摘要: 对顺磁性材料磁光特性和维尔德常数的研究通常采用量子理论, 但传统的量子理论仅考虑了电子跃迁偶极矩的影响, 难以对维尔德常数进行全面系统的描述. 本文在考虑跃迁偶极矩影响的基础上, 以受迫振动对电偶极矩修正的方式计入外磁场与光电场对电子运动的影响. 首先从微观层面分析了顺磁性材料磁光效应及维尔德常数的内在机理, 而后通过经典电子动力学理论和量子理论分别分析了电子的能级跃迁和外场作用下非跃迁位移对电偶极矩的贡献, 进而推导得到顺磁性材料的极化率, 构建了维尔德常数的解算模型. 以典型顺磁性磁光材料铽镓石榴石为例, 量子计算了Tb
3+ 离子在自旋-轨道耦合、晶场及有效场作用下的能级及波函数, 最终分别定量求解得到传统量子理论和本文方法下的维尔德常数. 对比分析发现: 相比传统量子理论, 利用本文方法计算得到的结果与实验数据更为吻合, 具有一定的优越性.
关键词: 顺磁性 /
维尔德常数 /
能级跃迁 /
电偶极矩 English Abstract Discussion on Verdet constant solution model of paramagnetic magneto-optical materials Cai Wei 1,2 ,Xu You-An 1 ,Yang Zhi-Yong 1 ,Miao Li-Yao 1 ,Zhao Zhong-Hao 1 1.Armament Launch Theory and Technology Key Discipline Laboratory of China, Rocket Force University of Engineering, Xi’an 710025, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 61505254)Received Date: 30 May 2019Accepted Date: 22 August 2019Available Online: 01 October 2019Published Online: 20 October 2019Abstract: The Verdet constant is one of the key parameters to characterize the material magneto-optical properties. The quantum theory is usually used to study magneto-optical properties and calculate the Verdet constant of paramagnetic material. However, the traditional quantum theory only takes into account the influence of the electron transition dipole moments caused by the particle property of light, which therefore cannot formulate the Verdet constant of magneto-optical material accurately. In view of the shortcomings of the existing theory, in this paper we propose is a wave-transition model of the Verdet constant. Due to the special wave-particle duality of light, the contribution of the non-transition dipole moment to the Verdet constant, caused by the electric field of light wave, should not be ignored. According to the basic theory of magneto-optical effect, in this paper we first explore the intrinsic mechanism of the paramagnetic material’s Verdet constant at a microscopic level and analyze the deficiency of traditional quantum theory. Furthermore, the classical electronic dynamic theory and quantum theory are used to reveal the contribution of volatility and transition of the light to the electric dipole moment. The density operator and statistical algorithm are introduced to derive the polarizability tensor of the paramagnetic magneto-optical material, thus obtaining the Verdet constant expression of the paramagnetic magneto-optical material, from which the Verdet constant is formulated. Taking the paramagnetic magneto-optical material TGG for example, the splitting energy levels and wave function of Tb3+ ions in the spin-orbit coupling, crystal field and effective field are calculated by the quantum method, and finally the Verdet constants under the traditional quantum theory and the volatility transition contribution model are obtained quantitatively. The comparative analysis shows that the results calculated by the wave-transition contribution model are more consistent with the experimental data and more accurate than the results calculated through the traditional quantum theory. The idea and method put forward in this paper will provide reference for further exploring the magneto-optical effect mechanism of paramagnetic magneto-optical materials. Keywords: paramagnetic /Verdet constant /energy level transition /electric dipole moment 全文HTML --> --> --> 1.引 言 1845年, 法拉第发现在外磁场作用下, 入射的线偏振光经过某些特定材料后偏振面会发生偏转, 具有这种磁致旋光效应的磁光材料被用于磁光调制器、光纤电流传感器及光信息处理等各项领域[1 —4 ] . 磁光材料主要分为顺磁性和抗磁性两类, 其中顺磁性磁光材料具有较高的维尔德常数, 应用更为广泛.[5 ] 提出了一种描述维尔德常数的经典表达式, 由经典电磁场理论, 文献[6 ]推导了磁性介质中磁光效应的基本关系式, 结合介电常量张量和麦克斯韦方程, 利用宏观理论解释了磁光效应的物理过程[7 ] . 这些经典理论对大多数抗磁性材料适用性较好, 但在计算顺磁性材料的维尔德常数时将出现较大偏差[8 ] .3+ , Pr3+ , Nd3+ 等稀土离子, 离子中不成对的电子极易发生4f → 5d的能级跃迁, 利用量子理论对维尔德常数进行求解具有更高的精确性. van Vleck-Hebb和Hebb[9 ] 提出了维尔德常数的量子表达式及与温度之间的依赖关系, 文献[10 ]从分子-轨道能级的角度出发, 在微观层面解释了磁光效应, 文献[11 ]分析了顺磁性材料中的多种相互作用对维尔德常数的影响. 但传统的量子理论只考虑电子能级跃迁的影响, 忽略了外磁场与光电场作用下电子非跃迁位移所产生的电偶极矩.8 ]采用主导波长跃迁模型思想, 通过实验数据拟合得到了顺磁性维尔德常数的量子理论表达式, 进而得到波动跃迁性贡献下的维尔德常数. 但该方法仅将维尔德常数视为波动性和跃迁性两部分的简单叠加, 未阐明维尔德常数的内在机理, 理论依据不足.2.理论及模型构建 22.1.传统量子理论 2.1.传统量子理论 量子理论认为, 顺磁性磁光材料中存在具有非零轨道角动量的简并基态M J z 轴正向的外磁场作用下, 分裂成M J E m 1 , E m 2 , 当温度T 远高于居里温度T c且外部磁场H e 不太强时, 两个子能级上均有一定概率的电子分布[12 ] . 线偏振光可分解为左旋(LCP)和右旋(RCP)两束圆偏振光, 其携带的左旋光子和右旋光子在z 分量的自旋角动量分别为$ \hbar $ 和$ - \hbar $ . 根据角动量守恒定理, 当线偏振光通过外磁场作用下的磁光材料时, LCP和RCP的光子及其所具有的自旋角动量可以分别被E m 1 能级上的轨道左旋电子和E m 2 能级上的轨道右旋电子吸收, 轨道左旋电子和右旋电子分别跃迁至激发态n , 如图1 所示.图 1 顺磁性磁光材料中的能级跃迁Figure1. Energy level transition in paramagnetic magneto-optical materials.图1 所示的顺磁性磁光材料, 电子左旋跃迁与右旋跃迁的振动强度大小不等, 这种跃迁的不均匀性正是磁光效应及维尔德常数产生的根源.[9 ] :g 为Lande因子, μ B = he /(4πmc )为玻尔磁子, c 为光速, h 为普朗克常量, e 和m 分别为电子电量的绝对值和电子质量, ω 为入射光的频率, χ 为磁化率, C mn ω mn 1 )式表明顺磁性材料的维尔德常数是一系列跃迁作用的总和, 式中C mn ω mn 13 ]引入主导波长跃迁模型思想, 即只考虑对维尔德常数起主导作用的跃迁, 同时考虑入射光波长λ 和温度T 的影响, 得到TGG维尔德常数的拟合模型为[13 ] λ 0 为TGG的主导跃迁波长; T w 为居里-外斯温度; B , C , D 为实验拟合得到的常数. 在文中所述的温度和波长范围内, 虽然各样本的维尔德常数测试曲线的相似性很高, 但拟合得到的各种待定常数却有显著的差别. 以第二项中的常数B 为例, 文中4个TGG陶瓷样本中B 的拟合结果分别为–252, –262, –175, –115, 最大差别超过127%, 显然这样的拟合模型对每个样本都不相同, 普适性较差.2.2.维尔德常数解算模型 -->2.2.维尔德常数解算模型 (1 )式只考虑了电子的能级跃迁, 亦即跃迁偶极矩的影响, 而忽略了外磁场和光电场对电子回旋运动的影响. 本文认为: 入射偏振光在磁光材料中传播时, 光电场对所有电子均产生影响, 引起非跃迁偶极矩; 与此同时, 电子可分别吸收左旋光子或右旋光子, 产生能级跃迁, 引起相应的跃迁偶极矩. 两者共同作用于顺磁性磁光材料的维尔德常数.2.2.1.电偶极矩 -->2.2.1.电偶极矩 1)外磁场和光电场引起的非跃迁偶极矩E 0 为振幅, 波矢${{k}} = \dfrac{{n\omega }}{c}{{s}}$ , 其大小$k = \dfrac{{n\omega }}{c}s$ 为波数, s n 为介质的折射率, c 为真空中的光速, $\omega $ 为入射光频率, z z 轴坐标乘以z 轴方向的单位矢量, ${R_{\rm{e}}}\left\{ \psi \right\}$ 为取$\psi $ 实部的算子.z 轴正向传播, 故${{s}} \cdot {{z}} = $ ${{z}} $ , 并设E 0 平行于x ${n_{\rm{L}}}$ 和${n_{\rm{R}}}$ , 左旋电场和右旋电场可分别表示为${n_{\rm{L}}}$ 和${n_{\rm{R}}}$ 相差很小, 在许多运算中可以忽略其差别.z 轴正向来看, RCP和LCP各自对应的电场矢量分别呈现为两个绕z 轴顺时针和逆时针旋转的空间曲面; 但如果固定于z 轴上一点来观察, 则RCP和LCP各自对应电场在该点处垂直于z 轴的XY 平面内的旋转方向恰好相反, 分别为逆时针和顺时针旋转. 这种现象可以解释为“空右时左”或“空左时右”.图2 所示.图 2 电子运动及受力分析Figure2. Electronic motion and force analysis.图2 可见, 电子受到正电中心吸引力F 0 、光电场作用力F E 及洛伦兹力F B 的共同作用. 忽略阻尼项的影响, 电子的受力与运动方程为r ω 0 为电子运动的固有频率, E B i 为介质中的有效磁场. 注意到LCP和RCP电场分别驱动左旋电子和右旋电子[14 ] , 通过方程(5 )可分别求得轨道左旋电子与右旋电子的位移为${\omega _{\rm{L}}} = \dfrac{e}{{2m}}{B_{\rm{i}}}$ 为电子进动的拉莫尔频率, 由于${\omega _{\rm{L}}} \ll \omega $ , 故(6 )式常简化为${10^{15}}\;{\rm{ rad}}/{\rm{s}}$ , 在LCP和RCP的电场作用下, 顺磁材料中的束缚电子将跟上光波频率, 在XY 平面内产生两种方向相反的圆周运动方式, 角频率由${\omega _0}$ 变为$\omega \mp {\omega _{\rm{L}}}$ . 因此由外磁场和光电场引起的非跃迁偶极矩为8 )式采用了文献中常用的表示方法, “+”,“–”分别表示右旋和左旋.${\psi _m}$ , ${\psi _n}$ 分别为基态与激发态的波函数.${{P}}_{{\rm{w {\text{-}} t}}}^ \pm = {{P}}_{\rm{w}}^ \pm + {{P}}_{\rm{t}}^ \pm $ , 如图3 所示.图 3 总电偶极矩Figure3. Total electric dipole moment.2.2.2.单粒子系统在光场作用下的极化率 -->2.2.2.单粒子系统在光场作用下的极化率 维尔德常数主要取决于离子最外层电子的运动, 而单粒子系统容易受环境的影响, 系统的哈密顿量$\hat H$ 难以精确获知, 且波函数$\left| \varPsi \right\rangle $ 的初值也难以给定. 因此引入密度算符$\hat \rho = \left| \varPsi \right\rangle \left\langle \varPsi \right|$ 及统计算法, 则可观测量$\hat F$ 的平均值可表示为$\left| \varPsi \right\rangle $ 通过能量表象$\left\{ {\left| {{\psi _n}} \right\rangle } \right\}$ 来表示; 而ρ nm F nm ${\hat H_0}$ 为无外场时的哈密顿量, ${\hat H_{{\rm{int}}}}$ 为系统与光场的相互作用, ${\hat H_{{\rm{rad}}}}$ 为系统与环境的弱相互作用.$\dfrac{\partial }{{\partial t}}\hat \rho = \dfrac{1}{{{\rm{i}}\hbar }}\left[ {\hat H,\hat \rho } \right]$ , 因此(11 )式可表示为$\left| {{u_k}} \right\rangle $ 满足${H_0}\left| {{u_k}} \right\rangle = $ $ {E_k}\left| {{u_k}} \right\rangle $ , 以本征函数为基矢, 则${\hat H_0}$ 的矩阵元是对角的, 得${\gamma _{nm}}$ , (12 )式右边的第三项可表示为$\rho _{nm}^{\left({{\rm{eq}}} \right)}$ 为密度矩阵元在无外场条件下的初值, 注意到无外场时常处于热平衡态, 因此非对角元初值为0, 即$\rho _{nm}^{\left({{\rm{eq}}} \right)}= 0(n \ne m)$ , 而对角元表示各能级的填充几率, 服从玻尔兹曼分布.${H_{{\rm{int}}}} \ll {H_0}$ , 可以采用微扰理论对其进行处理. 引入表征光场微扰程度的微小项η , 系统与光场的相互作用可表示为$\eta {\hat H_{{\rm{int}}}}$ . 将密度矩阵元展开成η 的幂级数${{{P}}_{{\rm{w'}}}}=e{{r}}' = \dfrac{{{e^2}/m}}{{\omega _0^2 - {{(\omega \pm {\omega _{\rm{L}}})}^2}}}{{l}}$ , l ${\hat H_{{\rm{int}}}}$ 是光场的一阶函数, 对于密度矩阵元的求导只需考虑一阶效应, 由(12 )—(16 )式可得z = 0处的情况,17 ), 得${{\alpha }}$ 为${{\alpha}} $ 为二阶张量, 其分量形式为n , m 符号交换, 且因为${\omega _{mn}} = - {\omega _{nm}}$ , ${\gamma _{mn}} = {\gamma _{nm}}$ , 极化率可化简为${P^ \pm }$ 为复数, 根据厄米算符的复共轭特征, 可解得极化率的分量形式为${\beta _m} = \rho _{mm}^{\left(0 \right)}$ 表示电子处于基态能级${E_m}$ 的几率, 服从Zeeman分布, $\rho _{mm}^{\left(0 \right)} = \dfrac{{{g_m}}}{Z}{{\rm{e}}^{ - {E_m}/({k_{\rm{B}}}T)}}$ , 其中g m E m $Z = \displaystyle \sum \limits_m {g_m}{{\rm{e}}^{ - {E_m}/({k_{\rm{B}}}T)}}$ .2.2.3.法拉第旋转角及维尔德常数 -->2.2.3.法拉第旋转角及维尔德常数 法拉第旋转角及维尔德常数的求解通常从磁光材料的介电常数张量入手, 本文重点讨论立方晶系以上的磁光材料, 此时z 轴方向与x /y 轴方向的介电特性互不影响, 而x 轴与y 轴方向存在对称性. 根据厄米特性, 介电张量可写成如下形式[15 ] :${\varepsilon _{xx}}$ 与介质的折射率n 相关, 假定介质无吸收, ${\varepsilon _{xx}} = {n^2}$ ; 矩阵非对角元${\varepsilon _{xy}} = 4{\text{π}}N{a_{ij}}$ 则引起了磁光材料的法拉第旋转.[10 ] ${\gamma _{nm}} \ll \omega $ 可忽略不计, 则考虑磁场和光电场作用下的电子受迫运动后, 可得到顺磁性材料的维尔德常数为${L_n} = {\left[\dfrac{{{n^2} + 2}}{3}\right]^2}$ 为Lorentz-Lorenz局域场修正项.3.数据验证 选取典型顺磁性磁光材料TGG晶体为研究对象, 其维尔德常数主要取决于晶体中Tb3+ 离子由4f→5d的能级跃迁. 下文通过计算Tb3+ 离子的能级及波函数, 分别得到传统量子理论及本文方法下的维尔德常数并进行对比分析, 进而验证本文方法的可行性.3.1.Tb3+ 离子能级及波函数 3.1.Tb3+ 离子能级及波函数 Tb3+ 离子在晶体中受诸多作用的影响, 总哈密顿量为${\hat H_0}$ 为库仑相互作用, ${\hat H_{{\rm{LS}}}}$ 为自旋-轨道耦合, ${\hat H_{\rm{C}}}$ 为晶体场作用, ${\hat H_{\rm{i}}}$ 为有效场对离子的作用, ${\hat H_{\rm{S}}}$ 为磁相互作用(可忽略不计).$\dfrac{{{z^*}{e^2}}}{{4{\text{π}}{\varepsilon _0}r}}$ 为电子所处的周期性势场, $\xi $ 为自旋-轨道耦合系数, L S ${B_{k,q}}$ 为晶场参数, ${{\rm{Y}}_{k,q}}({\theta _j},{\varphi _j})$ 为球谐函数.${\hat H_{\rm{C}}}+{\hat H_{{\rm{LS}}}}$ 作为微扰量, 通过下列久期方程得到Tb3+ 离子在晶场及自旋-轨道耦合作用下的能级位移及波函数${\psi _{i1}}$ , ${\psi _{j1}}$ 为未微扰的本征波函数;${E_{m1}}$ 为自旋-轨道耦合和晶场引起的基态能级位移, ${E_{n1}}$ 为激发态能级位移. 考虑4f及5d多重态的耦合, 以4f基准态7 F6 为能级零点, 计算得到的部分能级位移如表1 所列.1 2 3 4 5 6 7 8 Tb3+ E m 1 41.6 49.7 84.9 89.2 267.5 272 303.2 310.5 E n 1 –863.2 –336.4 –56.3 784.6 1446.7 1996.2
表1 晶场及自旋轨道作用下的能级位移(单位为cm–1 )Table1. Energy level shift under the action of crystal field and spin orbit (in cm–1 ).z 轴平行的外部磁场时, 原子磁矩与有效场相互作用引起的能量将导致能级的进一步分裂. 将${\hat H_{\rm{i}}}$ 代入下列久期方程, 得到有效场作用下的能级位移及波函数,${H_{\rm{\nu }}} = \nu M$ 只作用于自旋, 且有效场对激发态能级的影响可忽略不计, 在一级近似下, 基态能级位移为${\psi _{i2}}$ , ${\psi _{j2}}$ 为晶场及自旋-耦合作用后的基态波函数. 玻尔兹曼常数${k_{\rm{B}}} = 1.3807 \times {10^{ - 23}}$ , 室温下${k_{\rm{B}}}T \approx 200\;{\rm{c}}{{\rm{m}}^{ - 1}}$ , 因此表2 中Tb3+ 离子的第1—4个基态能级上都有一定概率的电子分布, 由(33 )式计算得到的基态能级分裂列于表2 .1 2 3 4 Tb3+ ($ \pm 2.342 \mp 0.9516\nu \chi $) ($ \pm 0.46 \mp 0.1422\nu \chi $) ($ \pm 0.897 \mp 0.3641\nu \chi $) ($ \pm 1.49 \mp 0.6561\nu \chi $)
表2 有效场作用下的能级分裂(单位为cm–1 )Table2. Energy level splitting under the action of effective field (in cm–1 ).${E_m}={E_{m1}}+{E_{m2}}$ , Tb3+ 离子5d激发态与4f基态之间的能级间距为 38462 cm–1 [16 ] , 因此激发态的最终能级为${E_n}={E_{n1}} + $ $38462\;{\rm{ c}}{{\rm{m}}^{ - 1}} $ . Tb3+ 离子能级的分裂过程如图4 所示.图 4 Tb3+ 离子的能级分裂过程Figure4. Energy level splitting process of Tb3+ ions.3.2.维尔德常数计算 -->3.2.维尔德常数计算 根据表1 和表2 中的能级位移及由(31 ), (32 )式求得的波函数, 可解算得到左右圆偏振光激发下Tb3+ 离子全部的48个跃迁矩阵元$P_{\rm{t}}^ \pm $ ; TGG晶体的中心波长${\lambda _0} = 258 \;{\rm{nm}}$ [17 ] , 共振频率${\omega _0} = 2{\text{π}}c/{\lambda _0} = 7.{\rm{307}} \times {10^{15}} \;{\rm{ rad}}/{\rm{s}}$ , 拉莫尔进动频率${\omega _{\rm{L}}} = \dfrac{{e{\mu _0}}}{{2m}}{H_{\rm{i}}}$ , 其中e ≈ 1.60217662 × 10–19 C, m ≈ 9.109383 × 10–31 kg, ${\mu _0}$ ≈ 1.2566370614 × 10–6 H/m, 由此可计算得出非跃迁矩阵元${P_{{\rm{w'}}}}^ \pm $ .34 )式及(27 )式可知, 维尔德常数表达式的各项参数中, 只有拉莫尔进动频率${\omega _{\rm{L}}}$ 与外磁场相关, 由于${\omega _{\rm{L}}} \ll \omega $ , 因此弱磁场条件下的维尔德常数与外磁场大小无关.N = 1.274 × 1022 cm–3 , 磁化率$\chi = N{g^2}J(J + 1)\mu _0^2/\left[ {3{k_{\rm{B}}}(T - {T_{\rm{c}}})} \right]$ , 式中有效玻尔磁子数$p = g{[J(J + 1)]^{1/2}} = 9.72$ [17 ] , J 为内量子数, T c = 0.227 K为居里常数[18 ] . 取温度T = 298 K, 分别得到不同波长下利用van Vleck-Hebb传统量子理论及本文方法进行解算时的维尔德常数, 如表3 .λ/nm 457.9 532 632.8 830 1064 1300 V e –305.7 –190 –134.4 –61 –40.2 –20 V t –351.9 –236.2 –157.8 –83.2 –50.3 –32.9 V w-t –314.6 –198.7 –144.3 –68.9 –43.7 –23.1 注: V t 为Van Vleck-Hebb传统量子理论的计算值, V w-t 为本文方法的计算值, V e 为实验数据[19 —22 ] .
表3 不同理论下的维尔德常数(单位为${\rm{rad/(m}} \cdot {\rm{T)}}$ )Table3. Verdet constant under different theories (in ${\rm{rad/(m}} \cdot {\rm{T)}}$ ).图5 所示. 图5 中, V e 表示实验数据, V t 表示利用van Vleck-Hebb传统量子理论进行计算得到的值, V w-t 表示本文方法的计算值. 由图5 可见, 由于跃迁偶极矩对维尔德常数的贡献为负, 而非跃迁偶极矩的贡献为正, 两者效果相反. 因此计入电子回旋运动引起的非跃迁偶极矩后, 本文方法计算得到的维尔德常数V w-t 均低于传统跃迁模型的维尔德常数V t , 与实验数据更为相符. 同时随着波长的增大, 传统量子理论的计算值逐渐接近实验值, 这是由于随着波长的增大, 非跃迁偶极矩变小, 而跃迁偶极矩的值基本不变, 对维尔德常数贡献的比重进一步加大, 起决定性作用.图 5 维尔德常数随波长变化情况Figure5. Verdet constant varies with wavelength.V w-t 与实验数据V e 更为吻合, 说明相比传统量子理论, 本文方法具有一定的优越性. 但V w-t 与V e 之间还存在误差, 这是由于在模型构建及计算过程中, 忽略了哈密顿微扰的高级修正项、磁偶极子之间的相互作用及电场引起的Stark位移等微观参数对维尔德常数的影响.4.结 论 本文从微观层面分析了顺磁性材料中磁光效应和维尔德常数的产生机理及现有理论的不足, 并由此引入外磁场与光电场对电子运动的影响, 认为维尔德常数是跃迁偶极矩及非跃迁偶极矩共同作用的结果. 通过量子计算, 分别得到传统量子理论及本文方法下TGG晶体的维尔德常数, 与实验数据对比分析发现: 在一定程度上, 利用本文方法能够更为精确地求解顺磁性磁光材料的维尔德常数. 这也为进一步探索顺磁性材料磁光效应的内在机理提供了参考借鉴. 

 图 1 顺磁性磁光材料中的能级跃迁
图 1 顺磁性磁光材料中的能级跃迁










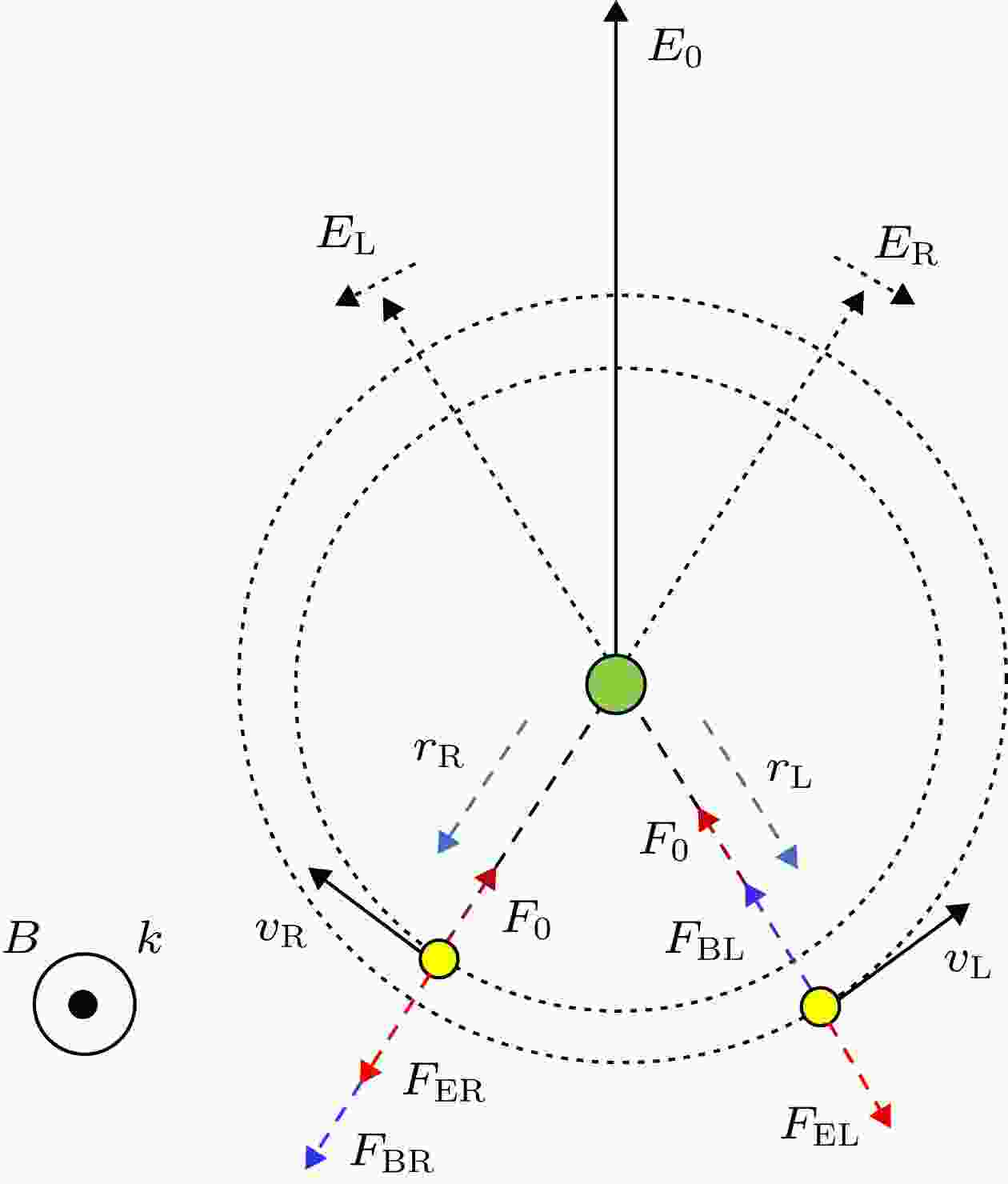 图 2 电子运动及受力分析
图 2 电子运动及受力分析







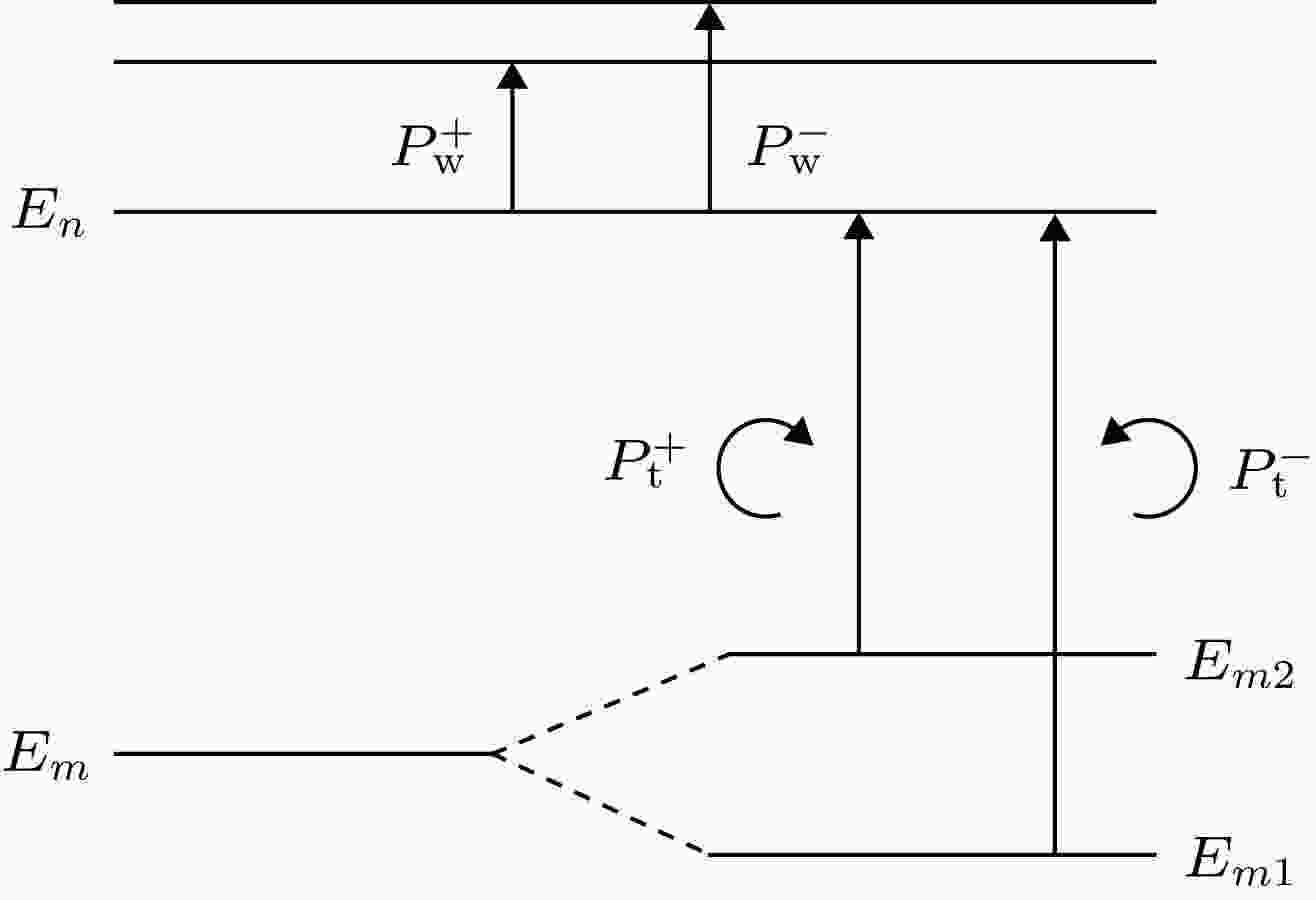 图 3 总电偶极矩
图 3 总电偶极矩

























































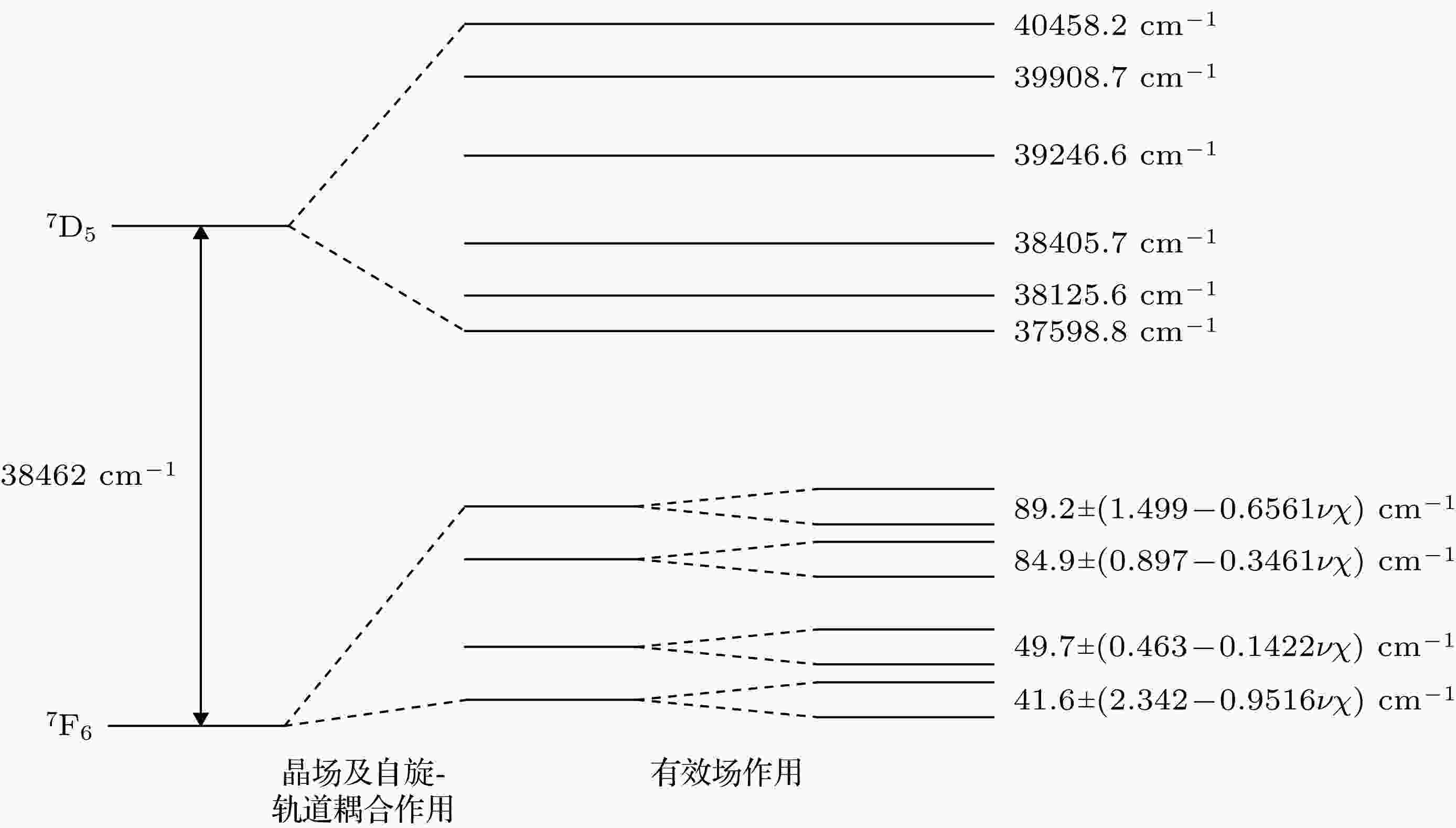 图 4 Tb3+离子的能级分裂过程
图 4 Tb3+离子的能级分裂过程











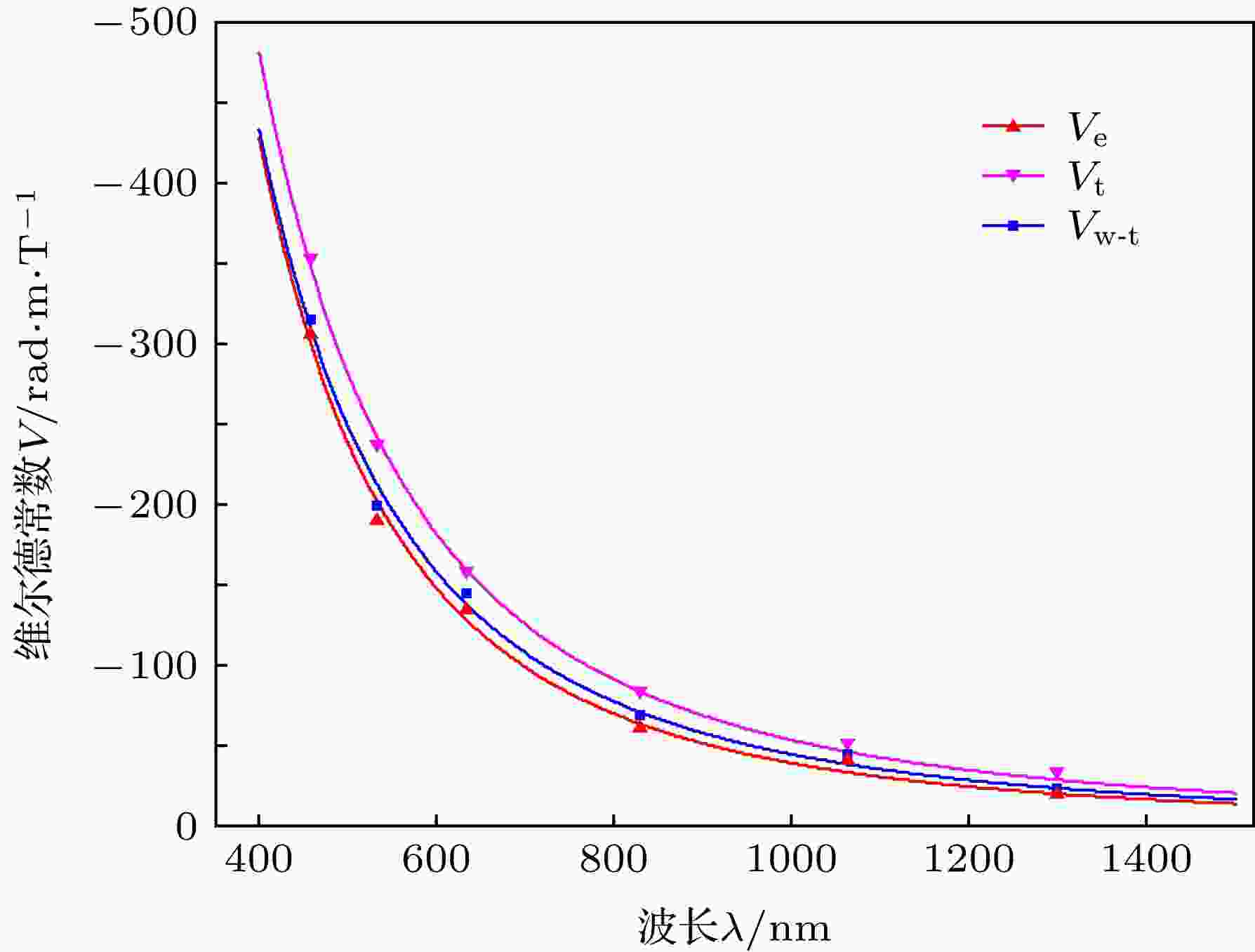 图 5 维尔德常数随波长变化情况
图 5 维尔德常数随波长变化情况