全文HTML
--> --> -->目前, 有关HiPIMS的研究主要是围绕上述问题进行的, 为了改善其放电稳定性, 包括直流、射频、中频在内的多种HiPIMS复合技术[8-11]被提出, 通过低功率的预离化基本消除了脉冲电流相对于脉冲电压的延迟现象, 同时减缓了“打火”频率, 提高了该技术的放电稳定性. 但是低功率的复合技术在等离子体束流中引入了太多未离化溅射原子, 使其离化率严重下降[12]. ?apek等[13]通过改变靶背面磁场强度来实现HiPIMS的稳定放电, 但是磁场强度大小和分布却十分依赖放电材料, 即不同的材料需要的磁场不同, 无法满足阴极的通用性. 多家电源公司或研究单位, 如Huettinger, Hauzer, Melec和哈工大等, 尝试通过改进电源技术, 减小“打火”反馈时间或通过电流归一化来实现放电稳定性和重复性, 事实上, 反馈再快, “打火”仍在发生, 电流的归一化也并不代表放电的完全一致[14,15]. 两年前我们提出了筒形阴极设计理念[16,17], 一方面利用类空心阴极效应[18]增强等离子体碰撞, 进而减缓离化对放电峰值功率的需求, 另一方面通过筒形结构缓解放电“打火”和材料差异对涂层产生的影响, 从而保证了不同材料的放电过程中等离子体束流离化率的一致性, 并实现了高质量薄膜的生长[19]. 然而, 在使用筒形阴极进行HiPIMS放电时, 其等离子体向基片上的输运只能依靠浓度差来驱动, 且溢出筒形阴极后呈发散状分布, 离子运动方向的不一致性导致损失较大, 薄膜沉积速率并没有得到明显的改善.
除了通过改变放电增强离子束流以外, 提高沉积速率的主要方法就是通过电场或磁场控制等离子体的输运过程, 减少离子损失, 使产生的离子尽可能多的沉积为薄膜. 其中电场方法主要是对基体施加偏压吸引离子向基体运动并沉积[20,21]和增加辅助阳极改变电子运动轨迹, 并由电子牵引离子向基体运动并沉积[17,22]. 但由于HiPIMS放电强度大, 等离子体密度高, 电场鞘层较薄, 对离子的作用有限, 且较高的偏压也会引起反向溅射, 因此对沉积速率的提高效果并不明显[23,24]. 磁场可以有效地约束电子运动路径, 进而牵引离子束流, 形成聚焦或扩散引出[25,26]. 比如扩散型的非平衡磁控溅射就是通过磁感线约束电子运动, 从而牵引离子增加薄膜沉积速率[27,28]; Anders和Brown [29]以及Li等[30]也曾通过添加直流电磁线圈在阴极前形成径向磁场, 显著增强了离子运动的方向性, 使得沉积速率提高.
鉴于此, 本文针对筒形阴极, 提出用电磁场约束离子束流的引出方案, 由于筒形阴极的放电平面与离子引出方向平行, 外加电磁场不仅可以约束输出离子的运动方向, 而且能够调控靶面的磁场, 对放电进行调节. 结果表明合适的线圈结构和磁场强度可以有效地增强HiPIMS放电, 且能明显提高薄膜沉积效率.
2.1.电磁场的实现
电磁线圈由直径为5 mm的铜导线缠绕而成, 通过控制线圈扎数分布实现对磁场强度分布的调节. 电磁线圈安装在筒形阴极两侧, 为了增加离子束流的沉积范围, 将电磁线圈设计成外扩型, 即不同位置的缠绕直径不同, 具体尺寸如图1所示. 在距离筒形阴极较近的位置用较厚的电磁线圈和较小的缠绕直径, 而在远端线圈的缠绕直径较大, 不同位置的磁场强度随到筒形阴极的距离增加而逐渐减弱, 其磁感线可与靶面背后永磁铁的磁感线相互作用, 形成对等离子体的连续作用. 电磁线圈形成的轴向(z方向)磁场, 一方面束缚进入线圈的电子, 使其沿磁感线方向做螺旋运动, 进而引导离子在等离子体自洽电势的作用下同时沿磁感线向基体运动; 另一方面作用于阴极靶面, 当电磁场与永磁体磁场方向一致时, 靶面横向磁场增强, 当电磁场与永磁体磁场方向相反时, 靶面横向磁场减弱, 且阴极与线圈之间的纵向磁场增强, 进而对等离子体放电产生不同影响.
图 1 筒形阴极及电磁线圈结构示意图Figure1. Schematic diagram of the cylindrical cathode and the electromagnetic coils.
2
2.2.模拟方法
针对外扩型的电磁线圈的仿真研究可分为两部分, 即电磁场仿真和等离子体输运过程仿真. 根据筒形阴极内外不同的物理过程, 对筒形阴极内的辉光和扩散区域和电磁线圈内的引出区域分别进行仿真. 由于筒形阴极具有旋转对称性, 可将其简化为一个旋转截面, 并设置柱坐标系进行计算. 图1中z轴(轴向)为中央旋转轴, r轴(径向)表示与z轴垂直的径向方向, 原点选取在筒形阴极的边缘.3
2.2.1.磁场模拟
在进行磁场仿真时, 所做简化如下: 选取尺寸为半径40 cm, 高80 cm的圆柱形空间作为电磁场的仿真区域, 固定其中心与筒形阴极的中心重合. 假设筒形阴极的永磁铁和电磁铁磁场只在仿真区域内起作用, 因此, 仿真区域的边界条件为磁绝缘边界条件. 仿真区域内的总磁场B相当于永磁铁的磁场Bmagnet和电磁铁磁场Bcoil的矢量和, 如(1)式所示, 其中永磁铁磁场Bmagnet和电磁线圈磁场Bcoil可分别通过方程组(2)和(3)进行求解.3
2.2.2.筒形阴极内等离子体运动仿真
利用粒子网格/蒙特卡罗法(particle in cell/ Monte Carlo collision, PIC/MCC)[31,32]对筒形阴极内部进行模拟, 分别计算不同电磁线圈电流(15, 10, 5, 0, –5, –10和–15 A)条件下的电磁场状态和等离子体在磁场作用下的运动和分布情况. 模型采用Matlab软件进行编辑, 为简化计算量, 模型只考虑简单的Ar气放电[33], 包括4种主要组分: 电子e, 氩原子Ar, 氩离子Ar+和激发态氩原子Arm, 各组分之间主要的反应如表1所列. 筒形阴极两侧的屏蔽罩为阳极并且接地, 靶面为阴极, 施加靶电压为–800 V, 放电气压为1 Pa, 初始等离子体密度设置为1×1013 m–3. 仿真开始时, 在模型中分别随机取3600个仿真离子和仿真电子, 每个粒子代表2×106个实际粒子. 由于仿真区域为规则的矩形, 初始时刻将仿真区域划分成多个尺寸为1 mm × 1 mm的正方形网格. 随着仿真的进行, 由于等离子体的德拜长度逐渐减小, 网格尺寸也随之减小并始终小于德拜长度. 为保证模型计算的准确性, 需要在仿真过程中考虑仿真粒子的三维速度. 模型的计算时间步长为1×1012 s, 每个步长后都利用泊松方程计算一次等离子体的自洽电势.| 序号 | 反应方程式 | 反应能量/eV | 反应类型 |
| 1 | $e + {\rm{Ar}} \to {\rm{A}}{{\rm{r}}^ + } + 2e$ | 15.76 | 电离 |
| 2 | $e + {\rm{Ar}} \to {\rm{A}}{{\rm{r}}^m} + e$ | 11.56 | 激发 |
| 3 | $e + {\rm{A}}{{\rm{r}}^m} \to {\rm{Ar}} + e$ | –11.56 | 退激发 |
| 4 | $e + {\rm{A}}{{\rm{r}}^m} \to {\rm{A}}{{\rm{r}}^ + } + 2e$ | 4.2 | 电离 |
| 5 | $e + {\rm{Ar}} \to {\rm{Ar}} + e$ | —— | 弹性 |
| 6 | ${\rm{Ar}} + {\rm{A}}{{\rm{r}}^ + } \to {\rm{Ar}} + {\rm{A}}{{\rm{r}}^ + }$ | —— | 弹性 |
| 7 | ${\rm{Ar}} + {\rm{A}}{{\rm{r}}^ + } \to {\rm{A}}{{\rm{r}}^+} + {\rm{Ar}}$ | —— | 电荷交换 |
表1Ar气放电的主要反应表
Table1.The main reactions of simple Ar gas discharge.
3
2.2.3.筒形阴极外等离子体输运仿真
本文以Cr+离子为例, 采用Comsol Multiphysics软件对等离子体中Cr+离子束流在磁场中的输运特性进行仿真, 计算在不同电磁线圈电流的条件下, 筒形阴极辉光区域外Cr+离子的密度分布, 并换算为沉积速率, 研究其随空间的变化. 由于离开离化区域后等离子体密度会显著下降, 因此可认为此时等离子体的德拜长度较大, 将仿真区域划分成尺寸为1 mm × 1 mm的正方形网格. 同时可认为仿真区域内等离子体整体呈电中性, 且Cr+离子只与背景气体Ar(1 Pa)发生弹性碰撞, 即忽略扩散过程中的电离和电荷交换. 因此Cr+离子密度n(m–3)可由连续性方程((6)式)描述.
2
2.3.放电测试
将配有电磁线圈的筒形阴极安装在自主设计的矩形真空腔(600 mm × 600 mm × 500 mm)内, 使用哈尔滨工业大学研制的HiPIMS电源进行放电[15], 其输出电压为0—1000 V, 脉宽为50—400 μs, 频率为50—300 Hz. 放电实验使用99.99%的高纯氩气作为工作气体, 溅射靶为高纯铬(99.9%). 放电时气压设置为1 Pa, 靶电压脉冲频率为100 Hz, 脉冲宽度为300 μs. 使用等离子体发射光谱仪(optical emission spectroscopy, OES) 测试筒形阴极中央的等离子体强度. 为了得到沉积速率随空间的变化, 将16 cm × 16 cm的基片放置在距离筒形阴极不同的位置进行Cr薄膜沉积, 并选取基片上不同的点进行厚度测量.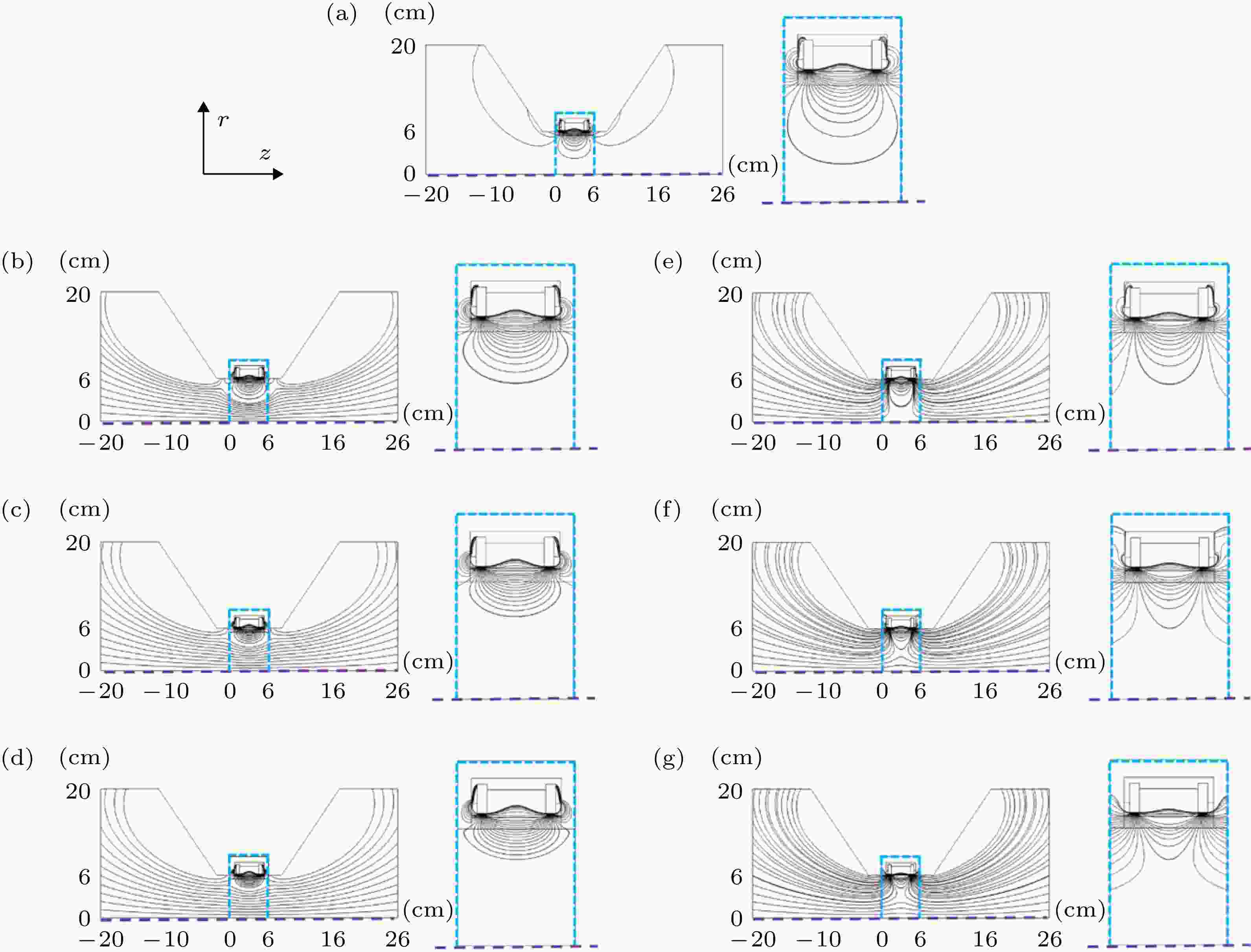
图 2 磁感线分布与电磁线圈电流的关系, 右侧为筒形阴极内的磁感线分布放大图 (a) 0 A; (b) 5 A; (c) 10 A; (d) 15 A; (e) –5 A; (f) –10 A; (g) –15 A. 图中紫色虚线为筒形阴极中央轴, 蓝色方框中的部分为筒形阴极的放大区域Figure2. The distribution of the magnetic induction line vs. the current in electromagnetic coils: (a) 0 A; (b) 5 A; (c) 10 A; (d) 15 A; (e) –5 A; (f) –10 A and (g) –15 A. The purple dotted line is the center axis of the cylindrical cathode and the magnified area of the cylindrical cathode is marked by the blue square.
筒形阴极靶面的轴向磁场Bz和径向磁场Br分别对靶面的放电刻蚀和电子溢出的速度有重要影响[36,37], 因此, 施加不同的电磁线圈电流, 其等离子体放电状态和演化趋势也将产生明显变化. 以图2中的磁场分布作为背景场, 用PIC/MCC模型对筒形阴极内Ar等离子体的演变趋势进行仿真(800 V, 1 Pa), 得到Ar+离子密度分布如图3所示, 为减少计算量, 数据取自等离子体演变基本稳定时, 即计算0.5 μs后. 仿真结果如图3所示, 仿真区域中的Ar+离子密度分布与对应的靶面附近磁感线的形状基本符合, 说明磁感线对等离子体分布产生了明显作用. 以等离子体密度高于1×1017 m–3的区域作为辉光区域, 其边界即离子密度等于1×1017 m–3的等值线, 如图3中蓝线所示. 当电磁线圈电流为正时, 如图3(b)—图3(d) 所示, 随电流的增加, 主要辉光区域的径向尺寸减小, 轴向尺寸增大, 说明靶面的放电宽度逐渐增大, 但电子从筒形阴极两侧边缘的逃逸更加容易. 随着等离子体放电的主要离化区域逐渐被磁感线压缩, 高密度等离子体远离中央轴, 导致电子在筒形阴极内部的径向震荡效果减弱, 即筒形阴极结构引入的空心阴极效应的作用效果随之减弱. 反之, 当电磁线圈电流为负时, 随线圈电流的增加, 如图3(e)—图3(g) 所示, 主要辉光区域的径向尺寸增大, 轴向尺寸减小, 说明靶面放电宽度减小, 但电子从筒形阴极边缘的逃逸减弱. 随着等离子体离化区域被径向拉伸, 并逐渐靠近中央轴, 电子在筒形阴极内部往复运动的效果增强, 离子在中央轴附近形成聚焦, 密度大幅上升, 表明空心阴极效应的作用随负向电流的增大而逐渐增强.
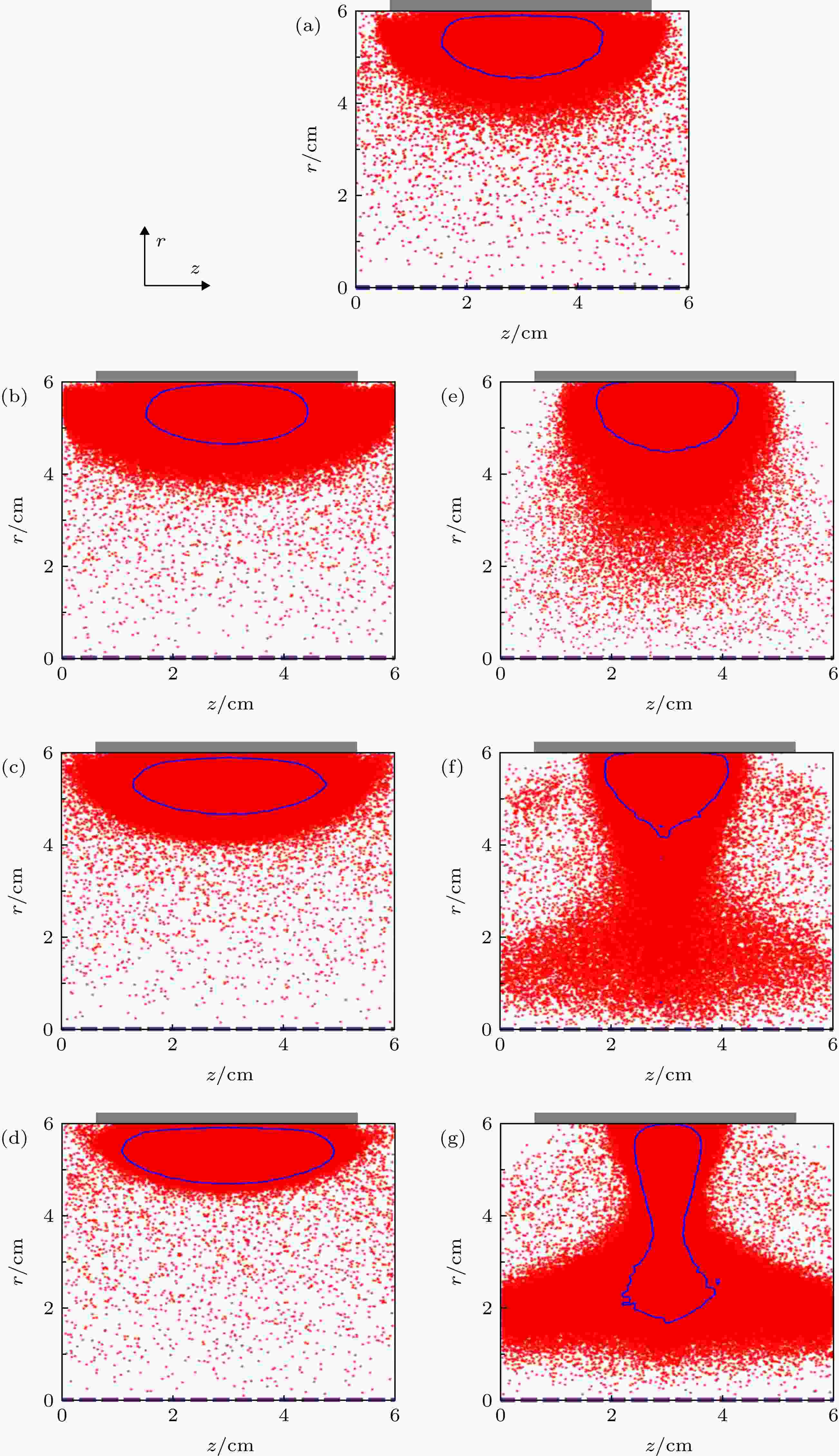图 3 不同电磁线圈电流条件下筒形阴极内Ar+离子分布 (a) 0 A; (b) 5 A; (c) 10 A; (d) 15 A; (e) –5 A; (f) –10 A; (g) –15 A. 图中紫色虚线为中央旋转轴, 灰色区域为靶材, 蓝线为1×1017 m–3的密度等值线Figure3. The Ar+ ion distribution in the cylindrical cathode vs. the current in electromagnetic coils: (a) 0 A; (b) 5 A; (c) 10 A; (d) 15 A; (e) –5 A; (f) –10 A and (g) –15 A. The purple dotted line is the center axis of the cylindrical cathode, the gray square is the target and the blue line is the contour line of 1×1017 m–3.
对图3中PIC/MCC模型的计算结果进行统计, 得到靶面放电宽度和离化区域内的最大等离子密度如表2所列. 当电磁线圈电流为正时, 随着电流的增大, 靶面的放电宽度逐渐增大, 靶面刻蚀更加均匀, 靶材利用率会增加. 在电磁线圈电流为15 A的条件下, 放电宽度最大达到4.2 cm, 靶面刻蚀区占整个靶面积的比例超过80%. 与靶面的放电宽度不同, 等离子体放电强度呈现出随线圈电流的增加而逐渐减弱的趋势, 这主要是因为电子在筒形阴极两侧边缘处的轴向逃逸严重, 等离子体得不到快速累积, 故离化区域内等离子体密度较低. 反之, 当电磁线圈电流为负时, 随着电流的增大, 靶面的放电宽度减小, 靶面刻蚀区面积减少, 在电磁线圈电流为–15 A的条件时, 放电宽度减小到只有2.3 cm, 靶面刻蚀区占整个靶面积的比例不足50%. 但电子逃逸被限制, 等离子体密度大大增加, 空心阴极效应的作用也增强, 在电磁线圈电流为–5 A时, 离化区域内的等离子体密度达到最高. 但随着电磁线圈电流继续增大, 靶面轴向磁场强度减小, 使电子的径向逃逸加快[37], 等离子体密度转而减小.
| 电磁线圈 电流/A | 靶面放电 宽度/cm | 最大等离子体 密度/m–3 |
| 15 | 4.2 | 4.63×1018 |
| 10 | 4.0 | 1.07×1019 |
| 5 | 3.6 | 2.93×1019 |
| 0 | 3.4 | 4.02×1019 |
| -5 | 2.9 | 6.80×1019 |
| -10 | 2.6 | 3.13×1019 |
| -15 | 2.3 | 7.41×1018 |
表2靶面放电宽度和最大的等离子密度
Table2.Target discharge width and maximum plasma density.
为验证磁场对筒形阴极放电阈值的影响, 测量了1.5 Pa条件下筒形阴极的HiPIMS起辉电压, 其随电磁线圈电流的变化如图4所示. 在电磁线圈电流由–15 A逐渐减小到0 A, 再增加到15 A的过程中, 起辉电压先减小后上升, 说明放电难度先下降后上升, 与表2中等离子体密度变化趋势相符合. 在电磁线圈电流为–5 A的条件下, 起辉电压最小, 为391 V, 此时, 径向磁场的增加减小了电子的轴向逃逸, 靶面轴向磁场均匀且足够大, 磁场强度保持在45 mT左右, 可有效阻止电子的径向逃逸, 使得尽可能多的电子在靶面积累[36], 等离子体密度迅速增加. 可见, 通过改变电磁线圈电流的大小和方向, 可对等离子体放电产生明显的增强或减弱作用, 改变等离子体放电区域的具体位置和几何形状, 调节空心阴极效应的作用效果, 实现对筒内等离子体放电状态的调控.
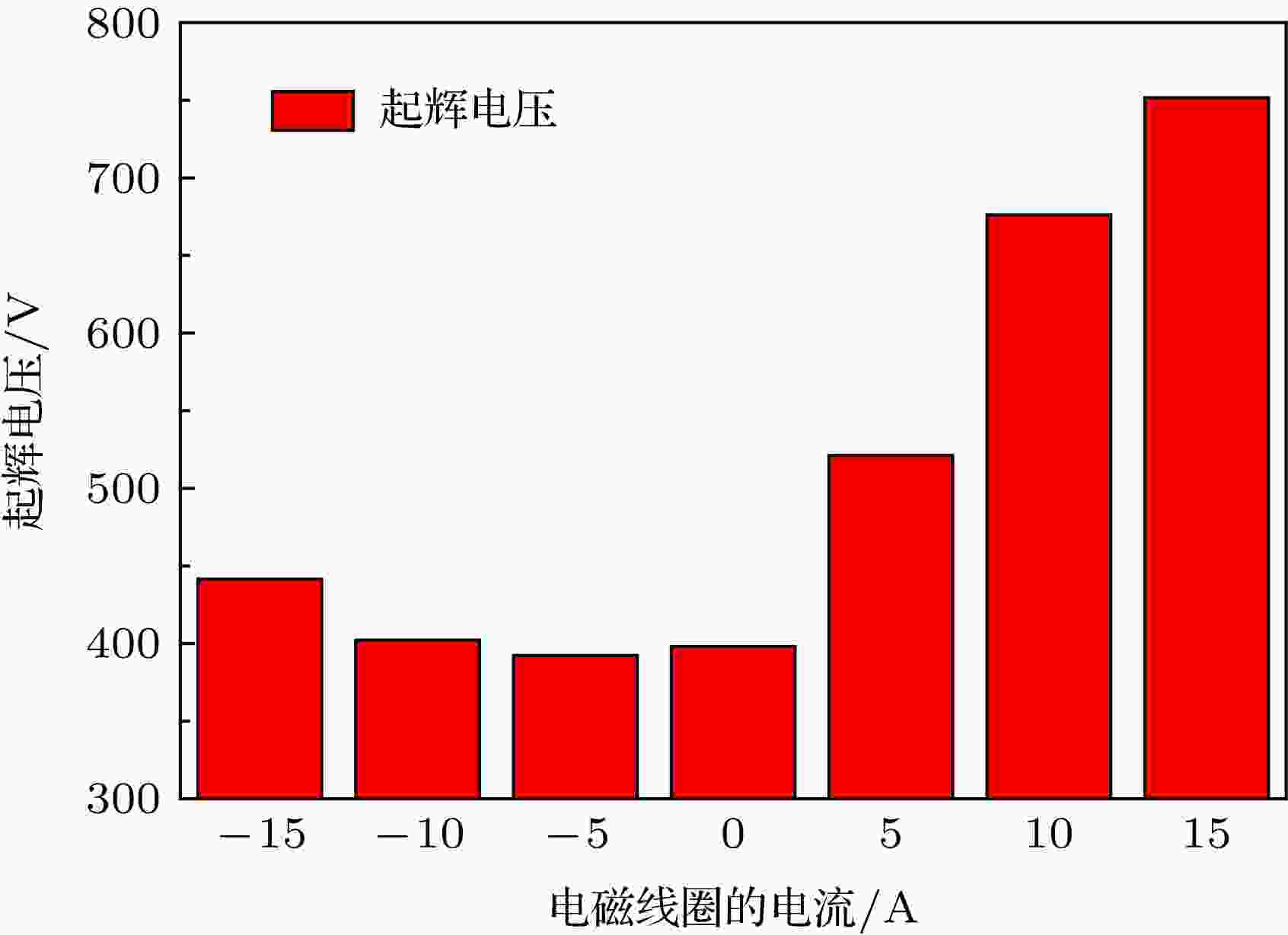图 4 HiPIMS放电的起辉电压随电磁线圈电流的变化Figure4. Threshold voltage of HiPIMS discharge vs. the current in the electromagnetic coil.
图5为不同电磁线圈电流条件下整个模拟空间的等离子体密度扩散分布图, 用来表征外加磁场对等离子体扩散路径的影响. 可以看出, 等离子体在模拟区域的运动仍然以扩散为主, 随着扩散距离的增加, 等离子体密度逐渐降低, 但是扩散过程中受到磁场作用, 其扩散路径和聚集位置发生了明显变化. 与电磁线圈电流为零时(即无外加磁场)相比(图5(a)), 电磁线圈提供的外加磁场减缓了等离子体的扩散损耗速度, 使得筒形阴极内的等离子体密度大大增加, 且效果随电磁线圈电流的增大而提高, 这是由于磁场使得电子在向外扩散过程中产生螺旋运动, 延长了运动路径, 从而产生累积, 使等离子体密度增加[26]. 在电磁线圈电流为正时, 由于筒形阴极两端的径向磁场被大大降低, 而靶面的轴向磁场却增加, 使得电子更容易从筒形阴极两端溢出, 而较难继续向筒形阴极中央轴运动. 在电子的带动下, 等离子体在放电区产生后即可一边向外输运, 一边向中央轴扩散, 在筒形阴极侧面形成相对均匀的等离子体密度分布, 如图5(b)—图5(d)所示. 随线圈电流的增加, 该趋势越来越明显, 在筒形阴极内径范围内均匀输出的距离也不断增加. 当电磁线圈电流为负时, 其等离子体密度分布结果与线圈电流为正时相反, 其靶面的轴向磁场减弱, 而阴极两端的径向磁场增加, 使得电子从筒形阴极边缘向外扩散的难度增大, 而向中央轴扩散更容易. 故在电子的带动下, 等离子体呈现出先向中央轴扩散, 然后再向外扩散的趋势, 在筒形阴极外形成一个高度聚焦的等离子体束流, 中心浓度高, 四周浓度低, 如图5(e)—图5(g)所示.
图 5 等离子体密度分布与电磁线圈电流的关系 (a) 0 A; (b) 5 A; (c) 10 A; (d) 15 A; (e) –5 A; (f) –10 A; (g) –15 A. 图中紫色虚线为中央旋转轴Figure5. The plasma density distribution vs. the current in electromagnetic coils: (a) 0 A; (b) 5 A; (c) 10 A; (d) 15 A; (e) –5 A; (f) –10 A and (g) –15 A. The purple dotted line is the center axis of the cylindrical cathode.
磁场能改变等离子体的沉积路径, 因此对等离子体沉积速率及其分布也会产生重要影响. 根据等离子密度数据计算特定位置的离子通量, 再除以计算出的离子通量最大值进行归一化处理, 即可获得相应位置上的归一化沉积速率, 如图6所示. 图6(a)为筒形阴极中央轴上距离阴极侧面出口不同处的沉积速率, 可见, 随扩散距离的增加, 其沉积速率逐渐减小, 两种线圈电流模式都增加了沉积速率, 并随电磁线圈电流的增大而增大, 说明电磁线圈的引入可以明显优化等离子体的沉积效率. 主要原因是磁感线的束缚作用限制了运动方向较偏而沉积到真空室壁上的等离子体损失, 使大部分离子束流沿磁感线运动并形成了有效沉积. 电磁线圈电流为正时, 等离子体向外运动的阻力较小, 而向中央轴运动的阻力较大, 故即使靠近阴极侧面出口位置处(0—3 cm时), 其沉积速率提升并不明显, 甚至在线圈电流较小时还出现少量的降低. 但随扩散距离的增加, 中央轴上的离子浓度得到不断补充, 使得中央轴上的沉积速率随扩散距离的增加衰减逐渐减弱, 因此其沉积速率相对不加线圈电流时有了明显提高, 尤其是距出口4 cm以上时沉积速率的改善效果更加明显. 但在电磁线圈电流为负时, 由于阴极两端的径向磁场大, 而靶面的轴向磁场小, 使得电子更倾向于向中央轴聚集, 然后向外扩散, 于是中央轴上的沉积速率远大于无线圈电流或线圈电流为正时, 尤其是距离阴极侧面出口越近, 其沉积速率越高.
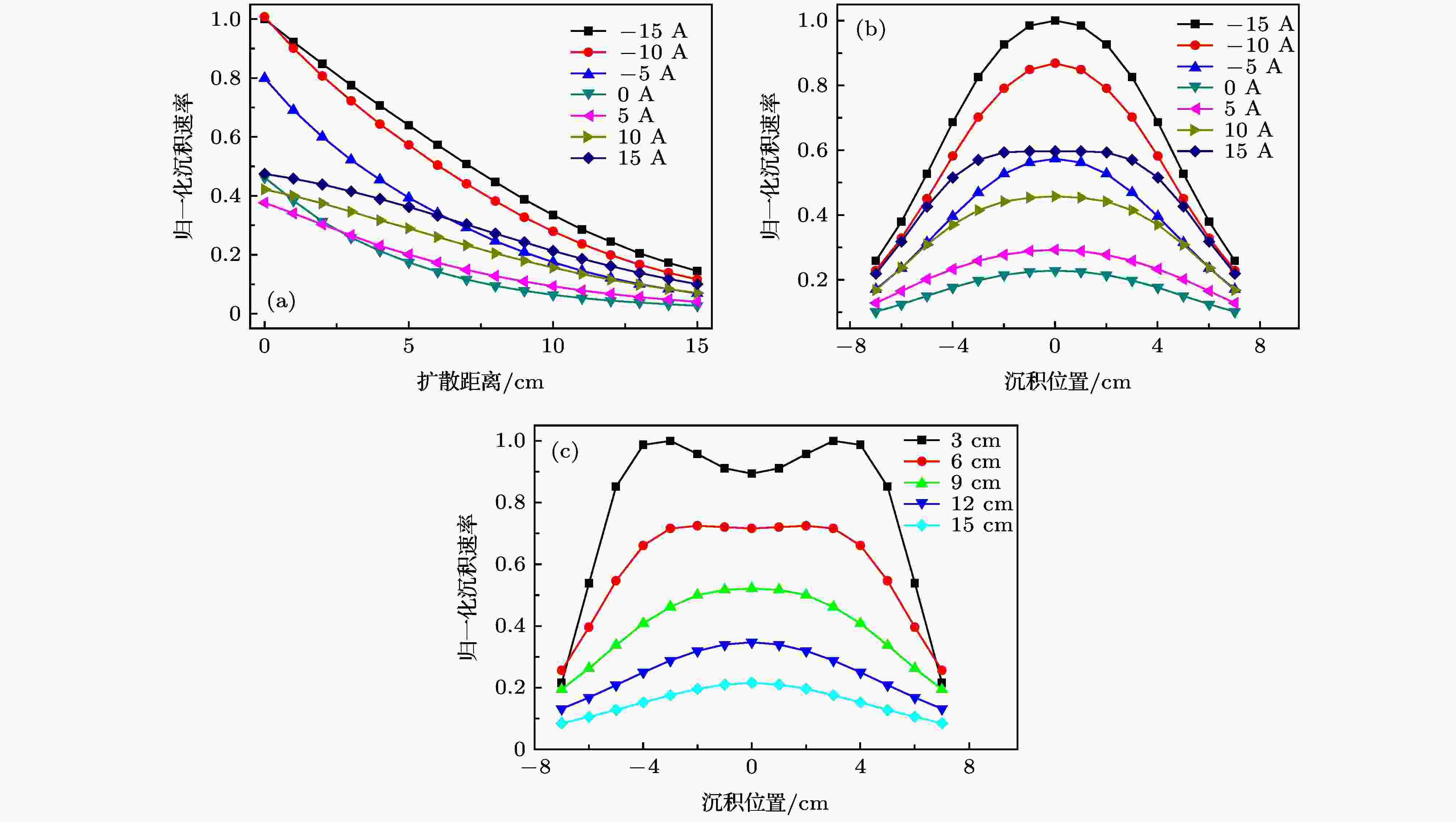图 6 沉积速率的空间分布 (a) 不同线圈电流下中央轴沉积速率随扩散距离的变化; (b) 不同线圈电流下距筒形阴极8 cm处截面上的沉积速率分布; (c) 线圈电流15 A时不同距离的截面上的沉积速率分布Figure6. Spatial distribution of the deposition rates: (a) Deposition rate on the central axis depends on the diffusion distance and the coil currents; (b) deposition rate at the distance of 8 cm from the cylindrical cathode at different coil currents; (c) deposition rate distribution at different distances from the cylindrical cathode when the coil current is 15 A.
图6(b)所示为在不同电磁线圈电流下, 距离筒形阴极侧面出口8 cm处沉积速率的径向分布, 相对无线圈电流的情况, 有线圈电流时的沉积速率均有增加. 当线圈电流为正时, 随线圈电流增加, 沉积速率增加, 其径向分布曲线逐渐出现一个平台, 宽度随电磁线圈电流的增大而增大, 说明此时在阴极侧面出口范围内离子沉积速率的均匀性较好, 尤其是线圈电流15 A时, 可在–4—4 cm的范围内保持较高速度的均匀沉积. 而当线圈电流为负时, 虽然沉积速率增加更明显, 可实现快速沉积, 但其沉积速率曲线在输出范围内成峰状, 中央轴上的沉积速率远大于两侧, 意味着输出范围内沉积均匀性较差. 但正是由于等离子体向中央轴的聚集, 使得其因漂移到真空室壁而损失的离子数量大大减少, 可实现更高的离子利用率.
为进一步研究距离阴极出口不同位置处的沉积速率的空间分布, 计算了线圈电流为15 A时不同位置的沉积速率径向分布, 如图6(c)所示. 在距离较小(3 cm)的截面上, 沉积速率分布不均匀, 曲线呈现两个峰, 对应于离子束流被引出的位置, 说明此时等离子体尚未在中央轴位置形成最大聚集. 随着扩散距离的增大, 中央轴处的等离子体得到补充, 曲线中央的凹陷逐渐消失形成平台, 在6 cm处形成最均匀的沉积. 随着截面距离的进一步增大, 两侧等离子体的消耗较快, 形成中心沉积速率大于两侧的现象.
为验证仿真结果, 在不同的线圈电流下进行HiPIMS放电测试, 放电总功率为3 kW, 其放电辉光照片如图7所示. 可见, 照片中的等离子体聚集情况基本与仿真结果(图5)一致, 即筒形阴极外等离子体辉光强度随线圈电流增加而增强. 当线圈电流为正时, 筒形阴极出口处的辉光在出口尺寸范围内分布均匀, 随着线圈电流的增加, 辉光范围变大, 辉光变亮, 说明等离子体束流密度增大, 且沿磁感线均匀输出, 如图7(a)所示. 当线圈电流为负时, 辉光区域呈现收缩状态, 集中从中央位置往外扩展. 随着线圈电流的增加, 辉光区域的长度增加, 辉光更亮, 意味着离子束流的聚焦程度增大, 引出效率大幅提高, 如图7(b)所示.
图 7 不同线圈电流时的等离子体束流辉光照片 (a) 线圈电流为正; (b) 线圈电流为负Figure7. The plasma flow pictures vs. the electromagnetic coil currents: (a) The coil current is positive; (b) the coil current is negative.
为了进一步验证线圈电流对空间的等离子体密度分布的作用, 采用等离子体发射光谱仪探测了筒形阴极中央轴上的发射光谱随线圈电流的变化规律, 如图8所示. 结果表明: 线圈电流为负时, 随线圈电流的增大, 光谱强度大幅增强, 说明筒形阴极中央的等离子体密度上升明显, 这主要来源于等离子体在中央轴位置的聚集以及空心阴极效应的增强. 在线圈电流为–15 A时, 光谱强度达到了无线圈电流时的4倍以上. 而线圈电流为正时, 随线圈电流的增加, 光谱强度逐渐减弱, 说明此时等离子体向中央轴的扩散受到抑制, 中央轴位置处的等离子体密度较低, 空心阴极效应因此减弱.
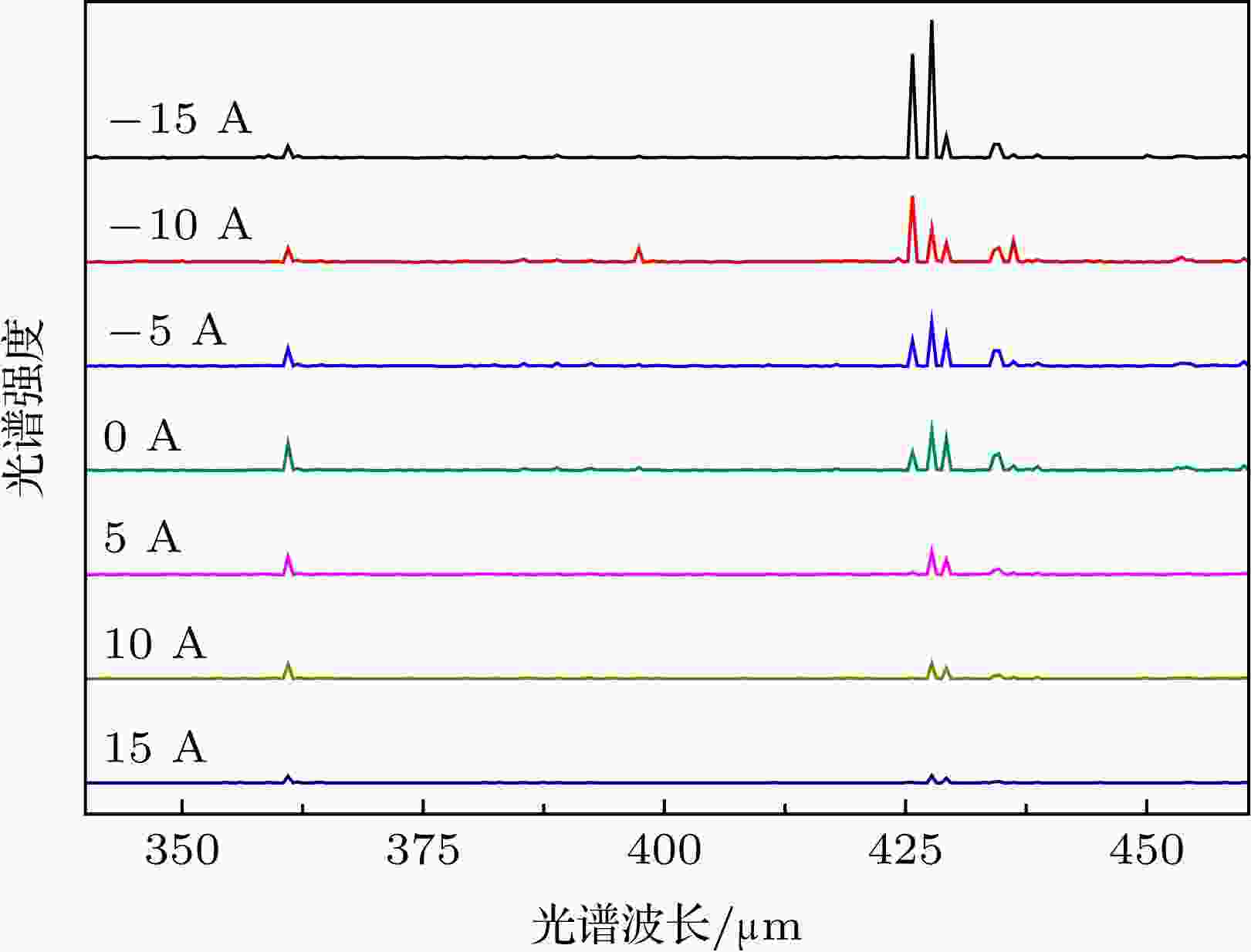图 8 不同的线圈电流时筒形阴极中央轴上的光谱强度Figure8. The OES intensity at the center axis of cylindrical cathode vs. the electromagnetic coil currents.
根据我们之前的工作[19], 无外加磁场情况下筒形阴极只能在直径为1.5 cm的范围内保持均匀沉积, 且在距离阴极出口15 cm处沉积速率不足40 nm/min. 配备电磁线圈后, 以纯金属Cr靶进行HiPIMS放电为例, 研究了线圈电流为15和–15 A时的Cr薄膜沉积速率, 结果分别如图9(a)和图9(b)所示. 可见, 在线圈电流为15 A时, 不同距离上的薄膜沉积速率较均匀, 且大体上随着与筒形阴极端口距离的增加呈现下降的趋势, 与仿真结果一致. 但当距离阴极出口较近(3 cm)时, 实验与仿真结果差异较大, 此时基片上的沉积速率相对仿真结果较低且均匀性较差. 这是由于实验中距离阴极较近的基片上会形成悬浮电位, 从而影响等离子体的扩散, 使离子向基片的运动受阻, 从而减少了沉积速率, 而仿真中忽略了基片悬浮电位对扩散的影响. 随着基片与阴极出口距离的增大, 整个基片上薄膜沉积均匀性得到明显改善, 其演化趋势与仿真结果(图5(c))相符合. 与无线圈电流相比, 线圈电流为15 A时薄膜的沉积速率略有提高, 但薄膜的均匀沉积范围显著增大. 图9(b)是线圈电流为–15 A时, 基片在距离筒形阴极出口15 cm处薄膜径向沉积结果, 可见, 基片中央部分的沉积速率远高于两侧, 与仿真结果相符合. 基片中央位置的沉积速率相对无线圈电流时提高4倍以上, 而两侧位置沉积速率与无线圈电流时类似, 只是略微提高.
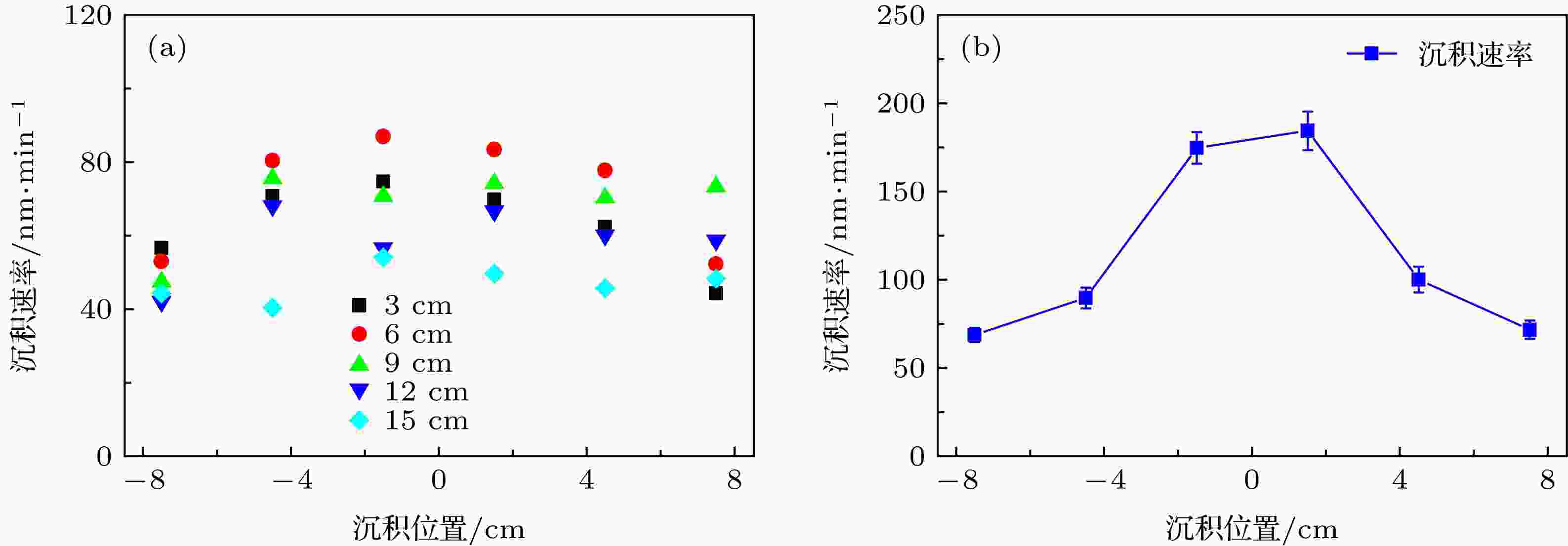图 9 (a)线圈电流为15 A时沉积速率的分布; (b)线圈电流为–15 A时沉积速率的分布Figure9. Distribution of the deposition rate when the electromagnetic coil current is (a) 15 A and (b) –15 A.
