全文HTML
--> --> -->过去人们在对于电磁波与等离子体相互作用的研究中, 在不同条件下发现了等离子体密度坑的产生. 如1982年, Cheung等人[3]在实验中发现了密度坑中的电磁孤子; 2002年, Borghesi等人[4]通过质子成像, 在实验中发现了由激光脉冲所产生的密度空泡. 密度坑和电磁孤子还可以在很多情况下产生, 如在临界密度附近由振荡双流不稳定性(oscillation two-stream instability, OTSI)所产生[5], 在1/4临界密度之上由受激布里渊散射(SBS)所产生[6], 在1/4临界密度处由受激拉曼散射(SRS)所产生[7,8], 以及在1/16临界密度处由二次SRS所产生[8,9]. 在空间等离子体中, 通过微波与电离层作用可以产生等离子体湍流和密度坑[10].
近年来, 随着人们对不同条件下激光与等离子体相互作用的深入研究, 关于电磁孤子以及密度坑的理论模拟工作已有了不少新的发现. 如2002年, Esirkepov等人[11]通过三维粒子模拟(particle-in-cell, PIC), 研究了在相对论情况下的电磁孤子的形成, 给出了孤子中电磁场的结构, 讨论了电磁孤子中库仑场对于离子的加速情况, 并发现了随着离子被加速而形成的准中性空腔(密度坑); 而盛政明等人[12]也研究了在不同条件下类似的过程; 2005年, Weber等人通过PIC数值模拟, 在密度为0.3nc的均匀等离子体(其中
综上所述, 等离子体密度坑在激光等离子体相互作用过程中是普遍存在的, 一旦这种密度坑形成, 将对激光在等离子体中的后续传输过程, 以及参量不稳定性的发展产生巨大影响. 然而针对激光惯性约束核聚变条件下的密度坑形成, 及其后续对参量不稳定性发展的影响, 目前尚未引起足够的关注.
本文通过PIC粒子模拟, 在激光直接驱动的参数条件下(激光强度为I ≈ 1015 W/cm2, 等离子体密度标长为L = 100 — 590 μm)[16], 研究了在不均匀等离子体中, 1/4临界密度附近受激散射的非线性演化过程, 主要内容为密度坑的产生过程及其产生机制, 以及密度坑产生前后SRS和SBS发展的变化情况, 并分析了等离子体温度对密度坑所产生的影响. 模拟结果发现, 等离子体在1/4临界面处, 由SRS所产生的密度坑, 对SBS也存在着抑制作用.
在本文的第2章节中, 我们采用一维粒子模拟的方法, 研究了在不同参数条件下, 在1/4临界密度附近密度坑产生的物理机制; 在第3章节中, 重点讨论了在1/4临界密度附近所产生的密度坑, 对于SRS和SBS不稳定性的后续发展的影响; 在第4章节中，对于研究内容作了总结.
描述非均匀等离子体参量不稳定性的线性模型采用了Wentzel-Kramers-Brillouin近似[21], 而这一近似在近nc/4处是不适用的. 在这一区域, SRS的前向散射与后向散射发生了强耦合, 散射光的波矢与群速度均为0, 因此需要用绝对不稳定性的模型来描述nc/4处SRS的行为. 以往的研究表明, 在非均匀等离子体中的绝对不稳定模式, 具有激发阈值低、时间增长率高、饱和幅度大等特性[9,22].
在与ICF相对应的参数条件下, 在均匀等离子体与非均匀等离子体中, 都有可能产生密度坑. 其中对于均匀等离子体中密度坑的产生机制, 已有了较为清楚的认识, 并可以用Zakharov方程[23,24]来描述. 而在非均匀等离子体中, 由于相位匹配都是局部的, 因此产生的散射光幅度都较低, 其有质动力很难驱动密度坑的产生. 而在nc/4处, 绝对SRS会产生很强的散射光, 因为在这一区域散射光的群速度为0, 所以光很难传播出去, 并在该密度处被等离子体捕获, 从而形成电磁孤子[15]. 随着越来越多的激光能量沉积在电磁孤子中, 当电磁孤子的光压大于等离子体的热压时, 密度坑就逐渐产生了.
我们采用了EPOCH中的一维粒子模拟程序[25], 研究了在大尺度密度范围下密度坑的产生过程. 由于密度坑的产生与SRS被等离子体捕获所产生的电磁孤子有着密切关系, 因此可以通过对与SRS相关的横场进行傅里叶分析, 找到电磁孤子的源项(波矢为0的频率成分), 从而分析电磁孤子以及密度坑的产生机制. 我们所采用的模拟参数如下: 入射激光为线偏振的半无限平面波, 强度为I0 = 2.4 × 1015 W/cm2, 与其相对应的归一化激光电场强度为
激光从x方向的左边界(x = 0)处入射, 并沿着x方向传播, 模拟总时长为4000个光周期(T0), 约13.2 ps. 图1(a)给出了在200—400 μm的模拟区域中, 离子密度的分布随时间的变化关系, 从中可以看到在300 μm, 也就是在1/4临界面处, 密度坑约在1500T0时刻开始产生, 约在2100T0时刻完全成型, 此时离子密度的空间分布如图1(b) 所示.
图 1 (a)随时间变化的离子密度分布; (b) 2100T0时刻的离子密度分布Figure1. (a) Temporal and spatial variation of ion density distribution; (b) the ion density distribution at 2100T0. The red dotted line marks the density cavity with the width of 2λ0.
由于非均匀等离子体中的nc/4密度处, 正是与绝对SRS散射光相对应的临界密度, 这使得大量的散射光被捕获, 从而形成电磁孤子. 被捕获的受激散射光的光压会推动周围的电子和离子, 从而损失能量并形成频率约为电子等离子体波频率一半的电磁孤子, 这种“半周期”电磁孤子的大小约为2πc/ωpe[26,27]. 在nc/4密度面附近, 由于电子等离子体波的频率为入射光频率的一半ωpe ≈ 0.5ω0, 所以电磁孤子的大小约为两倍的入射光波长2λ0. 因此, 当密度凹陷区域的空间尺度达到2λ0, 即该电磁孤子的大小时, 我们就认为密度坑完全成型了[15]. 因密度坑是由电磁孤子的有质动力所产生的, 所以首先需要估计电磁孤子的产生时间. 非均匀等离子体中绝对SRS的时间增长率为[28]
为了验证上述推论, 可以通过横向电场Ey来观察被捕获的光场. 横向电场Ey在空间中的分布随时间的变化如图2(a)所示. 随着入射光发生绝对SRS散射, 大量的散射光产生, 在t = 1300 T0左右, 可以在300 μm处(与其相对应的等离子体密度为nc/4)观察到电磁孤子. 在约t = 2000T0时刻, 在密度坑产生的空间位置处, 电磁孤子捕获了数倍于入射光强的光场. 通过对不同时间段, 200—400 μm空间范围内的等离子体中的横向电场Ey做傅里叶分析, 可以看到横向电场的波矢与频率分布的变化, 如图2(b)所示. 其中, ks = 0处的谱对应于被捕获的光场, 其频率约为0.5ω0, 即为nc/4处由绝对SRS所产生的散射光. 随着越来越多的散射光被捕获, 当散射光的光压大于电子的热压时, 有质动力将电子排开, 这一过程所形成的电荷分离场再将离子排开, 从而形成密度坑. 在形成密度坑的过程中, 被捕获的光场能量逐渐衰减, 用于对电子和离子做功, 与此同时, 被捕获的光场频率产生下移, 如图2(c)所示.
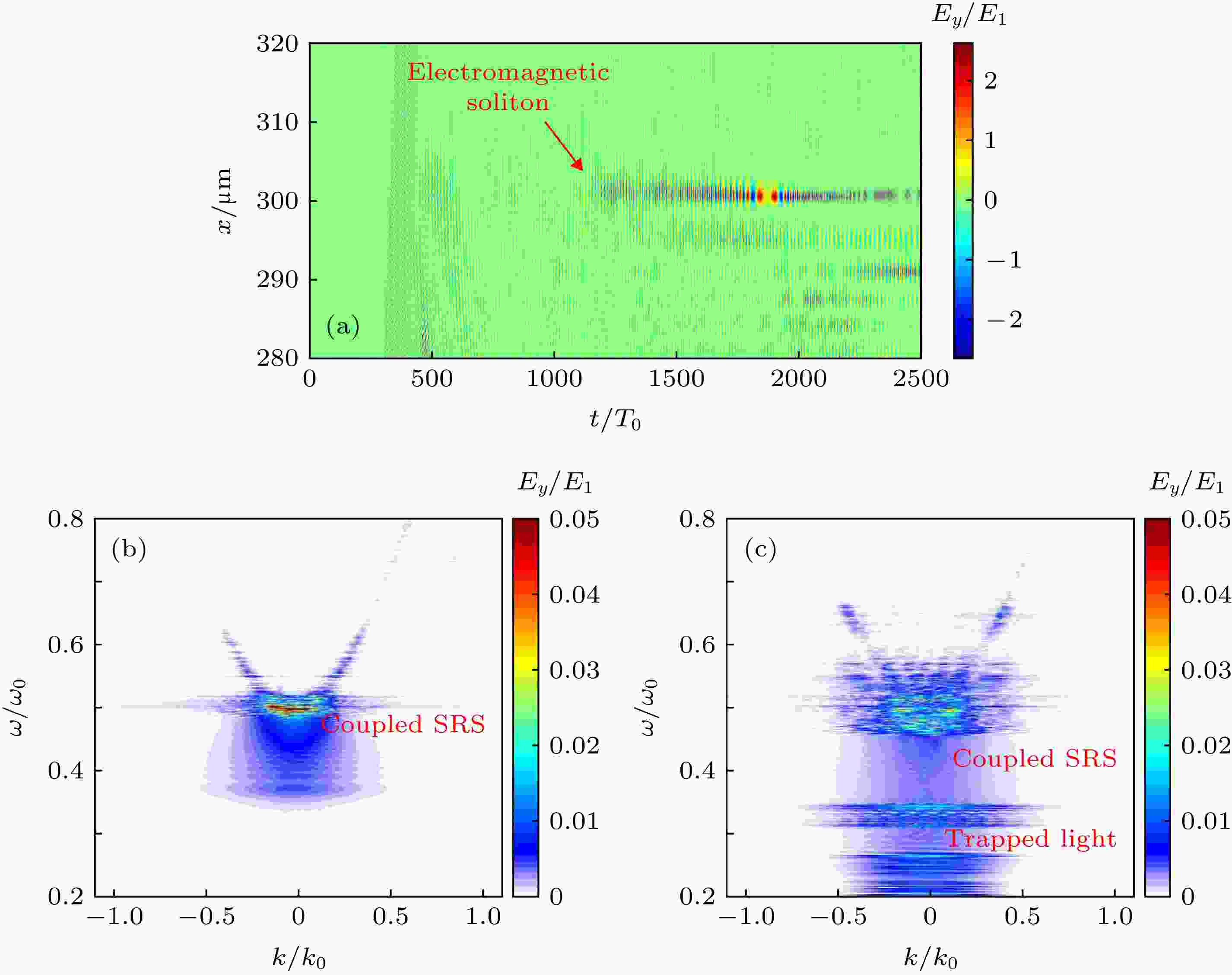图 2 (a)归一化电场Ey的时空演化图, 其中的归一化量纲El为入射激光的电场强度; (b) 0?2000T0, 200?400 μm等离子体中的电场Ey在k – ω空间中的分布; (c) 2000T0?4000T0, 200?400 μm等离子体中的电场Ey在k – ω空间中的分布Figure2. (a) Spatio-temporal evolution of the electric field Ey, Ey is normalized to El, which is the electric field intensity of incident laser; (b) distribution of electric field in (k, ω) space corresponding to the time window [0?2000]T0 and the space window [200?400] μm; (c) distribution of electric field in (k, ω) space corresponding to the time window [2000?4000]T0 and the space window [200?400] μm.
前面的计算结果表明, 在nc/4处密度坑的产生过程中, 离不开该密度处绝对SRS的产生和发展. 由于绝对SRS的散射光在nc/4处的群速度为0, 因此散射光不能在该密度处传播, 其作为电磁孤子产生的源项, 直接推动密度坑的发展, 因而该密度处的绝对SRS对密度坑的形成具有决定性的影响. 而在非均匀等离子体中, 绝对SRS的发展与很多因素有关, 如电子温度、离子声波以及等离子体密度标长等. 光强与等离子体标长对不稳定增长率的影响可以从(1)式推断出来, 当光强(a0)与等离子体密度标长(L)变大时, 随着绝对SRS增长率的增加, 电磁孤子的产生时间将变短. 而等离子体温度和离子声波的影响, 需要通过PIC模拟, 对比在不同的初始电子或离子温度下密度坑的发展情况, 来观察这些效应所带来的影响.
在下面的模拟中所选取的入射激光强度为I0 = 1015 W/cm2 (a0 = 0.027), 等离子体密度由0.05nc到0.3nc呈线性增长,
如将初始离子温度恒定为Ti = 100 eV, 在不同电子温度下的等离子体中, 密度坑的出现时间如图3(a)所示. 随着电子温度的上升, 绝对SRS不稳定性在等离子体中的增长率降低, 其产生的散射光幅度被衰减[29], 因此电磁孤子从SRS的背散光中获得足够能量的过程也变得更加缓慢, 从而使得散射光的有质动力产生密度坑的所需时间变得更长. 此外, 电子温度的上升还会导致热压力变强, 从而需要更强的有质动力来排开电子, 这也会导致密度坑的产生需要更长的时间.
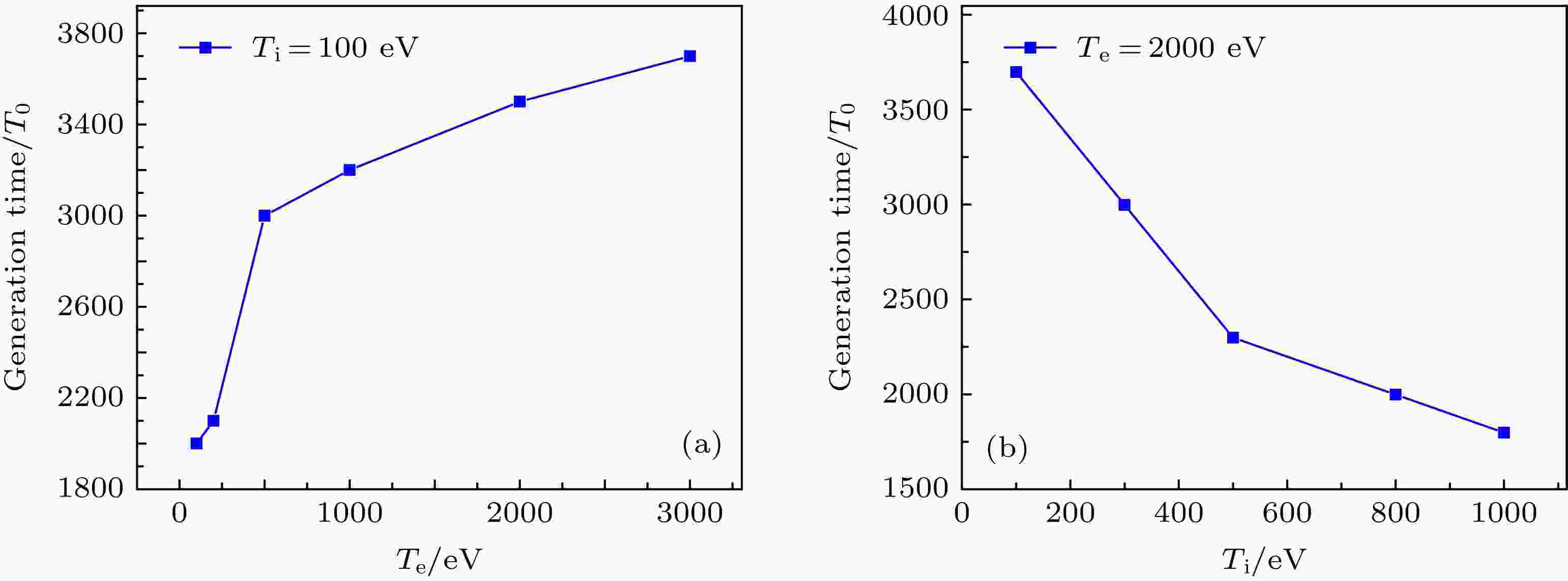图 3 (a)在不同的初始电子温度下, 1/4临界密度处等离子体密度坑的产生时间对比; (b)在不同的初始离子温度下, 1/4临界密度处等离子体密度坑的产生时间对比Figure3. (a) Comparison of the generation time of plasma density cavity with different initial electron temperatures at quarter critical density; (b) comparison of the generation time of plasma density cavity with different initial ion temperatures at quarter critical density.
如将初始电子温度恒定为Te = 2 keV, 通过改变初始离子温度, 来改变离子声波所受到的朗道阻尼, 在不同的初始离子温度下密度坑的产生时间如图3(b)所示. 当离子温度降低时, 随着离子声波所受到的朗道阻尼变小, SBS不稳定性在等离子体中发展起来. 根据SRS和SBS的非线性耦合理论, 当SBS所产生的离子密度扰动达到阈值时, SRS会随着SBS的发展而得到一定的抑制[24]. 当SBS的发展抑制了SRS的快速发展后, 电磁孤子从SRS的背散光中获得能量的时间变长, 从而使得有质动力推动密度坑发展的过程变得更长.
通过上述算例, 我们可以将非均匀等离子体中, 在nc/4附近密度坑产生时间的变化, 归结为如下几个因素的影响: 1)密度坑的参数取决于SRS的发展, 初始电子温度越低, 绝对SRS的增长率就越高, 且对应的电子等离子体波所受到的朗道阻尼越小, SRS就越容易发展起来, 密度坑也就越容易形成; 2) SBS的发展对nc/4面附近的绝对SRS产生明显的抑制作用, 初始离子温度越高, 离子声波被朗道阻尼抑制, SBS的份额越少, 其相应的SRS份额就越大, 密度坑也就越容易形成.
值得一提的是, 上述nc/4处密度坑的产生, 除了有被捕获的SRS散射光场的作用外, 还存在着局域的电子等离子体波的作用. 计算结果表明, 在该区域的SRS散射光场的振幅, 要比等离子体波电场的振幅高出一个数量级, 因此激光场对于有质动力对密度坑的产生, 起了主导作用.
在整个模拟过程中, 激光从x方向的左边界(x = 0)处入射, 模拟总时长为4000个光周期. 模拟给出的离子密度分布随时间的变化关系如图4(a)所示, 密度坑约在2000T0时刻, 最先在nc/4密度处产生. 随着模拟时间的增长, 在nc/4以下区域的对流SRS加热了电子温度, 使得朗缪尔波的频率上升, 从而导致了散射光频率的下降, 并使密度坑向低密度区域发展. 而密度坑扩散的另一原因, 是因为在第一个密度坑产生之后, 改变了该密度坑周围的密度分布, 从而在其周围形成了新的nc/4密度区域. 该区域会逐渐形成新的SRS绝对不稳定性, 并由此而产生新的电磁场捕获以及新的密度坑形成. 在这一新的密度坑形成后, 进一步改变了周围的密度分布, 并在更低的密度区域形成新的nc/4密度区域. 通过这样的过程, 从而形成了一系列的密度坑. 另外模拟结果还显示, 密度坑的产生会对于离子产生明显的加速效果, 而在密度坑产生之前, 由SBS所产生的离子声波, 只对离子产生轻微的加速效果. 随着密度坑的产生, 由电磁孤子的有质动力对周围电子的排空作用所形成的库仑场, 加速了密度坑中的离子, 如图4(b)所示. 离子的加速会提升离子声波的朗道阻尼, 从而抑制了SBS的增长.
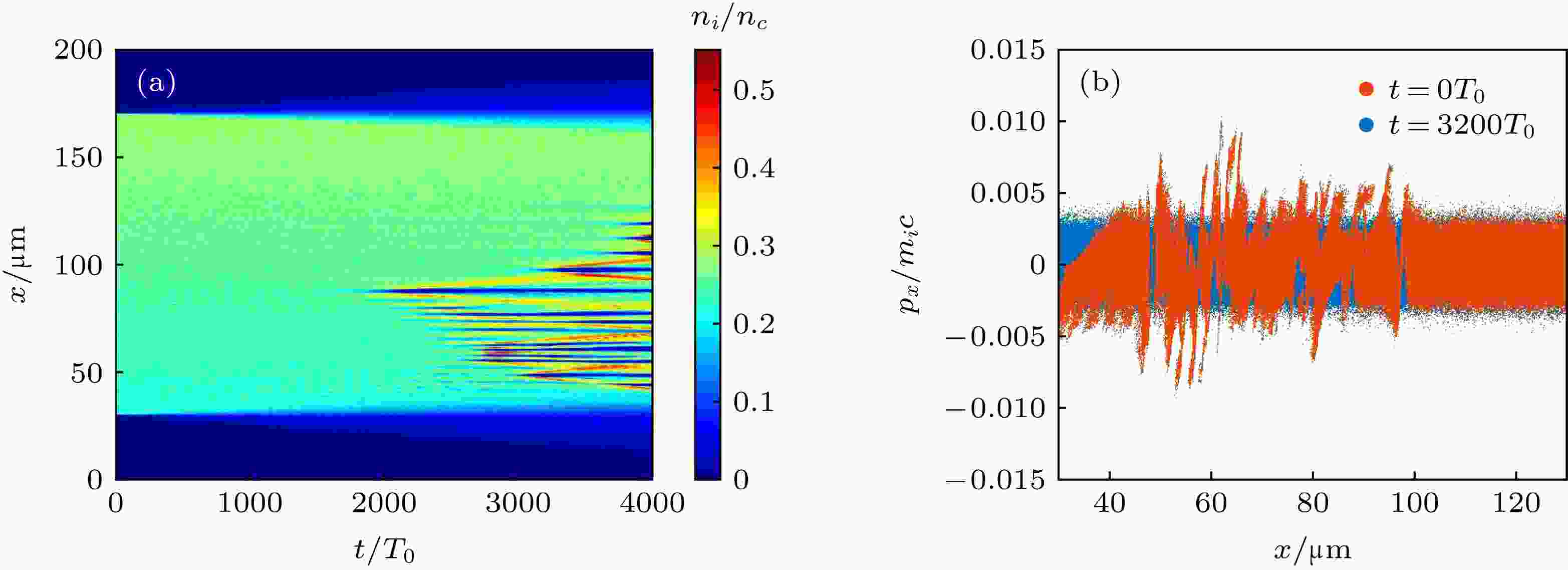图 4 (a)随时空变化的离子密度分布; (b)密度坑产生后, 在3200T0时刻, 密度坑附近的离子被加速到较高的能量Figure4. (a) Temporal and spatial variation of ion density distribution; (b) after the formation of density cavities, the ions near the density cavities have been accelerated to a higher energy at the moment of 3200T0.
除了密度坑形成过程中对离子的加速效果之外, 密度坑还将等离子体分割成多个不连续的部分, 从而形成了一连串具有很高密度梯度的等离子体段落. 大的密度梯度提高了在不均匀等离子体中, 参量不稳定性发展的光强阈值[30]. 另外, 这些不连续的等离子体密度坑, 破坏了参量不稳定性发展的相位匹配条件, 从而导致了不稳定性的抑制. 为了验证上述推测, 我们进一步分析了密度坑对于不稳定性的影响.
电荷分离场也就是纵向静电场, 在不稳定性中扮演着重要的角色. 通过观察纵向电场Ex的演化, 可以看到不稳定性发展的主要区域, 以及密度坑产生前后不稳定性强度的变化. 根据SRS所满足的三波匹配关系[1] ω0 = ωs + ωp和k0 = ks + kp可以得知, 与SRS和SBS两种不稳定性相对应的纵向场Ex的频率, 分别为ωpe ≈ 0.47ω0—0.51ω0和ωpi ≈ 0.005ω0, 与其相对应的波矢k分别为kpe ≈ k0, kpi ≈ 2k0, 其中ω0, ωs, ωpe则分别对应了入射光、散射光以及等离子体波的频率, 并与其相对应的波矢一一对应.
为了分析在不同空间位置处的不稳定性发展情况, 我们将纵向电场的时间分量进行一维傅里叶分析, 从而获得在不同的时间段中, 不稳定性的空间分布情况. 图5(b), 图5(d)和图5(f)给出了在不同的时间段中, 静电场在x-ω空间中的分布. 对比离子密度的时空分布, 由于密度坑将不稳定区域分隔为多个不连续的区域, 因而阻碍了等离子体波的产生与传输, 相应的不稳定性也就随之被抑制. 图5(d)和图5(f)表明了频率为ωpe ≈ 0.5ω0的电子等离子体波信号, 比早期密度坑在尚未形成时已大幅度减弱, 由此说明SRS的发展受到了极大的抑制.
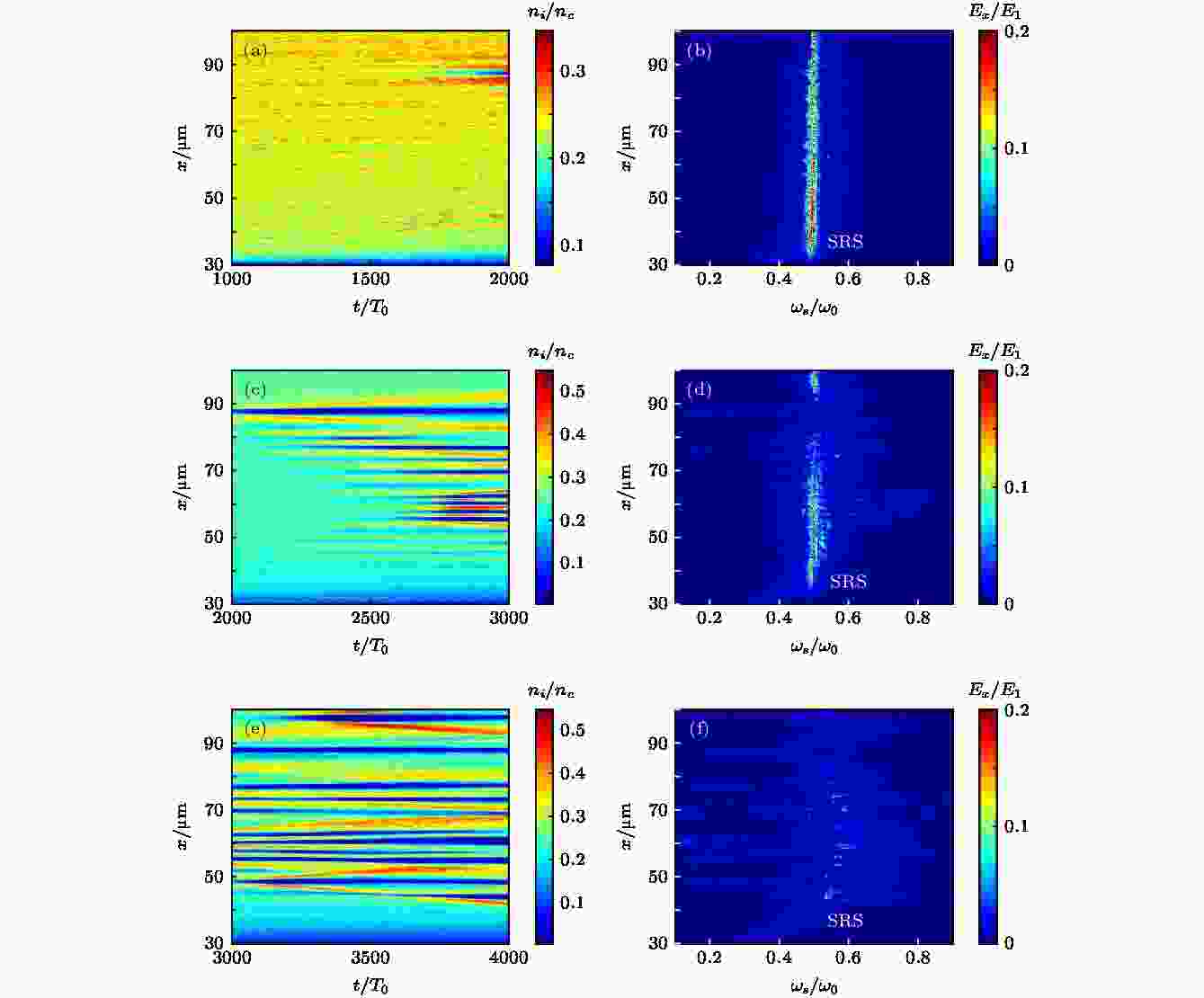图 5 (a), (c), (e)不同时间段中的离子密度在x – t空间中的分布; (b), (d), (f)不同时间段中的纵向电场Ex在x – ω空间中的分布; 这些离子密度以及纵向电场的分布, 分别反映了不稳定区域或激光等离子体不稳定性的发展情况Figure5. (a), (c), (e) Temporal and spatial variation of ion density distribution in different time windows; (b), (d), (f) the longitudinal field Ex in (x, ω) space. The ion and Ex distribution represent the development of instability regions and parametric instability, respectively.
在对于密度坑产生前后，不同时间段的纵场Ex进行二维傅里叶分析时, 可以获得Ex在k-ω空间的分布. 如图6所示, 图6(a)和图6(c), 图6(b)和图6(d)分别对应了在密度坑产生之前(0—2000T0), 与产生之后(2000T0—4000T0) SRS和SBS的静电模式分布. SRS所产生的朗缪尔波的波矢及其频率分别为kpe ≈ k0和ωpe ≈ 0.47ω0—0.51ω0, 比较图6(a)和图6(b)可以看出, 在密度坑产生后, 与SRS相对应的朗缪尔波强度已明显被抑制. SBS所产生的离子声波的波矢及其频率分别为kpi ≈ 2k0和ωpi ≈0.005ω0, 比较图6(c)和图6(d)还可以看出, 在密度坑产生后, 与SBS相对应的离子声波也被抑制了.
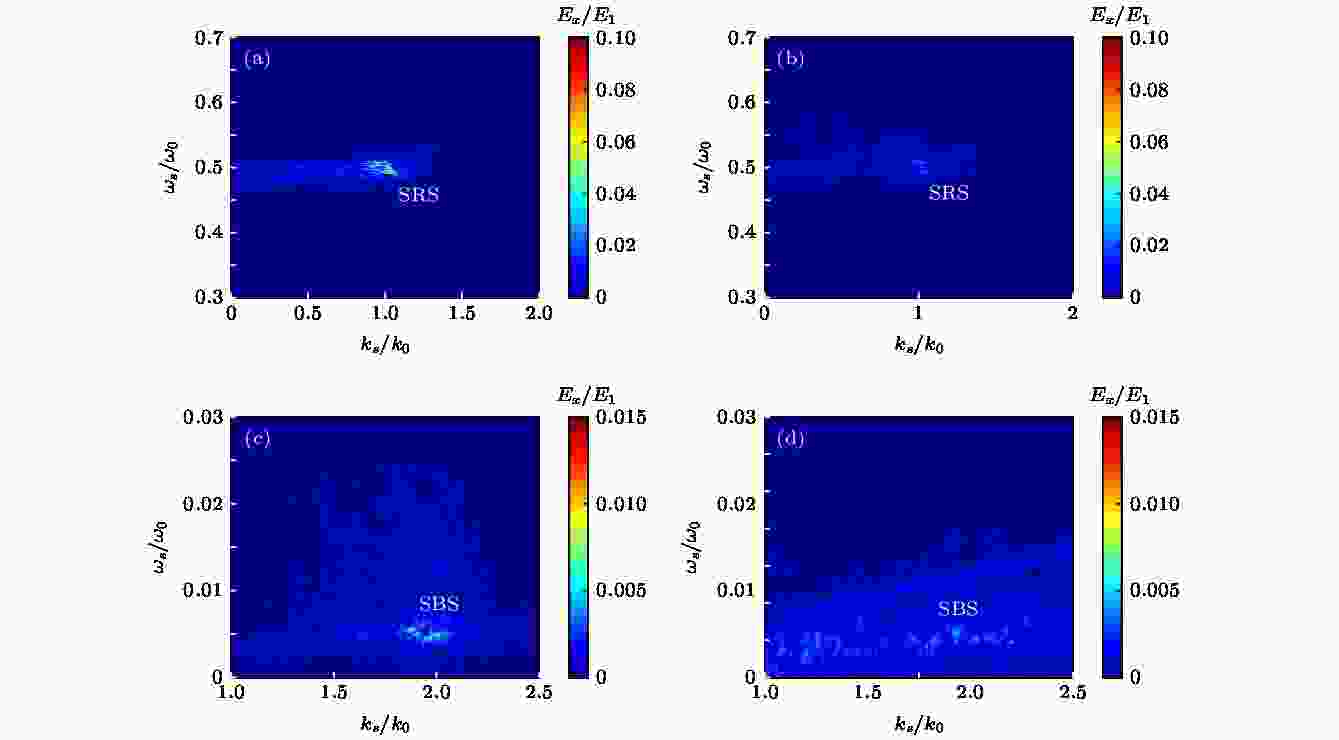图 6 (a), (c) 0?2000T0纵场Ex在k-ω空间的分布; (b), (d) 2000T0?4000T0纵场Ex在k – ω空间的分布, 相应频率与波矢的纵场Ex, 分别对应了SBS和SRS不稳定性的发展Figure6. (a), (c) The Ex distribution in (k, ω) space corresponding to the time window [0?2000]T0; (b), (d) the Ex distribution in (k, ω) space corresponding to the time window [2000T0?4000]T0. The longitudinal field Ex represents the development of SRS and SBS instabilities in the different time windows, respectively.
除了与不稳定性相对应的等离子体波的纵向静电场外, 还可以通过观察SRS和SBS所产生的背散光, 来分析不稳定性的发展情况. 同样根据三波匹配关系, 与SRS和SBS两种不稳定性相对应的背散光的频率约为
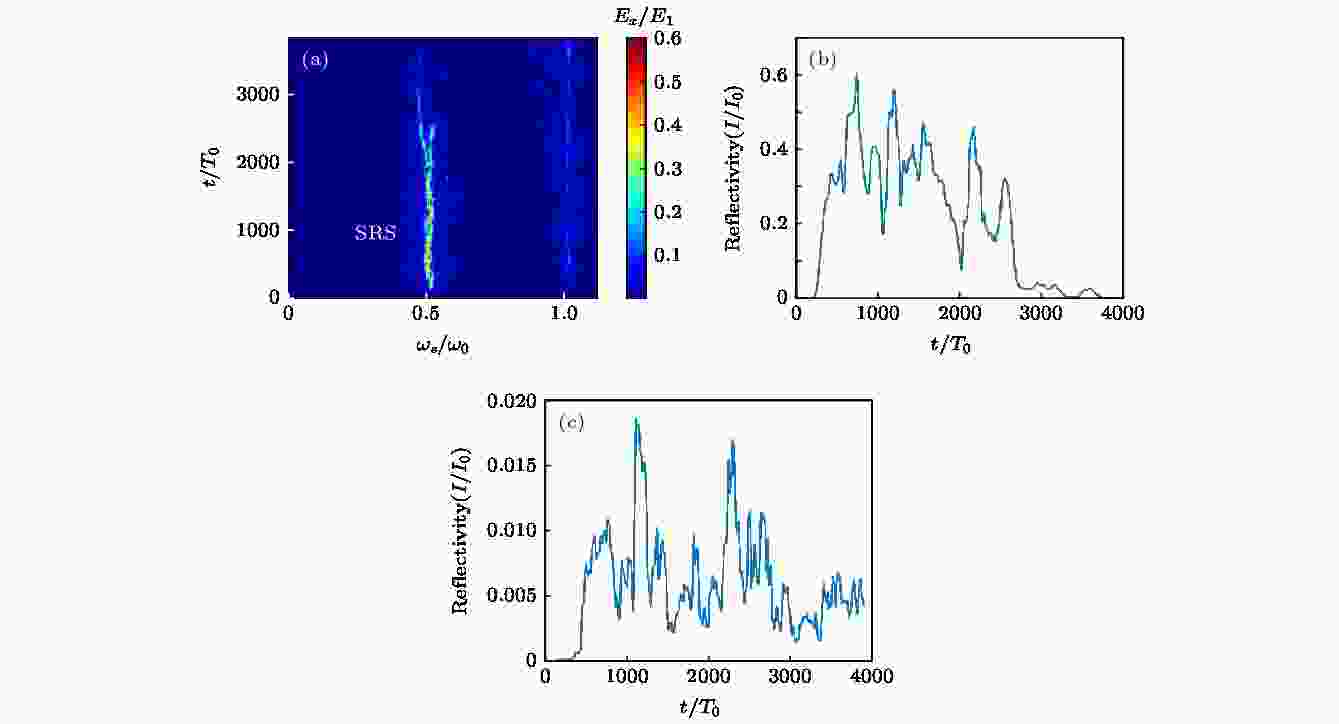图 7 (a)左行波在频率空间中随时间的变化; (b) SRS的份额随时间的变化; (c) SBS的份额随时间的变化Figure7. (a) The temporal evolution of left traveling wave in frequency space; (b) the temporal evolution of SRS; (c) the temporal evolution of SBS.
随着密度坑往低密度区域发展和密度坑的逐渐增多, 在这一过程中, SRS从以绝对不稳定为主, 转变为以对流不稳定为主. 当密度坑遍布了SRS的产生区域后, SRS几乎被完全抑制. 具体的SRS和SBS背散份额的变化, 我们可以通过对图7(a)中SRS和SBS相对应的频率成分积分后获得. 通过SRS和SBS不稳定性份额随时间变化的曲线, 如图7(b)和图7(c)所示, 以及离子密度分布的时空图, 可以看到随着密度坑在约t = 2000T0之后的大量产生, 不稳定区域被分割成多个不连续的部分, SRS和SBS均因此而受到了一定程度上的抑制, 其中SRS的抑制尤为明显.
综上所述, 由SRS绝对不稳定性所产生的散射光, 最先导致了nc/4处等离子体密度坑的产生. 由于密度坑的产生, 改变了周围等离子体密度的分布并形成了新的nc/4区域, 使得原本低于nc/4的区域产生了大量的密度坑. 随着大量的密度坑将不稳定区域分割成多个不连续的部分, SRS和SBS也都因此而受到了一定程度上的抑制.
由于一维模拟只能描述SRS和SBS散射, 而不能描述在多维几何条件下的激光成丝和双等离子体衰变, 特别是在三维几何条件下, 不仅会出现这些新的不稳定性, 而且线偏振激光的传输也将呈现各向异性[31], 因此有关密度坑的产生对于这些物理过程的影响, 还需要通过三维模拟来做更进一步的研究.
