摘要:为得到最大发光强度的红光上转换Er³⁺/Yb³⁺共掺Ba₅Gd₈Zn₄O₂₁荧光粉, 采用均匀设计初步寻找Er³⁺/Yb³⁺共掺杂的浓度范围, 再通过二次通用旋转组合设计, 建立了Er³⁺/Yb³⁺掺杂浓度与荧光粉在980 nm与1550 nm激光激发下红色上转换发光强度的回归方程, 最后利用遗传算法解得回归方程的最优解, 即在980 nm与1550 nm激光激发下红光上转换最大发光强度对应的Er³⁺/Yb³⁺掺杂浓度, 用高温固相法分别制备出两种激发下的最优解荧光粉样品. 经X射线衍射仪分析, 证明所制备样品均为纯相Ba₅Gd₈Zn₄O₂₁. 在980 nm激光激发下, 最优样品的红光为双光子过程; 在1550 nm激光激发下, 最优样品的红光为三光子过程. 测量了最优样品关于温度的上转换发射光谱, 发现样品的红光上转换发光强度随着温度的升高而减弱. 所得最优样品与NaYF₄∶Er³⁺/Yb³⁺红光商品粉进行比较, 在980 nm和1550 nm激光激发下, 最优样品红光上转换发光强度远强于NaYF₄红光商品粉发光强度. 在相同功率密度激发下, 980 nm激光激发下的最优样品比1550 nm激光激发下的最优样品红光上转换发光强度更强.
关键词: 均匀试验设计/
二次通用旋转组合设计/
红光上转换/
Ba₅Gd₈Zn₄O₂₁∶Er³⁺/Yb³⁺

English Abstract

全文HTML

--> --> -->

近年来, 随着稀土发光材料在光信息存储、显示、荧光探针、激光技术、激光防伪等领域的影响与应用不断扩大, 稀土掺杂的上转换发光材料得到了广泛的探讨与研究, 如今仍然有很多致力于提高上转换发光效率的研究^[1—4]. 在NaYF₄和氟化物光纤中观察到了高效的上转换发光, 但其应用通常受到化学和热稳定性能的限制^[5—7]. 与氟化物材料相比, 氧化物具有更好的稳定性和更简单的制备工艺^[8]. 在氧化物中, 具有低声子能量的Y₂O₃被认为是高上转换发光效率的理想材料, 并且Er³⁺/Yb³⁺共掺杂的Y₂O₃已经投入商业化生产^[9]. 在之前的研究中, Ba₅Gd₈Zn₄O₂₁也具有较低的声子能量, 且化合物材料的晶体结构稳定, 不易受到化学或物理环境的影响且具有良好的热稳定性, 因此是良好的上转换发光基质材料^[10—12]. 在Er³⁺/Yb³⁺共掺的发光材料中, 绿光与红光的发射比较明显, 且绿光与红光的发光强度随着Er³⁺/Yb³⁺离子浓度的变化而改变^[13]. 由于稀土离子掺杂的浓度范围较大且可能受到交互作用的影响, 于是如何科学高效地寻找离子掺杂浓度成为了研究焦点之一.
试验优化设计是一种可以通过少量试验来获取全面试验信息的科学试验方法. 试验优化设计有很多设计方法, 其中均匀试验设计和二次通用旋转组合设计是常用的优化设计方法. 均匀试验设计可以通过少量试验确定合理的试验范围, 二次通用旋转组合设计可建立研究对象的回归模型, 该回归模型不仅具有通用性、旋转性, 还能大量减少试验次数, 并可对所得的回归模型进行准确寻优. 尽管试验优化设计理论在很多研究领域得到了应用, 但将其应用于发光材料的合成研究还是一种科学新颖的方法^[14,15].
本文运用均匀试验设计和二次通用旋转组合设计相结合的试验方法, 对Er³⁺/Yb³⁺共掺Ba₅Gd₈Zn₄O₂₁上转换荧光粉的掺杂浓度进行寻优^[16]. 首先使用均匀试验设计的方法确定稀土离子的合理掺杂浓度范围, 再应用二次通用旋转组合设计的方法, 根据试验结果建立Ba₅Gd₈Zn₄O₂₁掺杂Er³⁺/Yb³⁺的二次回归方程, 对回归方程及各项系数进行显著性检验后, 通过遗传算法求得方程最优解, 即荧光粉红光最大发光强度对应的Er³⁺/Yb³⁺的最佳离子掺杂浓度^[17—19]. 试验采用高温固相法, 按Er³⁺/Yb³⁺最佳离子浓度制备出最优样品, 将最优样品与NaYF₄红光商品粉的发光强度进行比较, 并对其发光性质进行了研究^[20].

2

-->

2.1.实验方法

将实验用分析纯ZnO, BaCO_3, Gd₂O₃, Yb₂O₃, Er₂O₃作为原料, 将原料按一定摩尔系数比进行称量, 并将称量好的原料置于洗净的玛瑙研钵内, 充分研磨至原料混合均匀, 将得到的混合物装入刚玉坩埚内, 然后放入马弗炉中, 在1300 ℃下保温4 h, 自然降温冷却后得到块状样品, 将其研磨成粉末状, 即为所需的样品^[8].
使用日本岛津Shimadzu-6000型X射线衍射仪(XRD)对样品的晶体结构进行表征, 采用Cu靶${{\rm{K}}_{{\rm{\alpha }}1}}$辐射源作为X射线源. 测量的$2\theta $角度范围为10°—70°. 再用1550 nm光纤激光器和980 nm光纤激光器分别对样品进行激发, 并使用日立F-4600荧光光谱仪测定样品的上转换发射光谱, 试验中的光谱仪的光电倍增管所用电压为400 V. 采用实验室自制的DMU-TC 450温度控制器对样品的温度进行控制.
2 -->

2.2.试验优化设计

3 -->

2.2.1.均匀试验设计

为寻找Ba₅Gd₈Zn₄O₂₁荧光粉在1550 nm和980 nm激光激发下的最大红色发光强度所对应的Er³⁺/Yb³⁺掺杂浓度, 选用U₉(9⁶)进行均匀设计. 使样品在1550 nm和980 nm激光激发下得到上转换发射光谱, 并分别对发射光谱中的红色发光部分积分, 得到的积分强度见表1. 通过比较, 在1550 nm和980 nm激光激发下得到最强红光对应的Er³⁺/Yb³⁺浓度分别是Er³⁺为6%, Yb³⁺为7.875%和Er³⁺为8%, Yb³⁺为6.5%. 以这组Er³⁺/ Yb³⁺离子浓度为参考, 确定Er³⁺/Yb³⁺的掺杂浓度范围分别为Er³⁺ 4%—9%, Yb³⁺ 4%—9%, 将此浓度范围用于二次通用旋转组合设计中.

因素试验 序号	x1 (Er3+)/ mol%	x2 (Yb3+)/ mol%	y1550 nm	y980 nm
1	1(1)	4(5.125)	3328.2	62033.4
2	2(2)	8(10.625)	11605.2	101937.9
3	3(3)	3(3.75)	32949.3	90471.5
4	4(4)	7(9.25)	38447.2	99822.8
5	5(5)	2(2.375)	79416.9	69237.5
6	6(6)	6(7.875)	145038.5	123959.0
7	7(7)	1(1)	132225.6	38588.2
8	8(8)	5(6.5)	155258.0	112564.1
9	9(9)	9(12)	105986.7	75933.5

表1均匀试验设计
Table1.Uniform experimental design.

3 -->

2.2.2.二次通用旋转组合设计

为了使二次通用旋转组合设计具有通用性、旋转性等优异性质, 并符合建模和检验的要求, 因此需要进行因素编码, 表2是此次二次通用旋转组合设计的因素编码表. 二次通用旋转组合设计试验的方案与结果如列于表3. 共进行13组样品试验, 并分别对样品的红光部分进行积分, 积分面积分别用${y_{1550\;{\rm{nm}}}},{y_{980\;{\rm{nm}}}}$来表示.

zj(xj)	z1(Er3+)/mol%	z2(Yb3+)/mol%
z2j(2)	9	9
z0j + ${\varDelta _j} $(1)	8.2680	8.2680
z0j(0)	6.5	6.5
z0j – $ {\varDelta _j}$(–1)	4.7320	4.7320
z1j(–2)	4	4
${\varDelta _j} = \dfrac{{{z_{2j}} - {z_{1j}}}}{{2r}}$	1.7680	1.7680
${x_j} = \dfrac{{{z_j} - {z_{0j}}}}{{{\varDelta _j}}}$	${x_1} = \dfrac{{{z_1} - {\rm{6}}.{\rm{5}}}}{{{\rm{1}}.{\rm{7680}}}}$	${x_2} = \dfrac{{{z_2} - {\rm{6}}.{\rm{5}}}}{{{\rm{1}}.{\rm{7680}}}}$

表2自然因素水平编码表
Table2.Natural factors level codes.

序号	x0	x1	x2	x1x2	x12	x22	y1550 nm	y980 nm
1	1	1	1	1	1	1	129443	76365
2	1	1	–1	–1	1	1	124201	54268
3	1	–1	1	–1	1	1	120440	89291
4	1	–1	–1	1	1	1	100410	65430
5	1	1.414	0	0	2	0	127744	67758
6	1	–1.414	0	0	2	0	101623	73300
7	1	0	1.414	0	0	2	112067	82410
8	1	0	–1.414	0	0	2	109503	53292
9	1	0	0	0	0	0	120229	86752
10	1	0	0	0	0	0	123993	80120
11	1	0	0	0	0	0	124176	82245
12	1	0	0	0	0	0	118780	96762
13	1	0	0	0	0	0	108829	86738

表3二次通用旋转组合设计的试验方案及红光发光强度
Table3.Red luminescence intensity and experiment scheme of quadratic general rotary unitized design.

2

-->

3.1.数据分析与结果讨论

根据试验结果中的红光部分可初步建立在编码空间中的回归方程:

$\begin{split}{y_{1550\;{\rm{nm}}}} =\;& 119201.32 + 8716.12{x_1} + 3612.18{x_2} \\ &- 3697.04{x_1}{x_2} - 694.11x_1^2 \\ & - 2643.5x_2^2,\end{split}$

$\begin{split}{y_{980\;{\rm{nm}}}} =\;& 86523.21 - 3990.74{x_1} + 10891.21{x_2} \\ &- 440.77{x_1}{x_2} - 7403.85{x_1^2} \\ & - 8742.68{x_2^2} .\end{split}$

对上述红光的回归方程分别使用T-检验及F-检验来进行回归系数和方程显著性的检验, 检验的结果见表4, 其中(1)式代表1550 nm激光激发下的红光发光强度与Er³⁺/Yb³⁺浓度的二次回归方程, (2)式代表980 nm激光激发下的红光发光强度与Er³⁺/Yb³⁺浓度的二次回归方程. 对回归方程进行F-检验, 显著性水平均小于0.01, 说明回归方程(1)和回归方程(2)的置信度为99%. 对回归方程进行失拟检验, F₁, F₂均小于F_0.25(3, 4) = 2.05, 说明回归方程(1)和回归方程(2)均不失拟.

方差来源	偏差平方和1	偏差平方和2	自由度	t1统计量及F1比	t2统计量及F2比	显著性水平α1	显著性水平α2	显著性1	显著性2
x0	—	—	1	42.61	30.19	0.001	0.001	****	****
x1	—	—	1	2.30	1.03	0.1	0.4	***	*
x2	—	—	1	0.95	2.80	0.4	0.02	*	***
x1x2	—	—	1	1.18	0.14	0.4	0.9	*	不显著
x12	—	—	1	0.29	3.05	0.8	0.02	不显著	***
x22	—	—	1	1.11	3.60	0.4	0.02	*	***
回归	991488682.6	1960893448	5	12.03	18.77	0.01	0.01	****	****
剩余	115427203	146280989.8	7	—	—	—	—	—	—
失拟	43457130.87	15074730.26	3	1.11	0.37	0.01	0.01	****	****
误差	156531329.6	164236197.2	4	—	—	—	—	—	—
总和	1106915886	2107174438	12	—	—	—	—	—	—
注: ****极高显著水平(α ≤ 0.01); ***高显著性水平(α ≤ 0.1); **显著水平(α ≤ 0.25); *较显著水平(α ≤ 0.4).

表4红光的T-检验及F-检验方差分析
Table4.T-test and F-test with analysis of variance of red light

对回归方程系数进行T-检验, 将回归方程(1)中不显著项$x_1^2$和回归方程(2)中不显著项${x_1}{x_2}$数据剔除, 因此在编码空间中1550 nm与980 nm激光激发下Ba₅Gd₈Zn₄O₂₁∶Er³⁺/Yb³⁺共掺离子浓度与红色发光强度的二次回归方程分别为

$ \begin{split}{y_{1550\;{\rm{nm}}}} =\;& 119201.32 + 8716.12{x_1} + 3612.18{x_2} \\ &- 3697.04{x_1}{x_2} - 2643.5x_2^2,\end{split}$

$\begin{split}{y_{980\;{\rm{nm}}}} =\;& 86523.21 - 3990.74{x_1} + 10891.21{x_2}\\& - 7403.85{x_1^2} - 8742.68 {x_2^2}.\end{split}$

根据表2, 可得自然空间回归方程为

$ \begin{split}{y_{1550\;{\rm{nm}}}} =\, & - 11824.82 + 12617.75{z_1} + 20724.97{z_2}\\& - 1182.74{z_1}{z_2} - 845.70z_2^2, \\[-13pt] \end{split}$

$\begin{split}{y_{980\;{\rm{nm}}}} =\, & - 157089.70+28534.69{z_1} + 42520.15{z_2} \\&-2368.61{z_1^2} - 2796.92{z_2^2}.\\[-13pt] \end{split}$

利用遗传算法分别求出上述方程的最优解, 1550 nm激光激发下红光最优样品Er³⁺, Yb³⁺离子浓度分别为8.95%, 6.00%; 980 nm激光激发下红光最优样品Er³⁺, Yb³⁺离子浓度分别为6.02%, 7.53%. 按照得出的最优浓度分别制备了1550 nm和980 nm激光激发下的红光最优样品, 并测量其上转换发射光谱. 经测试计算, 1550 nm激光激发下最优样品的红光上转换发光强度积分是y_{1550 nm} = 188570, 980 nm激光激发下最优样品的红光上转换发光强度积分是y_{980 nm} = 91530.
图1为1550 nm激光激发下Ba₅Gd₈Zn₄O₂₁∶Er³⁺/Yb³⁺样品的上转换发射光谱, 可以明显看到红光的发光强度很强, 相比之下绿光的发光强度较弱, 蓝光的发光强度非常弱, 插图是1550 nm激光激发下1号样品与最优样品发光强度对比图, 可以看到最优样品在1550 nm激光激发下比1号样品的发光更强. 图2给出了980 nm激光激发下Ba₅Gd₈Zn₄O₂₁∶Er³⁺/Yb³⁺样品的上转换发射光谱, 红光发光较强, 绿光发光较弱, 蓝光的发光强度非常弱, 插图是980 nm激光激发下3号样品与最优样品的发光强度对比图, 可知最优样品在980 nm激光激发下比3号样品的发光更强. 其中红光的发光中心位于662 nm, 对应于⁴F_9/2 → ⁴I_15/2能级跃迁^[21,22].
图 1 Er³⁺/Yb³⁺共掺Ba₅Gd₈Zn₄O₂₁在1550 nm激光激发下的上转换发射光谱(插图为1号样品与最优样品的发光强度对比)
Figure1. Up-conversion emission spectra of Er³⁺/Yb³⁺ co-doped Ba₅Gd₈Zn₄O₂₁ phosphor under 1550 nm laser excitation. Inset picture shows the luminescence intensity of No. 1 sample and the optimal sample for comparison.

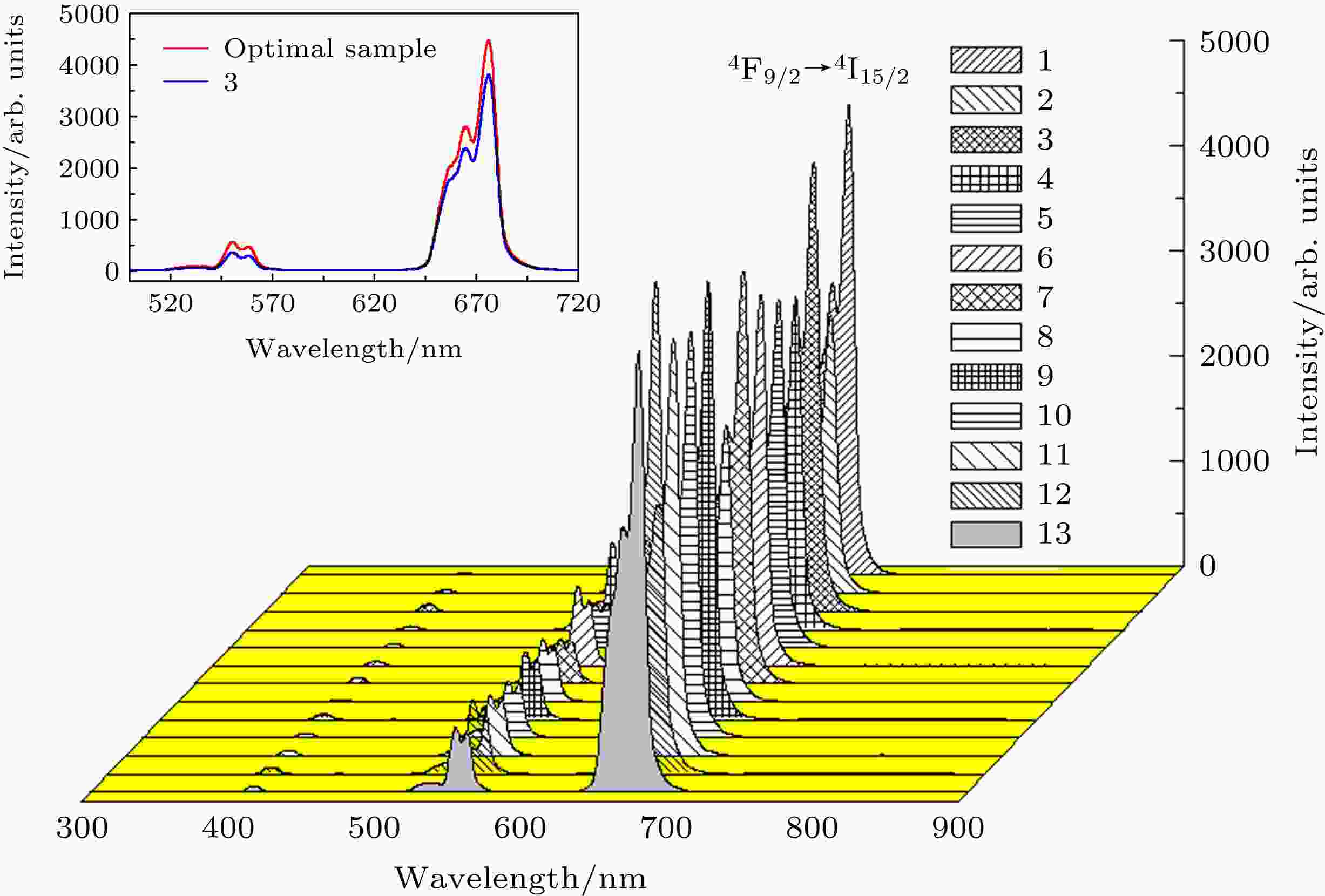图 2 Er³⁺/Yb³⁺共掺Ba₅Gd₈Zn₄O₂₁在980 nm激光激发下的上转换发射光谱(插图为3号样品与最优样品的发光强度对比)
Figure2. Up-conversion emission spectra of Er³⁺/Yb³⁺ co-doped Ba₅Gd₈Zn₄O₂₁ phosphor under 980 nm laser excitation. Inset picture shows the luminescence intensity of No. 3 sample and the optimal sample for comparison.

2 -->

3.2.最优样品的晶体结构表征

图3(a)对应着Er³⁺/Yb³⁺共掺中Yb³⁺最大浓度样品的XRD图样, 图3(b)对应着Er³⁺/Yb³⁺共掺中Er³⁺最大浓度样品的XRD图样, 图3(c)对应着1550 nm激光激发下红光最优样品的XRD图样, 图3(d)对应着980 nm激光激发下红光最优样品的XRD图样; 图3(e)给出了Ba₈Gd₅Zn₄O₂₁粉末衍射的标准卡片JCPDS card No. 51-1686. 经过对比可以看出, 图3(a)—(d)的XRD图样与标准卡片的衍射峰位置一致, 于是可以确认合成的Ba₈Gd₅Zn₄O₂₁∶Er³⁺/Yb³⁺粉末样品为纯相. 由于Gd³⁺与Er³⁺/Yb³⁺的离子半径接近, 所以并没有使共掺的Ba₈Gd₅Zn₄O₂₁的晶体结构发生改变而产生衍射峰的偏移^[23].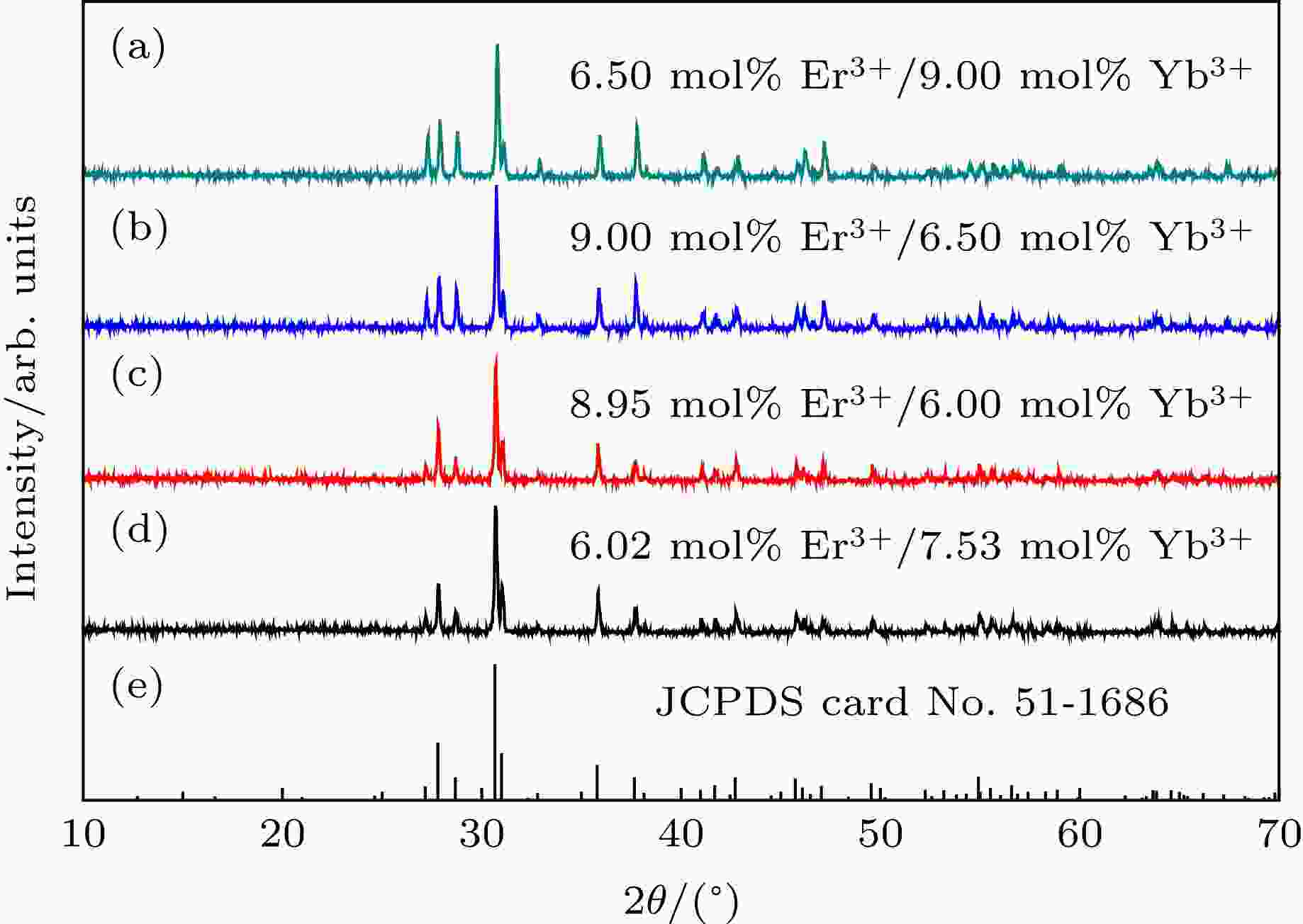
图 3 样品的XRD与标准卡片JCPDS No.51-1686图样
Figure3. XRD patterns of samples, and standard peaks of Ba₈Gd₅Zn₄O₂₁ (JCPDS No.51-1686) are included for comparison.

2 -->

3.3.最优样品的上转换发光机制

为了进一步探索研究最优样品的上转换发光机制, 将最优样品分别在不同工作电流的1550 nm和980 nm激光下激发并对红色发光部分积分. 另外, 为了避免由于激发功率密度过高而对样品产生激光致热效应, 把激光器工作电流控制在相对较低的范围内, 使得对发光机制的分析误差更小. 已知稀土离子的上转换发光过程是由稀土离子吸收两个或两个以上的长波长光子而产生一个短波长光子的过程, 由于在上转换发光过程发光强度${I_{{\rm{up}}}}$与抽运电流${i_{{\rm{LD}}}}$之间的关系满足

${I_{{\rm{up}}}} \propto {\left( {a{i_{{\rm{LD}}}} - b} \right)^n},$

通过此关系进行非线性拟合, 得出n值^[24]. 图4为不同波长激发下红光上转换发光强度与抽运工作电流的依赖关系, 通过对最优样品的分析可以发现, 样品在1550 nm激光激发下红光的n值为2.83, 这与三光子过程的理论值基本相同, 说明最优样品在1550 nm激光激发下实现红光与绿光上转换均为三光子过程, 而拟合数值的细微差异可能是由于求得的积分面积或是拟合过程造成的; 样品在980 nm激光激发的情况下红光的n值为1.83, 可以说明最优样品在980 nm激光下实现红光上转换为双光子过程.
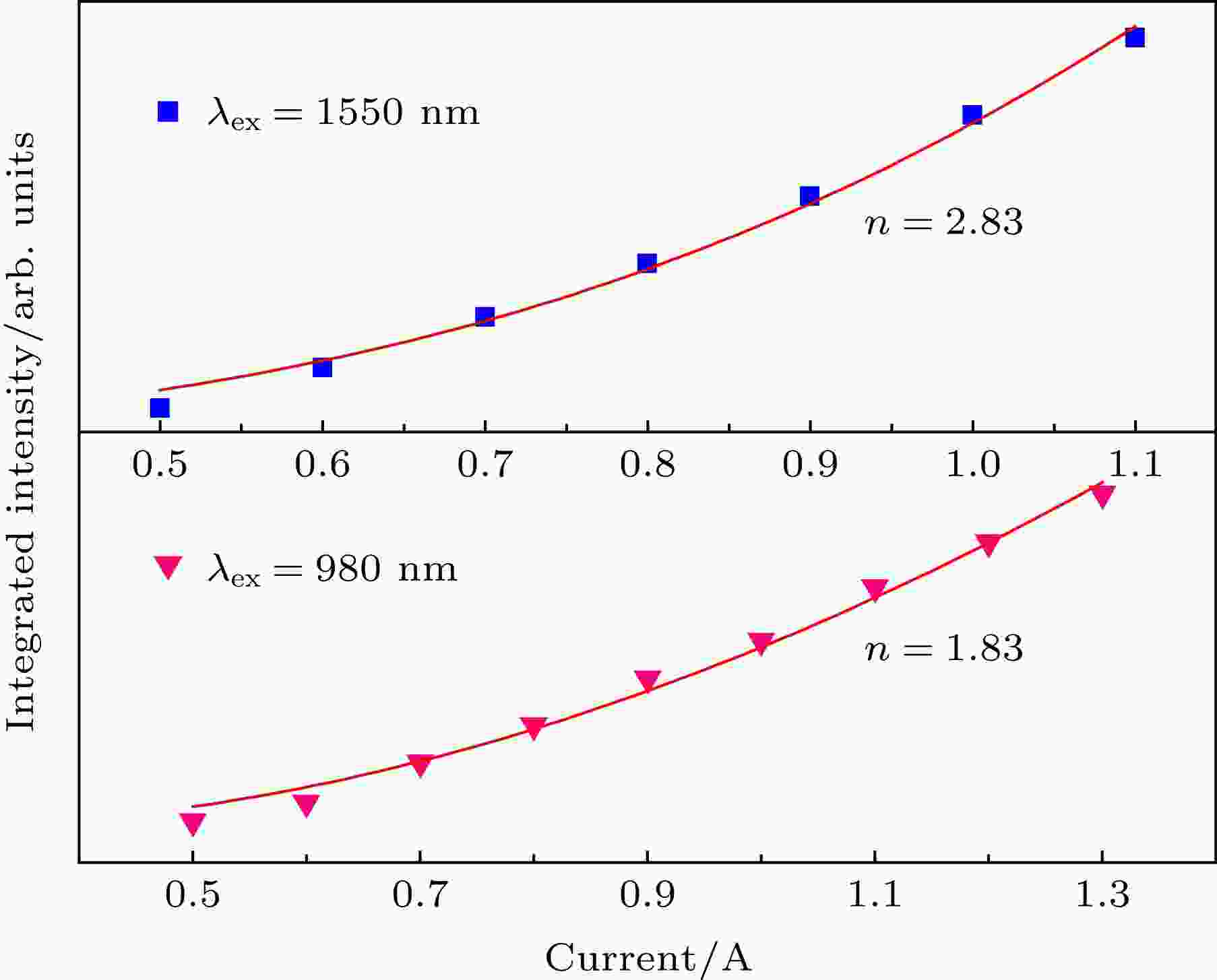图 4 上转换发光强度积分与激光器工作电流的依赖关系
Figure4. Dependence of the integrated intensity of up-conversion luminescence on laser working current.

2 -->

3.4.温度对最优样品红光上转换发光的影响

为了研究温度对Ba₈Gd₅Zn₄O₂₁∶Er³⁺/Yb³⁺粉末上转换发光的影响, 改变温度, 对最优样品进行上转换发射光谱的测量, 并求出红光发光部分的积分面积. 图5(a)和图5(b)分别是980 nm和1550 nm激光激发下最优样品的红光上转换发光强度随温度的变化, 图中红光的上转换发光强度随着温度的升高而呈现下降的趋势.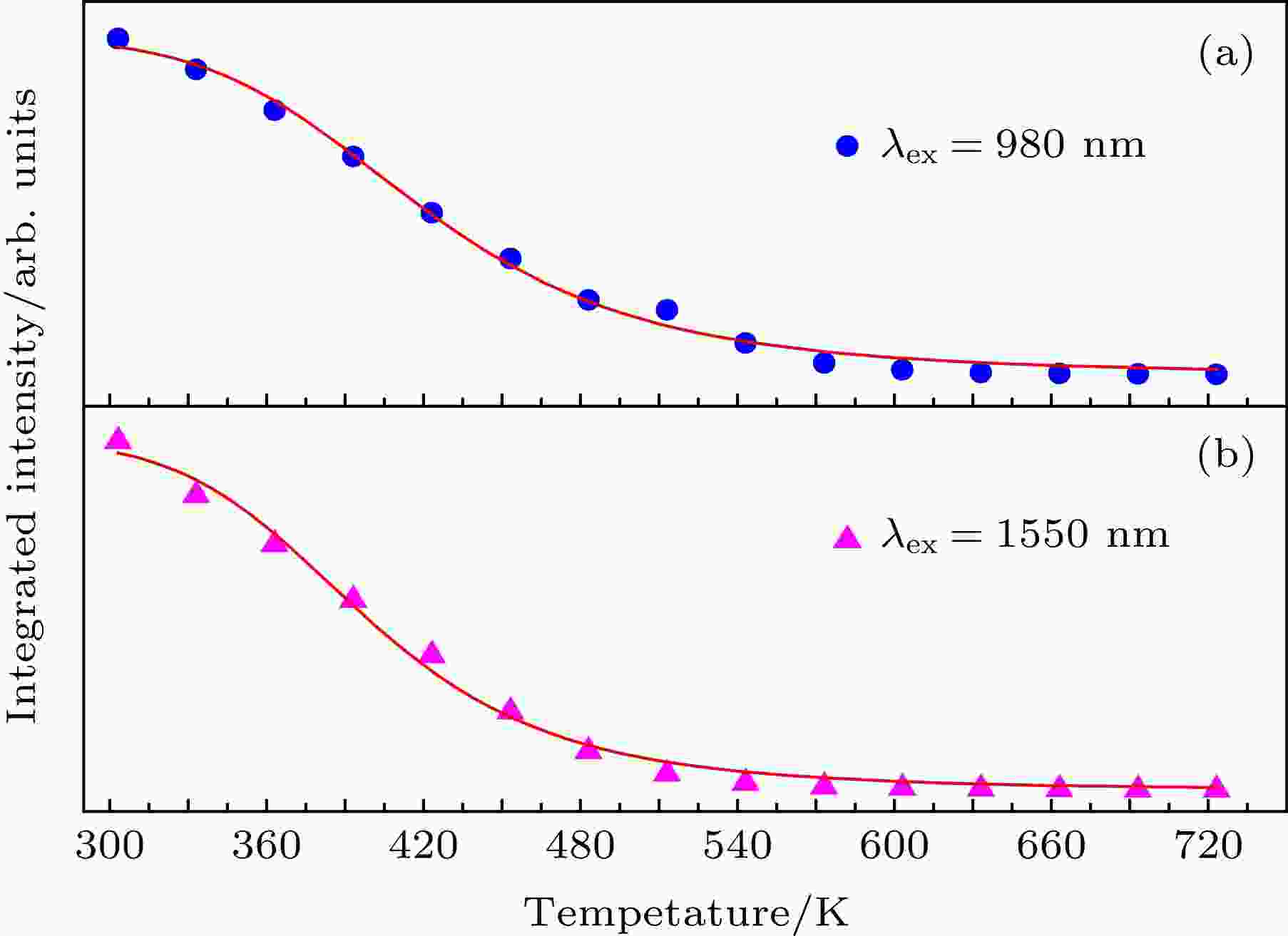
图 5 最优样品在(a) 980 nm与(b) 1550 nm激光激发下的红色上转换发光强度随温度的变化
Figure5. Dependence of red up-conversion luminescence intensity on temperature under (a) 980 nm and (b) 1550 nm excitation for optimal samples.

2 -->

3.5.最优样品与NaYF₄∶Er³⁺/Yb³⁺红光商品粉的发光强度比较

在980 nm和1550 nm激光激发下, 通过改变抽运工作电流分别测得NaYF₄∶Er³⁺/Yb³⁺红光商品粉与最优样品的红光上转换光谱, 积分后进行比较, 如图6所示. 图6(a)和图6(c)为最优样品红光上转换发光强度积分; 图6(b)和图6(d)为NaYF₄∶Er³⁺/Yb³⁺商品粉末的红光上转换发光强度积分. 通过对比可以看出, 此次制备的最优样品荧光粉红光上转换发光强度远强于NaYF₄商品粉, 并且随着抽运电流的增强, 两者发光强度差呈增大趋势.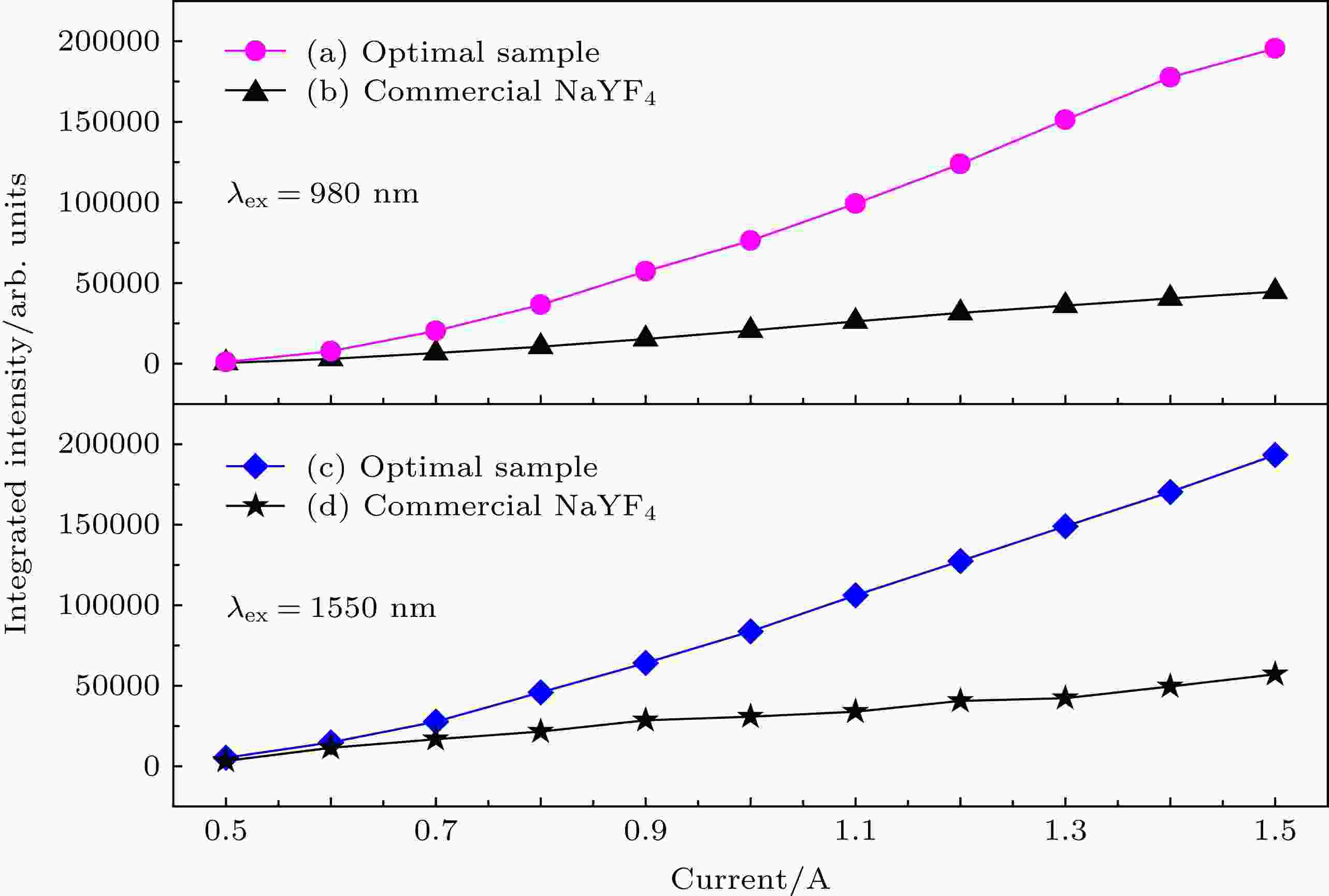
图 6 在(a), (b) 980 nm和(c), (d) 1550 nm激光激发下最优样品与NaYF₄商品粉末发光强度的比较
Figure6. Dependence of red up-conversion luminescence intensity compared with commercial phosphor of NaYF₄ under (a), (b) 980 nm and (c), (d) 1550 nm excitation for optimal samples.

图7为980 nm和1550 nm激光激发下最优样品与NaYF₄商品粉末的红光发光强度的倍数比.
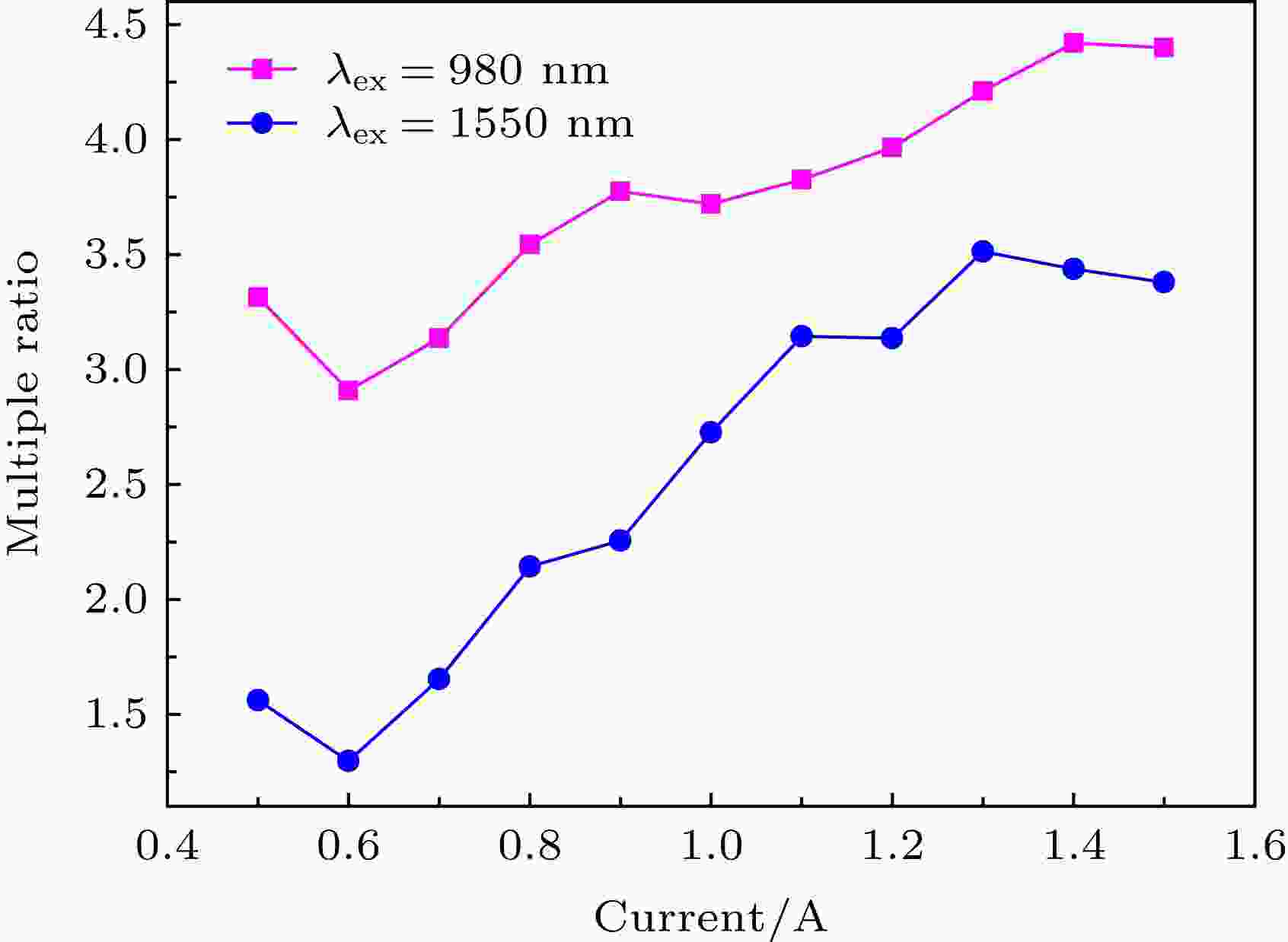图 7 在980 nm和1550 nm激光激发下最优样品与NaYF₄商品粉末发光强度的倍数比
Figure7. The Multiple ratio of red up-conversion luminescence intensity compared with commercial phosphor of NaYF₄ under 980 nm and 1550 nm excitation for optimal samples.

将最优样品在相同激发功率密度下进行红光上转换发光强度的比较, 如图8所示, 图8(a)是1550 nm激光激发下的最优样品的红光上转换发光强度积分, 图8(b)是980 nm激光激发下的最优样品的红光上转换发光强度积分. 可以看出, 在相同激发功率密度的情况下, 980 nm激光激发下的最优样品比1550 nm激光激发下的最优样品红光上转换发光强度更强.
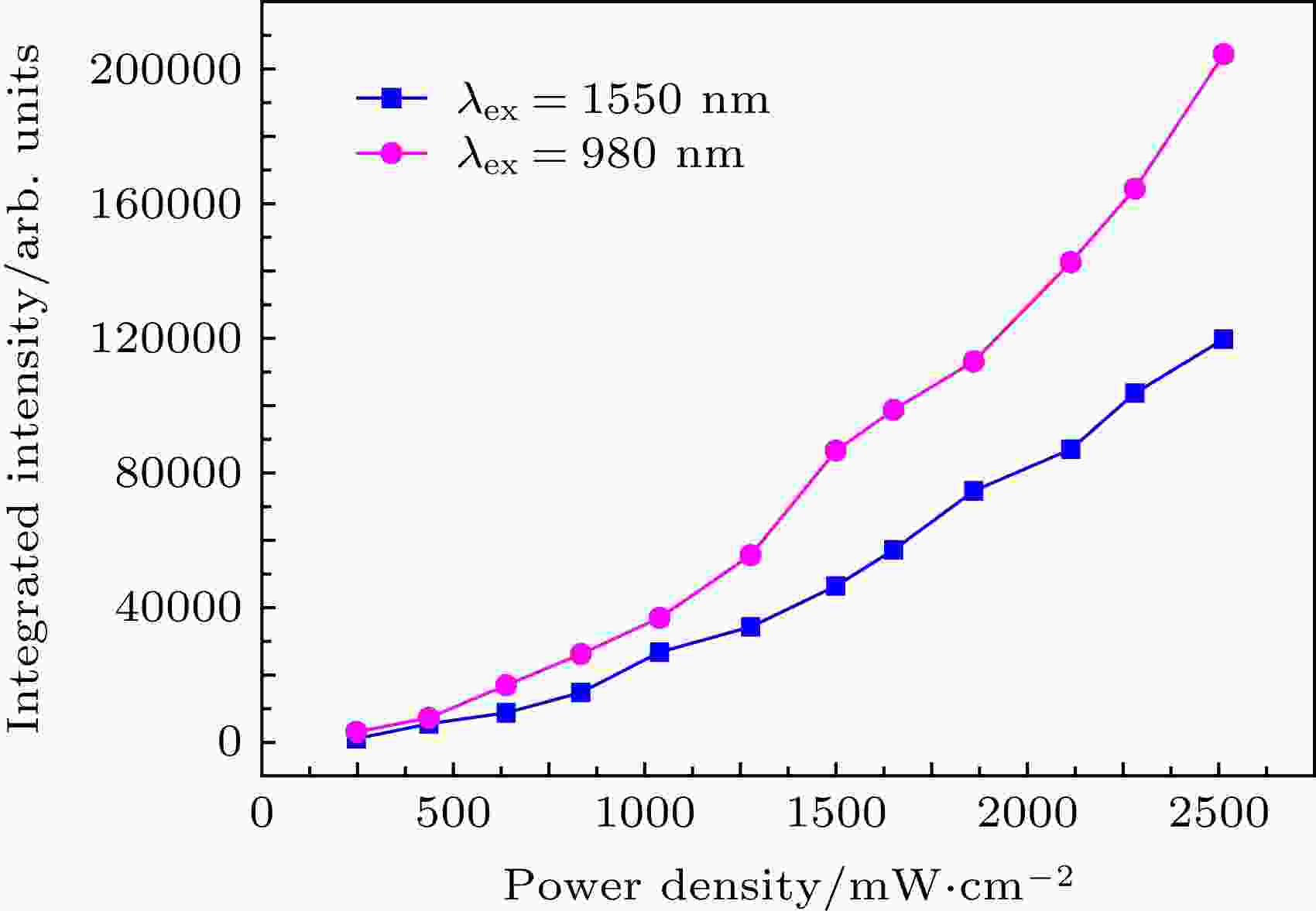图 8 相同功率密度下最优样品的红光上转换发光强度比较
Figure8. Comparison of red up-conversion luminescence intensity of optimal samples at the same power density.

本文采用均匀设计和二次通用旋转组合设计相结合的方法, 获得了在980 nm和1550 nm激光激发下红光最大发光强度的Ba₅Gd₈Zn₄O₂₁∶Er³⁺/Yb³⁺荧光粉的最优掺杂浓度. 用高温固相法分别制备出最优样品, 经过XRD衍射仪检验分析, 最优样品均为纯相. 在1550 nm激光激发下, 测得了上转换发射光谱, 由强度制约关系分析, 发现最优样品的红光上转换发光为三光子过程; 同样, 在980 nm激光激发下, 测得上转换发射光谱并由强度制约关系分析, 发现最优样品的红光上转换发光为双光子过程. 将制得的最优样品与NaYF₄∶ Er³⁺/Yb³⁺红光商品粉进行发光强度的对比, 样品发光强度远强于NaYF₄商品粉的发光强度, 并且随着抽运电流的增强, 两者发光强度差值呈增大趋势. 在相同激发功率密度的情况下, 980 nm激光激发下的最优样品比1550 nm激光激发下的最优样品红光发光强度更强. 该研究结果证明了试验优化设计的科学性和高效性, 同时为发光材料的研究制备提供了一种新的方法.