摘要:近年来, 金属半导体纳米激光器作为超小尺寸的光源被广泛地研究, 其在光子集成回路、片上光互连、光通信等领域具有潜在的应用价值. 随着谐振腔体积的减小, 激光器损耗也迅速增加, 这阻碍了激光器进一步的小型化. 本文提出一种基于双凹型谐振腔的金属半导体纳米激光器结构. 该结构具有圆柱形的反射端面和内凹的弯曲侧壁, 能够使谐振模式集中于腔中心并减小辐射损耗, 从而提升品质因子和降低激光器阈值. 本文利用时域有限差分方法数值计算了三种不同曲线侧壁的双凹腔性能. 数值仿真结果表明, 相比于传统胶囊型腔结构, 本文提出的双凹腔结构的品质因子提高24.8%, 激光器阈值电流降低67.5%, 能够有效提升激光器性能. 该结构在超小型金属半导体纳米激光器领域具有重要应用价值.
关键词: 半导体激光器/
微腔/
表面等离激元

English Abstract

全文HTML

--> --> -->

亚波长半导体激光器近年来在光子集成回路(photonic integrated circuits, PICs)、片上光互连、光通信等领域应用广泛^[1-5]. 为了缩小激光器尺寸, 多种不同谐振腔机制被提出并实验验证, 如微盘激光器^[6]、光子晶体激光器等^[7]. 特别是自2007年Hill等^[8]首次利用金属包层的半导体纳米柱结构实现激射以来, 金属半导体纳米激光器因其尺寸小、调制频率高等优势成为了近年来的研究热点.
在目前的各类金属半导体纳米激光器的研究中, 主要有基于回音壁模式(whispering-galley mode, WGM)的圆柱形腔^[9-12]和基于法布里-帕罗模式(Fabry-Perot mode, FPM)的矩形腔^[13-16]等两种谐振腔结构. 前者通常具有较高的品质因子, 后者因为FPM的反射损耗, 通常品质因子较低, 但具有模式能量易于耦合到集成波导中等优势. 为了提高基于FPM的金属半导体激光器的性能, 我们于2014年提出了一种胶囊型谐振腔(capsule-shaped cavity, CSC)结构^[17], 利用圆柱形的反射端面形成高斯型谐振模式, 使得光场能量集中在腔中心, 以减少其在金属侧壁的能量分布, 从而减小金属损耗. 随后, CSC型结构的有效性被实验证实^[18,19]. 实验研究表明, CSC型结构对橫电(transverse electric, TE)模式的品质因子提升更大, 从而能够抑制横磁(transverse magnetic, TM)模式的激射, 使其在光子集成和PICs等领域具有更好的应用价值. 然而, 随着CSC型谐振腔尺寸的缩小, 其金属损耗迅速增大, 品质因子迅速降低从而导致难以实现激射, 因此目前实验成功的CSC型激光器尺寸在1.6 μm × 1 μm量级.
为了进一步提升FPM的金属半导体纳米激光器性能, 我们提出并数值仿真验证了一种新型的谐振腔结构—高斯型谐振腔(Gaussian-shaped cavity, GSC)^[20], 其几何结构遵循高斯光束传播的波前分布, 同时具有圆柱形的反射端面和曲线型的束腰, 用以形成高斯型的谐振模式. 相比于相同体积的传统矩形腔和CSC型结构, GSC型结构能够使光场能量更加集中于谐振腔中心, 从而远离金属侧壁并减小金属损耗. 同时, GSC型结构的曲线侧壁使得谐振模式垂直于金属侧壁的电场分量减小, 从而有效抑制了表面等离激元(surface plasmon polaritons, SPPs)模式的激发, 提高了限制因子和品质因子, 降低了激光器阈值. 然而, 由于GSC型腔的几何结构遵循高斯光束传播的波前分布关系, 并不能独立优化反射端面的曲率半径和侧壁曲线的形状, 因而限制了超小型光源的设计和应用范围.
本文提出并通过数值仿真研究了一种新型的适用于金属半导体纳米激光器的双凹型谐振腔结构. 该结构的反射端面为圆柱形, 侧壁设计为独立可调的内凹曲线, 从而可以优化谐振模式, 获得更小的谐振腔体积和更高的品质因子. 本文利用时域有限差分(finite-difference time-domain, FDTD)方法对1.55 μm波长范围的不同曲率的反射端面和不同曲线的侧壁结构组成的双凹腔的品质因子、限制因子、阈值增益、阈值电流等物理性质进行了系统的研究, 数值仿真结果证明了本文提出的新型双凹腔结构相比于CSC结构具有更小的体积、更高的品质因子和更低的阈值, 对于极小尺寸的金属半导体纳米激光器的设计和应用具有重要意义.

本文提出的双凹型金属半导体纳米激光器谐振腔结构带有圆柱形的反射端面和内凹的弯曲侧壁. 侧壁的曲线独立可调, 可设计成一次函数、二次函数(如抛物线型等)、三角函数(如余弦函数)等. 以抛物线型为例, 其谐振腔结构示意图如图1所示. 本文针对1.55 μm波长的通信波段进行设计, 谐振腔的半导体材料有源层是厚度为300 nm的InGaAs, 其下层为500 nm厚的p掺杂InP包层, 上层为500 nm厚的n掺杂InP包层, 并使用100 nm厚的n掺杂InGaAs作为接触层. 半导体侧壁及反射端面由厚度为30 nm的绝缘体材料SiO₂覆盖, 整个谐振腔由100 nm厚的金属Ag包裹.
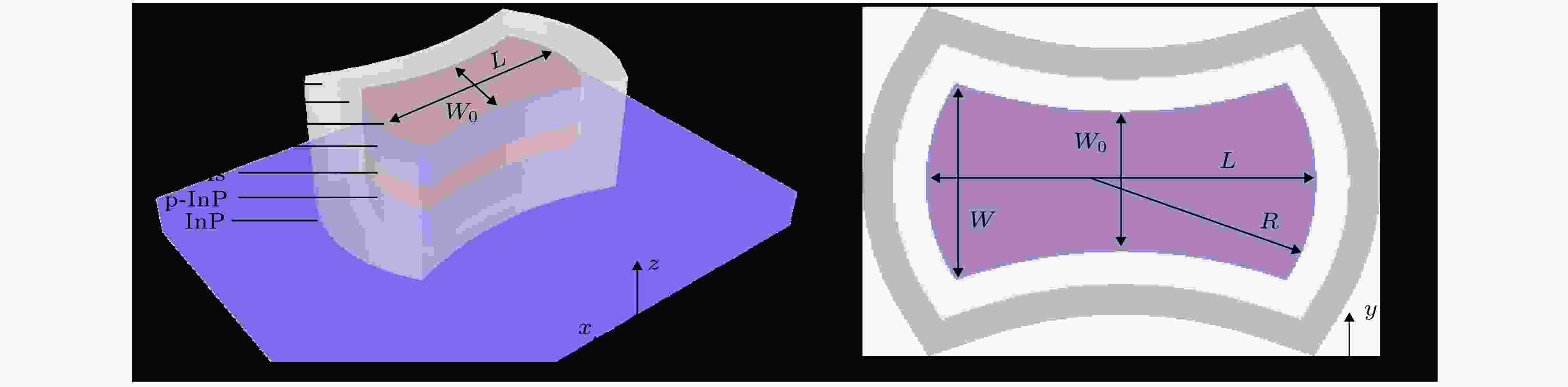图 1 双凹型金属半导体纳米激光器谐振腔示意图　(a)结构示意图; (b)俯视图
Figure1. Schematic of double-concave cavity of metallic semiconductor nanolaser: (a) The structure; (b) top view of the double-concave cavity.

该双凹型谐振腔的俯视图如图1(b)所示, 腔长为L, 谐振腔的最大宽度为W, 侧壁束腰宽度为W₀. 谐振腔的反射端面是具有一定曲率的圆柱面, 曲率半径为R, 侧壁曲线独立可调. 在本文中, 以一次曲线、抛物线和余弦函数形式的弯曲侧壁为例, 利用三维全波FDTD方法对双凹型谐振腔结构进行数值仿真研究. 半导体和介质材料InGaAs、InP、n-InGaAs、SiO₂的折射率分别设置为3.53, 3.17, 3.6, 1.45. 在数值仿真中, 根据Drude-Lorentzian模型, 我们利用实验值^[21,22]拟合了金属材料Ag的介电常数. 计算边界设置完美匹配层来吸收反射波, 计算区域采用5 nm的均匀网格, 用以保证良好的收敛性和较快速的计算时间.
通过计算得到的谐振腔品质因子Q可以分解成辐射品质因子Q_rad和耗散品质因子Q_diss. 前者来源于谐振腔辐射的能量损耗, 后者主要来源于金属材料的损耗, 它们遵从以下关系^[17,23]:

$\frac{1}{Q} = \frac{1}{{{Q_{{\rm{rad}}}}}} + \frac{1}{{{Q_{{\rm{diss}}}}}}.$

通过在数值仿真中将金属损耗设置为零, 重复相同谐振腔结构的计算, 得到的品质因子即为Q_rad^[17], 再由(1)式可得到金属损耗相关的Q_diss. 并由归一化的InGaAs有源层光场能量计算出谐振模式的限制因子Γ^[17,24], 则激光器的阈值增益g_th可表示为^[17,24]:

${g_{{\rm{th}}}} = \frac{1}{{\varGamma {v_{\rm{g}}}{\tau _{\rm{p}}}}},$

其中v_g是光在有源层的群速度, τ_p表示谐振模式中的光子寿命, 可以用${Q/{\left( {2{\text{π}}f} \right)}}$表示.
相应地, 阈值电流I_th可以通过半导体激光器的速率方程理论进行估值^[17,24]:

${I_{{\rm{th}}}} = \frac{{qV\left( {BN_{{\rm{th}}}^{\rm{2}} + CN_{{\rm{th}}}^3} \right)}}{{{\eta _{\rm{i}}}}}, $

${N_{{\rm{th}}}} = {N_{{\rm{tr}}}}\exp \left( {\frac{{{g_{{\rm{th}}}}}}{{{g_{{\rm{o}}N}}}}} \right), $

其中q是电子的单位电荷, V是有源层的体积, B和C分别为双分子复合系数和俄歇复合系数, N_th表示阈值载流子密度, N_tr表示透明载流子密度, g_oN是经验系数. 简便起见, 电流注入效率${\eta _{\rm{i}}}$设为1. 本文参考室温下与InP晶格匹配的InGaAs材料参数, 将(3)式和(4)式中的各系数设置为$B = 1.0 \times {10^{ - 10}}\;{{{\rm{c}}{{\rm{m}}^{\rm{3}}}}/{\rm{s}}}$, $C = 4.15 \times {10^{ - 29}}\;{{{\rm{c}}{{\rm{m}}^{\rm{6}}}}/{\rm{s}}}$, ${N_{{\rm{tr}}}} = 1.1 \times {10^{18}}\;{{{\rm{c}}{{\rm{m}}^{{\rm{ - 3}}}}}/{\rm{s}}}$, ${g_{{\rm{o}}N}} = 1000\;{\rm{ c}}{{\rm{m}}^{{\rm{ - 1}}}}$^[25-27].

本文利用三维全波FDTD方法对提出的新型双凹腔结构的金属半导体纳米激光器进行了数值仿真研究. 作为参照组, 我们首先研究具有直线侧壁的CSC型谐振腔结构. 理论和实验研究表明, 相比于TM模式, 圆柱形反射端面对TE模式的Q值提高更大^[17-20]. 此外, TE模式能够更好地限制谐振模式, 并通常兼容于PICs中其他光器件, 因此本文主要研究TE模式. 腔长度L设定为700 nm, 宽度W设定为520 nm, 计算不同反射端面曲率的谐振腔品质因子. 图2绘制了谐振腔Q值随着反射端面曲率半径R的变化关系曲线, 其中L/R = 0 (R = ∞)对应传统的矩形谐振腔, 其在宽度W = 520 nm时对应的Q值为95. 由图2可见, 随着曲率端面的引入, 谐振模式向腔中心集中, 因而辐射损耗减小, 辐射品质因子Q_rad得到显著提高. 而耗散品质因子Q_diss主要来源于金属损耗, 与谐振模式在腔内金属侧壁的分布有关, 随着反射端面曲率的减小, 呈现先增大后减小趋势, 在L/R = 1.43附近达到最大值, 并决定了谐振腔品质因子Q的变化趋势, 这与我们之前工作的研究结论一致^[17-19]. 另一方面, 已有研究表明, 在腔长L固定时, CSC型谐振腔的Q值随着宽度W的减小而显著下降, 这是由于宽度减小时, 谐振光场在腔的金属侧壁上的分布变大, 产生更强的SPP模式, 从而金属损耗增加, 品质因子减小, 阻碍了进一步缩小谐振腔尺寸^[17-19].
图 2 CSC型谐振腔(L = 700 nm, W = 520 nm) Q值与曲率半径R的关系
Figure2. Q values of the capsule-shaped cavities (L = 700 nm, W = 520 nm) as functions of the radius of curvature R.

为了克服这一困难, 本文提出了一种新型的双凹腔结构, 其反射端面是曲率独立可调的圆柱形结构, 内凹的弯曲侧壁由表1中的曲线方程所定义, 它与反射端面的曲率无关, 因而也是独立可调的. 该新型结构具有更小的体积, 并能够减小辐射损耗, 有效提高Q_rad, 从而在进一步缩小谐振腔尺寸的同时有效提高品质因子Q. 为了与作为参照组的CSC型结构进行比较, 我们设定双凹腔的长度L = 700 nm, 最大宽度W = 520 nm, L/R = 1.43, 此参数下对应的CSC型腔结构的品质因子为最大值141 (见图2). 本文研究了由表1定义的三种不同侧壁形状的双凹腔, 其侧壁曲线分别为一次函数、抛物线和余弦函数. 表1中各曲线方程的坐标原点为腔中心, 参数a₁、a₂、a₃和b由腔长度L、宽度W、束腰宽度W₀和反射端面曲率R所决定.

侧壁曲线类型	侧壁曲线方程
一次函数型	y = |a1x| + W0/2
抛物线型	y = a2x2 + W0/2
余弦函数型	y = a3cos(bx) + W/2

表1双凹型谐振腔的侧壁曲线方程
Table1.Curve equations of the sidewalls of the double-concave cavities

我们首先研究不同形状侧壁的双凹腔品质因子Q与束腰宽度W₀的关系, 如图3所示. 这里W₀/W = 1时对应了直线侧壁的CSC型谐振腔. 当W₀/W < 1时, 一方面, 谐振腔的侧壁内凹, 形成了弯曲侧壁, 谐振腔体积变小, 金属侧壁处光场分布增大, 从而增加了金属损耗. 另一方面, 弯曲侧壁导致TE模式的垂直于侧壁的电场分量减小. 由于SPPs模式只能由垂直于金属-介质界面的电场分量激发, 因此弯曲侧壁可以有效抑制SPPs模式的激发, 降低金属损耗. 在此两方面因素共同作用下, Q_diss值随着W₀/W的减小, 整体呈现出减小趋势, 但在某些几何结构下金属损耗减小, Q_diss值增大, 如图3(c)所示. 例如, 一次函数型和另两种双凹腔结构的Q_diss值分别在W₀/W = 0.85和0.9附近时最大. 另一方面, 随着束腰宽度的减小, 谐振模式受到调制, 除了金属损耗, 辐射损耗也相较于CSC型结构发生变化. 如图3(b)所示, 辐射损耗相关的Q_rad值随着W₀/W的减小, 呈现出先减小, 再显著增大至极值后缓慢减小的趋势. 与CSC型结构不同的是, 由于双凹腔结构的辐射损耗有效减小, Q_rad值决定了谐振腔的品质因子Q的变化趋势, 如图3(a)所示. 例如, 一次曲线型腔在W₀/W = 0.75时Q值最大, 为174, 抛物线型腔和余弦函数型腔在W₀/W = 0.8时, Q值达到最大, 分别为175, 176. 由此可见, 本文提出的双凹腔结构在CSC型结构对Q值进行优化的基础上, 通过引入弯曲侧壁的几何结构, 降低了辐射损耗, 有效提高Q_rad值, 以实现更小体积谐振腔结构下的品质因子提升.
图 3 三种曲线侧壁的双凹型谐振腔(L = 700 nm, W = 520 nm, L/R = 1.43)的品质因子Q、辐射品质因子Q_rad和耗散品质因子Q_diss与W₀/W的关系　(a) Q; (b) Q_rad; (c) Q_diss
Figure3. Quality factors Q, radiation quality factors Q_rad and dissipation quality factors Q_diss of three double-concave cavities with curved sidewalls (L = 700 nm, W = 520 nm, L/R = 1.43) as functions of the W₀/W: (a) Q; (b) Q_rad; (c) Q_diss.

图4描述了Q值最大处的三种双凹腔结构的谐振模式(TE模式)在经过腔中心的xy、yz和xz截面上的归一化电场强度分布图. 所有谐振腔结构的几何参数详见表2. 图4(a)—(c)所示的是CSC型腔结构, 谐振模式主要集中在半导体层, 但是在侧壁部分(特别是腔反射端面附近)有较大的SPPs模式分布, 金属损耗较大. 图4(d)—(l)所示的是三种双凹腔结构的谐振模式, 其归一化的金属损耗相比于CSC型腔结构均未改善, 这与图3(c)的结论一致. 图4(g)—(i)和4(j)—(l)所示的是分别是抛物线型和余弦函数型谐振腔结构, 它们相比于图4(d)—(f)所示的一次函数型谐振腔结构具有更加平滑的弯曲侧壁, 因此具有相对较低的金属损耗. 值得注意的是, 如上文所述, 由于双凹腔型结构具有更低的辐射损耗, 图4(d)—(l)所示的谐振模式依然具有更高的品质因子.
图 4 不同谐振腔结构的谐振模式(TE模式)的归一化电场强度|E|²在穿过腔中心的xy、yz、xz平面的分布图　(a)— (c)为胶囊型腔; (d)— (f)为一次函数型腔; (g)— (i)为抛物线型腔; (j)—(l)为余弦函数型腔. 所有腔的几何参数详见表2
Figure4. Normalized electric field intensity distribution |E|² of the resonant mode (TE mode) in the xy-, yz- and xz-planes crossing the cavity center: (a)–(c) The capsule-shaped cavity; (d)–(f) the linear-function-shaped cavity; (g)–(i) the parabola-shaped cavity; (j)–(l) the cosine-shaped cavity. All the geometric parameters of the cavities are listed in Table 2 in detail.

参数	胶囊型	一次函数型	抛物线型	余弦函数型
L/nm	700	700	700	700
W/nm	520	520	520	520
W0/W	1.00	0.75	0.8	0.80
L/R	1.43	1.43	1.43	1.43
V/λ3	0.267	0.258	0.257	0.258
λ/nm	1564	1552	1550	1551
Q	141	174	175	176
Г	0.460	0.441	0.440	0.445
gth/cm–1	2190	1870	1850	1830
Ith/μA	800	290	280	260

表2四种谐振腔的金属半导体纳米激光器的几何参数和数值仿真结果
Table2.Geometric parameters and simulation results of the metallic semiconductor nanolasers with four types of cavities.

为了进一步研究该新型双凹腔侧壁的内凹程度对金属半导体纳米激光器性能的影响, 我们根据数值仿真得到的Q值和谐振模式分布, 利用(2)式—(4)式, 计算了基于上述三种腔结构的金属半导体纳米激光器的限制因子、阈值增益和阈值电流随束腰宽度W₀的变化关系, 见图5. 这里, 体积V定义为金属半导体腔的总体积(包括绝缘体层和金属层). 由图5(a)可见, 当W₀/W < 1时, 随着束腰宽度W₀减小, 三种双凹腔结构的限制因子总体均呈现下降趋势, 但是在W₀/W = 0.8和0.85附近取得局域极大值, 这是束腰半径减小引起的金属损耗增大和辐射损耗减小共同导致的结果. 由图5(b)和图5(c)可见, 阈值增益与阈值电流随着束腰宽度W₀的减小, 呈现出先增大后减小的趋势, 一次函数型和另两种双凹型腔结构分别在W₀/W = 0.75和0.8处取得最小值. 并且, 抛物线型和余弦函数型腔结构在W₀/W ∈ [0.7, 0.85]的较大束腰宽度范围内, 都比CSC型腔结构具有更小的阈值, 因而对于半导体微加工的制造公差具有较好的容忍度, 有较好的应用价值.
图 5 三种曲线侧壁双凹型谐振腔(L = 700 nm, W = 520 nm, L/R = 1.43)的金属半导体纳米激光器的限制因子Γ、阈值增益g_th和阈值电流I_th与W₀/W的关系　(a) Γ; (b) g_th; (c) I_th
Figure5. The confinement factor Γ, threshold gain g_th and threshold current I_th of the metallic semiconductor nanolasers with three double-concave cavities with curved sidewalls (L = 700 nm, W = 520 nm, L/R = 1.43) as functions of the W₀/W: (a) Γ; (b) g_th; (c) I_th.

表2列出了图5中阈值最低处的三种双凹腔结构的金属半导体纳米激光器的各性能参数. 相比于CSC型腔结构, 三种双凹型谐振腔均拥有更小的体积、更高的Q值以及更低的阈值. CSC型金属半导体纳米激光器的阈值增益g_th和阈值电流I_th经计算为2190 cm^–1和800 μA. 作为对比, 本文中引入曲线侧壁结构的三种双凹腔结构的激光器阈值增益g_th和阈值电流I_th都有效降低了. 以余弦函数型双凹腔结构为例, 其阈值增益g_th和阈值电流I_th分别为1830 cm^–1和260 μA, 相比于CSC型腔结构, 分别下降了16.4%和67.5%. 因此, 本文所提出的新型双凹腔结构可以有效地提高金属半导体纳米激光器的性能.

本文提出并理论研究了一种双凹型谐振腔结构的金属半导体纳米激光器. 该谐振腔结构具有圆柱形的反射端面和内凹的弯曲侧壁, 从而能够使谐振模式集中在腔中心并减小损耗. 本文设计了三种内凹侧壁的双凹腔结构, 并利用 FDTD 方法进行了计算. 数值仿真结果表明, 在总体积小至0.258λ³时, 双凹腔结构的品质因子和阈值电流分别比传统胶囊型腔结构提高24.8%和降低67.5%, 证明了该结构的有效性. 本文通过优化谐振腔的几何结构来提高纳米激光器性能, 因而可以兼容于其他技术方法如散热优化^[28,29]、微加工优化^[30-32]等, 进一步提高性能. 本文提出的双凹型谐振腔结构的金属半导体纳米激光器作为超小型化的光源, 在PICs、片上光互连、光通信等领域具有潜在的应用价值.