摘要:采用有限元法研究了由两个共振在基波处的金属开口环谐振器组成的立体“超构分子”中的二次谐波产生特性. 通过改变立体“超构分子”中两个金属开口环谐振器之间的相对取向角度, 使得在基波处共振的模式耦合发生变化, 从而调控了二次谐波中两个正交分量之间的振幅比和相位差, 获得了具有不同偏振态的二次谐波辐射.
关键词: 开口环谐振器/
二次谐波/
偏振调控

English Abstract

全文HTML

--> --> -->

随着微纳加工技术的不断进步, 微纳光子学在近几十年中得到了长足发展. 而在微纳光子学的发展过程中, 对一些新近发展起来的具有优异性能的纳米材料进行研究是不可或缺的. 例如, 碳纳米管^[1,2]、黑磷^[3]、少层铋烯二维材料^[4]、石墨烯-碲化铋^[5]等新型材料已经被用于光电探测、传感、饱和吸收超短脉冲产生以及超快光学等领域.
在光波的波前调控领域, 对于偏振调控, 目前主要还是集中于用波片、偏振片或者相位延迟器等宏观的器件来实现. 为了实现集成光学的效果, 人们提出了一些基于微纳材料的二维结构来调控光的偏振态^[6—10]. 比如, 在线性领域, L形金属纳米线由于对称性的破缺, 在正交方向上能产生不同频率的共振, 那么反射光在正交方向上的相位差和电场会随着纳米线的旋转而独立变化, 所以就可以用来调节反射光的偏振态^[11]. 或者采用两组亚单元的组合, 分别在正交方向上产生相应的线偏振光, 再通过亚单元之间的空间位错引入相位差, 从而将入射的线偏振光转化为各种椭圆偏振态^[12]. 另外, 还可以采用双圆形开口环的立体结构组成一个手性超分子, 它会在与入射偏振正交的方向上引入共振, 从而在不同波长下产生不同偏振态的透射光^[13]. 总之, 偏振调控的关键在于如何在两个正交方向上引入相位差. 但目前偏振调控还多局限在线性领域中的实现, 至于如何在非线性领域调控二次谐波(second harmonic generation, SHG)的偏振态, 目前鲜见报道.
微纳尺度下, 两个结构单元之间的耦合效应对于其模式特性起到了至关重要的作用^[14—18]. 超材料在光学频段既有电共振特性, 又有磁共振特性^[19], 所以电和磁的偶极子以及更高阶的多极子之间的耦合是其中的重要机制. 耦合体系内部不同的耦合形式可以帮助我们很好地理解从分子态到固体物理模型的演变. 由于超材料的体积小于光的波长, 材料内部的两个结构单元之间相互作用就会极大地增强^[20]. 每个微纳尺度的亚单元可以看成一个“超原子”, 它们的组合构成“超构分子”的过程中, 由于电磁耦合作用, “超原子”不同的排列方式或相对位置会带来“超分子”不同的光学特性的改变^[21], 这就为研究模式耦合及其应用带来了更多的调控自由度.
金属开口环谐振器(split ring resonators, SRR)由于在共振时表面存在环形电流^[22], 相当于一个磁偶极子, 所以可以看成一种磁性“超原子”. 本文研究了由两个SRR堆叠构成的立体超构分子中的SHG特性. 相比于单个SRR仅能产生电场沿着其臂的方向振动的线偏振SHG^[23], 在SRR超构分子中利用两个开口环超原子之间的耦合, 通过其开口方向的旋转可以引入电场在正交方向振动的两个SHG分量, 并且可以调控正交分量之间的振幅比和相位差, 从而可以获得具有不同偏振态的SHG辐射.

如图1(a)所示, 采用的超构分子结构由两个全同的金SRR上下间隔一定间距堆叠而成, 两个SRR之间开口的相对朝向夹角为φ. 本文所选用的SRR的结构参数分别为: 边长L = 230 nm, 臂宽W = 90 nm, 臂长b = 140 nm, 厚度T = 50 nm. 上层SRR上表面到下层SRR上表面的间距为D = 100 nm. 我们使用了有限元法(finite-element-method, FEM)仿真软件COMSOL Multiphysics对它们的线性光学性质进行了模拟. 在模拟计算中, 上层SRR的底部以及线偏振入射光的电场方向始终沿着x方向, 并且SRR超构分子处于均匀介质环境(空气, 折射率设为1)中. 金的介电常数采用了实验参数^[24]. 我们采用周期边界条件来模拟x和y方向的周期性, 并且将其周期设为P_x = P_y = 500 nm以保证在我们研究的基波以及SHG波段仅有零级衍射. 如图1(b)所示, 计算了上下开口环相对角度φ = 90°时超构分子的吸收谱. 此时, 上层SRR的磁等离激元模式可以被线偏振光直接激发, 而由于下层SRR的底部与线偏振入射光的电场方向垂直, 其磁等离激元模式无法被入射光直接激发. 但是, 研究发现该结构在吸收谱的$wl1$和$wl2 $处出现了两个明显的吸收峰. 为了说明这两个吸收峰的成因, 进一步在图1(c)中给出了这两个吸收峰对应波长处SRR表面的磁场垂直分量H_z. 可以看到, $wl1$波长处的两个SRR之间的磁场垂直分量有一个π的位相差(反相位), 而$wl2$处的两个SRR之间的磁场垂直分量是同相位的. 这两种不同的磁场垂直分量分布表明我们在图1(b)中所观察到的两个吸收峰对应于两个磁偶极子相互作用后形成的反对称和对称模式, 与模式耦合作用会导致能级劈裂的预测相一致^[25].
图 1 (a)由两个金属SRR上下堆叠组成的超构分子结构示意图; (b)上下两个SRR相对开口朝向夹角为φ = 90°时超构分子的吸收谱; (c)与吸收谱中两个吸收峰对应的波长wl1和wl2处SRR表面的磁场垂直分量H_z分布图
Figure1. (a) Schematic diagram of SRR-based meta-molecule; (b) absorption spectrum of the meta-molecule consisting of two SRRs with a twist angle φ = 90°; (c) distributions of magnetic field component H_z on the surface of the SRRs at wavelengths corresponding to two absorption peaks wl1 and wl2.

在保持上层SRR开口取向以及入射波电场方向不变的前提下, 进一步计算了上下层SRR之间相对开口朝向夹角φ从0°变化为180°时的超构分子的吸收谱的变化, 如图2(a)所示. 可以看出, 在每个开口朝向夹角的吸收谱中都展现出了类似图1(b)中的对称和反对称耦合模式所对应的两个吸收峰的现象. 并且, 随着开口朝向夹角从0°增加到60°, 两个吸收峰之间的距离逐渐变小, 在60°左右时达到最小, 继续增加开口朝向夹角从70°增加到180°, 两个吸收峰之间的距离又开始逐渐变大. 这是由于随着开口朝向夹角的变化, 双层开口环的电耦合和磁耦合共同作用导致耦合强度的变化所致. 基于流体力学的模型^[26], 我们在FEM仿真软件COMSOL Multiphysics中将基波处SRR表面附近的电场转化为二阶非线性表面电流, 并以此作为产生SHG的源, 计算了不同开口朝向夹角下的SHG产生强度随基波波长的变化, 如图2(b)所示. 可以看出, 与超构分子线性吸收谱峰值之间距离的变化趋势相对应, SHG强度的峰值也随角度发生了先靠近后分开的情况, 这体现了基波处模式的耦合效应对于SHG具有显著的调控.
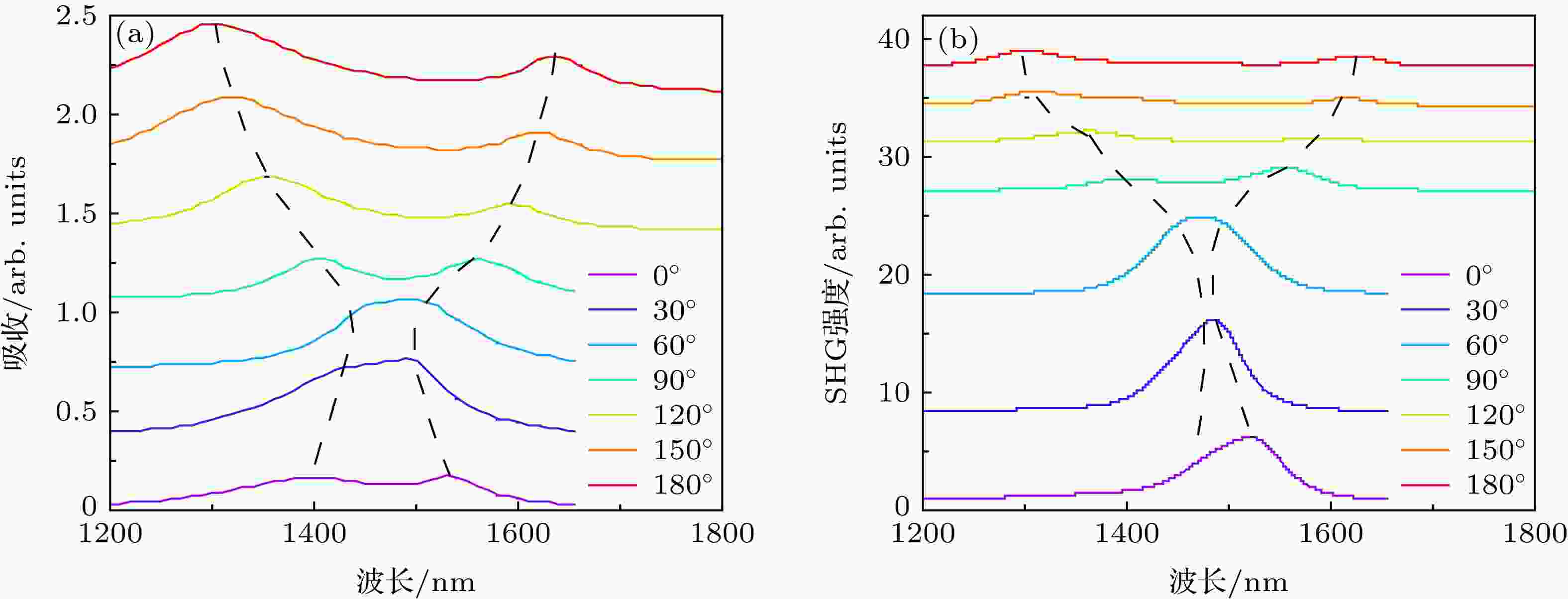图 2 双层相对角度改变时, (a)吸收谱和(b) SHG强度的变化, 黑色划线代表每条线左右峰值的连线
Figure2. (a) Absorption spectrum and (b) the SHG intensity with the relative angle of the two layers changing. The black dash line represents the line connecting the left and right peaks of each line.

我们知道单个SRR结构在入射基波偏振沿着其底边方向时, 所产生的SHG也是一种线偏振, 并且电场振动方向与SRR底边相垂直, 即沿着SRR臂的方向. 而在由两个SRR组成的超构分子中, 我们已经在图1中展示了即使下层SRR无法被入射基波直接激发的情况下, 也可以通过先激发上层SRR的磁共振模式, 继而通过模式耦合作用从而将下层SRR的磁共振模式激发出来. 由于SRR中SHG辐射的电场振动方向是与其臂的方向平行的, 因此在我们研究的超构分子中, 上层SRR将提供SHG的y分量, 而调节下层SRR的开口方向, 使得上下两个SRR的开口朝向夹角不为0°或180°时, 下层SRR产生的SHG就会具有x分量, 这就为调控SHG的偏振态提供了一个可能的途径.
我们选取相对角度从30°到150°每隔30°变化的5个参数, 分别给出了这五种结构下的远场SHG强度、SHG辐射的y和x分量的振幅比E_y/E_x和相位差δ, 如图3(a)—(c)所示. 可以看到, 由于下层SRR的开口偏离了y轴, 引入了SHG在x方向的电场分量, 因而SHG在两正交方向上的电场不再以y分量为主导, 振幅比E_y/E_x总体在1左右变化. 与此同时, SHG辐射的电场两正交分量之间的相位差δ在所选波段内都有比较大的变化.
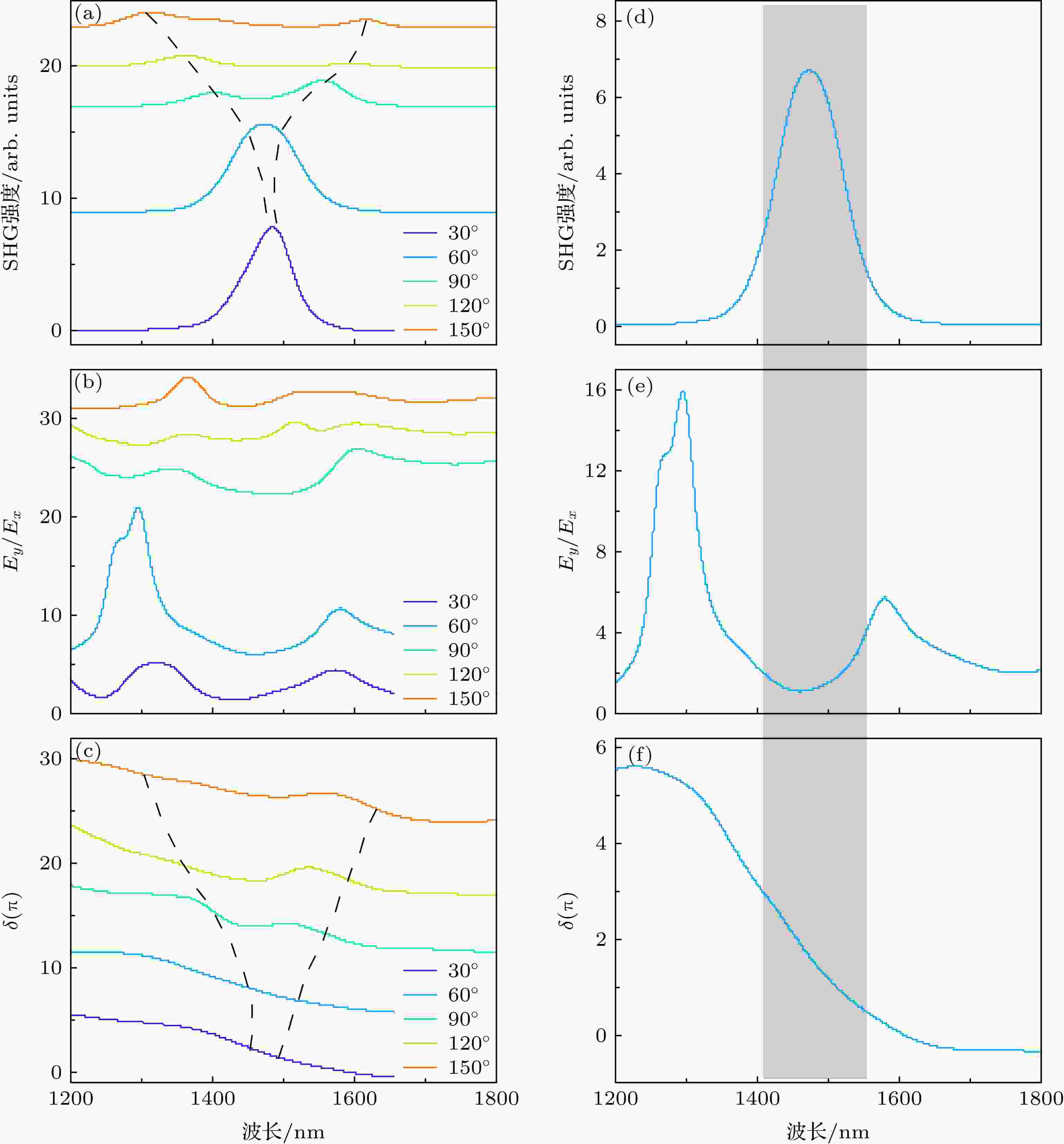图 3 双层相对角度为30°—150°时的远场SHG强度 (a)、SHG辐射的y和x分量的振幅比E_y/E_x (b)和相位差δ (c)随着波长的变化; 双层相对角度为60°时的远场SHG强度 (d)、SHG辐射的y和x分量的振幅比E_y/E_x (e)和相位差δ (f)随着波长的变化; 其中阴影区域表示SHG效率较大的一段波长区域
Figure3. When the relative angle of the two layers changes from 30° to 150°, (a) SHG intensity, (b) amplitude ratio of SHG in the y and x directions and (c) the phase difference of SHG in the y and x directions as a function of wavelength; when the relative angle of the two layers is 60°, (d) SHG intensity, (e) amplitude ratio of SHG in the y and x directions and (f) the phase difference of SHG in the y and x directions as a function of wavelength. The shaded area indicates a wavelength region where the SHG efficiency is relatively large.

值得一提的是, 不同角度下SHG在y和x方向上的相位差随波长变化的斜率有所不同, 且对于吸收谱明显劈裂为两个共振峰的90°, 120°, 150°, 相位差存在两次斜率较大的变化, 由图3(c)中黑色辅助线可以看出, 这两次明显变化对应的波长与各自线性谱的两个峰位是符合的. 而在两峰位之间相位差的变化则相对比较平缓, 这说明共振会带来相位差的较大变化. 这是由于双层SRR之间的耦合作用在磁共振时会得到极大的增强, 能量就从上层SRR转移到下层SRR. 而两层SRR分别提供SHG沿着开口方向上的分量, 所以y和x方向上的相位差会受到共振明显的调制.
为了实现SHG辐射较为丰富的偏振态, 要在保证固定波段内SHG效率的前提下, 尽量让两正交方向的振幅比E_y/E_x接近于1, 同时相位差δ能有较大的变化. 综合考虑这些因素, 我们以上下夹角为60°的双层SRR为例来展示可以获得的SHG偏振态. 把其对应的远场SHG强度、SHG辐射的y和x分量的振幅比E_y/E_x和相位差δ在图3(d)—(f)中单独显示, 发现超构分子在1410—1550 nm这段基波波长范围内都具有较高的SHG效率, 且SHG在y和x分量间的振幅比在1—4之间变化, 相位差也具有超过360°的全相位变化.
那么有了SHG两个正交分量的相位差和振幅比的信息, 就可以得出SHG偏振态. 对于一个面向波的传播方向的观察者来说, 传播的电场在两个正交方向上的分量会遵循这个经典的关系式:

${\left( {\frac{{{E_x}}}{{\left| {{E_x}} \right|}}} \right)^2} + {\left( {\frac{{{E_y}}}{{\left| {{E_y}} \right|}}} \right)^2} - 2\frac{{{E_x}}}{{\left| {{E_x}} \right|}}\frac{{{E_y}}}{{\left| {{E_y}} \right|}}{\rm{cos}}\delta = {\rm{si}}{{\rm{n}}^2}\delta ,$

其中E_y和E_x分别是SHG电场的y和x分量, δ就是两个分量之间的相位差. 如前面所述, 在接近吸收峰时, 两个分量之间的相位差δ变化比较大. 我们在SHG产生效率较高的波段选择了6个特殊的波长1410, 1430, 1460, 1480, 1510以及1550 nm, 使得δ近似以90°的步长变化, 并分别求出这些波长处SHG的两个正交电场分量, 并和δ一起代入(1)式. 通过导入数值计算软件Matlab, 得到了SHG的偏振态对应的电场矢量轨迹, 结果如图4所示. 可以看出, 随着基波波长的改变, 激发出的SHG椭圆偏振态的长轴发生了旋转, SHG在远场出现了椭圆偏振、近线偏振和近似圆偏振, 实现了SHG偏振态的变化, 同时SHG的产生效率又保持在较高的水平.
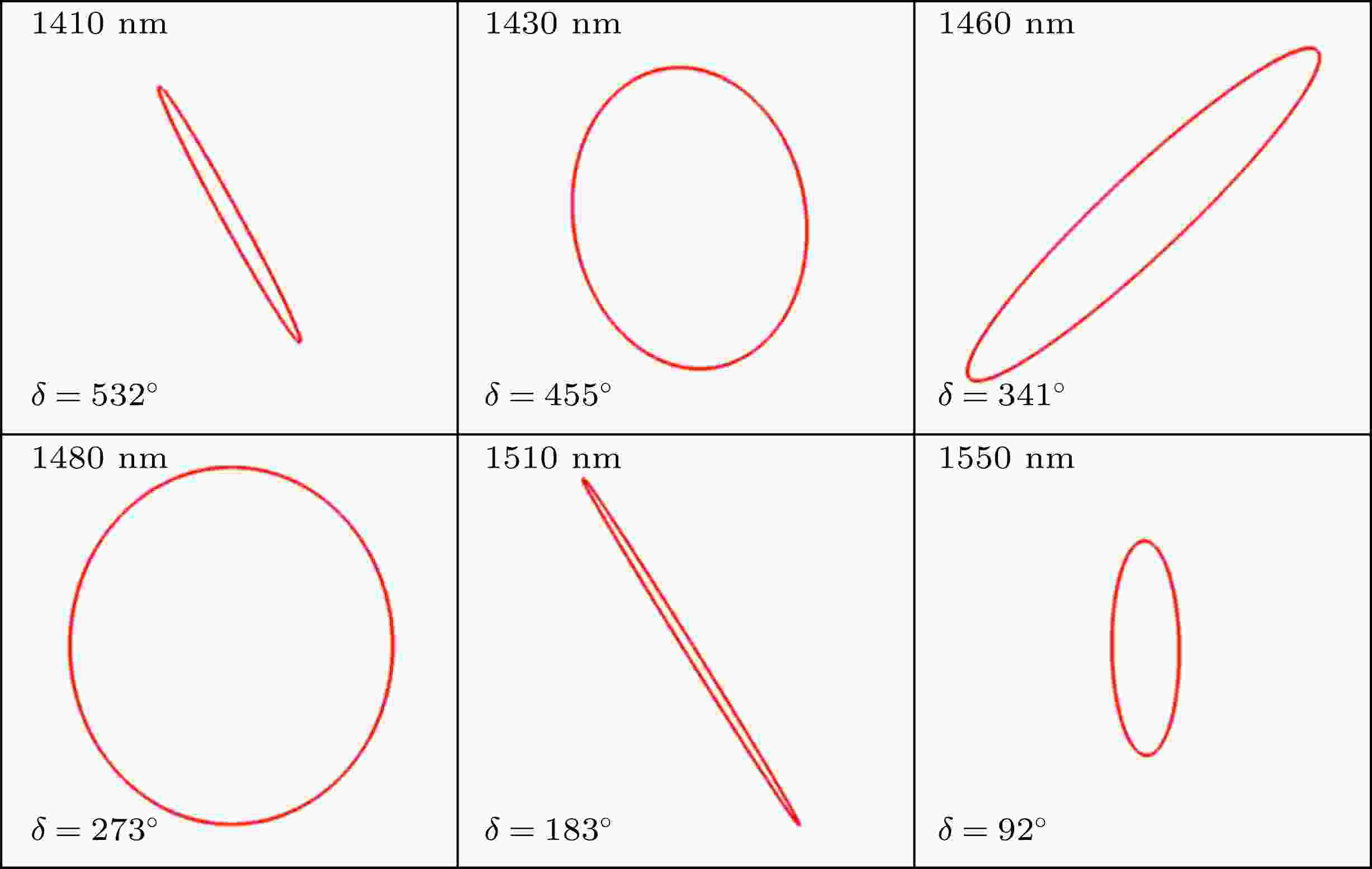图 4 双层相对角度为60°、不同波长的基波入射时, 远场SHG偏振态的变化
Figure4. Polarization of the far-field SHG changes when the relative angle of the two layers is 60°, and the the fundamental wave of different wavelengths is incident.

另外, 非线性偏振转换器件的工作环境有时需要固定基波波长就可以产生不同偏振态的非线性信号. 于是又按照图3选取了固定的基波波长1500 nm, 根据此波长处不同角度时的SHG强度和振幅比, 求出了不同角度下SHG的两个正交电场分量E_y和E_x, 并和相应的相位差δ一起代入(1)式. 再导入数值计算软件Matlab, 得到了固定波长下, 远场SHG偏振态随相对角度的变化, 结果如图5所示. 可以看出, 随着双层SRR相对角度的变化, 固定的基波激发出的SHG椭圆偏振态的长轴发生了旋转, 展示了近线偏振和椭圆偏振态的变化.
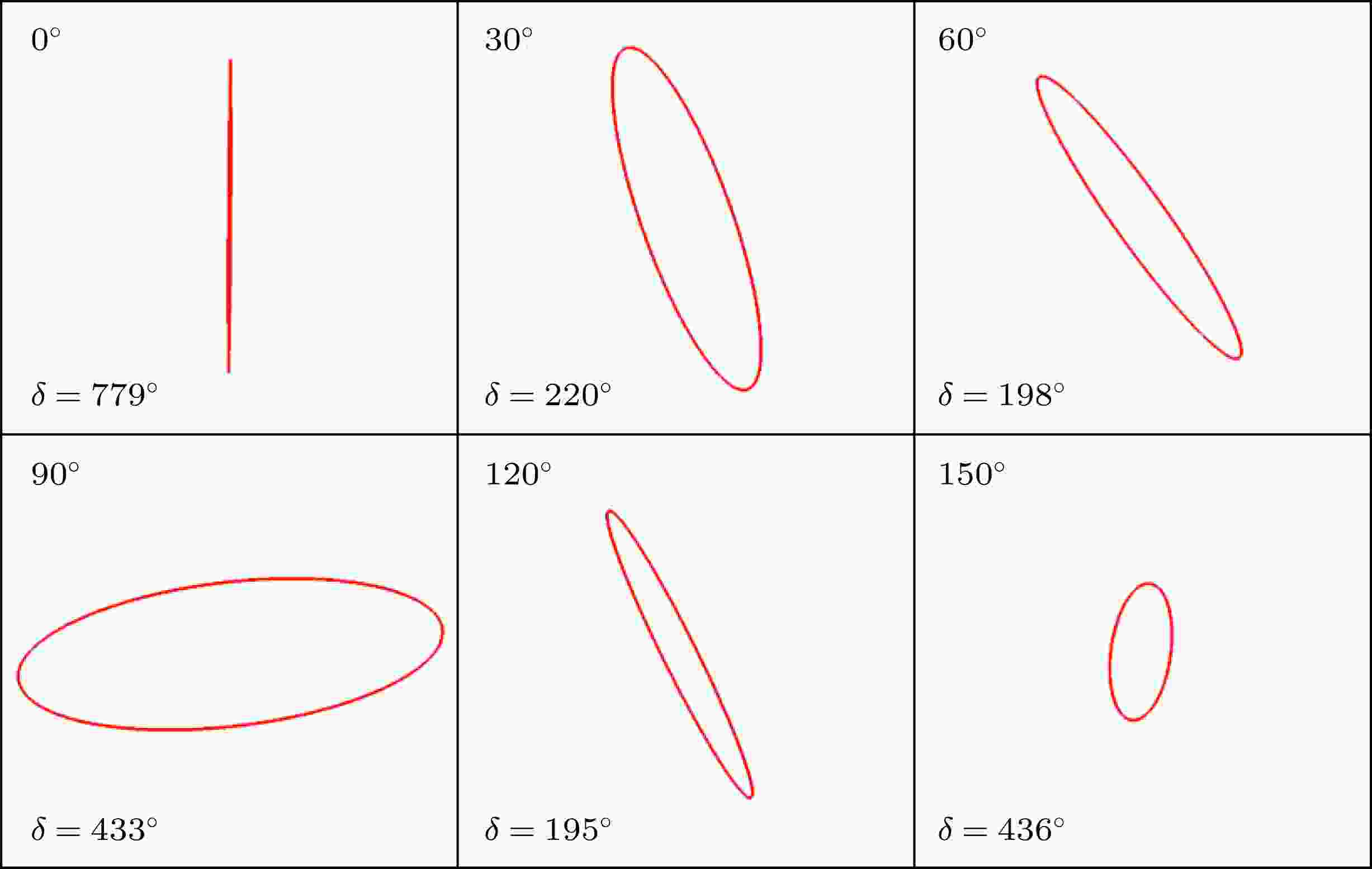图 5 基波波长为1500 nm入射时, 不同相对角度的结构的远场SHG偏振态的变化
Figure5. When the incidentwavelengthis 1500 nm, the polarization of the far-field SHG changes with the relative angle of the two layers

本文利用双层金属SRR组成的超构分子中存在的模式耦合特性, 通过调节上下层金属开口谐振器之间的相对开口方向, 使得超构分子的SHG辐射能够同时具有两个正交分量. 在SHG产生效率较高的波段内, 产生了依赖基波波长改变的SHG两个正交分量振幅比和相位差的变化, 从而实现了椭圆偏振、近线偏振、近圆偏振等多种偏振态的SHG辐射. 也可以用不同相对角度的SRR超构分子的组合, 在固定的基波激发下, 获得不同偏振态的SHG辐射.