摘要:提出一种集成在微桥结构中的二维亚波长周期钛(Ti)金属圆盘阵列结构, 以增强太赫兹微测辐射热计的吸收率. 基于严格耦合波分析方法, 建立吸收结构模型, 研究了不同结构的Ti圆盘阵列及其在微桥阵列结构中的太赫兹波吸收特性. 周期Ti圆盘阵列结构降低了金属的表面等离子体频率, 在太赫兹波段激发伪表面等离子体激元并实现共振增强吸收. 共振吸收频率由周期、直径等Ti圆盘阵列的结构参数决定, 圆盘厚度则对太赫兹波吸收率有重要影响, 微桥结构中的谐振腔结构可降低共振频率并增强耦合效率. 设计的微桥探测结构以较小的Ti圆盘阵列周期(37 μm)实现突破衍射极限的太赫兹波约束, 在3.5 THz (波长85.7 μm)实现接近90%的太赫兹波吸收率, 满足太赫兹微测辐射热计小尺寸、高吸收及工艺兼容的要求.
关键词: 太赫兹/
微测辐射热计/
伪表面等离子体激元/
严格耦合波分析

English Abstract

全文HTML

--> --> -->

太赫兹(Terahertz, THz)波是指频率在0.1—10.0 THz (波长30 μm—3 mm)范围内的电磁波, 位于毫米波与红外波之间, 是国际上重要的前沿交叉领域. 太赫兹波具有瞬态性、宽带性、低能性、穿透性、光谱特征吸收等很多独特的性质, 因此, 太赫兹技术在安全检测^[1,2]、生物医学^[3,4]、材料化学^[5]、能源环境等领域具有重要的应用价值. 在太赫兹技术开发和应用中, 太赫兹信号的探测具有举足轻重的意义. 目前, 太赫兹探测方法主要基于能够直接测量太赫兹信号的两种效应: 光子效应以及光热效应. 太赫兹光子探测器对太赫兹波的探测通过吸收太赫兹波能量后产生的光电效应来实现, 包括肖特基二极管^[6]、场效应管(FET)^[7]、超导-绝缘体-超导混频器(SIS)^[8]、量子阱(QW)探测器^[9]等. 光子探测器探测灵敏度高, 响应时间短, 但对波长具有选择性, 且往往需要制冷, 制作成本高. 光热探测器通过吸收太赫兹波的能量, 然后转换为电阻率、温度和自发极化强度变化等进行探测, 主要有热释电探测器、测辐射热计和高莱探测器. 其中, 热释电探测器和测辐射热计能够实现室温工作、阵列化、宽光谱的连续太赫兹波探测. 但热释电探测器的制备基于热释电晶体材料(如钽酸锂), 无法与硅基CMOS电路集成, 并且为保障探测性能必须采用厚度很薄的晶体材料^[10]. 微测辐射热计以微桥结构为基本单元, 制备二维焦平面探测器阵列, 通过读取因吸收目标太赫兹波而引起的热敏薄膜电阻变化, 实现太赫兹波探测. 因此, 在集成性、阵列化及成本方面, 微测辐射热计在太赫兹波探测成像领域具有巨大的优势.
由于太赫兹波处于与红外光相邻近的波段, 而微测辐射热计型红外探测器技术已非常成熟. 红外微测辐射热计在太赫兹辐射源的照射下可以用于太赫兹波段的探测与成像^[11-13], 但传统的红外微测辐射热计微桥结构无法对波长较长的太赫兹波进行谐振吸收, 导致器件对目标辐射的吸收极低(< 4%), 难以提供较高的响应与灵敏度^[14]. 因此, 需要增加太赫兹波吸收层. 金属薄膜由于电阻损耗可以吸收太赫兹波, 且具有低热容、高热导及与微桥结构的制备工艺兼容等优点, 成为太赫兹微测辐射热计中吸收材料的首选^[15-17], 表面修饰可进一步提高金属薄膜的有效吸收面积^[18], 但金属薄膜吸收太赫兹波的理论上限仅50%^[19]. 将天线、超材料等吸波结构集成到微桥结构中可有效提高太赫兹微测辐射热计的吸收率. 法国CEA-Leti实验室制备出11 μm高的介质谐振腔结构, 采用多层天线耦合的方法, 显著提高了太赫兹波吸收率和探测灵敏度^[20,21]. 但是, 高谐振腔微桥结构的制备与电学连通实现难度较大, 多层天线结构复杂, 集成性与工艺兼容性有待改善.
在光学波段, 表面等离子体激元(surface plasmon polaritons, SPPs)是金属与介质交界面处自由电子气的集体共振, 能够将电磁波约束在纳米级别的尺寸结构中, 具有克服衍射极限和在亚波长尺寸内操纵光束的能力^[22,23]. 而金属的等离子体频率一般位于可见光和紫外波段, 在微波和太赫兹波段类似于理想导体, 电磁波渗透能力很弱, 所以表面电子和电磁波的相互耦合作用非常微弱, 使得SPPs表面电磁模式变得非常微弱^[24]. 2004年, Pendry等^[25]提出了伪表面等离子体(spoof surface plasmon polaritons, sSPPs)理论, 在金属表面构造周期性的光栅结构和孔洞结构, 等效降低了表面等离子体频率, 光能量通过金属表面产生渗透作用, 达到亚波长约束的效果.
本文将二维周期金属钛(Ti)圆盘结构与太赫兹微测辐射热计微桥结构阵列相结合, 在太赫兹波段激发sSPPS共振增强吸收. 基于严格耦合波(rigorous coupled-wave analysis, RCWA)分析方法, 建立吸收结构模型, 研究圆盘直径、周期、厚度等吸收层结构参数以及真空腔、反射层、支撑层等对太赫兹波吸收特性的影响, 实现对共振吸收频率与太赫兹波吸收率的调制. 基于小的Ti圆盘阵列周期(37 μm), 微桥探测结构在较低的太赫兹频率(3.5 THz)下突破衍射极限, 获得接近90%的太赫兹波吸收率.

微测辐射热计型室温太赫兹探测器阵列由许多MEMS微桥结构的像元在焦平面上二维重复排列构成, 每个像元对辐射进行测量. 其基本原理为: 太赫兹辐射被像元中的吸收层吸收后引起温度变化, 进而使氧化钒热敏电阻的阻值变化; 氧化钒热敏电阻通过MEMS绝热微桥支撑在硅衬底上方, 并通过支撑结构与制作在硅衬底上的COMS读出电路(ROIC)相连; 读出电路将热敏电阻阻值变化转变为差分电流并进行积分放大, 经采样后得到热图像中单个像元的灰度值. 为了提高探测器的响应率和灵敏度, 要求探测器像元微桥具有良好的热绝缘性, 同时为保证成像的帧频, 需使像元的热容尽量小以保证足够小的热时间常数. 本文中室温太赫兹微测辐射热计焦平面阵列的探测单元微桥结构如图1(a)所示. 每个微桥结构由桥面(敏感区域)以及支撑桥面的两条桥腿组成. 细长的桥腿同时用作机械支撑、电学和热学通道. 桥面尽量轻、薄以减小热质量. 桥面层自下而上包括氮化硅(Si₃N₄)支撑层、氧化钒(VO_x)热敏薄膜、钝化层(Si₃N₄)和金属薄膜(Ti)太赫兹波吸收层. 在衬底上制作反射层(Ti), 与桥面之间形成谐振腔(约2 μm), 但由于太赫兹波的波长较长, 该谐振腔并无明显的增强吸收的效果, 在没有太赫兹波吸收层的情况下, 微桥结构的太赫兹波吸收率极低(2.6%—4%). 为了增强太赫兹波的吸收, 在桥面的顶部集成了一层超薄Ti薄膜作为太赫兹波吸收层. 与其他金属薄膜相比, Ti薄膜厚度容易控制且可以通过反应离子刻蚀工艺实现图形化, 具有很好的工艺兼容性.
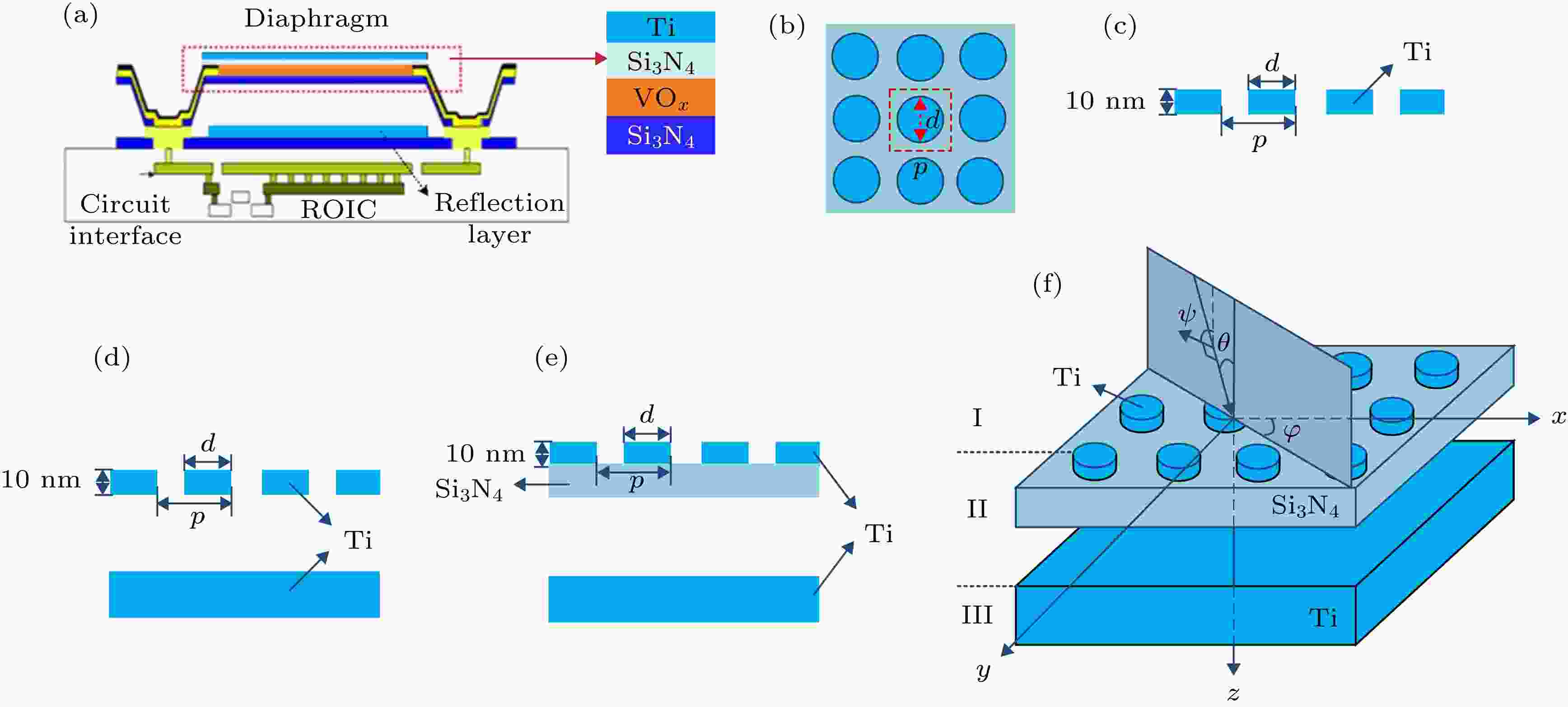图 1 吸收结构图　(a) 太赫兹微测辐射热计焦平面阵列的探测单元微桥结构; (b)二维亚波长Ti圆盘阵列俯视图; (c) 周期Ti圆盘阵列剖面图; (d) 增加反射层的吸收结构; (e) 增加反射层及支撑层的吸收结构; (f) 直角坐标系下的入射平面波与吸收结构模型
Figure1. Absorption structures: (a) Pixel structure of THz microbolometer focal plane array (FPA); (b) top view of a two-dimensional subwavelength Ti disk array; (c) sectional view of a periodic Ti disk array; (d) absorption structure with a reflection layer; (e) absorption structure with reflection layer and supporting layer; (f) absorption structure illuminated by a plane wave with a rectangular Cartesian coordinate system attached.

本文采用简化的结构分析Ti金属薄膜吸收层在微桥结构阵列中的太赫兹波吸收特性. 设计圆盘状Ti金属薄膜并集成到每个微桥单元结构中, 形成周期为p、直径为d的二维亚波长金属圆盘阵列, 其俯视图和剖面图分别如图1(b)和图1(c)所示. 增加反射层与增加反射层及支撑层的吸收结构分别如图1(d)和图1(e)所示. 采用RCWA方法计算并分析不同吸收结构的太赫兹波吸收特性. RCWA方法对计算区域进行严格划分, 并对不同区域的电场和磁场进行傅里叶级数展开以及耦合叠加, 将对Maxwell方程的求解转化成对特征函数的求解, 最后结合边界条件求得问题的本征值^[26,27]. 对于图1中的周期性微结构, RCWA方法能够非常精确且快速地计算出其各级反射、透射以及吸收光谱.
RCWA方法将集成在微桥结构中的Ti金属圆盘阵列看作是两个相互垂直的方向上周期排列的二维光栅^[28]. 吸收结构被划分为三个区域: 区域Ⅰ为入射区域, 其介质为真空, 介电常数为ε_d; 区域Ⅲ为出射区域(光栅基底区域), 对于图1(c)所示的单层Ti金属圆盘阵列, 基底介质为真空, 对于图1(d)和图1(e)所示的吸收结构, 基底材料为金属Ti(反射层); 区域Ⅱ为周期性光栅区域, 对于图1(c)和图1(d)所示的吸收结构, 由金属Ti与真空构成, 对于图1(e)所示的吸收结构, 由金属Ti, Si₃N₄与真空谐振腔构成.
图1(f)为平面波入射到图1(e)所示的吸收结构的立体模型, 在附加的直角坐标系中, x轴和y轴平行于Ti金属圆盘阵列的两个周期方向, z轴垂直于光栅平面. 入射平面波的传播方向由入射角θ, 方位角φ和极化角ψ决定, 光栅区域的电场矢量利用傅里叶级数展开可表示为

$\begin{split} {E_{\rm{g}}}\!\! =\!\!\; & \!\mathop \sum \nolimits_m \!\mathop \sum \nolimits_n\! \left[{S_{xmn}}\left(z \right){e_x} \!+\! {S_{ymn}}\left(z \right){e_y} \!+\! {S_{zmn}}\left(z \right){e_z}\right] \\ &\times{{\rm{exp}}} \left[ - {\rm{j}}\left({{k_{xm}}x + {k_{yn}}y} \right) \right],\end{split}$

其中${k_{xm}} = {k_{x0}}{\rm{sin}}\theta - mK$, ${k_{yn}} = {k_{y0}}{\rm{sin}}\theta - nK$, ${k_{x0}} = {k_{y0}} = k\sqrt {{\varepsilon _{\rm{d}}}} {\rm{sin}}\theta {\rm{cos}}\varphi $, k为波矢, m, n为衍射的级数, K为光栅矢量($K = 2{\text{π}}/p$), ${S_{mn}}\left(z \right)$为第mn级光栅区域谐波场的归一化振幅.
光栅区域的电场振幅满足亥姆霍兹方程, 而且该区域上下边界处的电场与磁场满足连续性边界条件, 即沿边界面的切向方向电场强度(E)与磁场强度(H)连续, 沿边界面法向方向电位移(D)与磁感应强度(B)连续. 求解麦克斯韦旋度方程并利用电磁场边界条件, 可将S_mn(z)表示为特征值的函数^[29]:

${S_{mn}}\left(z \right) = \mathop \sum \nolimits_i {C_i}{w_{imn}}{\rm{exp}}\left({{\lambda _i}z} \right),$

其中λ_i和w_imn为特征值与特征向量, C_i的值取决于边界条件. λ_i和w_imn可通过matlab的eig函数求解4N × 4N矩阵特征值问题得到(N为空间谐波级数, 本文中取N = 20). 利用电磁场表达式匹配边界条件可以得到各级次反射衍射效率r_mn与透射衍射效率t_mn如下:

$\left\{ {\begin{split}& {{r_{mn}} = {{\left| {{R_{mn}}} \right|}^2}{\rm{Re}}\left({\frac{{{k_{1,zmn}}}}{{{k_0}\sqrt {{\varepsilon _{\rm{d}}}} s{\rm{cos}}\theta }}} \right),}\\& {{t_{mn}} = {{\left| {{T_{mn}}} \right|}^2}{\rm{Re}}\left({\frac{{{k_{3,zmn}}}}{{{k_0}\sqrt {{\varepsilon _{\rm{d}}}} s{\rm{cos}}\theta }}} \right),}\end{split}} \right.$

其中R_mn为区域Ⅰ中反射光的归一化电场矢量振幅, T_mn为区域Ⅲ中透射光的归一化电场矢量振幅.

$\begin{split}& {k_{L,zmn}}\left\{ {\begin{aligned}& \sqrt {k_0^2n_L^2 - k_{xm}^2 - k_{xm}^2},~k_{xm}^2 + k_{yn}^2 \leqslant k_0^2n_L^2, \\& - \sqrt {k_{xm}^2 + k_{yn}^2 - k_0^2n_L^2},~k_{xm}^2 + k_{yn}^2 > k_0^2n_L^2,\end{aligned}} \right.\\ & L = 1,3,\end{split}$

其中n_L为L (1或3)区域的折射率, k₀ = ω/c为光在真空中的波数. 最终得到光栅区域的吸收率为

$A = 1 - R - T = 1 - \mathop \sum \nolimits {r_{mn}} - \mathop \sum \nolimits {t_{mn}}.$

Ti在不同频率下的介电常数为${\varepsilon _{{\rm{Ti}}}} = {\left({{n_{{\rm{Ti}}}} + {\rm{i}}{k_{{\rm{Ti}}}}} \right)^2}$, n_Ti与k_Ti值如图2(a)所示^[30]. Si₃N₄材料的${n_{{\rm{S}}{{\rm{i}}_3}{{\rm{N}}_4}}}$与${k_{{\rm{S}}{{\rm{i}}_3}{{\rm{N}}_4}}}$值如图2(b)所示^[31]. 真空谐振腔厚度为2 μm (n_d = 1). 太赫兹波垂直入射到吸收结构上, 则θ = 0, φ = 0, ψ = 90°(TE极化).
图 2 Ti与Si₃N₄的材料参数　(a) Ti在不同频率下的n_Ti与k_Ti值; (b) Si₃N₄在不同频率下的${n_{{\rm{S}}{{\rm{i}}_3}{{\rm{N}}_4}}}$与$ {k_{{\rm{S}}{{\rm{i}}_3}{{\rm{N}}_4}}} $值
Figure2. Material parameters of Ti and Si₃N₄: (a) n_Ti and k_Ti values of Ti at different frequencies; (b) ${n_{{\rm{S}}{{\rm{i}}_3}{{\rm{N}}_4}}}$ and $ {k_{{\rm{S}}{{\rm{i}}_3}{{\rm{N}}_4}}} $ values of Si₃N₄ at different frequencies.

当固定频率的入射电磁波与金属表面的自由电子耦合形成振荡, 沿着交界面方向传播, 并沿着垂直于交界面方向指数衰减, 这种被激发出的电磁波称为表面等离子激元. 在可见光与近红外频段, 金属与介质材料分界面的表面等离子波具有如下色散关系^[32]:

$\beta = {k_x} = {k_0}\sqrt {\frac{{{\varepsilon _{\rm{d}}}{\varepsilon _{\rm{m}}}}}{{{\varepsilon _{\rm{d}}} + {\varepsilon _{\rm{m}}}}}},$

其中β为传播常数, ε_d, ε_m分别为入射区与金属层的介电常数, 金属的介电常数满足Drude模型, k_x为沿x方向的波数. 在太赫兹波段, 金属是良导体, 金属区域的介电常数远远大于介质区域的介电常数, 难以激发出表面等离子激元. 但是周期结构的亚波长金属阵列可以显著降低等离子体频率, 与入射太赫兹波匹配^[33], 产生一种在表面束缚且被增强的电磁波, 称为伪表面等离子激元. 其匹配条件满足

${k_{{\rm{sSPPs}}}} = {k_0}{\rm{sin}}\theta + m{G_x} + n{G_y},$

其中m, n为整数, ${G_x} = {G_y} = 2{\text{π}}/p$, p为x与y方向的金属结构周期. 当垂直入射时, θ = 0°, 则(7)式可简化并得到激发出的伪表面等离子体激元的谐振频率为

${f_{{\rm{sSPPs}}}} = \frac{\omega }{{2{\text{π}}}} = \left({m + n} \right)\frac{c}{p}\sqrt {\frac{{{\varepsilon _{\rm{d}}} + {\varepsilon _{\rm{m}}}}}{{{\varepsilon _{\rm{d}}}{\varepsilon _{\rm{m}}}}}} .$

可见, 入射到周期结构的太赫兹波满足匹配条件即可激发伪表面等离子体激元, 而谐振频率随着周期结构的周期增大而降低.

首先基于RCWA方法计算了如图1(c)所示的单层周期Ti圆盘阵列的太赫兹波吸收特性. 金属圆盘厚度(t)为10 nm, 设置直径(d)为28 μm, 周期(p)为37 μm, 该结构在1.5—8 THz的太赫兹波反射率(R)、透射率(T)与吸收率(A = 1 – R – T)如图3(a)所示. 图3(a)中插图显示了厚度为10 nm的连续Ti薄膜在该频段的太赫兹波反射率、透射率与吸收率. 连续Ti薄膜表现出宽频太赫兹波吸收特性, 但由于反射率较高(> 70%), 吸收率较低(约25%). 当形成二维周期结构后, 在较低的频率处, 周期Ti圆盘阵列具有很高的透射率(约95%). 随着频率增大, 透射率降低, 反射率升高. 吸收率与反射率的变化趋势相似. 在6.5 THz处, 二维周期Ti圆盘阵列结构的等离子体频率与入射太赫兹波满足波矢匹配条件, 激发伪表面等离子体激元, 引起共振吸收, 峰值吸收率约为45%, 此时透射率仅为10%左右. 设置金属圆盘厚度为10 nm, 改变直径(d)与周期(p), 得到在3.5 THz (波长为85.7 μm)下Ti圆盘阵列的太赫兹波吸收率随着直径周期比(d/p)的变化曲线, 如图3(b)所示. 可以看出, 随着周期的增大(35—100 μm), 吸收率总体呈现先增大后降低的规律, 周期略小于波长时可获得最优的吸收率. 当d/p在0.5—0.8之间时, 周期p = 65 μm的Ti圆盘阵列在3.5 THz频率处的吸收率更高; 当d/p为0.9时, 周期p = 85 μm的Ti圆盘阵列具有更高的太赫兹波吸收率. 当周期进一步增大至大于波长(p = 100 μm)时, 吸收率又较低. 这与前述共振吸收频率随着周期增大而降低的结论一致. 在相同的周期下, 随着直径增大(即d/p增大), 圆盘间的间隙减小, 吸收率逐渐增大. 较小的间隙有助于圆盘之间的耦合效应及其与入射光的波矢匹配, 从而实现共振增强吸收.
图 3 单层周期Ti圆盘阵列的太赫兹波吸收特性　(a)周期Ti圆盘阵列的太赫兹波反射率(R)、透射率(T)与吸收率(A)曲线(p = 37 μm, d = 14 μm, t = 10 nm), 插图为厚度10 nm的连续Ti薄膜的太赫兹波反射率(R)、透射率(T)与吸收率(A)曲线; (b)不同直径周期比(d/p)的Ti圆盘阵列在3.5 THz频率处的太赫兹波吸收率
Figure3. Terahertz wave absorption characteristics of single-layer periodic Ti disk array: (a) Terahertz wave reflection (R), transmission (T), and absorption (A) curves for periodic Ti disk arrays (p = 37 μm, d = 14 μm, t = 10 nm), inset: Reflection (R), transmission (T), and absorption (A) curves for a continuous Ti film with a thickness of 10 nm; (b) terahertz wave absorption at 3.5 THz for Ti disk arrays with different ratios of diameter and period (d/p).

图3表明, 要在较低的频率处获得较高的太赫兹波吸收率, 需要Ti圆盘阵列具有较大的周期. 为了满足太赫兹微测辐射热计大阵列、小像元的要求, 固定圆盘阵列的周期(p)为37 μm, 金属Ti薄膜厚度(t)为10 nm, 在圆盘阵列的下方增加真空腔(高度2 μm)与Ti反射层, 如图1(d)所示. 当圆盘直径(d)为28 μm时, 该吸收结构与连续Ti薄膜在不同频率下的太赫兹波反射率、透过率与吸收率如图4(a)所示. 增加反射层之后, 透射率基本为0, 此时, 吸收率A = 1 – R. 当反射率最小时, 吸收率达到最大值. 与单层Ti圆盘阵列结构相比, 吸收峰值频率(共振频率)降低至5 THz, 此时反射率为47%左右, 吸收率达到了50%. 真空腔的引入使太赫兹波吸收率有所增大, 同时降低了吸收结构的等效介电常数, 使得伪表面等离子体共振频率${f_{{\rm{sSPPs}}}}$降低. 而对于连续Ti薄膜, 增加真空腔后仍然具有宽频太赫兹波吸收特性, 但吸收率有所降低, 这是因为Ti反射层增强了太赫兹波的反射导致的.
图 4 带有真空腔、反射层与支撑层的Ti圆盘阵列的太赫兹波吸收特性　(a) 增加真空腔与反射层后连续Ti薄膜与Ti圆盘阵列(p = 37 μm, d = 28 μm)在不同频率下的太赫兹波反射率、透过率与吸收率; (b) 增加支撑层后连续Ti薄膜与不同直径(d)的Ti圆盘阵列(p = 37 μm)在不同频率下的太赫兹波吸收率
Figure4. Terahertz wave absorption characteristics of periodic Ti disk arrays with resonant cavity reflection layer and supporting layer: (a) Terahertz wave reflection (R), transmission (T) and absorption (A) curves for continuous Ti film and periodic Ti disk arrays with resonant cavity and reflection layer (p = 37 μm, d = 28 μm); (b) terahertz absorption curve for continuous Ti film and periodic Ti disk arrays with different diameters (d) and a supporting layer (p = 37 μm).

在实际器件中, Ti圆盘阵列制备在为微桥结构的桥面支撑层上. 因此, 在吸收结构中增加一层Si₃N₄薄膜用作支撑层, 如图1(e)所示. Si₃N₄支撑层的厚度为400 nm, 圆盘阵列的周期(p)为37 μm, 改变圆盘直径, 吸收结构在不同频率下的太赫兹波吸收率如图4(b)所示. 可以看出, 随着圆盘直径的增加, 伪表面等离子体共振频率降低, 且吸收率有所增大. 当圆盘直径d = 34 μm时, 共振吸收频率为3.5 THz, 峰值吸收率达到为55%. 增加了Si₃N₄支撑层后, 增加了谐振腔的高度, 进一步降低了吸收结构的等离子体共振频率. 而随着圆盘直径的增加, 即圆盘间隙减小, 圆盘间的耦合增强, 损耗增大, 吸收率也得到增强.
当改变Si₃N₄支撑层厚度时, 吸收结构(p = 37 μm, d = 34 μm)在不同频率下的太赫兹波吸收率如图5(a)所示. 可以看出, 当Si₃N₄厚度在0.2—0.6 μm之间变化时, 共振吸收频率与峰值吸收率变化不大. 但随着Si₃N₄厚度的增大, 在较低频率处的吸收有明显增强. 在3 THz频率处, Si₃N₄厚度为0.2 μm时, 吸收率仅为33%, 而当Si₃N₄厚度为0.6 μm时, 吸收率增大至54%. 在2.5 THz处, 吸收率从13%增大至30%. 因此, Si₃N₄厚度的增加改善了吸收结构的宽频吸收特性. 但由于Si₃N₄薄膜贡献了微桥探测结构的大部分热容, 且对微桥结构的力学支撑性能有较大影响, 因此, Si₃N₄支撑层的厚度需要折中考虑.
图 5 不同Si₃N₄支撑层厚度与Ti圆盘厚度的吸收结构的太赫兹波吸收特性　(a)不同Si₃N₄支撑层厚度(h)的吸收结构在不同频率下的太赫兹波吸收率(p = 37 μm, d = 34 μm, t = 10 nm); (b)不同Ti圆盘厚度(t)的吸收结构在不同频率下的太赫兹波吸收率, 插图为不同Ti圆盘厚度(t)的吸收结构在3.5 THz下的峰值吸收率(p = 37 μm, d = 34 μm)
Figure5. Terahertz wave absorption characteristics of periodic Ti disk arrays with different thicknesses of supporting layer and Ti disks: (a) Terahertz absorption at different frequencies for absorption structures with different thicknesses (h) of Si₃N₄ support layers (p = 37 μm, d = 34 μm, t = 10 nm); (b) terahertz absorption at different frequencies for absorption structures with different thicknesses (t) of Ti disks; Inset: Peak absorption rate at 3.5 THz for absorbing structures with different thicknesses (t) of Ti disks (p = 37 μm, d = 34 μm).

为了得到金属层厚度对太赫兹波吸收率的影响, 研究了具有不同厚度Ti圆盘阵列的吸收结构在不同频率下的太赫波吸收率, 如图5(b)所示. Ti圆盘阵列的周期为37 μm, 圆盘直径为28 μm. 可以看出, 当Ti圆盘阵列的厚度变化时, 吸收结构的共振吸收频率保持不变(3.5 THz), 这说明共振吸收频率与金属圆盘厚度无关, 仅由圆盘阵列周期、直径以及支撑层厚度等吸收结构参数决定. 图5(b)中插图显示了峰值吸收率随着Ti圆盘阵列厚度的变化曲线, 表明当Ti圆盘阵列厚度从10 nm开始增大时, 峰值吸收率先增大, 在厚度为40 nm时达到最大值(86%), 然后开始有所下降, 这是因为其反射率增大引起的. 改变Ti圆盘阵列厚度可以调节吸收结构的等效阻抗, 当其等效阻抗与自由空间阻抗相匹配时, 所有入射光被限制在吸收结构中, 反射率基本为0, 从而获得很高的吸收率. 从图5(b)还可以看出, Ti圆盘阵列厚度的增大会显著降低在较高频率处的吸收率, 使得吸收峰变窄.
为了证明集成在微桥结构中的Ti圆盘阵列对太赫兹波的增强吸收作用, 计算了吸收结构中的场分布. 假设入射太赫兹波为垂直入射的TE波(由于吸收结构在x, y方向的对称性, 对入射波没有偏振选择性), Ti圆盘阵列的周期为37 μm、直径为34 μm、厚度为40 nm, Si₃N₄支撑层厚度为400 nm, 真空腔高度为2 μm, 反射层厚度为200 nm, 该吸收结构在峰值吸收频率处(3.5 THz, 如图5(b))的电场分布如图6(a)与图6(b)所示. 图6(a)为yz平面的电场分布, 表明电场主要分布在Ti圆盘阵列层表面; 图6(b)为xy平面的电场分布, 可以看出电场主要分布在Ti圆盘边缘与圆盘之间. 这与亚波长周期金属结构在太赫兹波段激发伪表面等离子体激元的特性相符. 太赫兹波能量被限制在Ti圆盘阵列层, 形成伪表面等离子体共振, 并因为Ti金属薄膜的欧姆损耗而被吸收. 同时, 支撑层、真空腔、反射层与Ti圆盘阵列层形成谐振腔结构, 进一步增强了太赫兹波与Ti圆盘阵列吸收层的相互作用, 使得在较低频率处获得了高太赫兹波吸收率.
图 6 共振吸收频率(3.5 THz)下吸收结构的电场分布　(a) yz平面上吸收结构的电场分布; (b) xy平面上吸收结构的电场分布(p = 37 μm, d = 34 μm, t = 40 nm)
Figure6. Electric field distribution of the absorption structure at the resonance absorption frequency (3.5 THz): (a) Electric field distribution in the yz plane; (b) electric field distribution in the xy plane (p = 37 μm, d = 34 μm, t = 40 nm).

本文将二维周期Ti圆盘阵列集成在微桥结构中, 以增强太赫兹微测辐射热计的吸收率. 基于RCWA方法, 研究了Ti圆盘阵列及其在微桥阵列结构中的太赫兹波吸收特性, 探讨了微桥结构与周期Ti圆盘层尺寸参数对太赫兹波吸收的影响. 研究表明, 通过构造周期圆盘结构, 可以有效降低金属的表面等离子体频率, 实现伪表面等离子体共振增强吸收. 共振吸收频率由结构的几何参数(周期、间隙)决定, 通过改变结构参数可以激发不同频段的表面等离子体激元. 支撑层、真空腔与反射层的引入进一步降低了共振频率并增强了耦合效率. 当Ti圆盘阵列的周期为37 μm、直径为28 μm、厚度为40 nm时, 微桥吸收结构在3.5 THz (波长85.7 μm)获得接近90%的吸收率. 本文突破衍射极限, 以小尺寸的吸收结构实现亚波长太赫兹波约束, 为太赫兹微测辐射热计探测器提供了一种简单高效、工艺兼容的增强吸收与探测性能的方法.