摘要: 体点导热问题是电子器件散热优化方面的基础问题之一, 已有研究大多建立在傅里叶导热定律的基础上, 但随着电子器件的特征尺度降低到微纳米量级, 导热优化需要考虑非傅里叶效应. 本文结合声子玻尔兹曼方程的数值解和对声子平均自由程进行插值的固体各向同性材料惩罚方法, 发展了微纳米尺度下弹道-扩散导热的拓扑优化方法. 在弹道-扩散导热机制下, 体点导热的拓扑优化得到的材料分布明显不同于扩散导热下的树状分布, 且会随努森数的变化而变化, 与拓扑优化的插值方式和声子弹道输运有关. 随着弹道效应的增强, 尺寸效应使得材料分布中微小结构的等效热导率低于粗壮结构, 因而拓扑优化结果朝着增多粗壮结构、减少微小结构的方向发展. 弹道效应足够强时, 填充材料聚集在低温边界附近, 主干和枝合并, 呈团状分布.
关键词: 体点导热 /
拓扑优化 /
微纳尺度 /
声子玻尔兹曼输运方程 English Abstract Topology optimization of the volume-to-point heat conduction problem at micro- and nano-scale Li Han-Ling Cao Bing-Yang Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 51825601, 51676108, 51621062).Received Date: 15 June 2019Accepted Date: 16 August 2019Available Online: 01 October 2019Published Online: 20 October 2019Abstract: The volume-to-point (VP) heat conduction problem is one of the fundamental problems of cooling for electronic devices. The existed reports about the VP problem are mainly based on the Fourier’s law which works well at the macroscopic scale. However, the length scale of modern electronic devices has reduced to micro- and nano-scale, at which optimization methods that are capable of dealing with the non-Fourier heat conduction are desired now. In this paper, phonon Boltzmann transport equation (BTE) and solid isotropic material with penalization (SIMP) method are coupled to develop a topology optimization method for ballistic-diffusive heat conduction. Phonon BTE is transformed into equation of phonon radiative transport, which is solved by the discrete ordinate method. To realize the topology optimization, SIMP method is adopted to penalize the phonon extinction coefficient, which equals to the reciprocal of phonon mean-free-path, and an explicit constraint on the global gradient of the nominal material density is used to ensure the solutions being well-posed and mesh-independent. By using the developed topology optimization method, it is found that the optimal material distributions for the VP problem in ballistic-diffusive heat conduction significantly deviate from the traditional tree-like structure obtained in diffusive heat conduction, and the results vary with the Knudsen number (Kn ). This is related to the different coefficient interpolation ways in the SIMP method and phonon ballistic transport. When Kn → 0, instead of converging to the conventional tree-like structure which fully stretches into the interior zone, the new method gradually produces the result obtained by the topology optimization which interpolates the reciprocal of the thermal conductivity in diffusive heat conduction. As Kn increases, the high thermal-conductive filling materials show a trend to gather around the low-temperature boundary, and there are more thick and strong trunk structures, less tiny and thin branch structures in the optimized material distributions. In addition, the ratio of the optimized average temperature to the value of the uniform material distribution $\left( {T_{{\rm{ave}},{\rm{opt}}}^{\rm{*}}/T_{{\rm{ave}},{\rm{uni}}}^{\rm{*}}} \right)$ also increases. The dependence of the topology optimization results on Kn can be attributed to the size effect of the thermal conductivity caused by phonon ballistic transport. In the diffusive heat conduction, filling materials with different length scales have the same efficiency to build high thermal-conductive channels. However, with ballistic effect enhancing, size effect makes the effective thermal conductivities of the branch structure lower than those of the trunk structure, as the former is smaller than the latter. As a result, the branch structures are less efficient compared with the trunk structures in terms of building high thermal-conductive channels, and the optimal material distributions have more trunk structures and fewer branch structures. When the ballistic effect becomes significant enough, say at Kn = 0.1, the topology optimization gets a dough-like material distribution in which branches merge into trunks. The proposed topology optimization method have the potential to provide guidance in designing nanoscale electronic devices for improving the heat dissipation capability.Keywords: volume-to-point heat conduction problem /topology optimization /micro- and nano-scale /phonon Boltzmann transport equation 全文HTML --> --> --> 1.引 言 以芯片为代表的电子器件, 在当代社会中扮演着不可替代的重要角色. 随着电子器件向小型化、集成化的方向发展, 器件的特征尺寸已经降低至微纳米量级[1 ] , 器件内的功率密度大幅增加. 2012年, 芯片内的平均热流密度便已达到250 W/cm2 左右[2 ] . 高功率密度会让电子器件温度升高, 产生局部热点, 导致其可靠性和寿命显著下降[3 ] . 因此, 电子器件的热管理已经成为相关领域发展面临的关键挑战之一[4 —7 ] . 根据电子器件内热点分布和传热结构布局等因素, 进行散热仿真和优化改进, 对实际产品的设计和制造有着重要意义.[8 ] , 如图1 所示. 给定体积的区域代表芯片, 区域内的均匀内热源代表焦耳加热, 产生的热量通过边界处一小段温度为${T_0}$ 的低温热沉流出, 其余边界绝热. 现提供数量有限的高导热填充材料, 希望寻找合适的填充材料分布方式, 构造高导热通道, 让整个系统的温度(平均温度或最高温度)降到最低. 关于体点导热问题, 人们采用多种优化方法进行了研究, 包括构型理论[8 ] 、仿生优化[9 ] 、拓扑优化[10 —13 ] 、模拟退火和遗传算法[14 ] 等. 尽管这些方法都能有效降低系统温度、提高散热能力, 但所得的高导热填充材料分布方式不尽相同, 这与优化问题自身带有的局部最优性和多解性有关. 当优化问题改变时, 不同方法的性能优劣也可能发生变化. 在各类优化方法中, 拓扑优化方法因其能够改变结构的拓扑构型、具备理论上的最高设计自由度而受到人们的青睐. 利用拓扑优化, 设计者不仅可以实现设计对象某方面性能的显著提升, 而且所花费的设计时间更少, 能得到传统经验之外的具有启发性的新结果[15 ] . 体点导热问题的拓扑优化会得到填充材料充分伸入内部区域、整体呈树状的材料分布, 其散热性能明显优于其他方法所预测的结构[11 ] .图 1 体点导热问题示意图Figure1. The schematic diagram of the VP problem.[13 ] , 这在宏观尺度下是合理的, 但对微纳米尺度下的导热过程, 傅里叶导热定律不再成立[16 —22 ] , 热仿真及热优化必须考虑非傅里叶效应. 声子是电子器件半导体中的主要载热子[23 ] , 声子弹道输运和声子相干是微纳米尺度下发生非傅里叶导热的两个重要原因[5 ] . 声子弹道输运的强度可由努森数$Kn$ 来表征, 其定义为材料声子平均自由程l 和系统特征尺寸L 的比值, 即$Kn = l/L$ . 宏观尺度下, 系统尺寸远大于声子平均自由程($Kn \to 0$ ), 声子间散射充分, 声子按扩散方式传递, 导热过程遵循傅里叶导热定律. 但当系统尺寸与声子平均自由程相当($Kn \sim 1$ )甚至更小($Kn < 1$ )时, 声子不经历散射而直接抵达边界, 这样的过程称为弹道输运, 会导致傅里叶导热定律失效[24 ] . 在微纳米结构中, 部分声子发生弹道输运, 其余声子仍按扩散方式运动, 对应的导热机制称为弹道-扩散导热[25 ,26 ] . 声子弹道输运会引起热导率的尺寸效应, 表现为系统的等效热导率与系统尺寸正相关, 尺寸减小会造成等效热导率降低[27 ,28 ] , 系统热点温度升高[29 ] . 此外, 在给定温度边界处, 由于弹道输运的非平衡本质, 边界处的温度并不连续, 会出现温度跳跃现象[30 ,31 ] . 声子相干则主要出现在特征尺寸和声子波长相当的系统中[32 ] , 例如石墨烯这样的二维材料和超晶格这样的特殊结构[33 —35 ] . 声子相干通过改变声子群速度、弛豫时间和态密度等因素来影响导热过程[36 ] . 对常用的半导体材料硅, 室温下声子平均自由程约为300 nm[37 ] , 声子波长小于10 nm[17 ] , 而目前大多数电子器件的特征尺寸在100 nm量级[1 ] , 故本文主要关注声子弹道输运引起的非傅里叶导热. 关于微纳米尺度下弹道-扩散导热过程的优化, 前人曾结合动力学理论和拓扑优化来处理[38 ] , 但其优化目标只是特定点之间的温差, 无法考虑系统整体的温度. 目前, 尚缺少适用于微纳米尺度下弹道-扩散导热过程的一般性优化方法, 关于弹道效应对优化结果的影响也缺乏系统的认识.$Kn$ 的变化而变化, 这与SIMP方法的插值方式和声子弹道输运有关.2.优化方法 22.1.声子玻尔兹曼输运方程 2.1.声子玻尔兹曼输运方程 声子的运动规律符合声子BTE, 稳态、弛豫时间近似下的声子BTE写作f 是声子分布函数; ${{{v}}_{\rm{g}}}$ 是群速度矢量; ${f^0}$ 是平衡态声子分布函数, 即玻色-爱因斯坦分布; $\tau $ 是弛豫时间. 联合求解(1 )式和能量守恒方程, 就可以获得声子的微观运动规律和分布函数, 进一步可计算得到温度、热导率等宏观热性质.[39 —41 ] 来求解声子BTE, 此方法最早用于辐射输运方程的求解, 相关计算方法的发展较为成熟. 根据声子和光子的类比, 可定义声子辐射强度$I =\!\displaystyle \sum \!\!{\displaystyle\int {{v_{\rm{g}}}f\hbar \omega D\left( \omega \right)} {\rm{d}}\omega } $ , 其中$\omega $ 表示声子频率, $D\left( \omega \right)$ 表示态密度, “$\displaystyle\sum $ ”表示对声子极化的求和. 利用此定义, 可以将声子BTE转化为声子的辐射输运方程(equation of phonon radiative transfer, EPRT)[42 ] s $\kappa = 1/l$ 为声子消光系数, ${I_0} = \displaystyle\sum {\displaystyle\int {{v_{\rm{g}}}{f^0}\hbar \omega D\left( \omega \right)} {\rm{d}}\omega } $ 是声子平衡态辐射强度. DOM解EPRT的基本思路是[18 ] : 假设I 在某个立体角单元内不随方向变化, 则整个立体角空间可被划分为多个控制角度, 每个控制角度对应的单位方向矢量是${{{s}}_i}$ , 每个离散方向上的EPRT可写作${{{s}}_i} \cdot $ $\nabla {I_i} = \kappa \left( {{I_0} - {I_i}} \right)$ , 求解此式可得不同方向的辐射强度${I_i}$ , 再利用加权求和得到$\displaystyle\int {I{\rm{d}}\varOmega } = \sum\nolimits_{i = 1}^N {{w_i}{I_i}}$ , 其中${\rm{d}}\varOmega $ 表示立体角的微分, ${w_i}$ 是与角度划分方式相对应的权系数, N 是控制角度的总数. 稳态下, 含内热源的能量守恒方程为$\nabla \cdot {{q}} = {\dot q_{\rm{s}}}$ , 其中${{q}}$ 是热流密度矢量, ${\dot q_{\rm{s}}}$ 是单位体积的内热源功率. 利用热流密度和声子辐射强度的关系, 最终得到DOM求解EPRT的导热方程组为3 )式中包含N + 1个等式, 与未知的声子辐射强度数量相对应, 方程组封闭.[43 ] , 而如何在这样的非平衡态下定义温度一直存在争议[44 ] . 本文采用等效平衡温度的概念[45 ,46 ] , 认为空间内某个离散单元在发射能量时, 产生的声子服从玻色-爱因斯坦分布, 根据发射能量反解出的分布函数中的温度, 便是等效平衡温度. 使用DOM离散辐射强度后, 等效平衡温度的计算式为$4{\sigma _{{\rm{phonon}}}}{T^4} =$ $ \displaystyle\sum\nolimits_{i = 1}^N {{w_i}{I_i}} $ , 其中${\sigma _{{\rm{phonon}}}}$ 是声子斯特藩-玻尔兹曼参数[47 ] . 使用这种等效平衡温度的好处是, 在接近扩散导热时, 解声子BTE所得结果能够与傅里叶导热定律的结果相吻合[39 ] .2.2.拓扑优化 -->2.2.拓扑优化 拓扑优化本质上属于大规模0—1整数规划问题, 区域内的每个点要么是空洞, 要么是实体. 这样的离散优化问题在数学上是病态的, 解的存在性、收敛性以及求解算法的实现都存在着巨大的困难[48 ] . 实现拓扑优化的关键是对优化问题进行适当的正则化处理, 将设计变量由离散的变为连续的, 从而能够直接使用针对连续设计变量优化问题的求解方法. 在这方面, SIMP方法[49 ] 是经典而常用的技巧, 其核心思想是将材料性质设定为关于相对密度的幂函数, 从而将设计变量转变为连续的相对密度. 考虑到(2 )式作为描述非傅里叶导热的本构方程, 仅有声子消光系数$\kappa $ 是与材料类型有关的性质[38 ] , 于是本文提出对$\kappa $ 进行插值的SIMP方法来实现拓扑优化. 空间中任意位置的消光系数写作$\rho $ 是值在[0, 1]区间上连续分布的相对密度变量; ${\kappa _{\rm{s}}}$ 和${\kappa _{\rm{f}}}$ 分别是基底材料和填充材料的消光系数, 亦即各自声子平均自由程的倒数; p 是值大于1的惩罚因子. 惩罚因子的作用是在优化过程中对介于0和1之间的中间密度值进行惩罚, 使得$\rho $ 的值逐渐趋向于0和1两个端点值, 从而在优化结果中得到清晰的空洞($\rho = 0$ )和实体($\rho = 1$ )分布. 关于SIMP方法插值方式的选择, 将在下一节结合优化结果做进一步讨论.[50 ] . 为了得到可靠的优化结果, 需要引入更多的正则化处理以抑制数值不稳定性. 本文采用对相对密度变量$\rho $ 的全局梯度施加显式约束的方法[15 ] , 即在目标函数中增加关于$\rho $ 的全局梯度的权重惩罚项, 以约束$\rho $ 的变化程度. 至此, 可写出通过求解EPRT来获得温度分布的二维体点导热拓扑优化的数学模型为:${T_{{\rm{ave}}}}$ 是系统平均温度, ${T_{{\rm{ave}},{\rm{ref}}}}$ 是人为选取的参考温度, $\alpha $ 是相对密度变量全局梯度的权重系数, $\overline {\nabla \rho } $ 是无量纲的相对密度变量梯度, $A = {a^2}$ 是二维区域的面积, $\phi $ 是预先给定的高导热填充材料占整个区域的比例. 对平均温度和设计变量梯度进行无量纲化的目的是使二者通过线性求和构成实际的目标函数g . 现在的模型以降低系统平均温度为优化目标, 如果目标是减小系统的最高温度, 则可以将优化对象变更为文献[51 ]中提到的几何平均温度, 其他设置不变. 需要说明的是, 因为本文的关注点是如何在导热优化中考虑声子弹道输运并分析弹道输运对优化结果的影响, 所以优化模型中并未考虑不同材料之间的界面热阻, 这样可以更直观地反映弹道效应的影响. 界面热阻对现有优化结果的影响将在第3节中进行讨论.5 )式的拓扑优化的流程图如图2 所示, 包括以下步骤: 1)初始化, 对区域进行离散并任意给定一组$\rho $ 的初始值; 2)系统重分析, 根据SIMP方法插值得到当前设计点对应的消光系数, 再求解EPRT和稳态能量守恒方程获得声子辐射强度, 进而计算平均温度和目标函数; 3)灵敏度分析, 计算目标函数和约束函数对设计变量的导数; 4)优化求解, 根据导数信息, 确定满足约束且减小目标函数的设计变量演化方向(可行下降方向), 并计算最佳步长, 更新当前设计变量值; 5)收敛判断, 满足收敛条件时结束迭代, 输出结果; 否则重复步骤2)—4).图 2 体点导热拓扑优化的流程图Figure2. The flow chart of topology optimization for the VP problem.3.结果与分析 在体点导热问题中, 设置低温边界与区域边长的比值为$c/a = 0.1$ , 低温边界的温度为${T_0} = 300\;{\rm{K}}$ , 填充材料体积占比为$\phi = 0.1$ , 设计变量初始值取为$\rho = \phi $ , 即材料均匀分布. 定义无量纲空间坐标为$X = x/a$ , $Y = y/a$ , 参考文献[12 ]定义无量纲温度${T^*} = \dfrac{{{k_{\rm{s}}}\left( {T - {T_0}} \right)}}{{{a^2}{{\dot q}_{\rm{s}}}}}$ , 其中${k_{\rm{s}}}$ 是基底材料热导率, 这样无量纲化的好处是消除了内热源功率、热源面积、热导率和边界温度具体值对优化结果的影响, 使填充材料和基底材料间导热性能差异成为优化结果的决定因素. 在数值计算中, 用数量为$n \times n$ 的方形网格离散计算域, 网格尺寸为$h = a/n$ . DOM的离散方向数设定为$N = 24$ , 此值既能避免求解温度场时出现过强的“射线”效应[41 ] , 又不至于让计算量过大. 参考文献[52 ], 相对密度变量梯度的无量纲化方式为$\overline {\nabla \rho } = h\nabla \rho $ , SIMP方法的惩罚系数取经典值$p = 3$ . 为了提高求解效率, 对声子BTE使用灰体近似, 迭代过程中的灵敏度分析使用伴随方法[53 ] , 优化求解则采用构造原问题局部近似模型的移动渐进方法(method of moving asymptotes, MMA)[54 ] . 收敛准则设定为$\left| {{\rho ^j}} \right|/$ $\left| {{\rho ^{j - 1}}} \right| \leqslant 0.001$ , 其中上标j 表示迭代次数, 认为满足此条件时设计变量、目标函数值都达到稳定. 考虑到大部分区域为基底材料, 用基底材料的平均自由程来计算努森数, 即$Kn = {l_{\rm{s}}}/a$ .3.1.扩散导热的体点优化 3.1.扩散导热的体点优化 在进行求解声子BTE的拓扑优化之前, 先在傅里叶定律适用的条件下实现体点导热的拓扑优化, 以检验所发展的拓扑优化方法. 尽管凡是在实体和空材料间构造连续函数并对中间密度值进行惩罚的方法都可称为SIMP方法, 但通常都是对本构方程的系数进行插值[15 ] . 对基于傅里叶定律的拓扑优化, 本构方程中与材料性质有关的系数是热导率, 对应SIMP方法的插值公式为$k\left( \rho \right) = {k_{\rm{s}}} + $ $ \left( {{k_{\rm{f}}} - {k_{\rm{s}}}} \right){\rho ^p}$ , 其中${k_{\rm{f}}}$ 是填充材料热导率. 此时, 填充材料和基底材料导热能力的差异通过热导率比${k_{\rm{f}}}/{k_{\rm{s}}}$ 来体现, ${k_{\rm{f}}}/{k_{\rm{s}}}$ 越大, 传导同样热量所需要的高导热材料横截面积越小, 因而在相同的填充量下填充材料能够更远地延伸到区域内部, 形成的树状结构的“树枝”更为细长, 优化效果也更好[12 ] . 对本文提出的优化模型, 本构方程中与材料性质有关的系数是声子消光系数$\kappa $ , 对应的插值公式为(4 )式. 根据动力学理论, 热导率和声子平均自由程间的关系为$k = \dfrac{1}{3}C{v_{\rm{g}}}l$ , 其中$C$ 是材料比热, ${v_{\rm{g}}}$ 是声子群速度的大小. 材料的比热、群速度通常是确定的, 于是有${k_{\rm{f}}}/{k_{\rm{s}}} \propto {l_{\rm{f}}}/{l_{\rm{s}}}$ , 意味着不同材料导热性能的差别主要源自声子平均自由程的差别[55 ] . 此时(4 )式中关于声子消光系数$\kappa $ ($ = {l^{ - 1}}$ )的插值, 对应于傅里叶导热定律下对热导率倒数${k^{ - 1}}$ 的插值, 而非传统的对热导率k 的插值. 在${k_{\rm{f}}}/{k_{\rm{s}}} = 500$ , $\alpha = 0.05$ , $n = 80$ 的条件下, 分别对k 和${k^{ - 1}}$ 进行插值, 基于傅里叶导热定律的拓扑优化得到的结果如图3 所示. 设定${k_{\rm{f}}}/{k_{\rm{s}}} = 500$ 是为了让填充材料和基底材料的导热能力存在较大差异, 更直观地体现优化的效果, 且实际电子器件中绝缘材料和导电材料的热导率通常也相差2个数量级[1 ] . 文献中关于傅里叶导热定律下体点导热拓扑优化的研究也大多采用此热导率比值. 图3 左侧表示$\rho $ 在区域内的分布情况, 白色代表基体材料($\rho = 0$ ), 黑色表示填充材料($\rho = 1$ ), 颜色越深意味着该位置的$\rho $ 值越接近于1; 右侧则是无量纲温度${T^*}$ 的分布. 插值k 的拓扑优化得到了充分伸入内部区域、含多个分岔和枝的树状填充材料分布, 如图3(a) 所示, 符合文献[10 —13 ]中的结果, 对应的无量纲温度平均值是$T_{{\rm{ave}}}^* = 0.021$ . 插值${k^{ - 1}}$ 的优化结果则由图3(b) 给出, 填充材料集中在区域下半平面, 与低温边界相接触, 向区域内伸展的过程中只形成了2处分岔, 此时$T_{{\rm{ave}}}^* = 0.113$ . 与图3(a) 相比, 图3(b) 中填充材料的主干更短、更宽, 枝数量更少, 对应的平均温度和最大温度更高. 在扩散导热条件下, 不同形状、尺寸的填充材料热导率相等, 具有相同的构建高导热通道的能力. 为了降低温度, 填充材料要设法伸入内部区域, 缩短高导热通道和区域内热源间的距离, 所以图3(a) 的结果要比图3(b) 更好. 受制于SIMP方法的插值方式, 图3(b) 得到的是体点导热优化的某个局部最优解, 但填充材料仍然有向区域内伸展的趋势. 图3 的结果表明, SIMP方法的插值方式会影响拓扑优化的效果, 对本构方程的系数进行插值是更合理的选择. 以傅里叶导热定律为例, 尽管插值${k^{ - 1}}$ 的拓扑优化也能收敛, 但对应的是优化问题的某个局部最优解, 优化效果不如插值k 的结果好. 类似地, 当导热的本构方程变成(2 )式时, SIMP方法应当对方程的系数$\kappa $ 进行插值.图 3 扩散导热下不同插值方式对材料分布和温度分布的影响 (a)插值k ; (b)插值${k^{ - 1}}$ Figure3. The effect of interpolation ways on the material distributions and temperature distributions in diffusive heat conduction: (a) Interpolating k ; (b) interpolating ${k^{ - 1}}$ .$\alpha $ 的取值也很重要, 因为$\alpha $ 显著响着拓扑优化解的数值稳定性[15 ] . 保持${k_{\rm{f}}}/{k_{\rm{s}}} = 500$ 不变, 并使用对k 的插值, 扩散导热条件下拓扑优化得到的填充材料分布随$\alpha $ 和n 的变化如图4 所示. 整体来看, 填充材料的形状都呈树状, 与图3(a) 的结果大致相同, 但细节上存在不少差异. 当$\alpha = 0$ 时, 随着网格密度的增大, 高导热通道的主干周围会出现越来越多狭长的末梢, 这是因为拓扑优化的数值解天然地存在着网格依赖性. 当$\alpha = 0.05$ 时, 由于引入了对设计变量全局梯度的约束, 拓扑优化结果的网格依赖性得到有效抑制, 网格细化并未导致太多狭长末梢. 进一步增大到$\alpha = 0.1$ , 不同网格密度下拓扑优化结果间的差异更小, 网格无关性更好. 但是, 比较相同网格密度的拓扑优化结果发现, 增大$\alpha $ 的值后, 中间密度值对应的灰色区域增多, 填充材料和基底材料之间的边界变得模糊, 这是控制设计变量全局梯度的代价. 综合考虑后, 本文的拓扑优化选择$\alpha = 0.05$ , $n = 80$ , 此时所得结果具有较好的网格无关性和较清晰的材料边界, 且计算量相对较少.图 4 扩散导热下拓扑优化得到的材料分布随$\alpha $ 和n 的变化Figure4. The material distributions obtained by topology optimization in diffusive heat conduction varying with $\alpha $ and n .3.2.弹道-扩散导热的体点优化 -->3.2.弹道-扩散导热的体点优化 根据上文确定的参数设置, 对(5 )式进行数值迭代, 获得了体点导热在弹道-扩散导热机制下的拓扑优化解. 设定${l_{\rm{f}}}/{l_{\rm{s}}} = 500$ 以便和傅里叶导热定律下的结果对比, 不同$Kn$ 下优化得到的材料分布和温度分布如图5 所示. 总体来看, 填充材料集中在区域下半平面, 与低温边界充分接触, 其形状完全不同于图3(a) 所示的伸入内部区域且含多个枝的树状结构, 而与图3(b) 的材料分布更为接近. 如3.1 节所述, 本文采用的插值$\kappa $ 的方法, 对应于傅里叶定律下对${k^{ - 1}}$ 的插值, 因而优化结果与插值${k^{ - 1}}$ 的结果相似. 可以预见的是, 在$Kn \to 0$ 时, 导热过程接近纯扩散导热, 优化会趋向于傅里叶定律下插值${k^{ - 1}}$ 的结果. 但受声子弹道输运的影响, 图5 与图3(b) 仍然存在明显的差异. 当$Kn = 0.002$ 时, 低温边界处几乎无温度跳跃, 区域内无量纲温度的最大值$T_{\max }^* = 0.29$ , 略高于图3(b) 中的0.23, 表明大部分声子以扩散方式导热, 但仍有部分声子发生了弹道输运, 这是因为填充材料的声子平均自由程已和区域尺寸相当(${l_{\rm{f}}} \sim a$ ). 此时填充材料在低温边界处连通, 主干呈“U”型, 两侧共有6处外凸的细枝. 增大$Kn$ 至0.01, 靠近低温边界处${T^*} = 0.06$ , 发生了一定的温度跳跃, $T_{\max }^*$ 则是0.44, 约为图3(b) 结果的2倍, 表明弹道效应增强. 此时填充材料分布的“U”形主干开口变大、宽度变厚, 枝数量减少为2个. 当$Kn = 0.1$ 时, 填充材料的体声子平均自由程已比区域尺寸大一个数量级, 边界处无量纲温度的跳跃值接近0.6, 区域内峰值温度($T_{\max }^* = 1.76$ )几乎是图3(b) 结果的6倍, 弹道效应已十分显著. 此时, 填充材料聚集在低温边界附近, 除了顶部有凹陷外, 其它方向的伸展长度基本一致, 主干和枝合并形成团状分布.图 5 弹道-扩散导热下拓扑优化的材料分布和温度云图随$Kn$ 的变化 (a) Kn = 0.002; (b) Kn = 0.01; (c) Kn = 0.1Figure5. The topology optimization obtained material distributions and temperature distributions varying with Kn in ballistic-diffusive heat conduction: (a) Kn = 0.002; (b) Kn = 0.01; (c) Kn = 0.1.图3 和图5 中出现的5种材料分布进行热仿真, 得到的$T_{{\rm{ave}}}^*$ 值列于表1 , 括号内的数据表示$T_{{\rm{ave}}}^*/T_{{\rm{ave}},{\rm{uni}}}^*$ 的值, 即相对于材料均匀分布时$T_{{\rm{ave}}}^*$ 的变化程度. 表1 显示, 不同努森数下, 本文发展的拓扑优化方法所对应的$T_{{\rm{ave}}}^*$ 值最低, 如表中加粗数据所示, 表明所预测的材料分布方式确实是最优的, 验证了声子BTE和拓扑优化相结合的优化方法的正确性. 以$Kn = 0.1$ 时为例, 解傅里叶定律的拓扑优化所得的材料分布, 对应的$T_{{\rm{ave}}}^*/$ $T_{{\rm{ave}},{\rm{uni}}}^*$ 值大概为80%, 而解声子BTE的拓扑优化得到的材料分布, 对应的$T_{{\rm{ave}}}^*/T_{{\rm{ave}},{\rm{uni}}}^*$ 值在70%左右, 进一步下降了10个百分点, 其中又以$Kn = 0.1$ 条件下的拓扑优化所得的构型效果最好, $T_{{\rm{ave}},{\rm{opt}}}^*/$ $T_{{\rm{ave}},{\rm{uni}}}^* = 69.9\% $ . 此外, 对相同的材料分布方式, 随着$Kn$ 的增大, $T_{{\rm{ave}}}^*/T_{{\rm{ave}},{\rm{uni}}}^*$ 的值增大, 表明添加高导热材料所能带来的优化效果变差. 例如对图3(a) 所示的树状结构(扩散导热条件下插值k 的拓扑优化结果), $Kn = 0.002$ 时, $T_{{\rm{ave}}}^*/T_{{\rm{ave}},{\rm{uni}}}^*$ 是33.7%, 但$Kn = 0.01$ 时此值上升到53.2%, $Kn = 0.1$ 时只有86.0%. 图5 和表1 的结果共同表明, 弹道-扩散导热机制下, 体点导热问题的最佳材料分布会随着弹道效应强度的变化而变化, 基于傅里叶定律的拓扑优化所得的材料分布不再是最优的. 因此, 对微纳米尺度下的散热优化问题, 在设计阶段必须要考虑声子弹道输运的影响. 值得一提的是, 如果将现有优化模型中对$\kappa $ 的插值改为对其倒数l 的插值, 优化模型的收敛性会严重恶化, 材料分布会出现严重的棋盘格问题和大量的中间密度值.Kn $T_{{\rm{ave}}}^*$(括号内数据为$T_{{\rm{ave}}}^*/T_{{\rm{ave}},{\rm{uni}}}^*$) 均匀分布 分布1 分布2 分布3 分布4 分布5 0.002 0.98(100.0%) 0.33 (33.7%) 0.21 (21.4%) 0.11 (11.2%) 0.12 (12.2%) 0.21 (21.4%) 0.01 1.07(100.0%) 0.57 (53.2%) 0.41(38.3%) 0.30 (28.0%) 0.29 (27.1%) 0.33 (30.8%) 0.1 2.29(100.0%) 1.97 (86.0%) 1.84 (80.3%) 1.64 (71.6%) 1.62 (70.7%) 1.60 (69.9%) 注: 分布1和2分别是扩散导热条件下插值k 的拓扑优化结果、插值${k^{ - 1}}$的拓扑优化结果, 分布3—5分别是弹道-扩散导热条件下$Kn$为0.002, 0.01, 0.1时的拓扑优化结果.
表1 不同材料分布在不同努森数下对应的无量纲温度平均值Table1. The average dimensionless temperature of different material distributions at different Knudsen numbers.图5 中拓扑优化得到的最优材料分布, 发现随着$Kn$ 的增大, 弹道效应增强, 填充材料从低温边界向内部区域发展的趋势减弱, 且分布形状中微小的枝所占的比例减少, 粗壮的主干所占的比例增多, 这可以由弹道输运产生热导率的尺寸效应来解释. 不同于扩散导热, 弹道-扩散导热机制下, 结构的等效热导率会随尺寸的减小而降低. 因为微小枝的尺寸比粗壮主干的尺寸更小, 所以前者的等效热导率比后者更低, 前者在构建高导热通道方面的性能不如后者; 且随着弹道效应的增强, 这种能力上的差别会增大. 在$Kn$ 较小时, 不同尺寸的填充材料间导热性能差异较小, 影响优化效果的主要还是热源和高导热通道的距离, 所以图5(a) 的结果像图3(b) 那样有一些分岔, 且伸入内部区域较多. 随着$Kn$ 的增大, 弹道效应增强, 结构等效热导率的降低对优化效果的影响加强, 拓扑优化倾向于产生等效热导率相对较大的粗壮结构, 而非伸入内部区域的微小分散结构. $Kn = 0.1$ 时, 尽管基底材料声子平均自由程仅为系统特征尺寸的0.1倍, 但填充材料的声子平均自由程已经是系统特征尺寸的50倍, 整个系统的弹道效应已十分显著, 团状的填充材料分布在构建高导热通道方面的性能最优, 但由于填充材料比例限制, 通道只能覆盖低温边界附近的区域. 弹道导热极限下, 拓扑优化的结果中填充材料聚集在低温边界附近, 沿各个方向的伸展长度基本相同, 呈半圆形团状分布. 图5(c) 的结果已经较为接近弹道极限下的结果. 温度分布中低温区域的轮廓反映了填充材料所形成的高导热通道的效果. 在图3 和图5 中, 低温区域的轮廓都与填充材料的形状大体一致, 表明所有填充材料都有效地形成了高导热通道. 根据上述分析, 在弹道效应较强时, 如果填充材料的形状中含有较多的微小结构, 由于这些小尺寸结构在构建高导热通道方面是低效的, 对应区域的温度将无法得到有效降低, 温度轮廓将势必不同于填充材料的形状. 作为检验, 给出扩散导热条件下插值${k^{ - 1}}$ 的拓扑优化所预测的材料分布(图3(b) )在$Kn = 0.1$ 时的温度场如图6 所示. 尽管材料分布与图3(b) 相同, 但图6 的温度轮廓明显不同于图3(b) , 反而与图5(c) 的温度轮廓更为接近, 说明填充材料中粗壮的主干形成了高效的导热通道, 但细小的枝因为等效热导率更低, 所以在导热方面是相对低效的, 未能有效降低所在区域的温度.图 6 扩散导热下插值${k^{ - 1}}$ 的拓扑优化所得的材料分布在$Kn = 0.1$ 时的温度分布Figure6. The temperature distribution for the material distribution obtained by topology optimization which interpolates ${k^{ - 1}}$ in diffusive heat conduction at $Kn = 0.1$ .${k_{\rm{f}}}/{k_{\rm{s}}} = 500$ 的条件下, 但因为弹道输运主要通过热导率的尺寸效应来影响拓扑优化结果, 所以改变${k_{\rm{f}}}/{k_{\rm{s}}}$ 的值不影响体点导热拓扑优化结果随弹道效应强度的定性变化. 定量上, 体材料热导率比的值越大, 发生弹道输运时不同尺寸结构等效热导率的差异越大, 相同努森数下弹道输运对拓扑优化结果的影响越显著. 界面热阻会使得材料间界面处出现温度不连续, 导致系统总热阻增大, 平均温度升高[4 ] . 双层材料间界面热阻的影响会随着材料尺寸的减小而增大[56 ] , 如果在拓扑优化中考虑界面热阻, 为了降低界面热阻对导热的阻碍作用, 优化结果会朝着增大结构尺寸的方向发展. 图5 中随着弹道效应的增强, 填充材料构型也明显表现出粗壮结构增多、微小结构减少的趋势, 这表明虽然现在的优化模型未考虑界面热阻, 但所得的结果有利于抑制界面热阻的作用.4.结 论 针对微纳米电子器件的散热优化设计, 结合声子玻尔兹曼方程和固体各向同性材料惩罚方法, 发展了适用于微纳尺度下弹道-扩散导热的拓扑优化方法. 声子玻尔兹曼方程被转化为声子辐射输运方程, 然后用离散坐标法求解以获得某个设计方案下的温度场; 拓扑优化则通过对声子平均自由程的倒数进行插值的固体各向同性材料惩罚方法来实现, 并采用对相对密度变量全局梯度施加显示约束的方法来确保解的适定性和网格无关性.Kn 的变化而变化, 表明微纳米尺度下的导热优化问题必须要考虑声子弹道输运的影响. 在Kn 较小时, 解声子玻尔兹曼方程的拓扑优化的结果会趋向傅里叶定律下于对热导率倒数进行插值的拓扑优化结果, 而非传统的插值热导率所对应的树状结构. 随着Kn 的增大, 拓扑优化结果中填充材料逐渐向低温边界附近聚集, 其构型中粗壮的主干结构所占比例增大, 微小的枝结构所占的比例降低, 且优化后系统平均温度和优化前系统平均温度的比值$T_{{\rm{ave}},{\rm{opt}}}^*/T_{{\rm{ave}},{\rm{uni}}}^*$ 增大.Kn 的相关性与声子弹道输运产生的热导率尺寸效应有关. 扩散导热机制下, 不同尺寸的填充材料热导率相同, 均能有效构建高导热通道; 但随着弹道效应的增强, 尺寸效应使得材料分布中微小结构的等热导率比粗壮结构低, 微小结构在提升系统导热性能方面的作用不如粗壮结构, 因而拓扑优化会向增多粗壮结构、减少微小结构的方向发展. 当弹道效应足够强时, 填充材料会聚集在低温边界附近, 主干和枝合并, 呈团状分布. 
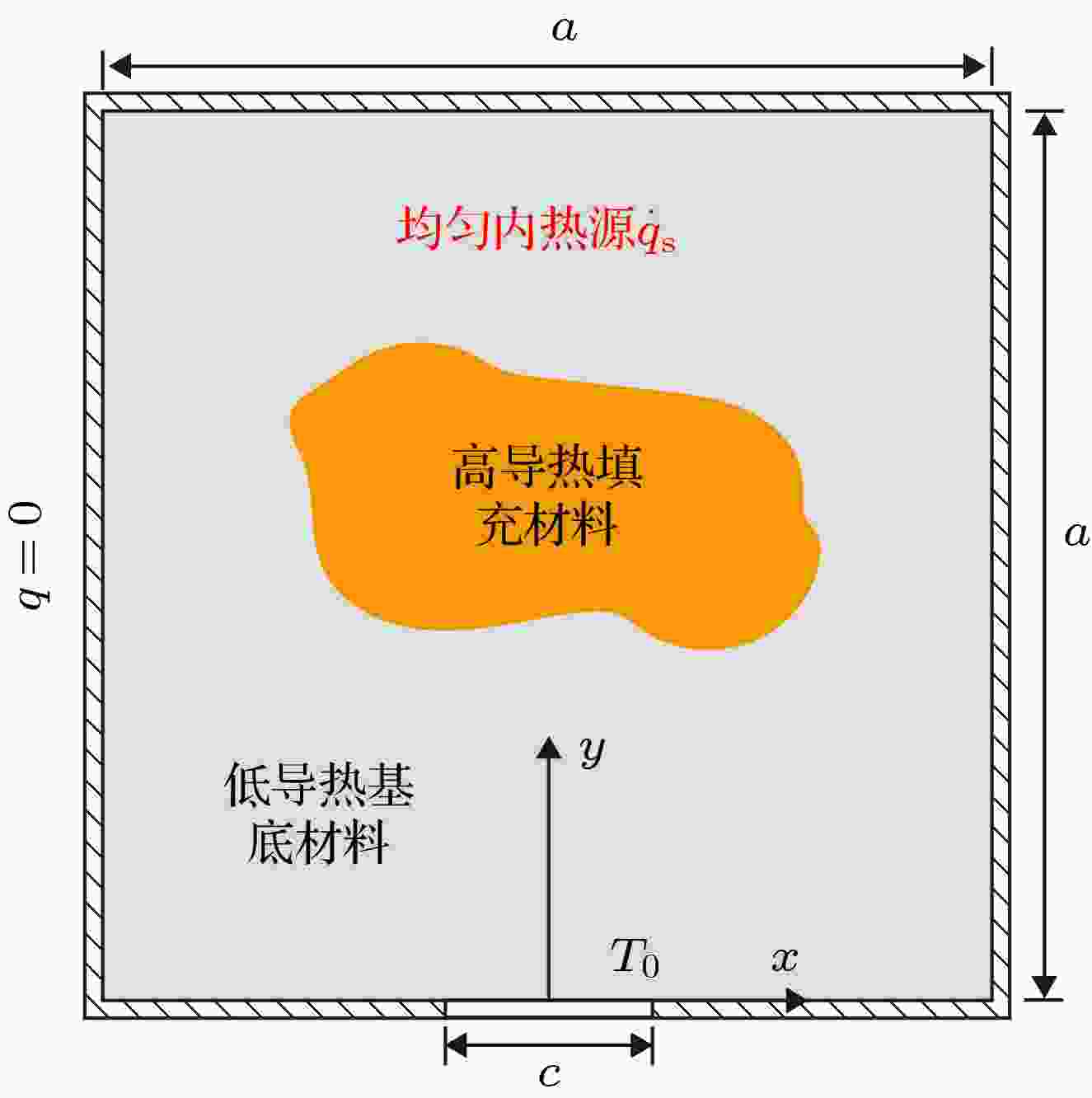 图 1 体点导热问题示意图
图 1 体点导热问题示意图























































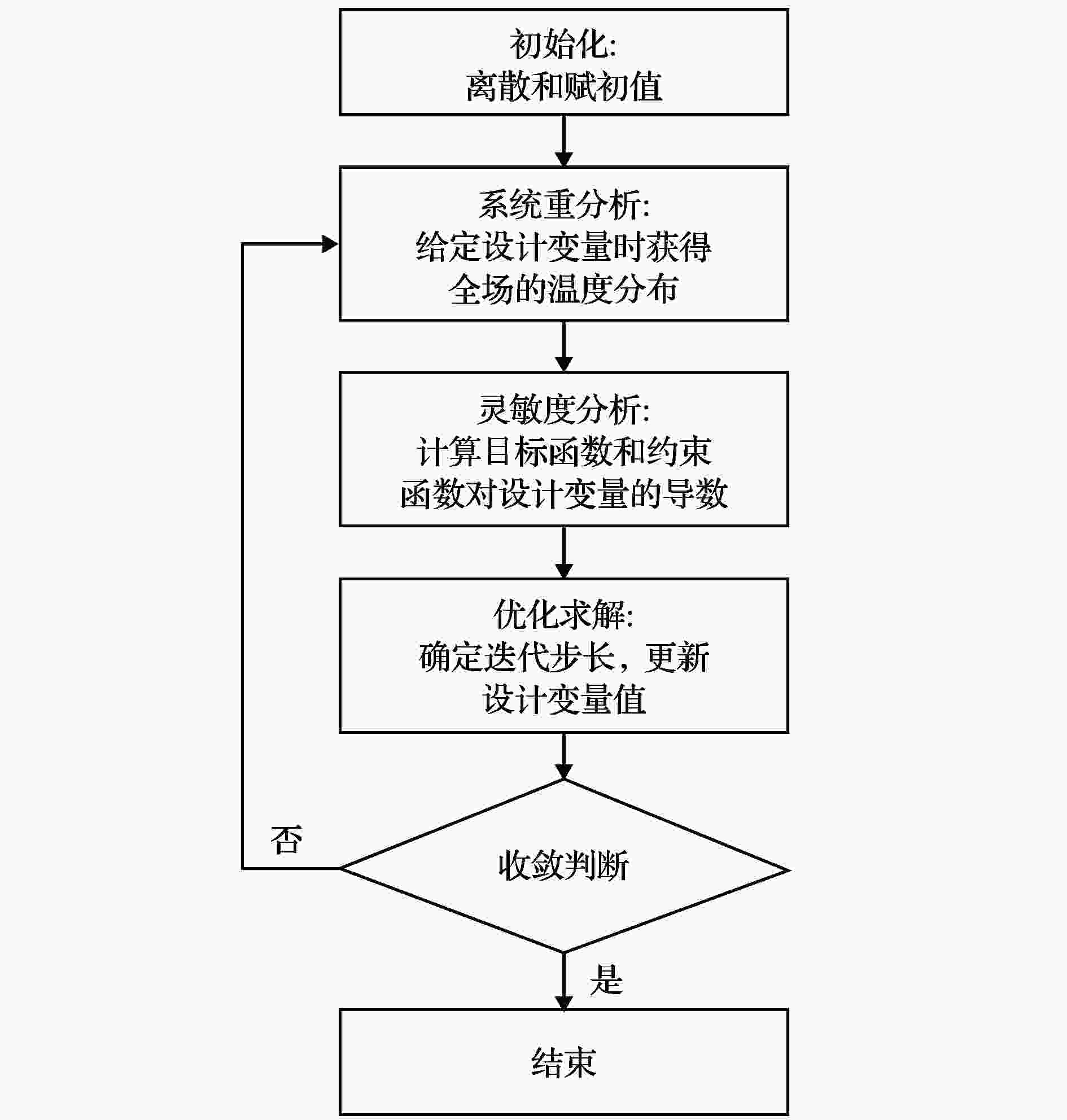 图 2 体点导热拓扑优化的流程图
图 2 体点导热拓扑优化的流程图



































































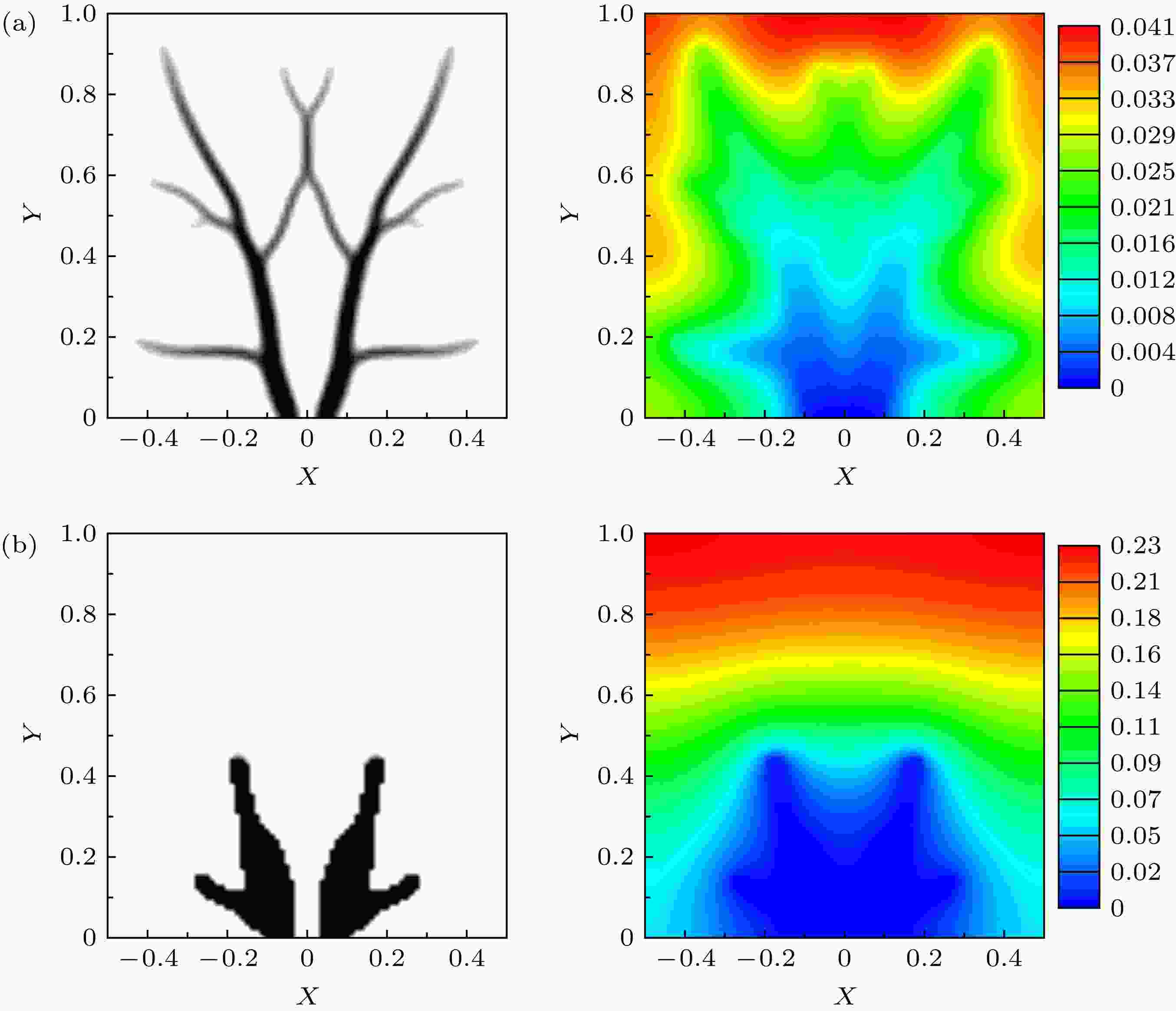 图 3 扩散导热下不同插值方式对材料分布和温度分布的影响 (a)插值k; (b)插值
图 3 扩散导热下不同插值方式对材料分布和温度分布的影响 (a)插值k; (b)插值

























 图 4 扩散导热下拓扑优化得到的材料分布随
图 4 扩散导热下拓扑优化得到的材料分布随
























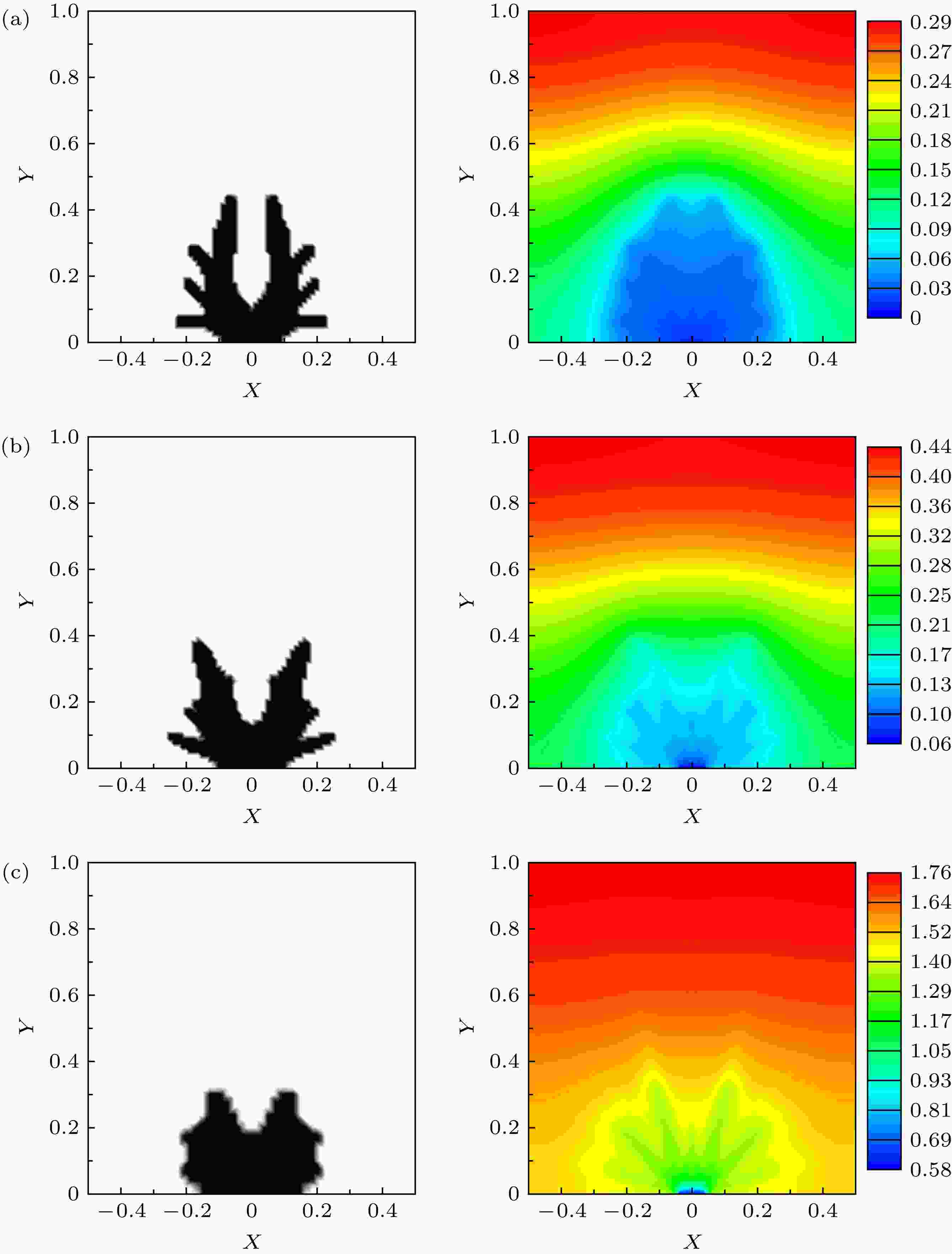 图 5 弹道-扩散导热下拓扑优化的材料分布和温度云图随
图 5 弹道-扩散导热下拓扑优化的材料分布和温度云图随






























































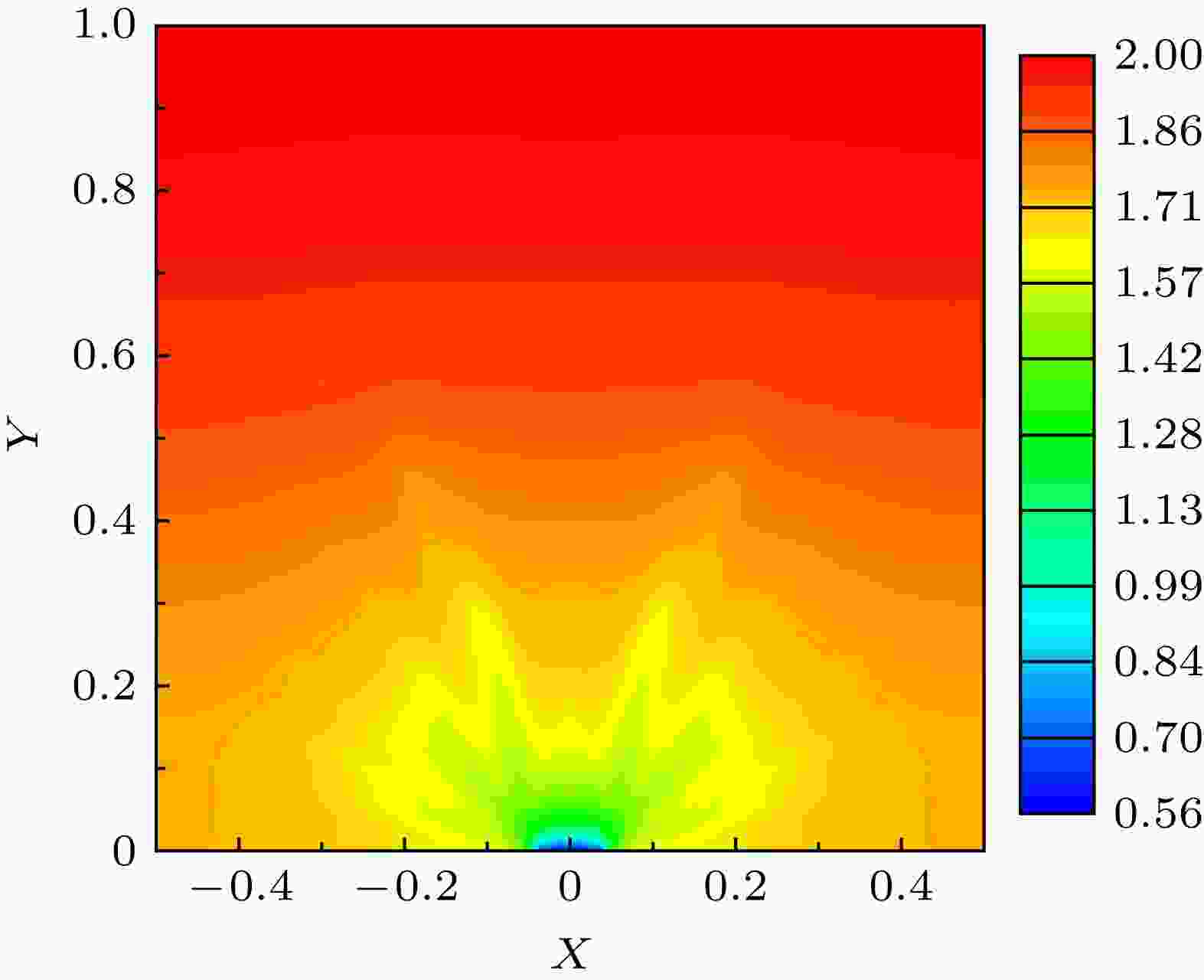 图 6 扩散导热下插值
图 6 扩散导热下插值







