摘要:等离激元光子学是现代光电子科学重要的组成部分. 除了传统的基于贵金属的等离激元研究, 随着新材料的快速发展, 越来越多具有新颖的等离激元性质的材料被发现. 典型的例子是具有高局域性和可调节性的石墨烯等离激元. 随着拓扑理论和实验的快速发展, 与石墨烯一样具有狄拉克线性色散的拓扑材料的等离激元光谱研究也取得了长足的进步. 本文首先介绍拓扑绝缘体和拓扑半金属的等离激元的谱学实验进展, 特别是光谱方面的进展. 随后对更多的有潜力适合二维等离激元研究的拓扑材料进行了展望.
关键词: 拓扑绝缘体/
拓扑半金属/
等离激元

English Abstract

全文HTML

--> --> -->

固体中的等离激元模式产生于光激发下电子的集体振荡, 其独特的色散关系使得等离激元可以突破光的衍射极限来实现纳米尺度光的传播和调控. 基于等离激元的激发、传导、调控和探测的等离激元光子学在生物、化学、能源和信息领域显现出了巨大潜力^[1]. 早期的等离激元研究主要集中于贵金属材料(金、银等)和二维电子气体系^[2], 等离激元光谱范围主要集中于可见光和近红外波段. 随着新材料尤其是二维材料的迅猛发展, 石墨烯等离激元得到了人们的广泛关注^[3,4], 其等离激元具有很强的光场局域效应^[5,6]和可调节性^[7], 因此在太赫兹波段的电子系统的动态响应和光学超材料研究中有很大的应用前景^[8,9]. 另外, 与传统半导体和金属相比, 石墨烯等离激元的色散和载流子浓度有独特的依赖关系^[7]. 这归因于石墨烯具有线性色散的能带结构, 也就是在费米面附近存在无质量的狄拉克费米子.
Das Sarma和Hwang^[10]计算了普通费米子(抛物线色散)和狄拉克费米子(线性色散)的等离激元在长波极限(q → 0)下的色散关系.

$\omega _1^{\left( {\rm{p}} \right)} = \sqrt {\frac{{2{e^2}{n_1}}}{{\kappa m}}} q\sqrt {\left| {\ln \left( {qa} \right)} \right|} + O\left( {{q^3}} \right), \tag{1a}$

$\omega _2^{\left( {\rm{p}} \right)} = \sqrt {\frac{{2{\text{π}}{e^2}{n_2}}}{{\kappa m}}} {q^{{1/2}}} + O\left( {{q^{{3/2}}}} \right), \tag{1b}$

$\omega _3^{\left( {\rm{p}} \right)} = \sqrt {\frac{{4{\text{π}}{e^2}{n_3}}}{{\kappa m}}} + O\left( {{q^2}} \right), \tag{1c}$

$\omega _1^{\left( {\rm{l}} \right)} = \sqrt {{r_{\rm{s}}}} \sqrt {\frac{g}{{\text{π}}}} {\upsilon _{\rm{F}}}q\sqrt {\left| {\ln \left( {qa} \right)} \right|} + O\left( {{q^3}} \right), \tag{1d}$

$\omega _2^{\left( {\rm{l}} \right)} = \sqrt {{r_{\rm{s}}}} {\left( {g{\text{π}}{n_2}} \right)^{{1/4}}}{\upsilon _{\rm{F}}}{q^{{1/2}}} + O\left( {{q^{{3/2}}}} \right), \tag{1e}$

$\omega _3^{\left( {\rm{l}} \right)} = \sqrt {{r_{\rm{s}}}} {\left( {\frac{{32{\text{π}}g}}{3}} \right)^{{1/6}}}{n_3}^{{1/3}}{\upsilon _{\rm{F}}} + O\left( {{q^2}} \right), \tag{1f}$

其中(1a)式—(1c)式((1d)式—(1f)式)为不同维度下普通费米子(狄拉克费米子)的等离激元色散. e代表电子电量, $\kappa $代表环境的介电常数, m代表有效质量, ${n_D}$, D = 1, 2, 3代表不同维度下的载流子浓度, q是等离激元的波矢, a代表了一维系统中的横向限制尺寸, ${v_{\rm{F}}}$是狄拉克费米子的线性色散速度, ${r_{\rm{s}}}$是结构因子(${r_{\rm{s}}} \equiv {{{e^2}}/{\left( {\kappa \hbar {v_{\rm{F}}}} \right)}}$). 从(1a)式—(1f)式中可以看出, 对于普通费米子, 无论维度如何, 等离激元频率始终与载流子浓度的1/2次方成正比($\omega _{\rm{D}}^{\left( {\rm{p}} \right)} \propto \sqrt n $). 然而狄拉克费米子的等离激元频率有不同的载流子依赖关系($\omega _{\rm{D}}^{\left( {\rm{l}} \right)} \propto {n^{{{\left( {D - 1} \right)}/{2 D}}}}$). 例如, 石墨烯等离激元的频率可以通过外加门电压的方法来调控^[7] (图1(a)和图1(b)). 不同门电压对应不同的费米面位置, 从而改变材料中的二维载流子浓度, 进而实现对等离激元频率的调控. 图1(c)展示了石墨烯中等离激元频率和载流子浓度的依赖关系. 可以看到${\omega _{\rm{P}}}$与n^1/2并不是图中虚线显示的线性关系(普通费米子的情形), 而是遵循${\omega _{\rm{P}}} \propto {n^{{1/4}}}$ (实线). 这证明了石墨烯中存在线性色散的狄拉克费米子.
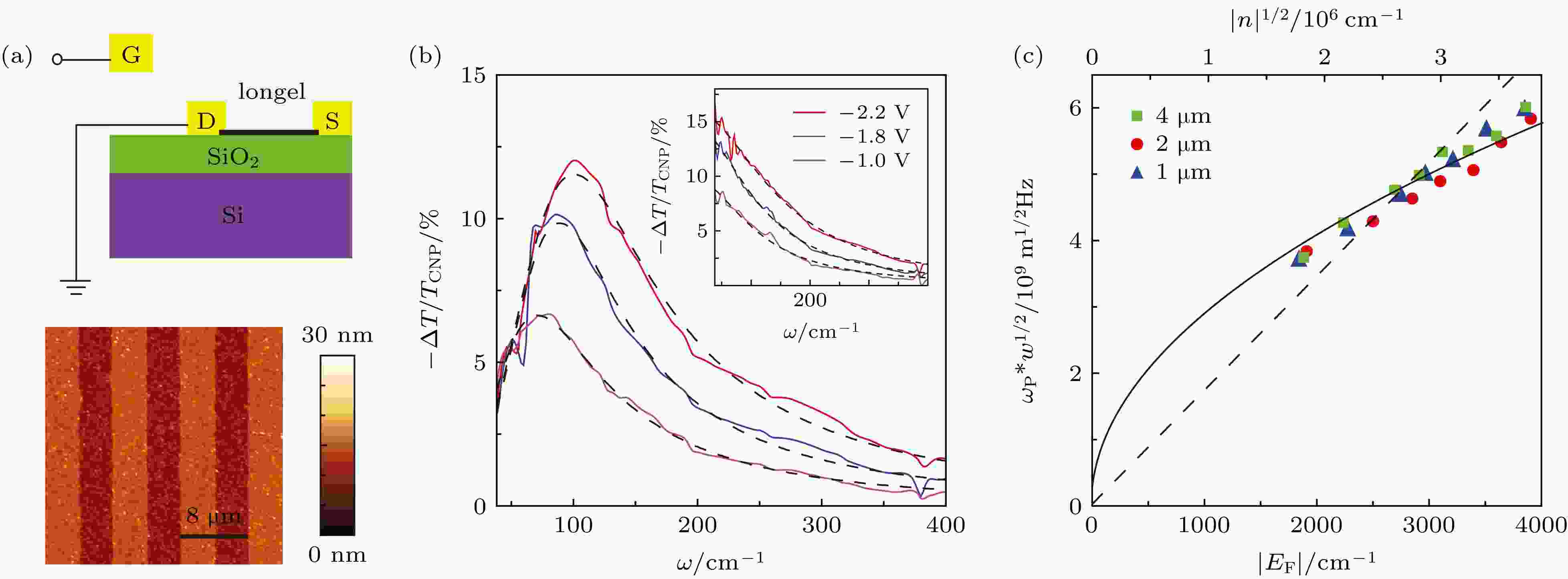图 1 石墨烯等离激元的电学调控^[7]　(a)器件示意图(上图)和石墨烯光栅结构AFM轮廓图(下图); (b)石墨烯光栅在不同门电压下的透射光谱图. 主图为入射光偏振垂直于光栅方向, 插图为偏振平行于光栅方向; (c)不同宽度光栅的等离激元频率随载流子浓度(费米面能量)的依赖关系
Figure1. Tunable plasmon resonance in gated plasmon ribbon array^[7]: (a) Schematic of the device (upper panel) and AFM image of a typical ribbon array (lower panel); (b) gate dependent plasmon resonance with light polarization perpendicular to the ribbon array. Inset shows the spectra with parallel light polarization; (c) normalized plasmon frequency as a function of Fermi energy and carrier density for different ribbon width.

随着拓扑材料的研究, 其他具有狄拉克费米子的材料被人们逐步发现, 如图2所示. 例如拓扑绝缘体材料^[11,12], 其体态具有能隙, 而表面态是具有线性色散关系的狄拉克费米子. 而近期, 一系列具有三维狄拉克费米子的拓扑半金属材料被人们提出和发现. 首先人们在包括 Na₃Bi, Cd₃As₂, ZrTe₅ 等材料中发现了三维狄拉克半金属^[13-17]. 这种材料的电子结构具有三维动量空间下的线性色散, 也就是三维的狄拉克点. 而理论进一步预言, 当材料的时间反演对称或空间反演对称性破缺时, 原来简并的三维狄拉克点会在能量或者动量方向分开变成两个受拓扑保护的具有相反手征的外尔点, 从而形成拓扑外尔半金属. 除了手征奇异性, 外尔半金属另一个特点是表面存在拓扑保护的费米弧, 它连接体内具有相反手征的外尔点在表面上的投影^[18-20]. 在实验中, 包括 TaAs, TaP, NbAs 和 NbP等被理论预测并被实验证明属于外尔半金属^[21-27]. 根据费米面附近的能带交叉点维度的不同, 科学家发现了拓扑节线(Nodal line)半金属材料^[28,29], 其在布里渊区中具有线性色散的交叉点形成连续闭合的一维曲线. 实验上一系列的拓扑节线半金属材料被发现和证实. 例如三维的PtSn₄^[30], ZrSiX (X = S, Se, Te)^[31-33], PbTaSe₂^[34]等, 二维节线费米子也在单层的Cu₂Si薄膜中被发现^[35]. 除了线性色散之外, 这些拓扑材料表现出一系列新颖的物理现象^[36,37], 如巨磁阻效应^[38]、负磁阻效应^[39,40]、反常霍尔效应^[41,42]、手征磁效应等^[17]. 而等离激元作为电子的集体振荡模式有很大机会受拓扑材料奇异电子性质的影响, 从而展现出不同于石墨烯和传统金属的一些特性. 另外, 拓扑材料的载流子普遍具有很高的迁移率, 十分有利于等离激元方面的研究^[37].
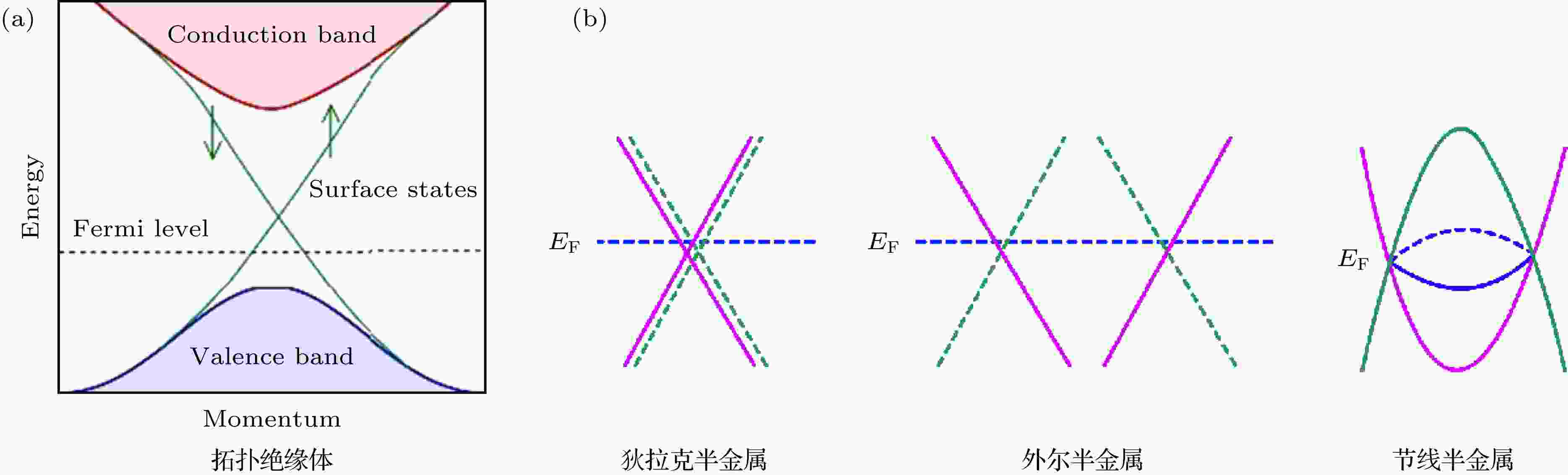图 2 不同拓扑材料的能带示意图　(a)拓扑绝缘体(来自维基百科); (b)拓扑半金属(来自文献[37])
Figure2. Band structures for different types of topological materials: (a) Topological insulator [from Wikipedia]; (b) topological semimetals^[37].

本文首先介绍拓扑材料等离激元的实验研究, 包括利用傅里叶变换红外光谱仪和电子能量损失谱对拓扑绝缘体、拓扑半金属材料的等离激元研究. 之后对潜在适合二维等离激元研究的拓扑材料进行展望.

拓扑绝缘体材料最吸引人的地方是其存在线性色散的表面态. 当光与表面态电子耦合时, 会产生二维等离激元振动模式^[43-45]. 从(1e)式和(1f)式可以看出, 二维等离激元相比于三维情形有不一样的动量依赖关系. 而对于拓扑绝缘体薄膜, 会存在上下两个表面, 对应于两个二维等离激元模式. 当薄膜的厚度远小于光波长时, 上下两个表面的等离激元模式会相互耦合, 最终形成一支声学支模式和一支光学支模式^[43]. 如图3(a)所示, 对于光学支模式, 电子密度波在上下面之间是同相位的, 而声学支正好相反, 是反相位的. 拓扑绝缘体表面态的另外一个性质是其电子的自旋和动量是锁定的, 并且上下表面的狄拉克圆锥正好反向. 这造成了在具有相同电子密度波相位的光学支等离激元模式中, 其自旋波相位是反相的. 而在声学支模式中, 虽然电子密度波是反相位的, 但是自旋波是同相位的. 最终光学支模式是一个纯电荷振荡模式, 而声学支变成纯自旋振荡模式^[43]. 两种模式的色散关系如图3(b)所示^[43]. 在长波极限下, 光学支模式(黑色实线)仍然遵循二维等离激元的色散关系$\omega \propto \sqrt q $ , 而声学支模式(红色实线)中等离激元频率与动量成线性色散关系$\omega \propto q$.
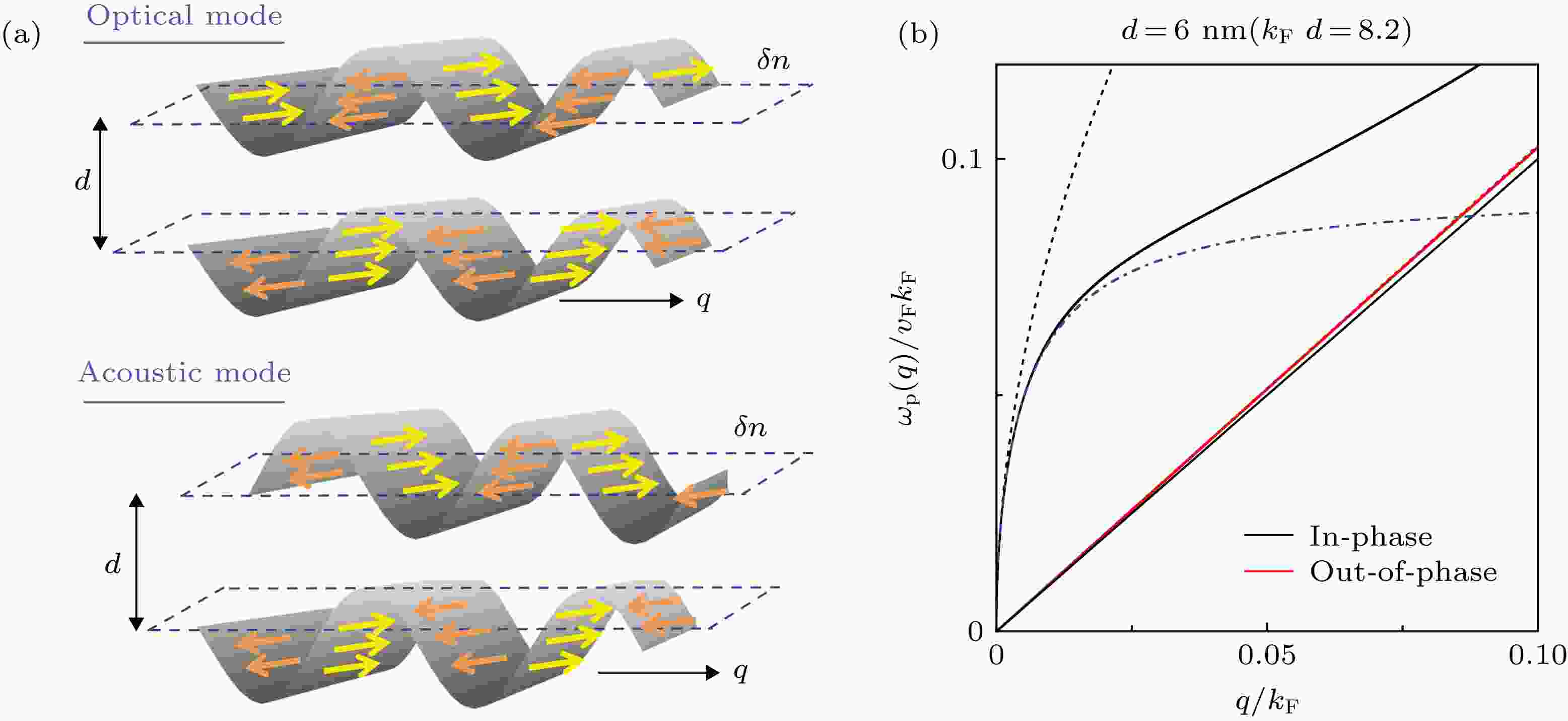图 3 拓扑绝缘体薄膜上下表面狄拉克等离激元的混合模式^[43]　(a)拓扑绝缘体薄膜光学支和声学支等离激元振动示意图; (b) 6 nm厚拓扑绝缘体薄膜的两支(同相位和反相位)等离激元模式色散曲线
Figure3. Hybrid plasmon modes in topological insulator thin slabs^[43]: (a) Schematic of optical mode and acoustic mode; (b) plasmon dispersion in 6 nm topological insulator film.

目前对于拓扑绝缘体材料的等离激元研究主要使用两种实验手段: 傅里叶变换红外光谱仪(FTIR)和电子能量损失谱(EELS). 前者需要在拓扑绝缘体薄膜表面制作周期性阵列来补偿光与等离激元之间的动量差, 进而实现利用光来激发等离激元的目的. 但是因为声学支模式是纯自旋振动, 不存在电子偶极矩, 所以无法采用光激发的方法来探测. 电子能量损失谱通过测量电子在非弹性散射过程中损失的能量和动量来测量材料体系中可能存在的激发态, 如带间跃迁, 等离激元模式等. 下面分别介绍采用这两种实验手段进行的拓扑绝缘体等离激元研究.
2

-->

2.1.基于傅里叶变换光谱的等离激元研究

从石墨烯等离激元的研究中可以知道, 由于光源的限制, 探测远红外(几个至十几个太赫兹)波段的二维等离激元需要大面积的薄膜样品. 意大利的Lupi 组的Pietro等^[46]利用分子束外延(MBE)方法在Al₂O₃衬底上生长了大面积的拓扑绝缘体Bi₂Se₃薄膜. 随后他们在薄膜上制备了光栅阵列(如图4(b)的插图), 利用傅里叶变换红外光谱仪, 测量了不同宽度的光栅阵列的吸收光谱. 图4(a)展示了在入射光偏振垂直于光栅阵列时的实验结果, 等离激元的信号表现为随着光栅宽度变化而逐渐移动的共振吸收峰. 值得注意的是, 因为与2 THz处Bi₂Se₃的红外活性声子存在耦合, 等离激元共振峰在声子附近表现出不对称的法诺峰型. 图4(b)展示了实验中得到的等离激元频率和动量的色散关系. 和一般的二维体系一致, 等离激元的频率表现出与动量的1/2次方成正比的关系. 但在拓扑绝缘体中, 等离激元存在两个贡献, 表面态狄拉克费米子和体态的普通费米子. Pietro等^[46]经过计算, 发现所测到的等离激元色散必须用狄拉克费米子的情况(图4(b)虚线)才能解释, 以此证明测到的是表面态的二维等离激元.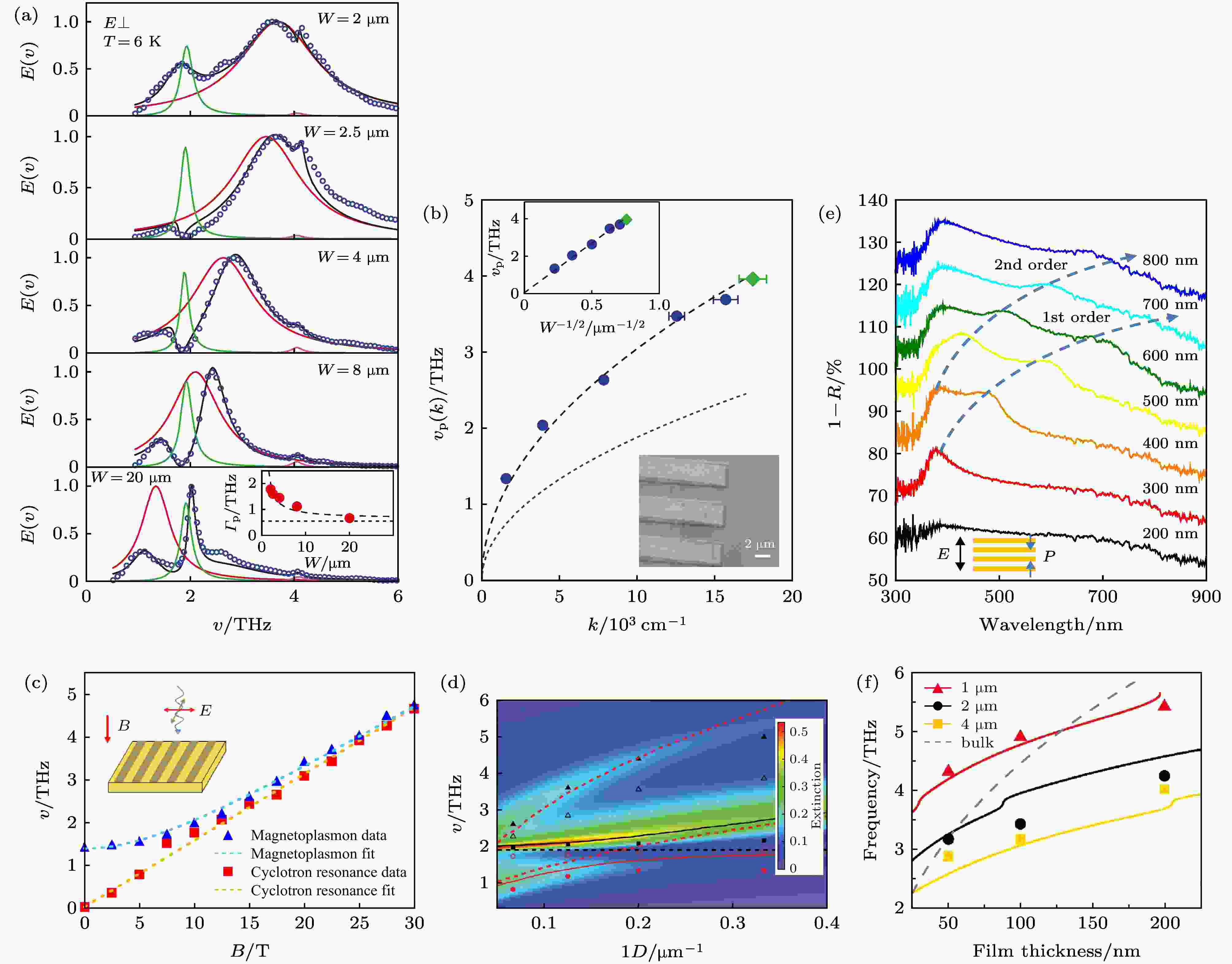
图 4 拓扑绝缘体等离激元的远红外和可见光远场光谱研究　(a)不同光栅宽度下拓扑绝缘体薄膜等离激元共振模式远红外吸收谱^[46]; (b)由(a)中实验得到的等离激元色散关系^[46]. 虚线和点线分别为考虑表面态电子和体载流子后计算的等离激元色散; (c)外加垂直于面的磁场后, 拓扑绝缘体薄膜光栅结构中磁性等离激元和回旋共振模式随磁场的变化关系^[47]; (d)圆环阵列结构下, 拓扑绝缘体薄膜等离激元色散关系^[48]; (e)可见到紫外波段拓扑绝缘体等离激元共振模式^[49]; (f)拓扑绝缘体薄膜光栅结构中等离激元共振模式随着薄膜厚度的依赖关系^[50]
Figure4. Far filed spectroscopic study of the plasmon modes in topological insulator films: (a) Extinction spectra of plasmon resonance modes in topological insulator ribbon arrays with different width; (b) plasmon dispersion extracted from Fig. (a). Fig. (a) and Fig. (b) from Ref. [46]; (c) magnetoplasmon mode and cyclotron resonance in topological insulator ribbon array as a function of external magnetic field^[47]; (d) plasmon dispersion in topological insulator microring array^[48]; (e) plasmon resonance modes of topological insulator ribbon array from visible to ultraviolet frequency range^[49]; (f) plasmon dispersion as a function of film thickness in topological insulator ribbon arrays^[50].

随后该组又进行了一系列的关于拓扑绝缘体等离激元的研究. 例如, Autore等^[47]测量了强磁场下磁性等离激元(光偏振垂直于光栅)和自由电子回旋共振(光偏振平行于光栅)的行为, 结果如图4(c)所示. 通过拟合得到表面态电子的有效质量约为0.18m_e. 之后, 该组在拓扑绝缘体薄膜表面制作了一系列的圆环阵列(图4(d))^[48], 在这样的结构中, 他们观测到了成键和反成键两种等离激元模式. 并且由于红外活性声子的存在, 这些等离激元模式同样表现出法诺振荡的谱型. 他们另一项工作是在生长的Bi₂Se₃薄膜中掺杂In, 来研究等离激元的半高宽随着掺杂浓度的变化关系^[51]. 实验结果发现, 在某个特定的掺杂浓度时, 半高宽会表现出突然的升高, 而这个浓度正好对应非平庸表面态到平庸表面态的相变位置, 证明了测量到的等离激元确实能反应表面态的信息.
另外, 其他一些实验组也对拓扑绝缘体的等离激元进行了光谱研究. Ginley和Law等^[50]研究了不同薄膜厚度和光栅宽度的等离激元模式(图4(f)), 他们发现实验结果不能仅仅用表面态的电子来解释, 而是需要考虑表面态和体态的共同作用. Ou等^[49]通过可见光波段的吸收谱研究, 发现拓扑绝缘体(Bi_1.5Sb_0.5Te_1.8Se_1.2)的等离激元不仅存在于远红外, 在可见光至紫外波段也有体现, 如图4(e)所示. 与上面提到的远红外模式不同, 这些等离激元共振模式来源于带间跃迁的载流子和表面载流子的共同贡献.
2 -->

2.2.电子能量损失谱等离激元研究

因为高能电子具有比较大的动量, 所以利用电子能量损失谱来探测等离激元不需要额外制作光栅结构来补偿动量. 随着技术的不断提高, 电子能量损失谱的能量探测范围和探测精度也在不断地进步. 从开始的探测高能激发(几个至十几个eV)到目前可以探测十几个meV的低能激发, 使得这项技术更加有利于探测等离激元模式, 尤其是在载流子浓度比较低的材料中.
最早, Nascimento等^[52]利用电子能量损失谱测量到, 在16.5 eV左右Bi₂Se₃存在体等离激元模式. 随后Liou等^[53]利用结合了(透射)扫描电子显微镜的EELS来对Bi₂Se₃进行具有空间分辨的探测. 如图5(a)所示, 当测量位置远离样品的边缘时, 测量到的结果主要是7 和17 eV两个体等离激元的峰. 但当探测位置逐渐移向样品边界时, 会在5.5和10 eV处出现两个新的峰. 作者认为这是来自表面等离激元的贡献. Politano等^[54]使用了更高能量探测精度的EELS. 通过高分辨率的测量, 他们测量到了两支等离激元色散(图5(b)), 分别指认为表面态的二维等离激元(${\omega _{{\rm{2 D}}}}$)和体载流子的表面等离激元(${\omega _{{\rm{SP}}}}$)模式. Kogar等^[55]做了类似的测量, 发现在这个频段研究表面态的等离激元必须综合考虑表面态载流子和体载流子的贡献. 2015年, 中国科学院物理研究所的Zhu等^[56]开发出了世界首台具有能量-动量二维解析能力的高分辨电子能量损失谱仪. 随后在2017年, Jia等^[57]对Bi₂Se₃进行了超低能的电子能量损失谱测量, 并观测到了反常的声学支等离激元模式(如图5(c)); 这个色散模式在很大的动量范围内都呈现出线性色散的特性. 而当采用磁性掺杂来破坏材料的拓扑表面态时, 这个线性色散的特性也同时消失, 证明该色散特性与表面态电子密切相关. 另外, 与普通电子的等离激元不同, 这个特殊的色散模式即使在高动量区间仍表现出弱衰减的特性, 进而作者推测这个性质和表面态的拓扑保护性质有关.
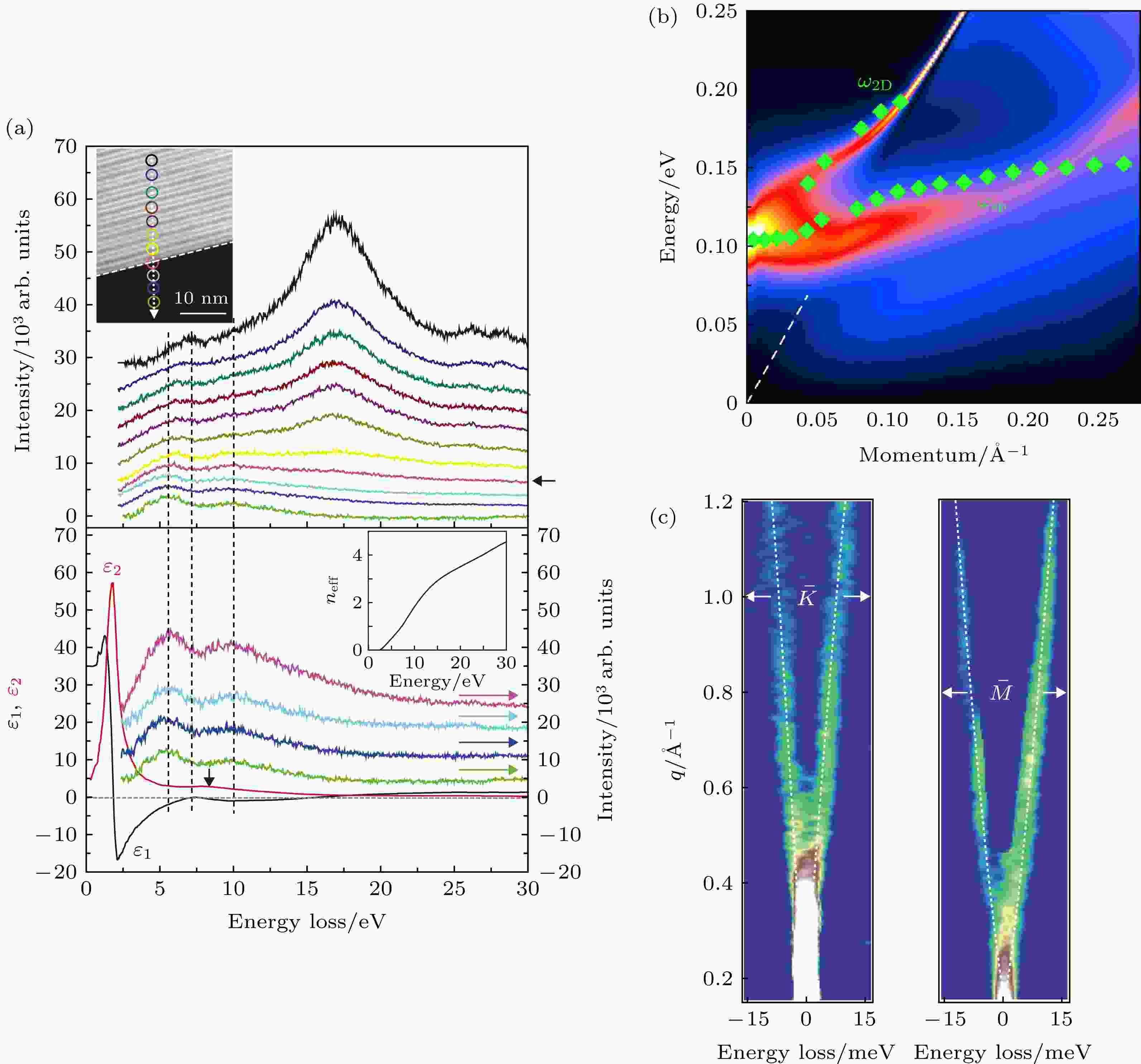图 5 拓扑绝缘体等离激元电子能量损失谱研究　(a)距离晶体边界不同位置处的能量损失谱(上图)和由上图黑线导出的介电常数(下图)^[53]; (b)高能量分辨EELS测量到的拓扑绝缘体等离激元色散模式^[54]; (c)高能量分辨EELS测量到的具有线性色散的声学支等离激元模式^[57]
Figure5. EELS study of plasmon modes in topological insulator: (a) EELS spectra at different spots from the edge (upper panel). Calculated permittivity from the black line (lower panel)^[53]; (b) plasmon dispersion derived from the EELS spectra with high energy resolution^[54]; (c) unusual acoustic plasmon modes with linear dispersion measured with high energy resolution EELS^[57].

拓扑半金属不同于拓扑绝缘体, 在体相中具有三维的狄拉克费米子, 可以看作是石墨烯的三维形式. 更重要的是, 拓扑半金属中电子存在一系列奇异的性质, 可以催生出很多新颖的等离激元应用. 例如在外尔半金属中, 动量空间分开的两个具有相反手征的外尔节点会在动量空间产生一个等效的外加磁场, 从而影响其等离激元模式^[58,59]. 另外, 外尔半金属的手征奇异性也会给包括本征和掺杂的外尔半金属的等离激元模式产生影响, 进而可以反过来利用等离激元来探测外尔半金属的手征奇异性^[59].
目前已经有一些实验上的努力来探测拓扑半金属等离激元的性质. 例如, Politano等^[60]利用电子能量损失谱在第二类狄拉克半金属材料PtTe₂中测量到了由狄拉克费米子贡献的体等离激元色散模式(图6(a)). 利用超高分辨电子能量损失谱, Chiarello等^[61]在中红外波段测量到了NbAs和TaAs晶体的表面等离激元模式(图6(b)), 并且发现这些模式的频率可以通过改变晶体表面吸附的化学气体成分来调节. Ashish等^[62]对Cd₃As₂薄膜在太赫兹波段的等离激元进行了研究, 他们利用热蒸镀的方法在石英衬底上蒸镀了大面积的Cd₃As₂薄膜, 随后在薄膜上做了一系列的周期性光栅阵列. 图6(c)展示了利用太赫兹光谱仪测量到的透射光谱, 其中谱线中的谷代表等离激元共振模式. 实验发现这些等离激元模式具有非常高的品质因子(Q ~ 3.7). 这来源于材料中载流子非常长的动量散射时间(约1 ps). 另外, 作者证明这些等离激元模式可以通过超快泵浦激光产生的光生载流子来调控, 为未来光电器件的研究提供了潜在的应用平台. 在第二类外尔半金属材料WTe₂中, Frenzel等^[63]通过对体材料单晶的各向异性反射谱测量, 计算得出了a轴和b轴方向的体等离激元频率. 如图6(d)所示, 材料的体等离激元频率具有各向异性, 这来源于材料面内各向异性的有效质量, 并且, 他们发现等离激元频率和有效质量比都有明显的温度依赖关系(图6(e)).
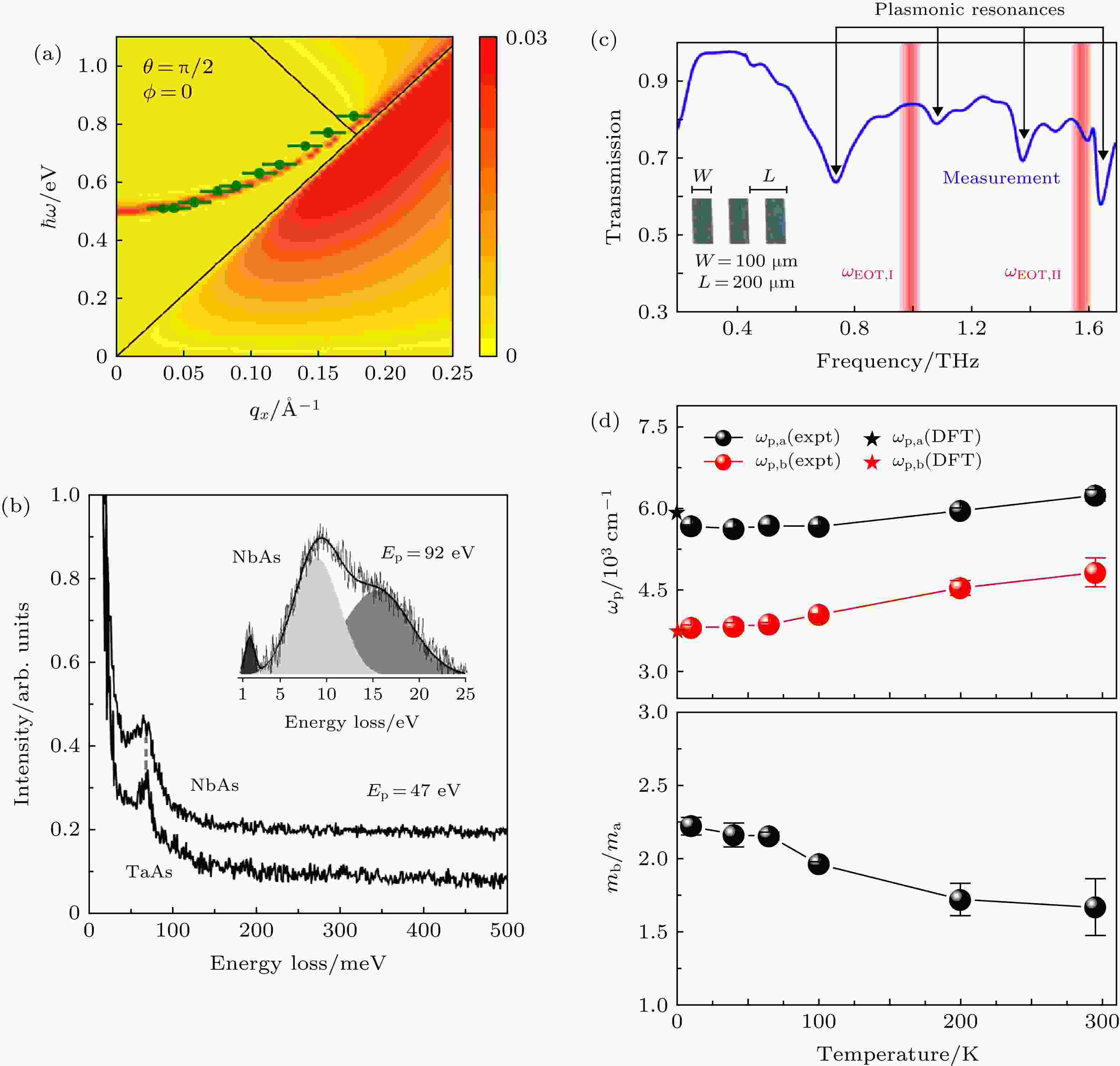图 6 拓扑半金属等离激元研究 (a)利用EELS测量PtTe₂中体等离激元色散模式^[60]; (b)超高分辨EELS下测到的NbAs和TaAs表面等离激元模式^[61]; (c)太赫兹波段Cd₂As₃薄膜的光栅结构中等离激元的远场透射谱^[62]; (d)和(e)由WTe₂体材料单晶的反射谱得到的各向异性体等离激元频率(d)和有效质量比(e)随温度的变化^[63]
Figure6. Experiments of plasmons in topological semimetals: (a) Bulk plasmon dispersion in PtTe₂ measured by EELS^[60]; (b) energy loss spectra of plasmon modes in NbAs and TaAs measured by EELS^[61]; (c) transmission spectra of plasmon modes of Cd₂As₃ in THz range^[62]. (d) and (e) temperature dependence of the anisotropic bulk plasmon and effective mass ratio in WTe₂^[63].

对石墨烯等离激元的广泛研究证明了二维等离激元无论从理论研究还是实际应用上都具有巨大的价值. 虽然目前已经有很多关于拓扑材料等离激元的实验报道, 但其中对于二维等离激元的研究相比于庞大的拓扑材料家族来说还是明显偏少^[45,64]. 随着拓扑材料的发展, 越来越多具有层状结构的拓扑半金属材料被发现. 例如具有层状结构的第二类外尔半金属材料WTe₂^[65], MoTe₂^[66], TaIrTe₄^[67]和同样具有层状结构的节线半金属材料ZrSiX (X = S, Se, Te)^[31-33]. 因为层间由相对弱的范德华力连接, 这些材料可以通过机械剥离等手段得到薄膜样品, 这为进一步研究二维等离激元提供了可能. 另外, 拓扑半金属材料具有一系列新颖的电子性质, 可以随着等离激元(电子的集体振荡)的形式表现出来, 为二维等离激元研究提供新的机遇.
1) 超高的电子迁移率. 许多拓扑半金属材料在低温下表现出可比拟甚至超过石墨烯的电子迁移率. 例如WTe₂体材料据报道有超过10000 cm²/(V·s)的迁移率; MoTe₂体材料的输运实验也证明了超过5000 cm²/(V·s)的迁移率. 虽然有实验报道随着材料厚度变小, 由于表面氧化和衬底的影响, 材料的迁移率会降低. 但是这可以通过选用高质量衬底和利用其他二维材料包裹保护的方法来改善, 典型的例子是氮化硼薄膜包裹的石墨烯^[68], 这种方法一方面防止了石墨烯表面与空气接触而造成的氧化或者杂质吸附, 另一方面高质量的氮化硼薄膜减少了衬底表面电荷不均匀性带来的散射. 以此结构为基础, 结合边接触的电极连接手段, Wang等^[69]测量到了石墨烯接近理论计算值的超高迁移率和低温下的弹道输运现象. Ni等^[70]利用扫描近场光学的手段观察氮化硼薄膜包裹的石墨烯表面等离激元的传播模式. 在这种高迁移率的样品表面上, 测量到的本征等离激元传播长度可以达到创纪录的10 μm. 因此同样具有超高迁移率的层状拓扑半金属材料为研究低损耗、远距离传播的二维等离激元提供了另一个理想平台.
2) 拓扑半金属材料的一些奇异拓扑性质会通过等离激元模式表现出来. 例如外尔半金属和节线半金属与普通金属相比等离激元频率有不同的载流子浓度依赖关系^[58,71]. 除了前文所提及的外尔半金属的手征奇异性带来的等离激元的新颖性质外, 当对外尔半金属外加磁场时, 所对应的极化激元会表现出一系列新颖的性质, 例如双曲色散特性、宽谱范围内的偏振转变等^[72]. 另外由于表面态(例如外尔半金属表面的费米弧)的存在, 拓扑半金属材料要考虑体载流子和表面态载流子对二维等离激元的共同贡献. Song和Rudner等^[73]计算了外尔半金属费米弧等离激元的色散关系, 并发现在高动量时费米弧等离激元具有双曲线型的色散特性. 此外, Hofmann和Das Sarma^[74]计算了三维拓扑半金属材料中等离激元频率随温度的变化关系, 他们发现在本征(无掺杂)系统中, 等离激元频率随温度升高而增大并具有超线性的依赖关系. 对于掺杂样品, 等离激元频率首先在低温区域随着温度升高缓慢下降, 然后在高温区域继续上升并重复超线性的依赖关系. 因此, 二维等离激元的温度依赖特性为证明拓扑半金属材料的拓扑性质提供了一个重要实验手段.
3)各向异性的电子结构带来的等离激元的各向异性. 第二类外尔半金属材料, 如WTe₂^[63], MoTe₂^[75], TaIrTe₄^[76]都具有面内的各向异性电子结构. 这不仅表现在各向异性的有效质量(各向异性的带内跃迁), 而且表现在各向异性的带间跃迁中. 例如, 北京大学Lai等^[75]和Ma等^[76]在MoTe₂和TaIrTe₄的二维薄膜上都测量到了各向异性的光电流, 并且这种各向异性随着激发光能量的减小而增大. 最近Nemilentsau等^[77]理论预言了在各向异性的二维材料中, 可能存在具有定向传播特性的双曲等离激元模式, 即等离激元的动量空间下的等能面色散为双曲型, 而不是各向同性材料的圆形色散. 他们提出形成这种奇特性质的前提是材料具有各向异性的电子结构. 因此, 同样具有各向异性电子结构的层状拓扑半金属材料为实现双曲等离激元提供了机遇.
然而, 相比于拓扑半金属材料在二维等离激元中的巨大潜力, 实际中的实验却并不多. 很重要的原因之一是, 无论是拓扑绝缘体材料还是拓扑半金属材料, 他们相对较低的载流子浓度决定了二维等离激元频率主要分布在太赫兹波段, 而这个波段等离激元的远场探测需要大面积高质量的薄膜样品和在远红外波段透光的衬底. 利用机械剥离的方法很难得到满足测量需求的大面积均匀薄膜. 虽然MBE方法可以生长大面积的薄膜样品, 但是由于晶格匹配的原因, 衬底往往无法自由选择, 使得很多材料只能生长在不适合远红外测量的衬底上. 所以在远红外友善的衬底(如硅衬底)上得到大面积薄膜成为了拓扑半金属二维等离激元研究首先要解决的问题.
一个潜在的解决办法是利用CVD方法生长大面积薄膜样品^{[78,79,80-85]}. 例如Zhou等^[78]利用CVD方法成功生长出了大面积的WTe₂和MoTe₂薄膜(图7(a)—7(c)), 并且衬底是远红外透明的Si/SiO₂衬底. 另外有很多组分别报道了利用Te粉末碲化金属薄膜的方法来制备WTe₂和MoTe₂薄膜, 图7(d)展示了制备原理^[79]. 首先在Si/SiO₂衬底上蒸镀金属薄膜(例如Mo), 然后在空气中和一定温度下进行氧化形成更加光滑致密的MoO₃薄膜. 随后再利用CVD方法, 在氢气氛围和700 ℃左右温度下, 用Te蒸气来碲化形成大面积的MoTe₂薄膜. 这种方法可以通过调节Te粉的量来实现可控的不同相的生长. 薄膜的厚度可以通过原始金属薄膜的厚度来调控, 最小可以生长3 nm左右厚度的薄膜(图7(e)). 香港中文大学Chen等^[82]利用类似方法生长出了大面积的WTe₂薄膜, 并利用扫描近场光学的手段看到了表面等离激元的迹象. 随着研究的不断深入, 相信有更多拓扑材料可以克服薄膜生长的障碍, 实现拓扑材料二维等离激元研究的新突破.
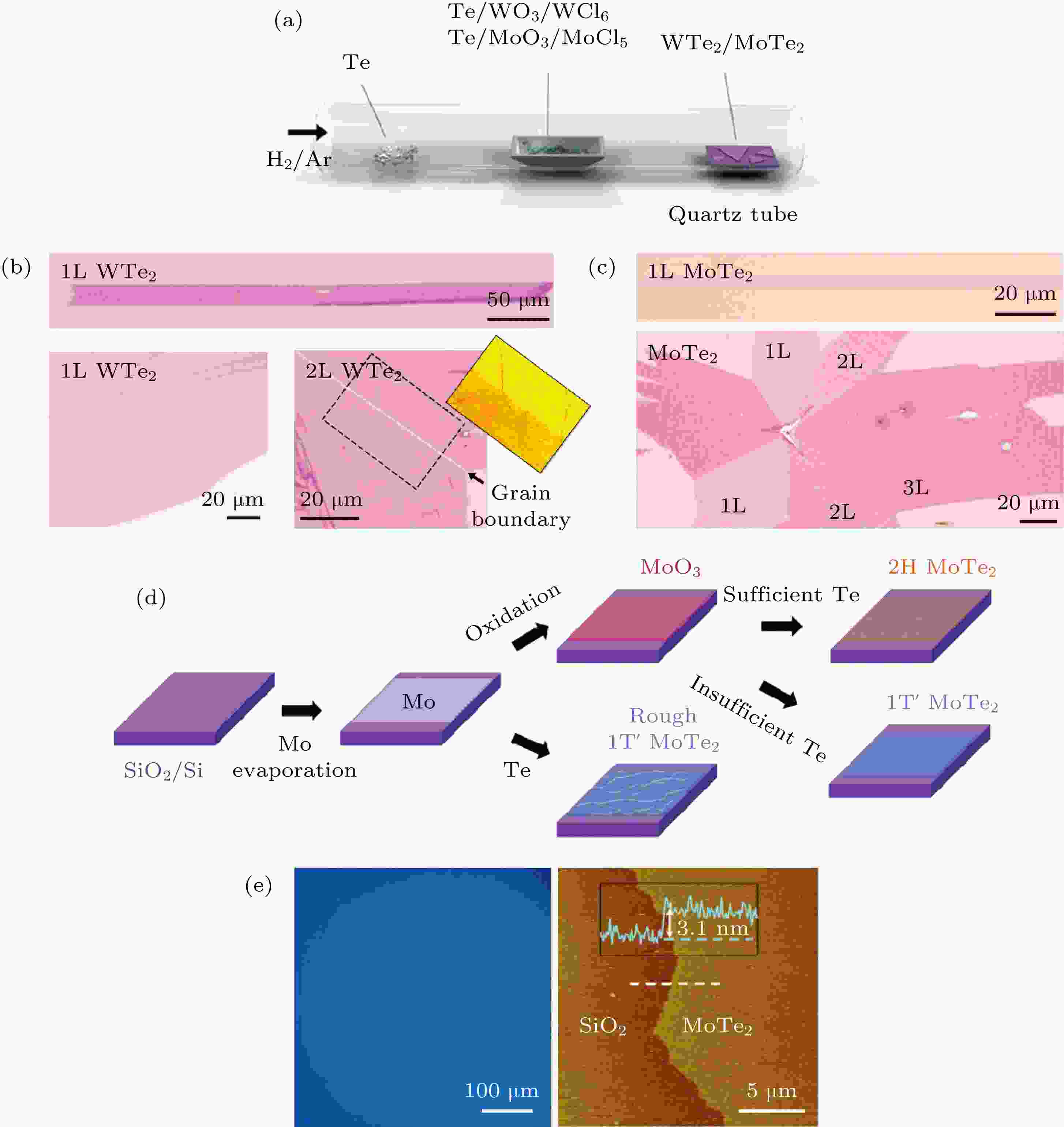图 7 大面积高质量拓扑材料薄膜CVD生长　(a)—(c) CVD方法生长大面积WTe₂和MoTe₂单晶薄膜^[78]; (d), (e)利用Te化金属薄膜的方法生长大面积多晶MoTe₂薄膜^[79]
Figure7. Synthesis of topological material films with large area and high quality by CVD method: (a) to (c) CVD growth of large area single crystal films of WTe₂ and MoTe₂^[78]; (d) and (e) large area MoTe₂ film grown from Mo^[79].