摘要:拓扑光子学、拓扑物理与光学的结合, 为凝聚态理论的验证以及新型光学器件的构建提供了新的视角. 紧束缚模型是凝聚态物理的重要研究手段. 我们发现, 将传统光子晶体的背景材料由通常的空气改为有效介电常数为负数的材料之后, 这样的光子晶体和紧束缚模型有一一对应的关系, 可以用于相关理论的验证. 通过数值仿真实验, 在蜂巢晶格负背景光子晶体结构中验证了之字形(zigzag)、胡须型(bearded)等界面态的存在性. 我们提出了两种实验构想, 以期在微波频段开发相应的凝聚态理论验证平台, 为拓扑物理的研究提供全新的工具. 我们也希望, 这些新理论的验证能为今后光学仪器的设计提供崭新思路.
关键词: 拓扑光子学/
紧束缚模型/
光子晶体/
表面/界面态

English Abstract

全文HTML

--> --> -->

拓扑绝缘体是一种特殊的量子材料, 其内部可看作是绝缘体, 但是材料表面却是导电的. 这种拓扑性质是受时间反演对称性保护的, 这使拓扑绝缘体区别于有普通表面态的材料. 电子在材料表面中的背散射被强烈抑制, 做无损耗传输. Haldane和Raghu^[1]在2008年发现在二维三角晶格光子晶体的光子能带中同样具有狄拉克点, 并提出将之用于光学单向传输波导的设计. 而在2011年Poo等^[2]的实验验证了Haldane的理论. 他们将铁电材料柱摆放成蜂巢晶格并外加磁场来打破时间反演对称性, 在其之字形(zigzag)边界, 观测到了沿着边缘柱子和空气之间单向传输的表面态^[3]. 并发现在此表面态的频率, 微波甚至能绕过在界面上的障碍物继续传输.
紧束缚模型是固体物理中非常重要的近似计算非金属晶体能带方法, 使用基于孤立原子的波函数的线性叠加的一组近似波函数来计算电子能带结构^[4]. 在不考虑电子自旋的情况下, 电子系统的哈密顿量可以表示为

$ H = \mathop \sum \limits_{\rm{i}} {\epsilon_0}c_i^{\dagger} {c_i} - \mathop \sum \limits_{\left\langle {i,j} \right\rangle } {t_{ij}}c_i^{\dagger} {c_j},$

其中${\epsilon_0} $是位能, 代表了孤立原子的性质, t_ij是耦合系数, 决定了原子之间的相互作用, $ c_i^{\dagger} /{c_j}$是产生/消灭算符. 对于非金属晶体, 原子之间的长程作用非常小, 几乎可以忽略, 因此紧束缚模型在很多时候仅需考虑最近邻原子之间的相互作用, 就能够得到和真实体系非常类似的结果. 仅考虑最近邻原子相互作用来写就拓扑绝缘体的哈密顿量的方法, 对于拓扑绝缘体的理论发展是非常具有价值的^[5].
Thouless, Haldane和Kosterlitz因为对物质拓扑相的研究获得了2016年的诺贝尔物理学奖. 拓扑是研究物质几何不变情况下的性质, 与具体的物态方程无关. 将拓扑的概念引入麦克斯韦方程, 拓扑光子学^[6]应运而生. 在很多凝聚态系统中, 有限尺寸材料的边界特性, 可以被紧束缚模型很好地描述; 但加工过程中不可避免地存在的位错等缺陷使得相应的实验观测非常困难, 影响了相关理论的验证和进一步发展. 而在光学系统里, 几何尺寸和光波/电磁波波长可比拟, 在加工制备的精度上, 光学材料比电子材料有着天然的优势. 而且近年光学实验技术的进步, 已经允许我们在微波实验中实现更精准的近场观测实验^[7-9]. 所以, 如果能够基于紧束缚模型打造一一对应的电磁波类比实验平台, 对可以用紧束缚模型描述的理论进行实验验证, 相信这个平台能够帮助推动相关理论的发展. 同时, 这些新理论也有可能为全新光学元件的开发打下基础.

2

-->

2.1.负背景的定义

将介电材料做周期性排列, 可以让和晶格常数可比拟的特定波长的光无法通过. 光子晶体^[10], 或人工带隙材料, 在发现的伊始就是电子晶体的光学类比. 早在1998年, Lidorikis等^[11]就提出可以利用紧束缚模型来对光子晶体能带进行描述, 并计算了四方晶格和蜂巢晶格光子晶体, 用紧束缚模型进行参数标定. 然而相关的研究并没有激发更多的紧束缚光子晶体的科研工作.
仔细分析传统光子晶体和紧束缚模型描述的电子体系, 可以发现一个很明显的区别. 真空对于电子而言明显是一个绝缘体; 而光和电磁波是能够在真空中传播的. 在紧束缚模型描述的电子体系中, 电子的波函数快速衰减, 原子之间是以倏逝波形式耦合的. 但对传统在空气/真空背景中插入柱子等的光子晶体, 同文献[10]一样, 电磁波显然在这些柱子之间并不是以倏逝波形式进行耦合的. 对于传统光子晶体, 因为光可自由在背景材料中传播, 只讨论最近邻的相互作用是不够的, 这就意味着很难用最近邻近似相互作用的紧束缚模型对传统光子晶体能带进行准确的描述. 而且如果想要描述拓扑绝缘体, 拓扑平庸的绝缘体也是一个重要的存在. 对光而言, 绝缘体并不是一个显然的材料(光子晶体在设计伊始就是尝试设计一个光的绝缘体), 这也给拓扑光子学的研究造成了一定的困难.
我们考虑采取的解决办法是将原有的真空背景更换为负材料, 即介电常数或磁导率为负的材料, 从而阻止光的正常传播. 本文因为仅考虑电场垂直于传播平面的偏振, 所以选用了介电系数为负值的材料. 这样, 因为有效折射率为虚数, 电磁波在这样的背景材料中只能处于倏逝波的模式. 这样的背景材料对光来说, 可以被认为是绝缘体. 同时, 在负背景介质光子晶体中, 电磁波主要会局域在内部插入的介质柱上, 以倏逝波耦合的形式影响介质柱的相互作用. 由于背景的有效介电常数是一个可以调节的参数, 它会极大地影响耦合的性质, 也为开展紧束缚模型理论相关的研究提供了便利.
本文主要研究具有六角蜂巢晶格的类石墨烯体系. 在2014年, Plotnik等^[12]研究人员利用光诱导晶体构造了类石墨烯的二维光纤阵列, 在实验上首次观测到了胡须形(bearded)的表面态, 并发现实验得到的真实光子能带和紧束缚模型的预测是一致的.
2 -->

2.2.负背景和紧束缚模型的对应

图1展示了我们的研究对象, 宽度为11个介质柱的蜂巢晶格类石墨烯光子晶体带. 每一个圆代表一根沿z方向无限高的介质柱. 考虑电场沿z轴的Transverse Magnetic(TM)偏振, 并沿x方向为无限延伸. 我们同时研究胡须形和之字形的界面态. 背景材料为相对介电常数ε = x, 相对磁导率μ = 1的材料(x < 0).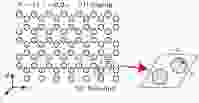
图 1 二维类石墨烯光子晶体结构示意图, 其蜂巢晶格原胞用红线标记. y轴方向上11个介质柱构成一个超原胞, 沿着x轴无限周期排列. 介质柱阵列的S1边界为之字形(zigzag)界面, S2为胡须形(bearded)界面, 介质柱半径r = 0.2a, a是蜂巢晶格的晶格常数
Figure1. The structure of a honeycomb-lattice graphene-like photonic crystal. Its honeycomb unit cell is indicated in red. A ribbon of 11 dielectric cylinders along the y direction is considered and it is periodically arranged in the x direction. The photonic crystal ribbon has zigzag (S1), bearded (S2) edges. The radius of cylinders shown here is r = 0.2a, where a is the lattice constant.

利用有限元数值仿真元件COMSOL Multiphysics仿真了这种具有负背景材料的类石墨烯光子晶体原胞的体能带. 由于该体系具有大量的变量, 我们重点关注背景介电常数x, 介质柱的尺寸y = r/a, 介质柱本身的材料介电常数z这三者, 并对比其中某一参数改变对光子晶体能带的影响. 在图2(a)中对比了四组不同的参数下, 第一布里渊区内的频率最低两条能带的能带结构.
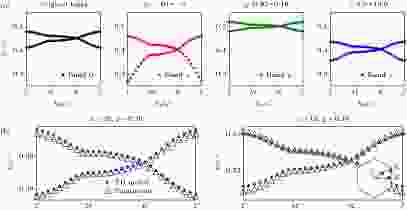图 2 (a)六角光子晶体最低的两条能带, 在布里渊区边界K点因为蜂巢晶格对称性具有狄拉克点. Band 0 对应了x = –10, y = 0.2, z = 8.5的能带, 即初始条件. Band x, y, z 在保持另两个初始值不变时, 改变了x = –5 (band x), y = 0.18 (band y), z = 10 (band z); (b) 左侧band (x = –20, y = 0.2, z = 8.5)和右侧band (x = –15, y = 0.18, z = 8.5) 对比了COMSOL计算的能带(点)以及用(5)式和(6)式拟合的紧束缚模型计算得到的能带(三角形)
Figure2. (a) A Dirac cone dispersion appears at K point for the lowest two photonic bands of the honeycomb photonic crystal structure we studied. Band 0 represents the band diagram when x = –10, y = 0.2, z = 8.5; Band x, y and z correspond to the situations that only one parameter from that of band 0 is changed: x = –5 (band x), y = 0.18 (band y), z = 10 (band z); (b) the comparison between calculated lowest two photonic bulk bands of band left (x = –20, y = 0.2, z = 8.5) and band right (x = –15, y = 0.18, z = 8.5) (in red dots) and corresponding bands calculated with tight-binding model with fitted parameters using equations (5) and (6) (in hollow blue triangles).

显然, x, y, z中任何一个参数的改变都会影响狄拉克点频率. 同时, 这两条能带在M点的频率间隔(能量差), 也随着参量在发生变化.
仅考虑最近邻的紧束缚模型来研究六角原胞, 这样的紧束缚模型是用位能${\epsilon_0} $和耦合强度t来进行描述的. 根据(1)式的哈密顿量, 可以解得六角晶体的第一和第二能带的解析值为

${E_ \pm } \!=\! {\epsilon_0} \pm t\sqrt {1\! +\! 4\cos \! \Big(\!{\frac{{\sqrt 3 {k_x}a}}{2}}\!\Big)\cos \!\Big(\!{\frac{{{k_y}a}}{2}}\!\Big)\! \!+\! 4{{\cos }^2}\!\Big(\!{\frac{{{k_y}a}}{2}}\!\Big)}.$

可以发现, 一阶紧束缚能带要求, 这两条能带应相对位能${\epsilon_0} $上下对称.
当$ {k_x} = \dfrac{{2{\text{π}}}}{{\sqrt {3 a} }}$, $ {k_y} = \dfrac{{2{\text{π}}}}{{3 a}}$(K点)时, 两条能带简并为

${E_ \pm } = {\epsilon_0},$

当$ {k_x} = \dfrac{{2{\text{π}}}}{{\sqrt {3 a} }}$, $ {k_y} = 0$(M点)时, 两条能带的能量差为

$\delta = {E_ + } - {E_ - } = 2t.$

也就是说, 从紧束缚模型, 我们找到了能带特性以及位能${\epsilon_0} $和耦合强度t两个参数的关系: 第一个狄拉克点的能量(频率)对应了位能${\epsilon_0} $, 而最低能量的两条能带第一布里渊区M点对应的能量差δ和t成线性关系δ = 2t.
通过这两个参数在能带的对应关系, 就很容易通过计算来发现光子晶体中的参数与紧束缚模型的对应关系, 结果如表1所列.

	Onsite energy ${\epsilon_0} $	t
背景材料介电常数|x|	↑	↓
晶体柱占空比y	↓	↑
晶体柱材料介电常数z	↓	↑
↑代表正相关, ↓代表负相关; x因为是负值, 所以这里取绝对值讨论.

表1参数和位能以及耦合系数的关系
Table1.Relationship between onsite energy, coupling ratio and parameters.

表1定性地总结了背景介电常数(x), 晶体柱占空比(y), 晶体柱材料介电常数(z)和(1)式哈密顿量中的位能${\epsilon_0} $, 耦合强度t的单调性.
为进一步简化问题, 我们固定光子晶体柱的材料为氧化铝(${\epsilon=8.5} $), 将TB模型中位能和耦合强度拟合为背景介电常数x和晶体柱占空比y的函数. 利用刚才分析得到的能带特性和紧束缚模型的关系, 可以数据拟合得出位能${\epsilon_0} $以及耦合强度t与背景介电常数x, 晶体柱占空比y的关系:

${\epsilon_o} = \frac{{0.1627{\rm{arccot}}\left( {0.0541x} \right) + 0.7461}}{y},$

$t = - 142.65{{\rm{e}}^{ - 0.2162\sqrt {\left( { - x} \right)} \left( {1 - y} \right) \cdot {\epsilon_0}}}{y^4},$

其中位能${\epsilon_0} $的拟合中调用了arccot函数, 是受到Soukoulis的拟合中根据函数变化趋势选择调用了tanh函数作为rescaling函数的一部分的启发^[11], 我们也根据函数的变化趋势选择了具有特殊单调性质的arccot函数. t中选用了exp函数主要是考虑在负背景下的倏逝波的电磁耦合. 系数$ \sqrt {\left( { - x} \right)} $对应了负背景介电常数下的虚数折射率的影响, $ \left( {1 - y} \right) $对应的两个介质柱之间的距离, 也就是倏逝波需要作用的距离. 至于位能${\epsilon_0} $对应了电磁波的频率, 自然也会影响衰减的波矢. 我们发现, 这样的函数在一定范围($ x \in \left( { - 30, - 15} \right)$, $ y \in \left( {0.15, 0.24} \right)$)内可以较准确地预测能带, 如图2(b)所示.
可以发现在图2(a)中, 对于band x的结果, 能带上下完全不对称, 这并不符合(2)式得出的“能带相对位能上下应当对称”的结论, 主要原因是当x的绝对值比较小的时候, 在负背景材料中的电磁波衰减较慢, 次紧邻乃至更远的相互作用不能完全被忽略, 所以这就不符合仅考虑最近邻的紧束缚模型. 同样的情况发生在介质柱比较粗(y比较大)的时候, 因为柱子间距比较小会导致之间的耦合很强. 但这也意味着我们的实验模型更接近真实体系, 并且具备能模拟考虑高阶近邻耦合的紧束缚模型的能力. 换句话说, 如果能够调控背景的介电常数, 那么我们的实验平台具有更多的调制性.

既然负背景光子晶体体系完全能够和紧束缚模型对应, 从而计算类石墨烯结构的体能带, 那我们就进一步开展有限石墨烯带特别是其界面态的研究(见图1的示意图). 图3中对比了利用紧束缚模型和负背景光子晶体计算的类石墨烯光子晶体带的能带结构, 其超原胞见图3右下角. 可以看到, 中间存在一条平坦的界面态能带. 从本征场分析可以发现, 靠近布里渊区中心的部分对应局域界面态, 出现在胡须状表面附近(位于超原胞的右侧), 靠近布里渊区边缘的部分局域界面态, 出现在靠近之字形表面(位于超原胞的左侧). 因此该负背景光子晶体也可以得到紧束缚模型预言的界面态信息.
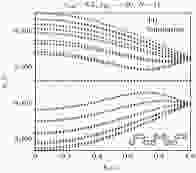图 3 宽度为11且有一个之字形边界和一个胡须形边界的光子晶体类石墨烯带超原胞, 利用(1)式, (5)式和(6)式的紧束缚模型得到的能带图像(红色)和仿真结果(蓝色)的对比; 其中背景常数x = –20, 占空比y = 0.2, 超原胞如图右下角所示
Figure3. The energy bands for a honeycomb-graphene-like photonic crystal ribbon (the background constant x = –20, filling ratio y = 0.2). Here we used the equations (1), (5) and (6) to derive the TB solution(red), as simulation results are marked blue. The supercell is depicted in the right-lower corner.

2014年Plotnik等^[12]的工作的有趣之处是发现在胡须状表面附近还存在一些新的Tamm表面态. 这不能通过直接紧束缚模型直接预言, 而是需要更改紧束缚模型的哈密顿矩阵中下边界上对应的位能值, Tamm界面态才会出现在理论能带中. Rechtsman等的解释是: 位能的大小也受到周围原子的影响, 边界上原子位能与内部原子不同. 利用我们负背景光子晶体结构直接COMSOL仿真的结果, 也观察到了一样的结论. 如图4所示, 在布里渊区边缘, 靠近体带的位置, 上下各存在一个局域在胡须状界面附近的Tamm界面态, 介质柱上电磁波的分布情况也与光纤阵列的实验结果完全相同.
图 4 利用负背景光子晶体系统数值计算得到的局域在胡须界面上的两个Tamm态, 界面态的色散用红色和体带(蓝色)区分. 此时负背景介电常数为–10, 上体带和下体带各有一Tamm态; 其对应的本征场在下方显示　(a) 下体带; (b) 上体带
Figure4. Band dispersion (in red dots) of Tamm-like bearded edge states calculated using photonic crystal system with background permittivity ${\epsilon} $ = –10. The bulk bands are in blue dots. Their corresponding eigenfield distributions localized on bearded edge are shown in the lower panels: (a) Lower bands; (b) upper bands.

在本文前述的数值仿真中, 使用了常数负背景介电常数来描述背景材料. 这仅仅是为了能更快地了解光子晶体系统与紧束缚模型的关系, 但实际实验中, 所有负介电常数的材料都是色散的. 另外, 因为我们主要研究了界面态的存在与否, 而界面态通常在一个较窄的频率范围存在, 所以如果主要关心界面态性质的话, 常数负背景不失为一个合理的模型. 我们提出了以下两个实验实现负背景的构型.
2

-->

4.1.金属柱阵列

金属在光学波段具有负的介电常数, 但我们希望背景材料的介电常数可控, 也不能有很强的损耗. 另外考虑到本课题组具备成熟的微波光子晶体相关的实验条件, 我们拟在微波波段开展相关实验. 而微波波段的有效负介电常数最早就是由Pendry等^[13]在1996年提出通过金属网线阵列加以实现的, 并由Simovski等^[14]和Belov等^[15]对该理论进行了发展. 金属中电子的集体行为可以用等离子体来描述, 电子的负电荷和晶格上的正电荷是相互抵消的, 但在受到外力作用时, 电子会产生位移, 导致局部出现正负电荷的堆积, 进而产生回复力, 这种情况就会导致电子群体的简谐振动. 此时用以下公式来描述其振动频率, 即等离子频率: $ \omega _{\rm{p}}^2 = \dfrac{{n{e^2}}}{{{\varepsilon _0}{m_{{\rm{eff}}}}}}$.
等离子与电磁波的相互作用对金属产生了重要的影响, 其介电常数可用以下公式描述: $ \varepsilon (\omega ) = 1 - {{\omega _p^2}}/{{{\omega ^2}}}$.
对于晶格常数在毫米量级、金属柱半径在微米量级的金属柱阵列, 它的等离子频率恰好在微波的范围, 这刚好满足了我们的需要.
通过仿真计算, 当晶格常数a = 17.045 m, 氧化铝柱半径r = 3.75 mm, 当插入一个晶格常数为4.9205 mm, 金属柱半径为0.0375 mm的三角晶格金属阵列时, 体系的等离子频率为13.9 GHz. 当插入介质柱以后, 该结构的有效介电常数和磁导率经修正后为$ \varepsilon = 1 - {{{\left( {17.03~{\rm{GHz}}} \right)}}^2/{{{\omega ^2}}}}$, μ = 1. 如图5所示, 我们比较了COMSOL计算的实际插满金属柱的六角原胞(见图5插图)的体能带. 这个结果和用负有效背景材料的结果符合. 而利用紧束缚模型, 符合程度并没有那么高, 这是因为此结构中的介质柱间的耦合依旧相对较大, 使用第一近邻的紧束缚模型仍会有误差.
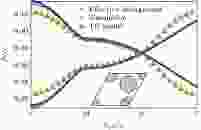图 5 金属柱背景下, 氧化铝蜂窝结构的光子能带(红色), 和其对应的背景替换为有效介质(蓝色)后得到的能带结果符合, 但用紧束缚模型(绿色)计算得到的能带略有差别. 原胞内的大圆代表介质柱, 小圆代表密集插入的细金属柱
Figure5. In the metallic background, photonic energy bands match well with the bands (Red) calculated with effective background constant (Blue). However, Tight Binding model’s result (Green) shows small variance compared to the real bands. In the schematic cell structure, bigger circle represents dielectric cylinder, while smaller circle represents thin metallic rod inserted.

2 -->

4.2.等离子体

除了使用金属线网格, 在微波波段, 依然可以使用等离子体材料放电来实现负介电常数^[16,17]. 通过外加电压来控制等离子体的浓度, 甚至可以进一步连续地控制介电常数的大小, 这样连续调控负背景的技术将给系统带来更大的便利. 我们也相信进一步将等离子体和光子晶体进行结合能实现更多创新实验.

拓扑光子学在过去的几年为拓扑物理和光学带来了重大的发展. 因为结构容易实现, 拓扑光子晶体被用于验证很多拓扑物理的相关理论^[18,19], 同样基于拓扑绝缘体的理论发展的光学单向传输器件^[20-22]也希望能为未来光通信提供新的思路. 因为电磁波和晶体中的电子不同, 在真空也可以传播, 因此光子晶体, 特别是空气/真空背景的光子晶体, 和紧束缚模型并没有良好的一一对应关系. 我们发现将背景材料改为具有负的介电常数的材料, 让电磁波在背景材料中以倏逝波存在, 这样具有负背景的光子晶体和紧束缚模型在一定参数空间下有一一对应的关系. 我们的数值模拟结果也验证了, 在类石墨烯光子晶体的之字形和胡须形界面上, 有界面态存在. 这些现象之前只能在光诱导光纤阵列的实验中才能被观测到. 同时, 我们提出了两种在微波实现负背景光子晶体系统的方法, 仿真和初步实验结果(未在本文发表)也证实了方法的有效性.
虽然本文的数值模拟仅仅研究了一个偏振下的二维情况, 但原则上没有任何难度就可以推广到三维, 在现有三维的光子晶体体系下紧束缚模型依旧是适用的. 而两个实验构想也都可以实现各向同性的有效三维负介电常数.和光诱导光纤阵列不同, 光子晶体系统无需使用光纤空间传播方向来代替时间轴来表达能量大小, 所以它完全可以对三维结构的拓扑性质进行研究. 同时, 如果采用等离子体放电的方式来构建背景负介电常数, 还可以通过对放电电压的调控来实现介电常数的连续可调, 为可调制拓扑光子学提供一个解决方案. 希望我们提出的微波实验验证平台, 能为研究拓扑物理提供全新的工具. 结合光学和拓扑物理学的新平台在凝聚态理论验证和新光学工具设计方面都有着非常大的潜力.