全文HTML
--> --> -->在拓扑半金属材料研究中, 许多实验表征手段都发挥了重要的作用, 例如输运、光学、扫描隧道显微谱学等. 而为了更好地探测拓扑半金属的电子结构, 获得材料电子的运动状态, 同时具有能量、动量分辨率的角分辨光电子能谱(ARPES)[21,22]是不可或缺的关键技术. ARPES测量不仅能给出单晶样品在三维动量空间中的能带色散、费米面、能隙等能带的综合信息, 还能获得载流子类型和浓度、有效质量、轨道对称性以及电子与其他自由度的多体相互作用等重要信息. 这些独特的能力使得ARPES在拓扑半金属的研究中占据了举足轻重的地位.
本文将系统回顾使用角分辨光电子能谱技术在拓扑半金属方面取得的研究成果, 对于具有代表性的材料总结其特征拓扑电子结构及物理内涵.
2.1.测量原理
角分辨光电子能谱技术基于光电效应现象: 用光照射材料, 如果光子能量大于材料的功函数, 那么材料内部的电子就能吸收光子从而逸出材料表面, 成为光电子(如图1(a)). 根据测得逸出光电子的能量和动量信息, 通过能量和动量守恒律, 能够反推出材料内部的电子运动行为, 即材料的能带结构.
图 1 (a)光电子能谱实验原理示意图; (b)光电子非弹性平均自由程与能量关系图; (c)光电效应过程的能量关系图示; (d) ARPES测量不同kz等能面示意图Figure1. (a) Illustration of a photoemission experiment; (b) curve of electric IMFP vs energy; (c) energetics of the photoemission process; (d) illustration different FSs measured by ARPES under different photon energies due to the kz dispersion in k-space of a 3D Fermi Surface.
ARPES测量信号主要来自于样品表面. 根据入射光不同能量, 出射的光电子动能在几至数百电子伏特左右, 根据图1(b)中电子非弹性平均自由程
ARPES的能量守恒过程如图1(c)所示. 测量出光电子的动能Ek之后, 通过能量守恒定律可以获得材料内部电子的束缚能EB = hν – Φ– Ek. 其中Φ为费米能EF和真空能级Evac之间的势垒(功函数).
电子动量可以被分解成两个方向来讨论: 平行于样品表面的动量k//(包括kx, ky)和垂直于样品表面的动量k⊥(kz). 由于表面势垒的存在, 只有k//在光电效应过程中守恒:
2
2.2.仪器设备
常见的ARPES系统由光源、电子能量分析器、样品操纵台、真空系统等组成.光源用以激发材料中光电子. 目前常用的供ARPES使用的光源包括: 深紫外激光、气体放电灯[26](如氦灯、氙灯等)和同步辐射光源[27]等. 深紫外激光光源往往采用倍频晶体(如?-硼酸钡(BBO), 氟代硼铍酸钾(KBBF)晶体等)或者气体非线性高次谐波过程产生深紫外激光. 氦灯能以冷阴极辉光放电的形式辐射出氦特征谱线, 常见能量为21.2 ev (He Iα)[28]. 同步辐射光源是最理想的ARPES光源, 它使用波荡器等在电子存储环内弯曲高速电子的运动轨道来获得同步辐射光. 同步辐射光具有较强亮度(第三代同步辐射光源可达到1011photons/s/0.01%BW@800 eV)且具有偏振及大范围光子能量调节能力[29], 广泛适用于各种材料体系的ARPES研究. 图2展示了一个典型的位于中国上海同步辐射光源的ARPES工作站(BL03U).
图 2 上海光源中同步辐射束线BL03U搭载的空间分辨角分辨光电子能谱实验工作站图Figure2. A picture of the synchrotron-based nano-ARPES workstation in SSRF BL03U.
电子能量分析器是收集并测量出射光电子的能量和发射角度(从而计算得到电子动量)的重要部件. 目前, 大多数ARPES装置使用的分析器是静电型半球型偏转分析器(hemispherical deflection analyzer, HDA), 它能在一次实验测量中提供沿某个动量方向的能带信息. 为了得到另一个动量方向的能带结构, 还需要改变样品角度或电子偏转电压以探测电子另一方向发射角的信息.
样品操纵台是安放、处理和操控样品位置和温度的设备. 通常有两个功能: 第一, 承载样品, 将样品送到测量位置, 并在测量中改变样品与能量分析器的相对角度和位置从而实现整个动量空间能带结构数据的获取; 第二, 通过冷却剂及加热器对样品温度进行控制, 测量电子结构随温度的改变.
真空系统由真空腔体和配套真空泵系统(含机械泵、分子泵、离子泵、钛升华泵及吸附泵等)构成. 它为测量提供超高真空环境(约10–11 Torr(1 Torr ≈ 133.322 Pa)), 以确保样品有较长寿命(较差真空中的残余气体分子会污染样品表面)和出射的光电子能到达电子能量分析器.
在拓扑狄拉克半金属中, 导带和价带交叠形成分立的四度简并的点—狄拉克点. 能带在狄拉克点附近行为满足狄拉克方程, 在各个动量方向均呈现线性色散关系(图3(a)). 狄拉克点受对称性(晶体对称性、时间及空间反演对称性)保护, 具有拓扑稳定性.
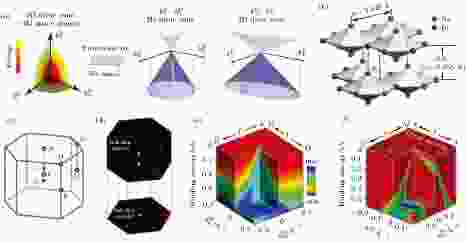图 3 (a)三维狄拉克费米子在能-动量四维空间示意图及其在不同三维能-动量子空间的投影; (b) Na3Bi的晶体结构示意图; (c) Na3Bi的第一布里渊区示意图; (d)在三维动量空间中的实验测量费米面(上半图)及其在表面布里渊区的投影(下半图) (e) (f)狄拉克点处沿kDy–kDx和kDy–kDz方向的三维光电子谱图Figure3. (a) Illustration of a 3D Dirac Fermion in 4D energy-momentum space and its projection onto different 3D subspace; (b) the crystal structure of Na3Bi; (c) 1st Brillouin zone of Na3Bi; (d) measured Fermi surface map across the whole 3D BZ (top panel) and its projection on the surface BZ (bottom panel) on pristine surfaces. 3D intensity plot of the photoemission spectra (e) along the kDy–kDx direction and (f) along the kDy–kDz direction at the Dirac point.
狄拉克半金属(DSM)可分为两类: 1)具有正立狄拉克锥, 满足洛伦兹不变性的第一类狄拉克半金属; 2)具有倾斜狄拉克锥, 破坏洛伦兹不变性的第二类狄拉克半金属. 经由调制费米能级, 第一类狄拉克半金属费米面能够只包含若干分立点, 而第二类狄拉克半金属则包含电子和/或空穴型口袋, 因此两者分别具有高磁阻、高迁移率和高载流子浓度、高电导率等电学输运重要性质.
2
3.1.第一类狄拉克半金属
首个经由理论预言且得到实验证实的第一类狄拉克半金属材料是具有三度旋转对称性的层状材料Na3Bi(图3(b)). 2012年, 物理所Wang等[12]的第一性原理计算预言, 在Na3Bi的动量空间中Γ-A方向存在一对三维狄拉克点(图3(e)). 这对狄拉克点由靠近费米面附近的导带和价带发生能带反转而相交形成, 其中, 价带顶大部分由Na(1)-3s提供, 导带底则大部分来源于Bi-6pxy轨道, 两带归属于不同的不可约表象. 由于体系同时存在空间和时间反演对称性, 能带相交形成的狄拉克点为4度简并. 并且, 该狄拉克点受Na3Bi晶体的三重旋转对称性的保护而得以稳定存在. 如果通过外加压力等方法打破晶体的三次旋转对称性, 则将引入相互作用项使其电子结构打开能隙变为绝缘体.随后, Liu等[18]用ARPES直接测得了Na3Bi的(001)解离面的能带结构, 并观测到了三维狄拉克点和狄拉克点附近沿各个动量方向的线性能带色散. 如图3(f)所示, 实验测得的沿着kz方向的费米面主要由A-Γ-A方向的两个点状费米面构成, 这两个点状费米面就是三维体狄拉克点. 进一步地, 在狄拉克点附近可以通过扫描kx–ky–E电子结构以及通过能量依赖扫描ky–kz–E电子结构, 验证围绕狄拉克点的电子能带呈现线性色散(三维狄拉克锥)(如图3(e)和图3(f)). 通过这些特征电子结构, ARPES直接证明了Na3Bi为三维拓扑狄拉克半金属.
在狄拉克半金属中, 一个狄拉克点往往可以看作是两个手性相反的外尔点重合而构成(由于旋转对称性的保护, 重合的外尔点没有发生“湮灭”而打开能隙), 那么可能会出现连接狄拉克点的拓扑表面态. 对Na3Bi而言, 这个拓扑表面态不会出现在(001)面上(在表面布里渊区中, 两个狄拉克点重合在一起), 但很可能会出现在与(001)面垂直的侧面解理面上(如沿(100)面解理[30,31], 图4(d)—图4(f)). 图4(b)和图4(c)展示了(100)面测得的能带结构, 可以观察到动量空间中Γ点附近连接两个狄拉克点的一对费米弧表面态(图4(a)和图4(b)). 由于晶格对称性的保护, 体态的三维狄拉克点和非平庸的表面电子态(如图4(b), 图4(c)和图4(f)中费米弧表面态SS)可以同时稳定存在, 沿
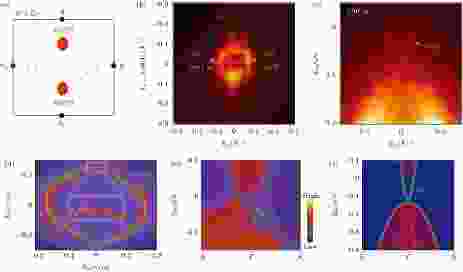图 4 (a)沿(100)解理的Na3Bi费米面示意图; (b) ARPES实验测得的费米面图像; (c)图(b)中沿α方向切出的能谱; (d)费米弧的理论自旋织构图; (e)沿
Figure4. (a) Schematic of Fermi surface in Na3Bi cleaved along (100) direction; (b) Fermi surface measured by ARPES experiment; (c) spectrum cut along α from (b); (d) theoretical calculated spin texture of Fermi arcs; (e) band structure along
除了Na3Bi之外, 通过理论计算和实验验证还发现了Cd3As2也是一种典型的拓扑狄拉克半金属[17,19,32]. Cd3As2具有较复杂形成缺陷序的晶体结构, 但其特征拓扑电子结构(三维狄拉克点构型和狄拉克锥)与Na3Bi较为类似. 此外, 相比Na3Bi, 此材料的优势是在空气中稳定, 并具有极高的体态电子迁移率(130 K时可达40000 cm2·V–1·s–1), 及相当大的线性量子磁阻等优良性质[33]. 最近, 研究者在Cd3As2纳米片中观测到手性异常导致的平面霍尔效应[34], 且获得了由外尔轨道形成的新型三维量子霍尔效应的直接证据[35]. 此外, 从此材料出发能够诱导出一系列拓扑相, 如在压力驱动下破坏晶体对称性后可被驱动至拓扑绝缘体和Weyl半金属态, 在二维极限下变为具有较大能隙的量子自旋霍尔绝缘体相等, 为研究新奇拓扑和拓扑相变提供了优良的材料平台.
2
3.2.第二类狄拉克半金属
由于凝聚态物理中的准粒子激发不需要遵循高能粒子的洛伦兹不变性, 在拓扑量子材料中研究者们可以观测到粒子物理学标准模型描述的基本粒子外的新型准粒子激发. 如第二类狄拉克费米子破坏了洛伦兹不变性, 其狄拉克锥色散会沿动量空间中的特定方向发生显著倾斜, 从而导致动量空间中能量-动量关系的剧烈变化. 例如在第二类狄拉克半金属PtSe2[36,37]中, 狄拉克锥在面内(kx–ky–E空间)呈现与第一类狄拉克半金属类似的正立锥形状(图5(a)—图5(c)), 而在面外(kx–kz–E方向)则呈现出显著倾斜的狄拉克锥形状(图5(d)和图5(e)). 此形状预示着较大的狄拉克型载流子浓度, 从而第二类狄拉克半金属带来高电导率等各项奇异物性.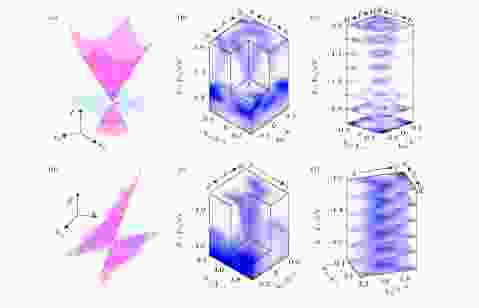
图 5 第二类狄拉克锥的三维示意图 (a)投影在kx–ky–E空间上的第二类狄拉克锥简图; (b) PtSe2中kx–ky面内切过第二类体狄拉克点的三维色散能谱图(光能24 eV), 狄拉克点由紫色箭头指出; (c)放大的图(b)中ARPES等能面堆叠图; (d)投影在ky–kz–E空间上的第二类狄拉克锥简图; (e)三维kz依赖的色散能谱图(光能18—33 eV); (f)放大的图(e)中ARPES等能面堆叠图Figure5. 3D visualization of type-II Dirac cone: (a) Schematic of type-II Dirac cone projected on kx-ky-E space; (b) 3D ARPES map (hν = 24 eV) which slices through the type-II BDP (pointed out by magenta arrow); (c) zoomed-in ARPES constant energy contours (CECs) of Fig.(b); (d) schematic of type-II Dirac cone projected on kx–kz–E space; (e) 3D kz-dependent map (hν = 18–33 eV); (f) zoomed-in ARPES CECs of Fig. (e).
下面以1 T相的过渡金属二硫化物类材料(如PtTe2[38], PdTe2[39-42]等)为例介绍第二类狄拉克半金属的形成机制. 成键、晶体场劈裂以及自旋轨道耦合会导致原子p轨道产生能级劈裂. 由于面外pz轨道与面内的px或py轨道相比具有更大的z方向延展性, 往往会表现出各向异性. 特别是, px或py轨道产生的能带(图6(b)中的E带)随kz变化而出现的色散变化很小, 而pz轨道产生的能带(图6(b)中的A1带)则受kz变化的影响很大. 当层间跳跃产生的影响大于晶体场劈裂时, A1带将与E带相交叉. 其中宇称相反的
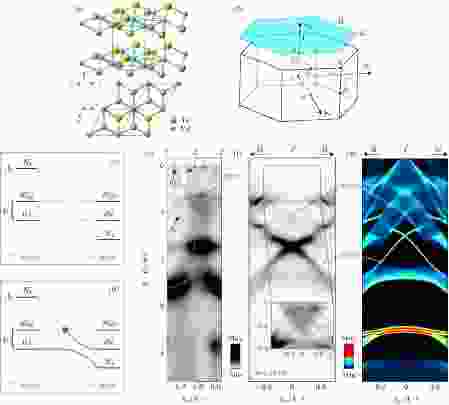图 6 (a) PdTe2型材料的晶体结构(及其俯视图)和(b)第一布里渊区(蓝色所示为(001)表面布里渊区); (c)忽略杂化和(d)考虑杂化时晶体场产生的能级随kz动量变化的演化, A1与E产生的能级在绿点处出现受保护的交界点; (e)沿Γ-A-Γ方向的ARPES能谱(横轴为光能80?132 eV对应的kz区间), 黄线为理论计算的能带; (f)沿表面布里渊区
Figure6. (a) Crystal structure (with its top view) and (b) 1st Brillouin zone (with surface BZ marked in blue) of PtTe2; (c) (d) evolution of crystal-field-derived levels with the out-of-plane kz momentum when hybridization is (c)neglected or (d)included, showing a protected crossing of the A1 and E-derived levels; (e) ARPES spectrum along Γ-A-Γ direction (kz corresponding to hv = 80?132 eV) with calculated bands (yellow lines) attached; (f) ARPES spectrum along
以过渡金属二硫化物中的PdTe2为例, PdTe2的晶体为如图6(a)所示的三角晶格(No.164 P-3m1空间群), 动量空间第一布里渊区为六棱柱(如图6(c)). 在ARPES实验随kz变化测量所得的Γ-A方向能谱(图6(e))中, 可以发现在靠近高对称A点的费米面以下约0.65 eV处, 能带R4与R5, 6交叉处出现与第一性原理计算预言(图6(e)中橙线和图6(g))相符合的第二类体态狄拉克点. 在入射光能为24 eV时, E-ky的能谱图中清楚地看到费米面下的第二类狄拉克点(如图6(f)中小图). Pt族过渡金属二硫化物体系中的第二类狄拉克半金属涉及三条以上能带的能带反转, 因此可形成丰富的拓扑非平庸表面态, 如图6(g)中在更高结合能能带反转产生的能隙中(费米面下约1.1和1.7 eV处)发现了由拓扑表面态交叉而成的狄拉克锥.
2
3.3.破坏时间反演对称性的狄拉克半金属
除上述介绍的同时满足时间和空间反演对称性的狄拉克半金属材料之外, 近期有理论预言存在破坏时间反演对称性的狄拉克半金属, 如CuMn As[43,44], FeSn[45,46], EuCd2As2[47,48], EuCd2Sb2[49] 等. 这给狄拉克半金属的材料探索拓展了新的方向.如华中科技大学的Hua等[50]通过DFT计算预言层间反铁磁材料EuCd2As2是仅有一对狄拉克点的反铁磁狄拉克半金属. 在该体系中, 尽管时间反演对称性被打破, 但系统具有在非点式空间操作和时间反演联合操作下的对称性, 这和体系的空间反演对称性一起确保了体系能带的两重简并和体狄拉克点的四重简并. 近期ARPES研究则观察到了EuCd2As2顺磁相中由于自旋涨落破坏时间反演对称性诱导的外尔半金属态[48].
此外反铁磁的Kagome层状材料FeSn被理论预言处于反铁磁狄拉克半金属态. 该狄拉克点源自Kagome对称性下的面内局部Fe3d轨道[45], 受到时间-空间反演联合对称性和非同构S2z对称性保护. 打破某一对称性能够将无质量狄拉克费米子转换为无质量的外尔费米子或有质量的狄拉克费米子[46].
磁性狄拉克半金属为研究拓扑和强关联电子的耦合以及自旋电子器件等应用探索提供一个理想的平台, 因此成为了拓扑材料研究的新热点之一.
在凝聚态物理体系中, 从拓扑狄拉克半金属出发, 通过打破晶体对称性或者时间反演对称性的保护, 研究者们可以实现拓扑外尔半金属态, 其中四重简并的狄拉克点分离为一对两重简并且手性相反的外尔点, 不同手性的外尔点之间会有费米弧表面态(非闭合的费米面)相连接, 这种表面态投影形成的费米弧以及体态外尔锥是外尔半金属(WSM)根本的特性. 这些非平庸的拓扑能带结构能导致一系列重要的物理现象, 包括手性反常、三维量子霍尔效应、非局域电磁效应等.
破缺时间反演或者空间反演对称性, 是形成外尔半金属相的先决条件(但若两者同时破缺, 能带交叉会形成四度简并的狄拉克点). 与狄拉克半金属一样, 也可以把外尔半金属分为第一类和第二类外尔半金属.
2
4.1.第一类外尔半金属的角分辨光电子能谱研究
34.1.1.空间反演对称性破缺的外尔半金属
虽然最早的拓扑外尔半金属在破坏时间反演对称性的体系中(如HgCr2Se4[51]及Y2Ir2O7[11])被预测, 但由于实验和样品制备的困难, 拓扑外尔半金属相在破坏空间反演对称性的系统中获得实现, 首个发现的外尔半金属体系是TaAs家族化合物, 由中国科学院物理所的Lv等[52, 53]、普林斯顿大学的Xu等[20]及清华大学的Yang等[54, 55]完成了实验发现. TaAs晶体为体心四方结构(如图7(a)), 空间群为破坏空间反演对称性的I41md (No.109). 中科院物理所Weng等[56]通过理论计算预言其动量空间布里渊区中存在12对24个手性相反的外尔费米子, 图7(c)中红色和蓝色标出的点即手性分别为–1和+1的外尔点, 其中8个外尔点(称作W2)分布在ΓΣΧ面上, 而另外16个外尔点(称作W1)分布于面外的布里渊区中, 不同手性的成对外尔点之间由费米弧表面态相连(如图7(c)(iii)), 这些特征拓扑电子结构证实了TaAs外尔半金属的性质. 外尔点附近的贝里曲率呈刺猬状分布, 这与实空间中点电荷产生的电场分布类似, 手性为–1的外尔点的贝里曲率皆从内向外发散, 手性+1的则反之, 这表明了它们是“动量空间中的磁单极子”(如图7(b)).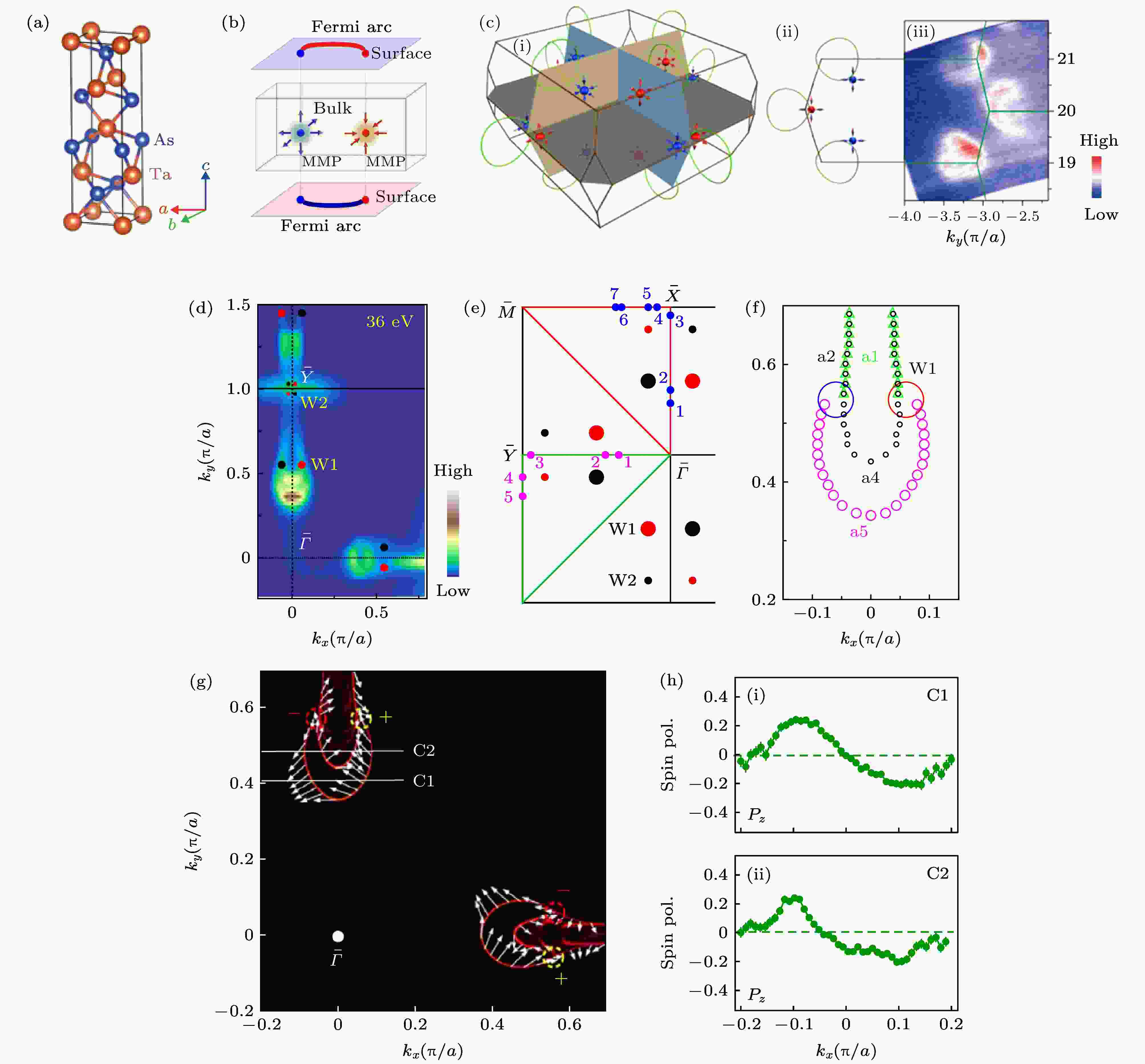
图 7 (a) TaAs的晶体结构; (b)有自旋极化费米弧的外尔半金属电子结构图示(红色和蓝色分别代表不同的手性. 为清晰起见, 图中只画出了顶面和底面的表面态); (c)理论计算的第一布里渊区中外尔费米子及费米弧位置及其(ii)俯视图, (iii)为费米能级处ky–kz面上(kx = 0)光电子强度谱的等能面能谱, 绿线为ky–kz面上的布里渊区边线; (d)ARPES实验(光能36 eV)所得的kx–ky费米面; (e)选取闭合路径计算能带穿越费米面数目的示意图, 紫色及蓝色圆点代表能带穿越
Figure7. (a) Crystal structure of TaAs; (b) schematic of a WSM electronic structure with spin-polarized Fermi arcs connecting projections of two bulk Weyl nodes (The red and blue colors represent opposite chirality. For clarity, only surface states on the top and bottom surfaces are indicated); (c) (i) calculated position of Weyl Fermions and Fermi arcs in 1st BZ with its (ii) top view; (iii) shows the photoemission intensity plot at EF in the ky–kz plane at kx = 0 (The green lines represent the BZ structure in the ky–kz plane.); (d) Fermi surface measured by ARPES experiment (hv = 36 eV); (e) illustration of band numbers crossing an arbitrary k loop. Blue and magenta circles indicate the locations where the bands cross the enclosed k loop
利用基于同步辐射的ARPES实验能够在TaAs的(001)面上直接观测到这些特征拓扑电子结构. 如图8所示, 通过使用较高光能的光子, 能够抑制表面电子态的影响, 从而主要测量来自于体态的光电子能谱[20]. 经过调整光子能量探测到合适的布里渊区位置, ARPES实验能够观测到成对出现的外尔点和呈现线性色散的外尔锥. 而通过较低光子能量对表面电子态更为敏感的ARPES测量, 能在费米面上观察到连接不同手性外尔费米子投影的费米弧. 如图7(d)所示, 在成对外尔费米子投影W2和W1附近, ARPES测量能找到多套表面态, 其中包含有平庸表面态及非平庸费米弧态(如图8(f)中圈出的连接成对外尔点W1的两条弧线). 对其中的费米弧的具体认定尚有争议, 但其存在性可以通过选取闭合路径计算穿越费米面数目为奇数次的方式证明(图7(e)) [52]. 此外, 费米弧具有非平庸自旋织构(如图7(g)中白色箭头所示). 图7(h)中揭示了通过自旋分辨ARPES方法测量TaAs的费米面自旋织构情况. 沿着C1, C2方向能够观察到在费米弧不同区域Pz方向自旋的符号改变(图7(h)).
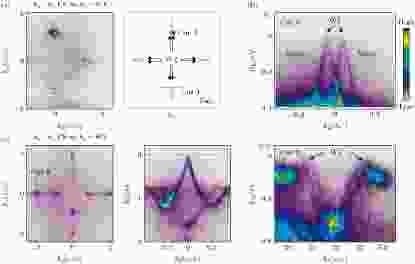图 8 软X射线ARPES下TaAs中体外尔锥和外尔点观测图 (a) kz穿过外尔点W1时候采得的费米面及其理论简图; (b) (i)沿图(a)中cut1, cut2方向切出的角分辨光电子能谱图; (c) kz穿过外尔点W2时候采得的费米面及沿cut3方向切出的能谱; 过外尔点W1, W2均可看到线性色散外尔锥Figure8. Observation of bulk Weyl cones and Weyl nodes in TaAs using SX-ARPES: (a) Measured and first principles calculated kx-ky Fermi surface maps at the kz value that corresponds to the W1 Weyl nodes; (b) ARPES spectra cut along (i)cut1 and (ii)cut2 from Fig. (a); (c) measured kx-ky Fermi surface maps at the kz value that corresponds to the W2 Weyl nodes as well as the spectrum cut along cut3. Linearly dispersive Weyl cones of both W1 and W2 can be observed.
除了TaAs之外, 研究者发现同族化合物TaP[57], NbP[55,58], NbAs[59]均为拓扑外尔半金属, 且成功观测到了体外尔锥及表面态费米弧等特征电子结构. 通过结合理论计算和ARPES测量能带结构, 研究者们可以系统研究此家族材料能带结构的系统演化[55]. 根据理论预言, 如图9(a)中所示, NbP, TaP, TaAs内原子质量增大时, 晶体中自旋轨道耦合作用增强, 因此具有不同手性成对外尔点的间距以及连接两外尔点的表面态费米弧长度会逐渐增加. 图9(b)—图9(d)中是三种不同材料通过ARPES实验测得的能谱, 直观地展示了费米面上外尔点的分离以及费米弧的变化. 其中不同材料中的外尔点的劈裂ΔK1及费米弧与其他表面态的分裂ΔK2随着SOC增强结果总结于图9(e).
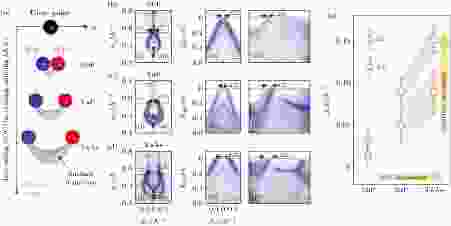图 9 (a) TaAs家族中不同自旋轨道耦合强度材料中手性相反外尔点的位置演化图; (b)—(d)高分辨ARPES测量的NbP, TaP和TaAs的(i)勺状费米面以及(ii) (iii)沿C1, C2红虚线方向的能谱; (ΔK1和ΔK2分布代表外尔点、费米弧的分离程度); (e)统计得到的ΔK1和ΔK2随三种不同材料自旋轨道耦合强度变化图像Figure9. (a) Illustration of the separation of Weyl points (with opposite chirality, marked as WP+ and WP–) in different materials of TaAs family with increasing spin-orbital coupling effect; (b)–(d) high-resolution ARPES measurements on the (i) spoon-like FS and (ii, iii) associated band dispersions indicated by the red dotted lines for NbP, TaP and TaAs, respectively (ΔK1 and ΔK2 represent the separation between the Weyl points and Fermi arcs, respectively.); (e) summary of the extracted ΔK1 and ΔK2 from the three compounds, plotted against the SOC strength
3
4.1.2.时间反演对称性破缺的外尔半金属
除了空间反演对称性破缺的材料, 拓扑外尔半金属相也能在破坏时间反演对称性的材料中获得. 与空间反演对称性破缺的外尔半金属相比, 时间反演对称性破缺的外尔半金属(也常被称为磁性外尔半金属)有其独特的优点. 例如这类材料最少可以只包含一对外尔点(如图10(b)所示), 从而被誉为外尔半金属材料中的“氢原子”. 此简单性更有利于通过调控参数(磁性、电子关联及拓扑序等)实现手性反常效应、手性磁效应、显著的反常霍尔效应甚至量子反常霍尔效应等(如图10(a)). 同时, 时间反演对称性破缺的外尔半金属也是制备自旋电子器件的重要候选材料之一. 然而, 由于材料制备和实验表征等诸多困难, 在2011年被理论预言的磁性外尔半金属材料体系(如Mn3Sn[60], HgCr2Se4[51]等)至今一直没有被证实. 最近发现的Co3Sn2S2材料中(晶格结构及动量空间布里渊区如图10(c)和图10(d)所示)[61,62], 低温(175 K)发生的铁磁相变形成了时间反演对称性破缺. Liu等[61]利用先进的同步辐射高分辨角分辨光电子能谱手段, 完整观测到了磁性Weyl半金属的两大标志性特征: 线性色散的Weyl体能带(图10(f))和连接Weyl点的拓扑表面态费米弧(SFA)(图10(e)), 从而在实验上首次证实了Co3Sn2S2材料确为时间反演对称性破缺的外尔半金属.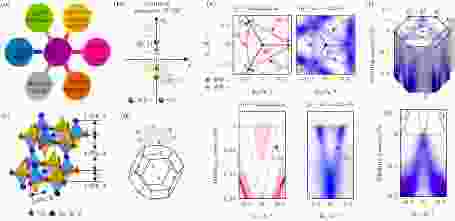
图 10 磁性Weyl半金属Co3Sn2S2 (a)磁性Weyl半金属及其丰富的近邻量子态; (b)时间反演破缺使狄拉克费米子(DP)劈裂产生一对手性相反的外尔费米子(WP)示意图; (c) Co3Sn2S2晶体结构及(d)动量空间中(001)面外尔点和费米弧表面态分布示意图; (e)费米弧表面态所形成费米面的理论计算(i)和实验结果(ii)比较以及费米弧表面态能带色散的理论计算(iii)和实验结果(iv)比较; (f)费米面上的Weyl点(i)及其能带(ii)的三维演示; (ii)中过Weyl点的线性色散为(i)中灰色平面位置所切取, 红色的叠加曲线是理论计算结果Figure10. Magnetic Weyl semimetal Co3Sn2S2: (a) Exotic neighboring states of the magnetic WSM can be achieved by tuning parameters such as magnetism, thickness, and electron correlation; (b) illustration of DP splitting (into one pair or two Weyl points) caused by time reversal symmetry broken in simplest magnetic WSMs. Magenta and green color of the Weyl points represent positive (+) and negative (–) chirality, respectively; the arrows illustrate the Berry curvature. k: momentum; s: spin; WP: Weyl point; IS: inversion symmetry; (c) crystal structure of Co3Sn2S2 and (d) schematic of the bulk and surface Brillouin zones along the (001) surface of Co3Sn2S2, with the Weyl points marked and connected by SFAs (yellow line segments); (e) comparison of the calculated (i) FS, (iii) band dispersion from both bulk and surface states and the corresponding experimental data of (ii) FS, (iv) band dispersion at 124 eV; (f) (i) 3D ARPES spectra intensity plot measured with Weyl points emerge (marked by green arrows). (ii) The band measured at 10 K, cutting from (i) with grey surface, shows a linear dispersion across the Weyl point, agreeing well with the calculations (red curves overlaid).
2
4.2.第二类外尔半金属
与拓扑狄拉克半金属类似, 当外尔费米子破坏洛伦兹不变性时, 会出现所谓第二类的拓扑外尔半金属[63]. 第二类外尔半金属的特征电子结构, 表现为沿某个动量方向显著倾斜的两个相互交叠的外尔锥且外尔锥的两个二重简并点处有受拓扑保护的费米弧表面态相连(图11(a)), 此类特征电子结构会带来各向异性磁输运性质如手性异常、反常霍尔效应等一系列奇异物理性质.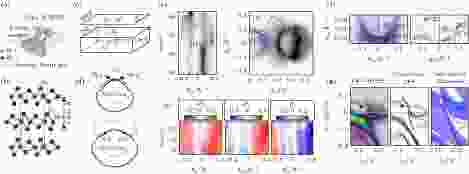
图 11 (a)第二类外尔费米子在动量空间中示意图; (b) Td-MoTe2的晶体结构及其(c)第一布里渊区示意图; (d)理论计算的W1和W2外尔费米子及费米弧在等能面上的位置; (e) (i)温度30 K下沿
Figure11. (a) Schematic illustration of type-II Weyl Fermions in the momentum space; (b) crystal structure and (c) 1st Brillouin zone of Td-MoTe2; (d) calculated W1 and W2 Weyl Fermions and Fermi arcs on CECs; (e) (i) photon-energy dependent ARPES data (T = 30 K) plot along
首个实验上发现的第二类外尔半金属体系是Td相的二碲化钨及二碲化钼(WTe2和MoTe2)[64-68]. 由于其较强的自旋轨道耦合强度, MoTe2体现出了较明显的拓扑电子结构. MoTe2的晶格结构是三层Te-Mo-Te原子层堆叠而成的单斜晶胞(No.31 Pmn21空间群)(如图11(b)). 根据理论计算(图11(c)), 显著倾斜的外尔锥与费米面相切, 形成空穴口袋和电子口袋, 两者相交处形成成对的外尔点(根据不同的计算假设, Td-MoTe2中外尔点位置处于费米能级EF以上5[69]—55 meV[70], 而外尔点数量为4个[70-74]或8个[66-69,75,76]). 而连接外尔点的表面态费米弧分布在空穴口袋和电子口袋之间的狭小能隙里(图10(d)). ARPES技术直接测得了MoTe2作为第二类外尔半金属的基本特征—显著倾斜的狄拉克锥和拓扑表面态费米弧. 对应于图11(d)中理论计算的费米面, 可以分辨图11(e)(ii)中电子、空穴口袋的位置并找到体带的表面态、费米弧等迹象. 特别地, 我们注意到, 由于理论预测的外尔点位置处于费米面之上, ARPES直接在费米面测得的信号来自于费米弧的投影. 清华大学Wan等[77]利用泵浦-探测ARPES技术测量未占据态能带结构, 并成功获得了外尔点和费米弧的直接实验证据(如图11(g)). 此外, 图11(e)(i)为温度30 K下在ky ≈ 0.05 ?–1处沿
同时, 研究者们通过理论研究发现, 通过样品参数调制(晶格常数、掺杂等)能够诱导出第二类外尔半金属的拓扑相变, 使得外尔点的个数, 费米弧的连接方式等发生变化, 导致材料出现不同的拓扑性质. 例如, 由于W和Mo原子的不同原子质量及自旋轨道耦合作用强度, 研究者们通过在WxMo1–xTe2[79]中改变W和Mo在晶格中的占比来获得不同晶格常数和费米弧拓扑性质的第二类外尔半金属[70,80]. 继WTe2/MoTe2[81-83]之后, 已证实的第二类外尔半金属还有LaAlGe[84], Ta/NbIrTe4[85-87]等. 第二类外尔半金属相较于已发现的第一类外尔半金属而言有更少的外尔点数量和费米面上非零的电子态密度, 这将会为研究反常霍尔效应等新奇的电子效应提供很好的平台.
5.1.多重简并外尔半金属
对于拓扑半金属, 除狄拉克半金属之外, 晶体对称性能够保护多重对称性, 如三重、六重简并费米子可以在有半整数角动量费米子激发的空间群中找到, 受非点式空间群对称性或者时间空间反演对称性保护[88-92]. 此种不连续的分立空间对称性导致的新型费米子突破了人们对基本粒子的认识. 除了对基础物理理解的突破, 具有多种简并度的费米子有着独特的表面态和输运特性[91-93]. 在理论预言的若干种材料中, 第一性原理的计算结果预言在几种碳化钨结构材料的电子能带结构中具备三重简并点[94,95]. 中国科学院物理研究所的Lv等[96]对上述体系材料中的MoP这一材料进行ARPES电子结构表征, 验证了MoP的电子结构中具备三重简并的费米子存在.MoP晶体处于No.187 P6/mm空间群, 具有C3Z旋转对称性, 以及My和Mz镜像对称性(图12(a)和图12(b)). MoP的能带计算显示, 在Γ—A方向上, 存在多重能带简并情况, 图12(d)和图12(e)绘制出无自旋轨道耦合以及有自旋轨道耦合这两种情况下三重简并点所在的位置. 当无自旋轨道耦合时, Γ-A方向上存在一个三重简并点, 由一个非简并的dZ2轨道能带和一个二重简并的eg(dxy和
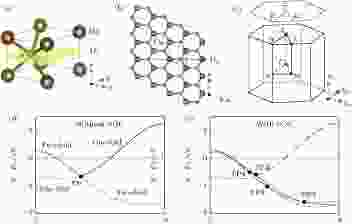图 12 MoP的晶体结构及动量空间Γ—A方向能带结构图示 (a) MoP的三维晶体结构及(b) Mz方向(黄色面)俯视图; (c)体布里渊区和投影的(001)表面布里渊区; (d)不考虑及(e)考虑自旋轨道耦合时沿Γ—A方向的理论能带结构. 交叉点处的黑点表示三重简并点. 颜色混合标注的曲线表示双重简并能带, 纯色曲线表示非简并带Figure12. Crystal structure and band structure of MoP along the Γ–A line in the momentum space: (a) Three-dimensional crystal structure of MoP and (b) the top view of the lattice showing the C3Z rotation symmetry with respect to molybdenum (brown spheres) or phosphorous (green spheres) and the My mirror plane (horizontal red line); (c) bulk Brillouin zone and the projected (001) surface Brillouin zone; (d) (e) calculated band structures along Γ–A (d) without and (e) with SOC. The black spots at the crossing points indicate the triply degenerate points. The curves with mixed colors represent doubly degenerate bands, curves with pure color represent non-degenerate bands.
对MoP的ARPES结果显示, 在布里渊区中, 沿C2的高对称A点附近的能谱上可以观察到两个二重简并能带, 如图13(b)所示. 沿A—Γ方向演化时, 两条能带中处于上部的能带保留其二重简并的特性, 而处于能量下部的W形状能带则劈裂成了上下两支非简并的能带, 如图13(c)所示. 其中下部的一条非简并上支能带沿着A-L方向与电子口袋状二重简并能带接触, 从而形成一个三重简并点(如图13(a)和图13(e)中TP1), 位于Γ—A方向上kz = 0.75π/c处.
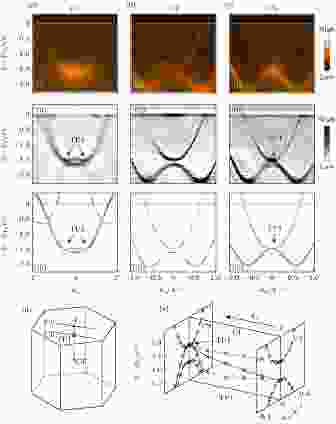图 13 拓扑简并点TP1附近的电子结构 (a)—(c)沿C1, C2, C3方向((i)—(iii))的ARPES及其能带曲率谱图与理论计算能带色散; (d) C1, C2, C3方向在体布里渊区中的位置示意图; (e)沿C1演化的TP1点附近能带分布三维色散图. C1能谱由(100)解理面采得而C2, C3由(001)解理面采得Figure13. Electronic structure near TP1. (a)-(c) (i) ARPES, (ii) curvature intensity plots and (iii)calculated band structure along (a) C1, (b) C2 and (c) C3; (C1, C2, C3 are blue and green lines indicated in (d)) (e) 3D plot of the band dispersions along C1 near TP1. Spectrum along C1 is recorded on the (100) cleavage surface; those along C2 and C3 are obtained on the (001) cleavage surface.
2
5.2.新型手性费米子
手性一词指一个物体不能与其镜像相重合的现象, 相对论中的手性讨论了自旋与动量的关系, 如外尔费米子就是一种具有手性的粒子. 如固体中包围能带简并点的费米面具有非零的Chern数, 则该简并点具有手性, 而此时费米面上的低能准粒子激发是具有磁荷的手性费米子. 手性相反的简并点在表面上的投影被费米弧表面态所连接. 如狄拉克点和三重简并点都可以看成是一对手性相反的外尔点的叠加, 但可以通过外加条件破缺对称性(如外加磁场), 退简并成手性的外尔费米子.发现外尔费米子之外的新型手性费米子具有重要的科学意义. 2019年科学家们在手性晶体CoSi[97,98], AlPt[99], PdBiSe[100]等体系中预言并发现了若干非常规的新型手性费米子, 以CoSi为例, 在其体态布里渊区的中心Г和顶角R点分别存在三重和四重能带简并点. 与MoP, WC中的三重简并点和Na3Bi, Cd3As2中的四重简并的狄拉克点不同, 它们是陈数C = ± 2的手性的简并点, 而费米面上的低能准粒子激发是磁荷为2的手性费米子, 分别被命名为spin-1(图14(a)(iii))和charge-2费米子(图14(a)(iv)). 由于CoSi中一个布里渊区仅容纳一对新型的手性费米子, 且两种手性相反的新型费米子间相隔极远, 横跨一整个布里渊区(如图14(b)(ii)). spin-1和charge-2费米子在(001)面上的投影由穿过整个表面布里渊区的费米弧相连接(图14(e)中蓝线), 这给出了CoSi中存在新型手性费米子的确定证据. 与CoSi类似的材料还有RhSi[98], AlPt[99]等, 其中AlPt为具有磁荷为4的手性费米子, 处于布里渊区中的高对称点, 分别被命名为spin-1和spin-3/2.
图 14 (a)四种费米子的能带示意图; (b)外尔半金属(上)与CoSi(下)中连接手性相反费米子投影的费米弧图示; (c) CoSi的晶体结构及(d)第一布里渊区示意图; (e)三维动量空间中手性边界态与费米弧示意图; (f), (g)理论计算和实验得出的CoSi费米面结果; (h)沿图(g)中Loop1和Loop2所示切出的k//面内能谱Figure14. (a)Schematics of the band structures of a Weyl Fermion, a Dirac Fermion, a spin-1 Fermion and a charge-2 Fermion; (b) schematics of the Fermi arcs connecting the projections of Fermions with opposite chiralities for Weyl semimetals(up) and CoSi (down); (c) crystal structure and (d) 1st Brillouin zone of CoSi; (e) diagram of chiral edge states and Fermi arcs in 3D momentum space; (f), (g) theoretical and experimental results of Fermi surface in CoSi; (h) in-plane (along k//) spectra cut along Loop1 and Loop2 in Fig. (g).
6.1.拓扑节线半金属
在三维动量空间中, 两条能带的交叉闭合不仅可能形成独立的零维交叉点(如狄拉克点、外尔点); 还有可能形成连续的一维曲线, 这样的半金属材料被称为节线半金属[101](如图15(a)). 在这类材料中, 节线的存在是受对称性保护的, 一旦对称性破缺, 则能带交叉的节点线处会完全打开能隙或者闭合的节线变成几个独立的能带简并点.
图 15 (a)狄拉克点与节点线图示; (b) MSiS(M = Zr/Hf)材料的晶体结构和(c)第一布里渊区(及(001)表面布里渊区)示意图; (d) ZrSiS中光能436 eV下(kz = 0)测得的三维能谱图, 展示了的节点环能带结构; (e)沿kz方向演化的狄拉克节点线图示及对应的从Γ-X-Γ到Z-R-Z的ARPES能谱; (f)理论计算和实验得出的ZrSiS费米面(i) (iii)表面态及(ii) (iv)纯体态结果; (g) Co2MnGa中的鼓面表面态图示Figure15. (a) Schematic illustration of Dirac node and Dirac nodal line in the momentum space; (b) crystal structure and (c) 1st Brillouin zone (together with surface BZ) of MSiS (M = Zr/Hf); (d) 3D intensity plot of spectra measured in ZrSiS with hv = 436 eV, showing the band structure of the nodal ring when kz = 0; (e) schematic of the band structure hosting a Dirac nodal line along kz direction as well as corresponding ARPES spectra from Γ-X-Γ to Z-R-Z; (f) calculated and measured Fermi surface of ZrSiS with surface and bulk states respectively; (g) schematic of topological drumhead surface states in Co2MnGa.
节线半金属最初是在2011年由Burkov等[102]首次提出的, 随后研究者们通过第一性原理计算预言了一大批候选材料, 如MSiS(M = Zr或Hf)、Cu2Si薄膜[103]、MgSrSi型材料[104]等. 截至目前, 已被实验研究证实是节线半金属的有PbTaSe2[105], PtSn4[106-107], MSiS(M = Zr, Hf)型材料[108-111], IrO2[112], InBi[113]等材料, 甚至在铍、镁等碱土金属单质[114]中, 也发现了与理论结果相符合的狄拉克节线量子态. 其中, MSiS系列的材料能带结构较为理想, 费米面附近节线、表面态差别明显[115], 下面以它为例子来介绍节线半金属.
MSiS型晶体为四方结构(No.129 P4/nmm空间群), 自然解理面为(001)面, , 实验测得的动量空间中能带色散如图15(d)所示. 理论预言在高对称R—X及M—A方向上存在一类节线, 在Γ—M方向附近存在另一类节线. 第一类节线受非点式空间群对称性保护, 在自旋轨道耦合作用下稳定, 但其具有平庸的拓扑数, 而第二类节线结构具有非平庸拓扑数, 但其在自旋轨道耦合作用下能打开能隙. 通过光能依赖的ARPES实验, 能够测得第一类节线结构, 如图15(e)所示, Γ—X—Γ方向上在费米面下约0.6 eV处产生狄拉克点, 并且随着R-X方向kz变化, 能带简并处的狄拉克点始终存在并在能量方向上下浮动, 构成了一条典型的节线. 而第二类节线由于处于费米面附近, 其整体结构较难测量完成. 此外2019年物理所的Fu等[116]通过软X射线ARPES测量空气中解理的ZrSiS样品得到了与图16(f)(ii)纯体带计算相符的干净体态费米面(图16(f)(iv)), 在体态中偏离高对称的方向时(如图16(a)中分别偏离X—M, L—H, R—A方向的C4, C5, C6), 节点线会出现劈裂并沿所在面的法线方向(如图16(b)中的kx方向)形成狄拉克锥型的能带交叠(如图16(b), 图16(c)和图16(d)), 这就在布里渊区的边界kx=π或ky=π处（例如R-X-M-A面）构成了二维的节点面结构[116].
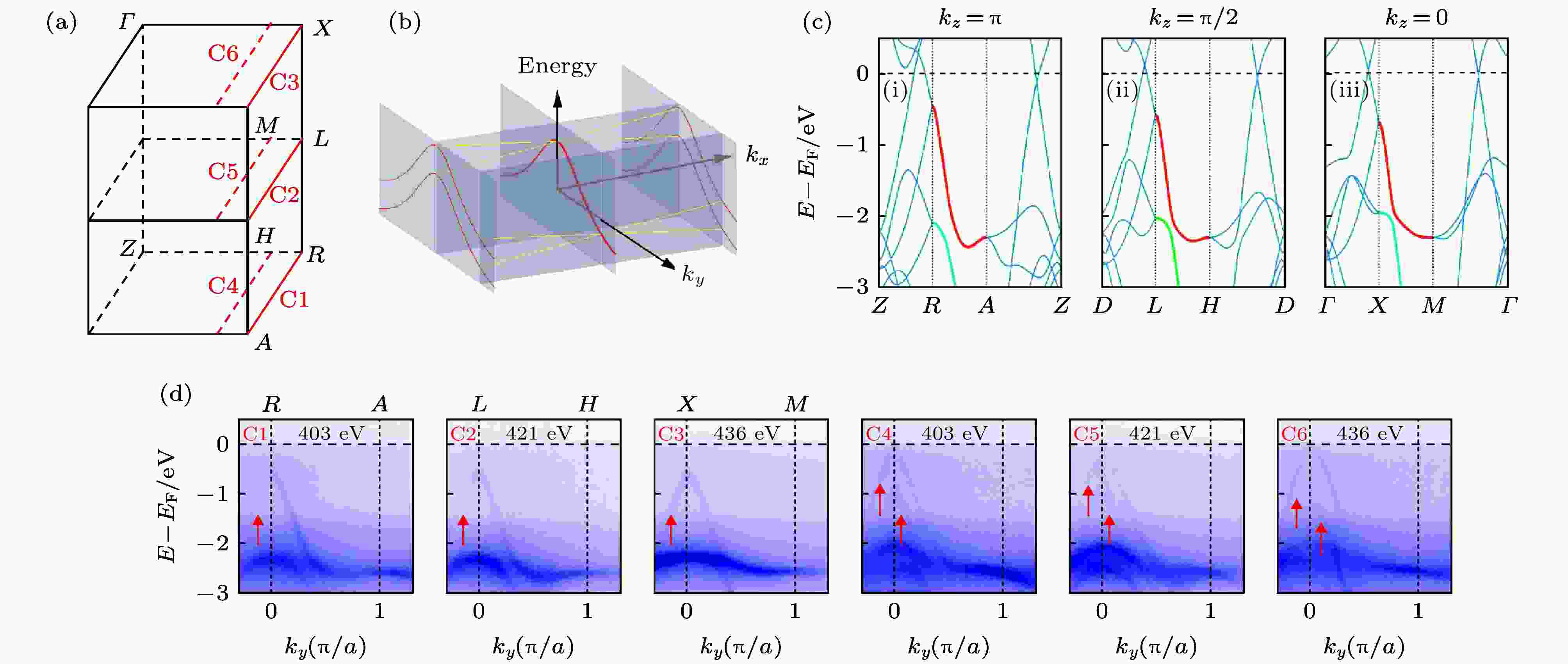图 16 (a) ZrSiS的布里渊区局部放大图; (b)节面附近任意kx-ky面上的节线能带劈裂图示; (c)理论计算的R—A, L—H, X—M方向上的节点线能带色散; (d)沿图(a)中C1—C6方向的ARPES能谱, 红色箭头所指为劈裂前后的对应能带Figure16. (a) Zoomed-in Brillouin zone of ZrSiS; (b) Schematic plot of the band splitting of nodal line in an arbitrary kx-ky plane near the nodal surface; (c) calculated nodal line dispersion along R–A, L–???????H and X–???????M direction; (d) ARPES spectra along C1–C6 cuts in Fig. (a), with nodal lines before and after spliting pointed out by red arrows.
拓扑节线半金属另一个重要特征拓扑电子态是围绕着拓扑非平庸的节线结构会产生所谓的鼓面表面态, 最近在铁磁性节线半金属Co2MnGa中被实验观察得到[117](如图15(g)). 在表面平带中引入电子关联效应或超导配对, 还有望实现分数拓扑态、高温超导等新奇物态.
除了上文所说的节点线、节点环(如图17(a)(i))之外, 多个节点环在动量空间中还可能出现相互交叠, 形成相互嵌套的节点环(图17(a)(ii))、节点链结构(图17(a)(iii)), 甚至是更加复杂的节点结(图17(a)(iv))等. 其中在节点链半金属中, 由于节点线之间出现了简并点, 电子结构可能出现比四重简并的狄拉克点更高简并度的节点(例如图17(b)中J点). 较为典型的节点链半金属是AlB2[118]型结构的TiB2[119,120], 其晶体为中心对称的六方结构(No.191 P6/mmm空间群, 如图17(d)), 第一布里渊区如图17(b)所示, 动量空间中除了A点附近的费米面有类似电子和空穴口袋的结构之外, 绝大部分的费米面都全是由节点环构成的. 根据第一性原理计算, 布里渊区中存在两个节点链的镜像对称平面: Γ-K-M面和Γ-A-H面(图17(c)), 节点环与能带在Γ-K-M面上投影如图17(e)所示, r1节点环围绕K点与其他布里渊区中的r1节点环相连接构成闭合图像, r2节点环与r1节点环在J点处相交叉. 图17(f)为通过ARPES实验在80 eV入射光条件下测得的费米面, 可以明显看到围绕K点的r1节点环的存在, 同时也能清晰地看到沿Γ—K方向r2节点环在费米面上绕Γ点的放射状投影, 两节点环的交叠处J点由黑色虚线圈出. 由于r2节点环嵌在Γ-A-H面中, 实验中通过改变不同的入射光子能量(光能从50 eV变至124 eV), 可以获得如图17(g)中的囊括了不止一个布里渊区的Γ-A-H费米面, 图中纵轴的光能对应kz动量方向的演化, 与图17(c)的理论计算对比, 可以证实空心圈圈出的路径即为穿过J点的r2节点环在动量空间中的分布色散.
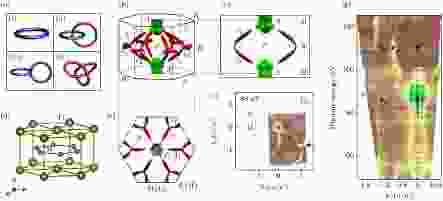图 17 (a)四种节线形成的拓扑结构; (b)三维动量空间中TiB2的理论计算体态费米面图示; (c)节点链结构在A-Γ-J面上的投影; (d) TiB2的晶格结构示意图; (e)节点链结构在Γ-M-K面上的俯视投影; (f) ARPES实验80 eV下测得的费米面图; (g)光能依赖ARPES实验测得的节点链结构Figure17. (a) Schematics of four topological configurations formed by nodal lines; (b) calculated bulk FSs in the 3D BZ and the (c) projected calculation on the A-Γ-J surface, respectively; (d) crystal structure of TiB2; (e) top view projection on Γ-M-K surface of the nodal chain calculation. (f) Fermi surface measured using ARPES at 80 eV; (g) nodal chain measured using hv-dependent ARPES experiment.
由于晶体中宇称-时间对称性和镜像反射对称性的保护, 节点链的存在与否受自旋轨道耦合作用影响几乎可以忽略, 所以除TiB2之外, ZrB2[121]等相似结构的二硼化物中也发现了类似的节点链结构. 这类材料中的节点线和动量空间其他能带没有互相干涉, 因此可以为进一步研究狄拉克节点线费米子提供一个理想的研究平台.
2
7.1.掺杂调控外尔半金属的拓扑电子结构
在外尔半金属的掺杂调控研究中, 以体掺杂的形式改变体系的自旋-轨道耦合强度, 能用来改变成对外尔点在动量空间中的分离程度及费米弧的长短[55,80]; 以表面掺杂的方式改变表面化学环境被报道能操纵费米弧并实现拓扑Lifshitz转变[122].如前所述, 通过改变化学配比方式, 能够调节TaAs家族和MoxW1?xTe2家族的外尔点分布、间距及费米弧的长度及连接方式等重要拓扑结构. 此外用钾原子修饰表面以改变表面的化学环境, 被证明能操纵第一类外尔半金属NbAs的费米弧表面态[122,125]. 图18(a)展示了NbAs的(001)解离面(砷截止面)的费米面, 拓扑表面态贡献的费米弧位于勺子顶端, 而勺子其余部分则为平庸表面态. 然而, 表面钾原子修饰后, 费米面由勺子-领结的结构变成了“8”字形结构, 并且该“8”字形纯粹地由两个长的费米弧构成的, 平庸的表面态不复存在(图18(b)). 更重要的是, 通过钾修饰后, 费米弧连接外尔点的方式发生了根本改变(对比图18(a)(iv)和 图18(b)(iv)): 修饰之后的费米弧跨过布里渊区边界连接了新的一对外尔点, 从而发生了拓扑Lifshitz转变[122]. 这为将来基于拓扑半金属的器件开发及应用提供一个具有可操作性的重要方向.
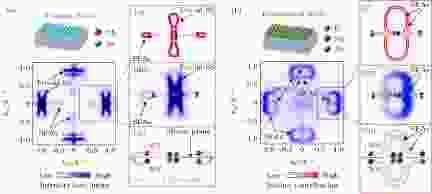图 18 原位表面钾原子修饰诱发的拓扑Lifshitz转变 (a)和(b)分别是解离的NbAs的(001)面和钾原子修饰的电子能带结构. (i)到(iv)分别是实验测得的费米面、
Figure18. Topological Lifshitz transition induced by in-situ potassium decoration: (a) and (b) are band structures of the pristine and in-situ potassium-decorated NbAs (001) surface, respectively. (i) - (iv): Measured Fermi surface, calculated and measured Fermi surface patch around
2
7.2.维度调制的拓扑相变
维度也是调控体系能带的一个重要参量. 如前所述, 三维体块的WTe2被理论和实验证实为第二类外尔半金属[63,81,82]. 当层状的WTe2被制备成为二维单层薄膜后, 能带结构则变为具有45 meV的能隙的间接带隙半导体(图19(b)), 且STM研究显示在边界处有拓扑非平庸边界态(图19(c))[123,126]. 进一步, 输运研究在单层WTe2测到了量子化电导平台[127], 这些证据共同证明单层WTe2是本征二维拓扑绝缘体(量子自旋霍尔效应绝缘体). 因此, 我们通过改变WTe2系统的维度在同一种材料中实现了拓扑相转变.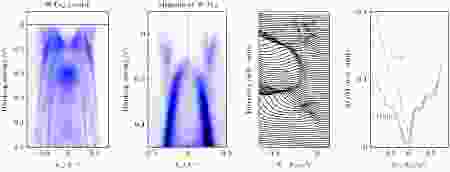
图 19 单层WTe2的量子自旋霍尔绝缘体态 (a) WTe2单晶的沿着
Figure19. (a) Band dispersion of WTe2 crystals along
