摘要: 运用密度矩阵理论研究了气固界面准
$\Lambda$ 型四能级原子系统的非线性选择反射光谱. 基于刘维尔方程给出了一阶近似条件下探测光场的解析式. 在探测场为弱场时, 分析了信号场拉比频率、失谐量和耦合场失谐量对反射光谱线型的影响. 数值模拟表明: 信号场参与产生的选择反射峰线宽可以利用信号场拉比频率进行调节, 通过调节信号场频率失谐量可以实现选择反射峰到透明窗口的转化, 选择反射峰和透明窗口的位置可以通过耦合场失谐量实现调谐. 利用三种电子跃迁路径以及缀饰态理论对所得结果进行了解释. 本文结果为研究气固界面原子的量子相干和动力学过程提供理论参考.
关键词: 选择反射光谱 /
电子跃迁 /
缀饰态 /
准Λ型四能级系统 English Abstract Selective reflection spectrum in a quasi-lambda four-level atomic system Meng Teng-Fei Tian Jian-Feng Zhou Yao-Yao Department of Physics, Taiyuan Normal University, Jinzhong 030619, China Fund Project: Project supported by the National Natural Science Foundation of China(Grant No. 11804246)Received Date: 17 July 2019Accepted Date: 17 September 2019Available Online: 05 December 2019Published Online: 05 January 2020Abstract: Selective reflection (SR) from the interface between transparent medium and dilute vapour is caused by the atomic vapor near the interface. The sub-Doppler structure in SR is due to the deexcitation caused by the collision between atomic vapor and the wall. Beacuse the interaction region between atomic vapor and incident light is on the order of a few hundred nanometers, SR has low optical loss and high spatial resolution. The experimental device of SR is simple. Because of the above characteristics, the SR has been widely studied and applied. The nonlinear SR spectrum of quasi lambda-type four-level system at gas-solid interface is studied theoretically in this paper. By sloving the density matrix equations, the approximate analytic solution of the matrix element associated with the probe field is obtained at normal incidence when the intensity of the probe field is very weak. The effect of the Rabi frequency, the detuning of the signal field and the detuning of the coupling field on the lineshape are analyzed by numerical simulation, respectively. Three peaks and two transparent windows appear in SR spectrum when the detuning of coupling field and signal field are both zero. The middle peak is generated due to the participation of signal field, and the other two peaks are caused by the other two fields. The linewidth and the amplitude of the middle peak can be changed by varying the Rabi frequency of signal field, and the other two peaks have little effect on the Rabi frequency of signal field. The signal generated due to the participation of signal field can be transformed from peak to transparent window when the detuning value of the signal field is equal to the Rabi frequency of coupling field. When the detuning value of the signal field is not equal to the Rabi frequency of coupling field, a dispersion-like signal between reflection peak and transparent window is generated due to the participation of signal field. The position of peak and transparent window can be manipulated by controlling the detuning value of the coupling field. When the detuning value of coupling field decreases from zero, three peaks all shift to red detuning direction. When the detuning value of coupling field is blue-detuned and increases, three peaks all shift to blue detuning direction. The numerical results can be explained by using the various electric transition pathways and dressed state theory. This study is helpful in investigating quantum coherence and dynamic process of atoms at gas-solid interface.Keywords: selective reflection spectroscopy /electron transition /dressed state /quasi lambda-type four-level system 全文HTML --> --> --> 1.引 言 一束光入射到透明介质和原子蒸气组成的界面时, 在原子近共振线区域由于受激辐射而产生反射, 并形成一尖峰光谱, 称之为选择反射光谱[1 ] . 对于该反射光谱, 原子碰壁导致完全退激发, 使光谱呈现亚多普勒结构; 与入射光作用的原子蒸气厚度为百纳米量级, 对光的损耗小、空间分辨率高; 实验装置简单. 由于存在上述特点, 该反射光谱获得广泛的研究和应用, 包括电磁诱导透明[2 -4 ] 、Aulter-Townes 分裂[5 ,6 ] 、四波混频[7 ] 、光的群速度改变[8 ,9 ] 、全光开关[10 ] 、密集气体的偶极-偶极相互作用[11 ,12 ] 、磁场测量[13 ,14 ] 等.[15 -17 ] 、$ \Lambda- $ [4 ,18 ,19 ] 、$ {\rm V} $ -[20 ] 和$ \Xi- $ [21 ,22 ] 型三能级原子系统. Nienhuis 等[15 ] 发展了一套分析二能级原子系统的选择反射理论, 给出了入射光角度及饱和效应对反射光谱的影响, 进一步地在正入射条件下将选择反射理论推广到$ \Lambda $ 型三能级原子系统, 并对暗共振产生的透明窗口做了研究[18 ] . 2012年, Thomas[8 ] 在该三能级系统中研究了入射光角度大于全反射临界角的倏逝场的电磁诱导透明. 2014年Stern等[10 ] 利用V型三能级系统选择反射光谱研究了Fanno共振并设计出全光开关, 2016年Meng等[20 ] 研究了该系统中泵浦光引起的饱和效应及其对光谱线型的影响. 除此之外, 纳米薄池[23 ] 、Fabry–Perot干涉仪[17 ] 、多层池[24 ] 等装置也被用于研究选择反射光谱. 在泵浦光、探测光和气固界面三能级原子系统的基础上加一束信号光场, 可以得到四能级系统选择反射光谱. 人们利用自由空间四能级系统可实现微波电场的精密测量[25 ] , 空间分辨率可达到100 μm, 利用气固界面形成的约100 nm厚气体薄膜, 选择反射光谱可提高微波测量的空间分辨率, 实现测量系统的小型化. 除此之外, 选择反射光谱还能为研究基于自由空间四能级系统的交叉相位调制[26 ] 、量子相位门[27 ] 、克尔非线性增强[28 ] 和群速度控制[29 ] 等装置提供一种小型化的途径. 本文首次考虑一种基于碱金属原子的准$ \Lambda $ 型四能级原子系统, 包含两个基态超精细能级和两个激发态超精细能级. 与$ \Lambda $ 型三能级原子系统相比较, 除光学耦合场和探测场外, 附加了一个射频场作用于两个激发态精细能级之间, 即$ \Lambda $ 型三能级系统中的光学耦合场被换作光学-射频双光子耦合场, 准$ \Lambda $ 型四能级原子系统的选择反射性质与$ \Lambda $ 型三能级系统有着明显的不同.2.理 论 本文考虑的模型为折射率为$ n $ 的电介质和原子蒸气组成的气固界面系统, 如图1(a) 所示. 气固界面处于$ z = 0 $ 的$ x-y $ 平面, 电介质处于$ z < 0 $ 的区域, 原子蒸气处于$ z > 0 $ 的区域, 原子沿z 轴正方向或反方向运动. 探测场、耦合场和信号场经电介质入射到界面, 然后再反射回电介质, 入射角分别为$ \theta_{\rm p} $ ,$ \theta_{\rm c} $ 和$ \theta_{\rm s} $ . 本文考虑三个电磁场正入射的情况, 也就是$ \theta_{\rm p} = \theta_{\rm c} = \theta_{\rm s} = 0^{\circ} $ (当不同激光有一定夹角时, 反射光谱的反射峰和透明窗口的位置、幅度等主要光谱特性变化很小.). 准$ \Lambda $ 型四能级原子的能级图如图1(b) 所示, 包含有两个低能级$ |1\rangle $ 和$ |4\rangle $ , 两个高能级$ |2\rangle $ 和$ |3\rangle $ . 探测场作用于能级$ |1\rangle $ 和能级$ |2\rangle $ 之间, 耦合场作用于能级$ |2\rangle $ 和能级$ |3\rangle $ 之间, 信号场作用于能级$ |3\rangle $ 和能级$ |4\rangle $ 之间. 三个电磁场的角频率分别为$ \omega_{\rm p} $ ,$ \omega_{\rm c} $ 和$ \omega_{\rm s} $ , 拉比频率为$ \varOmega_{\rm p} $ ,$ \varOmega_{\rm c} $ 和$ \varOmega_{\rm s} $ , 波矢为$ k_{\rm p} $ ,$ k_{\rm c}$ 和$ k_{\rm s} $ . 以碱金属铯原子为例, 能级$ |1\rangle $ ,$ |2\rangle $ ,$ |3\rangle $ 和$ |4\rangle $ 分别为6S1/2 (F = 3), 6P1/2 (F = 3), 6P1/2 (F = 4)和6S1/2 (F = 4).图 1 (a)探测场、信号场和耦合场入射到气固界面示意图; (b)准$ \Lambda $ 型四能级原子系统能级示意图Figure1. Gas-solid interface with a probe field, a signal field and a coupling field (a) and level diagram of quasi lambda-type four-level atomic system (b)[30 ,31 ] . 而气固界面附近的原子与电介质界面碰撞之后激发态原子产生退激发, 气体原子不再各向同性, 需用包含$ z $ 参量的密度矩阵$ {{\rho}} $ 描述其状态, 该密度矩阵遵循刘维尔方程[32 ] . 为了获得不含时间变量的准$ \Lambda $ 型四能级原子系统的密度矩阵方程组, 引入约化密度矩阵$ {{\sigma}} $ ,$ \Lambda $ 型四能级原子系统的密度矩阵方程组为$ \omega_{21} $ ,$ \omega_{32} $ 及$ \omega_{34} $ 分别表示$ |2\rangle\rightarrow|1\rangle $ ,$ |3\rangle\rightarrow|2\rangle $ 及$ |3\rangle\rightarrow$ $|4\rangle $ 的跃迁频率, $ v_{z} $ 表示原子在$ z $ 方向的运动速度分量, $ \Delta_{\rm p} $ ,$ \Delta_{\rm c} $ 和$ \Delta_{\rm s} $ 分别表示探测场、耦合场和信号场的频率失谐量. $ \gamma_{21} $ 和$ \gamma_{24} $ 分别表示能级$ |2\rangle $ 到能级$ |1\rangle $ 和$ |4\rangle $ 的自发弛豫速率. 类似地, $ \gamma_{31} $ ,$ \gamma_{32} $ ,$ \gamma_{34} $ 分别表示能级$ |3\rangle $ 到能级$ |1\rangle $ ,$ |2\rangle $ ,$ |4\rangle $ 的自发弛豫速率.2a )–(2j ), 引入拉普拉斯变换$ p $ 为空间变量$ z $ 的拉普拉斯变换量. 方程组(2a )–(2j )左边微分项的拉普拉斯变换可表示为2a )–(2j )两边进行拉普拉斯变换的方程组可用于描述原子与气固界面碰撞之后原子的状态. 假定原子在碰壁之后完全退激发, 则$ {{\sigma}} $ (z = 0) 的非零项为$ {{\sigma}}_{11} $ . 碰壁之前的原子与电磁场相互作用足够长时间, 原子布居达到了稳定状态, 可以用$ {{\sigma}} $ 的定态方程组描述. $ {{\sigma}} $ 的定态值通过以下表达式得到2a )–(2j )中包含$ \varOmega_{\rm p} $ 的项只有${{\rm i}\varOmega_{\rm p}}/{2}\sigma_{11}\neq 0 $ , 其余项都为零[32 ] . 利用(2e )–(2g ) 的拉普拉斯变换形式可计算得到描述探测场的拉普拉斯变换的约化密度矩阵元$ \sigma_{21} $ :$ p = -2 {\rm i}k_{\rm s} $ . 结合(6 )式和(7 )式可得到相应的定态解:$ \widehat{\sigma}_{21} $ 和$ \overline{\sigma}_{21} $ 的解析表达式可用于分析探测场的选择反射光谱.[15 ] T 是一个无量纲的量, 可以表示为$ N $ 是原子数密度, $ {{u}}_{21} $ 为跃迁偶极矩, $ {{E}}_1 $ 为原子蒸气中探测场的振幅, $ {\phi} $ 可表示为$ \phi_+ $ 和$ \phi_- $ 分别为正速度(碰壁之后)原子和负速度(碰壁之前)原子对选择反射光谱的贡献.$ W(v_{z}) $ 为归一化的麦克斯韦-玻尔兹曼速度分布函数. 利用(7 )式、(9 )式、(12 )式、(13a )式和(13b )式可数值分析准$ \Lambda $ 型四能级原子系统选择反射光谱.3.结果与分析 图2 所示为不同信号场拉比频率的选择反射光谱, 通过matlab数值模拟频率失谐量$ \varDelta_{\rm p} $ 和方程(12 )中$ \phi $ 的依赖关系获得, 横坐标为探测光的频率失谐量, 以$ k_{\rm p}v_0 $ 为单位, $ v_0 $ 为原子的最概然速度. 纵坐标为原子蒸气反射强度. 对应方程(10 )等号右边第二项. 探测场的拉比频率为$ \varOmega_{\rm p} = 5\times $ $10^{-3}k_{\rm p}v_0 $ , 耦合光场的拉比频率和频率失谐量分别为$ \varOmega_{\rm c} = 0.8 k_{\rm p}v_0 $ 和$ \varDelta_{\rm c} = 0 $ , 信号场的频率失谐量为$ \varDelta_{\rm s} = 0 $ , 自发弛豫速率$ \gamma_{21} = \gamma_{24} = \gamma_{31} = \gamma_{34} = 2.5\times $ $10^{-2}k_{\rm p}v_0 $ , $ \gamma_{32} = 2.5\times10^{-6}k_{\rm p}v_0 $ , 耦合场波数为$ k_{\rm c} = 2.5\times10^{-6}k_{\rm p} $ , 信号场波数为$ k_{\rm s} = k_{\rm p} $ . 这些参数为碱金属原子的典型值.图 2 不同信号场拉比频率的准$ \Lambda $ 型选择反射光谱Figure2. The quasi lambda-type SR spectroscopy under different Rabi frequencies of signal field$ \varOmega_{\rm s} = 0 $ , $ 0.12 k_{\rm p}v_0 $ , $ 0.24 k_{\rm p}v_0 $ , $ 0.36 k_{\rm p}v_0 $ 时, 得到一系列的选择反射谱理论曲线. 如果没有外加信号光场, 即$ \varOmega_{\rm s} $ = 0时, 此系统为标准的梯形三能级结构, 在反射光谱的近共振区域有单个电磁诱导透明窗口. 利用不同电子跃迁路径形成的干涉可以对此进行解释, 当只有耦合场时, 该三能级系统会产生$ |1\rangle\rightarrow|2\rangle $ (路径1)电子跃迁和$ |1\rangle\rightarrow|2\rangle\rightarrow|3\rangle\rightarrow|2\rangle $ (路径2)电子跃迁, 两个反射峰和透明窗口由这两种电子跃迁路径辐射光子的干涉产生. 当存在信号光场时, 在前两种电子跃迁过程的基础上产生$ |1\rangle\rightarrow|2\rangle\rightarrow|3\rangle \rightarrow|4\rangle$ $\rightarrow|3\rangle\rightarrow|2\rangle $ (路径3)的电子跃迁, 对应地在电磁诱导透明窗口出现一个小尖峰, 所以第三种电子跃迁路径辐射光子参与的干涉产生电磁诱导反射峰. 从图(2) 中可以看出引入信号光场时两边的两个反射峰与只有耦合场时基本相同, 只是在透明窗口底部产生一个小尖峰或者是由一个透明窗口变为两个透明窗口, 所以第三种电子跃迁路径的辐射光与其他两种路径辐射光的干涉会产生小尖峰, 这种多个电子跃迁路径产生的干涉不影响前两种跃迁路径辐射光子干涉产生的两个反射峰和小尖峰之外的透明窗口其他区域. 在一定范围内连续改变信号光场的拉比频率$ \varOmega_{\rm s} $ , 中间小尖峰的幅度逐渐增大, 线宽也逐渐加宽. 对光的群速控制、光存储提供了理论参考.$ \sigma_{31}\neq0 $ 且$ \sigma_{41}\neq0 $ , $ \sigma_{31}\neq0 $ 且$ \sigma_{41} = 0 $ , $ \sigma_{31} = 0 $ 且$ \sigma_{41} = 0 $ 的理论曲线, 如图(3) 所示. $ \sigma_{ij} = 0 $ 或$ \neq0 $ ($ i = 3, 4, j = 1 $ )表示$ |i\rangle $ 和$ |j\rangle $ 之间的相干效应关闭或存在. 从图中可以看出当$ |1\rangle $ 和$ |3\rangle $ 之间、$ |1\rangle $ 和$ |4\rangle $ 之间的相干效应都不存在时, 四能级系统只存在饱和效应, 理论曲线只有一个反射峰. $ |1\rangle $ 和$ |3\rangle $ 之间的相干效应存在、$ |1\rangle $ 和$ |4\rangle $ 之间的相干效应不存在时, 理论曲线形成两个反射峰和一个透明窗口, 可以得出该透明窗口由$ |1\rangle $ 和$ |3\rangle $ 之间的相干效应产生. $ |1\rangle $ 和$ |3\rangle $ 之间的相干、$ |1\rangle $ 和$ |4\rangle $ 之间的相干效应都存在时, 理论曲线在近共振位置多出一个反射峰并形成两个透明窗口, 可以得出该反射峰和透明窗口由$ |1\rangle $ 和$ |4\rangle $ 之间的相干效应产生.图 3 $ \sigma_{31} $ 和$ \sigma_{41}$ 为0 = 0或$ \neq 0 $ 时的准$ \Lambda $ 型选择反射光谱Figure3. The quasi lambda-type SR spectroscopy in the present or absent of $ \sigma_{31} $ and $ \sigma_{41} $ 图4 给出了信号场频率失谐量 $ \varDelta_{\rm s} = - 1.6{k_{\rm p}}{v_0} $ , $ {-0.8 k_{\rm p}}{v_0} $ , $ -0.4{k_{\rm p}}{v_0} $ , $ {0.8 k_{\rm p}}{v_0} $ , $ {1.2 k_{\rm p}}{v_0} $ 的选择反射光谱, 图中$ \varOmega_{\rm s} = {0.36}k_{\rm p}v_0 $ , $ \varOmega_{\rm c} = 1.6 k_{\rm p}v_0 $ , 其余参数与图2 相同. 由图可知, 当$ \varDelta_{\rm s} $ 在零附近时, 随着失谐量$ \varDelta_{\rm s} $ 的增大, 路径1辐射光子和路径2 辐射光子的干涉产生的两个反射峰基本保持不变, 第三种路径辐射光子的改变会影响中间小尖峰的位置, $ \varDelta_{\rm s} = - {0.4}k_{\rm p}v_0 $ 与$ \varDelta_{\rm s} = {0.4}k_{\rm p}v_0 $ 时小尖峰会分别向红失谐和蓝失谐的方向移动. 连续改变信号场$ \varOmega_{\rm s} $ 的失谐量时, 小尖峰会连续移动, 两个透明窗口也会连续移动, 两个反射峰基本保持不变. 当$ |\varDelta_{\rm s}| = \varOmega_{\rm c} = {0.8}k_{\rm p}v_0 $ , 三种路径干涉产生的小尖峰将移动到路径1 和路径2 干涉产生的两个反射峰位置, 并且由尖峰变为了凹坑. 缀饰态理论能够很好地解释探测场选择反射特性的这种变化, 光场强度很强的耦合场使能级$ |2\rangle $ 劈裂为两个缀饰态能级$ |+\rangle $ 和$ |-\rangle $ , 如图5 所示, 原子形成$ |1\rangle\leftrightarrow $ $|+\rangle\leftrightarrow|4\rangle $ 和$ |1\rangle\leftrightarrow|-\rangle\leftrightarrow|4\rangle $ 的两个$ \Lambda $ 型三能级系统. 如果这两个$ \Lambda $ 型三能级系统分别单独作用, 将各自产生一个电磁诱导透明. 当$ \varDelta_{\rm s} = 0 $ 时, 这两个$ \Lambda $ 型三能级系统的双光子跃迁具有相反的频率失谐, 它们之间形成量子干涉, 使气固界面的选择反射特性发生改变, 在探测场的共振频率位置形成电磁诱导吸收(图中紫色箭头所示). 当$ \varDelta_{\rm s} = 0.8{k_{\rm p}}{v_0} =$ $ \varOmega_{\rm c}/2 $ 时, $ |1\rangle\leftrightarrow|+\rangle\leftrightarrow|4\rangle $ 的$ \Lambda $ 型三能级系统发生共振跃迁, 使右侧的反射峰变为电磁诱导透明(图中深黄色箭头所示). 同理$ \varDelta_{\rm s} = -0.8{k_{\rm p}}{v_0} $ 时左侧的反射峰变为电磁诱导透明(图中红色箭头所示). 当$ \varDelta_{\rm s} $ 为其他值的情况时, 在$ \varDelta_{\rm p} = \varDelta_{\rm s} $ 的频率位置附近有一个介于电磁诱导透明和电磁诱导吸收的类色散信号(图中黑色、蓝色、绿色和橘黄色箭头所示), 这是由于两个$ \Lambda $ 型三能级系统的双光子跃迁具有相反的频率失谐的跃迁路径和$ |1\rangle\leftrightarrow|+\rangle\leftrightarrow|4\rangle $ 或$ |1\rangle\leftrightarrow|-\rangle\leftrightarrow|4\rangle $ 的共振跃迁路径 同时起作用, 使选择反射特性呈现类色散型. 通过调节信号光场频率失谐量可以实现慢光和快光之间的转换.图6 给出了不同耦合场频率失谐量的反射光谱. 耦合场的频率失谐量$ \varDelta_{\rm c} = -0.2 k_{\rm p}v_0 $ , 0, $ 0.2 k_{\rm p}v_0 $ , $ \varOmega_{\rm s} = 0.18 k_{\rm p}v_0 $ , 其余参数与图2 相同. 可以看出, $ \varDelta_{\rm c} = -0.2 k_{\rm p}v_0 $ 时, 相较于$ \varDelta_{\rm s} = 0 $ 时三个反射峰向红失谐的方向偏移, 透明窗口也向红失谐的方向偏移; $ \varDelta_{\rm c} = 0.2 k_{\rm p}v_0 $ 时三个反射峰向蓝失谐的方向偏移, 透明窗口也向蓝失谐的方向偏移. 进一步观察发现, 在一定范围内连续改变耦合场的失谐量$ \varDelta_{\rm c} $ , 透明窗口会连续移动, 三个反射峰会连续改变, 但透明窗口始终保持两个. 为进行不同频率微波电场测量提供了理论参考.图 4 信号场频率失谐量为$ {-0.8 k_{\rm p}}{v_0} $ , $ 0 $ , $ 0.8{k_{\rm p}}{v_0} $ 的准$ \Lambda $ 型选择反射光谱Figure4. The quasi lambda-type SR spectroscopy when the frequency detuning of signal field is $ {-0.8 k_{\rm p}}{v_0} $ , $ 0 $ , $ 0.8{k_{\rm p}}{v_0} $ 图 5 准$ \Lambda $ 型四能级原子系统缀饰态能级图Figure5. Dressed state picture in a quasi lambda-type four-level atomic system图 6 不同耦合场频率失谐量的准$ \Lambda $ 型选择反射光谱Figure6. The quasi lambda-type SR spectroscopy under different frequency detuning of coupling field4.结 论 本文理论研究了气固界面准$ \Lambda $ 型四能级系统的非线性选择反射光谱. 数值分析了外加信号场的拉比频率、频率失谐量和耦合场的频率失谐量对选择反射光谱的影响. 通过改变信号场拉比频率, 可调节选择反射光谱中间选择反射峰和中间两个透明窗口的线宽; 信号场频率失谐量的变化可实现电磁诱导吸收到电磁诱导透明的转变; 耦合场频率失谐量的变化, 可使得反射峰和透明窗口频率位置连续改变. 为了解释这些结果, 利用三种电子跃迁路径和缀饰态理论进行了详细分析. 研究结果对于研究气固界面附近原子系综的高分辨率光谱、量子相干效应、微波电场测量等领域的应用研究具有重要意义. 











































































































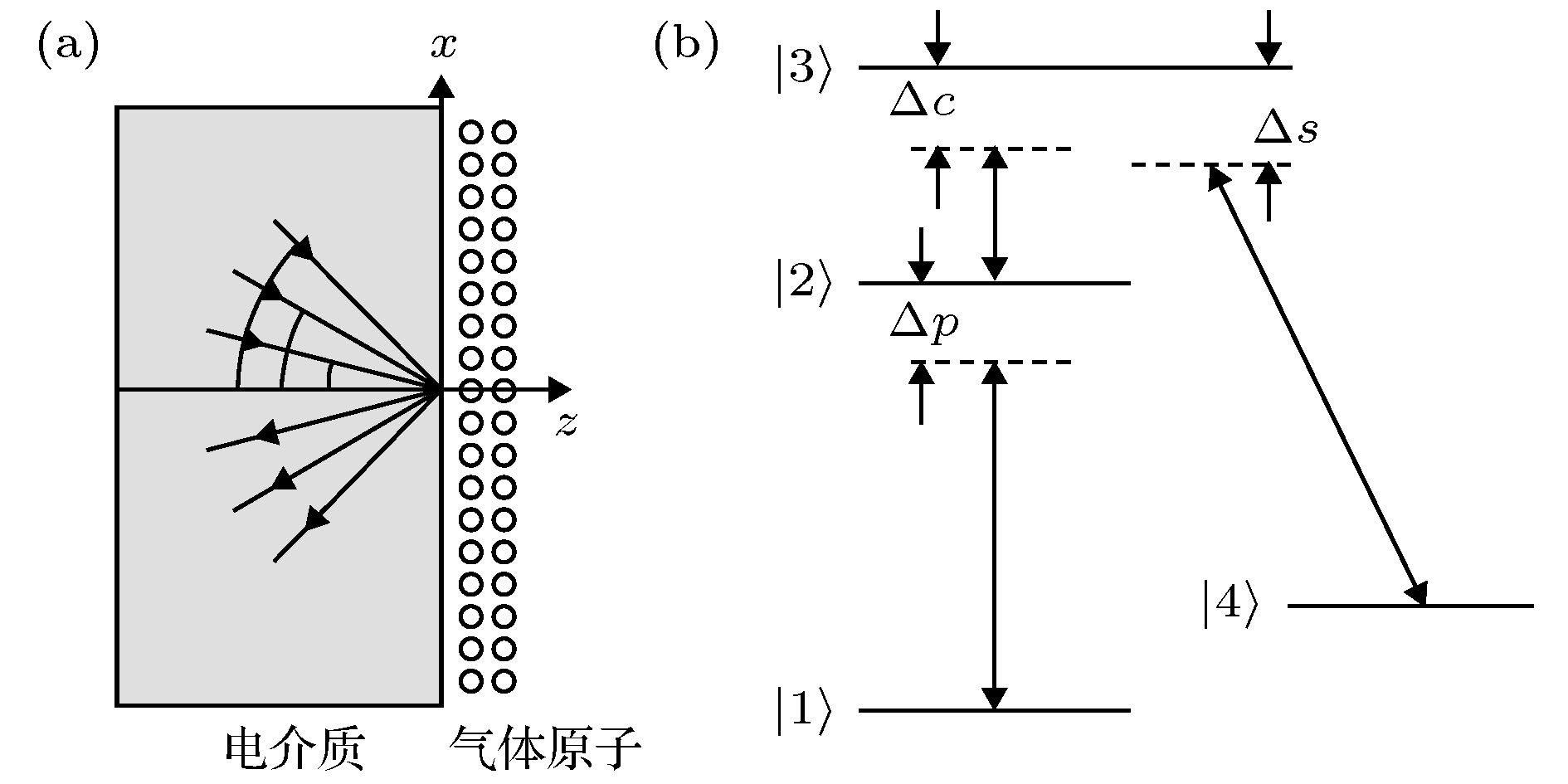 图 1 (a)探测场、信号场和耦合场入射到气固界面示意图; (b)准
图 1 (a)探测场、信号场和耦合场入射到气固界面示意图; (b)准











































































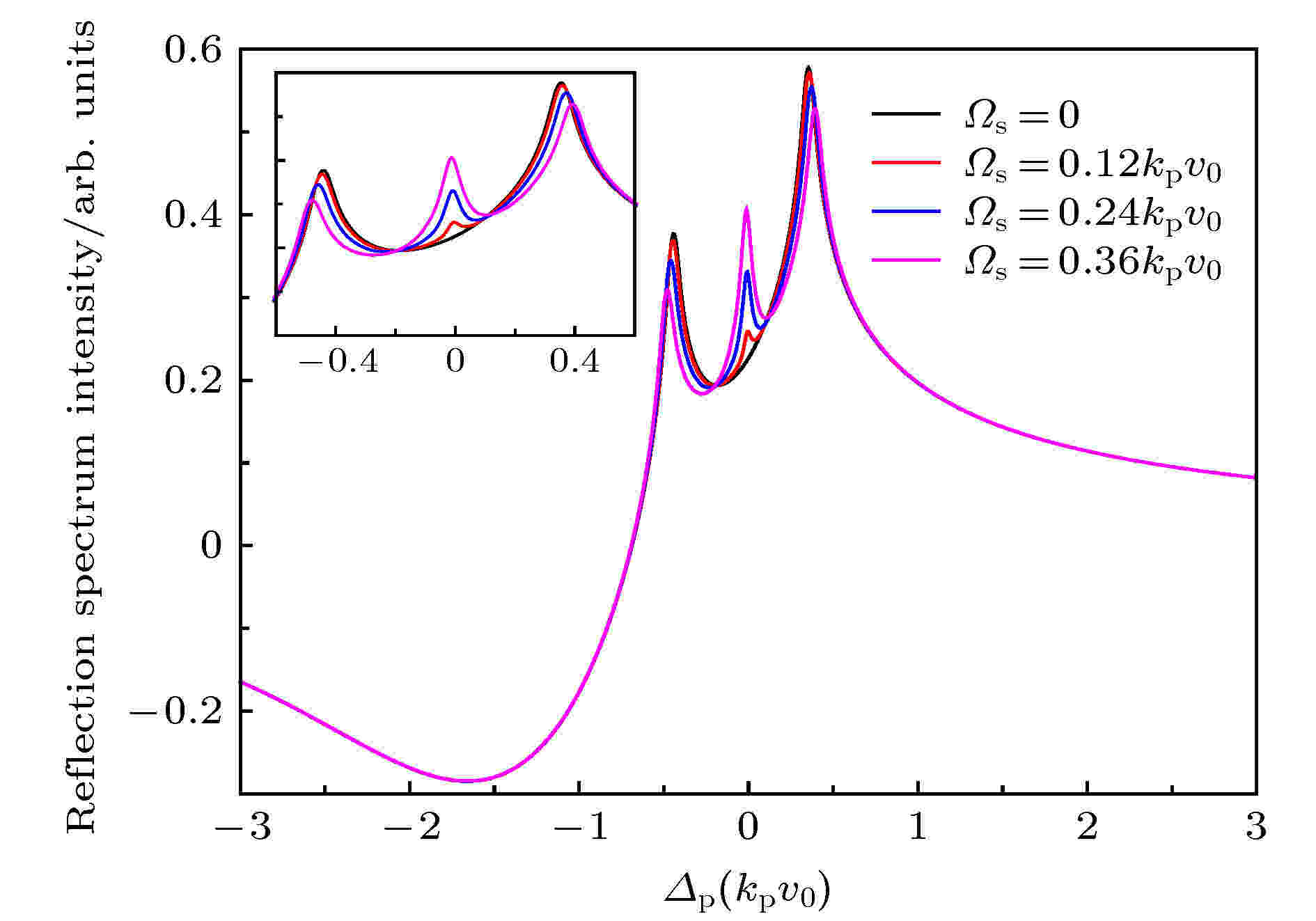 图 2 不同信号场拉比频率的准
图 2 不同信号场拉比频率的准



























































































































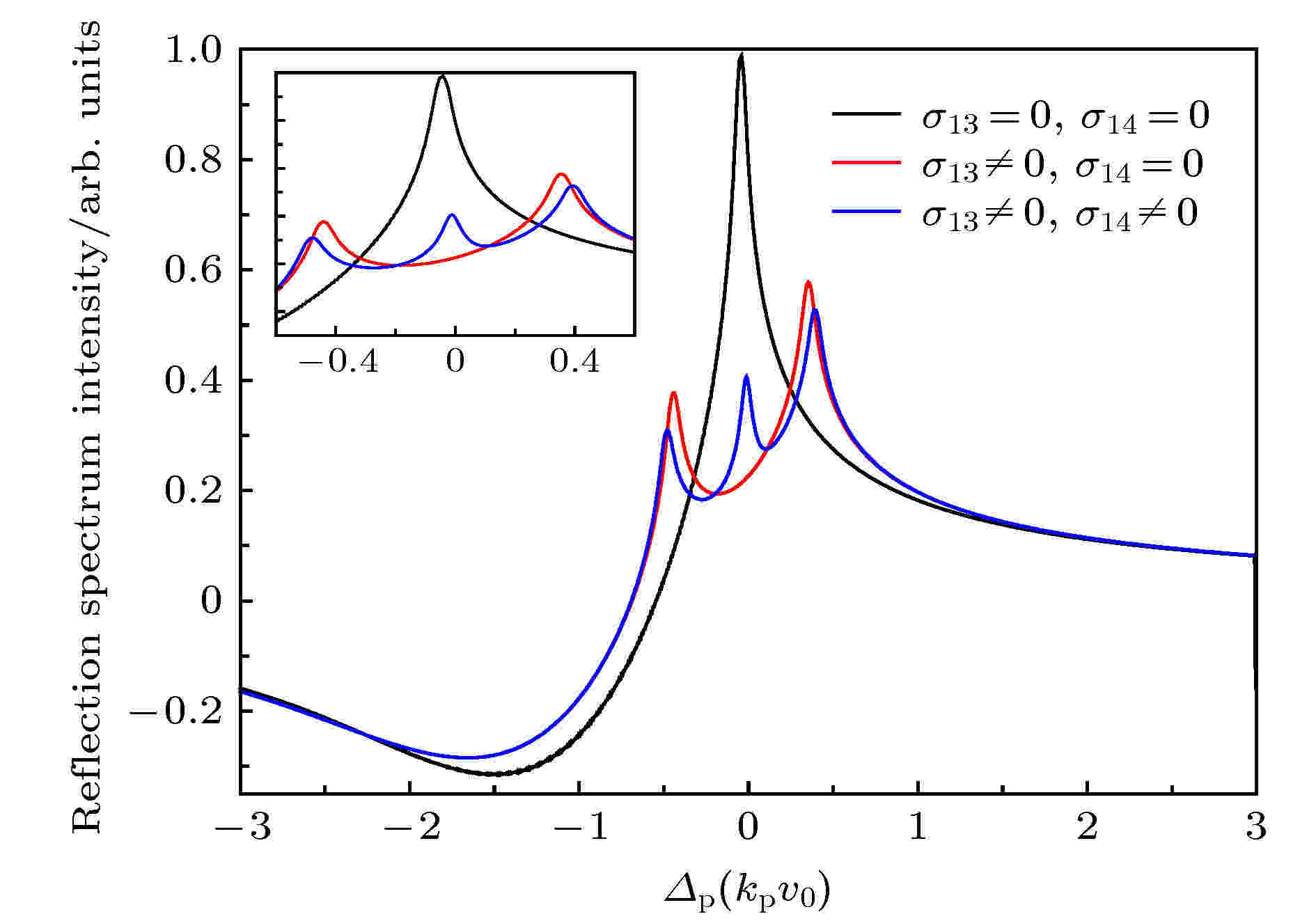 图 3
图 3 













































































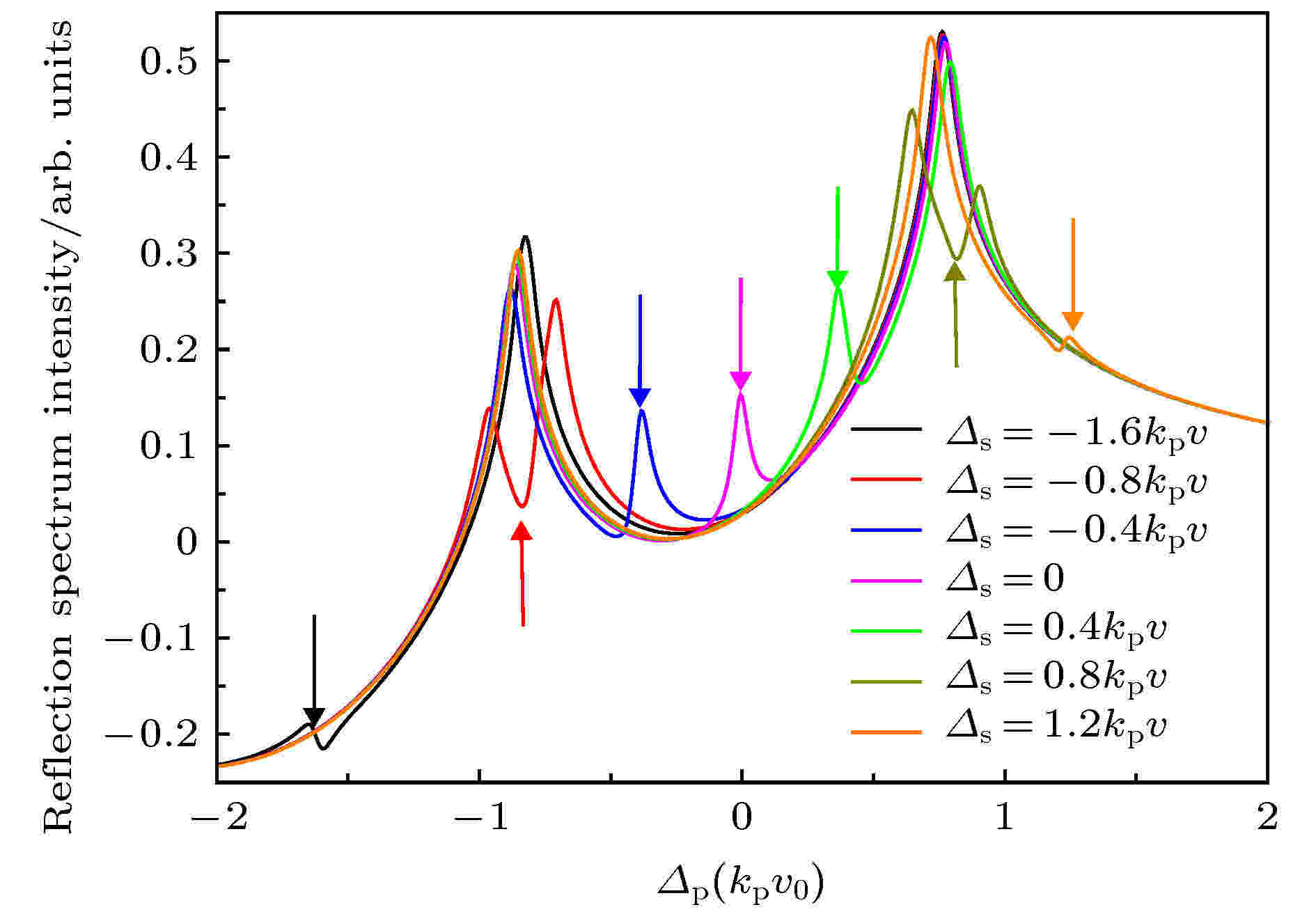 图 4 信号场频率失谐量为
图 4 信号场频率失谐量为






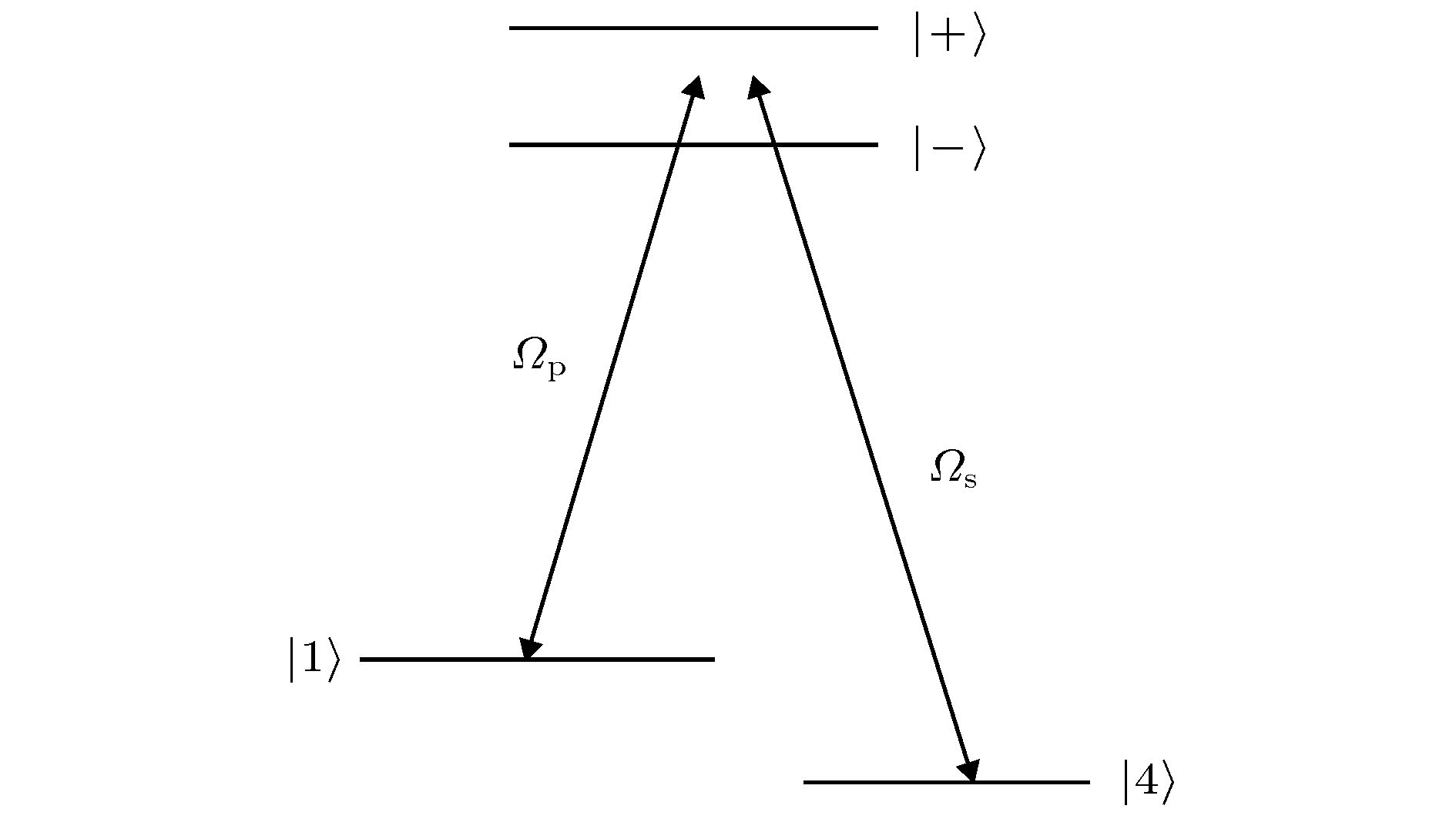 图 5 准
图 5 准
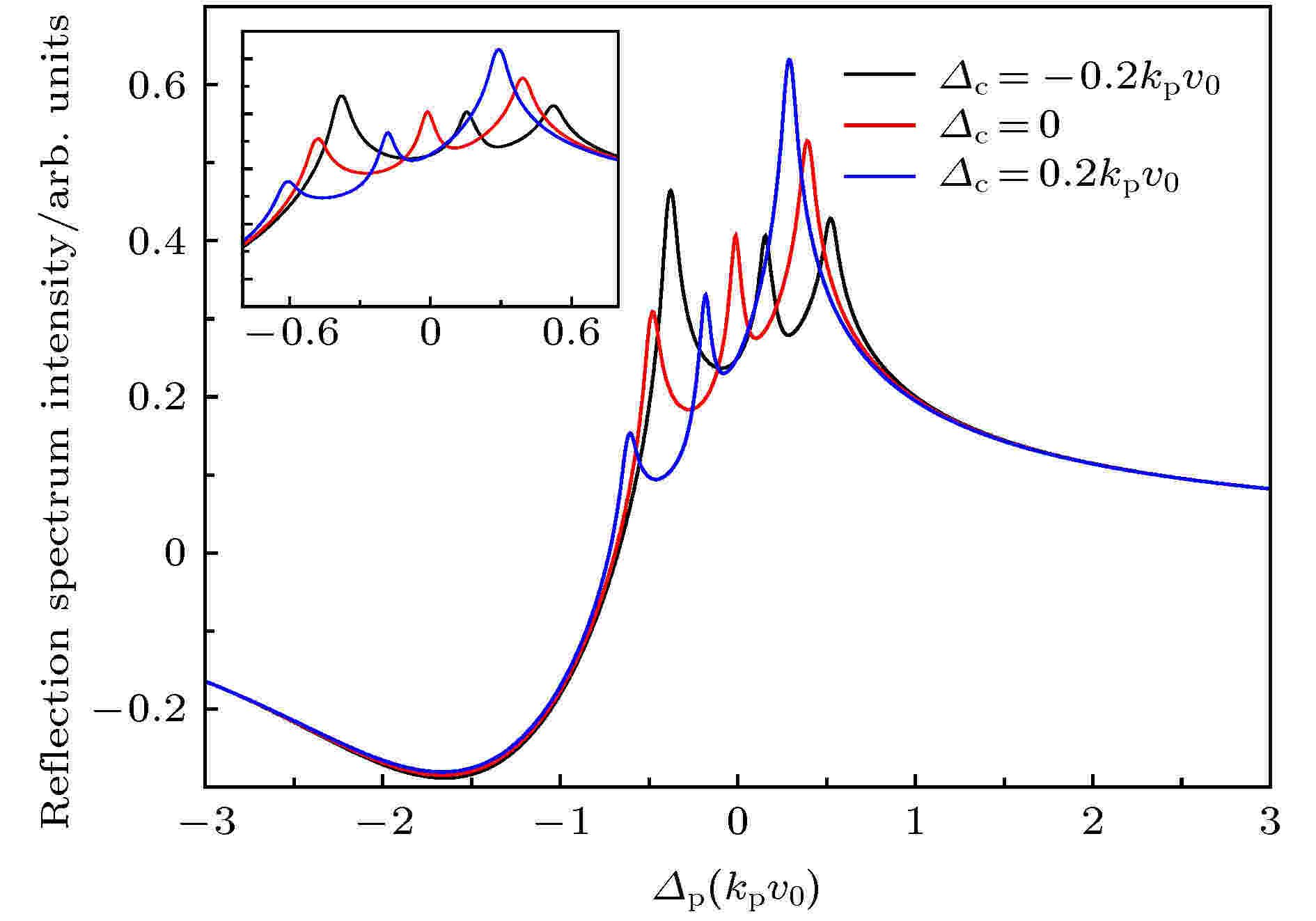 图 6 不同耦合场频率失谐量的准
图 6 不同耦合场频率失谐量的准


