摘要:光子对撞产生正负电子对的Breit-Wheeler过程, 是由能量直接产生物质的过程, 在物质的起源与光子物理理论的研究中有着极为重要的作用. 随着激光与物质作用产生γ光源品质的提升, 使得在实验室首次观测双光子对撞的Breit-Wheeler过程成为可能. 针对光子对撞机的数值模拟方法, 本文提出了一种基于严格的双光子对撞动力学过程的计算电子产额与动力学参数的数值方法. 在对Breit-Wheeler过程的模拟中, 根据光子的运动规律将光子划分为定量的区块, 检测区块的对撞, 然后在区块内部以动力学原理检测光子是否发生对撞, 该方法可以有效提升计算模拟的效率. 同时, 该方法与已经发表的理论结果进行了比较, 发现该计算结果与理论结果高度一致. 应用这一数值方法, 能够为Breit-Wheeler过程给出较为精确的模拟结果, 也可以为未来γγ对撞机的实验设计提供参照.
关键词: 光子对撞机/
正负电子/
Breit-Wheeler过程/
能量阈值

English Abstract

全文HTML

--> --> -->

根据爱因斯坦质能方程和量子电动力学理论^[1-3], 在一定条件下光子(能量)可以转化成物质如电子对、夸克对等^[4], 这对研究物质的起因有着举足轻重的作用, 与之相关的理论研究始于20世纪30年代, 然而直到1997年, 美国SLAC实验室才首次在试验中观测到多光子碰撞产生正负电子对的过程^[5]. 而对于两个高能光子的互作用过程, 也就是常说的光子对撞机^[6], 到目前为止实验中还未观测到. 在光子对撞机中, 光子的互作用过程发生的次数与光子数目和光子-光子截面成正比, 与光子束的脉冲宽度、两束光子束的交叉面积成反比^[7]. 在实验中, 不能观测到光子的互作用过程是由于已有γ射线源的流强和亮度还达不到实验要求. 相对于传统加速器产生的γ射线源, 激光与物质相互作用产生的光子射线源脉冲流强高、亮度高等特点^[8], 这使得单脉冲产生更多的正负电子对成为可能.
光子亮度的表达式$B \!=\! {n_{\rm{p}}}/(t \cdot \theta \cdot {\text{π}} \cdot {r^2} \cdot $0.1%BW), 式中n_p是光子数目, 光子束脉宽t的单位是秒, 光子束发散角$\theta $的单位是毫弧度, 光子束的半径r的单位是毫米, 0.1%BW是中心波长0.1%谱宽范围内的光子数目. 从上式可以看出光子亮度主要由以下参数决定: 光子数目、脉冲宽度、光子束源尺寸(焦斑大小)和发散角. 对于飞秒激光产生的超强辐射源, 其脉冲宽度与激光脉宽同量级, 焦斑大小近似于激光焦斑, 几微米到十几微米. 由于产生的光子数目与激光强度正相关^[9], 可以通过提升激光强度来获得更多的光子数目, 然而受限于当前和未来一段时间的激光技术, 激光强度不可能无限制提升. 因此, 增大γ射线的光子亮度切实可行的方案是减小光子束的发散角^[10]. 在已经报道的结果中光子束发散角(半角)均大于20°^[11-15], 存在巨大的提升空间. 近年来, 国内、外的相关团队已经开展了关于激光与物质相互作用产生高准直光源的一系列理论研究. 这其中包括中科院上海光机所提出的采用微型等离子体波导的系列方案^[16,17], 相关方案可以在波导中辐射高亮度、高准直度的x射线光源; 国防科技大学和南华大学、西北师范大学的相关研究团队在超强激光产生高品质gamma源和正电子源方面做了大量的基础性研究^[11,18-26]; 中科院物理所和上海交通大学相关研究团队, 也在超准直射线源方面做了大量工作^[27-30]; 美国德克萨斯大学奥斯汀分校的研究团队提出了复合靶方案^[12], 该方案可以有效提升能量为MeV光子的产额和准直度, 优化后的γ光子束发散角是30°左右; 北京大学^[10,31-34]以及深圳大学^[35]的相关理论团队研究了超强PW激光与通道等离子体相互作用以改善γ光源的准直性, 其PIC粒子模拟结果证明了通道等离子体可以有效改善γ光源的准直性.
光子对撞机可以分为两个作用区域, 一个是两个光子纯粹的散射过程, 其典型代表就是上海光机所即将开展的真空双折射实验^[36]; 另外一个区域则是两个光子对撞产生带电粒子的过程, 其典型代表就是Breit-Wheeler过程^[5]. 目前唯一的实验观测是在1997年由斯坦福直线型加速中心(SLAC)实现的, 将数目为10⁹的46.6 GeV高能电子束注入到强激光束中, 经康普顿散射产生的高能光子再与激光光子发生多光子的Breit-Wheeler过程^[5]. 20000次重复实验约能产生100个电子对, 但这一实验观测到的还不是双光子Breit-Wheeler过程. 法国波尔多大学的研究团队^[37]基于激光与铝箔的相互作用产生的MeV光子束设计了一种实验方案, 两束光子在一定距离下进行对撞, 并利用PIC模拟计算出10¹²的光子在一定距离外对撞可得到10³的电子. 另外该团队提出了一种特别的数值方法TrI LEns, 基于树代码对光子分组与检索对撞^[38], 对光子对撞过程实现了数值模拟; 帝国理工学院的研究团队提出一种实验方案, 以2 GeV的电子束打击金靶, 韧致辐射产生γ光, γ光与热黑体辐射空腔作用产生电子对. 根据蒙特卡罗模拟, 计算出400 eV的空腔内可产生超过10⁵的电子对^[39]. 北京大学的研究团队提出了利用两束10 PW激光分别聚焦到窄管靶中产生高度准直的γ光脉冲的实验方案, 利用宏粒子模拟, 可能得到10⁸的电子对产额^[7]. 上述三个团队提出的计算方案没有考虑光子束的局域分布不均匀的情况, 而光子束的局域分布也非常有可能影响对撞后的结果. 本文提出了一种全新的方法, 可以考虑光子束的实际分布, 同时简化对不会发生对撞的光子的处理, 在提升计算精度的同时还显著提高了计算效率.
为了模拟γ光束对撞产生正负电子的过程, 沿用北京大学的实验设计方案, 该方案有较高的可行性, 在未来技术进步之后可以为光子对撞机的真正实现提供参考. 本文的基本思想是: 将光子在空间中的分布划分成不同的区块, 然后以遍历法检测区块之间可能发生的对撞, 这只需很少的计算即可完成; 对于判断能够发生对撞的区块, 使用遍历法搜索每一对光子之间的对撞, 最终给出对撞的电子对产额以及电子的动量、动能参数. 这一算法的优点在于优先检测区块对撞可节省大量不必要的计算, 而严格按照动力学原理的双光子对撞检测能够给出最接近真实情形的结果. 本文使用单能光子束对撞得到的电子动量分布验证算法的正确性, 并基于10⁶量级光子束对撞, 计算电子产额与动量分布.

这一过程的反应式为

$\gamma + \gamma ' \to {\rm e^ + } + {\rm e^ - }, $

设双光子能量为E_γ1, E_γ2, 动量夹角为θ_p, 电子质量为m_e, 电子经典半径为r_e, 光速为c.
能量阈值条件为^[37]

${E_{{\rm{\gamma 1}}}}{E_{{\rm{\gamma 2}}}}(1 - \cos {\theta _{\rm{p}}}) > 2m_{\rm{e}}^2{c^4}, $

其经典截面为^[37]

${{\sigma }_{\gamma \gamma }}(s)\!=\! \frac{{\text{π}}}{2}r_{\rm{e}}^{2}(1-{{\beta }^{2}})\Big[ -2\beta (2-{{\beta }^{2}})+(3 \!-\! {{\beta }^{4}}){\rm{In}}\frac{1\!+\!\beta }{1\!-\!\beta } \Big],$

其中

$\beta = \sqrt {1 - 1/s} , $

$s = {E_{{\rm{\gamma 1}}}}{E_{{\rm{\gamma 2}}}}(1 - \cos {\theta _{\rm{p}}})/2m_{\rm{e}}^2{c^4}.$

假定两个光子能够满足能量阈值条件(2)式与截面条件(3)式, 将其视为一个质心系, 为简化推导, 设两个光子的动量均位于x-y二维平面上, 并令光速c = 1, 电子质量m_e = 1^[40]. 根据实验室系下的各光子动力学参数, 由洛伦兹变换得到双光子质心系的对应参数, 在质心系中, 光子对撞产生的正负电子能量分别为质心能量的1/2, 电子动量分布则是各向同性的. 得到质心系下电子动力学参数后, 再以洛伦兹变换得到实验室系下的相应参数.
设质心系下电子动量为${p'_{\rm{e}}}$, 在x, y方向的分量为${p'_{{\rm{ex}}}}, {p'_{{\rm{ey}}}}$, 电子总能量为${E'_{\rm{e}}}$; 实验室系下电子动量相应地设为${p_{{\rm{ex}}}}, {p_{{\rm{ey}}}}$, 电子总能量为${E_{\rm{e}}}$.
质心系下的正/负电子能量均为

${E'_{\rm{e}}} = \sqrt {2{E_{\gamma 1}}{E_{\gamma 2}}(1 - \cos {\theta _{\rm{p}}}} )/2, $

由爱因斯坦相对论能量方程, 质心系下的电子动量大小为

${p'_{\rm{e}}} = \sqrt {{E'}_{\rm{e}}^{2} - 1} ,$

正电子与负电子动量大小相等, 方向相反.
做出从质心系到实验室系的洛伦兹变换, 可求得实验室系下的电子动量值及能量值. 记

$ {{\beta _{{\rm{cm}}}}} = \frac{{ {{ p_{\gamma 1}}} + {{ p_{\gamma 2}}} }}{{{E_{\gamma 1}} + {E_{\gamma 2}}}}, $

${\gamma _{{\rm{cm}}}} = 1/\sqrt {1 - \beta _{{\rm{cm}}}^2} , $

对x轴, y轴方向的动量分量分别作洛伦兹变换, 合成后得到电子实验室系下的动量为

$ {{ p_{\rm{e}}}} = {{{ p'}_{\rm{e}}}} + \frac{{({\gamma _{{\rm{cm}}}} - 1)}}{{\beta _{{\rm{cm}}}^2}}({{ \beta _{{\rm{cm}}}}}\cdot { p'_{\rm{e}}}){{ \beta _{{\rm{cm}}}}}+ {\gamma _{{\rm{cm}}}}\mathop {{ \beta _{{\rm{cm}}}}} E'_{\rm{e}}, $

电子的实验室系能量为

${E_{\rm{e}}} = {\gamma _{{\rm{cm}}}}({E'_{\rm{e}}} + {{\beta _{{\rm{cm}}}}} \cdot \mathop {{{ p'}_{\rm{e}}}} ), $

正电子的动量、能量值的推导与负电子同理, 因此可以通过上述物理推导获得详细的电子动力学参数.

本文使用的数值分析思想是, 以空间坐标为基准将光子分为一定数量的区块, 给出区块的运动参数, 首先以遍历法判断区块的空间对撞以降低计算量, 对可能发生对撞的区块遍历其内部光子检测对撞, 输出所得电子的参数. 这一数值方法的优势在于, 区块间对撞的检测, 可大大降低遍历法的计算量, 而完全建立在物理学原理之上的光子阈值、截面条件可满足性的检测, 能够最大程度地提高计算结果的准确性.
为了检测基于光子对撞动力学过程的计算结果是否合理, 重复文献[40]中的一项工作, 将光子束取为单一能量2 MeV, 并且只具有横向的动量, 这样的两束光子束分别在180°, 60°条件下进行对撞. 由于所有光子能量动量均完全相同, 只需要进行部分光子对撞即可反映电子动量的分布特征. 由于这部分只考虑动力学过程, 无需考虑实际的产额, 在程序中增大光子截面以使单能光子对撞数增多, 取10⁴量级的光子进行对撞, 180°与60°下分别得到约10³, 10²量级的电子对, 输出负、正电子的动量分布图1与图2.
图 1 单能光子180°对撞时　(a)电子动量分布; (b)正电子动量分布
Figure1. (a) Electron momentum distribution; (b) positron momentum distribution of 180° collision of single-energy photons.

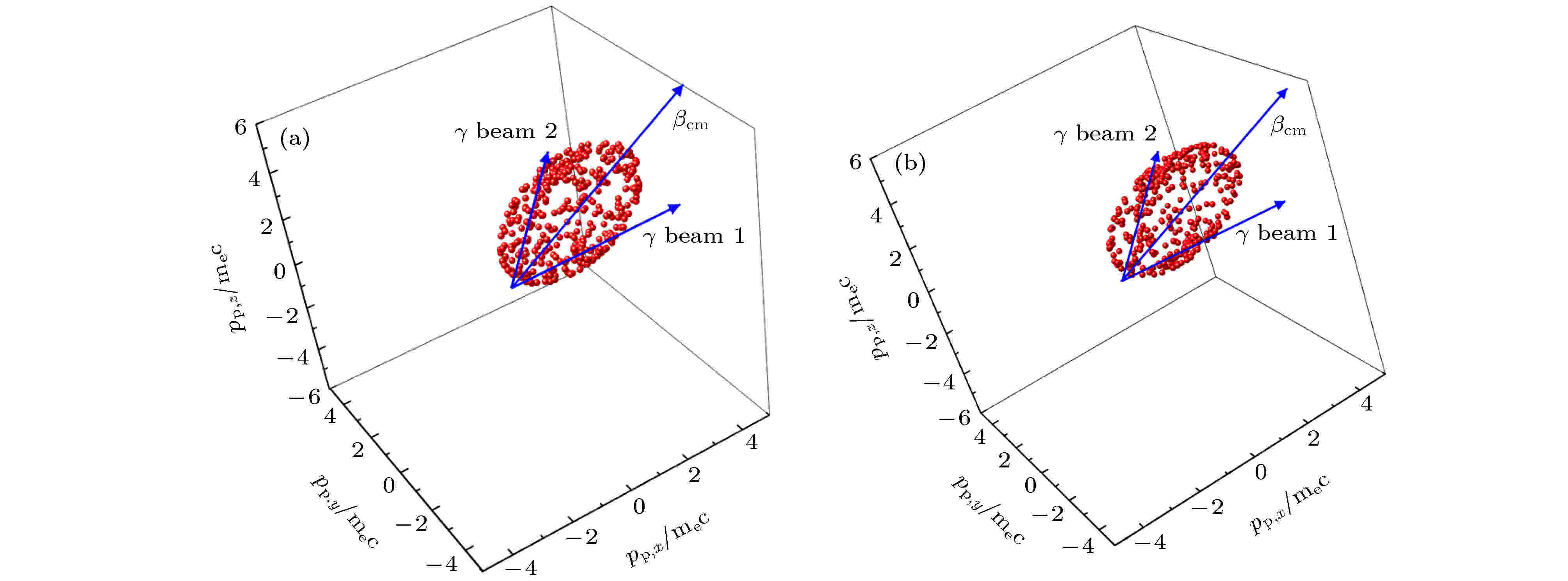图 2 单能光子60°对撞时　(a)电子动量分布; (b)正电子动量分布
Figure2. (a) Electron momentum distribution; (b) positron momentum distribution from 60° collision of single-energy photons.

在180°对撞时, 质心系相对实验室系没有相对速度, 质心系与实验室系中均应显示产生的电子动量方向随机, 电子能量恒为2 MeV, 因此实验室系的电子动量分布图应显示为以原点为球心的球面分布, 具有良好的各向同性. 电子动量的大小均相同, 约为4 m_ec. 在60°对撞下, 质心系相对实验室系有相对速度${\beta _{{\rm{cm}}}} = {\sqrt 3}/{2}c$, 在质心系中电子动量方向应显示各向同性, 电子能量恒为1 MeV; 而在洛伦兹变换后的实验室系内电子动量将发生在${\beta _{{\rm{cm}}}}$方向上的偏移, 电子能量大小受电子动量方向影响, 电子能量不为定值. 因此实验室系应显示出电子动量以质心速度方向为轴呈椭球形分布. 据(1)式计算得出电子动量大小分布于区间[–0.03, 6.74]m_ec. 图1, 图2中p_p的单位为m_ec, 图中显示的计算结果与前述分析一致.
以上两种对撞情形, 正电子的动量分布与负电子的几乎完全相同, 因为它们遵守相同的动力学原理, 计算所得的图像符合理论预期. 同时通过对比法国波尔多大学的研究团队所做的工作^[40], 该团队使用他们的算法, 同样对单能光子对撞下的电子动量分布进行了计算, 得到的180°、60°对撞的电子动量分布与该团队相同算例下的结果是一致的, 因此验证了该程序中双光子动力学模拟的准确性, 证明了本文算法的高效率和可靠性.

这一部分, 我们研究两束实际光子之间的对撞. 为方便起见, 我们以超强激光与通道靶相互作用产生的超准直γ光束^[10]为例, 对光子的对撞过程进行模拟. 具体模拟对象为两束10⁶量级的宏光子, 发散角为3°, 对撞角为170°, 光子束前端与对撞区域距离为70 μm, 第二束光子由第一束根据对撞角、对撞距离对称、平移变换得到. 以上参数与参考文献[7]中的设置一致, 以便进行模拟结果的对照分析.
图3给出了超强激光与通道靶相互作用产生得到的光子束的角-谱分布, 关于该光子束的更详细信息可以参考文献[10]. 我们对粒子模拟中获得的宏光子^[7]进行对撞计算, 计算中需要使用每个宏光子准确的位置、动量以及能量信息, 将以上信息导入本文使用的对撞模拟程序进行模拟, 就可以得到对撞后正负电子对的信息.
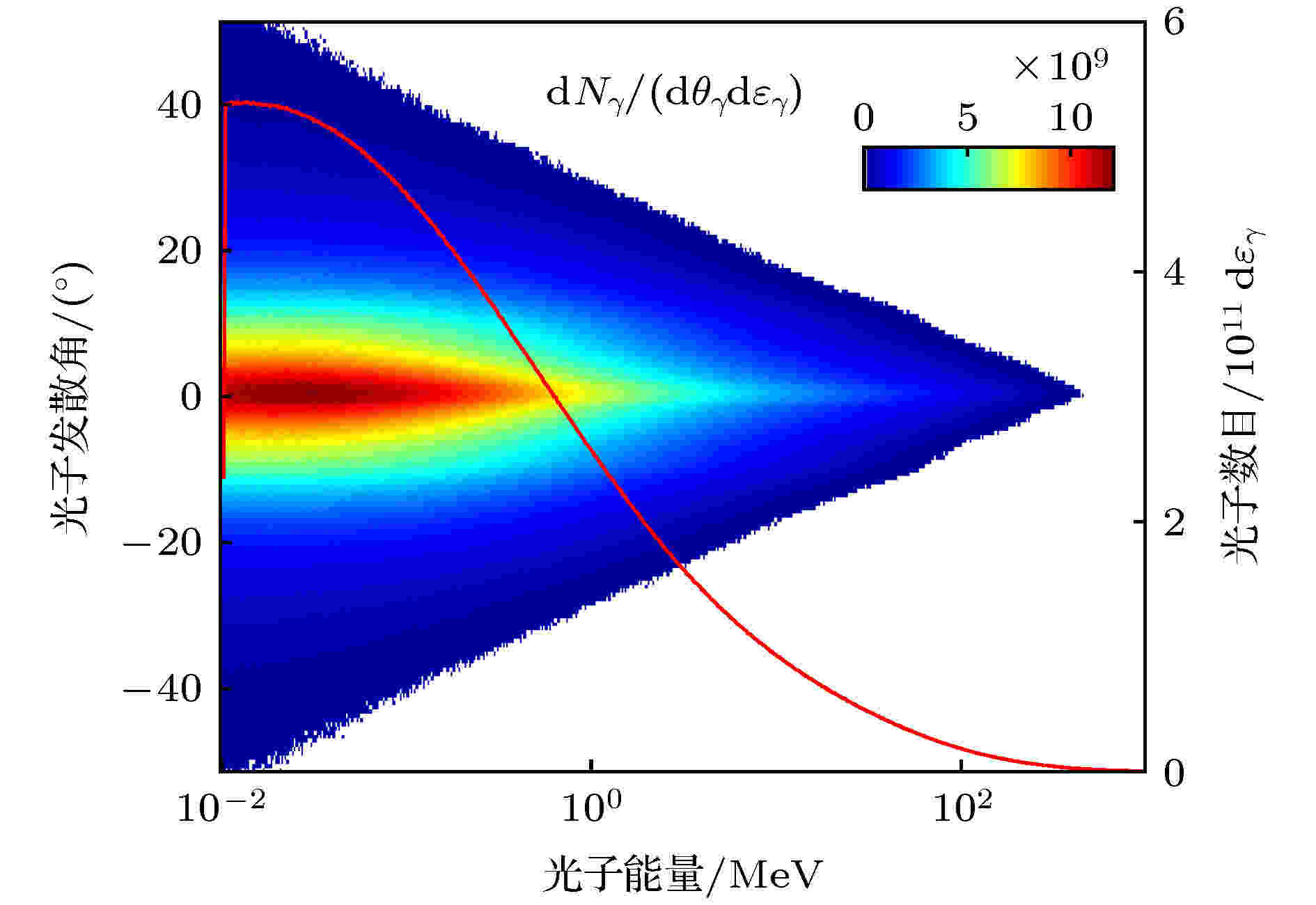图 3 粒子模拟程序得到的光子束角-谱分布^[7,10]
Figure3. Angle-spectral distribution of photon beams from particle simulator^[7,10].

具体的模拟过程与参数设置如下: 第一, 读取光子参数, 划分区块. 根据设定的对撞角与对撞距离, 对称变换出第二束光子, 将光子束以空间坐标相近为依据划分为多个区块; 这里划分区块有两种不同方式, 两种方式的区块内光子数目也不同, 可以互相对照结果以证明方法的准确性; 方法一(后文统称区块分法一)的设置是: 每个区块光子数量均为5000个. 根据光子束的实际空间分布, 先根据y坐标大小划分出几个较大的区块, 每个大区块的光子数均相同; 之后对每个大区块根据x坐标大小进行x方向上的划分, 保证各小区块的光子数为5000个. 最后一个大区块和最后一个小区块的光子数目与其他区块有所区别, 源于光子总数可能不是5000的整数倍. 由于光子分布的不均匀性, 各个区块大小有所不同, 计算时根据区块内所有光子的坐标来判断区块大小、边界坐标、中心坐标, 以保证计算的准确性. 方法二(后文统称区块分法二)的思想是: 根据光子束的初始分布区域划分出相同面积的一系列近似矩形的区块, 这种情形下区块内部光子数由光子的具体分布决定, 后续处理同区块分法一. 第二, 检索区块之间的对撞. 这一步的主要目的是剔除大量不会对撞的光子, 减少不必要的计算量. 在前一步的区块划分方式下每个区块可近似为矩形, 区块具有速度v, 取其为内部所有光子的平均速度; 进一步对两束光子的各个区块遍历检测整个运动过程中是否能发生空间上的相交, 方法是, 设定各个区块的中心坐标为区块内全部光子的坐标平均值, 在将区块近似视为矩形的前提下, 某两个区块中心坐标的距离极小值若低于两矩形对角线长度之和的一半, 则认为两区块在空间上会相交, 即可判定发生对撞. 事实上由于光子分布的不均匀性, 还可以将区块相交的判断阈值进一步缩小以提升计算速度. 第三, 检索光子的对撞. 根据每个光子的初始坐标、动能、动量各项参数, 遍历检测对撞区块的所有光子, 若两个光子可同时满足能量阈值条件与截面条件, 则判定发生Breit-Wheeler过程, 产生一对正负电子; 进而根据动力学原理计算正负电子的能量与动量.
计算得出, 两种区块分法产额相同, 均为8 × 10², 产额比例为1/10⁴. 为验证程序中所使用的动力学计算的正确性, 需要分析电子动量方向的分布规律并与文献[7]中的结果进行比较. 由于电子产额量级较小, 达不到类似于大量抽样的随机试验中获取统计规律的效果, 因此有必要获取更大的产额来分析比较. 将所有对撞截面增大10⁹倍, 计算得到的产额增大至1 × 10⁴, 产额增大的量级远小于截面增大的量级的原因是: 经数据分析, 截面条件要求的光子距离过小, 而170°对撞下绝大多数双光子的距离最小值处于远高于截面条件要求的距离范围, 因此在较小的截面范围内, 满足截面条件的光子对数量与截面的变化不构成线性关系. 在1 × 10⁴电子产额下, 负电子的动量极角分布(与正电子的动量极角分布几乎完全相同)如图4所示, 根据动力学原理分析, 对撞的情形以光子能量分类主要有三类: 1)高能光子与低能光子的对撞: 质心动量近似等于高能光子的动量, 而高能光子的动量极角根据其所属的光子束, 分别近似等于0°或170°. 在这种情况下, 电子动量在洛伦兹变换时, 受高能光子的影响较大, 动量极角将同样接近0°或170°. 且由于能量阈值条件易于满足, 低能光子的数量较多, 导致高能光子与低能光子对撞的事件相对较多, 对应了图4中存在大量极角接近0°或170°的电子. 2)高能光子与高能光子的对撞: 由于高能光子本身数量较少, 因此高能光子与高能光子对撞的概率较低, 事件较少. 3)低能光子与低能光子的对撞: 这一情形在对撞角接近180°时满足能量阈值条件的概率较大, 因此低能光子与低能光子的对撞主要在这一情形下发生, 质心动量趋近0, 因此对撞出的电子动量基本呈各向同性, 对应图4中极角远离0°或170°的电子数量分布较平均. 以上情形导致了电子动量方向显示出图4中的分布规律. 将这一极角分布结果对比文献[7]中的模拟结果, 可验证二者的极角分布保持一致, 证明了算法的正确性. 同时, 两种区块分法的产额相同, 电子动量分布趋势也相同, 说明了只要检索区块对撞时保证正确检索到可对撞的区块, 那么分区块的方式是不会影响到最终结果的. 这与算法的预设一致.
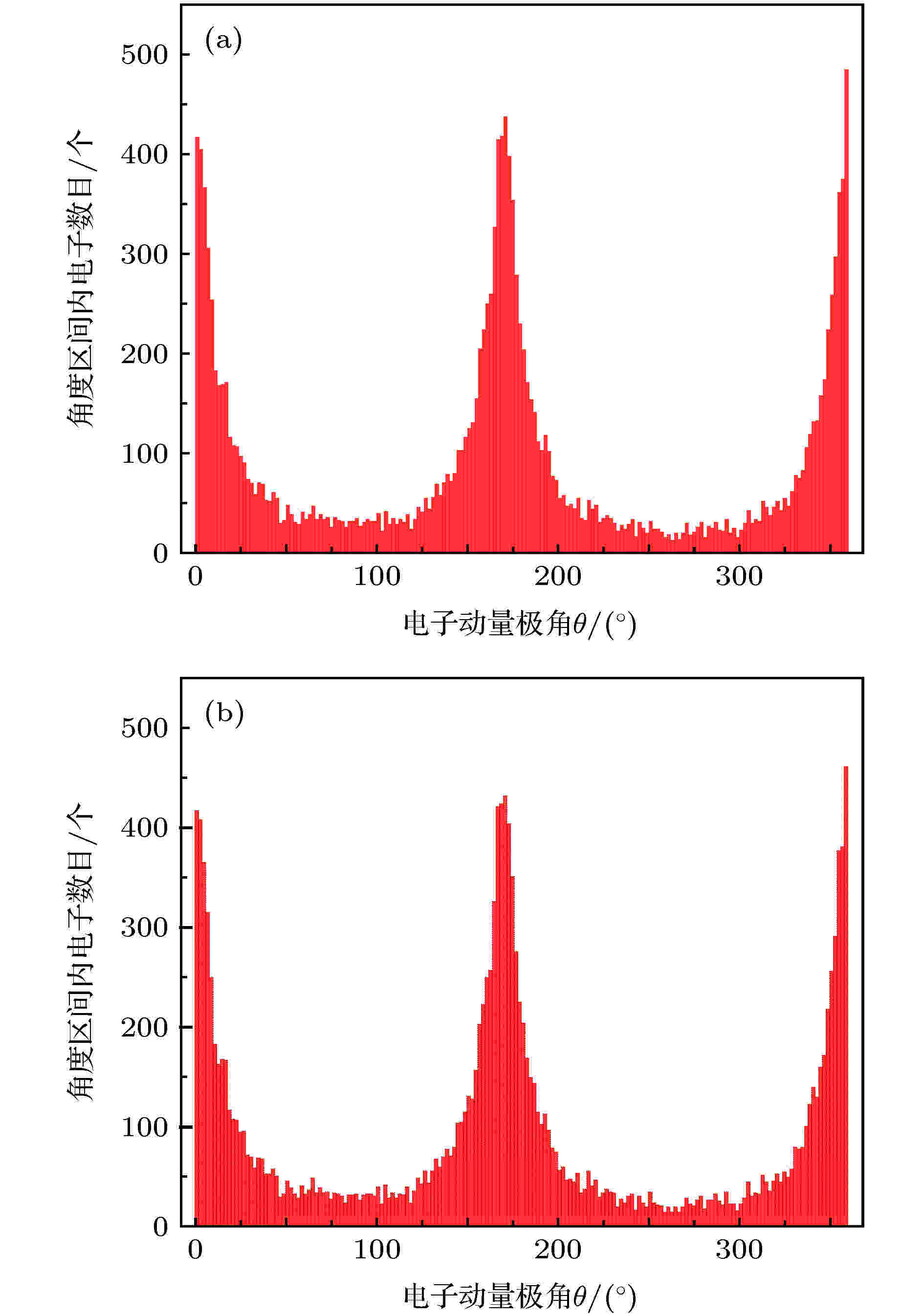图 4 10⁶光子170°对撞电子动量极角分布　(a)区块分法一; (b)区块分法二
Figure4. Polar angular distribution of electron momentum from 170° collision of 10⁶ photons: (a) the first block division; (b) the second block division.

改变光子束的对撞角, 其余条件不变, 计算电子的产额, 得出的两种区块分法下电子产额变化趋势如图5所示, 不同分法下的产额也相同. 随对撞角变小, 电子产额迅速降低. 变小的原因其一, 据(2)式对撞角变小导致双光子质心系能量降低, 满足能量阈值条件的光子对数目减少, 使得电子产额降低; 其二, 对撞角变小后, 光子对满足截面条件的概率降低. 因此接近180°的正对撞是提升电子产额的较佳选择. 由于本文没有严格考虑光子的权重, 因此没有和文献[7]严格比较绝对产额, 但对于不同对撞角, 正负电子对的相对产额的变化趋势是一致的. 通过上述与相关文献的直接比较, 证明了该模拟方法的有效性.
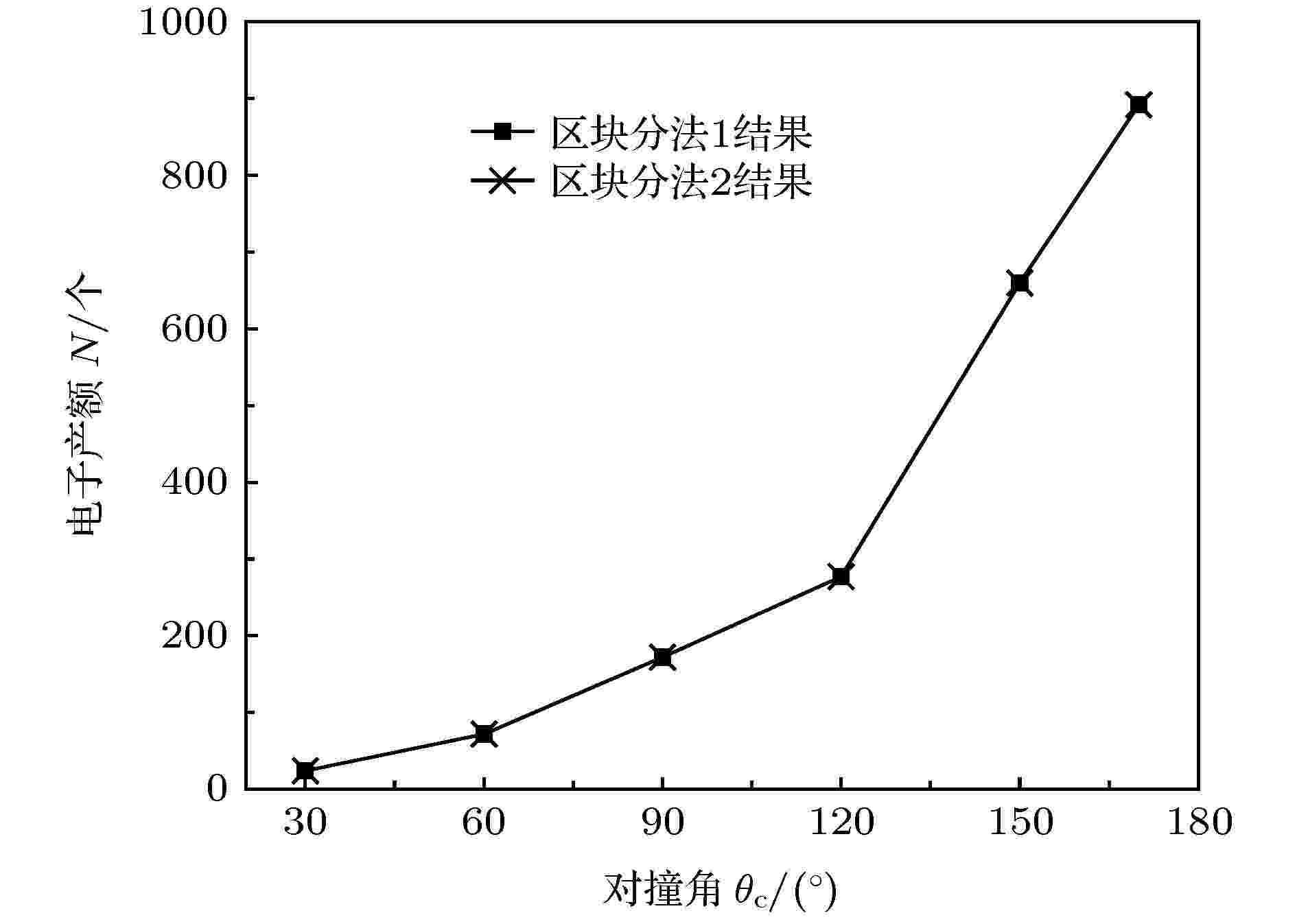图 5 电子产额随光子束对撞角的变化趋势
Figure5. The trend of electronic yield with the collision angle of photon beam.

在光子对撞机中, 正负电子对的产额与对撞区横截面的大小成正比, 而在对撞中两束光子束也无法做到完全对撞, 因此有必要研究对撞区域的偏移带来的影响. 在这一部分中, 将两束光的对撞角固定为170°, 改变另外一束光的纵向偏移值. 上述光子束的束腰宽度约为10 μm, 令其中一束光子在y方向上进行5 μm范围内的偏移, 步长取为1 μm, 其余条件均不改变, 计算对撞产额. 结果如图6所示.
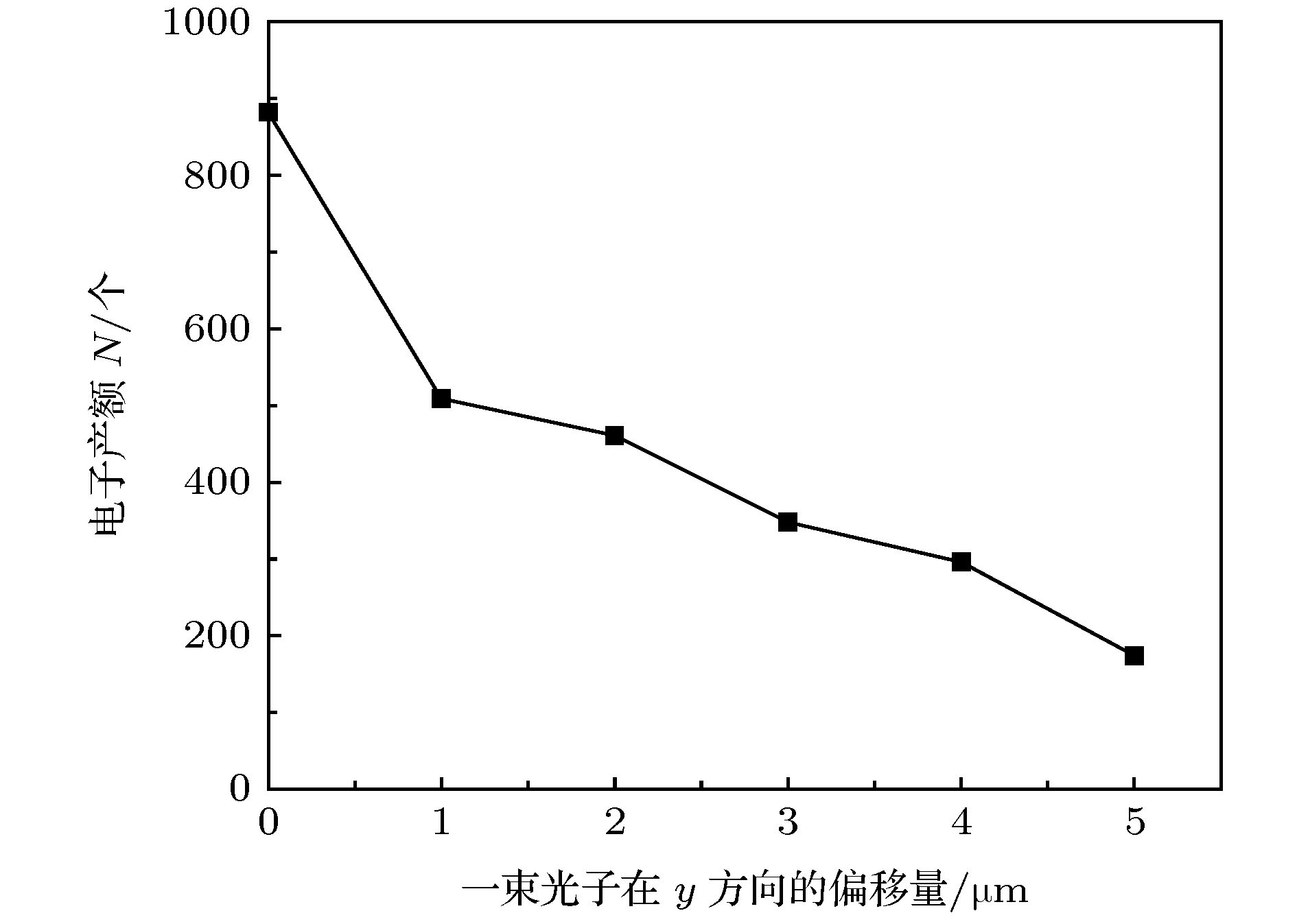图 6 电子产额随光子束偏移量的变化趋势
Figure6. The trend of electronic yield with the offset of photon beam.

根据计算结果可以得知, 在两束光子趋于完全对称之时, 有最大的电子产额; 由于Breit-Wheeler过程的截面非常小, 随着光子束初始位置的变化, 先前能对撞的光子不再满足截面条件, 且会有新的满足截面条件的光子出现对撞; 随着光子束的平移, 两束光子在空间上的有效对撞横截面积减小, 更多的光子无法与另一束光子作用, 因此电子产额下降; 一定程度上可认为有效对撞横截面积和实际参与对撞的光子数量N₀成正比, 而从概率的角度分析, 电子产额N近似有N～N₀²的关系, 则产额N随有效对撞横截面积S的变化趋势可以近似地用N～S²的关系来描述. 由于光子本身各类参数分布复杂以及Breit-Wheeler过程的截面非常小带来的敏感性的缘故, 计算结果与N～S²的关系略有偏差, 但基本上可以认为符合物理规律. 因此, 我们的计算结果也进一步说明了光子的空间位置分布对对撞会带来一定的影响, 在之前其他研究者的工作中, 均不能考虑光子的实际空间分布.
根据前文的详细分析, 这一工作能够总结出以下几点光子对撞结果的物理意义: Breit-Wheeler过程存在较高的能量阈值和极低的截面, 且截面对光子参数敏感性较高, 因此该过程的发生概率低, 绝大多数距离较远的光子之间都不会发生这一过程; 该过程的事件数受对撞角、光子能量、光子的空间分布等参数的影响较大. 由于光子束本身的能量分布特征, 据前文已有的基于双光子动力学的分析, 两束能量分布相同的准直光子束进行正对撞时, 高能光子(几个MeV)与低能光子(< 1 MeV)之间满足能量阈值条件的事件相对多, 进而能够发生较多的对撞, 基于动力学原理, 这类对撞产生的电子动量主要受高能光子的动量影响, 电子束准直性较好. 此外, 高能光子与高能光子、低能光子与低能光子对撞的事件数较少, 这两类对撞产生的电子动量方向较随机, 其分布趋近于各向同性. 当光子束从近似完全对称到发生空间上的相互偏移导致光子束对称性变差时, Breit-Wheeler过程的电子产额会受其影响而下降. 根据前文分析, 光子束的偏移会导致光子束有效对撞横截面积S的下降, 一定程度上, 电子产额N与S的关系可以用N～S²近似描述, 由于光子的具体空间分布而不能严格用N～S²来描述.
另外从理论计算与实验设计上进行一定的深入讨论: 其一, 若模拟三维空间下的运算, 可以仍然沿用先前从x、y方向划分近似矩形的区块的两种分区块方式, 进行类似的整个流程的计算; 如果光子束在z方向高度值较大, 可以在z方向上也对区块进行划分, 使计算更精确. 其二, 从实际实验的角度考虑, 观测Breit-Wheeler过程产生的电子时, 需要排除其它来源的电子的影响, 以文献[7]中的实验设计为例, 高能激光轰击微通道结构靶获得γ束流, γ束流中含有多种干扰Breit-Wheeler过程观测的噪声正电子, 通过文献[7]中的精确计算, 发现噪声水平比Breit-Wheeler信号水平低3个数量级以上, 不会对Breit-Wheeler过程的探测造成干扰. 在已有这一可行实验设置的基础上, 本文立足于提出一种更简单且可靠的数值方法, 可以为即将到来的光子对撞机提供有力的理论参考.

本文通过理论推导与数值模拟的方法对光子对撞Breit-Wheeler过程生成正负电子对这一物理过程进行了分析. 这一过程涉及大量光子的对撞, 需要对计算加以简化, 尽可能避免计算原本不会发生对撞的光子对. 本文利用分区块宏光子思想, 进行基于动力学原理的遍历法数值模拟, 在显著提升计算效率的同时还提高了计算准确度. 分区块方法能够有效考虑光子束的实际空间分布, 也有利于尽可能多地检索、剔除大量不会对撞的光子以提升计算效率; 基于动力学原理对可能对撞的光子区块做遍历检测计算, 能够给出最可信的电子产额等结果. 通过与国内外相关团队所研究的单能光子束对撞、实际光子束对撞的计算做对比, 得到了高度一致的结果, 证明了这一数值方法的有效性. 它可以为即将到来的光子对撞机提供有力的理论参考.