全文HTML
--> --> -->对于表面陷阱的影响, 采用钝化技术[17,18]或场板结构[19-21]可以使其有效降低, 而对于缓冲层陷阱, 尤其是缓冲层深能级陷阱对电流崩塌的影响仍得不到很好的解决, 因为这些陷阱可以抑制缓冲层泄漏电流以及短沟道效应, 它是器件正常工作所必需的[22]. 因此, 进一步研究缓冲层陷阱对电流崩塌的影响机理, 提出改善电流崩塌效应的方法是一个亟待解决的问题.
本文对传统AlGaN/GaN HEMT器件在缓冲层陷阱影响下的电流崩塌机理进行了研究, 结果表明栅边缘漏侧的电场峰值是导致电流崩塌效应的关键因素. 为进一步抑制电流崩塌效应, 提出了势垒层局部凹槽的AlGaN/GaN HEMT器件结构, 对新结构器件电流输运机理进行了研究. 计算机辅助设计(technology computer aided design, TCAD)仿真结果表明了新结构抑制电流崩塌效应的可行性和有效性[23].
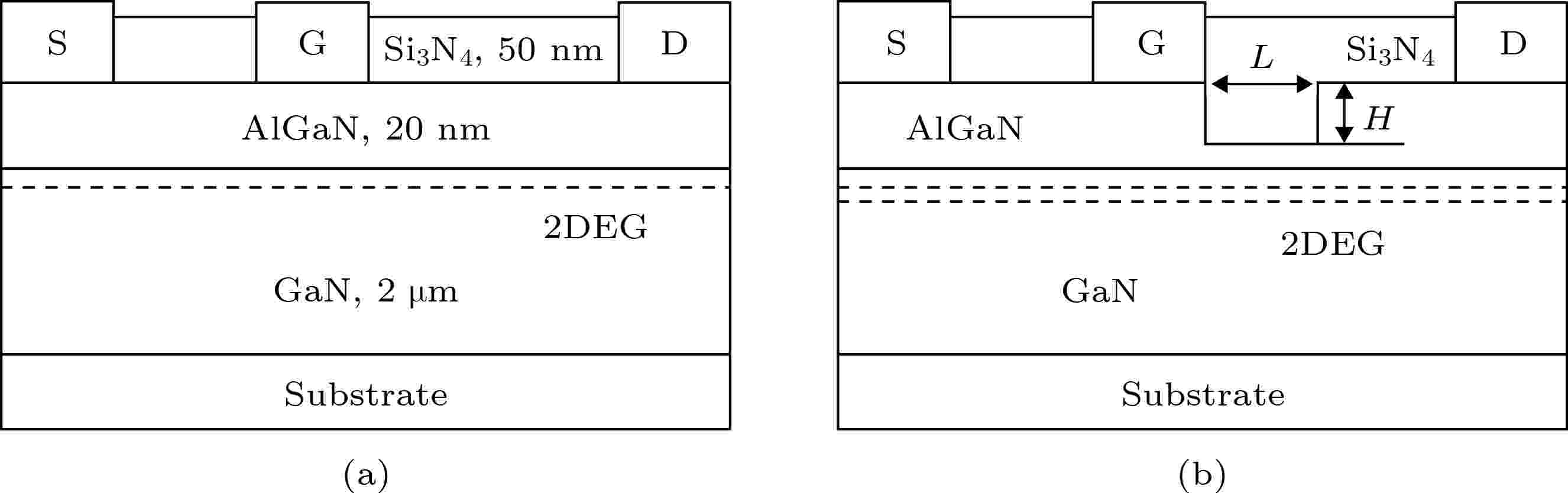图 1 AlGaN/GaN HEMT结构示意图 (a)传统AlGaN/GaN HEMT; (b)势垒层局部凹槽结构AlGaN/GaN HEMTFigure1. Schematic cross-section of AlGaN/GaN HEMT: (a) Conventional AlGaN/GaN HEMT; (b) AlGaN/GaN HEMT with barrier layer local groove structure.
3.1.电流崩塌效应机理
采用双脉冲技术对器件的电流崩塌效应进行研究, 脉冲波形及相关参数设置如图2所示, 静态偏置(VgQ, VdQ)为(–5 V, 20 V), 测试偏置(Vg, Vd)为(0 V, 5 V). 静态偏置时间持续到t = 10–7 s, 静态偏置到测试偏置的上升时间为t = 10–8 s, 测试偏置阶段从t = 1.1 × 10–7 s开始持续到t = 10 s结束.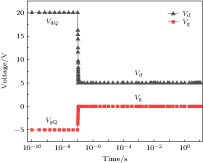
图 2 脉冲仿真电压偏置条件Figure2. Pulse simulation voltage bias conditions.
图3显示了传统AlGaN/GaN HEMT器件的电流崩塌变化曲线, 可以看出, 在t = 1.1 × 10–7 s时, 器件进入测试偏置阶段, 但输出电流未能直接达到稳定值, 而是保持在一个初始值持续一段时间(从t = 1.1 × 10–7 s 至t = 10–4 s)后才逐渐增大到稳定值, 图3所示结果表明AlGaN/GaN HEMT器件具有显著的电流崩塌效应. 为深入分析电流崩塌产生机理, 将测试偏置阶段分为三个部分, t = 1.1 × 10–7 s至10–4 s输出电流基本保持不变, 称为电流保持阶段; t = 10–4 s至2 × 10–2 s电流随时间增大, 称为电流上升阶段; t = 2 × 10–2 s之后, 输出电流几乎保持不变, 称为电流稳定阶段. 在t = 10–7 s之前器件处于静态偏置阶段, 栅压小于阈值电压, 栅下沟道耗尽, 器件工作在关断状态. 栅漏之间电势差较大(25 V), 2DEG获得能量跃迁至缓冲层, 被缓冲层陷阱俘获, 沟道2DEG浓度很小. t = 1.1 × 10–7 s栅压跃变为0 V, 器件处于测试偏置阶段, 栅下沟道可以很快响应, 但缓冲层陷阱的响应比较慢, 此时沟道中2DEG浓度较小, 电流未能达到稳定值而是保持在一个较小值的状态. 在t = 10–4 s时, 随着缓冲层深能级陷阱缓慢释放电子, 电流逐渐增大, 在t = 2 × 10–2 s时达到稳定状态.
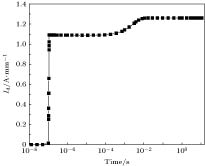图 3 双脉冲下的电流崩塌效应Figure3. Current collapse effect under double pulse.
在电流保持、上升和稳定这三个阶段中分别取t = 1 × 10–6 s, t = 1 × 10–3 s和t = 0.1 s三个时间点, 图4为这三个时间点2DEG浓度的变化情况. 在X = 2.0 μm, 即栅边缘漏侧, 2DEG浓度随时间的推移逐渐增大, 由于缓冲层陷阱的响应较慢, 沟道不能在栅压跃变后马上导通而是随着缓冲层陷阱缓慢释放电子逐渐导通, 这也是导致器件输出电流缓慢增加的原因.
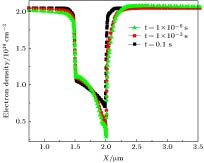图 4 沟道电子浓度曲线Figure4. channel electron concentration curves.
图5(a)—(c)分别为t = 1 × 10–6 s, t = 1 × 10–3 s和t = 0.1 s三个时间点上陷阱被电子占据情况, 可以看出随时间的增加缓冲层陷阱被电子占据的概率逐渐降低, 表现为陷阱释放电子的过程. 结合图4和图5可知, 电流逐渐趋于稳定状态是由于缓冲层陷阱释放电子导致的, 对比图5(c)与图5(d)(直流情况)可以看出两种情况的电子占据陷阱的情况几乎相同, 可知, 图5(c)处, 即t = 0.1 s时, 陷阱中已无净电荷释放, 输出电流Id趋于稳定.
图 5 不同时刻电子占据陷阱的概率分布情况 (a) t = 1 × 10–6 s; (b) t = 1 × 10–3 s; (c) t = 0.1 s; (d)直流情况Figure5. Probability distribution of electron occupying trap at different times: (a) t = 1 × 10–6 s; (b) t = 1 × 10–3 s; (c) t = 0.1 s; (d) direct current.
图6中(a)—(d)分别为t = 0.5 × 10–7 s, t = 1.05 × 10–7 s, t = 1.1 × 10–7 s和t = 1 × 10–6 s四个时间点对应的器件在栅边缘漏侧附近缓冲层陷阱被电子占据的概率分布情况. 可以看出, 测试偏置阶段之前, 器件处于缓冲层陷阱俘获电子的过程. 在刚进入测试偏置阶段时, 陷阱俘获电子的浓度达到最大. 由测试偏置阶段中陷阱释放电子的过程可知, 在栅边缘漏侧附近, 缓冲层陷阱释放的电子来自于静态偏置阶段及静态偏置阶段向测试偏置阶段的过渡状态中陷阱俘获的电子.
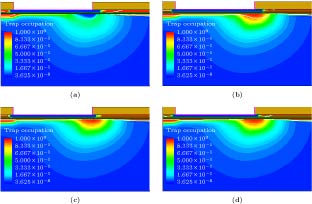图 6 电子占据陷阱的浓度分布情况 (a) t = 0.5 × 10–7 s; (b) t = 1.05 × 10–7 s; (c) t = 1.1 × 10–7 s; (d) t = 1 × 10–6 sFigure6. Concentration distribution of electron occupying trap: (a) t = 0.5 × 10–7 s; (b) t = 1.05 × 10–7 s; (c) t = 1.1 × 10–7 s; (d) t = 1 × 10–6 s.
图7和图8分别取t = 0.5 × 10–7 s, t = 1.05 × 10–7 s, t = 1.1 × 10–7 s, t = 1 × 10–6 s, t = 1 × 10–3 s及t = 0.1 s六个时刻, 栅边缘漏侧电场峰值及沟道电子浓度的变化情况. 可以看出, 电场峰值随时间推移逐渐减小, 在t = 1.0 × 10–7 s之前, 器件处于静态偏置阶段, 电场峰值最大, 栅边缘漏侧的沟道电子在这一高电场作用下发生跃迁进入缓冲层, 并被缓冲层中的受主陷阱俘获. 由于栅极下方的沟道耗尽, 栅边缘漏侧的沟道电子在被陷阱俘获后无法获得补偿, 导致该处沟道电子耗尽. 随着时间的推移, 器件进入静态偏置与测试偏置之间的过渡状态, 此时器件处于半导通状态, 栅极下方的沟道中已经开始产生电子, 并向栅边缘漏侧的沟道中进行电子补偿, 但由于栅漏间电势差仍较大, 在电场峰值作用下该处的电子会继续跃迁并被缓冲层中的陷阱俘获. 在测试偏置阶段, 栅下沟道已完全打开, 栅漏间电势差较小, 电场峰值也小到不足以使沟道电子发生跃迁, 为了维持平衡, 缓冲层陷阱开始释放电子, 导致栅边缘漏侧的沟道电子浓度逐渐增加, 沟道电子浓度分布趋于均匀, 沟道电场分布也随之趋于均匀, 最终电子浓度达到稳定状态. 由于输出电流的大小和沟道中2DEG密度有关, 所以输出电流也随着时间的变化发生变化, 形成了瞬态条件下的电流崩塌效应.
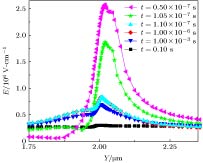图 7 栅极边缘处沟道电场Figure7. Channel electric field at the edge of the gate.
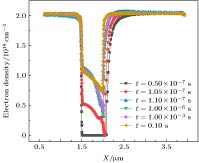图 8 栅极边缘电子浓度随时间的变化Figure8. Electron concentration at the edge of the gate as a function of time.
2
3.2.电流崩塌效应抑制
栅边缘漏侧的电场峰值是导致电流崩塌效应的关键因素, 本文提出的AlGaN/GaN HEMT新结构(如图1(b)所示), 基于势垒层局部凹槽结构可以显著降低栅边缘漏侧的电场峰值, 改善器件工作过程中的电流崩塌效应.图9为势垒层局部凹槽结构与传统结构在刚进入测试偏置阶段t = 1 × 10–6 s的横向沟道电场强度的分布. 可以看出, 相比传统结构, 凹槽结构在栅边缘漏侧处的电场峰值低, 同时电场分布向漏极方向扩展, 电场分布更加均匀. 这是由于沟道中的2DEG主要来自势垒层, 当其厚度低于能够产生二维电子气的临界厚度时, 费米能级在施主表面态能级之上, 几乎没有电离施主态电离, 无法形成2DEG. 随着厚度的增加, 在极化电场的作用下, AlGaN层的表面势逐渐升高, 表面导带下方的类施主陷阱能级相应升高. 当表面态能级到达费米能级后, 施主表面态发生电离, 释放电子, 2DEG浓度开始逐渐增加. 当势垒层厚度进一步增加, 表面态完全电离, 2DEG的浓度接近饱和时, 即使其厚度继续增大, 2DEG的浓度也不会出现明显的增加. 由2DEG的产生机理可知, 在一定范围内2DEG的浓度会随着势垒层厚度的增大而增大, 凹槽的引入, 减小了凹槽下方势垒层厚度, 该部分沟道的2DEG浓度有所降低, 使得凹槽结构栅边缘漏侧处的电场分布向漏极方向扩展, 分布更加均匀, 峰值电场小于传统结构.
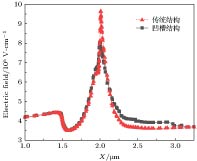图 9 凹槽结构与传统结构器件的沟道电场分布Figure9. Channel electric field distribution of groove structure and conventional structure device.
图10为凹槽的长L为1.0 μm, 高H为0.010 μm时, AlGaN/GaN HEMT势垒层局部凹槽结构与传统结构的电流崩塌曲线. 可以看出, 采用了凹槽结构的器件的电流崩塌量从13.59%降低到了10.56%, 性能提升了22.30%.
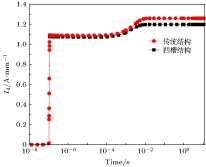图 10 凹槽结构与传统结构器件的电流崩塌对比Figure10. Comparison of current collapse between groove structure and conventional structural devices.
为进一步分析凹槽结构改善电流崩塌效应的有效性, 图11给出了在t = 1 × 10–6 s, t = 1 × 10–3 s及t = 0.1 s三个典型时间两种器件结构沟道电场分布情况. 可以看出, t = 1 × 10–6 s到t = 0.1 s之间, 势垒层局部凹槽结构的电场峰值变化量要远小于传统AlGaN/GaN HEMT器件.
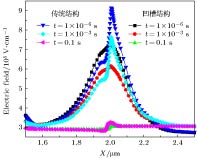图 11 凹槽结构与传统结构器件在不同时刻的沟道电场分布Figure11. Channel electric field distribution at different times for the groove structure and the conventional structure device.
图12给出了t = 1 × 10–6 s, t = 1 × 10–3 s及t = 0.1 s三个时间点下凹槽结构与传统结构沟道电子浓度分布, t = 1 × 10–6 s到t = 0.1 s时间范围, 凹槽结构沟道电子浓度的变化量小于传统结构, 导致凹槽结构电场的变化量小于传统结构, 从而导致图10中势垒层局部凹槽结构的电流变化量减小, 电流崩塌得以改善.
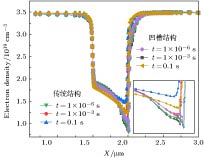图 12 凹槽结构与传统结构器件在不同时刻沟道电子浓度分布Figure12. Channel electron concentration distribution at different times for the groove structure and the conventional structure device.
沟道电子浓度的变化是由缓冲层陷阱俘获及释放电子造成的, 图13为在测试偏置阶段t = 1 × 10–6 s, t = 1 × 10–3 s及t = 0.1 s三个时间点下陷阱俘获电子浓度的变化情况, 表明凹槽结构和传统结构随时间的增加, 电子占据缓冲层陷阱浓度逐渐减小, 表现为释放电子的过程, 从而导致沟道电子浓度的增加. 器件进入测试偏置阶段时, 栅下沟道完全打开, 栅漏间电势差较小, 电场峰值小到不足以使沟道电子发生跃迁, 为了维持平衡, 俘获了电子的陷阱开始释放电子, 导致栅边缘漏侧的沟道电子浓度逐渐增加.
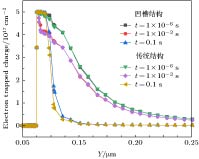图 13 电子占据缓冲层陷阱浓度随时间的变化Figure13. Electron occuping buffer layer trap concentration as a function of time.
综上可知, 栅边缘漏侧的电场峰值是导致传统AlGaN/GaN HEMT器件电流崩塌效应的一个重要因素, 新结构中通过引入凹槽结构降低了该处的电场峰值, 器件的电流崩塌效应得到了改善.
