摘要: 对比已有完善而系统理论的微分方程领域, 差分方程理论尚处于发展之中. 近年来离散可积理论的进展, 带来了差分方程理论的革命. 多维相容性是伴随离散可积系统研究出现的新的概念, 作为对离散可积性的一种理解, 提供了构造离散可积系统的B?cklund变换、Lax对和精确解的工具. 本文旨在综述多维相容性的概念及其在离散可积系统研究中的应用.
关键词: 离散可积系统 /
多维相容性 English Abstract Discrete integrable systems: Multidimensional consistency Zhang Da-Jun Department of Mathematics, Shanghai University, Shanghai 200444, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11875040, 11631007)Received Date: 28 October 2019Accepted Date: 14 November 2019Available Online: 05 December 2019Published Online: 05 January 2020Abstract: In contrast to the well-established theory of differential equations, the theory of difference equations has not quite developed so far. The most recent advances in the theory of discrete integrable systems have brought a true revolution to the study of difference equations. Multidimensional consistency is a new concept appearing in the research of discrete integrable systems. This property, as an explanation to a type of discrete integrability, plays an important role in constructing the B?cklund transformations, Lax pairs and exact solutions for discrete integrable system. In the present paper, the multidimensional consistency and its applications in the research of discrete integrable systems are reviewed.Keywords: discrete integrable systems /multidimensional consistency 全文HTML --> --> --> 1.引 言 离散系统泛指含有离散自变量的常差分、微分差分、偏差分系统、以及变换和映射等. 由于缺少导数、积分等局部化的数学工具, 对于非线性离散系统的研究, 往往伴随着新的数学概念、理论和方法的出现.[1 ] 、反散射变换方法的建立[2 ] 和Lax对概念的提出[3 ] , 参见文献[4 ]. 早期对离散可积系统的探索主要是可积离散化, 早在20世纪70年代: Case和Kac[5 ] 对Schr?dinger谱问题的离散以及Ablowitz和Ladik[6 —8 ] 对Ablowitz-Kaup-Newell-Segur(AKNS) 谱问题的离散 建立了基于差分的反散射变换过程; Hirota[9 -11 ] 对双线性方程的离散利用双线性B?cklund变换与Lax对的联系获得了一系列离散可积系统. 进入80年代后, 对离散可积系统的研究逐渐向形成独立于连续系统的研究方法, 系统进展有: 京都学派Date等[12 -16 ] 和?Ueno等[17 ] 对Sato理论的离散; 荷兰****Nijhoff等[18 -22 ] 和Quispel等[23 ] 基于Fokas和Abolwitz[24 ] 的直接线性化格式以及Levi和Benguria[25 ] 的变换与离散的同等性认识发展起来的构造和研究离散可积系统的系统方法. 进入90年代以后, 离散可积系统的显著进展包括: 超离散可积系统的提出及其连续极限的建立[26 ,27 ] , 基于奇点囿禁的奇点理论与可积性的联系的发现[28 ,29 ] , 奇点囿禁在可积性判别上的不充分性的发现[30 ] , 以及基于代数熵理论对可积性的判别[31 ] . 这些进展相继推动了超离散可积系统、离散Painlevé方程、可积性检验等方面的发展.[32 ] 基于有理曲面理论和Blow-up分析对离散Painlevé方程的分类, 揭示了离散Painlevé方程丰富的代数几何结构, Bobenko和Suris[33 ] 、Adler等[34 ] 和Nijhoff等[35 ,36 ] ****对于“多维相容性”的理解以及对若干离散可积系统的分类, 各种精确求解方法 在离散可积系统中相继实现[37 —45 ] , 等等, 一系列进展标志着对离散可积系统的研究进入到一个新的阶段. 2009年在著名的英国剑桥牛顿所(The Isaac Newton Institute for Mathematical Sciences)举办的为期半年的离散可积系统主题研讨活动, 是对当时离散可积系统蓬勃发展的一个反映.[4 ] . 在数学方面, 离散可积系统的发展伴随着离散几何和离散复分析的发展, 这与连续意义下可积系统丰富的几何背景以及分析的工具在其研究中的重要作用是分不开的. 对与离散可积系统相关的差分算子理论与复分析方面的研究, 如势函数的渐近性、散射理论、Riemann-Hilbert问题、解的长时间渐近分析、初边值问题等等, 建议参考文献[42 ,46 ]. 除了提及的上述进展, 还有如离散几何、对称理论、Galois理论、Lagrangian多形式理论等许多方面的重要进展. 值得指出的是, 最近由Hietarinta, Joshi和Nijhoff [47 ] 完成的一部专著《Discrete Systems and Integrability》已经出版. 读者可以参考了解其更多内容. 国际上每两年一届的SIDE会议(Symmetries and Integrability of Difference Equations)是离散可积系统及其相关问题的首要国际会议, 1994年始于加拿大Montreal, 至今已经成功举办13届, 其中SIDE-10于2012年在我国宁波召开.2.多维相容性 离散可积系统从未独立于连续系统. 下面首先来介绍两种引入离散变量的途径.2.1.离散变量的引入 2.1.离散变量的引入 离散化是引入离散变量的方式之一. 从熟悉的AKNS谱问题开始:$ u = u(x, t), \; v = v(x, t) $ , $ \eta $ 是谱参数, 为了方便, 记$ { M} = { M}(\eta, U) $ , $ U = (u, v)^{\rm T} $ . 定义$ ({ {\varPhi}}_{n+1}-{ {\varPhi}}_n)/\epsilon $ 替代导数$ { {\varPhi}}_x $ , 得到[7 ] 2 )式和$ { {\varPhi}}_{n+1} = { {\varPhi}}(x+\epsilon) $ 在$ \epsilon = 0 $ 展开, 并取$ \epsilon \to 0 $ , 则AKNS谱问题(1 )式可以作为领头项从AL谱问题(4 )式中恢复出来, 同时谱参数从$ \lambda $ -平面变到$ \eta $ -平面.2 )式是我们所熟悉的数值(差分)离散: 如图1 , 将区间$ [x_0, x] $ 等分成n 份, 步长为$ \epsilon $ . 在x 点, $ {\varPhi}_n $ 与$ {\varPhi}(x) $ 仍然表示相同的数值, 但是自变量的空间已经从实数域$ \mathbb{R} $ 变为整数域$ \mathbb{Z} $ . 差分离散是计算连续极限的基础, 但是对于可积系统而言, 差分离散(也称为直接离散)不足以保持原有系统的可积特征. 关于由AL谱问题(4 )式引出的半离散AKNS系统, 读者可以参考文献[48 —51 ].图 1 $[x_0, x]$ 上的数值离散Figure1. Numerical discretisation on $[x_0, x]$ $ \{H_n(x)\} $ 满足递推关系x 是自变量, $ \alpha $ 是参数. 由此方程可以建立Bessel函数的递推关系(参考文献[47 ]的第37页)x 和$ \alpha $ 互换了角色, x 是参数, $ \alpha $ 成为自变量. 再如, Painlevé II方程$ f'(t) $ 表示对t 的导数.[52 ] 在1973年发现形如w 满足势KdV方程$ u = w_x $ 满足KdV方程(6 ).7a )式可以建立KdV方程的解的非线性叠加公式. 首先在(7a )式中, 从同样的种子解w 出发, 分别记由$ \lambda = \lambda_1 $ 和$ \lambda = \lambda_2 $ 引出的$ \widetilde w $ 为$ w_1 $ 和$ w_2 $ , 即7a )式中取$ w = w_1, \; \lambda = \lambda_2 $ , 记$ \widetilde w = w_{12} $ , 有$ w = w_2, \; \lambda = \lambda_1 $ , 记$ \widetilde w = w_{21} $ , 有图2 .图 2 B?cklund变换解的交换性质Figure2. Permutation property of B?cklund transformation$ w_{12} $ 和$ w_{21} $ 能够相等(参考文献[49 ]). 进一步, 从(9 )式和(10 )式得到① [47 ] . 作为离散的方程时, (11 )式通常写为p 和q 分别是对应于n –方向和m –方向的方向参数.53 ,54 ]):$ u = {\rm e}^{\frac{{\rm i}\theta}{2}} $ 以后, 可以写为[11 ] 和Orfanidis[55 ] 先后得到, 与(16 )式只有部分符号差别, 经过同样的变换$ u = {\rm e}^{\textstyle\frac{{\rm i}\varphi}{2}} $ 以后, 可以写为[18 ] [58 ] 于1982年获得.9a )式中$ w_1 $ 可视为w 沿一个方向上的平移, (9b )式中$ w_2 $ 可视为w 沿另一个方向上的平移. 非线性叠加公式(11 )式是这两个方向上平移相容性的结果. 同时, (9a )式作为一个独立方程, 也可视为一个微分-差分方程.[25 ,59 ] 发现, 对于研究和理解离散可积系统具有重要意义. AKNS谱问题(1)式存在如下Darboux变换[60 ] :$ { U} = (u, v)^{\rm T} $ . 作为Darboux变换, $ \widetilde { {\varPhi}} $ 满足AKNS谱问题(1)式, 即$ \widetilde { {\varPhi}} _x = \widetilde { M} { {\varPhi}} $ , $ \widetilde { M} = { M}(\eta, \widetilde { U}) $ , 这相当于要求(1 )式与(22 )式相容, 即$ (\widetilde { {\varPhi}} )_x = (\widetilde{{ {\varPhi}}}_x) $ , 由此有22 )式引出一个新的半离散AKNS族[61 ,62 ] , 可视为微分-差分Kadomtsev-Petviashvili (KP) 方程族Lax三重组的对称约束的结果[63 ] . 若考虑两个不同方向上的Darboux变换21 ), 且在适当的连续极限下, (21 )式引出(20 )式(参考文献[43 ]). 显然, 由Darboux变换作为Lax对引出的4点方程$ \, { Q}({ U}, \widetilde { U}, {\widehat{ U }}, {\widehat{\widetilde{ U }}}; p, q) = 0 $ 即为4个解之间的非线性叠加公式. 更多的关于Darboux变换作为离散谱问题的例子可见文献[64 ].p 和q 分别表示n –方向和m –方向上的链参数. 如图3 所示.图 3 变换与平面网格Figure3. Map and lattice2.2.多维相容性 -->2.2.多维相容性 对于离散可积系统的研究需要引入新的概念. 下面介绍离散可积系统的“多维相容性”的概念.12 )式, 这一叠加关系可以重复下去. 为了方便,我们采用(26 )式中的符号, 将(12 )式写为l , 该方向上的平移表示为$ \, {\overline{u}} = u_{n, m, l+1} $ , 方向参数为r , 如图4 所示.图 4 相容立方体Figure4. Consistent cube$ (^{\widetilde{\; \; \;}}, p) $ 和$ (^{\widehat{\; \; \;}}, q) $ 互换下保持不变, 要求$ (\, \overline{\; \; }, r) $ 与另外两个方向之间也存在对称性, 则有27 )式定义在图4 中立方体的底面, (28a )式和(28b )式则分别定义在左侧和后侧. 如何体现这种维数扩充后的相容性? 首先, 由上述3个方程有l 以后的相容性体现在$\overline{ (29{\rm{a}})} = \widetilde{ (29{\rm{b}})} = $ $ \widehat{ (29{\rm{c}})} $ . 将(29a )式和(29b )式代入到$ \widehat{ (29{\rm{c}})} $ 算得$ (^{\widetilde{\; \;\; }}, p) $ ,$ (^{\widehat{\; \;\; }}, q) $ 和$ (\, \overline{\phantom{M}}, r) $ 下都保持不变, 说明从$ \overline{ (29{\rm{a}})} $ 和$ \widetilde{ (29{\rm{b}})} $ 也将得到同样的$ \widehat{\widetilde{\overline{u}}} $ .27 )的这种性质称~为该方程的3维相容性, 也称为27 )式自身的性质. 方程(17 )也具有同样的性质. 一般地, 对于一个定义在平面四方格上的方程图4 中立方体的6个面中, 得到$ {\widehat{\widetilde{u }}} $ , $ {\widetilde{\overline{u}}} $ 和$ {\widehat{\overline{u}}} $ , 代入到右侧的3个方程后得到同样的$ \overline{\widehat{\widetilde u}} $ , 则称方程(30 )具有3维相容性.d -维的离散方程, 如果嵌入到一个$ (d+1) $ -维链后, 所有的d -维子链都是相容的, 则称原d -维离散方程具有$ (d+1) $ -维相容性. 对于2维离散方程, 这种多维相容性即为3维相容性, 或CAC性质.2.3.ABS方程 -->2.3.ABS方程 本世纪初, 多维相容性逐渐被系统地认识并作为工具应用到离散系统的研究中[65 ,35 ,36 ,33 ] . 2003年, Adler, Bobenko和Suris (ABS)[34 ] 发表了他们在多维相容性的基础上对四方格方程的分类, 他们得到的方程列表被统称为ABS方程.30 )具有3维相容性的基础上, 进一步要求(30 )式满足:$ D_4 $ 下不变,30 )的一般形式可以设为$ k_i $ 都是待定系数; 四面体性质指$ \widehat{\widetilde{{\overline{u}}}} $ 只与$ {\widehat{\widetilde{u }}} $ ,$ {\widetilde{\overline{u}}} $ 和$ {\widehat{\overline{u}}} $ 有关, 而与u 无关, 即($ \widehat{\widetilde{{\overline{u}}}} $ , $ {\widehat{\widetilde{u }}} $ , $ {\widetilde{\overline{u}}} $ , $ {\widehat{\overline{u}}} $ )四个点在立方体(图4 )中构成一个四面体. ABS证明了满足上面3条要求的3维相容方程(30 )只有9个(允许存在M?bius变换), 并分别命名为H1, H2, H3(δ ), A1(δ ), A2, Q1(δ ), Q2, Q3(δ ), Q4:27 ), H3(δ = 0)为离散势mKdV方程(17 ) ($ u \to i^{n+m} u $ ), Q1(δ = 0)为离散的Schwarzian KdV方程, 也称为交比(cross-ratio)方程, A1(δ )在$ u\to (-1)^{n+m} u $ 下即为Q1(δ ), A2在$ u\to u^{(-1)^{n+m}} $ 下为Q3(δ = 0), Q4是著名的Krichever-Novikov方程的B?cklund变换的非线性叠加公式, 原型中系数用Weierstrass椭圆函数表示[34 ,66 ] , (33i )中Jacobi椭圆函数的参数化形式来自于Hietarinta[67 ] , 式中k 为Jacobi椭圆函数的模(modulus).2.4.离散Boussinesq型方程 -->2.4.离散Boussinesq型方程 离散的势Boussinesq方程是平面9点方程, 定义在$ 3\times 3 $ 格子上:$ P, Q $ 分别表示$ n, m $ 的方向参数, $ x_{ij} = x_{n+i, m+j} $ . 这类方程早期由Nijhoff等[68 -70 ] ****构造并研究. 借助于其他(因)变量, (34 )式可以改写为(参考文献[65 ])$ { u} = (x, y, z)^{\rm T} $ , 方程可以视为向量意义下的四方格系统, 并具有3维相容性.[71 ] 在(35 )式形式的基础上, 寻找了可能的离散Boussinesq型的3维相容系统, 代表方程为(考虑到对称性和M?bius变换):$ P, Q $ 仍然分别表示$ n, m $ 的方向参数, $ b_i $ 都是任意常数, 有的$ b_i $ 可以通过适当的变换去掉. 显然, [B-2]是(35 )式的推广. 文献[71 ]中还得到[C-4]方程, 现已证明与[C-3]之间存在M?bius变换, 故不再列出.2.5.不同方程间的3维相容性 -->2.5.不同方程间的3维相容性 离散的sine-Gordon方程(19 )不是3维相容的, 但是它与离散势mKdV方程(17 )一起可以实现立方体相容[72 ] . 在符号(26 )式下, 两个方程分别表示为39 )在变换$ u\to (-1)^n u $ 下成为(40 )式.图 5 离散sine-Gordon和势mKdV方程的相容立方体Figure5. The consistent cube for the discrete sine-Gordon equation and potential mKdV equation39 )和方程(40 )以如下方式放置于立方体的6个面:$ u, \widetilde u, {\widehat{u }}, {\overline{u}} $ 以后, $ {\widehat{{\widetilde{\overline{u}}}}} $ 是唯一的. 这说明两个方程按照如此方式放置于立方体的6个面时, 它们(在一起)具有3维相容性.73 ]给出了更多的例子. Adler等[74 ] 和Boll[75 ] 对这种情况进行了讨论. 详细结果列于Boll[76 ] 的博士学位论文中.2.6.高维的多维相容方程 -->2.6.高维的多维相容方程 对于定义在6面体上的8点3维(标量)离散方程, 如图6(a) , 目前已知的具有四维相容性(见图7 )的方程有[34 ] 图 6 定义3维方程的6面体以及8面体Figure6. Cube and octahedron for 3D equations图 7 围绕超立方体的4D相容性Figure7. 4D consistency around the hyper cube图6(b) , 要求这些方程具有4维相容性, Adler等[77 ] 于2011年进行了分类. 满足条件的方程共有5个:42a )式是离散的BKP方程, 又称为Miwa方程[78 ] ; (42b )式被认为是离散Schwarzian BKP, 首先从几何中得到[79 ] ; (43a )式由Hirota[80 ] 在1981年给出, 又称为离散广义Toda方程; (43b )式, (43c )式和(43d )式分别称为离散Schwarzian KP、离散势KP和离散modified KP方程, 最早由Nijhoff等系统构造(见文献[20 ]中(4)式和(23)式和文献[22 ]中(4.16)式); (43e )式由Date等于1982年获得(见文献[13 ]中(N-1)方程).3.多维相容性的应用 “多维相容性”不仅作为一类离散系统的可积性的理解, 还提供了研究手段, 可用于构造离散可积系统的B?cklund变换、Lax对、精确解等等.3.1.B?cklund变换 3.1.B?cklund变换 B?cklund变换始于对伪球面的构造. Bianchi[81 ] 首先证明了B?cklund给出的含任意参数的变换 可以保持sine-Gordon方程不变. 变换不仅是引入离散变量的一个渠道, 也是联系离散与连续的一座桥梁. 通常, auto-B?cklund变换指同一方程的解之间的变换, nonauto-B?cklund变换指不同方程的解之间的变换.30 ), 将其置于相容立方体的6个面中, 如图8 所示.图 8 相容立方体Figure8. The consistent cube$ {\overline{u}} $ 也视为方程(44a )的解时, 相容立方体侧面的两个方程44a )的一个B?cklund变换. 对于H1方程(33a )来说, 多维相容性为它提供的B?cklund变换是(28 )式.39 )和离散势mKdV方程(40 )而言, 它们合作构成相容立方体(见(41 )式). 此时, 左侧和后侧的两个方程, 即39 )的B?cklund变换. 不过这个变换没有对称性.δ )为例来解释如何利用相容立方体建立nonauto-B?cklund变换. 首先, 将Q2方程(33g )置于相容立方体的6个面. 然后在顶层方程$ {\rm Q}2({\overline{u}}, \widetilde{{\overline{u}}}, \widehat{{\overline{u}}}, \widehat{\widetilde{{\overline{u}}}}; p, q) = $ 0中引入关系$ \epsilon^2 $ 以后取极限$ \epsilon \to 0 $ , 顶层方程变为δ ). 此时, 立方体的左侧和后侧的两个方程, 经过替换(47 )式以及取极限以后, 得到δ )之间的nonauto-B?cklund变换.73 ]中表3. 除了上述方法, B?cklund变换可以利用Yang-Baxter映射以及ABS方程的分解性质来构造, 相关内容读者可以分别参考文献[82 ]和文献[83 ].3.2.Lax对 -->3.2.Lax对 众所周知, B?cklund变换与Lax对存在密切联系, 对于多维相容系统来说, 这种联系更加直接. 下面以H1方程(33a )为例, 利用其3维相容性引出的B?cklund变换构造它的Lax对.28 )式改写为$ {\overline{u}} = g/f $ , 得到$ { {\varPhi}} = (g, f)^{\rm T} $ , 上式改写为$ \gamma_i $ 可视为 分式线性形式(50 )式写成矩阵形式(51 )式后保留的原分子、分母的公因子, 一般取为$ \gamma_1 = \dfrac{1}{\sqrt{|{ M}|}}, \; \gamma_2 = \dfrac{1}{\sqrt{|{ N}|}} $ , 对于H1来说, $ \gamma_i $ 可以取为任意常数. 相容性$ {\widehat{\widetilde{{ {\varPhi}} }}} = \widetilde{\widehat{{ {\varPhi}} }} $ 引出33a ).51 )式中, 取$ {\varPhi} = (\phi_1, \phi_2)^{\rm T} $ , $ \gamma_1 = \gamma_2 = 1 $ , 从$ \widetilde { {\varPhi}} = { M}{ {\varPhi}} $ 中消去$ \phi_1 $ , 得到[84 ] .$ { Q}(u, \widetilde u, {\widehat{u }}, {\widehat{\widetilde{u }}}, p, q) = 0 $ , 其Lax对为(参考文献[85 ])$ \gamma_1 = \sqrt{|{ M}|}, \; \gamma_2 = \sqrt{|{ N}|} $ . 显然, 将矩阵谱问题改写成标量形式后, 可以发现所有的ABS方程都具有类似于(53 )式的二阶离散谱问题.M $ (^{\widetilde{\; \; }}, p) $ 换为$ (^{\widehat{\; \; }}, q) $ , 即得到N 86 ]中搜集了更多的利用3维相容性构造Lax对的例子. 对于由两个方程构成相容立方体时, 例如2.5节中的离散sine-Gordon方程和势mKdV方程, 由它们的相容立方体构造的离散sine-Gordon方程的B?cklund变换具有非对称性, 由此引出的离散sine-Gordon方程的Lax对也是非对称的:3.3.孤子解 -->3.3.孤子解 下面以离散势KdV (即H1)方程(33a )为例, 演示如何通过其B?cklund变换构造单孤子解(1-soliton solution (1SS)). 首先需要一个种子解. 取33a )的一个解, 其中$ \gamma $ 是任意常数.33a )的B?cklund变换是(28 )式, 即56 )式, 这里取$ r = -k^2 $ . 取u 为(57 )作为种子解, 设新解$ \overline{u} $ 形如$ \overline{u}_{} $ 是种子解(57 )沿l 方向的一次平移:v 是待定函数. 将(59 )式和(57 )式代入B?cklund变换(58 )式得到$ v = f/g $ 和$ { {\varPhi}} = (f, g)^{\rm T} $ , 将(61 )改写为$ \widehat{\widetilde{{ {\varPhi}}}} = \widetilde{\widehat{{ {\varPhi}}}} $ , 否则需要在上式的矩阵前乘上平衡因子(类似于(51 )式中的$ \gamma_i $ ). 进一步求解, 先后得到$ \rho_{0, 0} $ 为常数, 从(63 )式可得$ \rho_{0, 0} $ 后, 有59 )式, 离散势KdV方程(33a )的1-孤子解为N -孤子解. 相关内容可以参考文献[38 , 87 , 88 ].3.4.0-孤子解与不动点方法 -->3.4.0-孤子解与不动点方法 对于(33 )式中所列的ABS方程, $ u = 0 $ 一般都不是解, 而且也不易明显看出一些简单的解. “不动点方法”是在B?cklund 变换的基础上求解0-孤子解的方法. 从上一节的求解过程来看, 对于方程$ { Q}(u, \widetilde u, {\widehat{u }}, {\widehat{\widetilde{u }}};p, q) = 0 $ 的B?cklund变换(3.1), 其中的参数r 是孤子参数, 将作为离散谱在$ {\overline{u}} $ 中引出一个孤子. 现在, 如果孤子参数r 在变换中“失效”, 即$ {\overline{u}} = u $ , 则有33a ), 有57 )式.$ { Q}(u, \widetilde u, {\widehat{u }}, {\widehat{\widetilde{u }}};p, q) = 0 $ 在变换$u\to T(u) $ 下不变, 可在变换(3.1)中取$ {\overline{u}} = T(u) $ , 从而有δ )方程(33f ), 在$ T(u) = u+c $ 下不变, 对于的B?cklund变换(69 )式有$ (p, q)\to(\alpha, \beta) $ :δ )的线性0-孤子解:$ \lambda $ 是任意常数. 此外, Q1(δ )方程(33f ), 还在$ T(u) = -u $ 下不变. 此时的B?cklund变换(69 )式给出$ (p, q)\to(\alpha, \beta) $ :[89 ] , 其后又系统地应用于其他ABS方程0-孤子解的构造[37 ,38 ] . 当然, 也可以利用其他的方法构造0-孤子解, 例如, 利用方程间的B?cklund变换(如(48 )式), 从一个方程的0-孤子解得到另一个方程的0-孤子解.4.结 论 通过简单的描述和例子介绍了多维相容性的概念及其在离散可积系统中的应用. 对于多维相容性, 存在一定的几何背景, 换言之, 经典的初等几何中的点线之间的关系蕴含着若干离散可积系统的多维相容性(如文献[79 ,90 ]). 此外, 多维相容性也可以从平面波因子的对称性来理解. Miwa映射提供的离散的平面波因子[78 ] [37 ,45 ] 等途径来构造, 不难理解由此获得的离散可积系统具有多方向上的相容性. 
















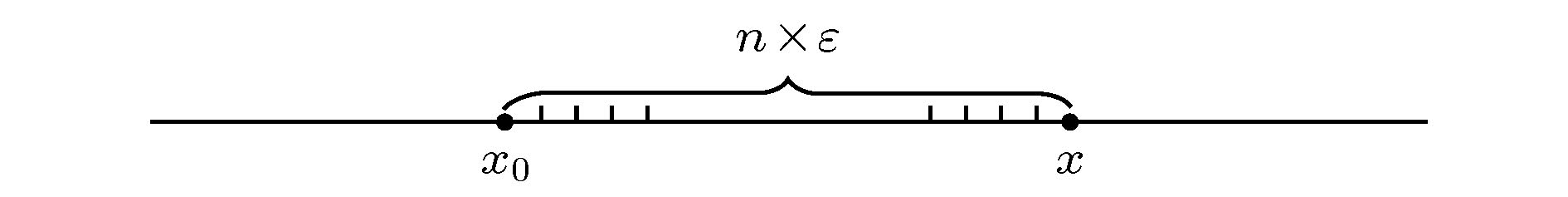 图 1
图 1 


















 图 2 B?cklund变换解的交换性质
图 2 B?cklund变换解的交换性质











 图 3 变换与平面网格
图 3 变换与平面网格
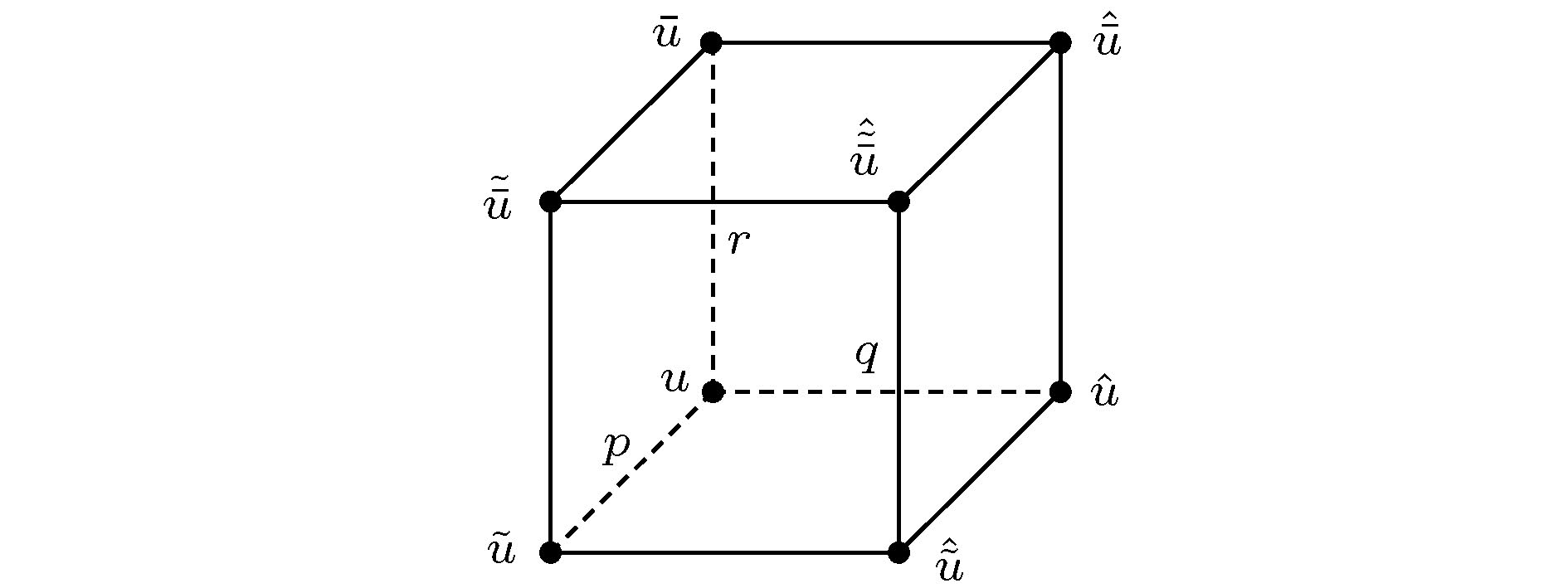 图 4 相容立方体
图 4 相容立方体




















































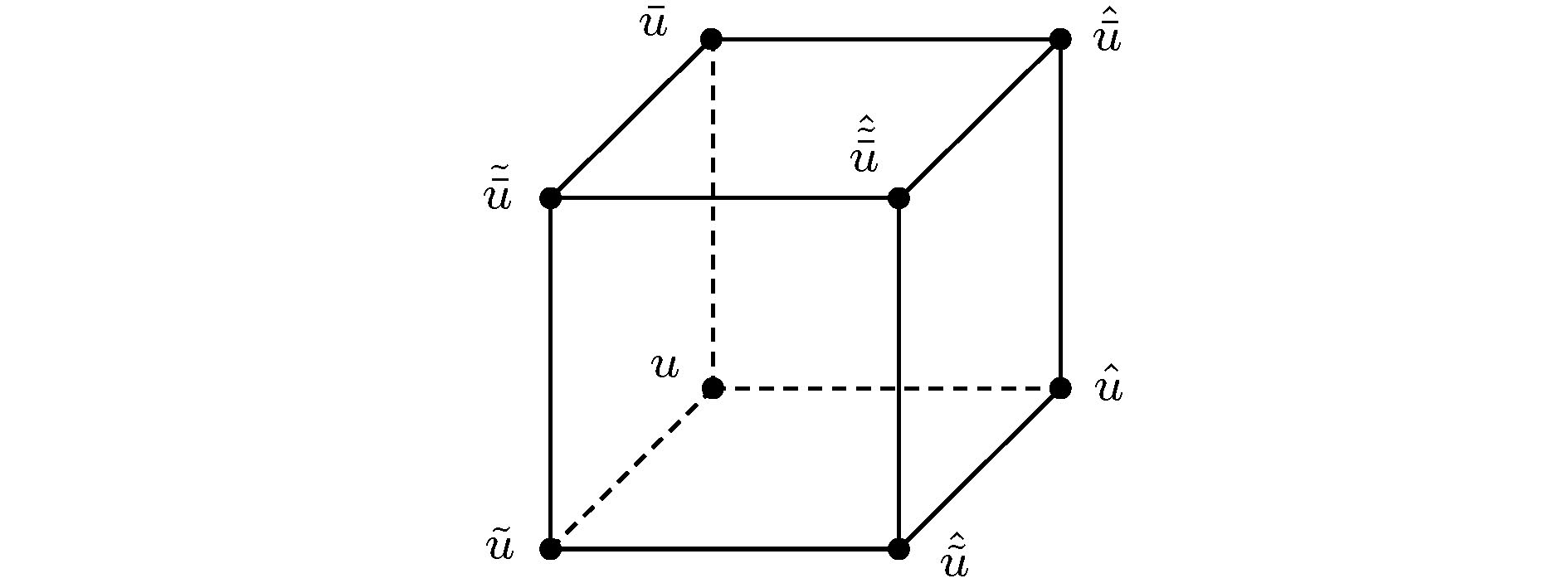 图 5 离散sine-Gordon和势mKdV方程的相容立方体
图 5 离散sine-Gordon和势mKdV方程的相容立方体

 图 6 定义3维方程的6面体以及8面体
图 6 定义3维方程的6面体以及8面体 图 7 围绕超立方体的4D相容性
图 7 围绕超立方体的4D相容性 图 8 相容立方体
图 8 相容立方体









































