摘要: 本文给出了一个可积的逆空时(逆空间-逆时间)非局部Sasa-Satsuma方程. 建立了这个方程的Darboux变换, 并且构造了这个逆空时非局部方程在零背景条件下的孤子解.
关键词: 可积的逆空时非局部Sasa-Satsuma方程 /
达布变换 /
孤子解 English Abstract An integrable reverse space-time nonlocal Sasa-Satsuma equation Song Cai-Qin 1 ,Zhu Zuo-Nong 2 1.College of Sciences, University of Shanghai for Science and Technology, Shanghai 200093, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos.11671255, 11801367)Received Date: 14 December 2019Accepted Date: 21 December 2019Available Online: 24 December 2019Published Online: 05 January 2020Abstract: In this paper, we introduce an integrable reverse space-time nonlocal Sasa-Satsuma equation. The Darboux transformation and soliton solutions for this nonlocal integrable equation are constructed.Keywords: integrable reverse space-time nonlocal Sasa-Satsuma equation /Darboux transformation /soliton solution 全文HTML --> --> --> 1.一个可积的逆空时非局部Sasa-Satsuma方程 耦合的Sasa-Satsuma系统$ R(X, T) = \pm Q^*(X, T) $ 下转化为经典的Sasa-Satsuma方程[1 -14 ] ,[2 ,3 ] .[15 ] 给出了一个逆空间的可积非局部NLS方程,[15 -24 ] . 作者在文献[20 ]中研究了一个逆空时可积非局部Sasa-Satsuma方程:$ R(X, T) = Q(-X, -T) $ , 则可得到如下逆空时非局部Sasa-Satsuma方程:5 )转化为如下形式:7 )也可以看作为一个逆空时非局部mKdV型方程. 本文的主要目的是建立逆空时非局部Sasa-Sasuma方程(7 )的Darboux变换, 并给出这个方程的孤子解.2.逆空时非局部Sasa-Satsuma方程(7 )的Darboux变换 我们注意到方程(7 )可以从系统$ v = u(-x, -t) $ 而得到. Sasa-Satsuma系统 (8 )和耦合系统(1)是等价的. 事实上, 在变换8 )在不同的约束条件下可以化为不同的方程: 当$ v = u $ 时, 系统 (8 )化为mKdV方程; 当$ v = u^* $ 时, 系统 (8 )化为一个复的mKdV型方程即经典的Sasa-Satsuma方程. Sasa-Satsuma方程(8 )是Lax可积的. 事实上, 系统 (8 )可由如下的线性谱问题$ { U}_{t}-{ V}_{x}+{ {UV}}-{ {VU}} = 0 $ 得到, 其中$ { {\varPhi}}(x, t;\lambda_j) $ 来表示线性谱问题(9 )在谱参数$ \lambda = \lambda_j $ 下的特征向量函数. 令${ {\varTheta}}_j = { {\varPhi}}'(x, t;\lambda_j){ M} $ , 那么可以直接验证9 )的伴随问题$ \lambda = -\lambda_j $ 下的特征函数, 这里上标$ ' $ 表示矩阵的转置, 矩阵M $ { {\varPhi}}(x, t;\lambda_j) $ 和$ \phi_l(x, t;\lambda_j) $ 分别简记为$ { {\varPhi}}_j $ 和$ \phi_{j, l} $ . 类似于文献[20 ], 我们可以获得Sasa-Satsuma方程(7 )的Darboux变换. 首先给出(8 )式的双Darboux变换. 作如下特征函数的变换:$ { {\eta}}_1 = ({ {\varPhi}}_{1}, { {\varPhi}}_{2}) $ ,8 )的线性谱问题(9 )变换为$ { P}[1] $ 与矩阵P $ { P}[1] $ 中的$ u[1], v[1] $ 与矩阵P $ u, v $ 有如下关系:$ { S} = { {\eta}}_1{ {\varOmega}}({ {\eta}}_1, { {\eta}}_1)^{-1}{ {\eta}}_1'{ M} $ , 则矩阵$ { P}[1] $ 与矩阵P 8 )的双Darboux变换被获得. 值得指出的是如果取约化$ v = u^* $ , 耦合Sasa-Satsuma方程(8 )约化为经典的Sasa-Satsuma方程. 我们在变换(13 )式中取$ \lambda_2 \!=\! -\lambda_1^* $ 及特征函数$ { {\varPhi}}_2 = \Big(\phi^*_2(x, t;\lambda_1), \phi^*_1(x, t;\lambda_1), \phi^*_3(x, t;\lambda_1)\Big)' $ , 那么变换后(16 )式的势函数满足$ v[1] = u[1]^* $ , 其表达式与文献[5 ,7 ,8 ]中得到的经典Sasa-Satsuma方程的势函数变换关系相同.P $ v = u(-x, -t) $ 并选取适当的参数使得$ S_{23} = S_{13}(-x, -t) $ , 那么$ { P}[1] $ 中的$ v[1] $ 就等于$ u[1](-x, -t) $ . 从而$ u[1] $ 与u 的关系实质上就是逆空时非局部Sasa-Satsuma方程(7 )的B?cklund变换. $ u[1] $ 是这个逆空时非局部Sasa-Satsuma方程的解.8 )的n 次双Darboux变换. 令$ { R} = ({ {\eta}}_1, { {\eta}}_2, \cdots, { {\eta}}_n) $ 并且$ { {\eta}}_k = ({ {\varPhi}}_{2 k-1}, { {\varPhi}}_{2 k}) $ ,$ u[n] $ 和$ v[n] $ 可以由矩阵$ { P}[n] $ 与矩阵P $ { a}, { b} $ 是一个$ 2 n $ 阶行向量, 那么根据等式关系$ { r}_l = (\phi_{1, l}, \phi_{2, l}, \cdots, \phi_{2 n-1, l}, \phi_{2 n, l}), \; l = 1, 2, 3 $ . 需要指出, 文献[5 ]给出了Sasa-Satsuma方程(即方程(8 )中取$ v = u^* $ )的Darboux变换, 但没有给出高阶Darboux变换. 这里给出了Sasa-Satsuma系统 (8 )的高阶双Darboux变换. 在约化$ v = u^* $ 下, 取$ \lambda_{2 j} = -\lambda_{2 j-1}^* $ 及特征函数${ {\varPhi}}_{2 j} = $ $ \Big(\phi^*_2(x, t;\lambda_{2 j-1}), \phi^*_1(x, t; \lambda_{2 j-1}), \phi^*_3(x, t;\lambda_{2 j-1})\Big)' $ , 即可获得Sasa-Satsuma方程的高阶Darboux变换.3.逆空时非局部Sasa-Satsuma方程(7 )的解 借助于Darboux变换, 我们将构造方程(7 )的解. 方程(7 )有指数形式的解$ u = r{\rm e}^{\kappa(x-(\kappa^2+6 r^2)t)} $ , 其中r 和κ 是任意的实数. 特别地, $ u = 0 $ 是一个解. 解对应的线性谱问题得到在谱参数$ \lambda = \lambda_j $ 时的特征函数为$ u[1] $ 和$ v[1] $ 如下:7 )的解, 需要选择适当的参数, 使得$ v[1] = u[1](-x, -t) $ . 经过分析, 我们发现在如下几种参数情况下:$ \alpha_1 = \alpha_2 = \beta_1 = \beta_2 = \dfrac{\sqrt{2}}{2} $ ;$ \alpha_1 = -\alpha_2 = \beta_1 = -\beta_2 = \dfrac{\sqrt{2}}{2} $ ;$ \alpha_1 = \beta_1 = 1, \alpha_2 = \beta_2 = 0, \lambda_1 = \dfrac{1-\sqrt{2}}{1+\sqrt{2}}\lambda_2 $ ;$ \alpha_1 = \alpha_2 = -\beta_1 = -\beta_2 = \dfrac{\sqrt{2}}{2} $ ;$ \alpha_1 = -\alpha_2 = -\beta_1 = \beta_2 = \dfrac{\sqrt{2}}{2} $ 图 1 可积的逆空时非局部Sasa-Satsuma方程(7 )的孤子解 (a) α 1 = α 2 = β 1 = β 2 = $ \dfrac{\sqrt{2}}{2}, \lambda_1 = {\rm i}, \lambda_2 = -{\rm i}/2 $ ; (b) α 1 = –α 2 = β 1 = –β 2 = $ \dfrac{\sqrt{2}}{2}, \lambda_1 = 1+{\rm i}, \lambda_2 = 1-{\rm i} $ ; (c) α 1 = β 1 = 1, α 2 = β 2 = 0 $\lambda_2 = {\rm i}, \lambda_1 = \dfrac{1-\sqrt{2}}{1+\sqrt{2}}\lambda_2 $ Figure1. Soliton solutions of integrable reverse space-time nonlocal Sasa-Satsuma equation (7 ): (a) α 1 = α 2 = β 1 = β 2 = $ \dfrac{\sqrt{2}}{2}, \lambda_1 = {\rm i}, \lambda_2 = -{\rm i}/2 $ ; (b) α 1 = –α 2 = β 1 = –β 2 = $ \dfrac{\sqrt{2}}{2}, $ $\lambda_1 = 1+{\rm i}, \lambda_2 = 1-{\rm i} $ ; (c) α 1 = β 1 = 1, α 2 = β 2 = 0 $\lambda_2 = {\rm i}, \lambda_1 = \dfrac{1-\sqrt{2}}{1+\sqrt{2}}\lambda_2 $ $ v[1] = u[1](-x, -t) $ . 从而逆空时非局部方程(7 )的解被构造. 对于情形(1)—(3), 有$ u(x, t) = u(-x, -t) $ , 而对于情形(4)—(5)有$ u(x, t) = -u(-x, -t) $ . 我们给出了对应于情形(1)—(3)的解$ u(x, t) $ 的图, 如图1 所示.4 ), 我们也给出了类似的双峰孤波解. 但对于本文研究的逆空时非局部可积方程(7 ), 并没有发现这样的双峰孤波解的存在. 从这个意义上说, 逆空时非局部可积方程(4 )和方程(7 )确有不同的性质. 逆空时非局部可积方程(7 )值得进一步研究. 






























































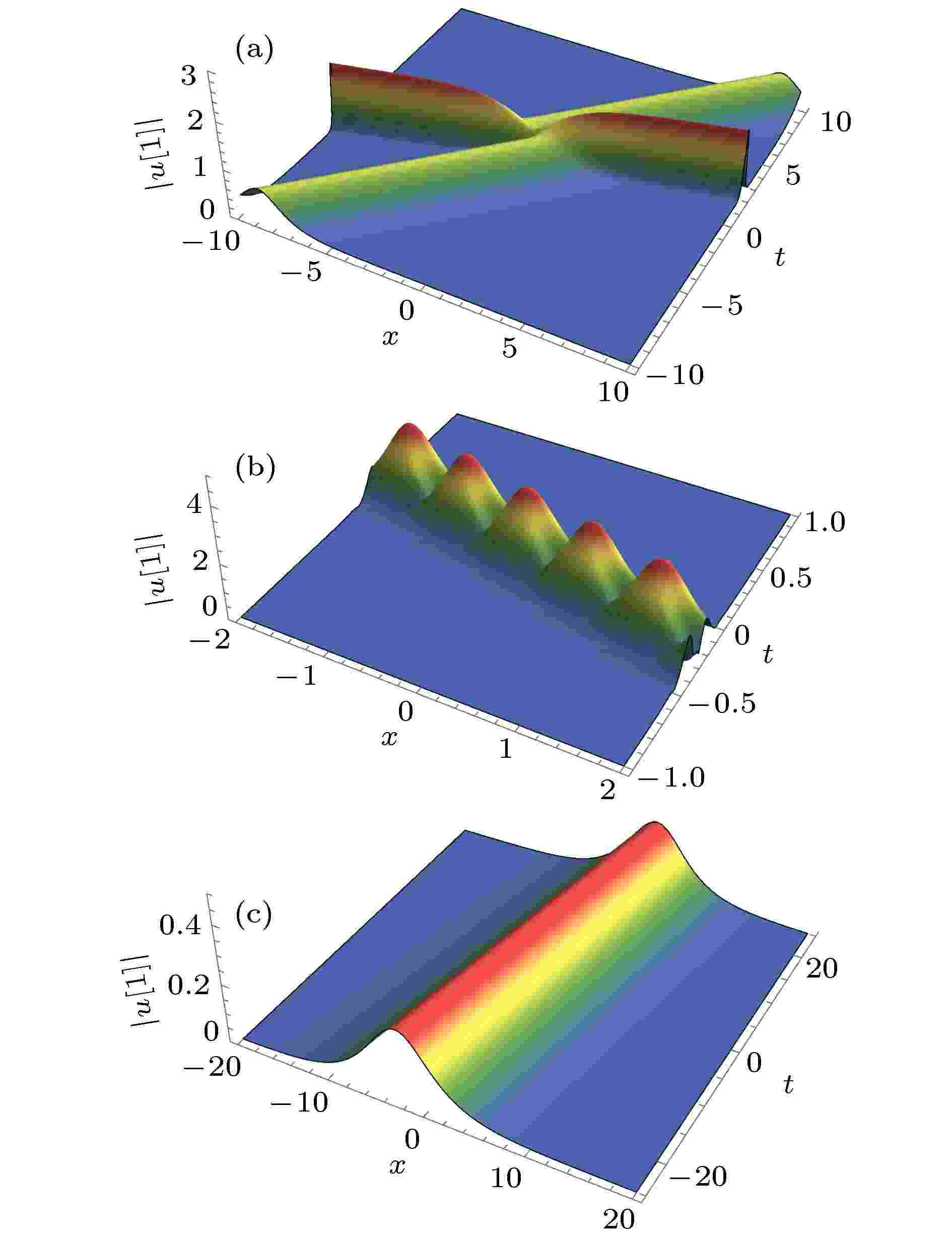 图 1 可积的逆空时非局部Sasa-Satsuma方程(7)的孤子解 (a) α1 = α2 = β1 = β2 =
图 1 可积的逆空时非局部Sasa-Satsuma方程(7)的孤子解 (a) α1 = α2 = β1 = β2 = 










