摘要: 本文研究了四阶色散非线性薛定谔方程的明暗孤立波和怪波的形成机制, 该模型既可以模拟高速光纤传输系统中超短脉冲的非线性传输和相互作用, 又可以描述具有八极与偶极相互作用的一维海森堡铁磁链的非线性自旋激发现象. 本文首先通过对四阶色散非线性薛定谔方程的相平面分析, 发现由其约化得到的二维平面自治系统具有同宿轨道和异宿轨道, 并在相应条件下求得了方程的明孤立波解和暗孤立波解, 从而揭示了同异宿轨道和孤立波解的对应关系; 其次, 基于非零背景平面上的精确一阶呼吸子解, 给出了呼吸子的群速度和相速度的显式表达式, 进而分析得出呼吸子的速度存在跳跃现象. 最后, 为了验证在跳跃点处呼吸子可以转化为怪波, 将呼吸子解在速度跳跃条件下取极限获得了一阶怪波解, 从而证实怪波的产生与呼吸子速度的不连续性有关.
关键词: 同异宿轨道 /
孤立波 /
怪波 /
速度不连续性 English Abstract Study on the generation mechanism of bright and dark solitary waves and rogue wave for a fourth-order dispersive nonlinear Schr?dinger equation Li Min 1 ,Wang Bo-Ting 1 ,Xu Tao 2 ,Shui Juan-Juan 1 1.Department of Mathematics and Physics, North China Electric Power University, Beijing 102206, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11705284 and 61505054), by the Fundamental Research Funds of the Central Universities (Grant No. 2017MS051)Received Date: 12 September 2019Accepted Date: 04 November 2019Available Online: 14 December 2019Published Online: 05 January 2020Abstract: In this paper, we study the generation mechanism of bright and dark solitary waves and rogue wave for the fourth-order dispersive nonlinear Schr?dinger (FODNLS) equation, which can not only model the nonlinear propagation and interaction of ultrashort pulses in the high-speed optical fiber transmission system, but also govern the nonlinear spin excitations in the onedimensional isotropic biquadratic Heisenberg ferromagnetic spin with the octupole-dipole interaction. Firstly, via the phase plane analysis, we obtain both the homoclinic and heteroclinic orbits for the two-dimensional plane autonomous system reduced from the FODNLS equation. Further, we derive the bright and dark solitary wave solutions under the corresponding conditions, which reveals the relationship between the homoclinic (heteroclinic) orbit and solitary wave. Secondly, based on the exact first-order breather solution of the FODNLS equation over a nonvanishing background, we give the explicit expressions of group and phase velocities, and reveal that there exists a jump in both the velocities. Finally, in order to verify that the breather becomes a rogue wave at the jumping point, we obtain the first-order rogue wave solution by taking the limit of the breather solution at such point, which confirms the relationship of the generation of rogue wave with the velocity discontinuity.Keywords: homoclinic and heteroclinic orbits /solitary waves /rogue wave /velocity discontinuity 全文HTML --> --> --> 1.引 言 孤子、呼吸子和怪波是自然界中三种典型的非线性波现象, 由于在非线性光学、玻色-爱因斯坦凝聚、大气物理以及等离子体等领域中的潜在应用而受到密切关注[1 -20 ] . 其中, 孤子在群速度色散和非线性效应均衡作用下可以保持不变的波形和速度稳定地传播, 从而在长距离、大容量和高速率光纤通信系统中有着重要应用[9 ] . 呼吸子的产生源于小扰动引起的平面波调制不稳定性[9 ] . 研究发现, 经典的非线性薛定谔方程(NLSE)具有两类呼吸子解: Kuznetsov-Ma呼吸子(简称KMB)[10 ] 和Akhmediev呼吸子(简称AB)[11 ] . 另外, 怪波在数学上可以通过NLSE的有理解(即KMB或AB呼吸子解的一种退化情形[10 ,11 ] )进行描述, 同时也可以作为在周期边界条件下不稳定Stokes波的一种同宿轨行为[12 ,13 ] . 怪波最早被用来描述在海洋中发现的来无影去无踪的大振幅畸形波[14 ,15 ] , 近年来也在非线性光学和水槽实验中被观察到[16 ,17 ] . 通常情况下, ****们认为只有非线性可以解释由能量的大量聚集而形成的高于周围波平均高度的单个水峰现象[18 ,19 ] , 并且认为调制不稳定性是怪波产生的初始过程[20 ] .21 ]在一个大的定向波池实验中讨论了平面波的调制不稳定性, 该研究为有限水深条件下怪波的产生给出了一定解释; 文献[22 ]通过光学实验研究了在连续波泵浦区域超连续统的时间特性, 从而指出怪波可由孤子之间的相互碰撞产生; 文献[23 ]借助数值模拟发现拉曼效应和三阶色散可以激发怪波的形成; 文献[24 ,25 ]在理论上指出由速度跳跃可以使得呼吸子演化为怪波, 并且非线性偏微分方程的行波解与对应的常微分方程的轨道存在对应关系, 即, 常微分方程中的同宿轨道和异宿轨道分别与非线性波方程中的孤立波和冲击波相对应, 而对于非线性薛定谔型方程, 其约化后的常微分系统的同宿轨道和异宿轨道则分别对应钟型的明孤立波解、冲击波解或倒钟型的暗孤立波解[26 ,27 ] .[28 -30 ] 的孤立波解和怪波解形式机制:$ q(x, t) $ 代表波的慢变包络振幅, x 和t 是归一化的空间和时间变量, $ \varepsilon^2 $ 是一个表示高阶线性和非线性强度的无量纲小参数, αj ($ j = 1, 2, \cdots, 8 $ )为实参数. 方程(1 )主要来源于光纤光学和磁力学: 在光学中可以模拟高速光纤传输系统中超短脉冲的非线性传播及相互作用[31 ] , 在磁力学中亦可描述具有八极与偶极相互作用的一维海森堡铁磁链的非线性自旋激发现象[32 ] . 特别地, 当参数取值为α 1 = 1, α 2 = 2, α 3 = 1, α 4 = 8, α 5 = 2, α 6 = 6, α 7 = 4, α 8 = 6时, 该方程是一个可积模型, 具有Lax对和无穷多守恒律[33 ] . 文献[34 ]借助双线性方法获得了方程(1 )的双线性形式及N 孤子解, 并通过渐近分析揭示了孤子的弹性碰撞现象. 文献[30 ]利用达布变换方法构造了呼吸子解和高阶怪波解的精确表达式.1 )经约化后得到的常微分方程的动力学性质, 分别给出同宿轨道和异宿轨道对应的参数条件, 并在相应条件下求得了方程(1 )的明孤立波解和暗孤立波解, 揭示了同异宿轨道与孤立波解之间的对应关系; 其次, 基于文献[30 ]获得的呼吸子解表达式, 分析了呼吸子的群速度和相速度随参数的变化关系, 进而确定速度发生跳跃的参数条件; 为了验证在速度跳跃的参数条件下呼吸子可以转化成怪波, 在该条件下对呼吸子解取极限得到一阶怪波解, 从而揭示怪波形成与速度跳跃之间的关联.2.方程(1 )的二维相平面分析及明暗孤立波解的产生条件 为了分析方程(1 )对应常微分方程的平衡点及相轨迹, 对方程(1 )做如下行波解约化:a , c , K 和$ \varOmega $ 都是实数, $ \phi(\xi) $ 是$ \xi $ 的实函数. 将其代入方程(1 )中, 得到关于$ \phi $ 的常微分方程:3 )的实部和虚部, 得到4 )式关于$ \xi $ 积分一次并取积分常数为零, 可得4 )式关于$ \xi $ 求一阶导, 得到$ \phi'''' $ 如下:6 )式和(7 )式消掉方程(5 )中的$ \phi'' $ , $ \phi''' $ 和$ \phi'''' $ , 有6 )两边同乘以$ 2\phi' $ , 得8 )关于$ \xi $ 求一阶导数, 有9 )和方程(10 )含有相同项, 两者需相容, 则参数满足以下条件:11 )式和(12 )式下, 方程(9 )和方程(10 )可同时化为如下常微分方程:13 )的二维平衡点类型及相轨迹, 在变换$ X\equiv\phi $ 和$ Y = \phi_{\xi} $ 下, 方程(13 )可等价于如下二维平面动力系统:15 )的平衡点的类型, 我们得出其相应的雅克比矩阵为$ \lambda_1, _2 = \pm\sqrt{-\beta_1-3\beta_2 X^{2}} $ .15 )的平衡点类型及解的稳定性分析如下:$ \beta_1/\beta_2\geqslant 0 $ 时, 系统只有一个平衡点(0, 0)并且在该点处J $ \pm\sqrt{-\beta_1} $ . 如果$ \beta_1>0 $ , 则(0, 0)点是中心点; 如果$ \beta_1<0 $ , 则(0, 0)点是不稳定鞍点.$ \beta_1/\beta_2<0 $ 时, 系统有三个平衡点: $ S_0(0, 0) $ , $ S_1(\sqrt{-\beta_1/\beta_2}, 0) $ 和$ S_2(-\sqrt{-\beta_1/\beta_2}, 0) $ . 对应这些平衡点, J 的特征值分别为$ \pm\sqrt{-\beta_1} $ , $ \pm\sqrt{2\beta_1} $ 和$ \pm\sqrt{2\beta_1} $ . 若$ \beta_1<0 $ , 则$ S_0 $ 是不稳定鞍点, 而$ S_1 $ 和$ S_2 $ 是中心点, 此时存在围绕中心点$ S_1 $ 和$ S_2 $ 绕至$ S_0 $ 的同宿轨道. 若$ \beta_1>0 $ , 那么$ S_0 $ 是中心点, $ S_1 $ 和$ S_2 $ 15 )存在的同宿轨道和异宿轨道, 选取特定参数画出系统(15 )在条件$ \beta_1/\beta_2<0 $ 下的相位图, 如图1 所示. 当取定$ \beta_1 = $ –1/10 和$ \beta_2 = 1/18 $ , 图1(a) 显示有一个鞍点和两个中心点, 随着时间的变化从鞍点出发的轨道最终会返回形成同宿轨道. 而当$ \beta_1 = 1 $ 和$ \beta_2 = -5/9 $ 时, 图1(b) 显示有一个中心点和两个鞍点, 并形成从一个鞍点到另一个鞍点的异宿轨道.图 1 系统(15 )的相位图 (a)同宿轨道(β 1 = –1/10, β 2β 1 = 1, β 2 = –5/9)Figure1. Phase portraits of System (15 ): (a) Homoclinic orbits (β 1 = –1/10, β 2 = 1/18); (b) heteroclinic orbits (β 1 = 1, β 2 = –5/9).[26 ,27 ] , 可以得出如下结论: 如果$ \beta_1/\beta_2<0 $ 且$ \beta_1<0 $ , 则方程(1 )具有明孤立波解; 而当$ \beta_1/\beta_2<0 $ 且$ \beta_1>0 $ 时, 方程(1 )有冲击波解或暗孤立波解. 通过(14 )式, 可以将条件$ \beta_1/\beta_2<0 $ 和$ \beta_1<0 $ 具体表示为$ 6 K^2\varepsilon^2\alpha_3-3\alpha_1+ $ 3c /2K < 0, α 5 – α 4 – α 6 > 0 且α 3 < 0或者$ 6 K^2\varepsilon^2\alpha_3-3\alpha_1+$ 3c /2K < 0, α 5 – α 4 – α 6 > 0且α 3 < 0. 同样地, 条件$ \beta_1/\beta_2<0 $ 且$ \beta_1>0 $ 可具体写成$ 6 K^2\varepsilon^2\alpha_3-3\alpha_1+3 c/2 K<0 $ , α 5 – α 4 – α 6 > 0且α 3 < 0或者$ 6 K^2\varepsilon^2\alpha_3-3\alpha_1+ $ 3c /2K < 0, α 5 – α 4 – α 6 > 0且α 3 < 0.1 )中明孤立波解和暗孤立波解的存在性, 分别在同宿轨和异宿轨条件下利用哈密尔顿函数对系统(15 )进行求解. 令$ h^* = h_i = H(S_i)(i = 0, 1, 2) $ , 则有11 )式和(12 )式可知表达式(8 )与哈密尔顿函数(16 )式是等价的, 故可得$ \beta_1<0 $ 且$ \beta_2>0 $ 时, 则平衡点$ S_0 $ 是不稳定鞍点, 而平衡点$ S_1 $ 和$ S_2 $ 是中心点, 此时存在围绕中心点$ S_1 $ 和$ S_2 $ 至$ S_0 $ 的同宿轨道. 当$ h^* = h_0 $ 时, 由表达式(16 )得到21 )式代入变换(2 )式中得到方程(1 )的明孤立波解为$ \beta_1>0 $ 且$ \beta_2<0 $ 时, 那么平衡点$ S_0 $ 为中心点, 平衡点$ S_1 $ 和$ S_2 $ 是不稳定的鞍点, 此时存在异宿轨道. 当$ h^* = h_1 = h_2 $ 时, 由表达式(16 )得到24 )式代入变换(2 )式中得到方程(1 )的暗孤立波解为22 )式和(25 )式中选取恰当的参数值得到明暗孤立波的传播图形, 如图2 所示.图 2 (a)由明孤立波解(22 )式描述的明孤立波传输图形, 其中参数选取为 α 1 = 1, α 2 = 2, α 3 = 1, α 4 = 8, α 5 = 2,α 6 = 6, α 7 = 4, α 8 = 6, c = 1, K = 1, $\varOmega $ = 51/16, ε = 1, a = 1; (b) 由暗孤立波解(25 )式描述的暗孤立波传输图形, 其中参数选取为α 1 = –1, α 2 = 2, α 3 = 1, α 4 = –8, α 5 = –2, α 6 = –6, α 7 = –4, α 8 = 6, c = –7, K = 1, $\varOmega $ = –123/32, ε = 1, a = 1Figure2. (a) Propagation of bright solitary wave via Solution (22 ) with the parameters chosen as α 1 = 1, α 2 = 2, α 3 = 1, α 4 = 8, α 5 = 2, α 6 = 6, α 7 = 4, α 8 = 6, c = 1, K = 1, $\varOmega $ = 51/16, ε = 1, a = 1; (b) propagation of dark solitary wave via Solution (25 ) with the parameters chosen as α 1 = –1, α 2 = 2, α 3 = 1, α 4 = –8, α 5 = –2, α 6 = –6, α 7 = –4, α 8 = 6, c = –7, K = 1, $\varOmega $ = –123/32, ε = 1, a = 1.3.呼吸子的速度跳跃点及怪波的形成条件 目前, 怪波解已经被发现存在于很多非线性发展方程中, 例如NLSE、Hirota方程、导数非线性薛定谔方程、Sasa-Satsuma方程、离散Ablowitz-Ladik方程以及变系数高阶非线性薛定谔方程等[35 -37 ] . 本节将基于方程(1 )在可积条件下求得的呼吸子解[30 ] , 分析呼吸子的速度跳跃现象以及怪波产生的条件.1 )中的参数为α 1 = 1, α 2 = 2, α 3 = 1, α 4 = 8, α 5 = 2, α 6 = 6, α 7 = 4, α 8 = 6, 得到如下形式:26 )的Lax对表示如下[30 ] :30 ]基于Lax对(27 )式给出了方程(26 )的一阶达布变换, 其中势函数变换关系如下:$ \varDelta_1 \!=\! -2 if_{1, 1}f_{2, 1}\mathrm{Im}(\lambda_1) $ , $ \varDelta_2 \!=\! f_{1, 1}f_{2, 2} \!-\! f_{1, 2}f_{2, 1},$ 其中$ f_{2, 1} = -f^{*}_{1, 2} $ , $ f_{2, 2} = f^{*}_{1, 1} $ , $ (f_{i, 1}, f_{i, 2}) $ $ (i = 1, 2) $ 是Lax对(27 )式相应$ \lambda = \lambda_i $ ($ \lambda_2 = \lambda^{*}_1 $ )的两组线性无关解.26 )的平面波解作为种子解:$ b = \varepsilon^2(a^4-12 a^2 c^2+6 c^4)+2 c^2-a^2 $ , $ a, \, b, \, c $ 分别代表波的波数、频率和振幅. 此时, 与$ q^{[0]} $ 对应的Lax对(27 )式的解为30 )式及特征函数(31a )式和(31b )式代入变换(29 )式中, 得到方程(26 )的一阶呼吸子解为[30 ] :图3 展示了由呼吸子解(32 )式描述的单个呼吸子的动力学演化, 其在演化过程中呈现出随时间的周期性震荡现象.图 3 解(32 )式描述的一阶呼吸子的动力学演化, 其中参数选取为$\xi=0$ , $\eta={1}/{2}$ , $c={2}/{5}$ 和$a=0$ Figure3. The propagation of one breather via Solution (32 ) with the parameters chosen as $\xi=0$ , $\eta={1}/{2}$ , $c={2}/{5}$ and $a=0$ .32 )来分析呼吸子的速度跳跃现象. 根据非线性波速度的相关理论[38 ,39 ] , 从表达式(32 )中可以看出, 呼吸子沿时间和空间轴方向发生周期性震荡, 其震荡性体现在三角函数部分$ {\rm{cos}}(2 G) $ 或$ {\rm{sin}}(2 G) $ , 且 G 中的$ k_2 $ 和$ w_2 $ 分别代表震荡的空间和时间频率, 震荡速度对应于呼吸子相速度$ V_{\rm p} $ . 另外, 呼吸子可以在$ (x, t) $ 平面上沿直线传播, 其传播轨迹由$ F = 0 $ 决定, 传播速度对应于呼吸子的群速度$ V_{\rm g} $ . 因此, 得到呼吸子解(32 )式的群速度$ V_{\rm g} $ 和相速度$ V_{\rm p} $ 的表达式如下:$ \eta\to\pm c $ 时, 群速度$ V_{\rm g} $ 和相速度$ V_{\rm p} $ 化简如下:35 )式和(36 )式中可以看出, 当$ \xi $ 沿不同方向趋于$ -a/2 $ 时, $ \sqrt{(a+2\xi)^2} $ 的符号是不同的, 从而导致群速度$ V_{\rm g} $ 和相速度$ V_{\rm p} $ 趋于不同的值, 即产生跳跃现象. 为了图形演示速度关于参数a 的跳跃现象, 我们在条件$ \eta\to\pm c $ 下, 保留参数a 且将其他参数取定, 即$ \varepsilon^2 = 1 $ , $ \eta = c $ , $ c = 1 $ 和$ \xi = 1 $ , 得到,图4 给出了群速度$ V_{\rm g} $ 和相速度$ V_{\rm p} $ 随参数a 的变化关系. 以$ V_{\rm g} $ 为例, 由图4 可清晰地看到群速度在$ a = -2 $ 处出现突然的跳跃. 为了更加说明该跳跃点, 我们计算了群速度在该点的左右极限, 发现$ \lim\limits_{a \to -2^-}V_{\rm g} = -54 \neq \lim\limits_{a \to -2^+}V_{\rm g} = 14 $ , 从而表明群速度在$ a = -2 $ 处不连续. 类似地, 相速度$ V_{\rm p} $ 在$ a = -2 $ 处的左右极限分别为14和–54, 也是不连续的, 即$ a = -2 $ 为跳跃点. 通过对表达式(37 )的分析, 速度跳跃点的出现是由于分母中包含$ \sqrt{(2+a)^2} $ , 从而导致$ V_{\rm g} $ 和$ V_{\rm P} $ 在$ a = -2 $ 点处不连续. 根据文献[24 ] 中关于临界频率的定义, 由于速度在波数$ a = -2 $ 处表现出了速度的不连续性, 因此该不连续点可以定义为方程(26 )的临界波数.图 4 呼吸子的群速度$V_{\rm g}$ (红实线)和相速度$V_{\rm p}$ (蓝虚线)随参数a 的变化关系Figure4. Group velocity $V_{\rm g}$ (red-solid line) and phase velocity $V_{\rm p}$ (blue-dot line) of the breather[24 ,25 ] . 为了验证方程(26 )中怪波的形成与速度跳跃的关系, 我们将呼吸子解(32 )式在$ \xi\to-{a}/{2} $ 和$ \eta\to c $ 条件下取极限, 即 $ \lambda_1 = \xi+{\rm i} \eta$ $ \to \lambda_0 = $ –a /2 + ic , 得到方程(26 )的一阶怪波解如下:$ \alpha_1 $ 和$ \alpha_2 $ 是两个非零的实参数. 图5 给出了由解(42 )式描绘的一阶怪波的动力学演化, 其中参数选取为$ c = 1 $ , $ \eta = 1 $ , $ \varepsilon^2 = 1 $ 和$ \alpha_1 = \alpha_2 = 1 $ . 通过极限计算, 当$ x\to \infty $ 或$ t\to \infty $ 时, 一阶怪波$ |q_{\rm{rw}}|^2 $ 在无穷远处高度为1, 从而说明了怪波的空间和时间局域性. 进一步, 借助数值近似计算可以验证$ |q_{\rm{rw}}|^2 $ 分别在点(0.3660257, –1)和(–1.3660251, –1)附近取得最小值$ 5.32932\times10^{-13} $ 和$ 5.3456\times10^{-13} $ , 在点(–0.4999952, –1)附近取得最大值9, 该值即为一阶怪波的振幅. 因此, 解(42 )式符合一阶怪波解具有一个极大值点和两个极小值点的特点, 且最高点振幅为背景波三倍以上. 以上分析表明方程(26 )的呼吸子解(42 )式在速度跳跃条件$ \xi\to-{a}/{2} $ 和$ \eta\to c $ 下转化成了怪波, 进而证明速度的不连续性可以产生怪波. 值得注意的是, 该速度跳跃条件与达布变换方法求怪波解[24 ] 时的谱参数取值相一致, 而该谱参数条件对应方程的调制不稳定区域[40 ] , 因此调制不稳定性与速度跳跃从不同角度揭示了怪波产生的条件.图 5 解(42 )式描述的一阶怪波的动力学演化, 其中参数选取为$\xi=1$ , $\eta=1$ , $c=1$ , $\alpha_1=1$ , $\alpha_2=1$ 和$a=-2$ Figure5. The propagation of first-order rogue wave via Solution (42 ) with the parameters chosen as $\xi=1$ , $\eta=1$ , $c=1$ , $\alpha_1=1$ , $\alpha_2=1$ and $a=-2$ .4.结 论 本文研究了一个在光纤光学和磁力学提出的四阶色散非线性薛定谔方程(1 ), 分别从动力学分析和速度不连续性两方面探讨了孤立波和怪波的产生条件.15a )和(15b ). 进而, 借助相平面分析方法讨论了系统(15a )和(15b )的平衡点类型及解的稳定性, 同时根据平衡点类型与相轨道的关系发现二维平面自治系统具有同宿轨道和异宿轨道, 并在相应条件下求解得到了方程(1 )的明孤立波解和暗孤立波解, 从而验证了同异宿轨道分别对应非线性方程的明暗孤立波解.$ \xi\to-{a}/{2} $ 和$ \eta\to\pm c $ 时, 群速度和相速度均关于波数存在不连续点, 即跳跃点或临界波数(见图3 所示). 同时, 从数学上指出了该跳跃点的出现是由于速度表达式中含有因子$ \sqrt{(a+2\xi)^2} $ . 为了验证呼吸子在速度跳跃点可以转化成怪波, 对一阶呼吸子解在速度不连续点处取极限获得了方程(26 )的一阶怪波解, 从而表明怪波的形成与呼吸子速度的不连续性有关. 另外, 如果取定速度表达式(35 )式和(36 )式中其他参数而只保留振幅参数c , 则群速度和相速度均不会出现不连续点, 如图6 所示. 在图6 中, 参数选取为$ \xi = {1}/{2}(-a+\sqrt{-4 c^2}) $ , $ \eta = 0 $ 和$ a = 1 $ , 此时群速度和相速度都是关于振幅参数c 的连续函数.图 6 (a) 群速度$V_{\rm g}$ 随振幅参数c 的变化(红实线)和(b)相速度$V_{\rm p}$ 随振幅参数c 的变化(蓝点线), 其中参数选取为$\xi={1}/{2}(\sqrt{-4 c^2}-a)$ , $\eta=0$ 和$a=1$ Figure6. Variation of the group velocity $V_{\rm g}$ (red-solid line) and phase velocity $V_{\rm p}$ (blue-dot line) about the amplitude parameter c with the parameters chosen as $\xi={1}/{2}(\sqrt{-4 c^2}-a)$ , $\eta=0$ and $a=1$ . 
































































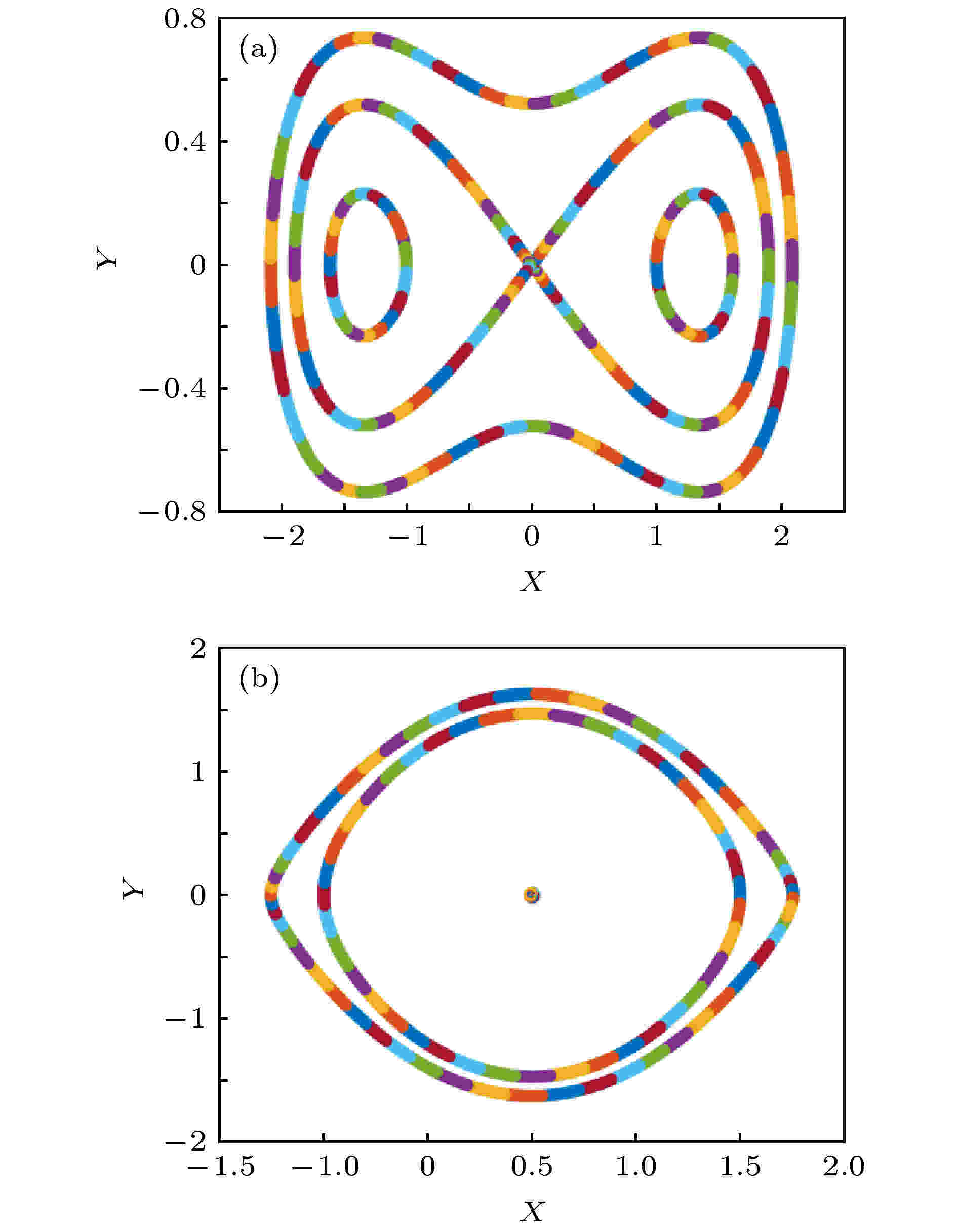 图 1 系统(15)的相位图 (a)同宿轨道(β1 = –1/10, β2 = 1/18); (b) 异宿轨道(β1 = 1, β2 = –5/9)
图 1 系统(15)的相位图 (a)同宿轨道(β1 = –1/10, β2 = 1/18); (b) 异宿轨道(β1 = 1, β2 = –5/9)



















































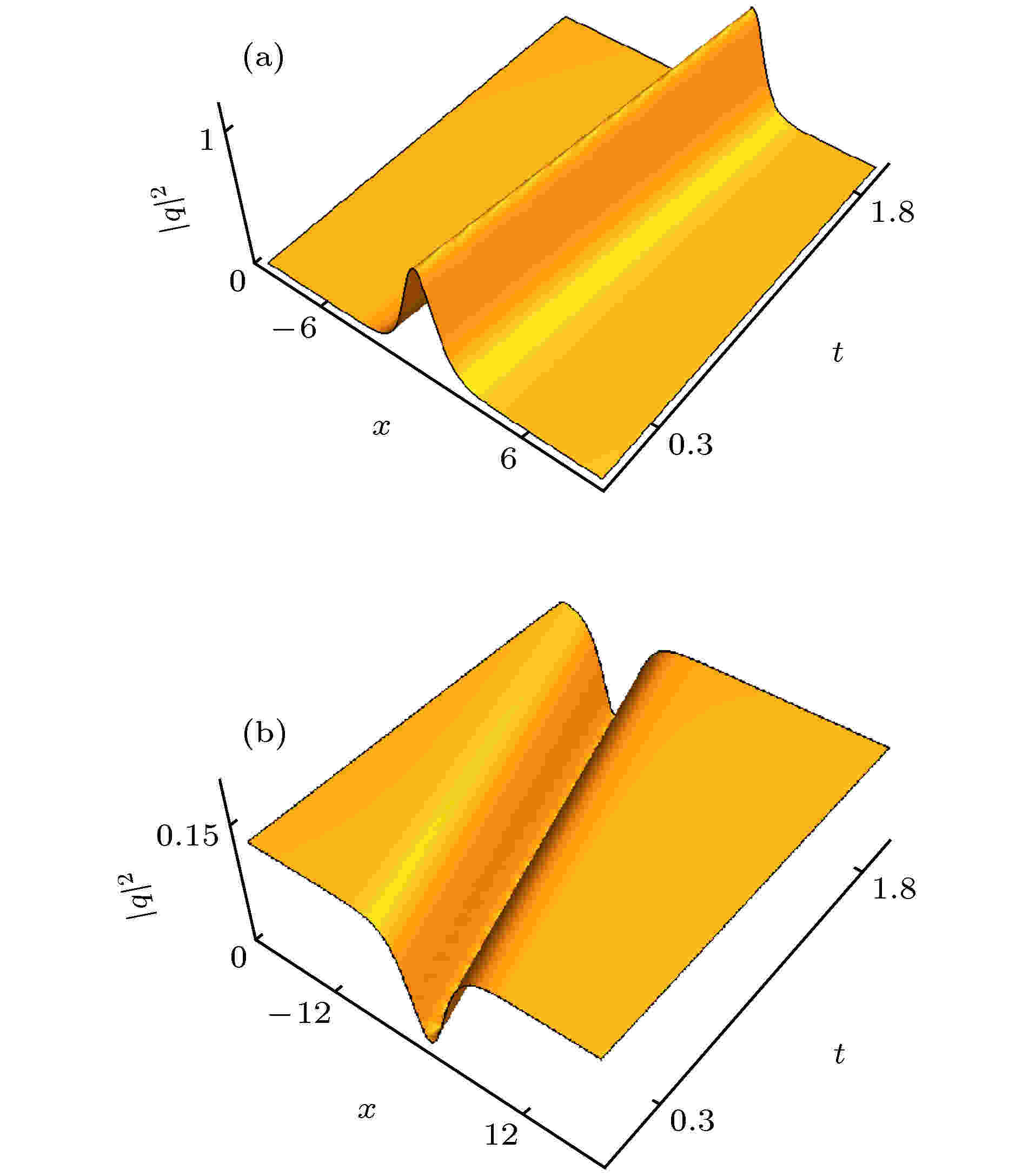 图 2 (a)由明孤立波解(22)式描述的明孤立波传输图形, 其中参数选取为 α1 = 1, α2 = 2, α3 = 1, α4 = 8, α5 = 2,α6 = 6, α7 = 4, α8 = 6, c = 1, K = 1,
图 2 (a)由明孤立波解(22)式描述的明孤立波传输图形, 其中参数选取为 α1 = 1, α2 = 2, α3 = 1, α4 = 8, α5 = 2,α6 = 6, α7 = 4, α8 = 6, c = 1, K = 1, 


















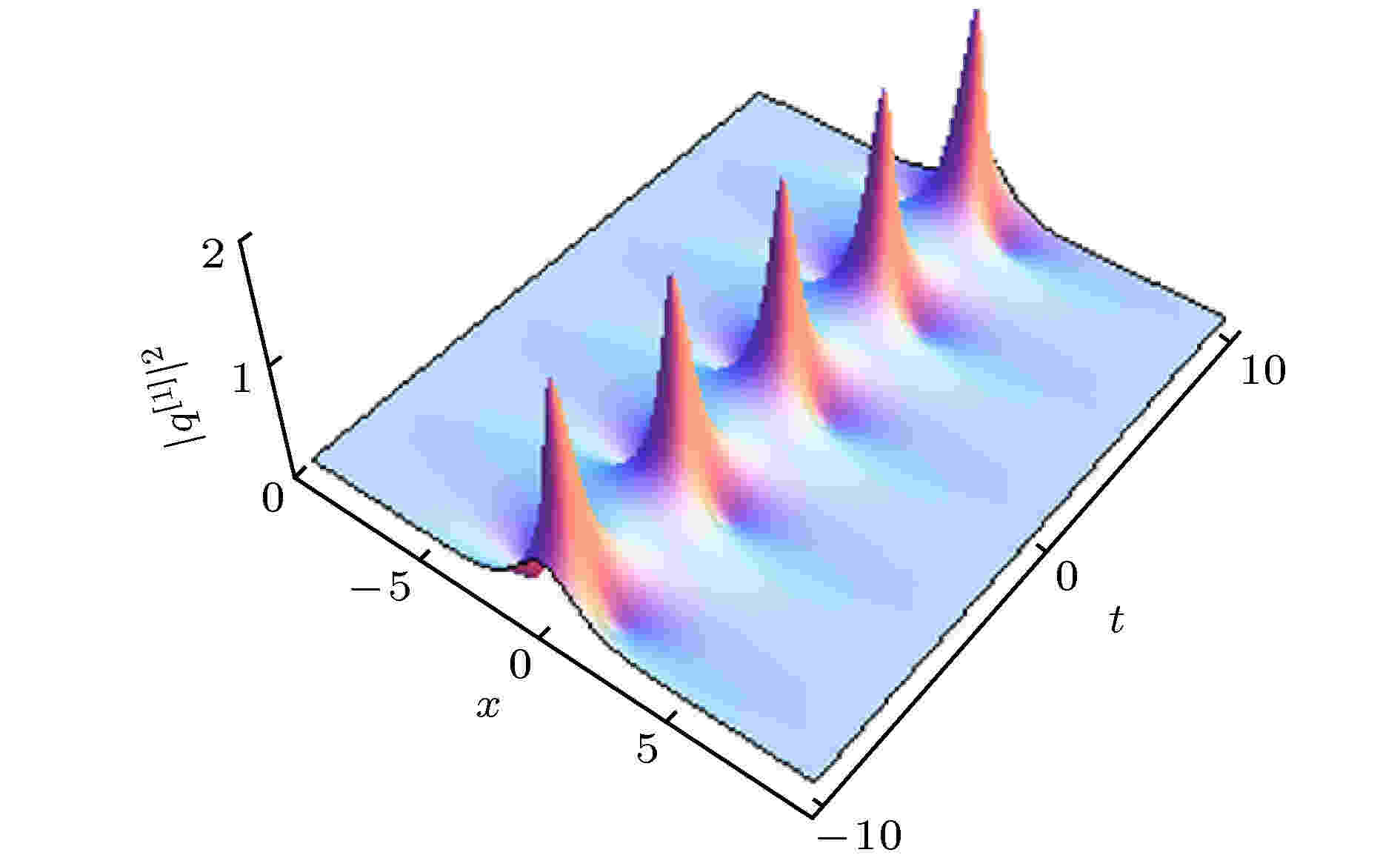 图 3 解(32)式描述的一阶呼吸子的动力学演化, 其中参数选取为
图 3 解(32)式描述的一阶呼吸子的动力学演化, 其中参数选取为






















































































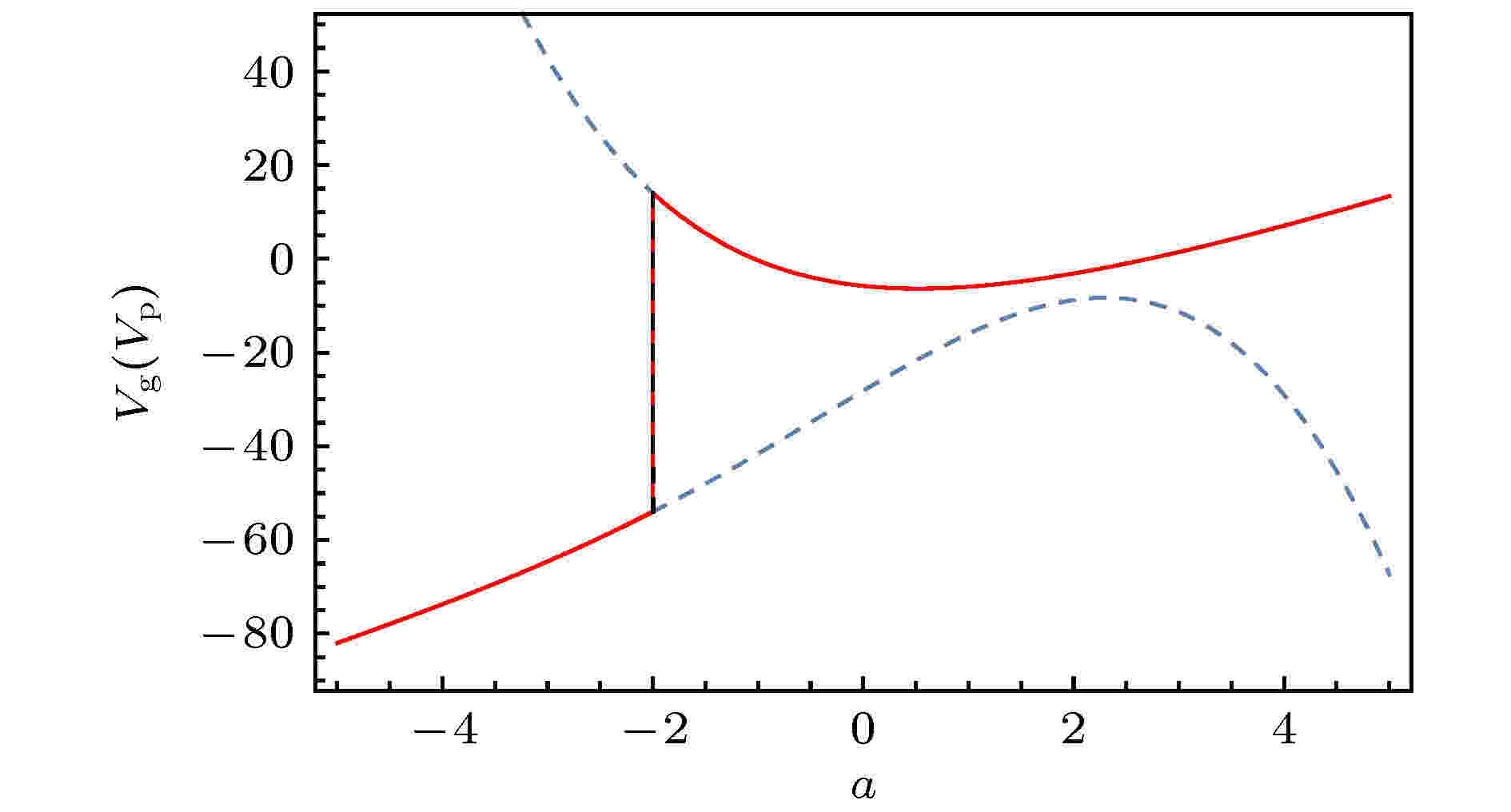 图 4 呼吸子的群速度
图 4 呼吸子的群速度























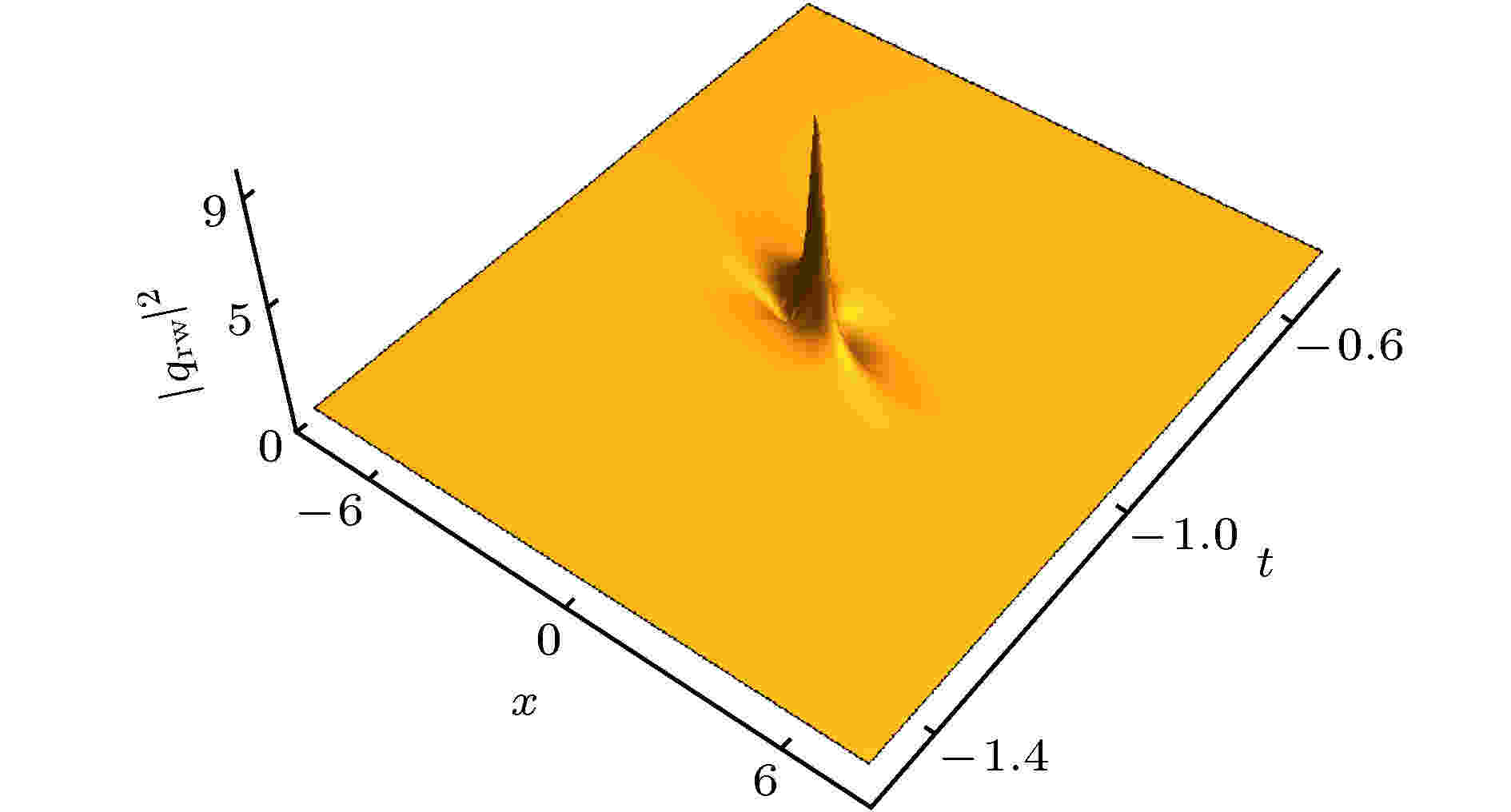 图 5 解(42)式描述的一阶怪波的动力学演化, 其中参数选取为
图 5 解(42)式描述的一阶怪波的动力学演化, 其中参数选取为

















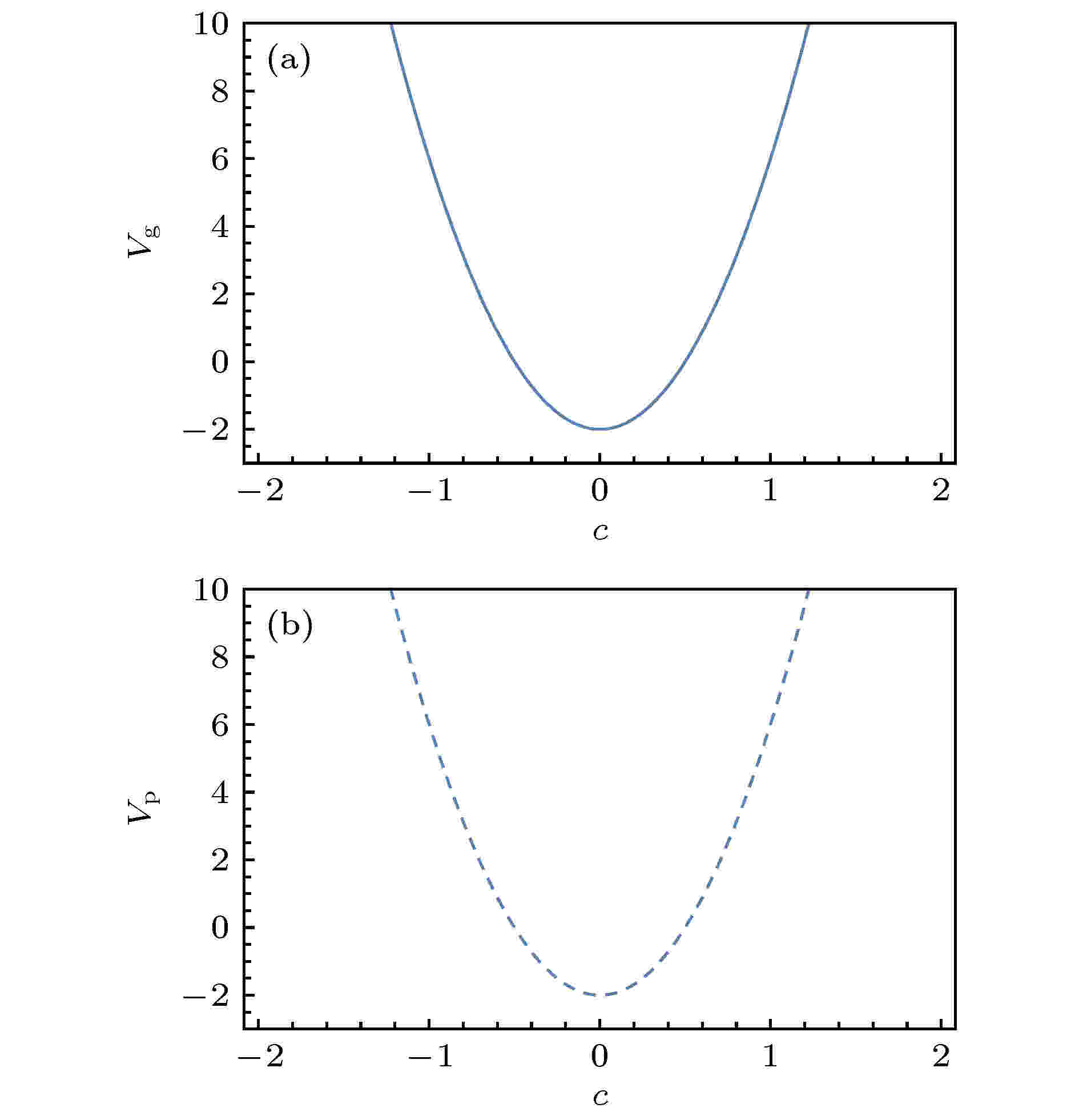 图 6 (a) 群速度
图 6 (a) 群速度









