删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

Boussinesq方程的Lax对、B?cklund变换、对称群变换和Riccati展开相容性

本站小编 Free考研考试/2021-12-29
摘要:Boussinesq方程是流体力学等领域一个非常重要的方程. 本文推导了Boussinesq方程的Lax对. 借助于截断Painlevé展开, 得到了Boussinesq方程的自B?cklund变换, 以及Boussinesq方程和Schwarzian形式的Boussinesq方程之间的B?cklund变换. 探讨了Boussinesq方程的非局域对称, 研究了Boussinesq方程的单参数群变换和单参数子群不变解. 运用Riccati展开法研究了Boussinesq方程, 证明Boussinesq方程具有Riccati展开相容性, 得到了Boussinesq方程的孤立波-椭圆余弦波解.
关键词: Boussinesq方程/
lax对/
B?cklund变换/
Riccati展开

English Abstract


全文HTML

--> --> -->
1.引　言
一般来讲, Boussinesq方程可写为
$ u_{tt}+\alpha u_{xx}+\beta (u^2)_{xx}+\gamma u_{xxxx} = 0, $
其中, 下角标x和t表示偏微分. Boussinesq方程可以用于描绘浅水波、等离子体、非线性晶格等众多物理现象[1-5].
由于该方程应用广泛, 一些特殊形式的或者修正的Boussinesq方程被推导出来研究. 例如, “坏”Boussinesq方程(也叫不适定Boussinesq方程)的形式为
$ u_{tt}- u_{xx}- (u^2)_{xx}- u_{xxxx} = 0. $
这个方程是在1872年由Boussinesq[1]提出来用于描绘浅水波问题的. Benny和Luke[6]发现这个Boussinesq方程非线性弱散色现象的一般近似. “好”Boussinesq方程的形式为
$ u_{tt}- u_{xx}- (u^2)_{xx}+ u_{xxxx} = 0. $
这个方程是作为描绘弦的非线性振动模型提出来的, 也可以用于描绘非线性介质材料中的电磁波[7]. 一种修正的Boussinesq方程的形式为
$ u_{tt}- u_{xx}- (u^2)_{xx}- u_{xxtt} = 0. $
这个方程也经常被称为“改进的”Boussinesq方程[8], 它由流体力学推导而来, 也可以用于描绘波在磁场中的传播, 并取代“坏”Boussinesq方程.
很多不同形式的Boussinesq方程, 是方程(1)的特殊形式. 本文旨在研究Boussinesq方程(1)的可积性、对称性和严格解. 在下文中, 如果没有特殊说明, Boussinesq方程指的是方程(1). 论文结构如下: 在第2节中, 从一个简化的Boussinesq方程的Lax对, 推导出Boussinesq方程(1)的一组Lax对; 在第3节, 对Boussinesq方程(1)进行截断的Painlevé展开, 得到Boussinesq方程的B?cklund变换; 第4节研究了Boussinesq方程的单参数群变换; 第5节讨论了Boussinesq方程的全点李对称性相似解; 第6节应用CRE (consistent Riccati expansion, CRE)方法证明了Boussinesq方程的CRE相容性. Boussinesq方程孤立波-周期波在第7节进行了讨论; 第8节是本文的结论和讨论.
2.Boussinesq方程的Lax对
当$ \alpha = 0 $,$ \beta = 1 $,$ \gamma = {1}/{3} $时, 方程(1)退化成
$ v_{\tau\tau}+ (v^2)_{\chi\chi}+\frac{1}{3}v_{\chi\chi\chi\chi} = 0, $
为了将方程(1)和方程(5)的变量进行区分, 我们将方程(1)中的变量$ \{u, x, t\} $对应地写成方程(5)中的$ \{v, \chi, \tau\} $. Weiss[9]通过研究方程(5)的painlevé性质, 推出了方程(5)的一组Lax对, 其形式如下
$ \psi_{\chi\chi\chi} = -\frac{3}{2} v\psi_\chi-\frac{3}{4}\psi v_{\chi}-\frac{3}{4}\psi{\int v_{\tau}\, {\rm d }\chi}+\lambda \psi \tag{6a},$
$ \psi_{\tau} = \psi_{\chi\chi}+v \psi \tag{6b}.$
方程(1)和方程(5)之间存在标度变换
$ \begin{split} & u(x,{\mkern 1mu} t) = {\left( {\frac{{3 \gamma }}{{{\beta ^2}}}} \right)^{\frac{1}{3}}}v\left( {\chi ,\tau } \right) - \frac{\alpha }{{2 \beta }},\\ &\chi = \pm \frac{{{\beta ^{\left( {\frac{1}{6}} \right)}} {3^{\left( {\frac{2}{3}} \right)}} x}}{{3 {\gamma ^{\frac{1}{3}}}}},\\ & \tau = \pm \frac{{{3^{\left( {\frac{5}{6}} \right)}} {\beta ^{\left( {\frac{1}{3}} \right)}} t}}{{3 {\gamma ^{\left( {\frac{1}{6}} \right)}}}}.\end{split}$
结合方程(5)的Lax对(6)式以及标度变换, 可以得到方程(1)的Lax对.
定理1 (Lax对定理)
Boussinesq方程(1)具有如下形式Lax对:
$\begin{split} \phi_{xxx} =\, & - { \frac { \sqrt{3\, \gamma } \beta\phi }{12\,\gamma ^{2}}} \, { \int } u_t\, {\rm d} x \! - { \frac { (2\,u\,\beta + \alpha ) }{4\,\gamma }} \phi_x \\ & - { \frac {\phi \,\beta \,}{ 4\,\gamma }} u_x \pm { \frac { \,\phi \,\lambda \,\sqrt{\beta }}{3\,\gamma }},\end{split} \tag{8a} $
$ \phi_t = \sqrt{3\,\gamma} \phi_{xx} + { \frac {\sqrt{3} \,\phi \,(2\,\beta \,u + \alpha )\,}{6\,\sqrt{ \gamma }}},\tag{8b} $
这里的λ代表谱函数, φ表示$ \{x, t\} $的任意函数.
3.与截断Painlevé展开相关联的B?cklund变换
截断Painlevé展开法, 是分析非线性系统最有效的方法之一[10-12]. 对Boussinesq方程(1), 可将u展开成
$ u = u_0+\frac{u_1}{f}+\frac{u_2}{f^2}, $
这里的$ u_0, u_1, u_2 $和f都是$ \{x, t\} $的函数, f是奇异流函数. 将(9)式代入到方程(1)中, 所得到的多项式中, f的所有不同阶次的系数都应该为零. 由$ f^{-6} $的系数为零, 可得到
$ {u_2} = - { \frac {6\,\gamma \, {f_{x}}^{2}}{\beta }}. $
由$ f^{-5} $的系数为零, 可得
$ {u_1} = { \frac {6\,\gamma \,{f _{{xx}}}}{\beta }}. $
由$ f^{-4} $的系数, 容易得到
$ {u_0} = { \frac {3}{2}} \, { \frac {\gamma \,{f_{{xx}}}^{2}}{\beta {f_{x}}^{2} }} - { \frac {2\,\gamma \,{f_{{xxx}} }}{\beta{f_{x}}}} - { \frac {1}{2}} \, { \frac {{f_{t}}^{2}}{\beta{f_{x}}^{2} }} - { \frac {\alpha }{2\,\beta }}\ . $
将(10)式–(12)式代入到$ f^{-3} $的系数中, 得
$ \gamma \left( { \frac {{f_{{xxx}}}}{{f_{x} }}} - { \frac {3}{2}} \,{ \frac {{f_{ {xx}}}^{2}}{{f_{x}}^{2}}} \right)_x + \left({ \frac {{f_{t}}}{ {f_{x}}}} \right)_t + { \frac {{f_{t}}\,}{{f _{x}}}} \left({ \frac {{f_{t}}}{{f_{x}}}} \right)_x = 0, $
方程(13)在M?bious变换下, 保持形式不变, 因此被称为Schwarzian形式的Boussinesq方程[9].
将(9)式—(13)式代到方程(1)中, 比较所得方程中$ f^0 $的系数, 可发现$ u_0 $也是Boussinesq方程的一个解, 这表示$ u = u_0 $是Boussinesq方程的一个自B?cklund变换. 而且, 对以上截断Painlevé展开进行总结, 可得到一个非自B?cklund变换.
定理2 (B?cklund变换定理)
如果f是Schwarzian形式的Boussinesq方程(13)的解, 那么
$ u = {u_0} = { \frac {3}{2}} \, { \frac {\gamma \,{f_{{xx}}}^{2}}{\beta {f_{x}}^{2} }} - { \frac {2\,\gamma \,{f_{{xxx}} }}{\beta{f_{x}}}} - { \frac {1}{2}} \, { \frac {{f_{t}}^{2}}{\beta{f_{x}}^{2} }} - { \frac {\alpha }{2\,\beta }} $
也是Boussinesq方程(1)的解.
定理3 (B?cklund变换定理)
如果f是Schwarzian形式的Boussinesq方程(13)的解, 那么
$\begin{split} u = \, & u_0+\frac{u_1}{f}+\frac{u_2}{f^2} = { \frac {3}{2}} \, { \frac {\gamma \,{f_{{xx}}}^{2}}{\beta {f_{x}}^{2} }} - { \frac {2\,\gamma \,{f_{{xxx}} }}{\beta{f_{x}}}}\\ & - { \frac {1}{2}} \, { \frac {{f_{t}}^{2}}{\beta{f_{x}}^{2} }} - { \frac {\alpha }{2\,\beta }}+\frac{{ 6\,\gamma \,{f _{{xx}}} }}{f\beta}-\frac{ { 6\,\gamma \, {f_{x}}^{2} }}{\beta f^2}\end{split}$
也是Boussinesq方程(1)的解.
4.单参数群变换
将$ { \dfrac {6\, \gamma \, {f _{{xx}}}}{\beta }} $代入Boussinesq方程(1)的对称决定性方程, 可发现$ { \dfrac {6\, \gamma \, {f _{{xx}}}}{\beta }} $是Boussinesq方程(1)的一个非局域对称. 为了将传统的点李对称和非局域对称结合在一起, 我们需要建立一个包含Boussinesq方程、Schwarzian形式的Boussinesq方程以及这两个方程的变换关系式的拓展系统, 其形式如下:
$ u_{tt}+\alpha u_{xx}+\beta (u^2)_{xx}+\gamma u_{xxxx} = 0, \tag{16a}$
$ \gamma \left( { \frac {{f_{{xxx}}}}{{f_{x} }}} - { \frac {3}{2}} \,{ \frac {{f_{ {xx}}}^{2}}{{f_{x}}^{2}}} \right)_x + \left({ \frac {{f_{t}}}{ {f_{x}}}} \right)_t + { \frac {{f_{t}}\,}{{f _{x}}}} \left({ \frac {{f_{t}}}{{f_{x}}}} \right)_x = 0, \tag{16b}$
$ u = { \frac {3}{2}} \, { \frac {\gamma \,{f_{{xx}}}^{2}}{\beta {f_{x}}^{2} }} - { \frac {2\,\gamma \,{f_{{xxx}} }}{\beta{f_{x}}}} - { \frac {1}{2}} \, { \frac {{f_{t}}^{2}}{\beta{f_{x}}^{2} }} - { \frac {\alpha }{2\,\beta }}, \tag{16c}$
$ f_x = g, \tag{16d}$
$ f_{xx} = h . \tag{16e}$
Boussinesq方程的对称$ \sigma^u $也相应地拓展为满足下式的四分量对称$ \{\sigma^u, \sigma^f, \sigma^g, \sigma^h\} $,
$ \sigma \!=\! \left(\!\!\! \begin{array}{cccc} \sigma^u \\ \sigma^f\\ \sigma^g\\ \sigma^h \end{array}\!\!\!\right) \!=\! \left(\!\!\!\begin{array}{cccc} { \dfrac {6\,\gamma \,{f _{{xx}}}}{\beta }} \\ -f^2\\ -2ff_x\\ -2{f_x}^2-2ff_{xx} \end{array}\!\!\!\right) \!=\! \left(\!\!\!\begin{array}{cccc} { \dfrac {6\,\gamma \,h}{\beta }} \\ -f^2\\ -2fg\\ -2g^2-2fh \end{array}\!\!\right)\ . $
对方程(16), 我们也可以研究它的全点李对称. 基于这个目的, 四分量对称$ \{\sigma^u, \sigma^f, \sigma^g, \sigma^h\} $应该满足Boussinesq方程的线性化的非线性系统. 按照点李对称的方法, 经过计算可得总的对称矢量为
$ \underline{V} = C_1 \underline{ V_1} +C_2 \underline{V_2}+C_3 \underline{V_3}+C_4\underline{ V_4}+C_5 \underline{V_5}+C_{6} \underline{V_{6}}\,, $
各个对称矢量为:
$\begin{split} & \underline{V_1} = \frac{x}{2}\partial_x + t\partial_ t-u\partial_u - { \frac {\alpha }{2 \,\beta }} \partial_u -\frac{g}{2}\partial_g-h\,\partial_h, \\ & \underline{ V_2} = \partial_x, \ \ \ \ \underline{V_3} = \partial_t, \\ & \underline{V_4} = -h\partial_u +{ \frac {\beta f^{2}}{6\,\gamma }} \partial_f +{ \frac {g\,\beta \,f}{3\,\gamma }}\partial_g +{ \frac {\beta (f\,h+g^2)}{3\,\gamma }}\partial_h,\qquad \qquad \\ & \underline{V_5} = -f\partial_f-g \partial_g-h \partial_h, \ \ \ \ \ \underline{V_{6}} = -\partial_f . \\[-10pt]\end{split}$
其中, $ \underline{V_1} $,$ \underline{V_5} $表示标度变换, $ \underline{V_2} $表示空间平移不变性, $ \underline{V_3} $代表时间平移不变性, $ \underline{V_4} $与非局域对称关联, 而$ \underline{V_{6}} $则表示相平移不变性.
由对称矢量(19)式, 可得到六个单参数不变子群:
$g_{\varepsilon}(\underline{V_1}) : \{x,t,u,f,g,h\} \longrightarrow \left\{x\,{\rm e}^{ \frac {\varepsilon }{2} },t\,{\rm e}^{\varepsilon },{\rm e}^{ - \varepsilon }\,u + { \frac { \alpha }{2\,\beta }}({\rm e}^{ - \varepsilon }-1),f,g\,{\rm e}^{ - \frac {\varepsilon }{2} }, h\,{\rm e}^{ - \varepsilon } \right\}, \tag{20a}$
$ g_{\varepsilon}(\underline{V_2}) : \{x,t,u,f,g,h\} \longrightarrow \{x+\varepsilon, \ t, \ u, \ f, \ g, \ h\}, \tag{20b}$
$ g_{\varepsilon}(\underline{V_3}) : \{x,t,u,f,g,h\} \longrightarrow \{x, \ t+\varepsilon, \ u, \ f, \ g, \ h\}, \tag{20c}$
$ \begin{array}{l} g_{\varepsilon}(\underline{V_4}) : \{x,t,u,f,g,h\} \longrightarrow \left\{ \begin{array}{ll} x,\ t, \ { u- { \dfrac {6\,\gamma \,\varepsilon ^{2}\,\beta \,g^{2}}{(\varepsilon \,\beta \,f - 6\,\gamma )^{2}}} + { \dfrac {6\, \gamma \,\varepsilon \,h}{\varepsilon \,\beta \,f - 6\,\gamma }}} , \ { \dfrac {6\, \gamma \,f}{6\,\gamma-\varepsilon \,\beta \,f }},\\ { { \dfrac { 36\,g\,\gamma ^{2}}{(\varepsilon \,\beta \,f - 6\,\gamma )^{2}}}},\ \ { { \dfrac {36\,\gamma ^{2 }\,( - 2\,g^{2}\,\varepsilon \,\beta + f\,h\,\varepsilon \,\beta - 6\,h\,\gamma )}{(\varepsilon \,\beta \,f - 6\,\gamma )^{3}}}} \end{array} \right\}, \end{array} \tag{20d}$
$ g_{\varepsilon}(\underline{V_5}) : \{x,t,u,f,g,h\} \longrightarrow \{x, \ t, \ u, \ {\rm e}^{( - \varepsilon )}f, \ {\rm e}^{( - \varepsilon )} g, \ {\rm e}^{( - \varepsilon )}h\}, \tag{20e}$
$ g_{\varepsilon}(\underline{V_6}) : \{x,t,u,f,g,h\} \longrightarrow \{x, \ t, \ u, \ f- \varepsilon, \ g, \ h\}. \tag{20f} $
从以上六个单参数不变子群, 可到到下列B?cklund变换定理.
定理4 (单参数群变换)
如果$ \{u(x, t), f(x, t), g(x, t), h(x, t)\} $是拓展的Boussinesq系统(16)的一组解, 则下列函数也是拓展的Boussinesq系统(16)的一组解,
$ \left\{ \begin{array}{ll} { \overline{u}_1 = {\rm e}^{ - \varepsilon }\,u(x {\rm e}^{ -\frac {\varepsilon }{2} },t {\rm e}^{-\varepsilon }) + { \dfrac { \alpha }{2\,\beta }}({\rm e}^{ - \varepsilon }-1)}, \qquad { \overline{f}_1 = f(x {\rm e}^{ -\frac {\varepsilon }{2} },t {\rm e}^{-\varepsilon })}, \\ { \overline{g}_1 = g(x {\rm e}^{ -\frac {\varepsilon }{2} },t {\rm e}^{-\varepsilon })\,{\rm e}^{ - \frac {\varepsilon }{2} }}, \qquad \qquad \qquad \ \qquad { \overline{h}_1 = h(x {\rm e}^{ -\frac {\varepsilon }{2} },t {\rm e}^{-\varepsilon })\,{\rm e}^{ - \varepsilon }} \end{array}\right \}, \tag{21a}$
$ \left\{ \overline{u}_2 = u(x-\varepsilon, t), \ \ \ \overline{f}_2 = f(x-\varepsilon, t),\ \ \ \overline{g}_2 = g(x-\varepsilon, t), \ \ \ \overline{h}_2 = h (x-\varepsilon, t)\right\}, \tag{21b}$
$ \{ \overline{u}_3 = u(x, t-\varepsilon), \ \overline{f}_3 = f(x, t-\varepsilon),\ \ \ \ \ \overline{g}_3 = g(x, t-\varepsilon), \ \ \ \overline{h}_3 = h(x, t-\varepsilon) \}, \tag{21c}$
$ \left \{\begin{array}{ll} { \overline{u}_4 = u(x,t)- { \dfrac {6\,\gamma \,\varepsilon ^{2}\,\beta \,g(x,t)^{2}}{(\varepsilon \,\beta \,f(x,t) - 6\,\gamma )^{2}}} + { \dfrac {6\, \gamma \,\varepsilon \,h(x,t)}{\varepsilon \,\beta \,f(x,t) - 6\,\gamma }}}, \ { \overline{f}_4 = { \dfrac {6\, \gamma \,f(x,t)}{6\,\gamma-\varepsilon \,\beta \,f(x,t) }}}, \\ { \overline{g}_4 = { \dfrac { 36 \gamma^{2}g(x,t)\,}{(\varepsilon \beta f(x,t) - 6 \gamma )^{2}}}},\ { \overline{h}_4 = { \dfrac {36 \gamma ^{2 } ( \varepsilon \beta f(x,t) h(x,t) - 2 \varepsilon \beta g(x,t)^{2}- 6 \gamma h(x,t) )}{(\varepsilon \,\beta \,f(x,t) - 6\,\gamma )^{3}}}} \end{array} \!\!\!\right\}, \tag{21d}$
$ \{ \overline{u}_5 = u(x,t), \ \ \ \overline{f}_5 = {\rm e}^{( - \varepsilon )}f (x,t),\ \ \ \overline{g}_5 = {\rm e}^{( - \varepsilon )}\,g(x,t),\ \ \ \overline{h}_5 = {\rm e}^{( - \varepsilon )}h (x,t)\}, \tag{21e}$
$ \{\overline{u}_6 = u(x,t), \ \ \ \overline{f}_6 = f(x,t)- \varepsilon,\ \ \ \ \overline{g}_6 = g(x,t), \qquad \ \ \ \overline{h}_6 = h(x,t) \}. \tag{21f}$

5.全点李对称相似解
对称性理论是求解偏微分方程的一种有效系统的方法[13-19]. 从对称矢量(19)式, 不仅可以得到单参数不变子群和群不变解, 而且可以得到Boussinesq的相似解和约化方程. 将约化方程的严格解和相似解相结合, 则可以得到所研究系统的严格解. 可得到下列四组非平庸情况.
情况1 $ C_1\neq 0, C_4\neq 0 $.
在种情这况, 群不变量可写为
$ \xi = { \frac {{C_{3}} + {C_{1}}\,t}{{C_{1}}\,(2\,{C _{2}} + {C_{1}}\,x)^{2}}}. $
相似解的形式为
$\begin{split}u= \,&{ \frac { {U}(\xi )}{(2\,{C_{2}} + {C_{1}}\,x)^{2}}} - { \frac {(4\,{C_{2}} + {C_{1}}\,x)\, \alpha\,{C_{1}}\,x}{2\,\beta( 2\, {C_{2}} + {C_{1}}\,x)^{2} }} \\ & - { \frac {6\,\gamma\,{C_{4}}\, {H}(\xi ) \,{\rm e}^{( - 2\, {F}(\xi )\,{C_{1}})}\, }{(2\,{C_{2}} + {C_{1}}\,x)^{2}\,\delta }}\\ & \times {\rm tanh}\!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ] \\ & +{ \frac {6\,\beta\,\gamma\,{C_{4}}^{2}\, {G}(\xi )^{2}\,{\rm e} ^{( - 2\, {F}(\xi )\,{C_{1}})} }{\delta ^{2}\,(2\,{C_{2}} + {C_{1}}\,x)^{2}\,}}\\ & \times {\rm sech}\!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]^{2},\end{split}\tag{23a}$
$ f \!=\! { \frac {3\,\gamma\,{C_{5}} }{C_4\,\beta}}-\frac{\delta}{C_4\,\beta} {\rm tanh} \!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} \!+\! {C_{1}}\,x ) \!+\! \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ],\tag{23b}$
$\begin{split} g =\, &{ \frac { {G}(\xi )\,{\rm e}^{( - {F}(\xi ) \,{C_{1}})}}{\,(2\,{C_{2} } + {C_{1}}\,x)}} \\ & \times{\rm sech}\!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]^{2},\end{split}\tag{23c}$
$ \begin{split} h = & { \frac { {H}(\xi )\,{\rm e}^{( - 2\, {F}( \xi )\,{C_{1}})}}{(2\,{C_{2}} + {C_{1}}\,x)^{2}\,}} \\& \times{\rm sech}\!\left[{ \frac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]^{2} \\&+{ \frac {2\,\beta\,{C_{4}}\, {G}(\xi )^{2}\, \,{\rm e}^{( - 2\, {F}(\xi )\,{C _{1}})}}{(2\,{C_{2}} + {C_{1}}\,x)^{2}\,\delta }} \\& \times\frac{{\rm sinh}\!\left[{ \dfrac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]}{{\rm cosh}\!\left[{ \dfrac {\delta \, {\rm ln}(2\,{C _{2}} + {C_{1}}\,x ) + \delta {F}(\xi )\,{C_{1}} }{3\,\gamma\,{C_{1}}}}\right ]^3} , \end{split}\tag{23d}$
其中$ \delta = \sqrt{6\, \gamma \, \beta \, {C_{4}}\, {C_{6}} + 9\, \gamma ^{2}\, {C_{5}}^{2}} $, 约化函数$ \{U(\xi), $$ F(\xi) $, $ G(\xi), H(\xi)\} $需要满足相应的约化方程. 这种情况的约化方程非常长, 这里省略不写.
情况2 $ C_1\neq 0, C_4 = 0 $.
$ \{\sigma^u, \sigma^f, \sigma^g, \sigma^h\} $包含$ C_4 $, 而$ C_4 $是与非局域对称相关联的, 那么如果令$ C_4 = 0 $, 则相似解会变得更加简化. 这样, 相似解为:
$ u = - { \frac {4\,x\, \alpha \,{C_{1}}\,{C_{2}} + x^{2}\,\alpha \,{C_{1}}^{2} - 2\, {U}(\xi )\,\beta }{2\,\beta \,(2\,{C_{2}} + {C_{1}}\,x)^{2}} }\,, \tag{24a}$
$ f = (2\,{C_{2}} + {C_{1}}\,x)^{\left( - \frac {2\,{C_{5}}}{{C_{1}}}\right)}\, {F}(\xi ) - { \frac {{C_{6}}}{{C_{5}}}}\,,\tag{24b}$
$ g = (2\,{C_{2}} + {C_{1}}\,x)^{\left( - 1 - \frac {2\,{C_{5}}}{{C_{1}}}\right) }\, {G}(\xi )\,, \tag{24c}$
$ h = (2\,{C_{2}} + {C_{1}}\,x)^{\left( - 2 - \frac {2\,{C_{5}}}{{C_{1}}}\right ) }\, {H}(\xi )\, . \tag{24d}$
与情况一相比, 时间和空间的对称性都没有改变, 因此这种情况的群不变量与情况一相同, 仍为
$ \xi = { \frac {{C_{3}} + {C_{1}}\,t}{{C_{1}}\,(2\,{C _{2}} + {C_{1}}\,x)^{2}}}\ . $
将(24b)式代入(16d)式和(16e)式, 则变量f和g变成:
$ g = - 2\,(2\,{C_{2}} + {C_{1}}\,x)^{( - 1 - \frac {2\,{C_{5}}}{{C_{1}}})}\,({C_{1}}{F_{\xi }}\,\xi \, + C_{5} {F} ), $
$\begin{split} h =\,& 2\,(2\,{C_{2}} + {C_{1}}\,x)^{( - 2 - \frac {2 \,{C_{5}}}{{C_{1}}})} (2 {C_{1}}^{2} {F_{\xi \xi }} \xi ^{2}+ 3 {C_{1}}^{2} { F_{\xi }}\,\xi \\ & + {C_{1}} {C_{5}}{F} \, + 4\,{C_{1}} {F_{\xi }} {C_{5}} \xi + 2\,{C_{5}}^{2} {F} ),\\[-12pt]\end{split}$
将(24b)式代到(16c)式, 可以得到用和F表示的u的表达式, 将(24b)代入到(16b)式, 可以得到F满足的约束方程. 由于这两个式子都很长, 此处省略不写.
情况3 $ C_1 = 0, C_2\neq 0, C_4\neq 0 $.
(18)式和(19)式说明空间x和时间t的对称受到$ C_1 $的影响. 当$ C_1 = 0 $时, 群不变量ξ将比情况一和情况二的群不变量简单. 此时, 群不变量变为
$ \xi = \frac{C_2 t-C_3x}{C_2}, $
相似解为:
$ u = {U}(\xi)+{ \frac {3\,\gamma\, C_{4} {\rm e} ^{ \frac {\delta \,{F}(\xi) }{ 3\,{C_{2}}\,\gamma } } {H}(\xi) }{\delta \,\left[{\rm e}^{ \frac {\delta \,(x + {F}(\xi) )}{3\,{C_{2} }\,\gamma } } + 1\right] }} - { \frac {24\,\beta\,\gamma\,{C_{4}}^{2} {G}(\xi)^{2} }{\delta ^{2} \left[{\rm e}^{ \frac {\delta \, (x + {F}(\xi) )}{3\,{C_{2} }\,\gamma } } + 1\right]^{2}}}, \tag{29a}$
$ f = - { \frac {\delta }{ \beta \,{C_{4}}}} {\rm tanh}\left[ { \frac {\delta \,(x + F (\xi) )}{6\,\gamma\,{C_{2}} }} \right ] + { \frac {3\,\gamma \,{C_{5}}}{ \beta \,{C_{4}}}}, \tag{29b}$
$ g = - { \frac {2\, {G}(\xi) }{ {\rm cosh}\left[{ \dfrac {\delta \,(x + {F}(\xi) )}{3\,{C_{2}}\,\gamma }} \right] + 1} }, \tag{29c}$
$ h = { \frac { {\rm e}^{ \frac {\delta \, (2\,{F}(\xi) +x)}{3\,{C_{2}}\,\gamma } } {H}(\xi) }{\left[{\rm e}^{ \frac {\delta \,(x + {F}(\xi) )}{3\,{C_{2} }\,\gamma } } + 1\right]^{2}}} - { \frac {16\,\beta\,{C_{4}}\, G(\xi)^{2}\,{\rm e}^{ \frac {\delta \,(x+F(\xi)) }{3\,{C_{2}}\,\gamma } } }{ \delta \,\left[{\rm e}^{ \frac {\delta \,(x + {F}(\xi) )}{3\,{C_{2} }\,\gamma } } + 1\right]^{3}}} .\tag{29d}$
其中$ F(\xi) $满足
$ \begin{split}& 27 {C_{2}}^{2}\,{C_{3}}^{5} \gamma ^{2} {F_{\xi \xi }}^{3} + 4 {F_{\xi \xi }} {C_{3}}^{4}\,{C_{2}} \delta ^{2}\,{F_{ \xi }}^{3}\\ + & ( - 6 {C_{3}}^{3} {C_{2}}^{2} \delta ^{2} {F_{ \xi \xi }} + 9\,{C_{3}}^{5}\,{F_{\xi \xi \xi \xi }}\,{C_{2}}^{2}\,\gamma ^{2})\,{F_{\xi }}^{2}\\ + & \{[ 2\,{C_{2}}^{3}\,( 2\,\delta ^{2}\,{C_{3}}^{2}-9\,\gamma \,{C_{2}}^{4})\\ - & 36\,{C_{2}}^{2}\,{C_{3}}^{5}\,\gamma ^{2}\,{F_{\xi \xi \xi }} ]\,{F_{\xi \xi }} - 18\,{C_{2}}^{3}\,{C_{3 }}^{4}\,{F_{\xi \xi \xi \xi }}\,\gamma ^{2}\}\,{F_{\xi }} \\ - & {C_{3}}^{5} {F_{\xi \xi }}\,\delta ^{2}\,{F_{\xi }}^{4} \\ + & \left[36 \gamma ^{2} {C_{3}}^{4} {C_{2}}^{3} {F_{\xi \xi \xi }} + { \frac {{C_{2}}^{4}\,(9\, \gamma {C_{2}}^{4} - \delta ^{2} {C_{3}}^{2})}{{C_{3}}}}\right] \\ \times & {F _{\xi \xi }} + 9\gamma ^{2} {C_{2}}^{4} {F_{\xi \xi \xi \xi }} {C _{3}}^{3} = 0 . \\[-10pt]\end{split} $
将(29b)式代到(16c)式, 可得到关于Boussinesq方程的下列B?cklund变换.
定理5 (B?cklund变换定理).
如果F满足(30)式, 则Boussinesq方程的解为
$ \begin{split} u =& - { \frac {1}{6}} \, { \frac {({C_{2}} - {F_{\xi }}\,{C_{3}})^{2}\,\delta ^{2}\,}{\beta \,\gamma \,{C_{2}}^{4}}}{\rm tanh}\left[ { \frac {\delta \,(x + {F} )}{6\,{C_{2}}\, \gamma }}\right ]^{2} \\ &+ { \frac {\delta \,{C_{3}}^{2}\,{F_{\xi \xi }} }{{C _{2}}^{3}\,\beta }} {\rm tanh}\left[ { \frac {\delta \,(x + {F} )}{6\,{C_{2}}\, \gamma }}\right ] \\ &- \frac {1}{18 \gamma \beta{C_{2}}^{4}({C_{2}} - {F _{\xi }}\,{C_{3}})^{2} } \{ 3\,{C_{2}}^{2}\,(3\,\gamma \,{C_{2}}^{4} \\ & + 3\,{C_{2}}^{2} \,\alpha \,\gamma \,{C_{3}}^{2} - 4\,\delta ^{2}\,{C_{3}}^{2})\,{ F_{\xi }}^{2}\\ & + [36\,{F_{\xi \xi \xi }}\,{C_{3}}^{4}\,{C_{2}}^{ 2}\,\gamma ^{2} - 2\,{C_{2}}^{3}\,{C_{3}}\,(9\,{C_{2}}^{2}\, \alpha \,\gamma\\ &- 4\,\delta ^{2})]\,{F_{\xi }} - 27\gamma ^{2} {F_{\xi \xi }}^{2}\,{C_{3}}^{4}\,{C_{2}}^{2} \\ &- 2 \delta ^{2} {F_{\xi }}^{4} {C_{3}}^{4} - 36 {F_{\xi \xi \xi }} {C_{3}}^{3} {C_{2}}^{3 }\,\gamma ^{2} \\ &+ {C_{2}}^{4}\,(9\alpha \gamma {C_{2}}^{2} - 2 \delta ^2)+ 8\,\delta ^{2}\,{C_{2}}\,{F_{\xi }}^{3}\,{C_{3}} ^{3} \}. \end{split}$
情况4 $ C_1 = 0, C_2\neq 0, C_4 = 0 $.
这种情况下, 拓展系统(16)的相似解为:
$ u = {U} (\xi ), \tag{32a} $
$ f = {\rm e}^{\left( - \frac {{C_{5}}\,x}{{C_{2}}}\right)}\, {F}(\xi ) - { \frac {{C_{6}}}{{C_{5}}}}, \tag{32b}$
$ g = G(\xi )\,{\rm e}^{\left( - \frac {{C_{5}}\,x}{{C_{2}}}\right)}, \tag{32c}$
$ h = {H}(\xi )\,{\rm e}^{\left( - \frac {{C_{5}}\,x}{{C_{2}}}\right)}, \tag{32d}$
这里, 群不变量ξ为
$ \xi = \frac{C_2 t-C_3x}{C_2}. $
将(32b)式代入到(16b)式, 可得到$ F(\xi) $满足的约束方程. 将(32b)式代入到(16c)式, 则得到下列定理.
定理6 (B?cklund变换定理).
如果$ F(\xi) $满足(32b)式, 则Boussinesq方程的解可以写为
$ \begin{split} u = & - { \frac {1}{2}}\frac{1}{({F_{\xi }} { C_{3}} + {F} {C_{5}})^{2} {C_{2}}^{2} \beta} \left\{ [4\,\gamma {F_{\xi \xi \xi }}\,{C_{3}}^{4}\right. \\ &+ 2\,{C_{3}} {C_{5}} {F} (2\,{C_{5}}^{2}\,\gamma + \alpha \,{C_{2}}^{2})] {F_{\xi }} - 3\,\gamma \,{F_{\xi \xi }}^{2}\,{C_{3}}^{4} \\ & +{C_{2}}^{2} (\alpha \,{C_{3}}^{ 2} + {C_{2}}^{2}) {F_{\xi }}^{2} + 6\, \gamma \,{F}{F_{\xi \xi }}\,{C_{3}}^{2}{C_{5 }}^{2}\,\\ & \left.+ 4\,\gamma \,{F_{\xi \xi \xi }} {C_{3}}^{3} {F} {C_{5}} + {C_{5}}^{2} {F} ^{2} ({C_{5}}^{2}\,\gamma + \alpha {C_{2}}^{2})\right\} . \end{split} $

6.Boussinesq方程的CRE相容性
本节将通过CRE (consistent Riccati expansion, CRE)方法来讨论Boussinesq方程的严格解[20]. Riccati方程的形式为
$ R_w = a_0+a_1R(w)+a_2 R(w)^2, $
这里的$ a_0 $, $ a_1 $和$ a_2 $是任意常数. Riccati方程的严格解可写为
$ R(w) = -\frac{\sqrt{\theta}}{2\, a_2}\tanh \left(\frac{\sqrt{\theta}\, w}{2}\right)+\frac{ a_1}{2\, a_2}, $
其中,
$ \theta\equiv {a_1}^2-4a_0\, a_2. $
对于一个偏微分系统
$ \begin{split} & P(x, t, v) = 0,\ \ \ P = \{P_1, P_2,..., P_m\}, \\ & x = \{x_1, x_2,..., x_n\}, \ \ \ v = \{v_1, v_2,..., v_m\}, \end{split} $
我们可假设它可以展开为
$ v_i = \sum\limits_{j = 0}^{J_i} v_{i,j}R^j(w), $
这里的$ R(w) $是Riccati方程的严格解. 将(39)式代入到(38)式, 并令$ R^i(w) $的系数为零, 可得:
$ P_{j,i}(x,t,v_{l,k},w) = 0. $
如果系统(40)是自洽的, 则展开式(39)式是“CRE”, 且非线性系统(38)是“CRE”相容系统[20].
为了得到孤立波-周期波碰撞解, 可应用CRE方法. CRE方法可被用于证明一个系统是CRE相容系统, 并可用于寻求非线性系统的碰撞波解. 对Boussinesq方程, u可展开成截断展开的形式:
$ u = u_3+u_4 R(w)+u_5 {R(w)}^2,$
这里, $ u_3, \ u_4, \ u_5 $和w都是x和t的函数, $ R(w) $是Riccati方程的一个解.
将(35)式和(41)式代入到方程(1)中, 并令$ R(w) $所有阶次的系数为零, 可得
$\begin{split} {u_{3}} = & -\, { \frac { \gamma \,({a_{1}}^{2} + 8\,{a_{2}}\, {a_0})\,{w_{x}}^{2}}{ 2\, \beta }} - { \frac { \alpha + 6\,\gamma \,{w_{{xx}}}\,{a_{1}}}{2\,\beta }} \\ & - { \frac {2\,\gamma \,{w_{{xxx}}}}{{w_{x}}\, \beta }} - { \frac { {w_{t}}^{2} - 3\,\gamma \,{w_{{xx}}}^{2}}{2\,\beta \,{w_{x}} ^{2}}}, \\[-18pt]\end{split} \tag{42a}$
$ {u_{4}} = - { \frac {6\,{a_{2}}\,\gamma \,({w_{x}}^{2 }\,{a_{1}} + {w_{{xx}}})}{\beta }}, \tag{42b}$
$ {u_{5}} = - { \frac {6\,\gamma \,{w_{x}}^{2}\,{a_{2}} ^{2}}{\beta }},\tag{42c}$
这里w满足
$\begin{split} {w_{t}}^{2} {w_{ {xx}}}\, & - \gamma (4 {a _{2}} {a_0}\! -\! {a_{1}}^{2}) {w_{ {xx}}} {w_{x}}^{4} \!-\! ( \gamma {w_{ {xxxx}}}\! +\! {w_{ {tt}}}) {w_{x}} ^{2}\\ &+ 4 \gamma {w_{x}} {w_{ {xx}}} {w_{ {xxx}}} - 3 \gamma {w_{ {xx}}}^{3} = 0. \\[-10pt]\end{split} $
通过CRE和CRE相容性的定义, Boussinesq方程显然是一个CRE相容系统. 基于以上讨论, 可得到如下定理:
定理7 (CRE相容性定理)
Boussinesq方程是一个CRE相容系统. 如果w是相容性条件(43)式的一个解, 则下列形式的u也是Boussinesq方程的一个解.
$ \begin{split} u = & u_3+u_4 R(w)+u_5 {R(w)}^2 \\ = & - \,{ \frac { \gamma \,({a_{1}}^{2} + 8\,{a_{2}}\, {a_0})\,{w_{x}}^{2}}{ 2\,\beta }} - { \frac { \alpha + 6\,\gamma \,{w_{{xx}}}\,{a_{1}}}{2\,\beta }} \\ & - { \frac {2\,\gamma \,{w_{{xxx}}}}{{w_{x}}\, \beta }} - { \frac { {w_{t}}^{2} - 3\,\gamma \,{w_{{xx}}}^{2}}{2\,\beta \,{w_{x}} ^{2}}} \\ & - { \frac {6\,{a_{2}}\,\gamma \,({w_{x}}^{2 }\,{a_{1}} + {w_{{xx}}})}{\beta }} R(w) \\ & - { \frac {6\,\gamma \,{w_{x}}^{2}\,{a_{2}} ^{2}}{\beta }} R(w)^2, \end{split} $
这里的$ R(w) $和θ分别满足(36)式和(37)式.
7.孤立波-周期波碰撞解
从Boussinesq方程的CRE性质, 可进一步研究Boussinesq方程的严格解. 将(36)式代入到(44)式中可得
$\begin{split} u = & - { \frac {3}{2}} \, { \frac {{w_{x}}^{2}\,\gamma \,\,\theta }{ \beta }} {\rm tanh}\left( { \frac {w\,\sqrt{\theta }}{2}} \right)^{2}\\ & + { \frac {3\,\gamma \,{w_{{xx}}}\, \, \sqrt{\theta }}{\beta }}{\rm tanh}\left({ \frac {w\,\sqrt{\theta }}{2}} \right) - { \frac {\alpha }{2\,\beta }} \\ & - { \frac {\gamma \,(4\,{a _{2}}\,{a_{0}} - {a_{1}}^{2})\,{w_{x}}^{2}}{\beta }} - { \frac {2\,\gamma \,{w_{ {xxx}}}}{{w_{x}}\, \beta }}\\ & - { \frac {1}{2}} \,{ \frac { {w_{t}}^{2} - 3\,\gamma \,{w_{ {xx}}}^{2}}{\beta \,{w_{x}} ^{2}}} . \end{split} $
从(45)式可看到, 如果我们想知道u的具体形式, 那么需要先知道w的表达式. 如果w具有如下形式:
$ w = {k_{1}}\,x + \omega_1\,t + {a_{3}}\,E_{\pi}( {\rm sn}({k_{2}}\,x + \omega_2\,t, \,m), \,n, \,m), $
这里$ k_1, k_2, \omega_1, \omega_2, a_3, n $和m是常数, $ E_{\pi} $是第三类不完全椭圆积分. 将(46)式代入到(43)式中, 并令$ {\rm sn}({k_{2}}\, x + \omega_2\, t, \, m) $的所有不同阶次的系数为零, 可发现参数应该满足:
$ \left\{\begin{aligned} & {a_{0}} = { \frac {n\,{ a_{1}}^{2}\,{a_{3}}^{2} - 4\,m^{2} + 4\,m^{2}\,n - 4\,n^{2} + 4\, n}{4\, {a_{3}}^{2}\,{a_{2}}\,n}}, \\ & \gamma = { \frac {3\,[{k_{1}}^{2}\,{a _{4}}\,n^{2} - {k_{1}}\,{a_{4}}^{2}\,(1 + m^{2})\,n + m^{2}\,{a_{ 4}}^{3}]\,{k_{1}}\,{\omega _{2}}^{2}\,n\,{a_{3}}^{2}}{{k_{2}}^{2} \,[{k_{1}}^{2}\,({k_{1}} + 3\,{a_{4}})\,n^{2} - 2\,{k_{1}}\,{a_{4 }}\,({k_{1}} + {a_{4}})\,(1 + m^{2})\,n + m^{2}\,({a_{4}} + 3\,{k _{1}})\,{a_{4}}^{2}]^{2}}},\\ & {\omega _{1}} = - { \frac {{\omega _{ 2}} {k_{1}} [{k_{1}}^{2} (3 {a_{4}} - {k_{1}}) n^{2} - 2 {k _{1}} {a_{4}} (2 {a_{4}} - {k_{1}}) (1 + m^{2}) n + m^{2} ( 5 {a_{4}} - 3 {k_{1}}) {a_{4}}^{2}]}{{k_{2}} [{k_{1}}^{2}\,({ k_{1}} + 3 {a_{4}})\,n^{2} - 2 {k_{1}} {a_{4}} ( {k_{1}} + {a_{4}} ) (1 + m^{2})\,n + m^{2} ({a_{4}} + 3 \,{k_{1}})\,{a_{4}}^{2}]}},\end{aligned} \right. $
或
$ \left\{\begin{aligned} & {\omega _{1}} = - { \frac {1}{2}} \,{ \frac {{\omega _{2}}\,{k_{1}}}{{k_{2}}}}, \\ & \gamma = - { \frac {3}{16}} \, { \frac {{\omega _{2}}^{2}\,{a_{3}}^{2}\,(3\,{a_{4}} - 2\,{k_{1}}\,n)}{{k_{2}}^{2}\,{a_{4}}\,({k_{1}}\,n - {a_{4}})^{ 2}}}, \\ & m = \pm { \frac { \sqrt{( 2\,{k_{1}}\,n- 3\,{a _{4}})\,{a_{4}}\,{k_{1}}\,n\,({k_{1}}\,n - 2\,{a _{4}})}}{{a_{4}}\,( 3\,{a_{4}}- 2\,{k_{1}}\,n)}},\\ &{a_{0}} = { \frac {1}{4}} \, { \frac {{a_{1}}^{2}}{{a_{2}}}} - { \frac {(n - 1)\,({k_{1}}^{2}\,n + 2\,{k_{1}}\,n\,{a_{3}}\,{k_{2}} - {k_{1}}^{2} - 4\,{k_{1}}\,{a_{3}}\,{k_{2}} - 3\,{a_{3}}^{2}\,{ k_{2}}^{2})}{{a_{2}}\,( 2\,{k_{1}}\,n - 3\,{a_{4}} )\,{a_{3}}^{2}\,{a_{4}}}}, \end{aligned} \right. $
这里$ {a_{4}} = {k_{1}} + {a_{3}}\, {k_{2}} $.
将(46)式代入到(45)式中, 得:
$ u = { \frac {3}{2}} \, { \frac {(a_{4}-{k_{1}}\,n\,S^{2} )^{2} \gamma \theta T^{2}}{(n\,S^{2} - 1)^{2} \beta }} + { \frac {6 \gamma {a_{3}} {k_{2}}^{2} n S C {D} \sqrt{\theta }\,T}{(n S^{2} - 1)^{2} \beta }} - \frac{ [ a_5 S^{8} + a_6 S^{6} + a_7 S^{4} +a_8 S^{2} + a_9 ]}{2[({k_{1}} n S^{2} -{a_{4}} )^{2} (n S^{2} - 1)^{2} \beta ]}, $
其中
$ \begin{split} T\equiv \, &{\rm tanh}\left\{{ \frac {1}{2}} \,\sqrt{\theta }\,\left [{ k_{1}}\,x + {\omega _{1}}\,t + {a_{3}}\,E_{\pi}( {\rm sn}({k_{2}}\,x + \omega_2\,t, \,m), \,n, \,m)\right ]\right\}, \\ S\equiv\, &{\rm sn}({k_{2}}\,x + \omega_2\,t, \,m),\ C\equiv{\rm cn}({k_{2}}\,x + \omega_2\,t, \,m), \ D\equiv{\rm dn}({k_{2}}\,x + \omega_2\,t, \,m), \\ a_5 = \, & - n^{3} (2 n \gamma \theta {k_{1}}^{4} - \alpha {k_{1}}^{2} n - {\omega _{1}}^{2} n + 8 \gamma {a_{3}} {k_{2}}^{3} {k_{ 1}} m^{2}), \\ a_6 =\, & 2 n^3[ 8 \gamma a_{3}{k_2}^{3}k_{1} ( m^2 + 1)+ 4 \gamma {a_{4}} \theta {k_{1}}^{3}- \alpha {k_{1}}^{2} - \alpha {k_{1}} {a_{4}} - 2 {\omega _{1}}^{2} - \omega _{1} {a_{3}} \omega _2] - 4 n^{2}m^{2} {a_{3}}\gamma {k_{2}}^{3}( a_4 +3 {k_{1}} ), \\ a_7 = \, & 24 n\gamma {a_{3}}{k_{2}}^{3}( {a_{4}}\,m^{2} - n^2 {k_{1}}) + n^2( {\omega _{ 2}}^{2} {a_{3}}^{2} - 4\,\gamma \,{a_{3}}^{2} {k_{2}}^{4} - 12 \gamma {k_{1}}^{2} {a_{4}}^{2} {a_{1}}^{2} \\ & + 6 {\omega _{1}}^{2} + 48 \gamma {a_{2} } {k_{1}}^{2} {a_{4}}^{2} {a_{0}} + 6\,{\omega _{1}} {a_{3 }} {\omega _{2}} - 4 \gamma {a_{3}}^{2} {k_{2}}^{4} m^{2} + 6 \alpha {k_{1}} {a_{4}} + \alpha {a_{3}}^{2} {k_{2}}^{2} ), \\ a_8 =\, & 4 \gamma n^2 {a_{3}} {k_{2}}^{3} ({k_{1}}+3 {a_{4}}) +8n \gamma{k_{1}} {a_{4}}^{3} \theta - 16\,n\gamma {a_{3}} {k _{2}}^{3}a_{4}( m^{2} + 1) \\ & -2n( {a_{3}}^{2} {\omega _{2}}^{2} + \alpha {k_{1}} {a_{4}} + 2 {\omega _{1}}^{2} + 3 { \omega _{1}} {a_{3}} {\omega _{2}} + {a_{4}}^{2} \alpha), \\ a_9 = & {a_{4}}^{2} \alpha +( {a_{3}} {\omega _{2}} + {\omega _{1}})^{2} + 8 {a_{3}} \gamma {k_{2}}^{3} n {a_{4}} - 2 \gamma {a_{4}} ^{4} \theta,\end{split} $
上式中的参数满足(47)式或(48)式.
图1和图展示了满足约束关系(47)的解(49)式. 图1中的自由参数选为{n = 0.2, m = 0.5, a1 = 1, a3 = 1, k1 = 1, k2 = 1, $ \omega_2 = 1, \alpha = -0.8, \beta = 1 \} $, 图2中的自由参数选为{n = 0.2, m = 0.9, a1 = 1, a3 = 1, k1 = 1, k2 = 1, $\omega_2 = 1, \alpha = -0.8, \beta = 1 \} $. 图1和图2展示了亮孤子和周期波的碰撞行为. 图3展示了图1和图2中u的密度函数, 图3(a)对应图1, 图3(b)对应图2. 两种情况的周期波和孤立波的方向是一致的, 而碰撞处的形状则不相同.
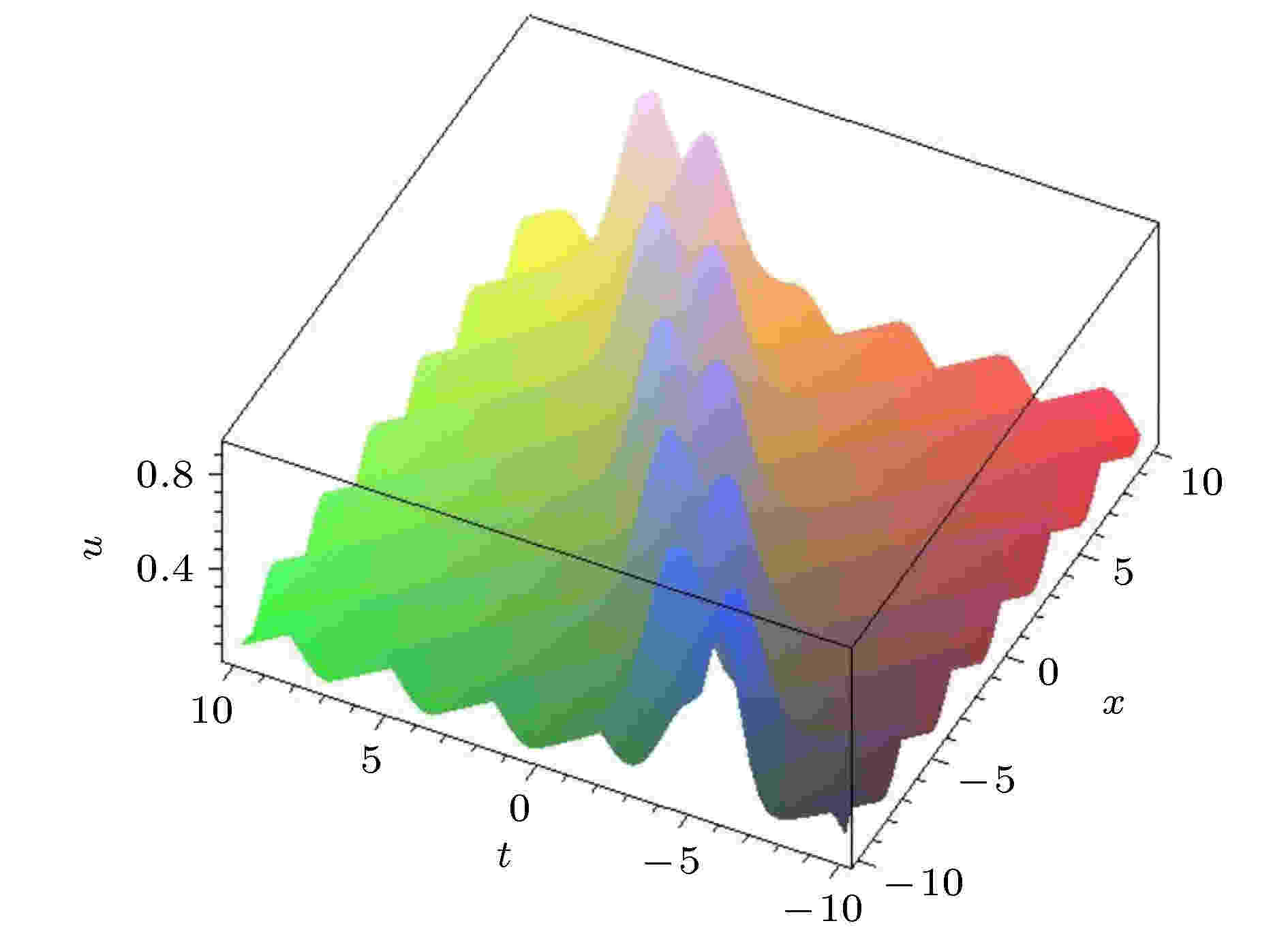图 1 满足(47)式的碰撞波解(49)式. 自由参数为{n = 0.2, m = 0.5, a1 = 1, a3 = 1, k1 = 1, k2 = 1, ω2 = 1, α = –0.8, β = 1}
Figure1. The solution (49) with Formula (47). The free parameters are {n = 0.2, m = 0.5, a1 = 1, a3 = 1, k1 = 1, k2 = 1, ω2 = 1, α = –0.8, β = 1}.

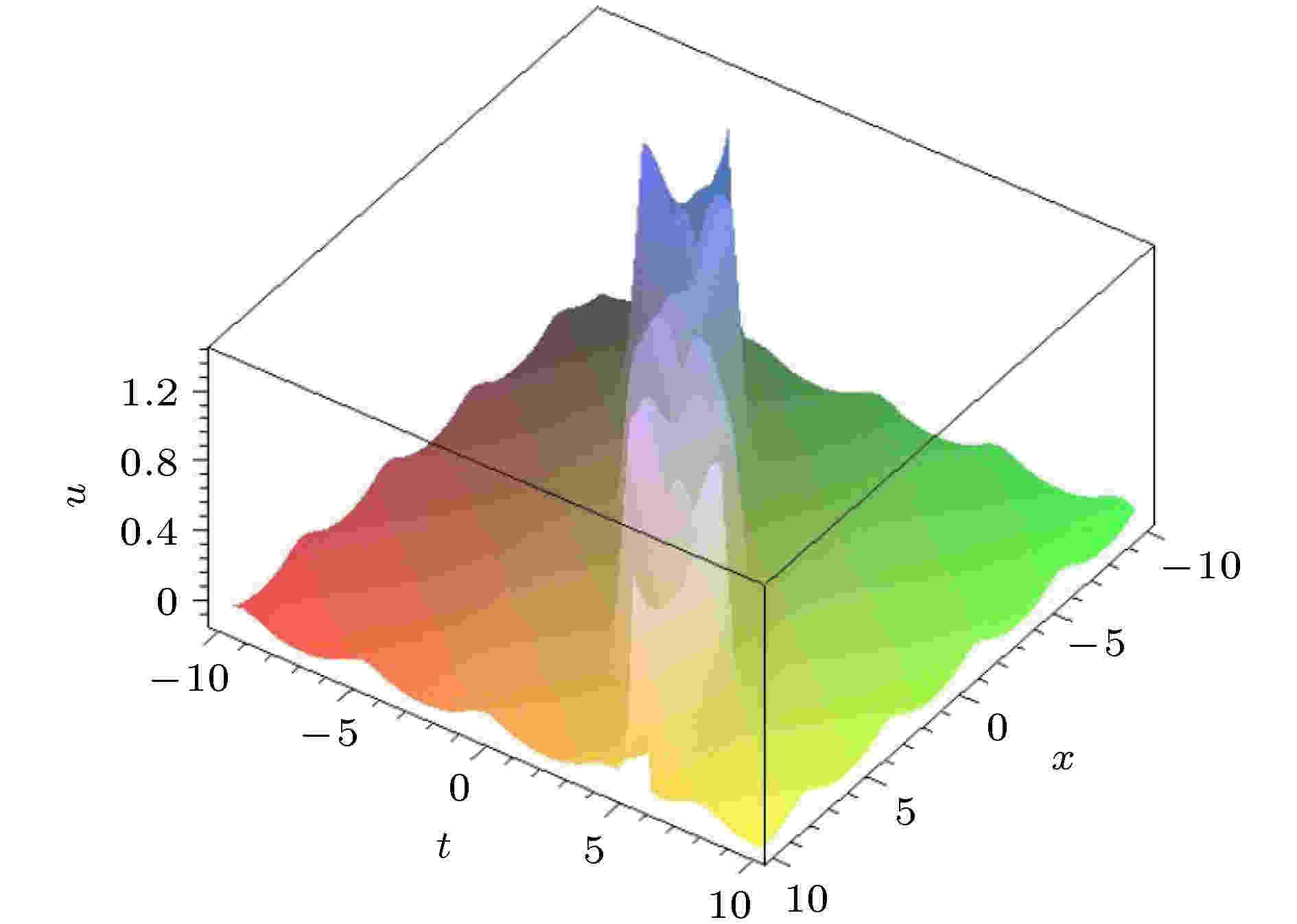图 2 满足(47)式的碰撞波解(49)式. 自由参数为 {n = 0.2, m = 0.9, a1 = 1, a3 = 1, k1 = 1, k2 = 1, ω2 = 1, α = –0.8, β = 1}
Figure2. The solution (49) with Formula (47). The free parameters are {n = 0.2, m = 0.9, a1 = 1, a3 = 1, k1 = 1, k2 = 1, ω2 = 1, α = –0.8, β = 1}.

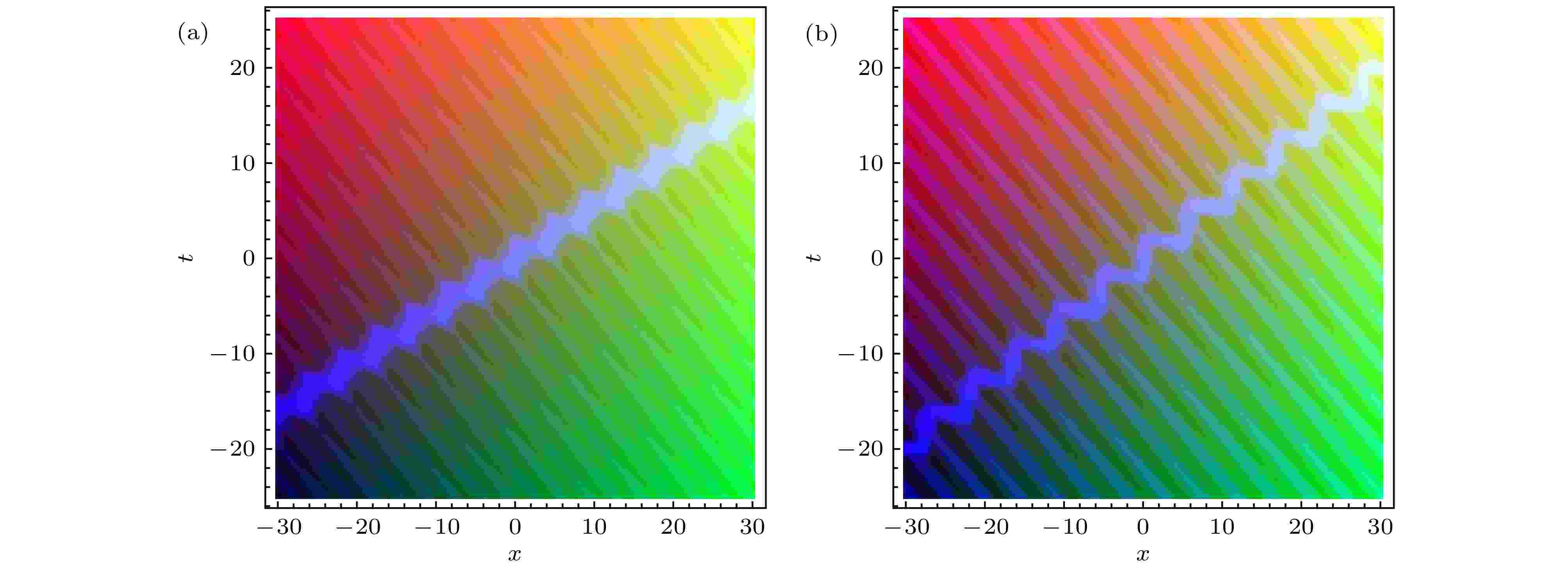图 3 u的密度函数图. 图(a)的参数与图1相同, 图(b)的参数与图2相同
Figure3. The density of u. The parameters of the Fig. (a) are the same as those of Figure 1 and the parameters of the Fig. (b) are the same as those of Figure 2.

图4和图5展示了满足参数限制(48)式的碰撞波解(49)式, 里边的周期波在扭结孤立波上运动, 而不是在常数背景上运动. 图4中的自由参数选为 {n = 0.4, a1 = 1, a2 = 1, a3 = 2.2, k1 = 1, k2 = –0.22, $\omega_2 = 1, \alpha = -400, \beta = 80 \} $, 其中(48)式中的m选“+”; 图5中的自由参数选为{n = 0.6, a1 = 2, a2 = 1, a3 = 4, k1 = 1, k2 = –0.12, ω2 = 0.1,$ \alpha = -14,\; \beta = 6 \} $, 其中(48)式中的m选“–”. 图6展示了图4和图5中u的密度函数, 图6(a)对应图4, 图6(b)对应图5. 图6清楚地展示了扭结孤立波和周期波的碰撞.
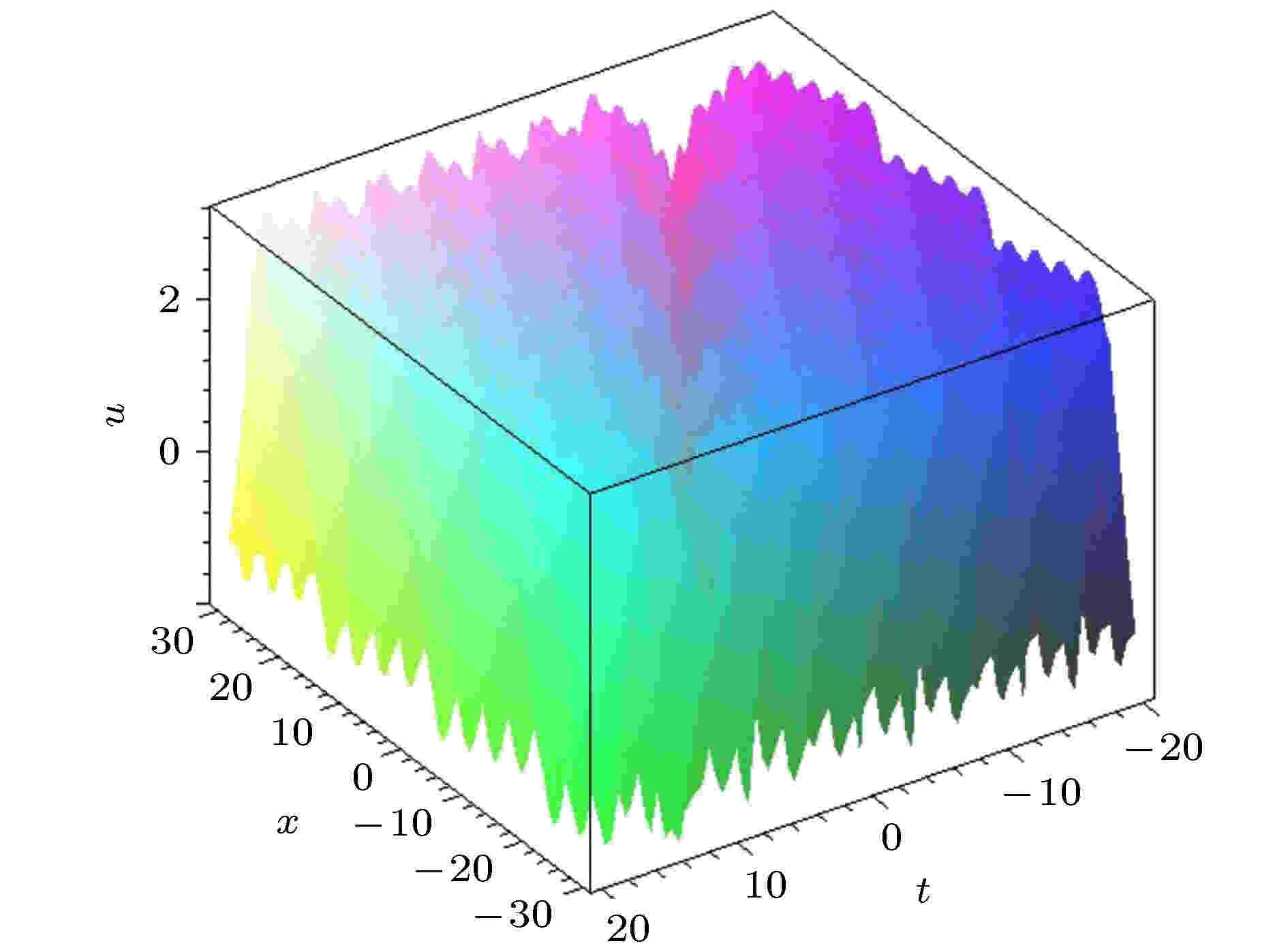图 4 参数关系满足(48)式的碰撞波解(49)式的演化图. 自由参数为 {n = 0.4, a1 = 1, a2 = 1, a3 = 2.2, k1 = 1, k2 = –0.22, ω2 = 1, α = –400, β = 80}
Figure4. The interaction solution (49) with parameter satisfying Formula (48). The free parameters are chosen as {n = 0.4, a1 = 1, a2 = 1, a3 = 2.2, k1 = 1, k2 = –0.22, ω2 = 1, α = –400, β = 80}.

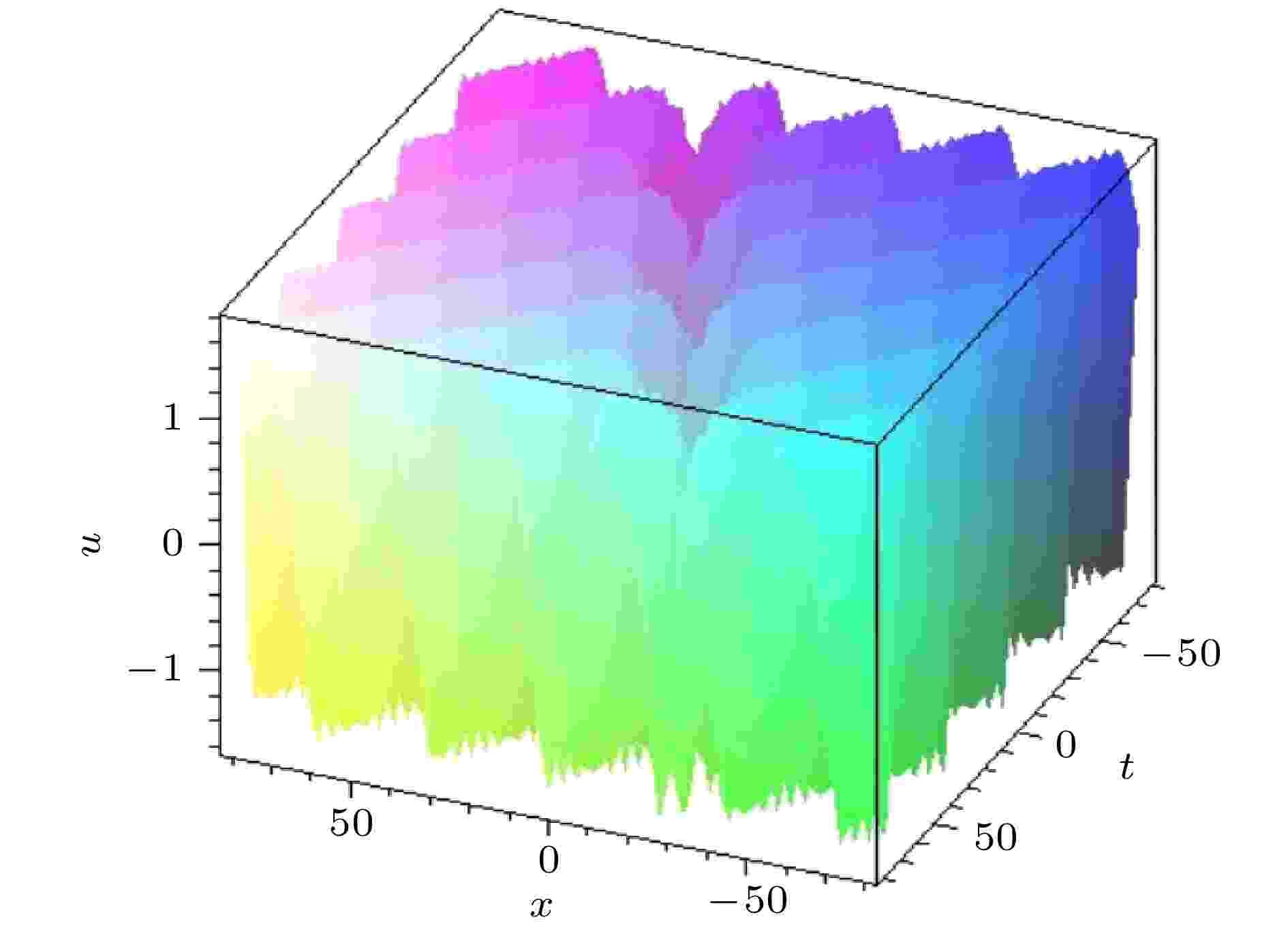图 5 参数关系满足(48)式的碰撞波解(49)式. 自由参数为{n = 0.6, a1 = 2, a2 = 1, a3 = 4, k1 = 1, k2 = –0.12, ω2 = 0.1, α = –14, β = 6}
Figure5. The interaction solution (49) with parameter satisfying Formula (48). The free parameters are selected as {n = 0.6, a1 = 2, a2 = 1, a3 = 4, k1 = 1, k2 = –0.12, ω2 = 0.1, α = –14, β = 6}.

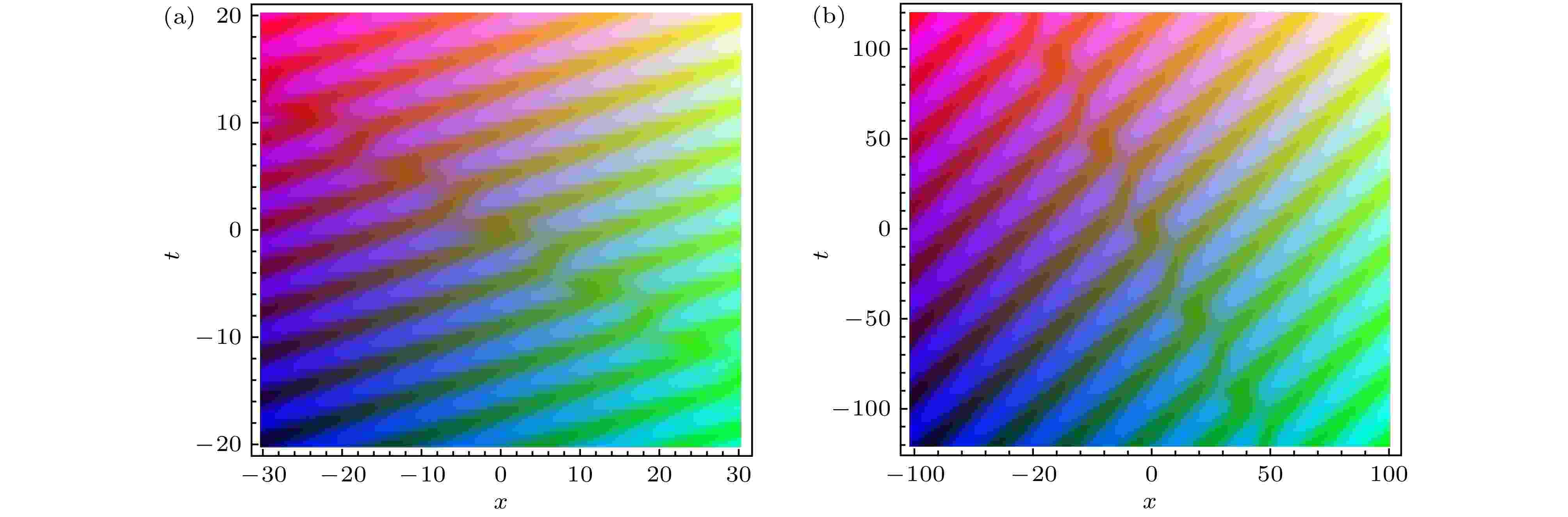图 6 u的密度函数图. 图(a)对应图4, 图(b)对应图5
Figure6. The density of u. The Fig. (a) is related to Fig. 4 and the Fig. (b) is corresponding to Fig. 5.

8.总结和讨论
本文推导了Boussinesq方程的Lax对, 说明Boussinesq方程是Lax可积模型. 运用截断Painlevé展开法研究了Boussinesq方程, 得到了Boussinesq方程的自B?cklund变换, 以及Boussinesq方程和Schwarzian形式的Boussinesq方程之间的非自B?cklund变换. 研究了Boussinesq方程的全点李对称, 得到了单参数群变换和单参数子群不变解. 运用CRE方法研究了Boussinesq方程, 证明了Boussinesq方程是一个CRE相容模型, 得到了Boussinesq方程的孤立波-椭圆余弦波碰撞解. Boussinesq方程广泛地应用于描绘流体动力学、电磁学、等离子体、非线性晶格等物理现象. 它作为一个著名的孤立子方程, 各种各样的激发模式, 以及它在各种物理情景中的应用, 值得不断深入研究.
感谢楼森岳教授和任博博士的宝贵讨论.
相关话题/系统 方程 空间 物理 流体力学
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 高阶Ablowitz-Ladik方程的局域波解及稳定性分析
    摘要:本文构造了一类高阶Ablowitz-Ladik方程的广义$(M,N-M)$-波Darboux变换,借助符号计算从不同背景出发研究了该模型丰富的局域波解,并利用数值模拟研究了这些解的动力学稳定性.关键词:高阶Ablowitz-Ladik方程/M,N-M)-波Darboux变换');"href=' ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一个可积的逆空时非局部Sasa-Satsuma方程
    摘要:本文给出了一个可积的逆空时(逆空间-逆时间)非局部Sasa-Satsuma方程.建立了这个方程的Darboux变换,并且构造了这个逆空时非局部方程在零背景条件下的孤子解.关键词:可积的逆空时非局部Sasa-Satsuma方程/达布变换/孤子解EnglishAbstractAnintegrabl ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 四阶色散非线性薛定谔方程的明暗孤立波和怪波的形成机制
    摘要:本文研究了四阶色散非线性薛定谔方程的明暗孤立波和怪波的形成机制,该模型既可以模拟高速光纤传输系统中超短脉冲的非线性传输和相互作用,又可以描述具有八极与偶极相互作用的一维海森堡铁磁链的非线性自旋激发现象.本文首先通过对四阶色散非线性薛定谔方程的相平面分析,发现由其约化得到的二维平面自治系统具有同 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 可积谐振系统中的极端波事件研究进展
    摘要:从微观角度上讲,单个极端异常波事件可视为可积模型方程的时空局域有理函数解.本文主要讨论了三类典型的可积谐振相互作用模型(即长波短波谐振方程,三波谐振相互作用方程,非线性薛定谔和麦克斯韦-布洛赫方程)的基阶Peregrine异常波解及其相关研究进展;明确指出了这些基阶异常波解形式具有普适性,可推 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 可积系统多孤子解的全反演对称表达式
    摘要:多孤子解是非线性数学物理系统的基本激发模式.文献中存在各种类型的表达式,如广田(Hirota)形式,朗斯基(Wronskian)或双朗斯基形式和法夫(Phaffian)形式.最近在多地系统的研究中,我们发现使用一种全新但等价的形式具有极为简洁和方便的优点.本文主要综述多种类型可积非线性系统的多 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 准Λ型四能级系统选择反射光谱
    摘要:运用密度矩阵理论研究了气固界面准$\Lambda$型四能级原子系统的非线性选择反射光谱.基于刘维尔方程给出了一阶近似条件下探测光场的解析式.在探测场为弱场时,分析了信号场拉比频率、失谐量和耦合场失谐量对反射光谱线型的影响.数值模拟表明:信号场参与产生的选择反射峰线宽可以利用信号场拉比频率进行调 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 隔板对流系统的热流特性及热量输入与传递特性
    摘要:采用DNS方法对隔板对流装置进行模拟计算,研究系统中热流特性以及热量输入与传递特性.讨论了热流的纵向和横向输运特性,在此基础上对传热通道和狭缝区域的热通量以及对应底板外界输入热通量进行了定量化分析.研究结果表明,通道中低温流体向下冲击底板而后转入水平运动,流入狭缝区域并不断被加热,只进行水平的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于1.06 μm波长的空间合作目标及碎片高精度激光测距试验
    摘要:常规卫星激光测距大多数采用532nm波长激光,但受激光能量和大气透过率低等瓶颈制约,在微弱目标探测如碎片激光测距、月球激光测距中使用难度较大.本文介绍了基于1.06μm波长的激光测距技术,分析了1.06μm测距技术在激光能量、大气传输、背景噪声、单光子探测等方面相对于532nm激光测距的优势, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于空间角度复用和双随机相位的多图像光学加密方法
    摘要:提出了基于空间角度复用和双随机相位的多图像光学加密新方法.加密过程中,首先将原始图像进行随机相位调制和不同距离的菲涅耳衍射;其次,将携带调制后图像的参考光与携带随机相位且具有不同立体角的参考光相干叠加,产生干涉条纹;最后,将不同方向的干涉条纹叠加形成复合加密图像.解密为加密的逆过程,将复合加密 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Shimizu-Morioka系统与Finance系统生成Lorenz混沌的微分几何策略
    摘要:从一种受控混沌系统生成另一混沌系统可增强保密通信的安全性,具备潜在应用前景.研究了如何通过状态变换以及单输入反馈,驱使受控Shimizu-Morioka系统与受控Finance系统生成Lorenz混沌动态.主要方法是运用微分几何理论,将上述三种系统等价转换为下三角形式,并尽量简化和一致化其方程 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.