摘要:在线社交网络逐渐成为人们不可或缺的重要工具, 识别网络中具有高影响力的节点作为初始传播源, 在社会感知与谣言控制等方面具有重要意义. 本文基于独立级联模型, 给出了一个描述有限步传播范围期望的指标—传播度, 并设计了一种高效的递推算法. 该指标在局部拓扑结构信息的基础上融合了传播概率对影响力进行刻画, 能够较好地反映单个节点的传播影响力. 对于多传播源影响力极大化问题, 本文提出了一种基于传播度的启发式算法—传播度折扣算法, 使得多个传播源的联合影响力最大. 最后, 将上述方法应用到三个真实网络中, 与经典指标和方法相比, 该方法不需要知道网络的全局结构信息, 而是充分了利用网络的局部结构信息, 可以较快地筛选出高传播影响力的传播源.
关键词: 社交网络/
影响力度量/
影响力极大化/
信息传播

English Abstract

全文HTML

--> --> -->

随着网络科学的快速发展, 节点的传播影响力越来越受到人们的关注. 在信息的传播过程中, 具有高传播影响力的节点可以加速信息的传播, 这对于宣传产品, 推送广告等方面具有重要的作用. 因此, 该领域的一个核心问题就是如何选择网络中的若干节点作为传播源, 使其传播影响力极大化, 又具体可分为单个传播源影响力排序问题和多个传播源影响力极大化问题(需要考虑不同传播源之间影响力的重叠).
对于网络中节点影响力排序问题, 最简单高效的方法是度中心性^[1], 它反映节点的邻居数, 例如微博中拥有粉丝数多的大V用户就具有很高的传播影响力. 后来, Chen等^[2]又给出了一个局部中心性指标, 该指标考虑了二阶邻居数, 但这两个指标在反映节点传播影响力时没有考虑传播概率的影响, 也无法充分反映节点的局部拓扑结构. 对于全局性的指标有介数中心性^[3]、接近度中心性^[4]、K核^[5]、特征向量中心性^[6]等. 而对于多源影响力极大化(influence maximization)问题, 最初由Domingos和Richardson^[7]提出, 后被Kempe等^[8]证明该问题是NP-Hard难问题. 一种最简单的选取策略就是选出某指标值最大的若干节点作为传播源, 但这种算法选出的各传播者之间可能会有较大影响力重叠. 因此, Leskovec等^[9]采用贪心算法来寻求初始传播集, 但这种算法的复杂度较大不适用于大型网络. Chen等^[10]提出两种改进的贪心算法新贪心算法和最大贪心算法, 这两种改进算法均比贪心算法的算法复杂度要低, 但在大型网络中仍具有较高算法复杂度. 后来, 一些特殊的启发式算法被提出, 度折扣算法^[11]就是其中一种高效的启发式算法, 它是对探索式算法的一种优化策略的改进, 具有较高的实用价值, 其基本思想为当节点的邻居节点已被选为传播源时, 会对该节点的度指标产生折扣效应, 从而达到了去重叠的目的. 再后来, Kimura等^[12]利用分解极大连通子图来寻找最优传播源, 基于此, 又提出了利用最大影响路径的方法^[13], 这种方法虽然大大降低了了算法复杂度, 但限制了只能在最短路径上传播. Wang等^[14]提出了一种结合动态规划的算法选择最优传播源, 提升了算法效率, Li等^[15]考虑积极消极影响力, 提出了一种新的模型, 尽管这些算法效率都很高, 但很容易陷入局部最优的情况, 效果不及贪心算法.
在线社交网络具有规模庞大, 结构复杂的特点, 运用节点的局部信息指标描述节点的传播影响力更具现实意义. 但目前的局部性指标均不能够很好的刻画节点的局部拓扑结构, 因此本文基于独立级联模型, 提出一种描述节点有限步传播范围期望的指标—传播度. 对于网络中的任一节点作为传播源, 我们充分分析信息在局部网络中的传播路径, 设计了一种精确的递推算法计算有限步后传播范围的期望值, 之后通过真实网络数据集仿真验证了该指标与节点传播影响力具有更高一致性. 另一方面, 在考虑多传播源影响力极大化问题时, 选择的各传播源影响力会发生重叠, 因此基于传播度提出了一种启发式算法—传播度折扣算法, 同样通过真实网络数据集仿真验证了该算法相较于经典方法具有更好的效果.
本文的主要贡献在以下几个方面:
1)提出了描述网络节点传播能力的指标—传播度, 用于描述节点在有限步后能够传播到网络节点范围的期望值. 并设计了计算该指标的迭代算法, 可以高效的计算节点的任意阶(步数)的传播度.
2)相较于传统指标, 传播度指标考虑了传播概率对节点传播的影响. 对于小型网络, 可以直接利用该算法计算节点的最终传播期望; 对于大型网络, 可利用低阶传播度刻画节点的传播影响力, 充分利用了节点的局部拓扑结构信息.
3)对于多传播源问题, 基于传播度指标提出了一种传播度折扣的算法, 能有有效地去除不同初始传播源间的影响力重叠, 相较于原有的度折扣算法有更好的选择效果.

独立级联模型(IC模型)是网络信息传播的一种最常用的模型, 当一个节点v被激活时, 它会以概率将其邻居节点u激活, 这种尝试仅进行一次, 在此之后, 节点v仍处于激活状态, 但不具有传播信息的能力. 根据该传播模型, 定义s阶传播度表示传播s步后所有节点被激活的概率之和. 由于网络结构十分复杂, 为了保证概率的计算不重不漏, 先提出两个辅助算法, 最终给出一个高效的递推算法.
2

-->

2.1.辅助算法一

为了更清楚地反映初始传播源的传播情况, 将节点的局部拓扑结构转化成树的形式, 并定义为该传播源的传播树, 该算法称为传播树算法. 根据信息在网络中的传播路线, 传播树是基于特定的单个种子节点的网络的另一种拓扑表示(简单的例子见图1). 图1(b)为图1(a)的传播树, 传播树的生成规则如下:
图 1 一个简单网络例子　(a)网络图; (b)图(a)对应的传播树
Figure1. A simple network example: (a) The network diagram; (b) the corresponding propagation tree of (a).

Step 1　确定一个种子节点作为${P_0}$代节点;
Step 2　将种子节点的邻居作为种子节点的孩子, 记为${P_1}$代节点, 令k = 1;
Step 3　对于${P_k}$代个体的任一个节点i, 将节点i的邻居且非节点i的祖先的节点作为节点i的孩子. 则将所有${P_k}$代个体的孩子记为${P_{k + 1}}$代个体;
Step 4　若${P_{k + 1}}$代个体数量大于0, 则令k = k +1, 返回Step 3; 否则, ${P_0}$到${P_k}$个体对应的树即为网络的传播树.
2 -->

2.2.传播度的计算公式及辅助算法二

3 -->

2.2.1.传播度的计算公式

在2.1节传播树概念的基础上, 先引入几个参量, 用${p_t}\left( u \right)$表示节点u在t时间内(包含t时刻)被感染的概率; ${f_t}\left( {{u_i}} \right)$表示${P_t}$代的第i个u节点在t时刻被感染的独立概率; ${f_t}(u_{i_1}, \cdots , i_n)$表示${P_t}$代的第${i_1}, \cdots , {i_n}$个u节点在t时刻被感染的联合概率; ${f_t}\left( u \right)$表示${P_t}$代的所有的u节点在t时刻被感染的联合概率. 那么独立概率计算公式为

${f_t}\left( {{u_{\left\{ i \right\}}}} \right) = {f_{t - 1}}\left( {{v_{\left\{ {\bar i} \right\}}}} \right) \times \beta \times \left( {1 - {p_{t - 1}}\left( u \right)} \right),$

其中${v_{\left\{ {\bar i} \right\}}}$节点为${u_{\left\{ { i} \right\}}}$节点的双亲节点, 且有

${p_s}\left( u \right) = \mathop \sum \nolimits_{t = 0}^s {f_t}\left( u \right),$

那么种子节点seed的s阶传播度的计算公式为

${d_s}\left( {{\rm{seed}}} \right) = \mathop \sum \nolimits_u {p_s}\left( u \right).$

3 -->

2.2.2.辅助算法二

由2.2.1节的介绍, 关键问题在于如何计算联合概率${f_t}\left( u \right)$, 因此提出了辅助算法二—联合概率算法. 在介绍算法前, 首先分析概率的传播公式, 假设u节点在t时刻(传播树的${{{P}}_t}$代个体中)出现N次, 此时节点u的双亲节点也有N个, 不失一般性, 记其双亲节点为${v_1}, {v_2}, \cdots {v_n}$, 其出现次数分别为${m_1}, {m_2}, \cdots {m_n}$次, 因此共有${m_1} + {m_2} + \cdots + $${m_n} = N $条传播路径在t时刻可能传播到节点u, 那么对于任意的$j \in \left\{ {1, 2, \cdots n} \right\}$, 节点u的双亲节点${v_j}$有$m_j$条路径通向u. 在${{{P}}_{t - 1}}$代个体中, 这${m_j}$条路径经过的节点${v_j}$在所有${v_j}$中的序号保存在集合${{{X}}_j}$中; 在${{{P}}_t}$代个体中, 这${m_j}$条路径经过的节点u在所有u中的序号保存在集合${{{Y}}_j}$中. 在计算${f_t}\left( u \right)$时, 首先考虑相同双亲节点间的联合概率,

${f_t}({u_{{Y_j}}}) = {f_{t - 1}}({v_{{j_{{X_j}}}}}) \times \beta ,$

进一步计算不同双亲间的联合概率,

${f_t}\left( u \right) = \!\bigg[ \!{1 - \mathop \prod \limits_{j = 1}^n \left( {1 \!-\! {f_t}\left( {{u_{{Y_j}}}} \right)} \right)} \!\bigg] \!\times \!\left( {1 \!- \!{p_{t - 1}}\left( u \right)} \right),$

其中集合${X_j}$只有一个元素时, 即为公式(1)所得的独立概率, 当${X_j}$含有多个元素时, 仍用该方法计算联合概率. 进一步,

${p_t}\left( u \right) = {p_{t - 1}}\left( u \right) + {f_t}\left( u \right).$

事实上, 该算法在编程时是一个计算联合概率${f_t}\left( {{u_w}} \right)$可调用函数, 当t – 1时间内传播树中各点的独立概率已递推求得, 用$F\left( {t, u, W} \right)$表示调用函数, 其算法的伪代码如表1所列.

辅助算法二	联合概率算法
输入	时间t, 节点u以及对于u的序号集W
输出	联合概率${{{f}}_{{t}}}\left( {{{{u}}_{{W}}}} \right)$
1.	if W只含一个元素 then
2.	找到该节点的双亲节点${{{v}}_{\left( {{i}} \right)}}$
3.	${{{f}}_{{t}}}\left( {{{{u}}_{{W}}}} \right) = {{{f}}_{{{t}} - {{1}}}}\left( {{{{v}}_{\left( {{i}} \right)}}} \right) \times {{\beta }} \times \left( {{{1}} - {{{p}}_{{{t}} - {{1}}}}\left( {{u}} \right)} \right)$
4.	else
5.	找到传播树种${{{P}}_{{t}}}$代序号集为W的u节点, 记其双亲节点为${{{v}}_{{1}}}, {{{v}}_{{2}}}, \cdots , {{{v}}_{{l}}}$, 出现次数为$ m_1, $$ m_2, \cdots , m_l$, 这些路径对于双亲节点的序号集分别为${{{X}}_{{1}}}, {{{X}}_{{2}}}, \cdots , {{{X}}_{{l}}}$, 对于节点u的序号集分别为${{{Y}}_{{1}}}, {{{Y}}_{{2}}}, \cdots {{{Y}}_{{l}}}$.
6.	for ${{j}} = 0 \to {{l}}$ do
7.	${{{f}}_{{t}}}\left( {{{{u}}_{{{{Y}}_{{j}}}}}} \right) = {{F}}\left( {{{t}} - {{1}}, {{{v}}_{{j}}}, {{{X}}_{{j}}}} \right) \times {{\beta }}$
8.	end for
9.	${{{f}}_{{t}}}\left( {{{{u}}_{{W}}}} \right) = \left[ {{{1}} - \mathop \prod \nolimits_{{{j}} = {{1}}}^{{l}} \left( {{{1}} - {{{f}}_{{t}}}\left( {{{{u}}_{{{{Y}}_{{j}}}}}} \right)} \right)} \right] \times \left( {{{1}} - {{{p}}_{{{t}} - {{1}}}}\left( {{u}} \right)} \right)$
10.	end if
11.	return ${{{f}}_{{t}}}\left( {{{{u}}_{{W}}}} \right)$

表1联合概率算法
Table1.Joint probability algorithm

2 -->

2.3.传播度递推求解

由方程(6)可知, 在计算${p_t}\left( u \right)$时, 需要知道${f_t}\left( u \right)$和${p_{t - 1}}\left( u \right)$. 而计算${f_t}\left( u \right)$时, 根据2.2节中的分析, 最终转化为计算t–1时间内(包含t–1时刻)传播树中各点的独立概率的计算式. 因此, 可以用递推算法最终求得传播度. 求解s阶传播度的算法流程伪代码如表2所列. 有了表2所列的递推算法, 便可以编程高效的计算节点的任意阶的传播度.

递推算法	求种子节点s阶传播度
输入	seed, ${{\beta }}$, s
输出	${{{d}}_{{s}}}$
1.	${\rm Tree }_{s} = {\rm FTree }(\rm seed)$ %获取节点${{seed}}$的s阶传播树
2.	赋初值${ { {p} }_{ {0} } }\left( { { {\rm seed} } } \right) = { { {f} }_{ {0} } }\left( { { {\rm seed} } } \right) = { {1} }$, 其他情况${{{p}}_{{t}}}\left( {{u}} \right) = {{{f}}_{{t}}}\left( {{u}} \right) = {{0}}$
3.	for ${{t}} = {{1}} \to {{s}}$ do
4.	for ${{{u}}_{{y}}} \in {{{P}}_{{t}}}$ do %遍历传播树中${{{P}}_{{t}}}$代的个体
5.	获得${{{u}}_{{y}}}$的双亲节点${{{v}}_{{x}}}$ %表示节点u所在传播树层中第x个u节点
6.	${{{f}}_{{t}}}\left( {{{{u}}_{{y}}}} \right) = {{{f}}_{{{t}} - {{1}}}}\left( {{{{v}}_{{x}}}} \right) \times {{\beta }} \times \left( {{{1}} - {{{p}}_{{{t}} - {{1}}}}\left( {{u}} \right)} \right)$
7.	end for
8.	for ${{u}} \in {{{P}}_{{t}}}$ do
9.	获得u的序号集W %指${{{P}}_{{t}}}$代节点u出现次序构成的集合
10.	计算联合概率${{{f}}_{{t}}}\left( {{u}} \right) = {{F}}\left( {{{t}}, {{u}}, {{W}}} \right)$
11.	end for
12.	for $u \in {\rm Tree}_{s}$ do
13.	${{{p}}_{{t}}}\left( {{u}} \right) = {{{p}}_{{{t}} - 1}}\left( {{u}} \right) + {{{f}}_{{t}}}\left( {{u}} \right)$
14.	end for
15.	end for
16.	${ { {d} }_{ {s} } }\left( { { \rm{seed} } } \right) = \mathop \sum \nolimits_{ {u} } { { {p} }_{ {s} } }\left( { {u} } \right)$
17.	return ${{{d}}_{{s}}}$

表2种子节点s阶传播度的算法流程伪代码
Table2.Pseudocode of the algorithm flow for s order progpagation of the seed node.

2 -->

2.4.仿真验证

综上所述, 对于一个网络, 确定初始种子节点, 先用传播树算法得到相应的传播树, 在利用递推算得到任何时刻任意节点的期望值${p_t}\left( i \right)$, 进而得到任意时刻的传播度值. 为了进一步验证算法的精确性, 我们基于独立级联模型对图1所示网络进行传播仿真. 选择不同的仿真次数, 比较情况见图2.
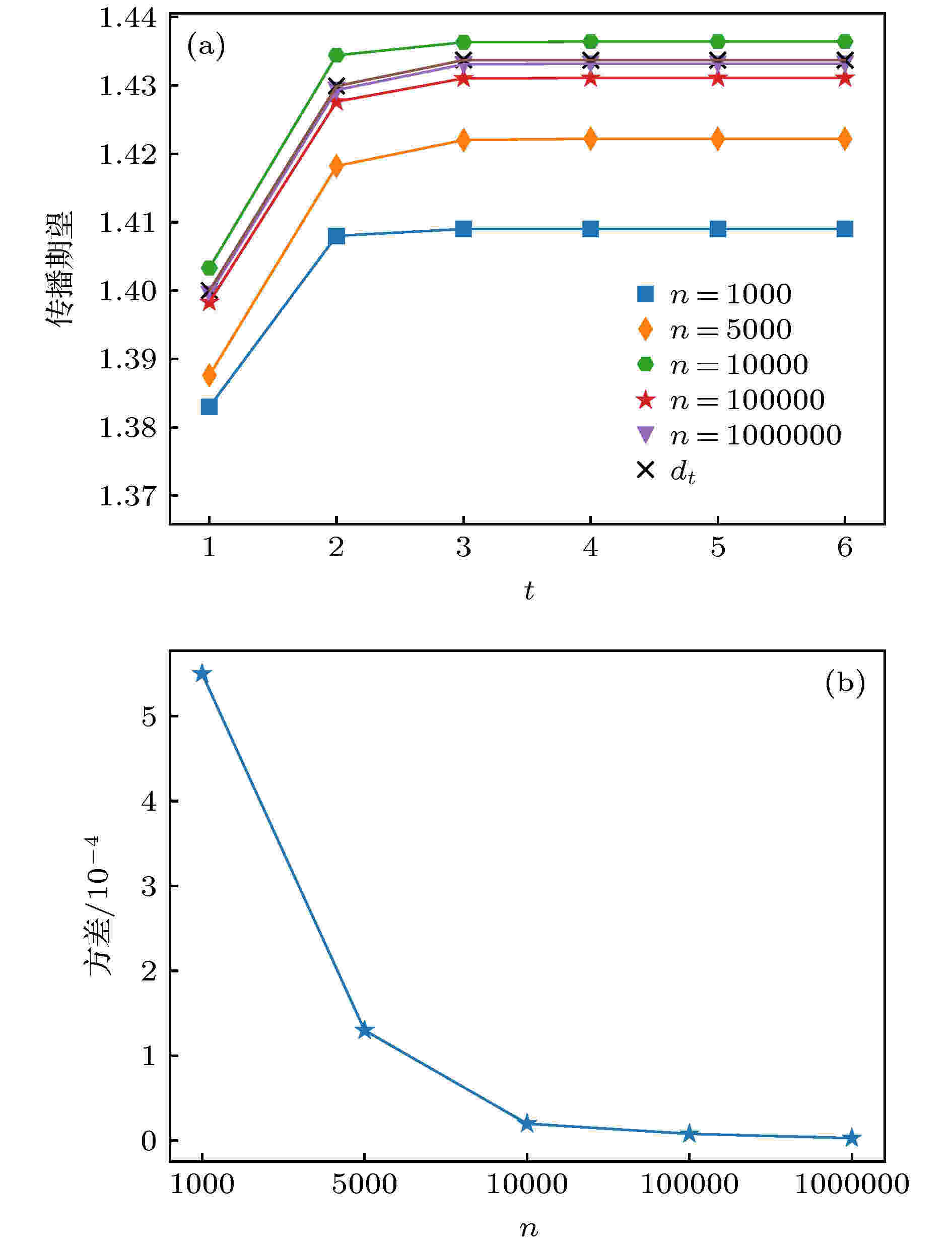图 2 (a)不同仿真次数下的近似传播期望值和传播度随时间的变化; (b)不同仿真次数的近似传播期望值与传播度的方差变化
Figure2. (a) Approximate propagation expectation and the degree of propagation over time for different simulation times; (b) variance of the approximate propagation expectation and the degree of propagation of different simulation times.

由图2可知, 模型计算的期望值是精确的. 有了传播度的指标后, 便可以用该指标来反应节点的传播影响力.
对于小型网络, 可以直接计算最高阶的传播度来反应节点的传播影响力, 该方法有两方面优势. 一方面, 在现实中, 出于商业考虑, 可能不会选取明显较优的核心节点, 如图1小型网络中的1号节点, 因此, 进一步比较2, 3号, 甚至5, 6, 7, 8号节点的传播影响力优劣具有重要意义. 另一方面, 网络中节点的传播影响力是与传播概率相关的, 而传播度指标可以很好地将传播概率融入到刻画节点传播影响力中去.
如图1所示, 节点最多传递四步, 因此利用上述方法计算所有节点的四阶传播度来反映节点的传播影响力. 为了比较各节点传播影响力的大小以及验证节点的传播影响力与传播概率相关, 图3给出了不同传播概率下各节点四阶传播度的变化情况.
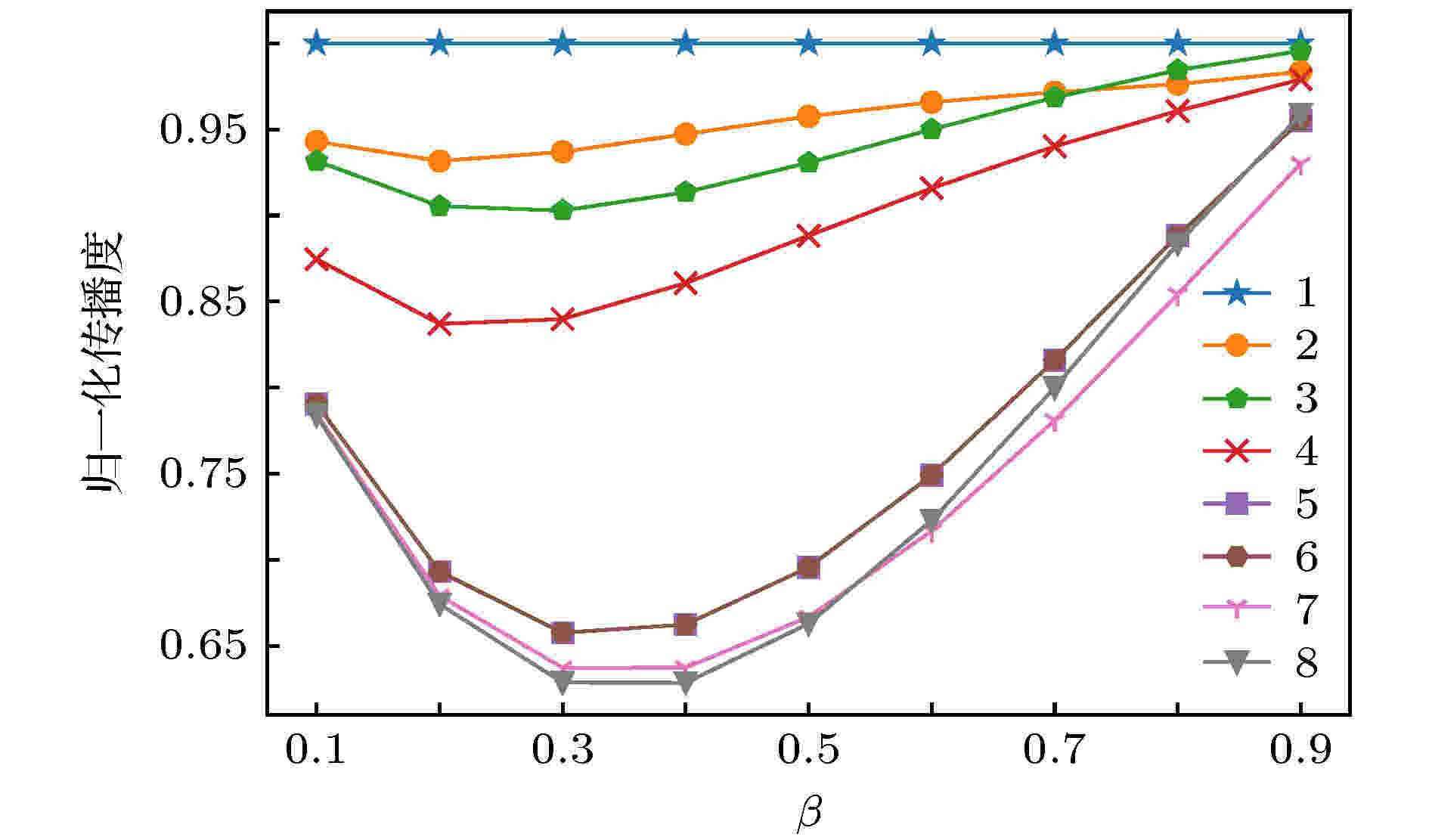图 3 图1中的网络各节点4阶传播度(归一化)随传播概率变化
Figure3. Changes of the 4th degree of propagation (normali-zed) of network node in Fig. 1 with the propagation pro-bability.

由图3可知, 随着传播概率不断增加, 各节点的传播影响力排序会发生明显变化, 且可以量化比较各节点传播影响力大小. 当传播概率较大时, 可以选择普通的节点作为传播源, 兼顾成本和传播能力两个方面. 后文将主要关注传播度在大型网络中识别高传播影响力传播源的作用展开详细讨论.

初始种子节点的传播影响力最大化问题分为单源和多源两种情况, 下面分别给出判别算法.
2

-->

3.1.单个节点的影响力排序

由传播度的定义知道, 一阶传播度为d₁ = $ 1 + \beta {d_{\rm seed}}$, 其中${d_{{\rm{seed}}}}$种子节点的度, 因此一阶传播度和节点度是等价的. 而二阶传播度事实上不仅反映了种子节点的一阶邻居和二阶邻居情况, 还反映了一阶邻居之间的连边拓扑关系, 例如, 种子节点的邻居节点很有可能实在第二步通过另一个邻居节点被传播的. 类似地, 考虑更高阶传播度时, 不仅反映了高阶邻居的情况, 还反映了较低阶邻居之间的拓扑关系.
2 -->

3.2.传播度折扣解决多源影响力极大化问题

关于多源传播影响力极大化问题, 一般采用启发式算法, 然而不同传播源的传播影响力会有较多“重叠”部分, 因此在算法进行的过程中需要采用去重叠过程. 由于定义的传播度是基于概率期望的, 基于这一特性, 去重叠过程是十分简便的, 下面进行理论分析.
考虑s阶传播度, 计算出所有节点的s阶传播度, 选择最大的一个节点加入种子节点集R的第一个节点, 其各节点的传播期望为${p_s}\left( i \right), i \in $$1, 2, \cdots , N\} $. 记ptotal为N阶向量, 表示考虑种子节点集R中所有节点的s阶传播度, 网络中所有节点未患病的概率. 不失一般性, 假设R中已有k个节点, 这些节点到网络中所有节点的传播期望值为$p_s^{\left( j \right)}\left( i \right), i \in \left\{ {1, 2, \cdots N} \right\}, j \in \left\{ {1, 2, \cdots , k} \right\}$, 表示R中的第j号种子节点到节点i的传播概率(仅考虑节点的s阶邻居内的节点). 则相应的ptotal值变为

${\rm{ptotal}}\left( i \right) = \mathop \prod \nolimits_{t = 1}^k \left( {1 - p_s^{\left( t \right)}\left( i \right)} \right),$

下面需要选择第k+1个节点, 任选一个节点v, 需要考虑节点v与已选种子节点集R的重叠情况, 进而求得节点v的有效贡献值. 一方面, 节点v是有效的, 说明已选节点没有传播到节点v, ptotal向量记录了已选节点未传播到其他节点的概率, 因此可以得到节点集R未传播到节点v的概率, 记为ptotal(v). 另一方面, 由于节点v可能传播到的节点可能已被传播, 因此需要引入折扣因子, 若节点v到节点u的传播期望值为${p_s}\left( u \right)$, 则引入折扣因子后变为${p_s}\left( u \right) \times {\rm{ptotal}}\left( u \right)$, 因此在选择第k+1个节点前, 先计算节点v的传播折扣度为

${\tilde d_s} = {\rm{ptotal}}\left( v \right) \times \mathop \sum \nolimits_{u \epsilon G.neis\left( v \right)} \left( {{p_s}\left( u \right) \times {\rm{ptotal}}\left( u \right)} \right),$

其中$G.neis\left( v \right)$表示节点v的s阶邻居内的节点(不包括v节点本身). 将候选者按传播折扣度排序, 选出最优者加入种子节点集合. 多次执行上述操作, 即可得到近似最优的传播影响力节点集.
2 -->

3.3.模型总述

综上所述, 算法的总流程图如图4所示. 从新定义的传播度指标出发, 充分考虑节点所有可能就近的传播路径和传播概率的大小, 分别对单源节点影响力排序问题和多源影响力极大化问题给出了解决方案. 对于小型网络, 我们在2.4节中指出, 可以计算最高阶的传播度从而可以精确的找出最优传播源. 对于大型网络, 将在第4节详细验证该模型的优势.
图 4 基于传播度的节点影响力极大化算法流程图
Figure4. Flow chart of node influence maximization algorithm based on propagation degree.

由渗流理论可知, 当传播概率较大且高于渗流阈值时, 单个节点就具有传播到全局的能力, 此时可以用全局传播概率(参见文献[16])反映节点的传播能力. 因此, 在检验算法效果时, 应分两种情况考虑: 一种是传播概率较小且低于渗流阈值, 此时用平均传播范围表示节点传播能力; 当传播概率较大时, 用全局传播概率来反映.
2

-->

4.1.数据集

为了评价模型, 采用如下3个不同领域的真实网络数据集(无向)进行仿真实验.
1) Deezer^[17]: 数据来源于音乐流服务网站Deezer提供的数据, 表示罗马尼亚用户朋友网络. 数据下载于: http://snap.stanford.edu/data/(简称SLNDC), 共有41773个节点, 平均度为6.024.
2 Email-Enron^[18]: 数据来源于安然电子邮件网络, 下载于SLNDC, 共有36692个节点, 平均度为10.020.
3) Facebook^[17]: 数据来源Facebook朋友网络, 下载于SLNDC, 共有13866个节点, 平均度为12.528.
2 -->

4.2.单源影响力排序效果

采用节点的仿真影响力值和传播度值的kendall’s tau系数^[19]来反映单源影响力的排序效果. 该指数反映了两个序参量的一致性, 大小介于–1和1之间, 当该系数越大时, 两个序参量越趋于一致. 该算法排序效果见图5和图6.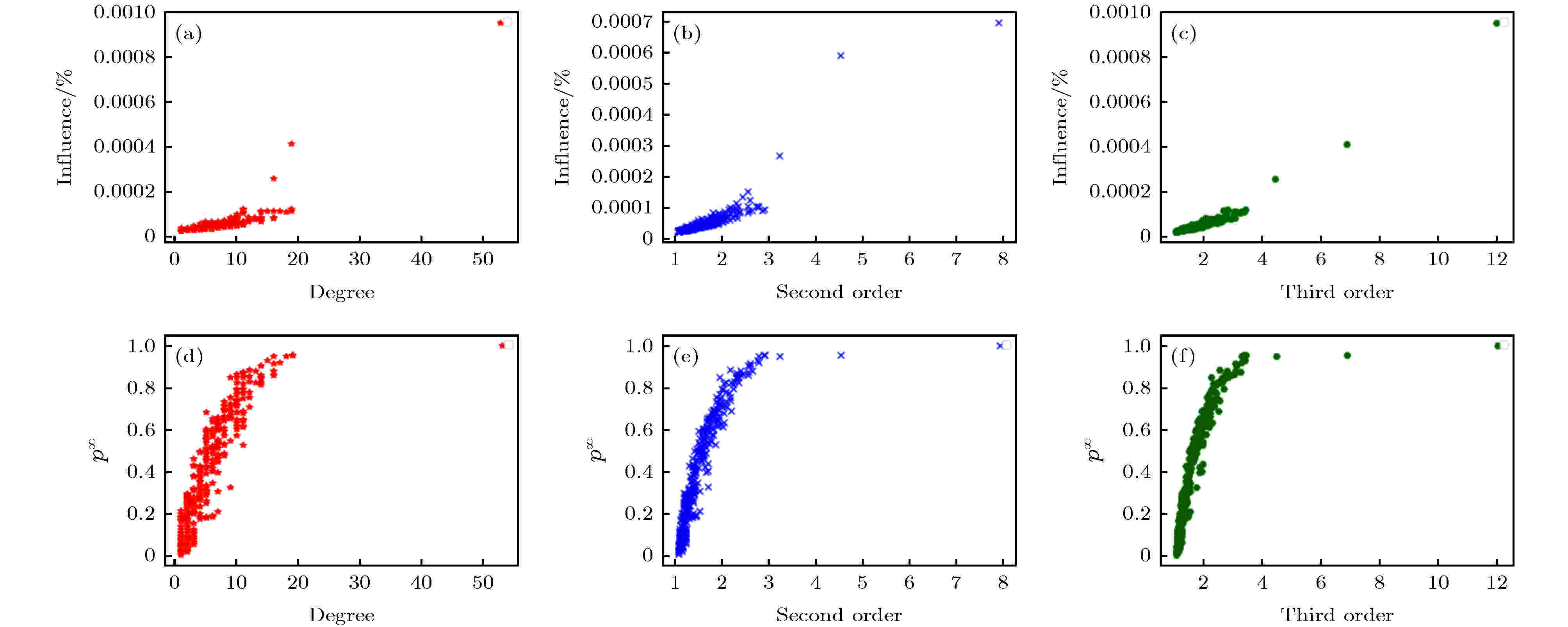
图 5 (a)?(c) 分别反映了Deezer网络随机挑选若干节点的传播能力与度, 二阶传播度, 三阶传播度的关系, 其中β = 0.06; (d)?(f) 分别反映了Deezer网络随机挑选若干节点全局传播概率(参见文献[12])与度, 二阶传播度, 三阶传播度的对应情况, 其中β = 0.12(这里通过仿真实验不难发现该网络的渗流阈值介于0.06和0.12之间)
Figure5. (a)?(c): Respectively reflects the relationship between the propagation capacity and degree, second-order propagation, and third-order propagation of several nodes randomly selected by the Deezer network, where β = 0.06; (d)?(f): Respectively reflects the global propagation probability of randomly selected nodes by the Deezer network (see reference[12]) Correspondence with degrees, second-order propagation, and third-order propagation, where β = 0.12 (here, it is not difficult to find through the simulation experiments that the percolation threshold of the network is between 0.06 and 0.12)

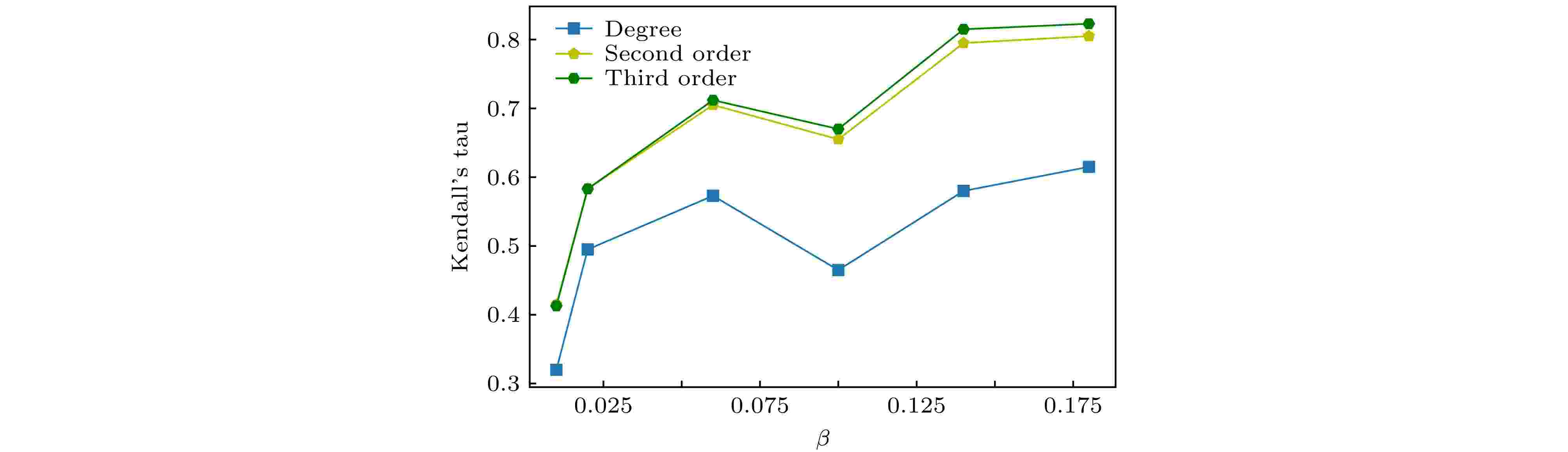图 6 不同传播概率下度, 二阶、三阶传播度与仿真传播能力的kendall’s tau系数
Figure6. Kendall’s tau coefficient for different propagation probabilities, second-order, third-order propagation and simulation propagation ability.

由图5和图6可知, 传播度相较于度, 高阶传播度相较于低阶传播度与节点的传播能力之间具有更高的一致性, 特别是在传播概率偏大时, 这种效果是明显的, 这种现象同样适用其他的真实网络.
目前最常用的节点重要度排序指标有k核^[20](coreness), 特征向量中心性^[6](eigenvenctor), 考虑节点最近邻居核次近邻居的多级邻居信息指标^[2](local centrality), 而介数中心性和接近度中心性由于其算法复杂度较高, 不适用于大型网络. 不同方法下的比较情况见图7和图8.
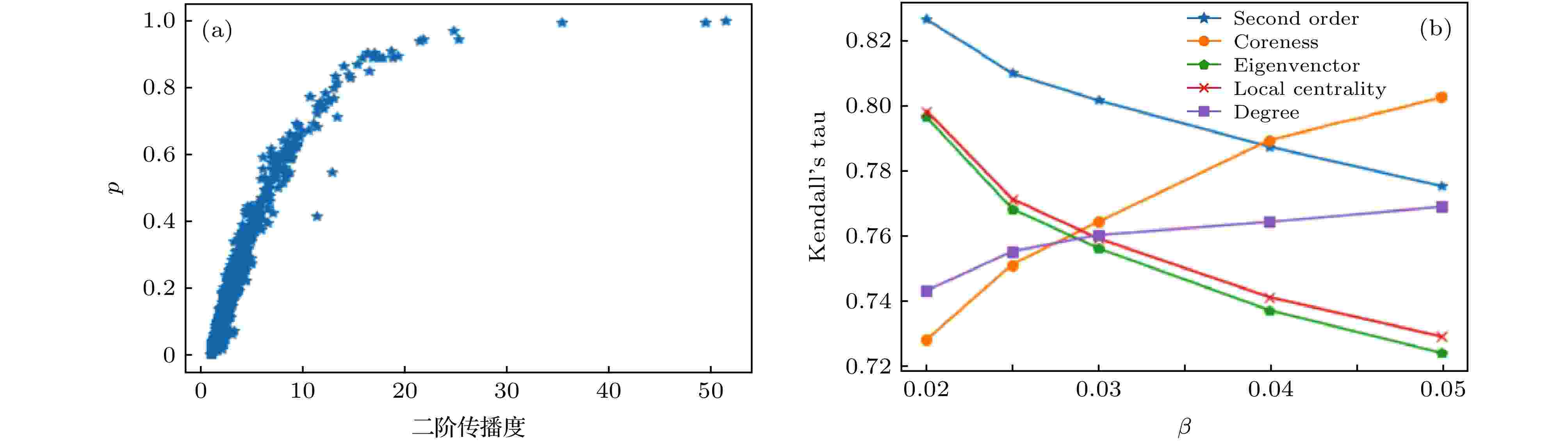图 7 (a)在Email-Enron网络中, 传播概率为0.02的情况下二阶传播度和全局传播概率p的关系; (b)各指标在不同概率下与传播能力的kendall’s tau系数
Figure7. (a) The relationship between the second-order propagation degree and the global propagation probability p in the case of the Email-Enron network with a propagation probability of 0.02; (b) the kendall's tau coefficient of each indicator with different propagation rates and propagation capabilities.

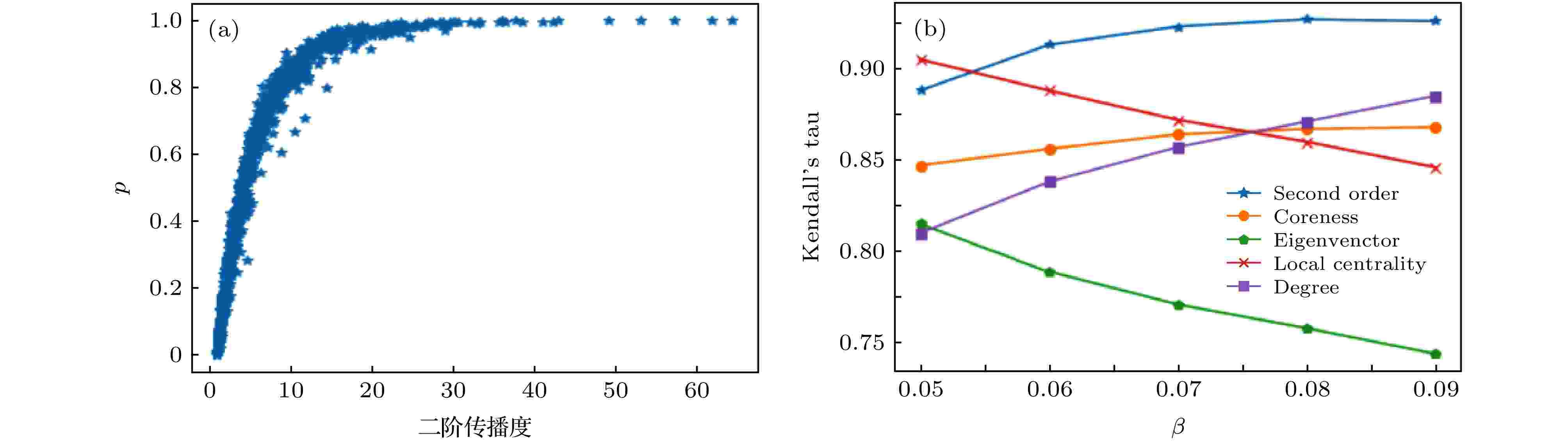图 8 (a)在Facebook网络中, 传播概率为0.09的情况下二阶传播度和全局传播概率p的关系; (b)各指标在不同概率下与传播能力的kendall’s tau系数
Figure8. (a) The relationship between the second-order propagation degree and the global propagation probability p in the case of a Facebook network with a propagation probability of 0.09; (b) the kendall's tau coefficient of each indicator with different propagation rates and propagation capabilities.

由图7和图8可以看出, 对于大型网络, 二阶传播度相较于其他指标在不同的传播概率和网络下具有更好的效果和更高的稳定性. 因此, 我们给出的传播度能更好地利用节点的局部拓扑结构来描述单源影响力排序.
2 -->

4.3.多源影响力极大化效果

通过实验发现, 分解极大连通子图等方法虽然算法复杂度低, 但由于做了过多近似, 效果不如算法复杂度较高的贪心算法, 因此这些方法不是本文研究的重点, 而是致力于贪心算法的一种改进算法. 为了验证传播度折扣算法的效果, 将该算法与最大度^[1] (degree), 核^[20] (coreness), 特征向量^[6] (eigenvenctor), 介数^[3] (betweeness), 折扣度算法^[11] (degreediscount)进行仿真比较. 同样, 也分两种情况来比较: 一种取传播概率较小且低于渗流阈值, 另一种取传播概率较大且高于渗流阈值. 算法效果见图9和图10所示.
图 9 在Deezer网络中(a)不同算法下传播范围随所选种子节点数量的变化和(b)不同算法下全局传播概率随种子节点数量的变化, 其中候选节点为度为6, 7, 8的9792个节点
Figure9. In the Deezer network, (a) the variation of the propagation range with the number of selected seed nodes under different algorithms; (b) the variation of the global propagation probability with the number of seed nodes under different algorithms. The candidate nodes are 9792 nodes with a degree of 6, 7 and 8.

图 10 (a), (b)和(c), (d)分别比较了Email-Enron, Facebook网络在不同算法下所选种子节点的传播性能
Figure10. (a), (b), and (c), (d), respectively, compare the propagation performance of Email-Enron, the selected seed node of the Facebook network under different algorithms.

由图9和图10可以看出, 传播度折扣算法能够较好的解决多源影响力极大化问题, 因此在利用局部信息去除影响力重叠时, 传播度折扣算法具有不错的效果.

在充分考虑节点局部拓扑结构信息的基础上, 提出了有限步传播范围期望的指标—传播度, 并设计了高效精确的递推计算方法. 在此基础上, 将该指标用于单源影响力排序问题, 实验证明, 该指标与节点的传播能力具有更高的一致性. 另外, 对于多源影响力极大化问题, 本文基于传播度的概念, 设计了一种启发式算法—传播度折扣算法, 相较于经典的算法, 具有更好的筛选效果.
给出了一种精确计算有限步传播范围期望的递推算法, 事实上, 当传播到达一定步数后, 即当传播步数较大时, 节点被传播的概率往往很小, 因此, 如何设置局部的递推终止条件, 引入较小的误差, 可以进一步优化算法, 计算更高阶的传播度, 这一问题有待进一步研究.