<script type="text/javascript" src="https://cdn.bootcss.com/mathjax/2.7.2-beta.0/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script>
<script type='text/x-mathjax-config'>MathJax.Hub.Config({tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]},"HTML-CSS": {linebreaks: { automatic: true},scale: 100}});</script>
摘要: 光束在自由空间中传播时容易受到大气湍流的影响, 其对传输光束的影响相当于附加一个随机噪声相位, 导致传输光束质量下降. 本文提出了一种基于深度卷积神经网络(convolutional neural network, CNN)的湍流相位信息提取方法, 该方法采用受湍流影响的光强图为特征提取对象, 经过对海量样本进行自主学习后, CNN的损失函数值收敛到0.02左右, 其在测试集上的平均损失函数值低于0.03. 训练好的CNN模型具有很好的泛化能力, 可以直接根据输入的光强图准确提取出湍流相位. 利用I5-8500 CPU, 预测
$C_{\rm{n}}^2 = 1 \times $ ${10^{ - 14}}\;{{\rm{m}}^{ - 2/3}} $ ,
$C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}}^{ - 2/3}}$ 和
$C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}}^{ - 2/3}}$ 三种湍流强度的湍流相位所需要的平均时间低至
$5 \times {10^{ - 3}}\;{\rm{s}}$ . 此外, CNN的湍流相位提取能力可以通过提高计算能力或者优化模型结构来进一步提升. 这些结果表明, 基于CNN的湍流相位提取方法能够有效的提取湍流相位, 在湍流补偿、大气湍流特性研究和图像重构等方面具有重要的应用价值.
关键词: 大气湍流 /
相位提取 /
深度卷积神经网络 /
Gerchberg-Saxton算法 English Abstract Extracting atmospheric turbulence phase using deep convolutional neural network Xu Qi-Wei 1,2,# ,Wang Pei-Pei 1,2,# ,Zeng Zhen-Jia 2 ,Huang Ze-Bin 2 ,Zhou Xin-Xing 3 ,Liu Jun-Min 1 ,Li Ying 2 ,Chen Shu-Qing 2 ,Fan Dian-Yuan 2 1.College of New Materials and New Energies, Shenzhen Technology University, Shenzhen 518118, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61805149, 61575127, 61490713, 61571188), the Natural Science Foundation of Guangdong Province, China (Grant No. 2016A030310065), the Educational Commission of Guangdong Province, China (Grant No. 2016KCXTD006), the Program of Fundamental Research of Shenzhen Science and Technology Planning, China (Grant No. JCYJ20180507182035270), Science and Technology Planning Project of Shenzhen, China (Grant No. ZDSYS201707271014468), and International Collaborative Laboratory of 2D Materials for Optoelectronics Science and Technology, China (Grant No. 2DMOST2018003)Received Date: 28 June 2019Accepted Date: 15 October 2019Published Online: 05 January 2020Abstract: When a light beam transmits in free space, it is easily affected by atmospheric turbulence. The effect on transmitted light is equivalent to adding a random noise phase to it, which leads its transmission quality to deteriorate. The method of improving the quality of transmitted beams is usually to compensate for the phase distortion at the receiver by adding reverse turbulence phase, and the premise of this method is to obtain the turbulence phase carried by the distorted beam. The adaptive optics system is the most common way to extract the phase information. However, it is inefficient to be applied to varying turbulence environments due to the fact that a wave-front sensor and complex optical system are usually contained. Deep convolutional neural network (CNN) that can directly capture feature information from images is widely used in computer vision, language processing, optical information processing, etc. Therefore, in this paper proposed is a turbulence phase information extraction scheme based on the CNN, which can quickly and accurately extract the turbulence phase from the intensity patterns affected by atmosphere turbulence. The CNN model in this paper consists of 17 layers, including convolutional layers, pooling layers and deconvolutional layers. The convolutional layers and pooling layers are used to extract the turbulent phase from the feature image, which is the core structure of the network. The function of the deconvolutional layers is to visualize the extracted turbulence information and output the final predicted turbulence phase. After learning a huge number of samples, the loss function value of CNN converges to about 0.02, and the average loss function value on the test set is lower than 0.03. The trained CNN model has a good generalization capability and can directly extract the turbulent phase according to the input light intensity pattern. Using an I5-8500 CPU, the average time to predict the turbulent phase is as low as s under the condition of $C_{{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}}^{ - 2/3}}$ , $ 5 \times {10^{ - 14}}\;{{\rm{m}}^{ - 2/3}}$ , and $1 \times {10^{ - 13}}\;{{\rm{m}}^{ - 2/3}}$ . In addition, the turbulence phase extraction capability of CNN can be further enhanced by improving computing power or optimizing model structure. These results indicate that the CNN-based turbulence phase extraction method can effectively extract the turbulence phase, which has important application value in turbulence compensation, atmospheric turbulence characteristics research and image reconstruction.Keywords: atmospheric turbulence /phase extraction /deep convolutional neural network /Gerchberg-Saxton algorithm 全文HTML --> --> --> 1.引 言 光在自由空间传输过程中不可避免地会受到大气湍流效应的影响[1 -6 ] , 在天文目标观测过程中, 大气湍流使得目标成像模糊, 光能分散, 分辨率严重受限[7 ] ; 激光光束在传输过程中受到大气湍流的影响会导致光束发生随机漂移[8 ] ; 在自由空间光通信系统(free space optical communications, FSO)中, 大气湍流容易使信号光发生相位畸变, 引发模式串扰, 使得FSO系统误码率上升[9 ] . 于是有许多****提出了抑制大气湍流影响的解决方案[10 ,11 ] . 在纠正大气湍流的影响时往往需要预先知道所受大气湍流的具体信息, 而传输光束受湍流影响后相当于附加了一个随机湍流相位, 因此从畸变的光束中提取湍流信息实际上也就是提取湍流相位. 传统的湍流相位提取方法多采用Gerchberg-Saxton (GS)算法[12 ] , Fu等[13 ] 利用CCD相机采集受大气湍流影响的高斯光束的强度分布, 利用GS算法最终可以得到影响高斯光束的湍流相位. 但是, 传统的GS算法无记忆性, 即每次预测都需要重新设置初始相位进行多次迭代, 并且容易出现迭代停滞. 另外, 利用随机并行梯度下降算法的自适应光学技术补偿大气湍流效应[14 ] 也是一种可行的方法, 但是随机并行梯度下降算法收敛效果和速度易受增益系数的影响. 若增益系数选择不正确易使优化曲线陷入局部极值, 增加了湍流补偿系统的不稳定性.[15 ] 通过无监督预训练方法初始化权值, 再进行权值微调, 解决了多层隐藏层的训练问题, 从此引发深度学习的研究热潮[16 ] . 深度学习因具有很好的非线性表达能力而可以精确地提取特征信息, 并且具有记忆功能而引起了各个研究领域的关注. 有研究者已经将其应用于光学领域的研究, Li等[17 ] 提出基于CNN的联合大气湍流检测与OAM (orbital angular momentum, OAM)键控解调技术, 在受强湍流影响的8-OAM系统中实现了达到99.5%的自适应解复用精确率. 但是该方案只能进行湍流强度(用大气结构率常数$C_n^2$ 来表示)的分类检测, 还没有实现大气湍流信息的提取, 不利于后续大气湍流补偿以及大气湍流信息的研究分析.$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}$ , $5 \times {10^{ - 14}}$ 和$1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ )影响下的高斯光进行了湍流相位提取. 结果显示本文提出的CNN模型对不同湍流都能实现准确而快速的相位提取. 另外, 在保持湍流强度一样的情况下, 对比了基于传统GS算法的湍流相位提取方法, 结果表明基于深度CNN的方法在训练过程中会自动根据输入和理想输出构建其中的映射关系, 并不需要初始化参数等系列操作, 具有较好的稳定性. CNN在训练过程中具有记忆功能, 训练好的CNN模型可以直接对湍流相位进行预测, 具有很好的泛化能力, 并且预测一次湍流相位的时间是毫秒量级, 大大缩短了湍流预测的时间.2.大气湍流 22.1.大气湍流模型 2.1.大气湍流模型 在大气湍流中, 折射率的随机分布扰乱了高斯光束的波前相位. 文献[17 ]指出大气湍流对高斯光传输的影响可以等效为高斯光在随机相位屏间自由传输. 随机相位屏的产生方法有两种: Zernike多项式展开法[18 ] 和功率谱反演法[19 ] . 本文采用经典的基于Andrews改进Hill谱的大气折射率变动频谱的功率谱反演法. 其中, Andrews分析定义更加符合真实大气湍流情况的大气折射率变动频谱表达式为[20 ] ${k_{\rm{l}}} = {{3.3} / {{l_0}}}$ ; ${l_0}$ 是湍流的内尺度; ${L_0}$ 是湍流的外尺度; ${k_{{x}}}$ 和${k_{{y}}}$ 分别是X 轴和Y 轴方向上的频率波数; $C_{\rm{n}}^2$ 为大气折射率结构常数, 常用来表示湍流强度. 相位谱与折射率频谱的关系为$\Delta Z$ 代表连续两相位屏的间距. 随机相位屏频域分布的方差为N 是栅格元素数目; $\Delta x$ 是栅格距. 相位屏在空间域的计算公式为C $N \times N$ 复随机数矩阵. 为了便于计算, 在笛卡尔坐标系中描述了相位扰动的随机分布, 然后通过快速傅里叶变换操作在频域中表示随机相位屏. 接着将复数形式的相位${\rm{\phi}} \left( {x, y} \right)$ 进行求模处理, 以得到可以直接加载到光束上的湍流相位. 为模拟高斯光在大气中的传输过程, 本文采用高斯光中最重要的基模高斯光(下文简称为高斯光), 并假设高斯光在Z 方向上传播, 则高斯光束的光场表达式可以表示为${U_0}$ 为常数; 截面半径${r^2} = {x^2} + {y^2}$ ; ${z_{\rm{R}}}$ 是高斯光束的共焦参数; 波数$k = {{2{\text{π}} } / \lambda }$ ; $\omega \left( z \right)$ 称为z 处的截面半径, 其中${\omega _{\rm{0}}}$ 为基模高斯光束的束腰半径; $R\left( z \right)$ 表示z 点处的波面曲率半径. (5 )式可以分成两部分, 乘号前面部分为振幅因子, 乘号后面部分为相位因子. 而大气湍流对高斯光束的影响主要是对相位产生影响, 在传播一定距离后, 湍流引起的相位起伏累积会引起复振幅发生变化, 导致光强发生畸变, 因此可以将大气湍流的影响等价于附加了一个随机相位, 主要对相位因子产生影响, 即此时受湍流影响的高斯光束的光场表达式为2.2.大气湍流模型仿真 -->2.2.大气湍流模型仿真 将光场在XY 面上的截面分成128 pixel × 128 pixel的二维像素矩阵, 所选取的大气折射率频谱为2.1 节的Andrews改进Hill谱的大气折射率变动频谱, 其他相关仿真参数见表1 . 湍流强度与大气折射率系数和源半径有关, 为了更方便描述湍流强度变化, 将光束束腰半径设为定值. 因此湍流强度可以由大气折射率结构常数$C_n^2$ 表示, 对于沿水平或准水平路径传播的应用, $C_{{n}}^2$ 可以假定为常数. 设置$C_{{n}}^2 \!=\! 1 \!\times\! {10^{ - 14}}$ , $5 \times {10^{ - 14}}$ 和$1 \!\times\! {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 这三种湍流强度, 根据表1 设置的参数, 最后得到如图1 所示的不同$C_n^2$ 对应的随机相位屏.Parameter Simulation Value Number of Grid Elements N 128 Grid spacing ${{\varDelta x} / {\rm{cm}}}$ About 0.047 Laser wavelength ${\lambda / {\rm{nm}}}$ 1550 Initial ${1 / {\rm{e}}}$ amplitude radius ${{{\omega _0}} / {\rm{cm}}}$ 2 Total path length ${L / {\rm{m}}}$ 20 Inner scale of Turbulence ${{{l_0}} / {\rm{m}}}$ $2 \times {10^{ - 4}}$ Outer scale of Turbulence ${{{L_0}} / {\rm{m}}}$ 50 Number of phase screens n 1
表1 仿真参数Table1. Parameter of simulation.图 1 各湍流强度下的随机相位屏 (a), (b) $C_{{n}}^2 \!=\! 1 \!\!\times\!\! {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (c), (d) $C_{{n}}^2 \!=\! 5 \!\!\times\!\!{10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (e), (f) $C_{\rm{n}}^2 \!=\! 1 \!\!\times\!\! {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ Figure1. Random phase screen at each turbulence intensity: (a), (b) $C_{{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (c), (d) $C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (e), (f) $C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ .图1(a) 与图1(b) 、图1(c) 与图1(d) 及图1(e) 与图1(f) 的湍流强度分别为$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ , $C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 和$C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ , 从不同湍流强度的相位屏的灰度变化范围可以发现, 随着湍流强度变强, 湍流相位振幅的峰值也越来越大. 这也与实际中湍流强度越强, 传输光束的畸变程度越严重相符合. 图1 的第一行和第二行为同等湍流强度下的两个随机相位屏, 因此其灰度起伏范围十分接近, 而造成上下两个大气湍流相位屏分布不一样的主要原因在于决定其相位分布的复数随机矩阵C 图2 所示为受不同湍流影响后的光斑图.图 2 各湍流强度影响下传输光束截面光斑 (a)初始高斯光束; (b), (c) $C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}}^{ - 2/3}}$ ; (d), (e) $C_{\rm{n}}^2 = 5 \times $ ${10^{ - 14}}\;{{\rm{m}}^{ - 2/3}} $ ; (f), (g) $C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}}^{ - 2/3}}$ Figure2. The cross-section spot of transmission beam at each turbulence intensity: (a) Initial Gaussian beam; (b), (c) $C_{\rm{n}}^2 = $ $1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (d), (e) $C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (f), (g) $C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ .图2(a) 为未受湍流影响的标准高斯光, 图2(b) —(g) 为高斯光分别受图1(a) —(f) 的湍流相位屏影响后的光强分布. 从光斑的变化趋势可以看出, 光斑畸变程度随着湍流的增强而增加. 当湍流强度$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 时, 光斑中心尚未发生严重漂移, 但已不再是对称的圆形光斑; 当湍流强度$C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 时, 光斑中心开始发生较小的漂移, 光斑形状发生较为严重的畸变; 当湍流强度$C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 时, 光斑中心已严重地漂移, 光斑形状也由最开始的圆形畸变成不规则形状. 引起这种现象的主要原因在于当湍流强度增强时, 湍流相位的波动幅值范围增大, 对传输光束的相位影响加剧, 引起更加强烈的相位起伏、光强起伏和光斑漂移等湍流现象, 最终导致光束畸变更加严重. 另外, 相同湍流强度的随机相位屏分布也存在差异, 进而导致图2(b) 与图2(c) 、图2(d) 与图2(e) 、图2(f) 与图2(g) 的光强分布有明显的区别, 但是畸变程度在同一等级. 这也可以证实得到的仿真结果不仅与理论分析相符合还与实际情况十分吻合, 所以该大气模型是准确的.3.基于深度CNN提取湍流相位 从上面的分析可以得出, 影响传输光束的大气湍流可以等效为一个湍流相位, 所以提取大气湍流信息就是从畸变光束中提取湍流相位. 为了准确提取高斯光束携带的湍流相位, 本文提出了一种基于深度CNN的大气湍流相位提取方法. CNN是一种学习效率很高的深度神经网络, 其核心是通过卷积核来进行特征提取, 低层的卷积层提取诸如边缘、线条、角度等特征, 而高层的卷积层提取更加抽象的高级特征, 同时还包括组合低层卷积层提取到的特征. 另外, 在训练过程中主要采用的优化算法包括反向传播算法[21 ] 和梯度下降算法[22 ] . 而这些卷积核的参数则是通过网络的损失函数根据反向传播算法进行优化调整, 在对大量样本进行有监督式学习训练后, 得到的CNN模型就可以对输入的受湍流影响的高斯光束进行直接的预测, 同时也减少了提取大气湍流相位的时间. 综合考虑大气湍流的复杂性与CNN各层的性能和作用, 提出了如图3 所示的CNN结构.图 3 提取湍流相位的CNN结构Figure3. The CNN structure of extracting the turbulent phase.图3 所示)共包含17层(不包括输入和输出层), 其中卷积层共有11层, 池化层共有3层, 反卷积层共有3层. 输入的是两幅单通道的二维图像, 一幅是标准的高斯光束, 另一幅是受大气湍流影响的高斯光束, 为了降低网络的时间复杂度, 两幅图像尺寸大小都被缩小到$64 \times 64$ . 经过卷积核大小为$5 \times 5$ 的第一层卷积层(Conv1)后得到32个大小为$64 \times 64$ 的特征图; 第二层还是卷积层(Conv2), 通过$3 \times 3$ 的卷积核后得到了32个大小为$64 \times 64$ 的特征图; 第三层是池化层(Pool1), 采用的是最大池化操作, 池化核尺寸为$2 \times 2$ , 步长为2, 非重叠池化, 所以输出特征图尺寸减半, 即此时特征图大小为$32 \times 32$ , 但特征图的数量没有变, 仍然是32个. 之后再经过两次相同的卷积层和池化层交替设置的结构后, 得到64个大小为$8 \times 8$ 的特征图, 再经过5层纯粹的卷积层, 所用的卷积核大小都为$3 \times 3$ . 在第十三层至第十五层添加了反卷积层, 卷积核大小都是$3 \times 3$ , 这里设置反卷积层的目的是为了还原湍流相位. 经过三层的反卷积层后再经过2层卷积核大小为$3 \times 3$ 的卷积层后就可以得到尺寸大小为$64 \times 64$ 的输出图像, 即影响传输高斯光束的湍流相位. 根据反向传播理论, CNN利用预测湍流相位与实际湍流相位构成的损失函数对上述的卷积核参数进行调整. 这里所用的评估索引为j 的样本误差损失函数为${\rm{Relu}}\left( x \right) = \max \left( {0, x} \right)$ ; ${p^{\left( j \right)}}$ 表示实际的湍流相位; ${\hat p^{\left( j \right)}}$ 表示CNN模型预测的湍流相位. 其具体表达式为$\theta $ 和b 分别表示卷积核和标量偏差, 这是模型的两个训练参数. ${a^{\left( j \right)}}$ 包含两幅单通道图像(一幅是标准的高斯光束, 另一幅是受大气湍流影响的高斯光束). 从(9 )式可以看出, 误差越小表示预测湍流相位与实际湍流相位更加接近, 且当两者相等时误差为0. (10 )式和(11 )式则是用来限制与实际湍流相位不相符的像素值. 对于给定的训练集, 这个误差只与模型的训练参数(卷积核$\theta $ 和标量偏差b )有关, 然后再将训练集中所有样本误差的平均来衡量模型预测的质量, 即:m 为采集的样本数.$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}$ , $5 \times {10^{ - 14}}$ 和$1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 三种湍流强度都分别设置了70000个训练集, 3000个测试集, 2600个校验集. 训练集用于对CNN模型进行训练, 在训练过程中最小化损失函数来不断优化模型参数, 校验集用于将训练过程可视化, 呈现不同训练迭代次数时CNN对湍流相位的预测效果. 训练好的CNN模型用测试集进行测试, 一个良好的CNN模型不仅追求训练误差小, 而且要求测试误差尽可能小. 若对CNN输入一个受大气湍流影响的高斯光束后, CNN的最终输出的湍流相位与仿真产生的随机相位屏的湍流相位一致, 则证明了该方法的可行性.$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 的训练损失函数的变化曲线如图4 所示, 其训练过程中使用校验集得到的预测湍流相位如图5 所示. 图5 中第一行是迭代次数分别为1, 100, 500, 4000, 8000, 14000时CNN模型输出的预测湍流相位, 第二行为与之对应的实际湍流相位, 即理想输出. 如果上下两幅图相似度越高则说明CNN提取到的湍流相位越精确. 图4 中损失函数曲线所标注的前三个点存在较高的损失值, 它表明预测结果和实际结果将会相差甚远. 这三个点分别对应着图5(a) 与图5(b) 、图5(c) 与图5(d) 、图5(e) 与图5(f) , 对比这三组图可以看出所预测的湍流相位与实际湍流相位的相似度很低, 并且整个输出图像比较模糊和混乱, 显然这不是理想的预测结果. 但是经过500次迭代后损失函数值有了明显的下降, 这表明整个网络在训练过程中不断地被优化. 如图5(g) 与图5(h) 、图5(i) 与图5(j) 、图5(k) 与图5(l) 中CNN预测的湍流相位无论是相位振幅分布还是图像细节都与实际湍流相位越来越吻合, 其损失函数值也有一个明显的下降过程. 综合图4 与图5 可以看出CNN模型的湍流相位预测能力经过一次次的迭代训练后变得越来越好.图 4 训练过程损失函数曲线Figure4. The loss function curve of training process.图 5 训练过程提取到的湍流相 (a)与(b), (c)与(d), (e)与(f), (g)与(h), (i)与(j)和(k)与(l)的迭代次数分别为1, 100, 500, 4000, 8000, 14000Figure5. The turbulent phase during the training process: The number of iterations of (a) and (b), (c) and (d), (e) and (f), (g) and (h), (i) and (j), and (k) and (l) is 1, 100, 500, 4000, 8000, 14000.图6 所示为三种不同湍流强度($C_{\rm{n}}^2 = 1 \times {10^{ - 14}}$ , $5 \times {10^{ - 14}}$ 和$1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ )的损失函数值随迭代次数变化的关系曲线, 从图6 中的损失函数的变化趋势可以看出, 经过一定迭代次数的训练, CNN模型都能得到很好的湍流预测结果, 同时也表明其性能并不会因为湍流强度的增加而变差. 图6 显示的曲线并不是光滑的, 而是存在着许多毛刺, 其原因是训练过程的损失函数值会根据本次网络参数更新, 预测湍流与实际湍流相位作比较而得出, 但并不是每次网络更新的湍流相位都可以保证比上一次更接近实际湍流相位, 所以损失函数值在局部是不断波动的, 但是整体上还是单调递减. 其次, 这三种湍流强度的下降趋势几乎一致, 且最后损失函数值都收敛到0.02左右, 说明了本文提出的基于CNN的湍流提取方法适用性强.图 6 各湍流强度损失函数曲线Figure6. The loss function curve at each turbulence intensity.图7 所示, 第一行、第二行和第三行分别是湍流强度$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}$ , $5 \times {10^{ - 14}}$ 和$1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 的仿真结果, 从图7 中可以看出CNN输出的预测湍流相位和理想输出湍流相位在相位振幅分布和图像细节方面都高度吻合. 而且提取效果并没有随湍流强度的变化而出现波动, 从而证明了基于深度CNN提取受湍流影响高斯光束的湍流相位这一方法是十分有效的, 并且还原效果并没有随着湍流强度的增强而出现显著恶化, 证明了该方法的普遍适用性. 另外, 对于每个湍流强度所设置的3000个测试集, 绝大部分仿真结果都可以获得如图7 所示的还原效果, 说明已经获得了泛化能力不错的CNN模型.图 7 不同湍流强度下, 经过CNN提取到的湍流相位 (a), (b), (c)初始高斯光束; (d), (e), (f) 受大气湍流影响的高斯光束; (g), (h), (i)实际的大气湍流相位; (j), (k), (l) CNN输出的预测湍流相位Figure7. The predicted turbulent phase based on CNN at each turbulence intensity: (a), (b), (c) Initial Gaussian beam; (d), (e), (f) Gaussian beam affected by atmospheric turbulence; (g), (h), (i) the actual turbulence phase; (j), (k), (l) the output phase of CNN.4.讨 论 为了证明基于深度CNN方法在大气湍流相位提取方面的优势, 本文还对目前普遍采用的GS算法湍流相位提取进行了对比研究. 利用GS算法提取湍流相位的第一步是对初始高斯光束做快速傅里叶变换(fast Fourier transform, FFT), 以确定相应光场函数的像平面分布. 然后其频域振幅由携带湍流相位的高斯光束的频域振幅代替. 接着经过快速傅里叶逆变换(inverse fast Fourier transform, IFFT), 这时的空域振幅再用入射高斯光振幅代替, 最后对其作FFT. 如图8 所示为两者输出的湍流相位与实际湍流相位的对比, 图8 中三行采用的分别是强度为$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 中的任意三种湍流分布. 从提取到的湍流相位的结果来看, 利用GS算法提取的湍流相位无论在相位振幅分布还是图像细节方面都远不如基于深度CNN模型输出的结果. 并且, 在多达1000次的仿真测试中发现, GS算法不总是可以得到图8(j) —(l) 的结果, 其还存在极小部分劣于图8(j) —(l) 的情况, 其中一个非常主要的原因是GS算法在一定程度上可以看成是一种误差减少算法, 它通过时域和频域的振幅约束, 每次迭代后误差都会下降, 最终重建出目标相位. 该方法适用于计算输入和输出面的光强分布存在严格的解析傅里叶变换对[23 ] , 但是实际应用中存在解析傅里叶变换对的情况毕竟是极少数, 尤其是在复杂的大气湍流中的应用. 这时, GS算法往往会出现收敛速度下降和收敛停滞, 导致提取的湍流相位不精确, 而基于深度CNN提取湍流相位的方法则在多达3000次的测试中都可以获得图8(g) —(i) 所展示的结果, 这体现了该CNN模型性能稳定.图 8 CNN与GS算法提取湍流相位效果对比 (a), (b), (c)受湍流强度为$C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 影响的高斯光束; (d), (e), (f)实际湍流相位; (g), (h), (i)基于CNN模型提取的湍流相位; (j), (k), (l) GS算法提取的湍流相位Figure8. The comparison of CNN and GS algorithm for extracting turbulence phase: (a), (b), (c) Gaussian beam affected by atmospheric turbulence with $C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ ; (d), (e), (f) the actual turbulence phase; (g), (h), (i) the predicted turbulent phase based on CNN; (j), (k), (l) the predicted turbulent phase based on GS algorithm.表2 所列). 表中显示训练好的CNN模型预测一个湍流相位所耗时间在毫秒量级, 并且几乎与湍流强度无关. 而GS算法一般都需要进行70次的迭代才可以得到比较好的输出[13 ] , 这意味着对于每一个相位的预测都需要花费0.4 s左右的时间, 其所花费的时间大约是CNN的100倍. 至此, 不难看出本文提出的方法在相位还原准确率和还原速度方面都优于GS算法.Data Set Average time/s GS algorithm (70 iterations) CNN model $C_{\rm{n}}^2 = 1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 0.39 0.0049 $C_{\rm{n}}^2 = 5 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 0.39 0.0048 $C_{\rm{n}}^2 = 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ 0.41 0.0051
表2 两方法预测时间对比Table2. The predicted time comparison of two methods.$C_{\rm{n}}^2 \in [1 \times {10^{ - 14}}\;{{\rm{m}} ^{{{ - 2} / 3}}},$ $ 1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}] $ , $C_{\rm{n}}^2$ 的具体值从该范围中随机选取, 产生70000个训练数据和2600个验证测试数据. 用训练集和验证集对CNN模型进行迭代训练和验证测试, 其结果如图9 所示, 图9(a) 为训练过程中的损失函数变化曲线, 随着迭代次数的增加, 损失函数值在不断下降, 当迭代次数达到1400次时, 损失值降到了0.0162. 另外, 在训练过程中调用验证集对CNN模型进行测试, 如图9(b) 为迭代次数分别为20, 500, 8000和14000时, CNN对应预测出的湍流相位. 与实际相位对比可以发现, 当迭代次数达到8000, CNN已经具备了较好的湍流相位预测能力. 由此可以得到结论, 我们提出的CNN模型结构在大气折射率结构参数随机变化的实际传输情况中, 同样具有很强的适应和泛化能力. 而对于更强的湍流, 可以考虑通过优化网络结构来抓取更多的特征信息, 从而实现湍流信息的预测.图 9 训练及验证测试结果 (a)训练过程损失函数曲线; (b)训练过程中利用验证集测试得到的预测湍流相位Figure9. Training and validation set test results: (a) The loss function curve of training process; (b) the predicted turbulence phase obtained by testing the validation set during training.[24 ] . 再加上现在人工神经网络, 包括卷积神经网络, 已经有很多算法和技术用于提高网络模型训练过程的训练速度[25 ] , 增加网络层深度[26 ] 和稀疏化编码[27 ] 等等, 这些方法在本文还未能得到巧妙地结合, 所以在CNN网络模型上的优化还有较大的提升空间.5.结 论 本文提出一种基于深度CNN模型的大气湍流相位提取方法, 该方法利用卷积层逐层提取湍流特征, 再经过海量样本集的有监督式的训练学习, 最终在三种湍流强度($C_{\rm{n}}^2 = 1 \times {10^{ - 14}}$ , $5 \times {10^{ - 14}}$ 和$1 \times {10^{ - 13}}\;{{\rm{m}} ^{{{ - 2} / 3}}}$ )的测试样本集上的平均损失函数值都低于0.03. 该方法还与传统的GS算法进行对比, 不仅在提取湍流相位的效果上获得了很大的提高, 而且预测时间缩短了两个数量级. 随着GPU的不断升级以及各种训练优化算法的提出使得训练时间大大减少, 这意味着可以进行更多次的参数调试以更接近最优模型, 所以该方法的应用与发展都有着非常好的前景. 




























 图 1 各湍流强度下的随机相位屏 (a), (b)
图 1 各湍流强度下的随机相位屏 (a), (b) 








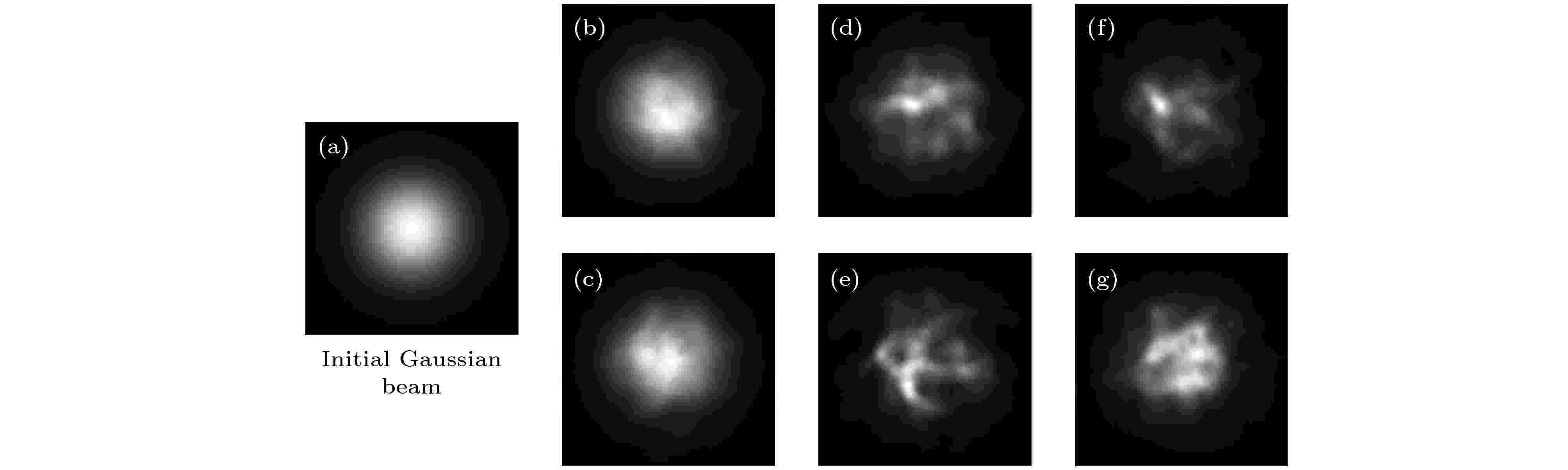 图 2 各湍流强度影响下传输光束截面光斑 (a)初始高斯光束; (b), (c)
图 2 各湍流强度影响下传输光束截面光斑 (a)初始高斯光束; (b), (c) 










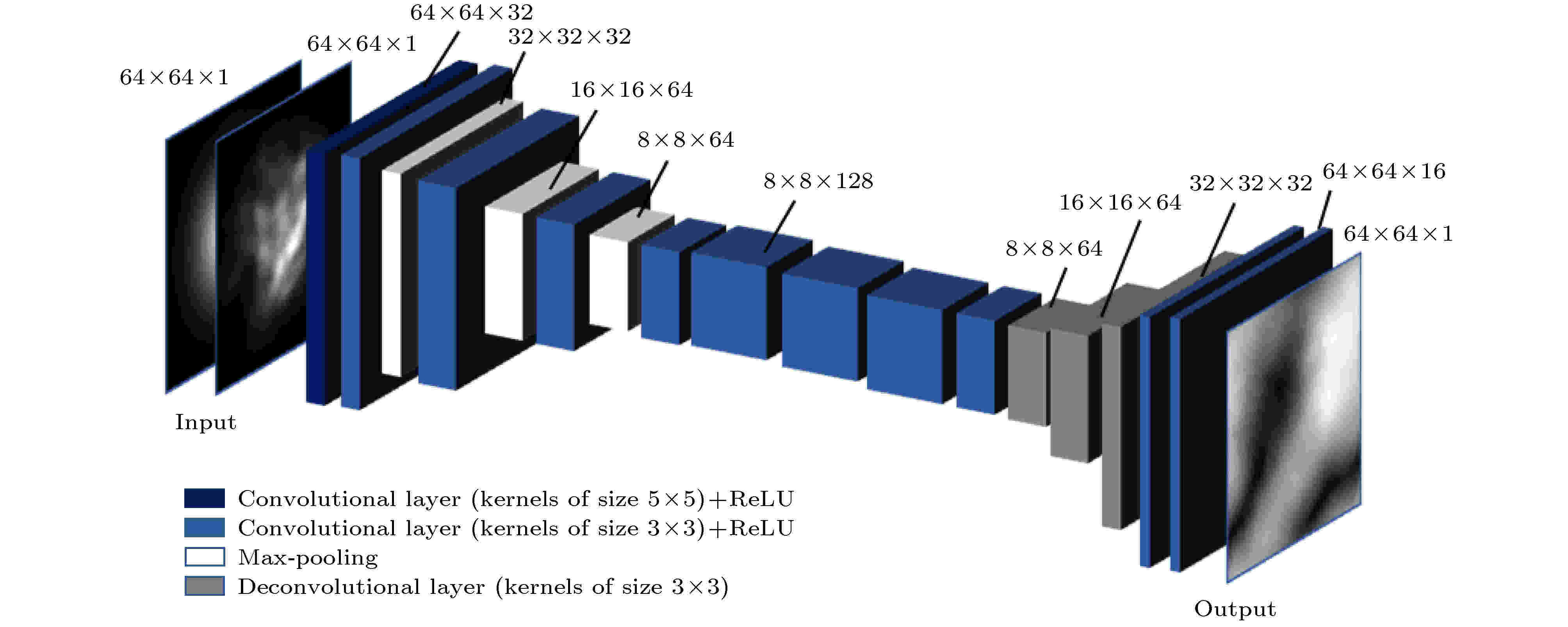 图 3 提取湍流相位的CNN结构
图 3 提取湍流相位的CNN结构















































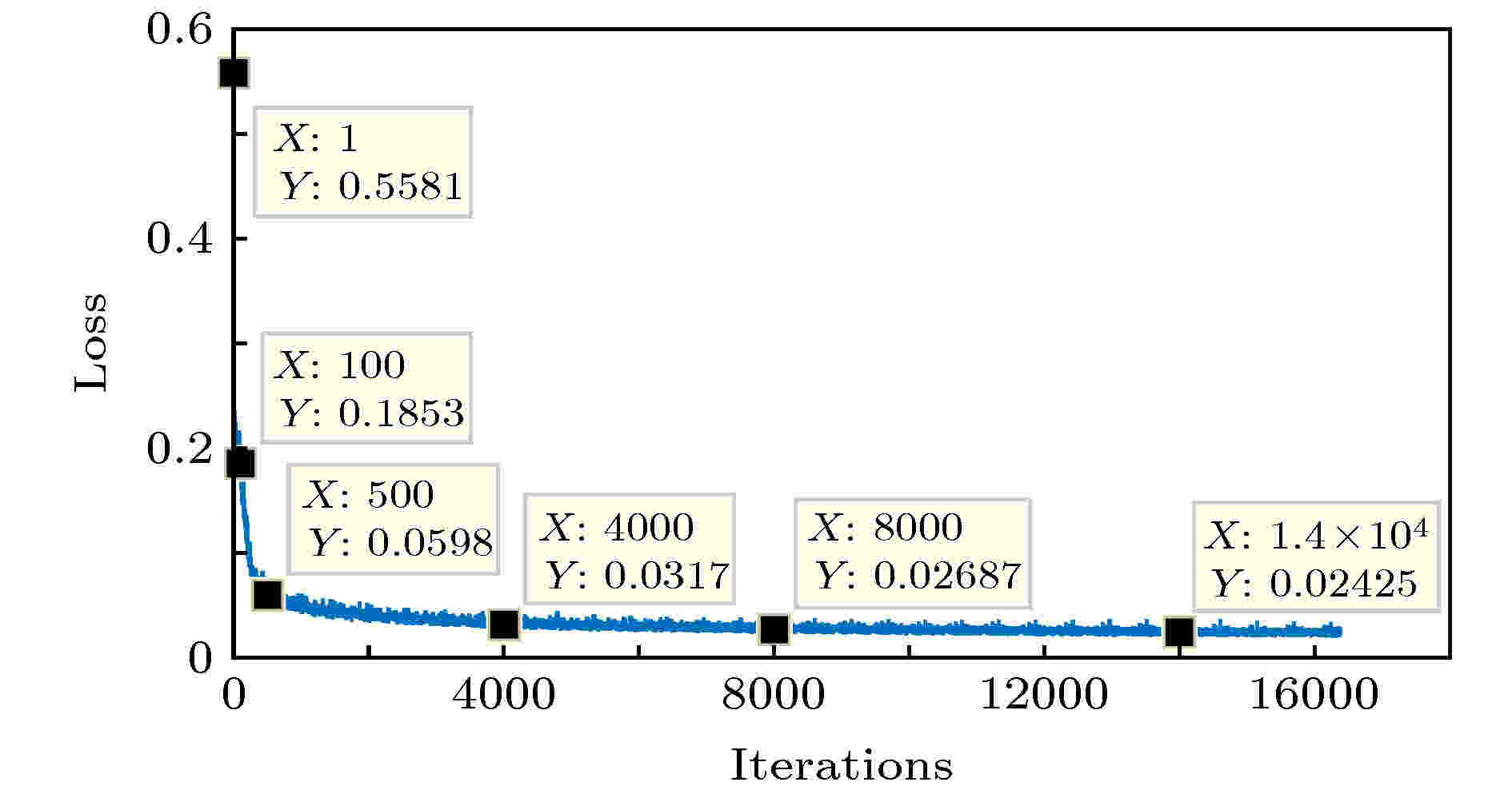 图 4 训练过程损失函数曲线
图 4 训练过程损失函数曲线 图 5 训练过程提取到的湍流相 (a)与(b), (c)与(d), (e)与(f), (g)与(h), (i)与(j)和(k)与(l)的迭代次数分别为1, 100, 500, 4000, 8000, 14000
图 5 训练过程提取到的湍流相 (a)与(b), (c)与(d), (e)与(f), (g)与(h), (i)与(j)和(k)与(l)的迭代次数分别为1, 100, 500, 4000, 8000, 14000


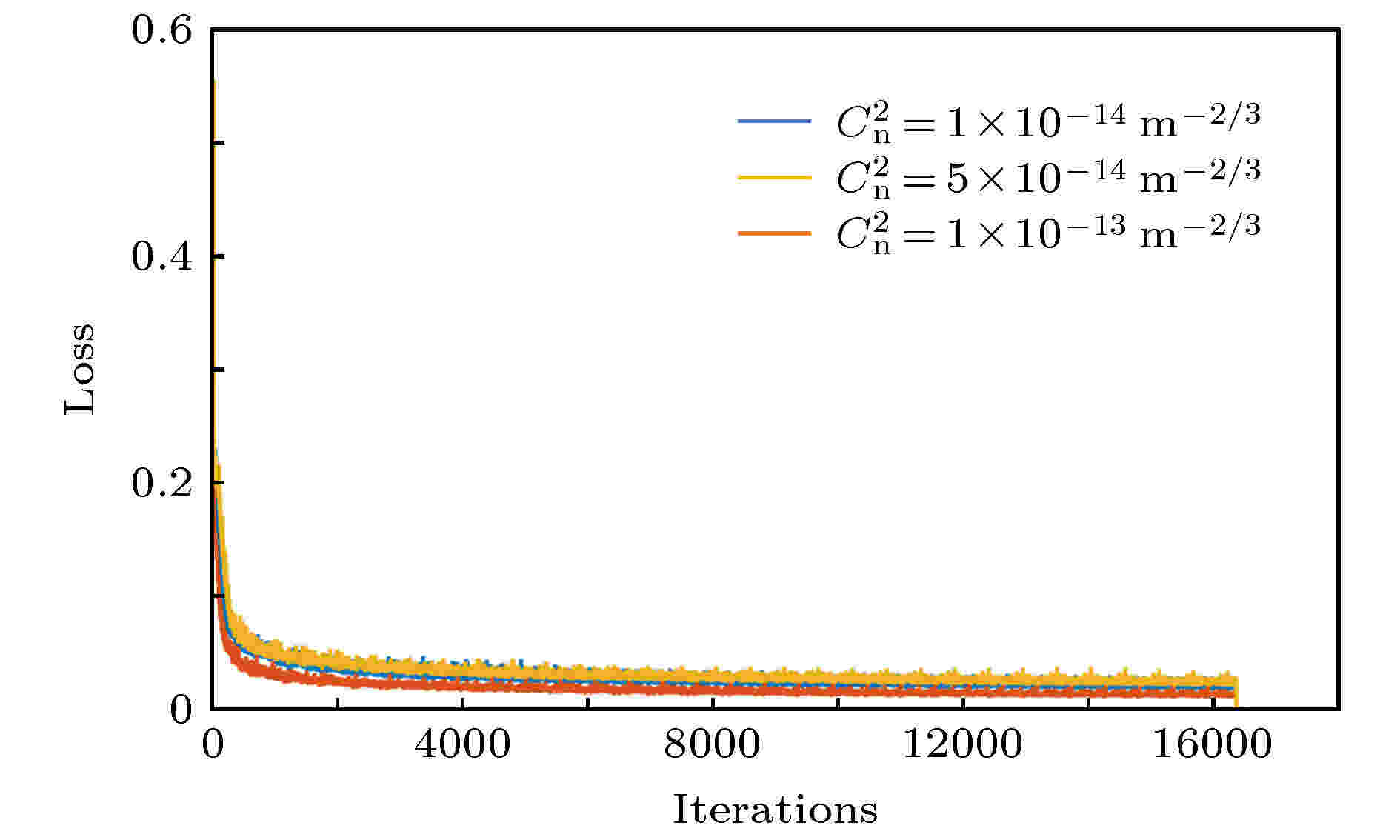 图 6 各湍流强度损失函数曲线
图 6 各湍流强度损失函数曲线


 图 7 不同湍流强度下, 经过CNN提取到的湍流相位 (a), (b), (c)初始高斯光束; (d), (e), (f) 受大气湍流影响的高斯光束; (g), (h), (i)实际的大气湍流相位; (j), (k), (l) CNN输出的预测湍流相位
图 7 不同湍流强度下, 经过CNN提取到的湍流相位 (a), (b), (c)初始高斯光束; (d), (e), (f) 受大气湍流影响的高斯光束; (g), (h), (i)实际的大气湍流相位; (j), (k), (l) CNN输出的预测湍流相位
 图 8 CNN与GS算法提取湍流相位效果对比 (a), (b), (c)受湍流强度为
图 8 CNN与GS算法提取湍流相位效果对比 (a), (b), (c)受湍流强度为




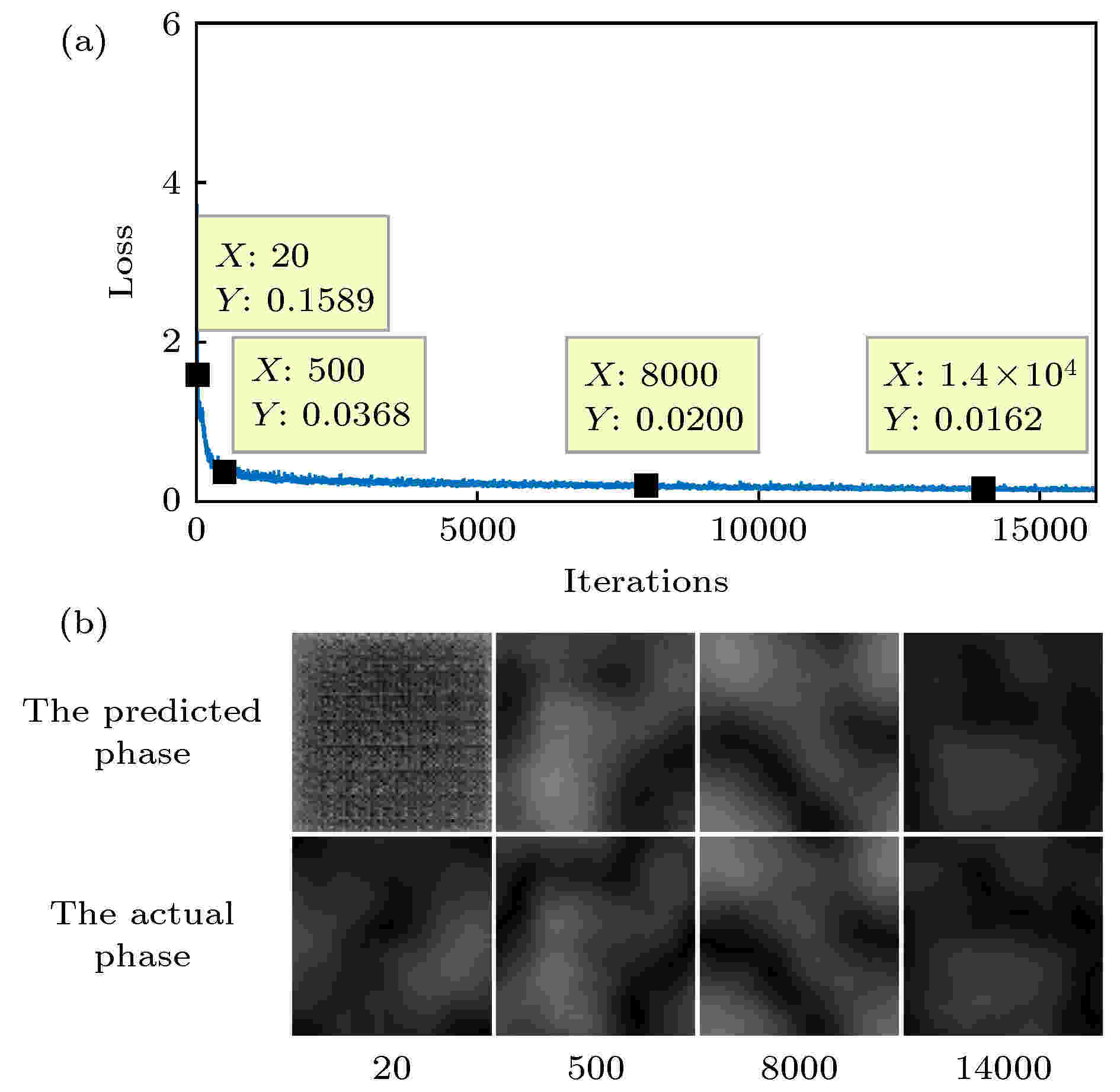 图 9 训练及验证测试结果 (a)训练过程损失函数曲线; (b)训练过程中利用验证集测试得到的预测湍流相位
图 9 训练及验证测试结果 (a)训练过程损失函数曲线; (b)训练过程中利用验证集测试得到的预测湍流相位










