摘要:为了有效控制海量数据时间序列网络的规模并使得网络更贴近实际, 符号化时间序列网络成为研究热点. 结合周期性时间序列的seasonal-trend-loess方法和符号化转化方法, 本文提出一种新的符号化时间序列建网方法. 该方法考虑了单个数据值的状态又结合了序列的长远变化趋势. 以符号模式为节点; 依时间顺序推移, 以节点间的邻接转换关系定义连边; 根据转换方向和转换频次确定连边的方向和权重, 建立有向加权网络. 分别以航空旅客吞吐量时间序列和因特网流量时间序列为实验数据构建的两个时间序列网络, 有明显差异的拓扑特征; 进一步对移动通信语音时间序列做了实证分析, 挖掘时间序列数据的本质规律.
关键词: 周期时间序列/
seasonal-trend-loess方法/
复杂网络/
拓扑特征

English Abstract

全文HTML

--> --> -->

将时间序列通过某种对应关系映射为复杂网络的思想最早由Zhang和Small提出, 这一创造性的想法为时间序列的分析方法提供了新的研究方向和视角. 2006年, Zhang和Small^[1]首次由伪周期时间序列构建了复杂网络. 之后, 时间序列网络方法成为热门的研究方向之一并被应用到许多领域, 如: 医学^[2]、金融学^[3]、交通运输^[4,5]. 目前, 普遍应用的时间序列建网方法有: 基于相空间重构法建网^[6,7]、基于可视图方法建网^[8,9]、基于递归法建网^[10]和基于符号模式建网^[11-13].
基于相空间重构法建网是经典的时间序列建网方法之一. Yue和Yang^[6]提出基于相空间建网方法分析时间序列. 将时间序列划分、重构, 转化为一系列长度一定的向量; 然后以向量为节点, 根据向量间的Pearson相关系数确定连边, 构建出一个无向无权网络. 应用该方法分析时间序列时, 确定向量的滞后期以及确定相关系数的阈值比较复杂. 为此, 一些科学家对相空间重构建网方法进行了改进. 其中, Gao和Jin^[7]引入伪最近邻方法^[14]估计嵌入维数和延迟时间, 使得由时间序列重构相空间变得更加精确, 从而可以根据复杂网络的拓扑特征得出最佳的相关系数阈值. 但是, 由于该方法在确定阈值时存在不确定性, 导致建立的网络的鲁棒性较差.
可视图建网方法^[8,9]是另外一种经典建网方法. 该方法将时间序列柱状图中的每个时间序列值视为一个网络节点, 如果柱状图中的两个柱体可以无障碍可视, 则柱体对应的两个节点之间连边, 从而构建出一个无向无权网络. 网络的总节点数等于时间序列数据值的总个数. 由于可视图建网方法的生成过程简便、网络鲁棒性较好, 使得该法应用于医学^[15]、地质学^[16]、经济学^[17]、天文学^[18]等众多领域. 根据类似的原理, Luque等^[19]于2009年提出水平可视时间序列建网方法. 周婷婷等^[20]提出有限穿越水平可视图时间序列建网方法, 高忠科等^[21]运用有限穿越水平可视图方法分析了两相流的形成动力学. 传统的可视图方法是有限穿越水平可视图方法在可视距为1时的特殊情况. 此外, 高忠科等^[22]还提出了多尺度有限穿越水平可视图时间序列建网方法, 它是水平可视图和有限穿越水平可视图的进一步拓展.
递归网络建网方法由Marwan等^[10]提出. Subramaniyam和Hyttinen^[23]应用递归网络建网方法分析了脑电图时间序列, 研究癫痫病患者的行为动力学. 近几年, 基于符号模式建网方法成为新的研究热点. 符号化时间序列建网方法考虑了节点之间的方向和权重, 构建的加权有向网络更加贴近实际. Karimi和Darooneh^[11]对平稳时间序列做符号化转化, 将时间序列映射为网络, 发现网络度的组合参数对不同流型之间的过渡非常敏感, 可以用来区分不同的流型. 之后, 曾明等^[12]提出符号化模式表征建网方法, 将原始时间序列标准化、符号化处理后, 映射为一个有向加权网络并分析了网络的拓扑性质. 符号化模式表征建网方法可以区分周期时间序列和混沌时间序列. 此外, Zhang和Na^[13]应用符号化模式表征的建网方法研究了空气质量指数等问题.
针对一类周期性时间序列, 本文提出一种基于STL (seasonal and trend decomposition using loess, STL)方法的符号化有向加权网络建网方法. 与其他的符号化建网方法相比, 本文提出的基于STL方法的时间序列建网方法以数据点为基元构建网络, 既考虑了单个数据的状态又融合了时间序列的长远变化趋势. 首先, 依据STL方法将时间序列转化为三个状态项: 季节项、趋势项和随机项; 然后, 使用符号化方法对状态值做区间划分和符号转化, 使得每个数据值表示为由状态符号构成的符号模式; 接着, 以符号模式为节点, 依时间顺序推移, 把数据间的邻接转换关系定义为节点间的连边; 最后以转换方向和转换频次作为连边的方向和权重, 建立有向加权网络.

2

-->

2.1.STL方法

STL方法是一种基于局部加权回归的时间序列分析方法^[24]. 运用局部多项式回归拟合方法, STL方法将时间序列表示为趋势、季节和余项三部分. 即时间序列Y_n = {y_i, i = 1, 2, …, n}通过STL可以转化为趋势T_n = {t_i, i = 1, 2, …, n}, 季节S_n = {s_i, i = 1, 2, …, n}和余项R_n = {r_i, i = 1, 2, …, n}; 其中n表示时间序列长度. STL方法由内循环和外循环组成; 内循环包含去趋势、周期序列平滑等六步; 外循环的主要作用是引入稳健性权重项, 以控制数据中异常值产生的影响. STL方法具有快速的计算速度和分析含缺失值时间序列的能力. 此外, STL方法对具有趋势和季节性成分的数据形成可靠估计, 使得这些数据不会被异常行为所扭曲.
2 -->

2.2.度与度分布

网络中, 节点的度k定义为直接与节点相连的连边的数目. 对于一个给定的有向加权网络G, 假设网络的权值邻接矩阵为W = (w_ij), 则节点i的加权出度和加权入度分别为

$s_i^- = \sum\limits_j {{w_{ij}}},\;s_i^ + = \sum\limits_j {{w_{ji}}},$

则节点i的加权度为

${s_i} = \sum\limits_j ( {w_{ji}} + {w_{ij}}).$

网络的加权出度分布p(s^–)定义为加权出度为s^–的节点被随机选中的概率. 类似地, 网络的加权入度分布p(s⁺)定义为加权入度为s⁺的节点被随机选中的概率. 实际应用中, 为了降低分布的尾部噪音, 常常采用累积分布分析网络的拓扑特征. 累积分布描述了序列中频数不小于某个特定值的概率. 本文分析了时间序列网络的累积加权入度分布, 累积加权出度分布和累积加权度分布.
在基于STL方法的符号化有向加权网络中, 节点的加权出度越大表示节点对应的数据值在时间序列中出现的频率越高, 这表明该节点向其他节点转化的次数越多. 如果节点的加权度值很小, 则说明该状态在时间序列中出现的频次很少, 可能是一些突发情况导致的时间序列值突然增大或减小.
2 -->

2.3.聚类系数与路径长度

网络中, 节点的聚集程度可以用节点的聚类系数来描述. 节点i的聚类系数定义为

${c_i} = \frac{1}{{{k_i}({k_i} - 1)}}\sum\limits_{j,k = 1}^{} {{a_{ij}}{a_{jk}}} {a_{ki}},$

其中, k_i为节点i的度, a_ij是邻接矩阵A = (a_ij)的元素. 当且仅当节点i, j, k构成一个三角形时, a_ija_jka_ki = 1, 否则a_ija_jka_ki = 0. 网络中所有节点的聚类系数的平均值定义为网络的聚类系数. 社会网络中, 节点的聚类系数可以表示“朋友的朋友也是朋友”的倾向性大小. 在基于STL方法的符号化有向加权网络中, 节点i的聚类系数越大, 表明符号模式i的相邻符号模式之间转换越频繁.
节点i和节点j之间的最短路径长度l_ij定义为从节点i到节点j的最短路径上连边的数量. 网络的平均路径长度L定义为任意两个节点的最短路径长度的平均值, 即

$L = \frac{1}{{{{\left[ {N(N - 1)} \right]} / 2}}}\sum\limits_{i \geqslant j} {{l_{ij}}}. $

2 -->

2.4.介　数

以经过某个节点的最短路径的数目刻画节点重要性的指标被称为介数中心性, 简称介数. 网络中, 节点i的介数用b_i表示, 定义为

${b_i} = \sum\limits_{s \ne i \ne t} {{{n_{st}^i}/ {{n_{st}}}}}. $

其中, n_st是从节点s到节点t的最短路径的数目, nⁱ_st为从节点s到节点t的n_st条最短路径中经过节点i的最短路径的数目. 从信息传输的角度看, 网络中介数越高的节点重要性越大, 对网络的信息传输影响越大.

针对一类具有周期性特征的时间序列数据, 本文提出基于STL方法的符号化有向加权网络建网方法. 原始时间序列数据经过STL分析以及符号化处理之后, 不仅保持了数据的信息量, 而且可以在短期细节和长期趋势两方面体现时间序列数据的特点. 具体的时间序列网络建立过程如下.
a) STL分析. 依据STL方法, 将时间序列转化为季节项、趋势项和余项之和, 即Y_n = S_n + T_n + R_n. 其中n是时间序列的长度, S_n = {s_i, i = 1, 2, …, n}是季节项, T_n = {t_i, i = 1, 2, …, n}是趋势项, R_n = {r_i, i = 1, 2, …, n}是余项.
b)符号化. 根据三个状态项对原时间序列的影响程度, 选用不同权重的符号化阶数对状态变量序列做层次划分. 得到三组符号化时间序列:

$\left\{ \begin{aligned}& g\left( {{S_n}} \right) = \left\{ {g\left( {{s_i}} \right),i = 1, \cdots,n} \right\}, \\& g\left( {{T_n}} \right) = \left\{ {g\left( {{t_i}} \right),i = 1, \cdots,n} \right\}, \\& g\left( {{R_n}} \right) = \left\{ {g\left( {{r_i}} \right),i = 1, \cdots,n} \right\},\end{aligned} \right.$

其中g(s_i), g(t_i), g(r_i)表示符号. 此时, 每个时间序列值表示为符号模式

${\rm{mod}}{{\rm{e}}_i} = g\left( {{s_i}} \right)g\left( {{t_i}} \right)g\left( {{r_i}} \right).$

c)构建网络. 以互不相同的符号模式为节点, 以两个不同符号模式的相邻关系作为连边, 以两个互异符号模式相邻的次数和符号模式的先后顺序作为连边的权重和方向, 建立一个有向加权网络.
为了实现对真实时间序列数据的比较分析, 在执行STL分析与符号化之前, 对原始时间序列数据{x_i, i = 1, 2, …, n}进行归一化处理. 采用归一化方法: y_i = (x_i – x_min)/(x_max – x_min). 归一化之后的时间序列{y_i, i = 1, 2, …, n}保持了原时间序列的周期性特征和变化趋势等特点, 并且取值范围在[0, 1].
在执行数据符号化时, 如果符号化阶数太小, 会导致时间序列信息的流失; 如果符号化阶数太大, 会使得符号模式过多, 不能体现符号化的优势. 因此, 考虑到准确体现时间序列特点和构建网络的规模需要适度, 经过多次试验才确定了最优的符号化阶数. 季节项的符号化阶数为m₁ = 8, 趋势项的符号化阶数为m₂ = 18, 随机项的符号化阶数为m₃ = 4.

为了验证所提出的基于STL方法的时间序列网络建模方法的有效性和实用性, 分别以具有非平稳特征的航空旅客吞吐量时间序列和具有平稳特征的因特网流量时间序列为例, 使用新方法建立有向加权网络. 分析网络的度分布、聚类系数、平均路径长度等拓扑性质, 从网络拓扑特征的角度对这两个实际时间序列做比较分析.
2

-->

4.1.航空旅客吞吐量时间序列网络

航空旅客吞吐量数据取自澳门国际机场专营股份有限公司(Macau International Airport Co. Ltd.)的官方网站. 时间序列跨度从1996年1月到2017年12月. 每月记录一次吞吐量数据, 表示该月内航空旅客的人数, 共有264条记录. 时间序列整体呈现上升趋势, 其周期为12. 此外, ADF检测结果显示, 该时间序列数据为非平稳性时间序列.
航空旅客吞吐量时间序列的STL分析如图1(a)—(d)所示. 季节项时间序列以周期规律呈现, 每个周期有12个值, 反映这个周期内数据波动的细微变化. 趋势项时间序列体现了原时间序列的变化趋势. 整体而言, 数据呈上升状态; 但是, 其中有两个时间段下降明显. 随机项时间序列为季节项和趋势项的残差值, 呈现不规则变化.
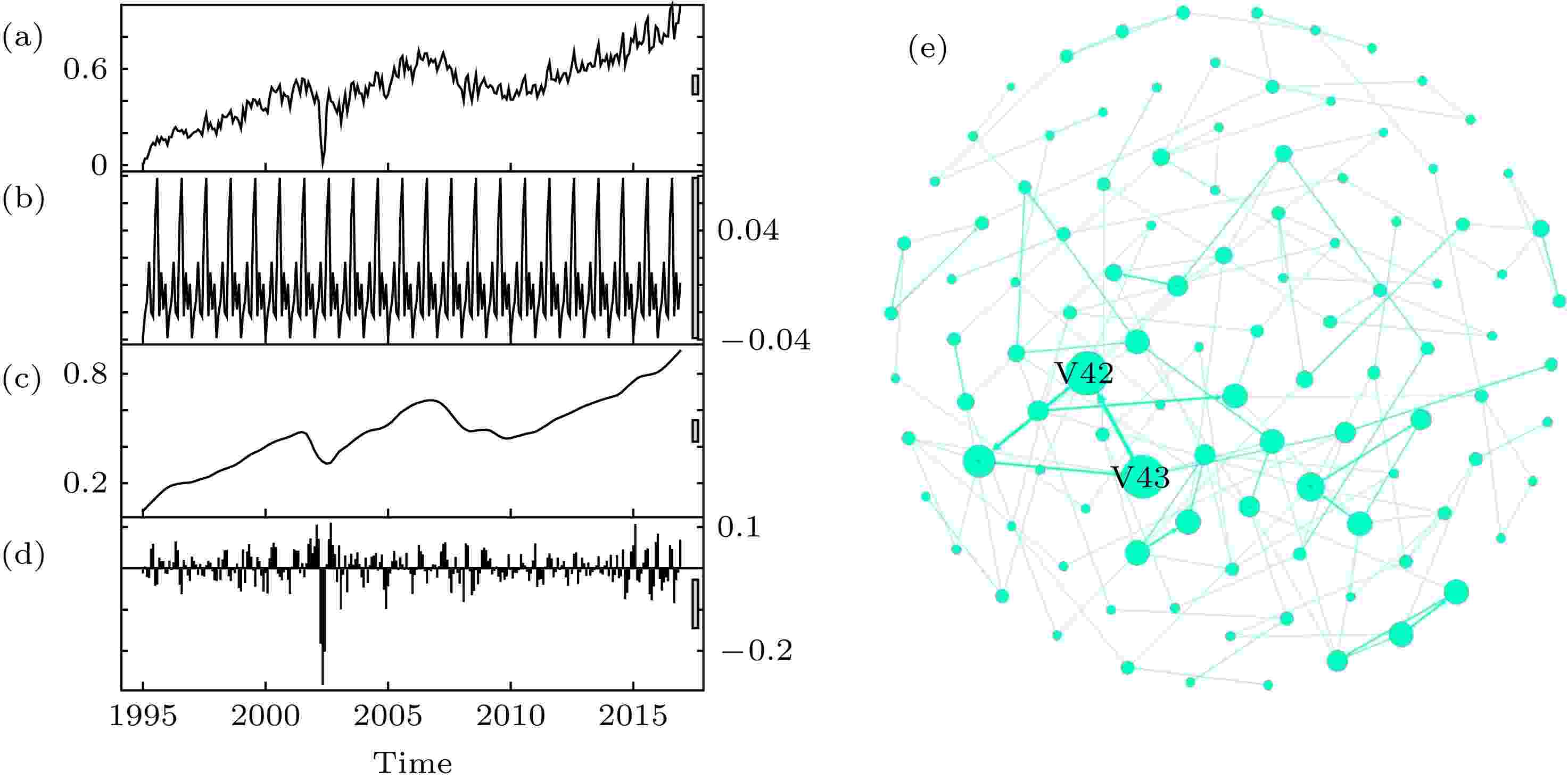图 1 (a)?(d)航空旅客吞吐量时间序列的STL分析　(a)原始时间序列; (b)季节项时间序列; (c) 趋势项时间序列; (d) 随机项时间序列; (e)航空旅客吞吐量时间序列网络
Figure1. (a)?(d) The STL analyzing for the air passengers throughput time series: (a) Original time series; (b) seasonal time series; (c) trend time series; (d) remainder time series; (e) the time series network of the air passengers throughput data.

图1(e)是航空旅客吞吐量时间序列网络. 该网络有107个节点, 178条有向边. 节点的面积大小与节点的加权度有关, 加权度越大, 节点的面积越大; 连边的宽度反映了连边的权重, 边权越大, 连边的宽度越宽. 网络中加权度最大的节点是V42和V43, 它们的加权度都是20; 网络中加权度最小的节点比较多, 加权度值为1. 网络中边权的最大值为7, 即图中连接V42和V43的边; 网络中边权的最小值为1. 航空旅客吞吐量时间序列网络的平均加权度为4.430, 聚类系数为0.169, 平均路径长度为13.355.
航空旅客吞吐量时间序列网络具有指数加权度分布. s⁺表示节点的加权入度, s^－表示节点的加权出度, s表示节点的加权度. 单对数坐标系下, 航空旅客吞吐量时间序列网络的累积加权度分布近似呈直线型, 拟合优度检验显示三个度分布均服从指数分布. 其中, 网络的累积加权入度分布服从指数为0.3990的指数分布(可决系数R² = 0.9280), 如图2(a)所示; 网络的累积加权出度分布服从指数为0.6151的指数分布(R² = 0.9960), 如图2(b)所示; 网络的累积加权度分布服从指数为0.2555的指数分布(R² = 0.9670), 如图2(c)所示.
图 2 航空旅客吞吐量时间序列网络度分布　(a)累积加权入度分布; (b)累积加权出度分布; (c)累积加权度分布
Figure2. The degree distribution of the time series network for air passengers throughput data: (a) The cumulative weighted in-degree distribution; (b) the cumulative weighted out-degree distribution; (c) the cumulative weighted degree distribution.

2 -->

4.2.因特网流量时间序列网络

因特网流量数据^[25]表示英国学术网络主干网的聚合流量. 数据时间截取于2005年1月16日至2005年1月26日. 每5 min记录一次流量数据, 1天有288条记录, 11天共产生3168条记录. 该时间序列是周期为288的周期性时间序列. ADF检测显示, 因特网流量时间序列为平稳时间序列.
图3(a)—(d)是因特网流量时间序列的STL分析图. 2005年1月16日、22日和23日分别为星期日、星期六和星期日, 这三天产生的因特网流量偏小. 星期一至星期五的流量时间序列整体趋势一致且较为稳定. 季节项时间序列以周期规律呈现, 包含11个周期, 每个周期有288个数据, 反映这个周期内数据波动的细微变化. 趋势项时间序列从星期一至星期五, 数据伏动较小, 呈现平稳状态; 在星期六、星期日, 数据伏动有明显的下降. 随机项时间序列呈现不规则变化.
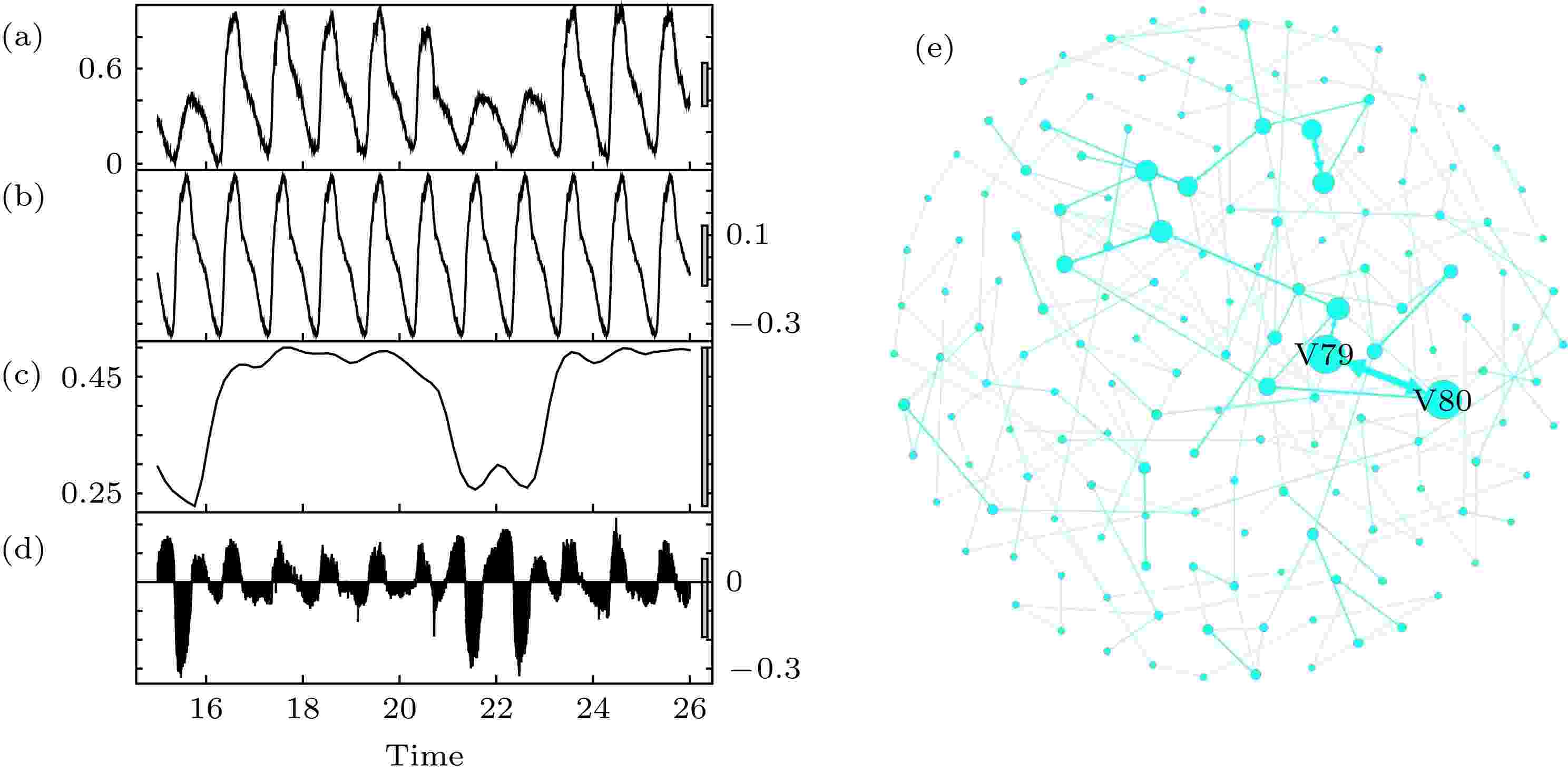图 3 (a)?(d)因特网流量时间序列的STL分析　(a)原始时间序列; (b)季节项时间序列; (c) 趋势项时间序列; (d) 随机项时间序列; (e)因特网流量时间序列网络
Figure3. (a)?(d) The STL decomposition results of the Internet traffic time series: (a) Original time series; (b) seasonal time series; (c) trend time series; (d) remainder time series; (e) the time series network of the Internet traffic data.

根据本文第3节提出的方法, 将因特网流量时间序列映射为一个有向加权网络(图3(e)). 该网络有160个节点, 244条有向边. 节点V79和V80的加权度值最大, 为54; 网络中存在大量加权度值较小的节点. 连边权重的最大值为22, 如图3(e)所示, 恰好是连接节点V79和节点V80的连边的权重. 因特网流量时间序网络的平均加权度为5.538, 聚类系数为0.249, 平均路径长度为25.61.
因特网流量时间序列网络的度分布服从幂律分布. 如图4所示, 在双对数坐标下, 累积加权度分布近似呈直线型, 拟合优度检验显示三个累积加权度分布均服从幂律分布. 其中, 网络的累积加权入度分布服从幂指数为1.202的幂律分布(可决系数R² = 0.9960), 如图4(a)所示; 网络的累积加权出度分布服从幂指数为1.202的幂律分布(R² = 0.9957), 如图4(b)所示; 网络的累积加权度分布服从幂指数为1.223的幂律分布(R² = 0.9940), 如图4(c)所示. 综上, 三个累积度分布均服从幂指数小于2的幂律分布. 因特网流量时间序列网络是一个无标度网络.
图 4 因特网流量时间序列网络的度分布　(a)累积加权入度分布; (b)累积加权出度分布; (c)累积加权度分布
Figure4. The degree distribution of the time series network for the Internet traffic data: (a) The cumulative weighted in-degree distribution; (b) the cumulative weighted out-degree distribution; (c) the cumulative weighted degree distribution.

2 -->

4.3.分析与比较

航空旅客吞吐量时间序列是非平稳时间序列, 因特网流量时间序列是平稳时间序列. 采用所提出的STL分析符号化时间序列网络建模方法, 得到网络的拓扑特征总结如表1所示. 航空旅客吞吐量时间序列的数据长度是10²数量级, 构建的加权有向时间序列网络的节点数为10²数量级; 因特网流量时间序列的数据长度是10³数量级, 构建的加权有向时间序列网络的节点数为10²数量级. 航空旅客吞吐量时间序列具有非平稳性. 随着时间的推移, 符号模式很大程度上不重复, 使得符号化时间序列的符号模式种类较多, 从而航空旅客吞吐量时间序列网络的节点数亦较多. 因特网流量时间序列的趋势项整体呈平稳状态, 对应的符号化序列不规则重复. 在转换成符号模式的过程中, 符号模式的重复率较高, 转换频率较大, 从而种类较少, 连边的权重较大. 所以, 因特网流量时间序列网络具有较少的节点数和较大的平均加权度.

时间序列				网络拓扑特征
	长度	周期		节点数	平均加权度	聚类系数	平均路径长度	加权度分布
航空旅客吞吐量	264	12		107	4.430	0.169	13.355	指数分布
因特网流量	3168	288		160	5.538	0.249	25.610	幂律分布

表1两类时间序列网络拓扑特征的比较
Table1.The comparison for topological characteristics of two kinds time series networks.

2

-->

5.1.时间序列数据

依据所提出的基于STL方法的时间序列建网方法, 将移动通信语音业务时间序列映射为一个有向加权网络. 删除数据记录不完整的周期, 并对初始数据进行归一化处理, 得到一个数值范围在[0, 1]的长度为52032的时间序列, 如图5(a)所示, 为前10个周期的语音时间序列数据. 通过STL分析, 季节项由长度为24的单周期季节趋势循环推移生成; 趋势项呈现不规则起伏变化.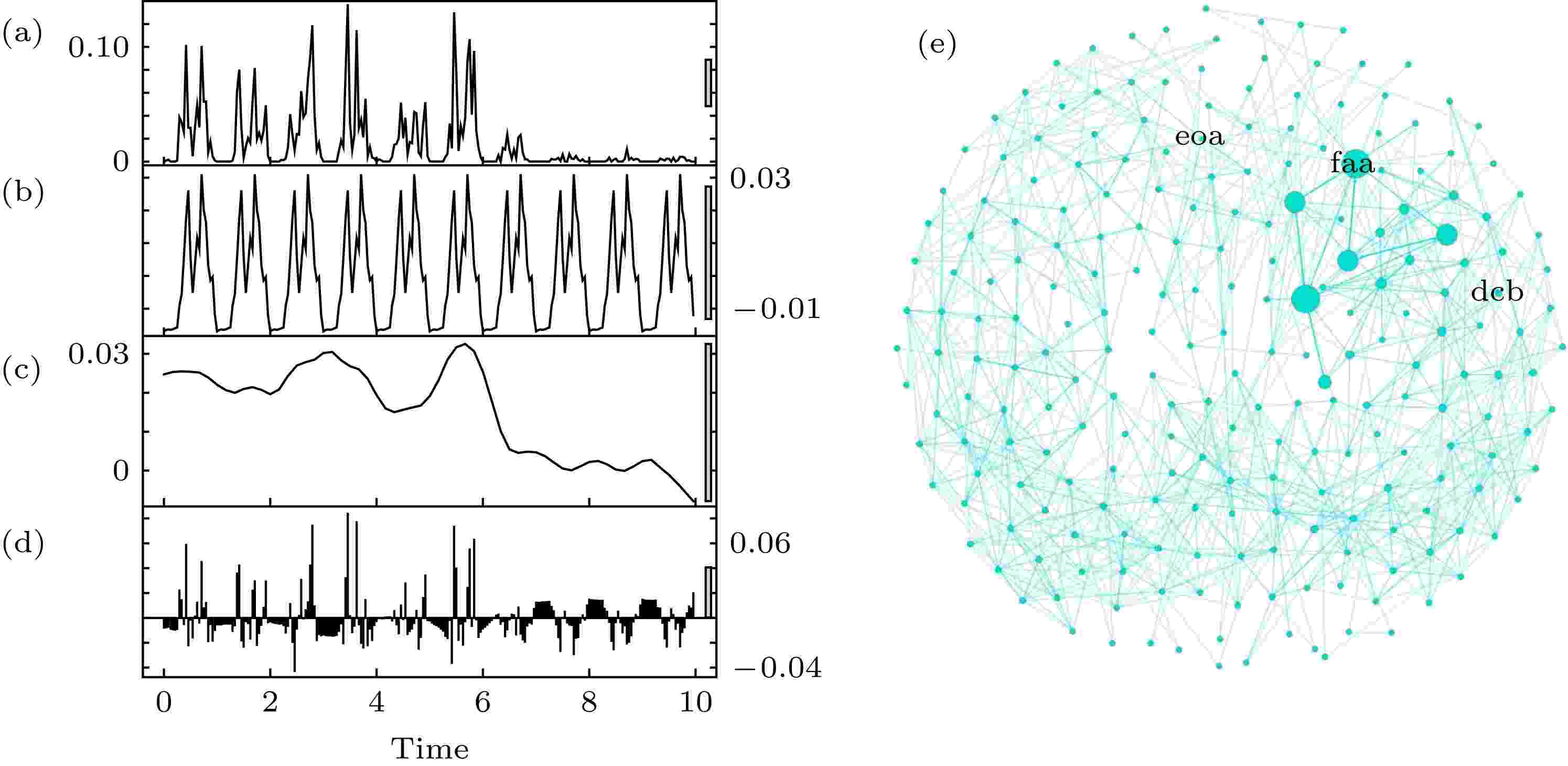
图 5 (a)?(d)语音时间序列数据的STL分析　(a)原始时间序列; (b)季节项时间序列; (c) 趋势项时间序列; (d) 随机项时间序列; (e)基于STL方法的语音时间序列网络
Figure5. (a)?(d) The STL analyzing for the mobile traffic data: (a) Original time series; (b) seasonal time series; (c) trend time series; (d) remainder time series; (e) based on the STL decomposition, the time series network of the mobile traffic data.

2 -->

5.2.时间序列网络

由语音时间序列数据建立的有向加权网络如图5(e)所示. 该网络有230个节点, 1275条边. 网络中, 节点加权度的最大值为7740, 连边权重的最大值为2555. 网络的平均加权度为260.626, 聚类系数为0.298, 平均路径长度为5.142.
语音时间序列网络的累积加权度分布服从幂律分布, 度分布如图6所示. 累积加权度在双对数坐标下呈近似线性关系. 网络的累积加权入度分布(图6(a))、累积加权出度分布(图6(b))和累积加权度分布(图6(c))均服从幂律分布. 语音时间序列网络是一个无标度网络.
图 6 语音时间序列网络的度分布　(a)累积加权入度分布; (b)累积加权出度分布; (c)累积加权度分布
Figure6. The degree distribution of the time series network for the mobile traffic data: (a) The cumulative weighted in-degree distribution; (b) the cumulative weighted out-degree distribution; (c) the cumulative weighted degree distribution.

2 -->

5.3.局部特征分析

通过网络的一些局部拓扑特征, 分析了语音时间序列数据值的特点. 移动通信语音时间序列网络依局部拓扑特征参数由大到小排序如表2所示. 依节点的聚类系数由大到小排序, 节点的符号模式如第一列所示; 依节点的加权出度由大到小排序, 节点的符号模式如第三列所示; 依节点的介数中心性由大到小排序, 节点的符号模式如第五列所示.

节点	聚类系数	节点	加权出度	节点	介数
dcb	1	faa	3874	eoa	9810.72
daa	1	aaa	3780	hia	9605.21
aac	1	haa	2597	faa	9295.21
deb	1	eaa	2570	eaa	8532.04
dfb	1	gaa	2564	haa	6180.21
dgb	1	daa	1279	aba	4185.66
egc	1	aba	890	ana	3933.32
aqb	1	fba	765	aoa	3649.48
aob	1	eba	564	fra	3475.81
dkb	1	hba	550	aga	3389.27

表2网络节点模式特征表
Table2.The table for characteristics of node patterns.

节点的聚类系数为1表示该模式的任意两个邻居模式之间都存在连边, 即该节点的邻居节点之间彼此相连, 如图5(e)中的节点dcb的聚类系数为1, 说明节点dcb的邻居节点之间也是相邻关系. 在时间序列中, 符号dcb对应于0点或1点. 这个时间位于趋势项时间序列的局部极大值处. 类似地, 其他聚类系数为1的节点对应于语音时间序列数据时, 均由趋势项的局部极大值或局部极小值映射而来. 这代表了一天的语音量高峰期或低谷期.
加权出度较大的节点对应于时间序列上局部极大值和局部极小值之间的时刻. 例如, 图5(e)中节点faa对应于语音时间序列上的12点、15点和19点等数据. 结合实际情况, 可知加权出度大的节点对应于时间序列上的上班时间与休息时间的过渡时刻. 对于周期性时间序列而言, 这样的数据较多, 使得对应的节点的加权度较大. 语音时间序列网络中, 一些节点的介数中心性很大, 这些符号模式对网络上信息的流动有较大的影响力. 节点eoa的介数中心性为9810.72, 该符号模式对应于时间序列中每天的14点和20点.

采用复杂网络的量化统计量挖掘时间序列的内在信息为时间序列分析方法提供了一个全新的视角. 其中, 时间序列网络建模是最重要的方法之一. 经典方法构建出无向无权网络, 主要有相空间重构法和可视图方法以及他们的拓展模型. 这些方法实施简便, 但是, 却忽略了时间的单向性和基元之间的关联程度的差异. 针对上述问题, 科学家们提出了符号化时间序列建网方法, 基于该类方法构建的加权有向网络更加贴近实际. 已有的符号化时间序列建网方法以时间序列相邻数据的变化趋势的符号组为基元, 考虑了数据的变化过程, 却忽略了数据值本身的特征. 本文提出的基于STL方法的时间序列网络方法, 既考虑了单个数据值的状态, 又考虑了时间序列的长远变化趋势. 以时间序列上的数据点为基元构建网络, 可以通过网络的局部拓扑特征体现时间序列单个数据值的信息.
本文提出的基于STL方法的时间序列建网方法, 结合周期性时间序列的STL分析和符号转化方法构建出一个有向加权网络. 首先, 依据STL方法将时间序列的每个数据值表示为三个状态值. 其次, 通过对状态值做区间划分和符号化转化, 将每个数据值表示为状态符号. 最后, 依时间顺序推移, 以节点间的邻接转换关系定义连边; 根据转换方向和转换频次确定连边的方向和权重, 建立有向加权网络. 有向加权网络的拓扑特征可以反映时间序列的特点: 1)周期时间序列经STL分析之后, 趋势项可以展示时间序列的长期变化特点; 2)对于平稳性周期时间序列, 其周期项的规则性和趋势项的平稳性, 使得在转换成符号模式时, 符号模式的重复率较高, 转换频率较大, 所以生成网络的连边的权重较大; 3)在有向加权网络中, 聚类系数较大的节点对应着时间序列的高峰期或低谷期; 而加权出度较大的节点对应着时间序列上的局部极大值和局部极小值之间的过渡时刻.
在构建网络时, 使用了航空旅客吞吐量时间序列、因特网流量时间序列和移动通信语音业务量时间序列. 它们的共性是均为周期性时间序列, 差异性表现在平稳性上. 本文研究重点是基于时间序列构建新的建网方法, 适用于具有周期性的时间序列. 时间序列表示为周期态、趋势态和随机态的符号形式, 这些时刻符号不仅体现时间序列值的细节变化, 而且反映时间序列的长期发展趋势. 在确定符号化阶数时, 需要通过实验验证, 尚缺乏普适性的规则. 未来将继续完善方法并探索它们在动态建模^[26,27]等领域的应用.