摘要: 通过线性耦合Brusselator模型和Lengyel-Epstein模型, 数值研究了双层耦合非对称反应扩散系统中图灵模之间的相互作用以及斑图的形成机理. 模拟结果表明, 合适的波数比以及相同的对称性是两个图灵模之间达到空间共振的必要条件, 而耦合强度则直接影响了图灵斑图的振幅大小. 为了保证对称性相同, 两个图灵模的本征值高度要位于一定的范围内. 只有失稳模为长波模时, 才能对另一个图灵模产生调制作用, 并形成多尺度时空斑图. 随着波数比的增加, 短波模子系统依次经历黑眼斑图、白眼斑图以及时序振荡六边形斑图的转变. 研究表明失稳图灵模与处于短波不稳定区域的高阶谐波模之间的共振是产生时序振荡六边形的主要原因.
关键词: 图灵模 /
非对称反应扩散系统 /
超点阵斑图 /
数值模拟 English Abstract Super-lattice patterns in two-layered coupled non-symmetric reaction diffusion systems Liu Fu-Cheng Liu Ya-Hui Zhou Zhi-Xiang Guo Xue Dong Meng-Fei College of Physics Science and Technology, Hebei University, Baoding 071002, China Fund Project: Project supported by National Natural Science Foundation of China (Grant Nos. 11975089, 11875014), the Natural Science Foundation of Hebei Province, China (Grant No. A2017201099), and the Postdoctoral Science Foundation of Hebei University, ChinaReceived Date: 06 September 2019Accepted Date: 31 October 2019Published Online: 20 January 2020Abstract: The coupling mechanism is one of most important approaches to generating multiple-scaled spatial-temporal patterns. In this paper, the mode interaction between two different Turing modes and the pattern forming mechanisms in the non-symmetric reaction diffusion system are numerically investigated by using a two-layered coupled model. This model is comprised of two different reaction diffusion models: the Brusselator model and the Lengyel-Epstein model. It is shown that the system gives rise to superlattice patterns if these two Turing modes satisfy the spatial resonance condition, otherwise the system yields simple patterns or superposition patterns. A suitable wave number ratio and the same symmetry are two necessary conditions for the spatial resonance of Turing modes. The eigenvalues of these two Turing modes can only vary in a certain range in order to make the two sub-system patterns have the same symmetry. Only when the long wave mode becomes the unstable mode, can it modulate the other Turing mode and result in the formation of spatiotemporal patterns with multiple scale. As the wave number ratio increases, the higher-order harmonics of the unstable mode appear, and the sub-system with short wave mode undergoes a transition from the black-eye pattern to the white-eye pattern, and finally to a temporally oscillatory hexagon pattern. It is demonstrated that the resonance between the Turing mode and its higher-order harmonics located in the wave instability region is the dominant mechanism of the formation of this oscillatory hexagon pattern. Moreover, it is found that the coupling strength not only determines the amplitudes of these patterns, but also affects their spatial structures. Two different types of white-eye patterns and a new super-hexagon pattern are obtained as the coupling strength increases. These results can conduce to understanding the complex spatial-temporal behaviors in the coupled reaction diffusion systems.Keywords: Turing mode /non-symmetric reaction diffusion system /super-lattice pattern /numerical simulation 全文HTML --> --> --> 1.引 言 自组织斑图是非线性动力学系统的一个典型特征, 普遍存在于自然界以及众多非线性系统中, 例如物理、化学以及生物系统等[1 -6 ] . 在过去的半个世纪内, 人们对斑图形成机理的认识有了突飞猛进的发展, 其中比较著名的就是反应扩散系统的图灵机制[7 ] , 一个均匀稳定态经历图灵失稳后会产生不随时间变化的空间周期性分布的结构, 例如条纹斑图和六边形斑图[8 ,9 ] .[10 -18 ] , 其中不同图灵模之间的相互作用可以产生各种复杂的多尺度时空斑图. 2002年, Yang等[11 ] 通过线性耦合双层反应扩散系统研究了图灵模之间的相互作用, 结果表明图灵模之间的波数比、子斑图对称性以及本征值高度是空间共振的三个必要条件. 该研究小组还发现仅仅是双层间的耦合作用也可以导致一种新的叉形分叉, 进而产生两个图灵模式. 这两个图灵模相互作用可以形成对称、非对称以及反相图灵斑图[12 ] . 在此基础上, 多个研究小组对图灵模相互作用机理进行了进一步研究. 例如Liu等[13 ] 在更广的本征值高度范围内获得了超点阵斑图, 并且在波数比接近4∶1时观察到一种新类型的白眼斑图. Catlla等[14 ] 发现当两个图灵模的波数比例为$\sqrt 2:1$ 时, 系统可以产生稳定的四边形斑图. 白占国等[15 -18 ] 详细研究了各种耦合条件对斑图的影响, 发现了多种超点阵四边形斑图, 包括大小点、白眼、点线和复杂超四边等.[19 -27 ] 之间的耦合, 例如两个Brusselator模型[19 ,20 ] 、两个Lengyel-Epstein模型[21 -23 ] 或者是两个Oregonator模型[24 ] 等. 在大多数非线性系统中, 同时存在着多种不同的非线性物理过程, 这些过程各自具有不同的斑图形成机理. 例如在介质阻挡放电系统中, 放电层与电介质层相互耦合, 可以产生种类繁多的时空斑图, 这些时空斑图通常由两套或者多套子结构相互嵌套而成[25 -27 ] , 因此有必要对不同物理过程之间的耦合进行详细研究. 然而到目前为止, 不同反应模型之间的耦合以及斑图选择机制还尚未见报道, 人们对不同斑图形成系统之间的耦合机制还不甚清楚.2.模型分析 为了研究不同系统形成的图灵模之间的相互作用, 本文采用线性耦合两个不同的反应扩散模型, 构建了一个双层耦合非对称反应扩散系统模型, 在无量纲的情况下, 该模型具有以下形式:$({u_1}, {v_1})$ 和$({u_2}, {v_2})$ , α 为两个子系统活化子之间的耦合强度; 方程$f(u, v)$ 和$g(u, v)$ 为每个子反应扩散系统的局部动力学方程, 不同的反应系统有着不同的具体表达式. 本文选取Brusselator模型和Lengyel-Epstein模型来充当两个子系统. 在无量纲的情况下, Brusselator模型的局部动力学方程具有下列形式:a 和b 是系统的控制参数.c 和d 是系统的控制参数. 对于子系统1和2, 其均匀定态解分别为$({u_{10}}, {v_{10}}) = (a, b/a)$ 和$({u_{20}}, {v_{20}}) = \left( {\dfrac{c}{5}, 1 + \dfrac{{{c^2}}}{{25}}} \right)$ . 本文中选取$c = 5 a$ , 则双层耦合系统的均匀定态解可以表示为A D λ , 本征值λ 与微扰模之间的关系被称之为系统的色散关系曲线. 通过系统的色散关系可以分析失稳模的性质以及系统的分岔类型.图1 给出了两个耦合系统处于图灵空间时的色散关系. 图1 中蓝色实线为本征值的实部, 代表模式的线性增长率, 红色虚线为本征值的虚部. 对于每一个子系统, 当活化子u 的扩散系数远小于禁阻子v 的扩散系数时, 系统经历图灵分岔并激发出图灵模. 该图灵模的波数大小为${k_c} = \sqrt[\leftroot{-1}\root{12}4]{{\dfrac{\varDelta }{{{D_u}{D_v}}}}}$ , 其中Δ 是与控制参数有关的常数. ${D_u}$ 相比于${D_v}$ 越小, 系统偏离分岔点越远, 图灵模线性增长率越高, 即图灵模的本征值高度越高. 因此通过调节模型中各变量的扩散系数, 可以使两个子系统均经历图灵分岔, 从而各自激发相应的图灵模式. 由于图灵模的波数与扩散系数成反比, 所以具有较小扩散系数的子系统的图灵模波数大(短波模), 称为${k_2}$ , 本征值高度为${h_2}$ , 而具有较大扩散系数的子系统的图灵模波数较小(长波模), 称为${k_1}$ , 相应的本征值高度为${h_1}$ . 图1(a) 和图1(b) 给出了两个图灵模波数比分别为1∶2和1∶3时的色散关系图. 研究发现, 只有长波模${k_1}$ 对短波模${k_2}$ 有影响, 而短波模${k_2}$ 对长波模${k_1}$ 没有影响. 因此长波模${k_1}$ 一般设置为失稳模.图 1 不同参数下耦合系统的色散关系 (a) D u 1D v 1D u 2D v 2α = 0.1; (b) D u 1D v 1D u 2D v 2α = 0.1Figure1. Dispersion relations of coupled systems under different parameters: (a) D u 1D v 1D u 2D v 2α = 0.1; (b) D u 1D v 1D u 2D v 2α = 0.1.3.模拟结果与讨论 采用欧拉向前差分的方法进行积分, 数值模拟在一个含有$128 \times 128$ 个空间格点的二维平面上进行, 时间积分步长取为$\Delta t = 0.01$ 个时间单位, 空间积分步长取为$\Delta h = 1.0$ 个空间单位, 扩散项在数值模拟中采取5点差分格式, 边界条件选用周期性边界条件, 初始条件为均匀定态加上一个很小的随机扰动. 如果没有特殊说明, 一般设置子系统2具有较大的扩散系数, 即激发长波模, 而观察子系统1中形成的各种斑图.3.1.两个图灵模波数比的影响 3.1.两个图灵模波数比的影响 固定两个图灵模的本征值高度(h 1 , h 2 ) = $ (0.20, - 0.55)$ 以及耦合强度$\alpha = 0.1$ , 通过改变两个图灵模的波数比值${k_1}:{k_2}$ , 研究不同波数比对斑图形成的影响. 如前文所述, 图灵模的波数大小取决于${D_u}$ 和${D_v}$ 的乘积, 而其高度取决于${D_u}$ 和${D_v}$ 的相对大小, 因此两个图灵模的波数${k_1}$ 和${k_2}$ 的大小可以通过其各自的${D_u}{D_v}$ 来控制. 波数大小确定后, 保持${D_u}{D_v}$ 的乘积不变, 改变二者的相对大小, 调节其本征值高度h .图2 给出了波数比分别为1∶2, 1∶3和1∶4三种比值下子系统1中形成的超点阵斑图及其相应的傅里叶频谱图. 图2(a) 是波数比为1∶2时得到的黑眼斑图, 其中每个中心点的浓度最低, 且周围环绕着一圈高浓度环, 整体呈现六边形阵列排布. 从其傅里叶频谱图可以看出, 该黑眼斑图包含三套不同波数的模式, 其波数值分别为${k_1}$ , ${k_2}$ 和q . 每一套波矢都组成一个完美的六边形结构, 其中${k_1}$ 和${k_2}$ 为两个子系统激发的图灵模 (${k_1}:{k_2} = 1:2$ ), 而q 是新生模式. 这三种模式之间满足空间三波共振关系: ${k_1} + {k_2} = q$ . 图2(b) 是波数比为1∶3时得到的白眼六边形斑图, 与黑眼斑图不同, 白眼斑图的中心为高浓度斑点, 周围依次围绕一圈低浓度环和一圈高浓度环, 然后被6个更高浓度的亮点包围, 整体也呈现六边形阵列结构. 分析其傅里叶频谱图可知, 该白眼斑图同黑眼斑图类似, 也包含上述三套满足空间共振关系的波矢, 唯一的区别是新生模式q 具有两套六边形结构, 即12个波矢. 通过几何关系可知, 此两套六边形之间的夹角为$\theta = 21.8^\circ $ . 图2(c) 是波数比为1∶4时得到的白眼斑图. 与图2(b) 相比, 每一个六边形晶胞中心的亮斑点浓度下降, 同时, 晶胞外围的六个亮点连接在一起, 形成了一个蜂窝状六边形结构. 它包含的波矢成分也较为复杂, 除了基本的图灵模${k_1}$ 和${k_2}$ 外, 还产生了各种高阶模$2{k_1}$ , $3{k_1}$ 以及这些模式共振而生成的新生模式q . 需要特殊说明的是, 图灵模式${k_2}$ 的强度较弱, 而高阶模$3{k_1}$ 的强度较强, 这意味着当波数比较大时, 子系统1中的斑图主要是失稳模${k_1}$ 及其激发的高阶模相互作用而形成.图 2 不同波数比下的超点阵斑图及其傅里叶频谱图 (a) 1∶2下的黑眼斑图, ${D_{u1}} = 13.5$ , ${D_{v1}} = 27.5$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (b) 1∶3下的白眼斑图, ${D_{u1}} = 6$ , ${D_{v1}} = 12.3$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (c) 1∶4下的白眼斑图, ${D_{u1}} = 3.4$ , ${D_{v1}} = 6.96$ , ${D_{u2}} = 21.9$ , ${D_{v2}} = 400$ . $\alpha = 0.1$ Figure2. Superlattice pattern and fourier spectrum under different wave number ratios: (a) Black eye pattern at 1∶2, ${D_{u1}} = 13.5$ , ${D_{v1}} = 27.5$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (b) white eye pattern at 1∶3, ${D_{u1}} = 6$ , ${D_{v1}} = 12.3$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (c) white eye pattern at 1∶4, ${D_{u1}} = 3.4$ , ${D_{v1}} = 6.96$ , ${D_{u2}} = 21.9$ , ${D_{v2}} = 400$ . $\alpha = 0.1$ .图3 给出了两个图灵模波数比为1∶5时所产生的振荡超六边形斑图. 图3(a) 为相应的色散关系曲线图, 由图3(a) 可知, 在${k_1}$ 和${k_2}$ 之间存在着一个虚部不为零的区域, 即短波不稳定性区域, 在此区域内的各个模式均随时间周期性振荡, 失稳模${k_1}$ 的高阶模$2{k_1}$ 和$3{k_1}$ 均位于此区域内. 在此情况下, 失稳图灵模${k_1}$ 与其高阶模$2{k_1}$ 和$3{k_1}$ 相互作用时, 就导致了一种正弦型时间振荡斑图的形成. 图3(b) 给出了三个不同位置处(分别标记为A , B , C )活化子${u_1}$ 随时间变化的图. 其中B 点为振荡六边形的中心斑点位置, 其格点坐标为(50, 76); A 点为两个中心亮斑的中心, 其格点坐标为(53, 59); C 点为三个中心亮斑组成的三角形中心, 其格点坐标为(65, 61), 如图3(c) 所示. 由图3(c) 可知, 三个位置处的振荡周期相同, 均为$T = {t_6} - {t_1} = 46$ 个时间单位, 但是相位不同, A , B , C 相位依次延迟. 另外, 这三点的振荡幅度也不相同, B 点处振荡幅度远高于其他两点. 图3(c) 显示了一个振荡周期内该振荡六边形斑图的时空演化过程. 在${t_1} = 24$ 时刻, 六边形亮斑结构浓度稍高于其它位置, 从而形成了一种具有晕结构的超六边形斑图. 在${t_2} = 30$ 时刻, 中心斑点浓度下降, 低于晕的浓度, 此时斑图呈现一种类似白眼斑图的结构. 在${t_4} = 47$ 时刻, 中心斑点处浓度降至最低点, 远远低于晕的浓度, 此时斑图呈现为简单的蜂窝六边形斑图. 随着时间演化, 中心斑点处浓度开始上升, 在${t_6} = 64$ 时刻开始显现出中心亮斑, 有意思的是单元中心由原来的一个斑点变为两个斑点, 并且每个单元外包围着6个暗点. 该时序振荡六边形斑图与对称耦合反应扩散模型获得的眨眼斑图[11 ] 有着很大的区别. 首先是形成机理不同, 该振荡六边形是失稳模与其高阶模相互作用而成, 而眨眼斑图则是失稳模与其次谐波模相互作用而成; 其次是振荡模式不同, 该振荡六边形呈现正弦式的振荡, 而眨眼斑图则呈现脉冲式的振荡.图 3 波数比为1∶5时的时间振荡超六边形斑图, ${D_{u1}} = 2.2$ , ${D_{v1}} = 4.5$ , ${D_{u2}} = 21.9$ , ${D_{v2}} = 400$ , $\alpha = 0.1$ (a) 色散关系曲线; (b) 三个位置处u 1 的时间变化关系图; (c) 一个振荡周期内的斑图演化过程Figure3. Oscillatory super-hexagon pattern with wave number ratio of 1∶5, ${D_{u1}} = 2.2$ , ${D_{v1}} = 4.5$ , ${D_{u2}} = 21.9$ , ${D_{v2}} = 400$ , $\alpha = 0.1$ : (a) Dispersion curve; (b) time variation of u 1 at three positions; (c) evolution of pattern in an oscillating period.3.2.图灵模强度对斑图的影响 -->3.2.图灵模强度对斑图的影响 图灵模的本征值高度h 代表了图灵模的线性增长率, h 越大, 表示增长率越快, 意味着图灵模强度越强. 在本节中固定两个图灵模波数比为1∶3以及耦合强度$\alpha = 0.1$ , 通过改变两个图灵模的本征值高度h 来研究图灵模强度对斑图形成产生的影响.${h_1} = 0.2$ , 讨论本征值高度${h_2}$ 对图灵斑图的选择及形成产生的影响. 图4 给出了${h_2}$ 逐步升高而获得的各种复杂斑图及其相应的傅里叶频谱图, 其中图4(a) —(d) 是${h_2} < 0$ 的情况, 图4(e) 是${h_2} > 0$ 的情况. 当${h_2} = - 2.56$ 时系统1呈现简单的蜂窝六边形斑图(图4(a) ). 由于${h_2}$ 较低, 该系统的本征模并不能被激发, 因此该六边形斑图完全是由系统2的失稳模调制形成. 随着${h_2}$ 的升高, 系统1中的本征模开始被激发, 如前文所述, 两个图灵模相互耦合, 形成了白眼斑图(图4(b) 和图4(c) ). 继续升高${h_2}$ 至–0.31, 白眼斑图失稳, 转变为一种新的超六边形结构, 该斑图中每个晶胞均由三个相邻的暗点排列而成, 这些暗点的空间波数为${k_2}$ , 晶胞之间以波数${k_1}$ 周期性排列(图4(d) ). 当${h_2} = 0.67$ 时, 系统1呈现单一的条纹斑图, 也就是说此时系统1的斑图完全由其自身的本征模所决定, 系统2的长波模对它的调制作用仅仅存在于背景中, 这可以通过傅里叶频谱图看出(图4(e) ).图 4 不同本征值${h_2}$ 下的复杂斑图及其傅里叶频谱图 (a) 蜂窝状六边形斑图${h_2} = - 2.56$ , ${D_{u1}} = 8.5$ , ${D_{v1}} = 12.5$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (b) 白眼斑图${h_2} = - 1.3$ , ${D_{u1}} = 7$ , ${D_{v1}} = 12.3$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (c) 白眼斑图${h_2} = - 0.55$ , ${D_{u1}} = 6$ , ${D_{v1}} = 12.3$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (d) 超六边形斑图${h_2} = - 0.31$ , ${D_{u1}} = 5.9$ , ${D_{v1}} = 12.7$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (e) 条纹斑图${h_2} = 0.67$ , ${D_{u1}} = 5.5$ , ${D_{v1}} = 16$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ . $\alpha = 0.1$ .Figure4. Complex patterns and Fourier spectrum under different eigenvalues ${h_2}$ : (a) Honeycomb hexagon pattern ${h_2} = - 2.56$ , ${D_{u1}} = 8.5$ , ${D_{v1}} = 12.5$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (b) white-eye pattern ${h_2} = - 1.3$ , ${D_{u1}} = 7$ , ${D_{v1}} = 12.3$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (c) white-eye pattern ${h_2} = - 0.55$ , ${D_{u1}} = 6$ , ${D_{v1}} = 12.3$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (d) super-hexagon pattern ${h_2} = - 0.31$ , ${D_{u1}} = 5.9$ , ${D_{v1}} = 12.7$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ ; (e) stripe pattern ${h_2} = 0.67$ , ${D_{u1}} = 5.5$ , ${D_{v1}} = 16$ , ${D_{u2}} = 22$ , ${D_{v2}} = 400$ . $\alpha = 0.1$ .h 还表征了系统远离初级分岔点的程度, h 越大, 偏离程度越高. 早期的研究表明[13 ] , 在初级分岔点附近, 系统一般选择为六边形斑图, 而当远离分岔点时, 选择为条纹斑图. 因此通过改变h 的大小还可以控制斑图的对称性类型. 图5 给出了${h_1}$ 分别为0.2和0.4两种情况下子系统1中形成的复杂斑图, 这里固定两个图灵模的波数比为1∶3, ${h_2} = - 0.5$ , 耦合强度$\alpha = 0.1$ . 当${h_1} = 0.2$ 时, 两个子系统中的斑图均为六边形斑图, 对称性相同, 因此可以满足空间共振关系, 从而形成了白眼斑图(图5(a) ). 但是当${h_1}$ 增大到0.4时, 该失稳模呈现出条纹结构, 与另一个图灵模的对称性不匹配, 不满足空间共振关系, 因此在子系统1中仅仅呈现简单的重叠斑图, 即条纹结构和六边形的叠加(图5(b) ).图 5 不同本征值$ {h_1}$ 下的复杂斑图及其傅里叶频谱图 (a) 白眼斑图, $ {h_1} = 0.2$ , $ {D_{u1}} = 6.1$ , $ {D_{v1}} = 12.7$ , $ {D_{u2}} = 22.3$ , $ {D_{v2}} = 403$ ; (b) 条纹点状斑图, $ {h_1} = 0.4$ , $ {D_{u1}} = 6.1$ , $ {D_{v1}} = 12.6$ , $ {D_{u2}} = 20.3$ , $ {D_{v2}} = 464$ , $ \alpha = 0.1$ Figure5. Complex patterns and fourier spectrum under different eigenvalues ${h_1}$ : (a) White-eye pattern, ${h_1} = 0.2$ , ${D_{u1}} = 6.1$ , ${D_{v1}} = 12.7$ , ${D_{u2}} = 22.3$ , ${D_{v2}} = 403$ ; (b) stripe-spot pattern, ${h_1} = 0.4$ , ${D_{u1}} = 6.1$ , ${D_{v1}} = 12.6$ , ${D_{u2}} = 20.3$ , ${D_{v2}} = 464$ , $\alpha = 0.1$ .${k_1}$ , 当本征值高度处于0 < h 1 < 0.33时, 子系统自发选择六边形斑图; 当${h_1} < 0$ 时, 系统是稳定的, 无法激发图灵模; 当${h_1} > 0.33$ 时, 子系统选择条纹斑图. 对于图灵模${k_2}$ , 其本征值高度范围需在$ - 2 < {h_2} < 0$ ; 若${h_2} > 0$ 时转变为失稳模, 此时子系统选择条纹斑图; 而当其本征值高度过小时, 尽管受到失稳模${k_1}$ 的激励作用, 但是依然无法激发出该本征模, 此时子系统处于均匀定态.3.3.耦合强度的影响 -->3.3.耦合强度的影响 耦合强度也是影响两个图灵模相互作用的一个重要因素. 由于各个参量共同影响两个图灵模的大小和强度, 本文中改变耦合强度的同时对扩散系数进行微调, 以保证两个图灵模的大小${k_1} = 0.2$ , ${k_2} = 0.6$ 和本征值高度$({h_1}, {h_2}) = (0.2, - 0.55)$ 始终保持恒定, 从而研究耦合强度对斑图形成的影响. 图6 给出了不同耦合强度下获得的超六边形点阵斑图. 模拟研究发现, 耦合强度不仅可以影响斑图的振幅大小, 还影响了其空间结构的具体形式. 如果耦合系数足够小, 失稳模对子系统1的影响可以忽略不计, 此时子系统1呈现稳定的均匀状态. 当耦合系数$\alpha = 0.01$ 时, 子系统1开始受到失稳模${k_1}$ 的调制和激发, 系统形成白眼斑图, 但是此时的活化子浓度的变化范围非常小(图6(a) ). 图6(b) 为耦合系数$\alpha = 0.1$ 时模拟得到的白眼斑图, 从图6(b) 中可以看出, 活化子浓度的变化范围变大, 图灵模${k_2}$ 的强度也开始增强. 继续增大耦合强度α , 子系统1中活化子浓度的变化范围持续增加, 并且其空间形貌逐渐开始变化. 图6(c) 是模拟获得的一种新型超六边形斑图, 此超点阵斑图虽然整体也呈现六边形阵列结构, 但是每一个晶胞单元中心不再是一个圆斑点, 而是形成了一个线段, 这可能是六边形斑图和条纹斑图共同竞争的结果. 图6(d) 给出了耦合强度$\alpha = 0.3$ 时得到的新白眼斑图, 与图6(b) 不同, 此白眼斑图在中心亮点周围还包围着一圈高浓度环, 环外排列着一组六边形斑点. 从傅里叶频谱图中可以看出, 耦合强度很大, 此斑图也是由两个图灵模${k_1}$ 和${k_2}$ 直接耦合而成.图 6 不同耦合强度下的超六边形斑图 (a) 白眼斑图, $\alpha = 0.01$ , ${D_{u1}} = 5.8$ , ${D_{v1}} = 11.4$ , ${D_{u2}} = 22$ , ${D_{v2}} = 367$ ; (b) 白眼斑图, $\alpha = 0.1$ , ${D_{u1}} = 6.3$ , ${D_{v1}} = 12.9$ , ${D_{u2}} = 21.8$ , ${D_{v2}} = 395$ ; (c) 新型超六边形斑图, $\alpha = 0.2$ , ${D_{u1}} = 6.1$ , ${D_{v1}} = 13$ , ${D_{u2}} = 22$ , ${D_{v2}} = 432$ ; (d) 新白眼斑图, $\alpha = 0.3$ , ${D_{u1}} = 6.3$ , ${D_{v1}} = 13.98$ , ${D_{u2}} = 22$ , ${D_{v2}} = 460$ Figure6. Super-hexagon patterns with different coupling strength: (a) White-eye pattern, $\alpha = 0.01$ , ${D_{u1}} = 5.8$ , ${D_{v1}} = 11.4$ , ${D_{u2}} = 22$ , ${D_{v2}} = 367$ ; (b) white-eye pattern, $\alpha = 0.1$ , ${D_{u1}} = 6.3$ , ${D_{v1}} = 12.9$ , ${D_{u2}} = 21.8$ , ${D_{v2}} = 395$ ; (c) new super-hexagon pattern, $\alpha = 0.2$ , ${D_{u1}} = 6.1$ , ${D_{v1}} = 13$ , ${D_{u2}} = 22$ , ${D_{v2}} = 432$ ; (d) new white-eye pattern, $\alpha = 0.3$ , ${D_{u1}} = 6.3$ , ${D_{v1}} = 13.98$ , ${D_{u2}} = 22$ , ${D_{v2}} = 460$ .4.结 论 通过线性耦合两个不同的反应扩散模型(Brusselator模型和Lengyel-Epstein模型)研究了不同系统间两个图灵模之间的相互作用以及斑图的形成和选择过程. 模拟结果表明合适的波数比以及相同的对称性是不同反应扩散系统的图灵模之间相互共振的必要条件. 只有长波模子系统对短波模子系统有调制和激发作用, 因此超点阵斑图只能出现在短波模子系统中. 在不同的波数比下, 短波模子系统内可以形成包括黑眼斑图和白眼斑图在内的多种超点阵斑图. 为了保证两个子系统斑图具有相同的对称性, 两个图灵模的本征值高度必须处于$0 < {h_1} < 0.33$ 和$ - 2 < {h_2} < 0$ . 当失稳模的高阶谐波处于短波不稳定区域时, 失稳模与其高阶模相互共振可以形成一种正弦型时序振荡六边形斑图. 耦合强度直接影响了图灵斑图的振幅大小. 本文的研究结果有助于人们进一步认知非线性系统中各种模式之间的相互作用机理. 





































 图 1 不同参数下耦合系统的色散关系 (a) Du1 = 12.6, Dv1 = 27.9, Du2 = 22, Dv2 = 420, α = 0.1; (b) Du1 = 5.3, Dv1 = 20, Du2 = 22, Dv2 = 500, α = 0.1
图 1 不同参数下耦合系统的色散关系 (a) Du1 = 12.6, Dv1 = 27.9, Du2 = 22, Dv2 = 420, α = 0.1; (b) Du1 = 5.3, Dv1 = 20, Du2 = 22, Dv2 = 500, α = 0.1



























































 图 2 不同波数比下的超点阵斑图及其傅里叶频谱图 (a) 1∶2下的黑眼斑图,
图 2 不同波数比下的超点阵斑图及其傅里叶频谱图 (a) 1∶2下的黑眼斑图, 

































































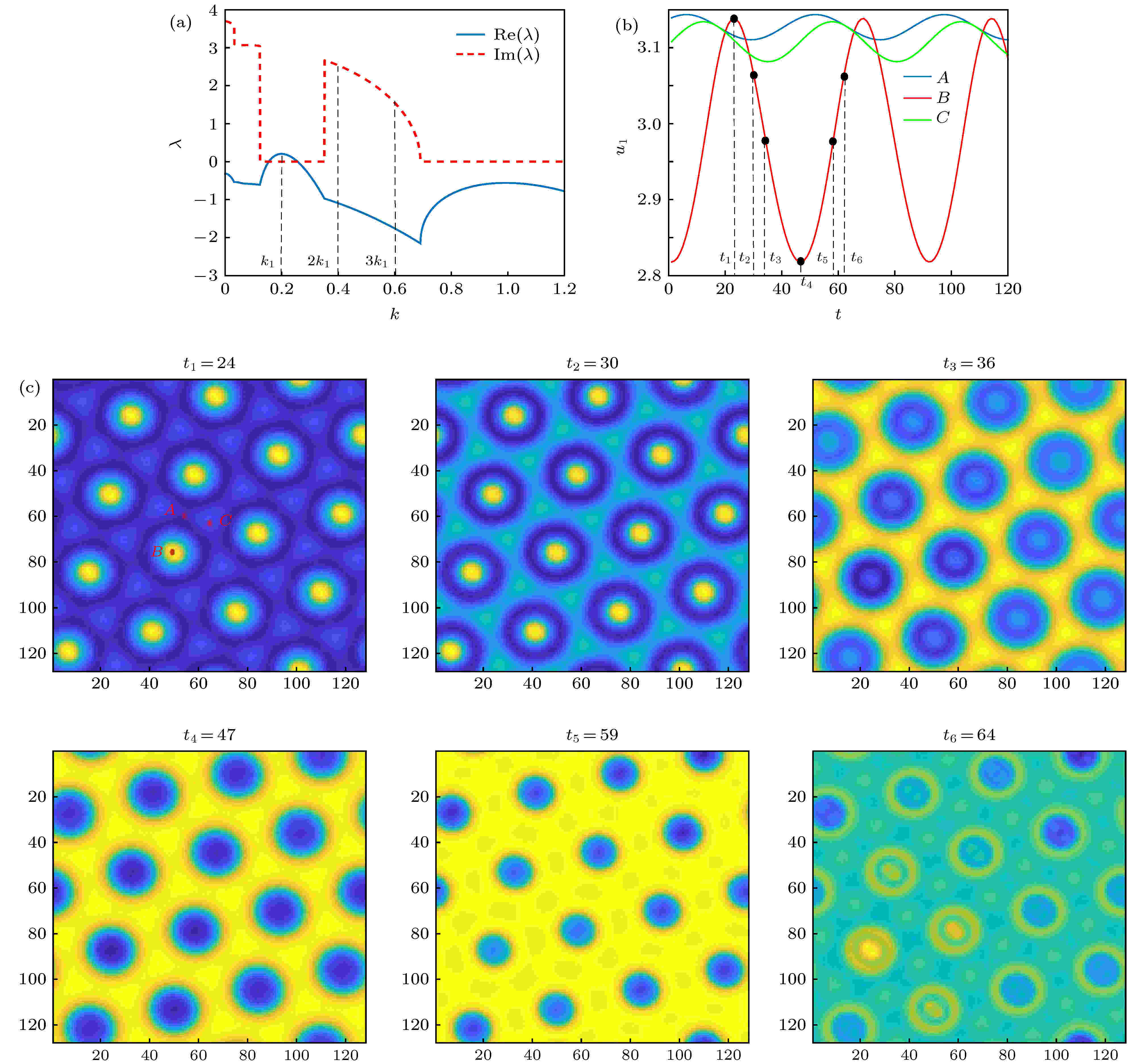 图 3 波数比为1∶5时的时间振荡超六边形斑图,
图 3 波数比为1∶5时的时间振荡超六边形斑图, 










































 图 4 不同本征值
图 4 不同本征值
















































































































































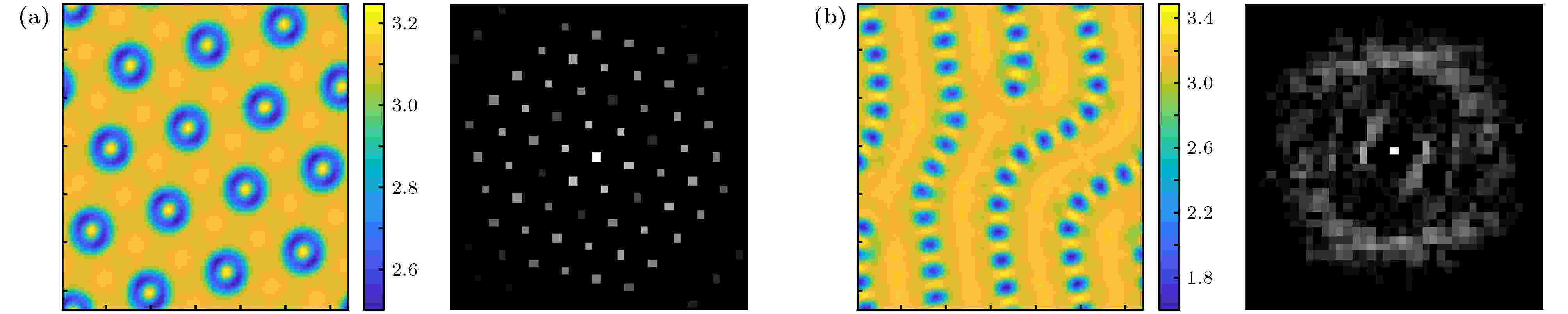 图 5 不同本征值
图 5 不同本征值


















































 图 6 不同耦合强度下的超六边形斑图 (a) 白眼斑图,
图 6 不同耦合强度下的超六边形斑图 (a) 白眼斑图, 

























































