摘要:超短超强激光脉冲在气体等离子体中激发的尾波场加速在过去40年里有了长足的发展, 人们已经在厘米加速距离内获得了数GeV的准单能电子加速, 激光尾波加速的最高电子能量已经达到8 GeV. 为了进一步提升加速电子束的稳定性和品质, 多种电子注入方式先后被提出. 本文研究了基于锐真空-等离子体边界面的密度跃变注入, 着重讨论了不同角度的倾斜边界面对注入电子品质的影响. 二维粒子模拟研究表明, 与倾角为0°的垂直边界面相比, 在合适的倾斜边界角下, 第二个尾波空泡内产生的注入电量可以有近三倍的提升, 同时偏振方向与入射面平行的驱动激光可以增加第一个空泡内注入电子的电量. 根据不同激光入射角度时尾波场中电子自注入的起始位置差异, 分析了电子电量与横向振荡增强的原因. 这些研究有利于提升基于Betatron运动的尾波场辐射及其应用.
关键词: 激光等离子体相互作用/
激光等离子体尾波加速/
电子注入

English Abstract

全文HTML

--> --> -->

超短超强激光在气体等离子体中激发的大幅尾波场有望成为新型大梯度粒子加速器和高频辐射源的加速结构, 自从20世纪70年代末被提出以来^[1], 已经有了长足的发展^[2]. 当一束相对论强度激光在等离子体内传播时, 会在等离子体内部激发电子的空间振荡, 该背景振荡在激光的后侧形成尾波结构, 其相速度接近于光速. 而尾波中的电子, 当其处于尾波场的加速区间, 且满足一定初始条件时, 能被尾波携带着加速前进, 获得比传统加速器中高3—4个量级的加速梯度. 利用这种机制, 目前实验室里已经在20 cm尺度内将电子从静止能量加速到峰值能量8 GeV^[3], 而中心能量在几个GeV的准单能激光尾波电子加速也已被广泛证实^[4-6].
在激光尾波加速中, 根据对输出电子束品质, 如电量、能散、发射度等要求的不同, 需要有效的控制电子注入的方式. 其中尾波波破自注入是最基本和最早被研究的注入方式, 如今已经发展出来多种控制注入的手段, 如密度梯度注入^[7,8]、对撞光碰撞注入^[9]和离化注入^[10-16]等. 除此之外, 另一种行之有效的注入方法是如图1所示的利用特殊的超音速喷嘴, 实现锐的真空-等离子体边界, 在分界面处产生由于密度突变造成的边界注入^[17]. 在锐的真空-等离子体边界处, 电子可以被激光场排出原来所处的等离子体区域, 在边界处形成电子薄层, 该薄层与激光后沿尾波处的背景离子形成电荷分离场, 一些从真空返回等离子体区域的电子会被该静电分离场注入到空泡中, 在空泡的尾部集聚, 形成一个被捕获并加速的致密电子束团.
图 1 真空等离子体边界激光尾波电子注入示意图
Figure1. Schematic of vacuum-plasma boundary injection in laser wakefield acceleration

在尾波中, 注入电子除了通常的纵向加速外, 当电子在尾波中有初始横向动量或横向位置偏移时, 会在尾波横向场的约束力下做横向周期性振荡, 发出频段为X射线的Betatron辐射^[18]. 为了利用激光尾波的Betatron辐射, 除了对电子进行纵向高能加速外, 人们还希望对注入电子的横向位置和动量加以控制^[19], 以得到品质更好的辐射源. 而上述发生在倾斜边界处的电子注入, 有望对该横向注入位置和动量予以控制.
采用二维粒子模拟(2D-PIC)程序OSIRIS^[20]研究倾斜边界对电子注入和最终束品质产生的影响. 在模拟中使用归一化的单位, 长度归一化到等离子体波长尺度L₀ = c/ω_p, 其中ω_p = 2πc/λ_p为等离子体频率, c是真空中的光速. 时间归一化到等离子体周期尺度$ T_0 = \omega_{\rm p}^{-1} $, 这里归一用的等离子体密度为n₀ = 2.76×10¹⁸ cm^-3, 对应的L₀ = 3.2 μm, T₀ = 10.7 fs. 初始入射激光脉冲具有纵向的高斯包络, 其在空间的归一化的电场强度分布为

$\begin{split}a\, &= {\rm{e}}E/(m\omega c) \\ &= {a_0}\exp \Big[ { - \frac{{{{\left( {\xi - {x_0}} \right)}^2}}}{{{d^2}}} - \frac{{{r^2}}}{{{\sigma ^2}}}} \Big]\cos \left( {\frac{{2{\rm{\pi }}}}{{{\lambda _0}}}\xi } \right),\end{split}$

其中ξ = x – ct, 纵向包络长度 d = 2.55 (对应实际所选激光的半高全宽为32 fs), 束腰半径σ = 10, 起始位置x₀ = –20, 聚焦位置在f₀ = 80, 这里a₀ = 3, λ₀ = 0.8 μm. 模拟中为了只研究倾斜角的影响, 将沿着倾斜面梯度方向的密度分布设为线性上升形状, 其归一化长度固定为L₀. 为了系统地做对比研究, 在6组不同的倾斜角度(0°, 15°, 30°, 45°, 60°, 75°)下观察电子注入的情况. 激光偏振垂直于模拟平面(即S偏振), 从左侧沿x轴正向入射到等离子体中.
本文将对该边界注入机制开展数值模拟研究, 以进一步获得对该机制的清晰理解, 并且根据模拟结果, 得到注入电子束品质(能散、电量和横向动量)对边界倾角和激光偏振方向的依赖关系, 为产生基于尾场的辐射源提供参考.

前人已经有过一些关于激光在等离子体锐密度跃变处产生电子注入的讨论^[21-24]. 我们发现当上升沿的密度变化梯度较短, 相对于尾波周期成为跃变过程时, 当一个短周期的激光脉冲由真空入射到等离子体中时, 激光首先与边界面处等离子体相互作用, 其有质动力会排开周围的电子, 使之偏离原来位置, 形成只有离子的正电荷区域与周边密集的电子峰, 在纵向形成向前传播的尾波. 在此过程中, 会有小部分电子被甩到激光后沿, 直接进入第一个尾波空泡内, 形成第一次注入; 同时大量由于纵向振荡被抛射至真空的电子与边界等离子体层形成正向的电荷分离场, 又将部分处在真空区域中的电子拖拽回等离子体, 正好处于第二个尾波空泡内, 形成第二次电子注入. 由于电荷分离场中的电子相比激光前沿碰撞接触的电子数量更多, 故注入第二个空泡中的电子会比第一个空泡中的电子要多很多. 研究表明通过控制激光和等离子体密度上升沿等参量, 可以有效控制边界电场的强度以及电子在这局部区域的运动, 从而改变注入电子束的电量和注入能量^[7]. Hu等^[24]发现通过多束脉冲激光的驱动, 还可以有效改善注入电子的品质. 为了在低密度情形下产生有效的自注入, 真空等离子体分界面上升沿长度L不能过长. 在模拟中保持L < λ_p (λ_p为等离子体波的波长), 才能有可观的电子被拖曳进真空, 形成足够强的电荷分离场, 发生边界自注入. 本文主要讨论当真空等离子体分界面为倾斜面时, 该倾斜角度对注入的影响, 这里将倾斜角度定义为激光传播方向与等离子体边界面法线方向的夹角. 研究表明与通常研究的0°入射锐边界注入不同, 当倾斜角度发生变化时, 注入电子的能量、电量以及横向动量均有较大的变化. 通过控制激光的入射角, 可以有效提升电子的注入电量和横向振荡幅度, 这为增强相应的Betatron辐射强度奠定了基础.

2

-->

3.1.倾斜角对注入电量与能量的影响

首先研究真空等离子体边界面倾角对注入电量和最终电子能量的影响. 如图2(a)所示, 数值模拟研究表明, 在锐真空-等离子体边界注入下, 通常电子会被注入到第一和第二个尾波中. 为了研究倾斜角的影响, 分别对注入到不同空泡的电子进行统计, 如图2(b)所示, 对第二个空泡中的超粒子, 统计它们的电量、动量和能量, 并随机选取其中的100个计算它们的轨迹.
图 2 倾斜角为0°时激光传播500T₀后等离子体密度与注入电子(γ ≥ 15)的位置分布　(a)注入电子的分布; (b)放大后第二个空泡中的电子分布
Figure2. Distributions of plasma density and injected electrons after 500T₀ propagation when the boundary slant angle is 0°: (a) Injected electrons; (b) electrons in the second bubble

分别对0—500T₀时间范围内不同倾斜角度情况下两个空泡中被加速电子进行统计, 在它们的相对论因子大于等于15时计入统计, 如图3所示. 从图3可以看出, 不同倾斜角度对应的激光电子加速到统计阈值(γ ≥ 15)所需的时长是不一样的. 简而言之, 倾斜角越大时, 激光后沿的尾波形成时间越晚, 电子越晚被捕获; 而低倾斜角情况下, 尾波形成较早, 电子被捕获时间也相对更早, 从而加速启动的更早.
图 3 激光传播过程中不同角度下的电子平均能量增长的情况　(a)第一个空泡内电子平均相对论因子γ的变化; (b) 第二个空泡内电子平均相对论因子γ的变化
Figure3. Average energy growth with time: (a) Average gamma factor of electrons in the first bubble; (b) average gamma factor of electrons in the second bubble

如图3所示, 虽然不同边界倾斜角度下的电子加速启动时间不同, 但到达统计能量阈值后的加速梯度则差别较小. 这是因为形成了尾波结构后, 电子在等离子体中的加速就与边界条件无关, 仅与当地尾波场强度和其在尾场中所处的相位有关. 换言之, 仅与此时的激光强度和等离子体密度有关(此时电子基本都处在尾波的末尾处, 所以电子在尾波中的相位差别不大). 由此可见, 为了合理比较不同倾斜角度下被加速电子的能量和电量, 应比较经过相同加速距离后电子的平均能量与电量, 而不是固定在某一个加速位置处比较这些信息.
图4对比了不同倾斜角度下注入电子经过相同加速距离(1 mm)后的平均能量和注入电量. 从图4(a)可以看出, 当倾斜角提升时, 第一个空泡与第二个空泡的电子的平均能量均有所下降, 在大倾斜角度下, 两个空泡的电子的平均能量则趋于相同. 一般而言, 因为第一个空泡电子的产生时间更早, 加速时间更长, 其相较于第二个空泡电子的平均能量也要更高. 而且由于第一个空泡加速电子束自身激发的尾场与激光尾场相位相反, 往往会造成后面的尾场强度小于第一个加速节处的尾场, 所以通常第二个加速空泡中电子的能量要小于第一个空泡. 而在当前的情形下, 则有所不同, 随着入射角的增大, 两个空泡之间加速电子平均能量的差别则渐趋于无. 这是因为此时激光碰撞一侧的时间比激光碰撞中心的时间要更早, 第一个空泡的电子虽然更早进入空泡受到尾波场加速, 但是注入第二个空泡的电子在注入前就已经从电荷分离场中获得了一些能量, 它的起始注入能量比第一个空泡电子要更高.
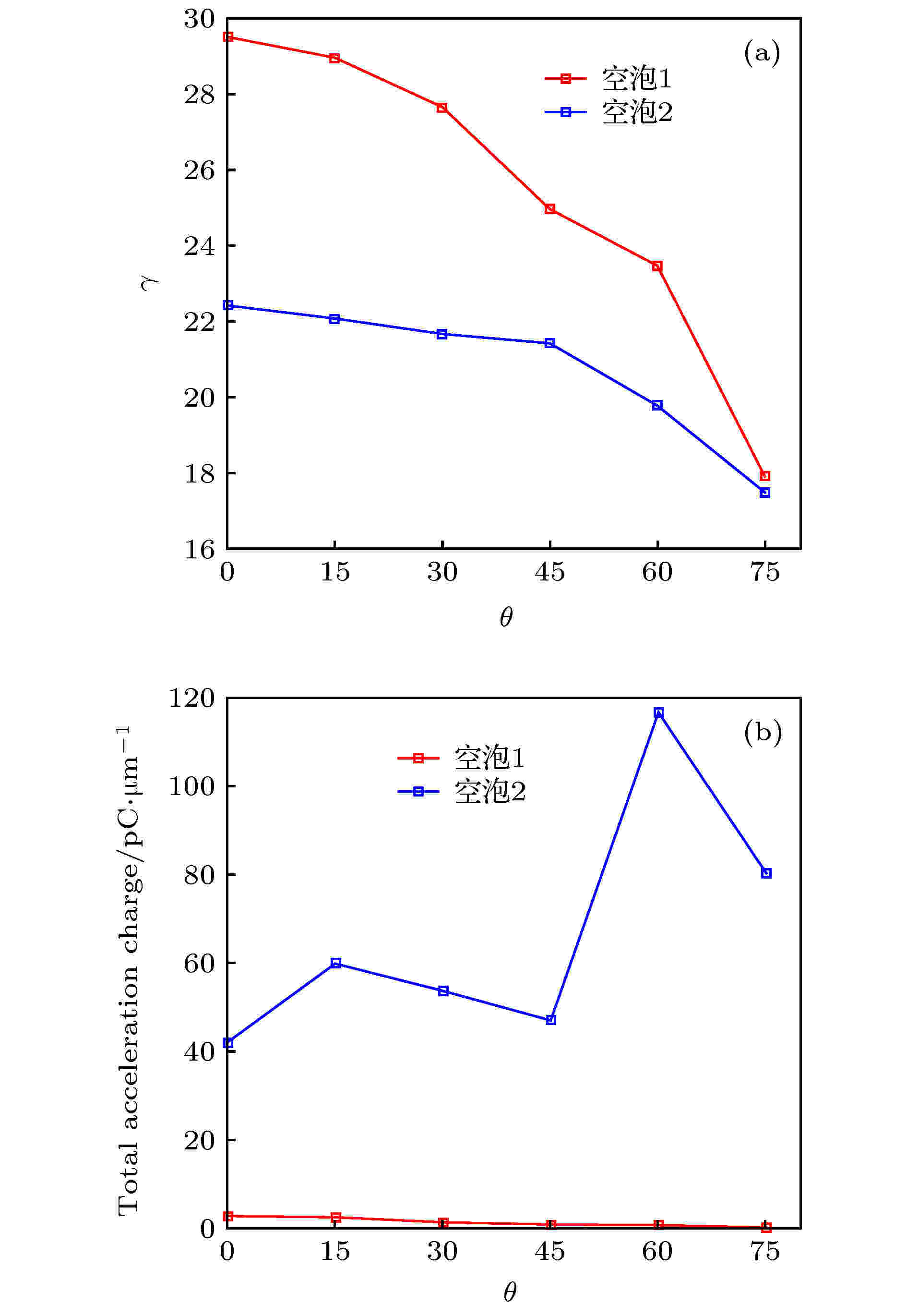图 4 不同角度下电子注入后经过相同加速距离后的加速情况对比　(a)被加速电子的平均能量; (b)被加速电子的总电量(单位归一化到 pC/μm)
Figure4. Electrons statistics after same acceleration length: (a) Average energy; (b) total acceleration charge (normalized to pC/μm).

图4(b)将不同倾斜角度下两个空泡内电子的电量进行比较, 在锐边界注入情形下, 第一个空泡的注入电量比第二个空泡少很多, 这种差异在倾斜角达到60°时最大, 此时第二个空泡的注入电子电量达到最高, 而第一空泡内电子注入量趋于0. 模拟中发现两个空泡中电子的平均能量其实相差并不是很大(见图4(a)), 所以最终加速电子束的总能量(以及激光到被加速电子的转换效率)依赖于被加速的电量, 它成为衡量加速效率的重要指标. 故对于锐边界注入, 具有较大注入电量的第二个空泡的电子会更适合应用, 这一点值得在应用研究中予以重点考虑.
2 -->

3.2.倾斜角对注入电子横向振荡的影响

除了关注加速电量外, 被加速电子束的横向振荡对于电子束的Betatron辐射也是非常重要的, 直接关系到辐射的强度和辐射谱分布. 为了明确倾斜边界对电子横向运动产生的影响, 研究了被加速电子的运动轨迹. 对两个特定的倾斜角度(0°和45°), 在不同的空泡中各选取100个被加速电子, 根据它们的轨迹分析注入特征.
如图5(a)所示, 在锐的倾斜情形中(0°), 注入电子沿着激光传输方向是基本对称的; 在边界倾斜角为45°时, 如图5(b)所示, 产生的注入电子则具有上下非对称性. 注入电子的这种上下轨迹不对称性是斜入射与0°入射激光的主要不同之处. 在边界面与入射光非垂直的情况下, 可以预见到激光单侧将与等离子体优先接触, 另一侧的接触时间则相对滞后, 此时仅有最先接触的那一侧附近的电子能够发生注入. 这种机制是导致二者的加速电子在统计上轨迹不同的原因, 同时也会导致电子在加速过程中横向振荡的不同.
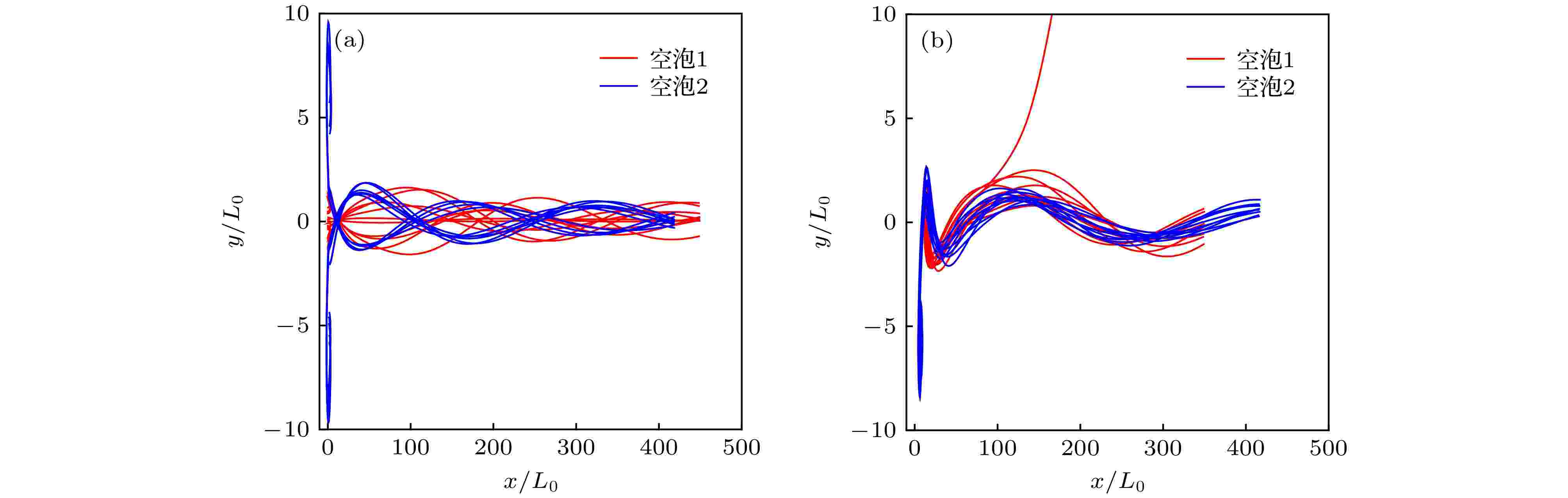图 5 不同倾斜角度下的第一个空泡(红色)和第二个空泡(蓝色)中注入电子的轨迹(为了显示清晰, 对两种倾角情形, 各自只选取了10个典型的电子)　(a) 0°; (b) 45°
Figure5. Trajectories of electrons in the first bubble (red) and second bubble (blue): (a) 0°; (b) 45°. Ten electrons’ trajectories have been selected for clearer view

图6显示了所有高能电子的横向动量的统计结果, 对于0°和45°的两种边界下, 空泡中被加速电子的横向振荡过程存在差异. 0°边界倾角时, 第一个空泡内注入电子的横向动量较小, 而第二个空泡内注入电子的横向动量则沿入射光两侧对称振荡, 幅度与45°倾角边界注入时类似, 但该倾角下第一个空泡内电子的振荡幅度也得到了增强(这是由于第一个空泡内电子注入较早, 但注入时空泡形成具有不对称性, 电子获得初始横向动量较大), 有利于强的Betatron辐射. 通常大的横向振荡幅度有望提升小型化台面X射线辐射源的强度和辐射谱的中心频率.
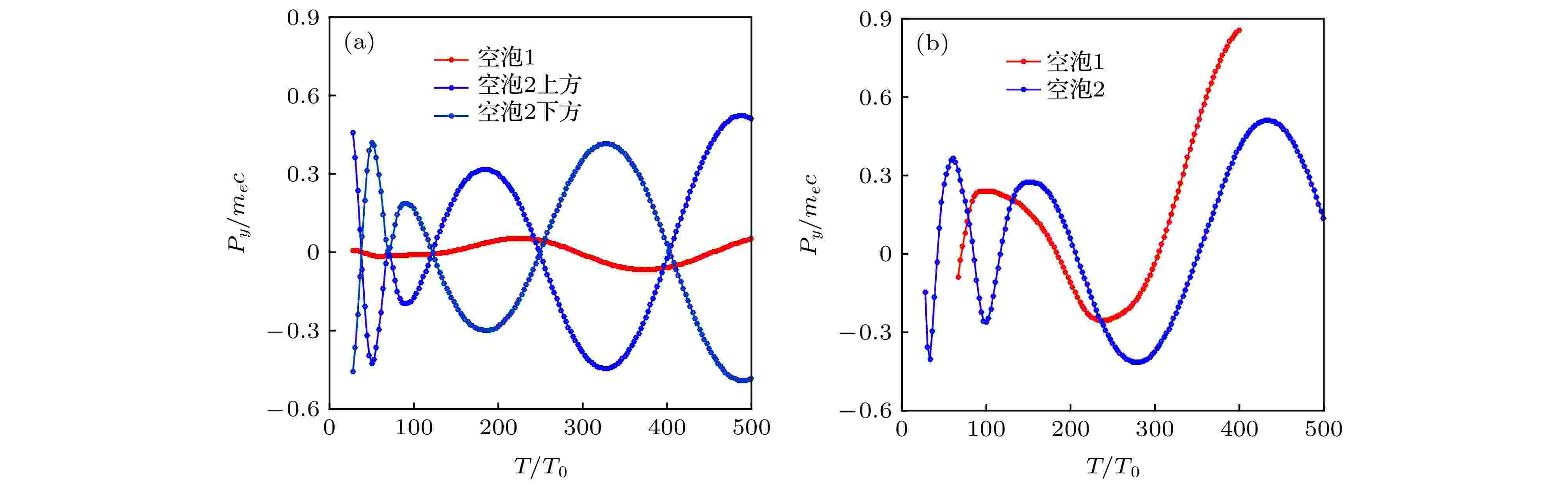图 6 (a) 0°倾斜边界角时注入空泡1 (红)和空泡2上下两侧注入电子(蓝)的平均动量; (b) 45°倾斜边界角时注入空泡1和空泡2电子的平均动量
Figure6. (a) Average transverse momentum of electrons in the first bubble (red) and second bubble (blue) when the boundary slant angle is 0°; (b) average transverse momentum of electrons in the first bubble (red) and second bubble (blue) when the boundary slant angle is 45°

2 -->

3.3.激光偏振方向对注入电子的影响

激光的电场方向对边界面注入过程也有一定的影响. 在二维模拟中, 当激光偏振方向与模拟平面垂直时(S偏振), 电子受到的激光作用仅表现为有质动力的作用而被光场排开; 而当激光偏振方向与模拟平面平行时(P偏振), 电子将在受到有质动力作用的同时也受到了激光电场的直接作用. 这种机制在激光斜入射高密度等离子体靶时会产生至关重要的作用^[25]: 电子在由真空拉回到等离子体的过程中时, 将会与入射和反射的激光相互碰撞, 部分电子会被激光在真空中直接加速. 在尾波加速的等离子体密度区间, 激光虽然不能被等离子所完全反射, 但是由激光前沿排开的电子在回流注入时也可能会与尾部的激光发生相互作用, 从而对注入产生影响.
基于此, 比较了45°边界下, S偏振和P偏振入射激光导致的尾场中注入电子的电量、横向振荡和能谱. 电量上, 如表1所列. 在第一个空泡中, P偏振入射激光注入电子比S偏振入射激光注入电子电量高三倍左右, 而第二个空泡中, 二者则相差甚小. 这证明了在斜入射机制下, 只有第一个空泡中的电子受到了类似Brunel过程^[26]中的激光电场的直接作用. 而在第二个空泡内的电子在注入过程中, 仅受到了激光场平均下来的有质动力和静电分离场的影响, 因此对驱动激光偏振依赖度不大.

电量/pC·μm–1	S偏振	P偏振
第一个空泡	1.24	3.88
第二个空泡	47.21	47.00

表1S偏振和P偏振激光45°入射时注入空泡中的电子电量
Table1.Injection charge of S-polarization and P-polarization incidence at 45°.

同时还比较了S偏振和P偏振在45°倾斜边界下注入电子的能谱分布. 发现P偏振注入电子的能谱谱宽相对较小, 相较于S偏振入射注入电子束团的能散更低, 但两者中心能量差不多. 这可能是由于P偏振第一个空泡中注入的电子稍多造成的. 从整体来看, 在这样的激光参数下, 注入以第二个空泡为主, 所以激光偏振效应对电子束的能谱和能量差别不大.

接下来分析倾斜边界下电子的注入轨迹. 如图7所示, 当激光传播至边界面时, 其有质动力排开光轴处的电子(图7(a)), 其中大部分电子被向前推进等离子体内部或从侧片被排开到真空区域, 与背景离子形成真空-等离子体电荷分离场(图7(b)). 部分被排开的电子受到该电荷分离场的牵引后溯回传播轴, 并在空泡尾部形成突出的密度峰(图7(c)). 在这个回溯过程中, 位置较靠前的电子继续被密度峰处的电场所散射, 并在峰前部聚集, 由于正好处于空泡内电子加速区域(图7(d)), 这些电子有可能会被空泡捕获并得到加速.
图 7 倾斜边界角为0°时的电子注入过程(等横向间距选取了3个粒子作为示意, 背景为等离子体密度, 线条代表粒子的真实轨迹, 圆圈代表粒子在该时刻的位置)　(a) T/T₀ = 20; (b) T/T₀ = 40; (c) T/T₀ = 60; (d) T/T₀ = 90
Figure7. Electrons’ injection trajectories when the boundary slant angle is 0°: (a) T/T₀ = 20; (b) T/T₀ = 40; (c) T/T₀ = 60; (d) T/T₀ = 90. Here the background color bar represents the plasma density, we have selected 3 particles with equally separation along the transverse direction. The blue and red lines represent the injection trajectories and the circles represent the particles’ positions at that time

第二次注入的电子先是被激光的有质动力和空泡前部正向电荷场作用进入真空区域, 而后受到静电分离场的吸引回溯, 并进入第二个空泡的负向电场区域被捕获加速. 0°边界倾斜角情况下这些电子基本位于激光两侧, 模拟中观察到少量电子(7%)于中心被拖曳向外经历回旋过程也进入第二个空泡, 而这一情况在非0°边界倾斜角情况下则仅局限于单侧(如图8所示). 在被捕获过程中, 第二次电子注入的允许范围较第一次注入范围更大. 相比较而言, 第一次注入发生的空间范围小, 被注入到第一个空泡的电子电量也就比注入到第二个空泡的电子电量少很多. 同时, 边界越倾斜, 激光与等离子体边界相互作用的时间也就越长, 被扰动进真空的电子也就越多, 这样第二次注入的所允许的起始范围就更大, 造成了最终被加速电子电量的不同.
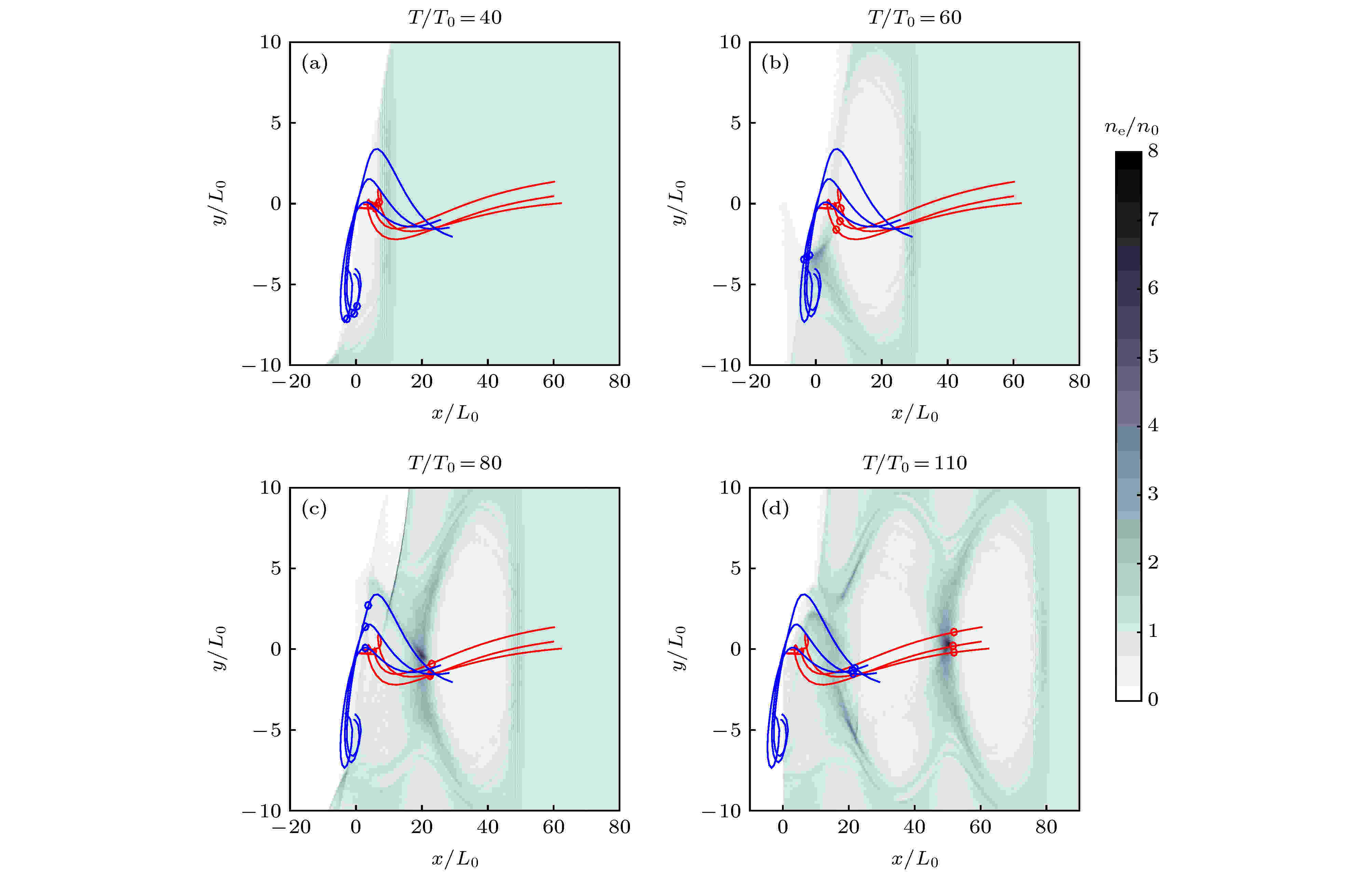图 8 45°入射下边界面产生电子注入的过程　(a) T/T₀ = 40; (b) T/T₀ = 60; (c) T/T₀ = 80; (d) T/T₀ = 110
Figure8. Electrons injection at 45° incidence: (a) T/T₀ = 40; (b) T/T₀ = 60; (c) T/T₀ = 80; (d) T/T₀ = 110

横向振荡幅度的差异来自于电子注入时起始位置的不同(如图9所示); 0°入射第一次注入的位置在激光传播的中轴线方向, 而第二次注入的电子起始位置对称地处在激光的两侧, 上下两侧电子的横向振荡幅度相同, 方向相反. 当真空等离子体边界面变为倾斜, 原本对称地处在激光两侧位置的注入电子区域仅保留了其中较早与激光碰撞的一侧, 横向振荡仅源于单侧的电子, 相较于0°入射产生的注入, 其注入位置的纵向长度有所增加.
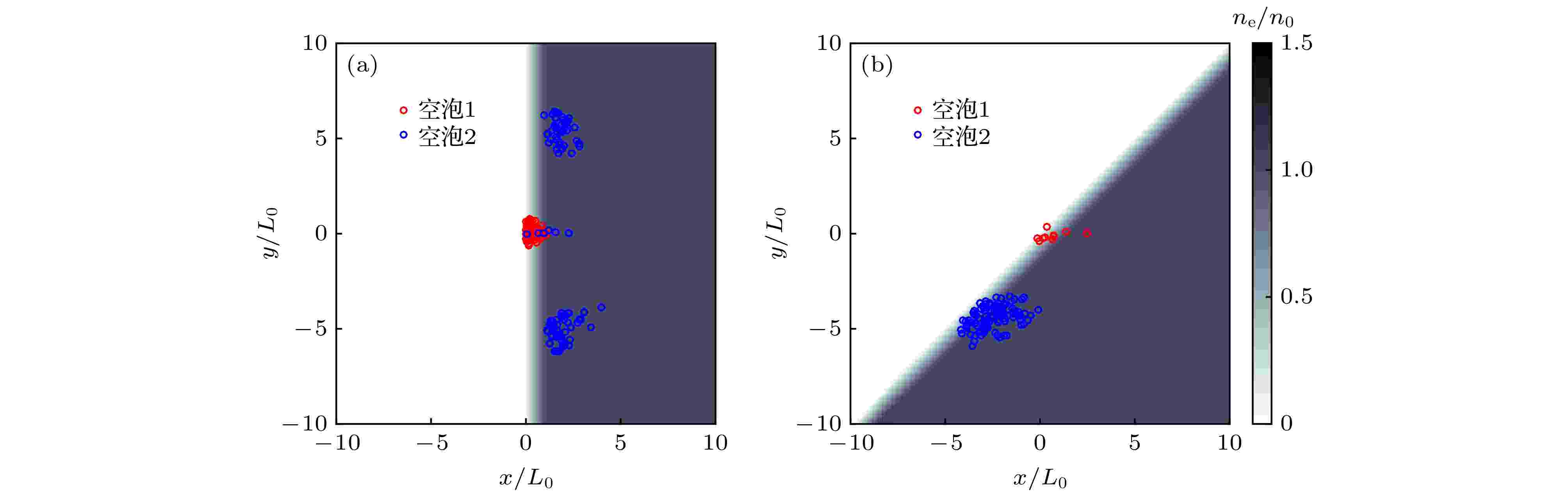图 9 (a)倾斜边界为0°情况下第一个空泡和第二个空泡内注入电子的起始位置; (b) 倾斜边界为45°入射下第一个空泡和第二个空泡内注入电子的起始位置
Figure9. (a) Original positions of the trapped electrons when the boundary slant angle is 0°; (b) original positions of the trapped electrons when the boundary slant angle is 45°

本文利用二维粒子模拟程序研究了一种发生于真空等离子边界位置处的尾场注入机制. 比较了不同倾斜边界角度对电子注入电量、能量和横向振荡的影响. 研究发现在给定激光强度下, 通过改变激光入射角、注入总电量和电子横向振荡幅度均可以发生改变, 分析了引起这些变化的原因. 这些研究对于控制初级电子束的注入, 将来与多级高能尾场加速相结合有助于对基于激光尾波的桌面型辐射源所需的大振荡、大电量电子束的产生提供参考^[27,28]. 在这里为了单独隔离出倾斜角度的影响, 在研究中选取了较为锐的真空等离子体边界(上升沿较短), 目前普通的气体喷嘴结构还较难实现这样的极端锐条件^[29], 然而通过选取合适的刀边在气体中形成冲击波等方法有望实现这样的上升沿结构^[30].