摘要: 时域色散精密控制是超短激光产生及其应用中的关键技术之一, 它通过控制各波长的光程产生相对延迟从而改变脉冲宽度. 展宽器是啁啾脉冲放大激光系统中对激光脉冲展宽的装置, 基于光线追迹法研究光线在展宽器中的传输路径, 可计算飞秒脉冲中各波长的光程, 进而计算脉冲展宽量并应用于系统设计. 由于展宽器的光程表达式复杂, 直接对其求导获得色散表达式较困难, 目前只能采用数值导数获得近似解, 这在计算过程中会引入误差, 不利于激光系统精确设计和优化. 本文介绍了一种易实现的求解展宽器色散的解析算法, 通过归纳展宽器光程表达式特点, 引入四个基元函数, 将光程表达式分解和反复代换, 可得到高阶色散的精确解析值. 本文首先对Martinez型展宽器重新光线追迹, 获得与Offner型展宽器一致的相位表达式, 其次通过解析算法获得了两种展宽器的精确高阶色散值, 最后将解析算法与数值算法的结果进行了比较. 该解析算法对于啁啾脉冲放大系统的参数设计具有实用价值.
关键词: 色散补偿 /
啁啾脉冲放大 /
脉冲展宽 /
高阶色散 English Abstract Analytical algorithem of stretcher dispersion in chirp pulse amplification laser system Wang Nan 1,2,3 ,Ruan Shuang-Chen 2,4 1.College of Physics and Optoelectronic Engineering, Shenzhen University, Shenzhen 518060, China Fund Project: Project supported by the Start-up Project of Scientific Research for New Teachers of Shenzhen University, China (Grant No. 2017020) and the Science and Technology Plan Project of Shenzhen, China (Grant No. JCYJ20170818142940246)Received Date: 18 September 2019Accepted Date: 28 October 2019Published Online: 20 January 2020Abstract: Dispersion control is one of many key techniques in ultrashort laser pulse generation and its applications. By controlling the optical path of wavelength in the laser pulse to generate relative time delay, the pulse width of laser can be changed. The stretcher is the optical scheme to broaden the pulse width in chirp pulse amplification. By using ray trace, the pulse stretch time can be evaluated. However, due to the complicated formula of optical path in stretcher, it is difficult to obtain an analytical expression of high-order dispersion by using direct derivative. In this case, the present numerical methods are commonly used and error would be introduced into the optical system design and optimization inevitably. In this paper we introduce an analytical algorithm of stretcher dispersion. By summarizing the characteristic of stretcher formula, four fundamental functions are introduced to help to calculate the analytical derivative. By substituting the separate terms of the expressions step by step, analytical calculation of stretcher dispersion can be realized. In this paper, the ray trace of Martinez stretcher is first introduced to achieve similar phase expressions to them of existing Offner stretcher, then accurate high order dispersion results are attained by using analytical method, finally the calculation results by using the analytical method and numerical method are compared with each other. The algorithm introduced into this paper for calculating the dispersion is practical and hopeful in designing the chirp pulse amplification laser systems.Keywords: dispersion compensation /chirp pulse amplification /pulse stretch /high-order dispersion 全文HTML --> --> --> 1.引 言 飞秒激光啁啾脉冲放大(CPA)是结合激光脉冲宽度操控与激光能量放大以实现超快超强激光输出的技术. 基于这种技术, 目前已经可以获得峰值功率10 PW以上[1 ] 的超强激光脉冲(1 PW = 1015 W), 为强激光与物质相互作用的研究提供了强大的技术工具. 峰值功率为太瓦量级的啁啾脉冲放大激光系统相比前者可以实现较高的脉冲重复频率, 在先进工业制造和生物医学领域具有优异的应用价值. 如在激光加工领域, 飞秒激光加工相比于传统的机械加工具有非接触的优点, 相比于长脉冲激光加工可以直接将介质等离子体化实现高精度的冷加工; 在生物医学领域, 飞秒激光可进行多光子成像获得比传统光学成像更深的穿透深度、超衍射极限的空间分辨率及更低的背景荧光噪声[2 ] , 也可以用于外科手术和靶向治疗. 当前的超快激光啁啾脉冲放大技术正向着产生更高的功率密度、更洁净的激光脉冲和以新激光材料为基础打造更低造价的新型激光系统等方向发展, 这些都需要可靠的光学理论模型作为支撑. 本文在理论上提出了一种超快激光啁啾脉冲放大系统中展宽器色散的解析计算方法, 对于精确计算展宽器色散、优化系统结构和设计新型激光系统具有实用价值.$\varPhi = KL$ 代入材料折射率方程并对光频率ω 求导进行色散分析[3 ] , 由于可以较方便地获得色散的解析表达式, 本文不再叙述过程. 对于复杂的展宽压缩光学系统, 则需要进行光线追迹进行光程计算. 早在1969年, Treacy[4 ] 就使用光线追迹对平行光栅对的相位和各阶色散进行了详细分析; 之后Fork等[5 ] 、Martinez等[6 ] 和张留洋等[7 ] 对棱镜对的色散进行了计算; Kane和Squier[8 ] 、Durfee等[9 ] 、郭淑艳等[10 ] 、徐婷婷等[11 ] 、苏娟等[12 ] 和Bucht等[13 ] 对棱栅对的色散进行了研究; Cheriaux等[14 ] 、Zhang等[15 ] 、蒋捷等[16 ] 、Wang等[17 ] 、田金荣等[18 ] 对Offner型展宽器进行了光线追迹与计算; Martinez[19 ] 、Zhang等[20 ] 、王勇等[21 ] 、宋晏蓉等[22 ] 和Su等[23 ] 对Martinez型展宽器进行了计算分析; 孙大睿等[24 ] 、Backus等[25 ] 、Zhang等[26 ] 对啁啾脉冲放大系统的色散优化给出了建议; 除此之外, 研究人员也分析了有限的光束宽度、光栅失谐、光栅拼接、非匹配光栅、曲面光栅、光谱宽度、面型平整度和球差等因素对展宽器或压缩器中脉冲的影响, 在这些方面有较多的文献报道, 本文不再展开介绍. 这些针对色散装置的研究为啁啾脉冲放大激光系统设计提供了很好的理论支持. 然而, 对于以上的展宽压缩光学系统装置, 由于相位表达式复杂, 难以直接推导出高阶解析导数表达式, 目前主要是通过设定自变量步长计算函数值再进行差商来进行数值求导的方法, 而这样会给系统引入误差, 不利于系统参数的设计和优化, 尤其是高阶数值导数值的误差会逐级累积增大; 另外步长越大, 使得偏离误差越大, 而步长越小, 计算量增大, 还会引入振荡误差, 也难以快速、精确地获得色散值, 不利于展宽器参数设计和色散的精密控制. 本文提出了一种解析算法, 并对Offner和Martinez型展宽器的各阶色散进行了解析计算, 也对数值算法和解析算法的结果进行了比较. 这种算法对于棱镜对、棱栅对等具有复杂相位表达式的解析导数求解也具有普遍适用性, 对于优化设计展宽器和精确补偿色散具有实用意义.2.Offner型展宽器和Martinez型展宽器的相位表达式 Offner展宽器和Martinez展宽器是啁啾脉冲放大激光系统中最常用的两种展宽器. 由于以前的研究人员针对展宽器的光线追迹过程各有描述, 有的为了简化计算也会使用近似, 从而使得色散计算过程和获得的展宽器相位表达式在表述和精度上都存在差异. 为了便于计算和比较, 本文首先对两种展宽器的相位表达式进行统一.图1 所示, 本文直接使用文献中的光线追迹结果作为进行计算的相位Φ 表达式[18 ] :图 1 Offner型展宽器的结构与光路图Figure1. Scheme of Offner stretcher.${\varPhi _{{\rm{Lo}}}}$ 是总光程引入的相位, ${\varPhi _{{\rm{Go}}}}$ 是光栅衍射相位修正因子, AB o , BC o , CD o , DE o , EF o , EA o 是展宽器中各段光路的表达式, 与文献[18 ]表述相同, 引用如下:θ 0 为光栅与OO' 的夹角, 是个初始设定值, 可以决定衍射光束在凹面镜上的位置, 此处设定为激光中心波长λ 0 在衍射后位于凹面镜的中心, 以最大程度地利用凹面镜实际使用面积. θ 1 —θ 5 分别为光线与水平线、凹面镜法线、凸面镜法线、凹面镜法线、光栅法线和光栅的夹角.Φ 的表达式[19 -22 ] , 为了统一描述和追迹方法, 本文对Martinez型展宽器重新进行光线追迹并获得与Offner型展宽器一致的相位表达式为:图2 所示, 其中的红色实线为传输光, 深黄色的虚线为光栅, 黑色的实线曲线和直线分别为凹面反射镜和平面反射镜, 黑色的虚线曲线为凹面镜相对于平面镜的镜像, 其余黑色虚线直线为辅助线. 光线从从A 点入射到光栅, 经凹面镜B 点、平面镜C 、凹面镜D 和光栅E 点后出射; θ 0 为光栅与OO' 的夹角, 选取为此时激光中心波长λ 0 的衍射光线为AO' ; θ 1 —θ 6 分别为光线与水平线、凹面镜法线、平面镜法线、凹面镜法线、光栅法线和光栅的夹角; 图中凹面镜圆心位于O 点, 圆半径为R ; 平面镜位于R /2处; 光栅凹面镜间距O'A 为L . BD' 延长线交OO' 于A' 点; DE' 延长线交OO' 于G 点; AF ⊥EF . 由几何关系和正弦定理, 可得各段光路的光程表达式为:图 2 Martinez型展宽器的结构与光路图Figure2. Scheme of Martinez Stretcher.Φ 关于光频率ω 的各阶解析导数是比较困难的.3.解析算法 通过分解各段光程表达式并循环代换的方式来获得解析计算结果. 观察相位式中的各段光路表达式可以发现, 所有式子都由四个初等函数构成, 即y = sin(x ), y = arcsin(x ), y = A /B , y = A + B . 为了求解解析解, 只需求解这四个初等函数的导数, 然后把所有表达式依次代入这4个函数即可. 以y = sin(x )为例, 参数x , y 都是光波长λ 或频率ω 的导数, 该初等函数的一阶到四阶导数使用简单的求导规则就可以获得:x 的各阶导数值, 代入(3 )式就可以获得参数y = sin(x )的各阶解析导数值. 同样的道理, 可得y = arcsin(x ), y = A /B , y = A + B 这三个初等函数的解析导数表达式(见附录 ). 只要已知输入参数x 或A 与B 的导数值, 就可以获得这三个初等函数的对应的解析值. 使用软件编程, 将以上表达式创建4个自定义函数, 保存为函数文件后, 对于各段光路反复调用这4个函数就能完成相位的求解.${\theta _1}$ 为例, 为了最终求解相位关于角频率的导数, 将追迹波长λ 变换为角频率ω , 得${\theta _1} = \dfrac{{\text{π}}}{2} - {\theta _0} - \arcsin \left( {\dfrac{{2{\text{π}}{\rm{c}}}}{{\omega d}} - \sin {\gamma _0}} \right)$ , 式中的${\theta _0}$ 是光栅与对称轴的夹角, ${\gamma _0}$ 是光线在光栅上的入射角, d 是光栅常数, c 是光速, 2和π是常数, 各阶导数为0; 角频率ω 是自变量, 其一阶导数为1, 高阶导数为0. 所以参照上述初等函数发现, $\dfrac{{2{\text{π}}{\rm{c}}}}{{\omega d}} = \dfrac{{2{\text{π}}{\rm{c}}}}{d\omega} = A/B$ , 其中此处$A = \dfrac{{2{\text{π}}c}}{d}$ , 各阶导数为0, $B = \omega $ , 一阶导数为1, 各阶导数为0, 代入到A /B 的解析导数式中, 可得$\dfrac{{2{\text{π}}c}}{{\omega d}}$ 的各阶解析导数值, 再代入A + B 的解析导数式中求得$\dfrac{{2{\text{π}}c}}{{\omega d}} - \sin {\gamma _0}$ 的各阶导数值, 继续代入arcsin(x )的解析导数表达式中求得$\arcsin \left( {\dfrac{{2{\text{π}}c}}{{\omega d}} - \sin {\gamma _0}} \right)$ 的各阶导数值, 再代入A + B 的解析表达式中求解得到$\dfrac{{\text{π}} }{2} - {\theta _0} - \arcsin \left( {\dfrac{{2{\text{π}}c}}{{\omega d}} - \sin {\gamma _0}} \right)$ 的各阶解析导数值, 这样就获得了${\theta _1}$ 的各阶解析导数值. 使用同样的方法, 依次得到${\theta _2}\text{---}{\theta _6}$ 、光程AB M 至EF M 以及最终的相位Φ 的各阶解析导数值. 虽然该过程需要把表达式分解成很多项依次代换, 但是使用程序设计很容易实现, 所以代换过程的程序的编写和运算都非常快, 并且计算结果是解析值, 比通常的数值运算更为精确.4.计算结果 基于上述算法, 对Offner型展宽器和Martinez型展宽器进行了编程计算. 使用的两种展宽器的计算参数如表1 所列.计算参数 Offner型 Martinez型 凹面镜曲率半径R /mm 1210 1210 光栅凹面镜间距L /mm 1005 400 激光光栅入射角γ 0 /(°) 22 22 光栅刻线密度/mm–1 1200 1200 展宽程数 2 2
表1 用于计算的Offner型与Martinez型展宽器参数Table1. Structural parameters of Offner and Martinez stretchers.6 fs2 . 使用高斯成像公式可得, Offner型展宽器的等效光栅对间距为$ 2(R-L)\cos\theta_0 $ , Martinez型展宽器的为$ 2(R/2-L)\cos\theta_0 $ , 此处两种展宽器参数对应的等效光栅对间距值都为332.407 mm.图3 所示. 红线给出的是Offner型展宽器的一阶到四阶色散, 其中图3(a) 为群延迟, 图3(b) 为群延迟色散或二阶色散, 图3(c) 和图3(d) 分别为三阶色散和四阶色散. 同理, 图3(a) —图3(d) 的蓝线分别给出的是Martinez型展宽器的一阶到四阶色散图. 可见采用该参数时, 两种展宽器提供的色散大概是相同的, 而Offner型展宽器在光谱边带处提供更大的色散量.图 3 Offner型与Martinez型展宽器700?900 nm的解析计算色散曲线 (a) GD; (b) GDD; (c) TOD; (d) FODFigure3. Analytical dispersion results of Offner and Martinez stretcher: (a) GD; (b) GDD; (c) TOD; (d) FOD.图4 给出, 其中图4(a) , (c) 为Offner型展宽器的结果, 图4(b) , (d) 为Martinez型展宽器的结果. 从图4(a) , (b) 中可以看出, 随着步长数值的增大, 二阶色散值的数值计算误差也相对于解析计算值增大, 所以数值计算的步长不宜过大. 图4(c) , (d) 为两种展宽器的四阶色散值, 其中红色点线的0.1 nm步长的值表现出显著振荡, 这是由于步长过小使得数值导数的分母过小, 引入了数值差分误差, 因而数值计算的步长也不宜过小. 本文通过多次模拟发现, 采用数值差商计算展宽器色散过程中, 为避免数值导数差分误差和累积误差过大, 仅进行二阶色散的计算时, 最佳步长可以选为0.0006 nm左右, 若进行四阶色散的计算, 最佳步长在0.3 nm左右. 通过对比数值求解与解析计算结果, 可以发现本文的解析算法计算可以避免数值计算的两种误差问题, 尤其在进行高阶色散的计算时表现出更好的实用性.图 4 (a) Offner型展宽器的二阶色散值; (b) Martinez型展宽器的二阶色散值; (c) Offner型展宽器的四阶色散值; (d) Martinez型展宽器的四阶色散值. 图中蓝色实线为解析计算值, 红色点线是步长为0.1 nm的数值计算值, 黑色虚线是步长为5 nm的数值计算值Figure4. (a) GDD of Offner stretcher; (b) GDD of Martinez stretcher; (c) FOD of Offner stretcher; (d) FOD of Martinez stretcher. Blue solid lines in the figure are analytical results; red dotted lines are numerical results with step of 0.1 nm; black dash lines are numerical results with step of 5 nm.5.总 结 介绍了一种啁啾脉冲放大激光中展宽器色散的解析计算方法. 基于光线追迹, 本文首先给出了与Offner型展宽器光线追迹结果相统一的Martinez型展宽器追迹公式, 进而使用初等函数循环代换的方式获得了两种展宽器的解析计算结果, 接下来本文对两种展宽器的数值计算结果与解析计算结果进行了比较, 最终获得了两种展宽器一阶到四阶色散的解析计算结果. 可以看出, 该方法得到的解析计算结果更为精确, 对于啁啾脉冲放大激光系统中的展宽器设计及色散优化提供了实用的工具; 另外本算法可以不依赖于特定程序设计语言的内置函数, 可以较好地进行推广, 能做成手机应用程序或可视化应用程序进行使用. 当然, 接下来研究的是综合整个啁啾脉冲放大系统的色散进行优化, 并结合色散测量装置FROG或SPIDER进行更为精确的色散控制, 以期待获得更好的色散补偿结果.附录 用于展宽器光线追迹解析算法的四个初等函数的四阶导数式y = sin(x )函数的一至四阶全导数:y = arcsin(x )函数的一至四阶全导数:y = A /B 函数的一至四阶全导数:y = A + B 函数的一至四阶全导数: 
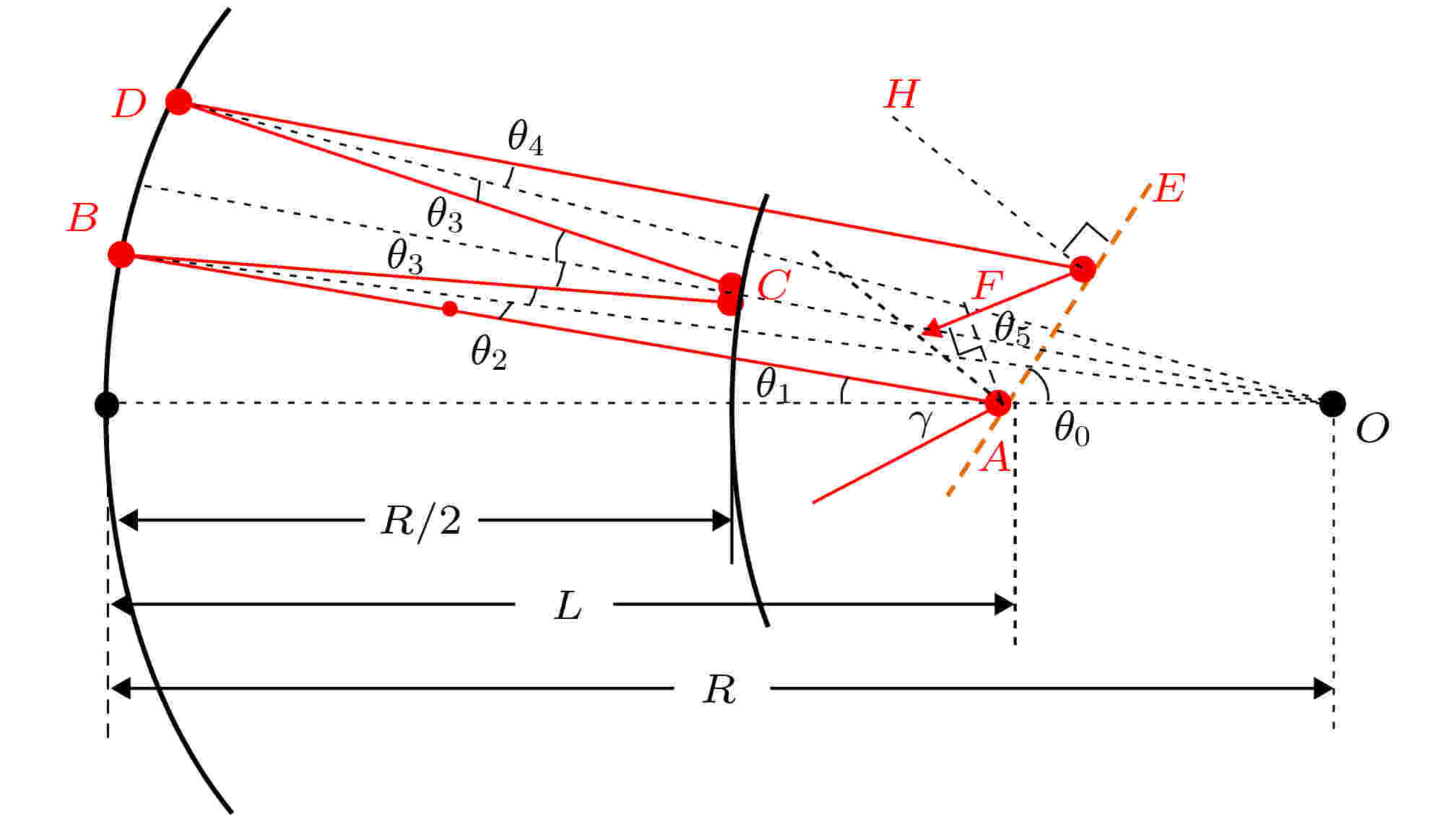 图 1 Offner型展宽器的结构与光路图
图 1 Offner型展宽器的结构与光路图

 图 2 Martinez型展宽器的结构与光路图
图 2 Martinez型展宽器的结构与光路图
















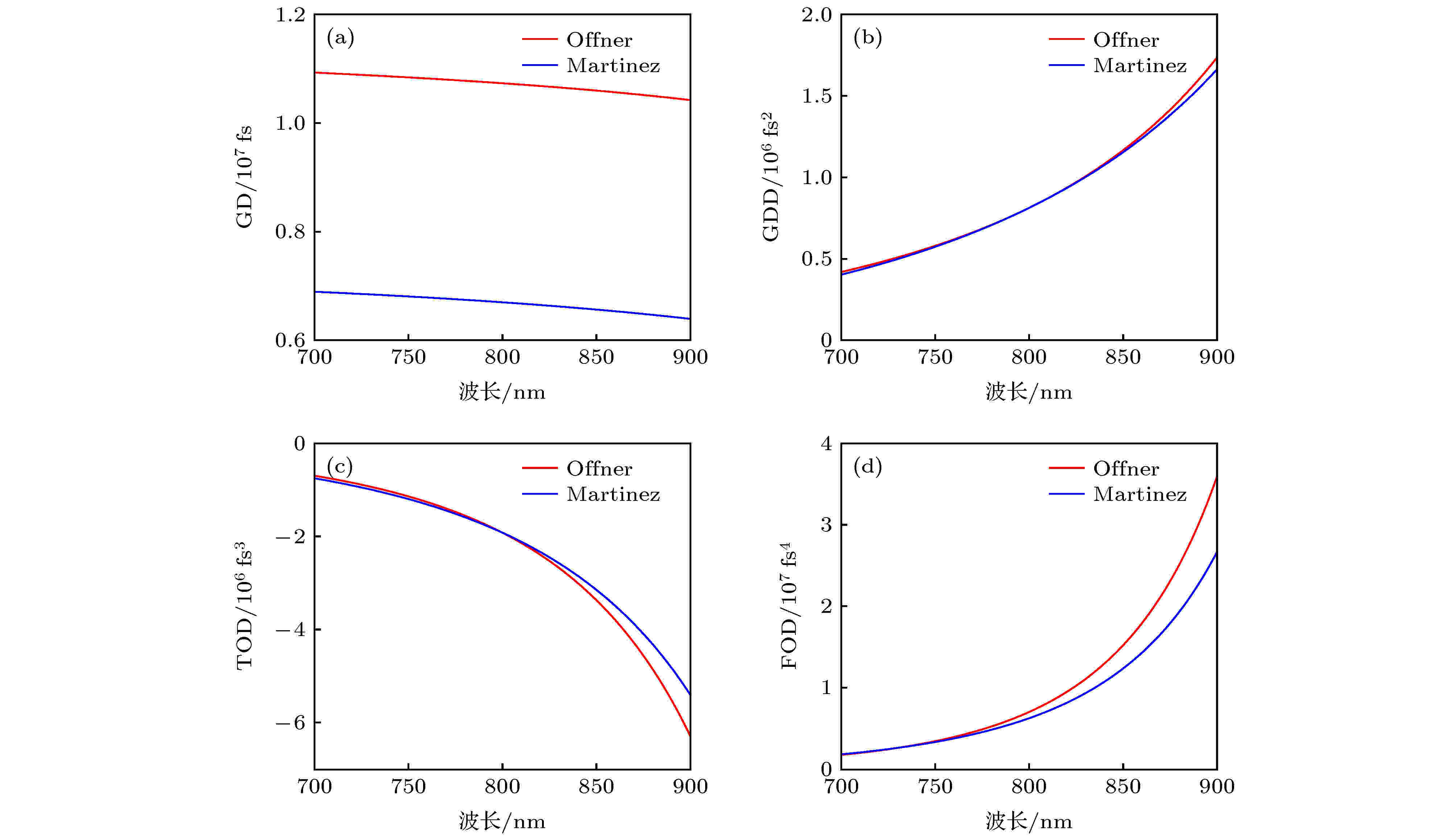 图 3 Offner型与Martinez型展宽器700?900 nm的解析计算色散曲线 (a) GD; (b) GDD; (c) TOD; (d) FOD
图 3 Offner型与Martinez型展宽器700?900 nm的解析计算色散曲线 (a) GD; (b) GDD; (c) TOD; (d) FOD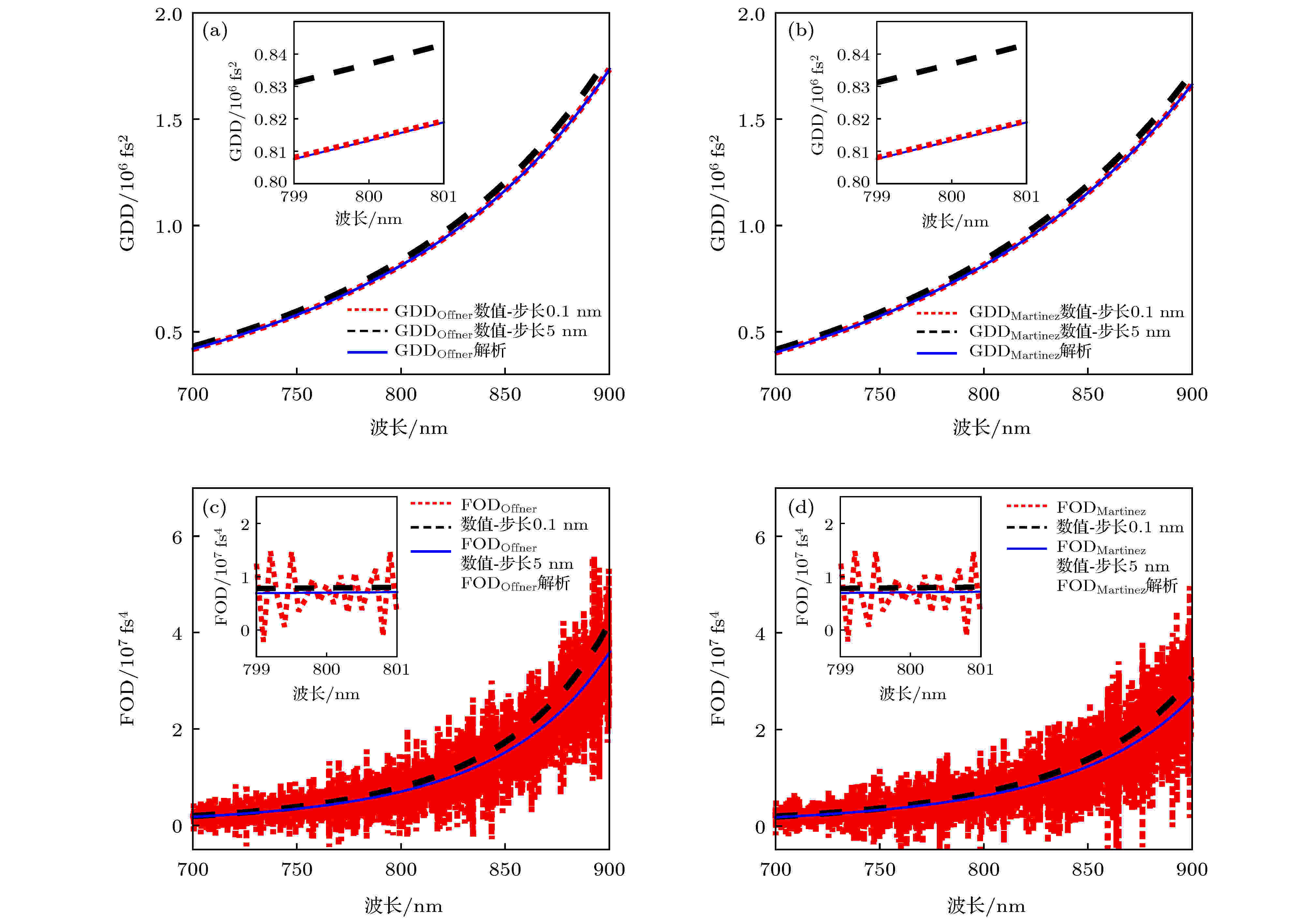 图 4 (a) Offner型展宽器的二阶色散值; (b) Martinez型展宽器的二阶色散值; (c) Offner型展宽器的四阶色散值; (d) Martinez型展宽器的四阶色散值. 图中蓝色实线为解析计算值, 红色点线是步长为0.1 nm的数值计算值, 黑色虚线是步长为5 nm的数值计算值
图 4 (a) Offner型展宽器的二阶色散值; (b) Martinez型展宽器的二阶色散值; (c) Offner型展宽器的四阶色散值; (d) Martinez型展宽器的四阶色散值. 图中蓝色实线为解析计算值, 红色点线是步长为0.1 nm的数值计算值, 黑色虚线是步长为5 nm的数值计算值