摘要:热辐射作为一种无处不在的物理现象, 对于科学研究和工程应用都具有重要意义. 传统上对热辐射的理解主要是基于普朗克定律, 它描述了物体通过辐射交换能量的能力. 而近年来的研究表明, 由于微纳光学材料在尺寸上远小于热辐射峰值波长, 它们的热辐射性质往往很大程度上有别于传统黑体辐射理论所描述的宏观物体. 更重要的是, 微纳光学材料的热辐射性质可以通过改变它们的几何尺寸和微观构型进行定量的优化设计与精确调控. 纳米光学材料与辐射制冷效应的结合, 给热辐射效应在能源和环境等相关领域的应用提供了极具前景的应用价值. 本文首先从热辐射的基本原理和规律出发, 介绍纳米结构热辐射增强的发展进程和最新进展, 包括二维材料间的近场热辐射机理以及尺寸效应导致的远场热辐射增强; 其次, 介绍了近年来纳米光学材料在辐射制冷应用中的重大进展, 包括可以实现高效日间辐射制冷的各种纳米光学材料设计; 最后, 进一步介绍了日间辐射制冷的各种实际应用, 包括建筑物制冷、冷凝水收集、舒适衣物与太阳能电池降温等. 此外, 展望了纳米光学材料的辐射制冷技术在推动荒漠生态环境的治理与改造方面的广阔未来.
关键词: 纳米光学/
辐射制冷/
近场增强/
冷凝水

English Abstract

全文HTML

--> --> -->

热的传递机制主要包括固体中的直接热传导, 气体液体的热对流以及物体间通过电磁波交换能量的热辐射传递. 地球上人类赖以生存的能量主要来自于太阳的热辐射传递. 热辐射理论发展于19世纪末. 德国物理学家基尔霍夫于1859年提出热辐射定律, 指出, 在热平衡状态下, 任何物体的热辐射系数与电磁波吸收系数直接相关, 其比值仅仅与波长和温度有关, 而与物体的材料特性无关, 并由此产生了理想黑体的假设, 即对所有波长的吸收系数都为1的理想物体, 其辐射谱仅是波长与温度的函数. 然而, 之后关于黑体辐射谱理论的建立, 历史上却并非一帆风顺. 瑞利和金斯先后独立按照经典热力学的能量均分定理进行研究, 可是, 瑞利-金斯公式仅能在黑体辐射谱的低频区域与实验结果符合, 而在高频区域显示出发散特性, 这与实验得到的高频(紫外频段)趋近于零的结果严重背离, 这种在紫外频谱与当时理论的差异被称为紫外灾难. 与之对应, 维恩利用热力学定理, 从实验数据出发, 推导出半经典能量分布曲线, 却在低频长波段与实验数据无法符合. 最终, 普朗克通过能量量子化的假设, 提出普朗克公式, 才终于完整地揭示了黑体辐射谱的物理图像. 对黑体辐射谱进行理论解释的成功, 也从此奠定了量子力学蓬勃发展的基础.
在此之后, 黑体辐射理论一直被视作解释物体与自由空间以及物体之间热辐射传热的基本理论^[1]. 值得注意的是, 黑体辐射理论是基于传统的宏观的光学体系建立的, 然而, 当物体的体积缩小到微观的纳米尺度, 或者辐射体之间的距离小于热辐射峰值电磁波对应的波长时, 却会出现不同于普朗克理论预期的现象^[2], 对此, 通常需要借助特定的理论方法进行修正, 而这些理论往往涉及复杂的数学公式和计算模拟. 如今, 随着技术手段的不断进步, 科研人员不仅仅可以在实验中直接测量物体在纳米尺度间隔下的热辐射过程, 甚至可以通过优化设计特定的微纳结构, 实现自然材料中所不具有的特殊的热辐射性质^[3].
关于纳米光学层面的热辐射特性可以从近场和远场两方面进行研究. 在近场方面, 相互靠近的物体因为其增强的近场耦合效应, 导致热传递的渠道增加, 所以表现为增强的近场辐射热传递^[4]. 这种辐射热传递, 是纳米科学中非常有特色的基本现象. 这种热传递方式还会影响光学材料的自身属性, 从而影响结构的整体光学特性^[5]. 近场辐射传导存在于多种应用领域, 例如集成电路中, 器件的散热问题是影响其工作的一个重要因素, 增强的近场辐射不但有助于器件散热, 而且有利于实现更高效的热电转换^[6].
对于远场热辐射, 近期的热点研究方向主要集中在辐射制冷等方面. 辐射制冷是指, 物体的热量通过大气的红外窗口, 以电磁波的方式传送到低温的宇宙中, 从而实现被动降温, 达到节约能源的目的^[7]. 有别于生活中常见的主动降温的方式(例如空调制冷), 被动降温不需要消耗大量的电能等额外的能源. 因此, 辐射制冷还存在非常多的潜在的应用. 例如, 利用辐射制冷生产冷凝水, 可以补充城市饮用水的供给, 而辐射制冷原理可以有效地增强冷凝效率, 为工业化大规模制造冷凝水提供了一种可能的解决方案. 在土地沙漠化治理方面, 可以利用辐射制冷得到的内外温差收集冷凝水, 增加沙漠中植物种植的成活率. 此外, 辐射制冷也同样可以集成到太阳能设备中, 进一步提高太阳能电池的转换效率以及寿命等.
本文从基本原理出发, 对纳米结构热辐射理论做直观的介绍, 并以此为出发点, 进一步介绍纳米材料和纳米结构热辐射在多个方面的研究进展和应用前景. 本文的内容既对热辐射理论进行基本概念的介绍, 同时也结合最新的科研进展, 介绍纳米光学材料以及纳米光学结构热辐射相关的技术和应用. 在文章的最后部分, 针对我国国情, 关于光伏应用、沙漠化治理、开源节流等卡脖子技术, 对于如果利用纳米光学热辐射技术, 展望了我们的预期方案, 并同时对方案进行了简要的可行性论证.
本文的内容安排如下: 首先, 介绍热辐射在纳米尺度下的原理和基本规律, 这里从一个基本纳米颗粒出发, 介绍其与自由空间进行热交换的规律, 并进一步推广到纳米颗粒在具体结构中的热辐射, 以及两个纳米颗粒间的热辐射情形, 由于纳米颗粒的热辐射速率与光学共振性质和它所处环境的光学态密度密切相关, 我们会详细阐述利用纳米光学的增强效应来增强热辐射速率的增强黑体辐射的相关原理. 其次, 介绍纳米结构近场热辐射增强的研究历史和进展, 包括近场热辐射在二维材料中的研究工作, 以及远场情况下纳米结构尺寸效应导致的热辐射增强. 再次, 介绍辐射制冷的研究进展, 包括各种可以实现高效辐射制冷的纳米光学结构和材料. 最后, 介绍辐射制冷的各种可能的应用, 包括集水、热机冷却、建筑物降温以及荒漠治理等.

图1(a)展示了黑体向自由空间辐射的情况. 考虑该黑体温度为T时, 其单位表面积向单位立体角Ω内辐射能量的速率. 按照黑体辐射的普朗克公式, 该情况下能量辐射速率的频谱表示为
图 1 (a) 黑体向自由空间的热辐射; (b)两个黑体间的热辐射
Figure1. (a) Free space radiation of black body; (b) the thermal radiation between two neighboring black bodies.

${I_{\Omega} }(\omega,T) = \frac{{{\omega ^2}}}{{4{{\text{π}}^3}{c^2}}}\frac{{\hbar \omega }}{{{{\rm{e}}^{{{\hbar \omega } / {{k_{\rm{B}}}T}}}} - 1}},$

其中, 玻色-爱因斯坦统计分布$ n(\omega, T) $$(n(\omega, T) = $$ {({{\rm{e}}^{{{\hbar \omega } / {{k_{\rm{B}}}T}}}} - 1)^{ - 1}}$)在ω = 0处的奇点被ω³抵消, 使得辐射谱存在极大值, 该极大值对应的波长称为维恩波长, 该波长仅随温度的变化被称为维恩位移定理. 对(1)式中的频率进行积分, 可以得到单位面积对自由空间单位立体角辐射能量的速率为

${I_{\varOmega} }(T) = {k_{\rm{B}}}^4{\text{π}}{(60{\hbar ^3}{c^2})^{ - 1}}{T^4} = {{\sigma {T^4}} / {\text{π}}}.$

如图1(a)所示, 黑体的单位表面积${\rm{d}}A$向外侧辐射能量时, 法向方向上(θ = 0o)所看到的面积为${\rm{d}}A$, 所以这个方向上能量的辐射速率最强, 若辐射方向与法向的夹角为θ, 则这个方向上看到的黑体面积为${\rm{d}}A\cos \theta $, 所以黑体能量辐射的角分布为$\cos \theta $. 通过对${I_{\varOmega} }(\omega, T)\cos \theta $在物体外半球方位角积分, 可以得到单位面积对自由空间辐射能量的频谱为

$I(\omega,T) = {(4{{\text{π}}^2}{c^2})^{ - 1}}\hbar {\omega ^3}n(\omega,T),$

进一步对$I(\omega, T)$中的频率进行积分, 可以得到黑体单位表面积对自由空间辐射的总能量速率为

$P(T) = \sigma {T^4},$

该公式被称为斯特藩-玻尔兹曼定律.
利用斯特藩-玻尔兹曼定律, 可以计算两个宏观黑体相距较远时的辐射热传递. 考虑如图1(b)所示的两个黑体. 按照(1)式中讨论的${I_{\varOmega} }(T)$的表达形式, 黑体1上的一个面积元${\rm{d}}{A_1}$向自由空间单位立体角内辐射的能量为${{{\rm{d}}{A_1}\sigma {T_1}^4} / {\text{π}}}$. 考虑到辐射的角向分布为$\cos {\theta _1}$, 和黑体2上的面积元${\rm{d}}{A_2}$对应的立体角为${\rm{d}} {A_2}{{\cos \theta } / {r_{12}^2}}$, 通过对两个物体表面积积分, 得到黑体1向黑体2辐射能量速率为$F\sigma {T_1}^4$, 其中$F = \displaystyle\int {{\rm{d}}{A_1}\displaystyle\int {{\rm{d}}{A_2}{{\cos {\theta _1}\cos {\theta _2}} / {{\text{π}}r_{12}^2}}} } $. 类似地, 可以写出黑体2向黑体1辐射能量的速率为$F\sigma {T_2}^4$. 最后, 黑体1向黑体2热辐射能量的净速率可以表示为^[8]

${P_{1 \to 2}} = F\sigma ({T_1}^4 - {T_2}^4).$

在纳米结构的热辐射中, 以上公式的假设有两点不会被满足: 1)纳米颗粒自身不是黑体, 并且纳米颗粒在特定波长的吸收截面可以远大于其几何截面; 2)以上对宏观物体的讨论基于传统光学, 主要考虑远场的贡献, 但是当两个纳米颗粒相距亚波长尺度时, 结构间的近场耦合会增强热辐射过程. 目前, 针对纳米结构的热辐射理论的基础, 主要是涨落-耗散定理^[9,10]. 在该理论基础上, 近年来一些研究发展出了各种数值计算的方法, 甚至可以解决复杂纳米结构中的热辐射计算模型等问题^[11]. 物体热辐射的微观机制的关键在于物体中电流在特定温度下的涨落, 该涨落电流会向自由空间辐射电磁波, 即电磁热辐射. 按照涨落-耗散理论, 电流的涨落与物体材料的内部耗散相联系, 该耗散一般由材料光学参数的虚部表示. 因为不同空间位置处的涨落电流不存在相位关联性, 所以热辐射电磁波一般不具有相干性. 本节主要介绍基于图1中所示的纳米颗粒的热辐射行为. 这些介绍可以帮助我们理解后文中详述的研究进展.
2

-->

3.1.黑体纳米颗粒对自由空间的热辐射

考虑一个温度为T₁的球型黑体颗粒与自由空间(温度为T₀)的热交换过程, 如图2(a)所示. 球型颗粒的半径为R, 则其表面积为4πR². 该球型黑体向自由空间辐射能量的频谱分布为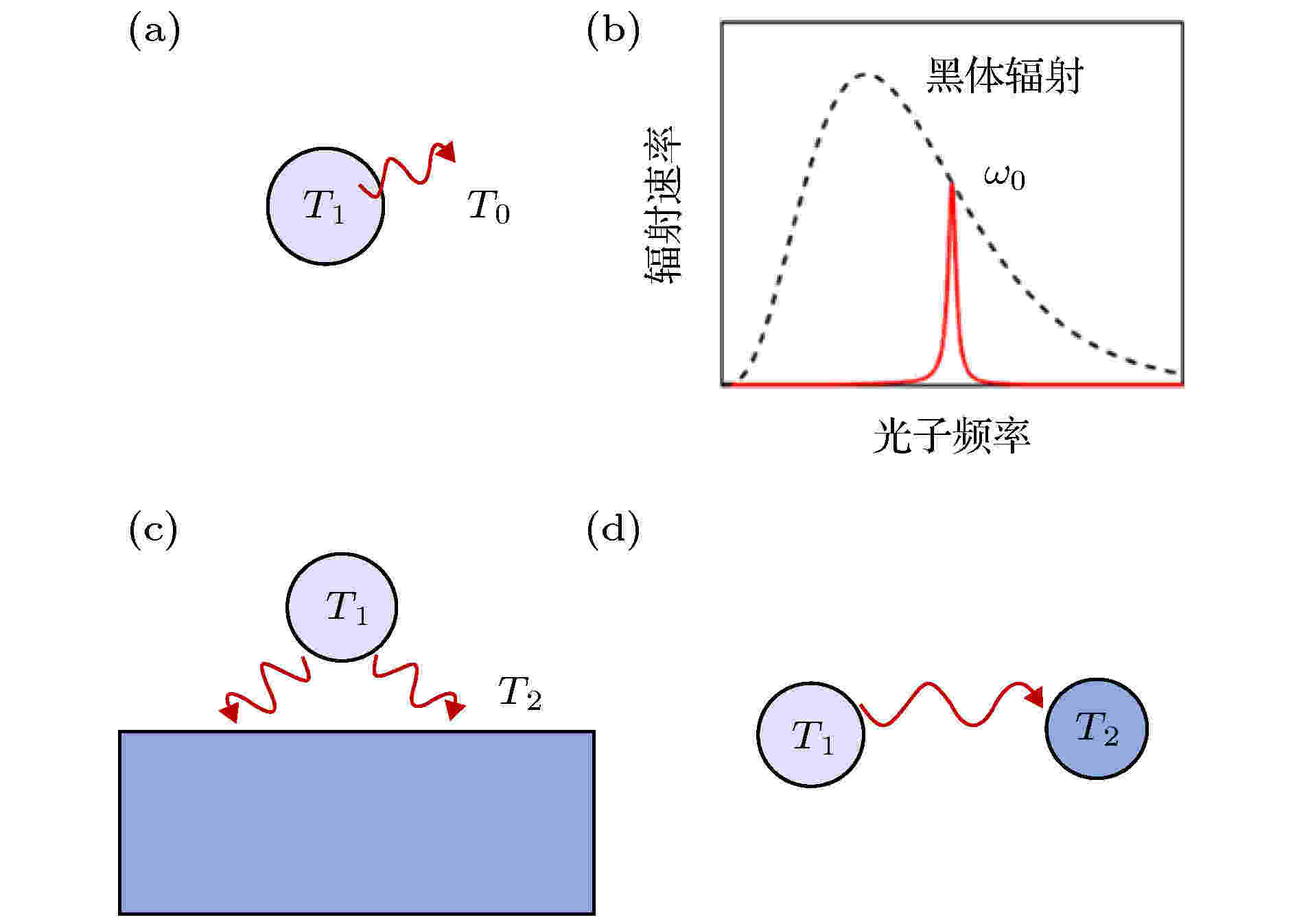
图 2 (a) 纳米颗粒与环境的热交换; (b)黑体辐射曲线(黑色虚线)和真实颗粒的辐射曲线(红色实线); (c)颗粒在一个衬底表面的热辐射; (d)两个颗粒间的热辐射能量交换
Figure2. (a) Thermal transfer between nanoparticle and surrounding media; (b) radiation spectrum of black body (black dashed line) and of true nanoparticles (red solid line); (c) thermal radiation of nanoparticle on the certain substrate; (d) thermal radiation enabled energy transfer between two nanoparticles.

${P_{\rm{e}}}(\omega ) = 4{\text{π}}{R^2}I(\omega,{T_1}) = C{{\text{π}}^{ - 2}}{c^{ - 2}}\hbar {\omega ^3}{n_1}(\omega ),$

其中C = πR²为该球型黑体的几何截面. 对该频谱分布在频率域积分, 可以得到斯特藩-玻尔兹曼定律对应的总辐射功率$P(T) = 4{\text{π}}{R^2}\sigma {T^4}$. 从这里开始, 我们用$n(\omega, {T_i}) = {n_i}(\omega )$表示对应温度T_i的玻色-爱因斯坦分布. 黑体一般是对宏观物体的定义, 其热辐射的传播一般按照几何光学描述. 但是, 在亚波长尺度, 例如当颗粒的尺寸小于颗粒对应温度的维恩波长时, 几何光学描述不再适用. 这里, 为了与后文中的真实纳米颗粒做比较, 我们依然将亚波长尺度的黑体颗粒理解为: 一个可以吸收所有投射在其几何截面上光子的亚波长球体. 黑体颗粒的辐射依然遵循黑体辐射曲线, 如图2(b)黑色虚线所示.
黑体的辐射为黑体吸收的逆过程. 在周围温度为T₀时, 环境中还充满着准平衡态的光子. 自由空间态密度为${\rho ^0}(\omega ) = {{{\omega ^2}} / {3{{\text{π}}^2}{c^3}}}$, 各光子态上的光子数分布由$n(\omega, {T_0})$决定, 则单位体积内的光子数可表示为${\rho ^0}(\omega ){n_0}(\omega )$. 单位时间内投射在颗粒上的光场体积为C. 黑体颗粒在3个垂直方向自由度的贡献相等, 可以直接写出黑体颗粒对环境光场中光子能量的吸收速率:

$\begin{split} {P_{\rm{a}}}(\omega )\; & = 3cC\hbar \omega {\rho ^0}(\omega ){n_0}(\omega ) \\& = C{{\text{π}}^{ - 2}}{c^{ - 2}}\hbar {\omega ^3}{n_0}(\omega ),\end{split} $

由以上讨论结合(4)式, 黑体颗粒对自由空间的净辐射速率为

$\begin{split} P(\omega ) \; & = {P_{\rm{e}}}(\omega ) - {P_{\rm{a}}}(\omega ) \\&= C{{\text{π}}^{ - 2}}{c^{ - 2}}\hbar {\omega ^3}\left[ {{n_1}(\omega ) - {n_0}(\omega )} \right].\end{split} $

2 -->

3.2.真实纳米颗粒的热辐射

真实的纳米颗粒并不是黑体, 其对电磁波的吸收和辐射具有选择性. 例如, 在金属纳米颗粒中, 由于表面等离激元共振的发生, 颗粒会较大概率地吸收满足共振频率的光子, 产生具有高度局域化的若干数量级的场增强^[12,13]. 这种效应已经产生多种重要的应用, 例如单分子拉曼光谱^[14]以及超灵敏光学传感器^[15]. 纳米颗粒这种对光吸收的选择性可以用光学定理描述, 当颗粒尺寸为亚波长时, 颗粒的吸收截面为${C_{{\rm{abs}}}} = 4{\text{π}}{c^{ - 1}}\omega {\rm{Im }}\left\{ {\alpha (\omega )} \right\}$. 其中, 颗粒的吸收正比于颗粒极化率的虚部${\rm{Im}} \{ \alpha (\omega )\} $, 即颗粒在共振位置存在更高的吸收. 以颗粒的吸收截面C_abs替换(5)式中的几何截面C, 就可以得到真实颗粒的热辐射速率:

$P(\omega ) = 4{{\text{π}}^{ - 1}}{c^{ - 3}}\hbar {\omega ^4}\left[ {{n_1}(\omega ) - {n_0}(\omega )} \right]{\rm{Im}} \{ \alpha (\omega )\} .$

所以, 一个真实纳米颗粒在绝对零度T₀ = 0 K时的自由空间的热辐射曲线受到其极化率虚部的调制. 真实纳米颗粒的辐射曲线如图2(b)红色实线所示. 当纳米颗粒的光学共振频率处存在最高的热辐射速率时, 由于表面等离激元共振的影响, 纳米颗粒的吸收截面C_abs可以大于其几何截面C. 此时, 颗粒的辐射速率可以超越对应黑体颗粒的辐射曲线(黑色虚线).
从(5)式中看到颗粒热辐射的速率决定于环境光场的态密度${\rho ^0}(\omega )$, 这一点与自发辐射过程类似. 对于一般情况, 例如图2(c)所示的颗粒在一个衬底表面的热辐射, 环境光场的态密度可以表示为(假设z方向垂直于衬底表面):

$\rho (\omega ) = {(2\omega )^{ - 1}}{{\text{π}}^{ - 2}}\sum\limits_{i = x, y, z} {{\rm{Im}} \left\{ {{G_{ii}}\left( {{{{r}}_0}, {{{r}}_0}, \omega } \right)} \right\}} .$

其中${G_{ii}}\left( {{{{r}}_0}, {{{r}}_0}, \omega } \right)$为颗粒位置r₀处的格林函数, 其意义为偶极子${p_i}({{{r}}_0})$与自身位置处产生的电场${E_i}({{{r}}_0})$的关系${E_i}({{{r}}_0}) = {G_{ii}}\left( {{{{r}}_0}, {{{r}}_0}} \right){p_i}({{{r}}_0})$. 以$\rho (\omega )$替换(5)式中的${\rho ^0}(\omega )$, 可以得到颗粒的吸收速率. 对(4)式进行类似修改, 最终可以得到颗粒在一般环境中的辐射速率:

$\begin{split} P(\omega ) =\; & 2{{\text{π}}^{ - 1}}\hbar \omega \left[ {{n_0}(\omega ) - {n_1}(\omega )} \right] \\& \times {\rm{Im}} \left\{ {\alpha (\omega )} \right\}\sum\limits_{i = x,y,z} {{\rm{Im}} \left\{ {{G_{ii}}(\omega )} \right\}} .\end{split} $

在自由空间中, 颗粒的热辐射可以展开为一系列光学平面波, 每一个平面波对应一个自由空间的光学态, 由这些光学平面波的叠加可以得到自由空间态密度${\rho ^0}(\omega )$. 在近场中, 如图2(c)所示的介电材料表面附近, 由于结构表面存在特殊的光学近场模式, 此时光学态密度$\rho (\omega )$高于自由空间态密度${\rho ^0}(\omega )$. 态密度的增加, 意味着颗粒的热辐射有更多的辐射通道, 所热辐射速率也随着增高. 从另一个角度讲, 偶极子产生的电场被表面散射作用在其自身上, 从而加快其自发辐射速率, 这种辐射速率增强也称为Purcell效应^[16]. 对于图2(c)中的情况, 当颗粒与衬底间距较远小于热辐射的维恩波长时, 可以采用静电近似. 假设衬底的介电常数为$\varepsilon (\omega )$, 则静电近似下格林函数可以表示为

${G_{xx}} = {G_{yy}} = \frac{G_{zz}}{2} = {(2 d)^{ - 3}} \dfrac{{{ {\varepsilon (\omega ) - 1}}}}{{{ {\varepsilon (\omega ) + 1} }}},$

其中d为颗粒与衬底的间距. 所以, 颗粒的热辐射速率随d减小而迅速增加.
2 -->

3.3.纳米结构间的热辐射

接下来考虑图2(d)所示的两个纳米颗粒间的辐射热传递过程. 假设两个颗粒的极化率分别为α₁(ω)和α₂(ω), 共振频率分别为ω₁和ω₂, 并且颗粒1和颗粒2的温度为T₁和T₂. 设定两个颗粒位于x轴上, 坐标分别为x₁和x₂. 颗粒1上的偶极子$p_i^1$产生的电场${G_{ii}}({x_2}, {x_1}, \omega )p_i^1$作用在颗粒2上产生偶极子${\alpha _2}(\omega ){G_{ii}}({x_2}, {x_1}, \omega )p_i^1$, 该偶极子会反作用在颗粒1上, 产生电场. 按照此过程, 当颗粒间距较小时, 忽略颗粒间的多次反射过程, 颗粒1处的格林函数由为${G_{ii}}\left( {{x_1}, {x_2}, \omega } \right){\alpha _2}\left( \omega \right){G_{ii}}\left( {{x_2}, {x_1}, \omega } \right)$. 在静电近似下, ${G_{ii}}\left( {{x_1}, {x_2}, \omega } \right) = {G_{ii}}\left( {{x_2}, {x_1}, \omega } \right) = {G_{ii}}$为实数, 具体形式为: ${G_{xx}} = {G_{yy}} = - {d^{ - 3}}$和$ {G_{zz}} = $$2{d^{ - 3}}$. 同理, 可以得到颗粒2处的格林函数为${\alpha _1}(\omega ){\left| {{G_{ii}}} \right|^2}$. 类比(8)式, 可以得到从颗粒1向颗粒2辐射能量的近似净速率:

$\begin{split} P =\; & 2{{\text{π}} ^{ - 1}}\hbar \omega {\rm{Im}} \left\{ {{\alpha _1}\left( \omega \right)} \right\}{\rm{Im}} \left\{ {{\alpha _2}\left( \omega \right)} \right\} \\& \times \left[ {{n_0}\left( \omega \right) - {n_1}\left( \omega \right)} \right]\sum\limits_{i = x,y,z} {{{\left| {{G_{ii}}\left( {\omega,{x_2},{x_1}} \right)} \right|}^2}},\end{split} $

由此可以看出, 当两个颗粒相距较近时, 热辐射的速率随间距的减小按照$ 1/d^6 $比率增加.

2

-->

4.1.近场热辐射增强

图1(b)中描述的是两个物体在远场时的辐射热传递, 这种传导由空间中自由传输的电磁波实现. 当物体间距小于热辐射电磁波的波长时, 物体表面的倏逝电磁波会对辐射热传递有显著贡献, 这种情况被称为近场辐射热传递. 考虑两个无线大的平行板, 当两者间距较大时, 平板间的辐射热传递速率由(3)式中的黑体间热辐射速率确定. 假设两个平行板的温度分别为T₁和T₂, 每个平行板单位面积的辐射速率按照斯特藩-玻尔兹曼定律确定, 该辐射能量会被彼此全部吸收, 所以单位面积热交换速率为$P(T) = \sigma ({T_1^4} - {T_2^4})$, 即对应(3)式中F = 1的情况. 这里, 物体间的热交换由自由传输的电磁波实现. 平行板表面同时还存在随着远离表面距离呈指数衰减的光学近场. 当平行板距离较大时, 光学近场对热辐射没有贡献. 当物体相距较近时, 例如小于平行板温度对应的维恩波长时, 物体表面的近场相互重叠, 如前文所述, 由于增加了热传输的通道, 平板间的辐射热传递也随之增高. 所以, 近场辐射热传递可以超过(3)式中由斯特藩-玻尔兹曼定律确定的热传导速率. 这种两个物体热传导速率随着间距缩小到微纳尺度下而迅速增加的现象, 是一种普遍现象. 这种现象可以从(8)和(9)式及其讨论中看出: 衬底附近颗粒的热辐射和两个纳米颗粒间的热辐射速率随着距离缩小在迅速增高.
这种热传输的近场增强, 在1969年由Hargreaves^[17]首先在平行板结构中在室温条件下观测到, 实验结果如图3(a)所示. 在该实验中, 两个镀铬的平行板被置于真空腔中, 平行板的平行度可以通过平行板不同位置的光学干涉实验和电学电容测量确认. 通过测量电导率, 可以确保平行板没有直接接触. 两个平行板分别作为发热体(323 K)和热接收体(306 K), 在达到热稳态分布时, 通过测量维持发热体温度的输入热量就可以确定两个平板间的辐射热导率. 实验中测量了平行板间距为1—5.8 μm时的热导率, 发现随着间距缩小至2.5 μm, 热导率开始显著增加. 之后, Domoto等^[18]又在真空和低温(4.2 K)条件下对类似的体系进行了重新测量, 结果如图3(b)所示. 其中, 热接收体的温度固定为环境温度, 图3(b)表示了不同发射体温度条件下, 热传递速率随距离的变化关系. 实验结果明确反映了不同情况下热导率随距离缩小而增高的现象. 之后, Polder和van Hove^[2]提出理论解释, 理论结果趋势上与实验结果相符. 直到2000年之后, 随着纳米技术的兴起, 一些研究开始对不同材料组成的平行板结构的近场辐射热导率进行测量. 2008年, Hue等^[19]在平行玻璃板结构中测量了热导率, 发现玻璃材料可以获得比金属材料更高的近场增强, 这是因为玻璃材料支持表面声子极化激元模式, 这种模式的激发可以产生更高的近场态密度. 之后, 又有研究对蓝宝石平行板和多层平行板结构进行测量^[20,21], 得到了近场辐射热导率随平行板间距变化的关系, 实验结果均与理论结果符合. 在以上实验中, 由于平行板的平行度和平整度都有极高的要求, 因此实验中可以达到的最小间距仅为1 μm.
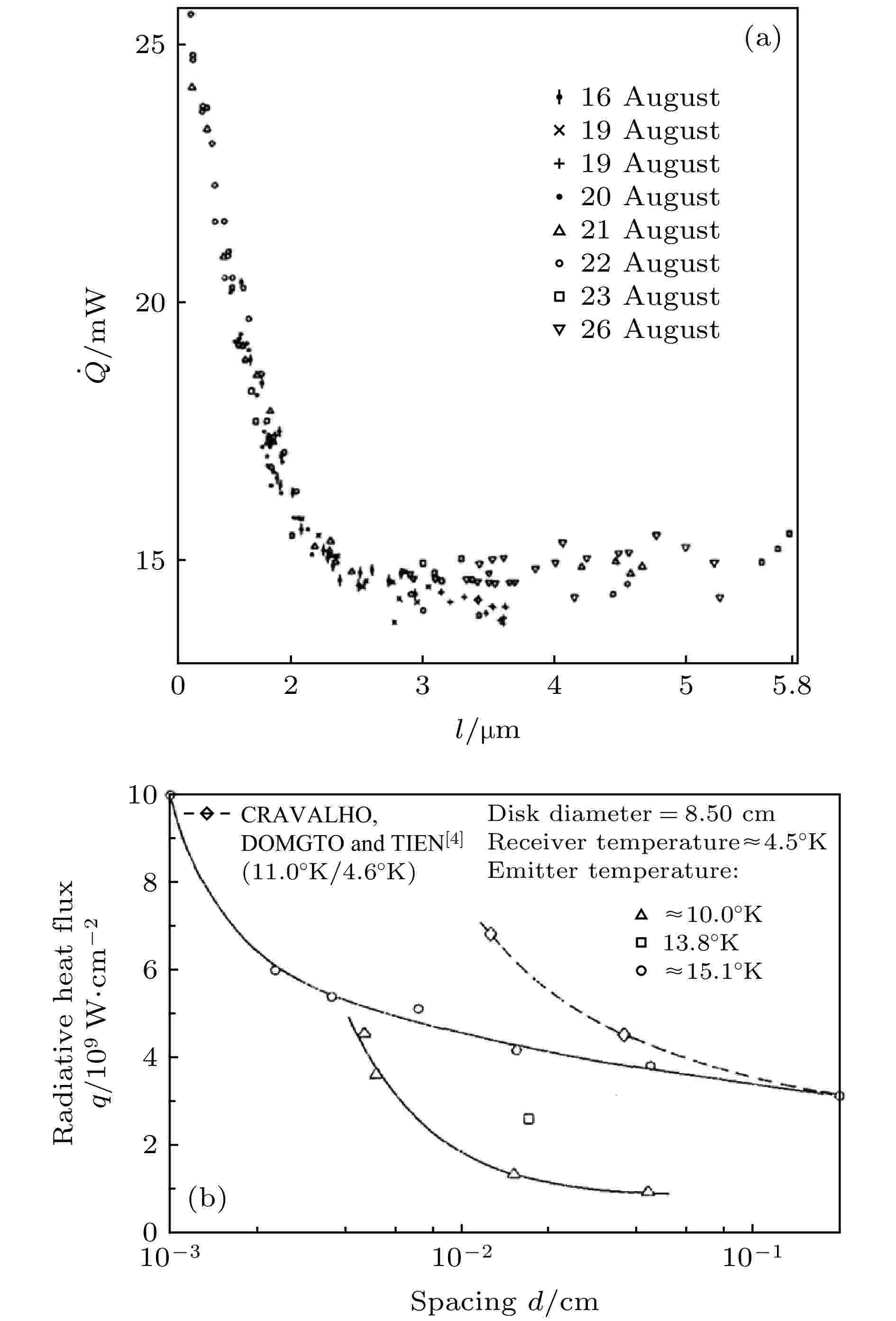图 3 平行板实验中在(a)室温^[17]和(b)低温^[18]条件下测得的热导率随间距的变化关系
Figure3. Distance dependent thermal conductivity of parallel plates, in the condition of (a) room temperature^[17] and (b) low temperature^[18].

20世纪80年代, 随着扫描隧道显微镜(STM)和原子力显微镜的诞生, Williams和Wickramasinghe^[22]设计了热轮廓扫描技术, 如图4(a)所示. 该技术通过在针尖上设计热电偶, 测量加热真尖和样品间的热电流, 进而对样品轮廓进行成像, 可以获得小于3 nm的垂直分辨率. 在这样高的垂直分辨率下, 针尖和样品间的近场辐射热导率对针尖和样品间距变化会十分敏感^[23]. 与平行板结构相比, 这种方法可以将针尖与样品的间距精确控制到1 nm, 但是这种结构中有效传热面积较小, 需要更加灵敏的技术手段来测量温度差导致的热电流. 针对这个问题, 有实验尝试使用球型的针尖从而提高有效传输面积^[24], 如图4(b)所示. 对于针尖样品结构, 从对图2(c)的讨论和(7)式中可以看到, 当针尖可以看作偶极子时, 其近场热辐射的速率正比于样品表面的电磁场态密度. 这个原理, 本质上与STM类似, 不同的是: STM中的隧道电流表示的是样品中局域电子态密度, 而非光子态密度. 在此启发之下, 2006年de Wilde等^[25]类比STM设计了热辐射扫描隧道显微镜, 其功能与近场光学扫描显微镜(NSOM)类似, 可以用来对样品的光学近场成像. 当然, 当针尖样品间距十分小时, 针尖不能仅仅理解为偶极子, 需要考虑具体形貌. 另一方面, 辐射热传递理论基于涨落-耗散理论, 其假设是材料中不同空间位置的涨落没有关联. 2005年Kittle等^[26]在实验工作中发现, 针尖到衬底的热辐射偏离了涨落-耗散理论, 如图4(c)所示; 只有同时考虑材料的非局域效应, 理论结果才能与实验结果相符. 2015年, Reddy研究组^[27]结合带有灵敏温控系统的定制扫描探针与微器件, 测量了间距小到2 nm尺度的辐射传热, 如图4(d)所示. 他们通过结合最先进的数值模拟, 得到了理论与实验良好符合的结果, 证明了理论的有效性.
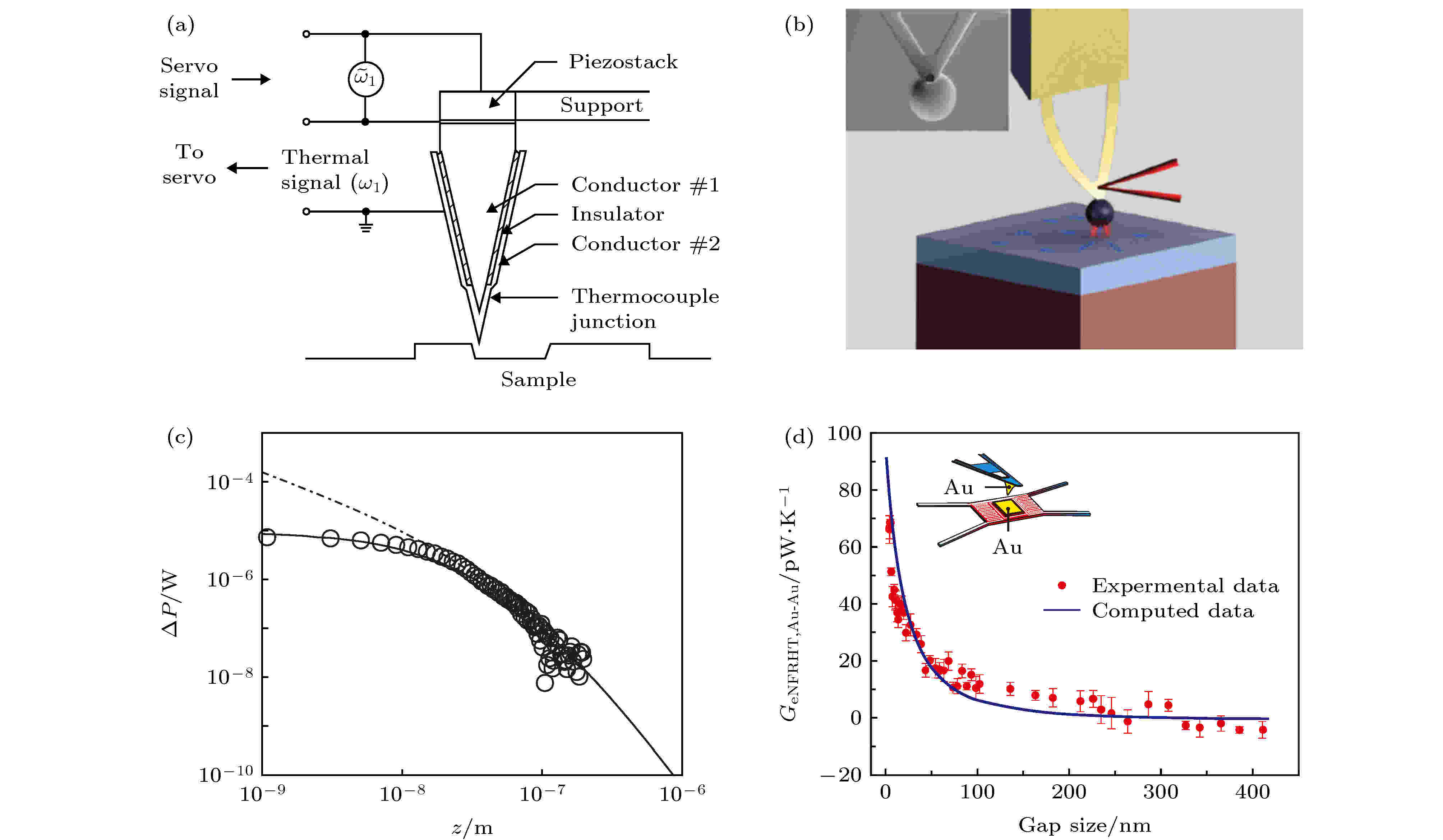图 4 (a)热轮廓扫描仪示意图^[22]; (b)测量近场热辐射的球型针尖示意图^[24]; (c)针尖热辐射测量中的非局域效应^[26]; (d)集成化微器件中的热辐射速率测量^[27]
Figure4. (a) Setup schematic of near-field thermal scanning microscopy^[22]; (b) schematic of spherical tips for near-field thermal scanning^[24]; (c) tips enabled nonlocal effect in thermal radiation^[26]; (d) thermal radiation speed of micro integration device^[27].

另一方面, 二维材料中的近场热辐射增强也是目前研究关注的方向. 例如, 石墨烯因为支持表面等离激元且其表面等离激元波长远远小于对应频率的真空波长, 所以在近场中具有极高的光学态密度. 2012年Ilic等^[28]在理论中发现, 当两个平行的石墨烯间隔在10—100 nm时, 辐射热传递的速率最大值为Stefan-Boltzmann公式的1000倍. 因为石墨烯中的等离激元共振可以由外加电极进行控制, 所以同时可以实现对辐射热传递速率的电调控. 如图5(a)所示, 当共振频率重合时, 两个颗粒间的耦合达到最大. 类似地, 当两层石墨烯具有相同的化学势时, 其中的耦合最强, 使得热传导速率最快. 2017年, Polini研究组^[29]在理论发现, 这种超越普朗克热辐射的现象, 在两层六方氮化硼包裹石墨烯的堆叠结构中同样存在, 如图5(b)所示. 这个工作针对这种堆叠结构进行研究, 是因为该结构可以实现石墨烯等离激元的低损耗传输^[30,31]. 而这种结构一直被用来研究石墨烯中的传输表面等离激元. 紧接着, Koppens研究组^[32]在实验中利用类似的方法, 验证了这种超越普朗克行为的超快热传导. 当石墨烯为有限尺寸时, 例如石墨烯圆盘, 可以支持局域化的表面等离激元共振, 从而进一步提高光学近场态密度. 2017年, de Abajo研究组^[33]在理论中发现, 在两个石墨烯圆盘间可以实现飞秒量级的辐射热传递, 如图5(c)所示. 甚至对石墨烯条带或者圆盘进行电压调制, 还可以调制辐射热传递的速率^[34].
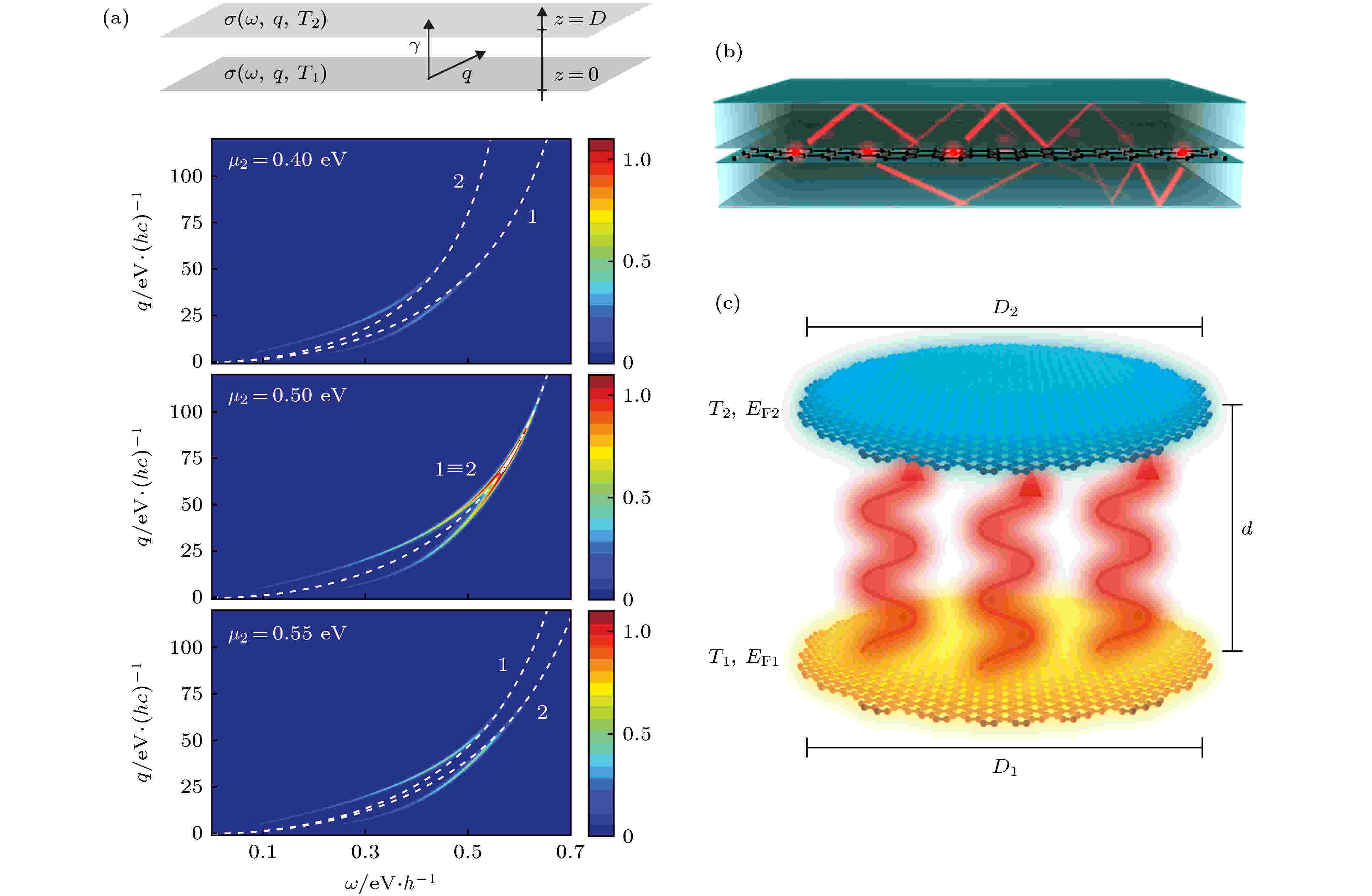图 5 (a)两层平行石墨烯间的近场热辐射传导^[28]; (b)氮化硼-石墨烯-氮化硼结构中的近场增强热辐射^[29]; (c)两个石墨烯圆盘中的超快热辐射^[33]
Figure5. (a) Near-field thermal radiation between parallel graphene^[28]; (b) near-field enhanced thermal radiation in boron nitride-graphene-boron nitride structure^[29]; (c) superfast thermal radiation between parallel graphene disc^[33].

2 -->

4.2.亚波长尺寸效应增强远场辐射热传递

以上讨论了物体间距小于热辐射波长时, 近场辐射热传递超越黑体辐射公式的情况. 另一方面, (3)式基于几何光学, 当两个物体相距较远时, 如果物体自身在某个方向上尺寸小于热辐射波长时, (3)式也不适用. 考虑如图2(c)所示的两个纳米颗粒相距较大距离时的热传导. 因为纳米颗粒在共振处(ω₀)的散射截面大于其几何截面, 如图2(b)所示, 所以颗粒在频率ω₀处的热辐射和热吸收的速率大于相同尺寸黑体颗粒. 但是, 计算总体的热辐射速率时, 需要对不同频率的贡献进行积分. 例如, 在图2(b)中偏离共振处很大范围内, 颗粒的热辐射曲线低于对应黑体颗粒的辐射曲线. 所以, 两个纳米颗粒远距离时的热辐射速率并不一定高于(3)式确定的辐射热传递速率^[35].
2018年, Fernández-Hurtado等^[36]对不同纳米结构的远场辐射热传递进行了研究, 发现对于一般金属颗粒和非金属颗粒, 当间距大于20 μm左右时, 热传导效率一般不会高于(3)式中的辐射热传递效率. 但是对于图6(a)所示的平行并列放置的纳米厚度的平板, 理论结果表明热传导效率可以远大于黑体辐射传导效率, 如图6(b)所示. 该比值随着平板厚度的减小而增高, 厚度减小为100 nm时该比值达到10³. 热传导效率可以远大于黑体辐射传导效率的原因如下: 一方面, 平板结构中只有平行相对的两个表面对(3)式中的黑体辐射有贡献, 当平板厚度缩减至纳米尺度时, 黑体辐射热传递的计算值也随之减小; 另一方面, 平板中支持沿着平板传输的包括倏逝场的模式, 两平板中该模式的耦合不会随平板厚度缩减而迅速降低. 随后, Reddy研究组^[37]在实验中验证了这种现象, 如图6(c)和图6(d)所示. 他们使用了带有嵌入式温度计的定制量热纳米结构进行测试, 实验和理论发现亚波长尺寸的平面薄膜之间的辐射热传递可以高出远场黑体辐射极限两个多数量级.
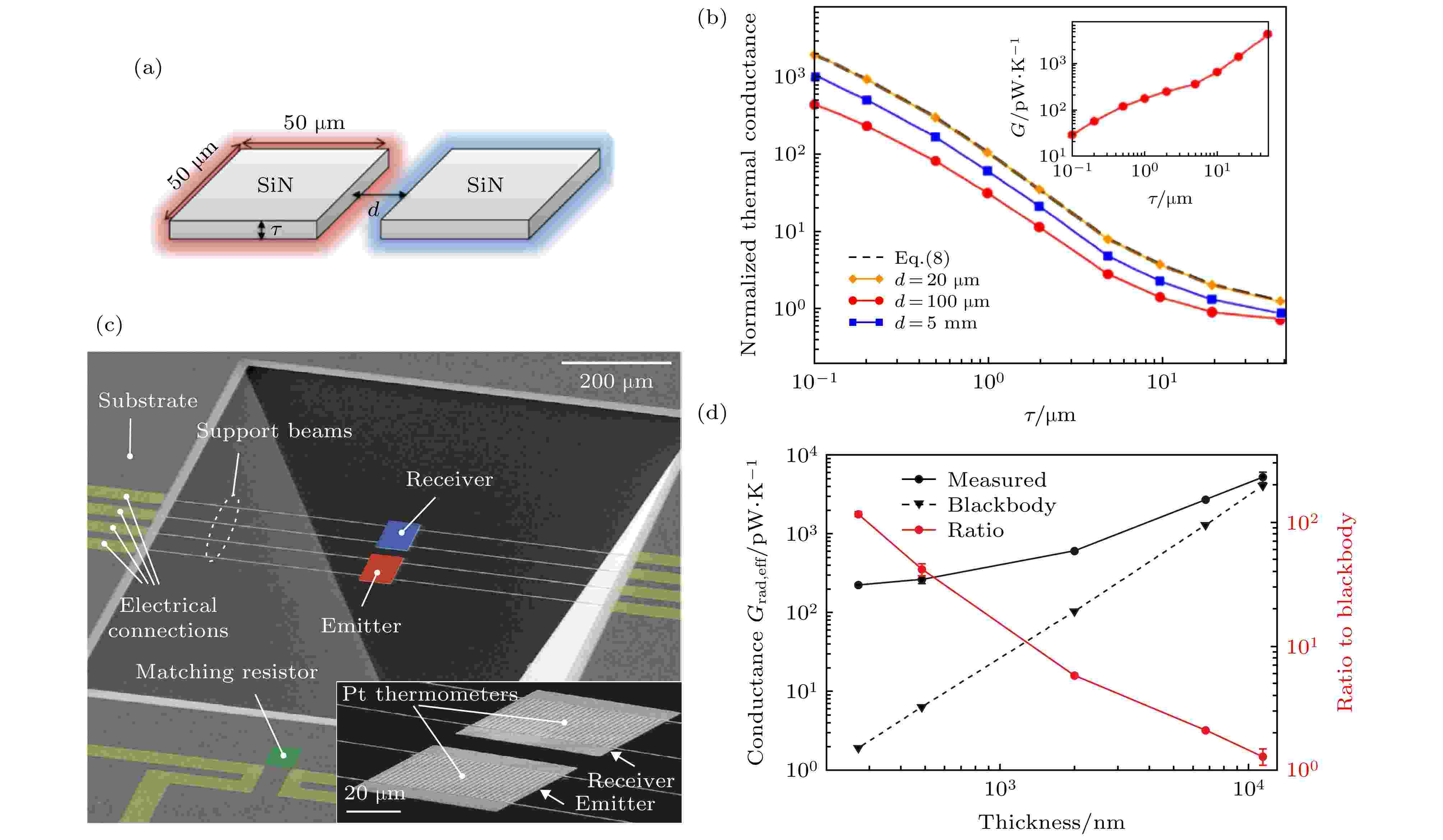图 6 两个并列纳米平板间的远场热辐射增强示意图(a)和计算结果(b)^[36]; 平行板热辐射结构(c)和实验结果(d)^[37]
Figure6. Schematic (a) and theoretical simulation result (b) of enhanced far-field thermal radiation between parallel nanoplate^[36]. Architecture (c) and experimental result (d) of thermal radiation between parallel plate^[37].

2

-->

5.1.辐射制冷原理

前文简明介绍了纳米结构近场以及远场热传导的相关研究. 纳米材料和纳米结构向自由空间的热辐射的相关理论已经日趋完善. 在相关应用领域, 利用大气红外辐射窗口进行被动降温的辐射制冷研究, 由于成本低廉、实用性高等特点, 近年来成为热辐射领域广受关注的热门课题. 辐射制冷的工作原理如图7(a)所示. 其基本原理是: 通过在密闭区域覆盖具有增强效应的红外辐射材料, 将该区域的热量以热辐射的形式释放到低温的宇宙空间. 地球大气层是包括N₂, O₂, CO₂, 水蒸气等在内的多种气体的混合, 可以吸收、散射和发射电磁波, 在天空明净的情况下(没有云/雾阻挡), 地球大气拥有一个透明的辐射窗口, 如图7(b)所示, 窗口的波长范围覆盖8—13 μm^[7]. 处于此波长范围内的电磁波可以直接穿透大气层到达宇宙空间, 只有很少一部分会被吸收. 为了使得制冷区域的能量可以通过该窗口传递释放到宇宙之中, 需要保证制冷器件的辐射光谱主要处于这个大气窗口中. 按照前文图2(a)以及(6)式的讨论, 我们知道热辐射的波长主要取决于辐射体的温度和材料的共振频率. 因此辐射制冷材料就是热辐射波长被调制到大气窗口波段的光学材料. 另一方面, 被制冷的物体还会通过其他途径从外部输入热量, 例如, 太阳光的直接照射可导致被照射区域内的温度升高. 所以, 辐射制冷材料还需要在太阳光光谱的主要能量分布范围内具有尽量高的反射率(严格说, 是尽量低的吸收率). 图7(a)中系统总热量流出的功率P_tot按照图所示过程可以表示为如下形式^[7,38]: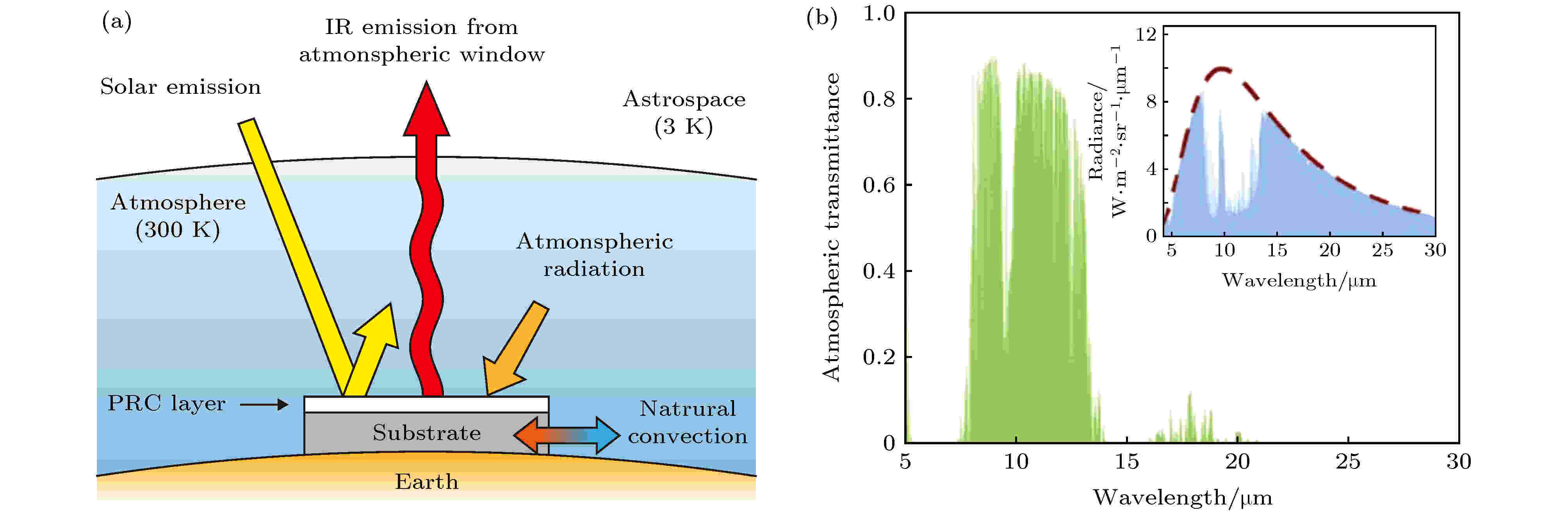
图 7 (a)辐射制冷中的热量转移过程示意图; (b)大气的辐射波段和对应黑体辐射强度的对比^[7]
Figure7. (a) Energy transfer schematic of radiative cooling; (b) radiation windows of atmosphere and the corresponding black body radiation^[7].

${P_{{\rm{tot}}}}({T_s},{T_a}) = {P_{{\rm{rad}}}}({T_s}) - {P_{{\rm{atm}}}}({T_a}) - {P_{{\rm{solar}}}} - {P_{\rm{c}}},$

其中P_rad为制冷区域表面向外的辐射功率(红色箭头), 其辐射谱由其表面温度T_s决定; P_atm为制冷区域从温度为T_a的大气中吸收辐射的能量的功率(橙色箭头); P_solar为制冷区域吸收的太阳辐射的功率; 此外, 制冷区域还会通过热传导和热对流交换直接从环境中吸取热量, 其功率为P_c. 当P_tot = 0时, 整个系统形成温度稳态分布, 制冷区域和外太空之间通过热辐射达到动态平衡状态, 此时制冷区域达到最低温度. 为了达到最佳制冷效果, 通常还需要尽量降低各种能引起温度上升的能量流入功率.
2 -->

5.2.辐射制冷进展

早在几个世纪前, 热带亚热带地区已经能够合理利用夜间的辐射制冷, 为建筑物降温和对水进行结冰脱盐. 在学术研究方面, 早期的辐射制冷器件主要使用自然存在或者化学合成的材料, 如白色颜料^[39,40]、高聚物薄膜^[41]、氧化硅(SiO)薄膜和其他固体材料^[35,42]等. 这些制冷器件虽然可以在大气窗口波段表现出一定的辐射特性, 但是辐射率不高, 限制了实际的性能. 并且由于缺少对光谱反射和吸收能力的精确设计和调制, 辐射器件在大气窗口波段之外也有明显的吸收, 因而早期^[40]的辐射器件不能达到稳定的显著低于环境温度的制冷效果^[41,43,44]. 所以, 这些器件一般只能工作在夜间, 需要避开太阳辐射带来的能量流入.
以光子晶体和超材料为代表的纳米光学材料的出现, 给应用于辐射制冷的光学性质设计带来新的思路^[45-49]. 经过设计的纳米光学材料可以克服自然材料的原有问题, 可以同时具有可见光波段高反射和大气窗口波段高吸收(辐射)的光学特点. 2013年, 斯坦福大学Fan研究组^[46]通过仿真设计出了在可见光波段高反射率和红外波段的高辐射率的光子晶体结构, 如图8(a)所示. 该光子晶体为具有周期孔洞的多层膜微纳结构, 在可见光波段有很高的反射率, 可以有效地避免日光照射带来的热量, 并在大气窗口波段有很强的辐射效果, 可以高效地将热量辐射到宇宙中. 计算表明, 这种多层膜结构可以实现日间制冷, 且功率超过100 W/m². 由于表面微结构加工复杂, 为了简化制作, Fan 研究组^[47]2014年简化了多层膜结构, 制作了由SiO₂, HfO₂和银膜组成的光子晶体, 结构如图8(b)所示. 这种多层膜结构使用银膜做衬底, 能够反射97%的太阳光, 同时在大气窗口波段能够较强地选择性地辐射电磁波. 该结构实现了太阳直接照射情况下低于环境温度的辐射制冷器件, 其工作效果如图8(c)所示. 当环境温度为20 ℃时, 在功率850 W/m²的太阳光下, 该制冷器件达到了低于环境温度5 ℃的制冷效果, 室温下的平均制冷功率达到40.1 W/m².
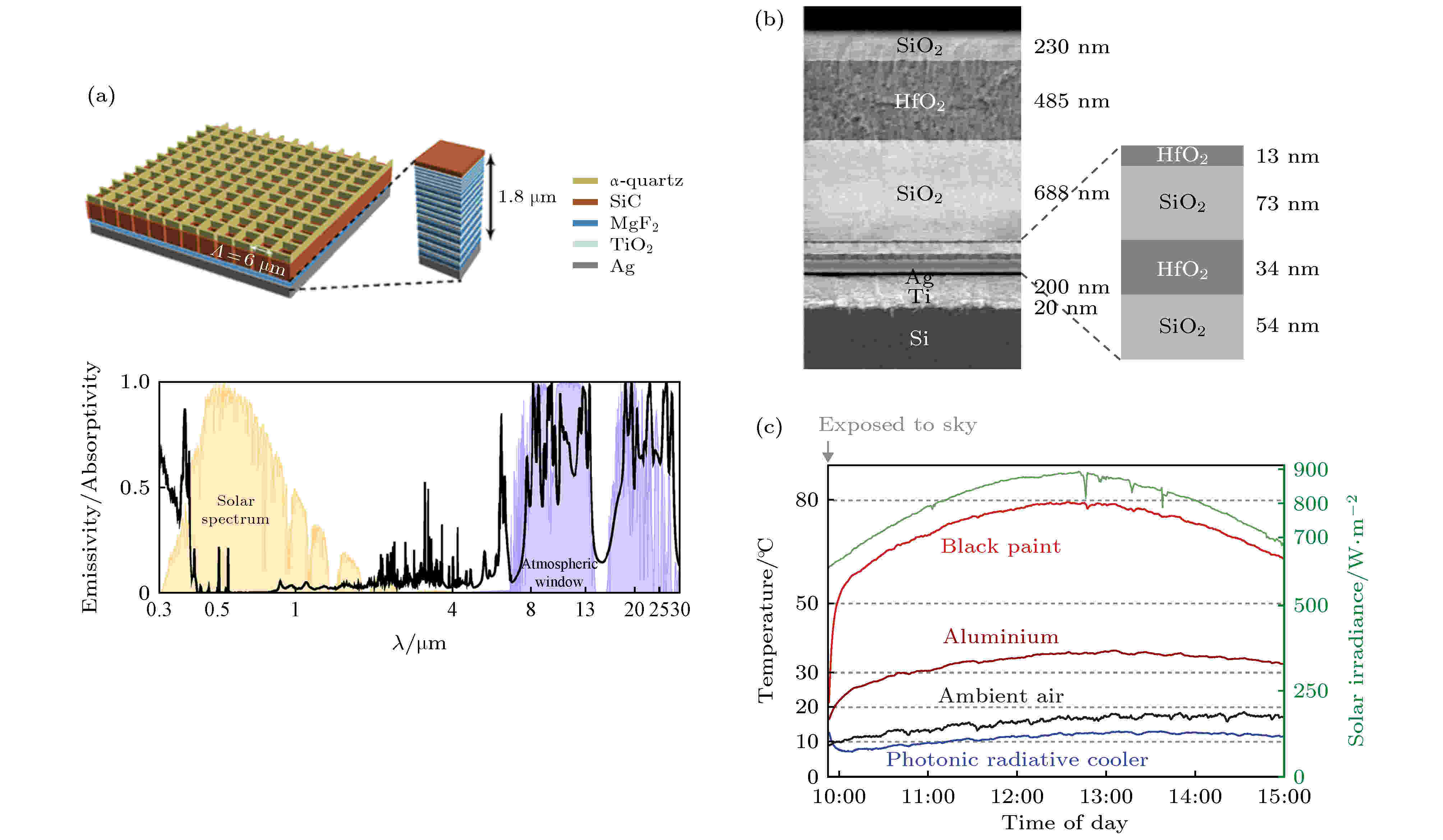图 8 (a)可实现日间辐射制冷的周期孔洞多层膜微纳结构(上图)及其吸收和辐射谱(下图)^[46]; (b)多层膜结构细节^[47]; (c)辐射制冷薄膜和其他薄膜对照物的温度变化曲线^[47]
Figure8. (a) Multi-layered hole array structure (top), of which the radiative cooling could work in the daytime, and the corresponding absorption and radiation spectra (bottom)^[46]; (b) detail of layered structure^[47]; (c) temperature comparison between the radiative cooling film and the other films^[47].

上述多层膜结构针对红外和可将光波段的光谱特性进行了优化设计, 能够实现较好的光谱选择性反射和吸收特性, 同时在实验中实现了较好的制冷效果. 然而, 通常情况下这些器件需要微纳加工手段来制作, 加工难度和成本问题严重限制了这类器件的大规模应用和推广. 针对上述问题, 2017 年美国科罗拉多大学的Yin和Yang团队^[50], 设计了一种嵌入平均直径为8 μm的SiO₂小球的聚4-甲基戊烯(methyl pentene copolymer, PMP)薄膜, 实现了可见光波段高透射, 大气窗口波段高发射(> 93%)的辐射制冷效果, 如图9(a)所示. 这种制冷器件利用PMP和SiO₂在可见光波段无吸收, 且SiO₂小球在红外波段有声子增强共振吸收的特点, 满足了辐射制冷器件的光谱性能需求, 日间制冷功率达到93 W/m². 该方案的突出优点是: 在实现了良好辐射制冷效果的同时, 材料廉价易得, 加工简单方便, 易于大规模制作.
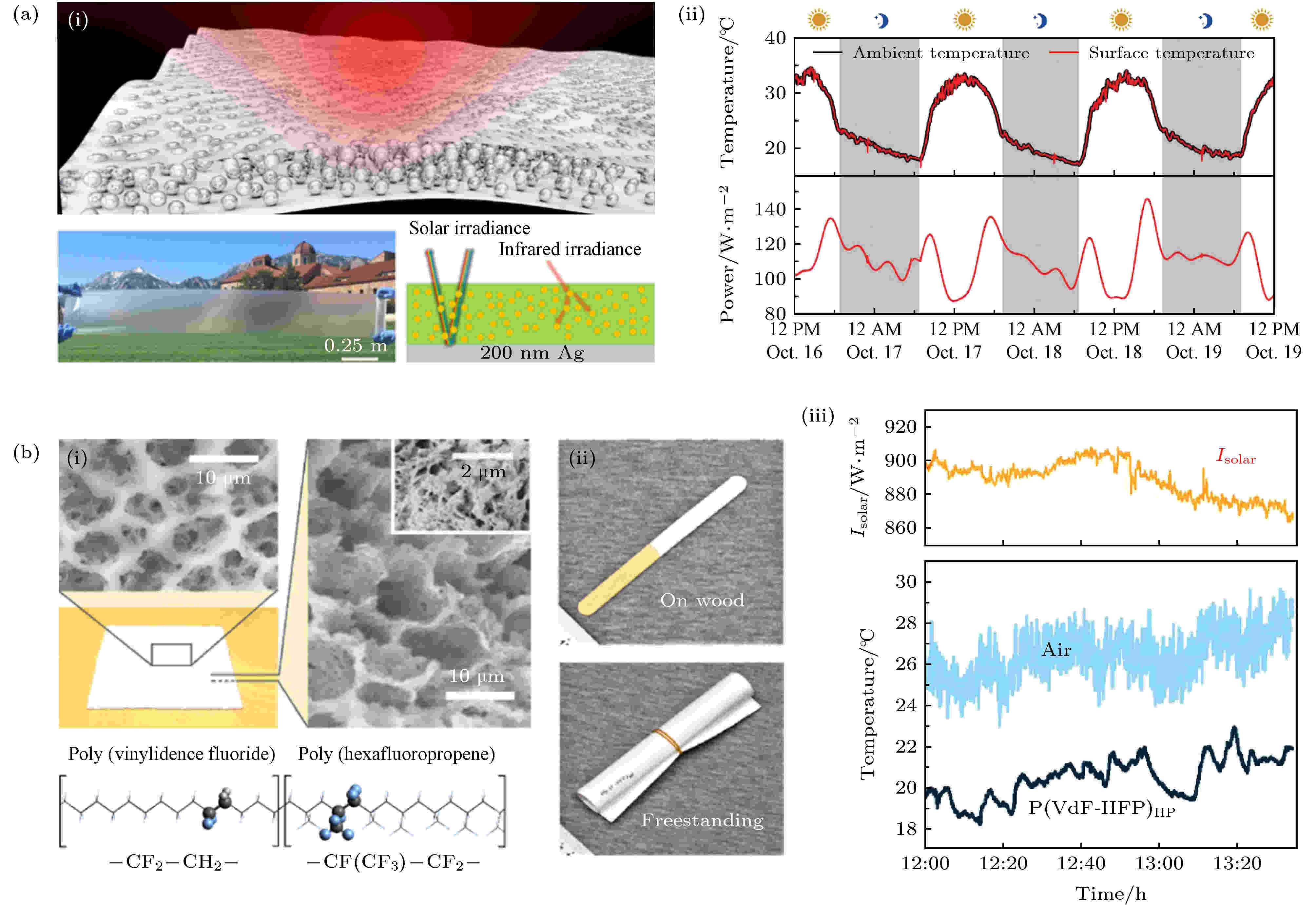图 9 低成本纳米结构辐射制冷材料　(a)二氧化硅小球掺杂的高聚物薄膜^[50], (i)结构示意图, (ii)连续三天的温度变化; (b) 涂布聚合物多孔薄膜^[51], (i)结构电子显微镜图及分子结构示意图, (ii)不同辐射制冷材料覆盖膜的照片, (iii)在中午时的能量变化以及辐射制冷降温效果曲线
Figure9. Low-cost radiative cooling materials: (a) SiO₂ beads embedded polymer film^[50], in panel (a), (i) structure schematic, and (ii) temperature changing in 3-days-nonstopping measurements; (b) coated porous polymer film^[51], in panel (b), (i) scanning electron microscope imaging and molecular structure schematic, (ii) camera picture of variously coated film, (iii) energy changing during noon time, and the corresponding radiative cooling efficiency.

2018年哥伦比亚大学的Yang和Yu研究团队^[51]制作了一种可涂布的聚合物混合材料(图9(b)). 将丙酮、水和聚偏氟乙烯-六氟丙烯(poly (vinylidene fluoride-co-hexafluoropropylene), P(VDF-HFP))三者混合, 由于这种高聚物溶于丙酮, 并具有很强的疏水性, 所以这三者的混合溶液中水会被P(VDF-HFP)排斥形成一个个大小不一的小液滴, 当丙酮和水逐步挥发以后, P(VDF-HFP)内部会形成网状的空气空洞. 这些微米到纳米尺度的空洞在可见光波段可以达到96%的高反射率, 可以较好地反射太阳光在可见光波段的能量从而大幅抑制物体温度的升高. 同时在红外窗口波段, 网状空洞的出现, 进一步加强了高聚物的发射率, 因此大气窗口最高辐射效率可以达到97%. 在740 W/m²的太阳光照射下, 这种材料的制冷功率大约为96 W/m². 达到比环境温度低5 ℃的制冷效果. 在图9(b)中的(ii)图可以看到, 这种材料可以涂布于多种物体表面, 使用方便, 并且它可以通过掺入一些染料来改变颜色和制冷性能. 相比于在高聚物中嵌入SiO₂小球的辐射制冷材料, 这篇文章提到的新型材料, 其制作难度进一步降低, 为辐射制冷的应用开拓了更广阔的空间.
2 -->

5.3.辐射制冷—日间建筑物冷却

2016年建筑物制冷系统消耗了全球室内用电总量的20%, 同时制造了全球温室气体排放总量的10%, 预计到2050年, 人类对制冷的需求会增长3倍^[52]. 所以, 提高制冷系统的效率, 是21世纪应对的能源挑战的重要部分. 空调需要降低的温度每减少1 ℃, 其电力消耗就会降低3%—5%^[53]. 被动降温制冷系统由于不需要额外的能量消耗就可以实现数摄氏度的温度降低, 因而可以很好地辅助空调降温, 有着巨大的应用前景^[7,54].
Ezekwe^[55]在1990年尝试将辐射制冷器件和热管阵列、冷水储藏箱结合, 将经过辐射制冷器冷却的水输送到水箱. 这套系统可以实现每晚628 kJ/m²的制冷量, 但限于其辐射制冷器件无法同时调整可见光和大气窗口波段的电磁波吸收, 该方案只能应用于夜晚. 2017年, Fan研究组^[54]将可在日间工作的辐射制冷薄膜和水循环系统结合起来, 研制出了流体制冷面板(fluid cooling panels), 装置原理图见图10(a). 该设备首先利用辐射制冷将作为冷媒的水的温度降低到室温以下, 再将水循环至建筑物各处, 达到为建筑物降温的目的. 这套系统没有液体的蒸发损耗, 无需特殊维护, 并且只消耗很少的电能. 在水的流量为0.2 lm^–2·min^–1, 辐射功率大约70 W/m² 的情况下, 该装置实现了将循环水的温度降低到低于环境温度5 ℃的制冷效果. 以一栋位于炎热干燥气候下的美国拉斯维加斯的两层建筑为例, 假如将这套流体制冷面板集成在该建筑上, 那么一个夏天用于制冷的电力消耗将降低21%, 可以节约能量14.3 MW·h. 美国科罗拉多大学的 Yang 团队^[56]同样将辐射制冷和水循环系统结合, 利用13.5 m²的辐射制冷表面, 实现在正午时刻607 W (45 W/m²)的制冷功率, 达到低于环境温度10.6 ℃的制冷效果, 如图10(b)所示. 这些实验展示了辐射制冷在建筑降温上的实际效果, 也同时预示了辐射制冷作为主动降温体系的辅助系统的巨大的应用前景.
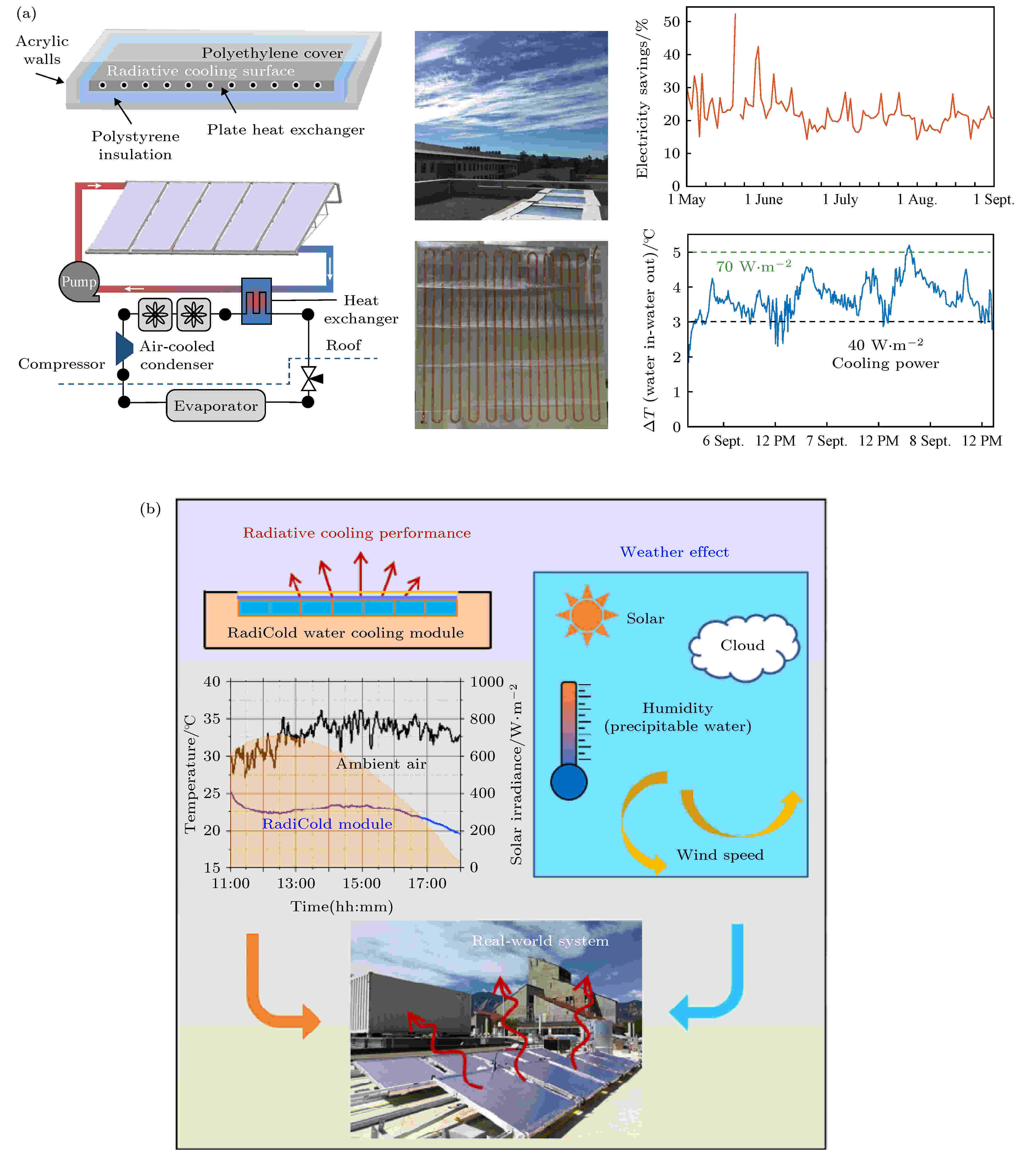图 10 (a) Fan团队制作的辐射制冷系统工作原理图及制冷效果^[54], 平均制冷功率超过40 W/m²; (b) Yang 团队搭建的建筑辐射制冷系统^[56]
Figure10. (a) General radiative cooling system, delivered by Fan’s group^[54], and the corresponding cooling result, of which the average cooling power is over 40 W/m²; (b) buildings used radiative cooling system, delivered by Yang’s group^[56]

2 -->

5.4.辐射制冷—舒适衣物

古人夏天喜欢穿着蚕丝制作的衣服, 因为蚕丝天然地具有可见光高反射、红外光高辐射的特性, 这与辐射制冷材料类似. 因此, 蚕丝是一种天然的穿戴用的自动降温的织物, 夏天穿着蚕丝制作的衣服会感觉十分凉爽. 而利用现代纳米技术设计制造的超材料纺织物可以达到超越蚕丝的辐射制冷效果^[57-60], 特别适合用于制作舒适衣物, 其概念如图11(a)所示^[59]. 一般的传统布料在阻挡可见光的同时也会阻止红外辐射透过, 而这种新型结构可以较好地反射太阳光, 同时在红外波段吸收人体产生的热辐射. 2016年, 斯坦福大学的研究人员研发了一种超级“凉爽”的纳米多孔聚乙烯(NanoPE)布料^[58], 该布料结构的电子显微镜图见图11(b). 这种新型布料在达到与传统衣料相当的透气性和耐穿性的同时, 还能让人们在夏天保持更舒适的体表温度. 如图11(c)^[59]和图11(d)^[58]所示, 在模拟实验中这种新材料显示出了优异的散热性能: 在模拟皮肤发热的装置上覆盖NanoPE材料之后, 表面温度只会上升0.8 ℃; 而同样条件下, 单面针织的棉布则会令温度增加3.5 ℃, 另外一种高密度聚乙烯纤维制成的无纺布材料也同样会使温度增加2.9 ℃. 最近, 研究人员还通过将氧化锌纳米颗粒嵌入聚乙烯, 来构筑新型光谱选择性纳米复合材料, 并用于人体室外活动的辐射冷却^[59]穿戴材料. 通过反射90%以上的太阳辐照度并且有选择地透过人体的热辐射, 这种纺织品可以使模拟皮肤在高峰日光条件下比普通棉织物减少5—13 ℃的热量. 类似的概念还被应用于各种各样的可穿戴设备的降温^[45,61]. 我们相信, 未来这种散热极佳的材料不仅可以用作衣料来加工各种衣物, 还可以应用在野外的帐篷, 以及露天停放的车辆遮阳罩, 甚至可以用在啤酒大棚等户外设施等情境中.
图 11 (a)辐射降温衣物的工作原理^[59]; (b)辐射降温织物的照片及扫描电子显微镜图^[58]; (c)皮肤温度降温效果^[59]; (d)降温织物在可见及红外波段的辐射谱^[58]
Figure11. (a) Principle of radiative cooling cloth^[59]; (b) camera picture and scanning electron microscope imaging of radiative cooling textiles^[58]; (c) cooling effect on human skin^[59]; (d) radiation spectrum of radiative cooling textiles, ranging from visible to infrared frequency^[58].

2 -->

5.5.辐射制冷—收集冷凝水

地球上水资源分布极不均衡, 存在大量水资源严重匮乏的沙漠干旱地区. 例如, 中东海湾地区, 各国所拥有的天然饮用水非常有限, 相当部分的饮用水需要通过海水淡化得到, 以色列甚至40%的饮用水都要从海水淡化获得^[62]. 海水淡化过程要消耗大量的能源, 因此, 能源问题和水资源问题常常相互交织. 即使在海水资源丰富的地方, 也往往不一定有足够的能源来将其净化以供使用^[63,64]. 在这种情况下, 几乎不需要额外消耗能源的被动式冷凝水收集技术引起了人们的极大兴趣.
有不少理论和实验工作研究了影响冷凝水收集效率的因素, 包括气候、湿度、风速、环境温度、云层覆盖情况、冷凝器朝向角度等, 而其中水蒸气凝结所必须的温度差是最重要的影响因素之一^[65-69]. 因此辐射制冷器件的制冷效率就成为冷凝效率的关键之一. 限于材料和加工技术手段, 绝大多数早期的辐射制冷露水收集系统只能在夜间工作. 而近几年日间辐射制冷技术的实验验证为全天候辐射制冷冷凝水收集铺平了道路.
斯坦福大学的Yu团队^[70]在2018年设计了一种多层膜器件, 利用辐射制冷降温效应实现了更高的露水收集效率, 如图12(a)所示. 这种器件以铝膜为基底并覆盖了150 nm的银反射层和100 μm的PDMS辐射层(图12(b)). 其辐射谱如图12(c)所示, 这套冷凝装置实现了0.3—4 μm波段的高反射和4—16 μm的高辐射效果^[70], 在白天可以达到低于环境温度8 ℃的效果. 在相同条件下, 这种辐射制冷器比商业的冷凝器有更高的冷凝速率和更长的有效工作时间. 这种冷凝器可以在24 h内实现两倍于商业制冷器的冷凝水效率, 如图12(d)所示.
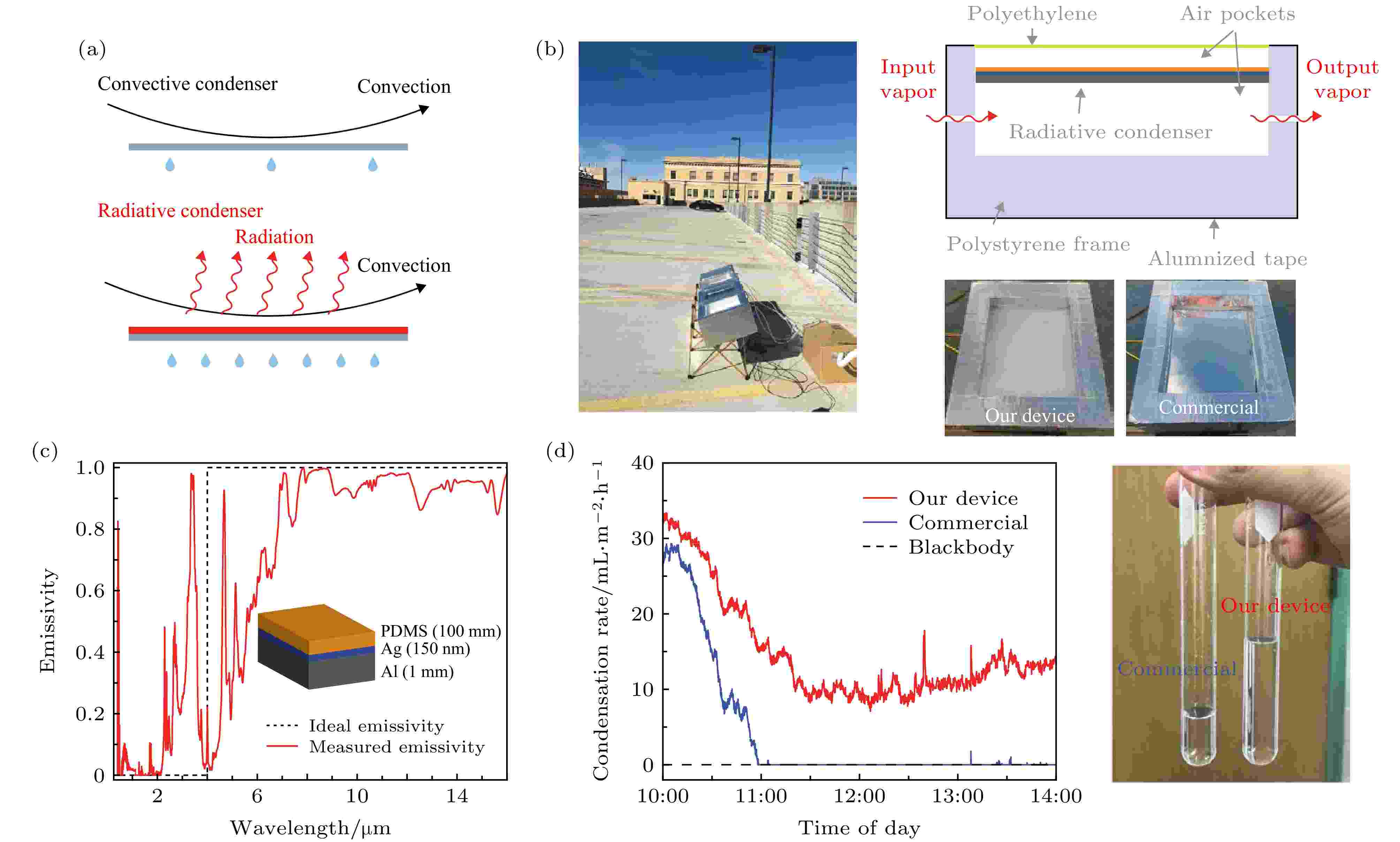图 12 (a)辐射制冷薄膜增加冷凝水量的工作原理^[70]; (b)多层膜冷凝水收集设备^[70]; (c)辐射制冷薄膜的发射谱以及(d)冷凝水增量效果^[70]
Figure12. (a) Principle of radiative cooling effect enabled condensate water^[70]; (b) multi-layered radiative cooling system for condensate water^[70]; emissivity spectrum (c) of multi-layered radiative cooling system, and (d) the dramatically increased condensate water^[70].

2 -->

5.6.辐射制冷—太阳能电池降温

太阳能电池在工作时会吸收绝大部分的太阳辐射能量, 但只有部分能够转化为电能. 其他能量都转为废热并导致太阳能电池的升温. 而高温环境对太阳能电池的性能和寿命明显不利^[71-73]. 如何给太阳能电池降温是困扰业界多年的问题.
2014年, 斯坦福大学的Shanhui Fan等^[71]首先提出利用辐射制冷薄膜, 可以实现对太阳能电池的降温. 他们在2017年测试了辐射制冷器件对业界普遍使用的单晶硅太阳能电池的降温效果, 将多层膜堆叠组成的辐射制冷结构和单晶硅太阳能电池结合起来进行测试^[73], 如图13(a)所示. 这种多层膜结构可以反射不参与产生光电流的太阳光谱部分, 同时最大化大气窗口波段的热辐射. 他们首先测量了对应器件在可见光和红外波段的相应吸收数据, 如图13(b)和图13(c)所示, 将实验测得数据代入模型计算后, 发现这种结构理想情况下可以给太阳能电池降温约5.7 ℃, 提高0.56%的太阳能转化效率. 但是, 值得注意的是, Gentle和Smith^[74]在一篇工作中指出, 在实际情况下, 其他热传递通道对太阳能电池的温度影响更大. 他们认为在正常工作状态下, 要用辐射制冷方式使太阳能电池比目前的工作温度低1.5 ℃在实际操作中有比较大的困难. 如果能够有效提高辐射制冷的降温速度, 使辐射降温的速度接近甚至达到热传导和热对流的速度, 我们相信辐射制冷对提高太阳能电池发电效率会产生本质的提升.
图 13 (a) I为商业太阳能电池照片, II为实验制作的银线电极及铝背电极的太阳能电池, 右图为太阳能电池覆盖上制冷薄膜的照片及其截面示意图^[73]; (b)各个器件的吸收谱, 分别为I图中太阳能电池板有无制冷薄膜下的吸收光谱和II图中器件的吸收光谱^[73]; (c)对应器件在大气窗口的辐射谱^[73]
Figure13. (a) Commercial solar cell unit (I) and the lab developed unit with silver wire electrode and alumina back electrode (II); the right figure shows the corresponding camera picture with coated cooling film and the detailed cross-section of the film^[73]; (b) absorption spectra comparison between commercial solar cells unit (Fig. 13(a) I) with or without radiative cooling film, and lab made solar cell unit (Fig. 13(a) II)^[73]; (c) radiation spectra of corresponding solar cell unit, in the frequency region of atmospherically radiative window^[73].

本文首先从纳米尺度下的热辐射基本原理出发, 介绍了纳米光学材料和结构以及二维材料的近场与远场增强热辐射效应. 接着, 对远场热辐射理论的一个重要的应用—纳米光学材料和纳米光学结构的辐射制冷效应—进行了原理上的阐释, 同时, 对于不同应用场景也逐一进行了简明扼要的介绍. 经过精确的微纳设计, 研究人员可以将物体自发辐射的波段调整在对应的大气窗口波段, 将物体的热能直接辐射到宇宙中, 从而达到对物体制冷的目的. 在过去的10年中, 辐射制冷已经成功地从只能在夜间工作的简单材料, 进化为可以在白天也有良好制冷效果的纳米光学材料. 而辐射制冷的应用场景也有了很大的拓展, 包括建筑制冷、增强冷凝水收集效率、舒适衣物与可穿戴设备、太阳能电池降温、发动机降温等. 但是另一方面, 自发辐射制冷应用技术也仍然处于开发阶段, 虽然在制作成本以及对环境条件的高度依赖性等问题上, 已经获得了极大成功, 但是, 自发辐射制冷的制冷功率弱也使得它目前很难完全替代主动制冷方式.
在可预见的未来, 辐射制冷有很大潜力作为传统制冷方式的最佳搭档, 有效地降低主动制冷所需要的能耗. 此外, 辐射制冷由于具备无排放、无需特殊维护、对环境很友好的优点, 十分适合各种户外应用场景, 例如户外活动板房的直接降温、干旱地区的冷凝水收集等维护成本较高, 难以使用传统制冷方法的场景. 尽管辐射制冷在环境依赖性、材料稳定性等方面还有很长的路要走, 但是天地广阔、未来可期.