删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

非规则形状介质内辐射-导热耦合传热的间断有限元求解

本站小编 Free考研考试/2021-12-29
摘要:采用间断有限元法(discontinuous finite element method, DFEM)求解非规则形状介质内的辐射导热耦合传热问题, 得到了典型非规则形状介质内辐射导热耦合传热问题的高精度数值结果. 和传统连续型有限元方法不同, DFEM将计算区域划分成相互独立的离散单元, 形函数的构造、未知量的加权近似以及控制方程的求解均在每一个离散单元上进行. 通过在单元之间施加迎风格式的数值通量, DFEM保证了整个计算区域的连续性, 因此这种方法兼具良好的几何灵活性和局部守恒性. 推导了辐射传输方程和能量扩散方程的DFEM离散格式, 验证了DFEM求解辐射导热耦合传热问题的正确性; 同时研究了不同几何形状介质内辐射导热耦合传热问题, 得到了典型非规则形状介质内辐射导热耦合传热的高精度数值结果.
关键词: 辐射导热/
耦合传热/
数值模拟/
间断有限元

English Abstract


全文HTML

--> --> -->
1.引　言
参与性介质内辐射导热耦合传热过程广泛存在于众多工程实际应用中[1-3], 如高温熔岩融化、材料加工等, 因此辐射导热耦合问题的研究对相关传热分析和工程设计具有重要的意义. 辐射传输方程是积分-微分型方程, 这类方程多通过数值解法进行求解, 如蒙特卡罗法[4-8]和修正的欧拉算法[9,10]. 由于辐射传输问题常常涉及复杂边界条件和非规则计算区域[11,12], 国内外****发展了多种数值方法[13-27]用以研究辐射传热问题. Mishra等[28,29]采用不同数值方法分别求解辐射传输方程和能量扩散方程, 发展了求解辐射导热耦合问题的混合方法.
虽然目前多种数值方法被成功应用于辐射导热耦合问题的求解, 然而非规则形状介质内辐射导热耦合传热的高精度数值求解仍旧面临较大的挑战[30]. 对于含有弯曲壁面的非规则形状介质而言, 辐射强度在界面附近等局部区域的变化率较大, 而传统连续型数值方法则是基于全局形函数对未知量进行加权近似, 没有考虑局部区域的大梯度辐射强度分布, 计算结果往往存在较大误差. 如文献[31]中即使采用较为细密的网格划分, 采用有限体积法所得辐射热流和温度分布曲线仍旧存在非常明显的振荡, 因此, 扩展高精度数值算法求解辐射导热耦合传热方程, 获得非规则形状介质内辐射导热耦合问题的高精度数值解具有重要意义.
间断有限元法(discontinuous finite element method, DFEM)[32]是在传统连续型有限元法(finite element method, FEM)基础上发展起来的一种高精度数值方法. 利用传统FEM的空间网格划分, DFEM利用相邻单元边界的数值通量从而释放了FEM强加的内部单元连续性. 由于DFEM形函数构造和控制方程求解均在每个离散单元上进行, 因此该方法兼具较好的几何灵活性和局部守恒性, 并被逐渐应用于辐射传输问题的求解[33-38]. 本文采用DFEM求解辐射传输方程和能量扩散方程, 将其扩展应用于辐射导热耦合传热问题的求解, 验证了数值结果的精确性并给出了典型非规则形状介质内辐射导热耦合传热问题的高精度数值解.
2.控制方程及DFEM离散
辐射导热耦合传热过程的控制方程包括辐射传输方程和能量扩散方程, 本文的求解思路是先求解辐射传输方程得到辐射强度信息, 然后再把辐射源项代入到能量扩散方程以得到温度场分布.
首先分析辐射传输方程. 参与性介质内辐射传输方程的离散坐标形式可写为
${{{\varOmega }}^m} \cdot \nabla I({{r}},{{{\varOmega }}^m}) + \beta I({{r}},{{{\varOmega }}^m}) = S({{r}},{{{\varOmega }}^m}),$
式中, I表示辐射强度, r表示坐标, Ω表示离散方向, β为衰减系数, 上标m表示离散方向. 为了书写简洁, $I({{r}}, {{{\varOmega }}^m})$在以下表达中缩写成I m. 考虑介质发射和散射, (1)式中的源项$S({{r}}, {{{\varOmega }}^m})$表示为
${S^m} = {\kappa _{\rm{a}}}{I_{\rm{b}}} + \frac{{{\kappa _{\rm{s}}}}}{{4{\text{π}} }}\sum\limits_{m' = 1,m' \ne m}^M {{I^{m'}}{\varPhi ^{m',m}}{\nu ^{m'}}}, $
式中, Ib表示黑体辐射强度, κa表示发射系数, κs表示散射系数, M = Nθ × Nφ表示角度离散个数, νm′表示Ωm′方向的权重, Φm′, m表示从方向Ωm′到方向Ωm的散射相函数.
在DFEM应用过程中, 计算区域首先被划分为紧密相邻的离散单元, 如图1(a)所示. 待求解的目标量(如辐射强度)在相邻单元边界上被认为是非连续的, 每个单元上的数值解是相互独立的, 如图1(b)所示. DFEM在每个离散单元上求解控制方程, 相邻单元之间通过数值通量相互连接, 从而保证了计算区域的连续性.
图 1 (a)空间网格; (b)相邻单元间数值通量示意图
Figure1. (a) Spatial mesh; (b) sketch of numerical flux across the adjacent elements.

以图1(b)中的单元e作为研究对象进行分析, 在该单元上对(1)式使用权函数$w\, ({{r}})$进行加权积分可得
$\int_{{A_e}} {w\,({{r}}){{{\varOmega }}^m} \cdot \nabla {I^m}} {\rm{d}}A = \int_{{A_e}} {w\,({{r}})( - \beta {I^m} + {S^m})} {\rm{d}}A.$
考虑辐射强度在相邻边界上的非连续性, 将高斯散度定理应用于(3)式可得
$\begin{split} &\int_{{A_e}} {w\,({{r}})\,{{{\varOmega }}^m} \cdot \nabla {I^m}} {\rm{d}}A + \int_{{\varGamma _e}} {w({{r}})\,\rlap{–} I_{{\varGamma _e}}^m\,{{{n}}_{{\varGamma _e}}} \cdot {{{\varOmega }}^m}} {\rm{d}}\varGamma \\=\, & \int_{{A_e}} {( - \beta {I^m} + {S^m})w({{r}})} {\rm{d}}A, \\[-15pt]\end{split}$
式中, ${{{n}}_{{\varGamma _e}}}$表示图1(b)所示的离散单元边界外法向单位向量, Γe表示离散单元边界, $\rlap{–} I_{{\varGamma _e}}^m$表示相邻边界上的数值通量, 定义为
$\rlap{–} I_{{\varGamma _e}}^m = I_{{\varGamma _e},{\rm{nei}}}^m - I_{{\varGamma _e}}^m,$
式中$I_{{\varGamma _e}, {\rm{nei}}}^m$表示图1(b)所示的与单元e相邻单元边界上的辐射强度, 定义为
$I_{{\varGamma _e},{\rm{nei}}}^m = \mathop {\lim }\limits_{\delta \to 0} I_{{\varGamma _e}}^m({{r}} + \delta {{{n}}_{{\varGamma _e}}}).$
本文数值通量的格式选取为迎风格式
$\rlap{–} I_{{\varGamma _k}}^m = \left\{\!\!\begin{aligned}& \rlap{-} I_{{\varGamma _k}}^m = I_{{\varGamma _k},{\rm{nei}}}^m - I_{{\varGamma _k}}^m, \quad \,{{{n}}_{{\varGamma _k}}} \cdot {{{\varOmega }}^m} \! < \! 0, \\ & \qquad \qquad \qquad \quad\qquad ~~ k = 1,2,3, \\ & 0,\quad \quad {{{n}}_{{\varGamma _k}}} \cdot {{{\varOmega }}^m} \!> \!0, \;k \!=\! 1,2,3,\end{aligned} \right.$
因此(4)式中的${\rlap{-} I^m}\, {{{n}}_{{\varGamma _e}}} \cdot {{{\varOmega }}^m}$可以写为
$\begin{split} & \rlap{–} I_{{\varGamma _k}}^m{{{n}}_{{\varGamma _k}}} \cdot {{{\varOmega }}^m} = \max (0, - {{{n}}_{{\varGamma _k}}} \cdot {{{\varOmega }}^m})\left( {I_{{\varGamma _k},{\rm{nei}}}^m - I_{{\varGamma _k}}^m} \right),\\ & \qquad ~\qquad \qquad k = 1,2,3.\\[-10pt] \end{split}$
在每一个单元上对未知量采用形函数近似, 单元e上的辐射强度分布可表示为
${I^m}({{r}}) \cong \sum\limits_{i = 1}^{{N_{\rm{n}}} = 3} {{\phi _i}({{r}})I_i^m} ,$
式中, ${\phi _i}({{r}})$表示定义在单元e上的形函数, $I_i^m$表示第i个节点在第m个离散方向上的辐射强度, Nn = 3表示单元e的3个节点. 将(9)式代入(4)式中, 并采用形函数${\phi _i}({{r}})$作为权重函数$w\, ({{r}})$, 可得单元e上辐射传输方程的DFEM离散格式为
${{{K}}^m}{{{I}}^m} = {{{H}}^m},$
式中Im = [I1, I2, I3]T表示离散节点上的辐射强度; 矩阵Km和Hm的元素表示为
$\begin{split}{{K}}_{ji}^m =\; & {{{\varOmega }}^m} \cdot \int_{{A_e}} {\nabla {\phi _i}{\phi _j}{\rm{d}}A} + \int_{{A_e}} {\beta {\phi _i}{\phi _j}{\rm{d}}A} \\ & + \sum\limits_{k = 1}^{{N_{\rm{b}}} = 3} {\max (0, - {{{n}}_{{\varGamma _k}}} \cdot {{{\varOmega }}^m})\int_{{\varGamma _k}} {{\phi _i}{\phi _j}{\rm{d}}\varGamma } } , \end{split} \tag{11a}$
$\begin{split} {{H}}_j^m =\; & {{{\varOmega }}^m} \cdot \int_{{A_e}} {{\phi _i}{\phi _j}S_i^m{\rm{d}}A} \\ &+ \sum\limits_{k = 1}^{{N_{\rm{b}}} = 3} {\max(0, - {{{n}}_{{\varGamma _k}}} \cdot {{{\varOmega }}^m})\int_{{\varGamma _k}} {{\phi _i}{\phi _j}I_{i,{\rm{nei}}}^m{\rm{d}}\varGamma } } , \end{split}\tag{11b}$
其中Nb = 3表示单元e的3个边界.
然后分析能量扩散方程. 能量扩散方程表示为
$ \nabla \cdot [k\nabla T({{r}})] = \nabla \cdot {{q}}({{r}}),$
式中, k表示热导率; $\nabla \cdot {{q}}({{r}})$为热辐射源项, 表示为
$\nabla \cdot {{q}}({{r}}) = {\kappa _{\rm{a}}}\left[ {4{\text{π}}{I_{\rm{b}}}({{r}}) - \int_{4{\text{π}}} {I({{r}},{{\varOmega }}){\rm{d}}{ \varOmega}} } \right].$
与辐射强度类似, 单元e上温度的形函数近似表示为
$T({{r}}) \cong \sum\limits_{i = 1}^{{N_{\rm{n}}} = 3} {{T_i}{\phi _i}({{r}})} .$
温度的数值通量表示为
${\rlap{-} T_{{\varGamma _k}}} = \left\{ \begin{aligned}& {T_{{\varGamma _k},{\rm{nei}}}} - {T_{{\varGamma _k}}}\quad \,\nabla \cdot {{{n}}_{{\varGamma _k}}} < 0, \; k = 1,2,3, \\ & 0\quad \quad \quad \quad\quad \;\;\;\;\nabla \cdot {{{n}}_{{\varGamma _k}}} > 0, \; k = 1,2,3.\end{aligned} \right.$
最后可得能量扩散方程的DFEM离散格式为
${{MT}} = {{N}},$
式中, T = [T1, T2, T3]T包含离散节点上的温度; 矩阵M和N的元素表示为
$\begin{split} {{{M}}_{ji}} =\; & k\int_{{A_e}} {\nabla {\phi _i}\nabla {\phi _j}{\rm{d}}A} \\ &+ k\sum\limits_{k = 1}^{{N_{\rm{b}}} = 3} {\max (0, - \nabla \cdot {{{n}}_{{\varGamma _k}}})\int_{{\varGamma _k}} {{\phi _i}\nabla {\phi _j}{\rm{d}}\varGamma } }, \end{split}\tag{17a} $
$\begin{split} {{{N}}_j} =\, & \int_{{A_e}} {\left\{ {{\kappa _{\rm{a}}}\left[ {4{\text{π}}{I_{\rm{b}}} - \int_{4{\text{π}}} {I({{r}},{{\varOmega }}){\rm{d}}\varOmega } } \right]{\phi _j}} \right\}} {\rm{d}}A \\ &+ \sum\limits_{k = 1}^{{N_{\rm{b}}} = 3} {\max \left( {0, - \nabla \cdot {{{n}}_{{\varGamma _k}}}} \right)\int_{{\varGamma _k}} {{\phi _i}\nabla {\phi _j}{T_{i,{\rm{nei}}}}{\rm{d}}\varGamma } } .\end{split}\tag{17b}$
至此, 辐射导热耦合传热控制方程的DFEM离散已经完成. 依次求解(10)式所示的辐射传输方程和(16)式所示的能量扩散方程即可得到离散节点的温度值.
3.模型验证
基于上述DFEM离散格式, 发展了MATLAB数值计算程序用以求解(11)和(17)式中的各项元素, 进而通过求解方程(10)和(16)得到辐射强度和温度分布. 本节将DFEM应用于求解二维方形介质内的辐射导热耦合传热以验证数值模型的正确性. 方形介质边长为L, 衰减系数为β, 光学厚度为τ = βL = 1.0. 所有壁面均为发射率ε = 1.0的黑壁面, 底边温度为Tb = 1000 K, 其他壁面温度为500 K, 普朗克数为Npl = kβ/(4σTb3), 其中k表示热导率, σ表示Stefan-Boltzmann常数, σ = 5.67 × 10–8.
首先进行网格无关性检验. 分别将方形区域的边界均匀划分为5, 10和15个单元, 二维计算区域离散为Ne = 62, 226和504个三角形单元. 图2(a)所示为角度划分为Nθ × Nφ = 10 × 20, 不同离散单元条件下介质对称线x/L = 0.5上的无量纲温度T/Tb的分布规律. 图2(b)所示为离散单元数Ne = 226, 不同角度划分Nθ × Nφ = 3 × 6, 5 × 10, 10 × 20和15 × 30条件下对称线上的无量纲温度分布. 由图2所示的结果可知, 离散单元Ne = 226, 离散角度Nθ × Nφ = 10 × 20条件下所得的结果满足网格无关性要求, 在该网格划分条件下采用DFEM求解本算例所需时间为25.38 s.
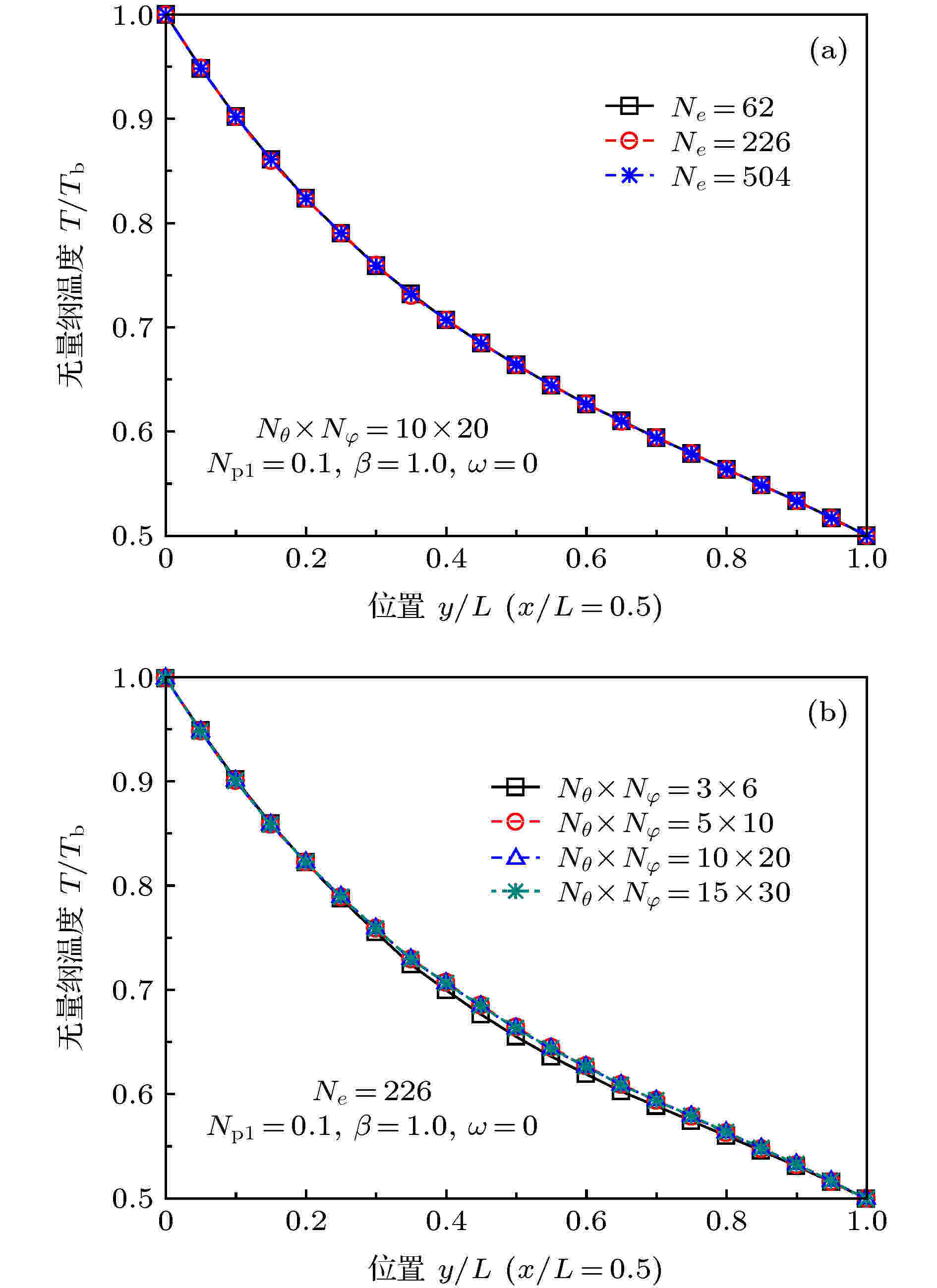图 2 方形介质对称线x/L = 0.5上无量纲温度T/Tb分布　(a)不同空间网格划分; (b)不同角度划分
Figure2. Dimensionless temperature T/Tb along the symmetry line x/L = 0.5 for the cases: (a) Different spatial discretization schemes; (b) different angular discretization schemes.

针对不同普朗克数Npl, DFEM所得无量纲温度分布如图3(a)所示, 并和文献[39]采用离散传递法(discrete transfer method, DTM)所得结果进行了比较. 针对不同的介质散射反照率ω = κa/β, DFEM和DTM所得无量纲温度的对比结果如图3(b)所示. 由图3(b)结果可知DFEM结果和文献DTM结果符合得很好, 验证了DFEM求解辐射导热耦合问题的正确性.
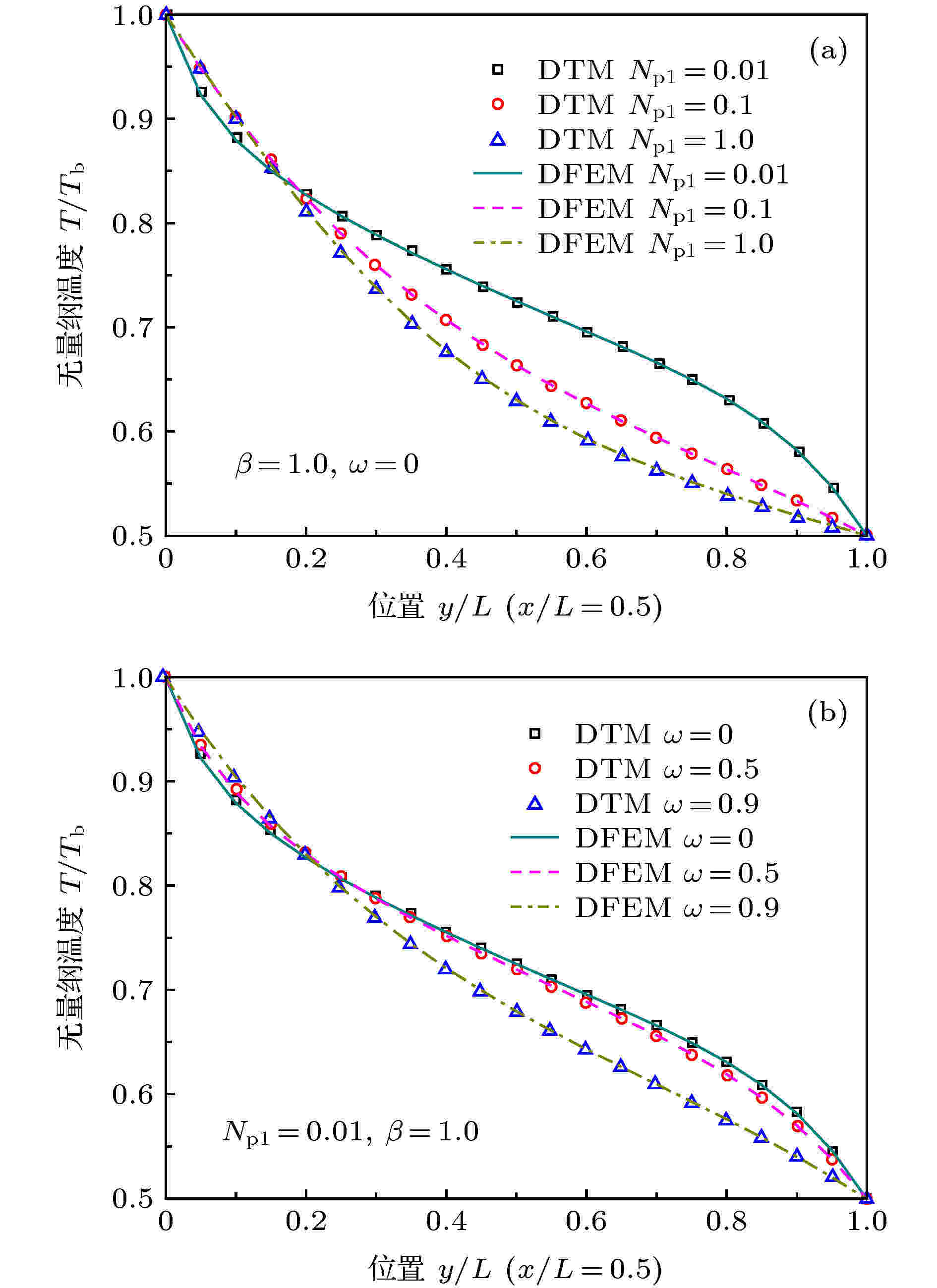图 3 方形介质对称线x/L = 0.5上无量纲温度的DFEM结果和DTM结果对比　(a)不同普朗克数; (b)不同散射反照率
Figure3. Comparison of dimensionless temperature along the square medium symmetry line x/L = 0.5 obtained by DFEM and DTM for the cases: (a) Different Planck numbers; (b) different scattering albedos.

图4所示为在Npl = 0.01, β = 1.0以及ω = 0.0条件下, 不同数值方法所得对称线x/L = 0.5上无量纲温度分布的对比结果. DTM是一种基于光线跟踪的数值方法[39], 避免了控制方程近似处理引起的误差, 因此采用该方法所得结果可视为该问题的基准解. 以DTM结果作为基准, 采用有限体积法(finite volume method, FVM)[29]所得结果最大误差为2.21%, 而本文DFEM结果的最大误差仅为0.68%, 说明DFEM结果更加精确.
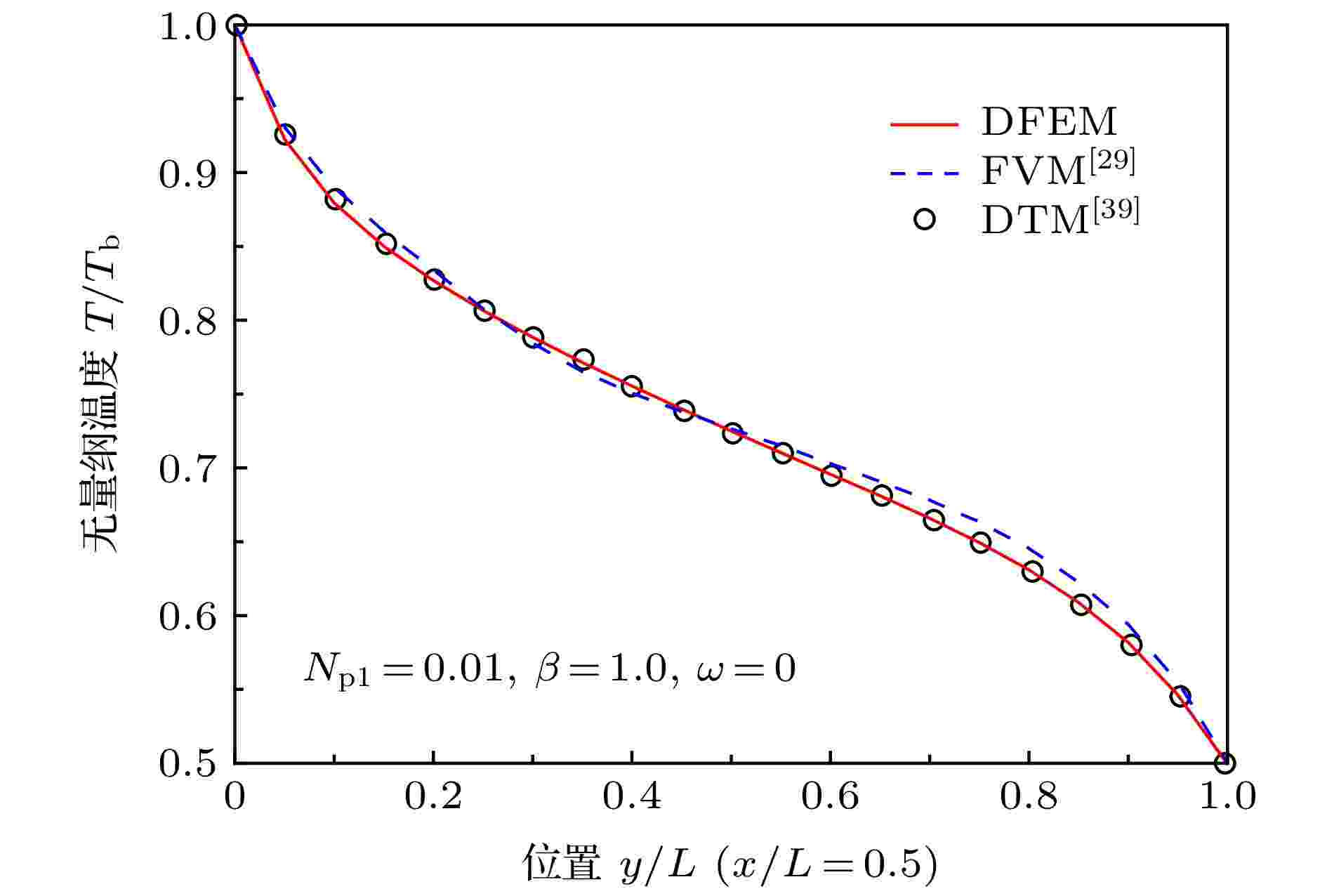图 4 不同数值方法得到的方形介质对称线上的无量纲温度对比
Figure4. Comparison of dimensionless temperature along the square medium symmetry line x/L = 0.5 obtained by different numerical methods.

4.结果和讨论
首先考虑如图5(a)所示的内含圆形壁面(半径Rc = 0.2 m)的半圆形(半径Rs = 1.0 m)介质内的辐射导热耦合问题. 介质衰减系数β = 1.0 m–1, 内部圆形壁面温度Tc = 400 K, 外部半圆形壁面和底边温度Ts = 300 K, 壁面均为黑壁面且发射率ε = 1.0. 采用DFEM方法求解沿着半径方向的无量纲温度分布. 方向离散为Nθ × Nφ = 20 × 40, 空间离散为如图5(b)所示的1768个三角形单元, 所得结果满足网格无关性要求, 采用DFEM求解本算例所需时间为182.69 s.
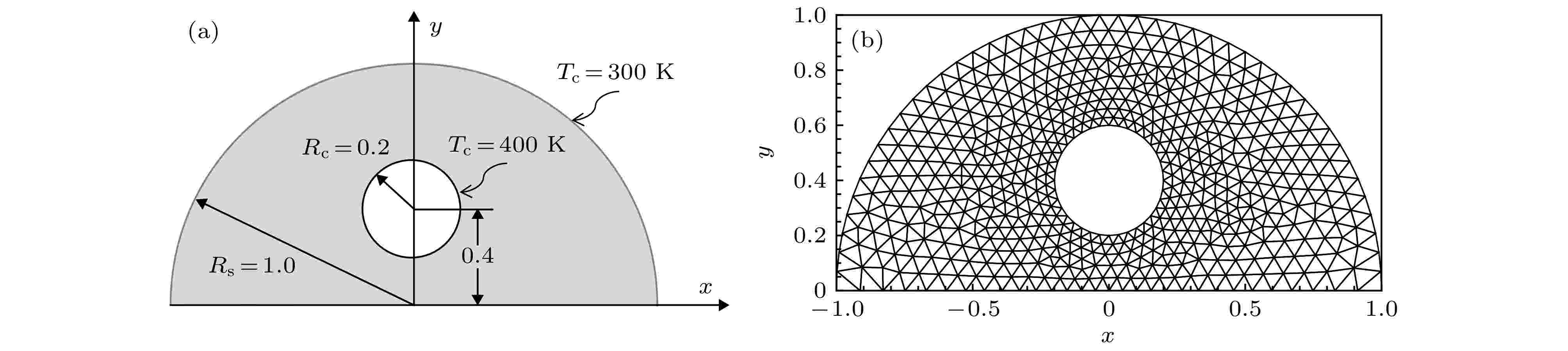图 5 内含圆形热壁面的半圆形介质　(a)结构示意图; (b)网格划分
Figure5. Semicircle medium with an inner circle hot boundary: (a) Geometry sketch; (b) spatial discretization.

在普朗克数Npl = kβ/(4σTs3) = 0.1条件下, 图6所示为采用不同方法(Fluent[31], 不同网格处理方式的FVM[31], 混合格子Boltzmann-有限体积法(LBM-FVM)[40]以及本文DFEM)所得的半圆形介质对称线x = 0上的温度分布. 由图6可知采用Fluent和LBM-FVM以及本文DFEM所得结果符合得较好; 而文献[31]采用FVM所得结果则具有较大的偏差, 这是文献[21]采用四边形网格处理弯曲壁面引起的计算误差所致. 图6所示结果表明, 和FVM相比, 本文发展的DFEM求解非规则形状介质内的辐射导热耦合问题更加精确.
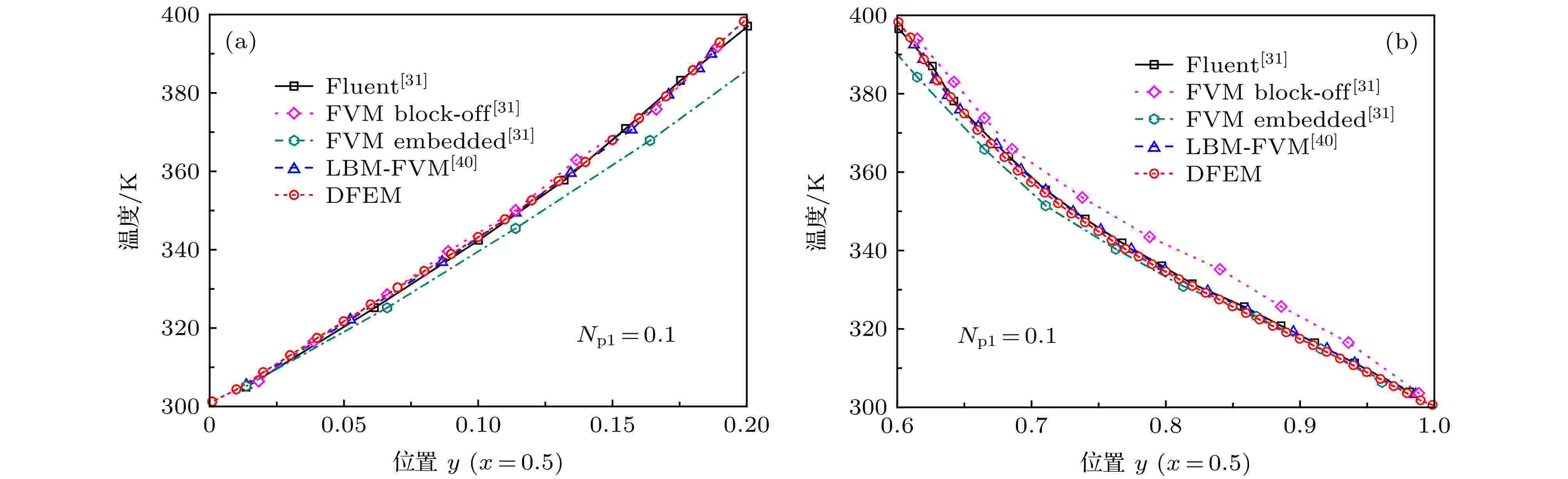图 6 不同数值方法得到的半圆介质对称线上温度分布　(a) y = [0.0, 0.2]; (b) y = [0.6, 1.0]
Figure6. Temperature distributions along the symmetric line of the semicircle medium obtained by different numerical algorithms: (a) y = [0.0, 0.2]; (b) y = [0.6, 1.0].

图7所示为普朗克数Npl = 0.1和1.0条件下半圆形介质底边y = 0上的总热流密度${q_{{\rm{total}}}}({{{r}}_{\rm{w}}}) = $$ - \left( {k\dfrac{{\partial T({{{r}}_{\rm{w}}})}}{{\partial n}} + \displaystyle\int_{{{{n}}_{\rm{w}}} \cdot {{\varOmega }} > 0} {I({{{r}}_{\rm{w}}}, {{\varOmega }})({{{n}}_{\rm{w}}} \cdot {{\varOmega }}){\rm{d}}{{\varOmega }}} } \right)$(负号表示方向)的分布规律. 由图7可知底边中点位置处的热流密度最强, 这是由于内部圆环温度较高, 底边中点距离高温圆环最近, 在辐射和导热共同作用条件下, 该位置处的换热强度达到最大. 由图7(a)结果可知, 当Npl = 0.1时, DFEM结果和Fluent结果吻合良好, 而LBM-FVM结果存在明显误差. 当普朗克数增大到Npl = 1.0时, 采用不同方法所得结果符合得比较好, 如图7(b)所示. 图7所示结果表明, 对于普朗克数较小即辐射占优的辐射导热耦合传热问题, DFEM所得结果更加精确.
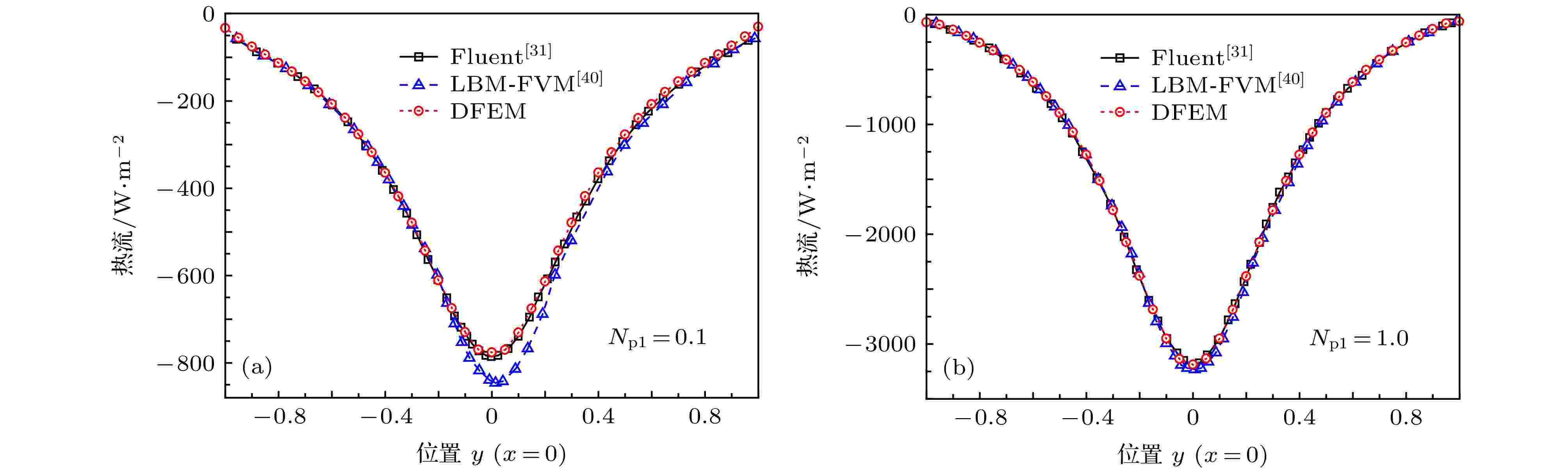图 7 不同普朗克数条件下半圆介质底边上总热流密度分布　(a) Npl = 0.1, (b) Npl = 1.0
Figure7. Total flux distributions along the bottom boundary of the semicircle medium under the situations with different Plank numbers: (a) Npl = 0.1; (b) Npl = 1.0.

接下来考虑如图8(a)所示的内含圆形热边界的非规则形状介质, 该模型可用来研究圆形热管和环境之间的辐射导热耦合换热. 介质尺寸(单位为m)在图8(a)中给出, 介质衰减系数为β = 1.0 m–1, 内部圆形边界温度为400 K, 其他边界温度为自然环境温度300 K, 所有壁面均为黑壁面且发射率为ε = 1.0. 计算区域离散为图8(b)所示的1142个三角形单元、方向离散为Nθ × Nφ = 20 × 40条件下所得结果达到网格无关性要求, 采用DFEM求解本算例所需时间为118.38 s.
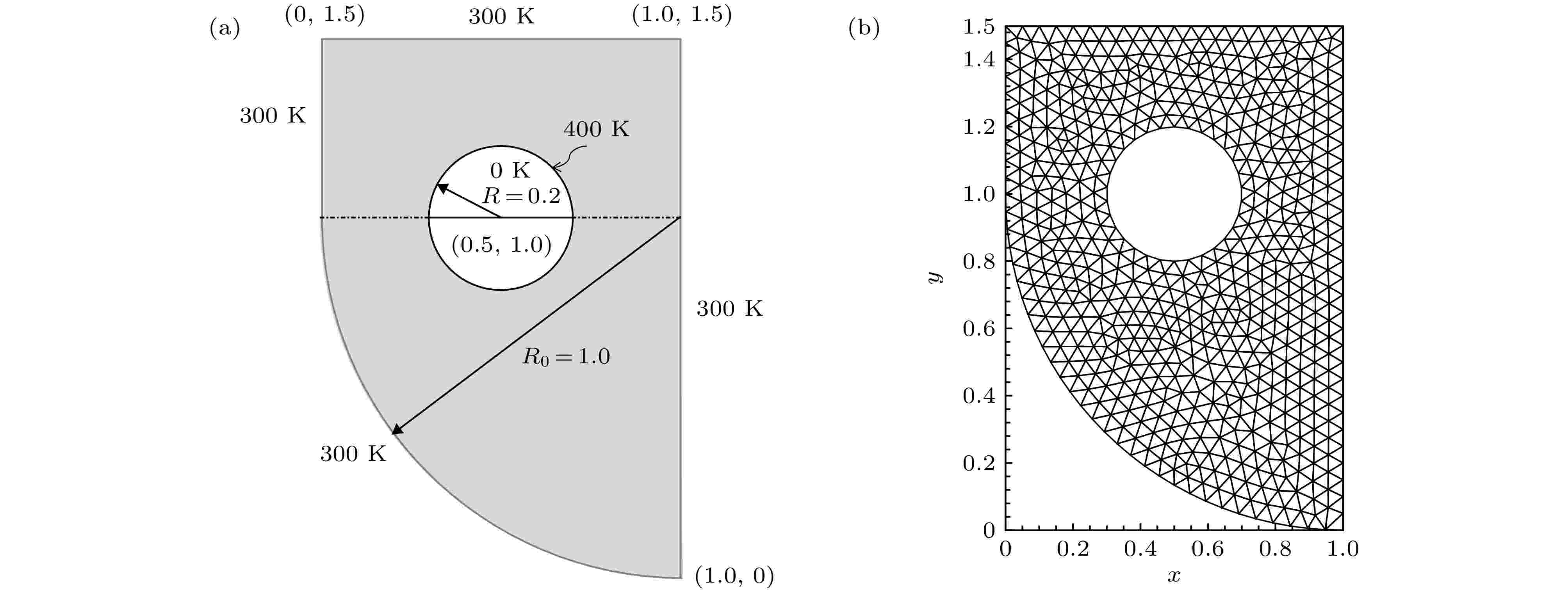图 8 内含圆形热边界的非规则形状介质　(a)结构示意图; (b)网格划分
Figure8. Irregular medium with an inner hot boundary: (a) Geometry sketch; (b) spatial discretization.

图9(a)所示为不同普朗克数Npl = 0.1和 1.0条件下非规则介质中线x = 0.5上的温度分布. 由图9(a)可知, 对于Npl = 0.1的辐射占优问题, 从壁面到圆环之间的温度梯度先减小后增加, 说明靠近圆环和弯曲壁面处的介质温度变化较为剧烈, 而中间区域介质的温度变化较为平缓; 对于Npl = 1.0的导热占优问题, 该区域内的温度梯度逐渐增加, 说明弯曲壁面附近处的介质温度变化较为平缓, 高温圆环附近处的介质温度变化剧烈; 圆环上方的介质温度变化剧烈程度也有所区别, 但由于该区间垂直高度较小, 因此该区间范围的介质温度沿y方向接近于线性减小.
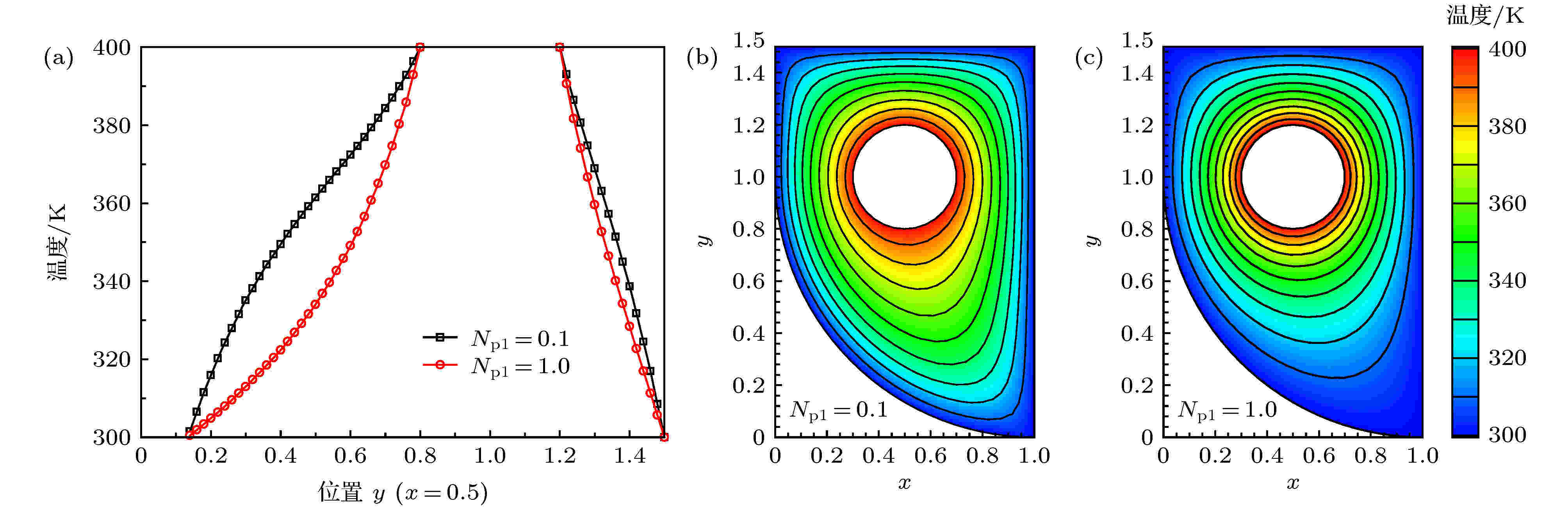图 9 (a)普朗克数Npl = 0.1和1.0时内含圆形热边界的非规则形状介质中线上温度分布; (b) Npl = 0.1时介质温度分布; (c) Npl = 1.0时介质温度分布
Figure9. (a) Temperature distributions along the centerline of the irregular medium with an inner hot boundary; (b) temperature distribution within the computation domain for the case of Npl = 0.1; (c) temperature distribution within the computation domain for the case of Npl = 1.0.

在中心线上的同一位置处, 普朗克数Npl = 0.1对应的介质温度总是高于Npl = 1.0对应的介质温度. 这是由于当Npl = 0.1时, 辐射传热作用显著, 相同位置的辐射源项较强, 因此介质温度更高. 图9(b)和图9(c)所示分别为同普朗克数Npl = 0.1和 1.0条件下的介质温度分布的等值线图, 图9中相邻两条等值线之间的温度差为10 K. 由图9(b)和图9(c)的对比结果可知, 当普朗克数Npl = 0.1时, 强烈的辐射效应能够使高温圆环能量传播得更远, 因此介质内的能量分布更加均匀; 当普朗克数Npl = 1.0时, 显著的导热效应导致温度从高温圆环向外迅速降低, 因此外部边界附近较大范围内的介质温度处于较低水平.
进一步考虑如图10(a)所示的内含两个高温圆环的矩形介质, 该模型可用来研究两个高温管道及其所处环境之间的辐射导热耦合换热. 矩形介质边长为Lx × Ly = 1.0 m × 1.0 m, 内部圆环半径为R = 0.1 m, 圆心位置分别为(x, y) = (0.3 m, 0.3 m)和(x, y) = (0.7 m, 0.7 m). 矩形介质边界和圆环边界之间充满衰减系数为β = 1.0 m–1的参与性介质, 内部两个圆形边界温度均为400 K, 其他边界温度为300 K, 所有壁面均为黑壁面且发射率为ε = 1.0. 计算区域离散为图10(b)所示的1262个三角形单元、方向离散为Nθ × Nφ = 20 × 40条件下所得到的结果达到了网格无关性的要求, 采用DFEM求解本算例所需时间为131.75 s.
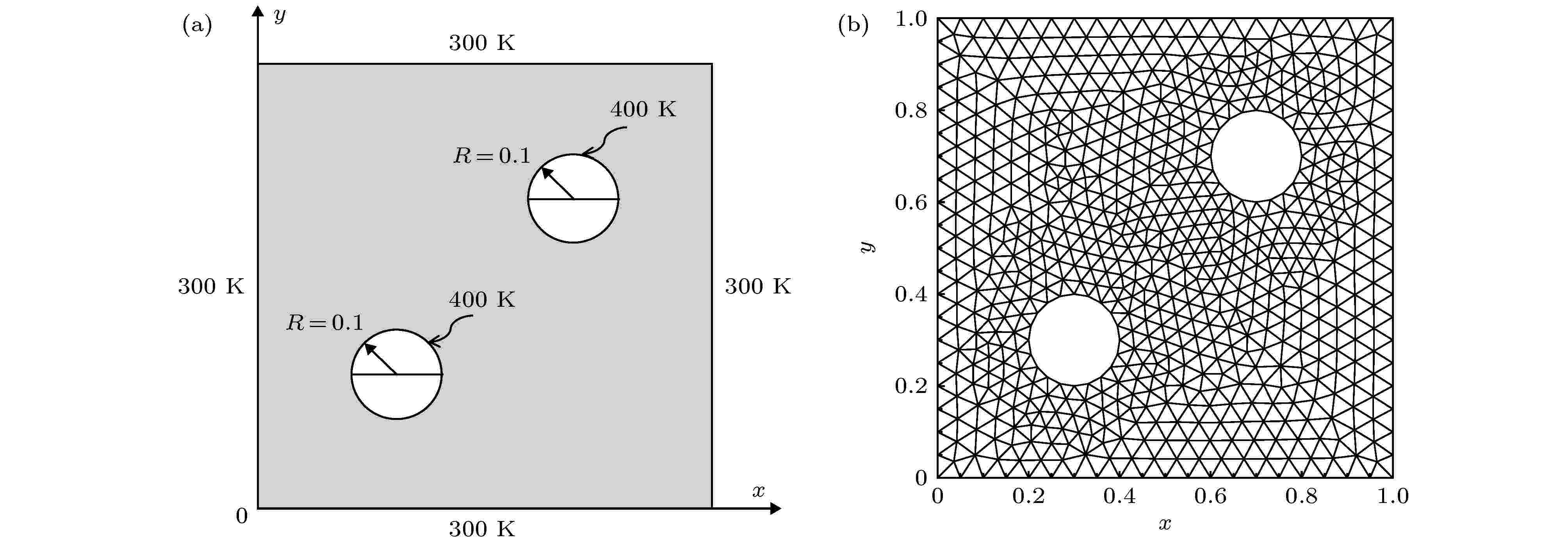图 10 内含两个圆形热边界的矩形介质　(a)结构示意图; (b)网格划分
Figure10. The medium the square medium with two circular hot boundaries: (a) Geometry sketch; (b) spatial discr etization.

在不同普朗克数Npl = 0.1和 1.0条件下, 中线x = 0.5上的温度分布如图11(a)所示, 可知介质中线温度在y = [0, 0.3]逐渐升高且温度变化剧烈程度逐渐降低, 再y = [0.3, 0.7]的介质保持较高的温度, 在y = [0.7, 1.0]逐渐降低. 在同一位置处, Npl = 0.1对应的介质温度高于Npl = 1.0对应的介质温度, 说明辐射效应作用对该模型中线上的介质温度具有显著的提升作用. 图11(b)和图11(c)所示分别为同普朗克数Npl = 0.1和 1.0条件下计算区域内温度分布的等值线图, 相邻两条等值线之间的温度差为5 K. 由图11(b)和图11(c)所示结果可知, 介质中心点位置(x, y) = (0.5 m, 0.5 m)周围存在一个温度梯度较小的区域, 且普朗克数越小, 该区域的面积越大. 以上结果表明辐射效应会弱化中心点位置处的温度梯度, 而导热效应则会强化该位置处的温度梯度.
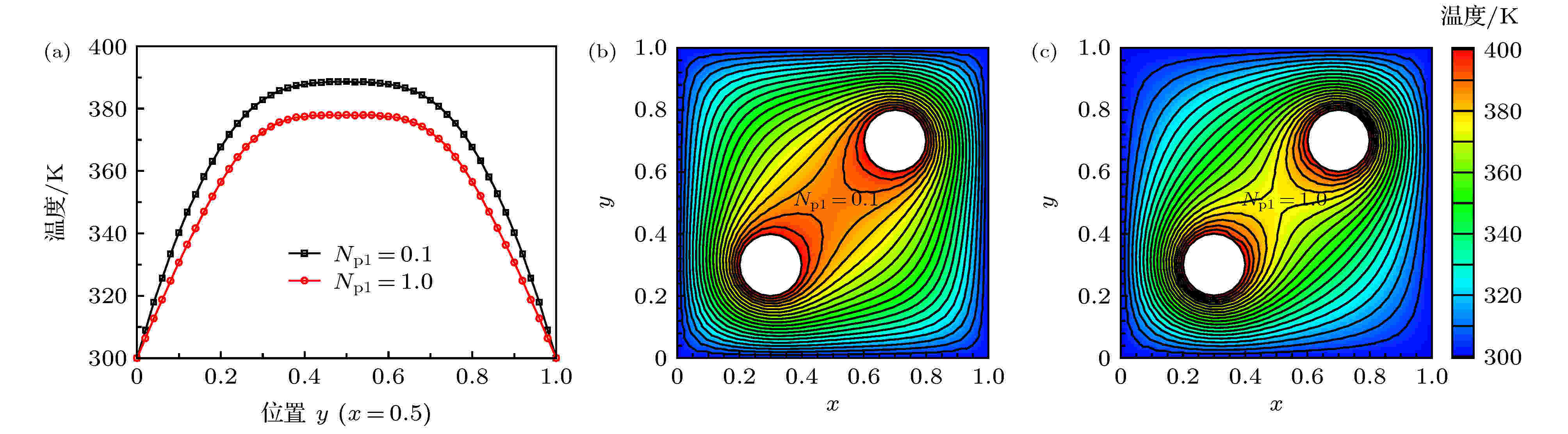图 11 (a)普朗克数Npl = 0.1和1.0时内含两个圆形热边界的矩形介质中线上温度分布; (b) Npl = 0.1时介质温度分布; (c) Npl = 1.0时介质温度分布
Figure11. (a) Temperature distributions along the centerline of the square medium with two circular hot boundaries; (b) temperature distribution within the computation domain for the case of Npl = 0.1; (c) temperature distribution within the computation domain for the case of Npl = 1.0

5.结　论
本文将DFEM扩展应用于求解辐射导热耦合传热问题, 采用非结构化三角形单元划分计算区域, 给出了辐射传输方程和能量扩散方程的DFEM离散格式, 验证了数值算法的正确性并研究了非规则形状介质内的辐射导热耦合传热问题. 研究结果表明: 本文发展的DFEM能够得到非规则形状介质内辐射导热耦合传热问题的高精度数值结果, 尤其是对于普朗克数较小的辐射占优问题; 非规则形状介质内的温度分布规律表明辐射效应会弱化热边界附近的温度梯度, 而导热效应则会强化热边界附近的温度梯度.
相关话题/辐射 传热 计算 控制 文献
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • Parity-time对称性对电注入半导体激光器的模式控制
    摘要:非厄米的描述对于开放系统有重要意义,满足parity-time对称性的哈密顿量,其参数在一定范围内可以使能量具有实的本征值.本文通过模拟,研究了损耗大小以及结构对称性对条形波导中的parity-time对称性的影响,并通过实验发现了电注入条件下由parity-time对称破缺导致的脊条波导模式 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 天线方向系数的一类计算逼近方法
    摘要:天线的方向系数是天线的核心性能指标之一,准确计算方向系数是高性能天线应用的核心要求.本文基于平面近场测试理论、实测数据和快速傅里叶变换算法,系统阐述基于近场测试来数值计算天线方向系数的原理,并进行深入的误差分析.本文选择一种方向图函数和方向系数已知的被测天线,来检验所讨论的误差评估方案.评估分 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 纳秒脉冲激光诱导空气等离子体的近红外辐射特性
    摘要:开展纳秒激光诱导空气等离子体近红外辐射特性的实验研究,对波长为532nm的脉冲ns激光诱导产生的空气等离子体的近红外光谱进行测量.结果表明:空气等离子体的近红外辐射在光谱范围为1100—2400nm内由连续谱和线状谱组成,光谱指认表明线谱主要来源于N,O原子的中性原子谱和氮分子的振动光谱.通过 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 热辐射输运问题的高效蒙特卡罗模拟方法
    摘要:惯性约束聚变研究中,热辐射光子在介质中的输运以及热辐射光子与介质的相互作用是重要研究课题,蒙特卡罗方法是该类问题的重要研究手段之一.隐式蒙特卡罗方法虽然能正确地模拟热辐射在介质中的输运过程,但当模拟重介质(材料的吸收系数大)问题时,该方法花费的计算时间将变得很长,导致模拟效率很低.本文以离散扩 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • TiAl电子态结构的<i>ab initio</i>计算
    摘要:应用完全活动基自洽场方法,结合N电子价态微扰近似(NEVPT2),对TiAl金属二聚体的基态和若干最低电子激发态的势能曲线进行了计算.完全活动空间由Al的3个价电子(3s23p1)轨道和Ti的4个价电子(3d24s2)轨道构成,计算基组选用Karlsruhegroup的价分裂全电子基组def2 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 空位及氮掺杂二维ZnO单层材料性质:第一性原理计算与分子轨道分析
    摘要:采用基于密度泛函理论的第一性原理计算方法,系统地研究了带缺陷的二维类石墨烯结构的ZnO(graphenelike-ZnO,g-ZnO)的几何结构、电子结构、磁性性质和吸收光谱性质.研究的缺陷类型包括锌原子空位(VZn_g-ZnO)、氧原子空位(VO_g-ZnO)、氮原子取代氧原子(NO_g-Z ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 碱金属和碱土金属掺杂二维GaN材料电磁特性的第一性原理计算
    摘要:基于密度泛函理论和投影缀加波赝势方法,采用广义梯度近似算法研究了碱金属(Li,Na,K和Rb)和碱土金属(Be,Mg和Sr)掺杂二维GaN单层的电子结构和磁学性质.研究表明,除Be原子位于GaN单层平面内之外,其余掺杂原子均略微隆起于平面.通过比较七种掺杂体系在不同环境下的形成能,发现在富N环 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 应用中国散裂中子源9号束线端研究65 nm微控制器大气中子单粒子效应
    摘要:采用设置和不设置镉中子吸收体两种方式,利用中国散裂中子源9号束线(CSNS-BL09)对65nm微控制器进行了大气中子单粒子效应辐照测试.测试中探测到的效应主要为单位翻转.测试结果表明,对于该款微控制器,热中子引起的中子单粒子翻转占比约65%;进一步分析表明,热中子与10B反应产生的0.84M ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 空间电子辐射环境中绝缘介质电荷沉积特性及陷阱参数研究综述
    摘要:空间电子辐射环境中绝缘介质充放电特性与介质表面电荷交换过程或内部电荷迁移过程密切相关.介质表面/内部电荷运动很大程度上取决于材料的微观特性,空间电荷与陷阱是反映绝缘介质微观特性的重要参数.本文综述了电子辐射环境中绝缘介质内部空间电荷和陷阱的形成、作用机理、测量方法、存在的问题及国内外研究现状. ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 半导体激光器储备池计算系统的工作点选取方法
    摘要:半导体激光器储备池计算系统的性能受很多因素的影响,如虚节点间隔、激光器的偏置电流和反馈强度等.对于光注入信号方式,注入强度和频率失谐的大小也会影响系统的性能,使得工作点更难确定.为此,本文以10阶非线性自回归移动平均任务为基础,提出一种选取半导体激光器储备池计算系统的最佳反馈强度与注入强度的方 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.