摘要:近来, 人们在凝聚态体系中发现了由拓扑不变量定义的物相, 其中最重要的有拓扑绝缘体、拓扑半金属和拓扑超导体等. 这些物相的拓扑性质由非平凡的拓扑数描述, 相应的材料被称为拓扑材料, 具有诸多新奇的物理特性. 其中拓扑超导体由于边界上有满足非阿贝尔统计的Majorana零能模, 成为实现拓扑量子计算的主要候选材料. 除了探索本征的拓扑超导体外, 由于拓扑性质上的相似性, 在不超导的拓扑材料中调制出超导自然成为了实现拓扑超导的重要手段. 目前, 人们发展了栅极调制、掺杂、高压、近邻效应调制和硬针尖点接触等多种技术, 已经成功地在许多拓扑绝缘体和半金属中诱导出了超导, 并对超导的拓扑性和Majorana零能模进行了研究. 本文回顾了本征拓扑超导候选材料, 以及拓扑绝缘体和半金属中诱导出超导的代表性工作, 评述了不同实验手段的优势和缺陷、分析了其超导拓扑性的证据, 并提出展望.
关键词: 拓扑绝缘体/
拓扑半金属/
非常规超导/
拓扑超导/
拓扑材料

English Abstract

全文HTML

--> --> -->

自从整数量子霍尔效应的研究将拓扑的概念引入凝聚态体系以来, 对材料的拓扑性质的研究已成为凝聚态物理领域最重要的方向之一. 材料的拓扑性质由它们的拓扑数表征, 这是一类倒易空间中受到对称性保护的积分不变量. 以整数量子霍尔效应为例, 著名的TKNN文章^[1]提出量子化的电导平台σ_xy可以由贝里曲率在布里渊区中的积分来描述,

${\sigma _{xy}} = - \frac{{{e^2}}}{h}C,$

$ C = \frac{1}{{2{\text{π}}}}\mathop \sum \limits_{{\rm{filled}}\;{\rm{band}}}\int{\rm{d}}^2k\int{\rm{d}}^2r\left( {\frac{{\partial {u^*}}}{{\partial {k_1}}}\frac{{\partial u}}{{\partial {k_2}}} - \frac{{\partial {u^*}}}{{\partial {k_2}}}\frac{{\partial u}}{{\partial {k_1}}}} \right), $

其中u为体系的波函数, k₁和k₂为二维布里渊区中的波矢, $\dfrac{{\partial {u^*}}}{{\partial {k_1}}}\dfrac{{\partial u}}{{\partial {k_2}}} - \dfrac{{\partial {u^*}}}{{\partial {k_2}}}\dfrac{{\partial u}}{{\partial {k_1}}}$为贝里曲率的一般表达式. C一定是整数, 被称为第一类陈数, 是布里渊区的拓扑不变量^[2,3].
正如曲面上属于不同分类的路径不能经过连续形变重合, 量子材料的拓扑类别在不闭合能隙的前提下也不会因为参数微调而改变, 因此拓扑性质通常具有很强的稳定性. 此外, 由于体态和真空属于不同的拓扑相, 在体态的边界会形成无能隙的导电通道, 受体态拓扑性质的保护, 不易受杂质、微扰的影响. 通常, 量子计算机最大的困难来自杂质、微扰所产生的退相干效应. 而拓扑量子计算, 也即利用拓扑性质开展的量子计算, 因其强的容错能力, 已成为最有前景的量子计算方式之一.
由于实际材料往往具有不同的对称性, 包括时间对称性、空间对称性、手征对称性、粒子空穴对称性等; 同时, 实际材料也具有不同的能带结构, 如绝缘体、半金属、超导等, 因此拓扑材料的种类异常丰富. 对于时间反演不变体系, Kane和Mele^[4]提出用${\mathbb{Z}_2}$拓扑数来进行分类, 区分出普通绝缘(${\mathbb{Z}_2}=0$)和拓扑绝缘体 (topological insulator, TI) (${\mathbb{Z}_2}=1$). 二维的拓扑绝缘体也被称为量子自旋霍尔效应 (quantum spin hall effect, QSHE) 体系, 其体态是有能带反转的绝缘体, 而一维边界上出现低耗散的、一对自旋和动量相反的边界态. 重要的二维拓扑绝缘体体系如HgTe量子阱^[5,6]、InAs/GaSb量子阱^[7,8]以及单层的过渡金属硫属化合物的1T' 相^[9,10]等在理论预测后基本得到了实验的证实. 在三维中, ${\mathbb{Z}_2}$不变量还可以用来区分弱和强的拓扑绝缘体^[11]. 三维拓扑绝缘体体态绝缘, 但边界上出现自旋轨道锁定的无带隙的导电通道, 即所谓表面Dirac锥的能带结构. 弱三维拓扑绝缘体相当于二维拓扑绝缘体的层叠, 因而表面态容易受到杂质的破坏. 强拓扑绝缘体的拓扑表面态则非常稳定, 因此, 在对三维拓扑绝缘体的研究中, 强TI受到更多的关注. 其中, Bi₂Se₃和Bi₂Te₃由于有较大的体态带隙(Bi₂Se₃的带隙大小约为0.3 eV)和单个Dirac锥的表面态^[12], 已经成为最具代表性的三维拓扑绝缘体. 其拓扑表面态的特性得到了输运^[13]、角分辨光电子能谱(angle-resolved photon emission spectroscopy, ARPES)^[14,15]和扫描隧道显微镜(scanning tunneling microscope, STM)^[16]的充分研究.
自2012年以来, 人们关注的重点开始转移到另一类拓扑材料—拓扑半金属上. 事实上, 在对拓扑绝缘体的研究中, 人们已经敏锐地意识到, 在拓扑绝缘体到普通绝缘体转变的临界点上, 体态能带闭合, 导带和价带交于一个点: 这可能是一种新的物态^[6]. 这一色散关系和三维拓扑绝缘体的表面态类似. 2012年, Young等^[17]预言, 在三维的能带中, 导带和价带可能在离散的点处相交, 在它周围色散关系成线性, 区别于常见的二次方色散关系. 在时间反演对称性和中心反演对称性的保护下, 这种离散点四重简并, 可以等效地用Dirac方程描述, 因此它们被称为Dirac点. Dirac半金属就是能带结构中有Dirac点的特殊半金属, 它们常被称为三维的石墨烯. 如果时间反演或中心反演对称性中任意一种被破坏, Dirac点会分成两个Weyl点. 每一个Weyl点带有非零的陈数, 陈数的正负反映Weyl点的手性. 一般的Dirac点不带有陈数, 因此它并不是稳定的. 只有在附加晶体对称性的保护下, Dirac点才能用镜面陈数和2维${\mathbb{Z}_2}$描述, 才是对微扰稳定的^[18]. 理论和实验都说明, 拓扑半金属可以作为研究新奇量子现象的平台: 非饱和的线性磁阻^[19-21]、负磁阻^[22,23]、非平凡的量子振荡^[24,25]、反常霍尔效应^[26]、面内霍尔效应^[27]以及非常规霍尔效应^[28,29]等在这些体系中都被实验观测到, 对它们的理解丰富了人们对材料拓扑性质的认识.
与此同时, 超导体作为一种被长期关注的量子体系, 也获得了从拓扑不变量角度的重新认识. 事实上, 超导体中准粒子的Bogoliubov–de Gennes (BdG)哈密顿量和绝缘体的哈密顿量有直接的类比关系^[30]. BdG哈密顿量下所有负能级态被完全占据, 因此, 可以在超导体中类比绝缘体定义拓扑不变量. 笼统地说, 如果一个超导体的某一种拓扑不变量取非平凡值, 它就可以被称为拓扑超导体^[31]. 拓扑超导体的重要特点是它的边界上会出现无能隙的准粒子激发. 理论上, 这种准粒子可以被视为Majorana费米子, 而零维受限的Majorana费米子可以被称为Majorana零能模. Majorana费米子是一种满足Dirac方程, 且为自身反粒子的粒子, 用二次量子化的语言, 即该粒子的产生算符等于其湮灭算符, ${{\gamma}} = {{{\gamma}} ^? }$. Majorana费米子满足非阿贝尔统计, 这是其他拓扑材料边界态所不具备的性质, 因此拓扑超导是实现容错性强的拓扑量子计算的重要途经^[32,33]. 在高能领域中, 人们猜测中微子可能是待证明的Majorana费米子; 而在天文学领域中, 一直无法被解释的暗物质, 也有可能由Majorana费米子组成. 值得注意的是, Majorana费米子为构成半个费米子的激发模态, 只有当两个Majorana费米子耦合在一起时, 才能表示一个凝聚态体系中的电子.
关于拓扑超导和Majorana费米子的理论预言, 最早由Read和Green^[34], 以及Kitaev^[35]分别提出. 他们通过理论模型证明, 二维和一维的时间反演对称无自旋p波超导态, 会分别在一维和零维边界上产生Majorana零能模. 对于通常的一维超导系统^[36], 哈密顿量可以写为$H\left( k \right) = {{h}}\left( k \right) \cdot {{\sigma}} $, 其中${{\sigma}}$为泡利矩阵, 参数${{h}}\left( k \right) = ({\rm{Re}}\varDelta \left( k \right), - {\rm{Im}}\varDelta \left( k \right), $$\varepsilon \left( k \right)) $张成二维球面且满足$\left| {{{h}}\left( k \right)} \right| = E\left( k \right)$, 其中$\varDelta \left( k \right)$为超导能隙, $\varepsilon \left( k \right)$为单粒子能量, E(k)为超导哈密顿量的本征值. 超导带来的粒子空穴对称性(particle-hole symmetry)要求$\varDelta \left( k \right) = - \varDelta \left( { - k} \right)$, 因此k = 0或π时, 超导能隙 Δ(k)=0, h(k)经过球面的南极点或北极点. 布里渊区[0, π]映射至球面的不同路径, 根据${{h}}\left( 0 \right), \;{{h}}\left( {\text{π}} \right)$的符号进行拓扑分类, 便能定义${\mathbb{Z}_2}$拓扑不变量. 若h(0)与h(π)反号, 则体系为拓扑非平凡的拓扑超导体. 特别地, 当拓扑超导体具有时间反演对称性时, 类似量子自旋霍尔效应, 也能定义时间反演对称意义下的新${\mathbb{Z}_2}$拓扑数. 对于二维拓扑超导系统, 与量子霍尔态类似, 拓扑分类由陈数给出. 非平凡的Majorana零能模会出现在p+ip超导体的量子磁通端点, 当对磁通进行交换作用时, 相当于对Majorana零能模进行交换作用, 因此二维p+ip或等效的p+ip拓扑超导体系提供了一个通过磁通对Majorana零能模进行编织的可行方案.
综上, 拓扑和超导的结合成为了凝聚态物理的重要领域, 以及实现量子计算的重要研究方向. 获得拓扑超导的重要手段, 除了寻找本征的拓扑超导体之外, 就是在拓扑材料(拓扑绝缘体和拓扑半金属)中调制出超导^[31,36,37]. 如今, 人们已经发展出多种调制手段, 如栅极调控、掺杂、高压、近邻效应调控和硬点接触等方式, 并已在不同的拓扑体系中诱导出了超导. 进一步地, 对这些拓扑材料中的超导的研究揭示了可能的非常规特性, 这为拓扑超导的实现提供了激动人心的可能. 本文将以实验手段为线索, 重点回顾在拓扑材料中调制出超导的代表性工作, 讨论其重要意义, 并评述不同调节方式的优势和缺陷. 最后, 对在拓扑材料中实现拓扑超导做出展望.

本征的拓扑超导体不需要借助过多的调制手段, 因此其中的Majorana零能模往往具有更强的稳定性. 但是根据Bardeen-Cooper-Schrieffer (BCS) 超导理论, 常见的超导体属于自旋单态配对, 因此叠加态包含自旋的自由度, 对于准粒子算符$a = uc_ \uparrow ^? + v{c_ \downarrow }$, 其反粒子${a^? } = {u^*}{c_ \uparrow } + {v^*}c_ \downarrow ^? $在形式上与原算符不同, 违反Majorana费米子的自反性要求. 因此, 通常从自旋三重态配对的手征p波超导体中寻找本征的拓扑超导. 理论上, 利用p波或d波来进行配对, 即无法用BCS理论解释的超导体都可称为非常规超导体, 由于其轨道削弱了电子之间的直接作用, 因此也能得到稳定的电子-电子配对. 受到广泛关注的铜氧化物高温超导体就被主流认为是d波配对的.
理论预言, 当电子之间相互作用在短程排斥而在长程吸引, 亦或体系具有多能带的特点时, 可能发现p波超导体^[38]. 实验上, He-3奇异态是最早发现的拓扑非平凡p波超流体^[39]. 之后, Maeno等^[40,41]以及Rice和Sigrist^[42]发现了可能的拓扑非平凡p波超导体Sr₂RuO₄. Sr₂RuO₄和高温超导体La₂CuO₄类似, 属于层状四方晶系, 但是却有着三条穿过费米面的能带. 实验证实Sr₂RuO₄具有自旋三重态配对和时间反演对称性破缺的p波性质^[43-45], 同时面内隧穿谱也探测到符合理论预测的安德列夫反射^[46], 因此Sr₂RuO₄很可能是具有非平凡的拓扑边缘态的手征p波超导体^[47,48]. 但是, 目前在He-3奇异态以及Sr₂RuO₄体系中尚无拓扑超导和Majorana费米子的直接实验证据.
类似的p波本征拓扑超导体候选材料, 有拓扑晶体绝缘体Sn_1–xIn_xTe, 包含三个不同超导相的重费米子金属UPt₃^[49], 以及低温下具有结构相变打开能隙的Dirac半金属Au₂Pb^[50-54]. 对于Au₂Pb, 输运和抗磁性实验证实了其在40 K左右的结构相变和在1.15 K以下的超导特性(图1), 而第一性原理计算则发现了体系中费米面附近拓扑非平凡的轨道结构. 最近, Xing等^[55]在第二类Weyl半金属TaIrTe₄中, 也发现转变温度为T_c = 1.54 K的准一维超导和拓扑非平凡的Shubnikov de-Haas (SdH) 量子振荡, 因此TaIrTe₄也可以作为研究拓扑超导的平台之一.
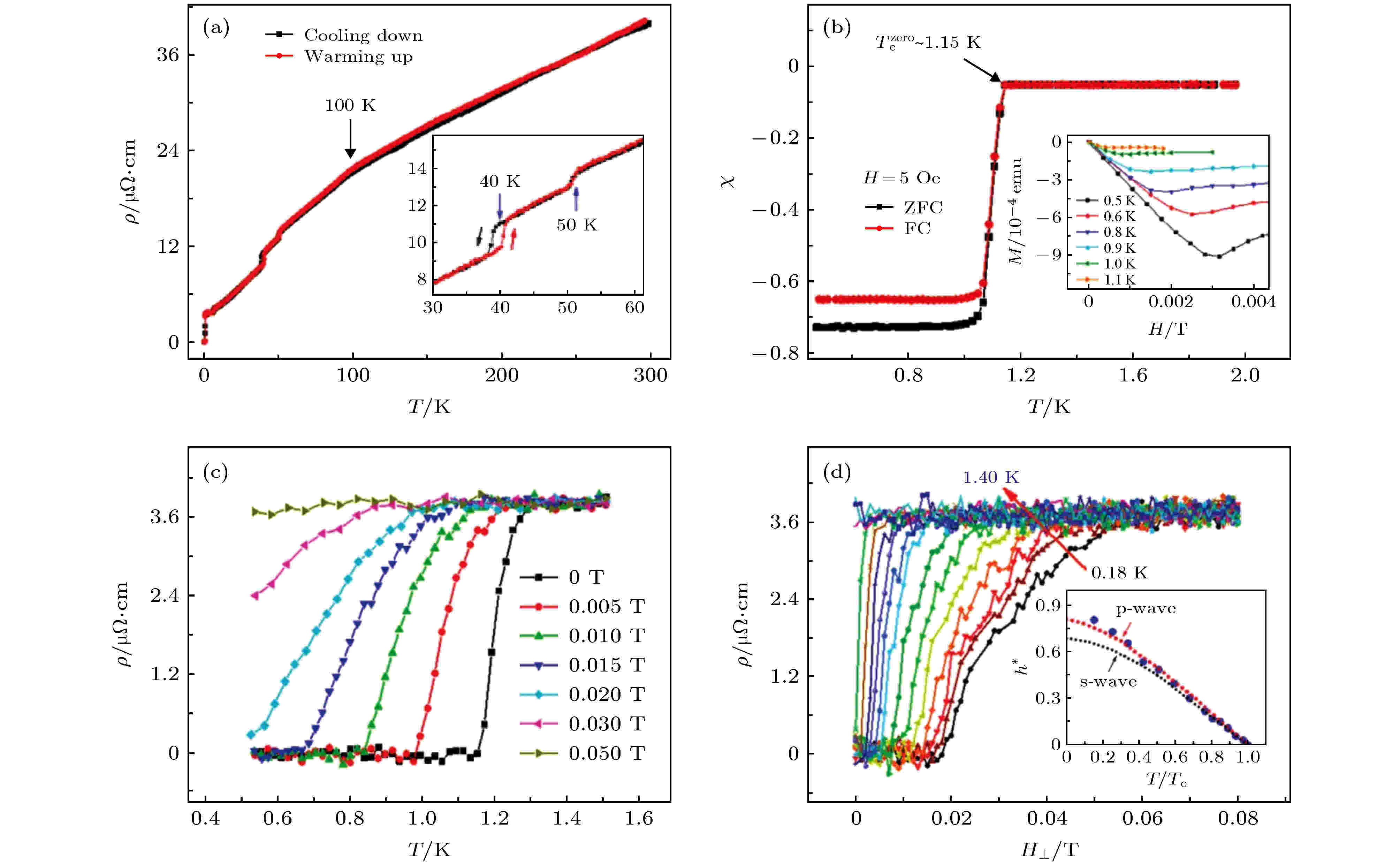图 1 Au₂Pb的输运测量　(a) Au₂Pb单晶的ρ(T)曲线, 插图为30—60 K的实验数据; (b) 温度对磁化率χ的依赖, 体现了低温下的Meissner效应, 插图为不同温度下的M(H)曲线; (c) 不同垂直场下的ρ(T)曲线; (d) 不同温度下的ρ(H_⊥)曲线, 插图为归一化的上临界场与温度的关系, 红色虚线为p波超导拟合, 而黑色虚线为WHH理论所描述的s波超导拟合. 引自文献[52]
Figure1. Transport measurements of Au₂Pb: (a) ρ(T) curves of Au₂Pb single crystal. Inset: close-up of the same data from 30 to 60 K; (b) temperature dependence of χ, shows the Meissner effect: sharp diamagnetic drops at 1.15 K. The inset presents low-field M(H) curves at various temperatures from 0.5 to 1.1 K; (c) ρ(T) characteristics at various H_⊥ up to 0.05 T. The ρ(T) obtained in zero field shows $ T_{\rm c}^{\rm onset} = 1.3~{\rm K},~T_{\rm c}^{\rm zero} = 1.18~{\rm K} $; (d) magnetoresistance of Au₂Pb crystal at various temperatures under H_⊥. Inset: normalised upper critical field ${h^*} = {H_{{\rm{c}}2}}/{T_{\rm{c}}}\left( {{\rm{d}}{H_{{\rm{c}}2}}/{\rm{d}}{T_{T{\rm{}} = T_{\rm{c}}}}} \right)$ as a function of normalised temperature t = T/T_c, with the red dashed line indicating the expectation for a polar p-wave state. The black dashed line indicates the WHH theory for s-wave superconductor. From Ref. [52].

此外, 在非中心对称的晶体中, 波函数的空间部分以及自旋部分都不能简单地写成对称或反对称的形式, 使得库珀对形成自旋单态和自旋三态的混合态^[56], 产生非平凡的拓扑能带结构. CePt₃Si是第一个被发现的非中心对称超导体^[57,58], 具有超导转变温度 T_c = 0.75 K 和反铁磁序转变温度 T_N = 2.2 K. 而在此之后发现的非中心对称超导体TaRh₂B₂和NbRh₂B₂等^[59], 还具有新奇的手征特性.
事实上, 由于具有p波特性的本征拓扑超导体候选材料非常有限, 更多的研究是通过栅极、高压、掺杂、超导近邻、以及点接触等方式对拓扑绝缘体和半金属进行调制, 进而产生可能的拓扑超导. 在相关研究中观测到可能的Majorana零能模信号, 为拓扑量子计算提供了候选平台.

栅极电压调控是半导体领域中常用的调节手段. 相比超导近邻效应的界面调控, 更加简单易行. 过渡金属硫族化合物 (TMD) 材料WTe₂的体态是第二类Weyl半金属, 而二维的单层结构则是一种拓扑绝缘体^[60], 其特点是在100 K的高温下仍然具有接近量子化的边缘态电导^[61]. 2018年, Fatemi等^[62]和Sajadi等^[63]几乎同时发现栅极电压调控能够使二维拓扑绝缘体WTe₂进入超导态.
Fatemi等^[62]将WTe₂通过范德瓦耳斯力包裹在两层氮化硼(BN)薄膜之间(图2(a)), 并通过这两层氮化硼薄膜来进行栅压调制(图2(b)), 连续地改变费米面位置和体系中的载流子浓度. 实验发现: 1)在很宽的一段栅压范围内, 都能看到零电阻态(图2(c)); 2) V-I特性曲线中低温时具有类似超导的非线性行为(图2(d)); 3)磁场抑制了V-I的非线性行为(图2(e)). 以上三点作为多重证据, 证实WTe₂在栅压调控下确实出现了超导. 同时, 文献[62]的补充材料中给出了超导螺旋边界态的初步证据, 预示着Majorana边界态的可能.
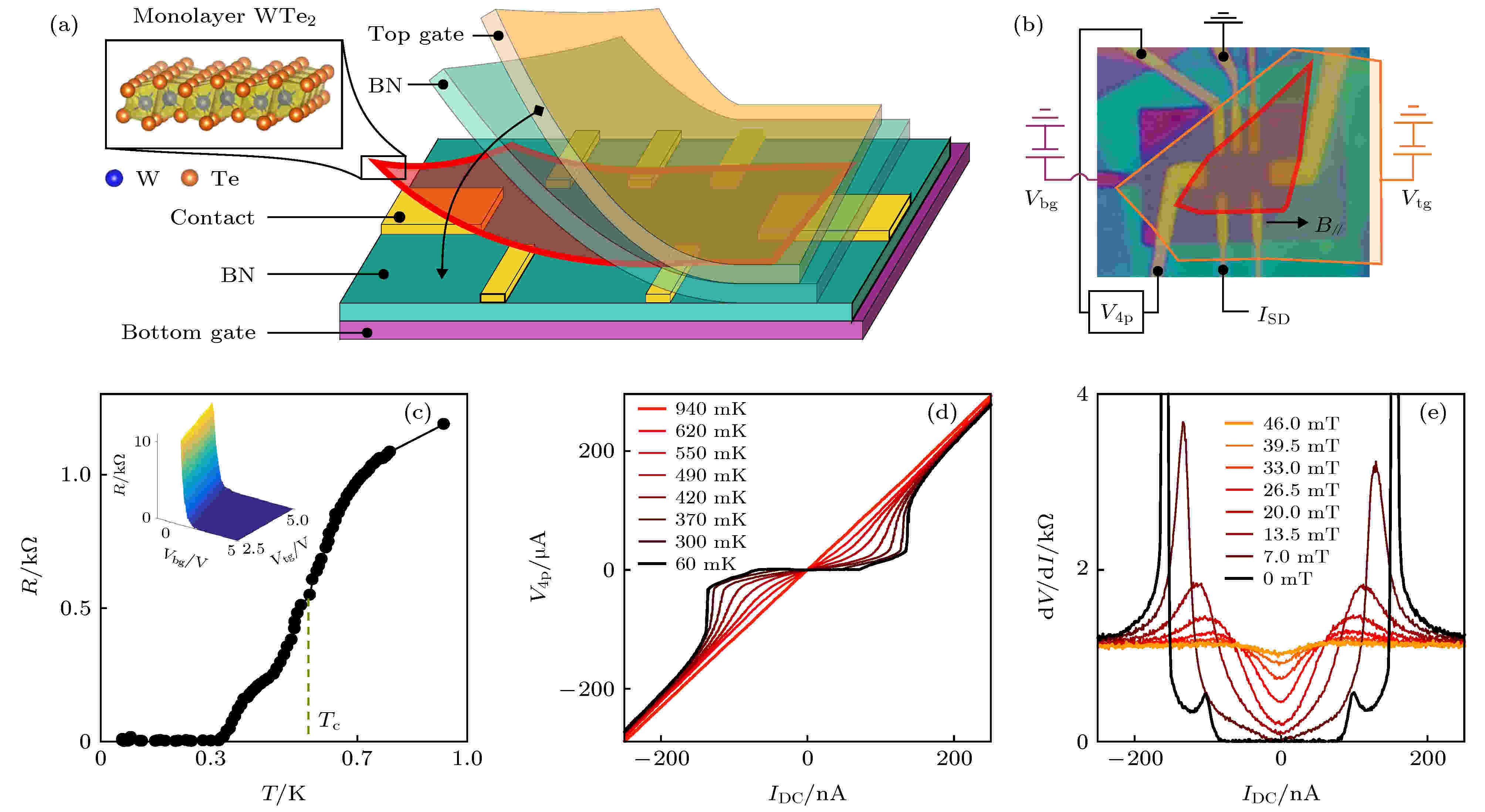图 2 Fatemi等^[62]的WTe₂栅压实验　(a)单层WTe₂晶体结构的示意图; (b) 实验样品的光学图像; (c) 底压为4 V、顶压为5 V时的R-T曲线, 插图表示60 mK时电阻随底压和顶压变化; (d)不同温度下的V-I特性曲线; (e)不同外磁场下的微分电导随电流变化曲线. 引自文献[62]
Figure2. Device schematic and superconductivity characteristics^[62]: (a) Cartoon illustration of the device structure and the crystal structure of monolayer WTe₂; (b) optical microscopy image of device 1; (c) temperature dependence of the resistance for V_bg = 4 V and V_tg = 5 V. The inset shows the resistance as a function of both gate voltages, at a base temperature of 60 mK; (d) V-I characteristics from base temperature (black) up to 940 mK (red); (e) nonlinear V-I behavior, captured by differential resistance curves, at base temperature for different perpendicular magnetic fields. From Ref. [62].

而Sajadi等^[63]同样用六方氮化硼薄膜对样品进行栅压的连续调控, 实验同样发现, 当载流子浓度高于临界值时WTe₂进入超导态(图3(a)). 此外, 实验中还发现了其他新奇的现象: 1) 极低温度下, 电阻值趋向一个与温度无关的常数, 预示着量子金属态的可能(图3(b)和图3(d)); 2) 在低温区域, R_xx随垂直场变化平滑, 却随平行场在2 T处出现突变(图3(e)和图3(f)); 3) 在很大的载流子浓度n_e范围内, lnR_xx-T曲线出现中间态平台, 然而该平台在微弱的垂直磁场下却立刻消失.
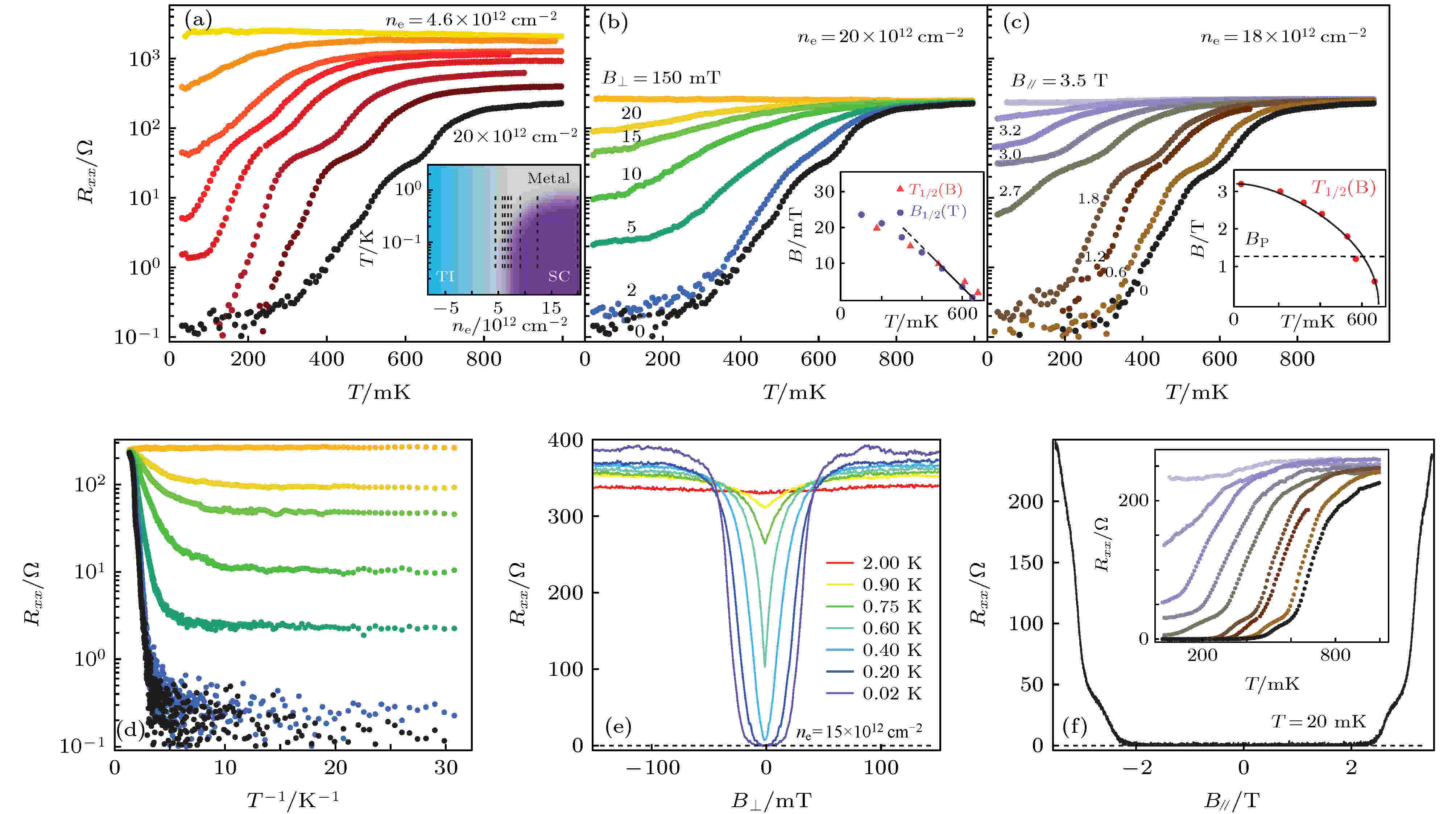图 3 Sajadi等^[63]的WTe₂栅压实验　(a)零外磁场下, 不同载流子浓度下的lnR_xx-T曲线, 其中出现明显的中间态平台. 插图为扫描线在相图中的位置; (b)载流子浓度n_e = 20 × 10¹² cm^–2时, 不同垂直场下的lnR_xx–T曲线. 插图: 扫温得到的特征温度 T_1/2和扫场得到特征磁场B_1/2; (c)载流子浓度n_e = 18 × 10¹² cm^–2时, 不同平行场下的lnR_xx–T曲线(B_// = 0 数据对应载流子浓度 n_e = 19 × 10¹² cm^–2; 剩余数据对应载流子浓度 n_e = 18 × 10¹² cm^–2). 插图: 特征温度T_1/2随平行场B_//的变化关系, 其中泡利极限B_P由灰色虚线表示; (d)不同垂直磁场下的lnR_xx–1/T曲线, 体现低温下电阻的饱和; (e)载流子浓度n_e = 15 × 10¹² cm^–2时, 不同温度下的R_xx–B_⊥曲线体现极低垂直磁场下电阻的升高; (f)和(e)相同载流子浓度下, 不同温度下的R_xx–B_//曲线, 体现相比(e)更为尖锐的电阻跳变. 插图: 线性坐标下(c)中的数据. 引自文献[63]
Figure3. Resistance characterization of WTe₂ device in the superconducting regime: (a) R_xx on log scale versus temperature T at a series of positive-gate doping levels n_e showing a drop of several orders of magnitude at low T for larger n_e. Inset: Locations of sweeps on the phase diagram; (b) effect of perpendicular magnetic field B_⊥ on resistance at the highest n_e value in (a). Inset: Chara-cteristic temperatures T_1/2 obtained from these temperature sweeps, as well as characteristic fields B_1/2 measured from field sweeps under similar conditions; (c) same as (b) but for the in-plane magnetic field B_// (the B_// = 0 data are for n_e = 19 × 10¹² cm^–2; the remaining data are for n_e = 18 × 10¹² cm^–2). Inset: Reduction of T_1/2 with B_//, fit to the expected form for materials with strong spin-orbit scattering (solid line). The Pauli limit B_P, assuming g = 2, is indicated by the dashed line; (d) data from (b) replotted to highlight the saturation of R_xx at low T; (e) sweeps of B_⊥ showing rise of resistance beginning at very low field; (f) sweep of B_// showing sharper onset of resistance comparing to (e). Inset: Data from (c) on a linear scale. From Ref. [63].

压强也是常用的实验调制手段, 在样品生长和电子态调控等方面有广泛应用. 作为一种调制超导的手段, 高压创造了目前最高的超导临界温度^[64]. 常见的材料杨氏模量在1—10² GPa量级, 因此, 在GPa量级的压强下, 可以预期样品的晶格常数及其各向异性会发生变化. 由此带来的色散关系的变化会调节费米面, 从而影响费米能级附近电子和空穴的态密度. 同时, 晶格畸变也影响着声子的色散关系, 由此带来的德拜温度T_θ的上升有利于超导的出现^[65]. 此外, 压强可能会改变材料竞争的基态之间的能量关系, 通过抑制某些结构相^[66]或是电荷密度波 (charge density wave, CDW) 态^[67], 也可能会促使超导的出现.
在拓扑体系中, 利用高压手段, 已经成功地在拓扑绝缘体和拓扑半金属中调制出了超导. 例如, 在典型的拓扑绝缘体Bi₂Se₃^[68,69]和Bi₂Te₃^[70,71]中, 通过金刚石对顶压砧技术施加高压, 人们已经获得了零电阻的超导态. 在Bi₂Te₃中, 超导在3.2 GPa左右开始出现, 4.8 GPa左右达到超导零电阻^[70]. 压强达到13.6 GPa时, T_c达到10 K左右, 上临界场H_c2则超过2 T^[70]. 有趣的是, 随着压强的进一步增大, T_c和H_c2逐渐降低(图4(a),(b)). 而在Bi₂Se₃中, 当压强达到28 GPa时, T_c达到7 K, H_c2达到4 T左右. 压强进一步增大时, T_c基本保持不变, H_c2则开始降低^[68] (图4(c),(d)).
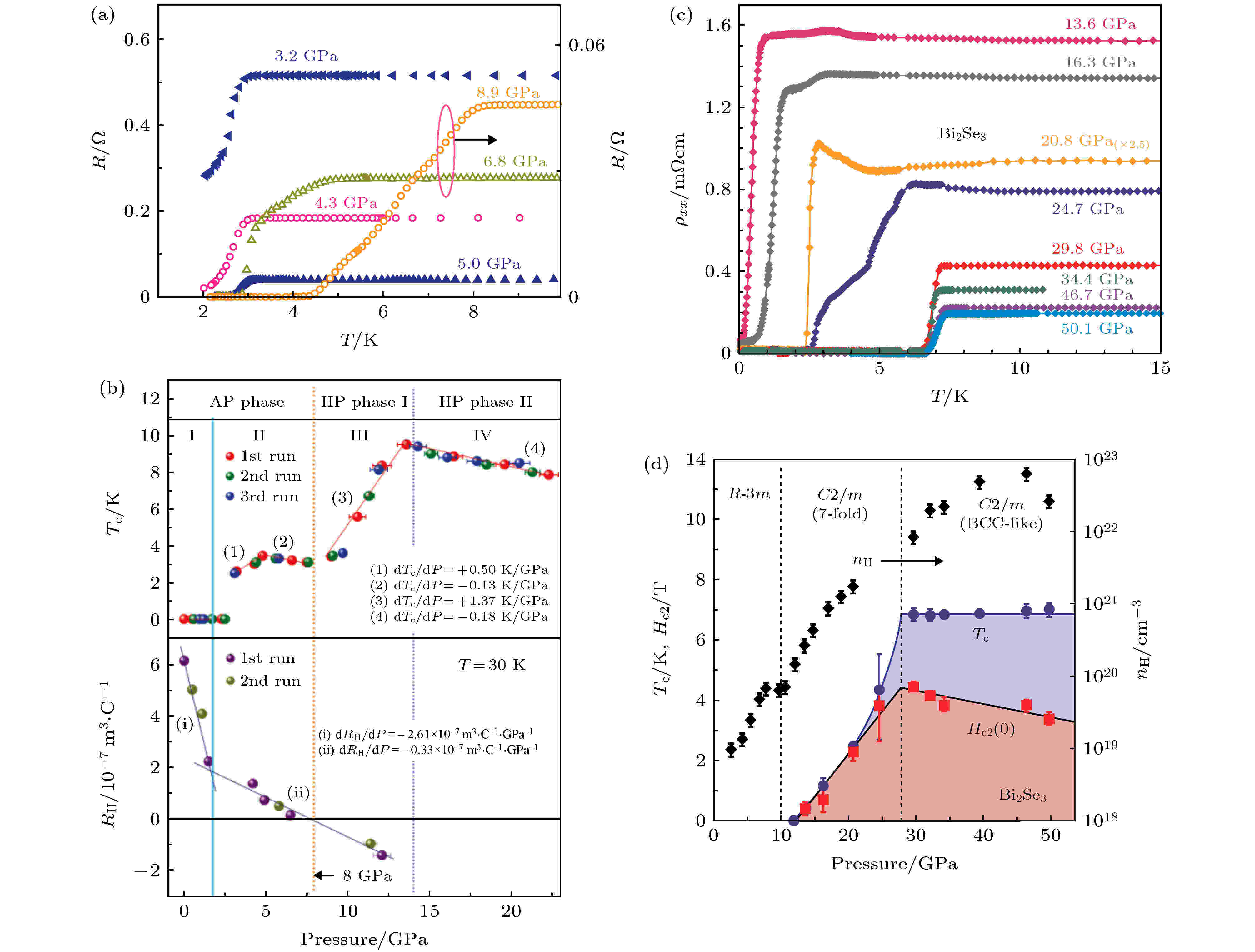图 4 高压诱导的Bi₂Te₃和Bi₂Se₃中的超导　(a) 不同压强下Bi₂Te₃中的超导相变^[70]; (b) Bi₂Te₃的相图和霍尔系数与压强的关系^[70]; (c) 不同压强下Bi₂Se₃中的超导相变^[68]; (d) Bi₂Se₃的相图和载流子浓度与压强的关系^[68]
Figure4. SC in Bi₂Te₃ and Bi₂Se₃ induced by pressure: (a) SC transition in Bi₂Te₃ at various pressures^[70]; (b) SC phase diagram and Hall coefficient as a function of pressure^[70] in Bi₂Te₃; (c) SC transition in Bi₂Se₃ at various pressures^[68]; (d) phase diagram and carrier density as a function of pressure in Bi₂Se₃^[68].

通过绘制超导相图可以看到, 随着压强变化, Bi₂Se₃和Bi₂Te₃的T_c表现出了不连续变化, 因此可能伴随着结构相变或是载流子类型的转变^[68,69,71]. 在Bi₂Se₃中, 超导相的出现和T_c-P关系的变化可以和X射线衍射(X-ray diffraction, XRD)测得的晶体结构相变很好地符合^[68]. 这说明Bi₂Se₃中的超导并不是出现在拓扑的六方晶系中, 其超导与拓扑的关系需要进一步计算研究. 而在Bi₂Te₃中, 研究指出超导在结构相变和p-n转变所需的压强以下就已经出现^[70]. 结合精修的XRD结果, 计算表明了超导和拓扑表面态的共存^[70], 从而确认Bi₂Te₃在4 GPa左右的压强下是超导-拓扑的近邻效应体系, 有可能在表面态实现Majorana费米子.
在拓扑Dirac半金属的代表Cd₃As₂中, 同样是使用金刚石对顶压砧技术, 11.7 GPa的压强诱导出了超导零电阻, 超导转变的开始温度为3.3 K (图5); 在13.5 GPa下上临界场外推为4.29 T^[72]. 虽然Cd₃As₂在2.57 GPa的单轴压下会发生四方到单斜的结构相变, 破坏了三维Dirac半金属相^[73], 但理论仍指出这一高压诱导的超导可能具有拓扑特性^[74]. 由于至今仍未能使用掺杂方法在Cd₃As₂中诱导出超导, 高压手段表现出了特殊的重要性.
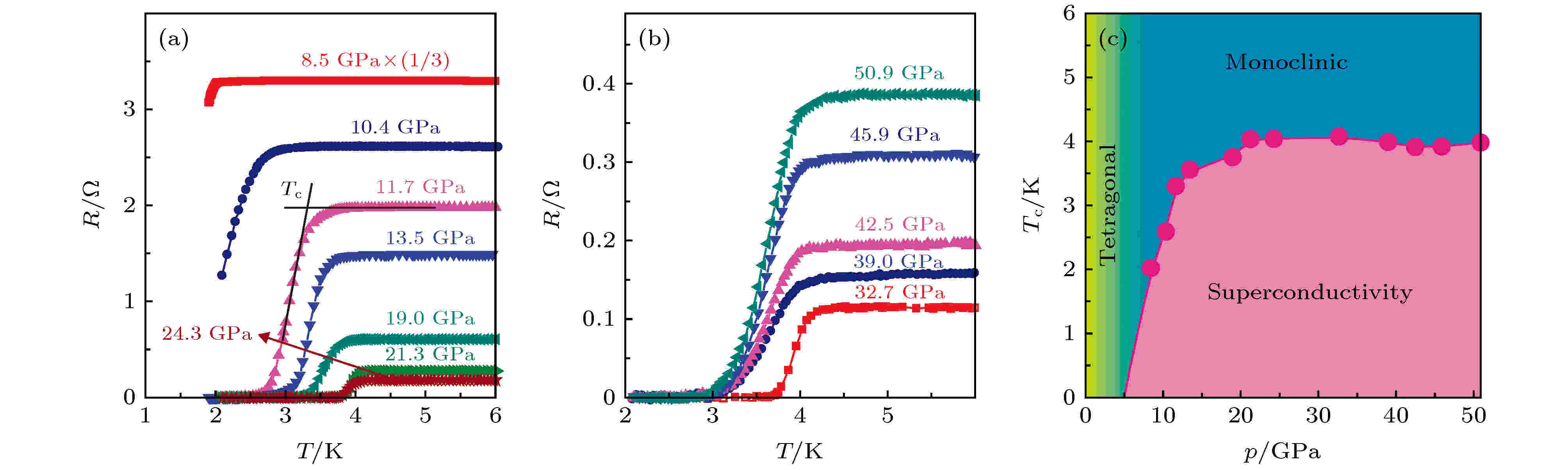图 5 高压诱导的Cd₃As₂中的超导　(a), (b)不同压强下Cd₃As₂中的超导相变; (c) Cd₃As₂在高压下的相图. 引自文献[72]
Figure5. Superconductivity in Cd₃As₂ induced by pressure: (a), (b) SC transition in Cd₃As₂ at various pressures; (c) phase diagram of Cd₃As₂ under pressure. From Ref. [72].

WTe₂和MoTe₂作为第二类Weyl半金属的典型代表, 其层状晶体结构使得它们对压强更加敏感. 在WTe₂中, 超导在10.5 GPa的压强下开始出现, 其超导起始转变温度在13.0 GPa的压强下达到了6.5 K^[75] (不同的工作中结果不尽相同). 密度泛函理论(DFT)计算发现, 随着压强的增大, 层间晶格常数比层内的更快地减小^[65]. 压强不仅使得费米面处的空穴和电子口袋变大, 还同时引入了新的口袋^[65]; 由此带来的费米面处态密度的增大有利于超导的出现(图6(a),(b)). 实验测量得到的相图^[75]还指出, 压强可能是一种引起量子相变的方式(图6(c)). 与此类似, MoTe₂的T_c也可以通过高压提高. 在施加的压强由常压增加到1 GPa的过程中, T_c迅速上升, 11.7 GPa时达到了最高的8.2 K^[66]; 进一步增大压强则导致T_c的降低, 使得T_c-P曲线表现为圆顶形^[66](图6(e)). 通过分析其他实验证据, 研究者认为这种迅速的超导增强可能与MoTe₂的1T' 和Td相之间的竞争有关^[66]. 对静水压下的MoTe₂的μ介子自旋旋转实验说明它的超导配对可能是拓扑非平凡的s^+–形式^[76]. 掺S的MoTe₂的拓扑超导研究给出了s^+–的实验证据^[77].
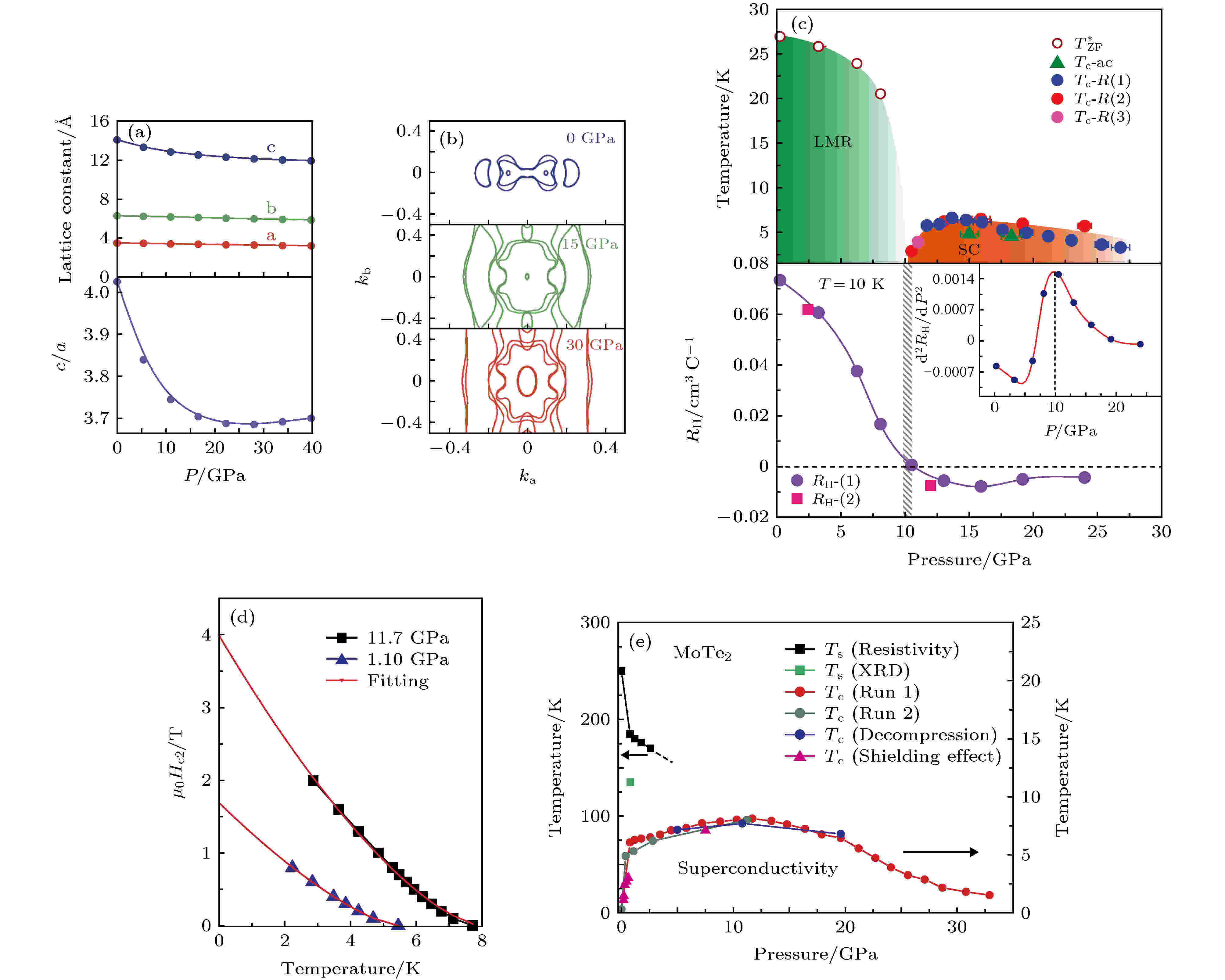图 6 在第二类Weyl半金属WTe₂中高压诱导的超导和MoTe₂中高压增强的超导　(a) DFT计算得到的WTe₂的晶格常数和各向异性随压强的变化^[65]; (b)费米面在k_ak_b面内的轮廓线, 随着压强的施加, 费米面显著变大, 费米面附近态密度增大, 从而有利于超导配对^[65]; (c)上半图为根据实验结果绘制出的WTe₂相图, 绿色区域是高磁阻区, 红色区域是超导相; 下半图为1 T, 10 K下的霍尔系数(R_H)和压强的关系, 插图是其二阶导数, 阴影部分指出R_H反号和超导出现的压强区域^[75]; (d) 高压增强的MoTe₂超导上临界场和温度的关系表现出多带超导的特征^[66]; (e) MoTe₂在高压下的相图, 其中黑色和绿色符号分别是用电阻-温度关系和XRD测得的从1T' 相到Td相的相变温度^[66]
Figure6. Pressure induced SC in WTe₂ and pressure enhanced SC in MoTe₂: (a) Lattice parameters and c/a as a function of applied pressure calculated by density functional theory (DFT)^[65]; (b) calculated evolution of Fermi surface contour in ab plane at various pressures. Fermi surface enlarges substantially with the application of pressure, which is favorable for the formation of Cooper pairs^[65]; (c) upper panel: measured phase diagram of WTe₂. Green and red region respectively correspond to large magnetoresistance (LMR) and superconductivity (SC). Lower panel: Hall coefficient R_H at 1 T and 10 K as a function of pressure. Inset is its second order derivative. The shaded area indicates where R_H sign changes and SC takes place^[75]; (d) upper critical field as a function of temperature of pressure enhanced SC in MoTe₂, whose behavior is reminiscent of multi-band SC^[66]; (e) phase diagram of MoTe₂ under high pressure. Black and green symbols represent 1T' to Td structural phase transition temperature measured by resistivity and XRD^[66].

除此以外, 在第一类Weyl半金属TaP中, 70 GPa的压强使得材料发生从四方到六角的结构相变, 伴随着超导的出现. 当压强被释放后, TaP可以保持高压结构相, 因而在常压下保持超导^[78]. 计算指出TaP的高压相也是Weyl半金属相. 而与其同家族的TaAs在14 GPa下就发生相同的结构相变, 但是超导转变在53 GPa以下都没有被发现^[79].
虽然高压在诱导拓扑材料中的超导方面取得了很大成功, 但它很难对这些超导的拓扑性质给出确定性的结论. 原因在于高压装置限制了研究手段的使用, 使得对高压超导的研究局限于电输运性质的测量等. 一些更直接的探测拓扑超导的手段, 如STM, 很难使用. 因此, 对于Bi₂Te₃, WTe₂和Cd₃As₂等拓扑材料中高压诱导的超导是否是拓扑的还没有确定性的证据. 高压诱导的拓扑超导的应用也受到限制. 此外, 高压常常会导致样品晶格常数的改变或结构相变, 因此只有在原位XRD或理论计算的辅助下才能充分理解高压下的物态.

掺杂是在电子电路领域最早使用的调控手段之一, 半导体之所以能够广泛地用于现代信息社会之中, 一定程度上凭借的是通过在其中掺入杂质原子灵活地改变其特性. 在现代的凝聚态物理研究中, 掺杂也是实现新奇的量子效应的手段, 比如量子反常霍尔效应最早就是在掺了Cr和Sb的Bi₂Te₃体系中得到实现^[80]. 掺入的杂质原子通过提供多余的电子或空穴, 改变费米面的位置, 就有可能形成有利于超导配对的电子结构, 从而诱导出超导态.
在拓扑材料中, 通过掺杂在Bi₂Se₃中诱导出的超导是最为著名的例子之一. 虽然理论指出Bi₂Se₃体态有较大的全局带隙^[12], 实验中看到的Bi₂Se₃却是电子掺杂的^[14], 从而在费米面处有非零的电子态密度. Hor等^[81]通过混合Cu, Bi和Se粉末共同熔融后冷却结晶, 获得了层间掺杂(Cu_xBi₂Se₃)和替代掺杂(Cu_xBi_2–xSe₃)的两种化合物. 输运实验发现, 当层间掺杂浓度合适(0.1 ≤ x ≤ 0.3)时, 样品表现出了清晰的超导特性(结构如图7(a)所示). x在0.12附近时超导最强, 开始转变温度T_c达到了3.8 K (图7(b)), 垂直于层和层内方向的临界磁场分别接近2 T 和5 T. 而在替代掺杂的样品中则没有观察到超导现象.
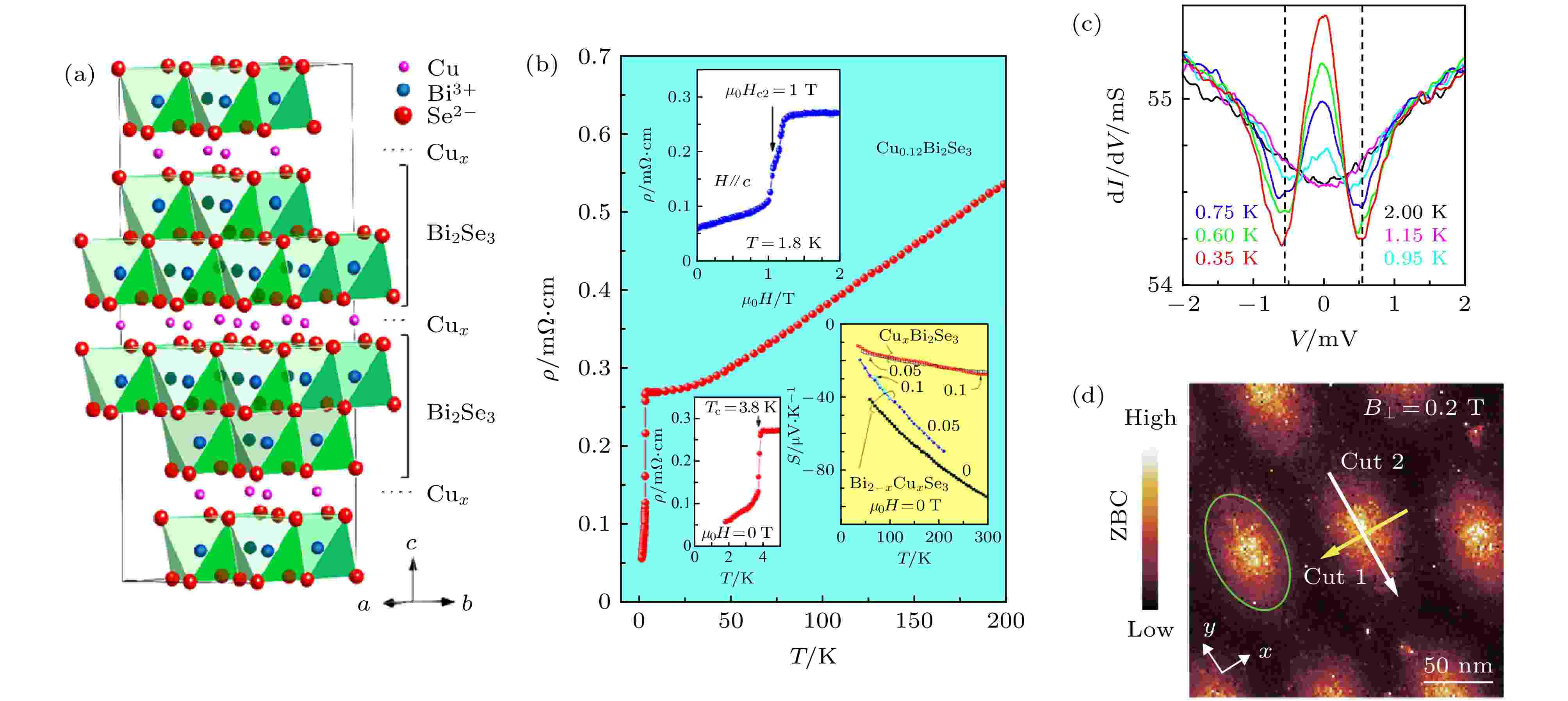图 7 Cu_xBi₂Se₃ 中的非常规超导　(a) 能够发生超导相变的层间Cu掺杂Bi₂Se₃结构示意图^[81]; (b) 输运测得的Cu_0.12Bi₂Se₃超导在电阻率-温度)(ρ-T)关系中的反映, 左下角插图是超导转变区的放大, 上方插图为超导转变中电阻率随垂直于面的磁场强度的关系, 右下方插图是不同掺杂方式和比例的样品Seebeck系数随温度的关系, 说明了填隙方式掺入Cu有更好的掺杂效果^[81]; (c)在点接触谱中观察到的Cu_xBi₂Se₃超导的ZBCP^[90]; (d) STM观测到的Cu_0.31Bi₂Se₃在电子温度310 mK和0.2 T的垂直磁场下磁通涡旋中的ZBCP^[84]
Figure7. Unconventional superconductivity in Cu_xBi₂Se₃: (a) Structure of Cu intercalated Bi₂Se₃ where superconductivity is possible^[81]; (b) resistivity-temperature) relation(ρ-T) relation of Cu_0.12Bi₂Se₃. Lower left inset magnifies the superconductivity transition region. Upper inset shows resistivity as a function of perpendicular magnetic field. A third inset shows Seebeck coefficients of differently doped materials, where we can see doping effect is stronger for intercalated Bi₂Se₃^[81]; (c) ZBCP in point contact spectrum (PCS) of superconducting Cu_xBi₂Se₃^[90]; (d) ZBCP observed in vortex cores of Cu_0.31Bi₂Se₃ surface under 0.2 T perpendicular magnetic field at effective electron tempearature 310 mK by STM^[84].

在Cu_xBi₂Se₃中诱导出的超导是否具有拓扑性, 自然成为人们所追问的问题. 作为拓扑绝缘体的代表, Bi₂Se₃有线性色散的拓扑表面态. 如果体态的超导能够通过近邻效应使表面态打开超导带隙, 这便很可能成为二维的拓扑超导体系^[82]. Wray等^[83]通过ARPES实验验证了在超导所需的掺杂范围内, Cu_xBi₂Se₃仍然存在线性色散的拓扑表面态并且和体态不简并, 从而外加磁场下其表面有可能存在包含Majorana零能模的磁通涡旋. 后续的STM实验已经看到了磁通涡旋中的零压电导峰 (zero bias conductance peak, ZBCP) (图7(d)), 但由于实验精度的限制, 还没有很好地和平庸的束缚态区分开^[84].
其他研究手段的引入揭示了Cu_xBi₂Se₃中更激动人心的可能. 在核磁共振(nuclear magnetic resonance, NMR)实验中, Matano等^[85]观察到在超导临界温度以下, Se原子核的奈特移位在层内表现出了两重对称性, 形成晶体的三重对称性的自发破缺. 同时考虑到比热测量指出的超导完全带隙^[86], Fu^[87]从理论上说明了这只可能源于Cu_xBi₂Se₃晶体点群D_3d的不可约表示E_u对应的奇宇称配对, 因此Cu_xBi₂Se₃中的体态超导可能是有向列性质的时间反演不变拓扑超导. Cu_xBi₂Se₃超导的向列性得到了比热实验^[88]和STM研究^[84]的验证. 进一步确定Cu_xBi₂Se₃中超导的拓扑性需要确定其费米面的形状. 通过SdH振荡和ARPES探测不同掺杂浓度下的费米面, Lahoud等^[89]发现, 掺杂浓度低时, 费米面是包含Γ点的封闭椭球; 掺杂浓度较高(能够诱导超导)时, 费米面是柱状开费米面. 在第二种情况下, 超导体的上下表面有完全的带隙, Majorana费米子存在于样品的侧面, 可以在样品表面的原子台阶处观察到. 实验上, Sasaki等^[90]使用软点接触方法测量得到了ZBCP(图7(c)). 然而, 超导区域的ZBCP却未能在STM实验中被观测到^[83], 这还有待进一步的研究.
在体材料中实现掺杂需要精确的原料配比和生长方式的控制. 在实际的材料制备的过程中, 产物中元素比例未必和原料元素配比相同^[91]. 同时, 这也对新材料的结构确定提出了挑战. 使用能量色散X射线谱(energy-dispersive X-ray spectroscopy, EDX)可以确定产物中元素配比, 但不能准确确定掺杂的具体方式. 原子的掺杂方式与掺杂的均匀性需要综合XRD、透射电子显微镜(transmission electron microscope, TEM)和理论计算等多种方式来确定. 在Hor等^[81]的Cu_xBi₂Se₃样品中, 磁化测量说明超导比例可能只有20%左右, 且没有出现超导零电阻, 表明样品中可能同时存在层间掺杂和替代掺杂两种掺杂方式. Kriener等^[92]使用电化学方法制备Cu_xBi₂Se₃样品, 将超导比例提高到了50%, 并可以更好地保证层间掺杂.
除了Cu原子之外, 在Bi₂Se₃中掺入Sr原子^[91]和Nb原子^[93-95]都能诱导出超导态, 它们超导的拓扑性也获得了一定的实验证据. 与Cu_xBi₂Se₃相比, Sr_xBi₂Se₃在空气中更稳定^[91], 而计算指出Nb_xBi₂Se₃可能有磁性的基态^[93].
在拓扑半金属中实现掺杂诱导的超导也是值得尝试的研究方向, 目前已经取得了一定的成果. 第二类Weyl半金属MoTe₂未掺杂时在常压下虽然可以发生超导相变, 但T_c只有0.1 K左右^[66]; 通过S掺杂得到的MoTe_1.8S_0.2超导临界温度达到了1.27 K^[77]. 比热和电输运的测量结果指出掺S的MoTe₂中的超导有双带特性, 并且可能是s^+–超导^[77]. STM研究进一步观察到了表面超导增强, 这被认为可能和Weyl半金属的费米弧表面态有关^[77] (图8). 此外, 在常压下不超导的第二类Weyl半金属WTe₂中, K掺杂可以诱导出T_c ≈ 2.6 K的超导态^[96].
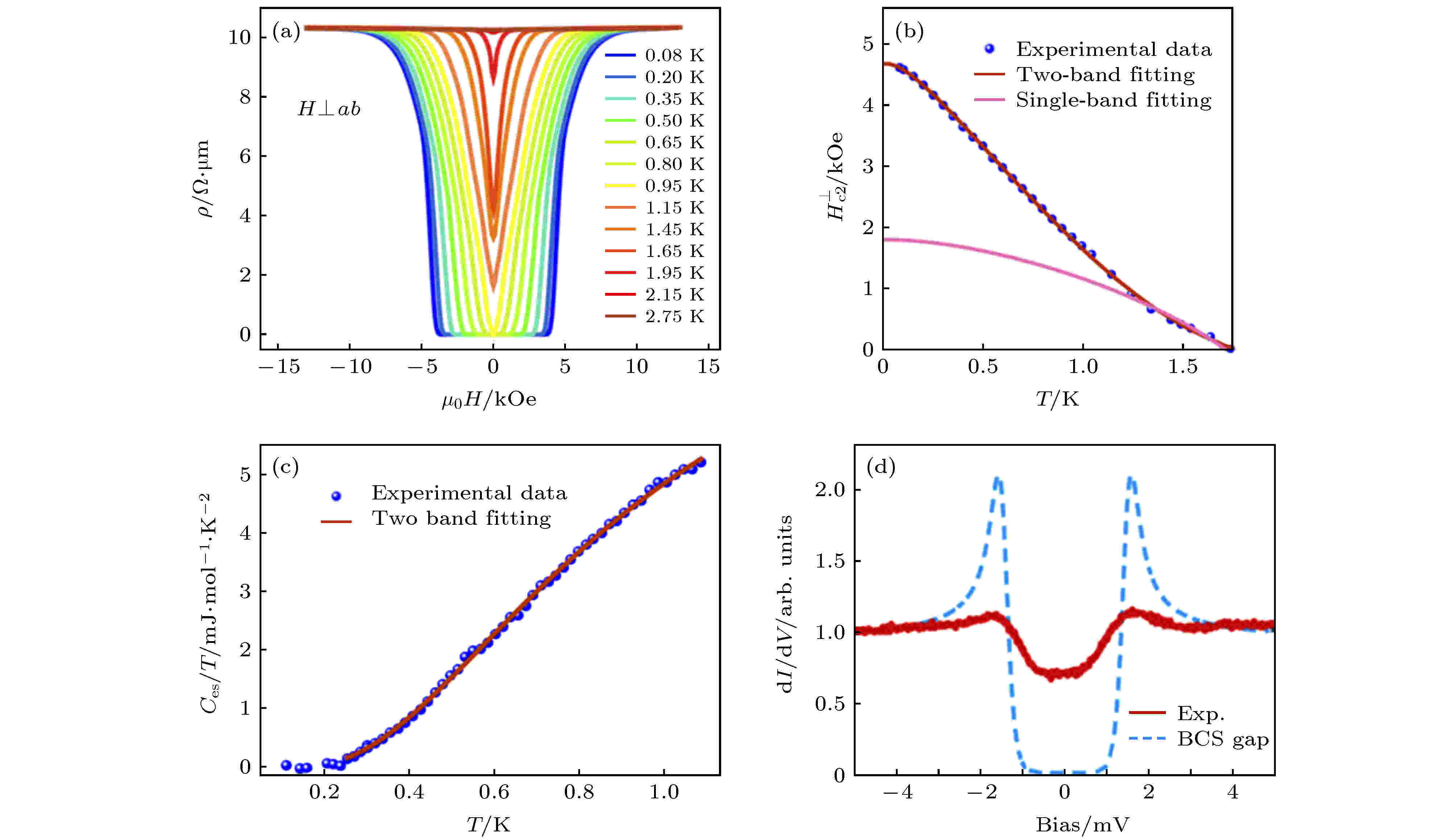图 8 掺S的MoTe₂(MoTe_1.8S_0.2)中的双带超导　(a) 不同温度下电阻率和磁场的关系, 在低温和低磁场下有明显的超导零电阻; (b) 超导的临界磁场和温度的关系, 可以用双带模型很好地拟合, 拟合参数指出很可能是非常规的s^+– 配对超导; (c) 超导电子热容和温度的关系, 可以用双带模型很好地拟合; (d) STM 在MoTe_1.8S_0.2的表面观测到的远大于体态的超导带隙, 谱形不能用常规的s波超导拟合. 引自文献[77]
Figure8. Superconductivity in S doped MoTe₂ (MoTe_1.8S_0.2): (a) ρ-B relation of MoTe₂ under various temperatures. Superconductivi-ty with zero resistance is clearly seen; (b) critical magnetic field as a function of temperature, which can be well fitted by a two-band mode. The fitting parameter supports unconventional s^+– pairing superconductivity; (c) superconducting electron heat capacity as a function of temperature can be well fitted by two-band mode; (d) superconductivity gap observed at the surface of MoTe_1.8S_0.2 by STM. The spectrum differs from what is expected for a conventional s wave superconductor. From Ref. [77].

近期, 另一种新的调控方式引起了人们的注意. 在第一类Weyl半金属TaAs家族中, Bachmann等^[97]使用聚焦离子束(FIB)对样品表面进行选择性曝光. 由于N族元素在样品表面的结合能不及ⅤB族元素, 在合理控制的离子轰击下, 样品表面会出现富金属层. 而Ta和Nb分别是T_c为4.5 K和9.2 K的超导体, 样品表面因此可以表现出超导特性, 从而形成了超导体和拓扑半金属的异质结.

近邻效应调制的拓扑超导信号, 最早在半导体纳米线中被实验发现. 其利用超导近邻效应和强自旋轨道耦合的相互作用, 产生等效的p波超导体^[98-100]. 这一方式得到的Majorana零能模并非来自内源的拓扑电子态, 而是来自外源的能带结构工程手段. 实际上更好的方式是利用拓扑绝缘体的内源性强自旋轨道耦合来实现拓扑超导. Fu和Kane^[101]在2008年理论提出可以用s波配对的常规超导体通过近邻效应在拓扑绝缘体中诱导出拓扑超导, 拓扑绝缘体使得系统受到时间反演对称性的保护, 在磁通涡旋处产生更为稳定的Majorana零能模. 随后Stanescu等^[102]进一步从微观角度对s波超导和拓扑材料界面的超导近邻效应进行研究, 发展出一套低能理论模型.
实验上, 上海交通大学贾金锋实验组^[103]通过分子束外延(molecular beam epitaxy, MBE)技术在NbSe₂衬底上生长出单晶Bi₂Se₃薄膜, 使用原位的STM/扫描隧道谱(scanning tunneling spectroscopy, STS)和ARPES, 发现了薄膜中超导和拓扑的共存. 由于涡旋中央准粒子态的最低能级很难被STM分辨, 因此通过普通的STM/STS技术很难区分Majorana零能模, 于是贾金锋实验组^[104]于2016年借鉴了He等^[105]提出的在一维拓扑超导中对于Andreev反射的自旋分辨探测手段, 利用磁性STM针尖对磁通涡旋(vortex)中的信号进行自旋分辨(图9). 如果体系处于拓扑超导状态, 处于磁通涡旋中央的自旋波函数总是严格指向外磁场方向, 所以实验中自旋向上和向下的电导通道出现的显著差别, 可以作为Majorana零能模的一项证据.
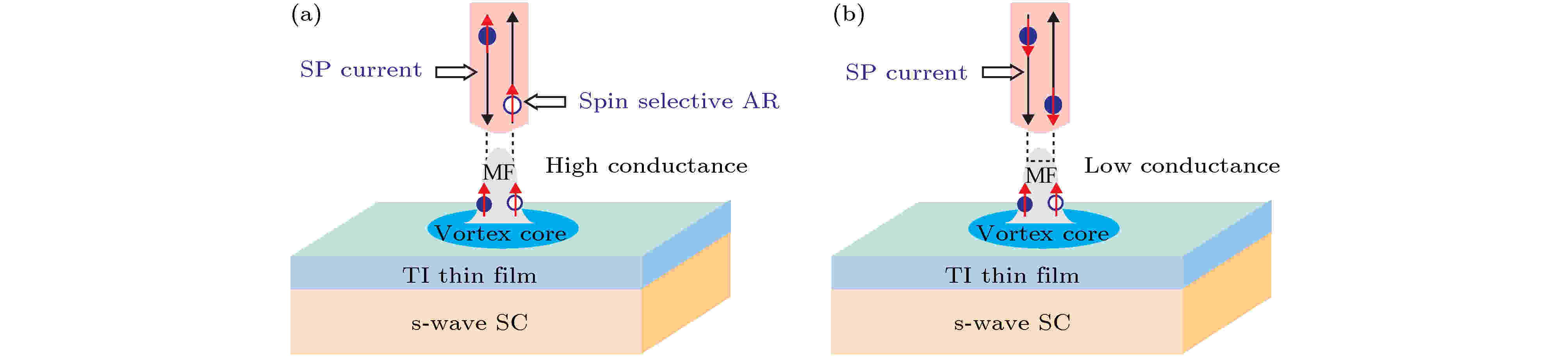图 9 自旋分辨针尖对Bi₂Se₃薄膜上磁通探测的示意图　(a)在涡旋中心自旋向上极化的Andreev反射具有高电导值, 因为一个自旋向上入射的零能电子被自旋向上Majorana零能模反射为空穴; (b)在涡旋中心自旋向下极化的安德略夫反射具有低电导值, 因为入射电子和Majorana零能模的自旋无法配对. 引自文献[104]
Figure9. Schematic diagram of a spin selective tip on a vortex: (a) Illustration of spin selective Andreev reflection in spin polarized (M↑) STM/STS on a vortex center r = 0 in an interface of a topological insulator and s-wave superconductor. An incoming spin-up electron of zero energy is reflected as an outgoing spin-up hole induced by Majorana zero mode with spin-up at r = 0, which gives out a higher tunneling conductance; (b) an incoming spin-down electron of zero energy is reflected directly because of the mismatch of the spins of the electron and the Majorana zero mode, which results in a lower tunneling conductance. From Ref. [104].

在对超导和拓扑性质的探索中, 输运实验也具有重要的作用^[106]. 美国宾夕法尼亚州立大学的研究组通过输运实验, 证实Bi₂Se₃纳米线中可能具有超导近邻效应调制出的拓扑超导信号. 他们通过超导钨电极探测到一维Bi₂Se₃纳米线中的超导电流和多重Andreev反射^[107]. 由于多重Andreev反射的通道长度远远大于正常输运的散射距离, 因此在Bi₂Se₃纳米线中近邻效应引发的拓扑超导电流倾向于弹道散射的表面态通道. 此外, Bi₂Se₃纳米线中的零压电导峰信号, 和徐洪起实验组^[108] Nb-InSb半导体纳米线的实验很类似, 预示着Majorana零能模在Bi₂Se₃纳米线体系中存在的可能性.
有趣的是, 高维拓扑绝缘体的一维hinge态也能通过近邻效应形成拓扑超导体. 最近J?ck等^[109]通过Nb的近邻效应, 在高阶拓扑绝缘体Bi台阶处的拓扑hinge态中诱导出可能的拓扑超导(图10). 由于只有在拓扑超导体的边界态才能产生Majorana零能模, 该实验组利用铁磁杂质对时间反演对称性的破坏作用, 在一维hinge态的边界探测到Majorana零能摸. 自旋极化的STM针尖排除了弱反局域化(week anti-localization), 近藤效应(Kondo effect)等自旋不分辨的干扰因素的解释, 也分辨出了正能量Shiba态(图10(c)中红色曲线)的贡献, 证实零压电导峰应当来自非平凡的Majorana零能模.
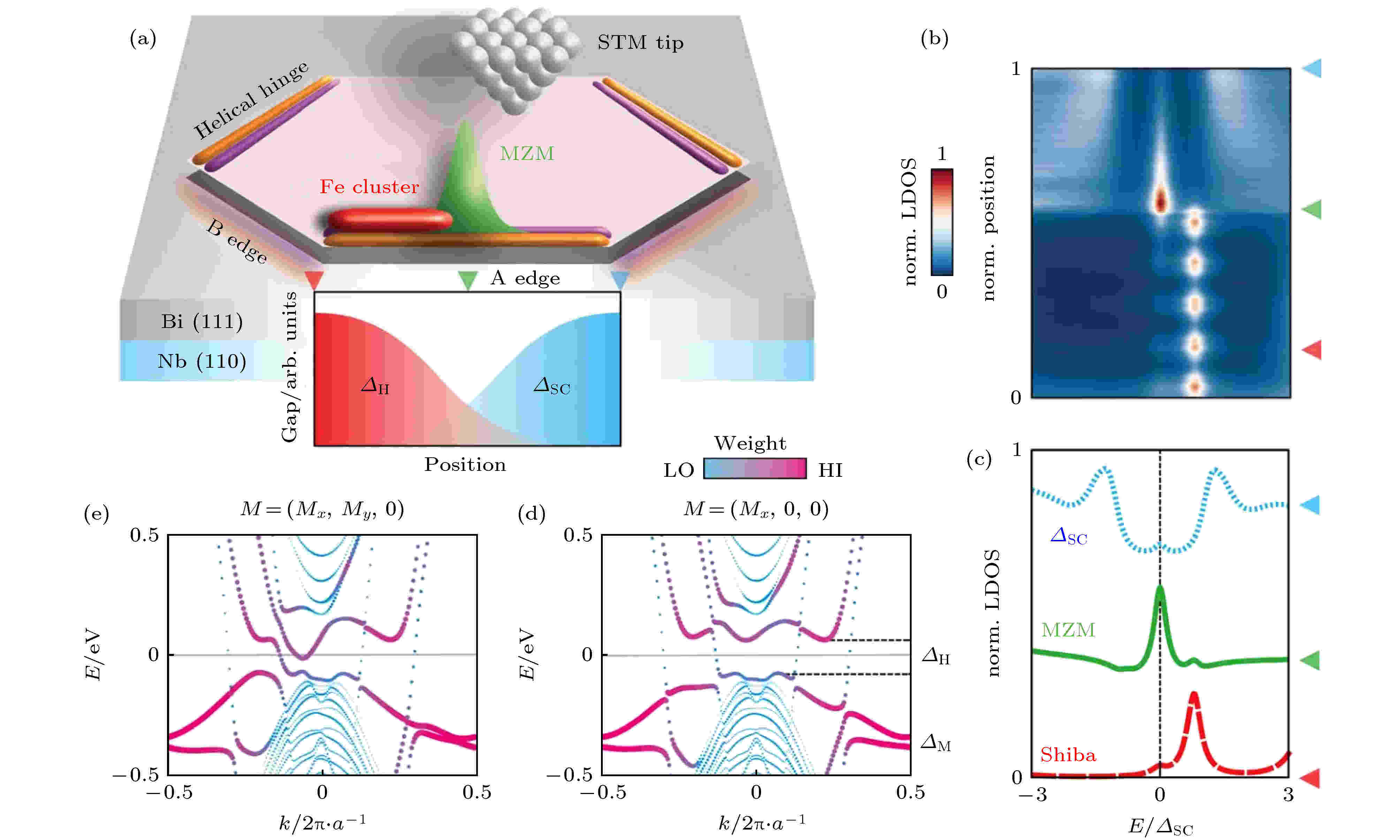图 10 Bi(111)双层台阶边界态的Majorana零能模　(a) Bi(111)面上双层台阶的卡通示意图, 其中Nb (110)衬底提供超导近邻效应, 铁原子簇提供质量壁垒; (b) 紧束缚模型计算得到的空间分辨低能局域态密度图, 其中各颜色箭头与图(a)中对应; (c) 三种颜色箭头所在位置的点谱; (d), (e) 由紧束缚模型计算的能带结构, (d)中磁场与边缘A平行, 而(e)中磁场包含垂直边缘A的分量, 其中Δ_H为铁磁杂化的能隙, 而Δ_M为高简并点的Zeeman劈裂. 引自文献[109]
Figure10. Topological superconductivity and Majorana zero modes in the topological edge state of a Bi(111) bilayer: (a) Schematic representation of a hexagonal Bi bilayer island sitting on the surface of a Bi(111) thin film and exhibiting topological helical states on every other edge. Topological superconductivity DSC is induced into these helical states by superconducting proximity from the underlying Nb(110) substrate. Attaching a ferromagnetic cluster to the bilayer edge can open a magnetic hybridization gap. An MZM is localized at the mass domain wall, which is realized at the cluster-helical edge state interface, and can be detected in STM experiments; (b) spatially resolved low-energy local density of states (LDOS) calculated from a tight binding model for the edge state cluster arrangement shown in (a). The LDOS is a spectroscopic line cut taken along the A edge in (a); (c) point spectra extracted from the calculated spectroscopic line cut shown in (b) (positions indicated by the colored triangles); (d), (e) calculated band structure along the G-M direction from a tight-binding model of a Bi(111) bilayer, for which the A edge is coupled to the spin-polarized d-bands of a ferromagnetic cluster, resulting in a magnetic hybridization gap and a Zeeman gap. In (d), the cluster magnetization is parallel to the A edge M = (M_x, 0, 0); in (e), it has an additional component of the same amplitude perpendicular to the A edge M = (M_x, M_y, 0); The wave function weight on the Bi(111) edge in contact with the cluster is represented by symbol size and position on color scale. The magnetic hybridization gap, spanning the entire Brillouin zone, and the Zeeman gap at the high-symmetry point are indicated. From Ref. [109].

此外, 大量其他Dirac材料也能由近邻效应诱导拓扑超导, 如三维Dirac半金属Cd₃As₂^[110], 以及具有奇异堆积结构的2M相的TMD材料WS₂^[111]. 除了拓扑材料, 超导衬底上一维铁磁系统也是一种能实现Majorana零能模的重要系统, 其中超导与铁磁的相互作用也是凝聚态的重要研究方向^[112,113]. 目前实验上在超导衬底上的铁原子链端点^[114]、铁基超导体中的磁通涡旋^[115], 以及单层FeSe上的Fe原子^[116]都发现了Majorana零能模的证据.

点接触是传统的研究材料超导特性的手段^[117]. 实验上, 可以通过微纳米加工、银胶连接和针尖接触等方式, 形成两种材料之间的局域隧穿结^[118] (图11). 通过测量微分电导谱, 可以得到样品超导序参量和配对机制等信息. 其中, 针尖点接触手段的基本实验构型如图11所示, 通过针尖和样品的直接接触形成隧穿结. 电流极和电压极分布在针尖和样品上, 使用锁相测量技术可以测得隧穿电导. 相较于STM技术对样品的无损害测量, 针尖点接触要求针尖直接接触样品, 它的优势在于: 1)针尖可以穿透样品暴露在外的表面, 与干净的样品表面接触; 2) 点接触电阻可以通过进针或退针来调节^[118]. 此外, 近些年来, 针尖点接触作为一种对样品施加局域调制的手段日益受到人们的关注. 针尖对局域施加的影响可以使得其进入新的物态. 针尖点接触诱导的超导态指使用非超导的针尖和样品观察到的超导谱形和其他超导特性. 具体而言, 针尖点接触的以下几种作用可能诱导超导态的出现.
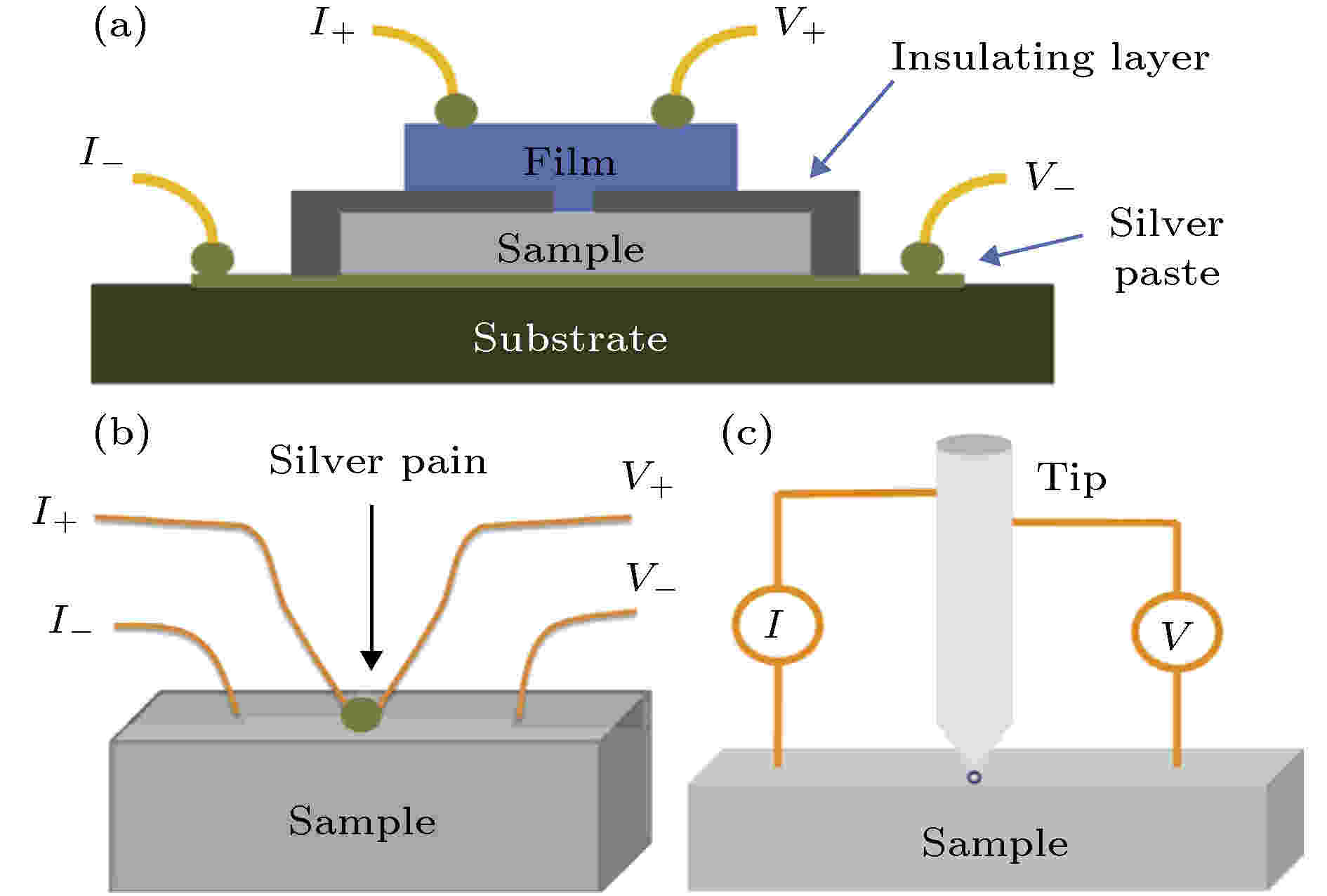图 11 三种点接触结构的示意图　(a) 用纳米微加工技术实现的隧穿结; (b) 使用银胶的软点接触; (c) 针尖硬点接触. 引自文献[118]
Figure11. Schematics of three common point contact confi-guration: (a) Tunneling junction fabricated by nanolithography; (b) soft point contact using silver paint; (c) hard point contact configuration, also called needle-anvil confi-guration. From Ref. [118].

1)局部压强. 针尖接触样品时对样品局部施加的压强与单轴压类似, 因此, 单轴压诱导的超导态也可能通过针尖点接触实现. 使用针尖点接触代替单轴压测量, 可以获得压强诱导的超导的谱学信息, 从而对其超导机制有更直接的理解. 这从一定程度上弥补了高压诱导超导的缺点.
2)局部掺杂效应. 金属针尖常被用于针尖点接触实验, 它们在和半金属、半导体、绝缘体接触时可以对其进行电子或空穴的掺杂, 从而改变样品局部的电子态密度, 可能有利于超导的出现.
3)界面效应. 在二维超导领域, 界面超导(如LaAlO₃/SrTiO₃界面^[119])和界面效应增强的超导(如FeSe/SrTiO₃界面^[120])是重要的研究课题. 针尖点接触形成了样品和针尖的界面, 因此在讨论诱导超导时界面效应也是不可忽视的.
在不同的点接触实验手段中, 局部掺杂效应和界面效应普遍存在, 而局部压强是针尖点接触所特有的. 而且, 在针尖点接触中, 三种效应同时存在, 区别它们贡献的强弱需要控制实验和细致的理论分析. 例如, 通过对比不同硬度的针尖点接触和银胶软点接触, 可以分析局部压强在诱导的超导中的重要性; 通过对比针尖点接触和单轴压诱导的超导, 可以分析掺杂和界面效应的影响等^[118].
针尖点接触诱导超导最重要的成果, 是在拓扑Dirac半金属单晶Cd₃As₂^[121]、多晶Cd₃As₂^[122]和Weyl半金属TaAs^[123,124]中诱导出非常规的超导态. 在Cd₃As₂中, 约10 GPa的单轴压可以诱导出超导态^[72]. 与之对应, 使用钨针尖可以实现针尖点接触诱导的超导, 而软点接触则不能诱导出超导态, 说明在针尖点接触诱导超导中压强会起作用^[121]. 50 GPa以下单轴压在Cd₃As₂中诱导的超导T_c最高达到4 K左右, 但在针尖点接触实验中却观察到了T_c高达7.1 K的超导态, 说明掺杂或界面效应在诱导Cd₃As₂超导中也是不可忽视的^[121]. 对点接触超导谱形的分析进一步揭示了超导的非常规特性. Cd₃As₂的点接触超导谱形包含了三个显著的特征: 1) 零压电导峰; 2) 对称分布的双电导峰; 3) 对称分布的双电导谷(图12(b)). 从Cd₃As₂体电子结构分析, 针尖诱导的超导有如下几种可能的机制: 谷间配对的常规s波超导; 谷内配对的准二维螺旋p波超导和表面态的准一维的拓扑超导^[121]. 其他机制, 如临界电流效应也可能解释实验中观察到的谱形的部分特征^[121]. 但在一个谱上同时观测到这三种特征更倾向于说明Cd₃As₂超导的非常规性, 并且可能是拓扑超导.
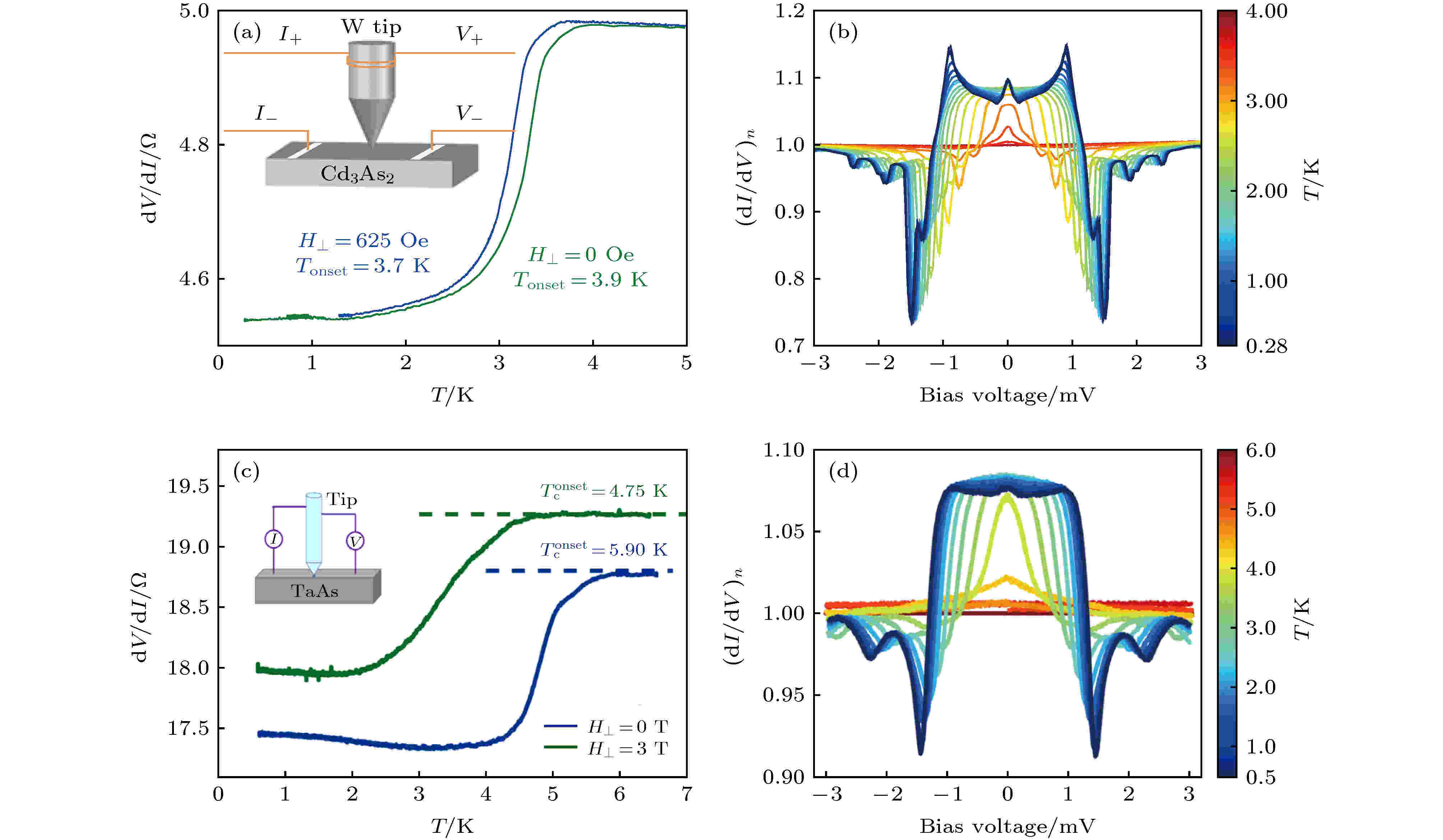图 12 针尖点接触在拓扑半金属Cd₃As₂和TaAs中诱导的超导　(a) Cd₃As₂中零偏压点接触微分电导与温度的关系, 电阻的下降可以被磁场抑制, 这意味着它代表超导相变, 插图是针尖点接触实验装置示意图^[121]; (b) 不同温度下归一化的钨针尖Cd₃As₂点接触微分电导谱^[121]; (c), (d) PtIr针尖点接触在TaAs中测得的超导^[123]
Figure12. Tip induced superconductivity in topological semimetal Cd₃As₂ and TaAs: (a) Zero-bias point contact differential resistance of Cd₃As₂ as a function of temperature with W tip, magnetic field suppresses resistance drop, which signals a SC transition^[121]; (b) normalized point contact differential conductance spectrum of Cd₃As₂ with W tip^[121]; (c), (d) superconductivity in TaAs induced by PtIr tip^[123].

在第一类Weyl半金属TaAs中, 尽管还没有高压诱导的超导的报道^[79], 针尖点接触已经成功地在其中诱导了超导, 展现了其较强的调制能力. 使用较硬的PtIr针尖, 通过步进电机的进针方式, 样品的超导临界温度达到了T_c = 5.9 K (图12(c)). 其点接触超导谱形表现出了丰富的结构: 1) 零压电导峰; 2) 零压附近的电导平台和对称的双电导峰; 3) 双电导谷^[123] (图12(d)). 而使用较软的银针尖以及手动进针的方式则观察到了不同的超导谱形^[124]. 可见, 针尖诱导的超导对针尖有很大敏感性. 针尖点接触诱导的TaAs超导是否是拓扑超导还需要进一步的实验和理论的检验.
针尖点接触作为一种调制和研究超导的实验手段, 还有很大的探索空间. 一方面, 目前实验参数的控制还不完善. 例如, 针尖和样品间的压强大小与有效接触面积的大小还没有很好的确定方法; 针尖作用下样品局部的晶格畸变或结构相变也还不能很好地判断. 在针尖的选择上, 拓展使用铁磁针尖, 可以研究非常规的p波与拓扑超导等. 另一方面, 通过和其他探针技术, 如针尖增强的拉曼谱学、STM等的结合, 研究在针尖点接触区域之外的声子模式和超导性质对于加深对针尖诱导的超导的理解有重要意义^[118]. 可以预期, 随着实验技术和理论模型的进步, 针尖点接触技术将在拓扑超导的探索中起到更大的作用.

拓扑超导与拓扑量子计算已经成为近年来人们最为关注的话题之一. 目前, 最引人注目的实现拓扑超导的方式是基于半导体纳米线和s波超导体的界面, 近期已经在其中实现了量子化的Majorana零能模^[100]. 与此相比, 利用栅极调制、掺杂、高压、针尖调制、近邻效应等方式在拓扑材料(拓扑绝缘体和拓扑半金属)中调制超导, 因材料自身的拓扑性质, 一旦确信有拓扑超导, 可能更容易普及和应用, 因此有广阔的发展前景.
本文重点介绍了一些潜在的本征拓扑超导体, 并重点讨论了目前已经成功地在公认的拓扑绝缘体和拓扑半金属中调制出超导的方法. 栅极、掺杂、高压和针尖点接触的调制手段, 可以增强材料本身的超导, 或在本来不超导的材料中诱导出超导. 此外, 通过超导近邻效应, 也可以在拓扑材料中诱导出超导. 使用这些方式调制得到的超导是否具有拓扑性质, 还需要通过对超导配对方式等的研究来确定.
值得指出的是, 拓扑超导目前还处在基础研究阶段. 本文只是揭示了拓扑超导的可能实现方案, 还远没有达到确认并应用拓扑超导的程度. 因此, 未来至少有两个方面还需要深入的研究: 一是找到更多的拓扑超导候选材料或在更多的拓扑材料中调制出超导态; 二是通过改善实验条件确认这些超导的拓扑特性. 在这些工作的基础上, 才能探索拓扑超导的应用可能, 如拓扑量子计算等. 总之, 拓扑材料中的超导是一个前景广阔的研究方向, 值得更多的关注和深入的研究.
感谢北京大学量子材料科学中心的刘彦昭、刘超飞的有益讨论.