摘要:作为一种快速、低成本和非接触的测量手段, 光学散射测量在半导体制造业中的纳米结构三维形貌表征方面获得了广泛关注与运用. 光学散射测量是一种基于模型的测量方法, 在纳米结构待测参数的逆向提取过程中, 为降低参数之间的耦合性, 通常需要将结构的光学常数作为固定的已知量, 即假设结构的材料光学常数不受光学散射仪入射光照的影响. 事实上, 这一假设对于半导体制造业中的绝大多数材料是成立的, 但某些感光材料的光学常数有可能随着入射光的照射时间增加而发生改变, 而由此产生的误差会在一定程度上传递给待测形貌参数的逆向提取值. 本文针对聚甲基丙烯酸甲酯光刻胶薄膜培片和光栅结构分别开展了光学散射测量实验与仿真研究, 结果表明该光刻胶材料的光学常数随着入射光照时间增加而变化, 进而导致光栅结构形貌参数的提取结果较大地偏离于真实值, 不容被忽视. 这一研究发现将为更进一步提高光刻胶纳米结构三维形貌参数的测量精确度提供理论依据.
关键词: 光学散射测量/
光刻胶纳米结构/
聚甲基丙烯酸甲酯/
光学常数

English Abstract

全文HTML

--> --> -->

纳米制造是指产品特征尺寸为纳米量级的制造技术, 是一个国家制造水平的重要标志之一^[1,2]. 纳米制造的工艺生产质量决定了纳米产业的发展前景, 而实现工艺质量监督、评估及优化的基本手段是测量. 由于具有非接触、非破坏性、低成本和易于在线集成等优点, 基于远场光学的光学散射仪测量技术^[3]除广泛应用于纳米薄膜材料的光学特性表征与膜厚测量外^[4,5], 也已成为一种周期性纳米结构关键尺寸的重要测量手段^[6-10]. 因此, 光学散射仪也被称为光学关键尺寸测量仪.
光谱椭偏仪是一种典型的光学散射仪, 其基本测量原理是通过将实际测量数据与模型仿真数据进行匹配来反演出待测纳米结构参数值^[11]. 其中, 测量数据由椭偏仪探测待测纳米结构的反射光或透射光而直接获得, 根据测量数据类型的不同, 测量仪器又可分为传统椭偏仪和Mueller矩阵偏振仪; 模型仿真数据的计算和待测参数值的反演提取则涉及到以下两个光学散射测量理论算法: 一是“正向”光学特性的建模; 二是“逆向”待测参数的提取. 正向光学建模是由已知的纳米结构参数、材料光学常数以及测量条件配置等, 利用电磁场理论计算出待测结构的理论数据^[12]; 逆向几何参数求取则是将实际测量数据与模型计算数据进行匹配反演得出待测参数值^[13]. 在以计算电磁波理论为基础的光学特性建模求解方法^[12,14,15]中, 由于严格耦合波分析(rigorous coupled-wave analysis, RCWA)可对任意周期性结构建模, 而且具有数值求解过程比较简单、实现相对容易、精度高等优点而得到了广泛应用^[16,17]. 纳米结构待测参数的逆向求解主要包括库匹配和非线性回归这两种方法^[18], 由于前者的建库过程相当耗时, 后者的操作过程简单直接, 因而具有迭代收敛快速特点的列文伯格-麦夸特(Levenberg-Marquardt, LM)非线性回归优化算法目前被广泛应用于光学散射测量中的待测参数逆向求解^[19,20].
在纳米结构三维几何形貌的逆向提取过程中, 为了降低待测参数之间的耦合性, 通常需要将已知的纳米结构参数、材料光学常数、入射测量条件配置等设为固定值, 而对待测的若干形貌参数进行浮动处理^[6-10]. 考虑到纳米结构测量数据的质量完全取决于测量仪器本身, 无法轻易改变, 目前已有诸多文献通过优化入射测量条件配置以提高待测参数的测量精确度. 例如, Vagos等^[21]基于不确定度与灵敏度分析进行了光学特性模型及方位角的优化; Littau等^[22]针对采用不同方式进行入射角范围的选取, 从而提高了角分辨型椭偏仪的测量精度; 文献[23, 24]中分析了不同来源的系统误差对纳米结构参数测量准确度的影响, 进而优化了测量入射角和方位角; 此外, 文献[25]中还结合全局灵敏度分析方法实现了测量方位角的优化, 提高了纳米结构形貌参数的测量精度.
总体而言, 上述优化方法均是通过合理地选择测量条件配置, 以降低测量随机噪声或者系统误差对纳米结构待测参数逆向提取结果的影响, 进而在一定程度上提高测量准确度或精密度. 结构的材料光学常数获取方式通常为测量同一工艺中尚未制作出形貌结构的薄膜培片, 而后在纳米结构三维形貌参数的光学散射测量过程中使用测得的光学常数并假设其固定不变. 这一假设对于半导体制造工业中的绝大多数材料是成立的, 但某些感光材料诸如聚甲基丙烯酸甲酯(polymethyl methacrylate, PMMA)光刻胶^[26,27]可能会随着椭偏仪入射光照射的影响而发生改变, 该误差则可能在一定程度上传递给待测形貌参数的逆向提取值. 为此, 本文结合实验与仿真开展了椭偏仪入射光照对PMMA光刻胶薄膜培片和光栅结构的光学散射测量研究, 以证明PMMA光刻胶光学常数随入射光照的变化对于纳米结构的光学散射测量不容忽视, 从而为更进一步提高光刻胶纳米结构三维形貌参数的测量精确度提供理论依据.

2

-->

2.1.基于RCWA的正向光学特性建模

利用RCWA理论对周期性光栅结构进行光学特性建模的基本步骤可分为: 1)由Maxwell方程组求得入射区域和透射区域的电磁场的表达式; 2)对光栅区域内的介电常数及电磁场按Fourier级数展开, 并由Maxwell方程导出耦合微分方程组; 3)分别在光栅区域的上下边界运用电磁场边界连续条件, 通过数学求解各级衍射波的振幅, 进而计算各级衍射波的衍射效率或衍射场的强度分布等.
以图1所示的光栅结构为例, 假设其周期为P, 占空比为f, 线高为d, 顶部线宽和底部线宽分别为D_TC和D_BC, 首先建立如图1(a)所示的直角坐标系, θ为入射角, 入射波波矢k₁所在的铅垂面与xoz平面夹角为方位角φ, 电矢量E与k₁所在平面的夹角为偏振角ψ. 然后, 将光栅截面进行纵向分层, 则可将图1(b)中的每个薄层等效为矩形光栅, 再将矩形光栅结构划分为3个区域, 即区域1 (入射/反射区域, z < 0), 区域2 (透射区域, z > d)以及光栅区域(0 < z < d). 区域1和区域2的复折射率分别记为n ₁和n ₂. 光栅区域包含了脊部和槽部两种介质的周期分布, 分别记其复折射率为n _rd和n _gr. 由于本文所研究对象的材料为各向同性材料, 因此光栅区域的相对介电常数ε仅为关于x的周期性函数, 而与z无关. 将光栅区域的相对介电常数展开成Fourier级数形式, 有
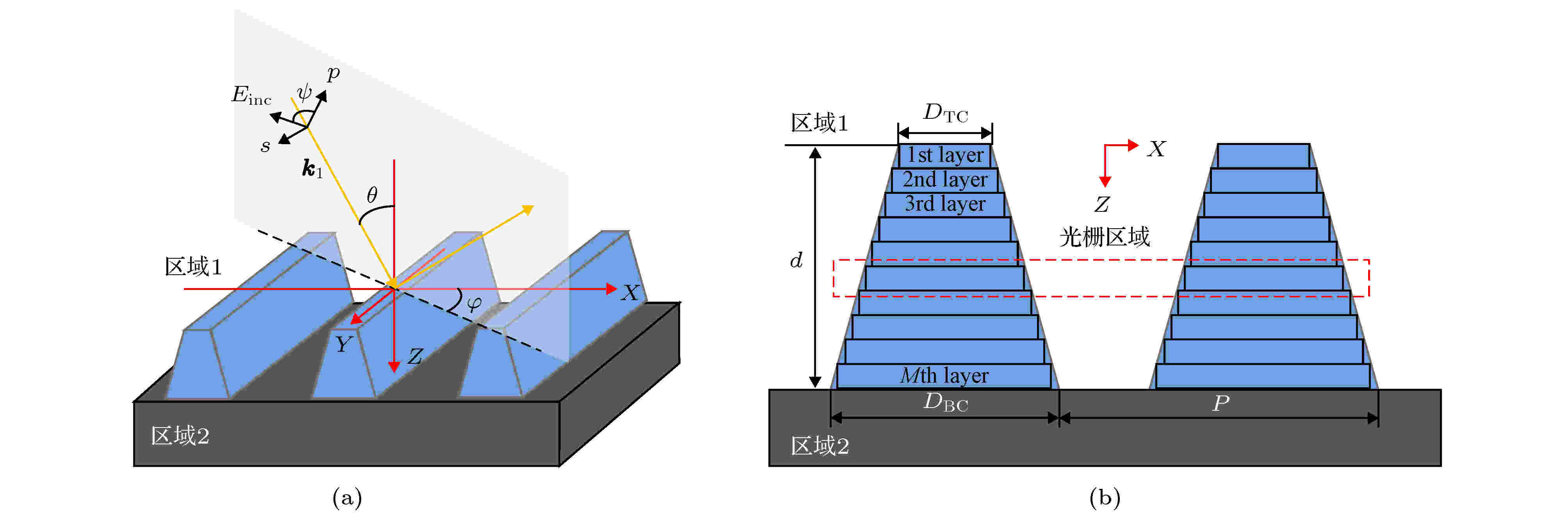图 1 (a) 线条光栅结构的几何形貌示意图; (b) RCWA建模的分层示意图
Figure1. (a) Geometry of the trapezoidal groove line grating; (b) layers division for inverse modeling based on RCWA.

$\varepsilon \left( x \right) = \sum\limits_g {{\varepsilon _g}\exp \left( {{\rm{j}}\frac{{2{\text{π}}g}}{P}x} \right)} ,$

其中ε_g表示相对介电常数的第g级Fourier展开分量.
将入射电场的振幅归一化后, 入射波的电场分量可表示成:

${{{E}}_{{\rm{inc}}}} = {{u}}\exp \left( { - {\rm{j}}{{{k}}_1} \cdot {{r}}} \right),$

其中, u为归一化的入射电矢量, k ₁表示入射波的波矢, r为平面波波面上任一点的位置矢量.
由Rayleigh展开可分别得到区域1 (z < 0)和区域2 (z > d)电场矢量的表达式:

${{{E}}_1} = {{{E}}_{{\rm{inc}}}} + \sum\limits_i {{{{R}}_i}\exp \left[ { - {\rm{j}}\left( {{k_{xi}}x + {k_y}y - {k_{1,zi}}z} \right)} \right]} , \tag{3a}$

${{{E}}_2} = \sum\limits_i {{{{T}}_i}\exp \left\{ { - {\rm{j}}\left[ {{k_{xi}}x + {k_y}y + {k_{2,zi}}\left( {z - d} \right)} \right]} \right\}} ,\tag{3b}$

式中, R_i和T_i分别表示第i级反射波和第i级透射波的幅值矢量; k_xi, k_y与k_l,zi分别表示第i级衍射波波矢的x, y与z分量,

${k_{xi}} = {k_0}({n_1}\sin \theta \cos \varphi - {\rm{i}}\lambda /\varLambda ), \tag{4a}$

${k_y} = {k_0}{n_1}\sin \theta \sin \varphi , \tag{4b}$

$\begin{split} {k_{l,zi}} =\, & \left\{\!\!\begin{aligned}& + {\sqrt {{{({k_0}{n_l})}^2} - k_{xi}^2 - k_y^2}, \;{{({k_0}{n_l})}^2} \!\geqslant\! k_{xi}^2 + k_y^2}, \\& -{{\rm j}\sqrt {k_{xi}^2 + k_y^2 - {{({k_0}{n_l})}^2}}, \; {{({k_0}{n_l})}^2} \!<\! k_{xi}^2 + k_y^2}, \end{aligned} \right. \\ & l = 1,2. \\[-10pt]\end{split} \tag{4c}$

在光栅区域(0 < z < d)内, 电场E_g和磁场H_g可以表示为空间谐波的Fourier级数展开式^[12]:

$\begin{split} {{ E}_g} = \, & \sum\limits_i \left[ {{S_{xi}}(z){\hat{ x}} + {S_{yi}}(z){\hat{ y}} + {S_{zi}}(z){\hat{ z}}} \right]\\ & \times \exp \left[ { - {\rm j}({k_{xi}}x + {k_y}y)} \right] ,\end{split} \tag{5a}$

$\begin{split}{{ H}_g} =\, & - {\rm j}\sqrt {\frac{{{\varepsilon _0}}}{{{\mu _0}}}} \sum\limits_i \left[ {{U_{xi}}{\hat{ x}} + {U_{yi}}(z){\hat{ y}} + {U_{zi}}(z){\hat{ z}}} \right]\\ & \times\exp \left[ { - {\rm j}({k_{xi}}x + {k_y}y)} \right],\end{split} \tag{5b}$

其中, ${{ S}_i}(z)$和${{ U}_i}(z)$分别为光栅区域内电场和磁场的幅值矢量, ${\varepsilon _0}$和${\mu _0}$分别为自由空间的介电常数和磁导率.
由Maxwell旋度方程, E_g与H_g有如下的耦合关系:

$\nabla \times {{ E}_g} = - {\rm{j}}\omega {\mu _0}{{ H}_g}, \tag{6a}$

$\nabla \times {{ H}_g} = {\rm{j}}\omega {\varepsilon _0}\varepsilon (x,y){{ E}_g}, \tag{6b}$

将(5)式代入(6)式, 消去E_gz与H_gz, 并应用逆规则^[28]后, 可得矩阵形式的耦合波方程组. 当所研究的结构具有非矩形面型(如图1所示)需要进行分层处理时, 应在光栅区域每一层中对电场E _g和磁场H _g进行展开, 并获得相应的耦合波方程. 最后在光栅区域内各层边界及光栅区域与反射区和投射区的分界面(z = 0和z = d)上考虑连续性条件, 即可得出反射波TE (ψ = 90°)模电场分量R _s和TM (ψ = 0°)模磁场分量R _p的幅值向量.
考虑到仪器探测设备主要检测的是光强信息, 基于RCWA模型输出的相应为反射率、椭偏参数或Mueller矩阵等光学特性参量的计算值. 其中, 反射率的计算公式为

$ D{E_i} = {\left| {{R_{{\rm{s}}i}}} \right|^2}{\rm{Re}}\left( {\frac{{{k_{1,zi}}}}{{{k_0}{n_1}{\rm{cos}}\theta }}} \right) + {\left| {{R_{{\rm{p}}i}}} \right|^2}{\rm{Re}}\left( {\frac{{{k_{1,zi}}/{n_1}^2}}{{{k_0}{n_1}{\rm{cos}}\theta }}} \right),$

其中R _si和R _pi分别表示第i级反射波TE模电场分量和TM模磁场分量的幅值向量.
由偏振光学可知, 待测样品的光学特性则可以用2 × 2阶Jones矩阵J或者4 × 4阶Mueller矩阵M来表征. 例如, 对应于待测样品的Jones矩阵J有

$\left[ \begin{gathered} {E'_{\rm p}} \\ {E'_{\rm s}} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{J_{11}}}&{{J_{12}}} \\ {{J_{21}}}&{{J_{22}}} \end{array}} \right]\left[ \begin{gathered} {E_{\rm p}} \\ {E_{\rm s}} \\ \end{gathered} \right],$

(8)式左右两边分别表示出射和入射至样品表面的Jones向量, E _p和E _s分别表示平行和垂直于入射面的电场分量. 由Jones矩阵J可求得椭偏参数:

$\rho = \tan \varPsi \exp ({\rm j}\varDelta ) = {{{J_{11}}}}/{{{J_{22}}}},$

其中, Ψ为振幅比角, Δ为相位差角. 当测量过程中不存在退偏效应时, 其Jones矩阵J和Mueller矩阵M之间存在如下关系:

${ M} = {({M_{ij}})_{4 \times 4}} = { U}({ J} \otimes {{ J}^{{*}}}){{ U}^{ - 1}},$

其中, $ \otimes $表示矩阵的Kronecker积; ${{ J}^ * }$为Jones矩阵J的共轭矩阵; 矩阵U定义为

${ U} = \left[ {\begin{array}{*{20}{c}} 1&0&0&1 \\ 1&0&0&{ - 1} \\ 0&1&1&0 \\ 0&{\rm j}&{ - \rm j}&0 \end{array}} \right].$

在实际测量过程中, 通常用Mueller矩阵中第1行和第1列的元素M₁₁对其进行归一化处理. 归一化的Mueller矩阵定义为

${ M}' = {({m_{ij}})_{4 \times 4}} = {{ M} / {{M_{11}}}},$

2 -->

2.2.基于LM局部优化算法的待测参数逆向求解

对于光学散射测量中的逆问题, 采用非线性回归法中的LM局部搜索算法对纳米结构的待测参数进行逆向求取, 该算法结合了梯度下降法和高斯-牛顿法, 是一种采用标准数值优化的快速算法^[29]. 不失一般性, 在参数提取过程中, 利用S维列向量表示一组需依据评价函数值的大小进行浮动变化的参数, 并记为x = [x₁, x₂, ···, x_S]^T, 其中x₁, x₂, ···, x_S可以表示光栅结构的顶部线宽、线高及侧壁角等待测参数; 将固定不变的参数组成的L维列向量记为a = [a₁, a₂, ···, a_L]^T, 其中a₁, a₂, ···, a_L可以是测量条件、材料的光学常数, 还可以是纳米结构的已知测量值的几何特征参数, 如薄膜厚度等; 数据拟合时, 采用χ²形式的评价函数来衡量测量和计算得到的椭偏参数或者Mueller矩阵元素之间的拟合误差.
以Mueller矩阵元素为例, 其测量值$m_{ij, k}^{{\rm meas} }$和计算值$m_{ij, k}^{{\rm calc} }({ x}, \;{ a})$之间的拟合误差表达式为

${\chi ^2} = \sum\limits_{k = 1}^{{N_{\lambda} }} {\sum\limits_{i,j = 1}^4 {{{\left[ {\frac{{m_{ij,k}^{{\rm meas} } - m_{ij,k}^{{\rm calc} }({ x},{ a})}}{{\sigma ({m_{ij,k}})}}} \right]}^2}} } ,$

其中下标i和j表示Mueller矩阵元素索引, 这里不包括元素m₁₁ (m₁₁ ≡ 1); k表示光谱点索引, ${N_{\lambda} }$为总的光谱点个数; $\sigma ({m_{ij, k}})$为测量Mueller矩阵元素${m_{ij, k}}$的标准差.
为了方便起见, 将测量得到的Mueller矩阵元素$m_{ij, k}^{{\rm meas} }$记为y_n, 而将计算得到的Mueller矩阵元素$m_{ij, k}^{{\rm calc} }({ x}, \;{ a})$记为${f_n}({ x}, \;{ a})$, 于是(13)式可以写为

${\chi ^2} = \sum\limits_{n = 1}^N {{w_n}{{[{y_n} - {f_n}({ x},\;{ a})]}^2}} ,$

其中, ${w_n} = {1 / {{\sigma ^2}({y_n})}}$为权值因子, $N = 15{N_{\lambda} }$. 再将(14)式写成矩阵形式:

${\chi ^2} = {[{ y} - { f}({ x},\;{ a})]^{\rm T}}{ W}[{ y} - { f}({ x},\;{ a})],$

其中, $ { y}= {[{y_1}, \;{y_2}, \; \cdots, \;{y_N}]^{\rm T} } $, ${ f}({ x}, \;{ a}) = [{f_1}({ x}, \;{ a}), $${f_2}({ x}, \;{ a}), \; \cdots, \;{f_N}({ x}, \;{ a})]^{\rm T}$, W为由权值因子w_n构成的$N \times N$阶对角矩阵, 即${ W} = {\rm diag}\left({1 / {{\sigma ^2}({y_1})}}\right., $$\left.{1 / {{\sigma ^2}({y_2})}}, \; \cdots, \;{1 / {{\sigma ^2}({y_N})}}\right) $. 因此, 纳米结构光学散射测量中的逆问题可以表述为

${\hat{ x}} = \mathop {\arg \min }\limits_{{ x} \in \varOmega } \left\{ {{{[{ y} - { f}({ x},\;{{ a}^ * })]}^{\rm T}}{ W}[{ y} - { f}({ x},\;{{ a}^ * })]} \right\},$

其中, ${\hat{ x}}$为最终提取的待测参数值, Ω为待测参数的取值范围, ${{ a}^ * }$为参数提取过程中向量a的给定值.
对于(16)式描述的逆问题, 本文利用LM优化算法提取待测参数的流程为: 首先设置一组迭代参数初值x₀, 然后利用所建正向光学特性模型计算出待测纳米结构对应的理论光谱, 通过定义某种评价函数来进行理论计算光谱与测量光谱的比对, 若评价函数值大于其预设的精度值, 则根据一定准则修改当前参数值, 重复上述过程, 直到评价函数值小于预设的精度值时则认为实现了理论计算光谱与测量光谱的最佳拟合, 即可得到待测参数的输出结果${\hat{ x}}$.

本文采用的实验仪器是一台由武汉某公司生产的双旋转补偿器ME-L型Mueller矩阵椭偏仪, 其实物图与基本原理图如图2所示, C_r1 (w ₁)为起偏臂的补偿器, C_r2 (w ₂)为检偏臂的补偿器, 二者在测量时将同步旋转且旋转角频率之比为5∶3^[30]; 仪器测量的光谱范围为210—1650 nm, 入射角范围为45°—90° (加聚焦组件入射角范围为55°— 75°), 样品台可360°旋转, 常规光斑直径约为3 mm (加聚焦组件时光斑直径约为200 μm), 单次数据测量时间为1—8 s, 测量参数包括反射率、椭偏参数及15个归一化的Mueller矩阵元素等.
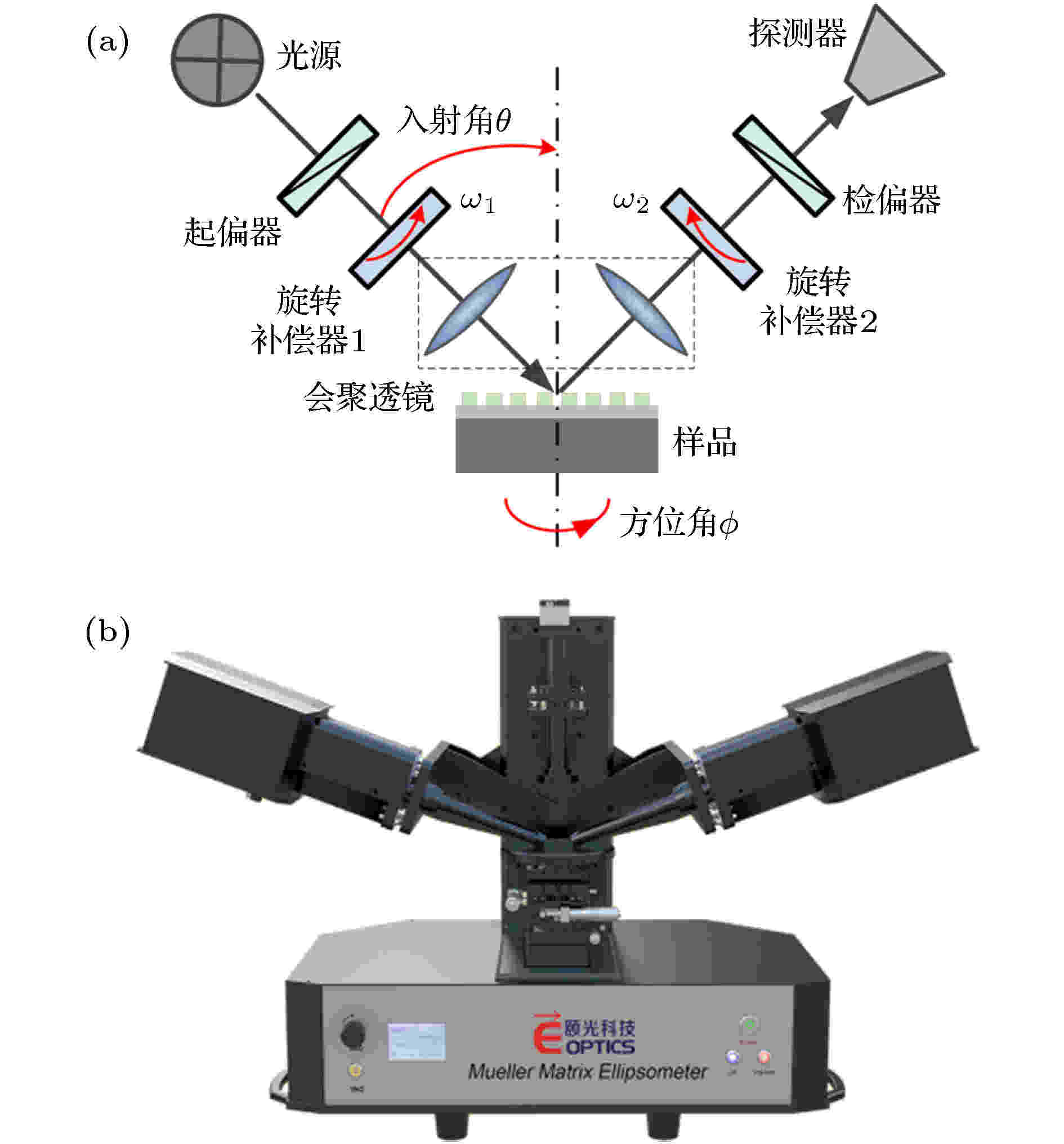图 2 双旋转补偿器型Mueller矩阵椭偏仪　(a)基本光路; (b)仪器
Figure2. Principle and instrument of the dual rotating-compensator Mueller matrix ellipsometer: (a) Principle; (b) instrument.

实验样品为光栅制作前期工艺中的两个薄膜样品, 样品1是基底为标准硅片(silicon, Si)的单层二氧化硅(silicon dioxide, SiO₂)薄膜结构, 其SiO₂薄膜厚度的名义值为100 nm, 如图3(a)所示; 样品2为在上述SiO₂薄膜结构表面旋涂了一层PMMA的光刻胶培片, 其PMMA薄膜厚度的名义值为385 nm, 如图3(b)所示. 其中, 第1个薄膜样品的待测参数包括SiO₂薄膜的厚度值d ₁、表面粗糙度c ₁及其光学常数折射率n ₁和消光系数k ₁; 第2个样品的待测参数为PMMA薄膜的厚度值d ₂、表面粗糙度c ₂及其光学常数折射率n ₂和消光系数k ₂.
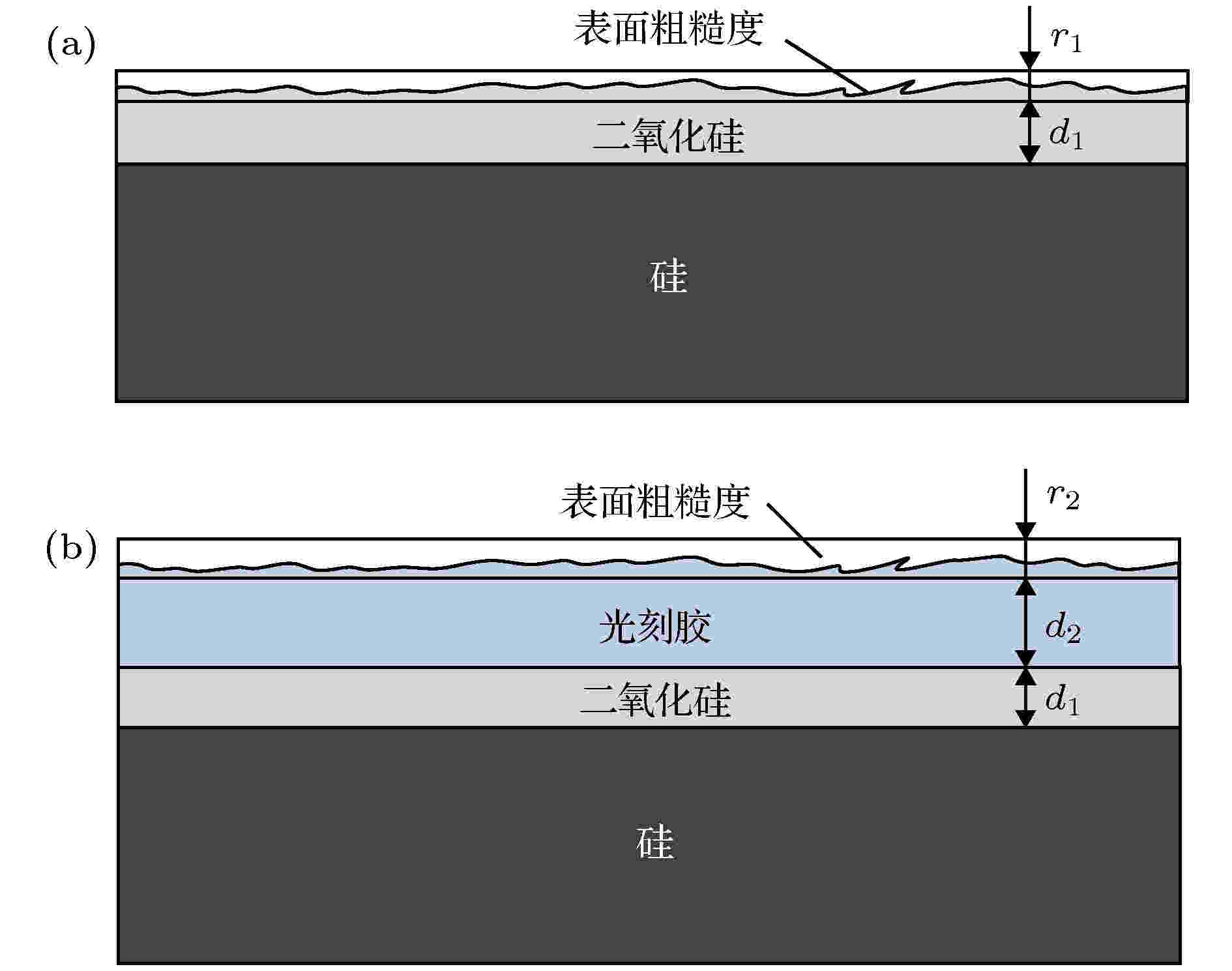图 3 (a) SiO₂薄膜样品; (b) 在SiO₂表面旋涂PMMA光刻胶后的薄膜样品
Figure3. (a) The SiO₂ sample; (b) the PMMA sample spinning coated on the surface of the SiO₂ film.

为了分析椭偏仪入射光对PMMA光刻胶的影响, 首先, 利用ME-L型Mueller矩阵椭偏仪在65°入射角下分别对图3所示的两个薄膜样品进行了20次重复性实验, 各获得20组椭偏参数测量数据, 由于仪器测量时间以及人工操作的时间消耗, 单次测量过程大约耗时15 s, 因此每个样品在入射光下的总暴露时间约为300 s. 然后, 利用上述LM迭代算法分别从每组椭偏参数测量数据中提取出薄膜样品的所有待测参数.
在样品1的参数提取过程中, 对于SiO₂光学常数中的n ₁和k ₁这两个待测参数, 我们采用Cauchy模型^[31]对其进行建模, 通过一个三项式来描述材料的折射率n ₁, 如(17a)式所示; Urbach尾部的指数吸收则采用(17b)式进行描述.

${n_1} = {A_n} + {10^{ - 2}}\frac{{{B_n}}}{{{\lambda ^2}}} + {10^{ - 3}}\frac{{{C_n}}}{{{\lambda ^4}}}, \tag{17a}$

${k_1} = {K_{{\rm{Amp}}}} \cdot {{\rm{e}}^{{e_{{\rm{Exponent}}}} \cdot \left[ {1.24{\kern 1pt} {\kern 1pt} \left( {\frac{1}{\lambda } - \frac{1}{{{\lambda _{{\rm{Bandedge}}}}}}} \right)} \right]}}{\kern 1pt} ,\tag{17b}$

其中, A_n, B_n和C_n描述折射率的色散; K_Amp(K振幅)和e_Exponent (指数)项描述消光系数色散的形状; λ_Bandedge一般设为定值400 nm. 模型中的A_n, B_n, C_n, K_Amp和e_Exponent均为待定系数. 对于样品表面的粗糙结构, 采用麦克斯韦尔-加内特等效介质模型(maxwell-garnett effective medium approximation, MGEMA)^[32]将其近似为一层均匀且各项同性的薄膜进行处理. 在此基础上, 将入射条件和基底硅的光学常数等设为已知值, 利用LM迭代算法分别对20组椭偏测量数据进行待测参数逆向求取, 并采用均方根误差(mean squared error, MSE)^[33]来衡量测量与模型计算数据之间的拟合程度, 待测参数包括d₁和r₁, 光学常数模型参数$n(\infty) $, E_g, A_i, B_i和C_i. 图4为SiO₂厚度d₁及其表面粗糙层厚度r₁的20组拟合值; 图5分别展示了第1, 5, 10, 15和20次所提取得到的各波长下折射率n₁与消光系数k₁值, 以及文献[34]中的SiO₂光学常数变化曲线.
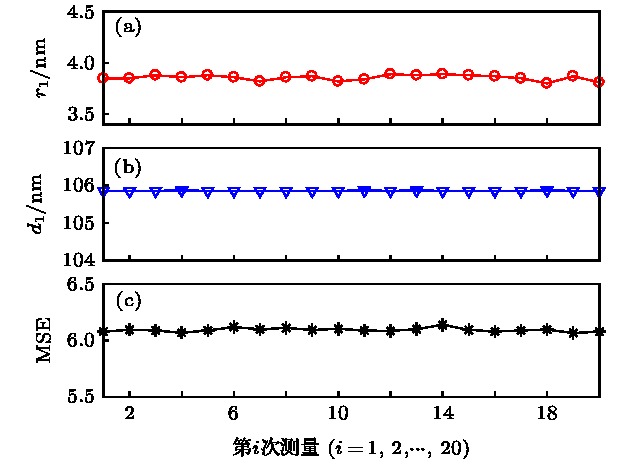图 4 拟合得到的20组SiO₂膜厚d₁及其表面粗糙度等效膜厚r₁　(a) r₁; (b) d₁; (c) MSE
Figure4. Extracted results of the thicknesses of SiO₂ film h₁ and equivalent surface roughness r₁: (a) r₁; (b) d₁; (c) MSE.

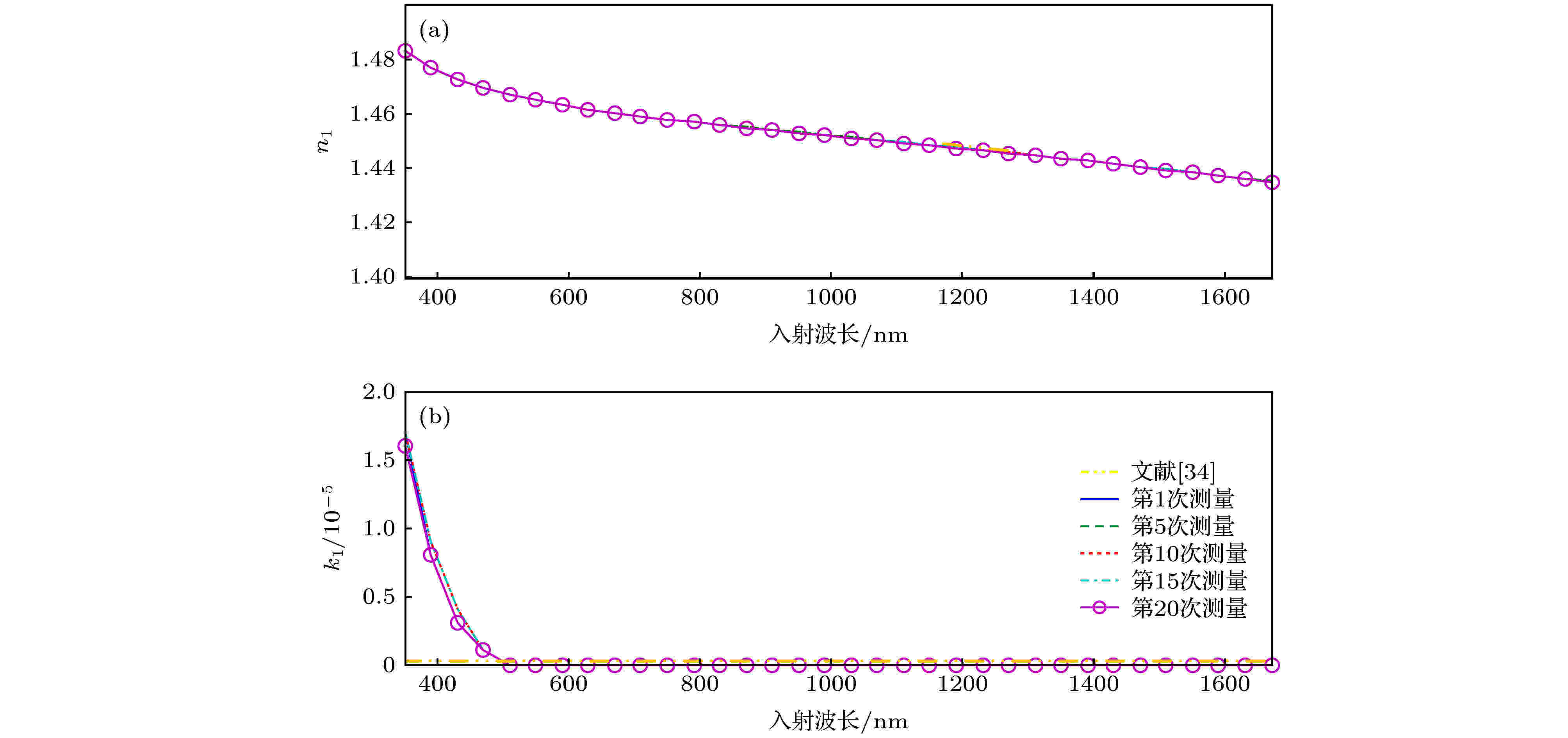图 5 拟合得到的第1, 5, 10, 15和20组SiO₂薄膜光学常数n₁和k₁的计算值, 以及文献[34]给出的折射率与消光系数　(a) n₁; (b) k₁
Figure5. Extracted results of the optical constants n₁ and k₁ of SiO₂ film calculated by Cauchy model and the ones from Ref. [34]: (a) n₁; (b) k₁.

对样品2的待测参数进行逆向提取时, 除了将入射条件(如入射角、入射波长等)、基底硅的光学常数等设为已知量, 还将SiO₂薄膜层的厚度、光学常数及粗糙度厚度均固定为样件一中20组提取结果的平均值; 对于PMMA光刻胶光学常数中的n₂和k₂这两个待测参数, 同样采用Cauchy模型对其进行建模, 其表面的粗糙结构也采用MGEMA模型将其等效为均匀且各项同性的一层薄膜. 在此基础上, 利用LM迭代算法分别对20组椭偏测量数据进行待测参数逆向求取, 待测参数包括d₂和r₂, 光学常数模型参数$n(\infty) $, E_g, A_i, B_i和C_i. 图6中的蓝色圆圈为PMMA光刻胶厚度d₂及其表面粗糙层厚度r₂的20组提取值, 图7分别展示了第1, 5, 10, 15和20次所提取得到的各波长下折射率n₂与消光系数k₂值. 此外, 将第1次提取得到的PMMA光学常数作为已知量后, 再从后续的19组测量数据中提取出待测参数d₂和r₂, 其拟合值如图6中的红色方形所示.
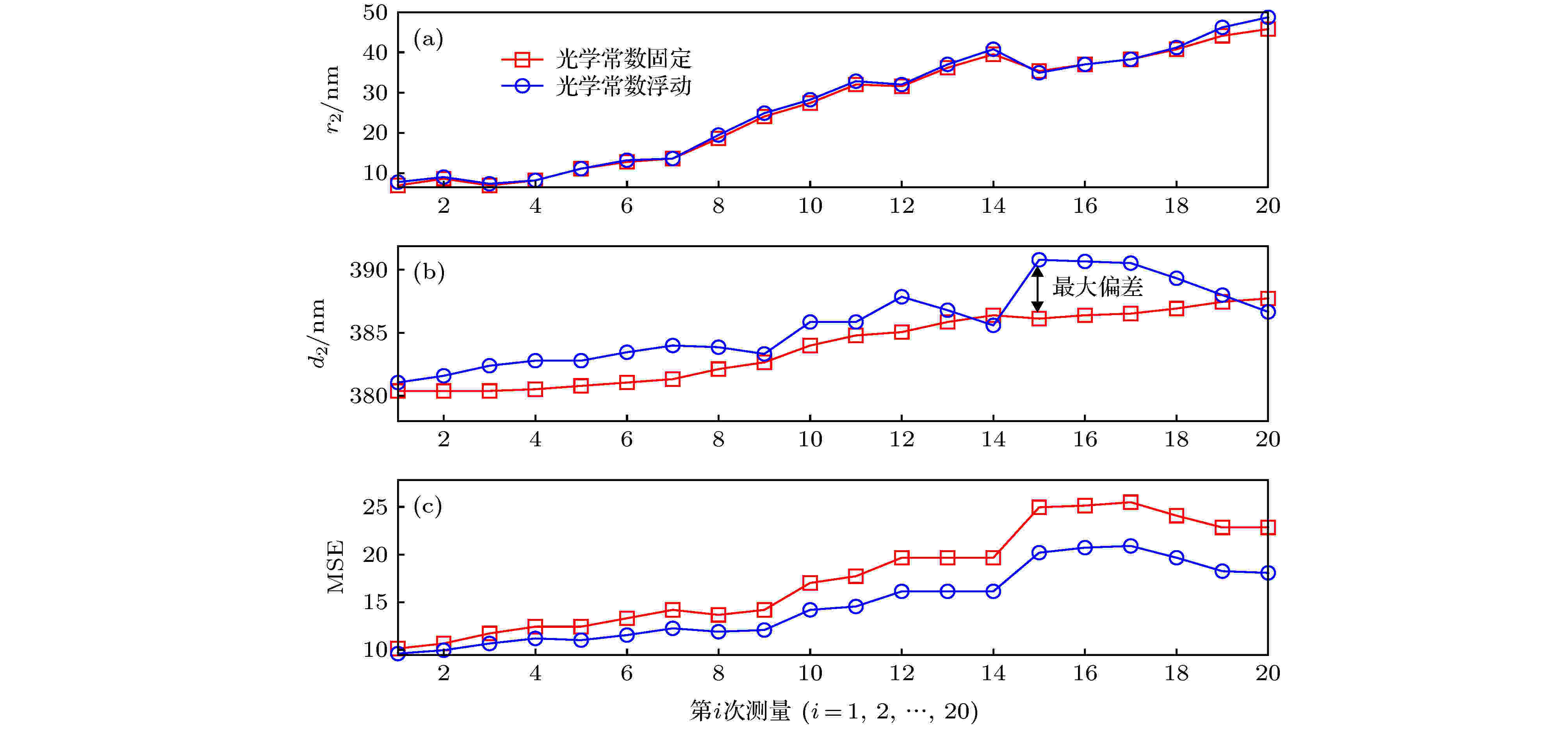图 6 拟合得到的20组PMMA膜厚d₂及其表面粗糙度等效膜厚r₂　(a) r₂; (b) d₂; (c) MSE
Figure6. Extracted results of the thicknesses of PMMA film d₂ and equivalent surface roughness r₂: (a) r₂; (b) d₂; (c) MSE.

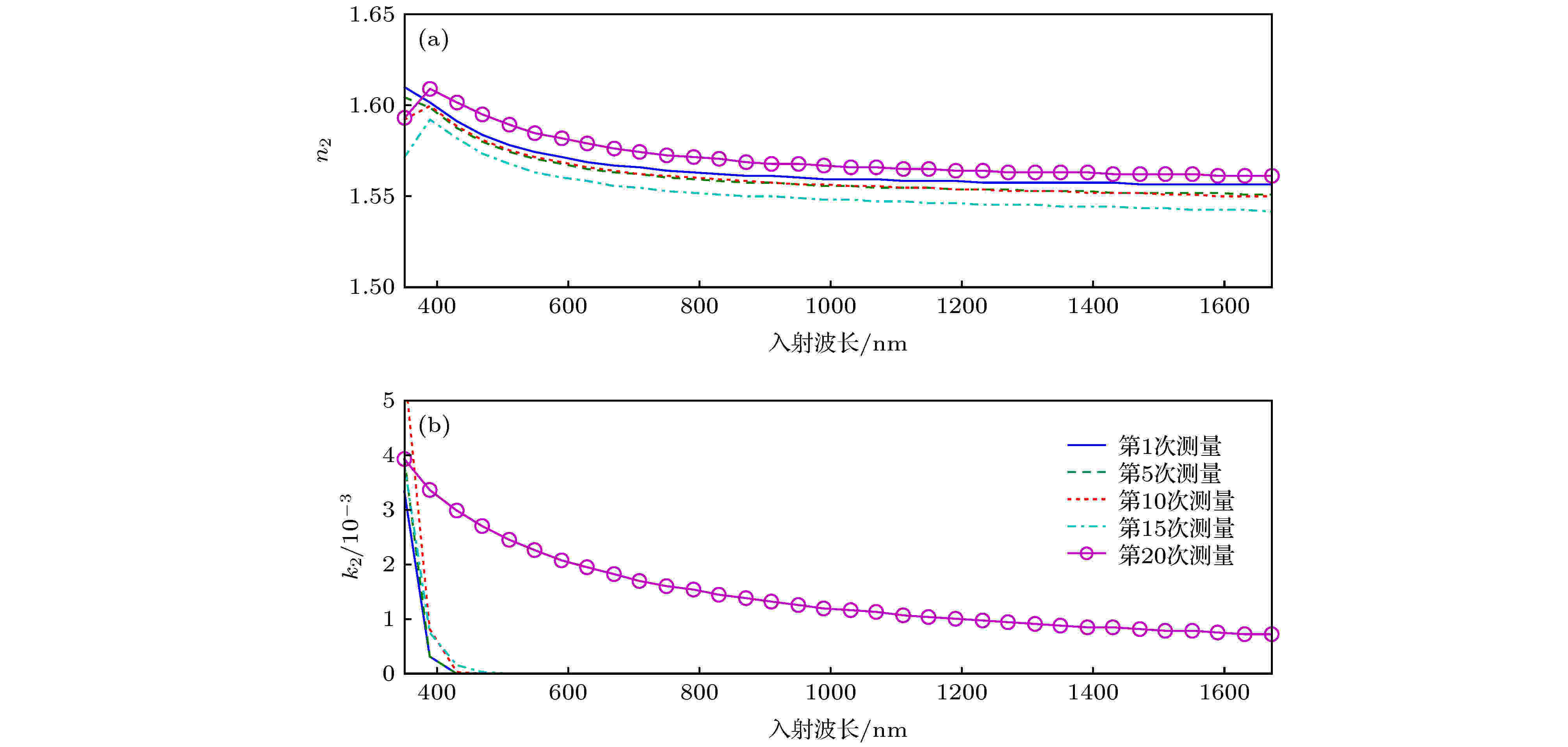图 7 拟合得到的第1, 5, 10, 15和20组PMMA薄膜光学常数n₂和k₂的计算值　(a) n₂; (b) k₂
Figure7. Extracted results of the optical constants n₂ and k₂ of PMMA film calculated by Cauchy model: (a) n₂; (b) k₂

从图4和图5可以看出, SiO₂薄膜样品折射率n₁的提取值与文献[34]中的结果几乎保持一致, 且k值的差别为10^–5量级(由于k很小, 可忽略不计, 故文献[34]中设定k = 0); SiO₂薄膜样品在20次重复性测量数据中拟合得到的折射率n₁、消光系数k₂以及薄膜厚度d₁几乎一致, 其表面粗糙度参数r₁的变化幅度也不大, 均位于3.82 nm左右. 由图6和图7可得, 随着入射光照射时间的增加, 重复20次提取得到的PMMA光刻胶折射率n₂、消光系数k₂、膜厚d₂以及表面粗糙度参数r₂均存在明显差异, 尤其是第20次得到的k₂变化更为剧烈, 可能的原因为PMMA光刻胶到达一定曝光时间后, 其光学特性进入非线性变化区域^[35]. 其中, 光刻胶厚度d₂大约在380—392 nm的范围内上下波动, 而表面粗糙度r₂的变化幅度较大且呈现上升趋势, 其第1次测量的拟合值为7.93 nm, 到第20次测量时为48.43 nm, 变化幅度高达40.5 nm. 对比图6(a)中光刻胶光学常数浮动(蓝色圆圈)与固定(红色方形)的提取结果可得, 光刻胶光学常数的变化对表面粗糙度r₂的测量结果影响较小, 而光刻胶厚度d₂ (红色方形)明显不同且小于在光学常数浮动时的拟合值(蓝色圆圈), 二者之间的最大差值达到3.5 nm. 此外, 在20次椭偏光谱数据的拟合中, 光学常数固定时得到MSE值均大于其浮动的结果, 即在光刻胶光学常数浮动时, 达到最佳拟合所对应的模型计算椭偏光谱与仪器测量光谱之间的匹配度更高. 上述实验结果表明, SiO₂材料不受入射光照射的影响, 而PMMA光刻胶薄膜样品, 尤其是其折射率n₂和消光系数k₂受到显著影响, 若在待测PMMA薄膜的光学散射测量中将其作为固定量, 则会较大地降低样品薄膜厚度的测量精确度.

在光栅结构三维形貌的光学散射测量中, 为了极大地降低待测参数之间的耦合作用, 通常需要事先测量结构刻蚀前的薄膜培片以确定光栅材料的光学常数, 从而在逆向提取待测形貌参数时将其设为固定值. 为分析PMMA光学常数的变化对光栅结构测量结果的影响, 以图8所示的PMMA光刻胶光栅为仿真对象, 结合上述PMMA薄膜样品的实验结果开展光栅结构待测形貌参数的逆向提取研究. 图8所示的PMMA光刻胶光栅是在薄膜样品2的基础上刻蚀后得到, 其几何形貌参数包括周期P、顶部线宽w₁、线高h以及底部线宽w₂.
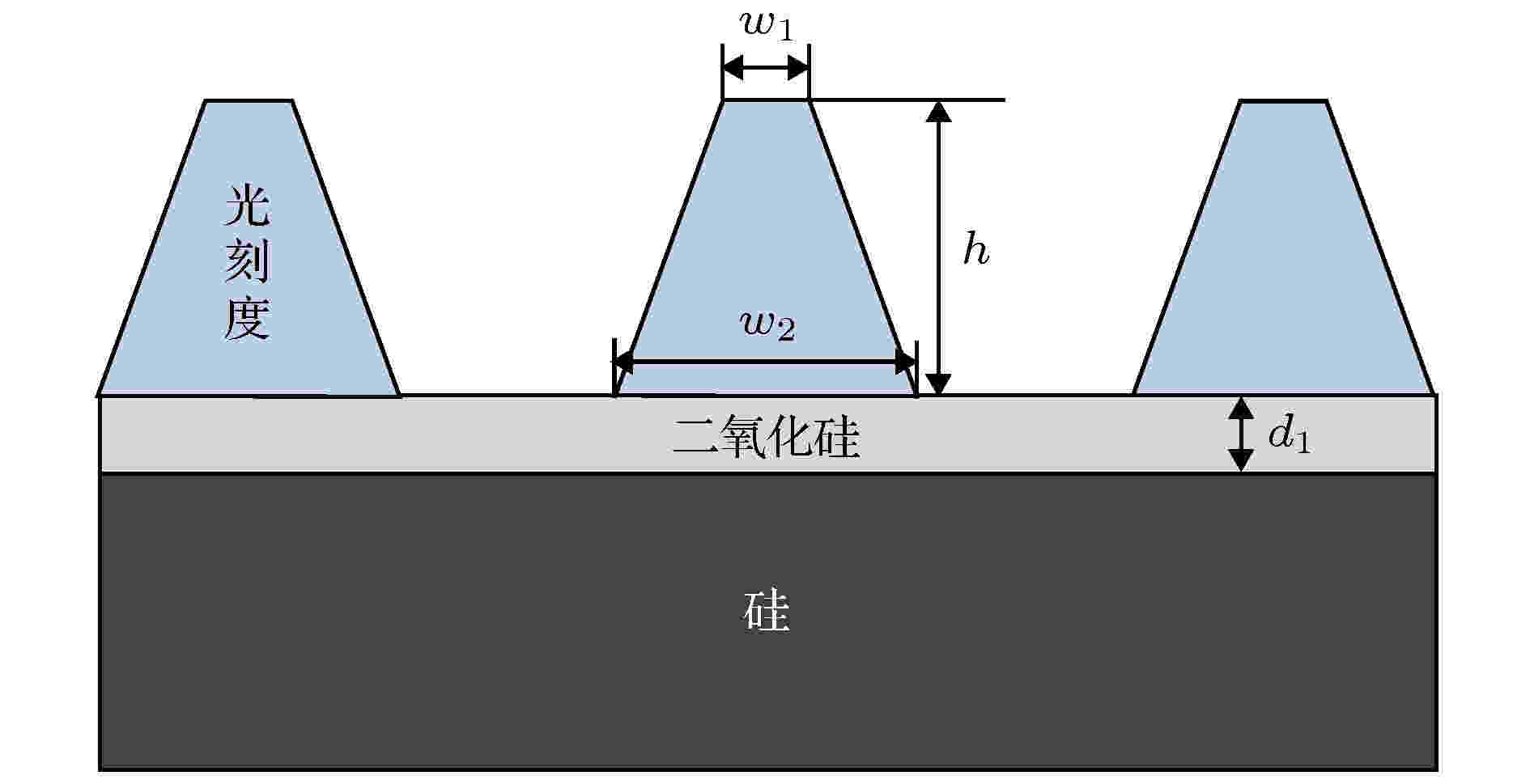图 8 PMMA光刻胶仿真光栅的结构示意图
Figure8. Geometry of the simulated PMMA grating sample

具体的仿真过程为: 假设光栅结构的真实尺寸为P = 800 nm, w₁ = 350 nm, h = 387.42 nm, w₂ = 365 nm, PMMA的光学常数n₂和k₂均取值为图7中的第20次拟合结果, 硅基底和SiO₂薄膜的光学常数、厚度等参数信息均与样品2的取值相同; 在入射角θ = 65°、方位角φ = 0°和入射波段为370—870 nm (步长为10 nm)的入射条件下, 利用所建立的基于RCWA的正向光学特性模型计算得到该PMMA光刻胶光栅的一组Mueller矩阵元素, 并将其看作“测量”光谱数据; 在其他参数保持不变的前提下, 将PMMA光学常数n₂和k₂的取值替换为图6中的第1次拟合结果后, 以顶部线宽w₁、线高h和底部线宽w₂为浮动的待测参数, 利用LM迭代寻优算法不断调用正向光学特性模型, 并将计算光谱与“测量”光谱进行匹配, 当二者实现最佳匹配后所对应的3个待测形貌参数的拟合值如表1所列, 图9所示为模型计算与“测量”光谱之间的拟合程度.

参数名称	真实值	拟合值	绝对误差
顶部线宽w1/nm	350.00	352.90	2.90
线高h/nm	387.42	387.90	0.50
底部线宽w2/nm	365.00	368.50	0.35

表1对比PMMA仿真光栅3个待测形貌参数的拟合值与真实值
Table1.Comparison of these three true dimensions and the extracted results of the simulated PMMA grating.

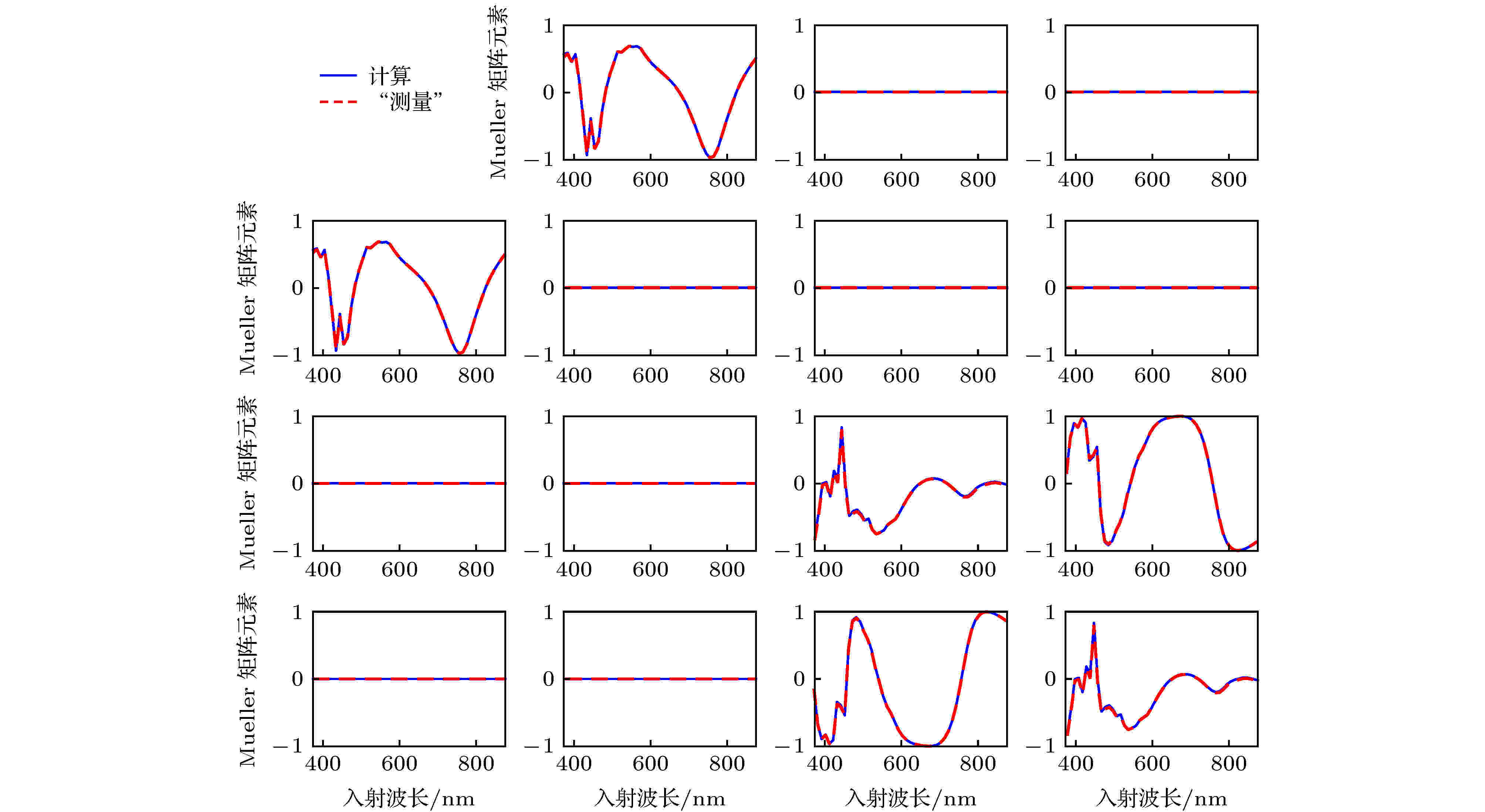图 9 在入射角θ = 65°、方位角φ = 0°的入射条件下, PMMA光刻胶仿真光栅的模型计算Mueller矩阵光谱与“测量”光谱之间的拟合曲线
Figure9. Fitting results of the calculated and the “ellipsometer-measured” Mueller matrix elements at the incidence and azimuthal angles fixed at θ = 65° and φ = 0°.

由表1可得, 在对“测量”光谱进行待测参数提取时, 改变PMMA光刻胶光学常数n₂和k₂的取值后, 3个结构参数顶部线宽w₁、线高h和底部线宽w₂的提取结果在一定程度上偏离于真实值. 其中, 引起待测形貌参数顶部线宽w₁的测量误差为最大, 达到了2.90 nm. 本文第3节中光刻胶薄膜的测量实验研究证明了光刻胶的光学常数受到椭偏仪入射光的照射影响后会发生明显的变化, 这里光刻胶光栅的仿真结果表明了光刻胶光学常数的变化将较大地降低光栅结构几何形貌参数的测量准确度. 因此, 针对半导体制造工业中光刻胶纳米结构的光学散射测量而言, 其光学常数会随着入射光照射时间增加而发生变化这个特性将不能再被忽略, 这对于实现光刻胶纳米结构三维形貌参数的高精确度测量具有较为重大的指导意义.

利用Mueller矩阵椭偏仪分别对SiO₂薄膜和PMMA光刻胶薄膜进行了包括光学常数、厚度和表面粗糙度的待测参数提取实验研究, 首次发现了PMMA光刻胶的光学常数(折射率和消光系数)受到入射光的照射影响会发生相应的改变. 结合实验得到的PMMA光学常数提取结果, 针对仿真的PMMA光刻胶光栅进行了几何形貌参数顶部线宽、线高和底部线宽的逆向提取研究, 结果表明光刻胶光学常数随入射光照射发生的变化对光栅形貌参数提取结果的影响较大, “材料光学常数不随入射光的照射而发生变化”这一假设条件将不再适用. 在后续的研究工作中, 我们将深入研究光刻胶材料折射率和消光系数受入射光照射的影响规律并建立相应的变化模型, 从而可进一步提高光刻胶纳米结构三维形貌参数的测量准确度.