摘要:在考虑光学微腔中二阶和三阶非线性效应的情况下, 引入了可同时描述腔内基频和倍频光场的演化过程的Lugiato-Lefeve方程, 分析了SiN微腔中二次谐波的产生, 并讨论了各参数对腔内基频和倍频光场的影响. 理论分析结果表明, 失谐参量为0时, 稳定后的基频光场为平顶脉冲的形式, 而倍频光场呈正弦分布; 失谐参量增加, 将导致腔内基频和倍频光功率在演化过程中出现振荡, 且最终稳定的光功率变弱, 稳定后的光场分布为周期性变化; 失谐参量的值过大, 会使得微腔光场处于混沌状态. 抽运光强较弱时, 腔内可形成稳定的光场分布; 抽运光强较强时, 会导致腔内色散以及非线性效应过强, 最终稳定的光场仍然呈周期性变化, 且抽运光功率越强, 光功率的演化曲线振荡越强. 此外, 选取特定的微腔尺寸, 微腔可工作于“图灵环”状态. 理论分析结果对研究光学微腔中二次谐波的产生有重要意义.
关键词: 非线性光学/
光学微腔/
二次谐波

English Abstract

全文HTML

--> --> -->

光频梳技术已经广泛地应用于绝对距离测量^[1]、光谱测量^[2]、光学频率测量^[3]等领域. 目前, 光频梳主要是基于锁模激光器实现的, 由于受到锁模激光器腔长的限制, 它们的重复频率一般为几十到几百MHz^[4,5]. 但是, 随着光频梳应用领域的不断拓展, 需要重复频率更高的光频梳, 例如: 在高分辨率天文光谱仪的波长定标中, 光频梳的重复频率要达到10—30 GHz^[6]. 传统的基于锁模激光器的光频梳已经无法满足需求, 因此, 一种新型的基于光学微腔的光频梳在近些年成为了研究热点^[7-9].
基于微腔的光频梳是利用级联的四波混频效应, 在光学微腔中产生一系列等间距的频率成分, 从而将单一的抽运频率扩展到一个非常超宽光谱范围. 微腔光频梳具有体积小、结构简单、易实现光学集成等优点. 通过理论研究证实, 微腔可工作于多种模式, 例如: 光孤子、图灵环、暗孤子、混沌等模式^[10], 并且这些工作模式也在实验中被观察到^[11-15]. 目前, 在光学微腔的理论研究中, 大多都是以Lugiato-Lefeve方程 (Lugiato-Lefeve equation, LLE)为理论模型, 通过求解LLE, 得到稳态时腔内的光场分布^[16]. 关于光学微腔中二次谐波的产生, 已经在实验中被观察到. Xue等^[17]通过四波混频的方法在正色散的光学微腔中同时观察到了Kerr光频梳和二次谐波的产生, 此外还建立了光学微腔中二次谐波产生的理论模型, 理论分析和实验结果相一致. Lin等^[18]也在片上集成的光学微腔中实现了高效率的二次谐波产生.
然而, 目前对微腔光频梳的理论研究采用的LLE, 只包含了腔内的损耗、色散、抽运项, 并没有考虑微腔中的非线性效应^[19]. 但是由于光学微腔本身体积很小, 腔内光功率密度较高, 因而腔内的非线性效应是无法被忽略的. 当考虑微腔内的二阶和三阶非线性效应时, 腔内会由于非线性效应产生二次谐波^[20]. 因此, 本文将在二阶、三阶非线性效应的基础上, 分析光学微腔内二次谐波的产生情况, 并研究各个参数对腔内基频光和倍频光光场产生的影响.

本文讨论以SiN为材料的光学微腔. SiN材料的光学微腔一般为以Si为基底的片上结构, 结构如图1所示, 抽运光通过微腔一侧的波导结构耦合进入微腔, 光在微腔传播过程中耦合进入另一侧的波导结构输出. 在这一过程中, 由于二阶、三阶非线性效应, 腔内会产生二次谐波. 为讨论微腔中的二次谐波产生情况, 引入包含二次谐波项的LLE来描述腔内基频和倍频光场在时间和空间上的演化, 分别用E₁表示基频光的光场, E₂表示倍频光的光场, 基频和倍频光场随时间和空间的变化关系满足以下方程^[17]:
图 1 SiN微腔结构示意图
Figure1. Structure of the SiN microresonator.

$\begin{split} \frac{{\partial {E_1}}}{{\partial z}} =\,& \bigg[ - {\alpha _1} - {\rm{i}}{\delta _1} - {\rm{i}}\frac{{k_1''}}{2}\frac{{{\partial ^2}}}{{\partial {\tau ^2}}} + {\rm{i}}{\gamma _1}{{\left| {{E_1}} \right|}^2}\bigg. \\ &+\bigg. {\rm{i}}2{\gamma _{12}}{{\left| {{E_2}} \right|}^2} \bigg]{E_1} + {\rm{i}}\kappa {E_2}E_1^* + {\eta _1}{E_{{\rm{in}}}}, \end{split}$

$\begin{split} \frac{{\partial {E_2}}}{{\partial z}} =\, & \bigg[ - {\alpha _2} - {\rm{i}}2{\delta _1} - {\rm{i}}\Delta k - \Delta {k{'}}\frac{\partial }{{\partial \tau }} - {\rm{i}}\frac{{k_2''}}{2}\frac{{{\partial ^2}}}{{\partial {\tau ^2}}}\bigg. \\ & +\bigg.{\rm{i}}{\gamma _2}{{\left| {{E_2}} \right|}^2} + {\rm{i}}2{\gamma _{21}}{{\left| {{E_1}} \right|}^2}\bigg]{E_2} + {\rm i}\kappa E_1^2,\\[-20pt] \end{split}$

其中, z为光沿微腔传播的距离; τ是光传播的时间, 即快时间; α₁和α₂分别为基频光和倍频光在腔内传播单位长度的损耗; 参量δ₁ = (ω₀ – ω_p)t_R/L为抽运光频率ω_p和微腔谐振频率ω₀之间的失谐参量, L为微腔的周长, t_R = L/c为基频光在腔内循环一周的时间; $k_1''$和$k_2''$分别表示基频光和倍频光的二阶色散, 它们的表达式为

$k_1'' = {\left. {{{\rm{d}}^2}k/{\rm{d}}\omega } \right|_{\omega = {\omega _{\rm{p}}}}},$

$k_2'' = {\left. {{{\rm{d}}^2}k/{\rm{d}}\omega } \right|_{\omega = 2{\omega _{\rm{p}}}}},$

$ \Delta k $和$ \Delta k' $分别为相位失配和群速度失配, 它们通过以下公式定义:

$\Delta k = {\left. {2k} \right|_{\omega = {\omega _{\rm{p}}}}} - {\left. k \right|_{\omega = 2{\omega _{\rm{p}}}}},$

$\Delta {k{'}} = {\left. {\frac{{{\rm{d}}k}}{{{\rm{d}}\omega }}} \right|_{\omega = {\omega _{\rm{p}}}}} - {\left. {\frac{{{\rm{d}}k}}{{{\rm{d}}\omega }}} \right|_{\omega = 2{\omega _{\rm{p}}}}},$

γ₁和γ₂分别为自相位调制的非线性系数; γ₁₂和γ₂₁是交叉相位调制的非线性系数; κ为二阶耦合系数; η₁为抽运光和腔内光场的耦合系数; 抽运光为连续光, 强度用E_in表示. 此外, 对于光学微腔还有一个重要参数, 即微腔的自由光谱范围(free spectral range, FSR), FSR = 1/t_R, 它也表示了微腔光频梳中梳齿之间的频率间隔. (1)式和(2)式中各色散、非线性、耦合等参数是由光学微腔的材料和结构决定的.
通过求解(1)式和(2)式, 可以得到微腔内基频和倍频光场的分布情况. 为了能够清楚腔内光场分布随时间的演化过程, 采用分布傅里叶法求解(1)式和(2)式^[19].

2

-->

3.1.光学微腔中二次谐波的产生

以SiN为材料的光学微腔为正色散. SiN材料的各项参数如下:

$\begin{split}& {\alpha _1}=4.94 \;\;{{\rm{m}}^{ - 1}},\\&k_1'' = 186.9\;\;{\rm{p}}{{\rm{s}}^{\rm{2}}} \cdot {\rm{k}}{{\rm{m}}^{ - {\rm{1}}}},\\&{\gamma _1} = 0.9\;\;{{\rm{m}}^{ - {\rm{1}}}} \cdot {{\rm{W}}^{ - {\rm{1}}}},\\&{\eta _1} = 3.07\;\;{{\rm{m}}^{ - {\rm{1}}}},\\&{\alpha _2}=9.87\;\;{{\rm{m}}^{ - {\rm{1}}}},\\&k_2'' = - 151.6\;\;{\rm{p}}{{\rm{s}}^{\rm{2}}} \cdot {\rm{k}}{{\rm{m}}^{ - {\rm{1}}}},\\&{\gamma _2} = 2.6\;\;{{\rm{m}}^{ - {\rm{1}}}} \cdot {{\rm{W}}^{ - {\rm{1}}}},\\ &\Delta k = - 854.66\;{{\rm{m}}^{ - {\rm{1}}}},\end{split}$

$\begin{split}&\Delta {k^{'}} = 6.17 \times {10^{ - 10}}\;{\rm{s}} \cdot {{\rm{m}}^{ - {\rm{1}}}},\\&{\gamma _{12}} = 0.72\;\;{{\rm{m}}^{ - {\rm{1}}}} \cdot {{\rm{W}}^{ - {\rm{1}}}},\\&{\gamma _{21}} = 1.44\;\;{{\rm{m}}^{ - {\rm{1}}}} \cdot {{\rm{W}}^{ - {\rm{1}}}},\\&\kappa = 1.3\;{{\rm{m}}^{ - {\rm{1}}}} \cdot {{\rm{W}}^{ - {\rm{1/2}}}}.\end{split}$

假设微腔直径为100 μm, 对应的FSR = 231.3 GHz. 微腔采用波长为1550 nm的连续光抽运. 微腔内的初始光场是由调制不稳定性产生的, 根据文献[21]可以假设腔内初始的基频光场E₁₀为高斯脉冲, 如${E_{10}} = {E_0}\exp \left[ { - {{\left( {\tau /{\tau _0}} \right)}^2}} \right]$. 由于初始光场源自于腔内的调制不稳定性, 因此初始光场的强度很弱, 因此假设初始光场的振幅E₀ = 0.1 W^1/2, 脉冲宽度τ₀ = 0.4 ps.
首先, 忽略抽运频率和微腔本征频率之间的频率失谐, 即失谐参量δ₁ = 0, 连续抽运光的强度E_in = 1 W^1/2. 在非线性效应的作用下, 腔内有二次谐波产生, 二次谐波随着光在腔内循环次数产生的光场分布如图2(a)所示, 可见初始产生的倍频光场较弱, 随着循环次数的增加, 腔内的倍频光场不断变强. 图2(b)和(c)表示腔内基频光和倍频光功率随循环次数不断增加, 并最终稳定于某一值, 此时腔内光场相对稳定, 稳定后基频光和倍频光光场分布如图2(d)和(e)所示, 基频光在腔内形成了一个较宽的脉冲, 且脉冲顶端较为平坦而倍频光场则类似正弦信号, 其功率和基频光相比相对较弱. 图2(f)和(g)是对应的光谱, 基频光和倍频光都在微腔内形成了梳状的光谱, 但倍频光谱宽要小于基频光的谱宽.
图 2 SiN光学微腔中二次谐波的产生 (δ₁ = 0, E_in = 1 W^1/2)　(a) 倍频光场在腔内的演化过程; (b) 基频光功率随光在腔内循环次数的变化曲线; (c) 倍频光功率随光在腔内循环次数的变化曲线; (d)基频场的稳定分布; (e)倍频光场的稳定分布; (f)基频光的光谱; (g) 基频光的光谱
Figure2. Second harmonic waves generates inside the SiN microresonator (δ₁ = 0, E_in = 1 W^1/2): (a) Evolution of the second harmonic waves; (b) curves of the fundamental frequency waves power and (c) the second frequency waves power vary with the round trip number; (d) stationary distribution of the fundamental frequency waves light field and (e) the second frequency waves light field; (f) spectra of the fundamental frequency waves and (g) the second frequency waves.

以上是失谐参数δ₁ = 0时腔内光场的演化情况. 下面讨论失谐参数δ₁不为0的情况. 假设δ₁ = 0.1, 抽运光强E_in = 1 W^1/2. 通过求解(1)式和(2)式, 得到微腔内基频光和倍频光功率变化如图3(a)和(b)所示. 对比图2(b)和(c)可以发现, 当微腔的抽运频率和本征频率发生失谐时, 腔内的基频光和倍频光功率在光循环过程中发生振荡, 且经过多次振荡后腔内最终稳定的光功率和图2(b)和(c)中的光功率相比, 强度明显减弱, 说明频率失谐会对腔内的光功率造成明显的损耗. 当腔内光功率稳定后, 腔内基频光和倍频光光场分布随循环次数的演化如图3(c)和(d)所示, 其中任意时刻光场的分布如图3(e)和(f)所示. 可见, 基频光在腔内最终形成了稳定的暗孤子, 而倍频光在腔内的光场仍然近似正弦信号, 但正弦信号的相位随着循环次数而变化.
图 3 发生频率失谐后, 微腔内光场变化情况 (δ₁ = 0.1, E_in = 1 W^1/2)　(a) 基频光功率和(b)倍频光功率随光在腔内循环次数的变化曲线; 光场稳定后, (c)基频光场和(d)倍频光场随时间的演化; (e) 基频光场和(f)倍频广场的稳定分布
Figure3. Light field evolution in the microresonator with the frequency detuning (δ₁ = 0.1 and E_in = 1 W^1/2): (a) Curves of the fundamental frequency waves power and (b) the second frequency waves power vary with the round trip number; evolution of (c) the fundamental frequency waves (d) the second frequency waves after the light fields are stable; stationary distribution of (e) the fundamental frequency waves light field and (f) the second frequency waves light field.

通过以上分析可知, 微腔的频率失谐参数δ₁会引起腔内基频光和倍频光功率的损耗, 并导致腔内光场分布发生变化. 因此, 接下来将分析失谐参数δ₁对微腔内二次谐波产生的影响.
2 -->

3.2.失谐参量对微腔内二次谐波的影响

假设抽运光场E_in = 1 W^1/2不变, 依次增加失谐参数δ₁, 得到微腔内基频光和倍频光功率变化曲线如图4所示. 图4(a)和(b)是δ₁取不同值时, 基频光在腔内循环过程中的功率变化曲线, 随着失谐参数δ₁的不断增加, 基频光的功率在趋于稳定的过程中振荡越来越明显, 当δ₁大于0.2后(图4(b)), 功率的振荡变得非常剧烈. 因此, 抽运光频率和微腔本征频率之间的失谐会导致腔内光场分布的不稳定. 图4(c)和(d)是失谐参数δ₁对腔内倍频光的影响. 和基频光的变化趋势一致, 倍频光功率在腔内经历先增大再减小的变化过程, 随着δ₁的增加, 曲线下降沿的抖动也越来越剧烈, 腔内最终稳定存在的倍频光功率总体呈下降趋势. 可以看到, δ₁ = 1时, 微腔内基频光和倍频光的功率变化曲线都出现了周期性的抖动, 腔内光场趋于稳定后, 光功率仍然保持周期性振荡. 图5(a)和(b)给出了腔内基频和倍频光场分布的演化, 光场分布随腔内光场循环的次数进行周期性的变化. 在光场变化周期中, 每隔100次循环选取一个时间点, 画出这些时间点腔内的光场分布的形状, 结果如图5(c)和(d)所示. 由图5(c)可见, 在某些时刻基频光在腔内可形成单脉冲形式的分布(图5(c)②③), 但也仍有脉冲分裂的情况存在(图5(c)④⑤). 图5(d)为倍频光在各个时刻的光场分布情况, 可以看出, 当失谐参量δ₁ = 1时倍频光在腔内仍然近似正弦分布, 正弦波的相位随时间不断变化.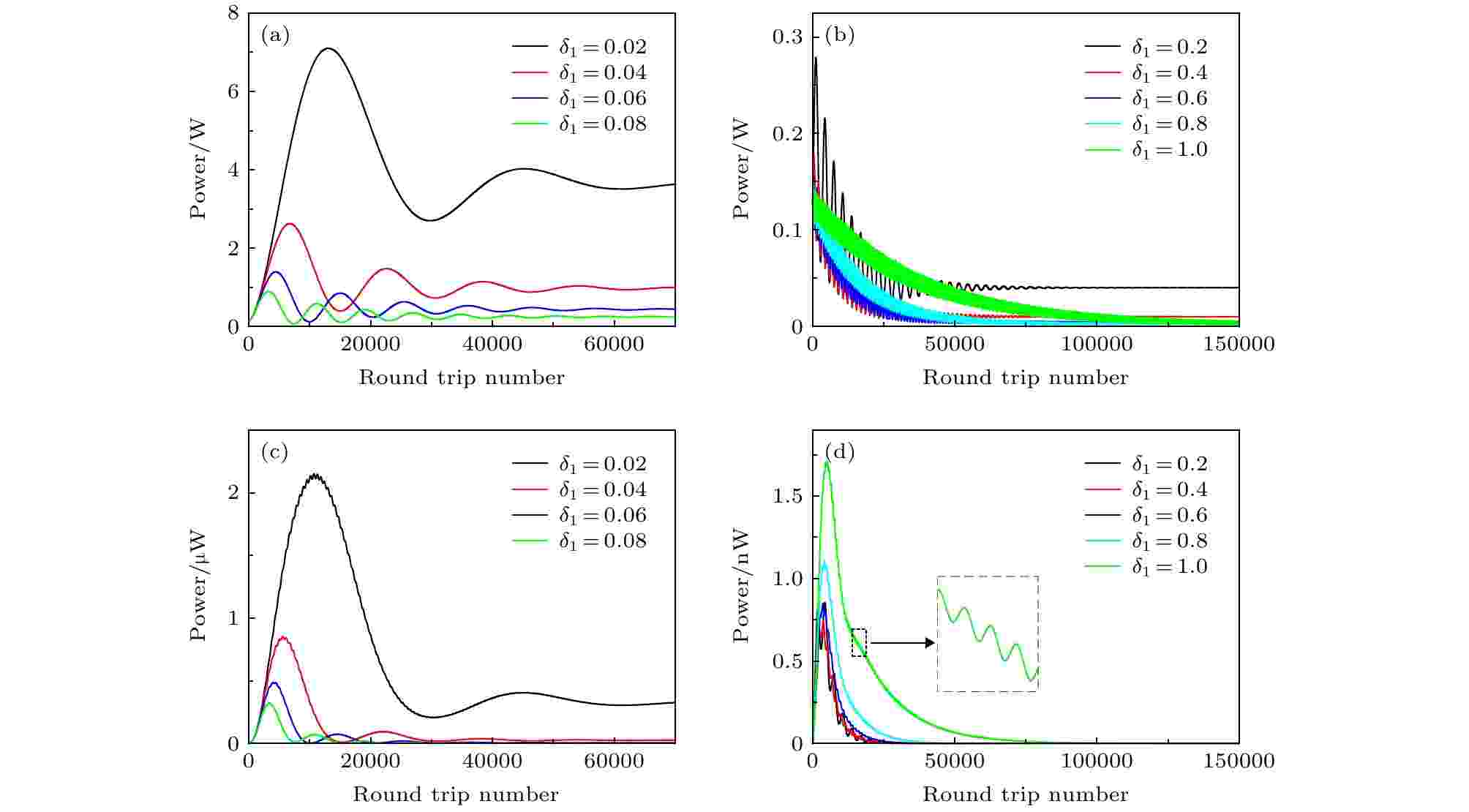
图 4 失谐参量δ₁取不同值时, 微腔内基频光和倍频光功率变化曲线　(a) 0.02 ≤ δ₁ ≤ 0.08时, 基频光功率变化曲线; (b) 0.2 ≤ δ₁ ≤ 0.8时, 基频光功率变化曲线; (c) 0.02 ≤ δ₁ ≤ 0.08时, 倍频光功率变化曲线; (d) 0.2 ≤ δ₁ ≤ 0.8时, 倍频光功率变化曲线
Figure4. Influence of the frequency detuning δ₁ on the power change curves: (a) Curves of the power variation for the fundamental frequency waves, 0.02 ≤ δ₁ ≤ 0.08; (b) curves of the power variation for the fundamental frequency waves, 0.2 ≤ δ₁ ≤ 0.8; (c) curves of the power variation for the second harmonic waves, 0.02 ≤ δ₁ ≤ 0.08; (d) curves of the power variation for the second harmonic waves, 0.2 ≤ δ₁ ≤ 0.8.

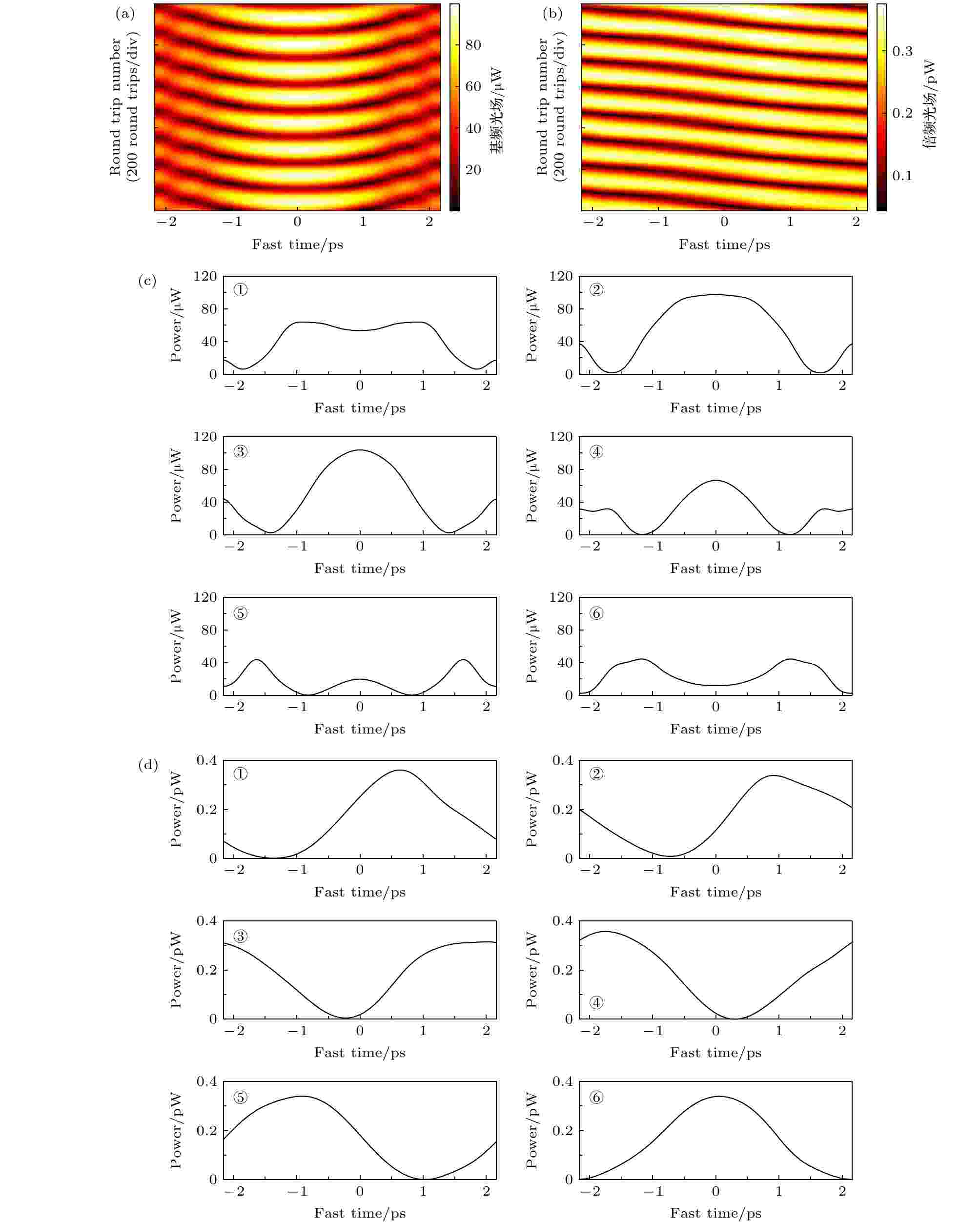图 5 失谐参量δ₁ = 1时, 腔内光场稳定后基频光和倍频光的光场演化　(a) 基频光场的演化; (b) 倍频光场的演化; (c) 基频光光场变化周期内, 光在腔内每循环100次, 绘制其波形; (d) 倍频光光场变化周期内, 光在腔内每循环100次, 绘制其波形
Figure5. Stable evolution of the dual light fields when δ₁ = 1: (a) Evolution of the fundamental frequency waves; (b) evolution of the second harmonic waves; (c) intensity profiles of the fundamental frequency waves at six different moments within a period, the waveforms are plotted every hundred times; (d) intensity profiles of the second harmonic waves at six different moments within a period, the waveforms are plotted every hundred times.

研究过程中, 我们进一步增大了失谐参量δ₁的取值, 结果发现当δ₁的值过大时, 腔内的基频光和倍频光的光场均呈现无规则的变化, 如图6(a)和(b)所示. 经过光场在腔内的长时间演化, 微腔中的光场在时间和空间上都没有形成稳定分布, 此时微腔内处于混沌状态^[22]. 任取某一时刻, 分别绘制基频光和倍频光的光场分布, 如图6(c)和(d)所示, 图6(e)和(f)分别为其对应的光谱. 可见, 混沌模式的光场表现为光功率随时间无规律地变化, 其相对应的光谱也是无规则的, 每一个梳齿对应的功率也是时刻发生变化的. 产生混沌的原因为失谐参量δ₁的值过大, 导致腔内光场的分布不稳定, 在色散以及高阶非线性效应的作用下, 腔内开始随机地出现毛刺以及功率较高的尖峰^[23]. 因此, 在利用光学微腔产生二次谐波光梳的过程中, 要尽量避免失谐参量δ₁过大, 即抽运频率要尽量接近微腔的本征谐振频率, 以免在腔内产生混沌状态.
图 6 失谐参量δ₁取值过大时, 腔内光场的混沌状态　(a) 基频光光场的混沌状态; (b) 倍频光光场的混沌状态; (c) 某一时刻基频光场的分布; (d) 某一时刻倍频光场的分布; (e) 与图(c)中光场对应的基频光光谱; (f) 与图(d)中光场对应的倍频光光谱
Figure6. Chaos inside the microresonator, when the value of detuning parameter is too large: (a) Chaos of the fundamental frequency waves; (b) chaos of the second harmonic waves; (c) intensity profile of the fundamental frequency waves in a moment; (d) intensity profile of the second harmonic waves in a moment; (e) spectrum of the fundamental frequency waves; (f) spectrum of the second harmonic waves.

失谐参量δ₁是抽运光频率和微腔谐振频率之间的失谐, δ₁的值越大, 表示抽运与微腔谐振之间的频率失谐越严重. 这种失谐会导致腔内光场不同的模式之间发生相互耦合, 因而使腔内基频和倍频光场的不稳定. 特别是当δ₁值过大时, 腔内光场的模式发生混乱, 因而产生不规则的光场分布. 根据以上分析, δ₁的值越小, 不仅可以有效避免混沌的现象产生, 同时还可获得较强的倍频光功率以及腔内稳定的光场分布.
2 -->

3.3.抽运功率对微腔内二次谐波的影响

微腔的抽运功率同样也会对腔内基频光和倍频光的功率以及光场分布产生影响. 我们保持失谐参量δ₁ = 0.1不变, 在此基础上, 不断增加抽运强度E_in, 得到微腔内基频光和倍频光功率变化曲线分别如图7(a)和(b)所示. 可明显看出, 随着抽运功率的不断增大, 腔内最终稳定后光功率也会越大, 且抽运功率的大小几乎不会影响腔内形成稳定光场所消耗的时间. 因此, 为了获得更高功率的倍频光, 可以增强抽运光的功率.
图 7 抽运功率对腔内光功率的影响　(a)腔内基频光功率的变化情况; (b)腔内倍频光功率的变化情况
Figure7. Influence of the pump power on the power change curves: (a) Power variation for the fundamental frequency waves; (b) power variation for the second harmonic waves.

然而抽运功率的增大也会导致腔内光场的不稳定. 将抽运光场强度E_in增大到100 W^1/2, 腔内基频光和倍频光功率变化曲线如图8(a)和(b)所示, 可见, 腔内的光功率经过大幅振荡衰减后趋于稳定, 稳定时期的光功率仍然保持周期性的小幅振荡. 当光功率稳定振荡后, 基频光和倍频光的光场演化如图8(c)和(d)所示, 光场分布同样呈周期性变化, 并且可以认为在任意时刻, 基频光和倍频光的光场在腔内是均匀分布的.
图 8 E_in = 100 W^1/2时, 微腔内光场的演化　(a) 基频光功率的变化曲线; (b) 倍频光功率的变化曲线; (c) 光场稳定后, 腔内基频光光场的周期性演化; (d) 光场稳定后, 腔内倍频光光场的周期性演化
Figure8. Evolution of the light field in the microresonator at E_in = 100 W^1/2: (a) Curve of power variation for the fundamental frequency waves; (b) curve of power variation for the second harmonic waves; (c) periodic evolution of the fundamental frequency waves; (d) periodic evolution of the second harmonic waves.

在此基础上进一步增大抽运光强度, 抽运光场E_in分别为800, 1000和1200 W^1/2时, 基频光和倍频光功率变化曲线如图9所示. 当E_in = 800 W^1/2时, 基频光的功率在腔内经过功率振荡后, 最终大约稳定于20 kW, 而倍频光功率在循环过程中增加, 达到峰值后迅速衰减, 然后趋向于稳定, 稳定部分的光功率也同样保持周期性振荡. 这是由于抽运光功率过高, 导致腔内二阶非线性效应明显, 较多的基频光转化为倍频光, 因而腔内累积的倍频光功率越来越大, 因此光在腔内循环过程中, 倍频光的功率有明显的增长. 当倍频光功率达到一定值时, 由频率失谐、色散、损耗引起的倍频光功率降低, 超过了由非线性效应产生的倍频光强度, 因而倍频光在功率增大到一定程度后会出现功率迅速衰减的现象, 所以在图9(b)中倍频光的功率会出现一个脉冲形式的变化曲线. 由于倍频光是由基频光通过非线性效应产生的, 因而在图9(a)中对应了一个向下的脉冲形状. 最终腔内形成的稳定光场, 基频光和倍频光功率都会在一定范围内等幅振荡 (如图9(b)中放大部分的曲线所示). 当E_in = 1000 W^1/2和E_in = 1200 W^1/2时, 腔内功率变化曲线如图9(c)—(f)所示. 抽运功率增加, 在图9(d)和(f)中, 倍频光功率变化曲线中出现了两个脉冲, 并且抽运光功率越强, 曲线中第二个脉冲的强度更大, 因此对应的基频光功率振荡也更加明显. 从LLE的(1)式和(2)式可以看出, 非线性效应的强弱和腔内光功率的大小是相关的, 腔内光功率越大, 由自相位调制和交叉相位调制引起的倍频效率也越高. 因此, 当抽运功率较弱时, 腔内基频和倍频光强也处于相对较弱的水平, 增益、损耗、色散、非线性之间相互作用可以达到相对平衡的状态, 最终基频和倍频光场均会趋于稳定. 而当抽运功率较强时, 腔内增益和非线性均表现为较强的作用, 此时腔内光场难以达到稳定状态. 因此, 光学微腔抽运功率过大, 会导致腔内光场处于不稳定的状态. 为保证腔内光场和光功率的稳定, 需要避免抽运功率过强的情况.
图 9 基频光和倍频光的功率变化曲线　E_in = 800 W^1/2时(a)基频光和(b)倍频光的功率变化; E_in = 1000 W^1/2时(c)基频光和(d) 倍频光的功率变化; E_in = 1200 W^1/2时(e)基频光和(f)倍频光的功率变化
Figure9. Curves of the power variation for the fundamental frequency waves and the second harmonic waves: Power variation for (a) the fundamental frequency waves and (b) the second harmonic waves at E_in = 800 W^1/2; power variation for (c) the fundamental frequency waves and (d) the second harmonic waves at E_in = 1000 W^1/2; power variation for (e) the fundamental frequency waves and (f) the second harmonic waves at E_in = 1200 W^1/2.

2 -->

3.4.微腔大小对腔内光场的影响

以上都是在微腔FSR = 231.3 GHz (对应的微腔半径为100 μm)的条件下进行的讨论. 但是研究中发现, 微腔半径的大小同样会对腔内光场产生影响. 设微腔FSR = 300 GHz, δ₁ = 0.1, E_in = 100 W^1/2, 得到腔内基频光和倍频光功率的随时间变换, 最终都收敛于某一值, 如图10(a), (b)所示, 即在围墙内可以得到稳定的基频、倍频的光场分布. 当光功率稳定后, 光场演化情况如图10(c), (d)所示, 由于微腔半径增大, 在腔内基频光与倍频光之间非线性作用的距离变长, 在较强的非线性作用下, 基频光和倍频光最终在腔内演化出16个脉冲, 在对应的光谱图中(图10(e), (f)), 每隔16 FSR, 就会有一个功率较大的梳齿, 此时微腔工作于“图灵环”模式(turing patterns)^[17].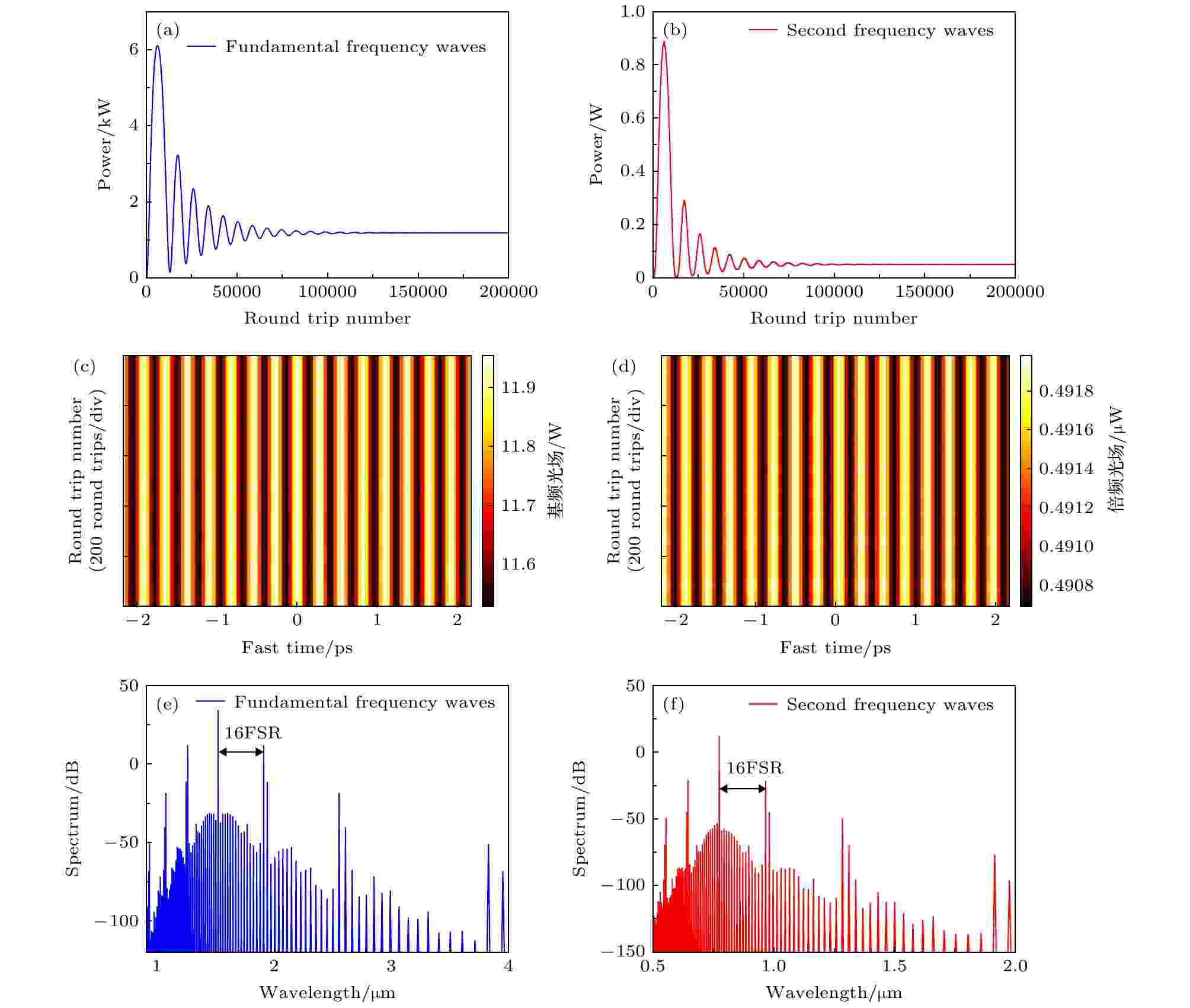
图 10 微腔FSR = 300 GHz时, 微腔内出现“图灵环”(E_in = 100 W^1/2, δ₁ = 0.1)　(a)基频光功率变化曲线; (b)倍频光功率变化曲线; (c) 腔内光场稳定后, 基频光光场随时间的演化; (d) 腔内光场稳定后, 倍频光光场随时间的演化; (e) 腔内光场稳定后, 基频光的光谱; (f) 腔内光场稳定后, 倍频光的光谱
Figure10. Turning patterns in the microresonator, when FSR = 300 GHz (E_in = 100 W^1/2, δ₁ = 0.1): (a) Curves of the power variation for the fundamental frequency waves; (b) curves of the power variation for the second harmonic waves; (c) evolution of the fundamental frequency waves; (d) evolution of the second harmonic waves; (e)spectra of the fundamental harmonic waves; (f) spectra of the second harmonic waves.

研究过程中发现, 可工作于“图灵环”模式的微腔FSR的取值范围较小. 将微腔的FSR减小为298 GHz, 腔内最终稳定的基频光场分布如图11(a)所示, 基频光的光场在腔内仍然为多脉冲的形式, 但脉冲的强度受到了调制, 这种调制在倍频光的光场分布中更为明显 (如图11(b)所示), 多脉冲的光场受到正弦信号的调制. 由于光场中包含了多个频率成分, 因此其光谱图中噪声较多, 在主梳齿附近会出现很多的毛刺. 进一步减小微腔的FSR, 当减小为295 GHz时, “图灵环”工作模式消失, 基频光和倍频光的光场均演化为正弦分布, 且正弦信号的相位随时间变化, 光谱也转化为很窄的梳状光谱(如图12所示).
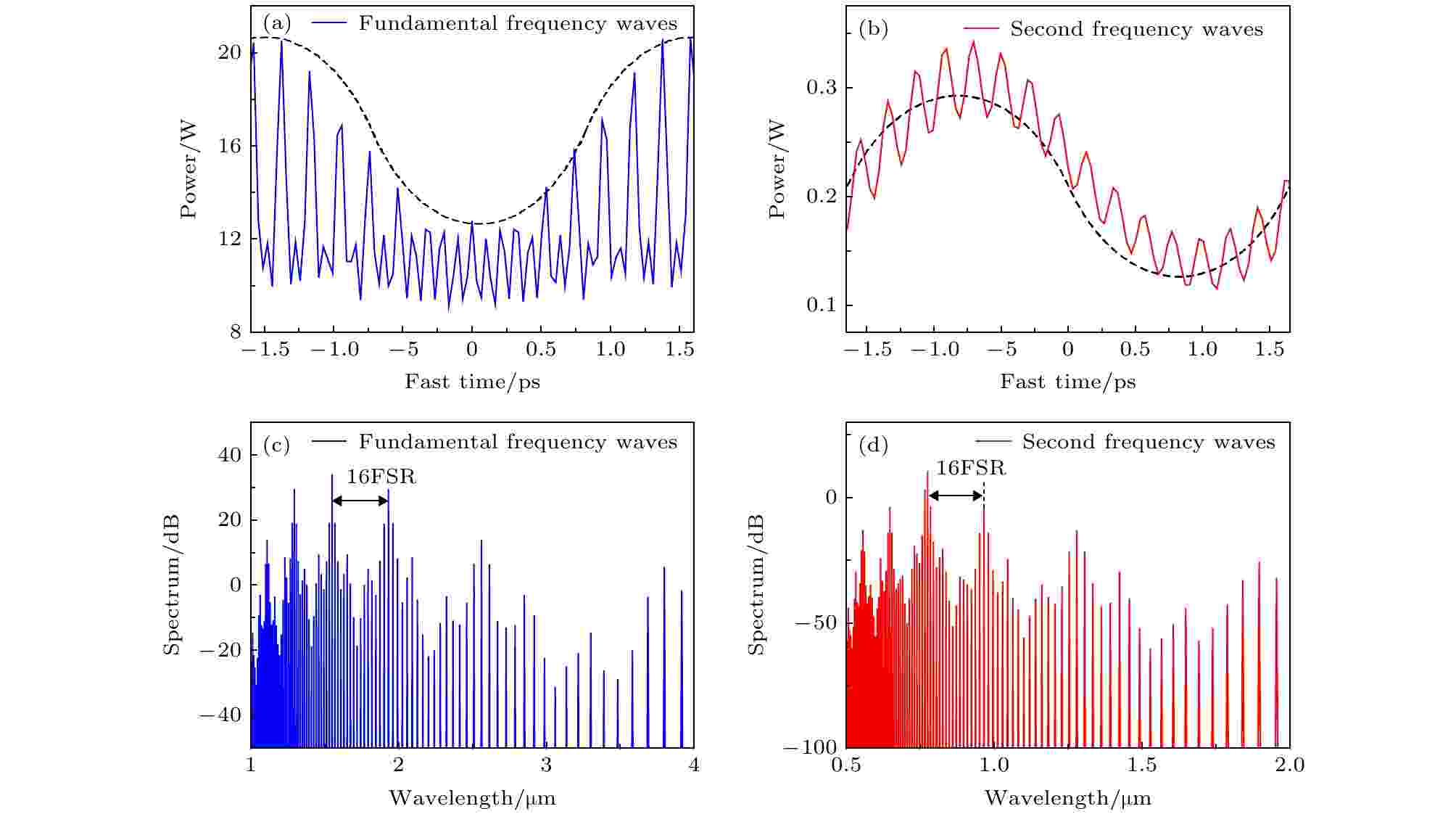图 11 微腔FSR = 298 GHz时, 稳定后的光场分布及光谱　(a)基频光的光场分布; (b) 倍频光的光场分布; (c) 基频光光谱; (d) 倍频光光谱
Figure11. Stable intensity profile and spectra of the fundamental frequency waves for FSR = 298 GHz: (a) Intensity profile of the fundamental frequency waves; (c) spectrum of the fundamental frequency waves; (b) intensity profile of second harmonic waves; (d) spectrum of second harmonic waves.

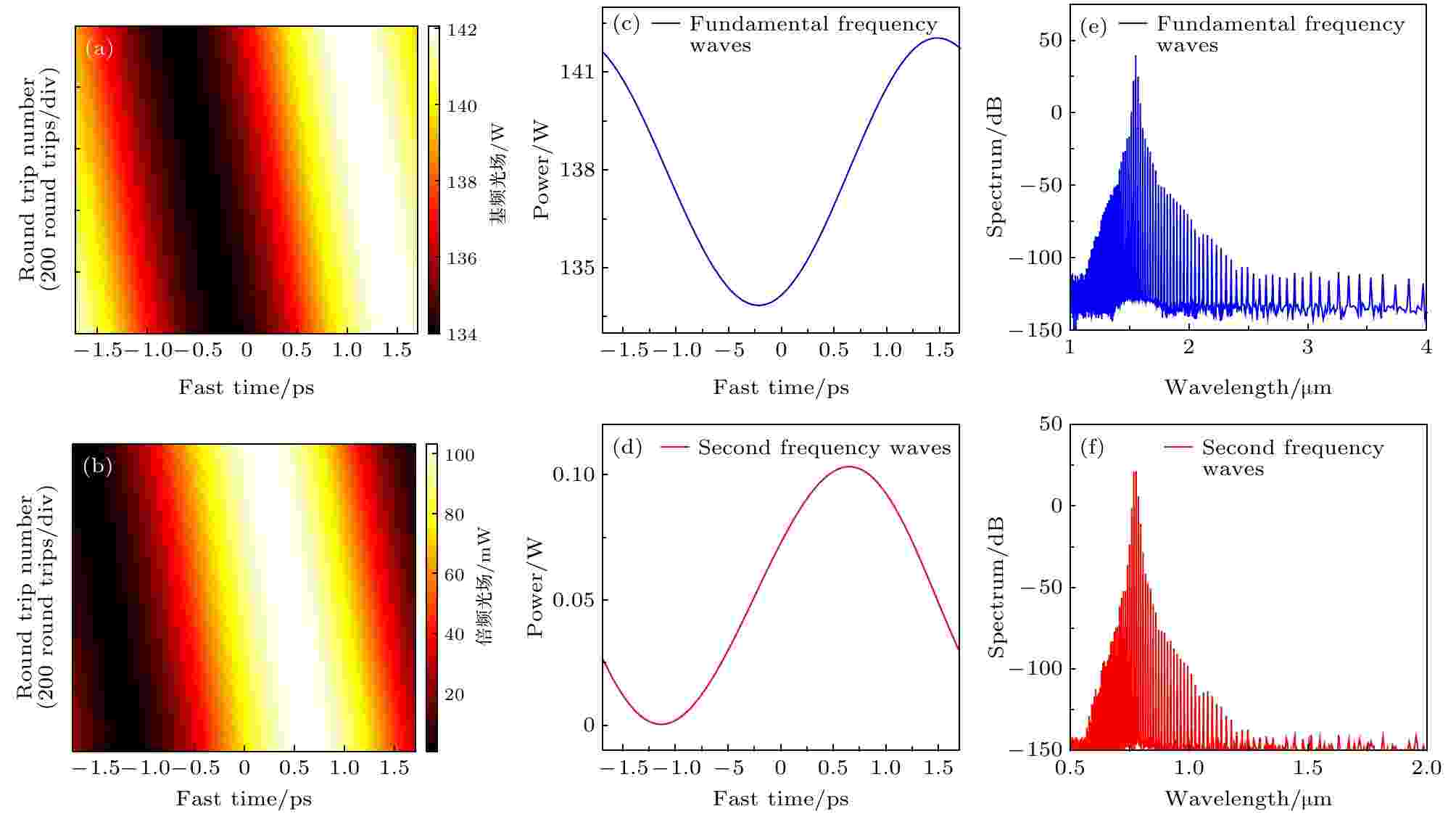图 12 微腔FSR = 295 GHz时, 稳定后的基频光和倍频光光场分布及光谱　(a) 基频光光场随时间的演化; (b) 倍频光光场随时间的演化; (c) 基频光场的瞬时分布; (d) 倍频光场的瞬时分布; (e) 基频光场的光谱; (f) 倍频光场的光谱
Figure12. Stable intensity profile and spectra of the fundamental frequency waves for FSR = 295 GH: (a) Evolution of the fundamental frequency waves; (b) evolution of the second frequency waves; (c) intensity profile of the fundamental frequency waves; (d) spectrum of the fundamental frequency waves; (e) intensity profile of the second harmonic waves; (f) spectrum of the second harmonic waves.

在考虑了光学微腔中二阶和三阶非线性效应的基础上, 引入了包含二次谐波项的LLE, 分析了SiN微腔中二次谐波的产生, 并讨论了各参数对腔内基频和倍频光场的影响.
研究结果表明, 当抽运频率和微腔谐振频率之间没有发生频率失谐, 即失谐参量δ₁ = 0.1时, 腔内的基频光和倍频光功率不断增强, 并最终达到稳定, 稳定后的基频光场为平顶脉冲的形式, 而倍频光场呈正弦分布. 当抽运频率和谐振频率之间发生频率失谐后, 腔内基频和倍频光功率在演化过程中出现振荡, 但最终稳定于某一值. 稳定后的光场也发生变化, 基频光场变为暗孤子的形式, 倍频光场仍然为正弦分布. 失谐参量δ₁增加, 将导致腔内基频和倍频光功率在演化过程中振荡变强, 且最终稳定的光功率变弱, 稳定后的光场分布为周期性变化. δ₁进一步增加会使得微腔光场处于混沌状态. 因此, 为保证微腔中二次谐波的产生以及腔内光场的稳定, 实验中应尽量减小抽运频率与微腔振荡频率之间的频率失谐.
当微腔抽运功率较小时, 增大抽运功率可有效增强腔内基频和倍频光场的强度; 而当抽运光强较强时, 会导致腔内色散以及非线性效应过强, 最终稳定的光场仍然呈周期性变化, 且抽运光功率越强, 光功率的演化曲线振荡越强. 因此, 为保证腔内光场和光功率的稳定, 需要避免抽运功率过强的情况.
光学微腔的尺寸同样会对腔内光场分布产生影响. 当选取微腔FSR = 300 GHz, 失谐参量δ₁ = 0.1, 抽运强度E_in = 100 W^1/2, 微腔工作于“图灵环”状态, 腔内基频和倍频光场均演化出稳定的16个脉冲, 相对应光谱每隔16 FSR, 就会有一个功率较大的梳齿. 当FSR减小后, 腔内多脉冲形式的光场受到了正弦信号的调制, 光谱中也出现较多的毛刺. 因此, 选择合适的微腔尺寸, 可以有效选择微腔的工作模式, 得到需要的光谱. 该理论分析结果对于实验中微腔参数和抽运参数的选取有重要意义. 此外, 本文中采用的微腔光场演化模型是二维模型, 忽略了光场在垂直方向上(y方向)的分布. 为了更精确地分析腔光场的分布和演化情况, 需要考虑光场在垂直方向分布情况时, 因而要引入三维的光场演化模型, 此时抽运光场是关于y的表达式, 腔内基频和倍频光场也和y有关. 关于微腔内基频和倍频光场三维模型的建立和分析, 将在后续的工作中进一步展开.