摘要:本文使用5—27 keV能量范围的电子轰击纯厚Al (Z = 13), Ti (Z = 22), Zr (Z = 40), W (Z = 74)和Au (Z =79)靶, 利用硅漂移探测器(SDD)收集产生的X射线, 给出了K, L壳层特征X射线产额的测量结果, 并将所得实验数据与基于扭曲波玻恩近似理论模型(DWBA)的蒙特卡罗模拟值进行了比较, 两者在小于或约为10%的范围内符合. 根据测得的特征X射线产额进一步得到了相应的内壳层电离截面或特征X射线产生截面. 通过对比电子入射角度为45°和90°的两种情况下解析模型与蒙特卡罗模拟的特征X射线产额, 发现在入射角度为90°时两者符合较好. 同时, 本文还给出了次级电子、轫致辐射光子对特征X射线产额的贡献, 该贡献与入射电子能量关系较弱, 表现出与原子序数较密切的相关性.
关键词: 特征X射线产额/
内壳层电离截面/
特征X射线产生截面/
蒙特卡罗模拟

English Abstract

全文HTML

--> --> -->

电子与原子的碰撞是一个复杂的过程, 通过分析不同能量的电子与物质碰撞后的产物可得到原子内部信息, 这些信息有助于研究电子-原子的相互作用过程和碰撞机理. 在原子与分子物理研究领域, 电子致原子内壳层电离截面、特征X射线产额与轫致辐射的研究一直都是重要研究内容, 在核医学、天体物理学、聚变等离子体物理学等学科中发挥着重要作用^[1], 而精确的电离截面数据对电子探针显微分析及材料科学领域中的电子输运模拟也具有重要意义^[2]. 迄今为止, 对电子致原子内壳层电离截面的测量已有大量的讨论与研究^[3-9]. 从理论研究方面来看, 相对较高能量的电子碰撞原子内壳层电离截面的研究开展得较为广泛^[10], 对于低能电子碰撞原子内壳层电离截面的研究工作, 现已提出了多种计算模型, 如包含库仑和交换修正的平面波玻恩近似理论(plane-wave Born approximation with Coulomb and exchange corrections, PWBA-C-Ex)^[9]、扭曲波玻恩近似理论(distorted-wave Born approximation, DWBA) 等^[11,12]. 由Segui等^[11]和Colgan等^[12]提出的DWBA理论, 即入射电子能量为从电离阈能至10倍电离阈能范围内中性原子的半相对论扭曲波玻恩近似理论, 考虑了入射电子波函数受靶原子作用下的扭曲效应和交换效应, 使其在低能电子入射时, 能更准确地计算其电离截面数据. Bote和Salvat^[13]结合了PWBA与DWBA两种理论, 计算了入射离子能量从电离阈能至1 GeV范围内的原子内壳层电离截面值. 在实验方面, 早期的电离截面测量大多使用薄靶方法完成, Long等^[14]和Liu等^[15]先后编评过一些相关的电离截面数据, 受当时实验条件等因素的限制, 其中靠近阈能附近的数据较少, 且Llovet等^[3]也曾指出, 尤其在L层与M层中, 实验值与理论值仍存在一定的差异. 随后, 许多****又陆续开展了相关的工作. 本小组发展了利用薄膜厚衬底的测量方法, 避免了制备自支撑薄靶的困难, 此方法需要使用蒙特卡罗模拟来修正入射电子在衬底上背散射的贡献, 以及入射电子轰击厚衬底产生的轫致辐射光子带来的影响^[16,17]. Wu等^[18]采用该方法测量了17—40 keV电子轰击Bi元素的Lα与Lβ壳层产生截面数据, 实验结果与DWBA及PWBA-C-Ex模型均符合较好. Fernandez-Varea等^[19]以沉积在碳衬底上的Al, Si和Ti的薄膜及其氧化物为靶, 测量了2.5—25 keV电子轰击的K壳电离截面, 修正氧化层所造成的影响后, 与文献[20,21]中的数据进行了比较, 结果与DWBA模型较为符合. 随后, An等^[22]在2006年的研究中提出了测量电子轰击电离截面的厚靶方法, 该方法不涉及样品厚度的确定, 避免了薄样品制靶以及厚度测量的问题, 并且在U < 5—6时(U = E/E_th, E为入射电子能量, E_th为电离阈能), 即入射电子能量为电离阈能5—6倍之内的情况下, 利用这种厚靶方法测得的电子轰击低、中Z元素原子的内壳电离截面或X射线产生截面的实验精度可以达到与薄靶方法相同的水平. 随后, Wu等^[23]和Zhao等^[24]陆续使用该方法进行了正电子或电子轰击Pb, Bi, Ag的特征X射线产生截面的测量工作. 迄今为止, 对电离截面测量数据大多集中在K壳层, L层和M层由于含有诸多子层, 为准确测量带来了一定的难度, 故相关数据较少, 诸多****间的数据也存在一定的差异^[3].
厚靶的特征X射线产额是评估蒙特卡罗模拟中所用理论模型和数据库准确性的重要依据, 涉及到内壳层电离截面、原子弛豫参数、电子和光子在材料中的传输参数等^[25,26], 特别是近年来在氚的β射线诱发X射线谱(β-ray induced X-ray spectroscopy, BIXS)分析方法中具有重要的应用价值^[27-29], 然而, 目前关于厚靶特征X射线产额的实验研究仍然较少^[24-26]. Bote等^[25]在几至40 keV能量范围内对C, Al, Si, Ti, Cu, Fe, Zr, W, Au, Pt等元素的Kα及Lα壳层厚靶实验特征X射线产额与蒙特卡罗模拟计算值进行了比较, 结果表明在其所关注的能量范围内, 基于DWBA的模拟值与实验值相差约10%, 且随原子序数增大, 基于DWBA的模拟值的准确度要明显更优于PWBA. Yadav等^[30]测量了10—25 keV电子撞击厚Ti靶的Kα壳特征X射线产额^[31]和厚Pt靶M层X射线产额, 结果与蒙特卡罗模拟计算值分别存在17%和12.5%的差异. Li等^[26]给出了5—29 keV电子撞击纯厚W, Mo和Zr靶的K, L, M壳层特征X射线产额测量结果, 与蒙特卡罗模拟值相差约为10%. 在进行实验谱的净峰面积获取时, Li等^[26]采用线性拟合来估计实验本底, 本文将使用蒙特卡罗模拟得到的轫致辐射谱作为扣除本底的依据, 进一步提高实验数据的准确性.
本文选择Al, Ti, Zr, W, Au元素作为研究对象, 虽然以前曾进行过它们中部分特征X射线厚靶产额的测量^[25,26], 但数据并不充分, 本工作在改进实验装置及数据处理方法的基础上, 得到了更高精度的一些新实验数据, 以进一步检验蒙特卡罗模拟及电离截面理论的精度; 同时, 这些元素的特征X射线厚靶产额还具有重要的应用价值, 例如Ti和Zr是重要的储氚材料, W是聚变堆第一壁候选材料^[32], 在氚的BIXS分析中都会利用到它们的特征X射线产额, Al和Au也常在BIXS方法中作为工作介质使用^[28], 因此, 这些元素X射线厚靶产额的精度对氚分析结果的准确度具有重要作用, 明确高精度厚靶产额实验数据和理论计算的差异也有助于评估BIXS方法结果的可靠性. 本文给出了Al的K, Ti的Kα, Kβ, Zr的Kα, Kβ, L及W, Au的Lα, Lβ, Lγ特征X射线的厚靶产额, 并对其中次级电子和轫致辐射光子致电离的贡献进行了研究. 在本文的实验几何下, Al的K, Ti的Kβ以及Au的Lβ, Lγ特征X射线厚靶产额实验数据为首次测量. 随后, 由实验的厚靶产额和蒙特卡罗模拟的初级电子产额得出了相应的K壳层电离截面和L壳层特征X射线产生截面. 针对电子分别在45°和90°入射时的特征X射线厚靶产额, 我们对解析模型结果与蒙特卡罗模拟值进行了对比, 并做了相应的讨论.

2

-->

2.1.实验装置

本实验所采用的装置与Zhao等^[33]和Li等^[34]的基本相同. 法拉第筒及靶置于KYKY公司生产的KYKY-2800B型扫描电子显微镜的真空靶室中, 由扫描电子显微镜中加热的灯丝发出电子束, 通过电场的加速、聚焦并垂直穿过法拉第筒顶部的小孔, 轰击与入射电子束成45°放置的厚靶. 铜制的法拉第筒壁厚5 mm, 能有效地阻止高能轫致辐射光子的穿透. 在法拉第筒的顶孔和侧孔间同时设有–100 V的偏压, 以阻止能量小于100 eV的电子逃逸. 入射电子束被法拉第筒收集后, 经ORTEC束流积分仪, 最后由定标器记录下来. 电子碰撞靶样品产生的特征X射线由水平放置的Amptek硅漂移探测器(silicon-drifted detector, SDD)记录. 通过调节束流强度, 使记录X射线谱的死时间控制在约2%的范围内. 与以前使用的装置相比, 本次实验中在探测器前方安装了由永磁铁构成的电子偏转器, 防止从靶上产生的背散射电子进入X射线探测器, 使得由蒙特卡罗模拟得到的轫致辐射谱与实验测得的本底谱符合, 用于本底的扣除. 实验装置示意图及照片如图1所示, 详细结构图见文献[33]的图1.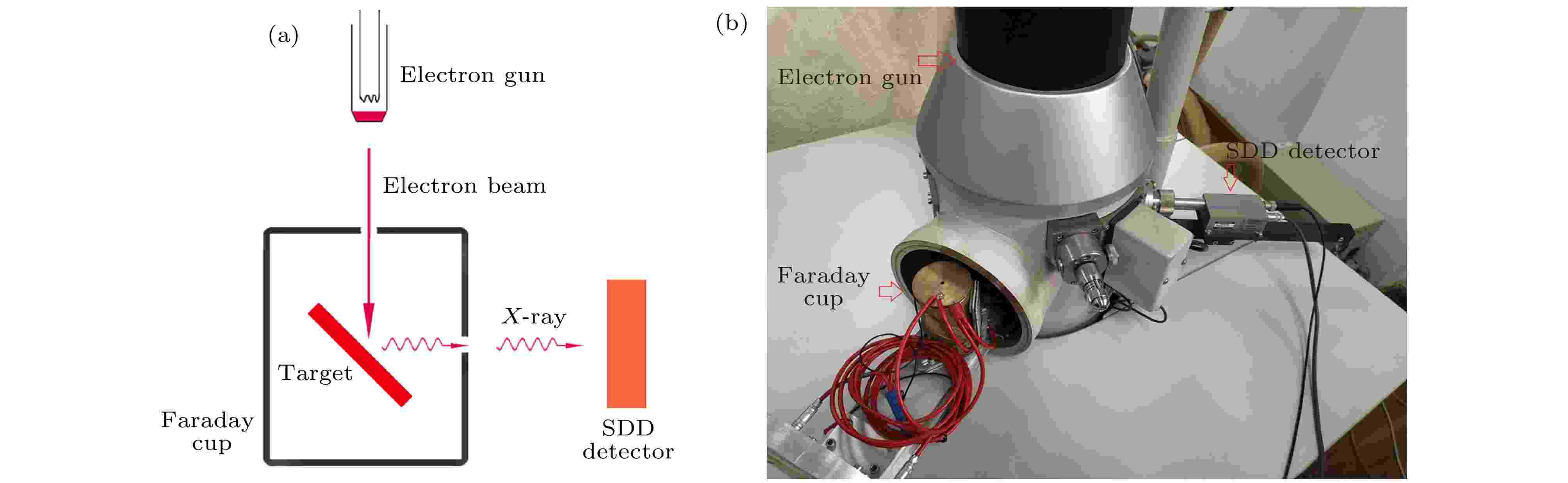
图 1 (a)实验装置示意图; (b)装置照片
Figure1. (a)The schematic of experimental setup; (b) photograph of experimental setup.

SDD探测器为美国Amptek公司生产的XR-100SDD型, 其Si灵敏层厚度为0.5 mm, 窗面积为20 mm²; 探测器的窗口为超薄C2窗, 由40 nm Si₃N₄薄膜、30 nm Al膜以及15 μm Si网格组成, 其开口面积占总面积的78%. 该C2超薄窗口的使用可以减少低能X射线的吸收, 并且可以检测到低至0.183 keV的硼Kα特征X射线.
在本次实验中所用到的厚靶由北京高德威金属科技开发有限责任公司提供, 靶厚为1.5 mm, 表面作抛光处理, 其中, Au靶直径为20 mm, Al, Ti, Zr及W靶直径为31 mm, 纯度均达99.99%.
2 -->

2.2.SDD探测器的效率刻度

探测器的效率刻度在特征X射线的定量测量中起着重要的作用. 本工作的探测器效率刻度采用标准放射源法, 该方法简单易行且精确度较高, 所用标准源为德国标准计量机构(Physikalisch-Technische Bundesanstalt, PTB)提供的⁵⁵Fe, ⁵⁷Co, ¹³⁷Cs和²⁴¹Am点标准源, 其活度不确定度约为1%—3% (k = 2). 低能区(< 3.3 keV)的效率刻度由于缺乏可用的标准放射源^[35], 故通过测量20 keV电子轰击各种厚靶产生的特征X射线谱(即特征峰法)来完成, 使用的厚靶为MgF₂, Si₃N₄, WS₂, CaF₂, Ti和Mn, 纯度大于99.9%, 同实验靶材一样, 也由北京高德威金属科技开发有限责任公司提供. 通过特征X射线实验产额与蒙特卡罗模拟结果的比值得到0.68—6 keV间效率刻度曲线的相对值, 然后再将低能区的相对效率值归一化到使用标准源获得的高能区的绝对效率值, 最终得到低能区的绝对效率值, 该部分工作在文献[34]中已完成.
采用这种方法确定的效率刻度不确定度主要来源于标准源, 在本文所关注的能量范围内约为1.6%, 相对于以前的工作^[33]效率刻度精度得到提高. 图2为SDD探测器效率刻度曲线.

2

-->

3.1.实验产额

本文测量了5—27 keV电子撞击厚Al, Ti, Zr, W, Au靶的特征X射线产额, 其计算公式如下: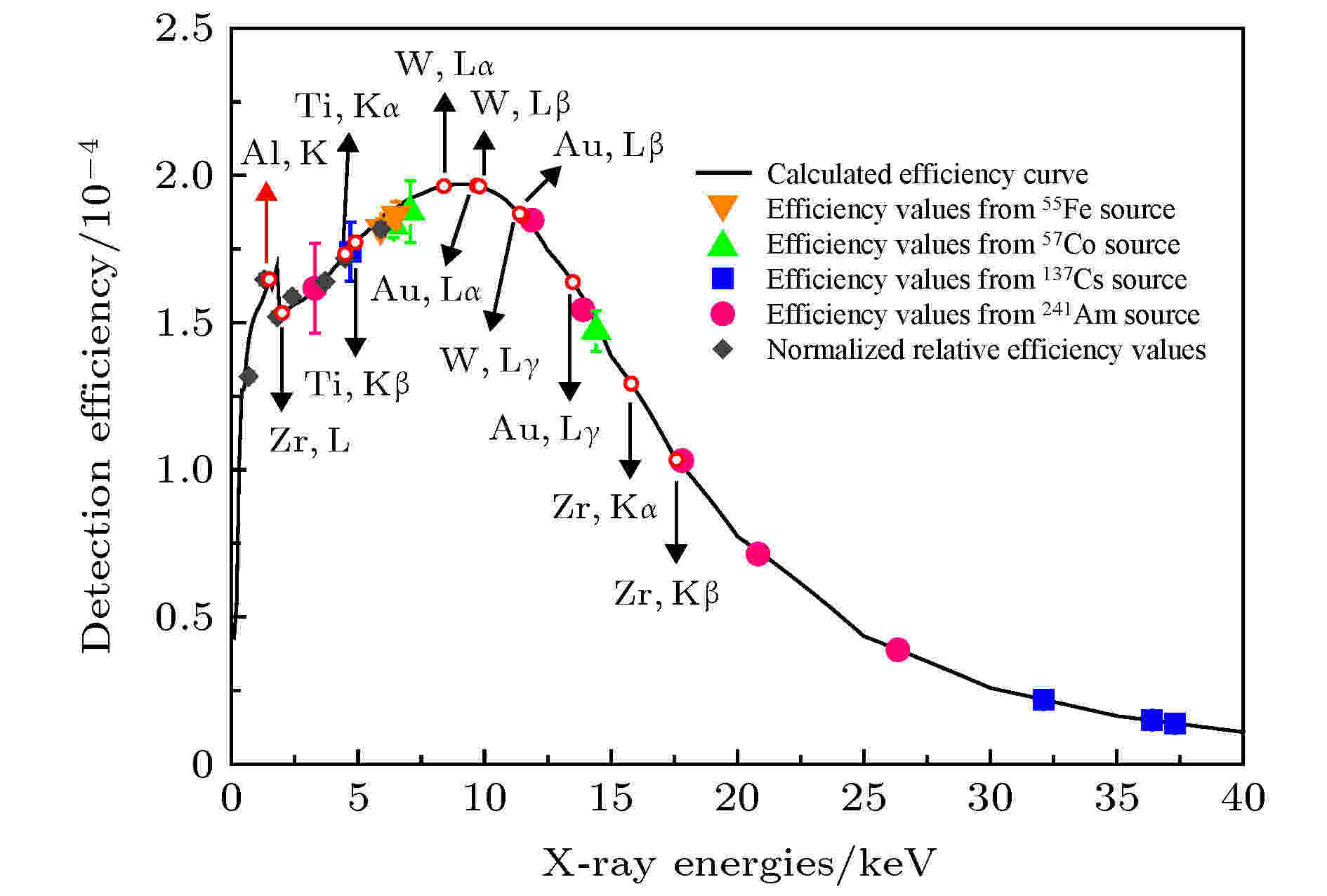

$Y\left({{E_0}} \right) = \frac{{{N_\chi }\left({{E_0}} \right)}}{{{N_{\rm{e}}}\varepsilon \left(E \right)\Delta \varOmega }}, $

其中N_X(E₀)表示入射电子能量为E₀时相应壳层的特征X射线净计数, N_e为总入射电子数, ε(E)表示光子能量为E时的探测器本征效率, ΔΩ为X射线探测器的立体角, 因子ε(E)ΔΩ/4π的值由图2中效率刻度曲线(实线)内插得到. 实验谱的X射线特征峰净计数N_X(E₀)由实验谱特征峰区计数减去蒙特卡罗程序PENELOPE^[2]计算出的轫致辐射谱本底得到, 以W元素为例, 结果如图3所示.
图 2 SDD探测器效率刻度曲线. 空心圆表示Al, Ti, Zr, W和Au的特征X射线位置, 实线表示根据探测器参数计算的效率值
Figure2. The X-ray detection efficiency of the SSD detector. The positions of the characteristic X-ray lines for Al, Ti, Zr, W and Au are indicated by the open circles. The solid line represents the theoretical values calculated based on the detector’s parameters.

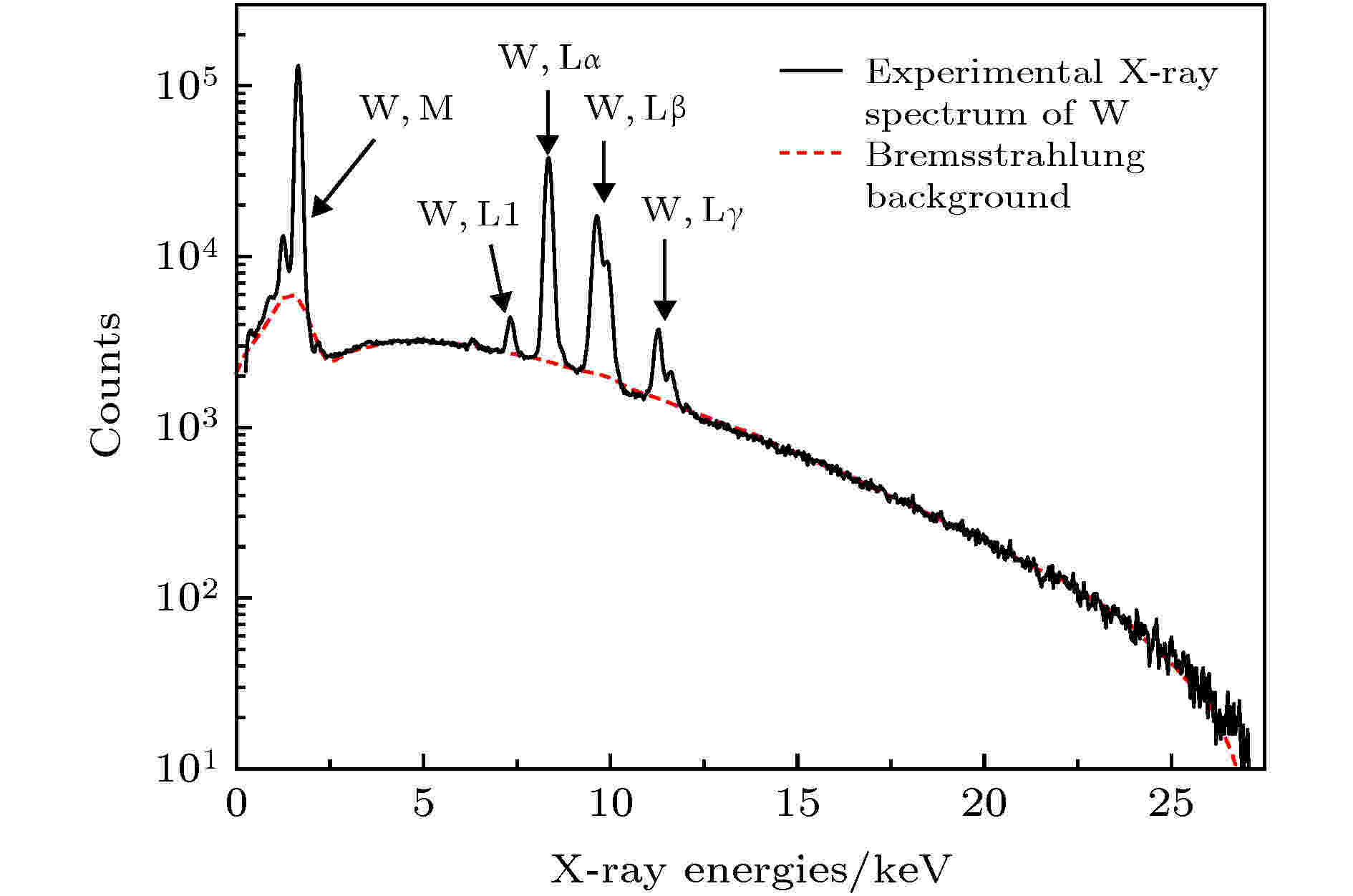图 3 27 keV电子入射厚W靶碰撞产生的实验谱(实线)与PENELOP模拟的轫致辐射本底谱(虚线)
Figure3. The experimental spectrum (solid line) and the bremsstrahlung background spectrum simulated by PENELOPE (dashed line) produced by 27 keV electron impact on thick W target.

2 -->

3.2.实验产额与PENELOPE模拟产额比较

PENELOPE(2008版)是一款目前广泛使用的模拟电子-光子输运的蒙特卡罗软件包, 它能在50 eV—1 GeV的能量范围内使用可靠的数值和解析物理模型相结合的方法模拟电子和光子的输运过程, 描述相应能区内电子和光子与物质的相互作用^[2]. PENELOPE程序对电子在厚靶物质中的输运过程考虑了电子的非弹性散射、弹性散射、内壳层电离及轫致辐射等物理过程. 在本文的能区范围, PENELOPE(2008版)程序采用了更为准确的基于扭曲波玻恩近似理论模型(DWBA)的内壳层电离截面^[11,13]来模拟特征X射线厚靶产额. 在本文的模拟计算中, 建立了与实验相同的几何模型, 如图4所示, 即电子垂直入射, 待测靶与水平成45°, 探测器水平放置. 在实验中, 探测器对靶的张角由探测器探头半径与靶中心距离决定, 为提高蒙特卡罗模拟的计算效率, 张角的半角取为30°, 计算表明这样设置不影响模拟计算结果^[33].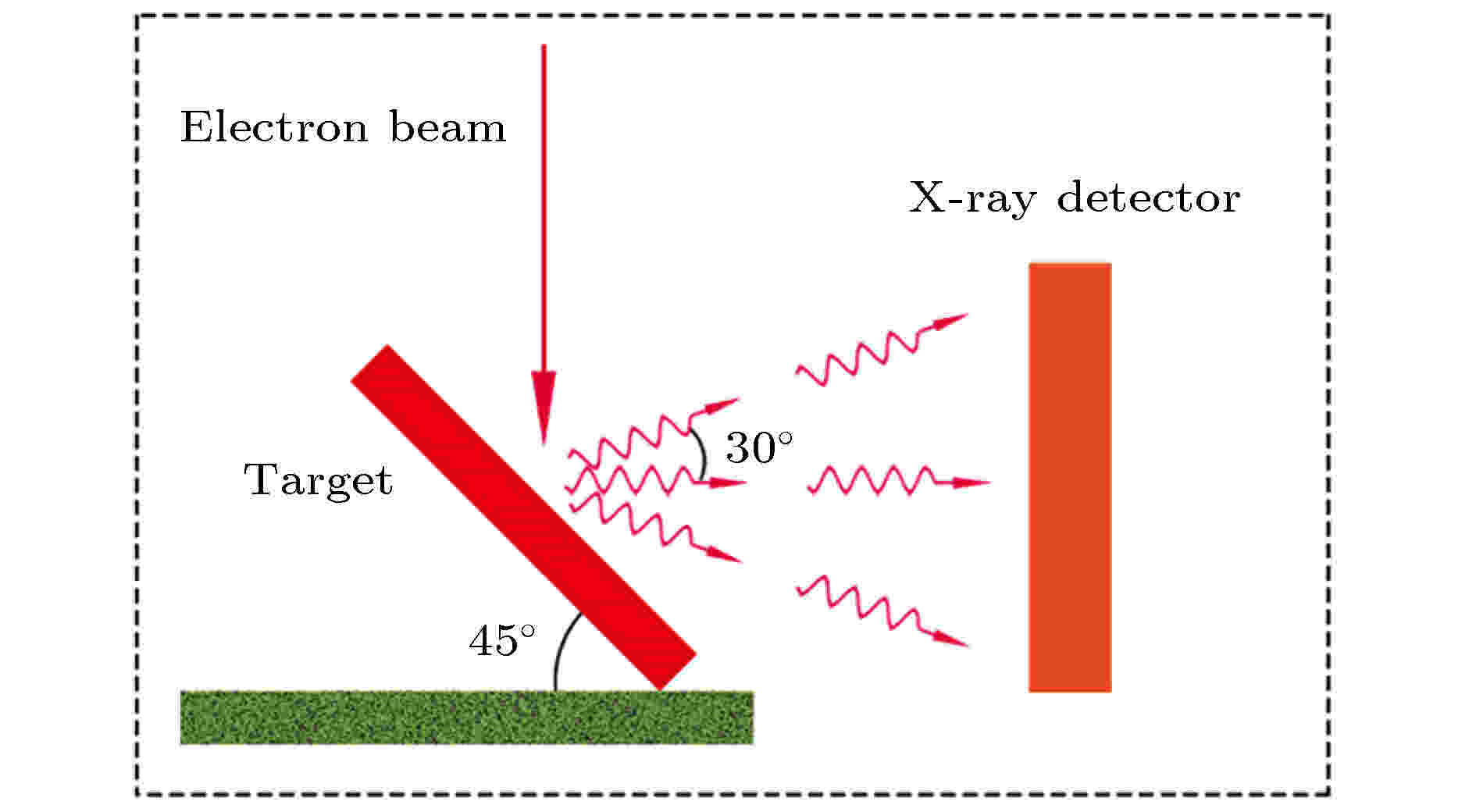
图 4 PENELLOPE模拟几何模型示意图
Figure4. The geometry used in the PENELOPE simulations.

在实验中, 由于受到筒内壁及靶的散射作用, 入射电子可能会经由法拉第筒的顶孔或侧孔逃逸, 导致实际记录电荷数损失. 因此本工作使用PENELOPE程序对法拉第筒的电子逃逸率进行了计算, 并以此来修正实验中的入射电荷数. 计算结果表明电子逃逸率随靶原子序数的增大而增大, 本文中涉及到的Al, Ti, Zr, W, Au元素在入射电子能量5—27 keV时对应的逃逸率分别约为2.2%—2.4%, 2.5%—2.7%, 2.9%—3.2%, 3.2%—3.6%和3.3%—3.7%, 修正后得到的实验产额与PENELOPE模拟产额结果如图5所示.




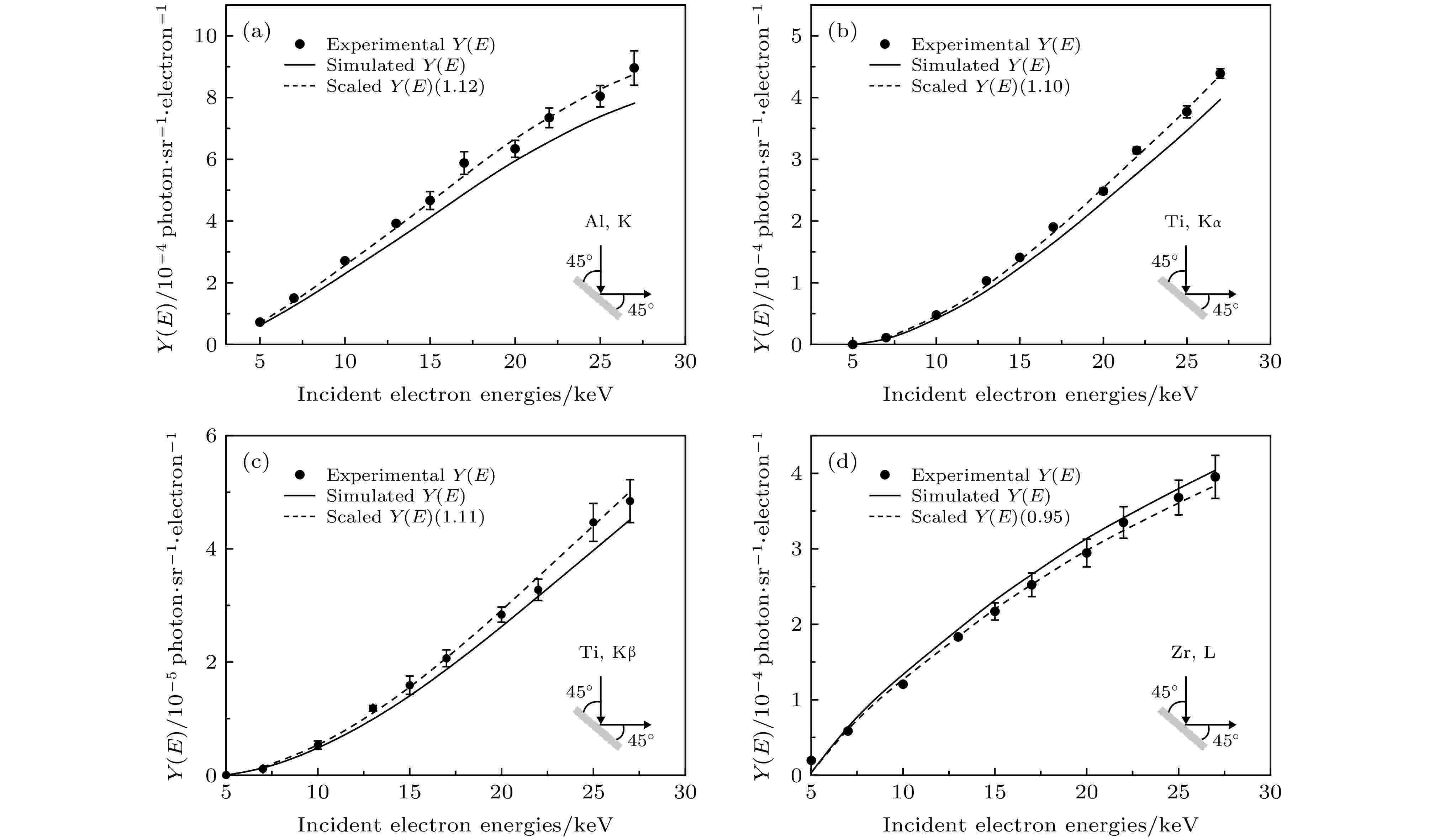
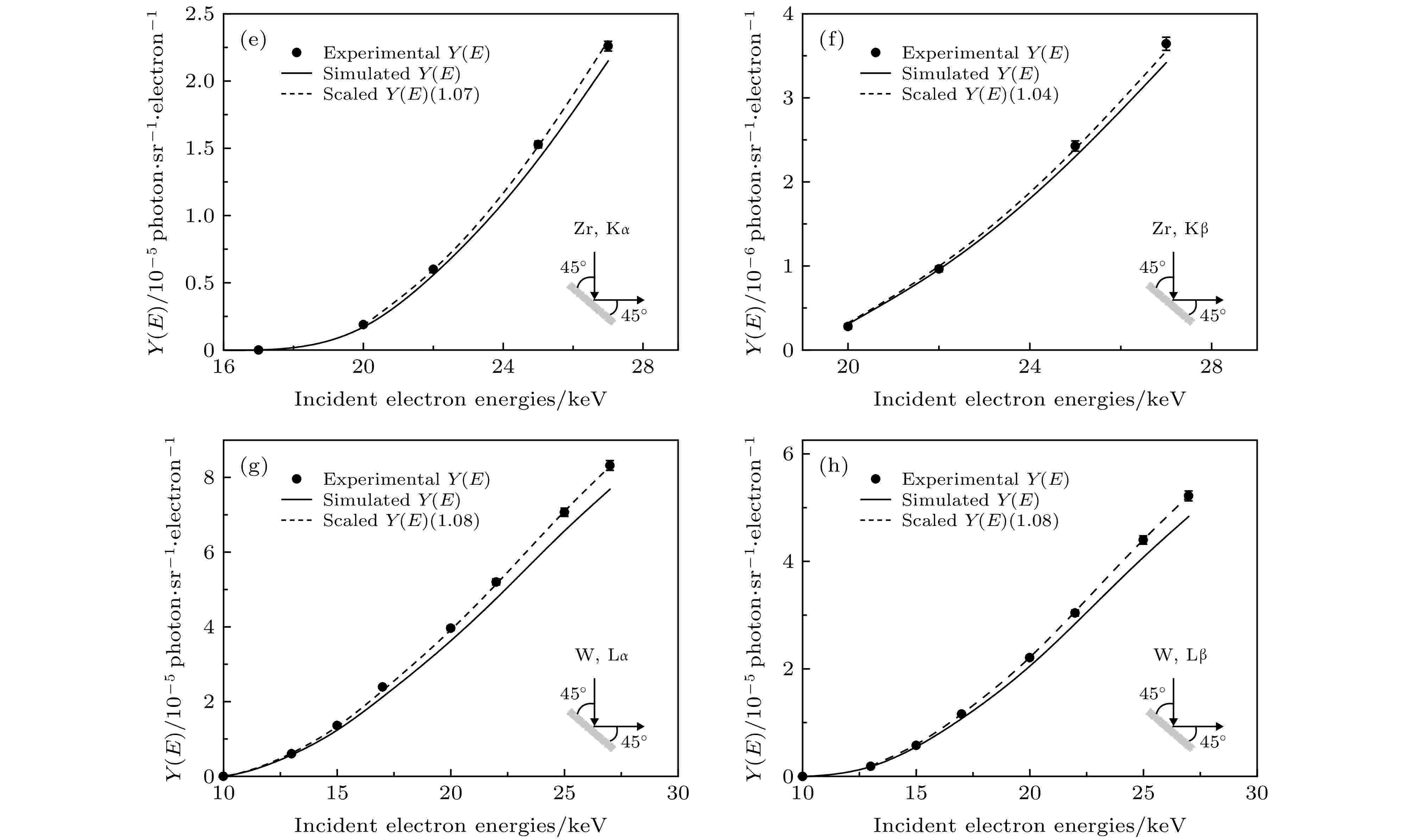
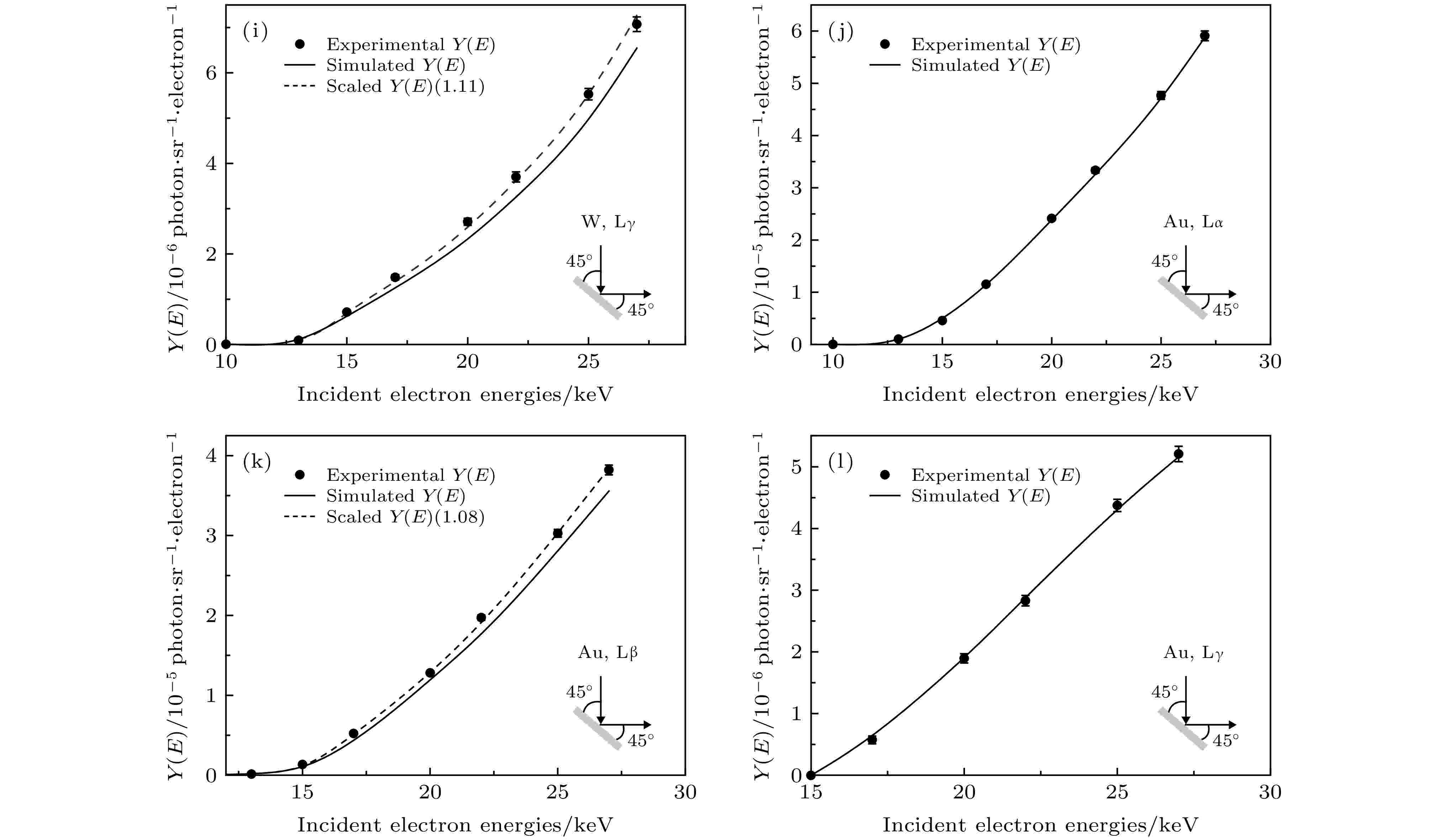图 5 实心圆点表示实验测得不同入射电子能量下的厚靶特征X射线产额, 实线代表相应的蒙特卡罗模拟值, 虚线为蒙特卡罗模拟值归一到实验数据值上的结果, 括号内为归一化参数, 缩略图为实验布局示意图
Figure5. Solid circles denote the experimental characteristic X-ray yields of thick targets at different incident electron energies. Solid curves represent the results of Monte Carlo simulations using the PENELOPE code. Dashed curves are the scaled results of Monte Carlo simulations by scaling factors that are given in parentheses. The insets show the schematic of experimental geometry.

本文测量了5—27 keV电子入射时Al的K, Ti的Kα, Kβ, Zr的Kα, Kβ, L及W, Au的Lα, Lβ, Lγ的厚靶特征X射线产额. 实验数据的不确定度主要来源于峰净计数不确定度(< 6.0%)及效率刻度不确定度(约1.6%), 总不确定度约为1.7—6.2%. 在图5中, 总体来看, 各元素的实验值与蒙特卡罗模拟值在约10%的范围内符合, 其中大部分实验数据与蒙特卡罗模拟值的符合程度小于10%. Al的K层特征X射线实验产额与模拟产额之间差异较其他元素略大, 原因可能来自于本底扣除时所产生的误差略大, 或者理论模拟本身的不准确性所致. 对于Ti元素, 使用Origin软件对实验谱进行解谱, 通过拟合来完成Kα和Kβ特征峰净面积的计算, Kβ峰面积较小, 其净峰面积采用K峰总面积减Kα峰面积的方法获得, 结果得到的Kα, Kβ实验产额分别在10%, 11%范围内与模拟值符合. Bote等^[25]对Shima等^[36]给出的一些特征X射线实验产额进行了分析, 其中Ti的Kα实验值比模拟值略低, 在其误差范围内与本文的实验数据符合良好. Zr元素的L, Kα, Kβ实验产额与模拟值均符合较好, 且与Li等^[26]的数据相比, 本文所获实验值与模拟值符合度更高. 对于W, Au的Lα, Lβ, Lγ, 可观察到实验产额不确定度随特征峰面积减小而略有增大, 与文献[25]中给出的W, Au的Lα数据相比, 虽然在高能端与模拟值偏差略有增大, 但总体上来看仍与本文结果较为符合. 文献[26]同时给出了W的Lα, Lβ, Lγ实验产额数据, 其中Lβ, Lγ的实验值与本文的实验数据在不确定度范围内取得了较好的一致性, Lα的数据略有差异, 整体来看本工作获得的实验值与蒙特卡罗模拟值符合程度更高.
2 -->

3.3.厚靶的解析模型分析

近年来, 厚靶的解析模型被应用于内壳层电离截面或产生截面的测量等方面^{[22,23,37,38]}, 因此, 对厚靶解析模型的比较分析非常有利于该模型的应用. 本文所采用的厚靶X射线产额解析模型, 对于电子轰击的情况, 基于如下假设: 1)入射电子在厚样品中直线运动, 即不考虑再扩散或散射效应; 2)忽略轫致辐射光子和其他二次粒子的贡献, 可以给出厚靶中电子引起的内壳电离的特征X射线产额${N_{\rm{X}}}$如下^[22]:

$\begin{split} \dfrac{{{N_{\rm{X}}}\left({{E_0}} \right)}}{{{I_0}}} =\; & \frac{{{N_A}}}{A}\frac{\varOmega }{{4{\text{π}}}}\varepsilon \int_0^{{E_0}} {{\sigma _{\rm{X}}}} (E) \\& \times \exp\bigg(- \mu _{\rm X}^{\tfrac{\cos\alpha}{\cos \beta }\textstyle\int_{\scriptstyle E}^{\scriptstyle E_0} \tfrac{{\rm d}{E^*}}{S(E^*)}}\bigg) \frac{{\rm d} E}{S(E )},\end{split}$

其中, E₀为入射电子能量, I₀为入射粒子数, N_A为阿伏伽德罗常数, A为原子质量数, εΩ/4π为探测效率, σ_X为特征X射线产生截面或电离截面, μ_X为样品内特征X射线的质量衰减系数, S(E)为质量阻止本领. α为入射粒子方向与靶表面法线之间的夹角, β为X射线探测器方向与靶表面法线之间的夹角. 对于本文的实验装置, α = 45°, β = 45°.
特征X射线来源于初级入射电子、次级电子和光子与靶物质的相互作用, 本文使用PENELOPE模拟了两种情况下各部分在总特征X射线产额中的贡献: 1) α = 45°, β = 45°; 2) α = 0°, β = 45°, 并与方程(2)解析计算的结果进行了对比. 方程(2)中使用的原子弛豫参数、内壳层电离截面、质量衰减系数和质量阻止本领均提取自PENELOPE数据库. 计算结果如图6和图7所示.




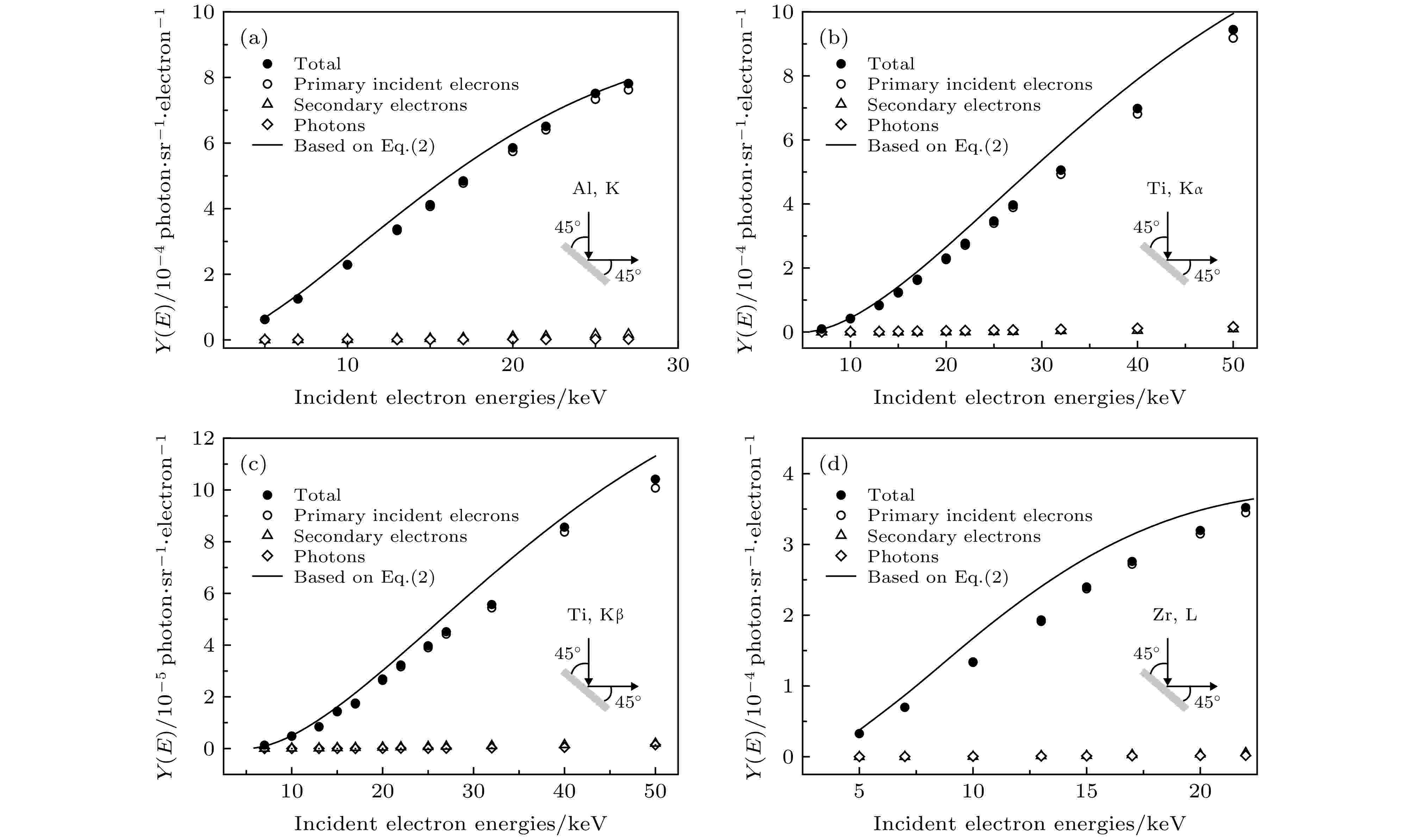
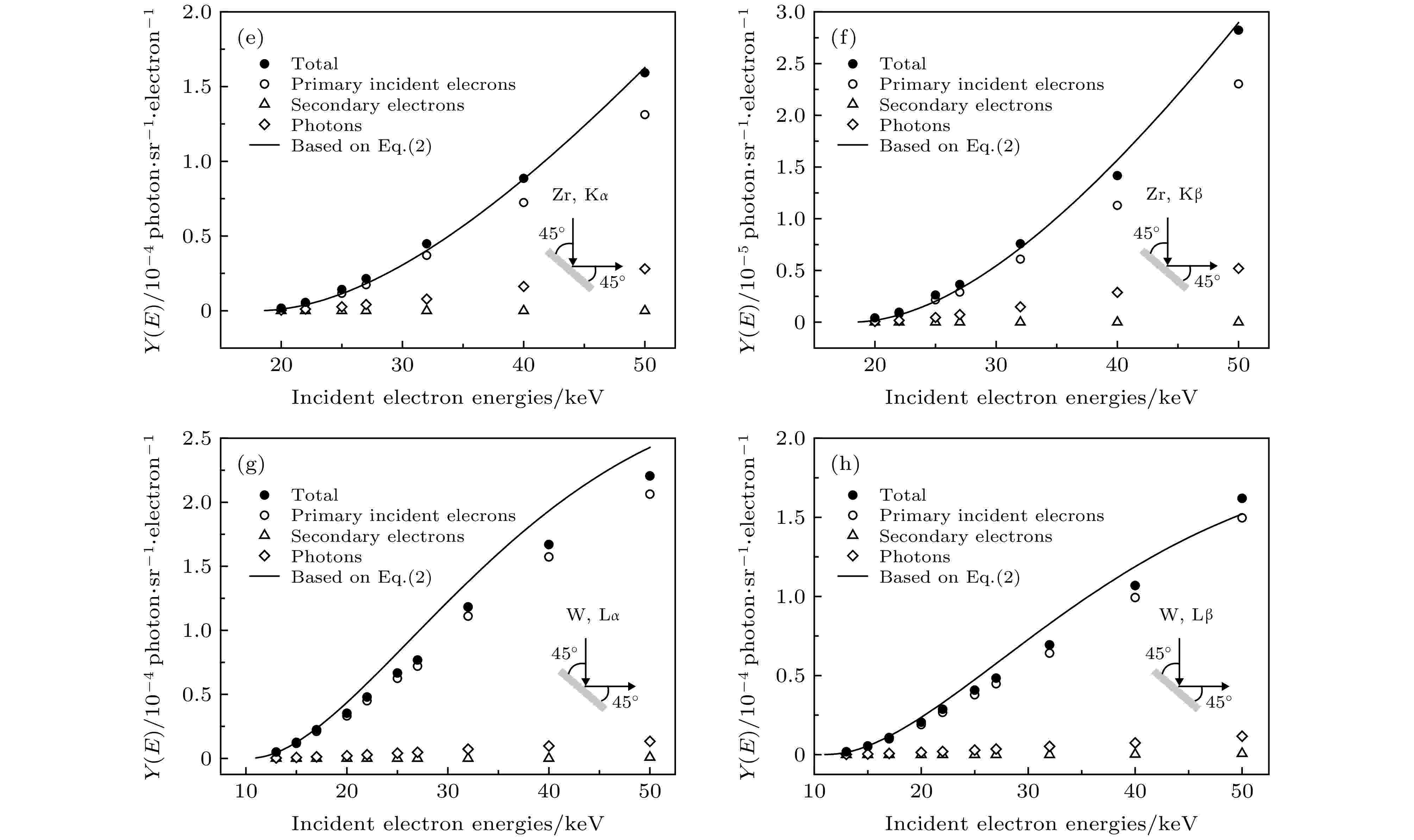
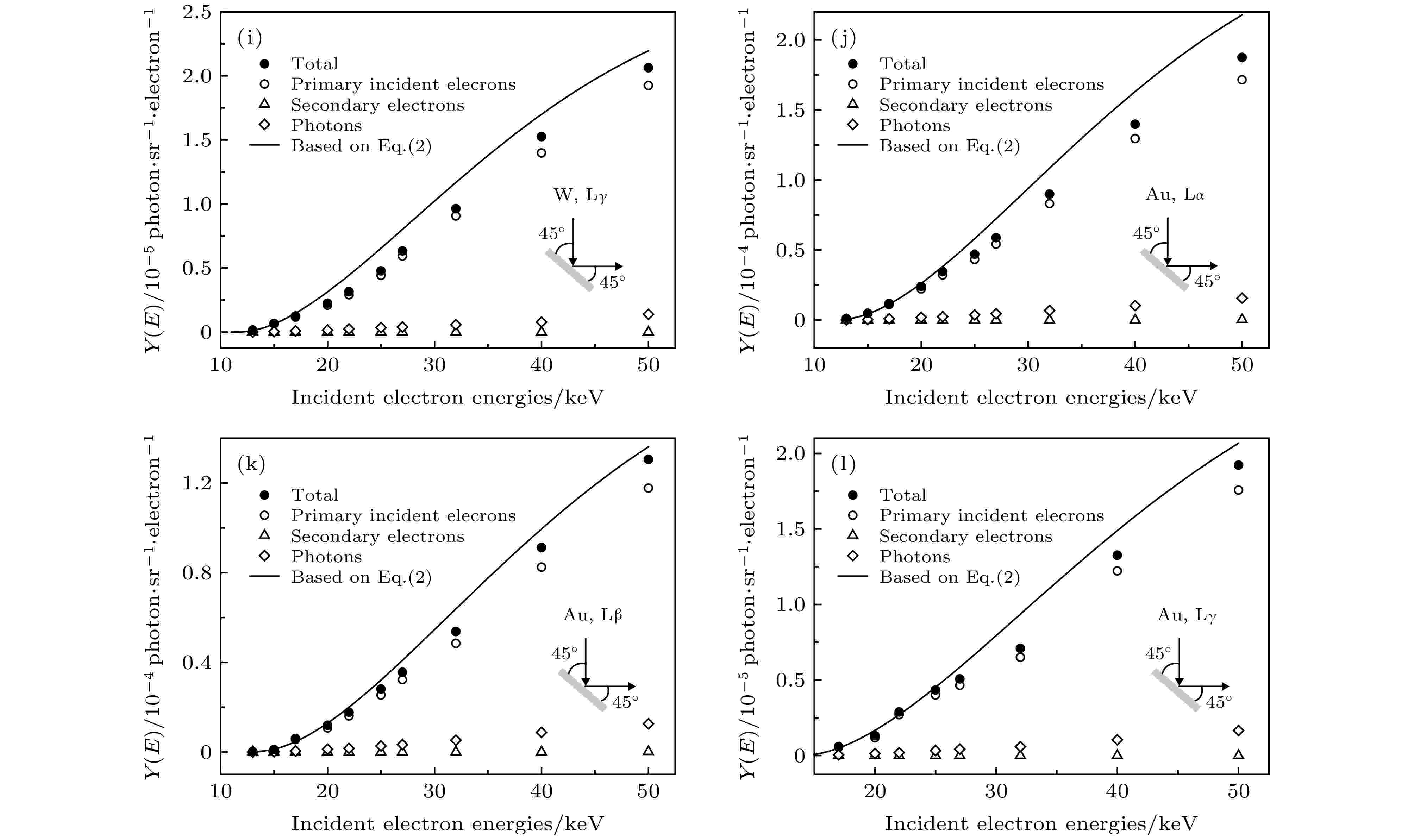图 6 α = 45°, β = 45°时由PENELOPE计算的特征X射线产额(实心圆点), 其中来自初级电子电离贡献表示为空心圆形, 次级电子电离贡献表示为空心三角形, 轫致辐射光子贡献为空心方形. 实线为方程(2)计算所得结果. 缩略图为计算几何示意图
Figure6. In the case of α = 45°, β = 45°, the solid dots represent the total characteristic X-ray yields calculated by PENELOPE, which include the contributions from the primary electron ionization (hollow circles), secondary electron ionization(hollow triangles) and bremsstrahlung photon ionization (hollow squares). The solid lines are the characteristic X-ray yields calculated by Eq. (2). The insets show the schematic of calculation geometry.





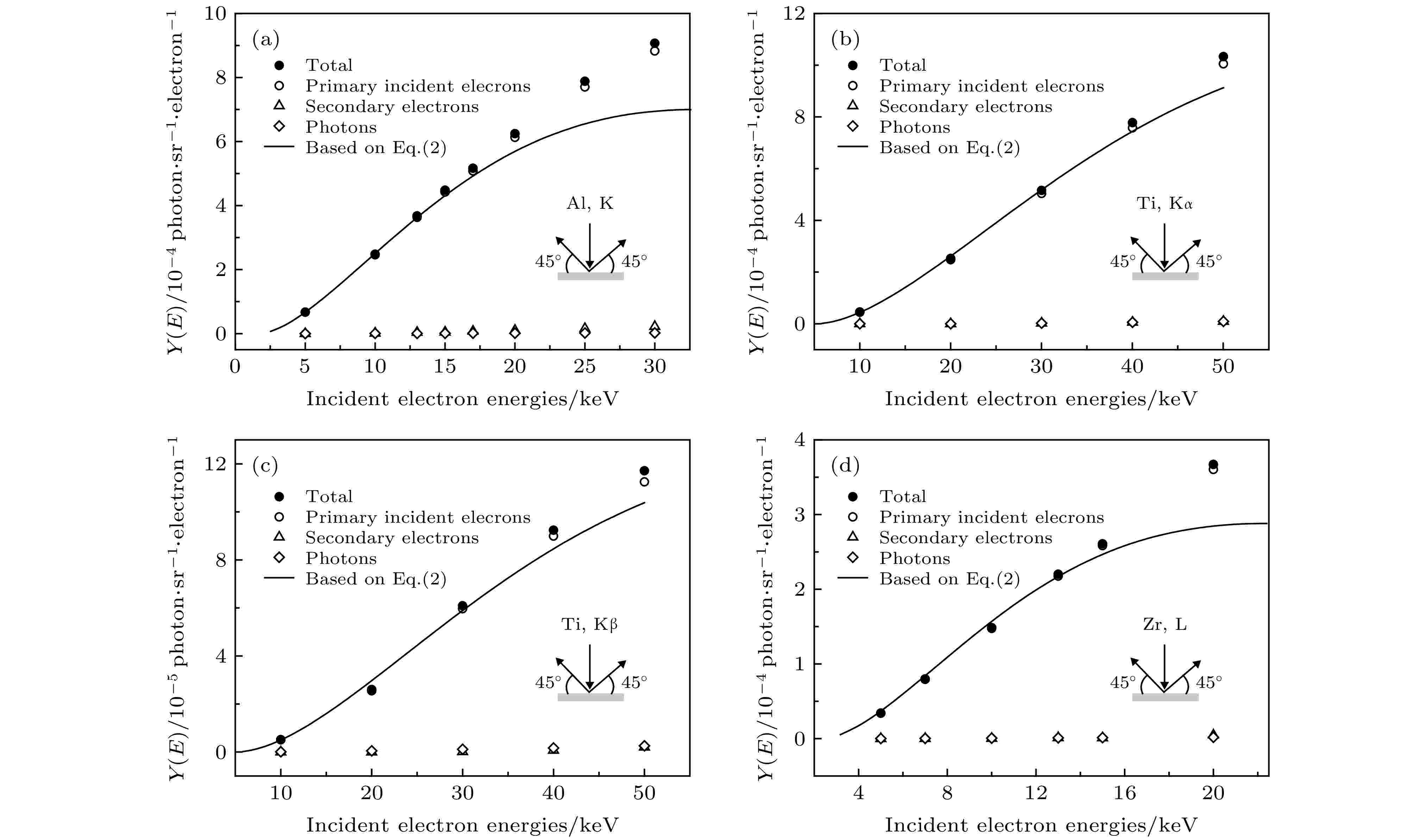
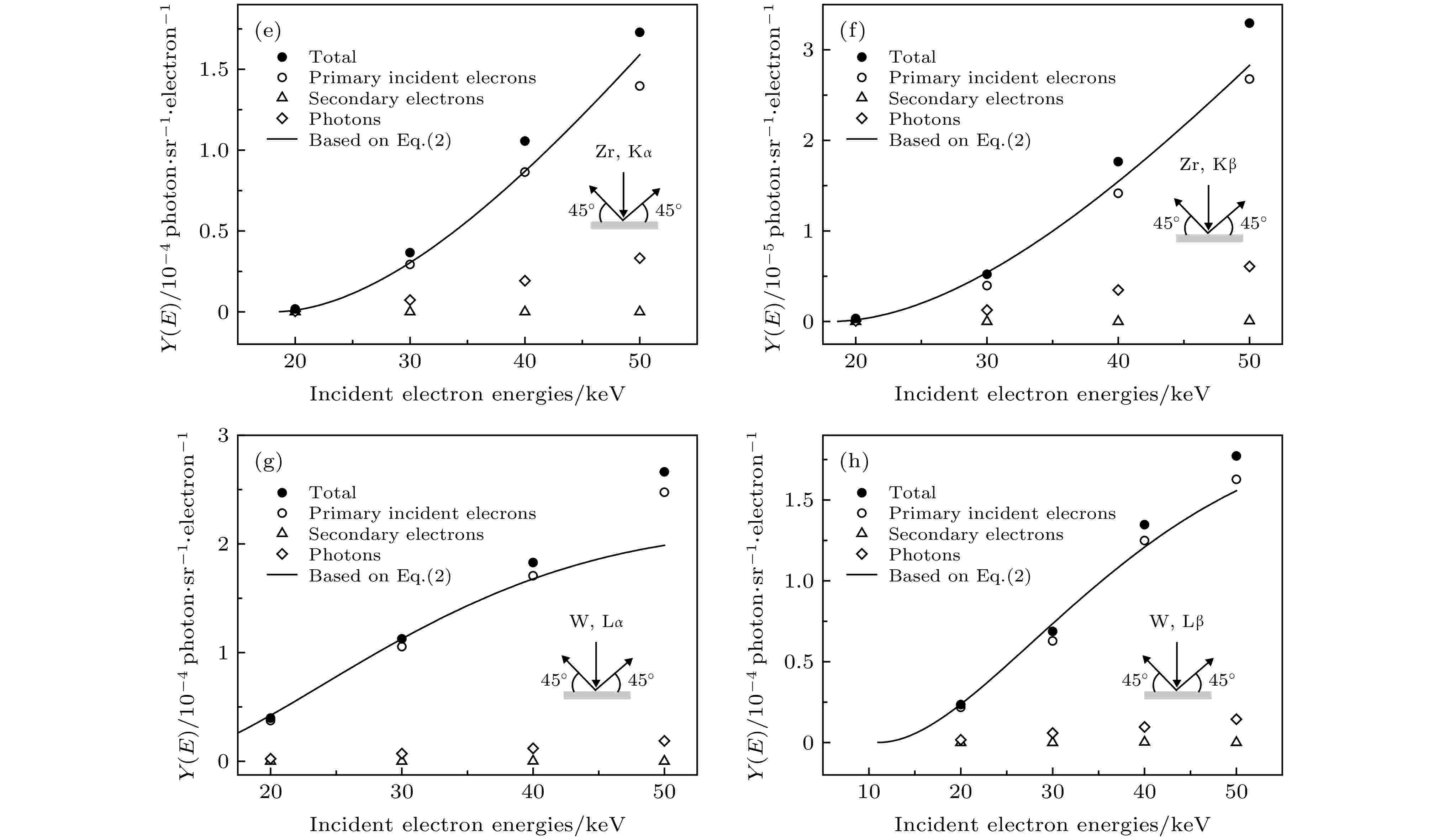
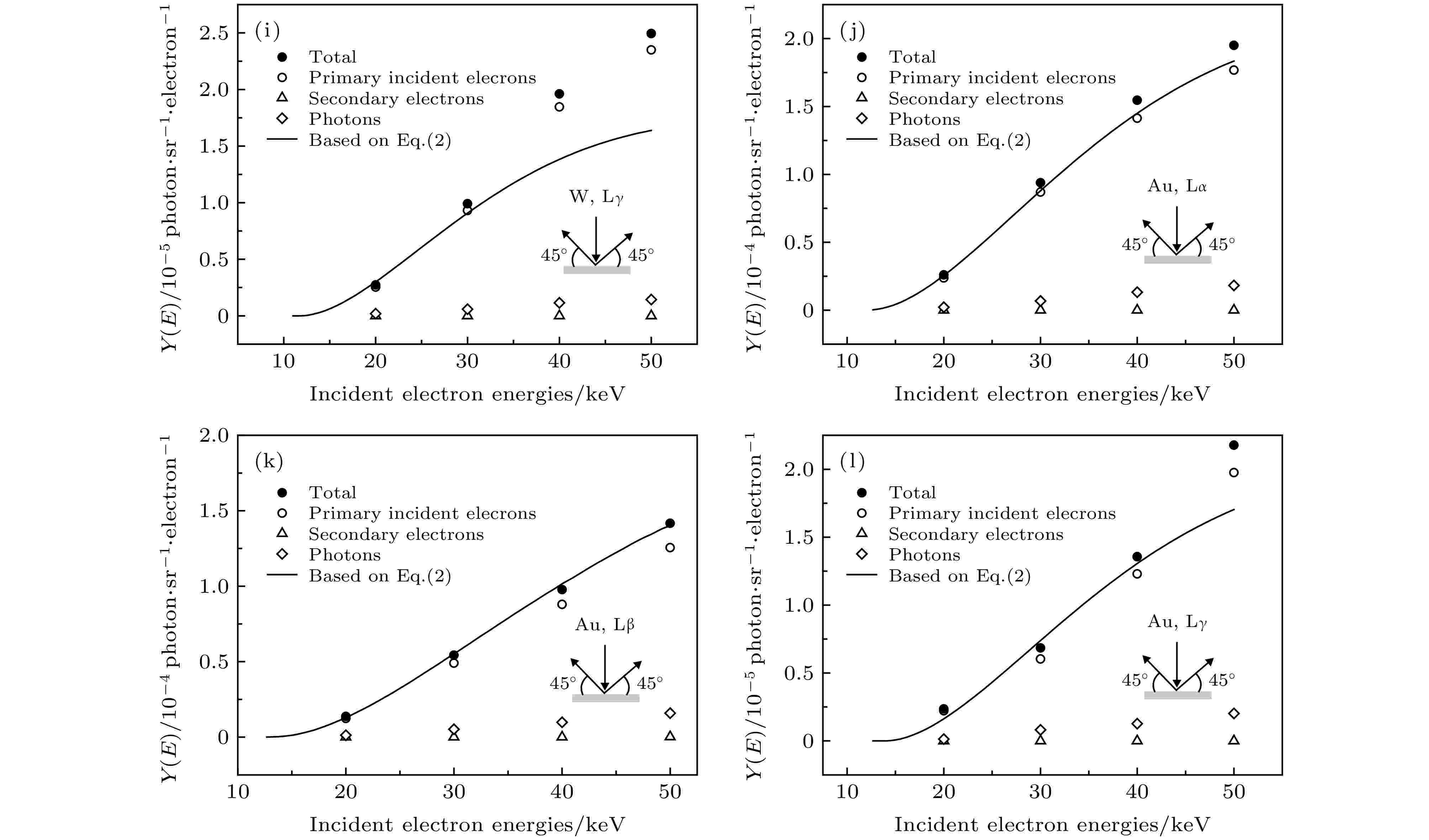图 7 α = 0°, β = 45°时由PENELOPE计算的特征X射线产额(实心圆点), 其中来自初级电子电离贡献表示为空心圆形, 次级电子电离贡献表示为空心三角形, 轫致辐射光子贡献为空心方形. 实线为方程(2)计算所得结果. 缩略图为计算几何示意图
Figure7. In the case of α = 45°, β = 45°, the solid dots represent the total characteristic X-ray yields calculated by PENELOPE, which include the contributions from the primary electron ionization (hollow circles), secondary electron ionization(hollow triangles) and bremsstrahlung photon ionization (hollow squares). The solid lines are the characteristic X-ray yields calculated by Eq. (2). The insets show the schematic of calculation geometry.

由图6可以看出, 对于低Z元素Al, Ti, 次级电子和光子在总产额中贡献仅占1%—2%; 在Zr的L层中, 该贡献也仅占1%—2%, 随着特征X射线能量越高, 即Zr的Kα和Kβ, 该贡献随之增大至17%—20%, 表现出与阈能的相关性; 对高Z元素W, Au的L层次级电子和光子所致电离占比约为7%—10%. 且对各元素的各层而言, 随着电子入射能量增加, 该比例大致保持不变. 通过对比图6和图7可以看到, 对于电子垂直入射的情况, 即在α = 0°, β = 45°时, 基于方程(2)的计算结果(实线)与蒙特卡罗计算的初级电子撞击电离(空心圆)符合程度要优于α = 45°, β = 45°的入射方式. 在图6中, 方程(2)计算值高于蒙特卡罗计算的初级电子撞击电离(空心圆)较多, 原因可能为在电子成45°入射厚靶时, 存在散射电子不能完全在靶内产生电离的情况, 而在垂直入射时这种作用则较轻, 故在α = 45°, β = 45°的情况下, 由(2)式计算的特征X射线产额与蒙特卡罗模拟的初级电子撞击电离产生的特征X射线产额差异较大. 同时, 从图7中也可看出, 在U < 5—6的范围内, 二者符合程度更佳^[22]. 本文使用的解析模型还有待进一步完善, 解析模型的改进也是人们目前感兴趣的问题^[38].
2 -->

3.4.电离截面及特征X射线产生截面

元素的特征X射线产额由初级电子、次级电子和光子的电离作用共同组成, 利用PENELOPE程序, 可以估算出入射初级电子、次级电子和光子对相应壳层特征X射线的贡献. Bote等^[25]指出, 内壳层电离的几率与弹性散射和外壳层电离相比很小, 故电子轨迹与蒙特卡罗模拟中使用的电离截面模型相关性很弱, 使用的PENELOPE可以很好地模拟如背散射系数、薄膜透射系数等诸多物理量, 因此, 特征X射线产额的模拟值大小主要由蒙特卡罗模拟中使用的电离截面或产生截面确定. 同时, 基于DWBA理论模型计算的理论特征X射线电离或产生截面值与实验值在形状上符合很好^[33], 因此可采用文献[33]的方法由厚靶的特征X射线产额来得出X射线产生截面或电离截面, 即通过实验与蒙特卡罗模拟的直接电离产额的比值确定为修正系数, 将蒙特卡罗模拟中使用的基于DWBA理论的截面数据乘以相应的修正系数得到实验截面值. 本文中的DWBA理论数据来自PENELOPE数据库, 根据文献[11,13]计算得到. 在Al, Ti的K层及Zr的L层中, 光子与次级电子电离仅占1%—2%, 对总电离贡献可以忽略, 故采用图5中所标注的归一化参数进行计算. 对于Zr的K层及W, Au的L层, 光子与次级电子电离贡献大于7%, 我们将实验初级电子电离产额与蒙特卡罗模拟初级电子电离产额相比得到新的修正系数, 其中, 实验初级电子电离产额由实验总产额减去蒙特卡罗模拟的次级电子与光子电离产额得到. 最终获得的内壳层电离截面及特征X射线产生截面与相应的修正系数如图8和图9所示.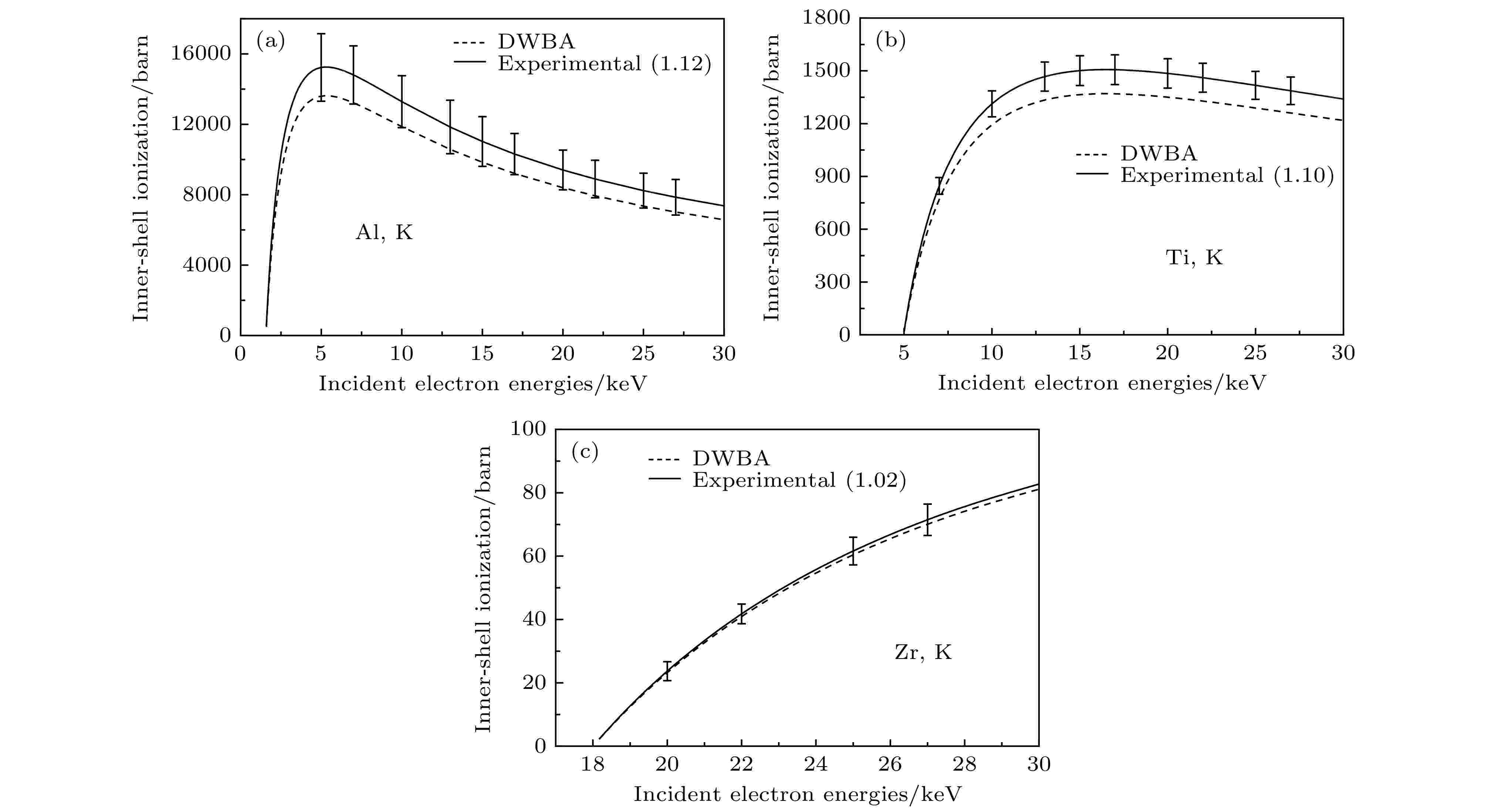
图 8 (a) Al, (b) Ti, (c) Zr元素实验K壳电离截面(实线)与DWBA理论值(虚线), 括号内为修正系数
Figure8. Experimental K-shell ionization cross sections of (a) Al, (b) Ti, (c) Zr (solid lines) and the DWBA theoretical values (dashed lines). The scaling factors are given in parentheses.

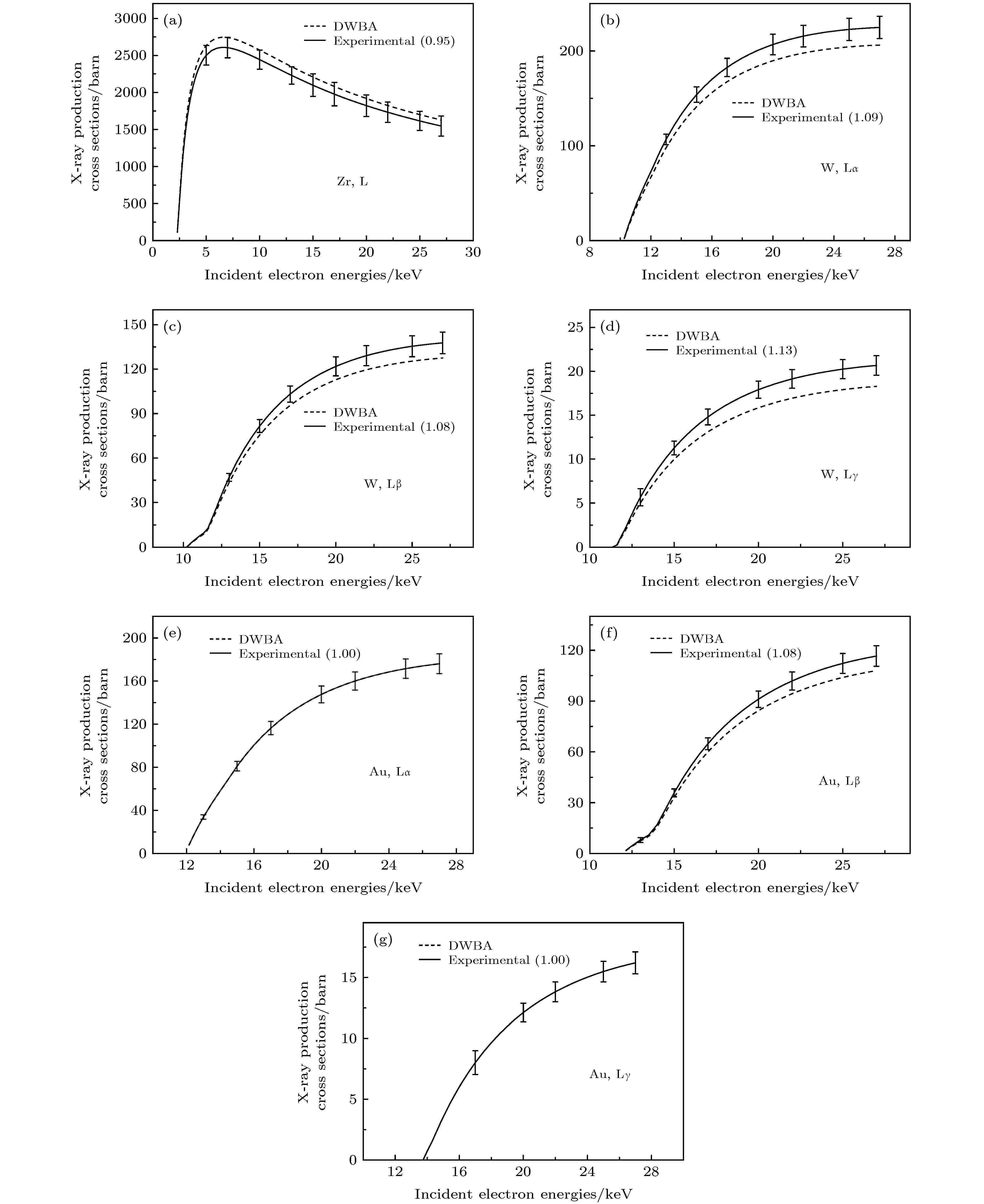图 9 (a) Zr, (b)?(d) W, (e)?(g) Au元素实验L壳特征X射线产生截面(实线)与DWBA理论值(虚线), 括号内为修正系数
Figure9. Experimental L-shell characteristic X-ray production cross sections of (a) Zr, (b)?(d) W, (e)?(g) Au (solid lines) and the DWBA theoretical values (dashed lines). The scaling factors are given in parentheses.

由此方法得到的特征X射线产生截面及电离截面的不确定度主要来源于实验产额及蒙特卡罗模拟产额的不确定度. 实验产额总不确定度 < 6.2%, 主要来自净计数(< 6.0%)及效率刻度(约1.6%); 蒙特卡罗模拟的不确定度中, 来源于电子的阻止本领及光子的质量衰减系数的不确定度约为5%^[33,37], 对于K壳层电离截面, 还存在荧光产额不确定度, 其中对Al, Ti, Zr元素分别为10%, 2%和4%^[39]. 综合以上不确定度来源, 得到Al, Ti, Zr的K层电离截面不确定度分别约为12.8%, 5.6%, 7.0%; Zr的L层特征X射线产生截面不确定度约为7.9%; W和Au的Lα, Lβ, Lγ特征X射线产生截面不确定度分别约为5.3%, 5.3%, 7.8%和5.4%, 5.5%, 5.8%.

1)本文通过改进的实验装置和数据处理方法, 测量了5—27 keV电子撞击厚靶所致Al的K, Ti的Kα, Kβ, Zr的Kα, Kβ, L及W, Au的Lα, Lβ, Lγ特征X射线产额, 不确定度为1.7%—6.2%, 并与蒙特卡罗模拟计算进行了比较, 大多数实验数据在小于10%范围内符合. 依据实验的厚靶产额数据得出了相应的内壳层电离截面或特征X射线产生截面值, 不确定度范围为5%—8%(Al除外, 由于其较大的荧光产额不确定度). 本文的研究表明, 目前广泛使用的电子原子碰撞内壳层电离理论模型(DWBA理论)及原子弛豫参数的结果与实验数据的差异小于或约为10%, 这些结论有助于相关理论计算的改进, 也对实际应用有价值, 例如对氚的BIXS分析方法, 该方法目前广泛应用于聚变堆材料的氚分析.
2)对于电子入射角度为45°和90°的两种情况, 基于方程(2)的解析模型计算值与蒙特卡罗模拟值的产额结果比较发现, 在90°入射时二者符合情况较好, 本文讨论了可能的原因, 并认为在45°(或其他角度入射)时解析模型的准确度有待进一步完善和提高.
3)同时, 基于扭曲波玻恩近似理论模型(DWBA)的内壳层电离截面, 本文还给出了次级电子、轫致辐射光子所产生的特征X射线产额的贡献度, 在本工作研究元素的低电离阈能壳层, 次级粒子的贡献度约为2%, 对高电离阈能壳层, 达到10%—20%, 这部分贡献与入射电子能量关系较弱, 表现出与原子序数的密切相关性.