摘要: 基于Floquet理论和传输矩阵方法, 理论研究了光场对电子隧穿两类磁电垒结构的自旋极化输运特性的影响, 计算结果表明光场对两类磁电垒结构中电子的输运有显著影响: 首先, 原来不存在自旋过滤特性的结构应用光场后会产生低能区域明显的自旋过滤效应; 其次, 原来存在自旋过滤特性的结构应用光场后自旋过滤明显增强, 增幅超过一个数量级. 这些为新的自旋极化源的产生和自旋过滤现象的深入研究有一定的指导性意义.
关键词: 自旋过滤 /
自旋极化 /
磁电垒 /
光场 English Abstract Light-field assisted spin-polarized transport properties in magnetic-electric barrier structures Li Chun-Lei 1 ,Xu Yan 1 ,Zheng Jun 2 ,Wang Xiao-Ming 3 ,Yuan Rui-Yang 4 ,Guo Yong 5,6 1.College of Elementary Education, Capital Normal University, Beijing 100048, China Received Date: 18 February 2020Accepted Date: 17 March 2020Published Online: 20 May 2020Abstract: Based on the Floquet theory and transfer-matrix method, We investigated the influence of light-field on the spin-polarized transport properties for electrons tunneling through two kinds of magnetic-electric barrier structures (the $\delta$ -doped magnetic-barrier can be realized in experiments by depositing two ferromagnetic stripes on top and bottom of a semiconductor heterostructure and the light-field can be realized by placing a hemispherical silicon lens on the back surface of the semiconductor substrate). Transport properties result from the interaction of electrons with the light-field by means of photon absorption and emission. It is found that the light-field can greatly affect the transmission probabilities as well as the corresponding polarizations. The distance between the adjacent peaks and the number of the transport peaks can be controlled by adjusting the frequency and the amplitude of the light-field, respectively. It is shown that a significant spin-polarization effect can be induced by such light-field in the kind of antisymmetric magnetic barrier structure ($B_{1}=-B_{2}$ ) and the light-field can greatly change the spin-polarization effect in the kind of symmetric magnetic barrier structure ($B_{1}=B_{2}$ ). When the frequency of the light-field increases, the spin-polarization shifts toward the low-energy end and gradually increases. These remarkable properties of spin polarization may be beneficial for the devising tunable spin filtering devices.Keywords: spin filtering /spin-polarized /magnetic-electric barrier /light-field 全文HTML --> --> --> 1.引 言 自从20世纪80年代磁调控量子结构的概念被提出以来[1 -3 ] , 磁调控半导体纳米结构得到了人们的广泛关注. 研究者从理论上相继提出了磁垒、磁量子阱、磁量子线、磁量子反点[4 ] 以及磁超晶格[5 ] 等结构. 实验方面, 现代刻蚀技术、电子微刻技术以及分子束外延技术的发展, 使****们实现了对相关领域的实验研究. 例如, 人们可以通过在半导体结构上沉积铁磁条等技术, 实现半导体异质结中二维电子气的磁调控, 这些实验的最新进展又为理论研究奠定了良好的实验基础. 源于自旋电子学的快速发展, ****们对磁调控半导体纳米结构中自旋输运特性的研究取得了显著成果, 研究重点主要集中在磁调控量子结构的共振劈裂、波矢过滤、磁阻性质以及自旋极化输运特性等方面. Peeters等[4 ] 提出磁量子反点的概念后, 再次掀起了人们对磁量子结构的深入研究. Guo等[6 -11 ] 在磁量子结构中做了一系列工作, 主要包括不同磁量子结构中电子的隧穿特性, 恒定电场下磁结构中电子的输运性质, 复杂磁结构中自旋极化隧穿特性等.[12 ] 提出反平行磁电垒结构并研究了其中电子的输运特性, 只是非常遗憾, 他们的计算中出现了错误. 随后Xu和Okada[13 ] 、Jiang等[14 ] 对相关结构进行了理论计算修正. Papp和Peeters[12 ] 的计算错误最终被秦建华等[15 ] 进行了最后修正, 同时给出了不同磁电垒结构的统一隧穿几率计算公式和显著增强磁电垒结构中自旋过滤特性的指导性意见. 此外, Lu等[16 -19 ] 和Li等[20 ] 在磁电垒结构及包含$ {\text{δ}} $ 势磁电垒结构中做了一系列相关工作, 对其中电子的隧穿特性给出了较为详细的研究.[21 -24 ] . 有关光子辅助电子隧穿的研究可以追溯到20世纪60年代[25 ,26 ] , 研究者首次在超导体-绝缘体-超导体结构中观测到光子辅助电子隧穿现象, 自此揭开了****对光子辅助隧穿研究的序幕, 各种理论研究方法不断被提出[27 -30 ] . 研究结果表明, 光场可以调控电子在低维结构中的隧穿特性. 这些研究为光子辅助电子隧穿在高速电子隧穿器件以及量子探测等相关领域的潜在应用提供了理论支持. 实验方面, 为了实现电子与光子的强相互作用, 主要采用蝴蝶结型电极与被试结构相连, 此外通过加装半球型透镜直接进行光波辐照[31 ] 或通过门电压连接时间周期场[32 ] 的方式来实现光子与电子的相互作用. 本文的研究目的在于通过研究两类代表性磁电垒结构中的电子自旋输运, 揭示其中光场对电子自旋输运的影响, 优化调控磁电垒结构中电子自旋过滤效应.2.理论模型 为了方便与不考虑光场时磁电垒结构中电子隧穿特性相比较, 文中研究的磁电垒结构与文献[15 ]的相似, 如图1 所示. 其中图1(a) 所示结构中$ B_{1} = -B_{2} $ , 即等效为两个反向等强度的$ {\text{δ}} $ 型磁垒; 图1(b) 所示结构中$ B_{1} = B_{2} $ , 即等效为两个同向等强度的$ {\text{δ}} $ 型磁垒, 这些结构在实验上可以通过在异质结上沉积金属铁磁条来实现. 这里铁磁条通常距离异质结面很近, 因此可以近似地由$ \delta $ 函数进行描述. 另外, 磁电垒结构中的电势垒$ U(x) $ 可以通过在铁磁条上直接加载偏压获得[12 ] . 图中$ V_{1}\cos(\omega t) $ 表示振荡幅度为$ V_{1} $ 振荡频率为$ \omega $ 的外加光场. 设二维电子气在$ (x, y) $ 平面内, 磁场方向为z 方向, 并且在y 方向均匀分布, 则磁场用$ \delta $ 函数可以表示为$B_{z}(x) \!=\! B_{1}\delta(x)\mp B_{2}\delta(x\!-\!L)$ . 其中$ B_{1/2} $ 分别是体系在$x \!=\! 0$ 和$x \!=\! L$ 处的磁感应强度. 根据朗道规范, 对应的磁矢势可以表示为${{A}} \!=\! [0, A_{y}(x), 0]0]$ , 从而$ A_{y}(x) = B_{1}l_{B}\varTheta(x){+}B_{2}l_{B}\varTheta(x-L) $ , 式中$ \varTheta(x) $ 为阶跃函数, 磁长度$ l_{B} = \sqrt{\hbar/(eB_{0})} $ . 应用抛物带有效质量近似方法, 该磁电垒结构中二维电子气的哈密顿量表示为图 1 光场$ V_{1}\cos(\omega t) $ 调制下两类磁电垒结构 (a)反向等强度$ {\text{δ}} $ 型磁电垒结构; (b)同向等强度$ {\text{δ}} $ 型磁电垒结构Figure1. The model field-driven magnetic-electric barrier structures: (a) $ B_{1} = -B_{2} $ ; (b) $ B_{1} = B_{2} $ $ m^{*}_{\rm e} $ 和$ m_{0} $ 分别为电子的有效质量和自由电子质量, $ p_{x} $ 和$ p_{y} $ 分别为电子在x 和y 方向的动量, $ U(x) $ 为体系的电势垒, $ g^{*} $ 为朗德有效因子, $ \sigma = +1/-1 $ 为对应z 方向电子的自旋向上和自旋向下的自旋本征量子数. 为了分析方便, 引入有效势$ U_{\rm {eff}}(x, k_{y}, \sigma) \!=\! \dfrac{[p_{y}\!+\!eA_{y}(x)]^{2}}{2 m^{*}_{\rm e}}\!+U(x)\!+\!\dfrac{eg^{*}\sigma \hbar}{4 m_{0}}B_{z}(x) $ , 同时对各物理量进行无量纲化处理, 即$ B_{z}(x)\rightarrow B_{0}B_{z}(x) $ , $ A_{y}(x)\rightarrow B_{0}l_{B}A_{y}(x) $ , $ r\rightarrow l_{B}r $ , $ E\rightarrow \hbar\omega _{\rm c}E $ , 其中$ \omega _{\rm c} = eB_{0}/m^{*}_{\rm e} $ 为回旋频率, $ B_{0} $ 为一特定磁感应强度. 考虑到$ (x, y) $ 平面内电子沿y 方向满足平移不变性, 同时包含时间周期场的作用, 根据Floquet理论电子的波函数可以表示为$ \varPsi(x, y, t) = \psi(x, t){\rm e}^{{\rm i}k_{y}y} $ , 这里$ k_{y} $ 为电子沿y 方向的波矢, $ \psi(x, t) $ 满足的一维薛定谔方程可以表示为$ V_{1}\cos(\omega t) $ 是时间周期函数, 根据Floquet理论, (2 )式有如下解的形式3 )式代入(2 )式, 分离变量后可以分别求得$ g(x) $ 和$ f(t) $ 的解. 经过计算[27 ,33 ,34 ] 可以得出:$ k_{{\rm e}n} $ , $ q_m $ 和$ k_{{\rm c}n} $ 为电子在对应区域吸收或发射n 或m 个光子的波矢, $ k_{{\rm e}0} $ 为$ x < 0 $ 区域$ n = 0 $ 时电子的波矢, 即与入射电子能量相对应的波矢, 各个波矢分别为:$J_{n-m}\left( {V_1}/{\omega}\right)$ 是第一类$ (n-m) $ 阶Bessel函数, 其中n 和m 为边带指标, 取整数, 对应反射和出射波形成的能量间隔为$ \omega $ 的边带. 根据$ {\text{δ}} $ 势场中波函数的跃变条件[35 ] , 利用传输矩阵方法, 可以计算出光子辅助电子隧穿磁电垒结构的透射几率$ P = (T^{+}-T^{-})/(T^{+}+T^{-}) $ .3.计算结果和讨论 23.1.无电势垒 3.1.无电势垒 图2 给出了$ U(x) = 0 $ 时反向等强度(B 1 = –B 2 )和同向等强度($ B_{1} = B_{2} $ )$ {\text{δ}} $ 型磁垒结构中电子的透射几率随电子入射能量的变化曲线, 其中图2(a) —图2(d) 对应$ B_{1} = -B_{2} $ 的情形, 图2(e) —图2(h) 对应$ B_{1} = B_{2} $ . 数值计算基于InAs系统, 计算参数选取为$ m^{*}_{\rm e} = 0.024 m_{0}, g^{*} = 15, B_{0} = 0.2\mathrm{T}, $ B 1 = 3, L = 1, 光场参数设置为$ V_{1}/(\hbar\omega) = 2 $ , 其中光子能量$ E_{\rm {photon}}(\hbar\omega) = 0, 1, 2, 3 $ 对应图2 中由上到下的各个情形. 图中实线表示自旋向上, 虚线表示自旋向下. 通过图2(a) 可以看出, 不考虑光场与电子的相互作用时, 自旋向上与自旋向下电子的透射几率完全相同, 即此时该结构不具有自旋过滤的特性, 相关结论已经由秦建华等[15 ] 给出, 本文为了与考虑光场与电子相互作用对比, 作为参考而给出. 对比图2(a) 和图2(b) —图2(d) 可以发现, 当有光子参与电子隧穿过程时, 电子的透射几率在低能区域出现了较大的区别, 电子隧穿通过光场调制的结构时出现了显著的自旋过滤效应. 此外, 在反向等强度$ {\text{δ}} $ 型磁垒结构中, 波矢$ k_{y} = -0.5 $ 时光场对电子隧穿的影响明显强于波矢为$ k_{y} = 0.5 $ 的情形, 这些为调控电子自旋过滤提供了一定的理论依据. 图2(e) —图2(h) 给出了同向等强度$ {\text{δ}} $ 型磁垒结构中($ B_{1} = B_{2} $ )电子的透射几率随电子入射能量的变化曲线, 计算结果显示, 同向等强度$ {\text{δ}} $ 型磁垒结构中, 不考虑光场与电子相互作用时(如图2(e) ), 也存在自旋过滤效应, 但是并不明显; 考虑光场对电子的辅助隧穿时, 可以看到在低能区出现了明显的辅助隧穿峰, 并且这些峰的位置与光子的能量直接相关, 即相邻辅助隧穿峰的能量间隔与光子能量($ E_{\rm {photon}} $ )相等, 这可以理解为低能入射电子隧穿过程的多光子吸收过程.图 2 电子隧穿磁垒结构透射几率谱 (a)?(d)反向等强度$ {\text{δ}} $ 型磁垒结构; (e)?(h)同向等强度$ {\text{δ}} $ 型磁垒结构Figure2. Transmission probabilities as the function of the incident energy: (a)?(d)$ B_{1} = -B_{2} = 3 $ ; (e)?(h)$ B_{1} = B_{2} = 3 $ 图3 给出了对应图2 的自旋极化度变化关系曲线. 其中图3(a) 和图3(b) 对应$ B_{2} = -3 $ 的情形; 图3(c) 和图3(d) 对应$ B_{2} = 3 $ 的情形, 图3(d) 插图对应$ B_{2} = 3 $ 时不包含光场时的电子极化度变化曲线. 图3 所示光场对低能区电子在上述两结构中的自旋过滤效应有明显的增强效应, 并且随着光子能量的增加, 增强呈现出正响应. 在一些特定条件下(B 2 = 3, $ k_{y} = -0.5, E = 5.36, E_{\rm {photon}} = 3 $ ), 自旋极化度甚至高达90%以上. 在同向等强度$ {\text{δ}} $ 型磁垒结构中, 对比图3(c) , 图3(d) 和图3(d) 中的插图可知, 包含光场时的自旋极化度比不包含光场时要高出一个数量级, 在$ k_{y} = -0.5 $ 时, 增强效应更加明显.图 3 自旋极化度随入射能量的变化 (a)?(b) $ B_{1} = -B_{2} $ ; (c)?(d) $ B_{1} = B_{2} $ Figure3. Spin polarization as the function of the incident energy: (a)?(b) $ B_{1} = -B_{2} $ ; (c)?(d) $ B_{1} = B_{2} $ 3.2.包含电势垒 -->3.2.包含电势垒 图4 给出了反向等强度$ {\text{δ}} $ 型磁电垒结构(图4(a) —图4(d) )和同向等强度$ {\text{δ}} $ 型磁电垒结构(图4(e) —图4(h) )在$ U(x) = 2 $ 时的电子透射几率变化关系曲线. 这里除了考虑了电势垒的影响, 其他参数与图2 完全相同. 作为对照, 图4(a) 和图4(e) 给出了不包含光场的透射几率曲线. 由图4 可以看出, 随着$ k_{y} $ 的增大, 透射几率曲线向高能区域移动, 这一点与图2 中不含电势垒的情形相同, 伴随光子能量增加, 电子在低能区域的透射几率明显增加. 然而, 在不考虑光场时可以达到完全透射的能量区域(例如$ B_{2} = -3, E = 11.46 $ )透射几率却明显减小, 这些计算结果表明光场与电子相互作用会伴随电子对光子的吸收和发射, 即低能入射电子因在光场辐照区吸收光子导致透射几率增加, 高能入射电子因为发射光子导致透射几率降低. 同样的结论在同向等强度$ {\text{δ}} $ 型磁电垒结构中也可以得到验证(见图4(e) —图4(h) ). 另外, 通过图4 可以看到, 光场在该结构中对电子隧穿过程的调制作用, 主要体现在通过改变光场频率可以明显改变自旋透射几率. 在反向等强型结构中, 不考虑光场调制作用时, 自旋向上和自旋向下的电子透射几率曲线完全相同; 考虑光场作用时, 不同自旋指向电子的透射几率随着光场频率的增加差异性明显增加. 在同向等强度型结构中, 自旋向上和自旋向下电子的透射几率因为光场的调制作用而出现了更为明显的分离, 这势必会引起自旋极化度的提高.图 4 电子隧穿磁电垒结构透射几率谱 (a)?(d) $ B_{1} = -B_{2} $ ; (e)?(h) $ B_{1} = B_{2} $ Figure4. Transmission probabilities as the function of the incident energy: (a)?(d) $ B_{1} = -B_{2} $ ; (e)?(h) $ B_{1} = B_{2} $ 图5 给出了包含电势垒时自旋极化度的变化曲线. 计算结果显示, 光场对磁电垒结构中低能区域电子的自旋极化度的影响较为明显, 并且$ k_{y} $ 为负值时光场的影响最为明显, 为零时次之, 为正值时影响最小. 图5(e) 中插图是同向等强度$ {\text{δ}} $ 型磁电垒结构中不包含光场作用时自旋极化度变化曲线, 对比可以发现光场对自旋极化度调节有显著增强作用. 此外, 如图5(a) —图5(c) 所示, 伴随光子能量的增加, 反向等强磁电垒结构中自旋过滤效应也随之增强, 即通过改变光场频率可以实现对该结构中自旋过滤效应的调控. 在同向等强磁电垒结构中(图5(d) —图5(f) ), 对比可以发现: 由于光场的调制作用, 自旋极化度增加了一个数量级, 伴随光子能量增加, 自旋极化度变化曲线发生了蓝移.图 5 自旋极化度随入射能量的变化关系 (a)?(c) $ B_{1} = -B_{2} $ ; (d)?(f) $ B_{1} = B_{2} $ Figure5. Spin polarization as the function of the incident energy: (a)?(c) $ B_{1} = -B_{2} $ ; (d)?(f) $ B_{1} = B_{2} $ 4.结 论 对比研究了电子隧穿两类不同磁电垒结构的自旋极化, 重点对比了包含光场与不包含光场时自旋输运的不同特性. 计算结果表明光场对所研究结构中电子的自旋隧穿有明显的调制作用: 在B 1 = –B 2 的反向等强度$ {\text{δ}} $ 型磁电垒结构中, 不施加光场时, 该类磁电垒结构中不存在自旋过滤效应, 当施加光场时, 可以使该结构具备自旋过滤效应, 并且在低能区域可以实现自旋极化度的明显增强; 在$ B_{1} = B_{2} $ 的同向等强度$ {\text{δ}} $ 型磁电垒结构中, 这类结构不施加光场也具备自旋过滤效应, 但是与考虑光场对比可以发现, 光场可以使自旋过滤效应明显增强, 增强程度超过一个数量级; 最后通过对比有无电势垒可以发现, 磁垒不变的情况下, 可以不考虑电势垒, 只施加光场来达到自旋过滤的优化调控. 
图 1 光场
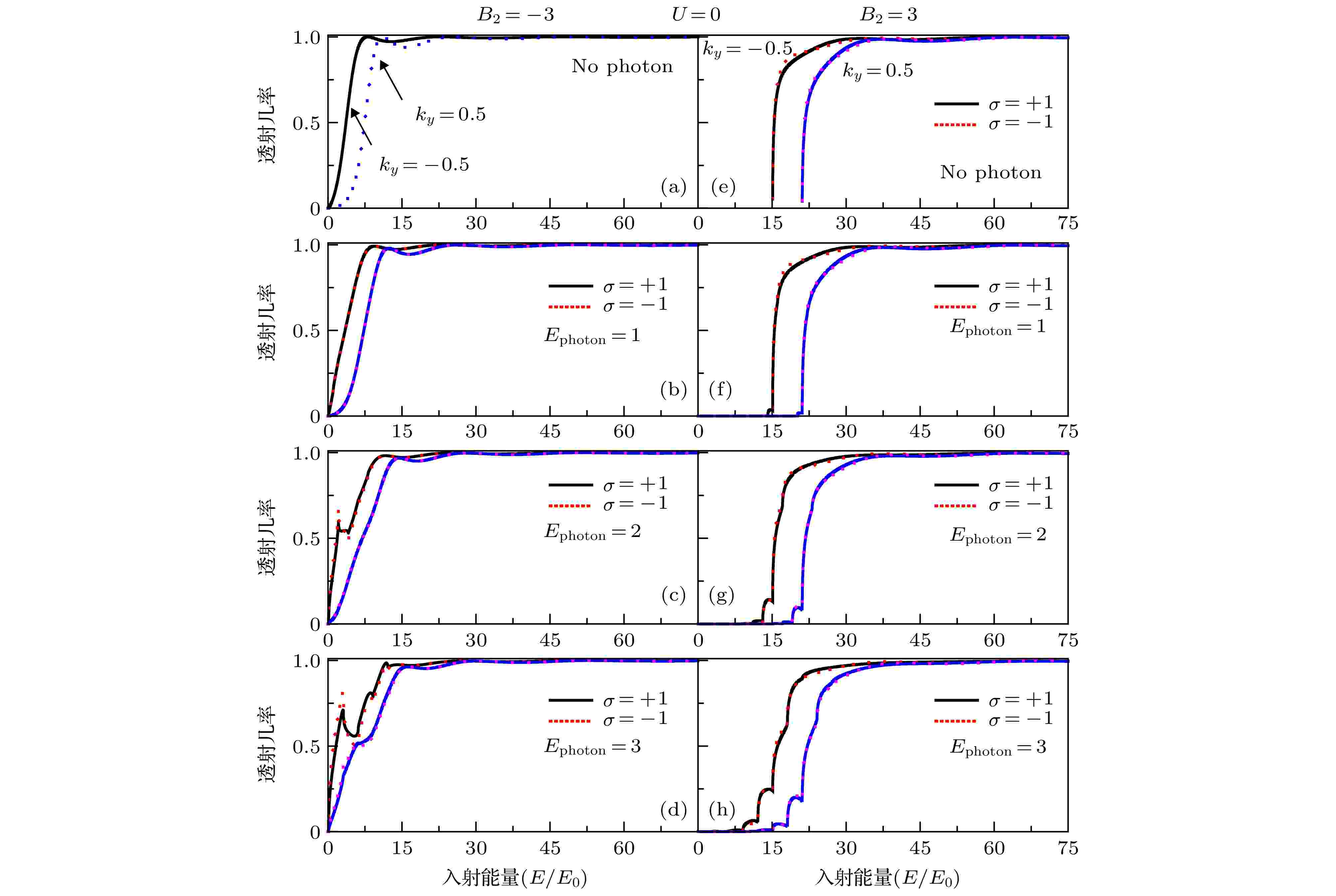图 2 电子隧穿磁垒结构透射几率谱 (a)?(d)反向等强度
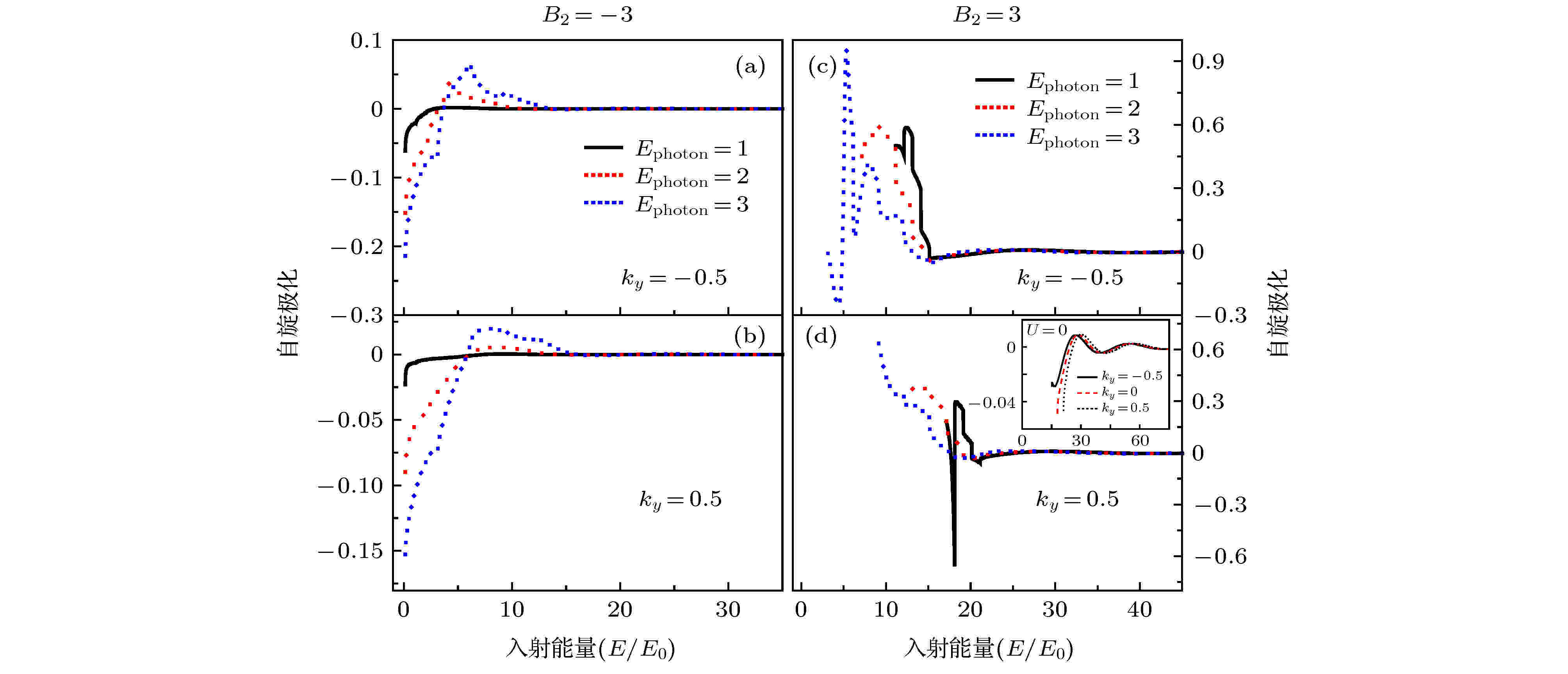图 3 自旋极化度随入射能量的变化 (a)?(b) 
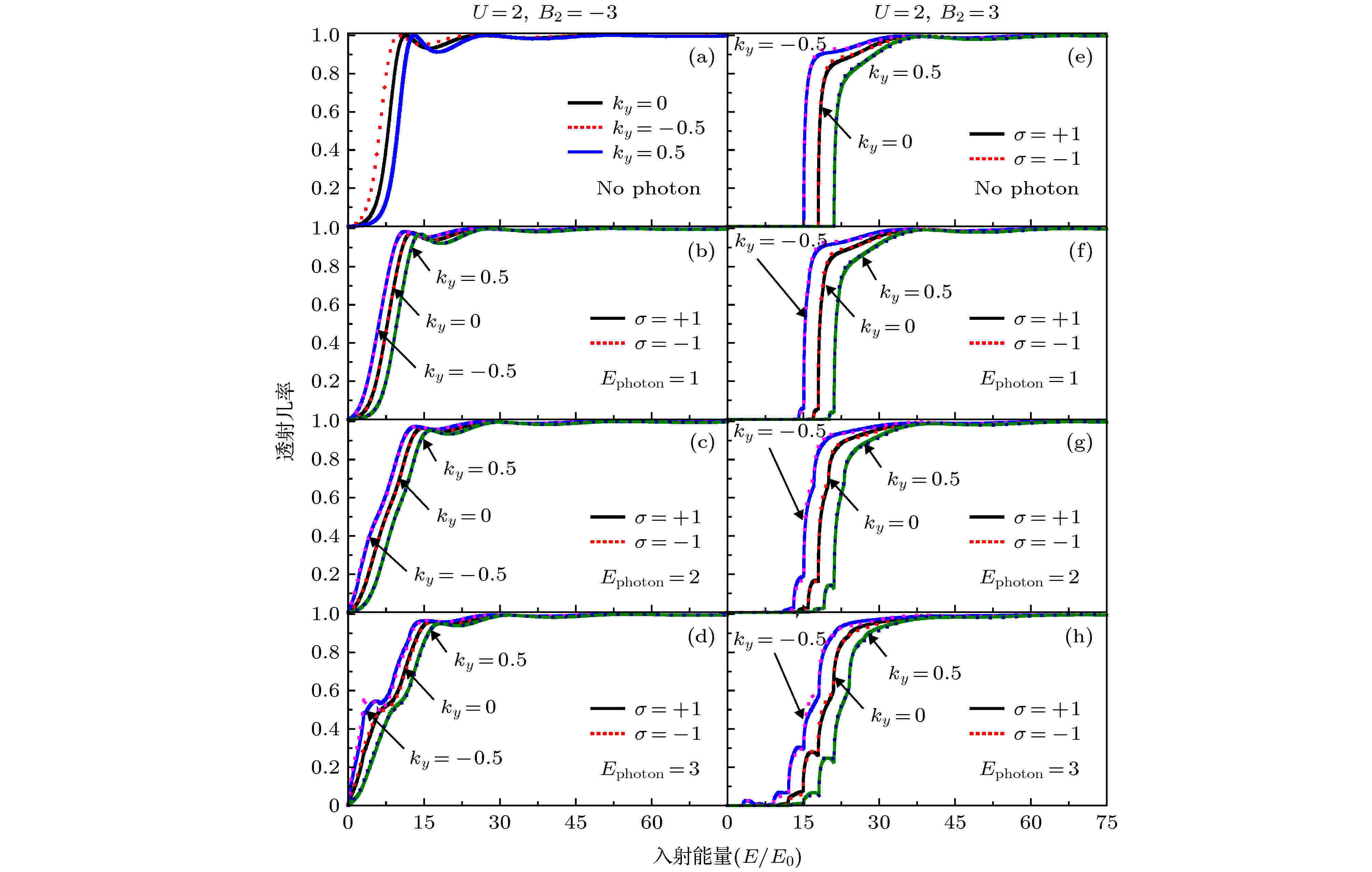图 4 电子隧穿磁电垒结构透射几率谱 (a)?(d) 
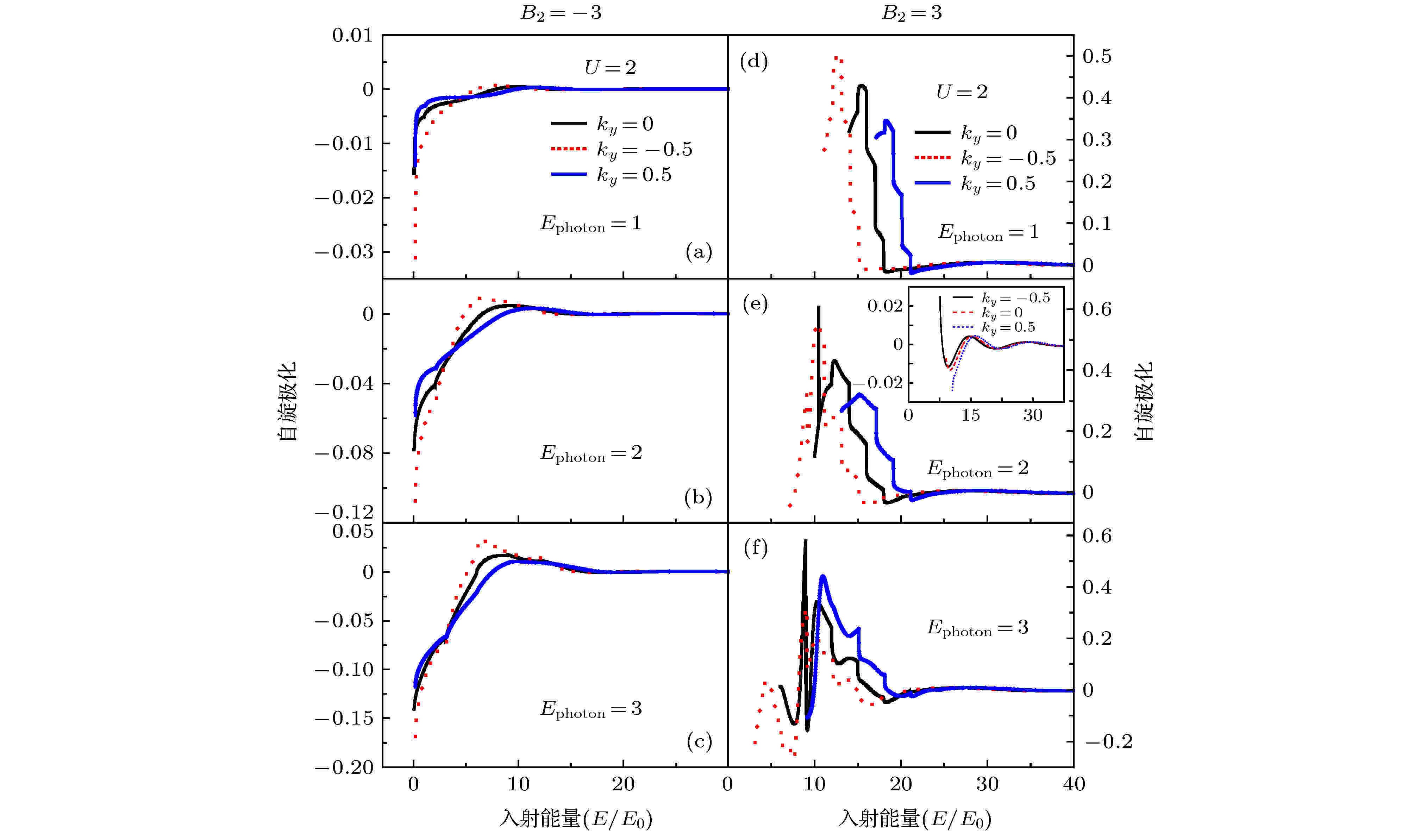图 5 自旋极化度随入射能量的变化关系 (a)?(c) 
