摘要:提出了一种磁流变液构成的类梯度结构, 并通过理论建模、数值计算和实验研究了该结构的振动传递特性. 磁流变液在磁场作用下具有液固转换的特殊理化性质, 而液固转换过程就是磁流变液的振动传递阻抗变化过程. 因此, 基于磁流变液的这一特性, 通过控制磁场, 构建了类梯度结构. 基于弹性波传递的一维波动方程, 建立了垂直入射的弹性波在类梯度结构中传递的波动方程. 然后, 使用连续介质的离散化方法和传递矩阵法进行求解, 得到振级落差的表达式, 对其进行数值计算, 分析类梯度结构的振级落差随弹性波频率和磁场强度的变化趋势. 最后, 对类梯度结构的振动传递特性进行了实验研究, 分析了磁场强度对类梯度结构振动传递特性的影响. 研究结果表明, 与均匀场作用的磁流变液相比, 类梯度结构对弹性波的衰减效果更好, 且该结构具备良好的可调控特性.
关键词: 磁流变液/
类梯度结构/
弹性波传递/
振级落差

English Abstract

全文HTML

--> --> -->

磁流变液是一种可快速响应的智能材料, 在磁场作用下, 其材料特性可以迅速发生变化, 且这个过程可控、可逆, 即在撤去磁场后, 磁流变液可在瞬间变回初始状态^[1-3]. 1948年, 美国****Rabinow^[4]首次提出磁流变液的概念. 在这之后, 人们开发了诸多基于磁流变液的智能设备, 例如阻尼器、离合器以及制动器等^[5-8]. 但是, 对于弹性波在磁流变液中传递和衰减的研究还很少.
Jozefczak等^[9,10]利用超声波传播光谱学研究了在外加磁场作用下铁磁流体的结构变化, 并通过实验研究了铁磁流体中超声波与磁场平行时超声波声速的时间响应特性. Bramantya等^[11-13]对超声波在磁流变材料内的传播特性做了大量的研究, 发现超声波在磁流体中传播速度和能量衰减的大小不仅与超声波频率、外加磁场强度、磁场方向和超声波传播方向的夹角有关, 还与温度和加上磁场后的弛豫时间有关. Lee等^[14]在Bolton提出的弹性多孔材料在随机入射和垂直入射下的弹性波传播特性的基础上, 结合Biot理论研究了流变材料的波传播模型, 实验结果和模型有较好的一致性. Mahjoob等^[15]研究了垂直入射场下, 可听声频段内的声波在磁流变液中的传播特性, 在低频段内模型与实验结果有较好的一致性, 且声波随着外部磁场的增加明显衰减, 整个频段内的衰减特性则表现出很强的非线性. Rodríguez-López等^[16]通过实验研究了磁感应强度以及磁场均匀性对超声波在磁流变液中传播速度的影响. 文娟等^[17]研究了磁场方向与超声波不同夹角的传播特性, 并设计了相关实验装置.
对于弹性波在磁流变液中传递和衰减的研究多数集中在声波上, 对于低频弹性波传递特性的研究相对较少. Liu等^[18]和Zhao等^[19]基于磁流变液的流变特性搭建了阻抗可调制结构, 并研究了弹性波在其中的传递特性, 结果表明通过调制磁流变液的材料特性可有效地控制弹性波的传递和衰减. 但是, 他们的研究是将磁场作用下的磁流变液等效为一种孔隙介质, 无法反映磁流变液材料特性的连续变化.
梯度结构是通过将不同参数的材料逐层叠加形成的结构, 其参数会发生阶梯性变化, 具有特殊的性质. Hasheminejad和Maleki^[20]对功能梯度材料的声学特性进行研究, 得到了水下多层球体壳的声学性能计算公式. 近年来, 人们不再满足于在宏观上将材料叠加, 而是转向研究在介质内部形成参数“类梯度”变化, 被称为材料属性梯度渐变结构. 在波传递介质研究中, 主要将材料属性梯度渐变结构分为三类, 分别是尖劈状梯度声学结构、波阻抗渐变结构以及梯度渐变特性介质. 其中, 波阻抗渐变结构是由波阻抗逐渐变化的非均匀介质制备成, 也被称为类梯度结构. 哈尔滨工程大学的杨德森院士等^[21]制备了阻抗梯度变化材料, 并研究了声波在其中的传递特性. 类梯度结构对弹性波有很优良的衰减作用, 而且能够实现阻抗匹配, 广受研究人员关注. 但是, 这种结构在设计完成后, 一般无法对外部激励的变化作出响应, 不具备适应性.
因此, 本文基于磁流变液的流变特性, 结合磁场的边缘效应, 构建一种类梯度结构, 并基于弹性力学提出了一种新的等效方法, 研究低频弹性波在该结构中的传递特性.
本文的主要内容如下: 首先, 构建磁流变液构成的类梯度结构, 建立弹性波在其中传递的波动方程. 其次, 为求解波动方程, 建立磁流变液的等效参数模型, 并通过实验对其进行修正. 然后, 对波动方程进行数值计算, 分析类梯度结构的振动传递特性随弹性波频率和磁场强度的变化趋势. 最后, 对类梯度结构的振动传递特性进行实验研究.

梯度结构能够实现阻抗匹配, 且对弹性波具有良好的衰减性能. 虽然梯度结构具有较强的可设计性, 但是一旦参数确定后性能也就固定了, 材料无法随着弹性波性质的变化做出响应. 磁流变液作为一种参数可调的新型智能材料, 可通过控制磁场实现磁流变液材料参数的连续变化. 因此, 本文将使用磁流变液构建一种参数可调的“类梯度”结构.
磁场存在边缘效应, 因此, 当磁场强度从大变小时, 处在磁场连续变化区域的磁流变液的阻抗也是连续变化的, 会形成一种材料参数连续变化的类梯度结构, 其原理如图1所示. 图中, $ (0—x_0) $段为无磁场作用区域, 磁流变液为黏滞液体, 阻抗值为一定值Z₀; $ (x_0—x_1) $段为磁场强度渐变区域, 磁流变液由黏滞液体转变为类固体, 且其阻抗随着磁场强度发生变化, 阻抗值为Z(x), 且Z₀ < Z(x) < Z₁, 即本文研究的类梯度结构, 可将其等效成由若干个厚度为d的匀质类固态磁流变液构成; $ (x_1—x_2) $段为磁场均匀分布区域, 该区域中的磁流变液转变为阻抗均匀分布的类固体, 其阻抗值为一定值Z₁.
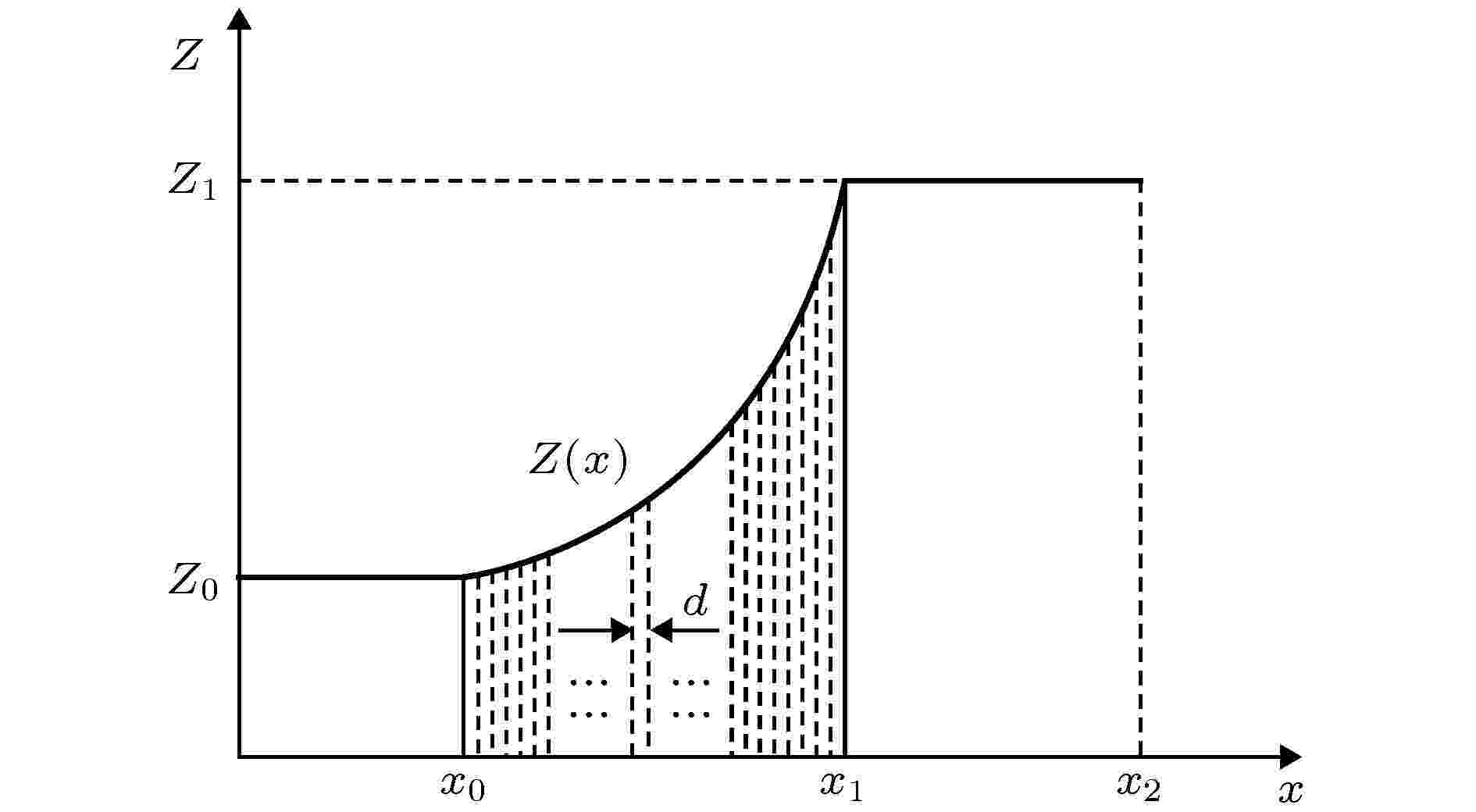图 1 阻抗分布示意图
Figure1. Impedance distribution diagram.

搭建磁流变液构成的类梯度结构的实验装置如图2所示. 可以通过改变电磁铁的数量调节磁场作用区域的厚度, 通过调节通入电磁铁中的电流大小改变磁场强度. 该结构主要包括引振活塞、阻抗管、电磁铁以及支撑单元. 弹性波通过引振活塞传递到阻抗管中的磁流变液中, 阻抗管被电磁铁围绕, 可通过改变通入电磁铁中的电流改变磁场强度的大小. 电磁铁和支架间使用销连接, 便于改变电磁铁的排布形式. 使用上述结构, 可形成一段磁场强度连续变化区域. 这个区域中的磁流变液就构成了本文要研究的类梯度结构.
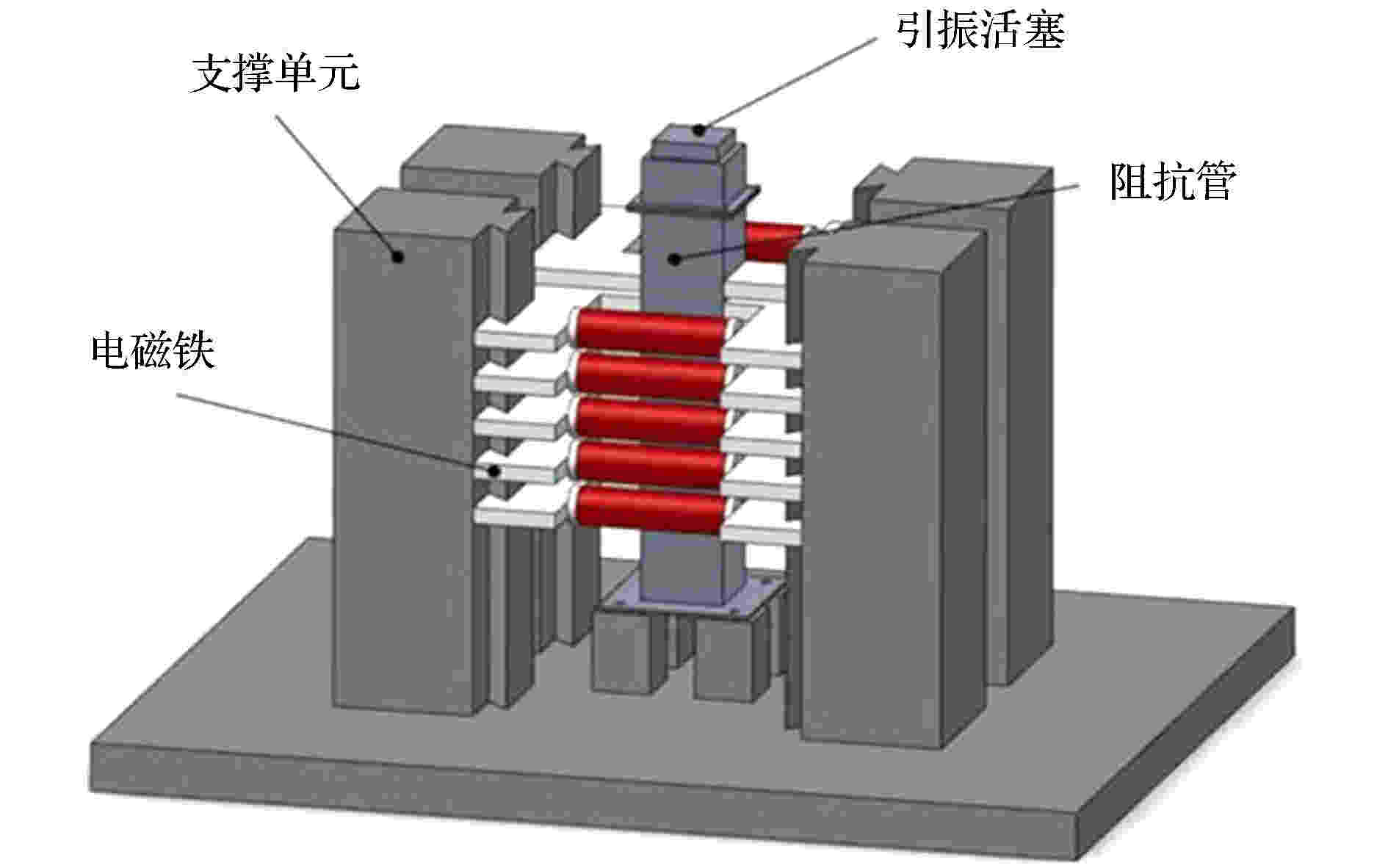图 2 磁流变液构成的类梯度结构示意图
Figure2. Schematic diagram of the experimental device for constructing gradient-like structure.

2

-->

3.1.理论建模

磁化后的磁流变液由黏滞液体转变为类固体. 因此, 在外加磁场作用时, 磁流变液主要变现出固相的特性. 本文将磁场作用下的磁流变液等效为一种材料属性受外界磁场控制的类固态介质, 使用振动理论中一维弹性波传递的波动方程, 建立垂直入射的弹性波在类固态磁流变液中传递的波动方程为

$c_{\rm{L}}^2\frac{{{\partial ^2}\xi (x,t)}}{{\partial {x^2}}} = \frac{{{\partial ^2}\xi (x,t)}}{{{\partial ^2}t}},$

其中, $\xi (x, t)$为弹性波的位移函数; ${c_{\rm{L}}}$为波速, 且${c_{\rm{L}}} = \sqrt {{K / \rho }} $, K为磁流变液的弹性系数, $\rho $为磁流变液的密度.
磁流变液的材料特性与磁场相关, 磁场强度的大小沿x方向发生变化, 所以本文研究的类梯度结构的材料特性只在单一坐标轴x方向上发生变化. 因此, 一维弹性波在类梯度结构中的波动方程可写为

$K(x)\frac{{{\partial ^2}\xi (x,t)}}{{\partial {x^2}}} = \rho \frac{{{\partial ^2}\xi (x,t)}}{{{\partial ^2}t}},$

其中$\rho $为磁流变液的等效密度; $K(x)$为弹性系数, 且$K(x) \!=\! \lambda (x) \!+\! 2\mu (x)$; $\xi (x, t)$为弹性波的位移函数.
2 -->

3.2.模型求解

当入射的弹性波是简谐波时, 其位移函数为

$\xi (x,t) = \xi (x){{\rm{e}}^{{\rm{i}}\omega t}},$

其中$\omega $为弹性波的角频率.
将(3)式代入(2)式中, 可得

$-{\omega ^{\rm{2}}}\rho \xi (x) = K(x)\frac{{{\partial ^2}\xi (x)}}{{\partial {x^2}}},$

令k(x)为

$k(x) = {\omega \bigg/ {\sqrt {\frac{{K(x)}}{\rho }} }},$

则(2)式可简化为

$\frac{{{\partial ^2}\xi (x)}}{{\partial {x^2}}} + {k^2}(x)\xi (x) = 0.$

(6)式为二阶齐次变系数微分方程, 无法使用特征方程进行求解. 此外, 由于系数函数k(x)与磁流变液的弹性模量、剪切模量、密度和泊松比等参数有关, 而上述参数又与外加磁场的磁场强度有关, 并不能保证系数k(x)一直满足微分方程的求解条件. 直接对其求解十分困难, 且不一定能求出精确解, 需要借助其他方法进行求解. 因此, 本文选择使用连续介质的离散化方法和传递矩阵法进行求解. 将类梯度结构沿着x方向进行微分, 微分成若干个厚度为d的匀质类固态磁流变液, 如图1所示.
类固态磁流变液中某质点的位移和应力可表示为

$\left\{ {\begin{aligned}& {{u_x} = \xi (x,t),} \\& {{\sigma _x} = (\lambda + 2\mu )\frac{{\partial \xi (x,t)}}{{\partial x}},} \end{aligned}} \right.$

对应的状态向量为

$\begin{split}\; & {{V}} = \left[ {\begin{aligned} {{u_x}} \\ {{\sigma _x}} \end{aligned}} \right] =\\ {}& \left[\!\!\!{\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {\rm{i}}{k_L}x}}}&{{{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}x}}} \\ { - {\rm{i}}(\lambda + {\rm{2}}\mu ){k_{\rm{L}}}{{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}x}}}&{{\rm{i}}(\lambda + {\rm{2}}\mu ){k_{\rm{L}}}{{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}x}}} \end{array}}\!\!\!\right]\left[ {\begin{aligned} A \\ B \end{aligned}} \right].\end{split}$

因此, 单层磁流变液入射点的状态向量V_in可表示为

$\begin{split}\;& {{{V}}_{{\rm{in}}}} = \left[ {\begin{aligned} {{u_{x{\rm{in}}}}} \\ {{\sigma _{x{\rm{in}}}}} \end{aligned}} \right] \\ ={}& \left[\!\!\!{\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}x}}}&{{{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}x}}} \\ { - {\rm{i}}(\lambda + {\rm{2}}\mu ){k_{\rm{L}}}{{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}x}}}&{{\rm{i}}(\lambda + {\rm{2}}\mu ){k_{\rm{L}}}{{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}x}}} \end{array}}\!\!\!\right]\left[ {\begin{aligned} A \\ B \end{aligned}} \right] \\ ={}& {{{\varGamma}} _{{\rm{in}}}}{{A}},\\[-15pt]\end{split}$

单层磁流变液射出点的状态向量V_out可表示为

${V_{{\rm{out}}}} = \left[ {\begin{aligned} {{u_{x{\rm{out}}}}} \\ {{\sigma _{x{\rm{out}}}}} \end{aligned}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}(x + L)}}}&{{{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}(x + L)}}} \\ { - {\rm{i}}(\lambda + {\rm{2}}\mu ){k_{\rm{L}}}{{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}(x + L)}}}&{{\rm{i}}(\lambda + {\rm{2}}\mu ){k_{\rm{L}}}{{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}(x + L)}}} \end{array}} \right]\left[ {\begin{aligned} A \\ B \end{aligned}} \right] = {{{\varGamma}} _{{\rm{out}}}}{{A}},$

入射点和射出点的状态向量之间的关系为

${{{V}}_{{\rm{out}}}} = {{{\varGamma}} _{{\rm{out}}}}{{{\varGamma}} '_{{\rm{in}}}}{{{V}}_{{\rm{in}}}} = {{{T}}_{\rm{g}}}{{{V}}_{{\rm{in}}}},$

其中${{{\varGamma}} '_{{\rm{in}}}}$为矩阵${{{\varGamma}} _{{\rm{in}}}}$的逆阵; ${{{T}}_{\rm{g}}}$为类梯度的传递矩阵.
因此, 当弹性波垂直射入厚度为d的匀质类固态磁流变液时, 其传递矩阵为

${{{T}}_{\rm{g}}} \!=\! \left[\!\!\!{\begin{array}{*{20}{c}} {\dfrac{{{{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}d}} + {{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}d}}}}{2}}&{\dfrac{{{\rm{i}}({{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}d}} - {{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}d}})}}{{2{k_{\rm L}}(\lambda + 2\mu )}}} \\ {\dfrac{{{\rm{i}}{k_{\rm{L}}}(\lambda + 2\mu )({{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}d}} - {{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}d}})}}{2}}&{\dfrac{{{{\rm{e}}^{{\rm{i}}{k_{\rm{L}}}d}} + {{\rm{e}}^{ - {\rm{i}}{k_{\rm{L}}}d}}}}{2}} \end{array}}\!\!\!\right].$

经过微分处理后, 类梯度材料的每一个微分层都可等效为参数不同的匀质类固态磁流变液. 因此, 可以借助相同的形式对弹性波的传递进行描述. 在每一层中, 位移和应力的关系为

$\begin{split}& \left[ {\begin{aligned} {{u_{id}}} \\ {{\sigma _{id}}} \end{aligned}} \right]= \\\; & \left[\!\!\!{\begin{array}{*{20}{c}} {\dfrac{{{{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} + {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}}}}{2}}&{\dfrac{{{\rm{i}}({{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}} - {{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}})}}{{2{k_{{\rm{L}}i}}({\lambda _i} + 2{\mu _i})}}} \\ {\dfrac{{{\rm{i}}{k_{{\rm{L}}i}}({\lambda _i} \!+\! 2{\mu _i})({{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} \!-\! {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}})}}{2}}&{\dfrac{{{{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} + {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}}}}{2}} \end{array}}\!\!\!\right]\\ & \times\left[ {\begin{aligned} {{u_{(i - 1)d}}} \\ {{\sigma _{(i - 1)d}}} \end{aligned}} \right],\\[-18pt]\end{split}$

其中i为层数, $1 < i \leqslant n$, n为总层数; d为微分后每一层的厚度; ${\lambda _i}, {\mu _i}$为微分后每一层匀质类固态磁流变液的等效拉梅常数, k_Li为弹性波在每一层中传递的波数.
因此, 弹性波在类梯度结构中传递时, 弹性波入射点和射出点的位移与应力的关系为

$\left[ {\begin{aligned} {{u_{\rm{L}}}} \\ {{\sigma _{\rm{L}}}} \end{aligned}} \right] = \prod\limits_{i = 1}^n {\left[ {\begin{array}{*{20}{c}} {\dfrac{{{{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} + {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}}}}{2}}&{\dfrac{{{\rm{i}}({{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}} - {{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}})}}{{2{k_{{\rm{L}}i}}({\lambda _i} + 2{\mu _i})}}} \\ {\dfrac{{{\rm{i}}{k_{{\rm{L}}i}}({\lambda _i} + 2{\mu _i})({{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} - {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}})}}{2}}&{\dfrac{{{{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} + {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}}}}{2}} \end{array}} \right]} \left[ {\begin{aligned} {{u_0}} \\ {{\sigma _0}} \end{aligned}} \right],$

弹性波在类梯度结构中传递的传递矩阵为

${{T}} = \prod\limits_{i = 1}^n {\left[ {\begin{array}{*{20}{c}} {\dfrac{{{{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} + {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}}}}{2}}&{\dfrac{{{\rm{i}}({{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}} - {{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}})}}{{2{k_{{\rm{L}}i}}({\lambda _i} + 2{\mu _i})}}} \\ {\dfrac{{{\rm{i}}{k_{{\rm{L}}i}}({\lambda _i} + 2{\mu _i})({{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} - {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}})}}{2}}&{\dfrac{{{{\rm{e}}^{{\rm{i}}{k_{{\rm{L}}i}}d}} + {{\rm{e}}^{ - {\rm{i}}{k_{{\rm{L}}i}}d}}}}{2}} \end{array}} \right]},$

类梯度结构入射点处的状态向量为

${{{V}}_0} = \left[ {\begin{aligned} {{u_0}} \\ {{\sigma _0}} \end{aligned}} \right] = \left[ {\begin{array}{*{20}{c}} {{U_0} + {U_1}} \\ {{\rm{i}}{K_0}{k_0}({U_1} - {U_0})} \end{array}} \right],$

其中K₀为入射点所处微分层的磁流变液的等效弹性系数, ${K_0} = \rho c_0^2$; k₀为该微分层的波数; U₀和U₁分别为入射点处的入射波振幅和反射波振幅.
类梯度结构射出点处的状态向量为

${{{V}}_{\rm{e}}} = \left[ {\begin{aligned} {{u_{\rm{L}}}} \\ {{\sigma _{\rm{L}}}} \end{aligned}} \right] = \left[ {\begin{array}{*{20}{c}} {{U_{\rm{L}}}} \\ { - {\rm{i}}{K_{\rm{e}}}{k_{\rm{e}}}{U_{\rm{L}}}} \end{array}} \right],$

其中K_e为射出点所处微分层的磁流变液的等效弹性系数, ${K_{\rm{e}}} = \rho c_{\rm{e}}^2$; k_e为该微分层的波数; U_L为射出点处的透射波振幅.
由传递矩阵法可得入射点处的状态向量V₀、射出点处的状态向量V₁以及传递矩阵T_g之间的关系为

${{{V}}_1} = {{{T}}_{\rm{g}}}{{{V}}_0},$

具体可表示为

$\left\{ {\begin{aligned}& {{u_1} = {T_{11}}{u_0} + {T_{12}}{\sigma _0},}\\& {{\sigma _1} = {T_{21}}{u_0} + {T_{22}}{\sigma _0},}\end{aligned}} \right.$

其中T_ij为传递矩阵T中第i行、第j列的元素, 即${{{T}}_{ij}} = {{T}}(i, j)$.
将(16)式和(17)式代入(19)式中可得磁流变液构成的类梯度结构的透射系数为

$\begin{split}& T = {{{U_{\rm{L}}}}}/{{{U_0}}} =\\ & \frac{{2{\rm{i}}({T_{11}}{T_{22}} - {T_{12}}{T_{21}}){K_0}{k_0}}}{{{K_0}{k_0}({\rm{i}}{T_{11}} - {K_0}{k_0}{T_{12}}) + ({T_{21}} + {\rm{i}}{K_0}{k_0}{T_{22}})}}.\end{split}$

使用振级落差作为衡量振动传递特性的参数指标, 振级落差越大, 该结构对弹性波的衰减效果越好. 振级落差的表达式为

$L = 20\lg \left({{{U_0}}}/{{{U_1}}}\right).$

将(20)式代入(21)式中可得磁流变液构成的类梯度结构中, 弹性波传递的振级落差为

$\begin{split} & L = 20\lg \left( {{1}/{T}} \right) = \\ {}& 20\lg \left[ {\frac{{{K_0}{k_0}({\rm{i}}{T_{11}} - {K_0}{k_0}{T_{12}}) + ({T_{21}} + {\rm{i}}{K_0}{k_0}{T_{22}})}}{{2{\rm{i}}({T_{11}}{T_{22}} - {T_{12}}{T_{21}}){K_0}{k_0}}}} \right].\end{split}$

当磁流变液受力或接收到外界传来的弹性波时, 其内部会产生相应的应力和应变, 一部分能量会因为磁流变液中铁磁颗粒的摩擦和碰撞而被耗散, 一部分能量会因为磁流变液本身的弹性被转化成势能储存起来. 因此, 磁流变液的剪切模量可表示为

${G^*}(H) = G'(H) + {\rm{i}}G''(H),$

其中$G'(H)$反映了磁流变液的储能特性, 其值主要受磁流变液的弹性的影响; $G''(H)$反映了磁流变液的耗能特性, 其值主要受磁流变液黏性的影响; H为磁场强度.
Sun等^[22]通过实验研究得到了该表达式的具体形式为

$G'(H) = 3.11 \times {{1}}{{{0}}^{ - {{7}}}}{H^2} + 3.56 \times {{1}}{{{0}}^{ - {{4}}}}H + 0.578,$

$G''(H) = 3.47 \times {{1}}{{{0}}^{ - {{9}}}}{H^2} + 3.{{85}} \times {{1}}{{{0}}^{ - {{6}}}}H + {{6}}.{{31}} \times {{1}}{{{0}}^{ - {{3}}}},$

其中, $G'(H)$为储能模量, 单位为MPa; $G''(H)$为耗能模量, 单位为 MPa; H 为磁场强度, 单位为Oersted (1 Oersted = 1/4π × 10^–3 A/m).
在外加磁场作用下, 磁流变液会变成类固态, 主要体现固态性质. 因此, 借鉴弹性力学中的相关关系, 计算磁流变液的等效拉梅常数为

$\left\{ {\begin{aligned}& {\mu = {G^*},} \\& {\lambda = \frac{{Ev}}{{(1 + v)(1 - 2v)}},} \\& {E = 2(1 + v){G^*}.} \end{aligned}} \right.$

磁流变液由载液、铁磁颗粒和添加剂组成, 其中, 添加剂的添加量一般非常小. 因此, 在计算磁流变液的等效密度时, 将添加剂的密度忽略不计. 磁流变液的等效密度为

$\rho = {\rho _{\rm{f}}}\theta + {\rho _{\rm{r}}}(1 + \theta ),$

其中${\rho _{\rm{f}}}$为磁流变液中铁磁颗粒的密度, ${\rho _{\rm{r}}}$为磁流变液的载液密度, $\theta $为体积分数. 将相关参数代入可得, 磁流变液的等效密度为$\rho = 2534.57$ kg/m³.
磁流变液本身属于固液两相体, 在磁场作用下虽然变成类固态, 主要体现固态性质, 但也能体现一部分液态性质. 但是, 本文使用的等效方法在一定程度上减小了磁流变液的液态特性对弹性波传递的影响. 在等效参数模型中, 最能体现磁流变液液态性质的就是复剪切模量的虚部, 即磁流变液的耗能属性. 因此, 应适当地将耗能模量进行放大.
由于磁流变液的参数会随磁场发生变化, 直接测量参数非常复杂, 且等效参数模型的数学意义大于物理意义, 直接测量的方式并不可行. 因此, 本文使用等效参数模型对匀质类固态磁流变液的振动传递特性进行研究, 和实验结果进行对比分析, 进而修正磁流变液的等效参数模型.
2

-->

4.1.均质磁流变液振动传递特性的数值计算

将全部参数和传递矩阵T_g代入(22)式, 使用MATLAB软件对其进行数值计算可得, 60 mm厚的匀质类固态磁流变液的振动传递特性随磁场强度B和频率f的变化趋势如图3所示.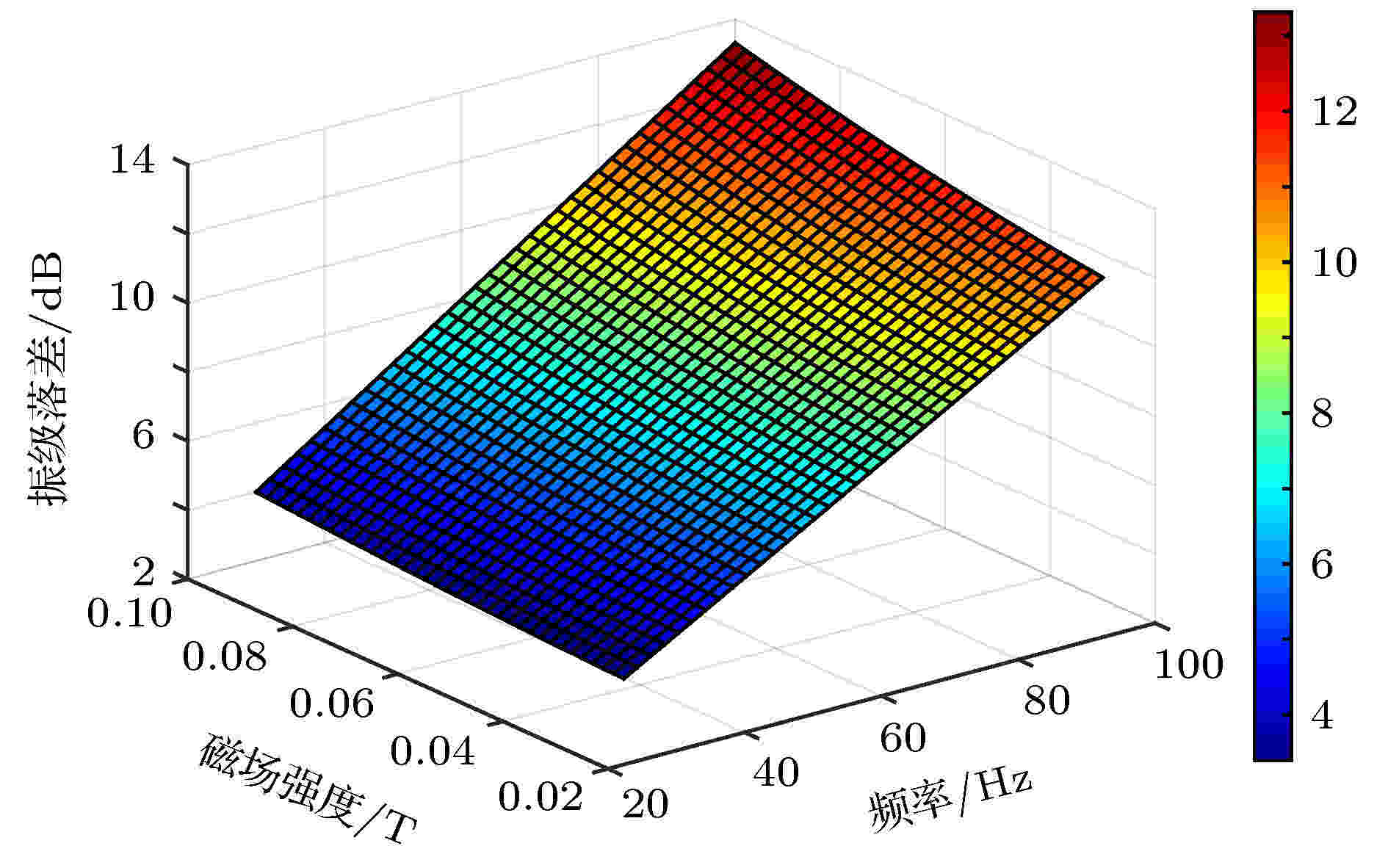
图 3 匀质类固态磁流变液的振动传递特性
Figure3. Vibration transfer characteristic of the homogeneous quasi-solid magnetorheological fluid.

由图3可得, 匀质类固态磁流变液结构的振级落差均大于0, 且振级落差的大小随频率和磁场发生变化. 证明磁流变液对弹性波具有衰减作用, 且衰减作用的大小与磁场强度和频率有关. 这是因为当外加磁场强度增大时, 磁流变液中的铁磁颗粒成链的程度随之增大, 场致结构也越发牢固, 相应地, 磁流变液的体积模量和剪切模量也随之增大. 因此, 磁流变液对弹性波的衰减作用随着磁场强度的增加而增大. 当输入的弹性波频率增加时, 弹性波的波速增加、波长减小, 磁流变液的阻抗对弹性波的影响越来越明显. 因此, 磁流变液对弹性波的衰减作用随频率的增加而增大. 综合以上两点分析, 数值计算的结果符合预期.
2 -->

4.2.均质磁流变液振动传递特性的实验研究

首先, 搭建了基于磁流变液的振动传递特性实验台, 如图4所示. 该实验台主要包括: 类梯度结构部分、振动信号发生部分以及数据采集部分. 其中, 类梯度结构部分主要包括阻抗管、电磁铁和台架, 振动信号发生部分包括信号发生器(YE1311)、功率放大器(YE5871A)和激振器(JKZ-2), 数据采集部分包括压电式振动传感器(LDT0-028K)、数据采集卡(USB_DAQ_HRF4626)和计算机. 选择阻抗管的材料为亚克力材料, 因为亚克力材料对磁场分布的影响很小且透光性好, 能实时观测到阻抗管内磁流变液的变化. 支撑部分选用铝合金材料, 能够最小化对磁场分布的影响, 且具备较好的力学性能以及加工性能. 磁流变液的型号为MRF-132DG, 其参数如表1所列.

性能名称	平均粒径	颗粒密度	载液密度	零场黏度	颗粒体积分数
	d/μm	${\rho _{\rm{f}}}$/kg·m–3	${\rho _{\rm{r}}}$/kg·m–3	$\eta $/Ns·m–2	$\theta $
参数值	5.5	6698	998	0.2425	27%

表1磁流变液性能参数
Table1.Characteristic parameters of the magnetorheological fluid.

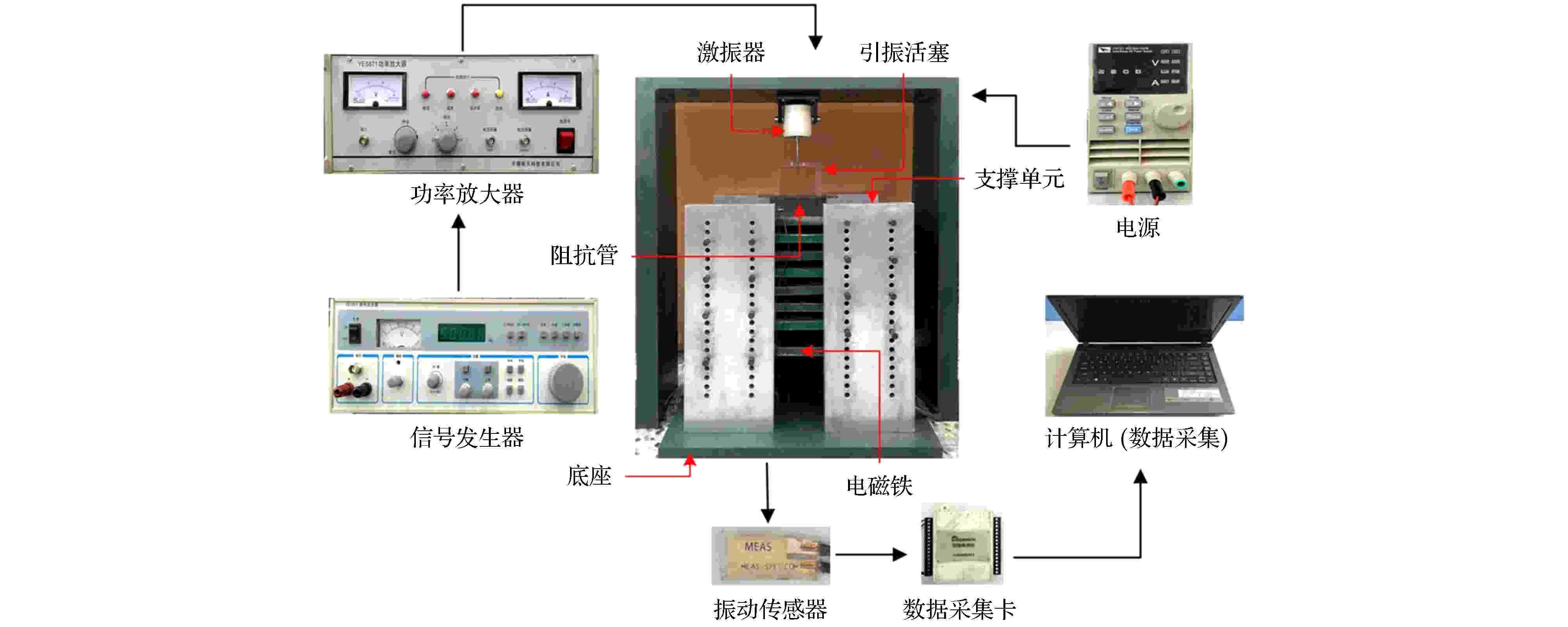图 4 实验台结构图
Figure4. Structure diagram of the experimental set-up.

在实验中, 由信号发生器产生正弦波激励信号, 以5 Hz为间隔, 调节输入正弦波的频率, 范围为30—100 Hz. 振动信号经过功率放大后作用于激振器. 激振器产生指定频率的正弦波, 通过引振活塞传递到磁流变液中. 传感器感知磁流变液中的弹性波传递, 将其转化成电压输出给数据采集卡, 然后传递到计算机上进行储存. 实验完成后, 调节电磁铁的输入电流, 使磁流变液所处的磁场发生变化, 变化范围为30—100 mT, 重复进行上述实验步骤. 实验结果和数值计算结果的对比如图5所示.
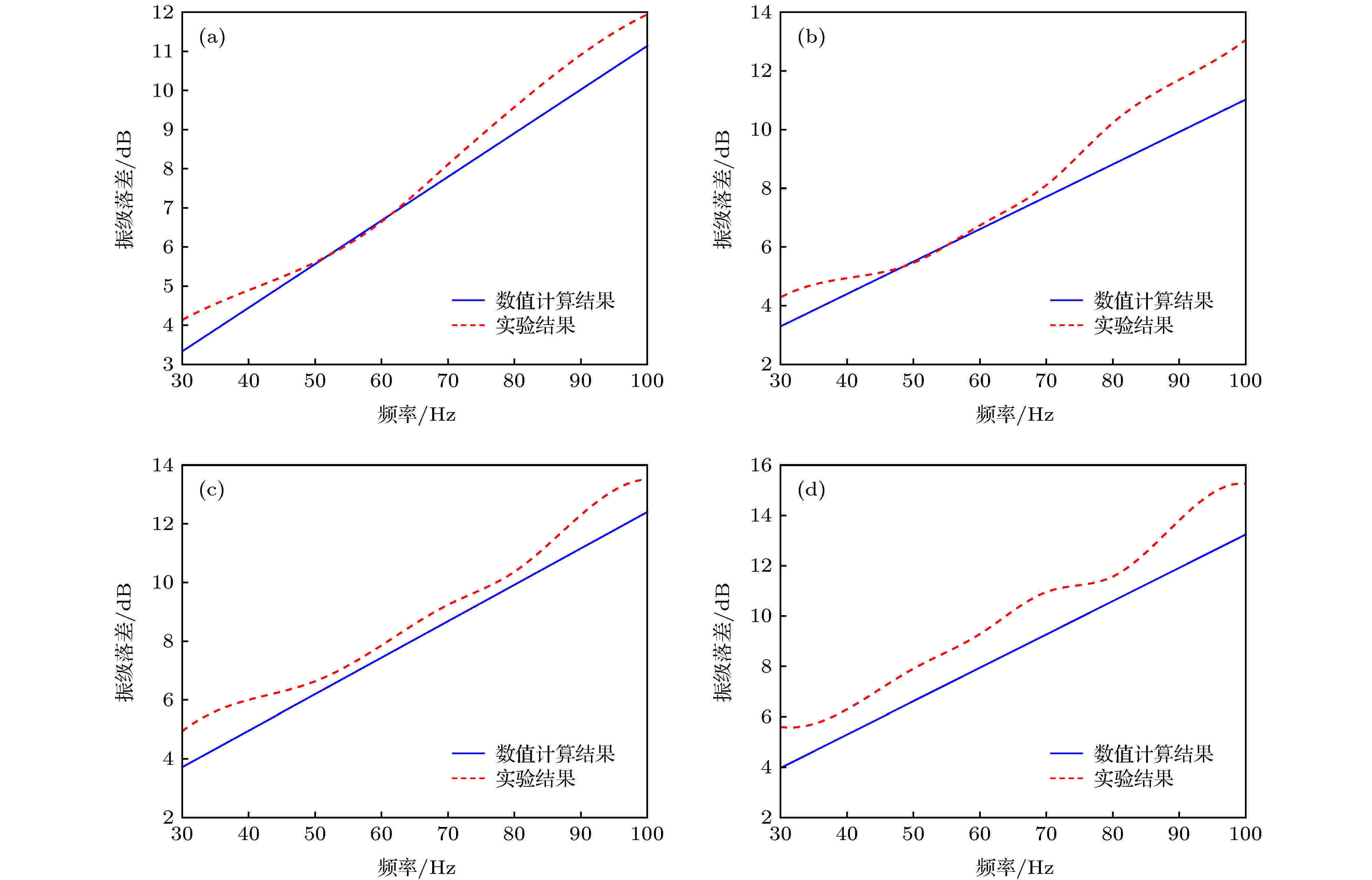图 5 不同磁场强度下的类固态磁流变液的振动传递特性对比　(a) 30 mT; (b) 50 mT; (c) 70 mT; (d) 100 mT
Figure5. Comparison of vibration transfer characteristic of quasi-solid magnetorheological fluid under different magnetic field: (a) 30 mT; (b) 50 mT; (c) 70 mT; (d) 100 mT.

2 -->

4.3.对比分析与模型修正

由图5可知, 数值计算结果和实验结果的变化趋势一致, 但在数值上仍存在一定的误差. 实验结果在数值上大于数值计算结果, 且磁场强度越大时误差就越大. 由上文分析可得, 造成此误差的主要原因是耗能模量. 因此, 需要将(25)式中的二次项和一次项系数进行放大.
将耗能模量模型的二次项和一次项放大共同倍数, 逐渐缩小修正区间, 提高修正精度. 首先将二次项系数和一次项系数同时放大2倍、5倍、10倍、15倍和20倍, 对修正后的模型进行数值计算, 可得到弹性波在类梯度结构中传递的振级落差. 以磁场强度为100 mT, 输入弹性波频率为100 Hz为例, 和实验结果进行对比, 结果如表2所列.

修正倍数	振级落差
	理论值/dB	实验值/dB	误差
2倍	9.6876	15.4419	37.31%
5倍	14.4739		6.27%
10倍	18.2995		18.51%
15倍	19.8275		28.40%
20倍	20.7795		34.57%

表2修正后的理论模型和实验结果对比
Table2.Comparison of numerical results and experimental results.

由表2可以看出, 当耗能模量的修正倍数在5—10倍之间时, 数值计算结果和实验结果之间的误差最小. 为了得到更加准确的修正系数, 应将此区间继续细分, 将数值计算结果和实验结果进行对比, 结果如表3所列.

修正倍数	振级落差
	理论值/dB	实验值/dB	误差
5倍	14.4739	15.4419	6.27%
6倍	15.5312		0.58%
7倍	16.4132		6.29%
8倍	17.1524		11.08%
9倍	17.7743		15.10%

表3修正后的理论模型和实验结果对比(5—10倍)
Table3.Comparison of numerical results and experimental results (5–10 times).

由表3可以看出, 当耗能模量修正倍数为6倍时, 将磁场强度为100 mT时外场作用下的磁流变液等效参数模型与实验结果最为接近, 误差仅为0.58%. 进一步对此修正系数进行验证, 以磁场强度为100 mT、输入弹性波频率为30—100 Hz为例, 对比数值计算结果和实验结果, 结果见表4.

输入弹性波频率	振级落差
	理论值/dB	实验值/dB	误差
30 Hz	5.1457	5.6042	8.18%
40 Hz	6.8610	6.7979	0.93%
50 Hz	8.5762	8.5199	0.66%
60 Hz	10.2915	10.2858	0.06%
70 Hz	12.0067	11.5679	4.3%
80 Hz	13.7219	12.8765	6.51%
90 Hz	14.4372	13.8086	4.55%
100 Hz	15.5312	15.4419	0.58%

表4修正后的理论模型和实验结果对比(30—100 Hz)
Table4.Comparison of numerical results and experimental results (30–100 Hz).

由表4可知, 当耗能模量修正倍数为6倍时, 频率在30—100 Hz内的平均误差为5.25%, 满足精度需求.
经计算, 可以求出进一步对所有磁场强度作用下的数值计算结果和实验结果进行对比分析和计算, 误差的变化曲线如图6所示. 由图6可知, 数值计算结果和实验结果之间的误差随磁场强度的增大而减小. 这是因为在磁场强度较小时, 磁流变液表现出液体的性质较多, 使用弹性力学理论建立的模型误差就相应地较大. 随着磁场强度的增大, 磁流变液中的场致结构就越牢固, 类固化程度就越高, 越来越体现出固态性质, 误差也就越小.
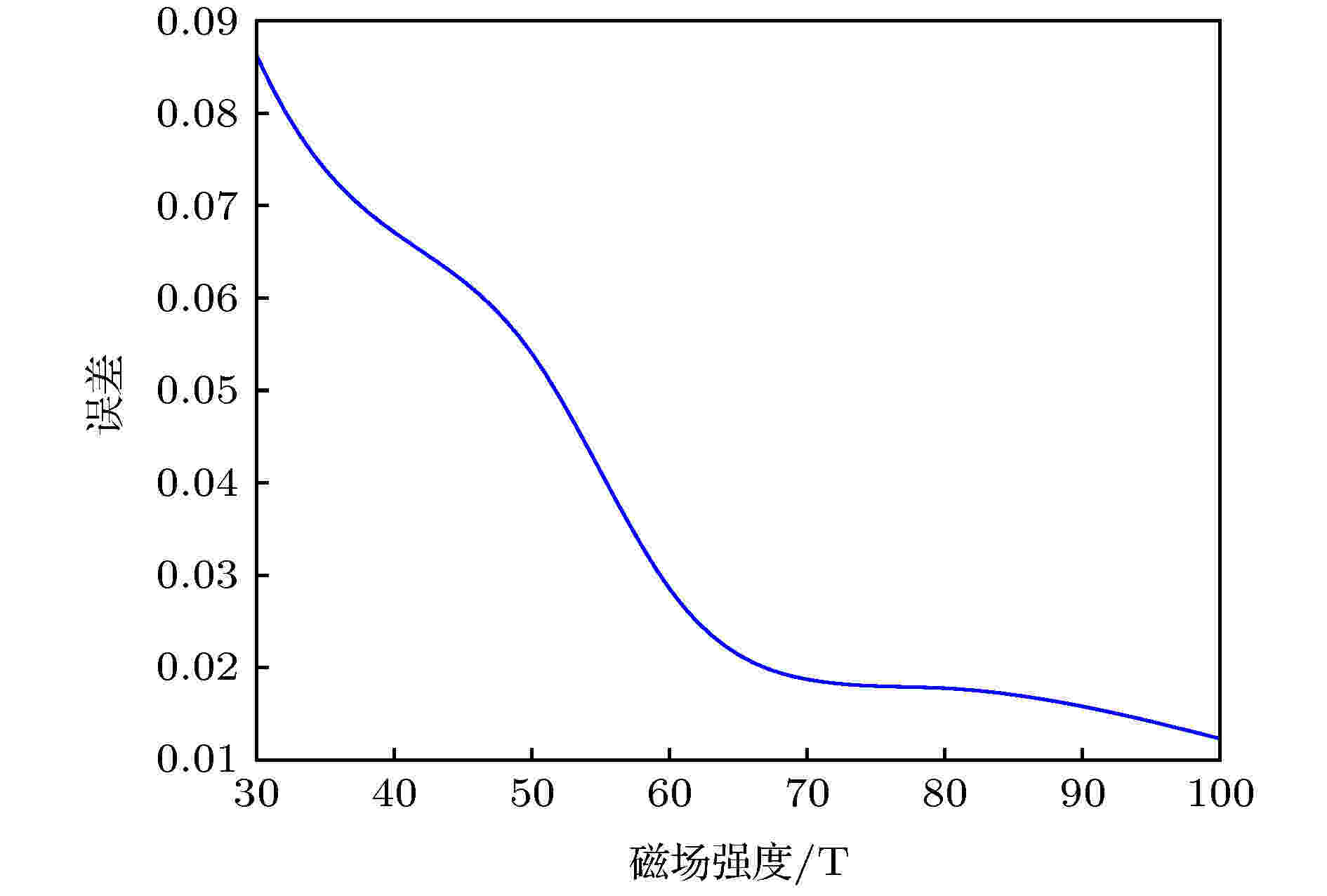图 6 理论结果和实验结果之间的误差
Figure6. Error between theoretical results and experimental results.

因此, 将复剪切模量中的耗能模量进行放大处理, 将其一次项和二次项系数同时放大6倍. 代入磁流变液的B-H关系可得, 修正后的磁流变液的耗能模量为

$\begin{split}{G''_n}(B) =\;& 5.43{B^6} \!+\! 5.42{B^5} \!+\! 13.35{B^4} \!+\! 8.01{B^3}\\ & + 9.63{B^2} + 1.61B + 0.083.\end{split}$

使用JMAG电磁有限元分析软件对类梯度结构中的磁场分布情况进行分析, 可以得到类梯度结构中磁场强度分布的表达式, 将其代入修正后的等效参数模型((24)式和(28)式)中, 即可得到类梯度结构中磁流变液的参数. 然后, 将其代入类梯度结构的传递矩阵((15)式)中, 对类梯度结构的振动传递特性进行数值计算.

2

-->

5.1.数值计算

将磁流变液的参数和传递矩阵T的相应元素代入(22)式, 使用MATLAB软件对其进行数值计算可得, 磁场均匀分布区域的磁场强度50, 70 和100 mT时, 类梯度结构的振动传递特性如图7所示.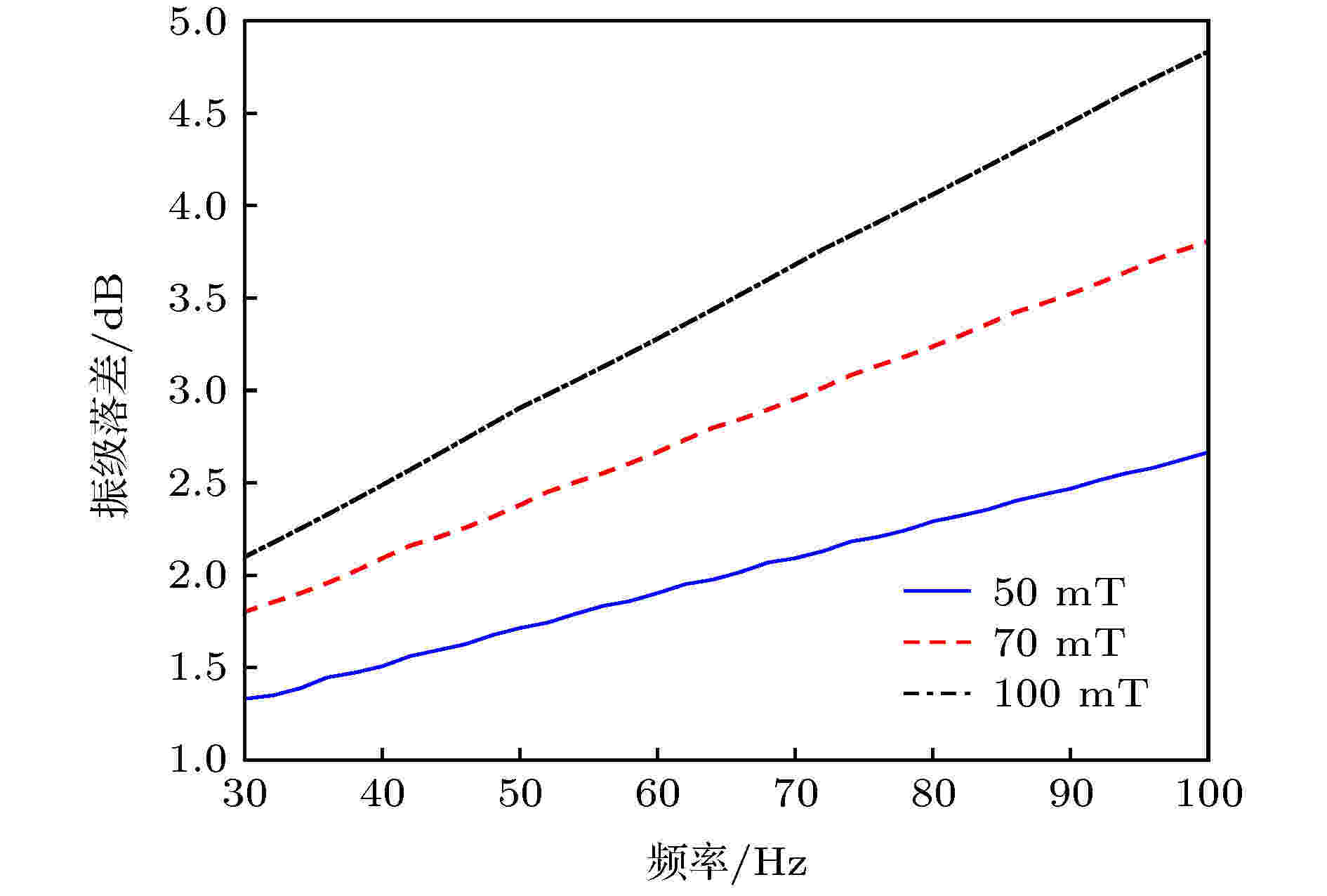
图 7 类梯度结构的振动传递特性
Figure7. Vibration characteristic of gradient-like structure.

由图7可知, 在不同大小的磁场强度作用下, 振级落差都随输入弹性波频率的增加而增大, 这表示磁流变液构成的类梯度结构对高频弹性波的衰减效果较好; 随磁场强度增加, 类梯度结构的振级落差越大. 这是因为磁场强度较大时, 磁流变液成链的程度也越高, 场致结构越牢固, 磁流变液的体积模量和剪切模量越大, 对弹性波的衰减作用更大. 此外, 磁场强度越大时, 曲线的斜率越大. 这是因为随着磁场强度增大, 磁流变液的固化程度越高, 越来越显示出固体的特性, 且固态介质对高频的衰减效果远低于低频.
2 -->

5.2.实验研究

保证磁场均匀作用区域的尺寸相同的情况下进行实验, 分别使磁场均匀分布部分的场强为50, 70和100 mT, 进行振动传递实验. 图8为不同磁场强度作用下, 实验测得的类梯度结构振动传递特性曲线. 图中, 蓝色实线表示磁场均匀作用区域的磁场强度为50 mT时的振动传递特性曲线, 红色虚线表示磁场强度为70 mT, 黑色点画线表示磁场强度为100 mT.
图 8 不同磁场强度作用下类梯度结构的振动传递特性
Figure8. Vibration characteristic of the gradient-like structure under different magnetic field intensity.

由图8可知, 在不同磁场强度作用下, 类梯度结构对弹性波的衰减作用均随频率的增加而增强. 这是由于频率越大, 弹性波的波长越小, 弹性波受类梯度结构的影响也就越大, 因此表现出的衰减作用越强. 随着磁场强度的增强, 类梯度结构对弹性波的衰减作用越大. 这是因为磁场强度越大, 磁流变液中的铁磁颗粒成链就越牢固, 其剪切模量和体积模量等也会随之增大, 因此, 弹性波在磁流变液中的传递需要消耗更多的能量, 即类梯度结构对弹性波的衰减作用越强. 此外, 磁场强度越大, 曲线的斜率就越大. 这是因为磁场强度越大时, 场致结构就越坚固. 因此, 相较于低频段而言, 高频段的弹性波受到的衰减效果就愈发明显, 在图像上就表现为斜率越大. 这与上文中对类梯度结构振动传递特性的分析结果一致.
为了验证类梯度结构的有效性, 将类梯度结构的振动传递特性和均匀场作用的磁流变液进行对比. 在实验中, 使用同一个阻抗管进行测量, 这样能保证对比的有效性, 实验结果如图9所示. 图中, 蓝色实线为类梯度结构的振动传递特性, 红色线虚为均匀场作用磁流变液的振动传递特性.
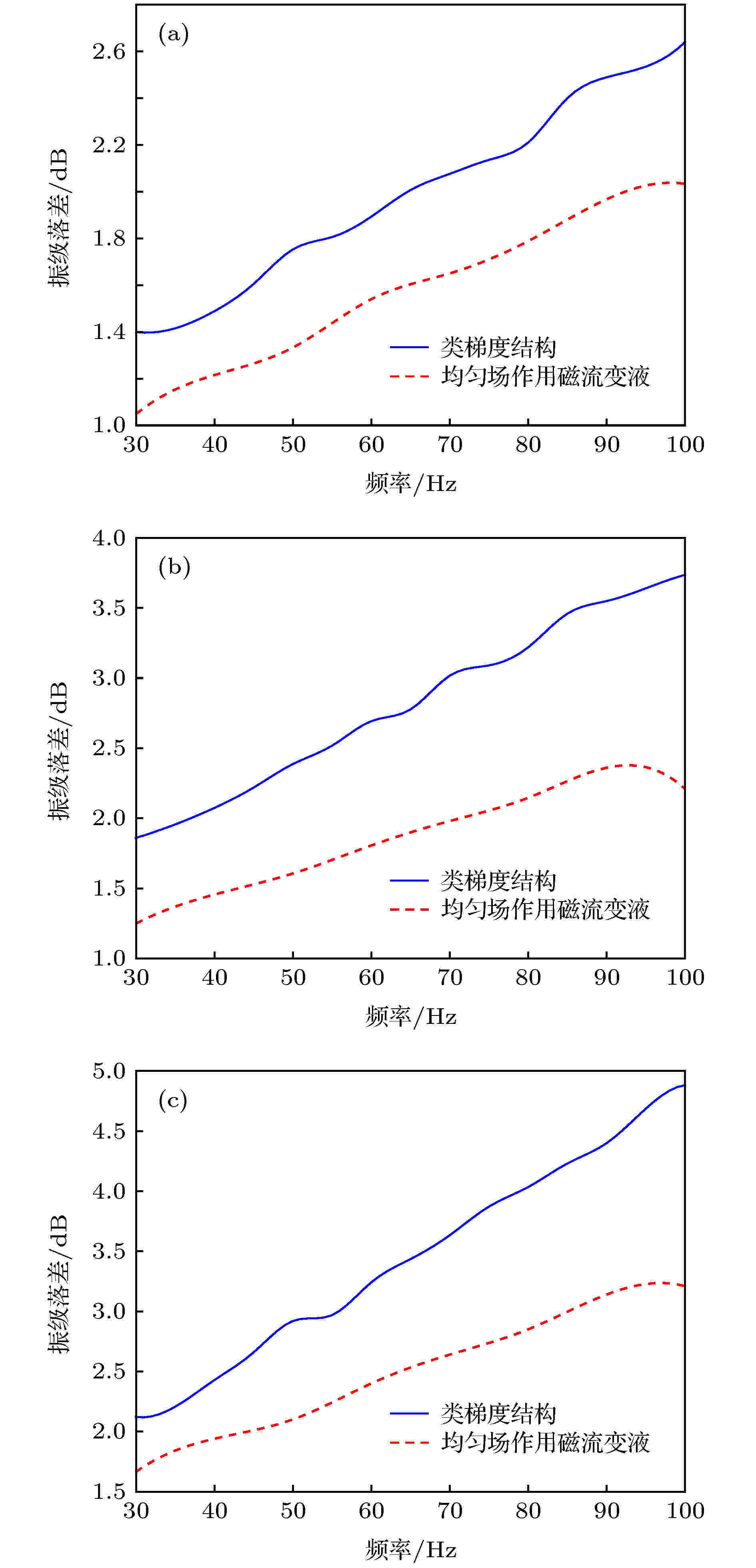图 9 类梯度结构与均匀场作用磁流变液对比图　(a) 50 mT; (b) 70 mT; (c) 100 mT
Figure9. Comparison between gradient-like structure and homogeneous magnetorheological fluid: (a) 50 mT; (b) 70 mT; (c) 100 mT

由图9可知, 均匀场作用磁流变液与类梯度结构的振动传递特性随频率的变化趋势大致相同, 都是随频率的增加而增大. 这是因为高频弹性波的波长较短, 受材料的阻抗影响较大. 同时, 从图9还能看出, 类梯度结构对弹性波的衰减效果优于均匀场作用的磁流变液.
为验证前面章节中所建立和修正的模型的有效性, 需要将数值计算结果和实验结果进行对比, 结果如图10所示. 图中, 蓝色实线为数值计算结果, 红虚线为相应的实验结果.
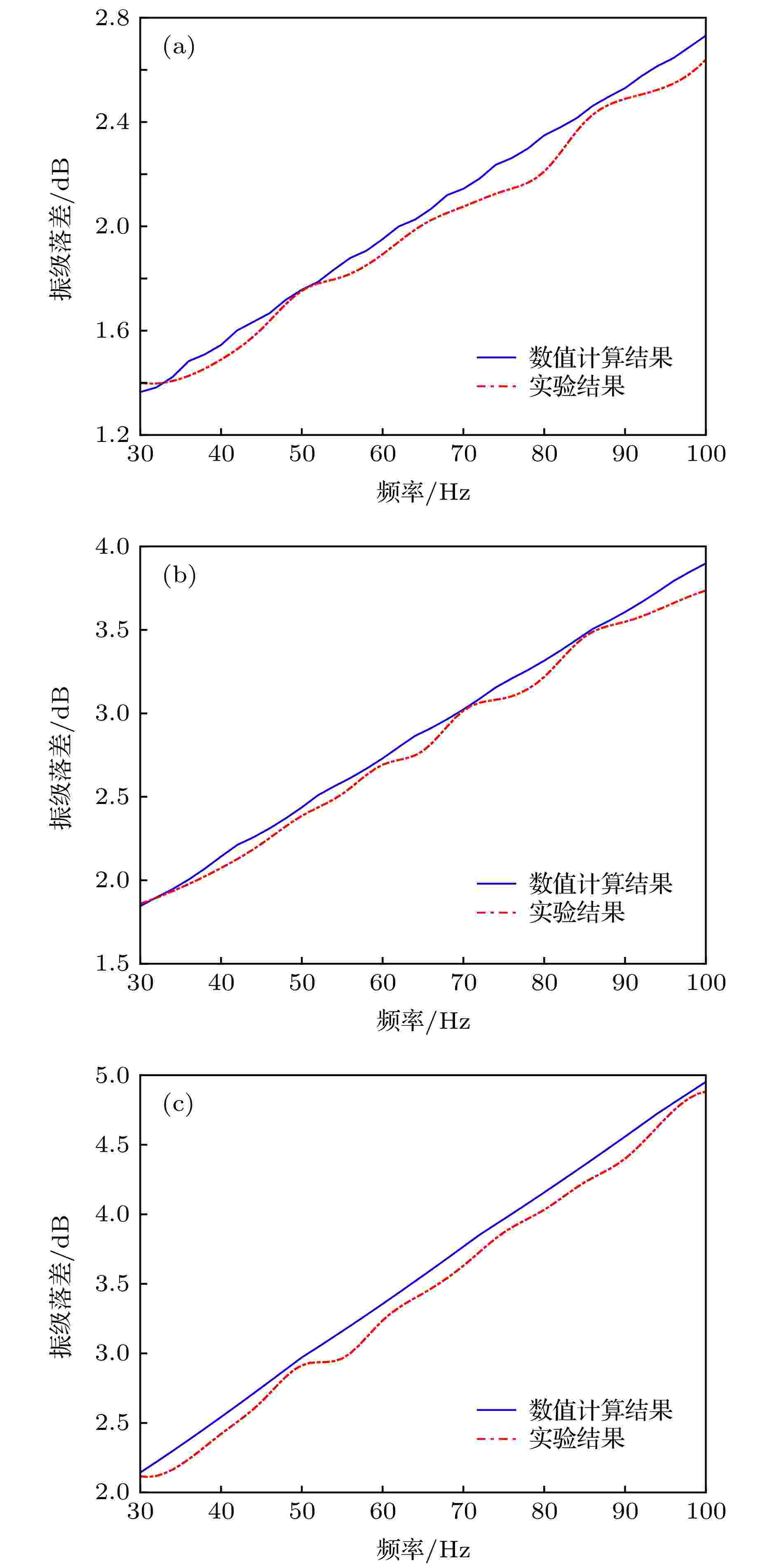图 10 类梯度结构振动传递特性的实验与理论对比图　(a) 50 mT; (b) 70 mT; (c) 100 mT
Figure10. Comparison between experimental and numerical results of vibration transfer characteristic of gradient like structure: (a) 50 mT; (b) 70 mT; (c) 100 mT

由图10可知, 数值计算结果和实验结果的变化趋势一致且符合程度较高, 证明对等效计算模型的精度较高, 符合实际情况. 但是, 这三组实验中, 实验结果普遍略低于理论分析结果, 这是因为磁流变液是固液两相体, 在磁场作用下虽然变成类固态, 主要体现固态性质, 但也能体现一部分液态性质. 虽然第三章中对理论模型进行了相应的修正, 增加了液相的影响, 但修正后的结果本就略高于实际值, 用于类梯度结构的振级落差求解也必然会存在误差. 此外, 磁流变液在磁场作用下并不是所有的铁磁颗粒都会成链, 仍有小部分存在液相中, 也会造成一定的误差. 经计算, 实验结果和相应的数值计算结果之间的平均误差如表5所列.

编号	实验参数/mT	误差
实验1	50	2.856%
实验2	70	2.233%
实验3	100	3.585%

表5实验与理论结果误差
Table5.Error between experimental and theoretical results.

由表5可知, 三组实验结果和数值计算结果之间的误差均小于5%, 一致性良好, 这说明前面章节中建立的计算模型和参数等效模型有效且精确.

本文基于磁流变液的固液转换特性, 通过控制磁场, 构建了类梯度结构, 并通过数值计算和实验的手段研究其振动传递特性. 结论如下:
1)搭建了磁流变液构成的阻抗分层调制结构装置和相应的振动传递测试实验装置. 该实验台利用外部连续分层排列的电磁铁可单独控制每一层磁流变液的阻抗, 进而调制出了“类梯度”结构;
2)类梯度结构对弹性波具有良好的衰减作用, 且表现出了优良的可调控特性. 随着磁场强度和弹性波频率的增加, 类梯度结构对弹性波的衰减作用逐渐增强. 在磁场强度为30—100 mT, 输入弹性波频率为30—100 Hz时, 该结构的振级落差最大可以达到4.9 dB, 比均匀磁场作用时的磁流变液高约一倍;
3)本文将磁场作用下的磁流变液等效为参数受磁场调控的类固体, 并使用弹性力学和黏弹性材料理论建立了等效参数模型. 经过对比分析, 数值计算结果和实验结果的平均误差约为3%, 这表明文中建立的数学模型和磁流变液的等效方法具备可行性和准确性.
实际工程中有些情况无法简化成一维弹性波的传递, 因此, 接下来还可以对倾斜入射的弹性波在类梯度结构中的传递特性进行进一步研究.