摘要:以典型的双稳态系统—屈曲梁结构为例, 基于等效模型, 结合解析、数值和实验手段, 研究了双稳态结构中的1/2次谐波共振特性、演化过程、参数调节规律及其对隔振特性的影响. 研究发现, 当非线性刚度系数或激励幅值增加到一定程度时, 系统会在一定带宽下产生显著的1/2次谐波共振; 随着激励幅值增加, 阻尼系统的1/2次谐波遵循“产生-增强-衰退-消失”的过程, 该过程对峰值频率和峰值传递率有重要影响; 适当提高非线性强度能有效改善双稳态结构隔振特性. 针对双稳态屈曲梁结构开展的实验验证了1/2次谐波特性和隔振特性变化规律.
关键词: 双稳态结构/
次谐波共振/
隔振/
屈曲梁

English Abstract

全文HTML

--> --> -->

非线性系统的独特性质, 如跳跃、分叉、混沌等, 为新型功能结构设计提供了新的思路与机理^[1-5]. 双稳态系统是一种典型的非线性系统, 其具有两个稳定平衡状态和一个不稳定平衡状态, 稳定平衡点之间的刚度为负值. 当能量输入较大时, 系统产生在两个稳定平衡状态之间的跳变跃迁运动, 导致强非线性现象^[6]. 应用双稳态结构设计的隔振系统具有高静态、低动态刚度特征, 可在保证高承载性能的情况下实现低频隔振^[7], 是双稳态系统的重要应用场景; 双稳态振子也可以实现高效的能量捕获和振动能量采集^[8-13]. 双稳态结构中存在次谐波共振, 次谐波能用于质量检测^[14,15]和拓宽双稳态能量采集器的工作频带^[16,17]. 目前, 国内外****对次谐波行为开展了一系列的研究工作^[18-20], 然而, 双稳态结构中1/2次谐波的产生机理、演化过程及其对隔振特性的影响尚待深入分析.
双稳态可利用磁铁、栓锁、铰链、弹簧、屈曲梁等结构产生^[21], 其中, 屈曲梁结构简单、适应性强, 是最具代表性的双稳态结构^[22-26], 大量****对其隔振特性开展了分析. 研究表明, 双稳态屈曲梁结构^[27]的突弹跳变^[28]、混沌响应^[29]、驱动力的位置^[25]和量值^[30]等都会影响其隔振特性. 然而, 其中的次谐波共振及其对隔振特性的影响的研究尚不完善, 参数影响规律有待揭示.
本文以典型的双稳态屈曲梁结构为对象, 基于解析、数值和实验方法系统研究双稳态系统中的1/2次谐波共振的产生机理、分岔过程、参数影响规律及其对隔振特性的影响. 研究结果为双稳态系统的设计与应用提供有益参考.

本文研究的对象如图1(a)所示, 主要部分为两个并列的双稳态圆弧. 双稳态圆弧可保证实际实验中加载配重后样件的稳定性. 该结构可视作两个非线性弹簧并联. 在结构振动的过程中, 两弹簧位移相同, 共同承受附加在结构上的质量. 所研究对象可简化为图1(b)所示的非线性弹簧振子模型, 为两组相同的弹簧振子结构并联. 屈曲梁几何参数为: 跨距l = 35 mm, 厚度t = 1 mm, 高度h = 5.25 mm, 宽度b = 56 mm. 双稳态屈曲梁结构试样使用3D打印的方法制备, 材料为TPU (热塑性聚氨酯弹性体橡胶), 其材料参数通过压缩实验测得: 密度ρ = 916.7 kg/m³, 弹性模量E = 17.9396 MPa, 泊松比ν = 0.385, 总配重M为0.93 Kg.
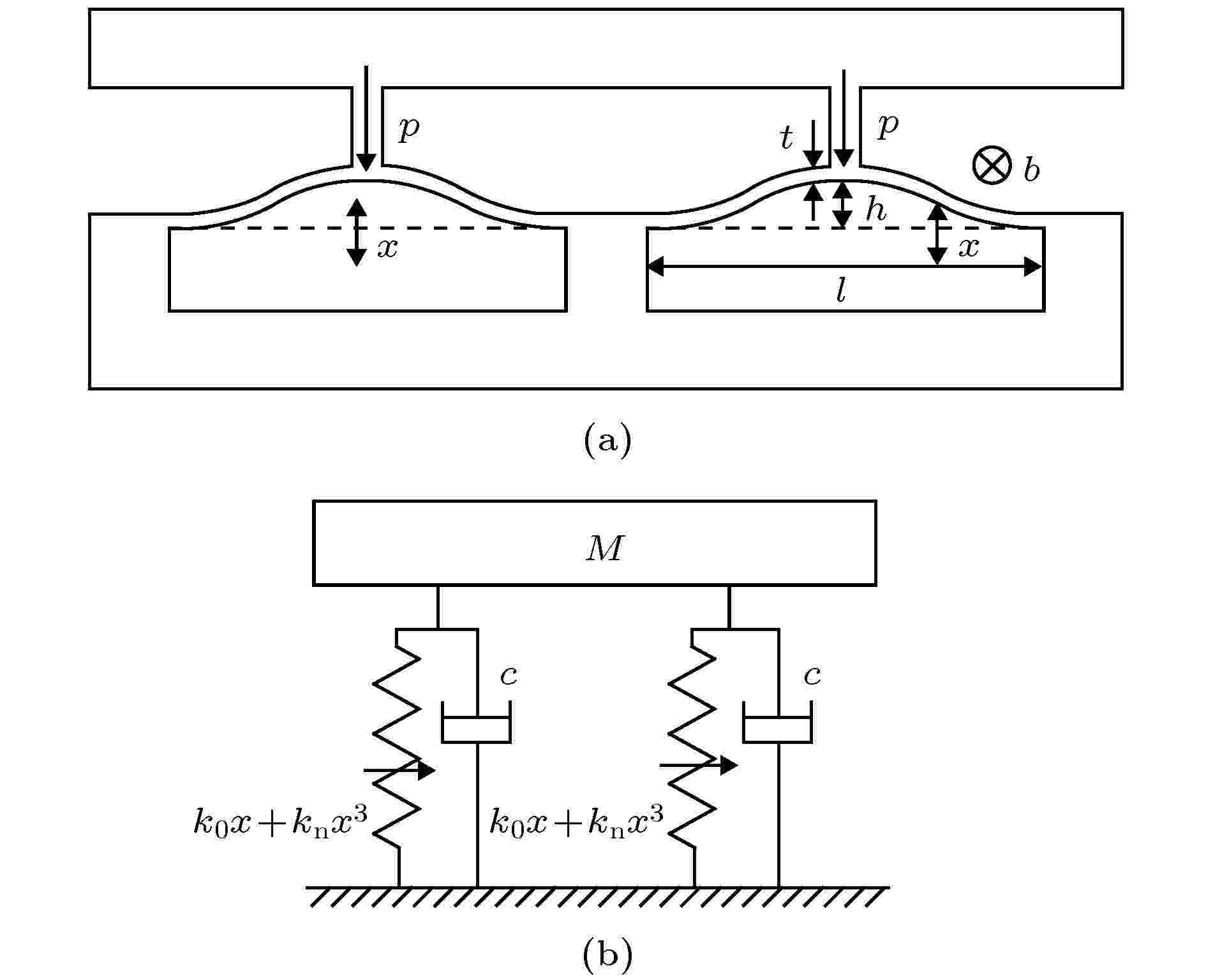图 1 (a)双稳态屈曲梁试样; (b)弹簧振子模型
Figure1. (a) Prototype of bistable buckling beam; (b) spring oscillator structure.

如图1所示, 外力p作用在屈曲梁结构中间位置, 该位置的位移为x. 每根屈曲梁都可等效为一个包含立方刚度非线性的双稳态系统, 但在理论解析和数值仿真分析过程中仅需取其中一个分析其动力学特性. 系统微分方程为

$m\ddot x + c\dot x + {k_0}x + {k_{\rm{n}}}{x^3} = - m\ddot u,$

其中质量m = M/2, c为阻尼系数, k₀为结构负刚度, k_n为立方刚度系数, u为激励位移, 则系统运动的绝对位移为x + u. 根据Jin等^[31]的研究, 屈曲梁所受外力与所发生位移的关系为

$\begin{split} F =\; & (3{{\text{π}}^4}{Q^2}/2)\varDelta \big[ {\varDelta - 3/2 - \sqrt {1/4 - 4/(3{Q^2})} }\,\big]\\ &\times\big[ {\varDelta - 3/2 + \sqrt {1/4 - 4/(3{Q^2})} }\, \big], \end{split}$

其中$ F = pl^3/(EIh) $, Δ = d/h, Q = h/t, 均为归一化后的参数, I为屈曲梁结构的惯性矩, d为受p外力时屈曲梁中间位置的变形量, x + d = h. 经验证, (2)式可准确描述屈曲梁结构所受外力与发生位移的关系. 利用(2)式可求得系统(1)的两个重要的参数(详见附录A):

$\begin{split}& {k_{\rm{n}}} = \frac{{3{{\text{π}}^4}EI}}{{2{l^3}{t^2}}},\\& {k_0} =- \left( {\frac{{3{{\text{π}}^4}EI{h^2}}}{{2{t^2}{l^3}}} - \frac{{2{{\text{π}}^4}EI}}{{{l^3}}}} \right).\end{split}$

求解得到的参数值分别为k_n = 0.28 N/mm³, k₀ = –7.5 N/mm. 在静态时, 系统处于其中的一个稳态平衡点. 当响应幅值非常微小时, 质点仅在该平衡点附近运动, 响应特性近似为线性的. 该平衡点附近的线性刚度为

${k_p} = {k_0} + 3{k_{\rm{n}}}{\varDelta ^2},$

因此, 双稳态系统在稳定平衡点附近的线性固有频率为${f_0} = \sqrt {{{{k_p}}/m}} /\left( {2{\text{π}}} \right)$. 本文中 f₀ = 29 Hz.
本文采用谐波平衡法求解该系统在给定激励下响应的解析解. 因阻尼对系统动力学特性的定性规律影响较弱, 为简化分析, 在解析分析中未考虑其影响. 实际试样中存在阻尼, 后文通过实验与仿真对比, 通过曲线拟合确定阻尼参数c = 30 kg/s. 设系统的激励为u = Ucos(ωt), 其中U为激励幅值, ω = 2πf为激励频率. 由于双稳态系统包含偏离0的响应项, 将系统的解设为x = A₀ + A₁cos(ωt). 代入方程(1)得

$\begin{split}& ({k_0}{A_0} + {k_{\rm{n}}}A_0^3 + 3{k_{\rm{n}}}{A_0}A_1^2/2)\\& + ( - m{A_1}{\omega ^2} + {k_0}{A_1} + 3{k_{\rm{n}}}A_0^2{A_1} \\& + 3{k_{\rm{n}}}A_1^3/4 - mU{\omega ^2})\cos \omega t\\& + (3{k_{\rm{n}}}{A_0}A_1^3/2)\cos 2\omega t + ({k_{\rm{n}}}A_1^3/4)\cos 3\omega t = 0.\end{split}$

令方程(5)的常数项和cosωt项的系数为零, 得

$\left\{ \begin{aligned}& {k_0}{A_0} + {k_{\rm{n}}}A_0^3 + 3{k_{\rm{n}}}{A_0}A_1^2/2 = 0,\\& - m{A_1}{\omega ^2} + {k_0}{A_1} + 3{k_{\rm{n}}}A_0^2{A_1} \\& + 3{k_{\rm{n}}}A_1^3/4 - mU{\omega ^2} = 0.\end{aligned} \right.$

给定U可通过方程组(6)求得A₀, A₁, 即可求得系统在激励u下的相对位移x. 因此, 结构的振动传递率为

$T = ({\text{响应幅值}})/({\text{激励幅值}}){\rm{ = }}\left| {{A_1} + U} \right|/\left| U \right|.$

本文采用MATLAB软件的Simulink模块对系统进行数值仿真分析. 针对系统的微分方程(1)建立系统的数值仿真模型, 如图2所示. 系统的激励u为正弦波, y = x + u为系统响应的绝对位移. 利用该模型, 可求解系统在给定激励下响应的数值解.
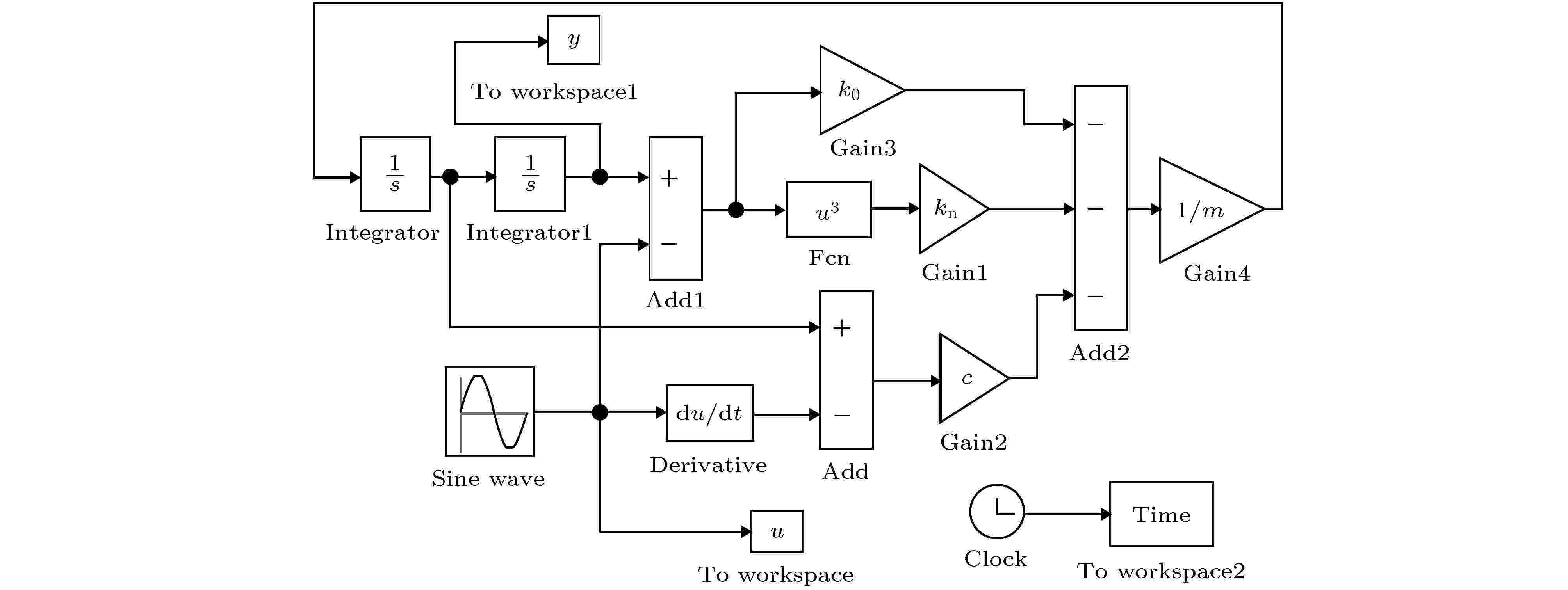图 2 Simulink数值仿真模型
Figure2. Numerical simulation model in Simulink.

2

-->

3.1.双稳态系统的1/2次谐波共振

给定U = 0.01 mm, 该系统的数值仿真结果与解析结果对比如图3所示. 实数解析结果具有3个分支, 双稳态系统的非线性使传递率曲线弯向左侧, 与软刚度非线性系统类似; 0—29 Hz频段, 解析解有两个根, 系统稳定状态下的响应对应的一般为幅值较低的解. 仿真结果与解析解的分支1和分支2一致性较好, 然而仿真结果中传递率在58 Hz处出现奇异峰值, 此频率恰好为系统主共振频率f₀的2倍, 因此可能产生了1/2次谐波共振现象. 但是根据(5)式得到的解析结果并没有预测出该奇异峰值, 原因在于以上理论没有考虑次谐波响应, 所以预测精度较低.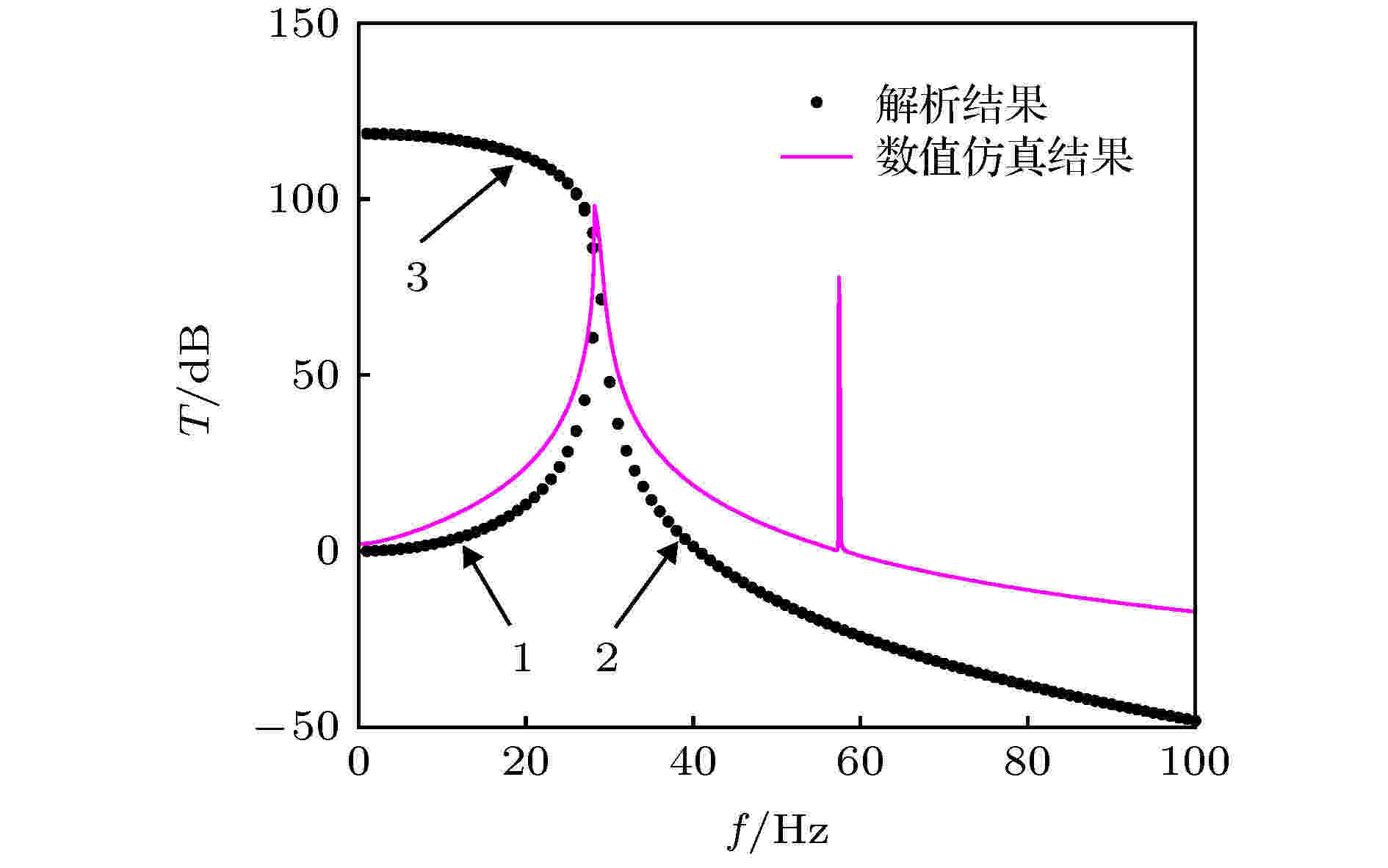
图 3 解析与数值分析结果对比
Figure3. Comparison between analytical and numerical results.

为了更准确地分析双稳态系统的响应特性, 在解设定时考虑1/2次谐波成分, 将系统的周期解表示为x = A₀ + A₁₂cos(ωt/2) + A₁cos(ωt)的形式, 其中A₁₂cos(ωt/2)为1/2次谐波成分. 代入方程(1)得

$\begin{split}& m[( - {\omega ^2}{A_{12}}/4)\cos (\omega t/2) - {w^2}{A_1}\cos (\omega t)]\\& + {k_0}[{A_0} + {A_{12}}\cos (\omega t/2) + {A_1}\cos (\omega t)]\\& + {k_{\rm{n}}}[(A_0^3 + 3{A_0}A_{12}^2/2 + 3{A_0}A_1^2/2 + 3A_{12}^2A/4)\\& + (3A_{12}^3/4 + 3A_0^2{A_{12}} + 3{A_{12}}A_1^2/2 \\&+ 3{A_0}{A_{12}}{A_1})\cos (\omega t/2) + (3A_1^3/4 + 3{A_0}{A_{12}}/2 \\& + 3A_0^2{A_1} + 3A_{12}^2{A_1}/2)\cos (\omega t) \\& + {\text{高次谐波}}) + m( - {w^2}U\sin (\omega t)] = 0.\end{split}$

令方程(8)的常数项、cos(ωt/2)项系数、cos(ωt)项系数为0, 得

$\left\{ \begin{aligned}& {k_0}{A_0} \!+\! {k_{\rm{n}}}A_0^3 \!+\! 3{k_{\rm{n}}}{A_0}A_1^2/2 \!+\! 3{k_{\rm{n}}}A_{12}^2{A_1}/4 \!=\! 0,\\& - m{\omega ^2}{A_{12}}/4 \!+\! {k_0}{A_{12}} \!+\! 3{k_{\rm{n}}}A_{12}^3/4 \!+\! 3{k_{\rm{n}}}A_0^2{A_{12}} \\& + 3{k_{\rm{n}}}{A_{12}}A_1^2/2 + 3{k_{\rm{n}}}{A_0}{A_{12}}{A_1} = 0,\\& - m{\omega ^2}{A_1}\! +\! {k_0}{A_1} \!-\! m{\omega ^2}U \!+ \!3{k_{\rm{n}}}A_1^3/4 \\& \!+\! 3{k_{\rm{n}}}{A_0}A_{12}^2/2 + 3{k_{\rm{n}}}A_0^2{A_1} \!+\! 3{k_{\rm{n}}}A_{12}^2{A_1}/2 \!=\! 0.\end{aligned} \right.$

给定U可通过方程组(9)求得A₀, A₁₂, A₁, 即可求得系统在激励位移u下的相对位移x. 因此, 考虑1/2次谐波共振时系统传递率的表达式变为

$\begin{split} T\;& = ({\text{响应幅值}})/({\text{激励幅值}})\\ & = \sqrt {{{({A_{12}} + U)}^2}+ ({A_1} + U{)^2}} /\left| U \right|,\end{split}$

此时, 基波与1/2次谐波的解相互耦合.
无阻尼情况下, 依然取U = 0.01 mm, 对比结果如图4所示. 解析结果除了具有与图3相似的3个分支外, 还具有另外一条向左弯曲的分支4, 且该分支实际上是由两条曲线构成. 分支3与分支4在$f \to 0$时源于相同的分岔, 当$f \to 2{f_0}$时, 分支4的两条曲线与分支2重合. 数值分析表明, 在0—57 Hz频率范围内, 真实响应对应于幅值较低的解, 与未考虑1/2次谐波相同; 在2f₀ = 58 Hz附近, 系统的响应发生突变对应的是分支2到分支4的跳变; 当激励频率远离2f₀时, 解再次从分支4跳变到分支2. 解析分析的主共振峰和1/2次谐波共振导致的奇异峰恰好与数值仿真结果十分符合. 系统在58 Hz正弦激励下的响应频谱如图5所示, 可以看出, 系统频域响应曲线除在58 Hz处有尖峰外, 在主共振29 Hz处也有一个明显的峰值, 甚至主共振的响应大于基波的响应. 这些分析都证明, 图3中2f₀的峰值是1/2次谐波共振引起的, 1/2次谐波共振导致高频能量向低频转移(而不是低频向高频转移), 无阻尼时导致主共振能量急剧增加从而使系统在2f₀激励下的总响应幅值传递率增加80 dB以上, 为系统隔振带来不利影响. 因此, 在实际使用双稳态隔振系统时, 需要设计恰当的结构和参数, 避免系统产生次谐波共振现象. 当系统存在强阻尼时, 高频向低频转移的能量能够被有效耗散.
图 4 考虑1/2次谐波时的解析-数值结果对比
Figure4. Comparison between analytical and numerical results with considering 1/2 sub-harmonics.

图 5 次谐波共振发生时的频谱
Figure5. Spectra for sub-harmonic resonance.

2 -->

3.2.幅值变化引起的分岔及次谐波产生过程

上文所分析的传递率为总幅值的传递率. 为更好地分析基波与1/2次谐波的耦合行为, 定义基波传递率为激励频率处的响应幅值与激励幅值之比, 即T₁ = A₁/U; 定义1/2次谐波传递率为1/2激励频率处的响应幅值与激励幅值之比, 即T₁₂ = A₁₂/U.
利用(9)式求得幅值变化引起的传递率分岔见图6(a), 图6(a)中的基波传递率曲线1和1/2次谐波传递率曲线突出呈现在图6(b)中, 图6(a)和图6(b)的Y轴分别为对数坐标和线性坐标. 图中粉色虚线所代表的T₁值对应的T₁₂ = 0, 因实际系统存在次谐波响应, 此虚线值可忽略. 基波传递率有两条连续曲线(曲线1和曲线2), 但是1/2次谐波的解仅有单个分支. U → 0时, 曲线1上的T₁ → –50 dB, 但曲线2上的T₁起始于很大的值; 由于激励幅值很小时系统呈线性规律, 因此曲线1代表了小幅值激励下系统的真实解. 0 < U < 0.04 mm时, 曲线1随激励幅值增加急剧增加, 表示系统已经开始出现非线性过程, 但此时T₁₂ = 0, 表明双稳态系统中无1/2次谐波响应. 随着U的进一步增加, 曲线1在U = 0.05 mm达到极大值后缓慢减小(几乎保持不变), 但是T₁₂在0.04 < U < 0.1 mm区间内急剧增加, 甚至T₁₂ $\gg $ T₁, 所以U = 0.04 mm为系统产生1/2次谐波共振的临界分岔点, 系统特性产生本质变化. 此后, 解析解表明T₁₂并不会随着U的增加而单调增加, 而是在T₁₂达到峰值后随着U的增加而减小. 结合曲线1可得, 1/2次谐波共振刚出现时并不会使基波传递率突变降低, 而是同步出现急剧增加的趋势, 这对振动抑制是不利的; 且即使T₁₂ $\gg $ T₁, T₁也不会显著降低从而导致显著的能量转化效应. 曲线2产生折叠, 且在U = 0.54 mm时出现鞍节点分岔, 该点可能引起T₁的突变.
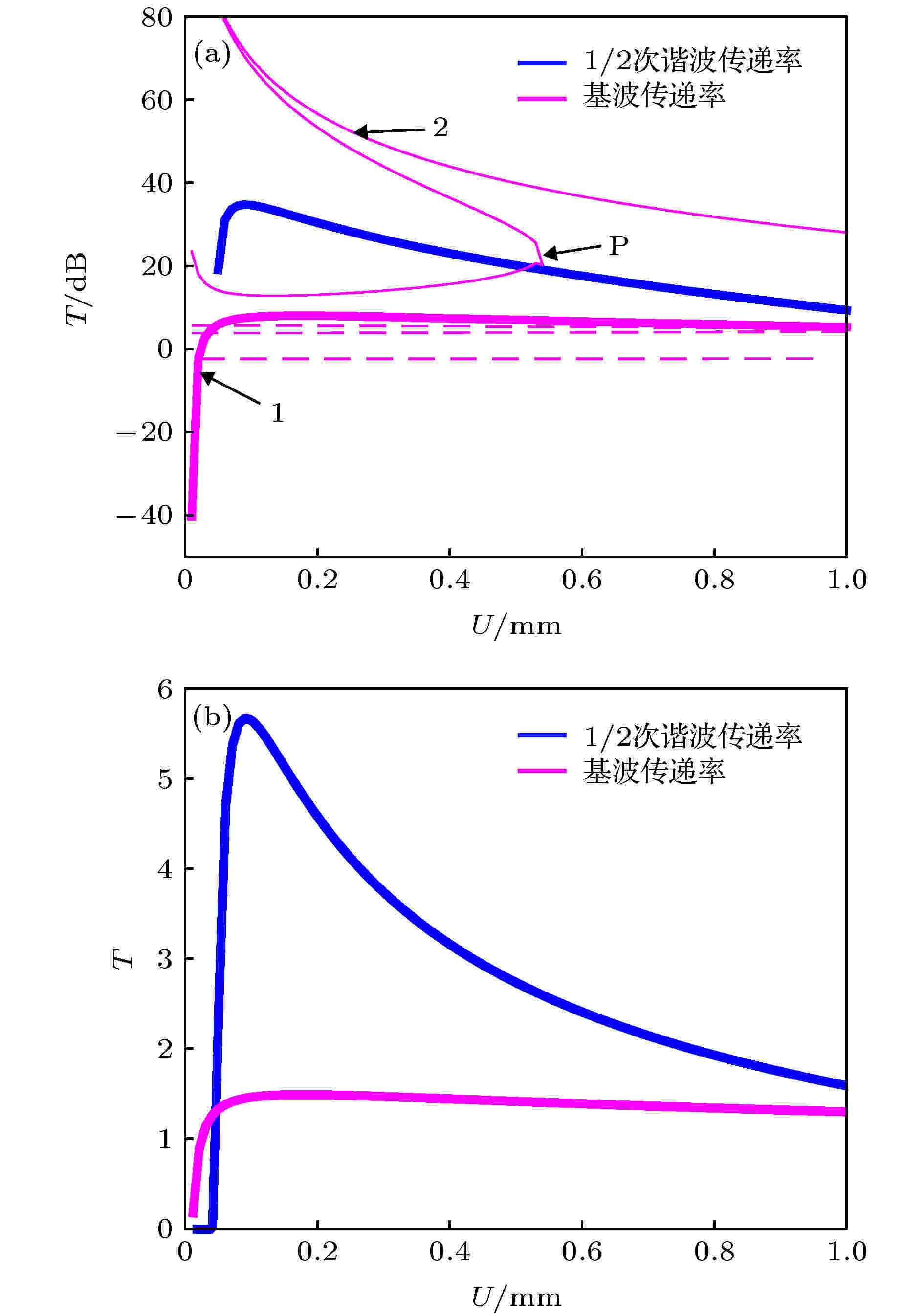图 6 解析求解的幅值变化对次谐波共振的影响　(a)对数坐标; (b)线性坐标
Figure6. Analytical results of the influence of amplitude on sub-harmonic resonance: (a) The Y coordinate of panel is logarithmic; (b) the Y coordinate of panel is linear.

图7(a)呈现了无阻尼情况下的数值仿真结果, 可见基波传递率呈现的规律与分岔分析中图6(b)(即图6(a)中曲线1)的规律恰好符合; 当U < 0.3 mm时, 图6(b)解析解与图7(a)数值解呈现的T₁₂变化规律一致; 但是当U > 0.3 mm时, 1/2次谐波共振的数值解出现波动, 单频激励下的响应频谱为连续谱, 主要的能量并不是集中在单频的1/2次谐波上, 而是集中在一个较宽的频带10—30 Hz内(图7(a)内插图), 因此系统的响应不再是周期或拟周期的, 这是典型的混沌响应特征.
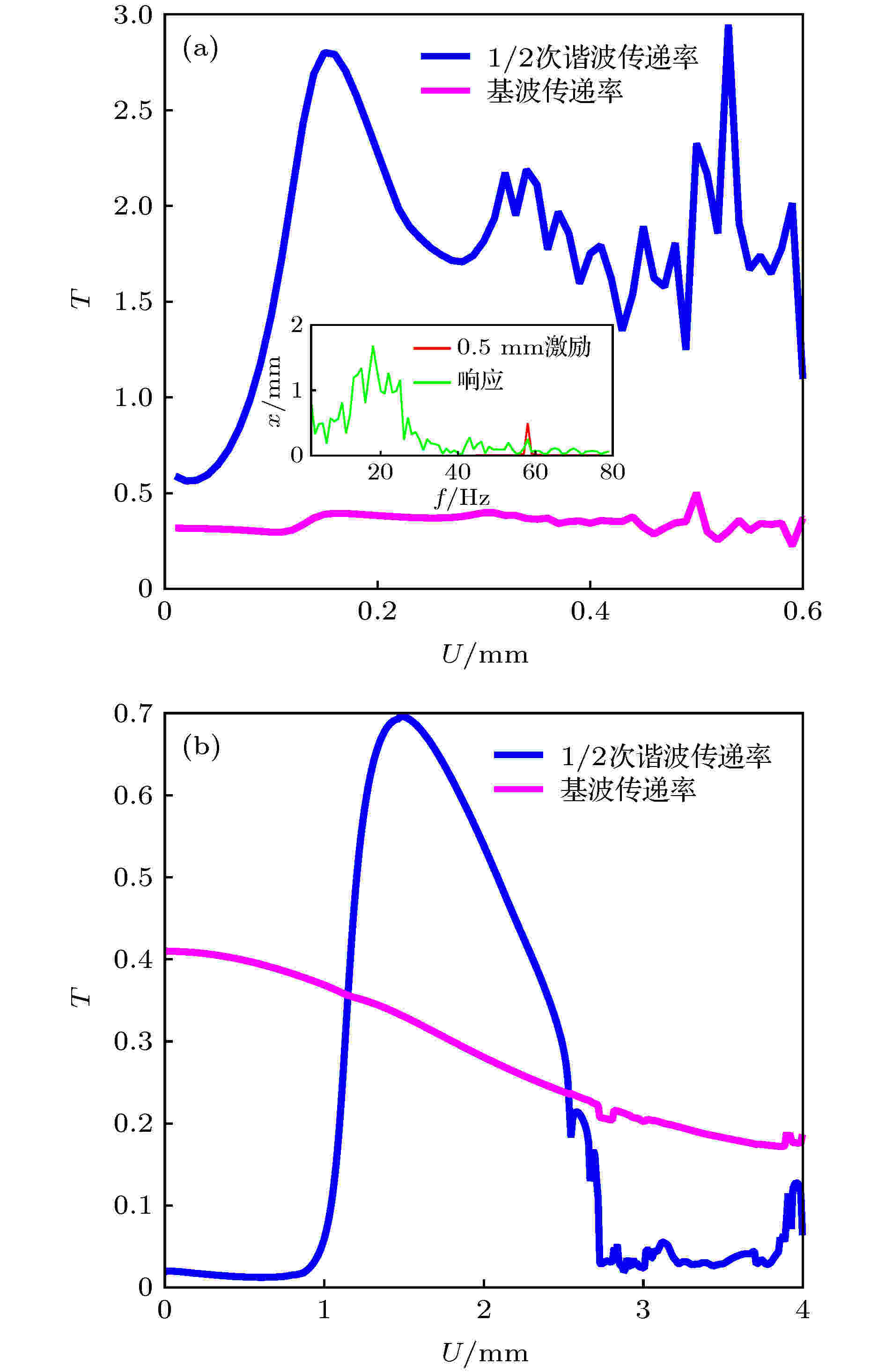图 7 幅值变化对次谐波共振影响的数值解　(a)无阻尼结果; (b)有阻尼结果
Figure7. Numerical results of the impact of amplitude on sub-harmonic resonance: (a) Results without damping; (b) results with damping.

图7(b)呈现了阻尼系数c = 30 kg/s时的数值仿真结果. 可见当系统中出现阻尼时, 基波传递率在0 < U < 4 mm的区间内从0.4单调降低到0.18, 产生1/2次谐波的临界值显著滞后于无阻尼结果, T₁₂在U = 1.6 mm时达到峰值0.7; 而且与无阻尼情形存在显著差异的是, 1/2次谐波产生之后并不是一直存在, 而是存在一个“产生-增强-衰退-消失”的过程, 这对实际应用具有重要启示. 在应用1/2次谐波时, 需要在恰当的幅值范围内调控; 而当需要避免1/2次谐波共振引起总幅值的增强效应时, 需要设计系统参数使之避开对应的幅值区间.

为了研究参数变化对双稳态系统隔振特性的影响规律, 本节分别阐明: 1)激励幅值U对频率偏移量的影响; 2)固定立方刚度系数k_n, 研究负刚度系数k₀变化对非线性系统隔振特性的影响; 3)固定负刚度系数k₀, 研究立方刚度系数k_n变化对系统隔振特性的影响. 得到参数变化对系统1/2次谐波共振现象和隔振特性的影响规律, 以此作为系统动力学特性优化的依据.
在以下分析中, 解析分析不考虑阻尼的影响$ (c=0), $ 在数值分析中, c = 30 kg/s, 分析系统参数变化的影响时, 激励幅值为0.3 mm.
2

-->

4.1.幅值变化对频率偏移量的影响

共振频率和共振峰峰值是双稳态系统振动特性的两个重要指标, 也是隔振应用中十分关注的两个变量. 前文分析表明, 在分析主共振时解析计算中可以不考虑次谐波的影响, 不同幅值下的数值和解析结果分别如图8中实线和点线所示. 在共振区域, 数值与解析结果趋势一致: 随激励幅值增加, 共振峰峰值降低, 共振点的位置向低频移动, 峰值传递率下降. 数值仿真结果还表明, 在一定带宽的激励下(图中为55—58 Hz), 均有1/2次谐波共振产生.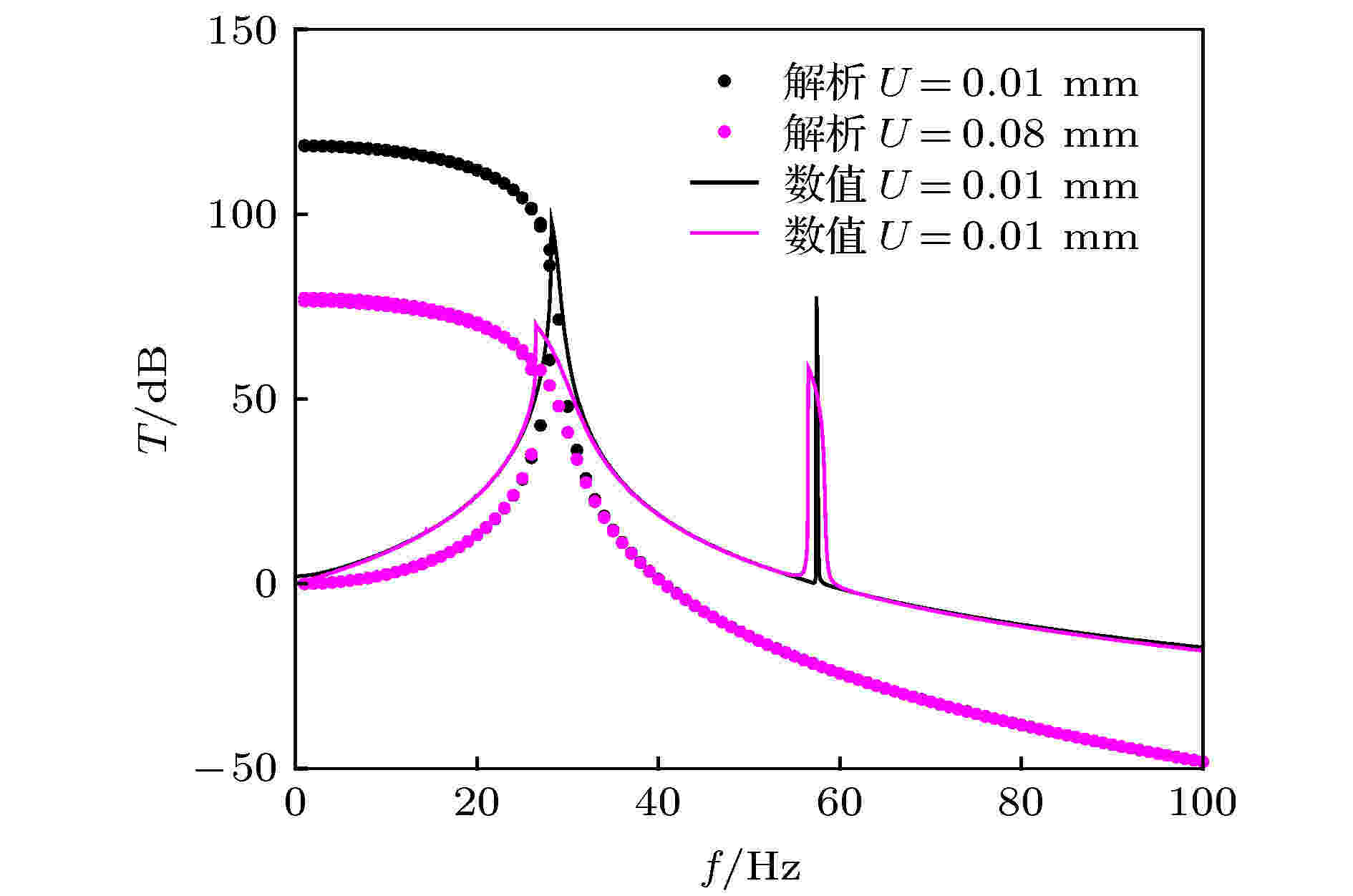
图 8 无阻尼条件下幅值变化对隔振特性的影响
Figure8. Influence of amplitude on vibration isolation characteristics without damping.

当考虑阻尼效应时, 上文所述共振频率偏移量会显著增加. 数值分析表明(图9), 随着激励幅值增加, 其共振频率从28 Hz降低到23 Hz, 频率前移了17.8%, 峰值传递率也随之下降. 但是激励幅值增加到一定程度(此系统为U > 1.05 mm之后), 系统的峰值频率(不一定是主共振)急剧跳变增大, 峰值传递率也跳变升高. 由图7(b)可知, 这一跳变点恰好对应于T₁₂ = T₁, 峰值频率和传递率升高的原因在于高幅值的1/2次谐波改变了系统的本质特性.
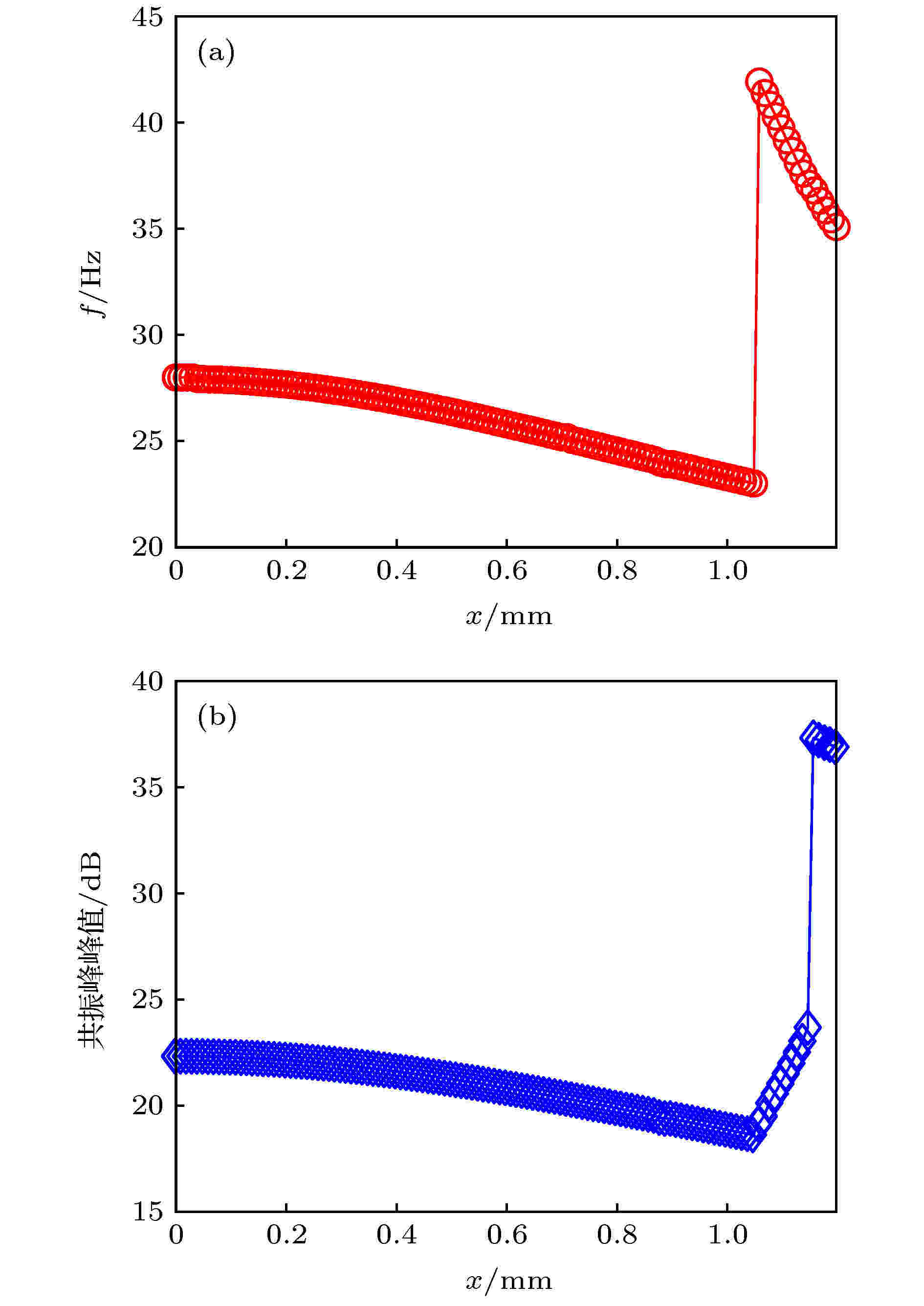图 9 有阻尼条件下幅值变化对频率偏移(a)和共振峰峰值(b)的影响
Figure9. Influences of amplitude on frequency shifting (a) and the peaks of harmonic resonance (b) with damping.

2 -->

4.2.负刚度系数k₀变化对系统隔振特性的影响

固定立方刚度系数k_n = 0.2 N/mm³, 通过改变双稳态屈曲梁结构的跨距l、厚度t、宽度b, 改变系统的负刚度参数, 变化k₀ = –0.2—–80 N/mm, 结果如图10所示. 解析和数值仿真结果均表明, 随|k₀|的增加, 系统共振点的位置向高频移动, 系统共振峰升高. 共振频率的变化规律与公式$\sqrt {{{|{k_0}|}/m}} /2{\text{π}}$相近, 但值略大于$\sqrt {\left| {{k_0}} \right|/m} /2{\text{π}}$.
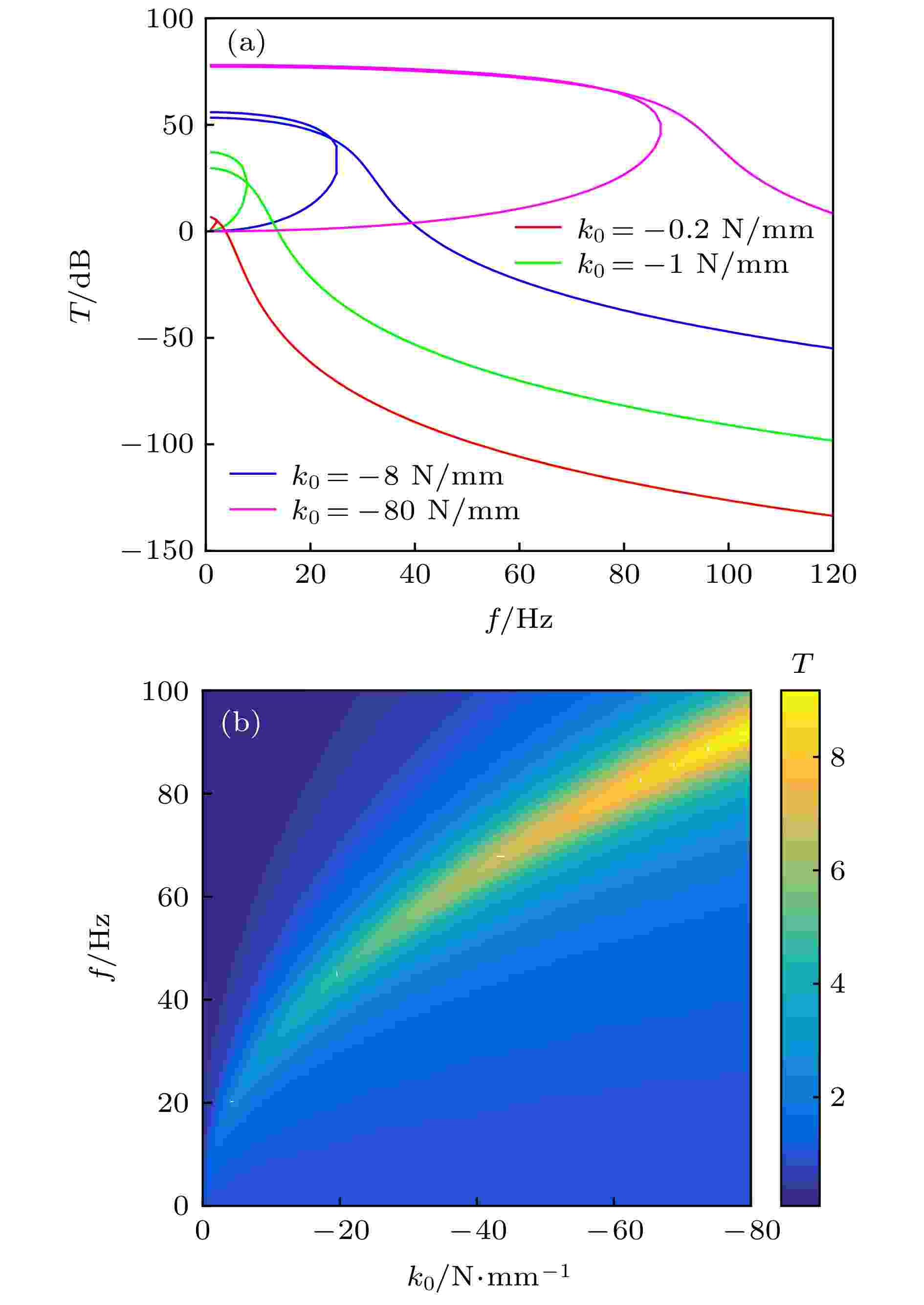图 10 固定k_n = 0.2 N/mm³, 负刚度系数k₀变化对系统隔振特性的影响　(a)解析结果; (b)数值仿真结果
Figure10. When k_n = 0.2 N/mm³, influence of k₀ on vibration isolation: (a) Analytical results; (b) numerical simulations.

2 -->

4.3.立方刚度系数k_n变化对系统隔振特性的影响

固定负刚度参数k₀ = –7.5 N/mm, 通过改变双稳态屈曲梁结构的高度h、跨距l、厚度t、宽度b, 改变系统的立方刚度系数, 变化k_n = 0.01—4 N/mm³, 结果如图11所示. 解析和数值结果均表明, 随着k_n的增加, 系统共振峰值频率略向低频偏移, 共振峰峰值降低. 与参数k₀理论分析结果相比, 参数k_n变化引起的效果远小于参数k₀变化引起的效果. 从图11(b)还可以看出, k_n的大小与1/2次谐波共振是否出现有关, 当k_n增大到一定值(此系统参数下约为2.6 N/mm³)时, 系统出现次谐波共振. 且传递率被1/2次谐波共振增强的频带在k_n = 2.6 N/mm³达到52—56 Hz, 进一步增加k_n还会拓展该频带, 表明强非线性下产生1/2次谐波共振现象.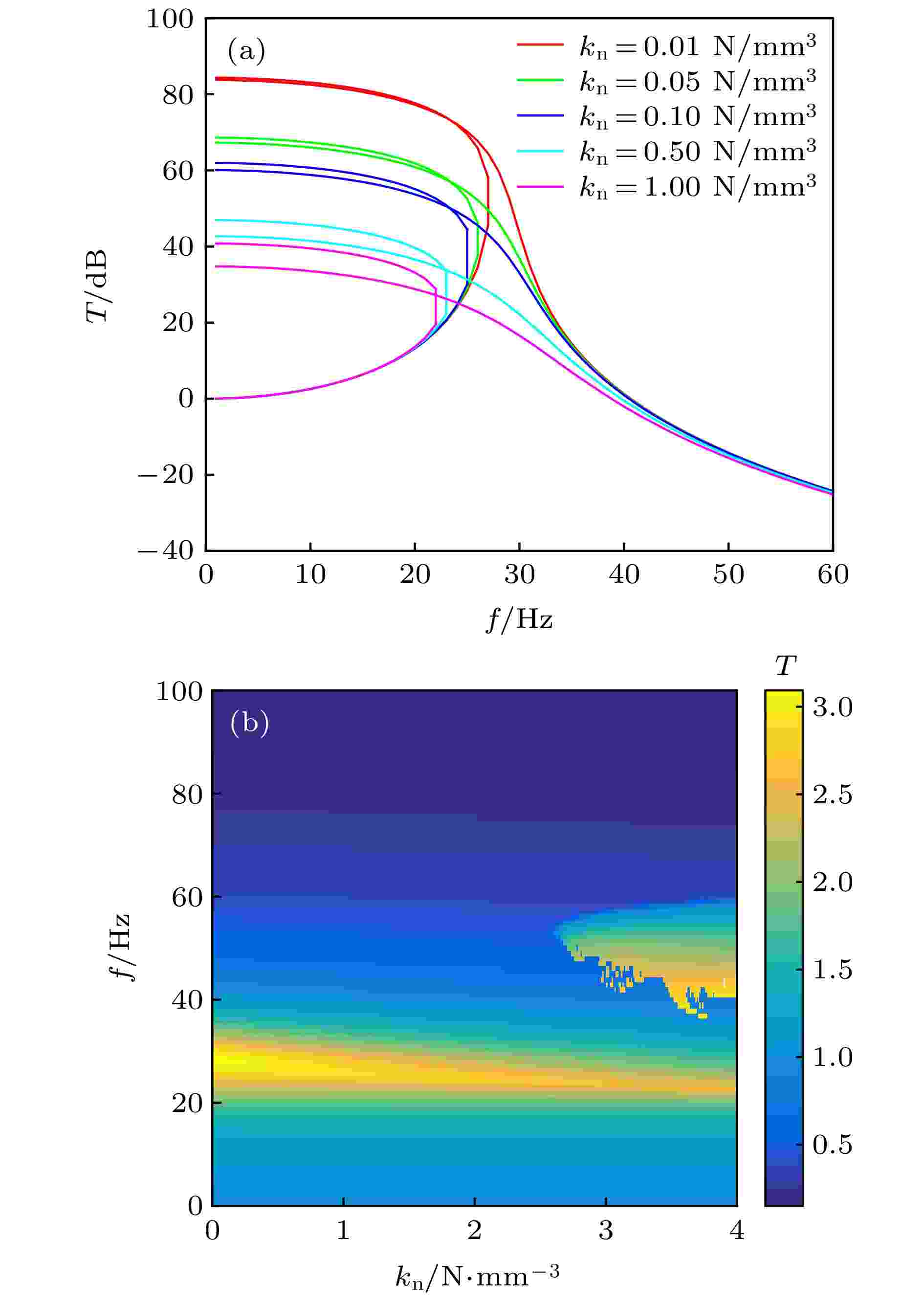
图 11 固定k₀ = –7.5 N/mm, 立方刚度系数k_n变化对系统隔振特性的影响　(a)解析结果; (b)数值仿真结果
Figure11. When k₀ = –7.5 N/mm, influence of k_n on vibration isolation: (a) Analytical results; (b) numerical simulations.

综上可得, 激励幅值影响系统的主共振频率; 负刚度系数k₀的变化主要引起系统共振点位置和共振峰大小的变化; 立方刚度系数k_n主要与系统次谐波共振的出现有关.

实验装置如图12所示, 通过功率放大器利用电磁激振器在屈曲梁底部施加激励, 利用激光扫描测振系统拾取结构的激励和响应, 利用电脑实现控制和数据采集等功能.
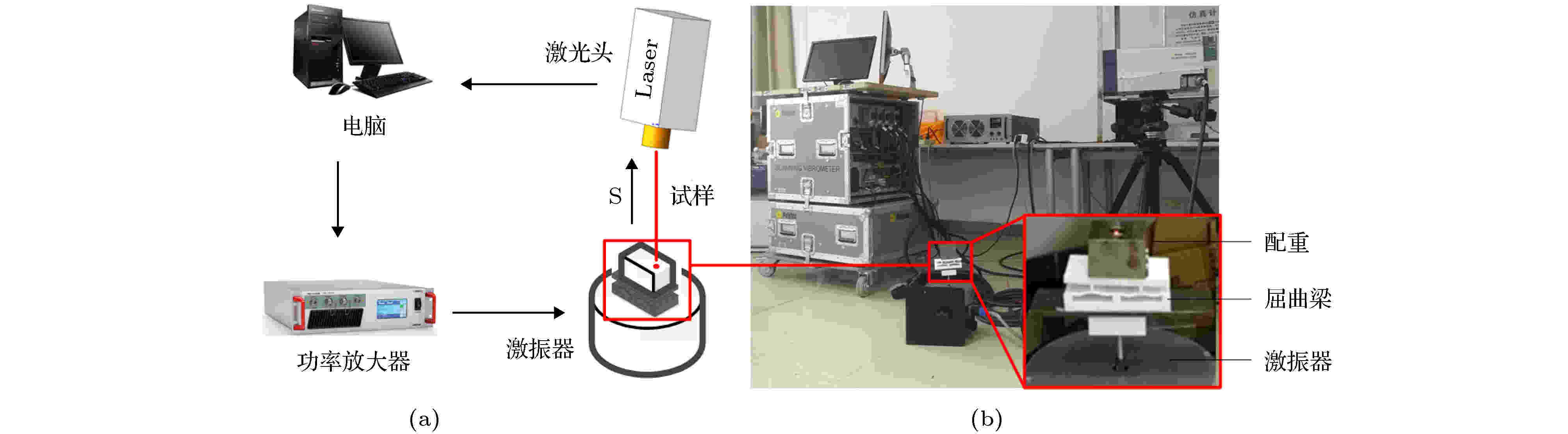图 12 (a)实验示意图; (b)实验装置
Figure12. (a) Experimental schematic diagram; (b) experimental setups.

2

-->

5.1.次谐波共振特性验证

为研究并验证该结构的1/2次谐波共振现象, 本文在实验中施加频率为55 Hz的正弦激励并研究系统的响应特性, 结果如图13所示. 图13(a)表明, 系统频域响应曲线除在55 Hz处有尖峰外, 在接近27.5 Hz处也有一个明显的峰值. 由此可知, 本文设计的双稳态结构确实可以产生显著的1/2次谐波共振响应, 时域响应曲线每2倍周期响应幅值被加强. 此外, 本文实验还表明, 1/2次谐波共振现象能在基波为40—60 Hz的宽带范围内观察到, 证明了1/2次谐波共振在较宽的带宽下均可产生.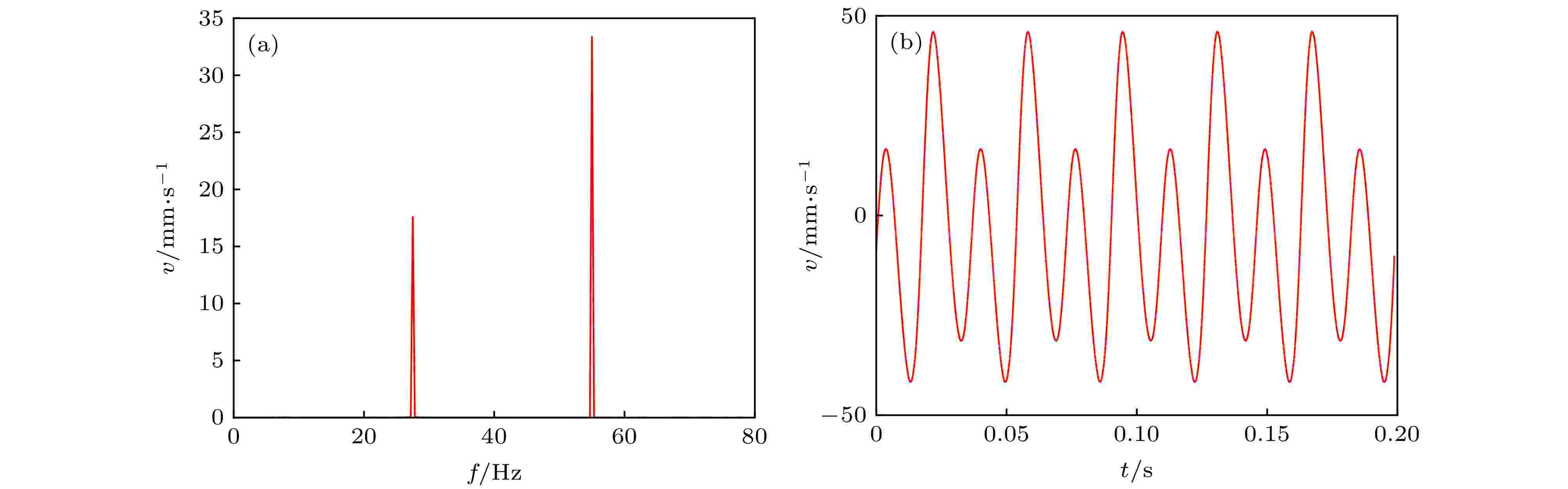
图 13 频率为55 Hz的正弦激励信号下系统的响应　(a)频域响应; (b)时域响应
Figure13. Response under sinusoidal excitation signal with frequency of 55 Hz: (a) Frequency domain; (b) time domain.

为从实验中验证激励幅值对系统次谐波共振的影响规律, 本文以40 Hz为例开展实验研究, 结果如图14和图15所示.
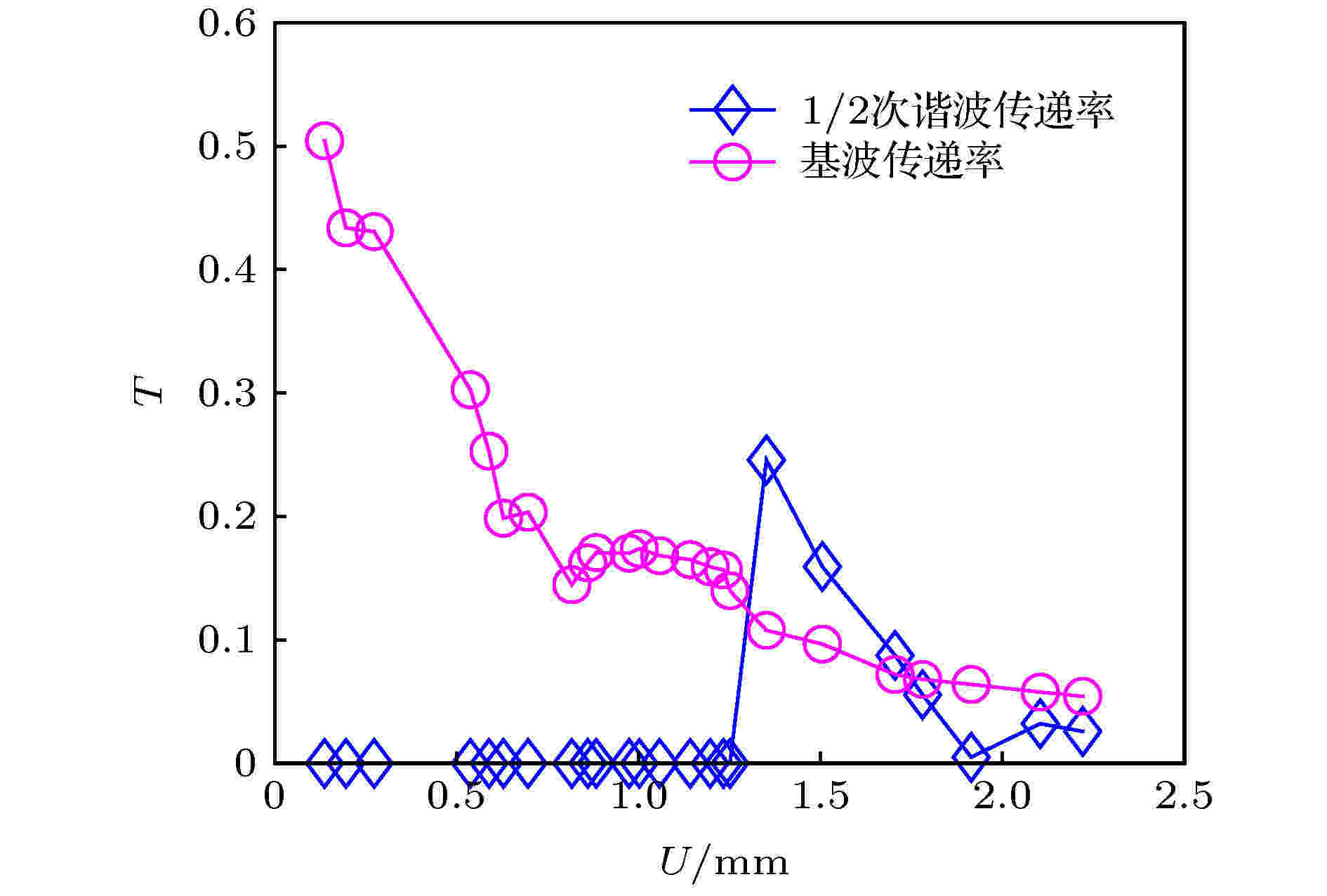图 14 激励幅值变化对1/2次谐波共振的影响
Figure14. Influence of excitation amplitude on the 1/2 sub-harmonic resonance.

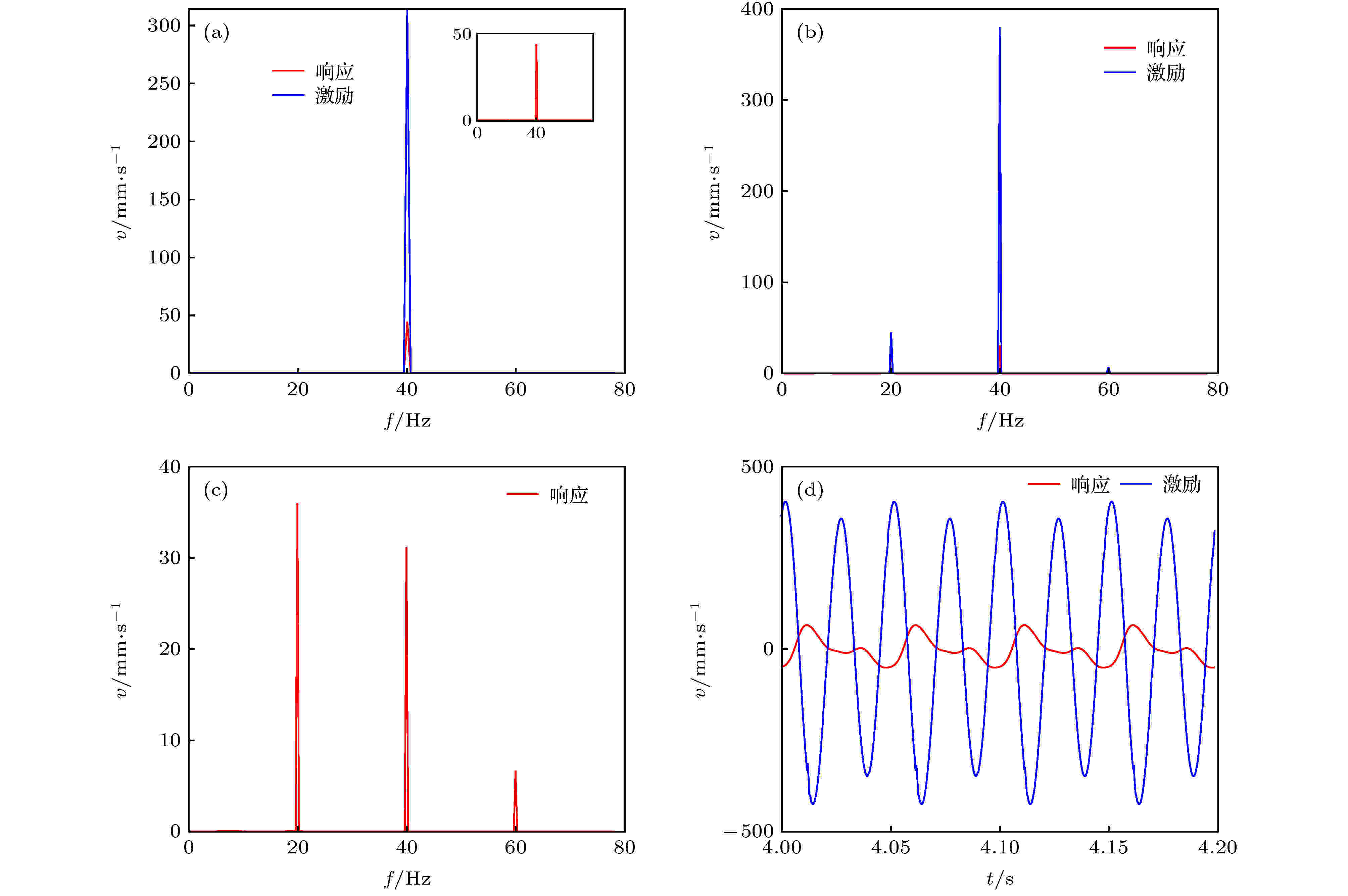图 15 系统40 Hz处的次谐波共振现象　(a) U = 1.251 mm时的响应和激励频谱; (b), (c)U = 1.351 mm时的响应和激励频谱; (d)U = 1.351 mm时的时域波形
Figure15. Sub-harmonic resonance phenomena at 40 Hz: (a) Response and excitation spectrum with U = 1.251 mm; (b), (c) response and excitation spectrum with U = 1.351 mm; (d) time-domain waveform with U = 1.351 mm.

图14呈现了激励幅值逐渐增加时基波和1/2次谐波的传递率. 随激励幅值的增加, 系统的基波传递率整体呈下降的趋势, 1/2次谐波传递率在激励幅值较小时为0, 在激励幅值为1.251 mm时向上跳变, 然后逐渐降低直至消失. 这一规律与图7呈现的特性完全一致, 证明了1/2次谐波共振的耦合特性以及次谐波的“产生-增强-衰退-消失”过程.
图15呈现了跳变前后的响应特性. 在跳变发生前(见图15(a)激励幅值U = 1.251 mm), 响应信号中仅包含基波成分. 但只需将激励幅值进一步增加(图15(b)U = 1.351 mm), 响应频谱(图15(c))除在40 Hz处有峰值外, 在20和60 Hz处也有明显的共振峰, 且20 Hz的频谱值更高, 1/2次谐波成分对系统响应的影响最大, 此时, 其时域波形产生2倍周期的显著畸变, 如图15(d)所示.
2 -->

5.2.隔振特性验证

为验证激励幅值对双稳态屈曲梁结构隔振特性的影响, 实验中施加扫频激励信号$ U_1, U_2\,(U_1 \! < \! U_2), $得到结构在不同激励幅值下的隔振特性, 实验与数值仿真结果对照如图16所示, 实验结果与数值仿真结果符合得较好. 实验证明, 随激励幅值增加, 双稳态屈曲梁结构的共振频率向低频移动且共振峰峰值降低. 因此, 适当提高非线性系统的激励幅值, 能有效改善系统的隔振特性.
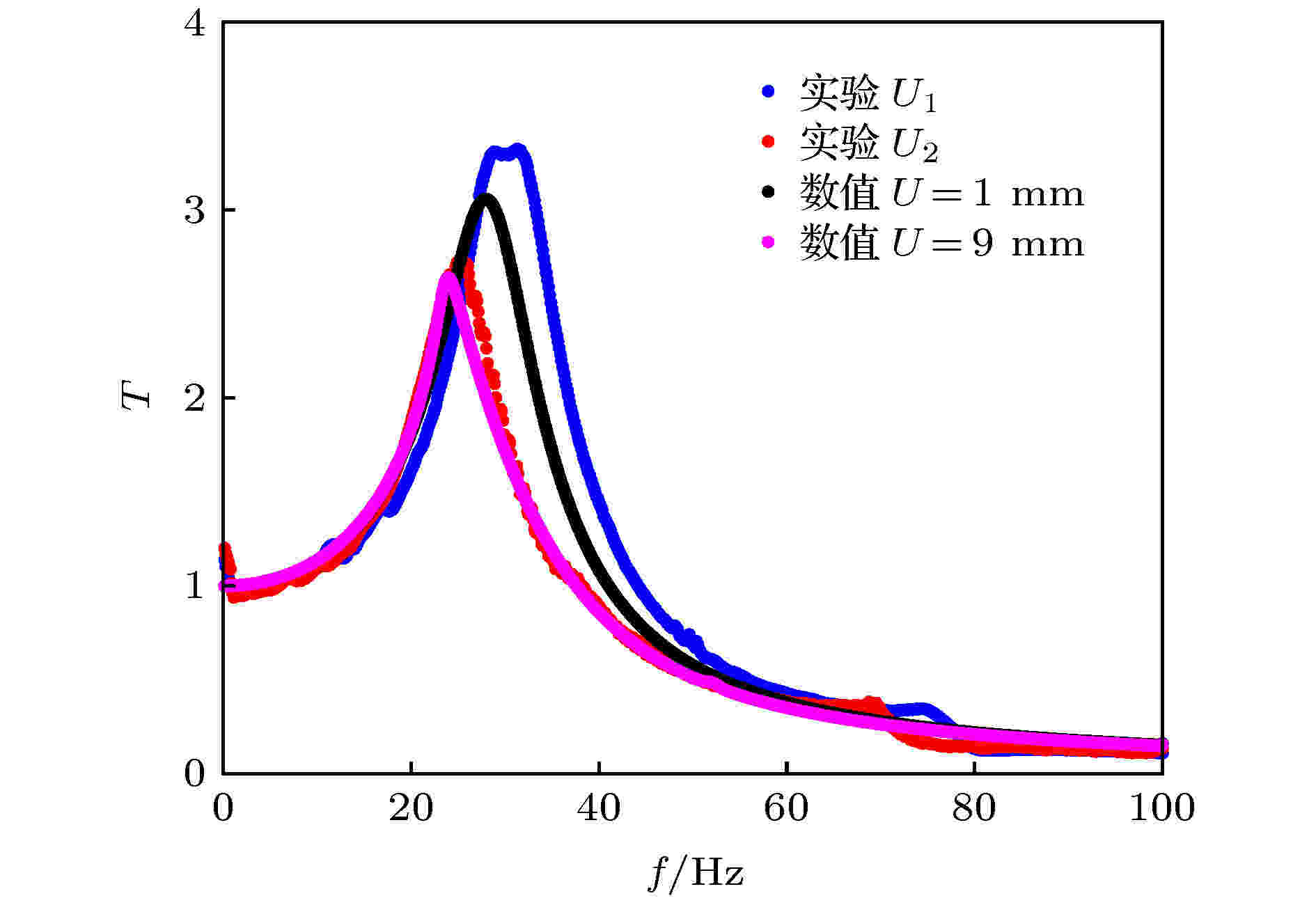图 16 实验-数值仿真结果对比
Figure16. Comparison between numerical and experimental results.

本文利用谐波平衡、数值积分和实验研究了典型双稳态系统—屈曲梁结构中的1/2次谐波共振、演化过程、参数调节规律及其对隔振的影响, 得到如下结论.
非线性强度增加到一定程度时会使系统产生显著的1/2次谐波共振, 使二倍固有频率附近的幅值传递率增加, 降低隔振效果, 且1/2次谐波共振能在一定带宽的激励下产生. 激励幅值较小时, 无次谐波共振现象; 激励幅值增加到一定程度时次谐波共振传递率急速增加, 但继续增加激励幅值会使次谐波传递率降低. 在激励幅值变化的过程中, 次谐波共振条件下基波和次谐波传递率产生分岔: 无阻尼时1/2次谐波的产生伴随着基波传递率增强过程, 但1/2次谐波传递率达到峰值并不会引起基波传递率的突变; 有阻尼时, 随着幅值增加, 1/2次谐波并不会在产生后一直存在, 而是遵循着“产生-增强-衰退-消失”的过程. 在这一过程中, 系统的峰值频率和峰值传递率先降低, 但是1/2次谐波传递率大于基波传递率时就引起峰值频率和峰值传递率的跳变增加.
负刚度参数k₀对系统主共振特性影响较大, 在给定激励幅值下, 随着|k₀|的增大, 系统共振峰向高频偏移且传递率升高; 非线性系数k_n主要影响系统次谐波共振特性, 对系统共振峰的峰值和共振点频率影响较小. 实验验证了理论分析结果.
非线性系统的次谐波共振会影响系统隔振区的隔振效果, 使系统在该频段的隔振效果变差, 在实际使用中应避开次谐波共振传递率增强的幅值区间; 而当需要应用次谐波的幅值增强效应时, 需调节参数使系统运行在“增强”幅值区间. 本文研究所揭示的规律和特性为双稳态结构的设计和应用提供指导.

利用(2)式求解双稳态屈曲梁机械结构理论模型的参数, 将其化为普通形式

$\small \begin{split} \frac{{p{l^3}}}{{EIh}} =&\; \frac{{3{{\text{π}}^4}}}{2}{\left( {\frac{h}{t}} \right)^2}{\left( {\frac{d}{h}} \right)^3} - \frac{{9{{\text{π}}^4}}}{2}{\left( {\frac{h}{t}} \right)^2}{\left( {\frac{d}{h}} \right)^2}\\& \; + \left[ {3{{\text{π}}^4}{{\left( {\frac{h}{t}} \right)}^2} + 2{{\text{π}}^4}} \right]\left( {\frac{d}{h}} \right),\\ p =&\; \frac{{3{{\text{π}}^4}EI}}{{2{l^3}{t^2}}}{d^3} - \frac{{9{{\text{π}}^4}EIh}}{{2{l^3}{t^2}}}{d^2} \\& \; + \left( {\frac{{3{{\text{π}}^4}{h^2}EI}}{{{t^2}{l^3}}} + \frac{{2{{\text{π}}^4}EI}}{{{l^3}}}} \right)d.\end{split}\tag{A1}$

将零点位置化到原点

$\small\begin{split}p\left( x \right)\; & = \frac{{3{{\text{π}}^4}EI}}{{2{t^2}{l^3}}}{\left( {x + h} \right)^3} - \frac{{9{{\text{π}}^4}EIh}}{{2{t^2}{l^3}}}{\left( {x + h} \right)^2} \\& \quad + \left( {\frac{{3{{\text{π}}^4}EI{h^2}}}{{{t^2}{l^3}}} + \frac{{2{{\text{π}}^4}EI}}{{{l^3}}}} \right)\left( {x + h} \right)\\& = \frac{{3{{\text{π}}^4}EI}}{{2{t^2}{l^3}}}{x^3} - \left( {\frac{{3{{\text{π}}^4}EI{h^2}}}{{2{t^2}{l^3}}} - \frac{{2{{\text{π}}^4}EI}}{{{l^3}}}} \right)x \\& + \frac{{2{{\text{π}}^4}EIh}}{{{l^3}}},\end{split}\tag{A2}$

取屈曲梁双稳态结构的几何、材料参数, 代入(A2)式得
x³项系数

$\small\frac{{3{{\text{π}}^4}EI}}{{2{l^3}{t^2}}} = 0.28\;\left( {{\rm{N}}/{\rm{m}}{{\rm{m}}^3}} \right),\tag{A3}$

x项系数

$\small - \left( {\frac{{3{{\text{π}}^4}EI{h^2}}}{{2{t^2}{l^3}}} - \frac{{2{{\text{π}}^4}EI}}{{{l^3}}}} \right) = - 7.5\;({\rm{N}}/{\rm{mm}}).\tag{A4}$