摘要: 界面力学性能是影响石墨烯/柔性基底复合结构整体力学性能的关键因素, 因此对该结构界面切应力传递机理的研究十分必要. 考虑了石墨烯和基底泊松效应的影响, 本文提出了二维非线性剪滞模型. 对于基底泊松比相比石墨烯较大的情况, 利用该模型理论研究了受单轴拉伸石墨烯/柔性基底结构的双向界面切应力传递问题. 在弹性粘结阶段, 导出了石墨烯双向正应变和双向界面切应力的半解析表达式, 分析了不同位置处石墨烯正应变和界面切应力的分布规律. 导出了石墨烯/柔性基底结构发生界面滑移的临界应变, 结果表明该临界应变低于利用经典一维非线性剪滞模型得到的滑移临界应变, 并且明显受到石墨烯宽度尺寸以及基底泊松比大小的影响. 基于二维非线性剪滞模型建立有限元模型 (FEM), 研究了界面滑移阶段石墨烯双向正应变和双向界面切应力的分布规律. 与一维非线性剪滞模型的结果对比表明, 当石墨烯宽度较大时, 二维模型和一维模型对石墨烯正应变、界面切应力以及滑移临界应变的计算结果均存在较大差别, 但石墨烯宽度很小时, 二维模型可近似被一维模型代替. 最后, 通过与拉曼实验结果的对比, 验证了二维非线性剪滞模型的可靠性, 并得到了石墨烯/聚对苯二甲酸乙二醇酯 (PET) 基底结构的界面刚度 (100 TPa/m) 和界面剪切强度 (0.295 MPa).
关键词: 石墨烯/柔性基底结构 /
泊松比 /
界面切应力传递 /
二维非线性剪滞模型 English Abstract Theoretical studies on bidirectional interfacial shear stress transfer of graphene/flexible substrate composite structure Bai Jia-Hao Guo Jian-Gang Tianjin Key Laboratory of Modern Experimental Mechanics, Department of Mechanics, Tianjin University, Tianjin 300354, China Received Date: 11 November 2019Accepted Date: 11 December 2019Published Online: 05 March 2020Abstract: Interfacial mechanical properties have a great influence on the overall mechanical performance of graphene/flexible substrate composite structure. Therefore, it is necessary to study interfacial shear stress transfer between graphene and flexible substrate. In this paper, a two-dimensional nonlinear shear-lag model (2D model) is presented. Taking the effects of Poisson’s ratio of the graphene and substrate into consideration, the bidirectional interfacial shear stress transfer between graphene and flexible substrate subjected to uniaxial tension is investigated by the 2D model when the Poisson’s ratio of substrate is larger than that of graphene. In the elastic bonding stage, the semi-analytical solutions of the bidirectional normal strains of the graphene and bidirectional interfacial shear stresses are derived, respectively, and their distributions at different positions are illustrated. The critical strain for interfacial sliding is derived by the 2D model, and the results show that the critical strain has a micron-scaled characteristic width. The width size of graphene has a significant influence on the critical strain when it is less than the characteristic width, but the size effect can be ignored when the width of graphene is larger than the characteristic width. In addition, the Poisson’s ratio of substrate can also affect the critical strain. Based on the 2D model, the finite element simulations are made to investigate the distribution of graphene's normal strains and interfacial shear stresses in the interfacial sliding stage. Furthermore, compared with the results obtained via one-dimensional nonlinear shear-lag model (1D model), the distributions of graphene’s normal strains and interfacial shear stresses calculated by 2D model show obvious bidimensional effects both in the elastic bonding stage and in the interfacial sliding stage when the width of graphene is large. There exists a compression strain in the graphene and a transverse (perpendicular to the tensile direction) shear stress in the interface, which are neglected in the 1D model. And the distributions of graphene’s tensile strain and longitudinal (along the tensile direction) interfacial shear stress are not uniform along the width, which are also significantly different from the results of 1D model. Moreover, the critical strain for interfacial sliding derived by the 2D model is lower than that obtained by the 1D model. However, when the width of graphene is small enough, the 2D model can be approximately replaced by the 1D model. Finally, by fitting the Raman experimental results, the reliability of the 2D model is verified, and the interfacial stiffness (100 TPa/m) and shear strength (0.295 MPa) between graphene and polyethylene terephthalate (PET) substrate are calculated.Keywords: graphene/flexible substrate structure /Poisson’s ratio /interfacial shear stress transfer /two-dimensional nonlinear shear-lag model 全文HTML --> --> --> 1.引 言 石墨烯是一种具有单原子层厚度的二维纳米材料[1 ] , 由于具有独特的电学、热学和力学性能[2 ,3 ] , 被认为在柔性电子器件和纳米复合材料等领域具有广阔的应用前景[4 ,5 ] . 在应用于柔性电子器件和纳米复合材料中时, 石墨烯通常被置于柔性基底上, 或嵌入基质中. 与碳纳米管/基体结构类似, 决定石墨烯/柔性基底复合结构的应用性能和可靠性的最关键问题之一在于其界面力学性能, 尤其是石墨烯与基底之间的剪切相互作用. 因此, 深入研究石墨烯与基底间界面切应力传递问题具有十分重要的意义.[6 ] 用拉曼实验技术对SU-8光刻胶/石墨烯/聚甲基丙烯酸甲酯 (PMMA)“三明治”结构界面的切应力传递进行了监测, 并且观察到与受较大应变载荷时碳纤维和基体间界面的断裂行为不同, 石墨烯与聚合物基底间的应力传递仍然通过界面摩擦进行. 这种界面纳米摩擦行为在Jiang等[7 ] 的实验中也被观察到, Jiang等利用原位拉曼光谱技术对置于单轴拉伸基底上石墨烯的应变进行了测量, 发现当基底受较大拉伸载荷时, 界面通过纳米摩擦作用进行切应力传递. 在Jiang等的研究中将这种界面摩擦行为称为界面滑移(下文沿用这一称谓), 并且计算得到基底所受拉伸应变载荷为0.3%时, 界面边缘开始出现滑移区域. 此外, Xu等[8 ,9 ] 和仇巍等[10 ] 在更大载荷范围对石墨烯/聚对苯二甲酸乙二醇酯 (PET)基底界面应力传递进行了研究, 同样在基底受到较大拉伸载荷情况下观察到了界面滑移行为, 并且发现石墨烯与PET基底间界面应力传递存在尺寸效应问题.[11 ] (剪滞理论)已经被广泛应用到受单轴载荷的石墨烯/柔性基底结构界面切应力传递问题的研究中. Gong等[6 ] 利用一维线性剪滞模型与实验结果进行拟合对比, 计算得出SU-8光刻胶/石墨烯/PMMA“三明治”结构的界面剪切强度约为2.3 MPa. Jiang等[7 ] 在线性剪滞模型基础上, 发展出了考虑界面滑移的一维非线性剪滞模型. 模型假设界面在弹性粘结阶段之后, 进入滑移阶段, 界面切应力大小随界面相对位移的增加保持不变. 利用该理论模型拟合实验数据, 获得石墨烯与PET基底间界面剪切强度为0.46—0.69 MPa. 另外, Guo 和Zhu[12 ] 以及Cui和Guo[13 ] 在理论研究中, 将受单轴载荷的石墨烯/基底结构沿加载方向上的单向界面切应力传递视为Ⅱ型裂纹沿界面切向的扩展, 并利用双线性内聚力模型近似代替一维非线性剪滞模型对该问题进行了研究, 计算了复合结构界面滑移的临界应变, 结果显示滑移临界应变明显受到石墨烯长度尺度的影响. 但是, 常用来作为石墨烯复合结构基底的柔性材料(PET, PMMA等)往往具有比石墨烯更大的泊松比[6 -10 ] . 然而一维剪滞模型只考虑了受单轴载荷的石墨烯/基底结构沿加载方向的界面切应力传递, 忽略了石墨烯和基底泊松效应引起的界面横向切应力传递作用, 可能会对石墨烯应变分布、界面切应力分布以及滑移临界应变的计算结果造成一定的影响.2.理论模型 22.1.问题描述 2.1.问题描述 一块长L 、宽W 的石墨烯薄膜完美地粘附在受单轴拉伸载荷的柔性基底上, 如图1 所示, 以O 为原点, 建立坐标系. 沿x 轴方向, 由于界面切应力作用, 基底的拉伸应变可以引起石墨烯薄膜的拉伸. 沿y 轴方向, 由于泊松效应, 石墨烯与基底产生横向压缩应变, 当基底泊松比相比石墨烯较大时(例如, PET泊松比为0.30—0.35[14 ] ), 基底压缩应变同样会通过界面横向切应力(垂直于拉伸方向)传递到石墨烯薄膜上. 所以, 石墨烯与受单轴拉伸载荷的基底间界面上实际存在双向切应力传递作用, 石墨烯实际处于二维应力状态下.图 1 受单轴拉伸载荷的石墨烯/基底结构示意图Figure1. Schematic diagram of the graphene/substrate structure under uniaxial tension.E , 泊松比为υ , 厚度为h . 基底杨氏模量为E s , 泊松比为υ s . 石墨烯的本构方程为:u , v , σx , σy , εx 和εy 分别代表了石墨烯沿x 与y 方向上的位移、正应力和正应变. 同时, 基底的位移与正应变有如下几何关系:u s , v s , ε sx 和ε sy 分别代表了基底沿x 与y 方向上的位移和正应变, 其中${\varepsilon _{{\rm{s}}y}} = - {\upsilon _{\rm{s}}} \times {\varepsilon _{{\rm{s}}x}}$ . 石墨烯与基底沿界面切向的相对位移为:δx 和δy 分别代表了石墨烯与基底沿x 与y 两个切向方向的相对位移.图2 所示. 仿照与石墨烯/基底结构相类似的矩形胶结补片结构与胶结接头结构求解双向应力解时的经典假设[15 -17 ] , 忽略石墨烯薄膜面内切应力, 从而得到平衡方程:图 2 石墨烯单元的应力状态示意图Figure2. The force balance of an element of graphene.τzx , τzy 分别代表界面沿x 与y 方向的切应力.2.2.二维非线性剪滞模型 -->2.2.二维非线性剪滞模型 一维非线性剪滞模型[7 ] 对石墨烯/基底结构单向界面切应力传递问题进行了描述. 界面局部处于弹性粘结阶段时, 切应力τ z iK 为界面刚度随基底与石墨烯界面相对位移δi 的增加而线性增加, 当切应力达到界面剪切强度τ c 后, 界面进入滑移损伤阶段, 切应力大小保持不变. 本构关系为:$d = 1 - {{{\delta _{\rm{c}}}} / {{\delta _{\rm{i}}}}}$ , δ c 为滑移起始时界面的相对位移.[18 -20 ] . Guo和Zhu[12 ] 以及Cui和Guo[13 ] 将石墨烯/基底单向界面切应力传递问题视为Ⅱ型裂纹扩展. 本文将石墨烯/基底双向界面切应力传递问题视为Ⅱ + Ⅲ型混合裂纹沿界面切向的扩展, 并仿照内聚力模型的做法, 将一维非线性剪滞模型(以下简称一维模型)扩展为可用于研究双向界面切应力传递的二维非线性剪滞模型(以下简称二维模型).图3 所示, 假设界面沿切向各向同性. 界面切应力合力τ m 为图 3 局部界面上一点的切应力分析Figure3. Analysis of interfacial shear stresses at local interface.δ m 为图4(a) 所示, 当界面处于弹性粘结阶段时, 界面切应力合力形式本构关系为${\tau _{\rm{m}}} = K{\delta _{\rm{m}}}$ , 分量形式本构关系为:图 4 (a) 二维非线性剪滞模型; (b) 双线性内聚力模型(Ⅱ + Ⅲ型混合模式)Figure4. (a) Two-dimensional nonlinear shear-lag model; (b) bilinear cohesive shear-mode (Ⅱ + Ⅲ) law.τ c , 界面滑移起始时, 切应力合力τ m 为7 )式— (9 )式, 得到滑移起始时界面实际相对位移δ m, c :τ m 大小保持不变, 方向与实际相对位移δ m 方向相同. 切应力合力形式本构关系为${\tau _{\rm{m}}} = \left( {1 - D} \right)K{\delta _{\rm{m}}} = {\tau _{\rm{c}}}$ , 分量形式本构关系为:$D = 1 - {{{\delta _{{\rm{m, c}}}}} / {{\delta _{\rm{m}}}}}$ .[12 ] 以及Cui和Guo[13 ] 利用研究Ⅱ型裂纹的双线性内聚力模型代替一维模型对石墨烯/基底结构单向界面切应力传递问题进行了研究. 而对于研究Ⅱ + Ⅲ型混合裂纹的双线性内聚力模型[21 ] (本构关系如图4(b) ), 当采用Benzeggagh-Kenane准则(B-K准则)判断断裂起始时, 断裂能G c 为δ m, f 表示混合裂纹断裂起始时界面的相对位移, G shear 代表Ⅱ + Ⅲ型混合裂纹起裂的能量释放率. 当${G_{{\rm{shear}}}} \to + \infty $ 时, ${\delta _{{\rm{m, f}}}} \to + \infty $ . 此时双线性内聚力模型的损伤变量D coh 为[21 ] ${D_{{\rm{coh}}}} \approx D$ 时, 两模型本构关系一致, 双线性内聚力模型软化阶段相当于二维模型的界面滑移阶段. 所以可以在ABAQUS中, 利用研究Ⅱ + Ⅲ型混合裂纹的双线性三维内聚力单元(沿垂直界面方向相对位移${\delta _z} = 0$ )代替二维模型对石墨烯/基底结构双向界面切应力传递问题进行仿真模拟研究.3.石墨烯正应变以及界面切应力分布的计算 23.1.弹性粘结阶段 3.1.弹性粘结阶段 当基底所受拉伸载荷较小时, 石墨烯/基底界面处于弹性粘结阶段, 此时采用二维模型弹性粘结阶段本构关系描述界面力学行为. 将(8 )式代入(4 )式, 结合(1 )式— (3 )式, 得到如下偏微分方程组:$A = \dfrac{K}{{Eh}}$ , $B = - \dfrac{{K\upsilon }}{{Eh}}$ , $C = - \dfrac{{K{\varepsilon _{{\rm{s}}x}}}}{h}$ , $D = - \dfrac{{K{\varepsilon _{{\rm{s}}y}}}}{h}$ . 相应边界条件如下, 沿石墨烯边缘$x = 0$ , $x = L$ 上有${\sigma _x} = 0$ 和15 )式进行求解, 得到σy 在$x = 0$ , $x = L$ 上边界条件为$y = 0$ , $y = W$ 上边界条件为${\sigma _y} = 0$ 与$\alpha = \sqrt {{K / {(Eh)}}} $ . 上述耦合偏微分方程组(14 )式已在文献[16 ]中得到了解决. 当基底受双轴拉伸载荷时(即${\varepsilon _{{\rm{s}}x}} > 0$ , ${\varepsilon _{{\rm{s}}y}} > 0$ ), 可以直接利用傅里叶级数法计算得到方程组中正应力σx 和σy 的半解析解, 将计算结果代入(4 )式即可求得界面切应力τzx 和τzy 的半解析解. 其结果具体形式如下:f mn ,x f mn ,y Φ m ,x Φ m ,y 附录 .${\varepsilon _{{\rm{s}}x}} > 0$ , ${\varepsilon _{{\rm{s}}y}} = - {\upsilon _{\rm{s}}} \times {\varepsilon _{{\rm{s}}x}} < 0$ ), 需使用叠加法计算. 取石墨烯杨氏模量$E = 1\;{\rm{TPa}}$ , 泊松比$\upsilon = 0.165$ [22 ] , 厚度$h = 0.335\; \;{\rm{nm}}$ , $L = W = 21.8\;{{\text{μ}}\rm{m}}$ , 基底 (PET) 泊松比${\upsilon _{\rm{s}}} = 0.33$ [14 ] . 根据文献[7 ]选取石墨烯/基底 (PET) 界面刚度$K = 74\;{\rm{TPa/m}}$ , 界面剪切强度${\tau _{\rm{c}}} = 0.5\;{\rm{MPa}}$ . 当基底所受拉伸载荷${\varepsilon _{{\rm{s}}x}} = 0.2 $ %时, 基底横向压缩应变${\varepsilon _{{\rm{s}}y}} = - {\upsilon _{\rm{s}}} \times 0.2 $ %, 复合结构处于弹性粘结阶段. 假设两种双轴拉伸加载情况. Case 1: ${\varepsilon _{{\rm{s}}x}} = {\varepsilon _{{\rm{s}}y}} = \xi$ %; case 2: ${\varepsilon _{{\rm{s}}x}} = \left( {0.2 + \xi } \right)$ %, ${\varepsilon _{{\rm{s}}y}} = \left( {\xi - {\upsilon _{\rm{s}}} \times 0.2} \right)$ % (ξ 可取任意大于${\upsilon _{\rm{s}}} \times 0.2$ 的值). 将case 1与case 2分别代入(17a )式、(17b )式和(18a )式、(18b )式进行计算, case 2– case 1即为基底受单轴拉伸载荷${\varepsilon _{{\rm{s}}x}} = 0.2$ %的结果(本文取$\xi = 0.3$ ), 石墨烯正应力为:19 )式代入(20 )式, 求得石墨烯正应变为:16 ], 由于篇幅原因此处不做记述.20 )式和(21 )式, 石墨烯正应变εx 和εy 分布如图5(a) 和图5(b) 所示, 界面切应力τzx 与τzy 分布如图5(c) 和图5(d) 所示. 从图5(a) 和图5(b) 中可以看出, εx 与εy 均在石墨烯薄膜中心区域达到最大, 且εy 最大值大约是εx 最大值的33%. 此外, 由于石墨烯泊松比引起的x 与y 方向的耦合效应, εx 在靠近边缘($x = 0$ 与$x = L$ )区域内沿宽度(y 方向)的分布与εy 在靠近边缘($y = 0$ 与$y = W$ )区域内沿长度(x 方向)的分布皆具有一定的不均匀性; 图5(c) 和图5(d) 结果显示, τzx 与τzy 在界面边角位置达到最大值, 且τzy 最大值大约是τzx 最大值的30%, 横向切应力τzy 的传递作用影响较大. 另外, 与正应变分布相似, τzx 沿宽度方向与τzy 沿长度方向的分布同样具有一定的不均匀性. 综上结果可知, 二维模型计算的石墨烯正应变分布与界面切应力分布表现出明显的二维应力分布状态, 这是一维模型所不能解释的.图 5 弹性粘结阶段 (ε sx = 0.2%) 时石墨烯正应变 (a) εx 和(b) εy 以及界面切应力 (c) τzx 和(d) τzy 的分布Figure5. Distributions of graphene’s normal strains (a) εx and (b) εy ; distributions of interfacial shear stresses (c) τzx and (d) τzy at the elastic bonding stage (ε sx = 0.2%).图6 ), 有限元模型建立具体过程详见3.3 节. 典型线分别选取沿石墨烯两个边缘($x = 0$ 和$y = 0$ )与两条中心线(x = $ {L / 2}$ 和$y = {W / 2}$ ). 从图6 中可以清楚地看出εx 和τzx 沿宽度方向分布以及εy 和τzy 沿长度方向分布的不均匀性, 而且理论模型结果与有限元结果符合较好.图 6 典型线处石墨烯正应变 (a) εx 和(b) εy 以及界面切应力 (c) τzx 和(d) τzy 的分布Figure6. Distributions of graphene’s strains (a) εx and (b) εy ; distributions of interfacial shear stresses (c) τzx and (d) τzy along several representative lines.3.2.滑移临界应变 -->3.2.滑移临界应变 将界面开始出现滑移区域时基底所受拉伸应变载荷定义为滑移临界应变ε sx c . 根据图5(c) 和图5(d) 可知, 弹性粘结阶段时最大切应力出现在界面的四个边角(图1 中点O , A , B 和D ), 所以界面边角位置最先发生滑移损伤. 当边角处切应力合力τ m 达到剪切强度τ c 时, 界面开始出现滑移区域. 由于结构对称性, 选取O 点处界面切应力进行计算, 根据(9 )式有16a )式和(16b )式代入(4 )式中可得:${\varepsilon _{{\rm{s}}y}} = - {\upsilon _{\rm{s}}} \times {\varepsilon _{{\rm{s}}x}}$ . 由(22 )式和(23 )式计算得到滑移临界应变ε sx c :[13 ] 利用一维模型研究了石墨烯长度尺寸对滑移临界应变的影响. 而依据二维模型推导 (24 )式可知, 石墨烯宽度尺寸以及基底泊松比大小同样会对滑移临界应变造成影响. 将3.1 节所述材料参数代入(24 )式, 图7 给出了不同基底泊松比情况下滑移临界应变ε sx c 随石墨烯宽度的变化关系. 从图7 可以看出, 滑移临界应变存在一个特征宽度, 当石墨烯宽度小于该特征量时, 滑移临界应变ε sx c 表现出明显的宽度尺寸效应, 石墨烯宽度越大, ε sx c 越小, 界面边缘越易发生滑移损伤; 当石墨烯宽度大于该特征量时, 宽度尺寸对ε sx c 的影响可被忽略. 对于本文选取的石墨烯与界面力学参数, ε sx c 的特征宽度大约为8 μm. 而通过分析 (24 )式中参数量α 可知, α 为界面刚度K 与石墨烯面内刚度Eh 比值的二分之一次方, 1/α 在微米量级, 所以滑移临界应变的特征宽度出现在微米量级是由界面力学性能与石墨烯自身力学性质所共同决定的. 另外, 对比图7 中三条曲线结果可知, 石墨烯宽度相同时, 基底泊松比越大, ε sx c 越小. 此外, 图7 还给出了一维模型与二维模型对滑移临界应变计算结果的比较. 结果显示, 一维模型过高估计了滑移临界应变ε sx c . 当石墨烯宽度大于8 μm, 基底泊松比为0.49时, 一维模型与二维模型计算结果的偏差可达11.3%, 但当石墨烯宽度小于0.5 μm时, 两种模型对ε sx c 计算结果的差别低于0.5%, 可被忽略.图 7 不同基底泊松比情况下滑移临界应变ε sx c 随石墨烯宽度W 的变化(线为理论值, 散点为有限元值)Figure7. Variation of the critical strain for sliding with the width of graphene at different Poisson's ratio of substrate (the lines are the theoretical results, and the scatter points are the FEM results).3.3.界面滑移阶段 -->3.3.界面滑移阶段 当基底所受拉伸载荷较大时, 界面开始出现滑移区域, 石墨烯/基底结构进入界面滑移阶段, 如图8 所示. 在ABAQUS中建立石墨烯/基底结构三维有限元模型, 计算界面滑移阶段时石墨烯正应变以及界面切应力的分布. 分别采用M3D4R单元与C3D8R单元对石墨烯和基底进行建模, 材料参数按照3.1 节所述进行设置, 基底 (PET) 杨氏模量${E_{\rm{s}}} = 3\;{\rm{GPa}}$ . 根据2.2 节所述方法, 采用具有双线性内聚力法则的三维COH3 D8单元代替二维模型对界面进行建模. 在切向两方向上, 分别设置界面刚度$K = 74\;{{{\rm{TPa}}} / {\rm{m}}}$ , 界面剪切强度${\tau _{\rm{c}}} = 0.5\;{\rm{MPa}}$ [7 ] . 在垂直方向上, 界面刚度和界面强度被视为惩罚参数, 设置为较大的数值, 防止垂直界面方向相对位移的产生. 当界面切应力合力达到剪切强度τ c 时, 界面进入软化阶段, 采用B-K准则判断断裂起始, 将界面切向断裂能设置为一个相当大的数值, 此时双线性内聚力模型软化阶段可近似替代二维模型界面滑移阶段.图 8 界面滑移阶段示意图Figure8. Schematic diagram of interfacial sliding stage.${\varepsilon _{{\rm{s}}x}} = $ 1%时, 复合结构进入界面滑移阶段. 石墨烯正应变εx 和εy 分布数值结果如图9(a) 和图9(b) 所示, 界面切应力τzx 和τzy 分布数值结果如图9(c) 和图9(d) 所示. 图9 结果显示, 界面滑移阶段时, 石墨烯正应变与界面切应力的分布同样表现出明显的二维应力分布状态. εx 与εy 仍在石墨烯中心区域达到最大, 而界面切应力则由于界面边缘发生滑移损伤, 最大值位置发生变化. τzx 在界面中心线 ($y = {W / 2}$ ) 上的滑移区域内达到最大, 而τzy 则在边缘线($y = 0$ 与$y = W$ )上滑移区域与弹性粘结区域交界点处达到最大值, 且τzy 最大值大约是τzx 最大值的60%, 横向切应力τzy 的传递作用进一步增大. 此外, 界面滑移区域的出现也使得εx , τzx 沿宽度方向分布与εy , τzy 沿长度方向分布的不均匀性进一步增大.图 9 界面滑移阶段 (ε sx = 1%) 时石墨烯正应变 (a) εx 和(b) εy 以及界面切应力 (c) τzx 和(d) τzy. 的分布Figure9. Distributions of graphene’s normal strains (a) εx and (b) εy ; distributions of interfacial shear stresses (c) τzx and (d) τzy at the interfacial sliding stage (ε sx = 1%).4.分析与讨论 24.1.与一维模型计算结果的对比 4.1.与一维模型计算结果的对比 根据3.1 节相关参数的取值, 将二维模型的计算结果与一维模型结果进行细致对比. 首先, 一维模型只考虑了沿拉伸方向的界面切应力传递, 忽略了界面横向切应力传递作用, 无法考虑石墨烯宽度以及基底泊松比大小对滑移临界应变ε sx c 的影响, 也无法对石墨烯压缩应变εy 以及界面横向切应力τzy 的分布进行计算. 3.2 节中已经将两模型对于滑移临界应变ε sx c 的计算结果进行了比较(如图7 所示), 并发现一维模型过高估计了复合结构的滑移临界应变, 但当石墨烯宽度小于0.5 μm时, 两种模型对ε sx c 计算结果的差别可以忽略. 而对于石墨烯压缩应变εy , 由于没有考虑界面横向切应力传递作用, 可认为一维模型对其的计算结果为图10 给出了基底受不同拉伸载荷作用下, 二维模型对石墨烯中心C 点处(如图1 所示)压缩应变ε y C ${\varepsilon _{{\rm{s}}x}} = 0.2\%$ ) 还是界面滑移阶段 (${\varepsilon _{{\rm{s}}x}} = $ 0.6%, 1%), 石墨烯宽度大于20 μm时, 由于界面横向切应力传递区域足够大, 基底横向压缩应变可以完全传递到石墨烯上, 此时$\varepsilon _y^C \approx - {\upsilon _s} \times {\varepsilon _{sx}}$ ; 当宽度小于20 μm, 大于0.5 μm时, 虽然基底横向压缩应变并未完全传递到石墨烯上, 但界面横向切应力传递对石墨烯中心C 点处压缩应变ε y C $\varepsilon _y^{C} \approx - {\upsilon _{}} \times \varepsilon _x^{C}$ , 与(25 )式计算结果相同, 此时由于传递区域过小, 界面横向切应力τzy 的传递作用可被忽略.图 10 不同基底应变下石墨烯中心C 点处压缩应变εy C 随石墨烯宽度的变化Figure10. Variation of compressive strain εy C at the center point C of graphene with its width when the strain of substrate is different.$y = 0$ ) 和中心线 ($y = {W / 2}$ ) 处, 将二维模型对石墨烯拉伸应变εx 和界面切应力τzx 的计算结果与一维模型的结果分别进行了比较(如图11 所示). 图11(a) 和图11(b) 给出了弹性粘结阶段 (${\varepsilon _{{\rm{s}}x}} = $ 0.2%)的比较结果. 由图11 结果显示, 二维模型对εx 和τzx 沿边缘线分布的计算结果与一维模型重合, 沿中心线分布的计算结果与一维模型具有一定差别. 图11(c) 和图11(d) 给出了界面滑移阶段 (${\varepsilon _{{\rm{s}}x}} = $ 1%)的比较结果. 结果显示, 界面滑移阶段时, 二维模型对εx 和τzx 沿两条典型线上分布的计算结果与一维模型结果均具有较大差别. 特别对于τzx , 由于二维模型考虑了界面横向切应力τzy , 界面滑移行为由τzx 与τzy 共同决定. 在界面滑移阶段, 沿界面边缘线 (y = 0) 上的滑移区域内存在较大的横向切应力τzy , 而在沿界面中心线 (y = W /2) 上横向切应力τzy 为零(如图9(d) ), 一维模型则没有考虑横向切应力τzy . 由此导致二维模型对τzx 沿界面边缘分布的计算结果与对沿中心线分布的计算结果以及一维模型结果均具有较大差异, 特别对于沿边缘线上x 小于5.6 μm的界面滑移部分, 差异更加明显.图 11 二维模型与一维模型结果的比较 (W = 21.8 μm) (a) εx 和(b) τzx 在弹性粘结阶段(ε sx = 0.2%); (c) εx 和(d) τzx 在界面滑移阶段 (ε sx = 1%)Figure11. Comparisons of the results obtained via one-dimensional and two-dimensional models (W = 21.8 μm): (a) εx and (b) τzx at the elastic bonding stage (ε sx = 0.2%); (c) εx and (d) τzx at the interfacial sliding stage (ε sx = 1%).εx 和τzx 沿典型线分布的计算结果与一维模型结果的差别可被忽略, 且εx 和τzx 沿宽度方向的分布基本均匀. 图12(a) 和图12(b) 给出了石墨烯宽度为1 μm时界面滑移阶段的比较结果, 两模型计算结果基本重合. 弹性粘结阶段时比较结果与之相似, 此处不做赘述.图 12 二维模型与一维模型计算结果的比较 (W = 1 μm) (a) εx 和(b) τzx 在界面滑移阶段 (ε sx = 1%)Figure12. Comparisons of the results obtained via one-dimensional and two-dimensional models (W = 1 μm): (a) εx and (b) τzx at the interfacial sliding stage (ε sx = 1%).εx 与界面切应力τzx 的计算结果与二维模型有一定误差, 尤其在界面滑移阶段时, 差别较大. 且通过二维模型结果可知, 石墨烯薄膜存在较大压缩应变εy , 界面横向切应力τzy 的传递作用不可忽略. 但当石墨烯宽度小于0.5 μm时, 针对本文所代入的界面力学参数, 一维模型与二维模型对滑移临界应变计算结果的差别低于0.5%, 对εx 与τzx 的计算结果基本重合, 且二维模型对εy 的计算结果约等于石墨烯自身泊松比所引起的横向压缩应变, 与一维模型根据(25 )式对其的计算结果相同, 此时界面横向切应力τzy 的传递作用可被忽略, 二维模型可近似被一维模型代替.4.2.与实验结果的对比 -->4.2.与实验结果的对比 许超宸[23 ] 利用原位拉曼光谱技术测量了放置在受单轴拉伸PET基底上的长方形石墨烯沿拉伸方向中心线上应变εx 的分布. 实验结果显示, 小尺寸石墨烯与基底完美贴合, 符合本文所建立模型的界面完美粘结假设. 本节利用二维模型与许超宸[23 ] 测得的小尺寸石墨烯 ($L = 20 $ μm, $W = 3\;{\rm{mm}}$ )的实验数据进行拟合对比, 确定界面参数, 验证模型可靠性.[23 ] 通过检测拉曼谱线中2D峰峰位ω 2D 对石墨烯应变分布进行测量. 2D峰频移变化Δω 2D 与石墨烯面内正应变分量之和${\varepsilon _x} + {\varepsilon _y}$ 有如下对应关系[24 ] :$\Delta {\omega _{2{\rm{D}}}} = {\omega _{2{\rm{D}}}} - \omega _{2{\rm{D}}}^0$ , $ \omega _{{\rm{2D}}}^{\rm{0}} $ 为被测位置2D峰初始峰位, γ 2D 为Grüneisen系数, 定义石墨烯面内正应变分量之和${\varepsilon _{\rm{m}}} = {\varepsilon _x} + {\varepsilon _y}$ . 依据(26 )式测量石墨烯应变, 首先要对$ - \omega _{{\rm{2D}}}^{\rm{0}}{\gamma _{{\rm{2D}}}} $ 项进行标定. Mohiuddin等[24 ] 的标定实验中考虑了泊松效应的影响, 选择石墨烯中心区域为观测点, 当基底所受拉伸载荷较小时, 2D峰峰位ω 2D 随基底拉伸应变ε sx 的增大线性变化, 此时认为石墨烯中心区域应变与基底应变协同一致, 即有27 )式代入(26 )式得到ω 2D 随基底拉伸应变ε sx 变化的线性段的斜率结合式(28 )式, 完成对$ - \omega _{{\rm{2D}}}^{\rm{0}}{\gamma _{{\rm{2D}}}} $ 项的标定. 但在许超宸[23 ] 的实验中, 采用了一维模型假设, 忽略石墨烯与基底的泊松比(假设${\upsilon _{\rm{s}}} = \upsilon = 0$ ). 利用2D峰线性变化段对$ - \omega _{{\rm{2D}}}^{\rm{0}}{\gamma _{{\rm{2D}}}} $ 项进行标定时认为$ - \omega _{{\rm{2D}}}^{\rm{0}}{\gamma _{{\rm{2D}}}} $ 项建立2D峰峰位ω 2D 与石墨烯应变的对应关系时, 假设${\varepsilon _y} = 0$ , 并根据(26 )式得到如下应变测定公式:26 )式可知, 实际与Δω 2D 成正比的是石墨烯面内正应变分量之和ε m . 并且根据 (28 )式与(29 )式对比可知, 许超宸忽略石墨烯与基底泊松比作用导致实验中标定的$ - \omega _{{\rm{2D}}}^{\rm{0}}{\gamma _{{\rm{2D}}}} $ 项实际为$ - \omega _{{\rm{2D}}}^{\rm{0}}{\gamma _{{\rm{2D}}}} $ ×(1 – υ s ), 所以其依据(30 )式测出的应变εx 与实际应变值可能存在一定的误差. 本文建立的二维模型考虑了石墨烯与基底的泊松比作用, 并解耦计算得到石墨烯拉伸应变分量εx 和压缩应变分量εy . 所以与许超宸[23 ] 实验数据拟合时, 需要考虑压缩应变分量εy , 将许超宸依据 (30 )式所测的实验数据乘以$1 - {\upsilon _{\rm{s}}}$ 项, 将其还原回实验精确测量值石墨烯面内正应变之和ε m . 此外在标定实验中, 许超宸只在石墨烯中心区域对$ - \omega _{{\rm{2D}}}^{\rm{0}}{\gamma _{{\rm{2D}}}} $ 项进行了标定, 并将之用于沿石墨烯整个长度上应变分布的测量中, 而$ - \omega _{{\rm{2D}}}^{\rm{0}}{\gamma _{{\rm{2D}}}} $ 项较为敏感[25 -27 ] , 可能会随标定位置的不同而改变, 所以其实验中相对准确的测量区域为石墨烯中心位置.3.3 节所述方法, 在ABAQUS中建立石墨烯/基底三维有限元模型. 图13(a) 给出了基底拉伸载荷${\varepsilon _{{\rm{s}}x}} =$ 0.25%时, 石墨烯面内正应变分量之和ε m 沿中心线 ($y = {W / 2}$ ) 分布的模拟值与实验测量值的拟合结果. 图中结果显示, 模拟值与实验值拟合良好, 从而确定界面刚度K 为100 TPa/m. 图13(b) 则给出了不同基底载荷作用下石墨烯中心C 点处$ \varepsilon_{\rm m}^{\rm C} $ 的模拟值与实验值的拟合结果, 由此确定界面剪切强度τ c 为0.295 MPa. 而许超宸[23 ] 通过一维模型拟合实验数据得到同尺寸石墨烯与PET界面剪切强度为0.314 MPa, Guo和Zhu[12 ] 通过一维模型拟合得到石墨烯与PET界面刚度为74 TPa/m.图 13 利用二维模型与实验数据拟合 (a) 基底拉伸应变ε sx = 0.25%时ε m 沿石墨烯中心线(y = W /2)的分布; (b) 不同基底载荷作用下石墨烯中心C 点处$ \varepsilon_{\rm m}^{C} $ 的大小Figure13. Fitting results of experimental data by using 2D model: (a) ε m along the centerline (y = W /2) when the tensile strain ε sx = 0.25%; (b) $ \varepsilon_{\rm m}^{C} $ at the center point C under different tensile loads.[28 ] , 放置在基底上的单层石墨烯, 当基底所受压缩应变载荷大于0.3%时, 石墨烯发生面外屈曲, 所以本文只在基底受较小载荷情况下, 用模拟值与实验值进行了拟合.5.结 论 考虑了石墨烯和基底泊松效应的影响, 本文提出了二维非线性剪滞模型. 对于基底泊松比相比石墨烯较大的情况, 利用该模型理论研究了受单轴拉伸石墨烯/柔性基底复合结构的双向界面切应力传递问题. 在弹性粘结阶段, 导出了石墨烯双向正应变和双向界面切应力的半解析表达式, 分析了不同位置处石墨烯正应变和界面切应力的分布规律. 导出了石墨烯/基底复合结构发生界面滑移的临界应变, 分析了石墨烯宽度以及基底泊松比大小对滑移临界应变的影响. 基于二维非线性剪滞模型建立有限元模型, 研究了界面滑移阶段石墨烯正应变和界面切应力的分布规律. 将二维非线性剪滞模型计算结果与一维非线性剪滞模型的结果进行了比较. 研究结果表明: 当石墨烯宽度较大时, 无论在弹性粘结阶段还是界面滑移阶段, 石墨烯正应变和界面切应力都呈现出二维应力分布状态, 石墨烯内存在较大的压缩应变分量εy , 界面上存在较大的横向切应力分量τzy , 这在一维模型中是被忽略的. 而且εx 和τzx 沿宽度方向的分布呈现出不均匀性, 与一维模型对其的计算结果具有显著差别. 滑移区域首先出现在界面的边角位置, 并且滑移临界应变ε sx c 存在一个微米量级的特征宽度, 当石墨烯宽度小于该特征量时, 宽度越大, 临界应变ε sx c 越小, 界面边缘更易发生滑移损伤. 但当石墨烯宽度大于该特征量时, 宽度尺寸变化对ε sx c 的影响可被忽略. 另外, 基底泊松比同样会对滑移临界应变ε sx c 造成影响, 基底泊松比越大, ε sx c 越小. 一维模型则会高估复合结构的滑移临界应变. 当石墨烯宽度很小时, 二维模型可以退化为一维模型, 界面横向切应力传递作用可被忽略.附录 3.1 节中(17a )式与(18a )式中参数具体表达式如下:$E = {A^2} - {B^2}$ , $F = A \times C - B \times D$ , $ d = \dfrac{{A{{\left( {{{m{\text{π}}}}/{L}} \right)}^2} + E}}{{{{\left( {{{m{\text{π}}}}/{L}} \right)}^2} + A}}. $ 17b )式与(18b )式中参数具体表达式如下:$G = A \times D - B \times C$ , $ d = \dfrac{{A{{\left( {{{m{\text{π}}}}/{L}} \right)}^2} + E}}{{{{\left( {{{m{\text{π}}}}/{L}} \right)}^2} + A}}. $  图 1 受单轴拉伸载荷的石墨烯/基底结构示意图
图 1 受单轴拉伸载荷的石墨烯/基底结构示意图
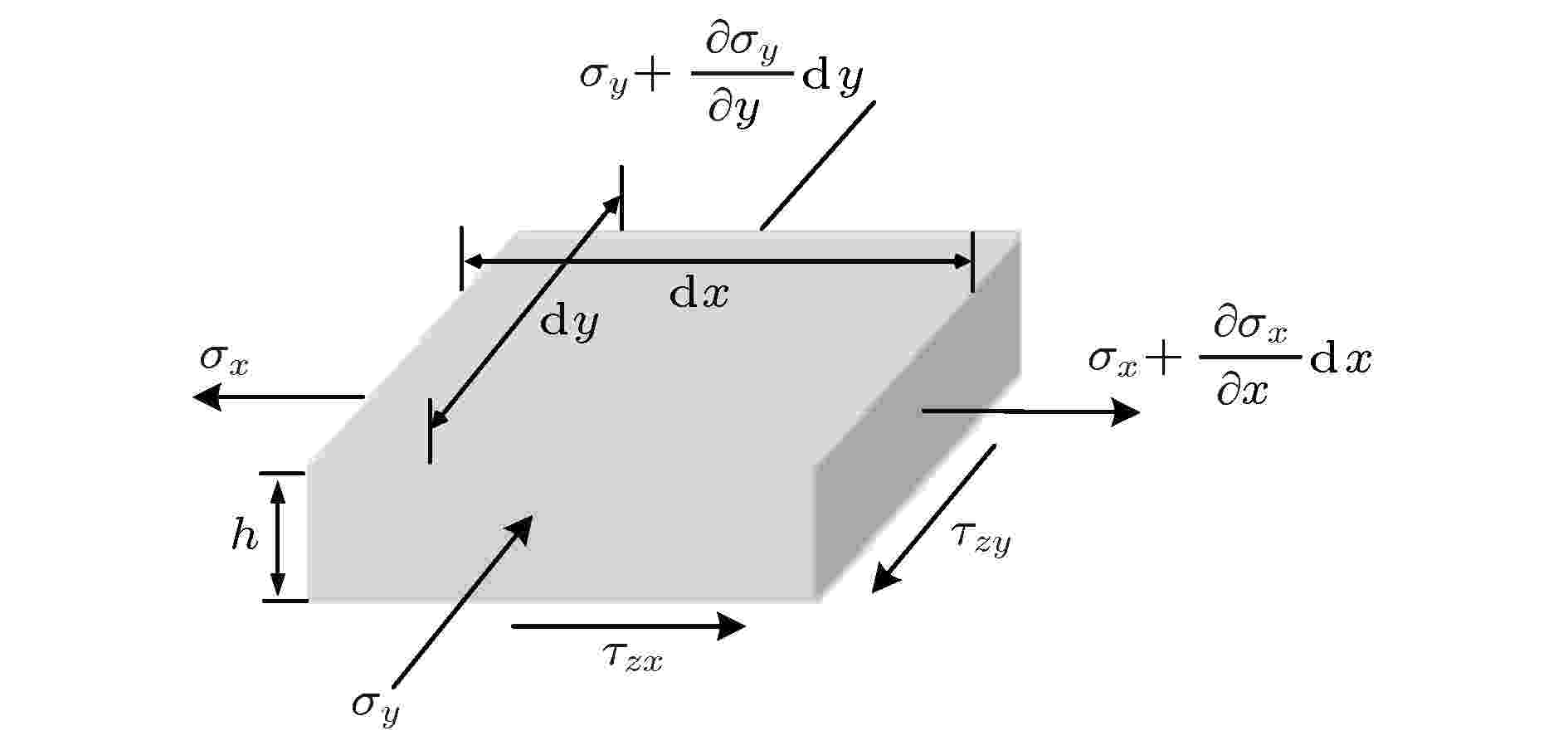 图 2 石墨烯单元的应力状态示意图
图 2 石墨烯单元的应力状态示意图
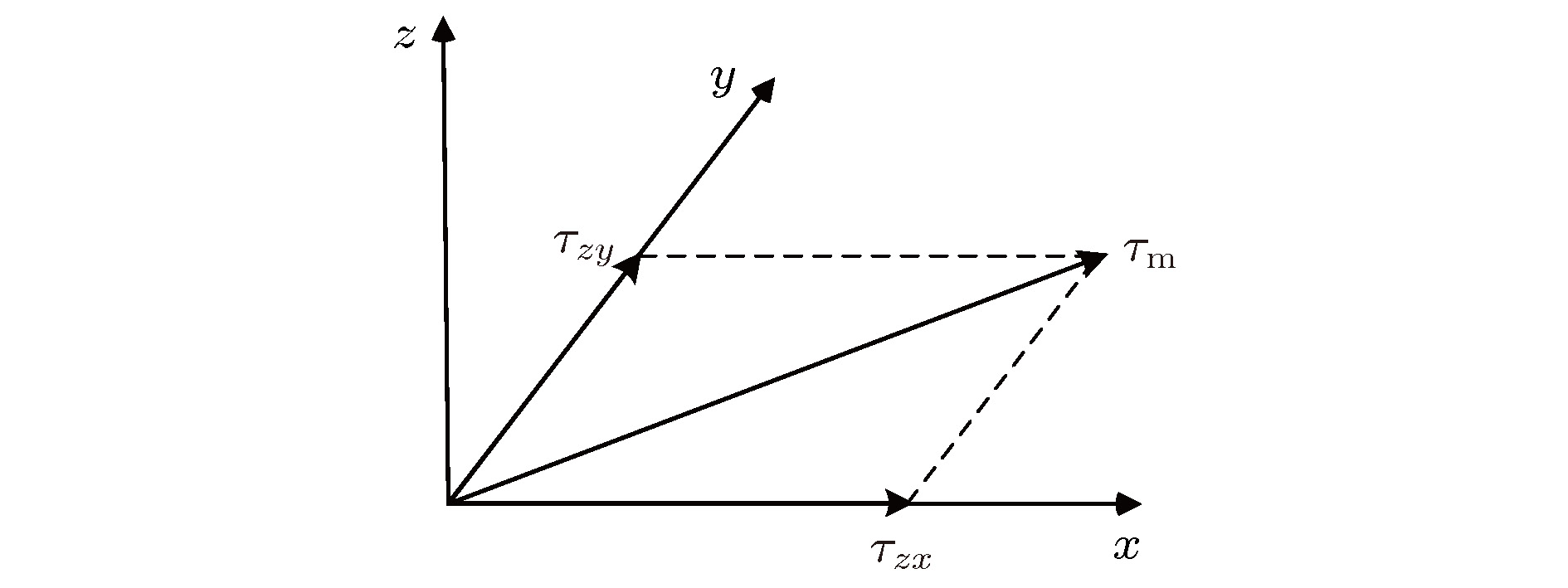 图 3 局部界面上一点的切应力分析
图 3 局部界面上一点的切应力分析
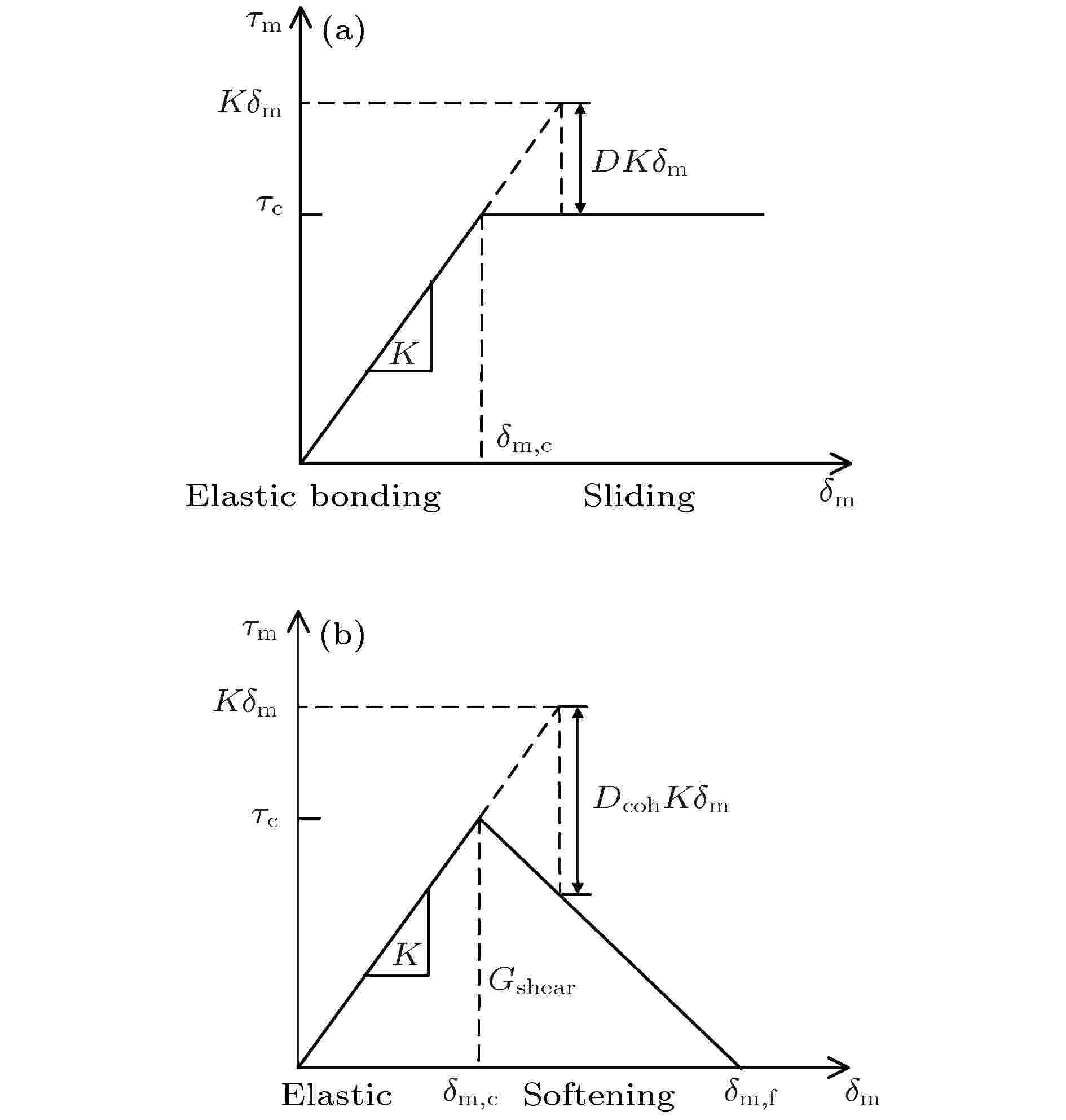 图 4 (a) 二维非线性剪滞模型; (b) 双线性内聚力模型(Ⅱ + Ⅲ型混合模式)
图 4 (a) 二维非线性剪滞模型; (b) 双线性内聚力模型(Ⅱ + Ⅲ型混合模式)









































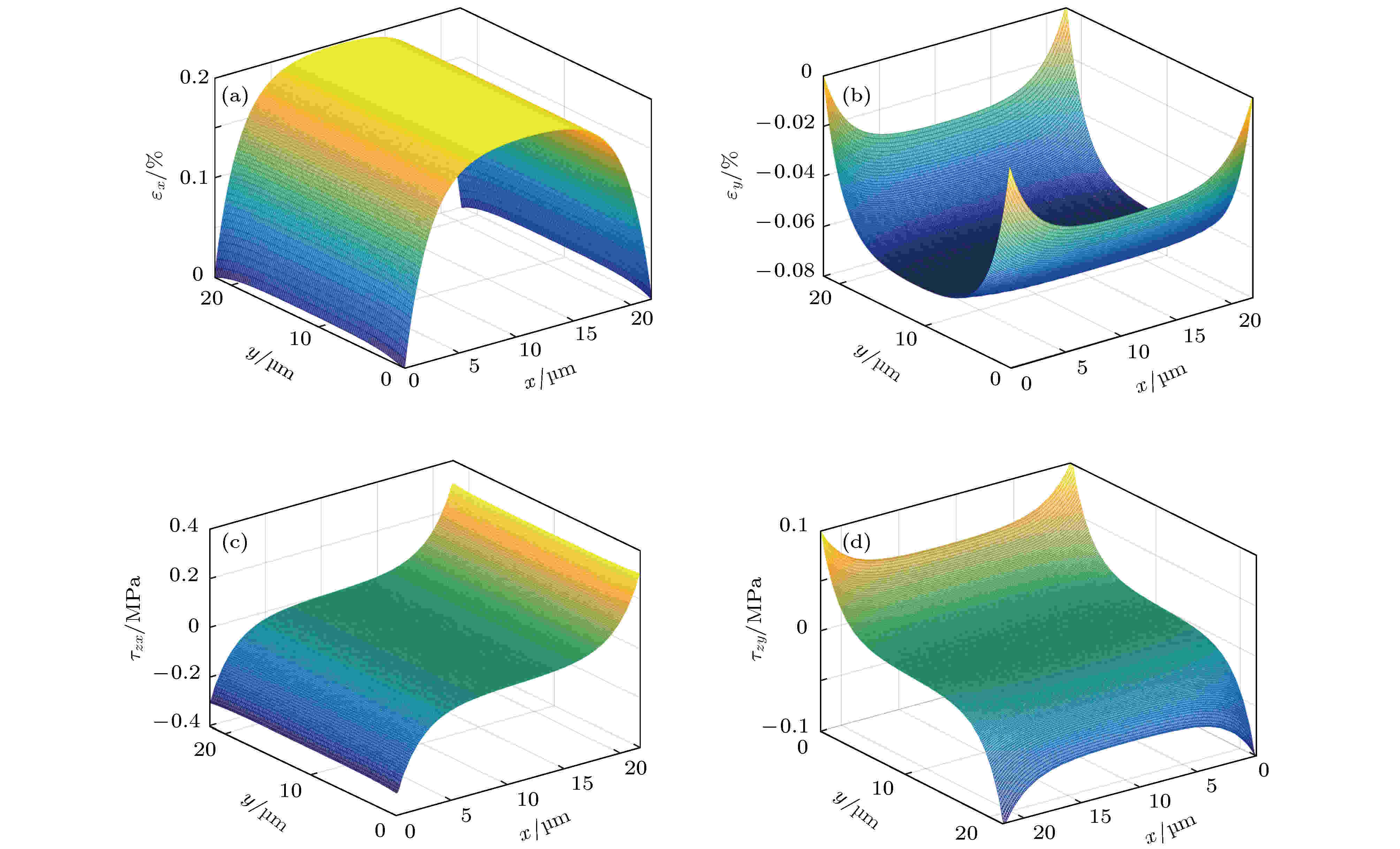 图 5 弹性粘结阶段 (εsx = 0.2%) 时石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy的分布
图 5 弹性粘结阶段 (εsx = 0.2%) 时石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy的分布



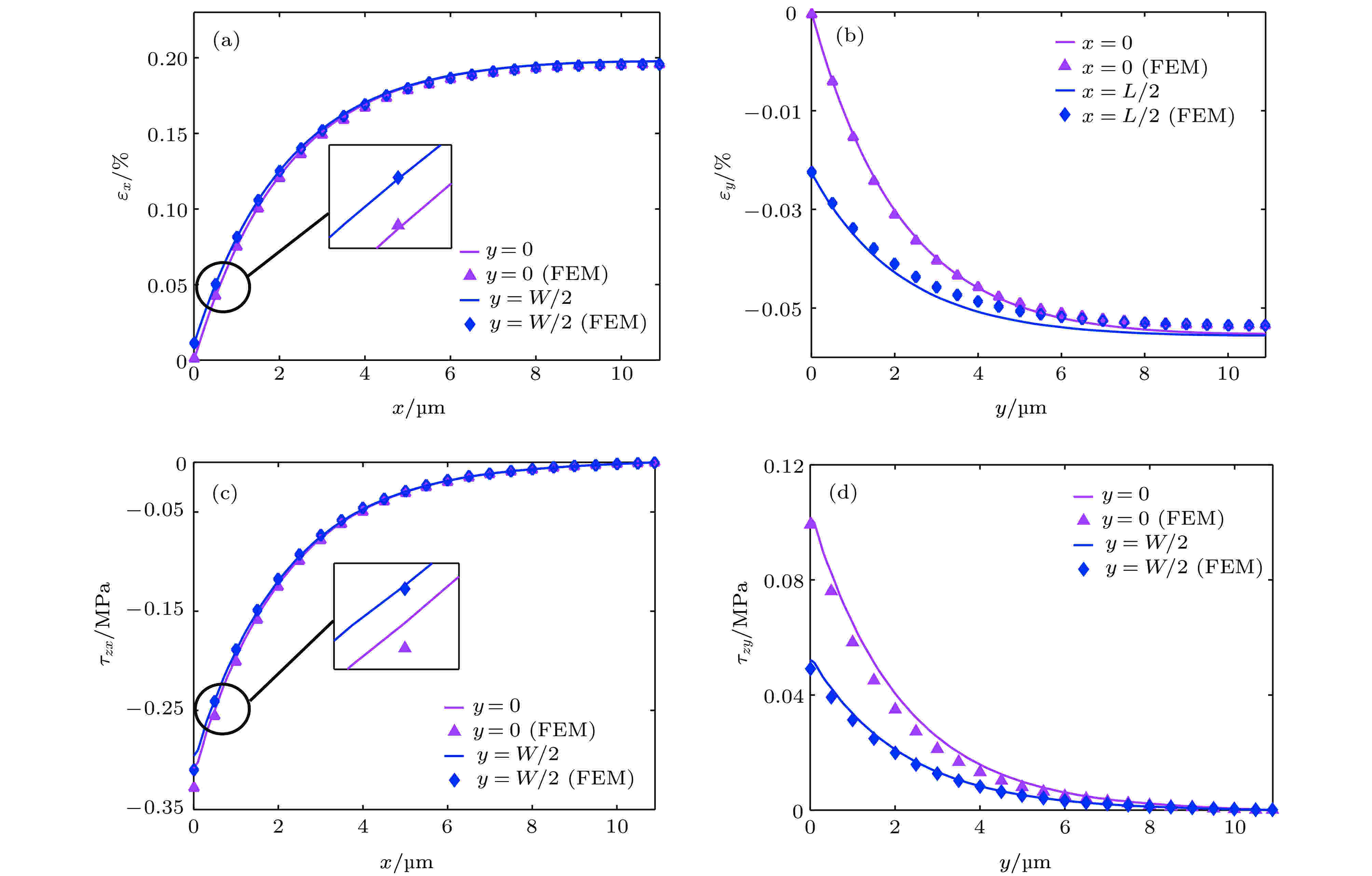 图 6 典型线处石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy的分布
图 6 典型线处石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy的分布
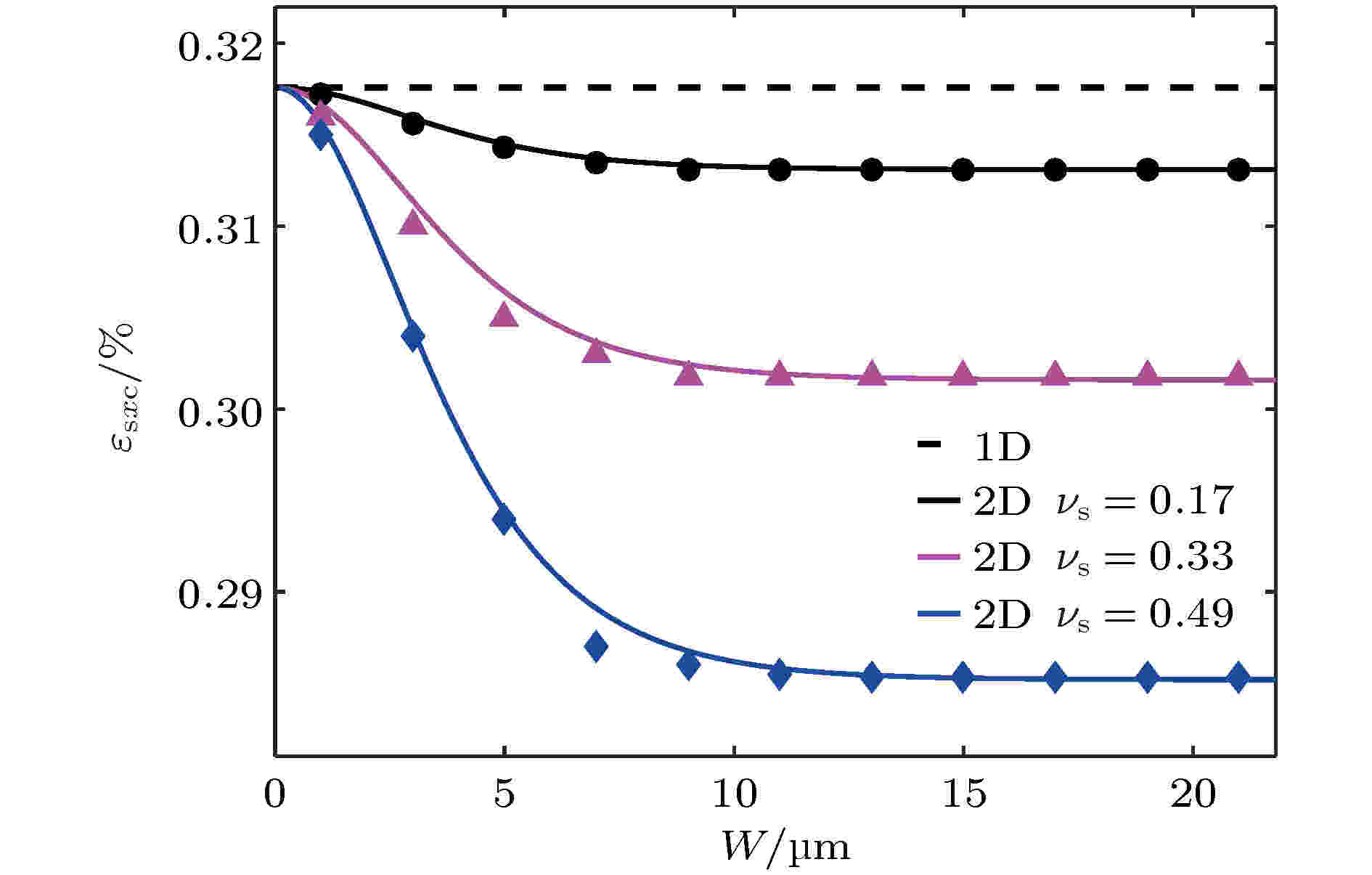 图 7 不同基底泊松比情况下滑移临界应变εsxc随石墨烯宽度W的变化(线为理论值, 散点为有限元值)
图 7 不同基底泊松比情况下滑移临界应变εsxc随石墨烯宽度W的变化(线为理论值, 散点为有限元值)


 图 8 界面滑移阶段示意图
图 8 界面滑移阶段示意图



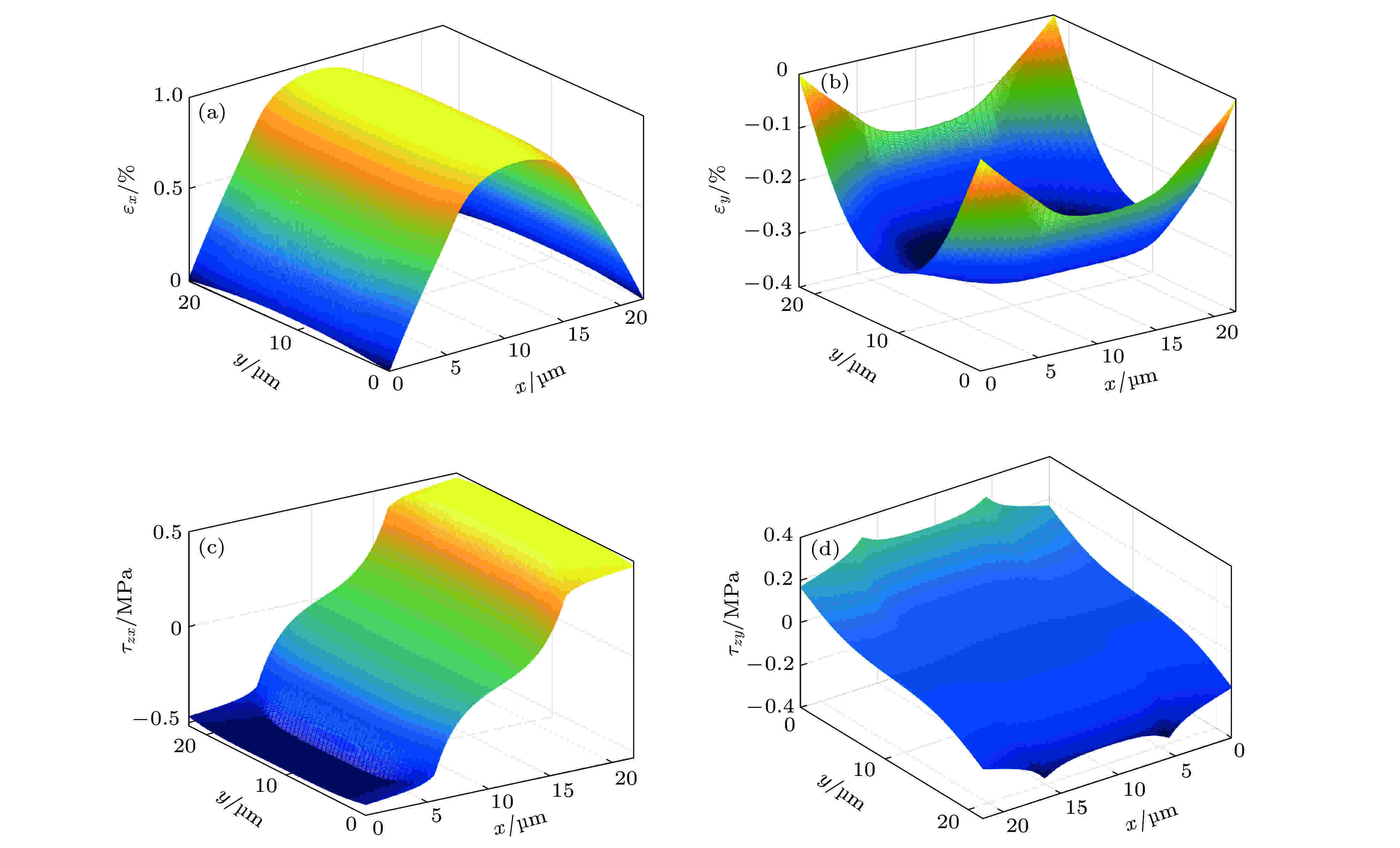 图 9 界面滑移阶段 (εsx = 1%) 时石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy.的分布
图 9 界面滑移阶段 (εsx = 1%) 时石墨烯正应变 (a) εx和(b) εy以及界面切应力 (c) τzx和(d) τzy.的分布



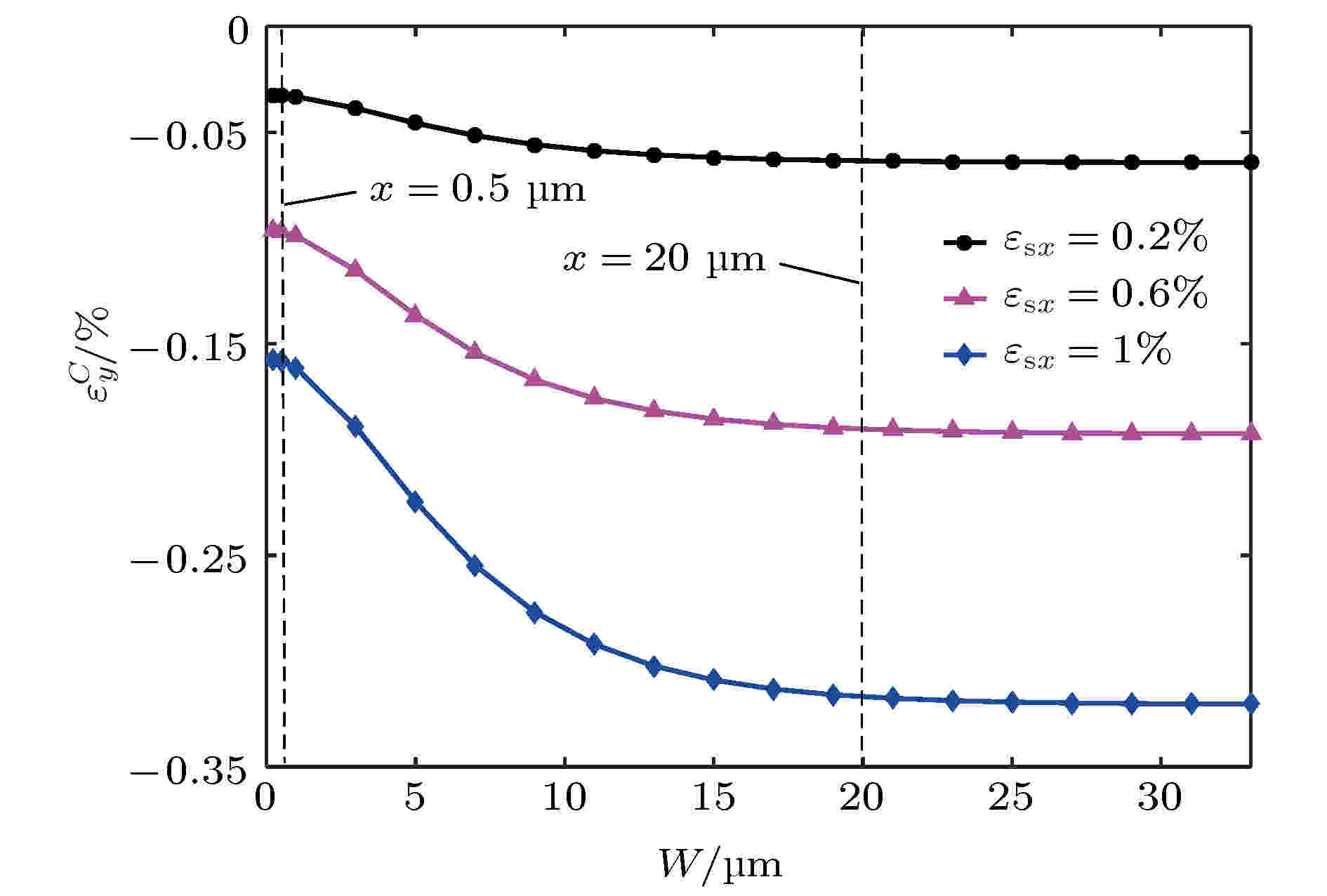 图 10 不同基底应变下石墨烯中心C点处压缩应变εyC随石墨烯宽度的变化
图 10 不同基底应变下石墨烯中心C点处压缩应变εyC随石墨烯宽度的变化





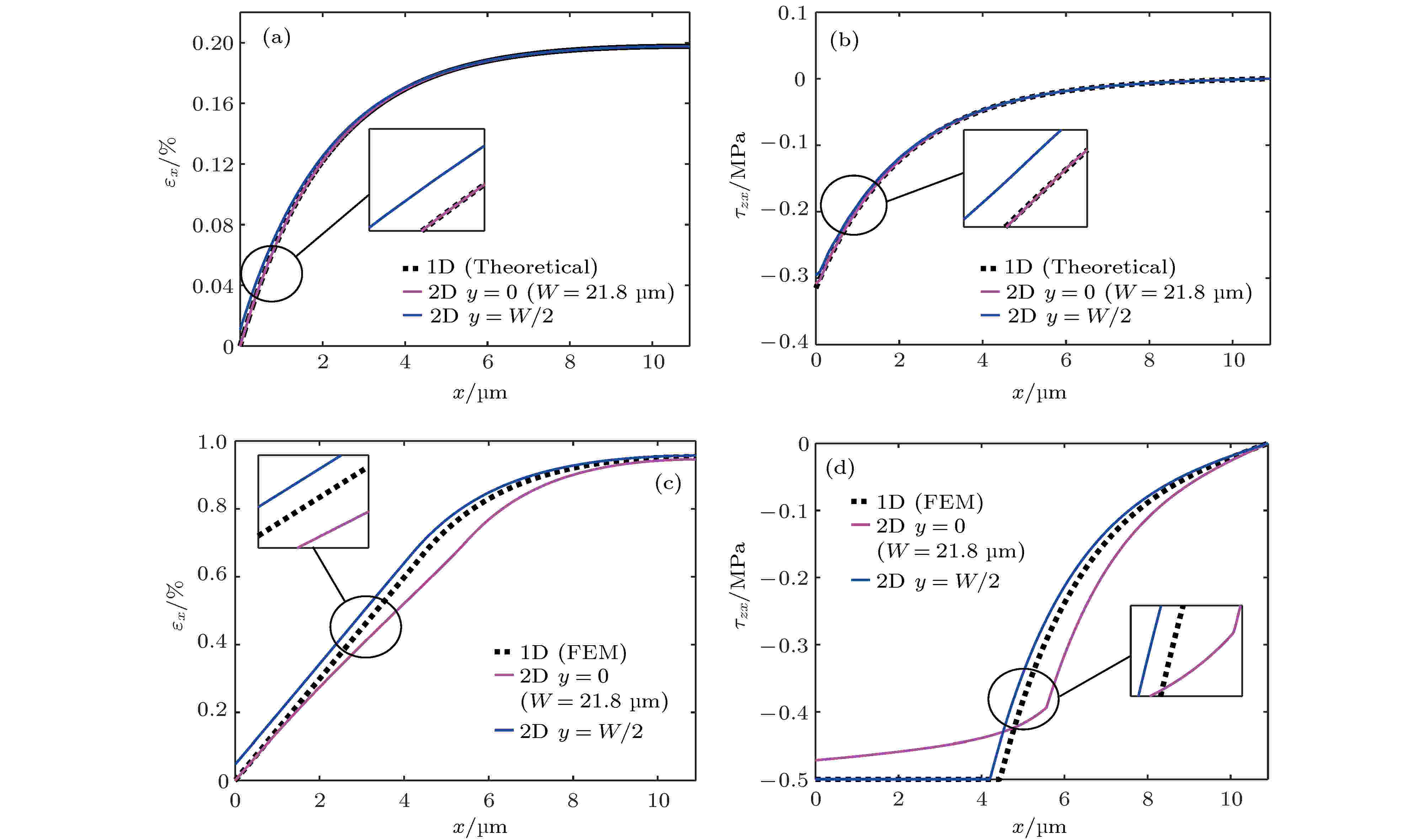 图 11 二维模型与一维模型结果的比较 (W = 21.8 μm) (a) εx和(b) τzx在弹性粘结阶段(εsx = 0.2%); (c) εx和(d) τzx在界面滑移阶段 (εsx = 1%)
图 11 二维模型与一维模型结果的比较 (W = 21.8 μm) (a) εx和(b) τzx在弹性粘结阶段(εsx = 0.2%); (c) εx和(d) τzx在界面滑移阶段 (εsx = 1%)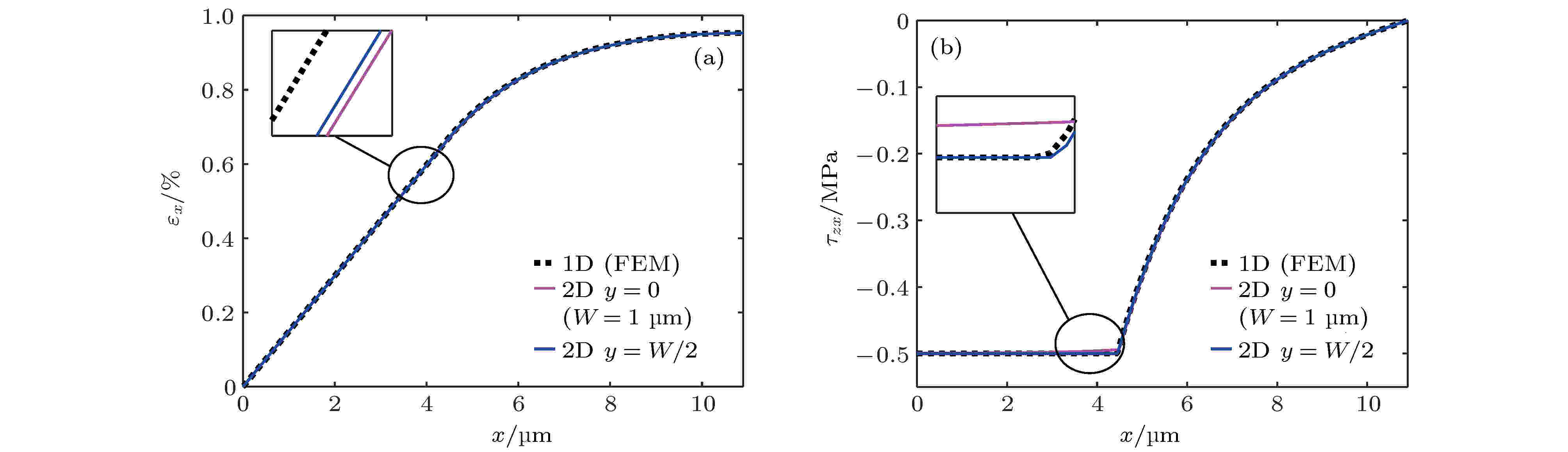 图 12 二维模型与一维模型计算结果的比较 (W = 1 μm) (a) εx和(b) τzx在界面滑移阶段 (εsx = 1%)
图 12 二维模型与一维模型计算结果的比较 (W = 1 μm) (a) εx和(b) τzx在界面滑移阶段 (εsx = 1%)

































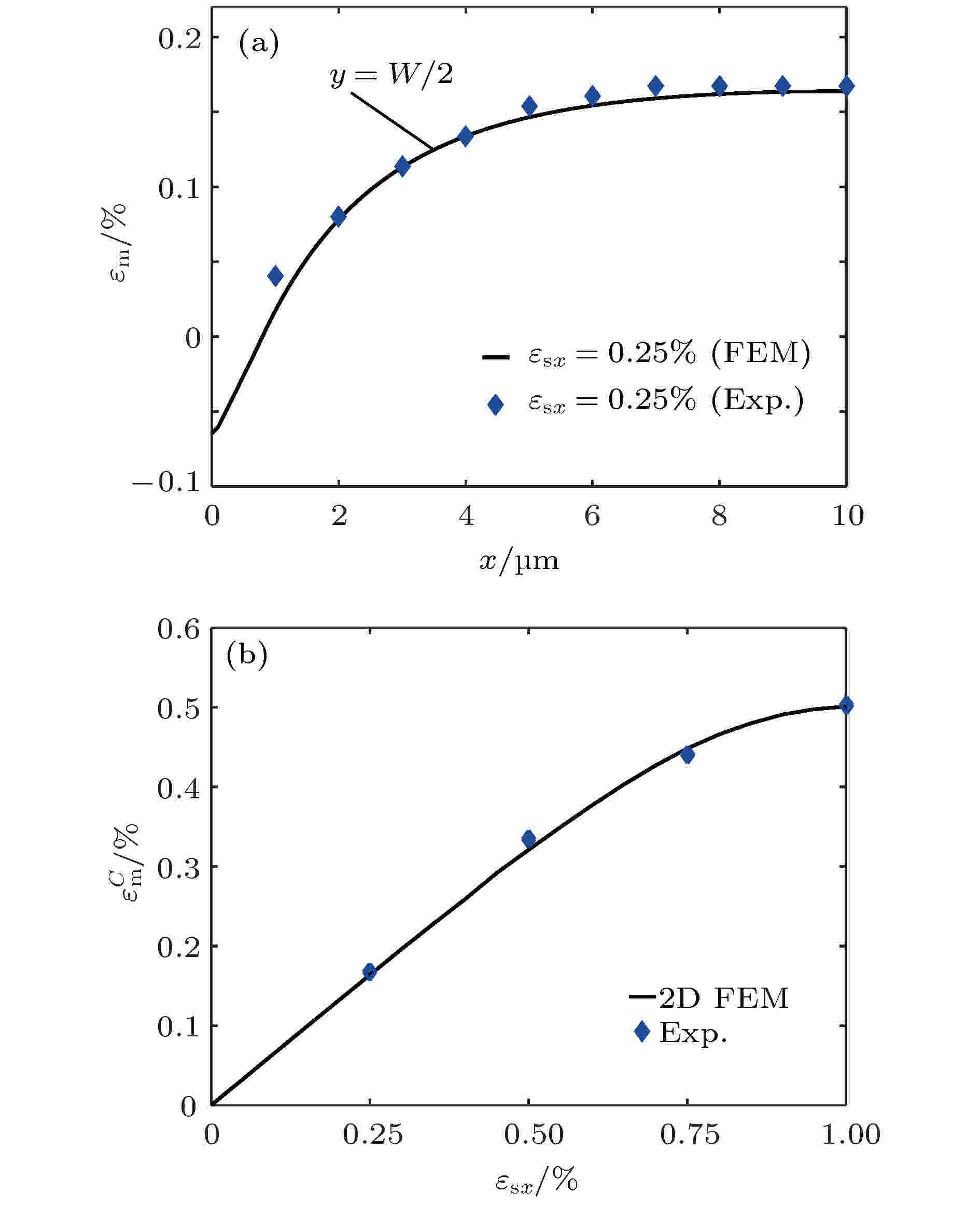 图 13 利用二维模型与实验数据拟合 (a) 基底拉伸应变εsx = 0.25%时εm沿石墨烯中心线(y = W/2)的分布; (b) 不同基底载荷作用下石墨烯中心C点处
图 13 利用二维模型与实验数据拟合 (a) 基底拉伸应变εsx = 0.25%时εm沿石墨烯中心线(y = W/2)的分布; (b) 不同基底载荷作用下石墨烯中心C点处






