全文HTML
--> --> --> 图 1 Fe3O4的电阻率随温度的变化关系. 样品I中FeO∶Fe2O3 = 1∶1.025, 样品II中FeO:Fe2O3 = 1∶1.08[1]
图 1 Fe3O4的电阻率随温度的变化关系. 样品I中FeO∶Fe2O3 = 1∶1.025, 样品II中FeO:Fe2O3 = 1∶1.08[1]Figure1. Temperature-dependent resistivity of Fe3O4 sample I with FeO∶Fe2O3 = 1∶1.025 and sample II with FeO∶Fe2O3 = 1∶1.08[1].
随着研究的不断深入, 天然Fe3O4单晶中杂质和缺陷的作用不能被忽略, 人们开始对合成Fe3O4单晶或多晶样品进行研究, 并更加关注Fe3O4的相变过程, 包括相变为一步或多步、一阶或高阶反应动力学, 低温相变后的晶格结构以及电荷有序的分布情况. 在早期的比热研究中, 人们对于Fe3O4中存在一个还是多个相变过程存在争议. 因此, 这一问题在二十世纪七、八十年代被广泛地讨论[14-22]. 最终, Matsui等[21]证实Fe3O4仅在120 K附近存在相变, 多个相变的出现是由于样品质量以及退火过程中引入的应力导致的.
Verwey相变导致Fe3O4的晶体结构、磁性和电输运特性发生变化. 因此本文将系统综述Verwey相变处Fe3O4的晶体结构、电子结构、磁性、电输运特性和铁电性的研究历史、现状、面临的挑战和对未来的展望.
2.1.Fe3O4的晶格结构
室温下Fe3O4为立方反尖晶石结构, 空间群为
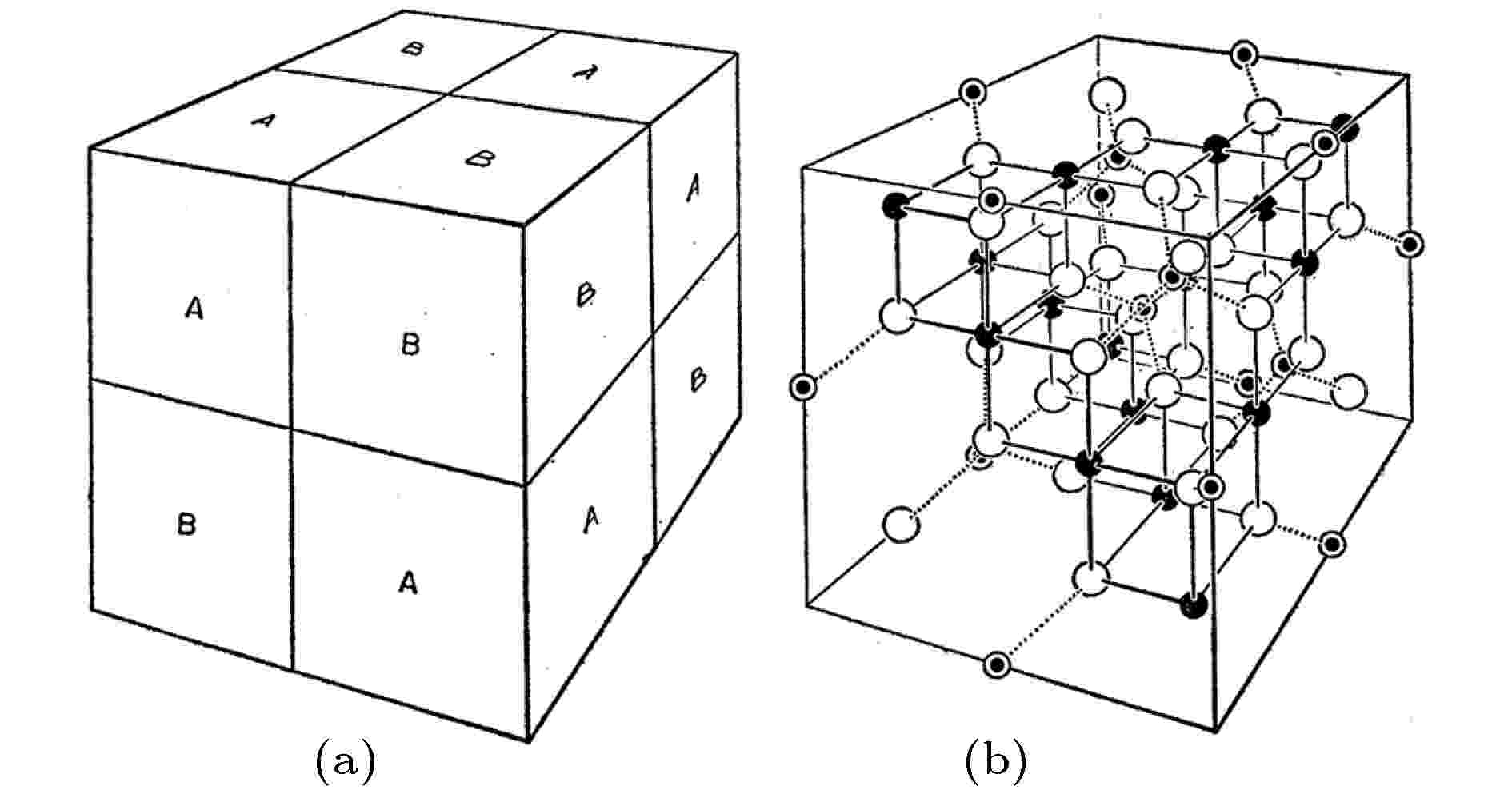 图 2 尖晶石晶胞 (a)次晶格的堆叠方式; (b)晶体结构[24]
图 2 尖晶石晶胞 (a)次晶格的堆叠方式; (b)晶体结构[24]Figure2. Spinel unit cell: (a) Stacking pattern of sub-lattices; (b) crystal structure[24].
Verwey转变温度以下, 立方Fe3O4晶格结构发生畸变, 对称性降低, 在Fe3O4内部形成孪晶, 使衍射结果受到影响, 不能获得准确的结构信息, 因此低温Fe3O4晶体结构并不是很清楚[25,26]. 磁对称性研究结果表明Fe3O4的磁各向异性具有单轴各向异性, 证明Fe3O4的晶体结构具有四方对称性或其他单轴对称性[27]. 在4.2 K, Fe3O4沿b轴方向的电极化随磁场方向的不对称部分可以通过改变加场冷却过程中磁场的方向实现反转, 表明在低温下Fe3O4晶胞为单斜晶系[28]. 电子衍射、X射线衍射和中子衍射结果相继证明低温相Fe3O4的晶体结构并不具有四方对称性, 而是在立方Fe3O4晶格的基础上发生菱方畸变, c轴方向晶格常数变为立方相的二倍, 并在c方向上出现滑移[29-33]. 最终, Iizumi等[34]利用三维中子衍射在10 K确定Fe3O4的晶体结构, 低温相Fe3O4的晶体结构具有单斜对称性, 空间群为Cc, 与立方Fe3O4相比, 低温相Fe3O4的晶格畸变为



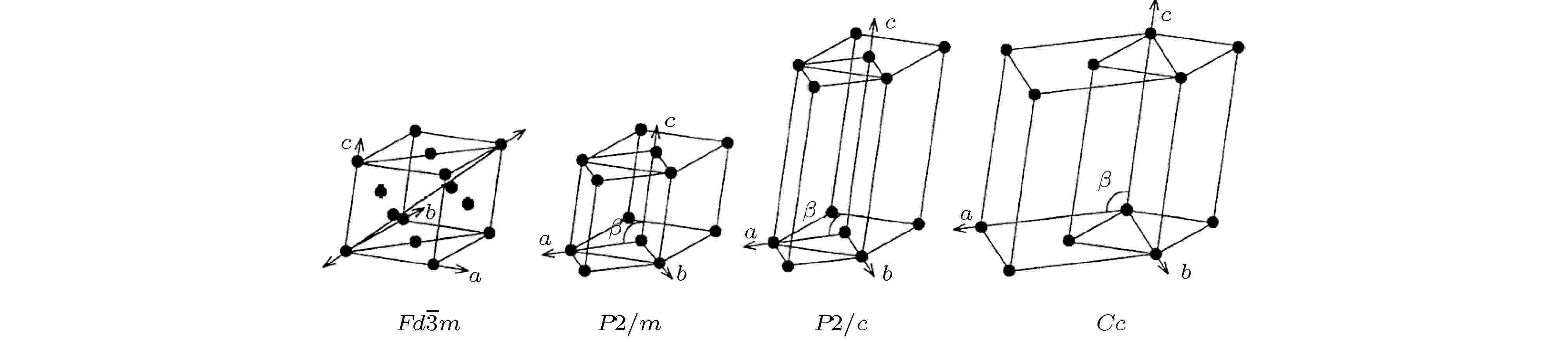 图 3 空间群为
图 3 空间群为
Figure3. Relationship between the unit cells referred to the structure with space group

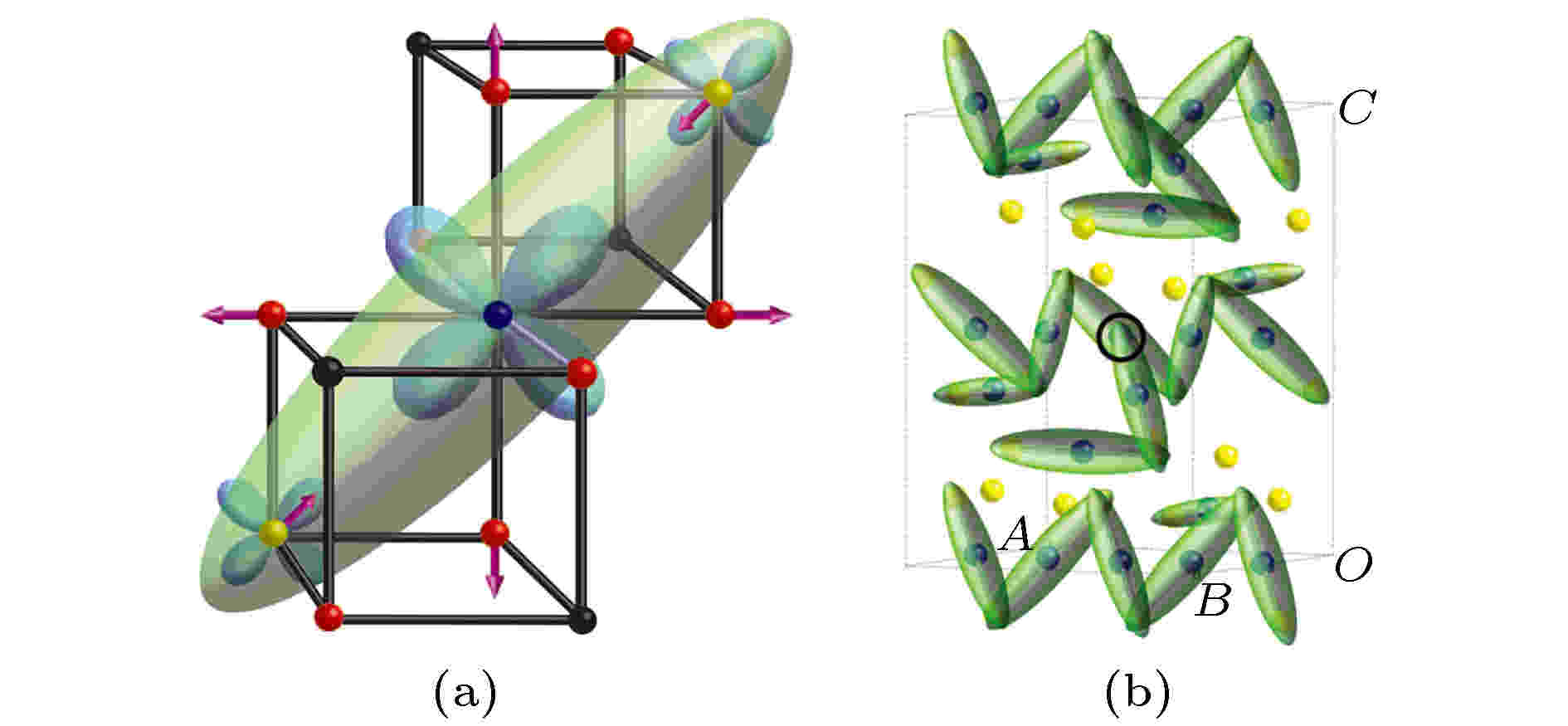 图 4 (a)三极化子和(b)三极化子分布的示意图[23]
图 4 (a)三极化子和(b)三极化子分布的示意图[23]Figure4. Schematic diagram of (a) trimeron and (b) distribution of trimeron[23].
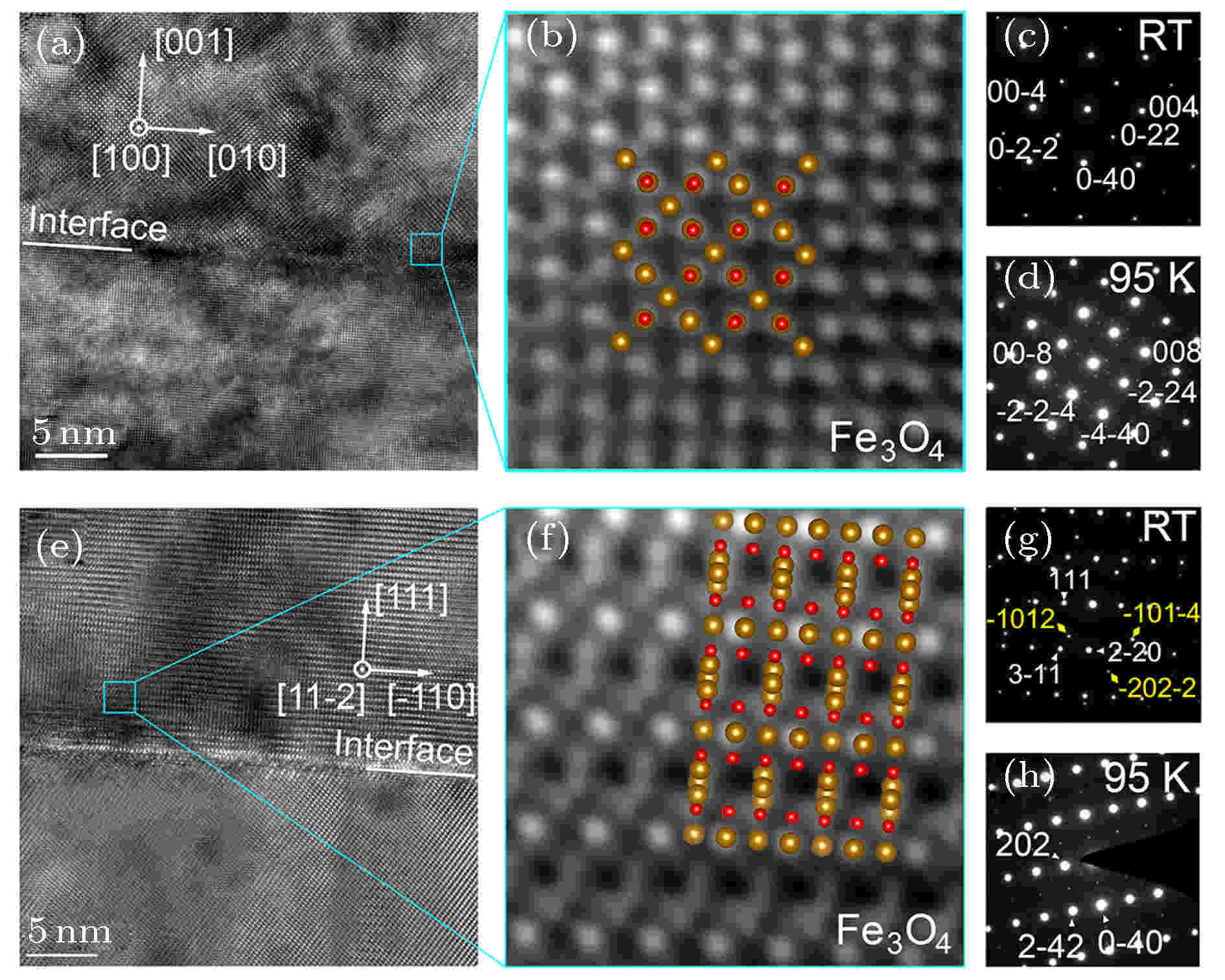 图 5 (a)?(d) Fe3O4(001)薄膜的TEM研究结果; (e)?(h) Fe3O4(111)薄膜的TEM研究结果. 室温和95 K的衍射斑点分别由室温相和低温相Fe3O4密勒指数标注. 图(g)中黄字为Al2O3密勒指数. 图(b)和图(f)棕球和红球分别代表Fe和O原子[41,43]
图 5 (a)?(d) Fe3O4(001)薄膜的TEM研究结果; (e)?(h) Fe3O4(111)薄膜的TEM研究结果. 室温和95 K的衍射斑点分别由室温相和低温相Fe3O4密勒指数标注. 图(g)中黄字为Al2O3密勒指数. 图(b)和图(f)棕球和红球分别代表Fe和O原子[41,43]Figure5. TEM results of ((a)?(d)) Fe3O4(001) and ((e)?(h)) Fe3O4(111) films. White Miller index above (below) TV are marked with cubic (monoclinic) Fe3O4. Yellow Miller index in Fig. (g) indicates Al2O3. Brown and red spheres in Fig. (b) and Fig. (f) represent Fe and O[41,43].
2
2.2.Fe3O4中的反相边界
Margulies等[42]利用内转换电子穆斯堡尔谱研究Fe3O4薄膜的磁性. 由于Fe3O4薄膜具有较大的形状各向异性, 磁矩应沿面内方向分布, 但Margulies等[42]发现Fe3O4的磁矩在面外方向具有分量. 此外, 在70 kOe (

Fe3O4单晶薄膜可以外延生长在MgO, SrTiO3(STO)和Al2O3基底上, 基底的晶格常数分别为4.212, 3.905和4.762 ?. 在这些基底中, O离子形成了Fe离子沉积的框架, 因此在MgO(001)和STO(001)基底上, Fe3O4沿[001]方向生长, 在Al2O3(0001)基底上Fe3O4沿[111]方向生长. MgO(001)和STO(001)基底具有面内四重对称性, Al2O3(0001)基底具有面内六重对称性, Fe3O4(001)和Fe3O4(111)在面内仅具有出二重和三重对称性. 因此对于在MgO(001)基底上生长的Fe3O4薄膜, Fe3O4晶胞在面内旋转90°, 等效于Fe3O4晶胞在面内



在APB处, FeA和FeB离子的排列方式与Fe3O4单胞不同, 引入了新的磁交换相互作用. APB处的磁交换相互作用见表1[46]. 在APB处, FeA–FeA位之间和FeB–FeB位之间出现强烈的反铁磁耦合, 降低了样品的饱和磁化强度, 并导致Fe3O4薄膜的饱和磁场增大[47]. Fe3O4薄膜的APB降低了样品的长程有序, 抑制了Verwey相变的一致性, 不同晶畴内的转变温度由于局部应力不同而产生差异, 因此Fe3O4薄膜的Verwey相变出现展宽.
| 交换相互作用 | 类型和角度 | 磁性和强度 | 出现位置 |
| FeB-O-FeB | 超交换, 180° | 反铁磁, 强 | APB处 |
| FeA-O-FeA | 超交换, 约140° | 反铁磁, 强 | APB处 |
| FeB-O-FeA | 超交换, 约120° | 反铁磁, 强 | 块体和APB处 |
| FeB-O-FeB | 超交换, 90° | 铁磁, 弱 | 块体和APB处 |
| FeA-O-FeA | 超交换, 约70° | 反铁磁, 弱 | APB处 |
| FeB-FeB | 直接 | 铁磁, 弱 | 块体和APB处 |
| FeA-FeA | 直接 | 反铁磁, 弱 | APB处 |
| FeB-FeA | 直接 | 铁磁, 弱 | APB处 |
表1外延Fe3O4(001)薄膜中APB处的磁交换相互作用[46]
Table1.Magnetic exchange interaction across APBs in the epitaxial Fe3O4(001) films[46].
2014年, McKenna等[48]采用第一性原理计算研究了Fe3O4(110)面的APB结构以及APB处的磁学和电学性质. 分析发现, 两种稳定的APB结构, APB–I为最稳定结构, 形成能较低, 为102 mJ·m–2, FeA, FeB原子的数量和块体结构中的相同且Fe离子位置未变化, 如图6所示[48]. 在APB–II中, APB两侧结构关于APB不具有镜面对称性, 因此优化后的原子位移更大, 且具有较高的形成能, 为954 mJ·m–2. 为了分析实际情况中存在哪一类APB, McKenna等[48]利用透射电子显微镜对退火的Fe3O4样品进行了结构表征, 证明样品中的APB为第一种类型. 此前, Celotto等[46]已经证明对Fe3O4样品进行退火会增加APB-I的密度, 由于APB-I具有更低的形成能, 因此McKenna等[48]只观察到APB-I. 也正是由于APB–I具有较低的形成能, 因此容易在生长过程中或通过热处理形成, 从而影响Fe3O4样品的性质.
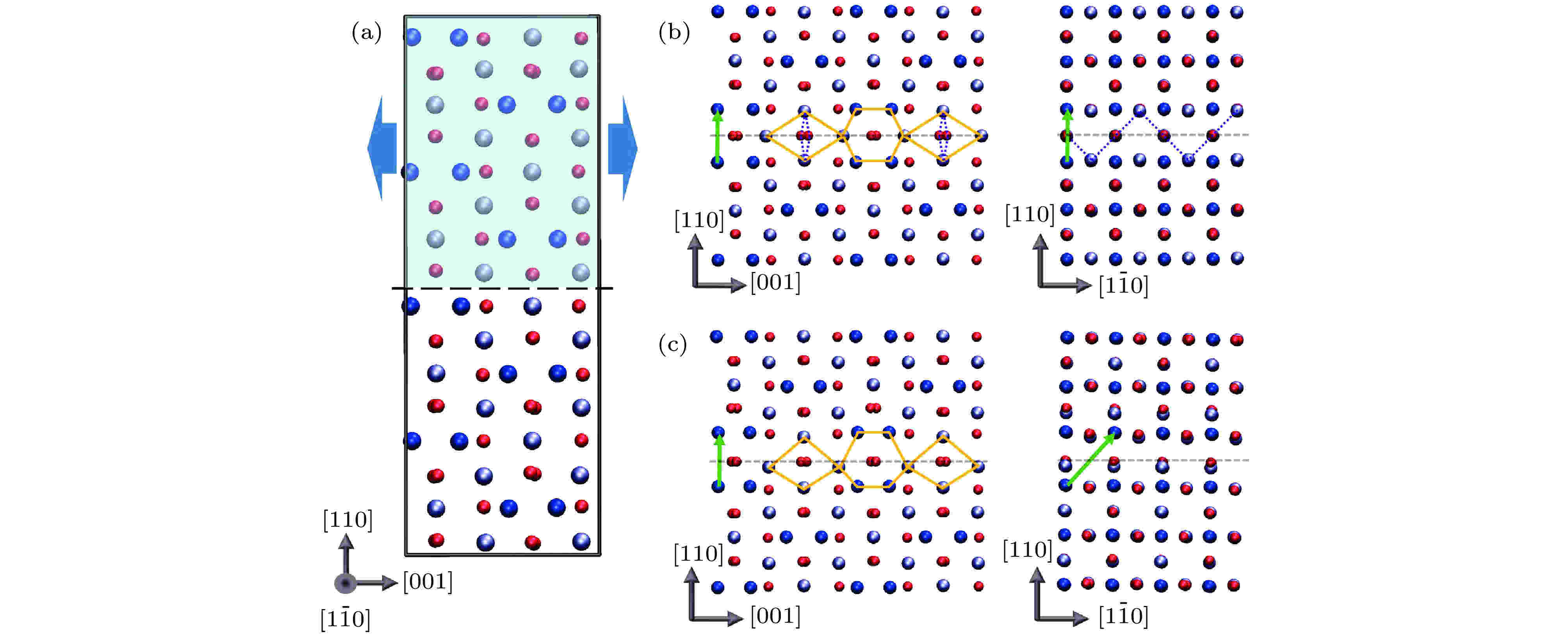 图 6 Fe3O4(110)面上APB的结构 (a)理想情况下Fe3O4的结构; (b)第一类APB(APB–I); (c)第二类APB(APB–II). APB的平移方向由绿色箭头表示, 红球为O原子, 蓝球为FeA离子, 灰球为FeB离子[48]
图 6 Fe3O4(110)面上APB的结构 (a)理想情况下Fe3O4的结构; (b)第一类APB(APB–I); (c)第二类APB(APB–II). APB的平移方向由绿色箭头表示, 红球为O原子, 蓝球为FeA离子, 灰球为FeB离子[48]Figure6. {110} APB defects in Fe3O4: (a) The ideal cubic Fe3O4 structure; (b) APB-I; (c) APB-II. The APB crystal translations are indicated by green vectors. Red, blue and gray spheres represent the oxygen atoms, tetrahedral Fe and octahedral Fe atoms[48].
2
2.3.低温相Fe3O4的孪晶界
低温相Fe3O4具有单斜对称性, c轴的倾斜使结构的各向异性增加. 由于c轴具有6个等价方向, 因此低温相Fe3O4单胞具有24个等价取向, 其中12种取向方式如图7所示[49]. 当样品经过零场冷却过程后, 单晶样品转变为多畴结构, 甚至多晶结构. 透射电子显微镜结果观察到三种孪晶界: 1) 孪晶界处单斜c轴方向发生90°旋转; 2) c轴方向关于孪晶界对称, 这种类型的孪晶界主要存在于大单斜畴内的精细结构中; 3) 孪晶绕c轴在ab平面内旋转90°[50]. de la Figuera等[51]利用扫描隧道显微镜在室温及78 K测量了单晶Fe3O4(100)样品的表面形貌, 结果表明在78 K, Fe3O4表面产生屋顶状的起伏, 如图8(a)和图8(b)所示, 起伏的夹角约为0.346°, 周期约为0.5 μm. 为证明这种起伏不是局部现象, de la Figuera等[51]利用低能电子显微镜观察了8.6 μm × 8.6 μm区域的结构随着温度的变化, 证明在温度低于TV时样品表面出现起伏, 当温度逐渐升至TV以上时, 这种起伏逐渐由中央向两侧退去. 因此, Figuera等[51]认为这种起伏是由Verwey相变引起的. 当Fe3O4发生Verwey相变后, β角增加了0.236°, Fe3O4形成了单斜结构(如图8(c)), 晶格基矢转变为a, b, c, 如图8(c)所示. 两个单斜晶格结合形成孪晶界, 经计算两表面形成的夹角约为0.34 ?, 与扫描隧道显微镜的结果一致, 证明表面起伏是由此导致的, 如图8(d)所示.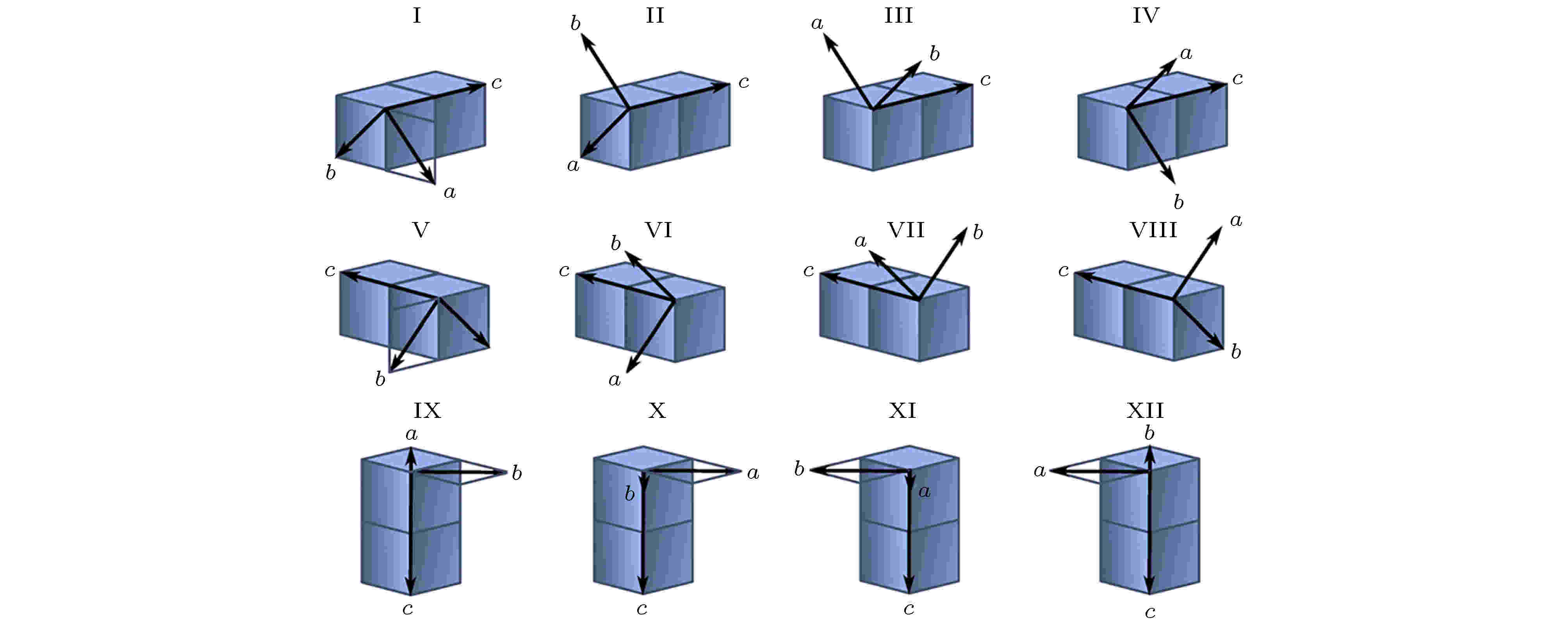 图 7 立方相和单斜相Fe3O4晶格的相关性[49]
图 7 立方相和单斜相Fe3O4晶格的相关性[49]Figure7. Symmetrically distinct crystallographic relationships between cubic and monoclinic phases of magnetite[49].
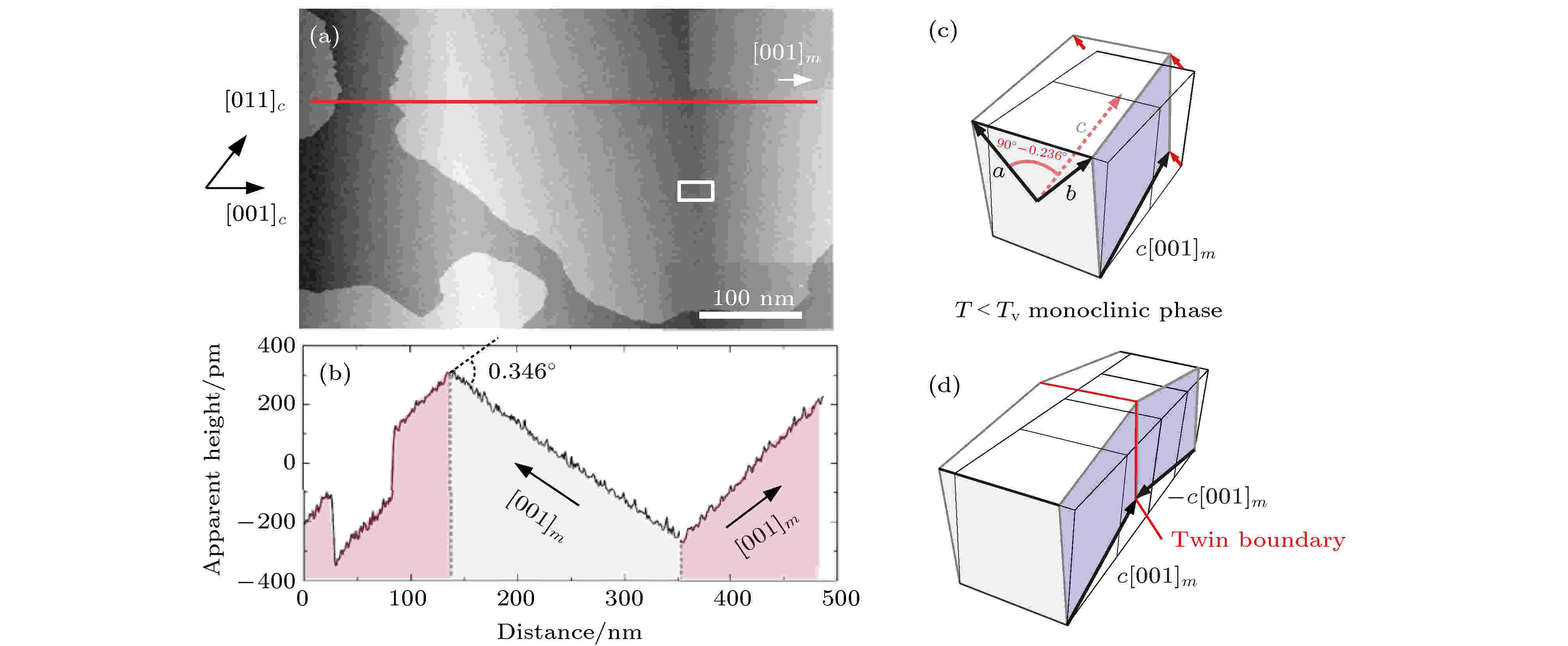 图 8 (a) Fe3O4薄膜的扫描隧道显微镜图像; (b)沿(a)中红线标记方向上的高度变化; (c)单斜结构Fe3O4; (d)由镜面对称单斜结构形成的Fe3O4[51]
图 8 (a) Fe3O4薄膜的扫描隧道显微镜图像; (b)沿(a)中红线标记方向上的高度变化; (c)单斜结构Fe3O4; (d)由镜面对称单斜结构形成的Fe3O4[51]Figure8. (a) STM image of Fe3O4(100) surface at 78 K; (b) profile along the line marked in red of (a); (c) the monoclinic unit cell of Fe3O4; (d) two mirrored monoclinic cells with opposite monoclinic c axis at a twin boundary[51].
孪晶界处的磁交换相互作用与立方相Fe3O4不同. 2018年, Liu等[43]和Chen等[52]先后通过微分相差扫描透射电子显微镜和磁输运测量的方法研究了低温相Fe3O4孪晶界处的磁耦合特性. Chen等[52]利用扫描透射电子显微镜对Fe3O4中的孪晶界结构进行研究, 确认了三种孪晶界结构, 如图9所示. 第一性原理计算结果表明在I型孪晶界处为铁磁耦合, 如图9(a)所示; II型和III型孪晶界处为反铁磁耦合, 如图9(b)和图9(c)所示[52]. 微分相差扫描透射电子显微镜结果证明低温相Fe3O4中这三种孪晶界处的磁耦合方式与计算结果一致[52]. Liu等[43]研究了高质量外延Fe3O4薄膜的磁电阻效应, 并拟合了不同温度下磁电阻曲线随磁场的变化关系. 对于Fe3O4(100)和(111)样品, 由APB密度决定的拟合参数从305 K的8.30和14.15增大到80 K的146.02和91.66. 由于在低温环境下APB不会产生移动或形成新APB, 因此可推测低温相Fe3O4的孪晶界具有反铁磁耦合特性[43]. 当温度降低至转变温度以下, Fe3O4薄膜的饱和磁化强度不断降低, 证明Fe3O4薄膜中存在相互抵消的磁矩, 表明孪晶界处具有反铁磁耦合[43]. 这种通过磁电阻效应间接获取孪晶界耦合方式的方法只适用于反铁磁耦合的边界, 因此无法检测到铁磁耦合的孪晶界.
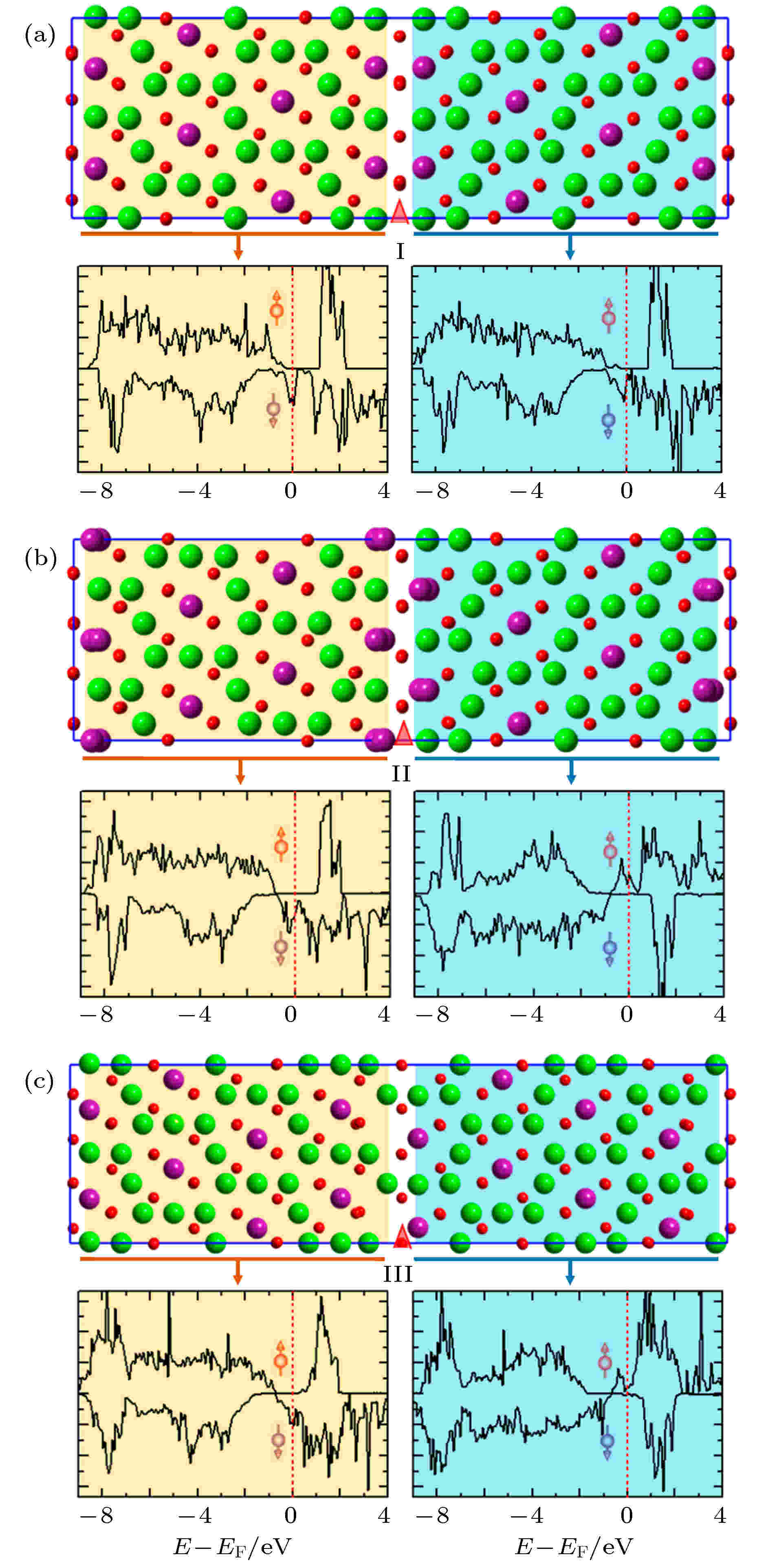 图 9 Fe3O4孪晶界处的自旋极化态密度图(density of states, DOS) (a) I型; (b) II型; (c) III型. 费米能级由红色虚线表示. 图中给出了弛豫后的模型. 态密度表明I型孪晶界处为铁磁耦合, II型和III型为反铁磁耦合[52]
图 9 Fe3O4孪晶界处的自旋极化态密度图(density of states, DOS) (a) I型; (b) II型; (c) III型. 费米能级由红色虚线表示. 图中给出了弛豫后的模型. 态密度表明I型孪晶界处为铁磁耦合, II型和III型为反铁磁耦合[52]Figure9. Spin-polarized DOS of Fe3O4 twin boundaries (TBs): (a) Type I TB; (b) Type II TB; (c) Type III TB. EF is represented by the red dashed lines. The relaxed atomistic models are also given for reference. The DOS suggest that the magnetic coupling across the type I TB is ferromagnetic and those across the type II and III TBs are antiferromagnetic[52].
3.1.Verwey相变温度以上Fe3O4的电子结构和磁性
Fe3O4的化学式可以写为

 图 10 Fe3O4中Fe离子的3d电子轨道排布和磁耦合示意图[53]
图 10 Fe3O4中Fe离子的3d电子轨道排布和磁耦合示意图[53]Figure10. Sketch map of the electronic ground state of Fe 3d electrons and magnetic couplings in Fe3O4[53].
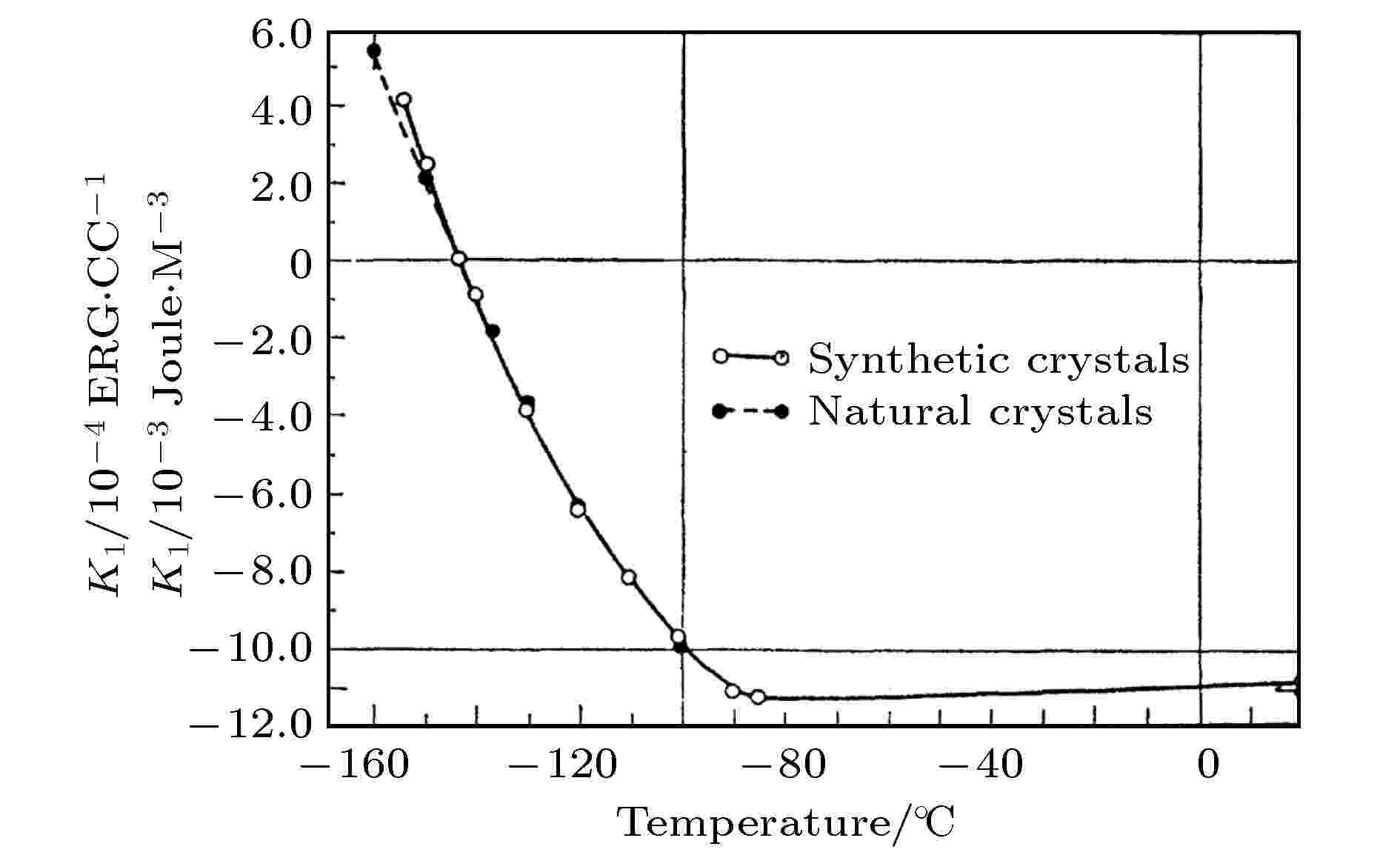 图 11 Fe3O4的磁各向异性常数K1随温度的变化关系[27]
图 11 Fe3O4的磁各向异性常数K1随温度的变化关系[27]Figure11. Temperature dependent Anisotropy constant K1 of Fe3O4[27].
2
3.2.Verwey相变温度以下Fe3O4的电子结构和磁性
33.2.1.电荷有序与轨道有序
当温度逐渐降低至120 K附近, Verwey[1]发现接近化学计量比的Fe3O4样品(Fe:O = 3∶4.075)的电阻率急剧增加, 在非化学计量的Fe3O4样品(Fe:O = 3∶4.24)中未出现这一现象. 这种对化学计量比的依赖关系表明在低温下电阻率的增大与某种有序行为相关. 通过测量不同Fe–O计量比的样品, Verwey[1,56]发现FeB位上Fe2+和Fe3+的比例对转变有影响, 认为Fe3O4电阻率的急剧增加来源于FeB位上的电荷有序. Verwey等[13]和Attfield[53]采用最简单的FeB四面体模型定义在FeB2+和FeB3+中出现的电荷有序现象, 如图12(a)所示. 后来的研究发现低温相Fe3O4的结构更加复杂. Anderson[38]提出, 在Verwey提出的模型中每个FeB4四面体内含有两个自旋向下的t2g电子, 最大程度地减少了库仑排斥作用, 结构高度简并, 这些FeB四面体由有序分布到无序分布的转换可能是Verwey相变的内在机制. 此后几十年, 关于Fe3O4中电荷有序的研究都基于Anderson条件, 即每个FeB4四面体由两个FeB2+和两个FeB3+离子组成, 包含两个自旋向下的t2g电子. Cullen和Callen[57]基于能带不稳定性利用纯电子机制下解释了Verwey相变. 在氧化物中, 局域电子倾向于通过形成小极化子使周围的晶格发生膨胀, 这些畸变与晶格的耦合使每个Anderson四面体中的两个电荷形成双极化子或分子极化子, 如图12(b)所示[58,59]. Seo等[60]认为FeB2+中自旋向下的t2g电子并非局域在FeB2+离子, 而是局域在类似由两个FeB2.5+形成的二聚体的弱Fe–Fe键内, 如图12(c)所示. van der Brink等[61]认为Fe3O4中的电荷有序是一种由FeB(3-δ)+–FeB(2+δ)+组成的部分电荷有序, 解释了低温相Fe3O4铁电性的来源.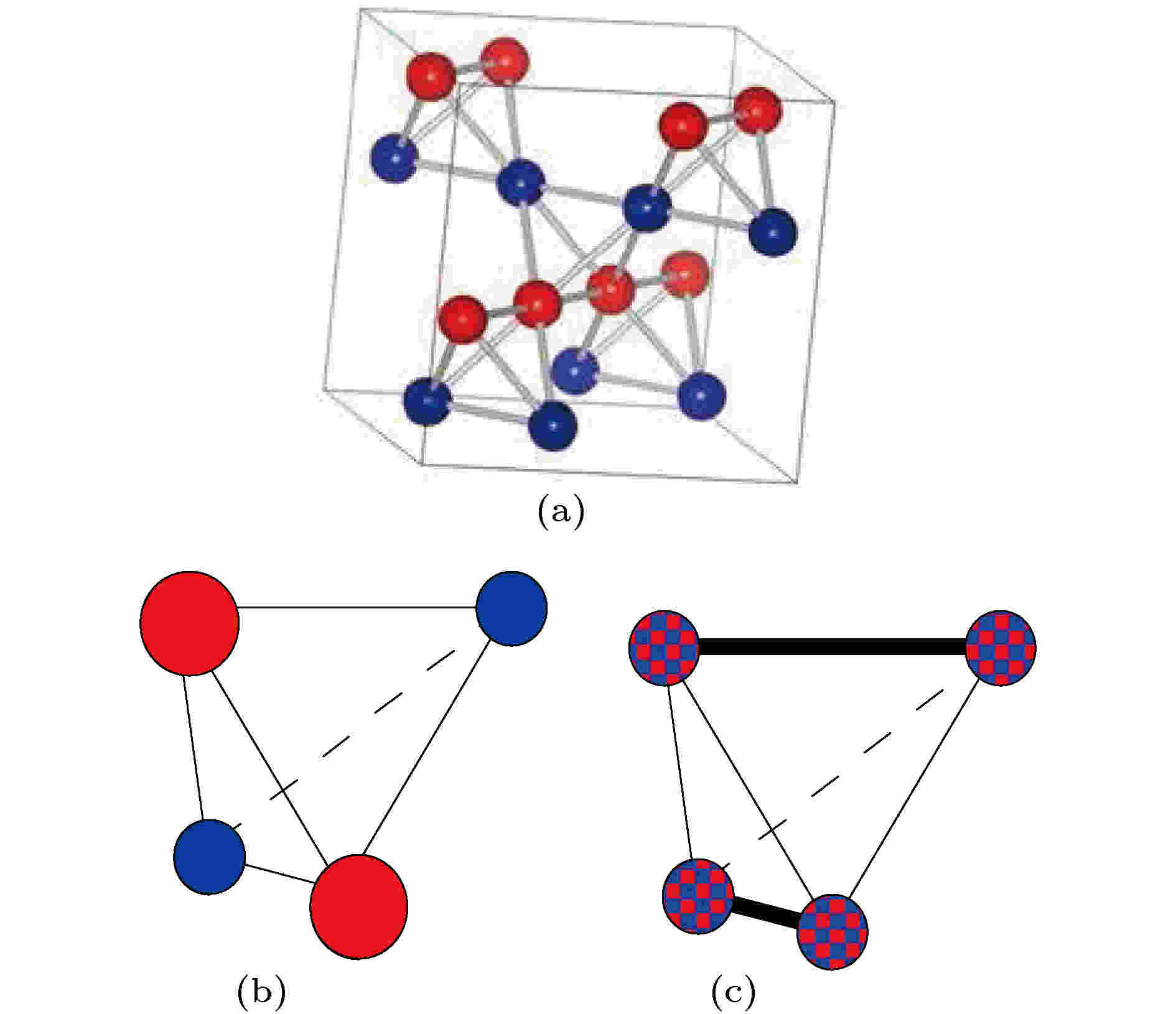 图 12 Fe3O4的FeB位的电子局域模型 (a) Verwey提出的简单四面体Fe2+/Fe3+电荷有序模型; (b)包含两个Fe2+和两个Fe3+的安德森四面体模型; (c) FeB4四面体内的键二聚化, 电子局域化在两个距离相近的FeB–FeB内, 由粗线表示[53]
图 12 Fe3O4的FeB位的电子局域模型 (a) Verwey提出的简单四面体Fe2+/Fe3+电荷有序模型; (b)包含两个Fe2+和两个Fe3+的安德森四面体模型; (c) FeB4四面体内的键二聚化, 电子局域化在两个距离相近的FeB–FeB内, 由粗线表示[53]Figure12. Models for electron localization on FeB sites of Fe3O4: (a) Verwey’s tetragonal model of Fe2+/Fe3+ charge order; (b) an Anderson tetrahedron of two Fe2+ and two Fe3+ ions; (c) bond-dimerization in the FeB4 tetrahedron, where the electrons are localized in two shortened FeB-FeB distances, shown as bold lines[53].
基于Pmca, Pmc21, P2/c和Cc空间群, Jeng等[36,54]计算了低温相Fe3O4的电子结构. 在P2/c空间群下, 利用GGA方法计算的Fe3O4表现出了半金属性. 当取库仑能U = 4.5 eV之后, Fe3O4具有0.2 eV的带隙, 这与通过光谱实验获得的带隙值0.14 eV接近[36,54]. 取U = 0, 4.0, 4.5, 5.0和5.5 eV, 对P2/c空间群的单斜和立方结构的Fe3O4进行计算, 分析了Fe3O4的带隙、电荷有序和轨道有序, 结果见表2. 即使将Fe3O4的对称性限制为立方晶系, 通过增加U值也可以使Fe3O4打开带隙, 对于单斜相Fe3O4, 较小的U值并不能使Fe3O4呈现绝缘态, 但随着U值的增大, 带隙值及电荷差明显增大, 因此认为Fe3O4的电荷、轨道有序是由电子相互作用驱动的, 由于4s和4p电子的屏蔽导致, 这种效应在过去的实验中未被发现. 在P2/c空间群下, FeB1 a, FeB1b和FeB4中自旋向下的t2g电子分别占据dyz, dxz和dxy轨道, 具有轨道有序特征, 如图13所示. 对比在P2/c, Pmca, Pmc21和Cc空间群下Fe3O4的带隙、电荷差、轨道有序以及体系总能量, 发现Cc空间群下Fe3O4是最稳定的. 特别地, 在Cc空间群中位于3/8c和7/8c层FeB中的两个自旋向下的t2g电子转移到2/8c和6/8c层的FeB中, 形成二聚轨道有序模型, 这与P2/c中的结果不同. 在Cc空间群下的Fe3O4最终形成75%的3∶1 (Fe3+:Fe2+ = 3∶1或Fe3+:Fe2+ = 1∶3)和25%的2∶2 (Fe3+∶Fe2+ = 2∶2)的混合电荷有序模型, 与此前认为的简单的3∶1电荷、轨道有序模型不同. 同时, 基于Anderson模型计算得到的熵变为2Rln2/mol (R为气体普适常数)[38], 实验上通过比热容测定的熵变为Rln2/mol, 基于这种混合电荷有序模型计算得出的熵变为(R/4)ln12/mol, 与实验值更接近.
| U/eV | P2/c | $Fd\overline 3 m$ | |||||||
| ↓gap/eV | CS/e | OO(P) | Et/eV·(f.u.)–1 | ↓gap/eV | CS/e | OO(P) | Et/eV·(f.u.)–1 | ||
| 0.0 | No | 0.00 | No(0.55) | –0.15 | No | 0.00 | No(0.34) | 0.00 | |
| 4.0 | No | 0.11 | Yes(0.98) | –0.15 | No | 0.10 | Yes(0.96) | –0.22 | |
| 4.5 | 0.2 | 0.15 | Yes(0.98) | –0.53 | No | 0.12 | Yes(0.96) | –0.27 | |
| 5.0 | 0.42 | 0.17 | Yes(0.97) | –0.75 | 0.11 | 0.16 | Yes(0.96) | –0.35 | |
| 5.5 | 0.63 | 0.19 | Yes(0.96) | –0.85 | 0.28 | 0.19 | Yes(0.91) | –0.47 | |
表2在P2/c和


Table2.Calculated charge separations (CS), orbital ordering (OO) and the total energy (Et) of Fe3O4 with

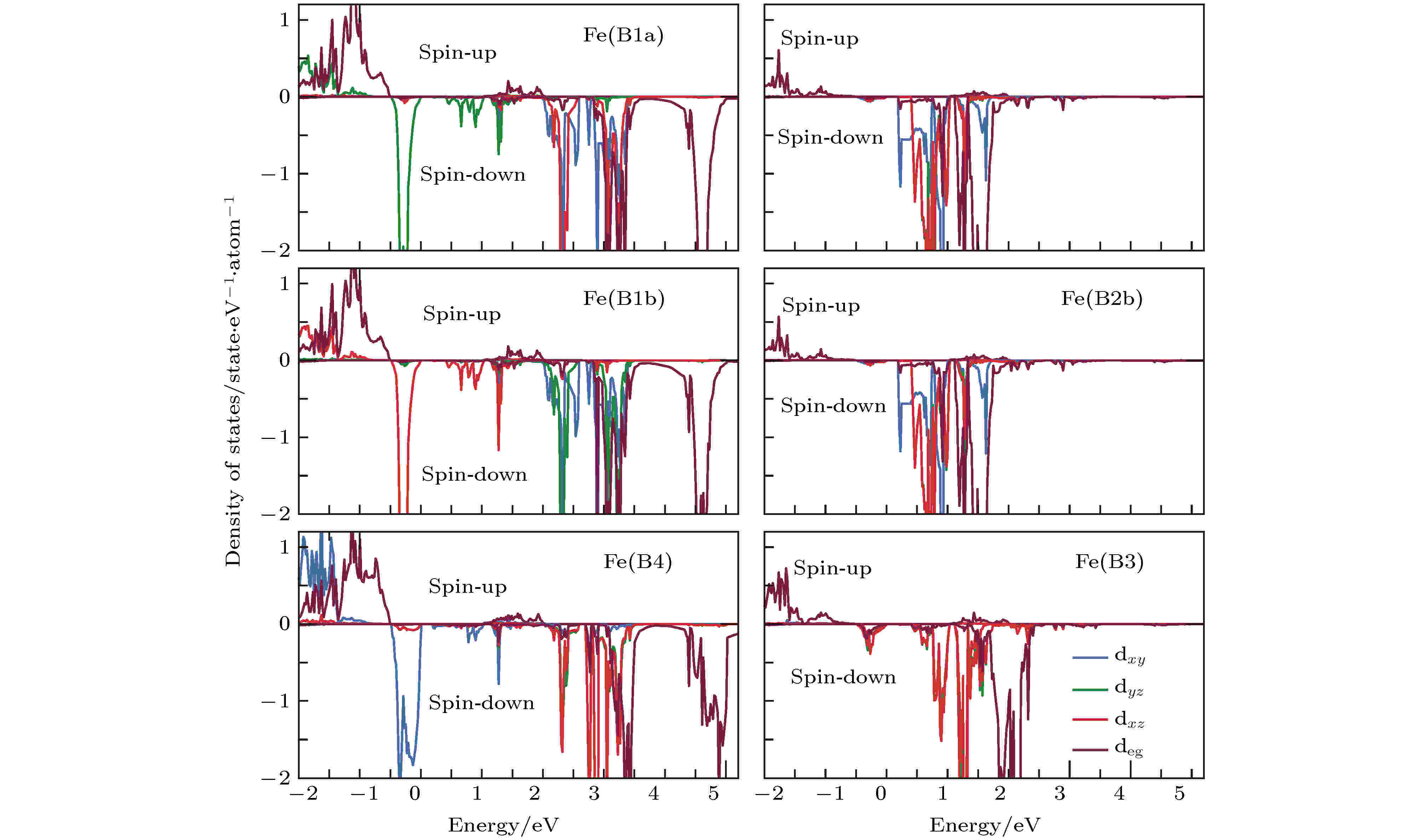 图 13 Fe3O4中FeB离子的态密度图, 费米能级位于EF = 0 eV处[54]
图 13 Fe3O4中FeB离子的态密度图, 费米能级位于EF = 0 eV处[54]Figure13. DOS of Fe3O4 with the monoclinic structure projected onto the FeB d orbitals. Fermi level EF is set at 0 eV[54].
2001年, García等[62]利用X射线共振散射研究了低温相Fe3O4的电子结构. 结果表明X射线反射强度对能量和方位角的关系在转变温度以上和以下不会发生变化, 证明低温下晶格c轴取向不会发生改变. 低温相Fe3O4没有发生明显的Fe3+和Fe2+的电荷有序. 在十种基于Cc空间群的模型中, 只有两个模型满足X射线散射结果, 具有电荷有序, 此时电荷量的差最多为0.5e[62]. 2006年, Nazarenko等[63]通过共振X射线衍射法研究了高纯度Fe3O4单晶样品. 此前, 对于Fe3O4的晶体学研究主要受到自吸收、孪晶、二次激发及多次散射等问题的限制, 不能得到精确结果, 这些限制可以通过共振X射线衍射解决. 根据Wright等[35]的报道, FeB应该存在两组电荷有序, 定义为δ12和δ34, 那么FeB会有四种价态, 分别为B1(




 图 14 δ12和δ34置信因子的等值图. 最佳值为δ12 = 0.12 ± 0.025, δ34 = 0.10 ± 0.06. Fe1电子占据数为5.38和5.62, Fe4电子占据数为5.40和5.60[63]
图 14 δ12和δ34置信因子的等值图. 最佳值为δ12 = 0.12 ± 0.025, δ34 = 0.10 ± 0.06. Fe1电子占据数为5.38和5.62, Fe4电子占据数为5.40和5.60[63]Figure14. Isovalue of the confidence factor. The best agreement is obtained for δ12 = 0.12 ± 0.025 electrons and δ34 = 0.10 ± 0.06 electrons, where the charge occupancies of Fe1 and Fe4 are 5.38, 5.62 and 5.40, 5.60, respectively[63].
Liu等[55]通过第一性原理计算研究了双轴应力对低温相Fe3O4的电荷–轨道有序和三极化子分布的影响. 当张应力超过4%时, FeB42离子的面外方向自旋向下的t2g电子轨道转变为面内方向的

3
3.2.2.磁各向异性
铁磁共振结果表明低温相Fe3O4的磁各向异性具有四方对称性或其他单轴对称性, 易磁化轴的方向沿某一室温相
2
3.3.Fe3O4的磁电阻效应
1950年, Domenicali[68]首先发现Fe3O4样品的磁电阻效应(magnetoresistance, MR), 低温相Fe3O4的MR比相变前更加明显, 然而并未给出MR数据. 1970年, Balberg[69]测量了77 K下块体Fe3O4的MR, 观察到负的MR, 发现MR随磁场的增大而增大, 在大于9000 G下逐渐饱和, 负MR值为–6%—–9%. 同时, MR与施加的电场大小相关, 证明负MR与自旋无序散射有关. 随着外加磁场增大, Fe3O4的磁有序程度增加, Fe离子的载流子在输运过程中的自旋散射降低, 因此负MR随磁场的增大而增大. Kostopoulos[70]研究了天然块体Fe3O4样品的横向磁电阻, 发现在相变温度以上为正MR, MR随温度的升高而降低, 随磁场增大而增大, 在5000 G附近正MR出现极大值. 当磁场进一步增大, 正MR降低, 当温度降低至相变温度以下, Fe3O4表现出负MR, 在相变温度处具有极大值. 考虑到转变温度处样品的电阻率变化较小, 天然Fe3O4的正MR可能来源于样品中的杂质[70].1997年, Gong等[71]利用脉冲激光沉积法在MgO(001)基底上制备不同厚度的外延Fe3O4薄膜, 研究了磁性和磁电阻效应. 在60—350 K范围内测量了厚度分别为660和150 nm厚的外延Fe3O4薄膜的ρ-T曲线, 在300 Oe磁场下测量了厚度为660 nm的Fe3O4样品的M-T曲线, 如图15所示[71]. 两个样品的Verwey转变温度为120 K, 但这两个样品在相变处都有展宽. 此前, Rozenberg等[72]对Fe3O4施加压强的研究结果表明, 随着压强的增加Fe3O4的Verwey转变温度降低. 因此, Gong等[71]认为相变的展宽来源于样品底层靠近基底部分受到晶格失配的影响产生形变, 进而影响转变温度. 为了证实此推测, Gong等[71]在MgO基底上生长了67 nm厚的样品, 此时Verwey转变温度为116.5 K, 证明Verwey转变温度随着薄膜厚度减小而降低.
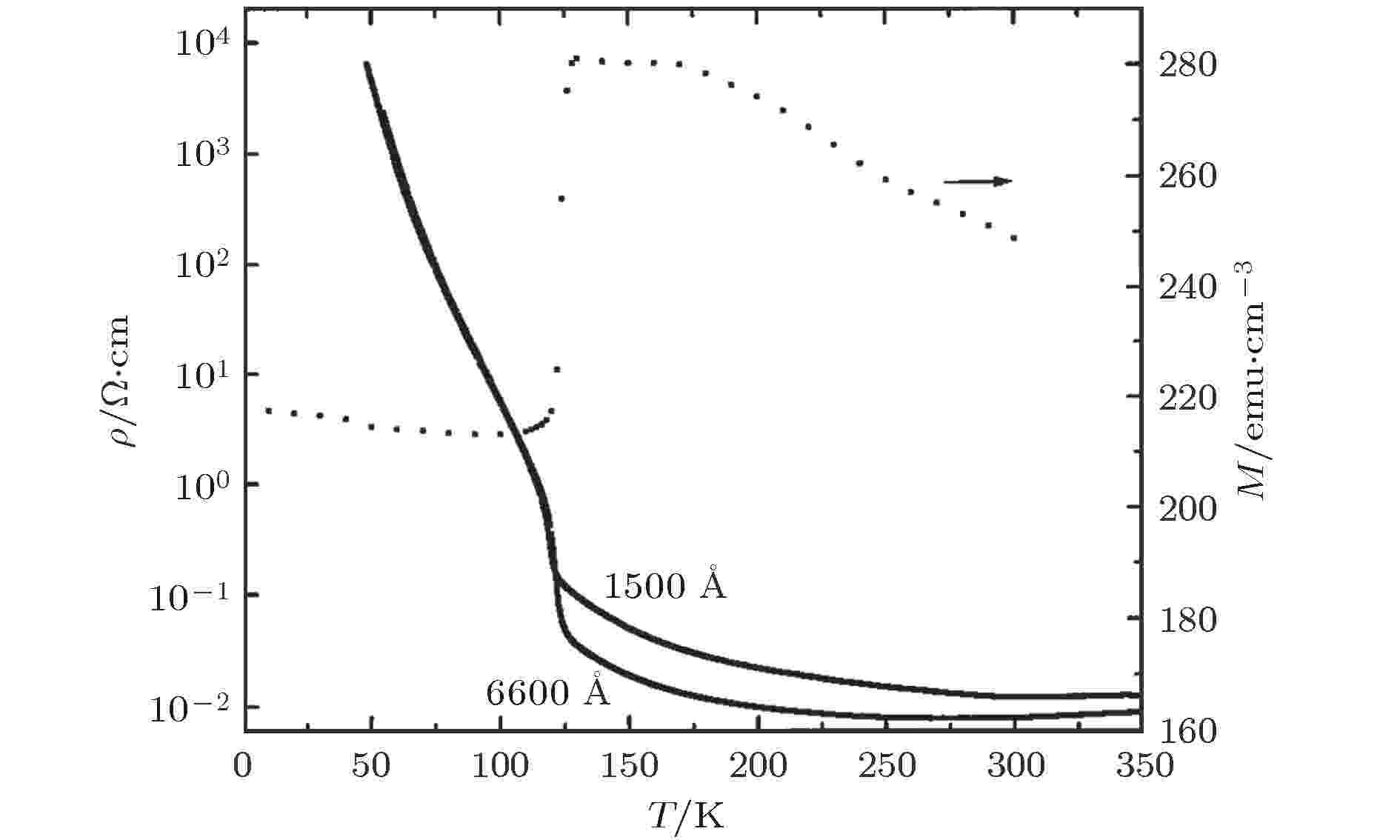 图 15 150和660 nm厚的Fe3O4外延薄膜的ρ–T曲线及300 Oe磁场下660 nm厚的Fe3O4外延薄膜的磁化强度随温度的变化关系[71]
图 15 150和660 nm厚的Fe3O4外延薄膜的ρ–T曲线及300 Oe磁场下660 nm厚的Fe3O4外延薄膜的磁化强度随温度的变化关系[71]Figure15. Temperature dependent resistivity of 150 and 660-nm thick Fe3O4 films in the temperature range of 60–350 K. The temperature dependent magnetization of 660-nm thick film at a magnetic field of 300 Oe[71].
Verwey转变温度以下, Fe3O4的输运特性依赖于转变温度以上时的状态, 因此, 磁电阻不仅依赖于降温时是否施加外磁场, 还依赖于降温前的磁化状态. 为了验证并消除这一影响, Gong等[71]将样品置于零场状态, 由300 K冷却至60 K测量样品的磁电阻效应, 测量完成后将样品加热至300 K, 再通过零场降温的方式将样品降至目标温度. 图16(a)和图16(b)为Fe3O4(660 nm)样品在70和115 K下的磁电阻[71]. 在初始阶段, 样品的电阻率为最大值, 当磁场由 ± 4 T降至0 T时, 电阻率小于初始状态. 在不同温度下, 测量样品的磁电阻效应, 在转变温度附近磁电阻出现极大值, 受到应力的影响, 磁电阻极大值出现展宽, 如图16(c)所示[71]. Verwey转变温度以上, Fe3O4薄膜的磁电阻效应迅速减小. 随着温度降低, 在105 K附近磁电阻出现极小值, 进一步降低温度, Fe3O4薄膜的磁电阻增大. 在60 K, 4 T条件下Fe3O4(660 nm)样品的磁电阻达到32%.
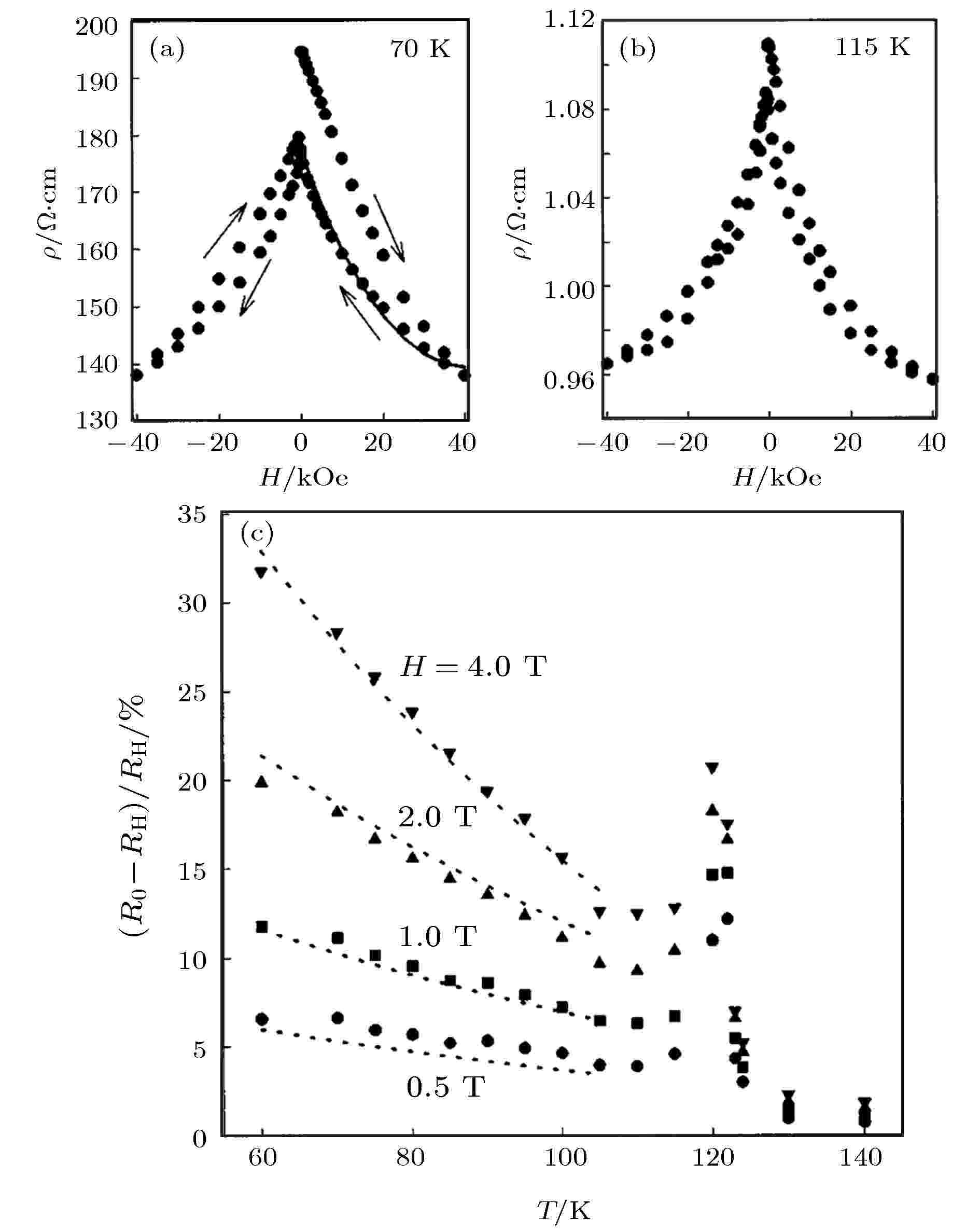 图 16 (a) 70 K和(b) 115 K下, 660 nm厚的Fe3O4薄膜的磁电阻随磁场变化关系; (c) 0.5, 1, 2和4 T磁场下磁电阻随温度的变化关系[71]
图 16 (a) 70 K和(b) 115 K下, 660 nm厚的Fe3O4薄膜的磁电阻随磁场变化关系; (c) 0.5, 1, 2和4 T磁场下磁电阻随温度的变化关系[71]Figure16. Magnetoresistance of 660 nm thick Fe3O4 films at (a) 70 K and (b) 115 K; (c) Temperature dependent magnetoresistance of 660-nm thick Fe3O4 film at the magnetic fields of 0.5, 1, 2, 4 T. The dotted lines are simulations using Mott’s formula[71].
2000年, Ziese和Blythe[73]系统地研究了Fe3O4单晶和薄膜的磁性、电性、各向异性磁电阻(anisotropic magnetoresistance, AMR)等性质. Ziese等将Fe3O4单晶加工成直径为4 mm、高度为13 mm的圆柱体, 圆柱轴体沿[110]方向. 同时, Ziese和Blythe[73]在MgO(001)基底上制备了厚度为200, 50和15 nm的Fe3O4薄膜. 对两类样品的电阻率和磁性进行测量, 结果如图17所示. 在Verwey转变温度附近, 单晶样品的电阻率明显地增大, 薄膜样品的变化较小, 这与之前Gong等[71]报道的结果一致, 对于15 nm的薄膜, 转变温度低于70 K. 研究结果表明对于不同样品, 从磁化强度和电阻率的温度依赖关系中获得的转变温度均保持一致. 但单晶样品的转变温度低于之前文献报道的结果[65,74], 其成分应为Fe3 × (1–0.0017)O4. 在样品面内施加平行或垂直于电流方向的磁场, 测量样品的磁电阻效应, 发现Fe3O4具有AMR效应, 磁场平行或垂直于电流方向的电阻率分别用


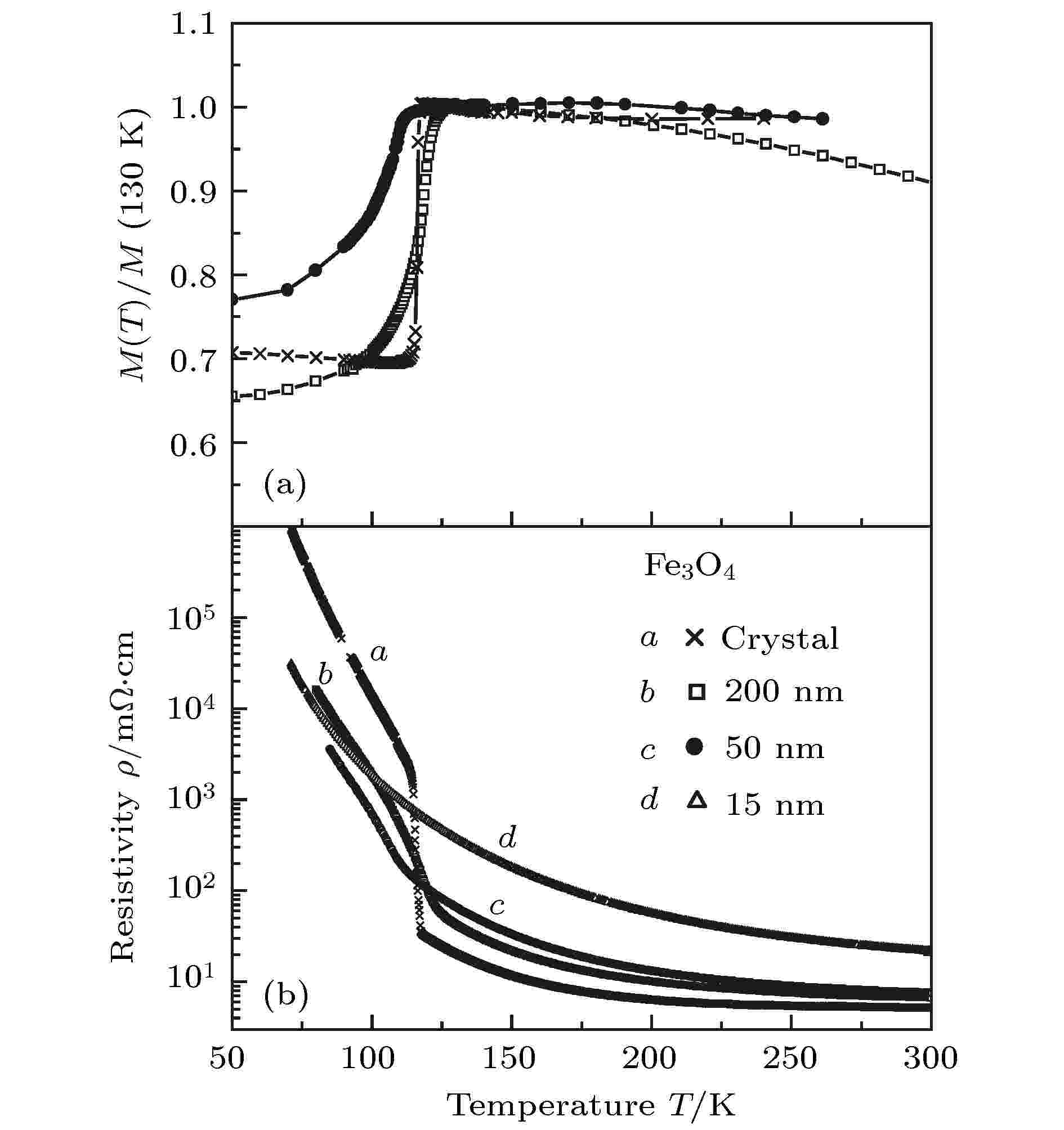 图 17 块体Fe3O4和200, 50和15 nm厚的Fe3O4薄膜的(a)磁化强度和(b)零场电阻率随温度的变化关系[73]
图 17 块体Fe3O4和200, 50和15 nm厚的Fe3O4薄膜的(a)磁化强度和(b)零场电阻率随温度的变化关系[73]Figure17. Temperature dependent (a) magnetization and (b) zero-field resistivity of Fe3O4 single crystal and films with the thickness of 200, 50 and 15 nm[73].
Eerenstein等[77]基于一维自旋链模型解释了Fe3O4薄膜的磁电阻行为. 对Fe3O4薄膜施加面内方向磁场, 反相边界处磁矩分布如图18所示. 此时一维自旋链的能量包括磁化能、反相边界处的反铁磁耦合能及APB两侧相邻磁矩之间的铁磁耦合能. 体系的能量可以表示为
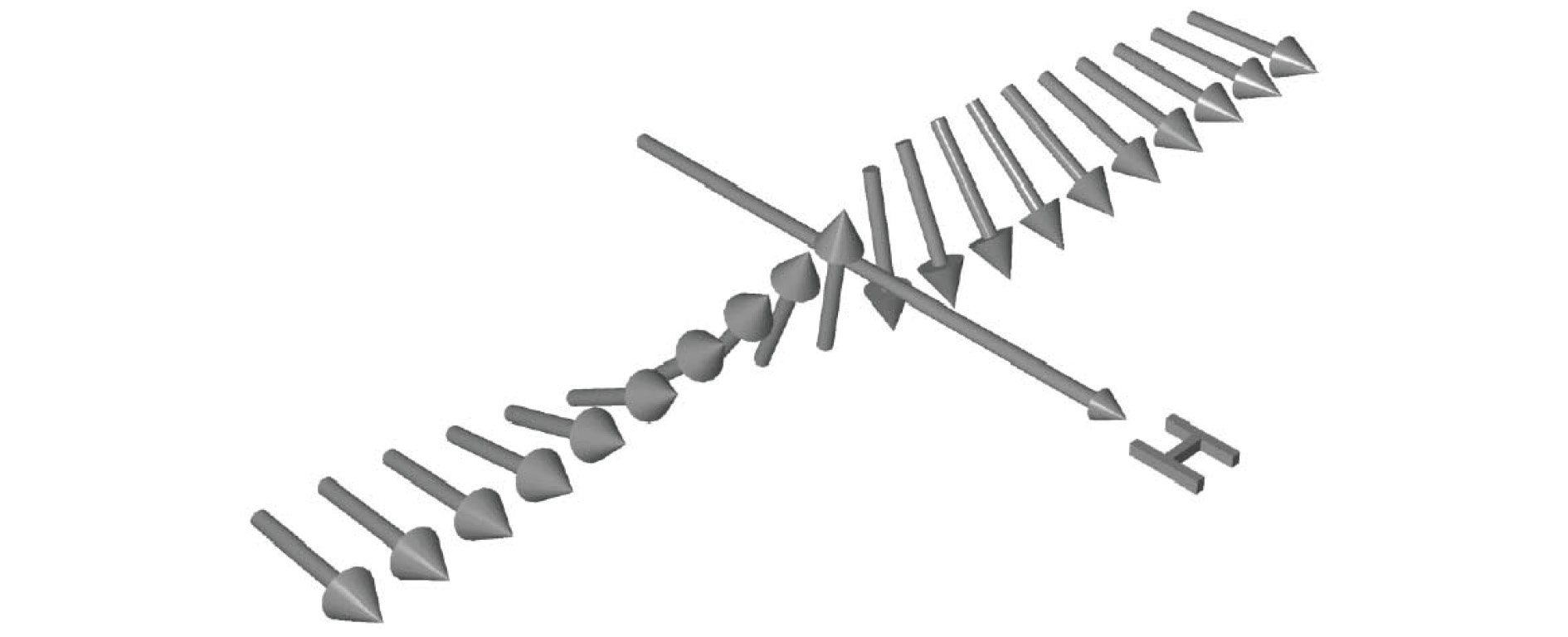 图 18 在磁场作用下, Fe3O4薄膜反相边界处的磁矩分布[77]
图 18 在磁场作用下, Fe3O4薄膜反相边界处的磁矩分布[77]Figure18. Spin orientation of two ferromagnetic chains with antiferromagnetic coupling at an atomically sharp boundary at a magnetic field[77].

2008年, Ramos等[81]对Fe3O4块体和薄膜的AMR进行研究. 在200 K以上, Fe3O4块体和薄膜的AMR具有二重对称性; 在200 K以下, AMR具有四重对称性, 如图19所示[81]. 通过测量样品的电阻随温度的变化关系, 发现在200 K下Fe3O4的电输运机制发生转变, 当温度低于200 K时, Fe3O4内部形成小极化子, 小极化子的出现使Fe–O位置发生偏移, 增强了Fe3O4的自旋-轨道耦合作用, 因此在200 K以下出现四重对称的AMR. 遗憾的是Ramos等未研究相变温度以下Fe3O4的AMR.
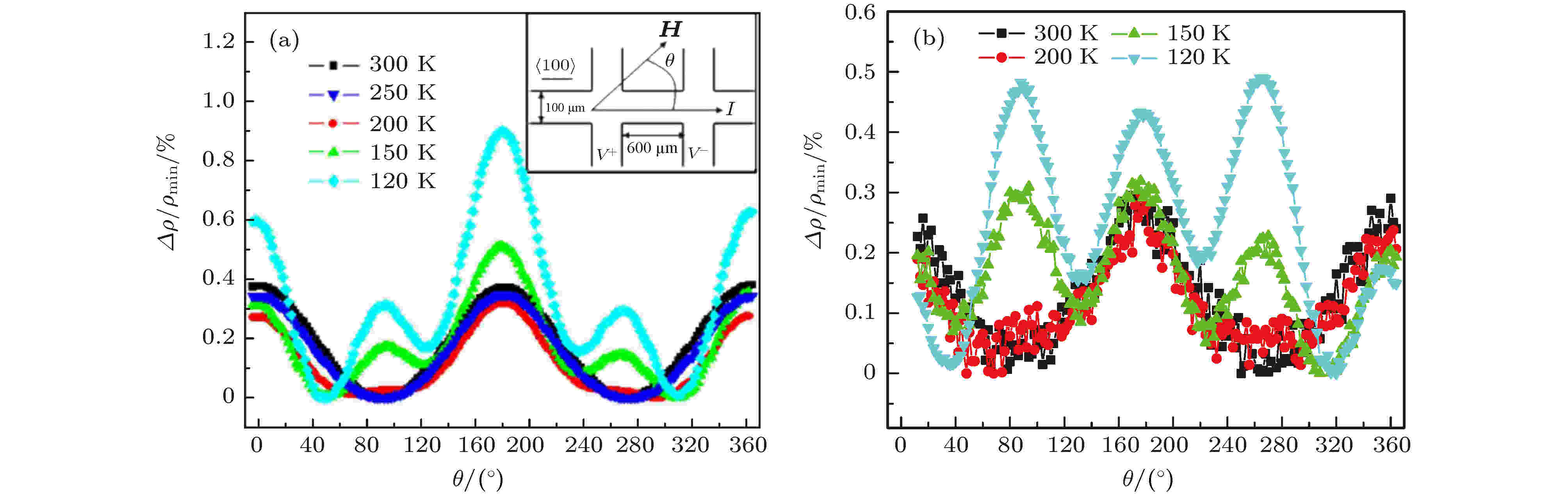 图 19 在5 T磁场下, (a) 67 nm厚的Fe3O4薄膜和(b) Fe3O4块体的AMR[81]
图 19 在5 T磁场下, (a) 67 nm厚的Fe3O4薄膜和(b) Fe3O4块体的AMR[81]Figure19. AMR of the (a) 67 nm thick Fe3O4 film and (b) Fe3O4 single crystal at a magnetic field of 5 T[81].
磁各向异性研究结果表明低温相Fe3O4具有单轴磁各向异性, 然而Li等[82], Hu等[83]和Ding等[84]对Fe3O4的AMR进行测量时发现, 当温度低于TV时AMR仍具有四重对称性, 与磁性对称性不一致. 2017年, Liu等[85]对高质量外延Fe3O4薄膜在Verwey相变温度附近的AMR进行了系统的研究, 结果表明当温度降低至TV—TV–15 K时Fe3O4(100)薄膜表现出二重对称的AMR, 随着温度继续降低, AMR的对称性逐渐由二重对称转变为四重对称, 如图20所示[85]. 在Fe3O4(111)薄膜中, 在50 kOe磁场下, AMR在不同温度下始终保持二重对称性, 在110 K, 2000—10000 Oe环境下, AMR在60°, 120°, 240°和300°出现极值, 接近六重对称性, 如图21(c)所示. 分析Fe3O4中三极化子的分布与AMR之间的联系, 当磁场平行于三极化子时AMR具有极小值, 如图21(b)和图21(c)所示. 因此, AMR对称性的变化可能和Fe3O4相变引起的结构变化相关, 通过测量Fe3O4(100)和(111)薄膜的拉曼光谱, 发现低于Verwey相变温度15 K附近出现单斜相Fe3O4的拉曼峰, 证明Verwey相变先后经历电荷有序和结构畸变两个过程.
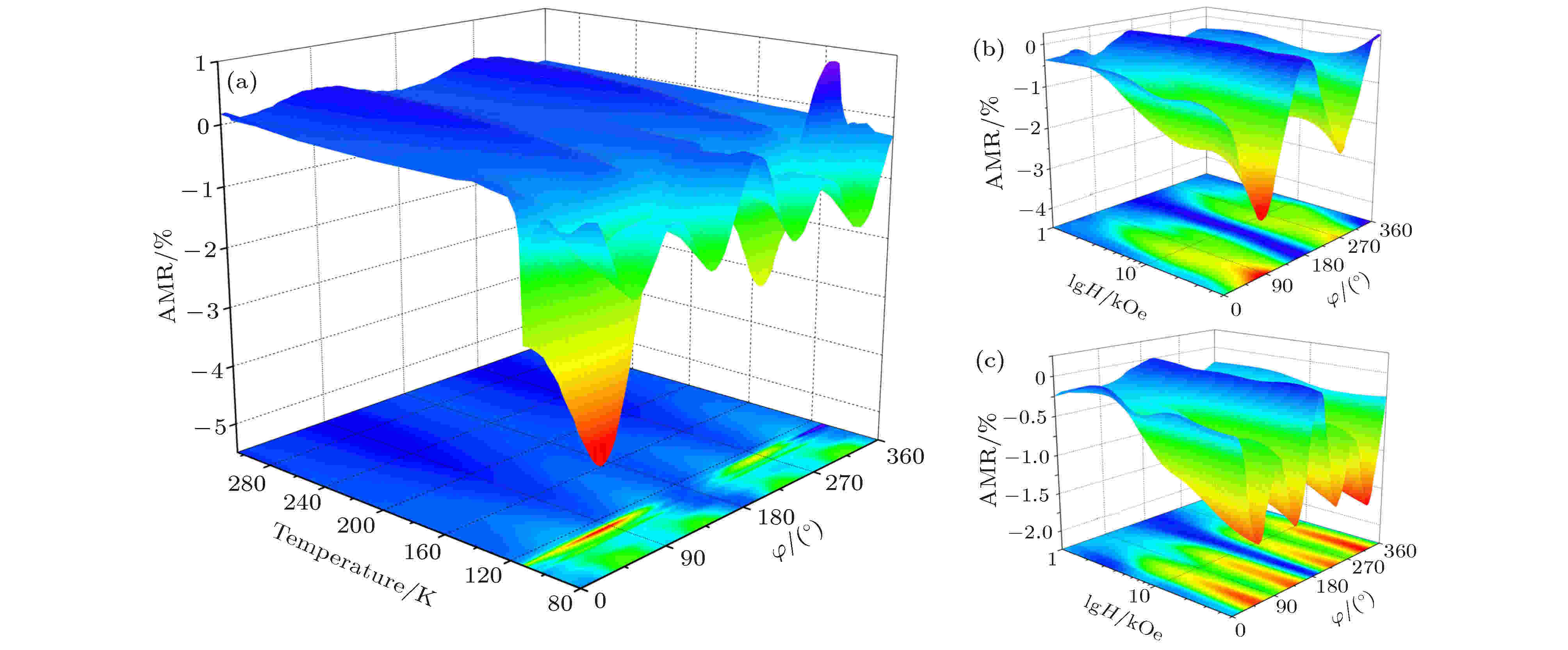 图 20 外延Fe3O4(100)薄膜的AMR (a) 50 kOe下AMR随温度的变化; (b) 110 K和(c)80 K下AMR随磁场的变化[85]
图 20 外延Fe3O4(100)薄膜的AMR (a) 50 kOe下AMR随温度的变化; (b) 110 K和(c)80 K下AMR随磁场的变化[85]Figure20. AMR of the epitaxial Fe3O4(100) film: (a) Temperature-dependent AMR at a 50 kOe magnetic field; AMR at (b) 110 K and (c) 80 K[85].
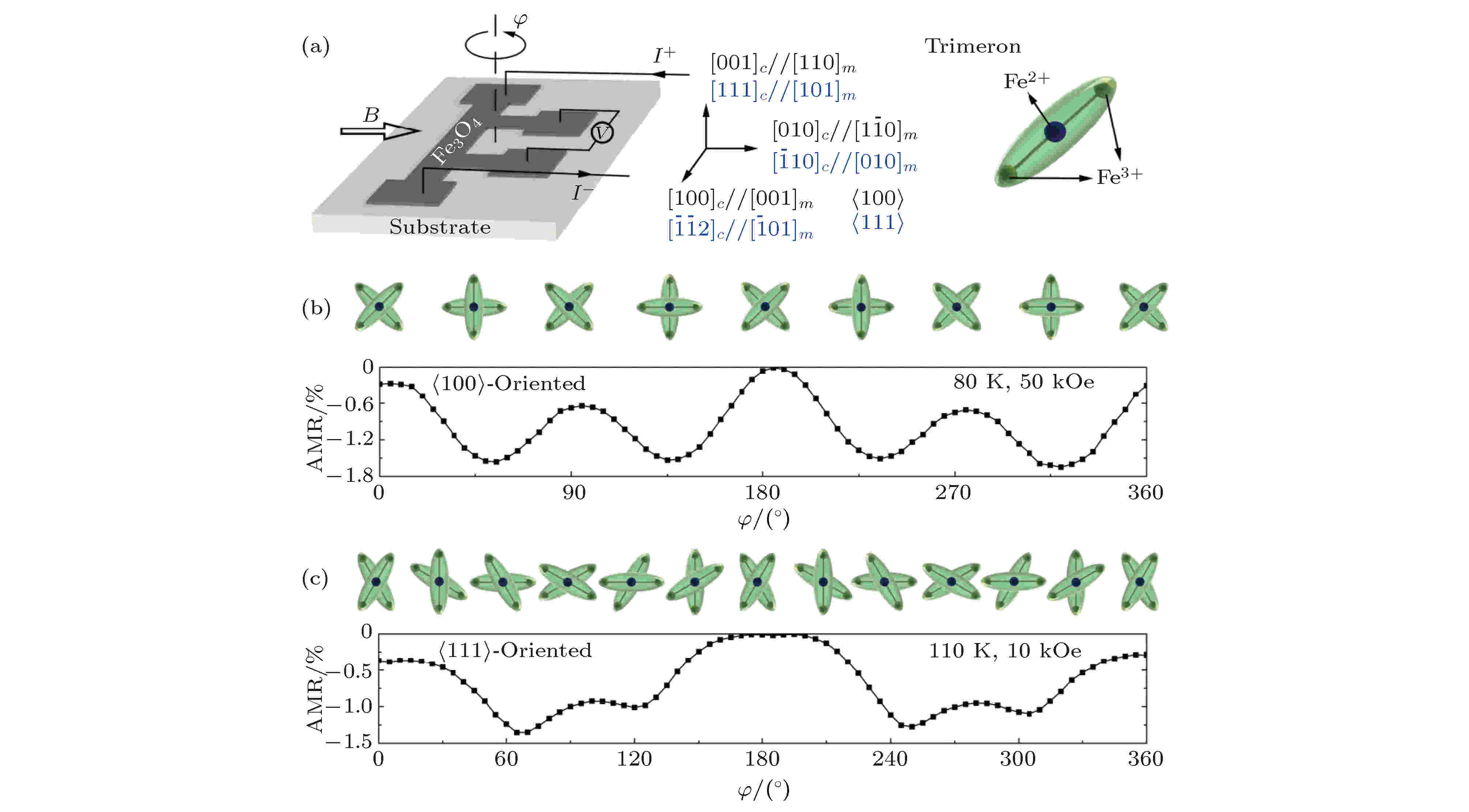 图 21 (a)测试示意图; (b) 80 K和50 kOe下, Fe3O4(100)薄膜的AMR与三极化子分布的关系; (c) 110 K和10 kOe下, Fe3O4(111)薄膜的AMR与三极化子分布的关系. 三极化子示意图如右上角所示[85]
图 21 (a)测试示意图; (b) 80 K和50 kOe下, Fe3O4(100)薄膜的AMR与三极化子分布的关系; (c) 110 K和10 kOe下, Fe3O4(111)薄膜的AMR与三极化子分布的关系. 三极化子示意图如右上角所示[85]Figure21. (a) Schematic of the measurements; (b) relation between AMR and distribution of in-plane trimeron of Fe3O4(100) film at 80 K and 50 kOe; (c) relation between AMR and distribution of in-plane trimeron of Fe3O4(111) film at 110 K and 10 kOe. The trimeron is shown in the upper right corner[85].
2
3.4.Fe3O4的铁电性
直至1970年, 人们还并不能准确地描述低温相Fe3O4的晶格结构, 因此Rado和Ferrari[86]期望低温相Fe3O4具有磁电耦合效应, 利用磁电耦合对称性的关系揭示Fe3O4的晶格对称性. 研究发现, 在4.2 K, 对Fe3O4单晶施加外磁场可以诱导出静电极化, 静电极化的大小和外加磁场具有非线性关系. 热力学分析结果表明这种非线性的磁电耦合效应来源于依赖电场的宏观磁各向异性. 不同方向测量的电极化对磁场的关系表明, 在4.2 K下Fe3O4为三斜结构. 此后, Iwauchi等[87], Kato等[28,88,89], Miyamoto等[90,91]对低温相Fe3O4的磁电耦合性质以及铁电性做了大量的研究.2009年, Alexe等[92]采用脉冲激光沉积和磁控溅射方法制备了Pd/Fe3O4/Nd:SrTiO3(001)异质结构, 在低温下研究了Fe3O4的铁电性. 40 K以上, 由于Fe3O4电阻率较小, 测量时出现漏电. 40 K以下, Fe3O4逐渐表现出铁电性, 外加电场可以翻转Fe3O4的铁电极化, 如图22(a)所示[92]. 20 K以下, Fe3O4铁电极化达到饱和, (001)方向的铁电极约为5.7 μC/cm2. Yamauchi等[93]通过第一性原理计算研究了低温相Fe3O4的自发铁电极化. 对称性分析表明P2/c空间群具有中心反演对称性, 因而具有顺电性(paraelectricity, PE). Cc空间群为非中心反演对称群, 因此在Cc空间群下Fe3O4具有铁电性(ferroelectricity, FE), 由于Cc空间群在b轴方向具有镜面对称性, 在b轴方向不具有电极化性质, 只在a, c轴方向上存在有限的极化矢量P, 如图22(b)所示[93]. 与Jeng等[36,54]报道的结果一致, 顺电相中的电荷有序为纯3∶1模式, 铁电相中为75%(3∶1)+25%(2∶2), 这两种电荷有序模型的区别可以理解为FeB12, FeB14和FeB12’, FeB14’互相发生了交换. 为了进一步研究铁电性, Yamauchi等[93]通过比较Berry相方法计算的极化矢量PBerry和点电荷模型(point charge model, PCM)得出的极化矢量PPCM, 发现P是由电荷有序的重新排列引起的, 因此Fe3O4是一种由电荷有序导致的具有较强电极化的多铁性材料.
 图 22 (a) Pd/Fe3O4/Nd:SrTiO3异质结构的电滞回线[92]; (b) P2/c (左图)和Cc空间群(右图)的FeB离子结构. 橙色和蓝色球表示Fe2+和Fe3+. 红色箭头表示电荷转移引起的电偶极矩[93]
图 22 (a) Pd/Fe3O4/Nd:SrTiO3异质结构的电滞回线[92]; (b) P2/c (左图)和Cc空间群(右图)的FeB离子结构. 橙色和蓝色球表示Fe2+和Fe3+. 红色箭头表示电荷转移引起的电偶极矩[93]Figure22. (a) Dielectric hysteresis loop of Pd/Fe3O4/Nd:SrTiO3 heterostructure[92]; (b) ionic structure of Fe octahedral sites with P2/c (left) and Cc (right) space groups. Orange and blue balls represent the Fe2+ and Fe3+ ions. Electric dipole moments caused by charge shifts are indicated by red arrows[93].
2018年, Liu和Mi[94]进一步研究了外加应力对低温相Fe3O4自发铁电极化的影响, 对比了基于点电荷模型、极化量子和贝利相位方法计算得到的Fe3O4铁电极化值. 基于点电荷模型, Liu等[94]首先确定了Fe3O4自发铁电极化的方向沿-x和-z方向. 利用贝利相位的方法, 在不受外加应力下, Fe3O4的自发铁电极化为(4.62, 0, 7.58) μC/cm2, 当应力由+6%的张应力转变至–6%的压应力时, z轴方向的自发铁电极化由6.09 μC/cm2增加至8.85 μC/cm2, 如图23所示.
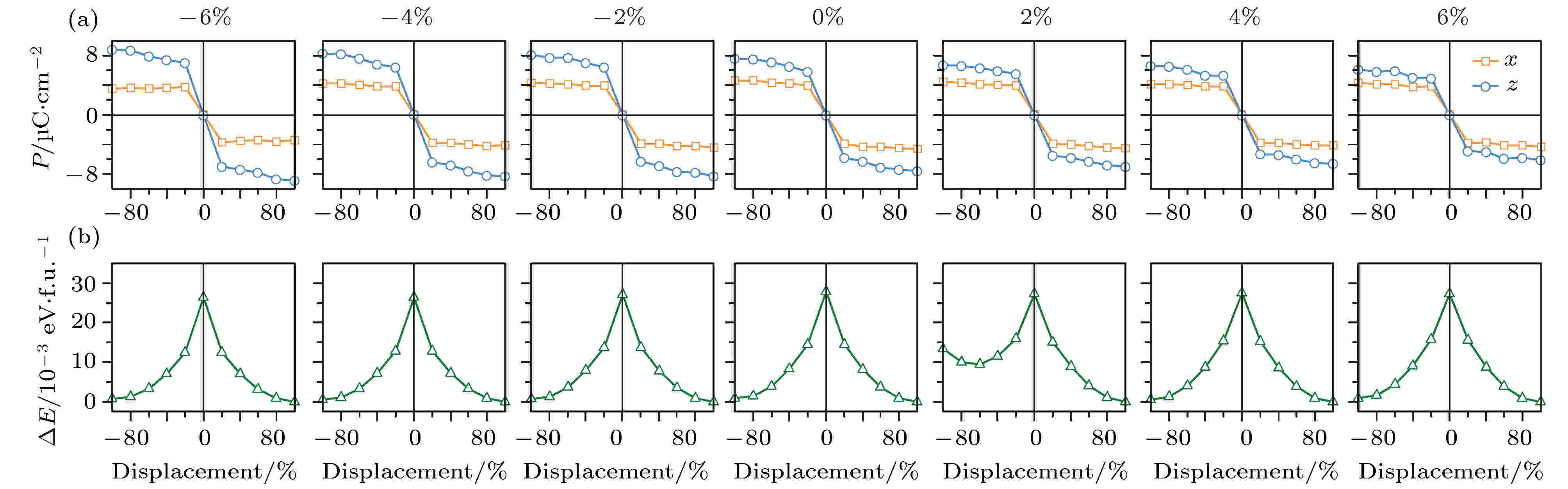 图 23 (a)低温相Fe3O4铁电极化在x, z轴方向的分量; (b)体系总能随应力的变化[94]
图 23 (a)低温相Fe3O4铁电极化在x, z轴方向的分量; (b)体系总能随应力的变化[94]Figure23. (a) Ferroelectric polarization along the x and z axes; (b) strain dependent total energy[94].
