摘要:为了研究欧姆损耗对高频真空电子器件工作特性的影响, 首先推导频率色散表面阻抗边界在三维共形粒子模拟软件UNIPIC-3D中的实现原理, 并通过对有耗边界矩形谐振腔和圆波导进行模拟验证了该阻抗边界算法的正确性. 采用有耗共形UNIPIC-3D模拟相对论太赫兹表面波振荡器和低电压平板格栅返波振荡器. 模拟结果表明, 对于表面波振荡器和平板BWO这种电磁场集中在金属慢波结构附近的太赫兹真空电子器件, 欧姆损耗会对器件的运行带来极大影响, 对于采用铜材料的器件, 输出功率会下降一半左右, 器件起振时间出现延迟, 但器件工作频率几乎不变. 为了提高相对论太赫兹表面波振荡器的效率, 在二极管和慢波结构之间增加了反射腔, 模拟结果表明, 在考虑器件表面损耗的条件下, 器件的工作频率保持不变, 输出功率由41 MW提高到60 MW.
关键词: 表面阻抗边界/
欧姆损耗/
粒子模拟/
太赫兹器件/
表面波振荡器/
返波管

English Abstract

全文HTML

--> --> -->

太赫兹(THz)波指频率在0.1—10 THz的电磁波, 在民生和国防领域都有广泛的应用^[1]. 在大多数应用中, 太赫兹源是关键. 对于低频段的太赫兹源, 真空电子器件是主要的产生途径^[2], 可产生百千瓦至数兆瓦的脉冲功率输出^[3-6]或数百毫瓦至数十瓦的连续波功率输出^[7-10], 因此, 国内外都在大力开展真空电子太赫兹器件的研究工作.
在真空电子太赫兹器件的设计方法中, 用的最多的数值方法是基于第一性原理的粒子模拟(particle-in-cell, PIC)方法^[11-16], 通过求解带电粒子运动的Newton-Lorentz力方程和电磁场Maxwell方程组, 实现对器件中电磁场与带电粒子非线性相互作用的模拟, 获得器件输出性能参数与器件结构参数和电子束参数之间的关系.
对于真空电子微波器件, 金属边界可以当做理想导体处理, 但对于毫米波尤其是太赫兹波, 电磁波对金属的趋肤厚度与器件的加工精度相当, 因此, 金属边界对太赫兹波的衰减较大, 从而大大影响了器件的工作特性^[17].
在模拟带欧姆损耗的器件时, 等效电磁参数方法、有限电导率方法以及表面阻抗边界条件是3种常用方法. 等效电磁参数主要用于带有超材料结构器件的模拟; 有限电导率方法需要对导电介质内部进行网格剖分, 主要用于模拟包含低电导率材料的器件, 对于良导体这类电导率很大的介质, 电磁波在其中的波长非常短, 网格尺寸会非常小, 导致计算量急剧增加; 采用表面阻抗边界, 只需要根据良导体表面切向电场与表面附近磁场的关系, 在导体边界处网格内磁场推进时进行一定修正, 就能考虑导体表面的损耗效应, 并不需要求解导体内部的场. 目前的研究中, 表面阻抗边界条件主要用于半无限大空间有耗介质表面以及介质表面涂覆层的电磁场分布研究. 文献[18]中在研究瞬态电磁脉冲对有耗地面附近电缆耦合问题时, 采用表面阻抗边界作为地面的边界条件来模拟有耗地面的反射. 文献[19]中利用表面阻抗边界条件研究了涂覆等离子体薄层的金属材料的电磁散射特性. 文献[20]中采用表面阻抗边界作为石墨烯材料的边界, 研究这类器件的电磁特性. 由于电磁波损耗是频率的函数, 金属边界对太赫兹波的衰减是色散问题. 本文给出三维粒子模拟软件在采用共形边界情形下的频率色散表面损耗边界条件, 并对损耗算法进行验证. 将损耗边界的粒子模拟方法应用于两种典型的真空电子太赫兹源(圆柱结构相对论表面波振荡器和平板结构非相对论返波管)的模拟.

粒子模拟中粒子推进和电磁场推进交替进行, 主要流程包括: 场推进、粒子推进以及场与粒子相互作用3部分, 互作用包括粒子所受电磁场力的插值以及粒子运动产生电流密度向网格的分配.
电场的计算采用时域有限差分方法^[21]. 如图1所示, 电场和磁场交错布置在网格边和网格面上, 通过在时间和空间上将Maxwell方程进行离散化, 用差分代替微分, 最终实现电磁场的推进. 这种处理使得每一个网格单元都满足法拉第感应定律和安培环路定律, 很好保留了电磁场旋度与通量之间的关联特性.
图 1 FDTD网格示意图
Figure1. Schematic of FDTD cell.

带电粒子运动遵循Newton-Lorentz力方程

$\frac{{\rm{d}}}{{{\rm{d}}t}}\gamma m{v} = q({E} + {v} \times {B}),$

$\frac{{{\rm{d}}r}}{{{\rm{d}}t}} = {v,}$

其中, γ为相对论因子, E和B是粒子所在位置处的电场和磁场,
对(1)式和(2)式进行离散可得

$\begin{split} & \frac{{{{u}^{n + 1/2}} - {{u}^{n - 1/2}}}}{{\Delta t/2}} \\=\, & \frac{q}{m}\left( {{E}^n} + \frac{{{{u}^{n + 1/2}} + {{u}^{n - 1/2}}}}{{2{\gamma ^n}}} \times {{B}^n} \right), \end{split}$

$\frac{{{{r}^{n + 1}} - {{r}^n}}}{{\Delta t}} = \frac{1}{{{\gamma ^n}}}{{u}^{n + 1/2}},$

其中, u = γv, 粒子速度的推进可以采用Boris旋转方法^[12]. 通过交替推进电磁场方程和粒子运动方程, 可以实现粒子和场互作用过程的自洽模拟, 得到粒子参数和电磁场时空分布.
随着真空器件工作频率的提高, 电磁场在器件金属壁面上的损耗也越来越大, 欧姆损耗的影响不能忽略. 尤其在太赫兹波段, 损耗对器件的起振时间、模式之间的竞争、输出效率及频带宽度都有很大影响^[17]. 为了使模拟结果更加符合真实情况, 需要在程序代码中加入阻抗算法, 用于模拟有耗介质对器件工作性能的影响. 如果直接采用有限电导率模型, 需要在金属区域内部进行网格剖分并求解, 但是金属内电磁波的波长非常短, 为了满足网格步长Δ小于λ/10的条件, 网格尺寸会非常小, 导致计算量急剧增加. 如果采用表面阻抗边界^[22], 只需要根据良导体表面切向电场与表面附近磁场的关系, 在磁场推进时加入导体表面上电场的作用, 就能考虑导体表面的损耗效应, 并不需要求解导体内部的场.
目前的粒子模拟软件多采用阶梯近似的方法来逼近模型边界, 采用阶梯近似网格在粒子模拟中会出现两个问题^[23]: 不能准确求解弯曲边界处的电磁场; 不能准确描述弯曲的阴极面上的粒子发射. 粒子模拟软件UNIPIC-3D基于射线与几何体的求交算法, 实现了三维复杂模型的共形网格生成技术^[23], 在共形网格上应用Maxwell方程组的离散积分方法对电磁场进行推进. 有些共形网格的面积可能会很小, 由稳定性条件可知过小面元会使时间步长缩短, 为了克服这个问题, UNIPIC-3D中采用Simple-Conformal共形算法^[23-26]. 以图2所示局部共形网格为例, 对磁场进行推进时需要计算局部真空面元上电场的环路积分:
图 2 局部共形网格
Figure2. Local conformal grid.

$ - \frac{{\partial {B_z}}}{{\partial t}}\Delta S = - {E_{x,2}}{\bar l _4} - {E_{y,1}}{\bar l _1} + {E_{y,2}}{\bar l _3},$

其中, ΔS为该共形网格面内除去PEC部分的面积, 带上标的长度量为相应边的有效长度. 有效长度根据环绕该边的4个共形面元的面积系数(共形面元面积除以完整网格面元)和该边的长度系数计算而来, 假设网格索引号为(i, j, k)的x方向某局部共形网格边的实际长度为l_x,ijk, 则该边有效长度的计算公式为

$\begin{split} {\overline l _x}_{,ijk} =\, & {l_{x,}}_{ijk} \cdot \min \left[ 2\min\left(\frac{{{s_{y,\;ij(k - 1)}}}}{{\Delta x\Delta z}},\frac{{{s_{y,\;ijk}}}}{{\Delta x\Delta z}},\right.\right.\\ &\left.\left.\frac{{{s_{z,\;i(j - 1)k}}}}{{\Delta x\Delta y}},\frac{{{s_{z,\;ijk}}}}{{\Delta x\Delta y}}\right),\frac{{{l_{x,}}_{ijk}}}{{\Delta x}}\right]\end{split}$

其中, Δx、Δy、Δz分别为x、y、z 3个方向的网格步长, s_{y, ijk}等4个变量为环绕该边的4个共形网格面元的面积.
考虑导体的高频损耗, 其核心问题是将理想导体的边界条件, 改为非理想导体的边界条件, 即其表面的切向电场分量不为零, 而是与附近的切向磁场满足如下形式的阻抗关系^[27]

${{{E}}_t} = {Z_{\rm{s}}}(\omega ) \cdot {{n}} \times {{{H}}_t}(\omega ), $

其中, n为指向导体外部的法方向单位矢量, Z_s为表面阻抗, 它与电磁场的角频率ω、金属材料的电导率σ和材料的磁导率μ有关, 且为复数形式,

${Z_{\rm{s}}} = (1 + {\rm{j}})\sqrt {\frac{{\omega \mu }}{{2\sigma }}} = \sqrt {\frac{{{\rm{j}}\omega \mu }}{\sigma }} . $

表面阻抗可以表示为表面电阻和表面电抗之和, 即Z (ω) = R (ω) + jL (ω). 在共形电场算法的基础上, 如果能在金属导体边界处利用电磁场的阻抗关系计算出金属边上的切向电场, 就可以在电场的回路积分上加上金属边上的电压用于磁场推进. 采用阻抗边界截断金属边界, 将计算区域限定于真空部分, 而不用考虑导体内部的场, 这样可以显著减少计算量.
(7)式给出了频域形式的阻抗关系, 为了将阻抗边界用于时域共形电磁场求解, 需要推导时域阻抗关系. 以z平面内x方向电场分量为例, 对(7)式进行逆傅里叶变换:

${E_x}\left( t \right) = \sqrt {\frac{\mu }{{{\text{π}}\sigma t}}} * \left[ {\frac{\partial }{{\partial t}}{H_y}(t)} \right]. $

将卷积写成积分形式并整理可得

${E_x}\left( t \right) = \sqrt {\frac{\mu }{{{\text{π}}\sigma }}} \int_0^t {\sqrt {\frac{1}{t}} } \left[ { - \frac{\partial }{{\partial \tau }}{H_y}(t - \tau )} \right]{\rm{d}}\tau .$

令t = nΔt, τ = αΔt, 对卷积中的时间项进行离散

${E_x}\left( t \right) = \sqrt {\frac{{\mu \Delta t}}{{{\text{π}}\sigma }}} \sum\limits_{m = 0}^{n - 1} {{Z_0}\left( m \right)} \frac{{H_y^{n - m + 1/2} - H_y^{n - m - 1/2}}}{{\Delta t}}.$

其中

${Z_0}\left( m \right) = \int_{\rm{m}}^{m + 1} {\frac{{{\rm{d}}\alpha }}{{\sqrt \alpha }}} . $

(11)式中计算离散卷积需要保存该网格边之前所有时间步的磁场值, 给编程带来困难. 为了简化离散卷积的计算, 可以对Z₀采用指数近似, 得到

${Z_0}\left( m \right) = \sum\limits_{i = 1}^N {{a_i}} {{\rm{e}}^{m{\alpha _i}}}, $

其中: N是近似项的数目, 一般取前10项即可; a_i为系数, 可以采用Prony近似的方法得到^[27]. 将Z₀写成这种形式后, 引入辅助变量

$\psi _i^n = \sum\limits_{m = 1}^{n - 1} {{a_i}{{\rm{e}}^{m{\alpha _i}}}\left[ {H_y^{n - m + 1/2} - H_y^{n - m - 1/2}} \right]} . $

可以证明ψ_i满足如下递推关系^[27]

$\psi _i^n = {a_i}{{\rm{e}}^{{\alpha _i}}}\left[ {H_y^{n - 1/2} - H_y^{n - 3/2}} \right] + {{\rm{e}}^{{\alpha _i}}}\psi _i^{n - 1}, $

以图2中包含金属边的共形网格单元为例, 考虑损耗的情况下, 推进磁场时需加上金属边l₂上电场对回路积分的贡献

$ \begin{split} {E_t}(t){l_2} =\; & {l_2} \cdot \sqrt {\frac{{\mu \Delta t}}{{{\text{π}}\sigma }}} {Z_0}\left( 0 \right)\frac{{H_z^{n + 1/2} - H_z^{n - 1/2}}}{{\Delta t}}\\ & + {l_2} \cdot \sum\limits_{m = 1}^{n - 1} {\psi _i^n} . \end{split} $

对于包含导体边界的局部共形网格面, 每次推进时需要加上金属边上电压对电场回路积分的贡献, 并将n+1/2时刻的H_z项进行合并, 最终完成计算, 得到n+1/2时刻新的磁场值后再按照(14)式对ψ_i进行更新, 为下一时间步的推进做准备.

为了验证表面阻抗边界算法的正确性, 首先模拟矩形谐振腔中电磁波的衰减过程. 对于起振后的谐振腔, 由于腔壁的损耗, 腔内电磁场的总能量W将随时间成指数衰减:

$W = {W_0}{{\rm{e}}^{ - 2\alpha t}}, $

其中, W₀是腔内某初始时刻电磁场的总能量, α是衰减常数. 该谐振腔横向(x-y截面)尺寸为25 mm × 12.5 mm, 高度为62.5 mm, 内壁电导率取10⁵ S/m, 根据理论公式可计算出该谐振腔的Q值为329^[28], 该谐振腔的基模为TE₁₀₁模, 对应的谐振频率为6.46 GHz. 在腔体中间加载沿y轴方向的线电压脉冲源进行激励, 电压波形为

$V\left( t \right) = \frac{{t - \tau }}{\tau }\exp \left[ { - 4{\text{π}}{{\left( {\frac{{t - \tau }}{\tau }} \right)}^2}} \right],$

其中, τ = 3 × 10^–10 s.
图3为模拟所得腔内偏离激励源一定位置的观测点处y方向电场随时间变化曲线, 可以看出: 1)该电压脉冲激励起腔内的谐振, 通过对时域波形进行FFT变换, 所得频率为6.51 GHz, 与理论值相符; 2)由于腔体表面的损耗, 起振后腔内电场振荡的幅度逐渐减弱. 如图3中蓝色曲线所示, 对电场幅值(上包络线)进行负指数拟合得到的指数项系数为–6.24 × 10⁷. 谐振腔Q值与角频率ω和衰减常数α的关系为Q = ω/2α, 由此可计算出谐振腔的Q值为325, 与理论值相符合较好, 验证了欧姆损耗算法的正确性.
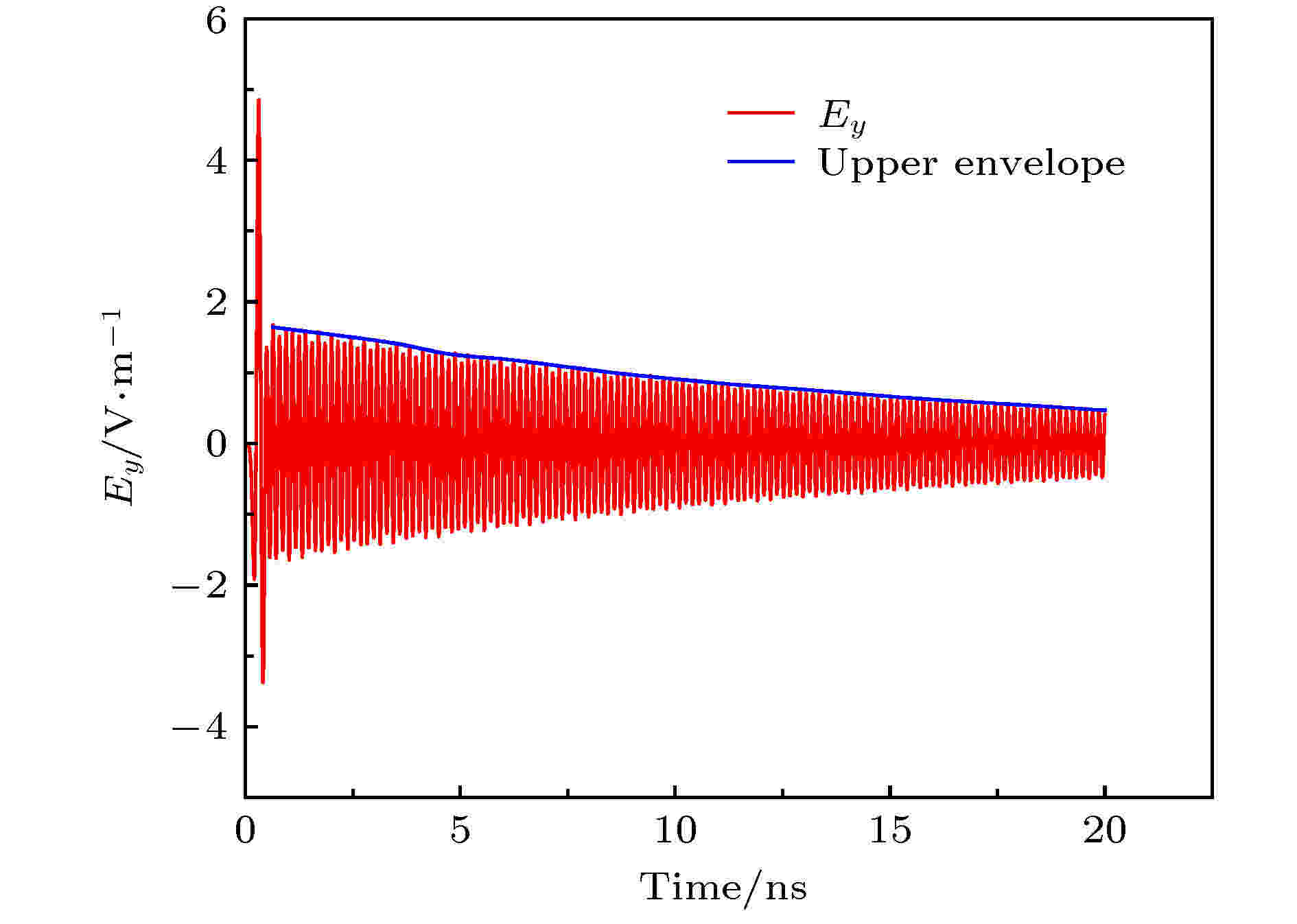图 3 谐振腔内诊断点处电场时间波形
Figure3. Time history of electric field inside a resonator.

另外, 采用新的损耗算法模拟了圆柱波导中电磁场的传播, 波导半径a = 0.5 mm, 长度为25 cm, 内壁电导率σ = 5.8 × 10⁷ S/m. 可以计算出波导壁面的电阻为

$R = \sqrt {\frac{{\omega \mu }}{{2\sigma }}} = 0.15213\;\Omega . $

在波导左侧端口加载TM₀₁模式电磁波, 该模式的截止频率f_c = 0.23 THz, 设置入射电磁波为频率f = 0.34 THz的正弦波, 右侧端口采用CPML吸收边界截断^[29]. 该波导中不同截面上电磁波功率幅值的计算公式为^[28]

$P\left( z \right) = {P_0}{{\rm{e}}^{ - 2\beta z}}, $

其中: P₀为注入功率的幅值; β为衰减系数, 由(21)式给出

$\beta \left( {{\rm{T}}{{\rm{M}}_{01}}} \right) = \frac{R}{{\eta a}}\frac{1}{{\sqrt {1 - {{({{{f_{\rm{c}}}}/f})}^2}} }}$

其中, η为真空中波阻抗. 由此可以计算出β = 1.09. 表1为模拟所得波导中距离输入端口不同距离的截面上Poynting通量的幅值及与理论解的对比, 可见采用损耗算法得到的结果符合理论解的预期.

距离/cm	理论值/P0	模拟值/P0	相对误差/%
5	0.8964	0.8933	0.3
10	0.8035	0.7969	0.8
15	0.7203	0.7105	1.4
20	0.6457	0.6335	1.9

表1圆波导中模拟Poynting通量与理论解的对比
Table1.Comparison of simulated and analytic Poynting flux in a circular waveguide.

对于高功率微波器件, 微波源的频率能达到几个GHz, 而对于太赫兹器件, 电磁波的频率可以达到百GHz以上, 由(8)式可以看出表面电阻和电抗都随频率的增大而增大, 因此电磁场频率越高, 金属表面的切向电场也越强, 欧姆损耗也更明显. 当采用紫外光刻蚀(UV-LIGA)技术加工太赫兹器件慢波结构时, 加工精度为微米量级, 材料表面粗糙度约为0.03 μm^[10]. 对于300 GHz的电磁波, 波长仅为1 mm, 可计算出该频率电磁波在金属铜中的趋肤深度仅为0.1 μm, 接近器件加工的表面粗糙度, 粗糙度会使阻抗变得更大.
2

-->

4.1.相对论表面波振荡器的模拟

太赫兹表面波振荡器是一种圆周对称契轮科夫器件, 通过采用慢波结构将器件中电磁波的相速度降到接近电子的群速度并与电子发生束波互作用而产生太赫兹波, 具有结构紧凑、功率高、适合重复频率工作等优点^[6]. Wang等^[6]研制了相对论太赫兹表面波振荡器, 包含无箔二极管、环形阴极、慢波结构、输出结构和外加引导磁场. 除了图中的准直段的反射腔外, 其结构如图4所示, 采用矩形慢波结构, 慢波段内半径为3 mm, p = 0.32 mm, h = 0.1 mm, d = 0.18 mm, 周期数为30. 380 kV的高电压波从左端口注入, 当阴极表面电场达到发射阈值后, 电子会自洽的向外发射, 发射电流约为2.2 kA, 引导磁场幅值为5.25 T. 在无耗和有耗边界条件下, PIC模拟得到的器件输出功率分别为91 MW和41 MW, 工作频率为0.377 THz, 电磁波模式为TM₀₁模^[30].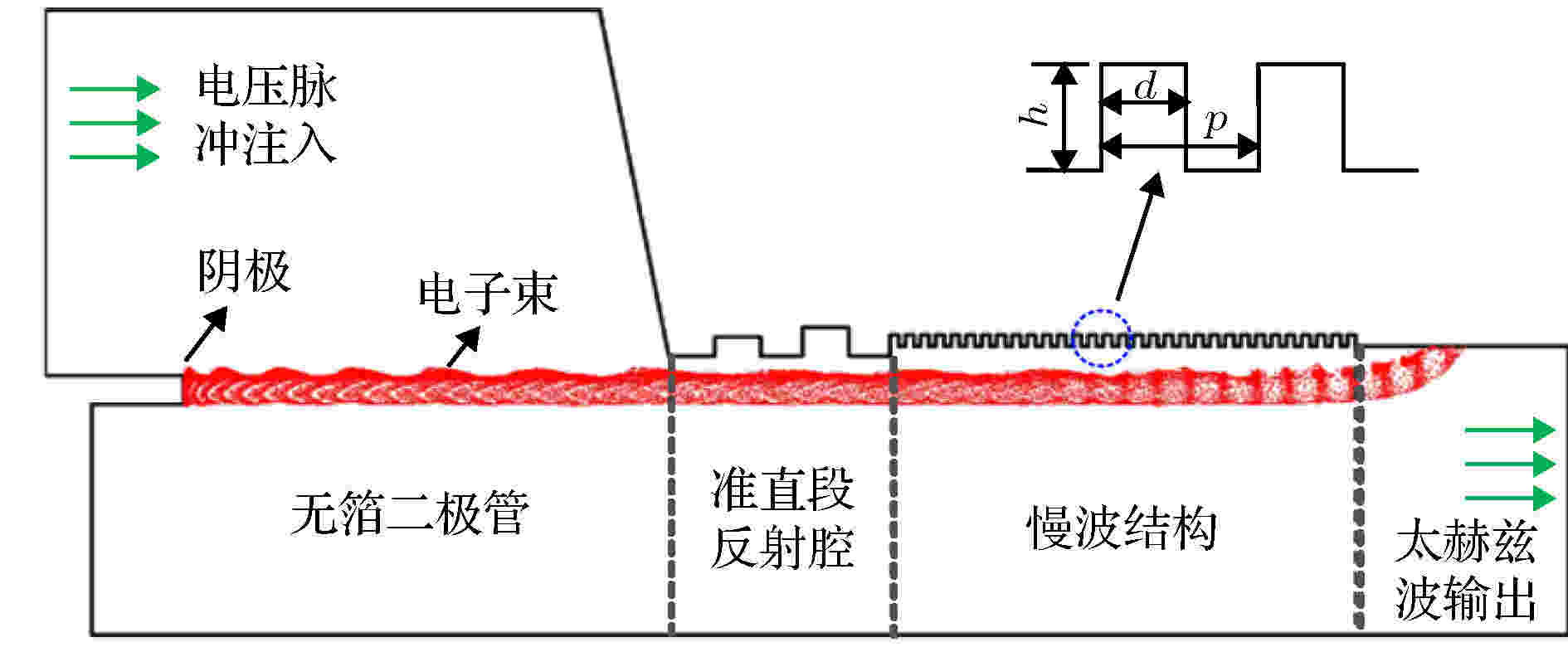
图 4 表面波振荡器示意图
Figure4. Schematic of a surface wave oscillator.

为了提高返波管高功率微波的产生效率, 在电子枪和慢波结构之间加入反射腔^[31-35], 如图4所示. 反射腔可以对电子束进行预调制, 并对器件中的返波进行反射, 增强慢波结构中电磁波的强度, 从而提高波束互作用效率. 本文采用加入损耗边界的UNIPIC-3D软件模拟了如图4所示的带反射腔的太赫兹表面波振荡器的工作过程. 波导输出端采用CPML吸收边界进行截断^[29]. 模拟中对器件壁面分别采用理想导体边界和非理想导体边界, 有耗边界采用铜的电导率σ = 5.8 × 10⁷ S/m.
图5是模拟得到SWO稳定起振后某时刻轴向电场云图, 可以看出器件中的波沿着慢波结构表面传输, 电场最强的地方集中在慢波结构附近, 这也是表面波振荡器工作的特点, 因而这类器件的欧姆损耗会更加明显. 从电场空间分布来看, 经过约两个慢波结构后电场的相位发生一次变化, 即器件工作在π模附近^[30]. 模拟得到的粒子空间分布如图4所示, 可以看出由阴极发射的电子注在管内同谐波发生互作用, 受到良好的密度调制, 群聚效果明显.
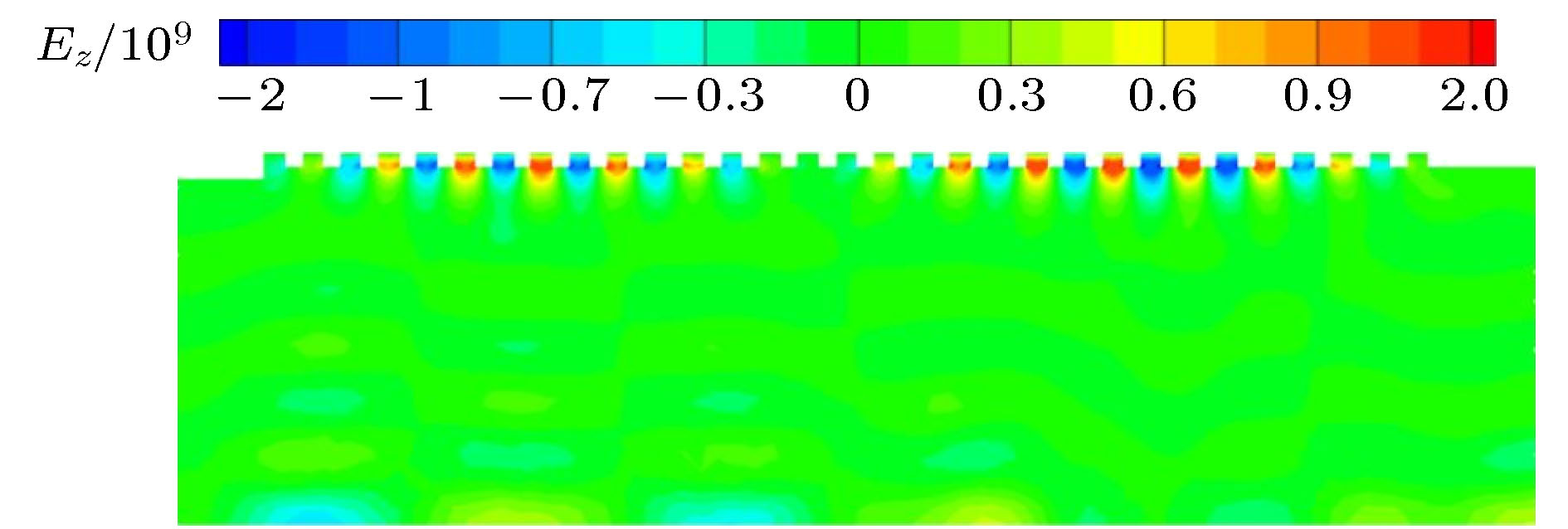图 5 SWO内z方向电场分布云图
Figure5. Contour of the Ez inside the SWO.

图6和图7分别为采用理想导体边界和有耗边界时靠近慢波结构的观测点处径向电场的时间变化曲线, 对其进行傅里叶变换可以看出器件的工作频率为0.337 THz, 电场的频谱纯度很高, 没有其他高次模出现, 表明在加入反射腔后器件的工作频率没有发生变化. 另外从图7可以看出加入表面损耗后, 电场时间变化曲线的包络曲线波动变大, 可能是因为考虑表面损耗后器件内能量分布发生了变化, 影响了器件的起振过程和后续的稳定输出.
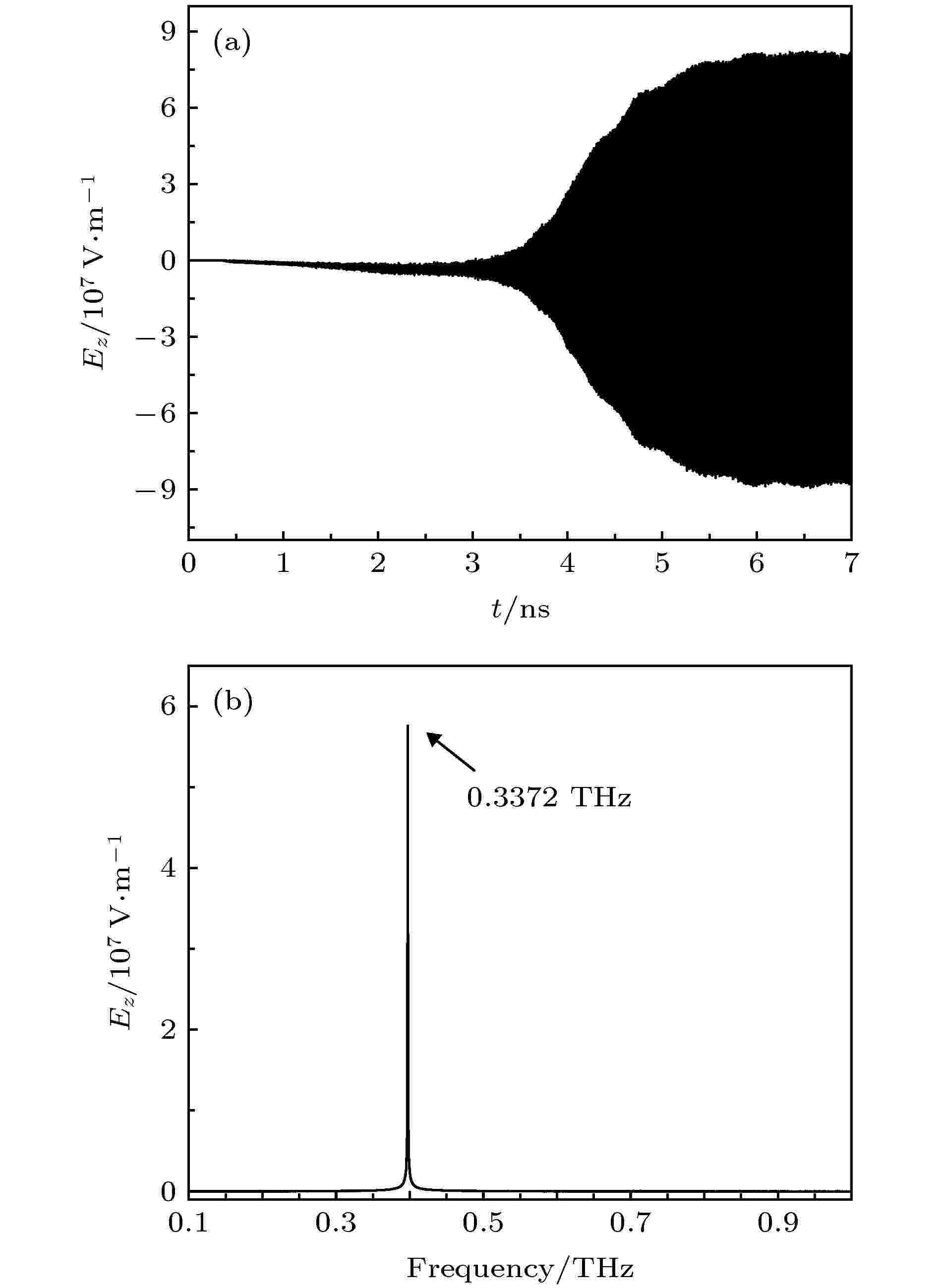图 6 理想导体SWO中　(a)电场时间波形; 电场频谱(b)
Figure6. Time history of the electric field (a) inside the SWO with PEC and its spectrum (b).

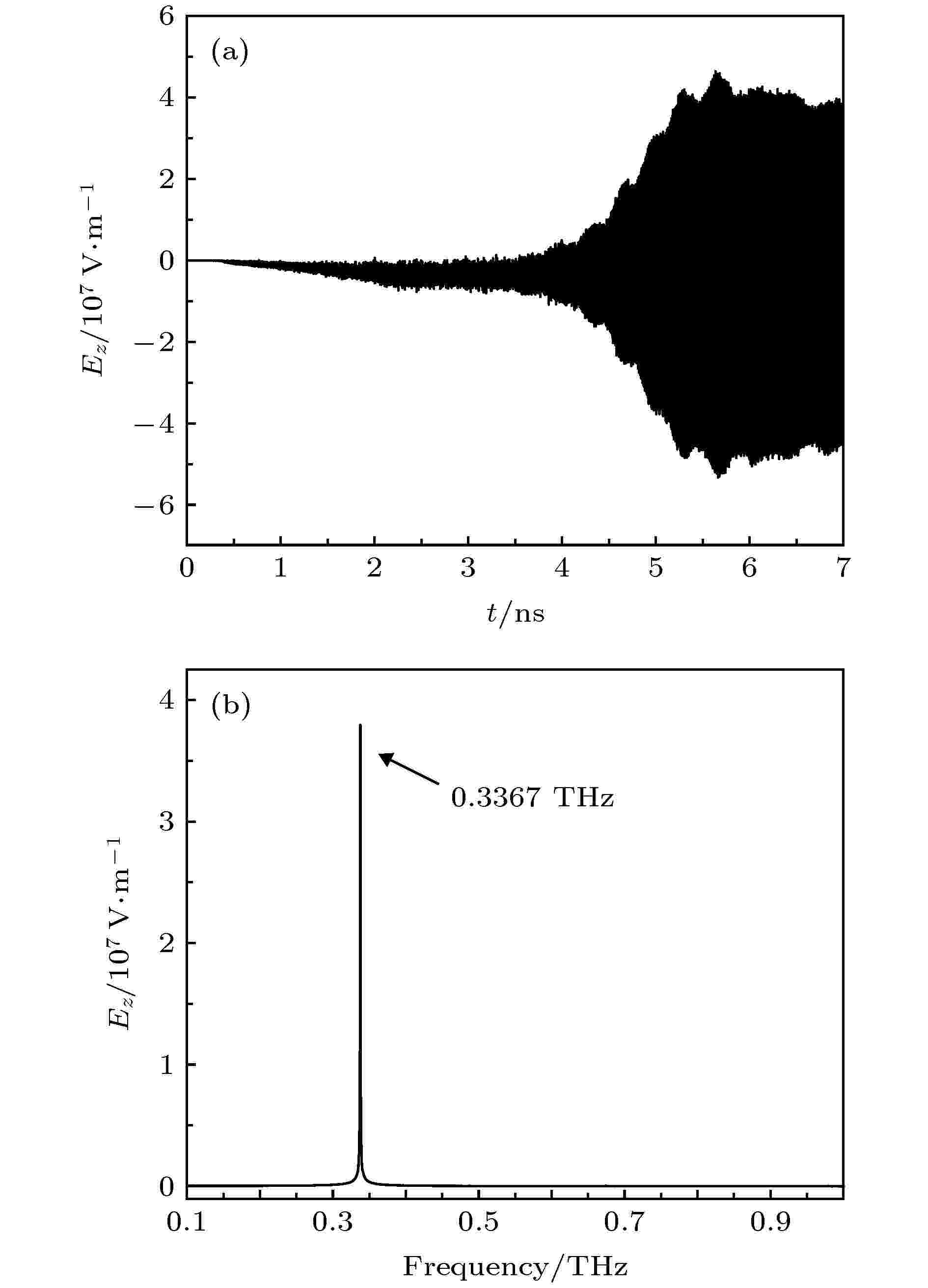图 7 有损耗铜材料SWO中　(a)电场时间波形; (b)电场频谱
Figure7. Time history of the electric field (a) inside the SWO with lossy copper and its spectrum (b).

图8为分别采用两种材料所得输出功率, 对比可以看出采用真实的金属材料边界后, SWO的输出功率下降非常明显, 这也解释了之前模拟得到的功率远大于实验测量功率的现象^[6]. 另外可以看出采用有耗边界以后, 该器件的起振时间发生了延迟. 为了加快器件的起振, 可以采用外加太赫兹源牵引器件快速起振^[36].
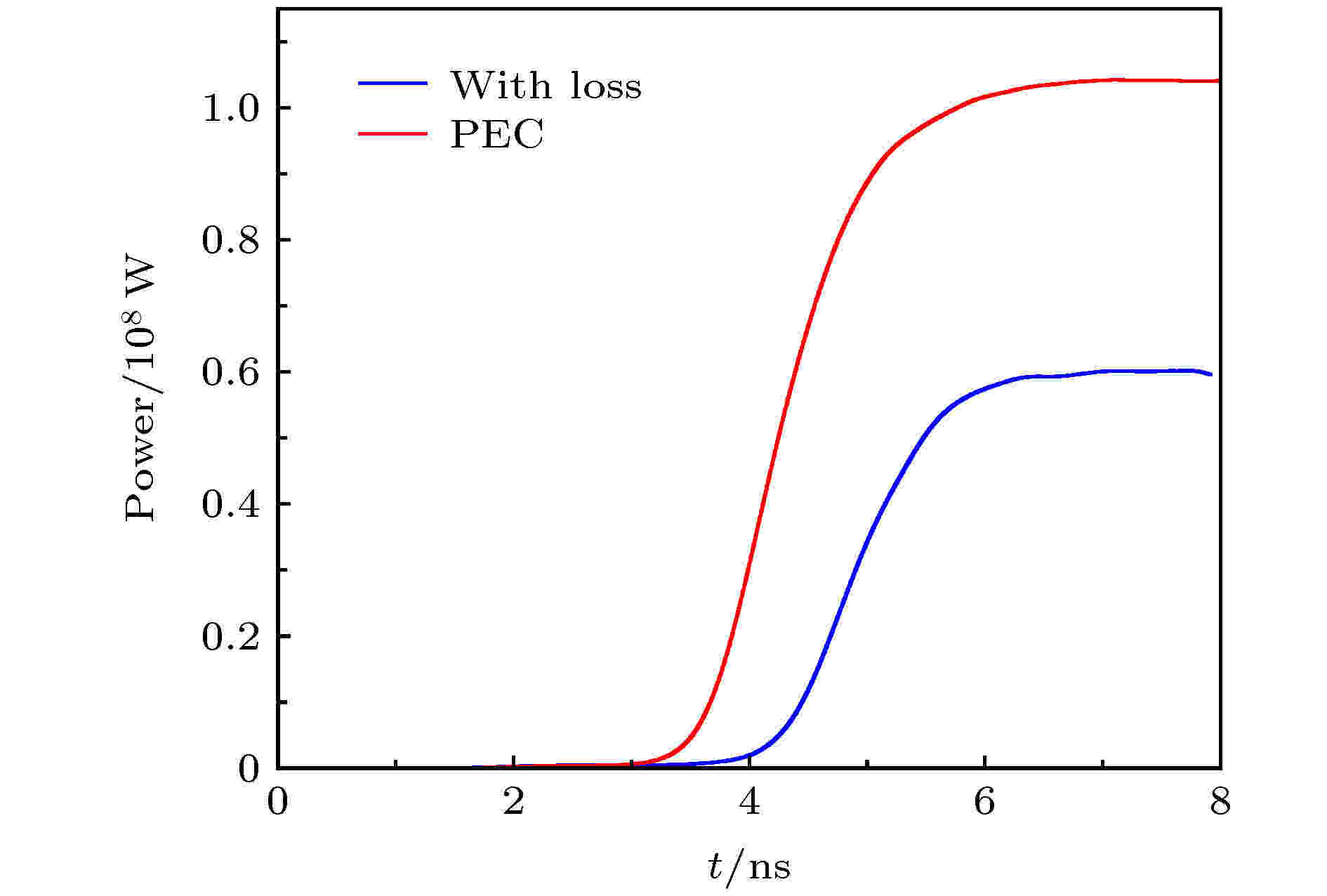图 8 SWO输出功率
Figure8. Output power from the SWO.

对比无反射腔的表面波振荡器^[6], 带反射腔的表面波振荡器的工作频率没有变化, 但输出功率有非常明显的增加, 在PEC情形下, 输出功率由91 MW增加到105 MW, 在考虑损耗边界条件下, 输出功率由41 MW增加到约60 MW.
2 -->

4.2.带状电子注平板返波管模拟

Xi等^[10]研制了低电压带状电子注平板返波管, 如图9所示, 主要由电子枪、慢波结构、收集极和外围波导及输出波导组成. 不同于上面的大功率SWO, 该平板返波管采用5 kV的低电压热阴极电子枪, 发射电流为200 mA. 采用带状电子注能减弱空间电荷力导致的束流扩散, 而平板格栅慢波结构则易于加工^[10]. 互作用段采用平板格栅慢波结构, 具体的几何参数如图中参数所示. 阴极发射面的尺寸为2.5 mm × 0.14 mm, 沿z方向加载了强度为0.9 T的引导磁场. 电子注沿+z方向传播并与慢波结构中的电磁波发生互作用. 产生的太赫兹波沿–z方向传播, 最终沿左下方输出波导输出.
图 9 平板BWO结构示意图(外围波导尺寸: 宽a = 7.2 mm, 高b = 1.8 mm; 格栅尺寸: 周期l = 0.1 mm, 宽w = 2.5 mm, 高h = 0.16 mm, 间距d = 0.058 mm; 格栅周期数140)
Figure9. BWO with planar structure.(a = 7.2 mm, b = 1.8 mm; l = 0.1 mm, w = 2.5 mm, h = 0.16 mm, d = 0.058 mm)

图10给出了起振后宏粒子z方向速度随纵向坐标的分布, 可以看出电子的速度以0.136倍光速为基准上下波动, 随着电子向前运动, 电子逐渐受到速度调制和密度调制而出现群聚, 电子的能量也逐渐降低, 表征着电子能量逐渐向太赫兹波能量发生转化.
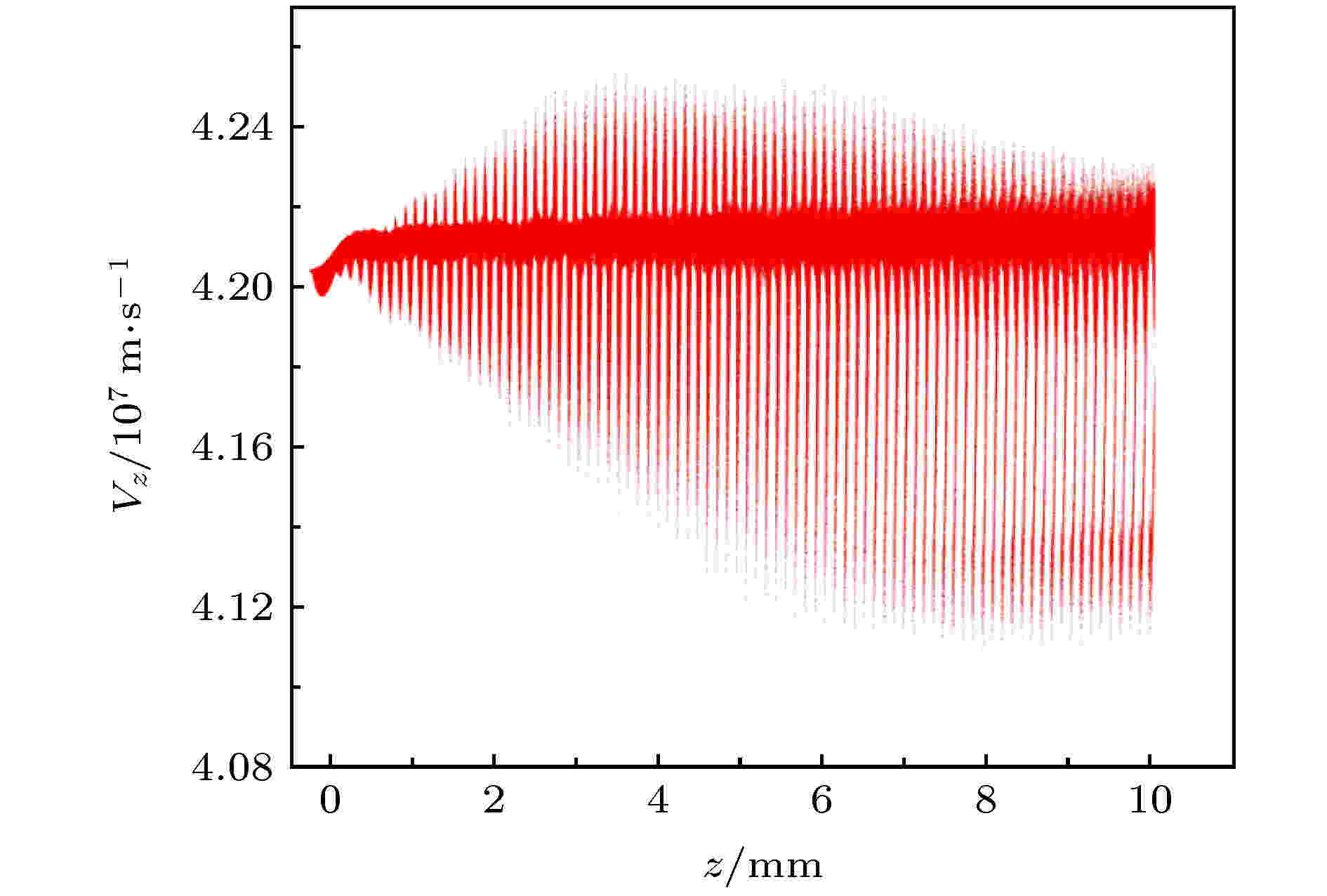图 10 BWO中电子相空间图
Figure10. Phase space of electrons in the BWO

图11(a)为采用理想导体边界时输出波导内诊断到的z方向电场时间波形. 图11(b)为考虑表面损耗时模拟得到相同位置处的结果, 选择铜材料. 可以看出, 输出电磁波的频率为0.34 THz, 没有其他模式. 采用理想导体边界所得监测点处电场的峰值约为采用有耗边界时的1.6倍, 欧姆损耗对器件中电场的幅值影响非常大.
图 11 BWO中电场波形　(a)无损耗; (b)有损耗
Figure11. Time history of electric field in the BWO with PEC (a) and lossy copper (b).

图12为输出波导段监测到的输出功率时间曲线, 采用理想导体边界时模拟到的输出功率约为1.8 W, 而采用有耗金属边界得到的输出功率约为0.65 W, 两者比值正好近似于前面电场峰值比值的平方. 另外, 对该器件实验测量到的输出功率约为0.18 W^[10], 可见采用损耗边界模拟到的结果更接近实测值, 至于模拟解与实测值出现的差距可能是因为太赫兹器件结构过于微细, 阴极电子枪的品质、器件加工及装配误差等都会对器件的工作状态带来很大影响. 另外, 考虑到这类器件加工时的粗糙度, 实际器件中的表面损耗也会更大. 从功率曲线还可以看出采用有耗边界后该BWO器件的起振时间也发生了延迟.
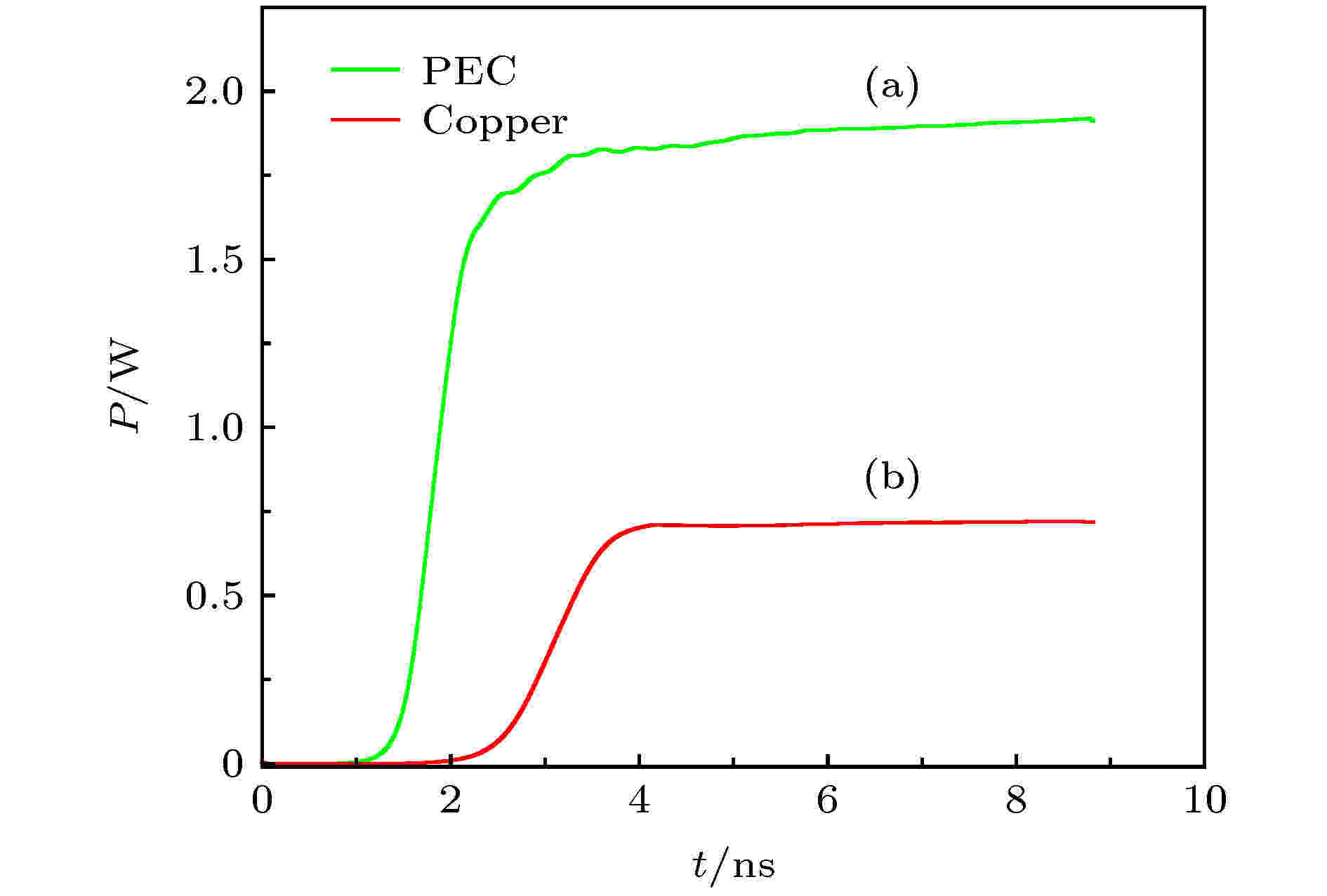图 12 BWO输出功率　(a) PEC边界的结果; (b)有耗金属边界的结果
Figure12. Output power from the BWO: (a) PEC ; (b) lossy copper.

本文介绍了UNIPIC-3D中共形算法的实现原理, 并推导了基于共形边界的频率色散表面阻抗边界算法, 采用矩形谐振腔和圆柱波导中电磁波的衰减, 验证了这种边界在模拟电磁波损耗方面的正确性. 然后采用UNIPIC-3D模拟了相对论表面波振荡器和低电压平板格栅返波管这两种太赫兹器件. 模拟结果表明, 对于表面波振荡器和平板BWO这种电磁场集中在金属慢波结构附近的太赫兹真空电子器件, 材料表面的欧姆损耗对器件的运行会带来极大影响, 采用铜材料时, 欧姆损耗会使输出功率下降一半以上, 起振时间发生延迟. 对于太赫兹波段电磁波, 它在金属中的趋肤深度变得接近器件表面加工粗糙度, 下一步将对表面粗糙度与阻抗的关系进行量化, 实现与粗糙度相关的表面阻抗算法, 为真空电子器件的模拟提供更真实的模拟技术.