删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

考虑界面接触热阻的一维复合结构的热整流机理

本站小编 Free考研考试/2021-12-29
摘要:建立了考虑变截面、变热导率及界面接触热阻效应的组合热整流结构的温度场及热整流系数的理论模型和有限元解. 数值算例证明了本文模型及算法的可靠性, 进而通过参数影响研究确定了若干几何及材料参数对结构热整流系数的影响规律, 揭示界面接触热阻对热整流效果的影响机理. 研究结果表明长度比、截面半径变化率、热导率、边界条件温差和界面接触热阻等因素必须通过优化设计才能得到最大的热整流系数, 同时界面接触热阻的引入也为调控热整流系数提供了一条新的途径.
关键词: 热整流/
组合结构/
接触热阻

English Abstract


全文HTML

--> --> -->
1.引　言
热整流是指在同样的温差下当温度梯度的方向不同时, 结构中的热流量或等效导热系数不一致的现象. 类似于电子二极管, 如果器件的热整流现象非常明显, 即为具有单向导热功能的热二极管. 基于热整流机理的热二极管[1]、热三极管[2]及热逻辑门[3]等器件为热计算机的实现提供了可能, 同时热整流机理及器件的相关研究也在节能、热防护、热斗篷、热幻像上有潜在的应用价值[4], 因此成为国内外研究的热点之一.
实现热整流的机理主要有非对称结构和非线性材料属性两类, 热整流效应的研究可以从微观和宏观两方面入手进行研究. 在微观上, 热整流一般基于微纳米材料器件, 此时需要考虑传热的微纳米尺度效应. 单小东等[5]采用Monte Carlo方法数值模拟了纳米梯形板导热的热整流现象. 张茂平等[6]和温家乐等[7]分别研究了非对称双链分子结构和异质结碳纳米管的热整流效率. Nobakht等[8]利用在结构中布置周期性分布的空穴来调控其等效热导率从而实现热整流的目的. Machrafi等[9]研究了不同纳米多孔硅组合结构的热整流效率. 鞠生宏等[10]采用非平衡态分子动力学方法研究带孔硅纳米薄膜的热整流效应. 李威等[11,12]基于非平衡分子动力学方法和量子修正研究了碳纳米管中的点缺陷以及Y形分子结对热导率与热整流效率的影响. Meng等[13]利用石蜡和六水氯化钙作为固液相变热二极管的材料, 对比分析长度比对整流效应的影响, 实验验证了理论的可靠性. Wang等[14]实验研究了石墨烯中热整流现象, 发现材料热导率随温度和空间的依赖性以及非对称声子散射这两种不同的热整流机理. Aiyiti等[15]在较低的温差下, 实验验证了Y形碳纳米管中的热整流现象, 实现了不同温差下的整流效果. 在宏观上, 热整流一般基于宏观块体材料结构, 可基于傅里叶传热定律来分析. Peyrard[16]最早提出一种利用两种材料热导率随温度变化的不同产生热整流的机制, 一种材料的热导率随温度升高而降低, 另一种材料的热导率则随温度升高而增加, 这样, 在热流方向不同时就会产生不同的等效热阻, 从而达到热整流的目的. Kobayashi等[17]则用实验验证了此种设想的可行性. Shih等[18]进一步研究了线性和非线性的温度相关热导率对热整流效果的影响. Sadat和Dez[19]给出了稳态条件下杆状、圆柱状和球形热整流器整流效果的理论解. Go和Sen[20]进一步给出了在宏观材料中实现热整流时其热导率应该满足的条件. Majdi等[21]也给出了优化热整流效果的设计方法. Sawaki等[22]和Tian等[23]分别采用变截面结构实现了热整流. Dames[24]给出了低温条件下(100—200 K)进行热整流器件设计的一般原则, 通过将热导率与温度之间的关系用幂函数来近似, 给出了整流系数的解析表达式. Yang等[25]研究了最优整流效率与两种材料温度依赖热导率之间的关系. 对于组合式热整流器, 界面的接触热阻也是影响热整流效果的一个重要因素, Sayer[26]据此提出一种利用界面接触热阻的变化来进行热流调控的方法. Chumak和Martynyak[27]利用周期性分布的粗糙表面来模拟实际的接触面, 利用接触传热的方向性研究了界面接触热阻对热整流的影响. 朱玉鑫[28]和汤宇轩等[29]也分别研究变厚度比组合材料结构的热整流特性, 并分析了界面接触热阻对整流效果的影响, 发现在界面接触热阻较小时可有效提高热整流的效果.
可以看出, 虽然国内外针对宏观热整流器件开展了的大量研究, 但是往往仅考虑一种因素的影响, 比如变截面或者温度依赖热导率, 限制了研究结果在实际热整流器件设计中的参考价值. Go和Sen[20]的研究已经表明, 如果系统的等效热导率可以写成分离变量的函数形式, 那么对于单一杆件将不会有热整流效果. 因此, 本文针对考虑温度依赖热导率和空间依赖横截面积的热整流器件, 同时考虑非完好接触引起的界面接触热阻的影响, 开展全面的理论研究和数值仿真, 定量研究各种因素对热整流系数的影响规律, 揭示其影响机理, 为实际热整流器件的设计提供重要的理论参考.
2.理论分析
2
2.1.问题描述
-->

2.1.问题描述

经典热整流器件由两种热导率温度依赖特性相反的材料组成. 热量正向流动时, 左边材料处于高温状态, 右边材料处于低温状态, 结构的等效热导率较高, 从而容易产生热量流动. 反之, 热量逆向流动时, 左边材料处于低温状态, 右边材料处于高温状态, 结构的等效热导率比较低, 热量流动困难, 从而实现热整流效应[30]. 本文模型以此类器件为研究对象, 如图1所示. 该热整流器由两段一维变截面结构组成, 其长度分别为L1和L2, 横截面积分别为A1(x1)和A2(x2), 材料的热导率分别为k1(T)和k2(T), 两杆接触界面为非完好接触, 存在接触热阻Rc, 器件的左右两端分别给定恒温边界条件.
图 1 变截面变热导率一维组合热整流器模型　(a) 热量自左向右正向流动; (b) 热量自右向左反向流动
Figure1. Schematic of the one-dimensional composite thermal rectifier model with variable cross section area and thermal conductivity: (a) Forward heat flows from left to right; (b) reverse heat flows from right to left.

假设结构温度场处于稳定状态, 此时无内热源的热量平衡方程可以写为:
$\begin{split}& {\frac{{\rm{d}}}{{{\rm{d}}{x_1}}}\left( {{k_1}\left( T \right){A_1}\left( {{x_1}} \right)\frac{{{\rm{d}}{T_1}}}{{{\rm{d}}{x_1}}}} \right) = 0,\;\; {0 \leqslant {x_1} \leqslant {L_1}} ,}\\& {\frac{{\rm{d}}}{{{\rm{d}}{x_2}}}\left( {{k_2}\left( T \right){A_2}\left( {{x_2}} \right)\frac{{{\rm{d}}{T_2}}}{{{\rm{d}}{x_2}}}} \right) = 0,\;\; {0 \leqslant {x_2} \leqslant {L_2}},}\end{split}$
其中, ${T_1}$和${T_2}$分别是两杆中的温度场.
在非完好接触界面处存在热量连续性条件:
${\left. { - {k_1}{A_1}\frac{{{\rm{d}} {T_1}}}{{{\rm{d}} {x_1}}} } \right|_{{x_1} = {L_1}}} = {\left. { - {k_2}{A_2}\frac{{{\rm{d}} {T_2}}}{{{\rm{d}} {x_2}}}} \right|_{{x_2} = 0}}. $
同时界面处根据接触热阻的定义有
$\frac{{{T_1}\left( {{L_1}} \right) - {T_2}\left( 0 \right)}}{{{R_{\rm{c}}}}} = - {k_1}{\left. {\frac{{{\rm{d}} {T_1}}}{{{\rm{d}} {x_1}}}} \right|_{{x_1} = {L_1}}} . $
热整流系数$\gamma $定义为
$\gamma = \max \left( {\left| {\frac{{{Q_{\rm{f}}}}}{{{Q_{\rm{r}}}}}} \right|,{\rm{ }}\left| {\frac{{{Q_{\rm{r}}}}}{{{Q_{\rm{f}}}}}} \right|} \right), $
其中, ${Q_{\rm{f}}}$是热量自左向右流动时器件中的热量, 其相应的边界条件为
${T_1}\left( 0 \right) = {T_{\rm{H}}},~~{\rm{ }}{T_2}\left( {{L_2}} \right) = {T_{\rm{C}}}; $
${Q_{\rm{r}}}$是热量自右向左流动时器件中的热量, 其相应的边界条件为
${T_1}\left( 0 \right) = {T_{\rm{C}}},~~{\rm{ }}{T_2}\left( {{L_2}} \right) = {T_{\rm{H}}}, $
其中${T_{\rm{H}}}$和${T_{\rm{C}}}$分别是高温和低温边界条件.
可以看出, 热整流系数$\gamma = 1$代表器件无热整流效果, 该数值越大代表热整流效果越明显.
2
2.2.有限元解
-->

2.2.有限元解

由于界面接触热阻的存在, 同时材料的热导率和截面积分别随温度和坐标变化, 因此一般情况下结构的温度场很难通过非线性方程组精确求得, 需要借助数值手段获取近似解. 这里采用有限元方法来求解[31], 将整体结构离散为若干等长度的热传导杆单元, 假设每个单元的热导率和横截面积都是恒定的, 如图2所示, 界面左右两侧的未知温度分别为${T_{\rm n}}$和${T_{\rm p}}$.
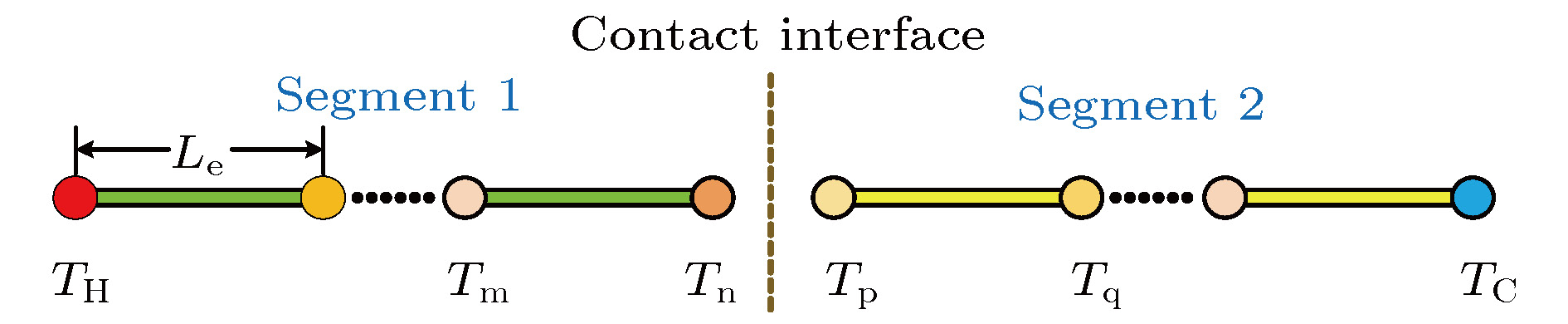图 2 热整流器的有限元模型
Figure2. Finite element model of the thermal rectifier.

采用线性温度场杆单元, 其单元热传导矩阵为
${{k}_{\rm{e}}} = \frac{{k\left( {\overline {{T_{\rm{e}}}} } \right)}}{{{L_{\rm{e}}}}}\left[ {\begin{array}{*{20}{c}}1&{ - 1}\\{ - 1}&1\end{array}} \right],$
其中, ${L_{\rm{e}}}$是单元长度, $k\left( {\overline {{T_{\rm{e}}}} } \right)$是单元平均温度$\overline {{T_{\rm{e}}}} $对应的热导率. 由于无内热源, 也没有对流或辐射等热边界条件, 因此等效载荷列向量为0.
对单元矩阵进行组装, 即可得到整体的矩阵方程为
${{KT}} = {{F}}, $
其中, K, T和F分别为结构总体热传导矩阵、节点温度列向量和节点等效载荷列向量.
两端恒温边界条件可以通过对角元素乘大数法引入, 界面处的温度跳变条件为
$\frac{{{T_{\rm n}} - {T_{\rm{p}} }}}{{{R_{\rm{c}}}}} = {k_1}\left( {\frac{{{T_{\rm{m}} } + {T_{\rm{n}} }}}{2}} \right)\frac{{{T_{\rm{m}} } - {T_{\rm{n}} }}}{{{L_{{\rm{e1}}}}}}. $
界面处的热流连续条件为
${k_1}\left( {\frac{{{T_{\rm{m}} } + {T_{\rm{n}} }}}{2}} \right)\frac{{{T_{\rm{m}} } - {T_{\rm{n}} }}}{{{L_{\rm{e}}}}} = {k_2}\left( {\frac{{{T_{\rm{p}} } + {T_{\rm{q}} }}}{2}} \right)\frac{{{T_{\rm{p}} } - {T_{\rm{q}} }}}{{{L_{\rm{e}}}}}. $
联立(9)式和(10)式, 可得:
$\begin{split}& {{T_{\rm{n}}} = \frac{{b{T_{\rm{q}}} + \left( {1 + ab} \right){T_{\rm{m}}}}}{{ab + b + 1}},}\\& {{T_p} = \frac{{{T_{\rm{m}}} + \left( {1 + a} \right)b{T_{\rm{q}}}}}{{ab + b + 1}},}\end{split}$
其中, $a = \dfrac{{{k_1}\left( {\dfrac{{{T_{\rm{m}} } + {T_{\rm{n}} }}}{2}} \right){R_{\rm{c}}}}}{{{L_{\rm{e}}}}}, \;\; b = \dfrac{{{k_2}\left( {\dfrac{{{T_{\rm{p}} } + {T_{\rm{q}} }}}{2}} \right)}}{{{k_1}\left( {\dfrac{{{T_{\rm{m}} } + {T_{\rm{n}} }}}{2}} \right)}}$.
界面处的温度跳变条件和热流连续条件基于(11)式通过给定左右两侧节点温度的方式引入, 通过迭代得到收敛解. 整体的求解流程为:
1) 初始化接触热阻Rc;
2) 基于(7)式组装形成结构总体热传导矩阵K;
3) 引入恒定边界条件基于(8)式求解节点温度列向量T;
4) 根据求得的节点温度和(11)式更新界面温度${T_n}$和${T_p}$, 如果满足收敛准则, 进行步骤5), 如果不收敛, 回到步骤2), 进行下一次迭代计算直到计算结果满足收敛准则;
5) 依据收敛的结构温度场结果计算结构的热流及热整流系数.
该有限元方法适用于任意截面形状和任意温度依赖的热导率, 同时可以考虑界面接触热阻对热整流系数的影响, 从而为实际复杂热整流器件的设计和分析表征提供了计算手段.
3.算例与讨论
2
3.1.数值算例
-->

3.1.数值算例

对于材料热导率和横截面积简单变化的情形, 结构的温度场可以给出理论解(参见附录), 本节给出基于本文有限元解和理论解及实验值[22]对模型温度场及热流量的比较, 以验证有限元解的可靠性. 理论解及各个参数的定义可以参见附录, 实验中采用的参数取值如下: L1 = L2 = 9.5 mm, 横截面积常数分别为 A01 = 3.06 mm2, AM1 = 2.08, A02 = 1.99 mm2, AM2 = 1.66, 所用材料为LaCoO3和La0.7Sr0.3CoO3, 其热导率常数k01 = 1.02 W · m–1 · K–1, k02 = 0.455 W · m–1 · K–1, 参考温度T0 = 60 K, 根据附录的理论解和2.2节的有限元解可以分别得到结构温度场及热整流系数的理论结果和数值结果, 在给定高温和低温边界条件分别为TH = 100 K和TC = 40 K时热整流器温度场的理论解、有限元解与实验结果的对比如图3所示. 低温端TC = 40 K不变, 高温端的温度边界条件分别取70, 80 , 90 和100 K时, 不同接触热阻条件下结构热量和热整流系数的理论解、有限元解与实验结果[22]的对比如图4所示.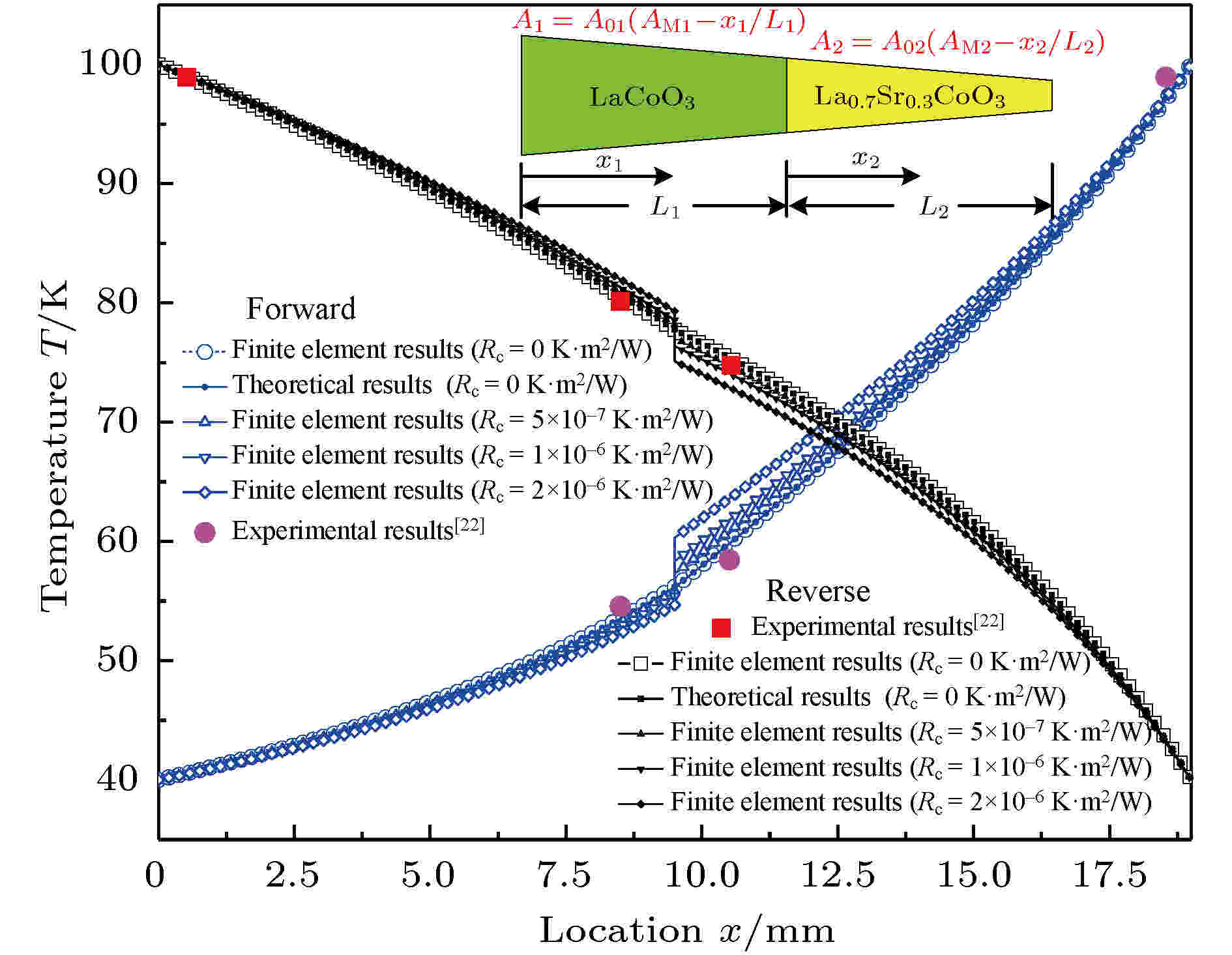
图 3 热整流器的温度场分布对比 (Reverse与Forward分别代表LaCoO3和La0.7Sr0.3CoO3材料位于高温端的情况)
Figure3. Comparisons of temperature distribution of the thermal rectifier (Reverse and Forward denote the case of that LaCoO3 and La0.7Sr0.3CoO3 materials locate in high-temperature side respectively).

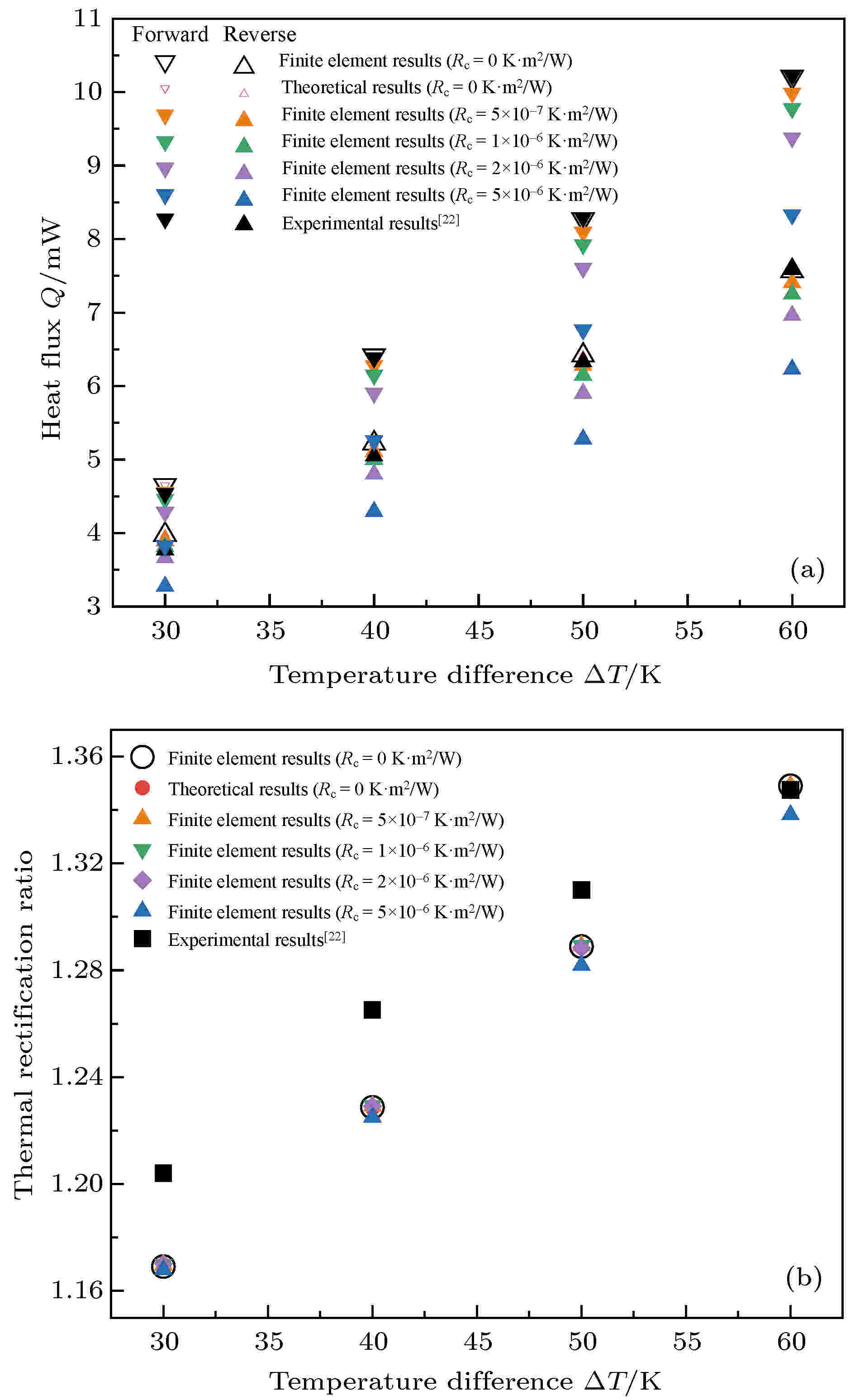图 4 不同温差下热整流器的响应　(a) 热量; (b) 热整流系数
Figure4. Response of the thermal rectifier with different temperature differences: (a) Heat flux; (b) thermal rectification ratio.

从图3和图4可以看出, 不考虑接触热阻时本文给出的理论解和有限元解完全吻合, 同时与文献中的实验结果[22]也吻合得很好. 考虑接触热阻的影响时, 热阻越大结构温度场、热流和热整流系数的计算结果与实验结果误差越大. 这表明, 实际结构的界面接触热阻确实很小, 不考虑界面热阻是合理的. 热整流系数的计算值与实验值有一定的误差, 随着结构两端温差的增加, 计算结果与实验结果的误差逐渐减小. 实验中通过杆件端部4个热电偶获得热整流器的温度场分布, 参考文献[22]中每个杆件的长度为9.5 mm, 但由于高低温热源位置处热电偶与端部位置还有一定距离, 实际高低温热源与热电偶测点位置距离略小于9.5 mm. 本算例表明本文提出的有限元仿真方法在分析变截面变热导率热整流模型时是可行的.
2
3.2.参数影响研究
-->

3.2.参数影响研究

本节利用常见的304不锈钢和纯铁分别作为组合结构的备选材料, 研究各种几何参数及温度边界条件对热整流系数的影响. 304不锈钢的热导率随着温度增加而增加, 而纯铁的热导率随着温度增加而降低, 这样的选择更加有利于实现较大的热整流系数. 假设杆1为不锈钢, 杆2为纯铁, 则304不锈钢和纯铁的热导率分别可近似表示为[32]:
$\begin{split}& {k_1}\left( T \right) = 11.01154 + 0.01478T,\\& \qquad \left( {300\;{\rm{ K}} \leqslant T \leqslant 1000\;{\rm{ K}}} \right),\\& {k_2}\left( T \right) = 117.2 - 0.15338T + 6.566 \times {10^{ - 5}}{T^2},\\& \qquad \left( {300\;{\rm{ K}} \leqslant T \leqslant 1000\;{\rm{ K}}} \right),\end{split}$
考虑双段的圆锥台组合杆件热整流器模型, 两杆件横截面积随坐标二次变化, 且在接触界面处有相同的横截面积${\text{π}}r_{\rm{c}}^2$, 假设杆件1的左端面横截面积${\text{π}}r_{\rm{1}}^2$, 杆件2的右端面横截面积${\text{π}}r_{\rm{2}}^2$, 引入横截面半径变化率${\beta _{{x_1}}}$, ${\beta _{{x_2}}}$, 接触界面半径与热整流器的左右端面半径关系为:
$\begin{split} {\beta _{{x_1}}} = \frac{{{r_{\rm{c}}} - {r_{\rm{1}}}}}{{{L_1}}},~~~ {\beta _{{x_2}}} = \frac{{{r_{\rm{2}}} - {r_{\rm{c}}}}}{{{L_2}}}.\end{split}$
则热整流器横截面积随两杆件局部坐标${x_1}$, ${x_2}$变化为:
$\begin{split}& {A_1}\left( {{x_1}} \right) = {\text{π}}{\left( {{r_{\rm{c}}} - {\beta _{{x_1}}}{L_1} + {\beta _{{x_1}}}{x_1}} \right)^{\rm{2}}},\\& {A_2}\left( {{x_2}} \right) ={\text{π}}{\left( {{r_{\rm{c}}} + {\beta _{{x_2}}}{x_2}} \right)^{\rm{2}}}.\end{split}$
模型示意图及与横截面面积随截面半径变化率变化趋势的关系如图5所示.
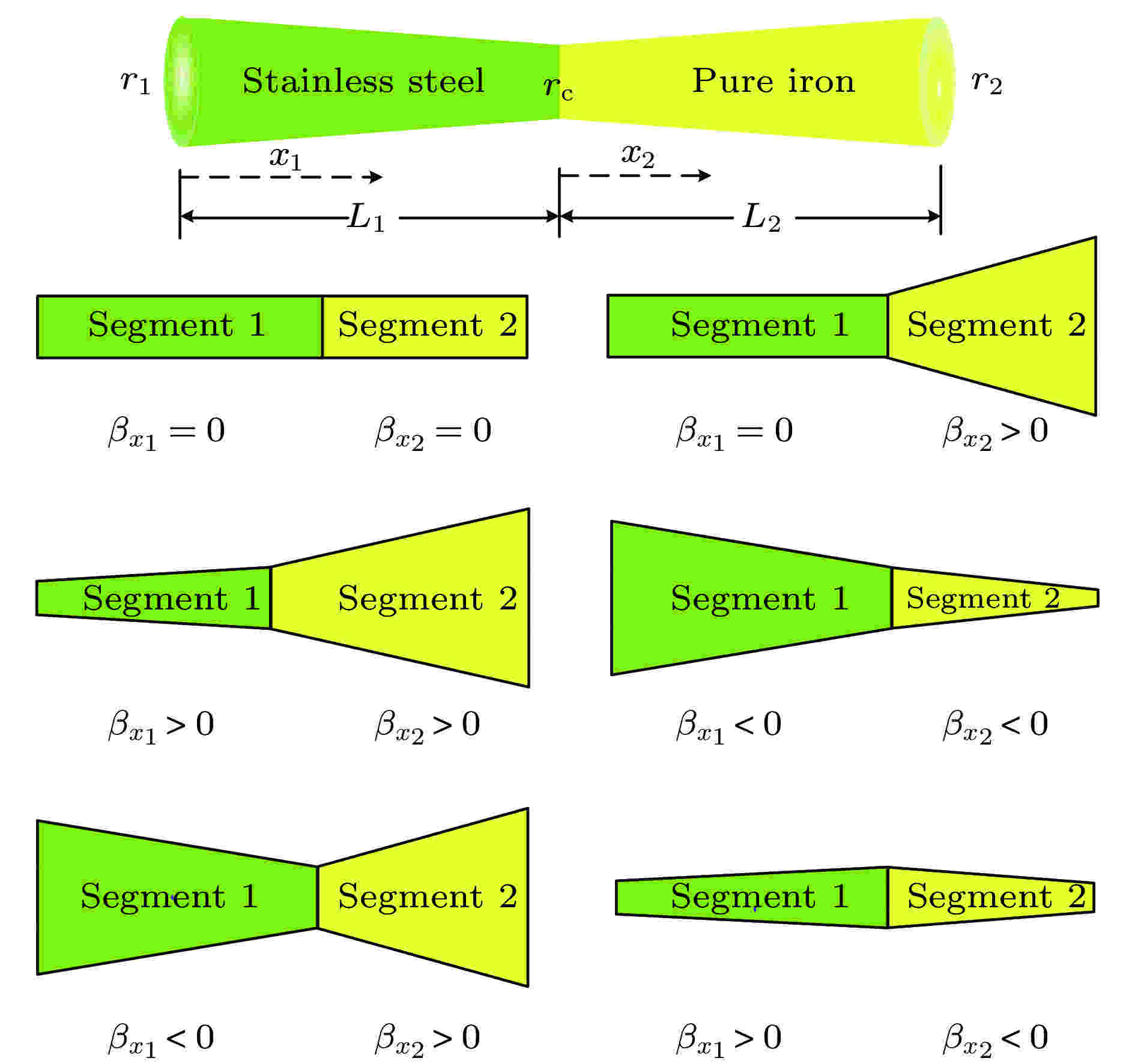图 5 横截面面积变化趋势与截面半径变化率的关系
Figure5. Relationship between cross-section area and cross-section radius change rate.

在本部分算例中, 给定组合模型的整体长度L = 300 mm, 界面半径${r_{\rm{c}}} = 10\;{\rm{ mm}}$, 由于模型横截面的等效半径不能为负, 同时考虑到一维稳态传热的基本假设, 截面半径变化率${\beta _{{x_1}}}$和${\beta _{{x_2}}}$的取值区间为$\left[ { - 0.03, {\rm{ }}0.03} \right]$. 这里, 截面半径变化率取为${\beta _{{x_1}}} = - 0.03$, ${\beta _{{x_2}}} = {\rm{}}0.03$. 算例1 (图6(a)): 两杆长度${L_1} = {L_2} = 150\;{\rm{ mm}}$, 长度比为0.5; 算例2 (图6(b)): 两杆长度${L_1} = 60\;{\rm{mm, }}\;{L_2} = 240\;{\rm{mm}}$, 长度比为0.2, 界面处的接触热阻设为${R_{\rm{c}}} = 1 \times {10^{ - 3}}\;{\rm{ K}} \cdot {{\rm{m}}^2} \cdot {{\rm{W}}^{ - 1}}$. 图6给出了结构左右两侧分别给定高温低温和低温高温边界条件时结构的温度场.
图 6 不同长度比热整流器的温度场　(a) 长度比0.5; (b) 长度比0.2
Figure6. Temperature distribution of the thermal rectifier with different length ratios: (a) Length ratio is 0.5; (b) length ratio is 0.2.

从图6可以看出, 存在界面接触热阻的情况下, 界面处出现了温度跳变, 由于两种不同的边界条件下通过结构的热量并不相同, 因此界面处的温度跳变量也不同. 算例1热量自左向右传递时轴向热量${Q_{\rm{f}}} = 16.176\;{\rm{ W}}$, 而自右向左传递时轴向热量为${Q_{\rm{r}}} = 13.593\;{\rm{ W}}$, 由(4)式可知该热整流器的整流系数为$\gamma = 1.190$. 算例2热量自左向右传递时轴向热量${Q_{\rm{f}}} = {\rm{22}}{\rm{.631\;W}}$, 而自右向左传递时轴向热量为${Q_{\rm{r}}} = {\rm{18}}{\rm{.067\;W}}$, 热整流器的整流系数为$\gamma = 1.253$.
为了进一步考虑结构各种几何参数及边界条件对热整流系数的影响, 图7—图9给出了热整流系数随长度比${{{L_1}}/L}$, 截面半径变化率${\beta _{{x_1}}}$和${\beta _{{x_2}}}$, 界面接触热阻${R_{\rm{c}}}$和边界温差$\Delta T$等因素的变化规律.
图 7 不同接触热阻下热整流系数随长度比的变化　(a) ${\beta _{{x_1}}} = $$ - 0.03$, ${\beta _{{x_2}}} = 0.03 $; (b) ${\beta _{{x_1}}} = - 0.03$, ${\beta _{{x_2}}} = - 0.03 $
Figure7. Variations of thermal rectification coefficient with length ratio under different contact thermal resistance: (a) ${\beta _{{x_1}}} = - 0.03, \; {\beta _{{x_2}}} = 0.03$; (b) ${\beta _{{x_1}}} = - 0.03, \; {\beta _{{x_2}}} = $ –0.03

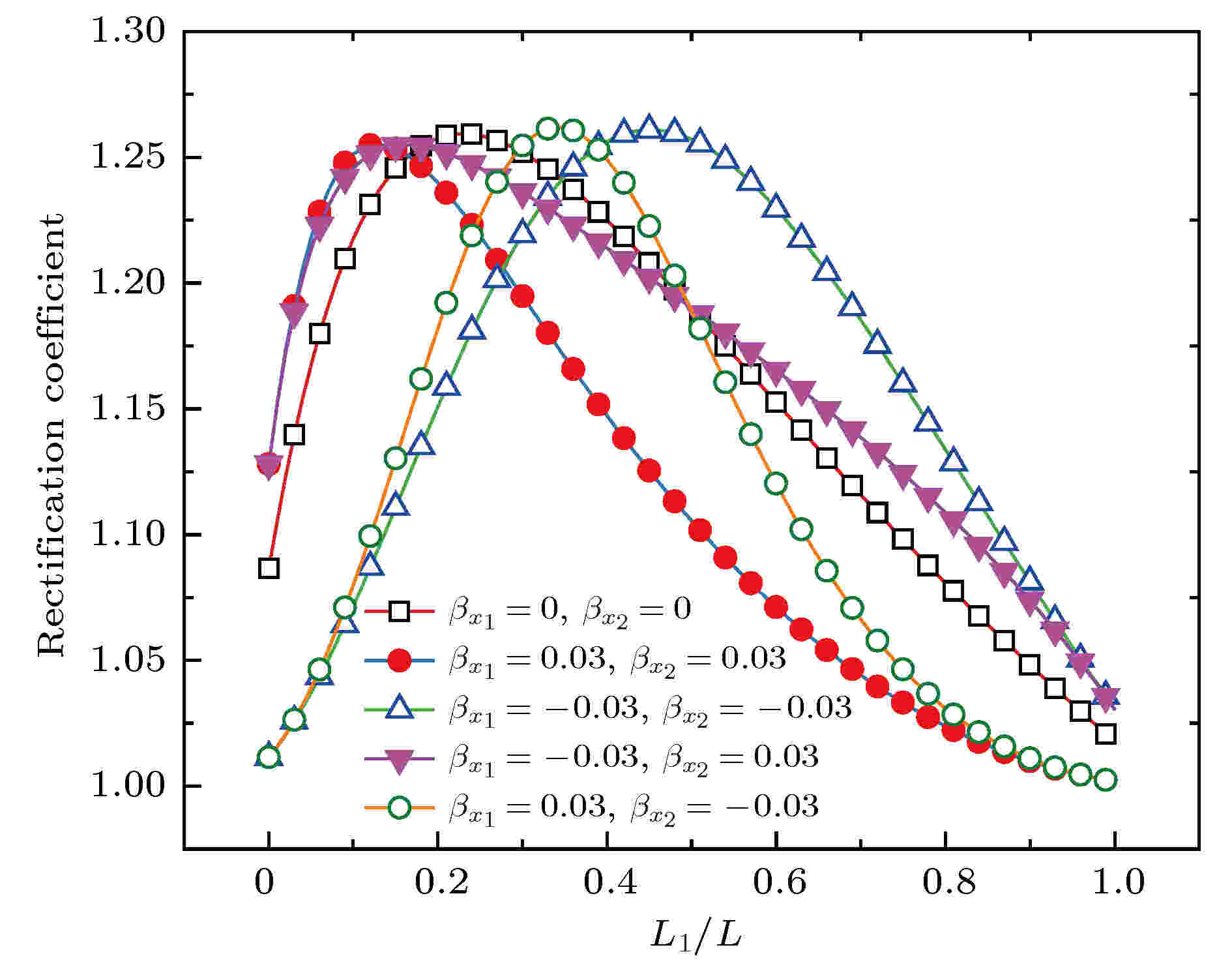图 9 不同长度变化率下热整流系数随长度比
Figure9. Variations of thermal rectification coefficient with length ratio at different length variation ratio.

保持结构总长度L = 300 mm不变, 在${T_{\rm{H}}} = 700\;{\rm{ K}}$和${T_{\rm{C}}} = 300\;{\rm{ K}}$的温度边界下, 结构热整流系数随着接触热阻和长度比及截面半径变化率的变化规律如图7所示.
从图7可以看出, 在不考虑接触热阻的情况下, 随着长度比的增加, 热整流系数先增加后减小, 截面半径变化率不同, 则极值点的位置不同, 最大的热整流系数保持不变. 对于固定长度的结构, 界面接触热阻越大, 则最大的热整流系数越小, 但是如果结构的长度比不固定, 那么在长度比较小和比较大时, 接触热阻越大热整流系数越大, 在此之间的中间区域, 接触热阻越大热整流系数越小. 如果长度比恒定, 那就可以通过界面接触热阻来调控结构的热整流系数.
热整流器的几何模型与长度比和截面半径变化率紧密相关, 当截面半径变化率恒定时, 随组合模型长度比的增加, 两杆件长度发生变化, 同时长度比的增加也影响着同位置截面面积的变化, 由(1)式与图6可以看出, 长度比增加的同时伴随着截面面积的变化并改变了温度场的分布趋势, 由于杆件1的热导率随温度的增加单调递增, 杆件2的热导率随温度的增加单调递减, 为扩大每段材料正反向等效热导率的差异, 杆件1整体的正向温度场应大于反向温度场, 杆件2整体的正向温度场应小于反向温度场, 即正反向温度场分布曲线无交点, 此时, 组合结构的整流效应最佳, 热整流系数最大. 因此, 随组合结构长度比的增加, 正反温度场分布曲线交点经历了有-无-有的过程, 热整流器的整流系数先增加后减小.
界面接触热阻的存在, 使得界面两侧温度出现跳变, 在小接触热阻的情况下, 温度跳变使得热量正向流动时提高了杆件1温度、降低了杆件2的温度, 热量反向流动时则降低杆件1的温度, 提高杆件2的温度, 增大了热整流器正反情况下等效热导率的差异性. 当界面接触热阻过大时, 界面接触热阻虽在一定程度上扩大等效热导率的差异性, 但同时会增加热整流器整体的热阻, 当由界面接触热阻导致整体热阻的增加占主导地位时, 反而会降低热整流器的整流效果. 对于不同长度比的热整流器, 存在一个最佳的界面接触热阻使得热整流器的热整流系数最大, 因此, 调节界面接触热阻是优化热整流系数的一种有效手段.
保持结构总长度L = 300 mm和低温端温度${T_{\rm{C}}} = 300\;{\rm{ K}}$不变, 同时界面接触热阻固定为${10^{ - 3}}\;{\rm{ K}} \cdot {{\rm{m}}^2} \cdot {{\rm{W}}^{ - 1}}$, 结构热整流系数随着两端温差$\Delta T$、长度比及截面半径变化率的变化规律如图8所示.
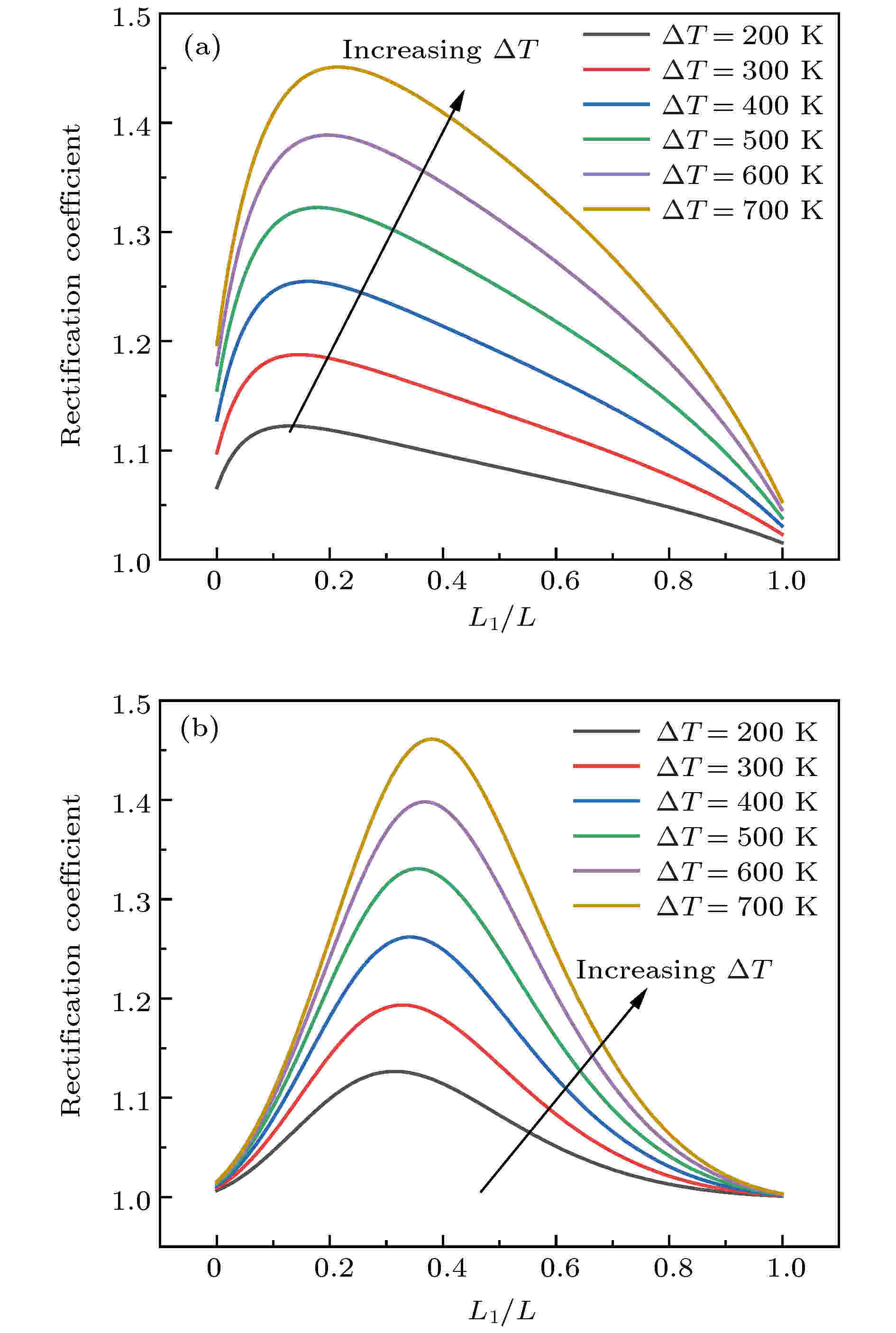图 8 不同边界温差下热整流系数随长度比的变化　(a) ${\beta _{{x_1}}} = $$ - 0.03, \; {\beta _{{x_2}}} = 0.03$; (b) ${\beta _{{x_1}}} = - 0.03, \; {\beta _{{x_2}}} = - 0.03$
Figure8. Variations of thermal rectification coefficient with length ratio at different boundary temperature differences: (a) ${\beta _{{x_1}}} \!=\! - 0.03, \; {\beta _{{x_2}}} \!=\! 0.03$; (b) ${\beta _{{x_1}}} \!=\! - 0.03,\; {\beta _{{x_2}}} \!=\! - 0.03$

从图8可以看出, 当结构截面半径变化率改变, 热整流系数随长度比的变化趋势略有不同, 即热整流系数随着长度比的增加先增加后减小, 而极大值对应的长度比随着边界温度差值和截面半径变化率的改变而变化. 随着边界温差的增加, 热整流系数逐渐增加, 极值处热整流系数增加趋势更为明显. 这是由于热整流器中一种材料的热导率随温度单调递增, 同时另一种材料的热导率随温度单调递减, 增大温差相当于增加了两种材料在正反温度边界条件下等效热导率的差异, 从而加大了结构整体等效热导率的差异, 进而提高了热整流系数. 当高低温边界温差为700 K时, 其热整流系数最大可达1.463.
保持结构总长度L = 300 mm和高低温边界温差400 K不变, 接触热阻恒定为${10^{ - 3}}\;{\rm{ K}} \cdot {{\rm{m}}^2} \cdot {{\rm{W}}^{ - 1}}$, 结构热整流系数随着长度比及截面半径变化率的变化规律如图9所示.
从图9可以看出, 无论截面半径变化率如何变化, 随着长度比的增加, 热整流系数的总体变化规律都是先增加后减小, 且最大值基本保持不变, 但是长度比和截面半径变化率必须满足一定的关系才能获得最大热整流系数. 如果左右两杆的横截面积都是随坐标递减的, 且递减规律一致, 那么两杆长度相等时有最大热整流系数, 而如果左右两杆的横截面积都是随坐标递增的, 虽然其递增规律一致, 但是最大热整流系数并未出现在两杆长度相等时. 这说明, 最大热整流系数的实现需要综合考虑各种材料参数和几何参数, 必须通过精细的计算分析才能获取最佳设计参数.
2
3.3.讨　论
-->

3.3.讨　论

一般来讲, 组合结构的热整流系数可以简单写为
$\gamma = \frac{{{Q_{\rm{f}}}}}{{{Q_{\rm{r}}}}} \propto \dfrac{{{{\left( {\dfrac{{kA}}{L}} \right)}_{\rm{f}}} + \dfrac{{{A_{\rm{c}}}}}{{{R_{\rm{c}}}}}}}{{{{\left( {\dfrac{{kA}}{L}} \right)}_{\rm{r}}} + \dfrac{{{A_{\rm{c}}}}}{{{R_{\rm{c}}}}}}},$
其中, ${\left( {\dfrac{{kA}}{L}} \right)_{\rm{f}}}$和${\left( {\dfrac{{kA}}{L}} \right)_{\rm{r}}}$分别为正反传热条件下的组合结构的等效热导率, ${R_{\rm{c}}}$为界面接触热阻, ${A_{\rm{c}}}$为界面接触面积.
从(15)式可以看出, 如果正反传热的等效热导率恒定不变, 那么增加界面接触热阻会使得(15)式的分子和分母同时增加, 此时结构的热整流系数必然是减小的. 而接触热阻实际上会使界面两侧的温度产生跳变, 从而改变了结构的整体温度场, 进而影响不同杆件的热导率, 使得结构的等效热导率发生变化, 使得增加结构的热整流系数成为可能, 而且存在一个最佳的界面接触热阻值来实现最优的热整流效果, 以上的数值计算结果也证明了这点. 在实践中该界面接触热阻可以通过在两杆之间增加垫片的方式实现, 通过设计垫片的厚度来实现不同的界面接触热阻, 从而实现最大的热整流系数.
4.结　论
建立了考虑界面接触热阻的变截面和变热导率的组合结构, 根据傅里叶热传导定律建立其热整流的理论模型, 给出了简单条件下温度场和热整流系数的理论解和一般条件下的有限元数值解. 数值算例验证了本文模型和算法的可靠性, 同时也得到了若干关键几何参数及材料参数特别是界面接触热阻对结构热整流效果的影响规律, 研究结果表明: 结构总体长度、长度比、截面半径变化率等几何参数, 热导率的变化规律和界面接触热阻等材料参数, 以及工作边界温度等环境参数对热整流效果都有较大的影响; 为了获取最大的热整流系数, 需要尽量提高正反两个方向上等效热导率的差别; 引入界面接触热阻是一个有效的调控结构热整流系数的技术手段, 在环境参数、几何参数和热导率变化规律确定的情况下, 通过调整界面接触热阻来实现最大的热整流效果是可行的.
附录　热整流系数的理论解
对于简单的截面积和热导率模型, 在不考虑界面接触热阻的条件下, 可以得到结构温度场和热整流系数的解析解. 假设两杆的截面积可表示为:
$\small\begin{split}& {A_1}\left( {{x_1}} \right) = {A_{01}}\left( {{A_{{\rm{M1}}}} - {{{x_1}}}/{{{L_1}}}} \right),\\&{A_2}\left( {{x_2}} \right) = {A_{02}}\left( {{A_{{\rm{M2}}}} - {{{x_2}}}/{{{L_2}}}} \right),\end{split}\tag{A1}$
其中${A_{01}}$, ${A_{{\rm{M1}}}}$, ${A_{02}}$和${A_{{\rm{M2}}}}$为截面积常数.
两杆材料的热导率可表示为:
$\begin{split}& {k_1}\left( T \right) = {k_{01}}{\left( {{T}/{{{T_0}}}} \right)^{ - 1}},\\&{k_2}\left( T \right) = {k_{02}}\left( {1 + {T}/{{{T_0}}}} \right),\end{split}\tag{A2}$
其中${k_{01}} = {\rm{}}1.02$, ${k_{02}} = {\rm{}}0.455$, 参考温度${T_0} = {\rm{}}60\;{\rm{ K}}$.
将(A1)式与(A2)式代入到无内热源的热量平衡方程(1)式, 结构分别在给定高温边界${T_{\rm{H}}}$和高温端界面温度${T_{{\rm{midH}}}}$的情况下以及给定低温边界${T_{\rm{C}}}$和低温端界面温度${T_{{\rm{midC}}}}$的情况下, 其温度场分别为:
$\begin{split}& {T_1}\left( {{x_1}} \right) = {T_{\rm{H}}}{\kern 1pt} {{\rm{e}}^{{C_1}/{C_2}}},\\& {T_2}\left( {{x_2}} \right) = \sqrt {\frac{{{C_4}}}{{{C_3}}} + \frac{{{C_5}}}{{{C_3}}} + {T_0}^2} - {T_0}.\end{split}\tag{A3}$
这里, 由于忽略了界面接触热阻的影响, 因此界面两侧温度相同. 且有
$\begin{split} & {C_1} = {\rm{}}\ln \dfrac{{{A_{{\rm{M1}}}}{L_1}}}{{{A_{{\rm{M1}}}}{L_1} - {x_1}}}\ln \dfrac{{{T_{{\rm{midH}}}}}}{{{T_{\rm{H}}}}},\\ & {C_2} = {\rm{}}\ln \dfrac{{{A_{{\rm{M1}}}}}}{{{A_{{\rm{M1}}}} - 1}},\\ & {C_3} = \ln \dfrac{{{A_{{\rm{M2}}}} - 1}}{{{A_{{\rm{M2}}}}}},\\ &{C_4} = \left( {{T_{{\rm{midC}}}}^2 + 2{T_{\rm{0}}}{T_{{\rm{midC}}}}} \right)\ln \dfrac{{{A_{{\rm{M2}}}}{L_2} - {L_2}}}{{{A_{{\rm{M2}}}}{L_2} - {x_2}}},\\ & {C_5} = \left( {{T_{\rm{C}}}^2 + 2{T_{\rm{0}}}{T_{\rm{C}}}} \right)\ln \dfrac{{{A_{{\rm{M2}}}}{L_2} - {x_2}}}{{{A_{{\rm{M2}}}}{L_2}}}. \end{split}$
界面热量连续性条件为
${\left. { - {k_1}{A_1}\frac{{{\rm{d}}{T_1}}}{{{\rm{d}}{x_1}}}} \right|_{{x_1} = {L_1}}} = {\left. { - {k_2}{A_2}\frac{{{\rm{d}}{T_2}}}{{{\rm{d}}{x_2}}}} \right|_{{x_2} = 0}}.\tag{A4}$
引入界面接触热阻:
$\frac{{{T_{{\rm{midH}}}} - {T_{{\rm{midC}}}}}}{{{R_{\rm{c}}}}} = - {k_1}{\left. {\frac{{{\rm{d}}{T_1}}}{{{\rm{d}}{x_1}}}} \right|_{{x_1} = {L_1}}}. \tag{A5}$
通过(A4)式与(A5)式迭代求解出界面两侧温度${T_{{\rm{midH}}}}$与${T_{{\rm{midC}}}}$.
热整流器件中通过任意截面的热量为
$Q = - k\left( T \right)A\left( x \right)\frac{{{\rm{d}} T}}{{{\rm{d}} x}}. \tag{A6}$
可得通过结构的正向热量为
${Q_{\rm{f}}} = \frac{{{A_{{\rm{01}}}}{T_0}{k_{01}}\left( {\ln {T_{\rm{H}}} - \ln {T_{{\rm{midH}}}}} \right)}}{{{L_1}\left( {\ln {A_{{\rm{M1}}}} - \ln \left( {{A_{{\rm{M1}}}} - 1} \right)} \right)}}. \tag{A7}$
将${T_{\rm{H}}}$和${T_{\rm{C}}}$互换即可得到反向热量的数值, 进而根据(4)式可得其热整流系数的理论解.
相关话题/结构 材料 实验 计算 设计
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 肖特基钙钛矿太阳电池结构设计与优化
    摘要:有机-无机杂化钙钛矿材料有高吸收系数、低廉的制作成本以及较为简单的制备工艺,在近年来表现出良好的发展前景.本文采用wx-AMPS模拟软件对平面结构钙钛矿太阳电池和肖特基钙钛矿太阳电池进行建模仿真对比,从理论上分析无载流子传输层的肖特基钙钛矿太阳电池的优势.结果显示,器件两侧电极功函数和吸收层的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于银纳米线电极-rGO敏感材料的柔性NO<sub>2</sub>气体传感器
    摘要:使用银纳米线作为材料制备柔性叉指电极,用还原氧化石墨烯(reducedgrapheneoxide,rGO)作为气体敏感材料制备出柔性气体传感器,并研究其对二氧化氮气体的响应特性以及柔韧性能.实验结果表明,制备的以银纳米线作为电极的rGO气体传感器可以实现室温下对浓度为5—50ppm(1ppm= ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Verwey相变处Fe<sub>3</sub>O<sub>4</sub>的结构、磁性和电输运特性
    摘要:作为典型的金属–绝缘体转变,Fe3O4的Verwey相变蕴涵的丰富物理现象与微观机制,因而受到了人们的广泛关注.在Verwey相变处,Fe3O4的晶体结构、电子结构以及磁各向异性等均发生转变,但其磁基态并未发生改变.与其他强关联体系相比,Fe3O4的Verwey相变不需要考虑磁交换耦合作用的变 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高效外腔倍频产生426 nm激光的实验研究
    摘要:利用与铯原子吸收线对应的852nm半导体激光作为基频光,泵浦基于周期极化磷酸钛氧钾(PPKTP)晶体的环形腔,进行高效外腔谐振倍频并产生426nm激光.在理论分析小角度环形腔内的热透镜效应基础上,发现晶体中等效热透镜中心位置并非在晶体的几何中心.在理论分析的基础上,实验上通过精密平移台精细调节 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 高熵合金短程有序现象的预测及其对结构的电子、磁性、力学性质的影响
    摘要:如何有效预测高熵合金的稳态结构,是开展研究其物理及化学等性能的基础.以FeCuCrMnMo合金为例,在有限晶胞尺寸内,采用蒙特卡洛结合密度泛函理论杂化计算方法(MonteCarlo/densityfunctionaltheory,MC/DFT)预测高熵合金的平衡态结构.与准随机近似方法(spe ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 石墨烯纳米网电导特性的能带机理：第一原理计算
    摘要:通过第一原理电子结构计算来研究有序多孔纳米网的电导特性变化的能带机理.能带结构分析结果表明:石墨烯纳米网超晶格(3m,3n)(m和n为整数)的电子本征态在布里渊区中心点发生四重简并;碳空位孔洞规则排列形成的石墨烯纳米网具有由简并态分裂形成的宽度可调带隙,无论石墨烯的两个子晶格是否对等.在具有磁 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 腔光子-自旋波量子耦合系统中各向异性奇异点的实验研究
    摘要:通过耦合三维微波腔中光子和腔内钇铁石榴石单晶小球中的自旋波量子形成腔-自旋波量子的耦合系统,并通过精确调节系统参数在该实验系统中观测到各向异性奇异点.奇异点对应于非厄米系统中一种特殊状态,在奇异点处,耦合系统的本征值和本征矢均简并,并且往往伴随着非平庸的物理性质.以往大量研究主要集中在各向同性 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Tl<sub>0.33</sub>WO<sub>3</sub>电子结构和太阳辐射屏蔽性能第一性原理研究
    摘要:节能减排已成为当今社会发展的主题,对节约能源、提高太阳能的高效综合利用的新型窗用透明隔热材料的理论设计和研究尤其重要.本文采用基于密度泛函理论的计算方法,研究了六方相三氧化钨Tl掺杂前、后的晶格参数、电子能带结构、形成能和光学性质.研究结果表明,Tl掺杂后晶格体积增大,系统能量降为负值,体系具 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 粉末颗粒气力加注特性实验研究
    摘要:粉末发动机是以粉末颗粒为燃料的新型发动机,具有多次起动和推力调节的功能.粉末加注是粉末发动机实验组织过程中的重要环节.本研究通过搭建粉末供应系统开展粉末气力加注实验,研究对比了集粉箱加注位置、流化气量对粉末气力加注特性的影响.考虑了供粉过程中储箱内粉末堆积密度的动态变化,并建立了相应的计算方法 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 入射光照对典型光刻胶纳米结构的光学散射测量影响分析
    摘要:作为一种快速、低成本和非接触的测量手段,光学散射测量在半导体制造业中的纳米结构三维形貌表征方面获得了广泛关注与运用.光学散射测量是一种基于模型的测量方法,在纳米结构待测参数的逆向提取过程中,为降低参数之间的耦合性,通常需要将结构的光学常数作为固定的已知量,即假设结构的材料光学常数不受光学散射仪 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.