摘要: 采用基于密度泛函理论的第一性原理平面波赝势方法, 计算了单层GeTe、表面氢化及氟化单层GeTe的晶体结构、稳定性、电子结构和光学性质. 计算结果表明, 经过修饰后, GeTe的晶格常数、键角、键长增大, 且均具有较好的稳定性. 电子结构分析表明, 单层GeTe为间接带隙半导体, 全氢化修饰、全氟化修饰以及氢氟共修饰(F, Ge同侧; H, Te同侧)则转变为直接带隙半导体, 且修饰后的能隙均不同程度减小. 载流子有效质量表明, 全氢化、全氟化以及氢氟共修饰GeTe (F, Ge同侧; H, Te同侧)的有效质量减小, 其载流子迁移率增强. 带边势分析结果显示, 单层GeTe能够光裂解水制氢和析氧, 而修饰后的GeTe的价带带边势明显下移, 其氧化性明显增强, 能够光裂解水析O
2 , H
2 O
2 , O
3 以及OH·等产物. 光学性质表明, 修饰后的GeTe对可见光区和红、紫外区的光谱吸收效果明显增强, 表明其在光催化领域有着广阔的应用前景.
关键词: 单层GeTe /
电子结构 /
有效质量 /
光催化性能 English Abstract Electronic structure and photocatalytic properties of H, F modified two-dimensional GeTe Fang Wen-Yu 1 ,Zhang Peng-Cheng 1 ,Zhao Jun 1,2 ,Kang Wen-Bin 1,2 1.School of Public Health and Management, Hubei University of Medicine, Shiyan 442000, Chin Received Date: 14 September 2019Accepted Date: 12 December 2019Published Online: 05 March 2020Abstract: Using the first principle calculation based on the density functional theory, we have systematically investigated the structure stability, electronic structure and photocatalytic properties of two-dimensional single-layered GeTe crystal structure modified by H and F. The results show that the lattice constant, bond angle and bond length of GeTe increase after being modified. The stability analysis shows that all the materials have excellent dynamical, mechanical, and thermal stabilities. The electronic structure analysis shows that the two-dimensional GeTe is an indirect bandgap semiconductor with an energy gap of 1.797 eV, and its energy band is mainly composed of Ge-4p and Te-5p, while it is converted into a direct bandgap semiconductor by H or F modification and H-F co-modification (F and Ge on one side, H and Te on the other), and their corresponding energy gaps are reduced to 1.847 eV (fH-GeTe), 0.113 eV (fF-GeTe) and 1.613 eV (hF-GeTe-hH). However, hH-GeTe-hF is still an indirect band gap semiconductor, and its energy gap is reduced to 0.706 eV. The results of the density of states show that part of the Ge-4p and Te-5p electrons are transferred to a deeper level due to the adsorption of H or F atoms, resulting in a strong orbital hybridization between them and the adsorbed atoms. The effective mass shows that the effective mass of H or F modified and H-F co-modified GeTe (F and Ge on one side, H and Te on the other) decrease, and their carrier mobilities increase. The carrier recombination rates of all modified GeTe materials are lower than that of the intrinsic GeTe, so the semiconductor will be more durable. The electron density difference shows that due to the electronegativities of atoms being different from each other, when H or F is used to modify GeTe, some electrons transfer to H and F atoms, resulting in the weakening of covalent bond between Ge and Te atoms and the enhancement of ion bond. The results of band-edge potential analysis show that GeTe can produce hydrogen and oxygen by photolysis of water. However, the valence band edge potential of the modified GeTe decreases significantly, and its oxidation ability increases considerably, the photocatalytic water can produce O2 , H2 , O3 , OH·, etc. Optical properties show that the modified GeTe can enhance the absorption of visible and ultraviolet spectrum, which indicates that they have great application prospects in the field of photocatalysis.Keywords: two-dimensional GeTe /electronic structure /effective mass /photocatalysis 全文HTML --> --> --> 1.引 言 自石墨烯[1 ] 发现以来, 二维材料的研究便吸引更多人们的关注, 过渡金属硫族化合物(transition metal dichalcogenide, TMDs)[2 -5 ] 、硅烯、锗烯、黑磷、砷烯、锑烯等类石墨烯二维材料的发现更加丰富了二维材料的种类[6 -10 ] . 但是现存的这些二维材料均存在一些不足, 例如: 石墨烯具有零带隙的特点[11 ] , 黑磷在空气中不太稳定[12 ] , 砷烯、锑烯制备难度相对较大等[13 ] , 因此在新型二维材料的电子结构和光催化等性质方面具有很大的研究价值. $\alpha $ -GeTe是一种具有层状结构的窄带隙直接半导体材料, 其能隙为1.65 eV[14 ] , 且载流子密度高达1021 cm–3 . 因此, $\alpha $ -GeTe在光电子及沟道器件等领域具有广阔的应用前景[15 ] . 目前, 对纳米尺度的$\alpha $ -GeTe已经有了一定的研究进展[16 ] , 但是对于二维GeTe的研究还比较少, 且主要集中在理论计算方面, 如Qiao等[17 ] 通过理论计算表明, 二维GeTe可以从体相GeTe剥离出来, 具有较高的电子和空穴迁移率, 并在太阳光谱的可见区域具有明显的光学吸收. 这些优良的性能使得单层GeTe有望成为一种很有前途的光催化剂. Singh等[18 ] 通过计算单层GeTe的结构、稳定性和电子性质, 证明单层GeTe具有较好的结构稳定性, 它的形成能与单层MoS2 差不多, 这表明它们的层状结构易于机械剥落, 且其半导体特征适用于光电子学和太阳能转换. Wan等[19 ] 研究了单层GeTe的铁电性能, 结果表明其本征居里温度高达570 K, 通过外电场可以有效地降低矫顽力场的极化反转, 扩展其调节极化开关动力学的潜力, 这些优点表明二维GeTe是一种很有前景的铁电集成应用候选材料.[20 ] 通过超声辅助液相剥离法制备出了单层的$\alpha $ -GeTe纳米片, 结果显示单层GeTe的厚度约为1.6 ?(1 ? = 0.1 nm), 其光学带隙为1.93 eV, 与理论计算值(1.85 eV)较为接近. 另外, 研究还表明单层GeTe在紫外光 (370 nm)的激发下发射出433 nm的蓝光, 可用于铁离子的检测. 再次说明了对于二维GeTe的研究具有非常重要的研究价值. 氢基和氟基是常见的化学基团, 常常用来修饰二维材料的表面, 用于调控材料的物理性质[9 ,21 ] , 且有关氢基或氟基修饰单层GeTe的研究尚未见报道. 本文主要基于密度泛函理论(density functional theory, DFT)系统研究H, F对单层GeTe能带结构、载流子有效质量、光学性质调控作用, 从而为实验上制备高性能的新型二维材料提供理论指导.2.模型与计算方法 体相GeTe 属于三斜结构, 其对称群为R -3M , 层内原子由较强的共价键结合, 层与层之间主要以范德瓦耳斯力相连, 实验上可通过电化学或机械剥离等方法得到其纳米级甚至单层结构[22 ] . 随着层数减少, GeTe的表面会由三斜结构向六方结构的转变, 单层GeTe为六方结构, 其对称群为P 3m 1, 如图1 所示. 为避免层与层之间弱范德瓦耳斯力的影响, 沿轴方向设置了20 ?的真空层. 单个原子或分子的吸附可以看成杂质的引入, 单层GeTe经过表面修饰后, 其结构和性质实质上已经改变, 可以认为是一种新的材料[23 ] . 本文选取氢基(—H)和氟基(—F)分别全表面修饰, 以及二者同时半表面修饰GeTe的计算模型, H和F全表面修饰记为fH-GeTe和fF-GeTe, H和F同时修饰时, 当H在Ge侧, F在Te侧, 记作hH-GeTe-hF, 反之记为hF-GeTe-hH, 其晶胞结构如图1(b) —(e) 所示.图 1 优化后的晶胞模型 (a) GeTe侧视图; (b) fH-GeTe俯视图; (c) fH-GeTe侧视图; (d) hH-GeTe-hF侧视图; (e) hF-GeTe-hH侧视图; (f) K 点路径Figure1. The optimized geometric structures: (a) side view of GeTe; (b) top view of fH-GeTe; (c) side view of fH-GeTe; (d) side view of hH-GeTe-hF; (e) side view of hF-GeTe-hH; (f) K point path.[24 ] 软件来完成, 采用周期性边界条件, 运用广义梯度近似GGA的PBE算法来处理电子相互间的交换关联能. 选取价电子组态分别为Ge (4s2 4p2 ), Te (5s2 5p4 ), H (1s1 ), F (2s2 2p5 ). 计算时选取的平面波截断能是E cut = 500 eV, 布里渊区积分采用15 × 15 × 1 Monkhorst-Pack特殊K 点对全布里渊区求和, 计算均在倒格矢中进行. 在自洽场计算中, 能量的收敛精度为2.0 × 10–6 eV·atom–1 , 每个原子上的受力不大于0.002 eV·nm–1 , 内应力收敛精度为0.01 GPa, 原子最大位移收敛标准为2.0 × 10–3 nm, 计算各种体系时均进行结构优化.3.结果与讨论 23.1.结构分析 3.1.结构分析 表1 列出了各晶体原子自由弛豫后的结构常数和吸附能E f 等, 其中a /b 为晶格常数, θ 为优化后的面内原子间夹角, l 为Ge原子与Te原子间的键长, l 1 和l 2 分别为Ge和Te原子与其修饰原子间的键长, σ 为优化后GeTe层的弯曲高度(buckling height), 所有参数均在图1 中做了标注. 从表1 可以看出, 单层GeTe的a /b 为3.95 ?, σ 为1.56 ?, 与Singh等[18 ] 计算结果基本一致. 单层GeTe经过H, F修饰后, 其晶格常数、键角、Ge—Te原子间键长均不同程度增大, 其中fH—GeTe和hF—GeTe—hH的键角增大至120°左右, 即Ge和Te原子此时处在一个准平面内, 此时它们的σ 值分别低至–0.08和–0.03, 负值说明Ge和Te分别凹陷至另一侧, 即原子有略微的“塌陷”. 由于原子的半径大小关系为Te (1.37 ?) > Ge (1.22 ?) > F (0.64 ?) > H (0.32 ?), 即H原子半径相对其他原子半径要小得多, 所以H与修饰原子间的键长较F修饰时要短. 很显然由于H和F原子的引入, 单层GeTe的结构明显发生变化, 这些结构的变化必然会引起其物理性质的改变.Structure (a /b )/? θ /(°)l /?l 1 /?l 2 /?σ /?E f /eVGeTe 3.95 91.22 2.76 — — 1.56 — fH-GeTe 5.09 119.92 2.94 1.60 1.69 –0.08 –5.80 fF-GeTe 4.18 93.08 2.88 1.79 2.04 1.58 –7.45 hH-GeTe-hF 4.02 92.04 2.97 1.59 2.08 1.56 –5.79 hF-GeTe-hH 5.21 119.99 3.01 1.81 1.69 –0.03 –7.74
表1 晶体的结构参数及吸附能Table1. Structural parameters for all chemically decorated GeTe.E f 为[25 ] E f 为吸附能, E 0 和E t 分别为修饰前后原胞的能量, Ex 为修饰原子(H, F)的能量, n 1 和n 2 是相应原子的摩尔分数. E f 越小, 说明体系越容易形成, 其结构越稳定. 基于(1 )式计算得到修饰后GeTe的吸附能如表1 所示, 从表1 中可以看出, 4种修饰模型计算出来的吸附能均为负值, 表明当H或F吸附在GeTe表面时为放热反应, 即修饰后的GeTe结构更为稳定. 同时, hF-GeTe-hH吸附能最低, 说明这种结构在实验中更容易实现.[25 ] . 图2 为GeTe修饰前后声子谱计算结果. 从图2 可以看出, 仅fF-GeTe在G 点出现微弱的虚频, 分析认为这主要是系统误差所造成的, 其他体系均没有虚频, 表明它们均具有很好的动力学稳定性. 同理, 为了分析各体系的热稳定性, 应用分子动力学计算方法[26 ] , 计算了各分子膜(2 × 2 × 1)在加热到500 K (时间步长为1 fs, 模拟2.5 ps)后的原子构型和能量的变化, 如图3 所示. 观察发现, 本征GeTe依然保持褶皱六元环结构, 修饰后的GeTe的形变则主要集中在H或F与竖直方向发生偏离, 即与y 轴间存在倾角, 但在整个过程中各体系均没有发现严重几何重构和键断裂现象, 表明这些单层分子膜可以作为独立的二维材料存在. 能量的变化只表现出轻微的振荡(1 eV内波动), 因此, 即使在500 K的高温下, 它们也可以保持很好的稳定性.图 2 声子谱 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hHFigure2. Phonon dispersion: (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH.图 3 分子动力学模拟计算的能量随时间的变化, 插图表示加热到500 K温度下最后的结构图 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hHFigure3. Variation of the total energy in the molecular dynamics simulation at 500 K for: (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH, during a timescale of 2.5 ps. The insets are the top (left panel) and side (right panel) views of the atomic structure snapshots taken from the molecular dynamics simulation.3.2.电子结构 -->3.2.电子结构 图4 为单层GeTe修饰前后的能带图和分波态密度图, 从图4(a) 可以看出, 本征GeTe的价带顶在G 点, 而导带底则处在M 与G 点之间, 说明其为间接带隙半导体, 能隙为1.797 eV, 这与文献[20 ]计算结果(1.85 eV)基本相符. 此外, 价带中的能带都有着较大的展宽, 说明Ge和Te的轨道电子共有化比较明显. 对照其分波态密度发现, 本征GeTe的电子结构主要由Ge-4p和Te-5p组成, Ge-4s和Te-5s的贡献很小. 尽管各轨道电子的贡献不一, 但是变化趋势几乎保持一致, 即各个轨道之间有着明显的杂化效应. H或F修饰单层GeTe后, 其能带结构发生很大变化, 最显著的特征是修饰后的能隙不同程度减小, 且fH-GeTe, fF-GeTe和hF-GeTe-hH由间接半导体转变为直接带隙半导体, 这使得它们能够与光直接耦合, 有利于对光子的吸收. 单从能隙宽度来看, 本征及修饰后的GeTe的能隙较窄, 均能够对太阳光谱产生响应, 这使得它们作为新型光催化材料成为可能. 修饰后的分波态密度的变化则主要表现为能级深处的峰值相对费米面附近两侧的分布变得更大, 观察发现, 这主要是由于H-1s态或F-2p态在能级深处有较强的分布, 且由于电负性的差异, Ge和Te原子周围有部分电子转移至H和F原子, 各原子轨道电子杂化更加强烈导致的. 比如, fF-GeTe在–4 eV附近有个明显的峰值, 该处峰值主要由F-2p电子和转移至F-2p轨道的Ge-4p和Te-5p, 各原子轨道电子在–4 eV附近杂化明显增强. 此外, 从能带的色散关系可以看出, fH-GeTe, fF-GeTe和hF-GeTe-hH价带顶的曲率变化明显比导带底的曲率变化快, 由于曲率的变化与半导体的载流子迁移率直接相关[27 ] , 因而光生空穴与光生电子的“步调”存在着较大的差异性; hH-GeTe-hF则依然为轻电子重空穴型间接半导体, 其能隙减小至0.706 eV. 另一方面, 修饰后GeTe的能级局域化程度也有了一些变化, 其中最显著的就是价带顶和导带底的能级均向费米面靠近, 且部分能级展宽, 这也是修饰后能隙变小的原因所在. 由于对晶体的光电性质起决定作用的主要是集中在费米面附近的电子分布, 修饰后的GeTe的导带底整体向费米面靠近, 且分布略有增加, 这有利于载流子在价带顶与导带底之间的跃迁. 然而对于价带顶部分, fH-GeTe, fF-GeTe和hF-GeTe-hH的态密度明显减小, 即价带顶能够跃迁至导带底的载流子更少, 这显然是不利的.图 4 能带图和态密度 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hHFigure4. Band structure and density of states: (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH.[28 ] :$\dfrac{{{\partial ^2}E}}{{\partial {k^2}}}$ 单位为$\dfrac{1}{{{{(2{\text{π}}/a)}^2}}}\;{\rm{eV}}$ ; a 为晶格常数, 单位为?; $\hbar $ 为约化普朗克常数, $\hbar = h/\left( {2{\text{π}}} \right)$ . 可知, 载流子有效质量的数值取决于价带顶与导带底的二次微分. 由于空穴一般位于价带顶附近, 电子一般位于导带底附近, 因此, 只需要计算导带底与价带顶的二次微分就可以计算电子与空穴的有效质量. 通过对价带顶(导带底)附近的E-k 数据用二次方程$E(k) = {E_0} + {d_1}k + {d_2}{k^2}$ 进行拟合, 则$\dfrac{{{\partial ^2}E}}{{\partial {k^2}}} = 2{d_2}$ , 此时(2 )式可以变换为[29 ] $ m_{\rm h}^* $ 表示光生空穴有效质量, $ m_{\rm e}^* $ 表示光生电子有效质量, $ D = \max(m_{\rm h}^*, m_{\rm e}^*)/\min(m_{\rm h}^*, m_{\rm e}^*) $ , 用于表征$ m_{\rm h}^* $ 和$ m_{\rm e}^* $ 的差异性. 通常来说, 载流子的迁移速度与它的有效质量成反比, 即光生电子或空穴的有效质量越小, 则其载流子的迁移速度就越大. 如果光生电子和空穴的迁移速度差异性越大, 两者的分离效率和非同步化程度越高, 则光生电子与空穴之间的复合率越低, 因此D 越大, 则说明半导体的载流子复合率越低, 半导体的光催化活性越好[30 ] . 基于(3 )式计算各体系的光生载流子有效质量如表2 所示, 计算结果均是基于能带图中所标识的价带顶与导带底的位置得来. 从表2 可以看出, 单层GeTe和hH-GeTe-hF的电子有效质量小于空穴有效质量, 它们属于轻电子重空穴型半导体, 且后者的载流子迁移率会小于前者; 而fH-GeTe, fF-GeTe以及hF-GeTe-hH则属于轻空穴重电子型半导体, 且它们的迁移率都比单层GeTe大. 观察D 值发现, 修饰后的D 值明显比未修饰的更大, 说明修饰后的GeTe的载流子复合率更低, 其光催化活性更有利.Effective mass GeTe fH-GeTe fF-GeTe hH-GeTe-hF hF-GeTe-hH $ m_{\rm h}^*/m_0 $ 0.54 0.24 0.23 1.50 0.30 0.52 0.39 0.27 0.91 0.49 D 1.04 1.63 1.17 1.65 1.63
表2 半导体的载流子有效质量Table2. The effective mass for all chemically decorated GeTe.[31 ] . 为了进一步研究掺杂原子对GeTe的电子结构影响, 做出了$\langle 0, 0, 1 \rangle$ 面的差分电荷密度, 如图5 所示. 图5 中差分电荷密度线保持同一刻度, 刻度条的数值表示差分电荷密度等高线数值的大小, 深蓝色表示得到电子, 亮黄色表示失去电子, 颜色越亮表示失去电子越多. 从图5 可以看出, 对于本征GeTe, 在Ge和Te原子之间有明显的电子重叠, 且原子周围等高线没有明显差异, 即Ge和Te原子之间主要以共价键形式存在. 当用H或F修饰GeTe时, 不难发现, Ge和Te原子间颜色变浅, 即电子减少, 且H和F原子周围则主要为亮黄色, 即它们主要表现为获得电子. 因此, 当H或F吸附在GeTe表面时, 会导致Ge和Te之间的共价性减弱, 离子性增强. 由于各原子的电负性满足Ge(4.6) < Te(5.49) < H(7.18) < F(10.41), 即H, F的电负性大于Ge和Te原子, 因此当用H或F修饰GeTe时, 会有电子转移至H和F原子, 由于F的电负性最大, 所以相比较而言会有更多的电子转移至F-2p态, 因而fF-GeTe的轨道杂化最强烈, 在价带深处的态密度分布形成很大的峰值, 这与前文态密度的分布规律相符.图 5 $\langle 0, 0, 1 \rangle$ 截面差分电荷密度图 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hHFigure5. Electron density difference $\langle 0, 0, 1 \rangle$ : (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH.3.3.光催化性质 -->3.3.光催化性质 为分析单层GeTe及其修饰后的光催化能力, 如光裂水制H2 , 析O2 , H2 O2 等, 计算上述5种体系的价带顶电势和导带底电势. 通常情况下, 相对于标准氢电极的氧化还原势, 材料带边对应的氧化还原电势可通过(4 )式, (5 )式给出[32 ] $\chi $ 表示材料的电负性, 可以通过计算构成材料各原子密立根电负性几何平均值得到; E e 为以氢为标准时自由电子的电势(4.50 V); E g 为能隙. 计算得到的各材料的电负性及氧化还原势如表3 所示, 并将其与光催化水的部分产物的电势做比较, 如图6 所示. 结合表3 和图6 可以看出, 单层GeTe的导带边电势为–0.37 V, 小于光裂水制氢的还原势(0 V), 且价带边电势1.42 V, 大于光裂水析氧的氧化势(1.23 V), 因而GeTe能够光裂水制氢和析氧. 修饰后的GeTe的电负性增大, 导致其带边势的氧化性明显增强, 几乎没有还原性. 分析发现, 修饰后的GeTe的氧化势均低于2.07 eV, 因此它们能够光裂水析O2 , H2 O2 和O3 , 其中fF-GeTe和hF-GeTe-hH的价带边氧化电势分别高达2.79 eV和2.90 eV, 除了能够产生以上产物外, 还可以产出羟基自由基(OH·), 而O2 , H2 O2 和O3 等产物都有较强的氧化能力, 可以直接氧化很多污染物, 即修饰后的GeTe的光生空穴具有很强的氧化能力, 在光催化领域有着广阔的应用前景.Structure GeTe fH-GeTe fF-GeTe hH-GeTe-hF hF-GeTe-hH $ \chi $ 5.03 6.01 7.23 6.59 6.59 CB/eV –0.37 0.76 2.68 1.74 1.28 VB/eV 1.42 2.25 2.79 2.44 2.90
表3 半导体的导带和价带的带边电势Table3. Reduction and oxidation potentials of CB and VB edges of all chemically decorated GeTe.图 6 半导体的导带与价带的带边电势示意图Figure6. Reduction and oxidation potentials of CB and VB edges of all chemically decorated GeTe.[33 ] $\omega $ 是频率, ${\varepsilon _1}(\omega )$ 和${\varepsilon _2}(\omega )$ 分别为实部和虚部. 吸收系数随光子能量变化的曲线如图7 所示, 可以看出, 单层GeTe和hH-GeTe-hF的吸收边分别约为1.8 eV和0.8 eV, 与它们的能隙值相吻合, 这是因为吸收边与光学带隙直接相关, 只有光子能量达到能隙大小, 才能产生光-电子耦合效应, 激发电子在价带与导带间跃迁. 而其他体系的吸收边分别为fH-GeTe (1.0 eV), fF-GeTe (0.1 eV)和hF-GeTe-hH (1.1 eV), 小于它们所对应的能隙(1.487, 0.113和1.613 eV), 前文提到这3种材料均属于轻空穴重电子型半导体, 即空穴的迁移率高于电子的迁移率, 导致价带顶的空穴复合更慢, 这些空穴允许浅处能级电子带内跃迁而产生光吸收现象, 从而能够吸收比能隙更小的能量的光子. 很显然, 修饰后的GeTe吸收边红移, 对低能量的光子(0—2.3 eV)的吸收效果明显增强, 即对可见光区和红、紫外区的光谱吸收效果明显增强, 这将有利于光催化效率的提高.图 7 半导体的吸收系数Figure7. Absorption spectra of all chemically decorated GeTe.4.总 结 采用了基于DFT的第一性原理平面波超软赝势方法, 计算了单层GeTe, H, F表面修饰单层GeTe的晶体结构、电子结构和光学性质. 计算结果表明: 单层GeTe是一种间接带隙半导体, 计算带隙为1.797 eV, 经过H或F修饰后, hH-GeTe-hF转变为窄带隙(0.706 eV)间接半导体, 而fH-GeTe, fF-GeTe和hF-GeTe-hH则由间接半导体转变为直接带隙半导体, 且能隙均不同程度减小. 半导体的光生载流子有效质量计算结果表明, 单层GeTe和hH-GeTe-hF属于轻电子重空穴型半导体, 即电子迁移率大于空穴迁移率, 而fH-GeTe, fF-GeTe和hF-GeTe-hH则属于轻空穴重电子型半导体. 通过分波态密度和差分电荷密度图分析发现, 由于H, F的电负性均大于Ge和Te, Ge和Te原子周围会有部分电子转移至H和F, 从而在能级深处形成强烈的轨道杂化效应, 同时Ge, Te之间的共价性减弱, 离子性增强. 通过计算半导体的带边电势发现, 单层GeTe能够光裂水制氢和析氧. 修饰后的GeTe的电负性增大, 导致其带边势的氧化性明显增强, 能够光裂水析O2 , H2 O2 和O3 , 且修饰后的GeTe对可见光区和红、紫外区的光谱吸收效果明显增强, 因而它们在光催化领域有着广阔的应用前景. 









 图 1 优化后的晶胞模型 (a) GeTe侧视图; (b) fH-GeTe俯视图; (c) fH-GeTe侧视图; (d) hH-GeTe-hF侧视图; (e) hF-GeTe-hH侧视图; (f) K点路径
图 1 优化后的晶胞模型 (a) GeTe侧视图; (b) fH-GeTe俯视图; (c) fH-GeTe侧视图; (d) hH-GeTe-hF侧视图; (e) hF-GeTe-hH侧视图; (f) K点路径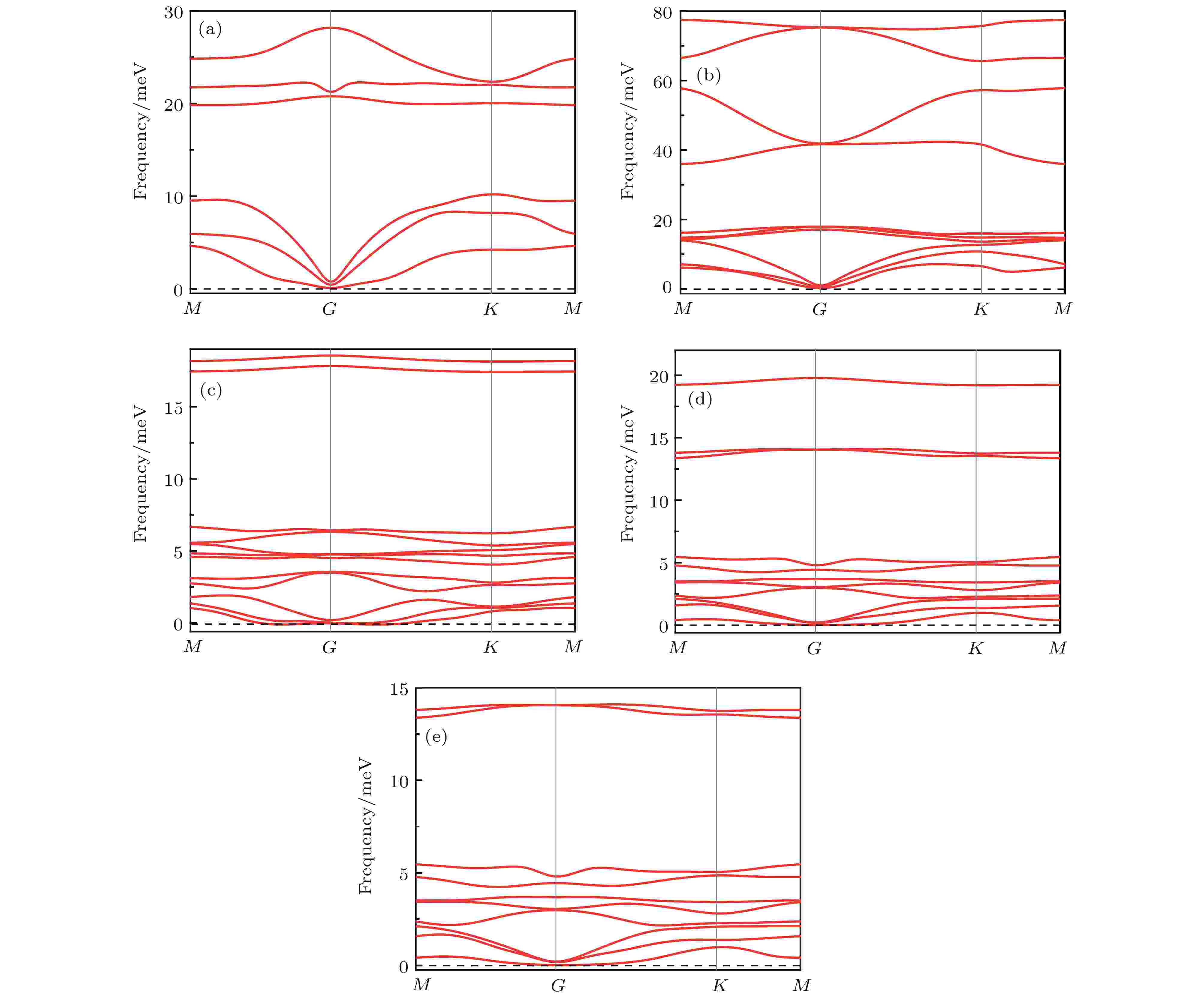 图 2 声子谱 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH
图 2 声子谱 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH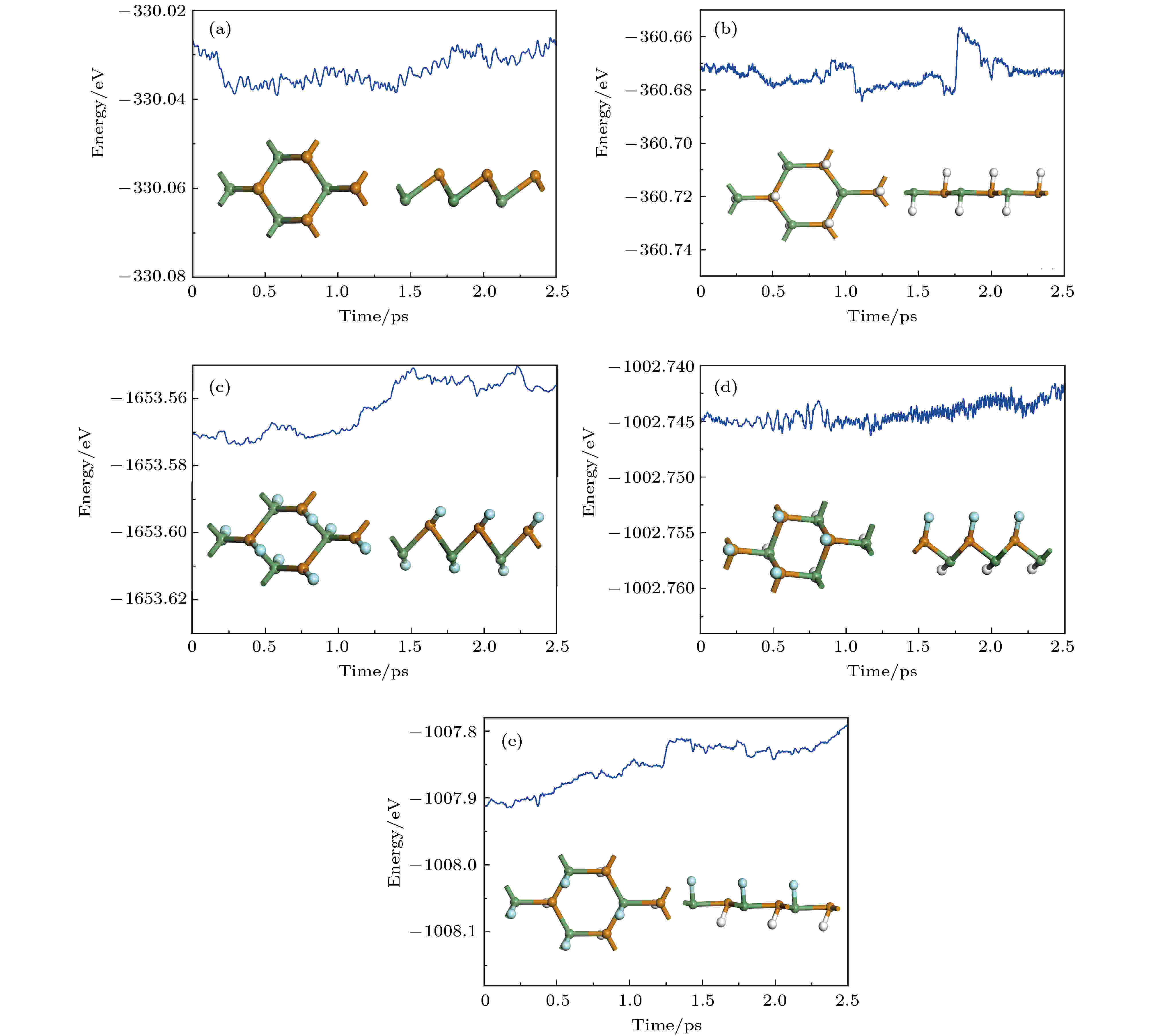 图 3 分子动力学模拟计算的能量随时间的变化, 插图表示加热到500 K温度下最后的结构图 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH
图 3 分子动力学模拟计算的能量随时间的变化, 插图表示加热到500 K温度下最后的结构图 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH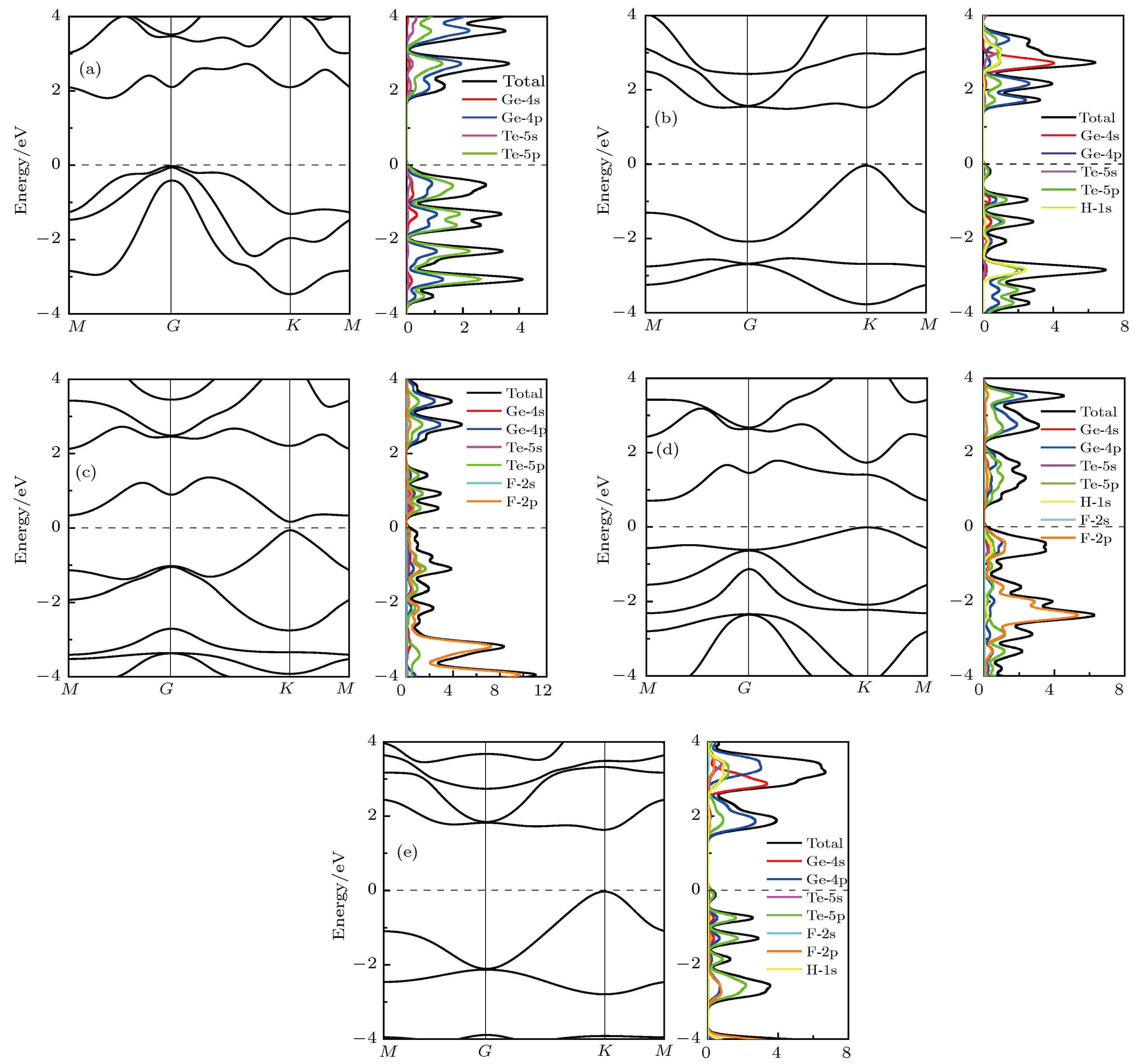 图 4 能带图和态密度 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH
图 4 能带图和态密度 (a) GeTe; (b) fH-GeTe; (c) fF-GeTe; (d) hH-GeTe-hF; (e) hF-GeTe-hH















 图 5
图 5 


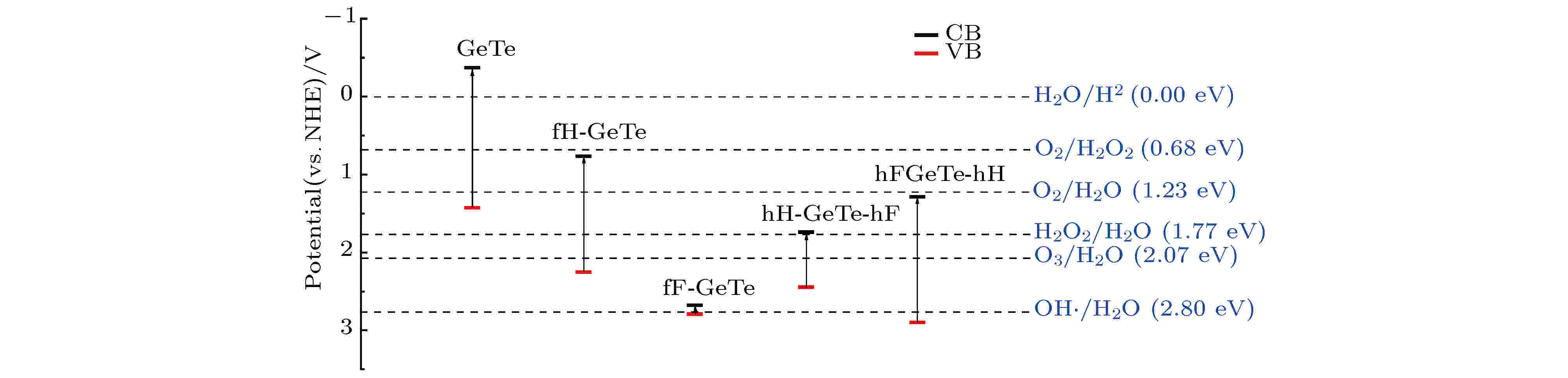 图 6 半导体的导带与价带的带边电势示意图
图 6 半导体的导带与价带的带边电势示意图


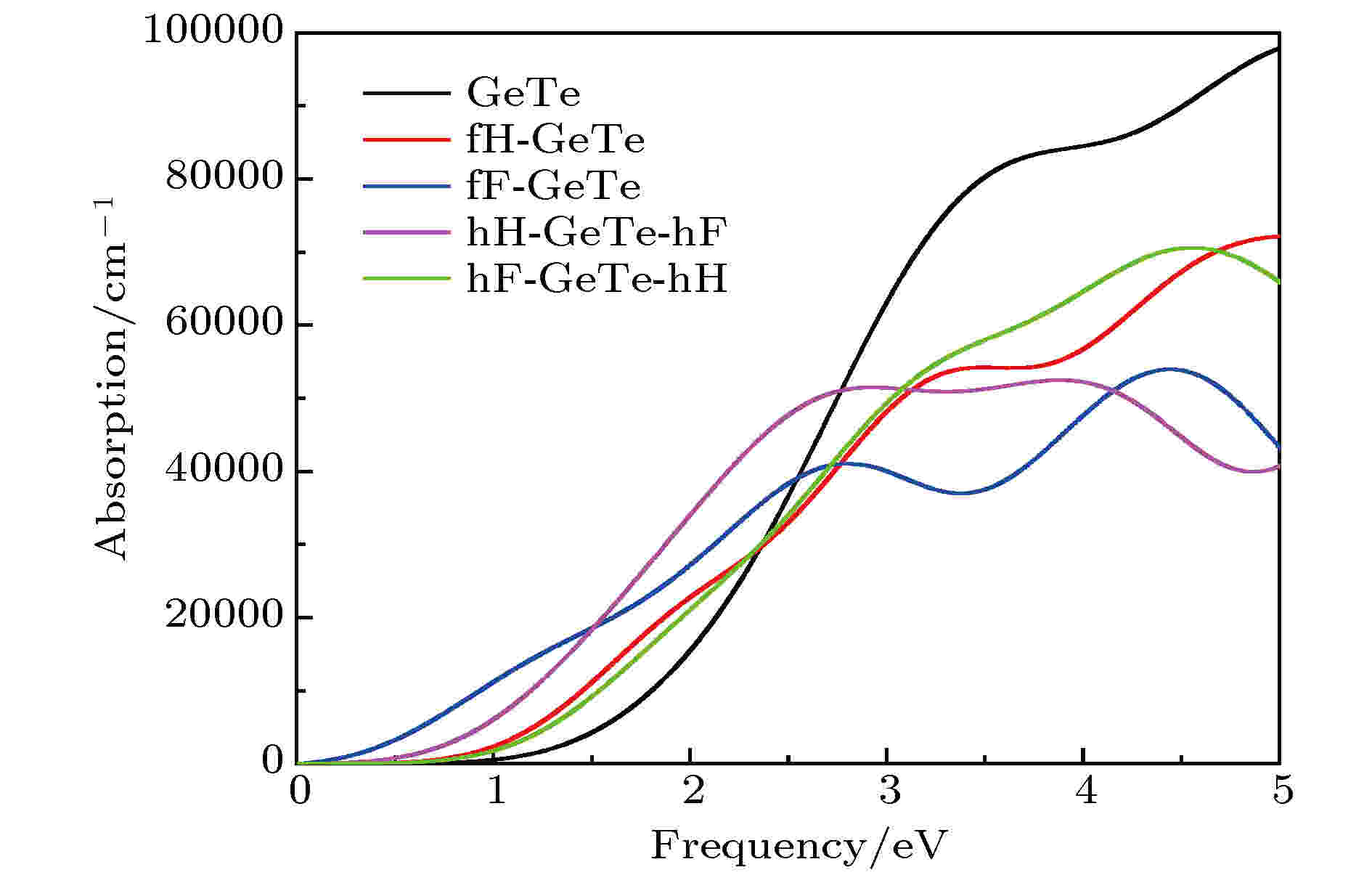 图 7 半导体的吸收系数
图 7 半导体的吸收系数