摘要:污水处理、油田采油、液态金属冷却反应堆和磁流体动力转换器等领域采用气力提升系统有其显著优势. 由于不同液体介质与气体介质密度对气力提升系统性能影响较大, 因此本文基于Fluent仿真软件, 采用欧拉模型、k-ω剪切应力输运湍流模型数值模拟了氮气-水、氮气-煤油、氮气-水银及空气-水、氩气-水、氮气-水下气力提升系统内气液两相流动行为, 分析了系统稳定时提升立管内气相体积分数、提升液体流量、提升效率、提升管出口处液体径向速度的变化规律. 研究结果表明: 1)氮气-水、氮气-煤油、氮气-水银系统中, 提升管内液体介质密度越大, 提升管内气相体积分数越小、提升液体流量越大、提升效率越高; 2)空气-水、氩气-水、氮气-水系统中, 提升管内气体介质密度越大, 提升管内气相体积分数越小、提升液体流量越大、提升效率峰值越小; 3)提升管出口处提升液体径向速度随气体充入量的不断增加而整体波动升高, 最终管轴中心附近液体速度较大, 管壁附近液体速度较小. 本文研究成果为污水处理、气举采油、液态重金属冷却核反应堆和磁流体动力转换器等应用领域的气力提升技术的优化提供科学的理论基础.
关键词: 气力提升系统/
数值模拟/
密度/
提升效率

English Abstract

全文HTML

--> --> -->

气力提升装置原理是通过向提升管内注入压缩空气, 通过管内外产生的压差来提升液体. 与传统机械泵相比, 其结构简单、无机械传动部件、无系统磨损; 提升技术易实现、耗能低、驱动能源来源广泛; 可在高温、高压、真空、放射性、腐蚀性的环境中使用, 也可在不规则形状的井中使用, 故研究气力提升系统具有重要的科学价值^[1-3]. 目前, 由于气力提升系统的维护成本较低、可靠性较高, 其在污水处理、抽吸海水、港口疏浚、油田采油、液态金属冷却反应堆和液态金属磁流体转换器等众多领域有着广泛的应用^[4-10].
气力提升系统因其与传统机械泵相比有着无可比拟的优越性, 从二十世纪五六十年代以来, 国内外****做了大量的研究. 1963年, Nicklin^[11]研究了影响小管径气力提升装置提升性能的影响因素. 1965年, Futer^[12]发明了一种用于提升固体的气提装置. 1975年, 日本的Kato等^[13]实验研究了气力提升管中的多相流. 1985年, Kouremenos和Staicos^[14]实验研究了不同的提升管长度和浸没比对提升管内流型转变的影响. 1996年, Kajishima和Saito^[15]运用漂移流动模型模拟了深海采矿下大尺度气力提升系统内两相流流动情况. 1999年, Khalil等^[16]研究九种浸没比和三种提升管长度对气力提升系统提升性能的影响. 2000年之后, Furukawa和Fukano^[17]实验研究了气力提升系统内三种不同黏度的液体对提升性能的影响. Pougatch和Salcudean^[18]采用多流体欧拉方法, 将水作为连续相, 气泡和固体颗粒作为离散相开展了二维数值模拟计算, 模拟数据与试验结果符合. Moisidis和Kastrinakis^[19]对短气力提升系统内的两相流动行为和流型转化进行了实验研究. 高嵩等^[20]对气液混输管线与立管系统严重段塞流问题进行了数值模拟, 深入分析了内部流动规律和流动特性. 李洪伟等^[21]对毫米级小矩形通道内氮气-水气液两相流流型特性进行了研究, 发现四种典型流型三谱切片差异明显, 环状流较泡状流与段塞流更为复杂. 胡东等^[22]为揭示气力提升技术进气方式对其特性的作用机理及过程, 研究了气孔数量对排液量、排沙量以及提升效率的影响. Tighzert等^[23]通过实验研究探讨气力提升系统提升效率随浸没比和注入空气量的变化趋势. Fan等^[24]在千岛湖四个不同位置同一水下深度, 改变喷射喷嘴设计和不同空气流量, 研究其对气力提升系统整体性能的影响. Wahba等^[25]基于流体体积模型和大涡模拟了提升管内两相流型特征及其变化. Zuo等^[26,27]对带有气力提升系统的加速器驱动次临界反应堆进行深入研究, 探讨了气力提升系统对整个冷却回路自然循环能力的影响; 此外还建立了适用于不同进气方式的气力提升模型^[28], 通过改变进气面积与气孔分布方式对泵的水力特性进行试验研究.
综上所述, 目前对气力提升装置研究多集中在提升管内主要结构参数, 如浸没率、充气量、压力、提升管管径等对气力提升性能影响, 以及提升管内多相流流动特性与流型转化的研究. 但对于不同介质下, 介质密度对气力提升系统水力特性影响研究较少. 然而, 在实际工程中, 例如污水处理和抽吸海底高养分海水时, 会用到气水两相流的气力提升系统; 石油开采时, 会用到气油两相流的气力提升系统; 加速器驱动次临界反应堆和液态金属磁流体动力转换器中, 会用到惰性气体和高密度的液态金属气力提升系统. 因此, 本文基于Fluent软件对不同液体介质(氮气-水、氮气-煤油、氮气-水银)的气力提升系统以及不同气体介质(空气-水、氩气-水、氮气-水)的气力提升系统的提升性能进行了较详细的数值模拟研究, 分析了不同工况下提升液体能力及提升效率的变化规律, 为污水处理、抽吸海底高养分海水、气举采油、液态重金属冷却核反应堆和磁流体动力转换器等应用领域的气力提升技术的优化提供科学的理论基础.

2

-->

2.1.模型建立及网格划分

根据气力提升装置原理可将其装置简化为 图1(a), 将一根竖直提升管插入蓄水池内, 由注气管线通过喷嘴注入提升管内(因注气管线尺寸太小, 忽略其影响), 不断充气, 使提升管内形成复杂的气液两相流动, 液相连续相为主相, 气相分散相为次相. 因气力提升装置一般均为圆柱形结构, 提升管外部蓄水池直径远大于提升管直径, 且蓄水池直径对气力提升系统提升性能影响不大, 只要保证计算过程中蓄水池水位保持不变, 即可将其简化为如图1(b)所示的二维轴对称结构, 图1(b)上部图形为计算模型结构图, 其下面为对其进行的网格划分图. 图中提升管管长为2 m, 管径为30 mm, 喷嘴截面面积为197.92 mm², 浸没比为0.5. 本次网格划分采用结构化网格, 蓄水池较提升管内网格划分更为稀疏, 经网格无关性分析, 当网格总数为169600, 最小网格尺寸为0.5 mm时, 误差最小, 模拟效果最好. 本次模拟计算过程中, 选择Phase Coupled SIMPLE算法, 基于压力求解器进行求解. 初始条件下, 假设蓄水池充满液体, 由于蓄水池与提升管是联通的, 提升管内液位与蓄水池持平, 蓄水池顶部与空气接触, 液体进口边界条件为压力入口, 进气口设置为速度进口, 其值为标准大气压; 提升段出口与大气连通, 边界条件为压力出口边界, 压力值为标准大气压. 为保证计算精度, 采用高精度离散格式对各变量在时间和空间上进行离散, 体积份额及湍流强度采用QUICK离散格式, 时间项采用二阶隐式离散格式, 其余保持默认设置.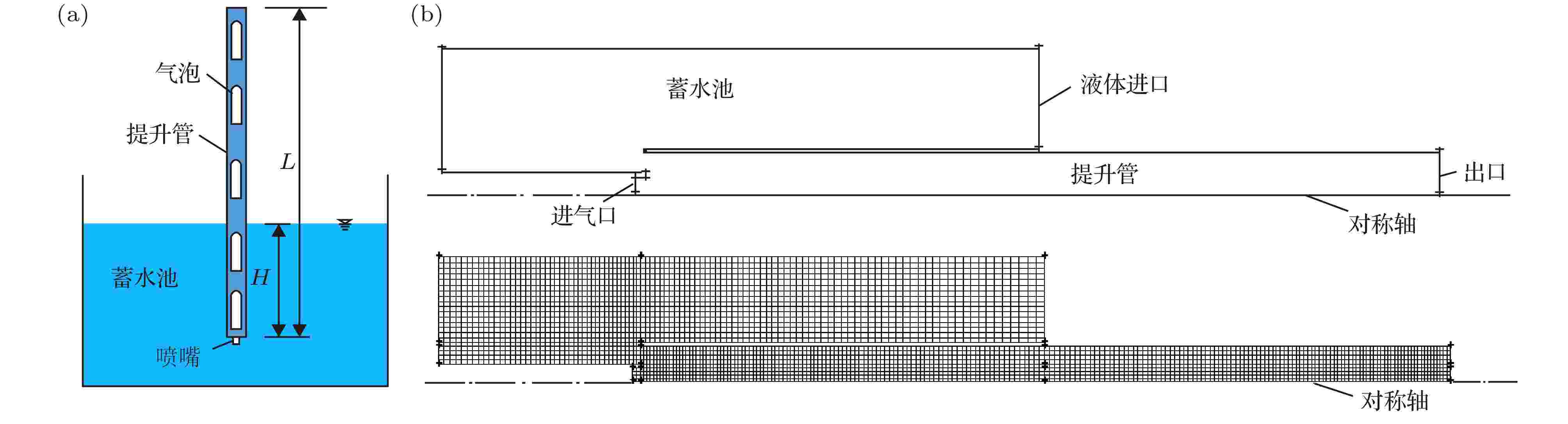
图 1 气力提升系统模型图　(a) 气力提升装置示意简图; (b) 模型及网格划分
Figure1. Model diagram of gas lift system: (a) Schematic diagram of gas lift system; (b) model and grid generation.

2 -->

2.2.控制方程^[29,30]

本文选用Eulerian多相流模型, 湍流模型采用k-ω剪切应力输运(shear stress transport, SST)模型研究气力提升系统中的多相流动.
质量守恒方程:

$\frac{\partial }{{\partial t}}\left( {{\beta _q}{\rho _q}} \right) + \nabla \cdot \left( {{\beta _q}{\rho _q}{{ v}_q}} \right) = \sum\limits_{p = 1}^n {({m_{pq}} - {m_{qp}})} + {S_p},$

式中${\beta _q}$, ${\rho _q}$, v_q分别表示第q项的体积分数、密度、速度; m_pq代表从p相到q相的质量传递, m_qp代表从q相到p相的质量传递, m_pq = –m_qp; S_p表示质量源项, 其值为0.
流体q相的动量守恒方程为

$\begin{split} &\frac{\partial }{{\partial t}}\left( {{\beta _q}{\rho _q}{{{v}}_q}} \right) + \nabla \cdot ({\beta _q}{\rho _q}{{{v}}_q}{{{v}}_q}) \\ ={}& - {\beta _q}\nabla p + \nabla \cdot {\overline{\overline \tau } _q} + {\beta _q}{\rho _q}{{g}} \\ &+ \sum\limits_{p=1}^n {\left[ {{K_{pq}}({{{v}}_p} - {{{v}}_q}) + {m_{pq}}{v_{pq}}} \right]} \\ & + \sum {{{{F}}_q}}, \end{split} $

式中${\overline{\overline \tau } _q}$为第q相压力应变张量, K_pq为相间动量交换系数, $\displaystyle\sum {{{{F}}_q}} $为外部体积力、升力、虚拟质量力等之和, g为重力加速度.

${K_{pq}} = \frac{{{\rho _p}f}}{{6{\tau _p}}}{d_p}{A_i},$

${\tau _p}=\frac{{{\rho _p}d_p^2}}{{18{\mu _q}}},$

$f = \frac{{{C_{\rm{D}}}{\mu _q}{A_i}\operatorname{Re} }}{{8{d_p}}}\left( {{{{v}}_p} - {{{v}}_q}} \right),$

${A_i} = \frac{{6{\alpha _{\rm{g}}}(1 - {\alpha _{\rm{g}}})}}{{{d_p}}},$

式中d_p是p相气泡的直径; ${\tau _p}$为颗粒弛豫时间; f为曳力函数; A_i为相界面密度; C_D为曳力系数; μ_q为液相分子黏性; α_g表示气相空泡份额, 也称截面含气率, 代表两相混合物流经任一截面时气相所占的面积与通道截面积之比.

$\begin{split}&{d_p}= \\{}& \begin{cases}\max \!\left\{\!{1.0 \!\times\! {{10}^{ - 5}},{d_{\min }}\exp\!\Big[\!{\dfrac{{ - K(\Delta {T_{{\rm{sub}}}}\!-\!\Delta {T_{\max }})}}{{{d_{\min }}}}}\!\Big]}\!\right\},\\ \quad\quad\quad\quad~ \quad\quad\quad\quad\quad\quad\quad\Delta {T_{{\rm{sub}}}} > 13.5\; {\rm K}, \\ {d_{\max }} \!-\! K( {\Delta {T_{{\rm{sub}}}} - \Delta {T_{\min }}} ), ~ \Delta {T_{{\rm{sub}}}} \!\leqslant\! 13.5\;{\rm K}, \end{cases}\end{split}$

$K = \frac{{{d_{\max }} - {d_{\min }}}}{{\Delta {T_{\max }} - \Delta {T_{\min }}}},$

其中$\Delta {T_{{\rm{sub}}}}$为液体过冷度; $\Delta {T_{\min }}$, $\Delta {T_{\max }}$为液体最小温差与最大温差; ${d_{\min }}$, ${d_{\max }}$为气泡最小直径与最大直径.
相间滑移速度v是因为气相与液相之间的速度不同, 两相之间存在相对速度:

${{v}} = {{{v}}_p} - {{{v}}_q}.$

基于均相湍流处理方法的k–ω SST模型^[31]的控制方程如下:

$\begin{split} & \frac{\partial }{{\partial t}}({\rho _{\rm{m}}}k) + \frac{\partial }{{\partial {x_i}}}({\rho _{\rm{m}}}k{u_{\rm{m}}}) \\ = \; &\frac{\partial }{{\partial {x_j}}}\left[ {\left( {{\mu _{\rm{m}}} + \frac{{{\mu _{{\rm{t}},{\rm{m}}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] \\ &+ {G_{k,{\rm{m}}}} - {Y_{k,{\rm{m}}}} + {\varPsi _{k,{\rm{m}}}} + {S_k}, \end{split} $

$\begin{split} &\frac{\partial }{{\partial t}}\left( {{\rho _{\rm{m}}}\omega } \right) + \frac{\partial }{{\partial {x_i}}}\left( {{\rho _{\rm{m}}}\omega {u_{\rm{m}}}} \right) \\ = \; &\frac{\partial }{{\partial x{}_j}}\left[ {\left( {{\mu _{\rm{m}}} + \frac{{{\mu _{{\rm{t}},{\rm{m}}}}}}{{{\sigma _w}}}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right]\\ & + {G_{\omega,{\rm{m}}}} - {Y_{\omega,{\rm{m}}}} + {\varPsi _{\omega,{\rm{m}}}} + {S_\omega },\end{split} $

式中ρ_m为混合物密度; v_m为混合物速度; μ_m为混合物分子黏度; μ_t,m为混合物湍流黏性; σ_k, σ_ω为湍流普朗特数; G_k,m, G_ω,m为湍流产生项; Y_{k, m}, Y_ω,m为k和ω因湍动产生的耗散相; Ψ_k,m, Ψ_ω,m为气液相相互作用导致的湍动能增量; S_k, S_ω为湍动能源项.
提升效率是评测气力提升系统性能的关键指标, 本文效率公式使用Oueslati和Megriche^[32]文中的效率公式:

$\eta = \frac{{{m_{\rm{L}}}}}{{{m_{\rm{G}}}}},$

式中${m_{\rm{L}}}$代表提升液体质量流量, ${m_{\rm{G}}}$代表充入气体的质量流量.

Oueslati和Megriche^[32]设置了一个气力提升实验系统, 用来研究在不同浸没比下液体温度对气力提升系统的影响. 装置如图2所示, 主要由供气装置、给水装置、加热装置及气液两相流发生装置构成. 提升管长为2 m, 管径为30 mm. 液体通过加热装置和温度计控制液体温度, 由给水罐及下降管调节提升管内的液面初始高度, 从而控制浸没比. 压缩机产生的空气通过管路系统传输到提升管内, 提升管的上端与蓄水槽相连, 被提升的液体通过提升管排入蓄水槽, 空气从蓄水槽中逸出, 被提升到蓄水槽中的水又通过管道流入给水罐, 其气体流量由气体流量计测量, 提升的液体流量通过液体流量计来测量, 整个实验构成了一个循环系统.
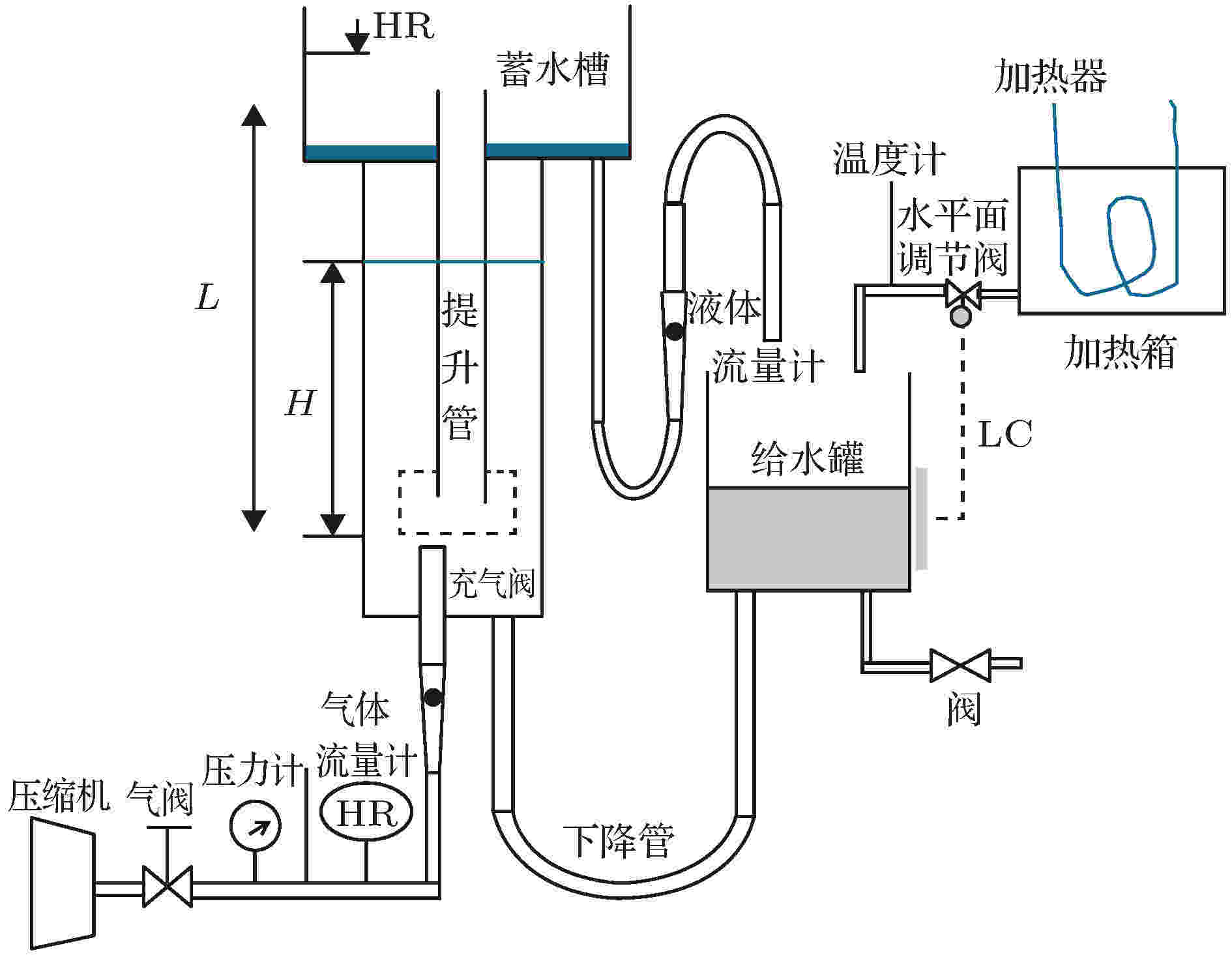图 2 实验装置图^[32]
Figure2. Experimental apparatus system^[32].

本文以Oueslati和Megriche^[32]所做的提升管管径为30 mm, 浸没比为0.5, 液体温度为60 ℃空气-水气力提升系统实验数据为依据, 验证本文数值模拟模型的准确性, 表1列出了提升液体流量实验值$ {Q}^{\prime}_{\rm L} $与模拟值Q_L的对比结果, 由表1可知实验数据与模拟数据符合较好, 故此模型可应用于气力提升系统数值模拟研究.

充气量QG/m3·h–1	提升液体流量 实验值$ Q′_{\rm L} $/m3·h–1	提升液体流量 模拟值QL/m3·h–1	误差/%
0.8163	0.4031	0.4597	14.0
1.6327	0.5700	0.8117	42.4
2.4490	1.2336	1.1817	4.2
3.2653	1.3676	1.3665	0.1
4.0816	1.3709	1.3786	0.6
4.8980	1.3735	1.3848	0.8
5.7143	1.3735	1.3705	0.2

表1实验结果与模拟结果的对比
Table1.Comparison of experimental and simulation results.

气力提升系统内气液两相流动特性与气液物性参数有关, 在出口边界设置适当的回流系数, 本文是在常温常压下, 当提升管管长为2 m、管径为30 mm, 浸没比为0.5时, 分别对不同液体介质(氮气-水银, 氮气-水, 氮气-煤油)、不同气体介质(氮气-水, 空气-水, 氩气-水)多种气力提升系统内的气液两相流动进行数值模拟研究, 探讨气体注入量对提升管内气相体积分数、提升液体体积流量、出口处提升液体速度、提升效率的影响. 表2列出了相关变量的物性参数.

变量	密度/kg·m–3	黏度/Pa·s	表面张力/N·m–1
氮气	1.1380	0.00001663
空气	1.2250	0.000017894
氩气	1.6228	0.000021250
水银	13529	0.001523	0.4840
水	998.2	0.001003	0.0728
煤油	780	0.0024	0.0260

表2物性参数表
Table2.Physical parameters table.

2

-->

4.1.气相体积分数变化趋势

图3描绘了不同液体和气体介质下, 提升系统稳定时, 提升管内气相体积分数β与充气量Q_G之间的变化规律. 由图3可知, 随着充气量不断增加, 气相体积分数先快速增加后增加缓慢, 这是因为在气量较低时, 管内主要以小气泡形式存在, 相界面密度较大, 相间曳力较大, 相间滑移速度减小, 管内气相体积分数随充气量的增加而迅速增大. 当气体注入流量不断增加时, 小气泡逐渐凝聚, 形成弹状流、搅混流、环状流, 相界面密度变小, 相间曳力变小, 相间滑移速度增大, 管内气相体积分数的增加速率变缓. 图3(a)描述了煤油、水、水银三种不同液体介质时, 提升立管内气相体积分数随氮气流量的变化关系. 由图3(a)可知, 煤油的气相体积分数最大, 水次之, 水银最大. 说明在相同气流量下, 液体介质密度越大, 气液两相间曳力越大、相滑移速度越小、管内气相体积分数越小. 图3(b)描述了当气体介质为氮气、空气、氩气来提升液体水时, 提升立管内气相体积分数随气流量的变化. 由 图3(b)可知, 在低充气量下, 提升管内三种不同气体介质下的气相体积分数相差不大, 然而当充气量超过1.6327 m³/h时, 管内气相体积分数发生较大差异, 氮气气相体积分数最大, 而氩气最小. 说明在相同气流量下气体介质密度越大, 相间曳力越大、相滑移速度越小、管内气相体积分数越小.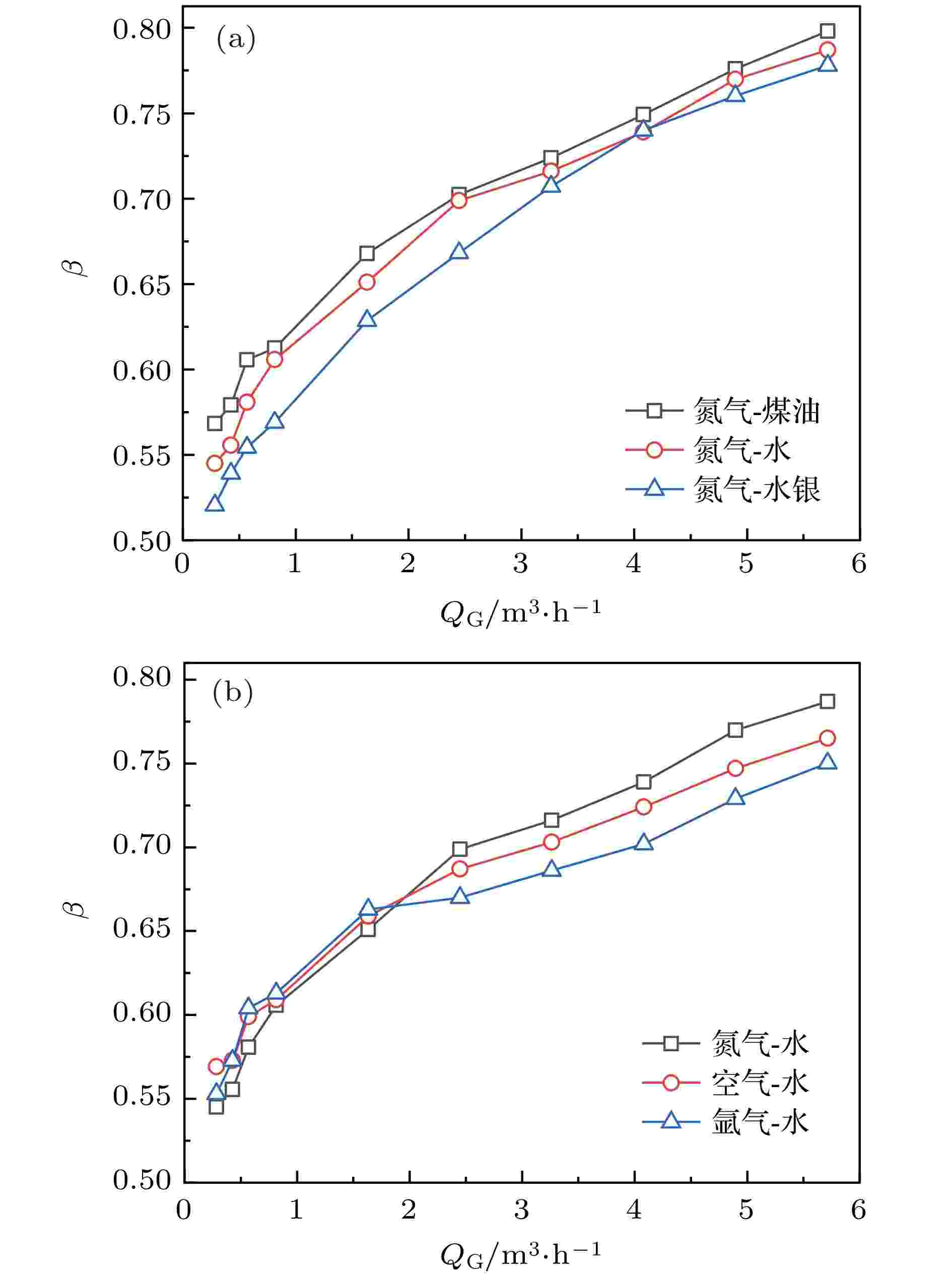
图 3 提升管内气相体积分数随充气量的变化　(a) 不同液体介质; (b) 不同气体介质
Figure3. Change of gas volume fraction with gas volume flow rate in lifting pipe: (a) Different liquid mediums; (b) different gas mediums.

2 -->

4.2.液体提升过程随时间演变规律

气力提升系统依靠向提升管内注入压缩气体产生提升压头, 使提升段内液体流动, 产生流量. 图4反映了不同液体介质和气体介质下, 当充入氮气量为4.0816 m³/h时, 提升液体流量Q_L随时间t的变化. 图5描绘了当充入氮气量为4.0816 m³/h时液态水提升过程的相位图. 图5中, 初始时刻提升管内液体液位与蓄水池液位持平, 气体经喷嘴注入到提升管段, 气泡在液体中上升, 0—0.4 s管内小气泡立刻聚集, 形成弹状气泡, 提升管内液体出现流动, 此时并未有液体从出口处排出, 0.9 s时刻当弹状气泡聚集足够大时, 管内又重新开始聚集新的弹状气泡. 初始时间段内因管内气量较少, 液柱较重, 气体从提升管下侧逸出, 随着时间推移, 提升管内气体体积分数逐渐增大, 提升管内形成气体通道, 气体不再向外逸出. 由图4可看出, 1.5 s左右液体逐渐从提升管内排出. 之后, 由图5可知, 管内气体占比越来越多, 在1.4—4.4 s提升管内主要为弹状流与搅混流, 10 s之后提升管气泡逐渐连通, 流型逐渐转变为环状流.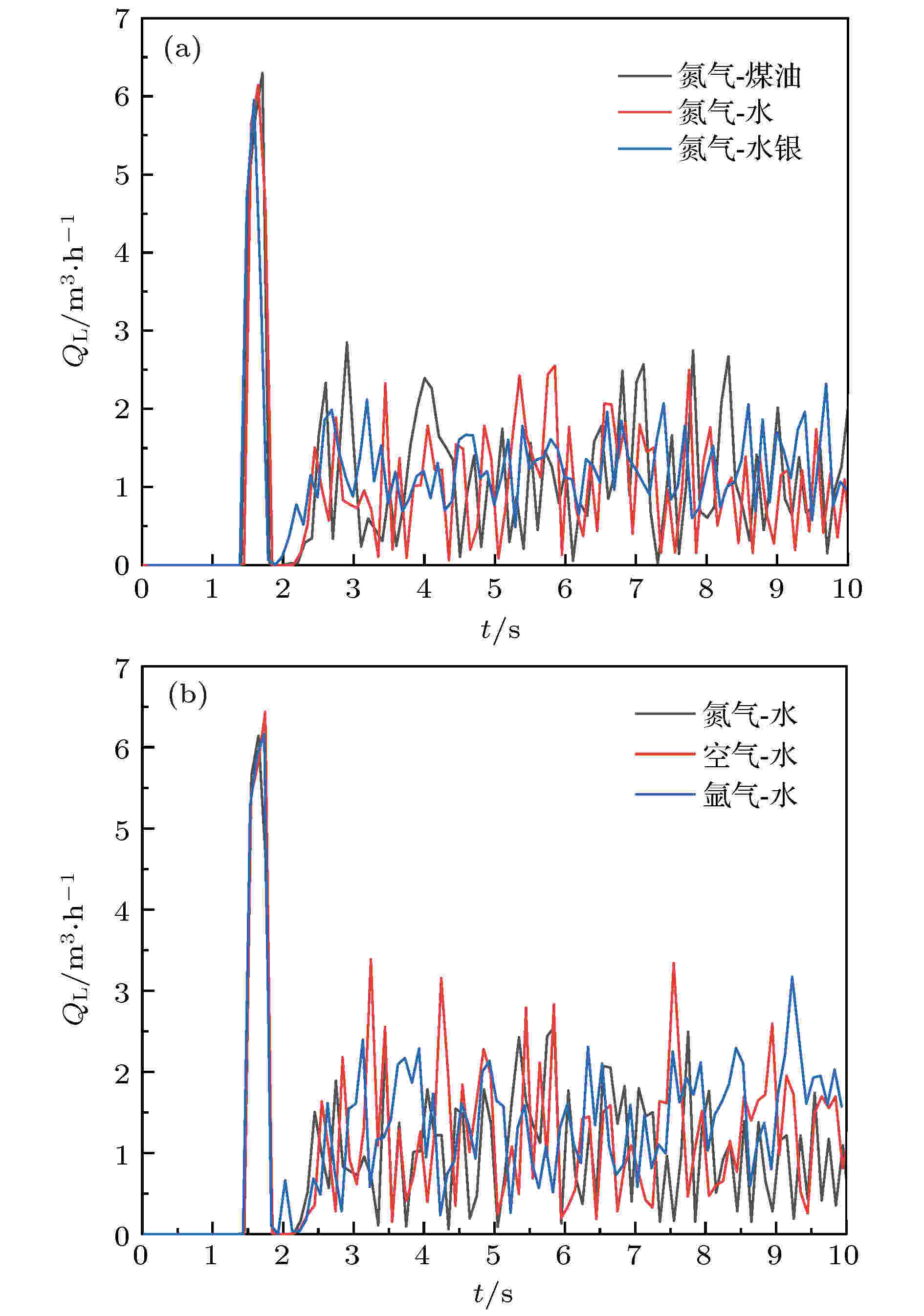
图 4 提升液体流量随时间的变化　(a) 不同液体介质; (b) 不同气体介质
Figure4. Change of liquid volume flow rate with time: (a) Different liquid mediums; (b) different gas mediums.

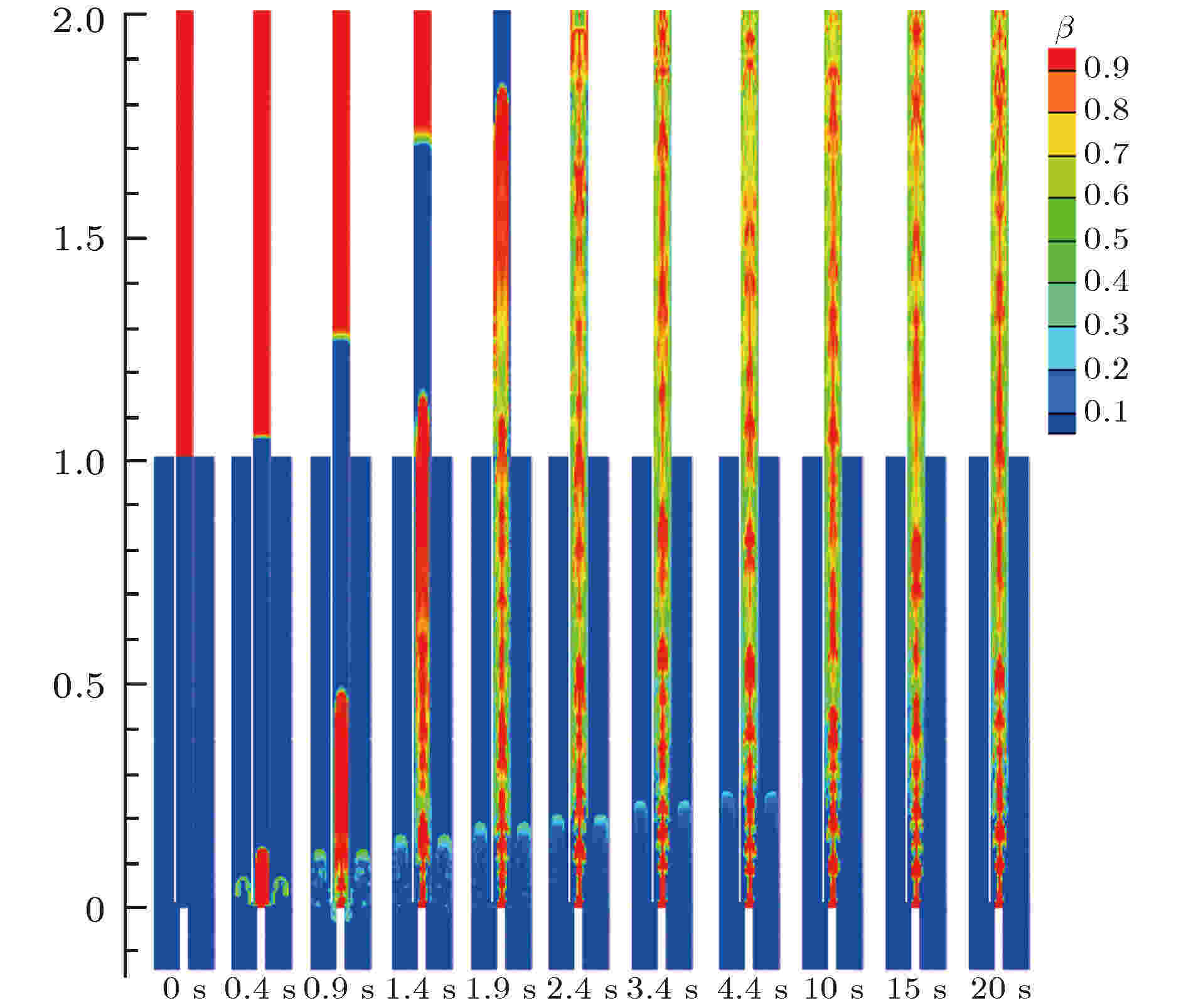图 5 液体提升过程相位图
Figure5. Phase diagram of liquid lifting process.

2 -->

4.3.提升液体体积流量变化趋势

图6为提升系统稳定时, 不同液体介质和气体介质下, 液体提升流量Q_L随气流量Q_G的变化关系图. 由图6(a)可知, 氮气-水银, 氮气-水, 氮气-煤油三种不同工况下, 提升液体流量随充气量的增加先迅速升高, 当气流量为3.2653 m³/h时, 水银提升流量达到峰值, 当充气量为4 m³/h附近时, 煤油及水提升流量达到峰值, 这是因为, 随着充气量的继续增加, 提升管内混合相密度越来越小, 蓄水池与提升管间的驱动力增大, 提升液体流量就越多. 继续增大充气量, 整个提升管内气相份额变大, 液相份额变小, 提升流量小幅度缓慢下降. 同一充气量下, 水银提升流量最大, 水次之, 煤油最小, 结合图7(a)不同液体介质提升管内总压降p随充气量Q_G变化图, 反映出液体密度越大, 提升管进出口总压降越大, 则越易提升液体, 提升流量越大.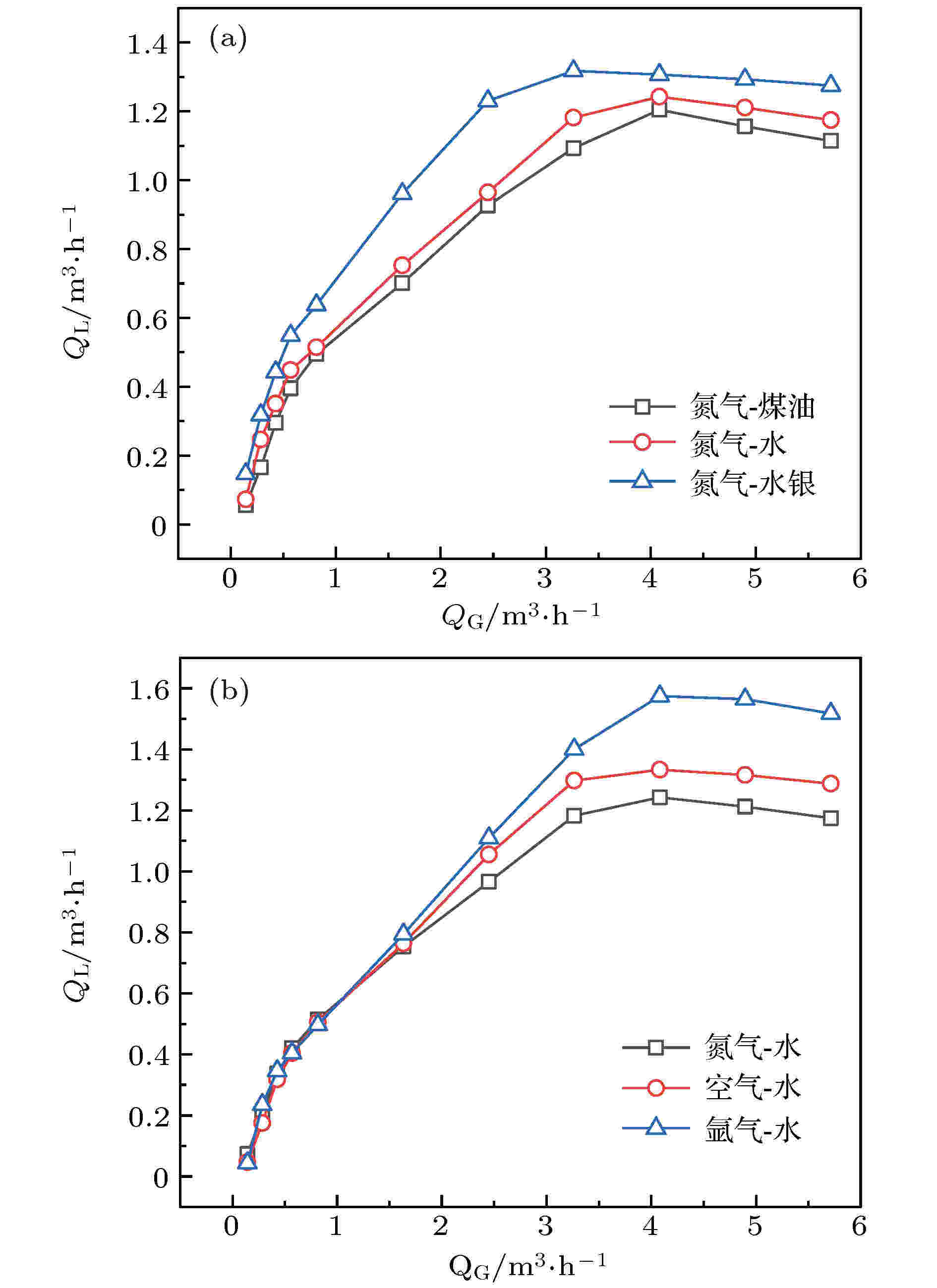
图 6 提升液体流量随充气量的变化　(a) 不同液体介质; (b) 不同气体介质
Figure6. Change of liquid volume flow rate with gas volume flow rate: (a) Different liquid mediums; (b) different gas mediums.

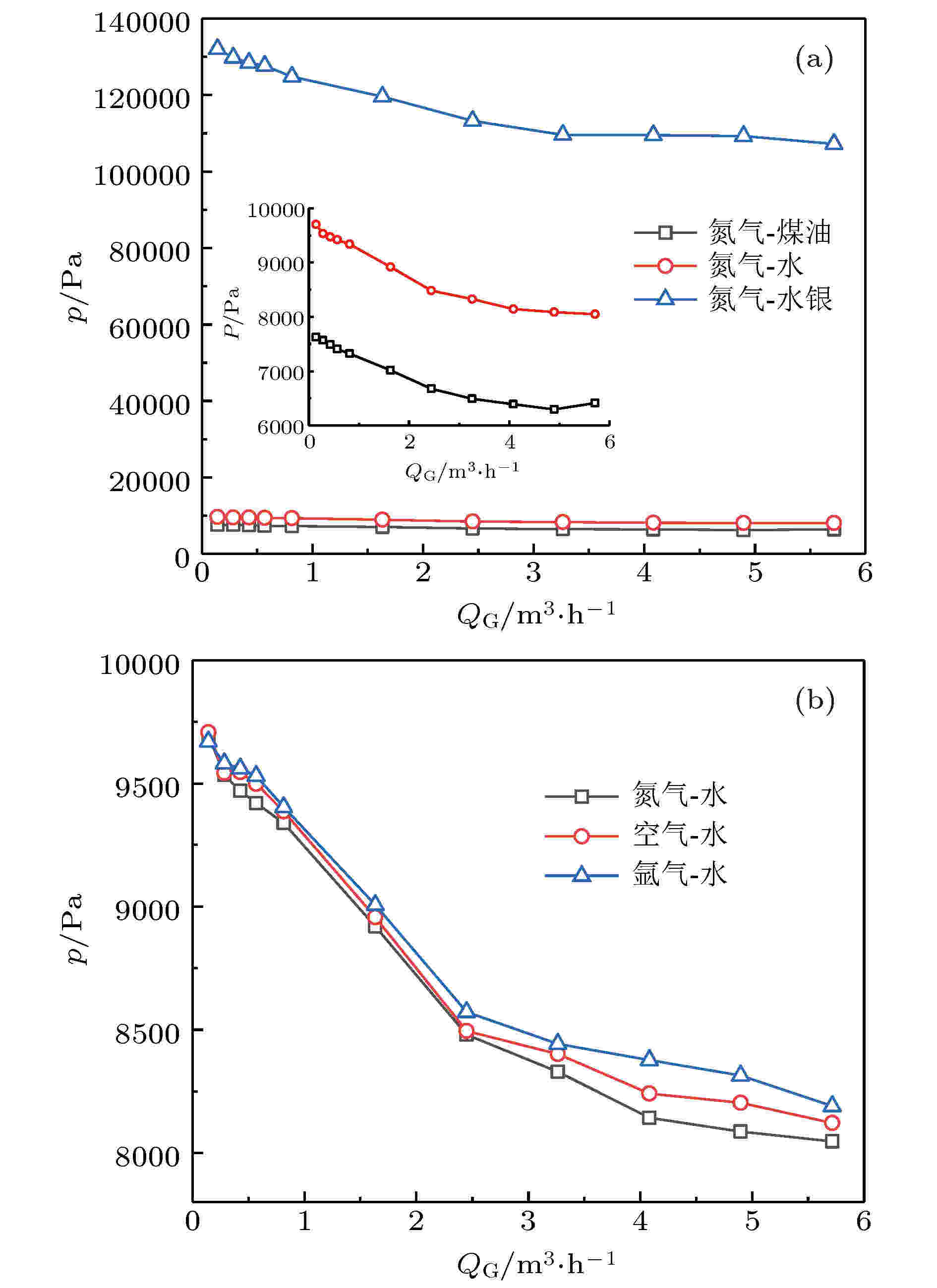图 7 提升管总压降随充气量的变化　(a) 不同液体介质; (b) 不同气体介质
Figure7. Change of total pressure drop with gas volume flow rate in lifting pipe: (a) Different liquid mediums; (b) different gas mediums.

由图6(b)可知, 氮气-水, 空气-水, 氩气-水三种不同工况下, 气流量较低时, 向提升管内水中充入不同密度的气体对提升液体流量的影响不大, 当充气量大于0.8 m³/h时, 三种气体提升的液体流量产生较大差异, 氩气提升流量最大, 空气次之, 氮气最小. 由图7(b)不同气体介质提升管内总压降p随充气量Q_G变化图可知, 氩气提升水提升管内总压降最大, 则其驱动力最大, 氮气最小, 驱动力最小. 说明气力提升系统的驱动气体密度越大, 液体越易提升.
2 -->

4.4.提升液体速度变化趋势

图8为系统稳定时不同液体和气体介质下, 气流量由低到高过程中提升管出口处提升液体速度沿径向分布图. 由图8(a)可知, 氮气-水银、氮气-水、氮气-煤油三种不同工况下, 管轴中心附近的液体速度较大, 管壁附近的液体速度较小. 这是因为喷嘴位于管轴中心, 致使气流量推动管轴中心液体向上流动, 而管壁是静止状态, 故引起管轴中心液体速度最大, 管壁最小. 当充气量小于0.8163 m³/h时三种液体出口速度相当; 充气量大于0.8163 m³/h时三种液体速度差异变大, 随着气流量增大, 提升管出口处三种液体的速度整体升高, 且径向速度出现较大波动, 由图6可知, 此现象是因为在低充气量下, 不同液体对提升流量影响较小, 进而提升管出口断面提升液体速度相当, 随充气量的增大, 不同液体间提升流量差值增大, 径向速度差值增大. 由图8(b)可知, 三种不同气体氮气、空气、氩气提升液体水时, 管轴中心附近的液体速度较大, 管壁附近的液体速度较小. 当充气量低于2.4490 m³/h时, 提升管出口处, 三种气体提升的液体速度相当, 当充气量大于2.4490 m³/h时, 三种气体提升的液体速度差异变大, 随着气流量增大, 液体速度整体趋势增大, 且三种不同气体提升液体的径向速度出现波动, 惰性气体氮气、氩气提升液体的速度增长幅度高于空气.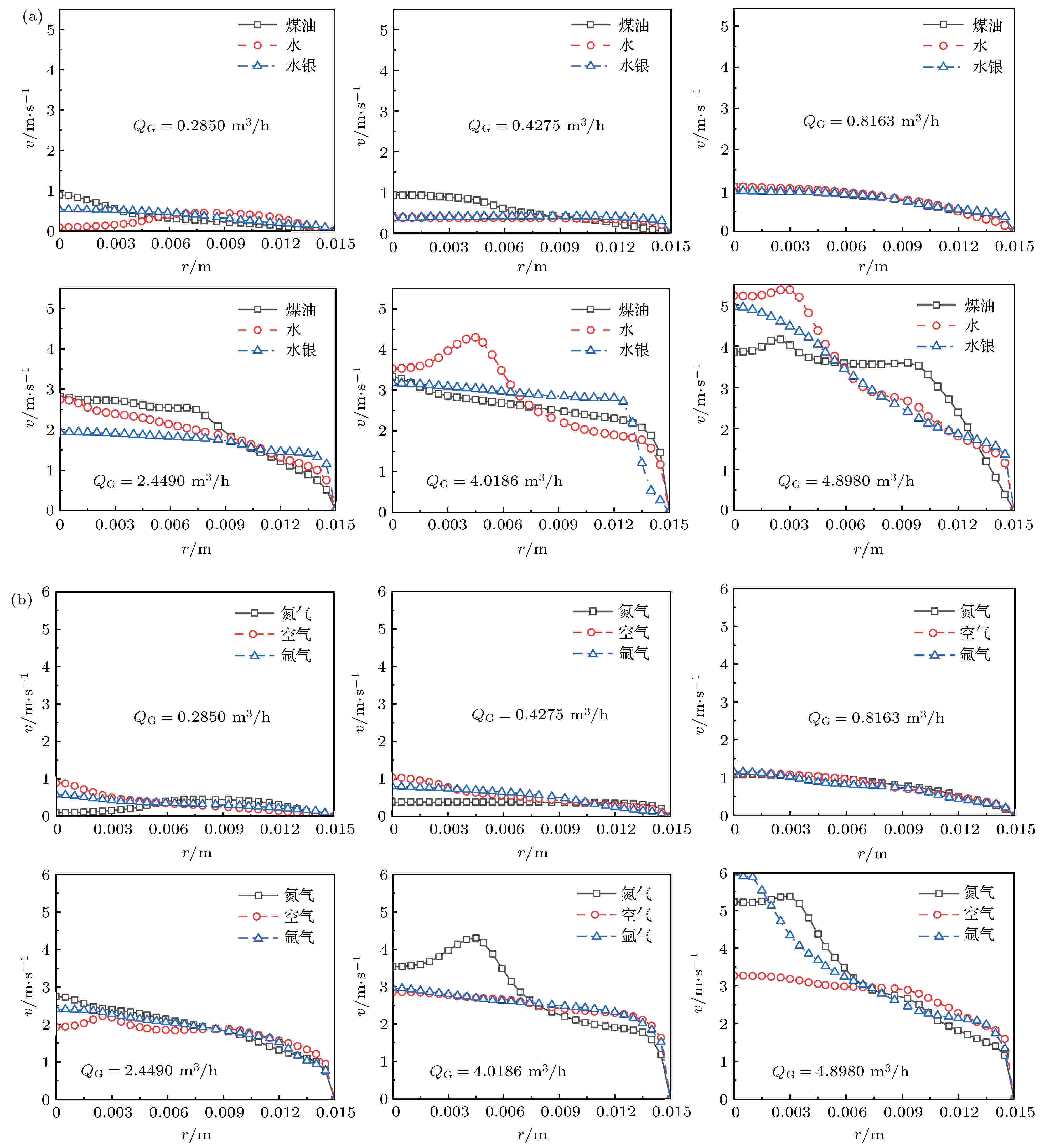
图 8 不同充气量下提升管出口处液体速度径向分布　(a) 不同液体介质; (b) 不同气体介质
Figure8. Liquid radial velocity at lifting pipe outlet under different gas volume flow rates: (a) Different liquid mediums; (b) different gas mediums.

2 -->

4.5.提升效率变化趋势

图9描述了不同液体介质和不同气体介质气力提升系统稳定时, 液体提升效率η随充入气体质量流量m_G的变化趋势. 图9(a)为氮气-煤油、氮气-水、氮气-水银三种工况下气力提升效率变化图, 由于煤油、水与水银密度差值较大, 故将其放大图置于该图右上角. 由图9(a)可知, 三种液体介质下, 提升效率均先升高后降低, 这是因为, 随着提升管内流型逐渐由泡状流过渡到弹状流, 气相体积分数越来越大, 液体提升量迅速升高, 提升效率增加, 后随着充气量不断增大, 提升管内液体提升速度变缓, 提升效率逐渐降低. 当液体介质为水银时, 提升效率明显大于液体介质为水和煤油, 说明液体密度越高, 提升效率越大. 图9(b)为氮气-水、空气-水、氩气-水三种工况下气力提升效率变化图, 由图9(b)可知, 三种气体介质下, 提升效率均先升高后降低, 但效率数值接近, 当气体质量流量m_G分别为0.4865, 0.5237和0.4625 kg/h时, 氮气-水、空气-水、氩气-水效率达到峰值, 其中氮气-水气力提升系统效率峰值点最高, 氩气-水最低, 这主要因为相同气体体积流量下, 气体介质密度不同, 气体质量流量不同, 故计算提升效率时气体密度越小, 对其效率影响越大, 计算结果反而越大. 随充气量的增大, 空气-水气力提升系统提升效率逐渐超过氮气-水, 继续增大充气量, 氩气-水气力提升系统的效率反超空气-水、氮气-水, 此后, 氩气-水提升效率最大, 氮气-水最小. 气体介质为氮气时提升效率峰值点最大, 空气次之, 氩气最小, 说明气体介质密度越大, 提升效率峰值点越小.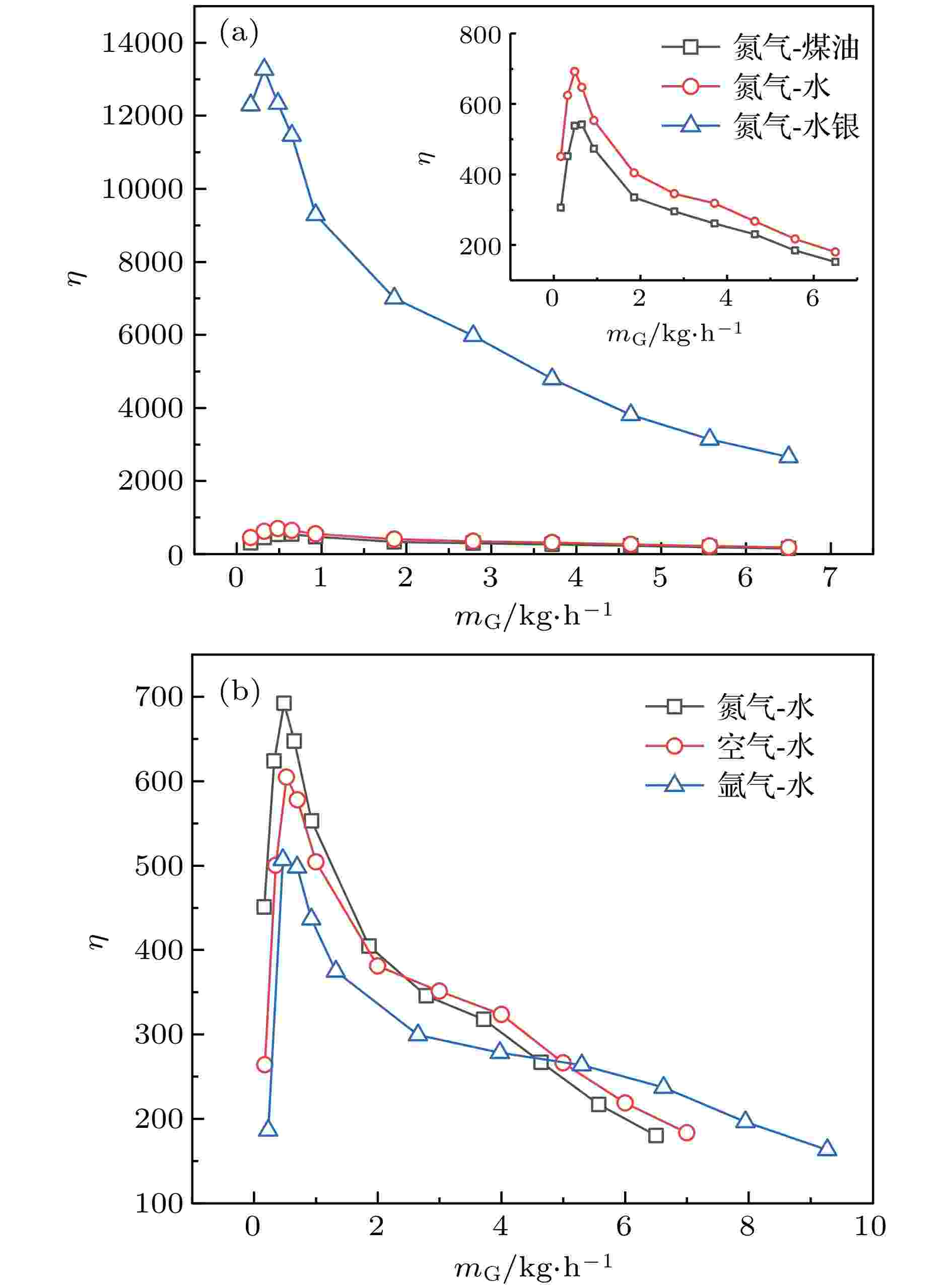
图 9 提升液体效率随充气量的人变化　(a) 不同液体介质; (b) 不同气体介质
Figure9. Change of lifting efficiency with gas mass flow rate: (a) Different liquid mediums; (b) different gas mediums.

本文通过Fluent软件对浸没比为0.5, 提升管径为30 mm, 在常温常压下三种不同液体介质氮气-水、氮气-水银、氮气-煤油与三种不同气体介质氮气-水、空气-水、氩气-水的气力提升系统进行了数值模拟, 探讨介质密度对气力提升系统提升性能影响, 结论如下:
1)同一介质下, 提升管内气相体积分数随充气量的升高先快速增加后增加速率变缓. 在相同气流量下, 液体介质密度越大, 气体介质密度越大, 管内气相体积分数越小;
2)同一介质下, 液体提升流量随注气量的增加先快速增多, 后增加缓慢, 到达最大值后又缓慢下降. 同一充气量下, 液体提升流量随液体密度和气体密度的增大而增大;
3)提升管出口处提升液体径向速度随气体充入量的不断增加而整体波动升高, 最终管轴中心附近液体速度较大, 管壁附近液体速度较小;
4)同一介质下, 随着充气量的增加, 提升效率先显著增加到达峰值后又降低; 同一充气量下, 液体介质密度越大, 提升效率越高; 气体介质密度越小, 提升效率峰值点越高.