摘要: 本文提出了一种基于新的五维多环多翼超混沌系统的数字图像加密方法. 首先, 将明文图像矩阵和五条混沌序列分别通过QR分解法分解成一个正交矩阵和一个上三角矩阵, 将混沌系统产生的五条混沌序列分别通过LU分解法分解成一个上三角矩阵和一个下三角矩阵, 分别将两个上三角矩阵和一个下三角矩阵相加, 得到五个离散后的混沌序列; 其次, 将明文图像矩阵分解出来的正交矩阵与五个混沌序列分解出来的五个正交矩阵相乘, 同时把明文图像矩阵分解出来的上三角矩阵中的元素通过混沌序列进行位置乱, 再将操作后的两个矩阵相乘; 最后, 将相乘后的矩阵通过混沌序列进行比特位位置乱, 再用混沌序列与其进行按位“异或”运算, 得到最终加密图像. 理论分析和仿真实验结果表明该算法的密钥空间远大于10
200 , 密钥敏感性强, 能够有效地抵御统计分析和灰度值分析的攻击, 对数字图像的加密具有很好的加密效果.
关键词: 五维超混沌系统 /
正交分解 /
比特位扰乱 /
数字图像加密 English Abstract Image encryption algorithm based on new five-dimensional multi-ring multi-wing hyperchaotic system Zhuang Zhi-Ben 1 ,Li Jun 2 ,Liu Jing-Yi 1 ,Chen Shi-Qiang 3 1.School of Science, Hubei Mimzu University, Enshi 445000, China Received Date: 05 September 2019Accepted Date: 21 November 2019Published Online: 20 February 2020Abstract: The complex structure of hyperchaos and its complex dynamic behavior have a good application prospect in the fields of image encryption, digital watermarking and information security. Therefore, it has become very important to generate chaotic attractors with multi-vortex and multi-winged multi-rings with complex topologies. In this paper, we propose a new five-dimensional hyperchaotic system capable of generating multi-ring and multi-wing, and carry out theoretical analysis and numerical simulation experiments on some basic dynamic characteristics of the chaotic system. Such as equilibrium point, dissipation, Lyapunov exponent, bifurcation diagram, phase diagram and so on. In the process of encryption, first, we decompose the plaintext image matrix and the five chaotic sequences into an orthogonal matrix and an upper triangular matrix by QR decomposition. The five chaotic sequences generated by the chaotic system are respectively decomposed into an upper triangular matrix and a lower triangular matrix by the LU decomposition method. The upper triangular matrix decomposed by the QR decomposition method and the lower triangular matrix decomposed by the LU decomposition method are respectively added to obtain five discrete chaotic sequences. At the same time, the five discrete chaotic sequences are added to the upper triangular matrix decomposed by the LU decomposition method to obtain the final five discrete chaotic sequences. Secondly, the orthogonal matrix decomposed by the plaintext image matrix is multiplied by five orthogonal matrices decomposed by five chaotic sequences. At the same time, the elements in the upper triangular matrix decomposed by the plaintext image matrix are chaotically arranged by the chaotic sequence, and then the two matrices after the operation are multiplied. Finally, the multiplied matrix is chaotically placed on the bit by a chaotic sequence. Then use the chaotic sequence to perform a bitwise XOR operation to obtain the final encrypted image. The theoretical analysis and simulation results show that the algorithm has large key space and strong key sensitivity. It can effectively resist the attacks of statistical analysis and gray value analysis, and has good encryption effect on digital image encryption. This image encryption algorithm using a combination of conventional encryption and chaotic encryption does not have a defined plaintext ciphertext mapping relationship.Keywords: five-dimensional hyperchaotic system /orthogonal decomposition /bit disturb /digital image encryption 全文HTML --> --> --> 1.引 言 在网络高速发展的今天, 保密通信已成为当今备受关注的一个热门话题, 其中混沌系统和超混沌系统的复杂结构和动力学行为在通信保密中有着很好的应用前景. 因此, 构造出能够产生具有复杂拓扑结构的超混沌系统是非常重要的.[1 -4 ] ; 二是在三维混沌系统的基础上, 增加一个新的状态反馈控制器来构造出超混沌系统[5 -7 ] , 这就使得到的新混沌系统满足超混沌系统的必要条件. 在构造的过程中, 必须将新增加的控制器反馈到原始的控制器中, 同时将原始控制器反馈到新的控制器中, 这两个操作能够使此系统的四个控制器之间互相影响, 可使得关系更加复杂; 三是通过多个正李氏指数来构造超混沌系统[8 ] . 1979年, Rossler首次提出了超混沌系统, 从此, 专家和****就相继提出了一些超混沌系统. 2014年与2015年, 彭再平等[6 ] 和刘杨[7 ] 分别提出的新的四维超混沌系统结构简单, 动力学特征复杂, 但不具有多环的特征, 且刘杨的系统方程处于混沌状态的参数不够大. 本文提出了一种五维多环多翼超混沌系统, 能够产生明显的多环和多翼, 系统处于混沌状态的参数范围大, 且系统方程结构简单, 没有平衡点.[9 ,10 ] . 因此, 专家和****提出了许多基于混沌的图像加密算法. 为了提高后续密码系统的安全性, 2016年, Zhang等[11 ] 提出基于3D比特位矩阵的混合置换架构; 2018年, Luo等[12 ] 根据密钥和明文图像信息, 设计了一种新颖的并行量化方法. 而在图像的加密过程中, 主要是改变其像素的位置和像素值的大小, 目前主要有三种方法, 一是在比特位上用混沌序列进行行列扰乱, 二是直接对明文图像进行像素位置扰乱和改变像素值的大小[13 -15 ] , 三是用可逆矩阵去乘明文图像矩阵. 针对方法一, 2018年, He等[16 ] 提出对比特位高位进行扰乱, Raza和Satpute[17 ] 提出先对高6位进行处理, 紧接着再对低6位进行扰乱, 但所用的混沌系统都不是超混沌系统, 也不能产生多环; 针对方法三, 2017年, Ahmad等[18 ,19 ] 提出用正交矩阵去乘以明文图像矩阵, 以达到改变像素值的目的, 但不能很好地克服计算机精度对复杂的混沌动力学特性迅速退化问题. 在本文提出的方案中, 当混沌系统的参数$f \in (0, 50)$ 时, 混沌系统都处于混沌状态; 将原文图像进行${\rm{QR}}$ 分解, 分别对正交矩阵${{Q}}$ 和上三角矩阵${{R}}$ 进行处理; 同时将混沌系统产生的5条混沌序列进行了${\rm{QR}}$ 分解和${\rm{LU}}$ 分解处理, 通过这些处理, 增大了穷举攻击的难度, 除穷举之外的一切基于明确的明文密文映射的攻击方法, 对该方法都将失效, 具有较高的安全性.2.相关知识 22.1.矩阵的一些基本性质及运算规律 2.1.矩阵的一些基本性质及运算规律 设${{Q}}$ 是一个正交矩阵, ${{P}}$ 为与${{Q}}$ 满足乘法条件的一般矩阵, 那么:${{Q}}$ 的逆一定存在并且有${{{Q}}^{ - 1}} = {{{Q}}^{\rm{T}}}$ ;${{{Q}}^{ - 1}}{{Q}} = {{{Q}}^{\rm{T}}}{{Q}} = {{Q}}{{{Q}}^{ - 1}} = {{Q}}{{{Q}}^{\rm{T}}} = {{E}}$ , (其中${{E}}$ 为单位矩阵);${{A}} = {{QP}}$ , 那么${{P}} = {{{Q}}^{ - 1}}{{A}} = {{{Q}}^{\rm{T}}}A$ ;${{{Q}}_1}, {{{Q}}_2}, ..., {{{Q}}_n}$ 都是与${{Q}}$ 具有相同行列的正交矩阵, 且${{{A}}_1} = {{{Q}}_1}{{{Q}}_2}...{{{Q}}_n}{{P}}$ , 则${{P}} = {{Q}}_n^{ - 1}{{Q}}_{n - 1}^{ - 1}...{{Q}}_1^{ - 1}{{{A}}_1}$ .2.2.矩形矩阵的正交分解与一般方阵的高斯消去法分解 -->2.2.矩形矩阵的正交分解与一般方阵的高斯消去法分解 矩形矩阵的正交分解又称${\rm{QR}}$ 分解. ${\rm{QR}}$ 分解是把一个$m \times n$ 的矩阵${{A}}$ 分解成一个正交矩阵${{Q}}$ 和一个上三角矩阵${{R}}$ . 即设矩阵$[{{Q}}{\rm{, }}{{R}}] = {\rm{qr}}({{A}})$ , 就可以把矩阵${{A}}$ 分解成一个正交矩阵${{R}}$ 是与矩阵${{A}}$ 具有相同大小的上三角矩阵, 矩阵${{Q}}$ 是$m \times m$ 矩阵, 并且还要满足${\rm{LU}}$ 分解. ${\rm{LU}}$ 是把任意一个方阵${{X}}$ 分解成一个下三角矩阵${{L}}$ 和一个上三角矩阵${{U}}$ . 即设矩阵$[{{L}}, {{U}}] = {\rm{lu}}({{X}})$ , 就可以把矩阵${{X}}$ 分解成一个下三角矩阵${{L}}$ 和${{U}}$ 都与方阵${{X}}$ 具有相同的大小. 并且满足3.新的五维多环多翼超混沌系统 1994年, Sprott[20 ] 总结了许多三维混沌系统, 其A系统方程如下:$w, v$ , 并将原始控制器$y$ 反馈到新的控制器$w$ 中, 将原始控制器$z$ 反馈到新的控制器$v$ 中, 这两个操作能够使此系统的五个控制器之间互相影响, 可使得关系更加复杂. 新构造出来的五维多环多翼超混沌方程如下:a , b , c , d , e , f , g 是系统参数，且均取大于0的数.3.1.Lyapunov指数谱分析 3.1.Lyapunov指数谱分析 混沌方程的主要动力学特性可以通过它的Lyapunov指数谱来进行分析. 当系统参数$a = 1.5$ , $b = c = d = e = f = g = 1$ 时, 该系统的Lyapunov指数谱如图1 所示. 从图1 中可以明显地看出, 该系统有两个Lyapunov指数为正, 一个Lyapunov指数为零, 还有两个Lyapunov指数为负, 因此系统(2)处于超混沌状态.图 1 Lyapunov指数谱Figure1. Lyapunov exponent diagram.3.2.平衡点分析 -->3.2.平衡点分析 令$\dot x = \dot y = \dot z = \dot w = \dot v = 0$ , 即$a, b, c, d, e, f, g$ 取大于0的任何值, 方程(3 )都没有解, 因此该系统方程无平衡点.3.3.分岔图分析 -->3.3.分岔图分析 方程参数$a = 1.5$ , $b = c = d = e = g = 1$ , 参数$f$ 在变化时, 关于$f$ 的分岔图如图2 所示. 从图2 中可以看出, 当$f \in (0, 50)$ 时, 系统(2)都是处于混沌状态. 因此, 该系统处于混沌状态的参数动态范围很大.图 2 系统(2)随$f$ 变化的分岔图Figure2. Bifurcation diagram of system (2) variation with $f$ .3.4.时间序列图 -->3.4.时间序列图 当系统参数$a = 1.5$ , $b = c = d = e = f = g = 1$ 时, $x, y, z, w, v$ 的值随时间$t$ 的变化序列图如图3 所示. 从图3 中也可以看出, 在系统参数$a = 1.5$ , $b = c = d = $ $e = f = g = 1$ 时, 系统(2)处于混沌状态.图 3 时间序列图 (a) $x\text- t$ 时间序列; (b) $y \text- t$ 时间序列; (c) $z \text- t$ 时间序列; (d) $w \text- t$ 时间序列; (e) $v \text- t$ 时间序列Figure3. Time series diagram: (a) $x \text- t$ time series; (b) $y \text- t$ time series; (c) $z \text- t$ time series; (d) $w \text- t$ time series; (e) $v \text- t$ time series3.5.五维多环多翼混沌相图 -->3.5.五维多环多翼混沌相图 当系统参数$a = 1.5$ , $b = c = d = e = f = g = 1$ 时, 系统(2)产生的多环多翼的三维相图如图4 所示. 方程(2 )产生的多环多翼的平面相图如图5 所示. 从图4 和图5 可以明显地看出, 该混沌系统能在多个方向上产生多环多翼.图 4 三维相图 (a) $x \text- y \text- z$ 三维图; (b) $x \text- y \text- w$ 三维图; (c) $x \text- y \text- v$ 三维图; (d) $x \text- z \text- w$ 三维图; (e) $x \text- z \text- v$ 三维图; (f) $x \text- w \text- v$ 三维图; (g) $y \text- z \text- w$ 三维图; (h) $y \text- z \text- v$ 三维图; (i) $y \text- w \text- v$ 三维图; (j) $z \text- w \text- v$ 三维图Figure4. Three-dimensional phase diagram: (a) $x \text- y \text- z$ Three-dimensional map; (b) $x \text- y \text- w$ Three-dimensional map; (c) $x \text- y \text- v$ Three-dimensional map; (d) $x \text- z \text- w$ Three-dimensional map; (e) $x \text- z \text- v$ Three-dimensional map; (f) $x \text- w \text- v$ Three-dimensional map; (g) $y \text- z \text- w$ Three-dimensional map; (h) $y \text- z \text- v$ Three-dimensional map; (i) $x \text- y \text- z$ Three-dimensional map; (j) $z \text- w \text- v$ Three-dimensional map.图 5 二维平面相图 (a) $x \text- y$ 平面; (b) $x \text- z$ 平面; (c) $x \text- v$ 平面; (d) $y \text- z$ 平面; (e) $y \text- w$ 平面; (f) $z \text- w$ 平面; (g) $z \text- v$ 平面Figure5. Two-dimensional plane phase diagram: (a) $x \text- y$ flat; (b) $x \text- z$ flat; (c) $x \text- v$ flat; (d) $y \text- z$ flat; (e) $y \text- w$ flat; (f) $z \text- w$ flat; (g) $z \text- v$ flat.4.算法描述 24.1.加密算法描述 4.1.加密算法描述 给定一个$M \times N$ 的灰度图像${{P}}$ , 加密步骤如下:Step1 输入灰度图像${{P}}$ , 通过${\rm{QR}}$ 分解把${{P}}$ 分解成一个正交矩阵${{E}}$ 和一个$M \times N$ 的上三角矩阵${{R}}$ ;Step2 输入超混沌系统的初始值${y_0} \!=\! [1, 0.1, 2, 0.5, 0.4]$ 和步长$l = 0.02$ , 求出迭代总时间$T = l \times (P \times P + $ 250). 其中$P = \max (M, N)$ ;Step3 调用ode45函数, 迭代系统(3), 产生5条混沌序列;Step4 分别把5条混沌序列作如下处理:$y(201:(200 + M \times N), i)$ 是把混沌序列$y(i)$ 的第201个值到第$200 + M \times N$ 个值取出来; ${\rm{reshape}}(y(201:(200 + M \times N), i), M, N)$ 是把取出来的$M \times N$ 个值转换成$M \times N$ 矩阵;Step5 第4步中的5个$M \times N$ 矩阵分别通过${\rm{QR}}$ 分解, 得到五个正交矩阵${{{{{E}}}}_1}, {{{E}}_2}, {{{E}}_3}, {{{E}}_4}, {{{E}}_5}$ 和五个上三角矩阵${{{R}}_1}, {{{R}}_2}, {{{R}}_3}, {{{R}}_4}, {{{R}}_5}$ ;Step6 改变初始值${y_0}$ , 重复步骤二到步骤五$n(n \geqslant 2)$ 次, 得到$5 n$ 个正交矩阵和$5 n$ 个上三角矩阵. 分别记为${{{E}}_{11}}, {{{E}}_{12}}, {{{E}}_{13}}, {{{E}}_{14}}, {{{E}}_{15}}, {{{E}}_{21}}, \cdots, {{{E}}_{n1}}, $ ${{{E}}_{n2}}, {{{E}}_{n3}}, {{{E}}_{n4}},{{{E}}_{n5}}$ ;Step7 第一步中的正交矩阵${{E}}$ 与第六步中的正交矩阵${{{E}}_{11}}, {{{E}}_{12}}, {{{E}}_{13}}, {{{E}}_{14}}, {{{E}}_{15}}, {{{E}}_{21}}, \cdots, {{{E}}_{n1}},$ $ {{{E}}_{n2}},{{{E}}_{n3}}, {{{E}}_{n4}}, {{{E}}_{n5}}$ 分别相乘, 得到矩阵${{E}}{{E}}$ ; 即${{E}}{{E}} = $ $ {{{E}}_{11}} \times {{{E}}_{12}} \times {{{E}}_{13}}\, \times \,{{{E}}_{14}} \,\times\, {{{E}}_{15}} \,\times {{{E}}_{21}}\, \times \,\cdots \times {{{E}}_{n1}}\, \times$ ${{{E}}_{n2}} \times {{{E}}_{n3}} \times {{{E}}_{n4}} \times {{{E}}_{n5}} \times {{E}}$ ;Step8 第三步中的五条混沌序列分别作如下处理:$P \times P$ 矩阵分别通过${\rm{LU}}$ 分解, 得到五个上三角矩阵${{{L}}_1}, {{{L}}_2}, {{{L}}_3}, {{{L}}_4}, {{{L}}_5}$ 和五个下三角矩阵${{{U}}_1}, {{{U}}_2}, {{{U}}_3}, {{{U}}_4}, {{{U}}_5}$ ;Step9 ${{{L}}_1}, {{{L}}_2}, {{{L}}_3}, {{{L}}_4}, {{{L}}_5}$ 与${{{U}}_1}, {{{U}}_2}, {{{U}}_3}, {{{U}}_4}, {{{U}}_5}$ 分别对应相加, 即${{L}}{{{U}}_1} \!=\! {{{L}}_1} \!+\! {{{U}}_1}, {{L}}{{{U}}_2} \!=\! {{{L}}_2} \!+\! {{{U}}_2}, $ ${{L}}{{{U}}_3} = {{{L}}_3} + {{{U}}_3},\; {{L}}{{{U}}_4} = {{{L}}_4} + {{{U}}_4}, \;{{L}}{{{U}}_5} = {{{L}}_5} + {{{U}}_5}$ . 然后分别取出${{L}}{{{U}}_i}(i$ $ = 1, 2, 3, 4, 5)$ 中的前$M$ 行与前$N$ 列位置上的元素, 从而得到五个$M \times N$ 矩阵. 分别记为${{M}}{{{N}}_1}, {{M}}{{{N}}_2}, {{M}}{{{N}}_3}, {{M}}{{{N}}_4}, {{M}}{{{N}}_5}$ ;Step10 ${{M}}{{{{{N}}}}_1}, {{M}}{{{{{N}}}}_2}, {{M}}{{{{{N}}}}_3}, {{M}}{{{{{N}}}}_4}, {{M}}{{{{{N}}}}_5}$ 与${{{R}}_1},{{{R}}_2}, {{{R}}_3}, {{{R}}_4}, {{{R}}_5}$ ${{{R}}_2}, {{{R}}_3}, {{{R}}_4}, {{{R}}_5}$ 分别对应相加, 即${{{B}}_{41}} = {{M}}{{{{{N}}}}_1}\!+ {{{R}}_1}, $ $ {{{B}}_{42}} \!=\! {{M}}{{{N}}_2} \!+\! {{{R}}_2}, {{{B}}_{43}} \!=\! {{M}}{{{N}}_3} $ $+ {{{R}}_3}, {{{B}}_{44}} \!=\! {{M}}{{{N}}_4} \!+\! {{{R}}_4},{{{B}}_{45}} \!=\! {{M}}{{{N}}_5} \!+\! {{{R}}_5} $ ;Step11 ${{{B}}_{41}}, {{{B}}_{42}}, {{{B}}_{43}}, {{{B}}_{44}}, {{{B}}_{45}}$ 转换成1行$M \times N$ 列的矩阵, 同时把每个矩阵中的所有元素转换成0—255之间的整数, 分别得到矩阵${{{B}}_{51}}, {{{B}}_{52}}, {{{B}}_{53}}, {{{B}}_{54}}, {{{B}}_{55}}$ ;Step12 ${{{B}}_{51}}, {{{B}}_{52}}, {{{B}}_{53}}, {{{B}}_{54}}, {{{B}}_{55}}$ 作如下处理:$i2 = 1, 2, 3, \cdot \cdot \cdot, M \times N$ ;Step13 ${{{B}}_{61}}, {{{B}}_{62}}, {{{B}}_{63}}, {{{B}}_{64}}$ 作如下处理:${\rm{mod}}$ 为求模运算, ${\rm{round}}(f)$ 是对$f$ 进行靠近取整;Step14 上三角矩阵${{R}}$ 的所有行的元素进行扰乱, 扰乱公式如下:${{Z}}(i3, :)$ 是矩阵${{Z}}$ 的第$i3$ 行的所有列, ${\rm{circshift}}({{A}}, k, 2)$ 是把行向量${{A}}$ 的所有元素按顺时针方向移动$k$ 个单位;Step15 将${{RR}}$ 的所有列的元素进行扰乱, 扰乱公式如下:${{Z}}(:, i4)$ 是矩阵${{Z}}$ 的第$i4$ 列的所有行, ${\rm{circshift}}(B, k, 1)$ 是把列向量${{B}}$ 的所有元素按顺时针方向移动$k$ 个单位;Step16 将${{EE}}$ 与${{R}}{{{R}}_1}$ 相乘, 得到矩阵${{E}}{{{E}}_1}$ , 即${{E}}{{{E}}_1} = {{EE}} \times {{R}}{{{R}}_1}$ ;Step17 将${{E}}{{{E}}_1}$ 转换成1行$M \times N$ 列的矩阵${{E}}{{{E}}_2}$ , 再把${{E}}{{{E}}_2}$ 中的所有元素都映射成0—255之间的整数, 映射公式如下:Step18 第十七步中经过映射公式处理了的${{E}}{{{E}}_1}$ 转换成二进制数, 得到矩阵${{E}}{{{E}}_2}$ ;Step19 ${{E}}{{{E}}_2}$ 中的每一行二进制数分别进行扰乱, 得到矩阵${{E}}{{{E}}_3}$ , 扰乱公式如下:Step20 ${{E}}{{{E}}_3}$ 中的每一列二进制数分别进行扰乱, 得到矩阵${{E}}{{{E}}_4}$ , 扰乱公式如下:Step21 将${{E}}{{{E}}_4}$ 转换成十进制数, 再把已经转换成十进制数的${{E}}{{{E}}_4}$ 转换成1行$M \times N$ 列的矩阵${{E}}{{{E}}_5}$ ;Step22 ${{E}}{{{E}}_5}$ 与${{{B}}_{65}}$ 进行按位“异或”运算, 得到一个新的序列${{E}}{{{E}}_6}$ , 把${{E}}{{{E}}_6}$ 转换成$M$ $ \times N$ 的矩阵${{E}}{{{E}}_7}$ , ${{E}}{{{E}}_7}$ 为最终的加密图像.4.2.解密算法描述 -->4.2.解密算法描述 Step1 输入图像矩阵${{E}}{{{E}}_7}$ , 同时与${{{B}}_{65}}$ 进行按位“异或”运算, 得到一个新的序列${{E}}{{{E}}_8}$ ;Step2 ${{E}}{{{E}}_8}$ 转换成二进制数, 然后把行列进行还原, 得到矩阵${{E}}{{{E}}_9}$ ;Step3 ${{E}}{{{E}}_9}$ 转换成十进制数, 得到矩阵${{E}}{{{E}}_{10}}$ , 再把${{E}}{{{E}}_{10}}$ 通过下列公式还原成${{E}}{{{E}}_1}$ ,$j = 1, 2, \cdot \cdot \cdot, M \times N$ ;Step4 在${{E}}{{{E}}_1}$ 的左边依次乘上${{{E}}_{11}}, {{{E}}_{12}}, $ $ {{{E}}_{13}}, {{{E}}_{14}}, {{{E}}_{15}}, {{{E}}_{21}}, \cdots, {{{E}}_{n1}}, {{{E}}_{n2}}, {{{E}}_{n3}}, {{{E}}_{n4}}, {{{E}}_{n5}}, E$ 的逆, 得到矩阵${{R}}{{{R}}_1}$ ;Step5 ${{R}}{{{R}}_1}$ 的行列进行还原, 得到矩阵${{R}}$ , 再把矩阵${{E}}$ 与${{R}}$ 相乘, 得到解密图像${{P}}$ .5.实验结果 25.1.实验平台 5.1.实验平台 PC机配置: Intel(R) Core(TM) i3-4170 CPU @ 3.70 GHz, 内存4 GB, Windows7 32位操作系统. 通过Matlab R2014 a编写程序实现上述加密算法.5.2.实验结果 -->5.2.实验结果 实验选取了经典的lena, baboon, boat灰度图像, 其大小均为512$ \times $ 512. 明文图像、加密图像和解密图像如图6 所示.图 6 数字图像加解密实验图 (a) lena原图; (b) lena加密图像; (c) lena解密图像; (d) baboon原图; (e) baboon加密图像; (f) baboon解密图像; (g) boat原图; (h) boat加密图像; (i) boat解密图像Figure6. Digital image encryption and decryption experiment: (a) Original Lena image; (b) encrypted Lena image; (c) decrypted Lena image; (d) original baboon image; (e) encrypted baboon image; (f) decrypted baboon image; (g) original boat image.; (h) encrypted boat image; (i)decrypted boat image.6.安全性分析 26.1.密钥空间分析 6.1.密钥空间分析 决定图像加密算法强度的最重要因素之一是密钥空间的大小. 本文的初始密钥由${y_0}$ 中的五个初始值、系统参数$a, b, c, d, e, f, g$ 、正交矩阵${{E}}$ 和原图像的最大值最小值组成, 以计算机精度为${10^{ - 15}}$ 计算的话, 本算法的密钥空间远大于${10^{200}} > $ ${2^{100}}$ . 如果一种图像加密算法的密钥空间大于${2^{100}}$ , 则它就是安全的[21 ,22 ] . 因此本算法是足够安全的.6.2.直方图分析 -->6.2.直方图分析 直方图可以很好地反映图像像素值的分布情况, 直方图越平坦则像素值分布就越均匀. 图7 分别是lena, baboon和boat的原图像直方图和加密后图像的直方图.图 7 明文图像和密文图像直方图 (a) lena明文直方图; (b) lena密文直方图; (c) baboon明文直方图; (d) baboon密文直方图; (e) boat明文直方图; (f) boat密文直方图Figure7. Histogram of plaintext and ciphertext images (a) Plaintext Lena image histogram; (b) ciphertext Lena image histogram; (c) plaintext baboon image histogram; (d) ciphertext baboon image histogram; (e) plaintext boat image histogram; (f) ciphertext boat image histogram.6.3.信息熵分析 -->6.3.信息熵分析 信息熵是最重要的随意因素之一. 计算公式如下:$p({m_i})$ 是${m_i}$ 的机率, $L$ 是${m_i}$ 的总数量. 对于灰度图像来说, 信息熵的最大值为8. Lena, baboon和boat加密前后的信息熵与文献[11 —17 ]的测试值如表1 所列. 仿真实验结果表明本算法具有良好的加密效果.图像 Lena图像 Baboon图像 Boat图像 原图像 7.4644 7.3713 7.1267 密文图像 7.9994 7.9994 7.9993 文献[11 ] 7.9992 7.9993 — 文献[12 ] 7.9994 7.9993 — 文献[13 ] 7.9971 — 7.9993 文献[14 ] 7.9960 — — 文献[15 ] 7.9993 7.9993 — 文献[16 ] 7.9993 7.9992 — 文献[17 ] 7.9974 — —
表1 明文图像与加密图像的信息熵分析表Table1. Information entropy analysis table of plain text and encrypted image.6.4.不动点比和灰度平均变化值分析 -->6.4.不动点比和灰度平均变化值分析 不动点比为图像加密后灰度值未发生变化的像素点占所有像素点的百分比, 计算公式如(15 )式所示; 而灰度平均变化值能更好地评价加密图像灰度变化的程度, 计算公式如(16 )式所示.$f(i, j) = \left\{ \begin{aligned} & 1, \;\;{g_{ij}} = {c_{ij}} \\ & 0, \;\;{g_{ij}} \ne {c_{ij}}\end{aligned} \right.$ . 由(15 )式计算出本算法的不动点比如表2 所列.图像 总像素数 不动点数 不动点比 Lena图像 262144 1015 0.39% Baboon图像 262144 1014 0.39% Boat图像 262144 999 0.38%
表2 加密图像不动点比分析表Table2. Encrypted image fixed point ratio analysis table.${{G}}$ 为明文图像, ${{C}}$ 为密文图像. 根据(16 )式计算出本算法的灰度平均变化值如表3 所列.图像 Lena图像 Baboon图像 Boat图像 灰度平均变化值 73.1937 70.8589 74.8383
表3 灰度平均变化值分析表Table3. Grayscale average change value analysis table.6.5.密钥敏感性分析 -->6.5.密钥敏感性分析 密钥的微小改变就会导致密文的极大改变, 这就是密钥敏感性. 实验以经典的lena图像为例. 图8 展示了本算法对初始密钥的敏感性. 图8(a) 是lena的明文图像; 图8(b) 和图8(c) 分别是用密钥${y_0} \!=\! [1, 0.1, 2, 0.5, 0.4]$ 和${y_1} \!=\! [1, 0.1000000000000001,$ $ 2, 0.5, 0.4]$ 加密的密文图像${{{Y}}_{\rm{1}}}$ 和${{{Y}}_2}$ ; 图8(d) 是${{{Y}}_1}$ 用${y_0}$ 正确解密的结果图; 图8(e) 和图8(f) 是${{{Y}}_1}$ 和${{{Y}}_2}$ 分别用错误的密钥${y_1}$ 和${y_0}$ 解密的结果. 图8 说明尽管密钥${y_0}$ 和${y_1}$ 之间仅有微小的变化, 密文图像${{{Y}}_1}$ 和${{{Y}}_2}$ 却不能相应的用密钥${y_1}$ 和${y_0}$ 正确解密.图 8 密钥敏感性测试图 (a)明文图像; (b)密文${{{Y}}_1}$ (密钥为${y_0}$ ); (c)密文${{{Y}}_2}$ (密钥为${y_1}$ ); (d) ${{{Y}}_1}$ 正确解密结果; (e) ${{{Y}}_1}$ 用${y_1}$ 错误解密结果; (f) ${{{Y}}_2}$ 用${y_0}$ 错误解密结果Figure8. Key sensitivity tests: (a) Plain-image; (b) cipher ${{{Y}}_1}$ with key ${y_0}$ ; (c) cipher ${{{Y}}_2}$ with key ${y_1}$ ; (d) right decrypted ${{{Y}}_1}$ ; (e) decrypted ${{{Y}}_1}$ with ${y_1}$ ; (f) decrypted${{{Y}}_2}$ with${y_0}$ .$D\left( {i, j} \right) = \left\{ \begin{aligned}& 1, \;\; {C_1}\left( {i, j} \right) \ne {C_2}\left( {i, j} \right) \\ & 0, \;\; {C_1}\left( {i, j} \right) = {C_2}\left( {i, j} \right) \end{aligned} \right.$ ; $M, N$ 为图像的大小, ${C_1}\left( {i, j} \right)$ 和${C_2}\left( {i, j} \right)$ 分别是两幅图像在$\left( {i, j} \right)$ 位置上的像素值. NPCR和UACI的值越大, 说明两幅图像之间的差异就越大. 为了更好地评价算法的密钥敏感性, 我们测试了分别用密钥${y_0} \!=\! [1, 0.1, 2, 0.5, 0.4]$ 和${y_1} \!= \![1, 0.1000000000000001,$ 2, 0.5, 0.4]加密的图像之间的NPCR和UACI的值, 测试值和文献[13 —16 ]的测试值如表4 所列. 从表4 可以看出, 测试结果良好, 因此提出的加密算法具有良好的密钥敏感性.图像 lena图像 baboon图像 boat图像 指标 NPCR UACI NPCR UACI NPCR UACI 本文算法 0.9964 0.3340 0.9962 0.3346 0.9958 0.3344 文献[13 ] 0.9962 0.3347 — — 0.9960 0.3340 文献[14 ] 0.9957 0.3508 — — — — 文献[15 ] 0.9961 0.3347 0.9961 0.3347 — — 文献[16 ] 0.9962 0.3344 0.9961 0.3349 — —
表4 密钥敏感性测试结果表Table4. Key sensitivity test result table.6.6.相邻像素相关性分析 -->6.6.相邻像素相关性分析 相邻像素的相关性用来评价图像加密算法在消除明文图像相邻像素相关性方面的效果. 本文分别在lena, baboon和boat的明文图像和密文图像中随机选取了5000个相邻像素点, 按(19 )—(22 )式计算明文图像与密文图像在水平方向的相邻像素的相关性系数、垂直方向的相邻像素的相关性系数和对角线方向的相邻像素的相关性系数. 测试结果如表5 所列. Baboon明文图像和密文图像在水平方向、垂直方向和对角线方向的像素相关性图如图9 所示.图像 水平方向相关系数 垂直方向相关系数 对角线方向相关系数 明文图像 密文图像 明文图像 密文图像 明文图像 密文图像 Lena 0.9762 –0.0084 0.9659 0.0461 0.9468 0.0131 Baboon 0.7204 –0.0050 0.8264 –0.0074 0.7046 –0.0322 boat 0.9621 0.0106 0.8252 0.0087 0.8327 –0.0423
表5 明文图像与密文图像相关系数测试结果表Table5. Plaintext image and ciphertext image correlation coefficient test result table.图 9 baboon图像加密前后三个方向上的相关性分析图 (a), (b)对角相邻; (c), (d)水平相邻; (e), (f)垂直相邻;Figure9. Correlation analysis chart in three directions before and after baboon image encryption: (a), (b) Diagonally adjacent; (c), (d) horizontally adjacent; (e), (f) vertically adjacent.表5 中可以看出, 明文图像在三个方向上的相关系数都大于0.6, 说明明文图像的相邻像素之间的相关性非常强; 而密文图像在三个方向上的相关系数都接近于0, 说明密文图像的相邻像素之间的相关性已被打破.图9 可以看出, 明文图像的像素点集中分布在对角线附近, 说明明文图像的像素点之间的相关性很强; 而密文图像的像素点分布得比较均匀、散乱, 说明密文图像的像素之间的相关性已被破坏. 因此提出的算法可以很好地降低图像相邻像素之间的强相关性, 对图像加密具有良好的效果.6.7.抗剪切能力分析 -->6.7.抗剪切能力分析 为测试该算法的抗剪切能力, 我们剪掉Lena加密图像中间60 × 60大小的图像, 如图10(b) 所示, 再对剪切过的加密图像进行解密, 解密图像如图10(d) 所示. 图10(a) 为原加密图像, 图10(c) 为原加密图像的解密图像. 对比图10(c) 和图10(d) 可以发现, 图10(d) 中有些点的像素值发生了改变, 但仍然可以显示出明文图像的大致信息. 因此, 加密图像在遭受剪切攻击后仍然具有一定的解密效果.图 10 抗剪切攻击能力分析图 (a)剪切前密文; (b)剪切后密文; (c)剪切前解密; (d)剪切后解密Figure10. Anti-shear attack capability analysis chart: (a) Ciphertext before cutting; (b) ciphertext after cutting; (c) decrypted image before cutting; (d) decrypted image after cutting.6.8.抗噪声能力分析 -->6.8.抗噪声能力分析 椒盐噪声是图像中常见到的一种噪声, 当影像讯号受到突如其来的强烈干扰、类比数位转换器或位元传输错误等都可能产生椒盐噪声. 为了测试本算法的抗椒盐噪声攻击能力, 我们对Lena加密图像加入1%的椒盐噪声, 加噪后的加密图像如图11(b) 所示, 再对加噪后的加密图像进行解密, 解密图像如图11(d) 所示. 图11(a) 为原加密图像, 图11(c) 为原解密图像. 对比图11(c) 和图11(d) 可以发现, 图11(d) 中有些点的像素值发生了改变, 但仍然可以显示出原始明文图像的大致信息. 这说明加密图像在遭受到椒盐噪声攻击后仍然具有一定的解密效果.图 11 抗噪声攻击能力分析图 (a)加噪前密文; (b)加噪后密文; (c)加噪前解密; (d)加噪后解密Figure11. Anti-noise attack capability analysis chart: (a) Ciphertext before adding noise; (b) ciphertext after adding noise; (c) decrypted image before adding noise; (d) decrypted image after adding noise.7.结 论 本文提出了一种新的五维多环多翼超混沌系统, 该系统结构简单. 对该混沌系统的基本动力学特征进行了理论分析和数值仿真实验, 包括Lyapunov指数谱、平衡点、分岔图、时间序列、相图等, 从相图中可以明显看出, 该混沌系统能够在多方向上产生多环多翼, 从分岔图可以看出, 该系统参数的动态范围很广. 同时, 将该五维多环多翼超混沌系统应用于物理混沌加密和代数加密的混合图像加密算法, 并对混合加密系统进行了数值仿真实验, 实验结果验证了该加密方法的正确性. 因此, 本文提出的加密算法在数字图像的保密通信中有很好的应用前景. 
图 1 Lyapunov指数谱
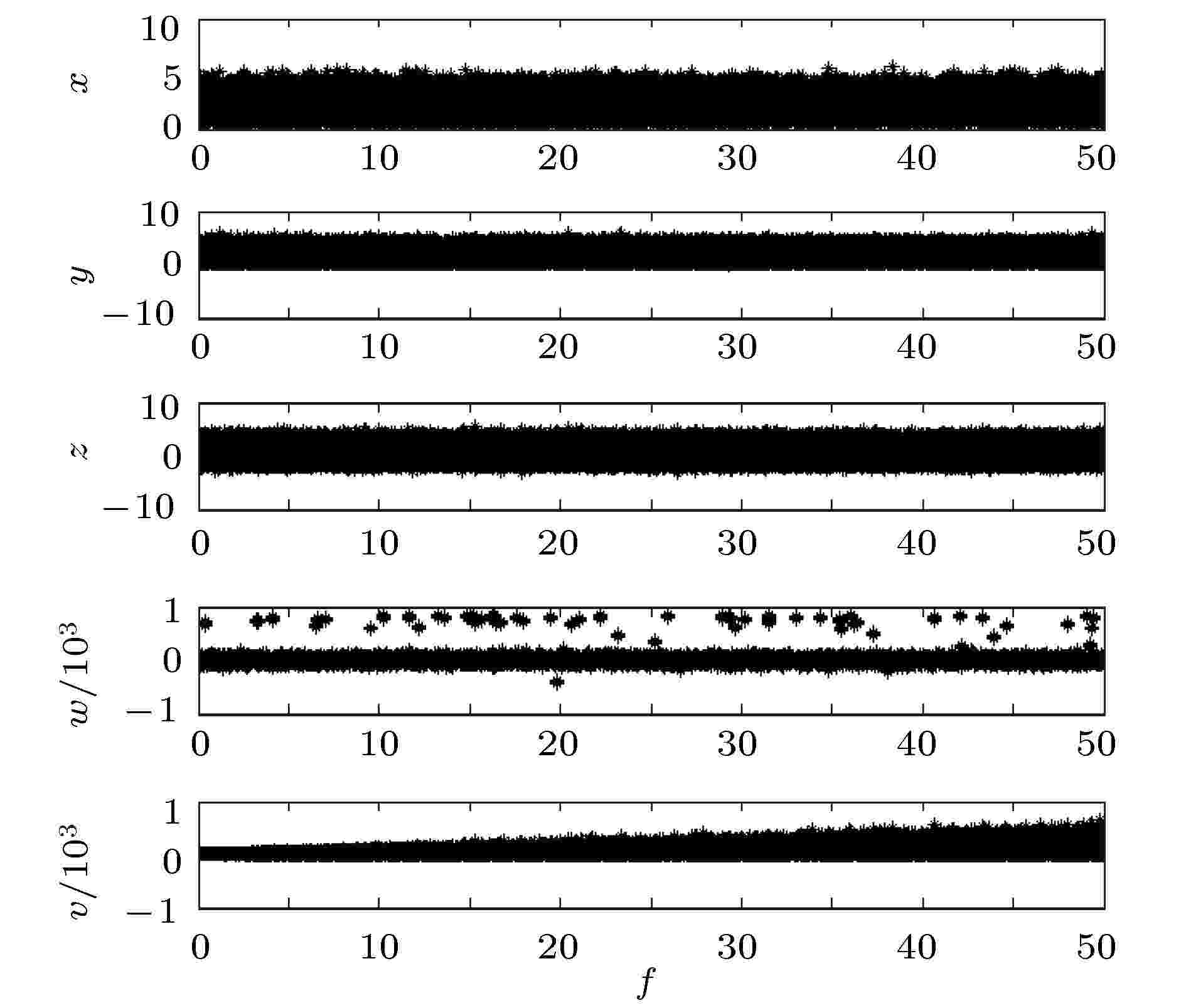图 2 系统(2)随
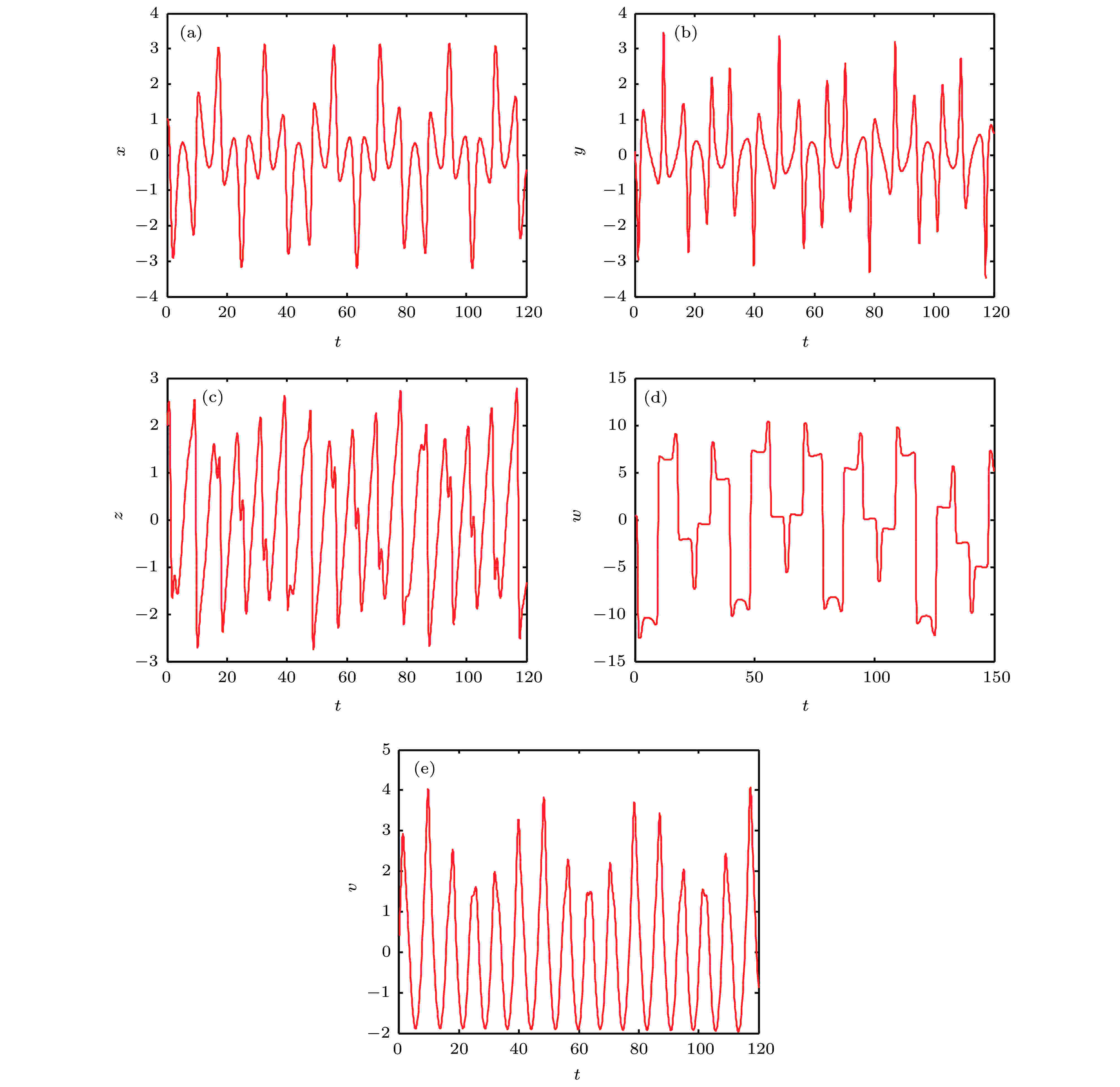图 3 时间序列图 (a) 
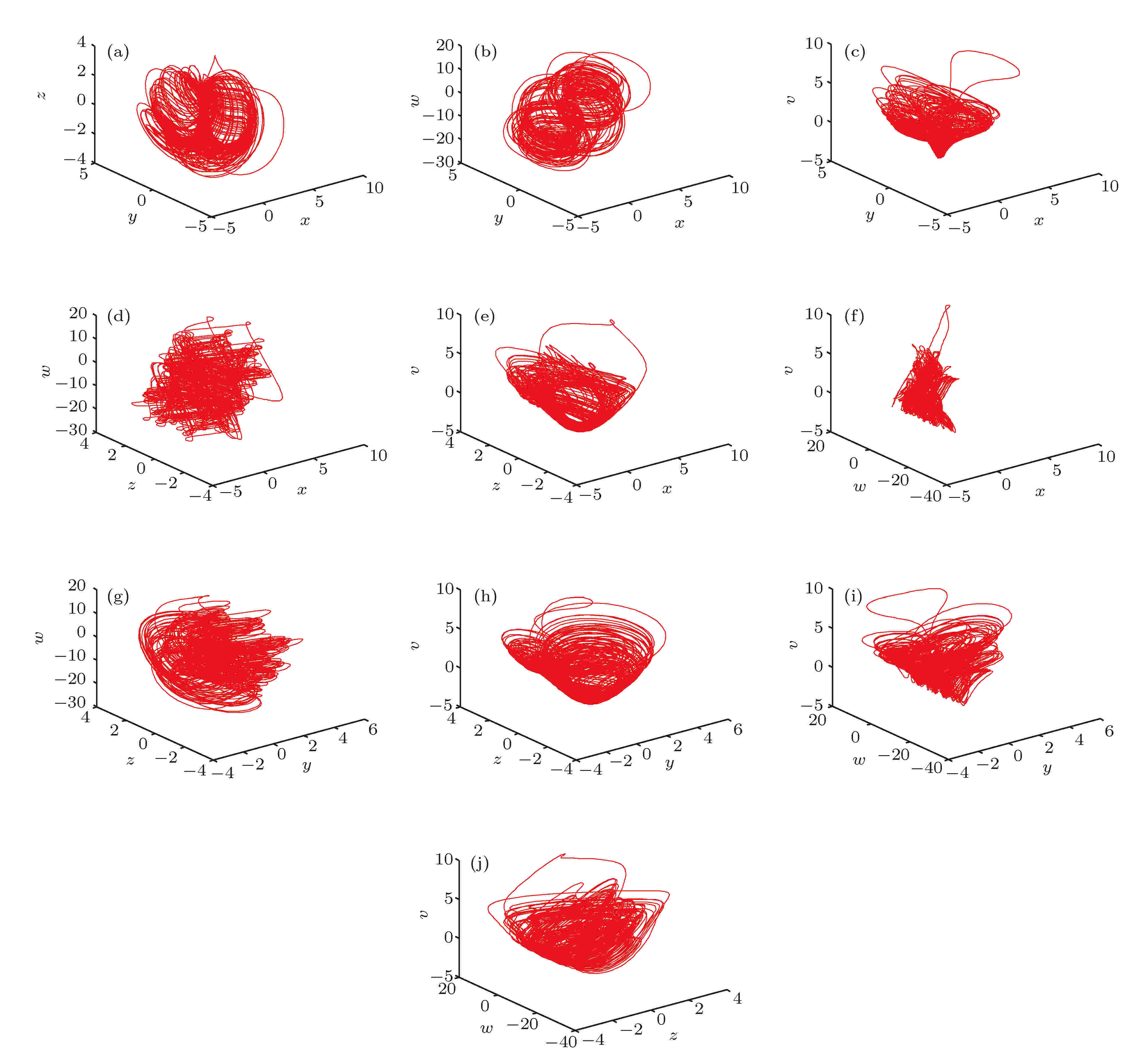图 4 三维相图 (a) 
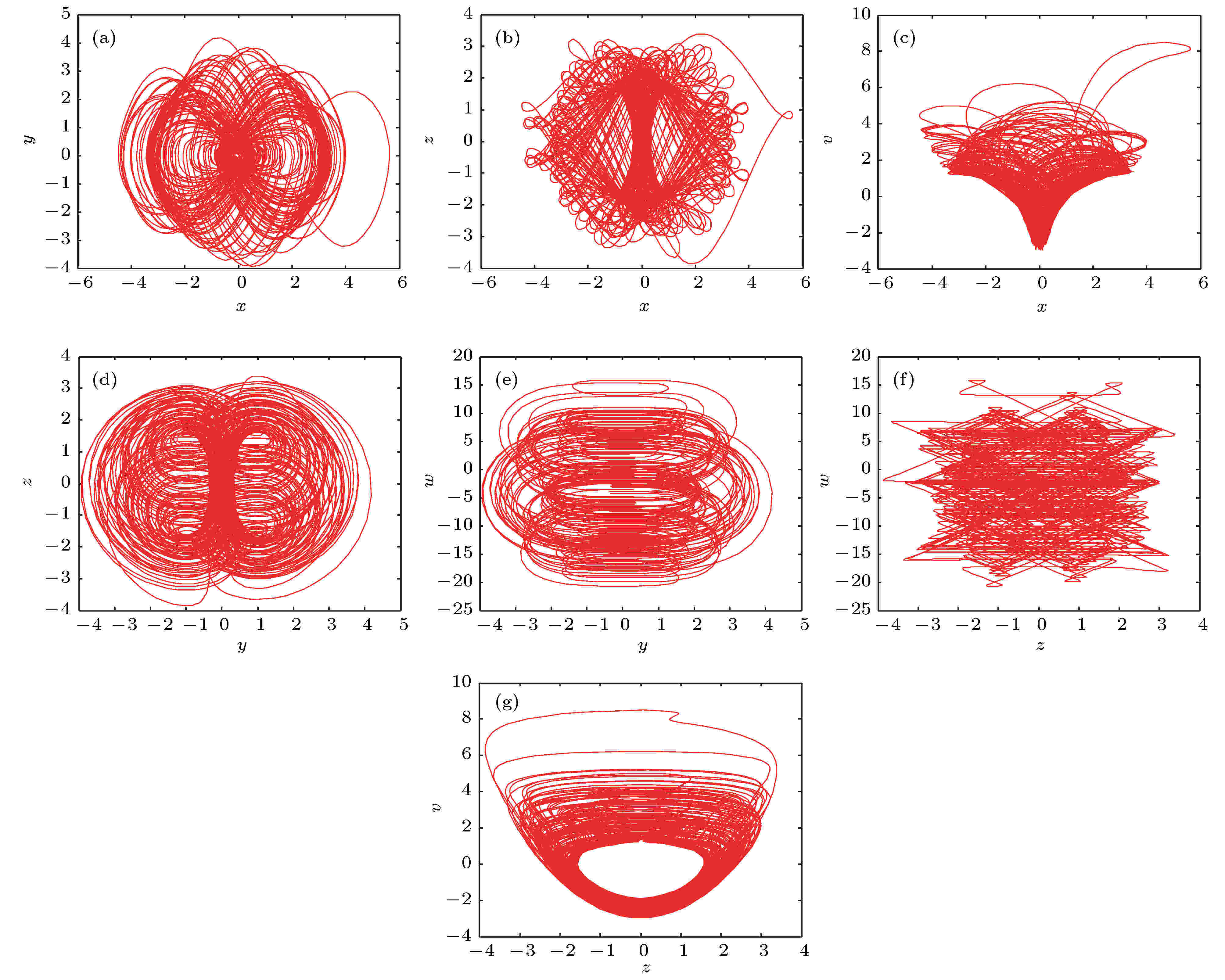图 5 二维平面相图 (a) 
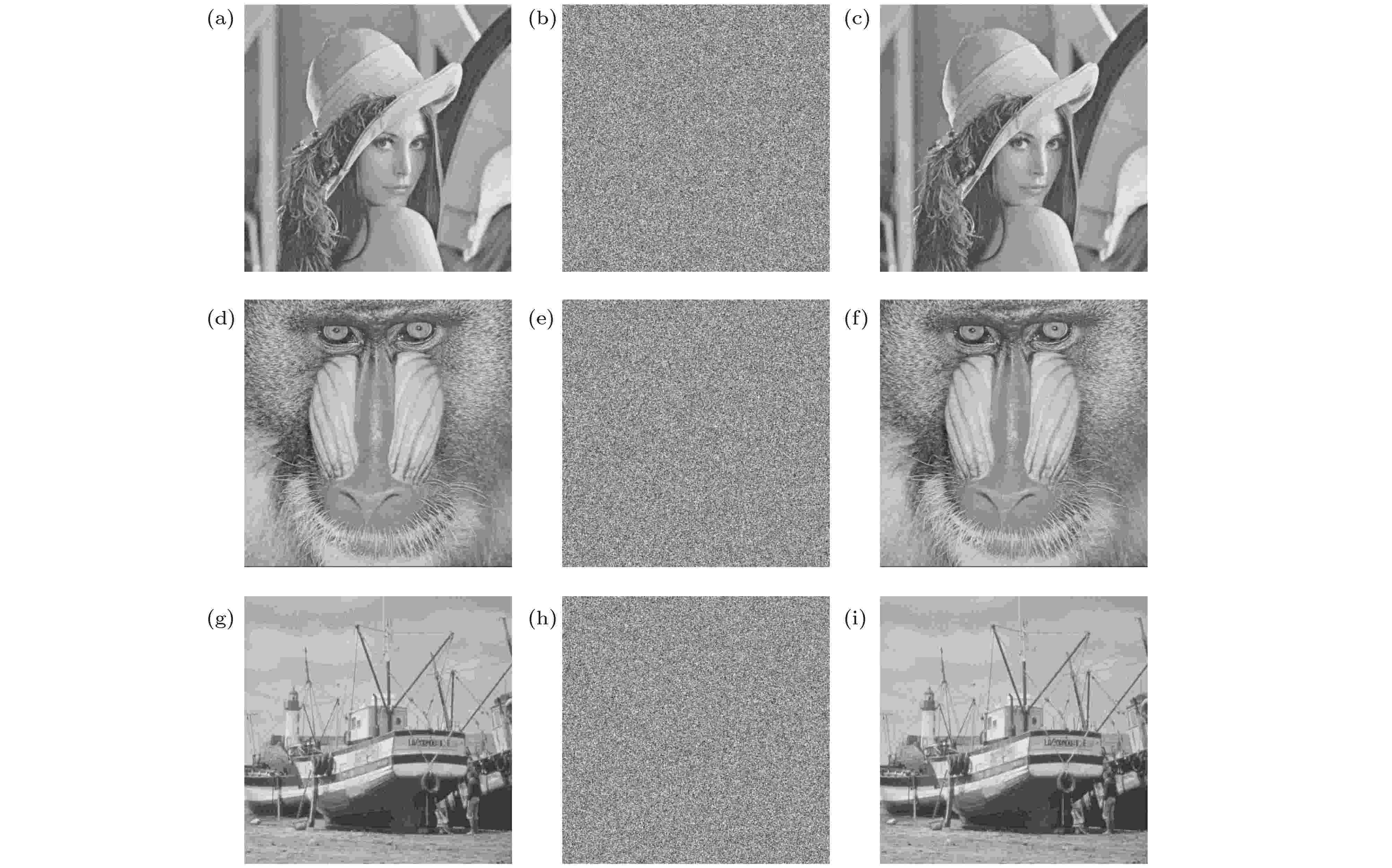图 6 数字图像加解密实验图 (a) lena原图; (b) lena加密图像; (c) lena解密图像; (d) baboon原图; (e) baboon加密图像; (f) baboon解密图像; (g) boat原图; (h) boat加密图像; (i) boat解密图像
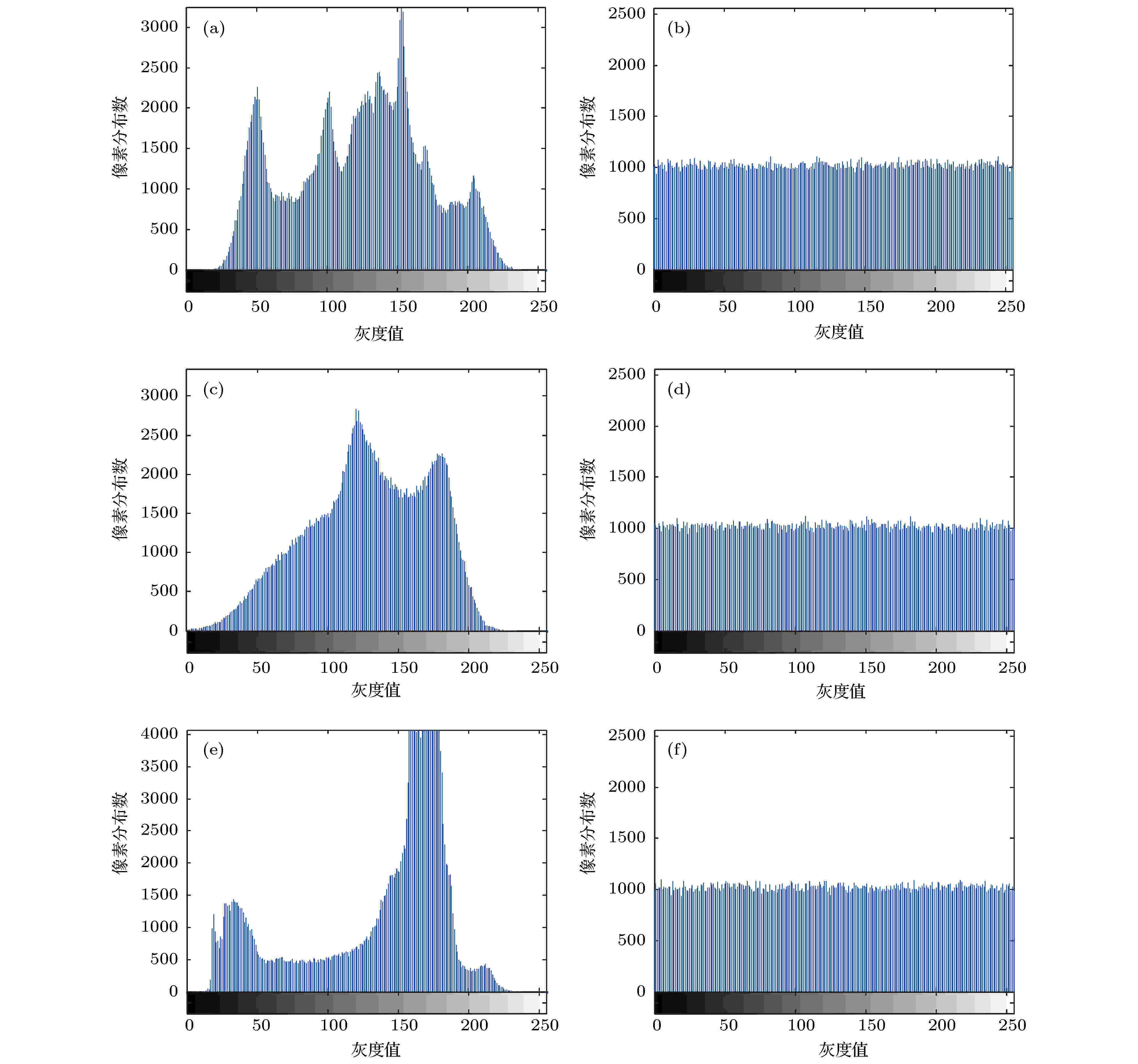图 7 明文图像和密文图像直方图 (a) lena明文直方图; (b) lena密文直方图; (c) baboon明文直方图; (d) baboon密文直方图; (e) boat明文直方图; (f) boat密文直方图
图 8 密钥敏感性测试图 (a)明文图像; (b)密文
图 9 baboon图像加密前后三个方向上的相关性分析图 (a), (b)对角相邻; (c), (d)水平相邻; (e), (f)垂直相邻;
图 10 抗剪切攻击能力分析图 (a)剪切前密文; (b)剪切后密文; (c)剪切前解密; (d)剪切后解密
图 11 抗噪声攻击能力分析图 (a)加噪前密文; (b)加噪后密文; (c)加噪前解密; (d)加噪后解密