全文HTML
--> --> -->在量子现象、特性实验载体的选择上, 光波一直都是主流和首选[12-15]. 这是因为相对于微波频段而言, 光波光子具有较高的能量, 不易被噪声光子影响, 相关器件成熟高效, 有关量子现象的制备在室温下即可实现. 微波的频率范围为300 MHz—300 GHz, 处于高频无线电频段与光频段的连接部分, 同时具有高频无线电和光的自由空间传输特性, 因此被广泛应用于通信、导航、雷达、成像等领域[16-19], 是经典应用中极为重要的信息载体. 在量子应用层面, 由于微波光子的能量较之光波光子低3个数量级, 受环境中的热光子影响较大, 量子现象的制备较为困难, 大多工作在超低温条件下, 使得微波的量子应用发展迟缓. 因此, 解决该问题的关键就是实现微波非经典量子态的有效制备.
随着技术和工艺的逐渐提高, 越来越多的研究者开始聚焦于在微波频段实现非经典量子态及其他量子特性[20-23], 甚至有****认为应将相关研究命名为“量子微波(quantum microwave)”, 以体现其与“量子光学(quantum optics)”的相应地位[24]. 围绕如何实现微波非经典态的有效制备, 研究者提出了许多方案, 相关的实验也得以开展, 取得了令人瞩目的突破, 其中包括一种被称为腔光力系统(cavity optomechanical system)的混合量子系统的方案[25]. 本文介绍了腔光力系统的基本原理, 对腔光力系统进行了分类, 详细介绍了使用腔光力系统制备微波非经典量子态的理论和实验进展, 归纳总结了该方案的性能优势和待解决问题, 并对其应用进行了分析、展望.
2
2.1.腔光力学及腔光力系统的发展
腔光力学是研究腔光力系统中光力相互作用特性及其内部的量子动力学的科学, 腔光力系统则是一种由广义光学谐振腔与广义机械振子构成的系统, 腔内的光模和声模通过光压相互作用, 从而实现模式间的有效耦合. 如图1所示[30], 其基本原理可以以经典的法布里-珀罗(Fabry-Perot, F-P)腔为例描述为: 法布里-珀罗腔由一个固定的腔镜和一个可移动的腔镜构成, 可移动腔镜一端连接弹簧, 激光从固定腔镜入射腔内, 进而对可移动腔镜造成光压并使其受迫振动, 同时腔内光场不断往返压迫腔镜, 腔镜的微小位移使得腔长改变, 从而使得腔内光场频率改变, 两者达到平衡后, 稳定的光场和简谐运动形成, 即光子与声子相互作用稳定进行, 这就是最简单的腔光力系统.
图 1 法布里-珀罗型腔光力系统原理图[30]Figure1. Schematic of Fabry-Perot cavity[30].
最早的腔光力学理论可以追溯到1967年, Braginsky等[31]指出可利用辐射压改变机械振子的性能, 从而实现弱力测量, 这是第一个关于腔光力系统的构想, 且该过程使用的是微波信号. 1983年, Dorsel等[32]用光信号也证明了光力效应. 1994年, Fabre等[33]提出使用一个含有可移动腔镜的腔光力系统可以降低入射光束的量子噪声, 并认为这样的腔光力系统在功能上等同于一个克尔介质, 这是首次将量子性质的讨论引入腔光力学. 此后, 腔光力学进入迅速发展时期, 目前已进入以微腔和纳米腔为主流的发展阶段.
腔光力系统, 尤其是微纳腔光力系统, 因其具有超高的品质因数、超高的振动频率、超轻的质量以及超高的灵敏度而广受青睐, 其应用已涉及弱力探测、冷却、光学双稳性、量子信息处理等多个领域[34-38].
2
2.2.常见腔光力系统
随着材料科学研究的不断深入以及加工能力的发展, 大量的腔光力系统已经问世, 其质量、机械振动频率、结构、材料、腔内的模式种类及数目等方面均存在差异. 图2从腔光力系统的质量和机械振动频率的角度, 展示了多种腔光力系统, 其质量范围从皮克到千克, 相应的机械振动频率可以从赫兹到兆赫兹级别, 被应用于不同的场景[39].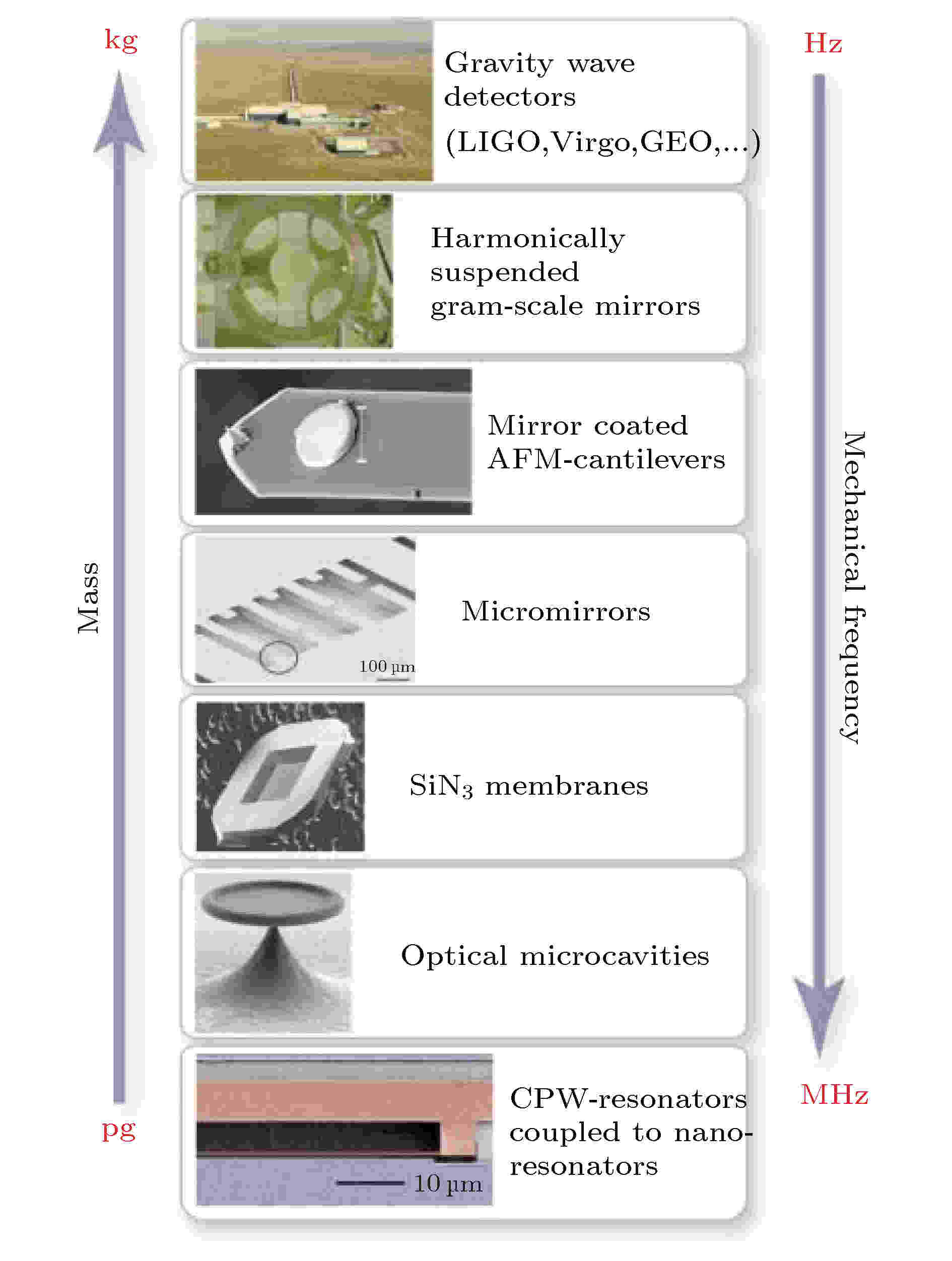
图 2 各种不同质量和机械振动频率的腔光力系统[39]Figure2. Cavity optomechanical systems with different mecha-nical vibration frequencies and masses[39].
在现有的技术条件下, 各种不同结构、材料的腔光力系统都已经被实验实现, 如法布里-珀罗腔、回音壁腔(微球腔、微环腔、微盘腔、微芯环腔)、振动薄膜腔、超导微波腔、光子晶体腔、玻色爱因斯坦凝聚腔[40]等, 选择其中5种主要的类型并介绍.
1)法布里-珀罗腔. 法布里-珀罗腔类型的腔光力系统是最早被提出的腔光力系统, 也是最为经典的腔光力系统之一. 法布里-珀罗腔最早在1899年由Fabry和Perot[41]作为干涉仪提出, 两镜相对面具有较高的反射率且相对长度可调, 故可通过调节精细度因数来增加光传输的有效距离, 当入射光频率满足腔的共振条件时, 腔镜对其将具有极高的透射率, 该过程如图3所示. 早期光力效应的观测实验中使用的结构也正是法布里-珀罗腔结构. 此后, 该结构得到广泛应用.
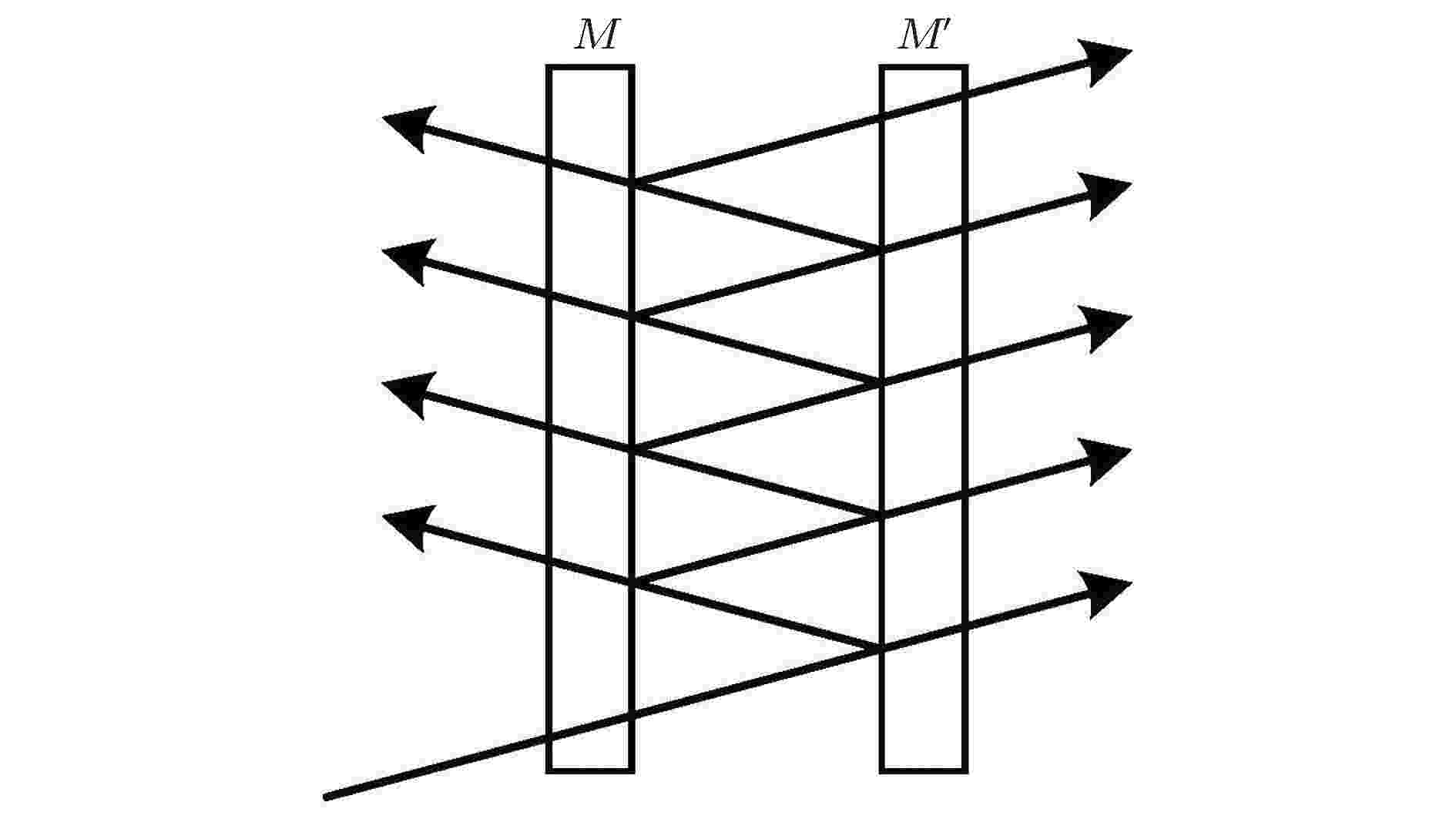图 3 法布里-珀罗干涉仪原理图Figure3. Schematic of Fabry-Perot interferometer.
2003年, Jing等[42]提出一种基于法布里-珀罗腔的纠缠转换方案, 该方案可以将纠缠态从传输光场中转移到腔的两镜上, 在其位置和动量中制备EPR (Einstein-Podolsky-Rosen)纠缠态. 2007年, Vitali等[43]提出一种经典强激光驱动的法布里-珀罗腔(腔镜质量在微克级别), 稳定的腔内模式纠缠可通过辐射压的方式产生, 其原理如图4所示.
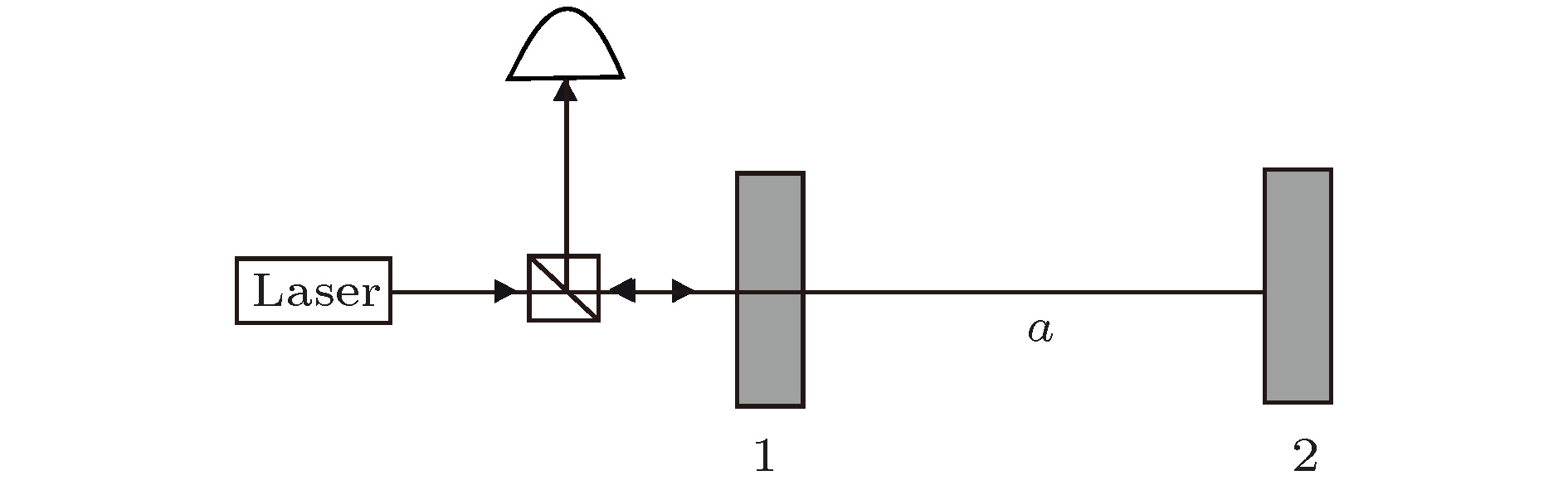图 4 Vitali团队[43]方案原理图Figure4. Schematic of proposal from Vitali’s group[43].
2009年, Regal等[44]提出了一种SiN底片的法布里-珀罗腔, 该结构具有极高精细度和品质因数, 可以同时对多个机械振动模式的动量进行冷却. 2015年, Bitarafan等[45]构造了一个曲顶式法布里-珀罗微腔光力系统(如图5所示), 该曲顶由数个a-Si/SiO2叠层及内含的圆形波导曲面所构成, 用以研究该微腔光力系统的热机械及热调谐特性. 系统获得的品质因数为9600, 且由于其腔模体积较小, 使得系统工作于强耦合模式, 其适用于传感、腔量子电动力学及腔光力学.
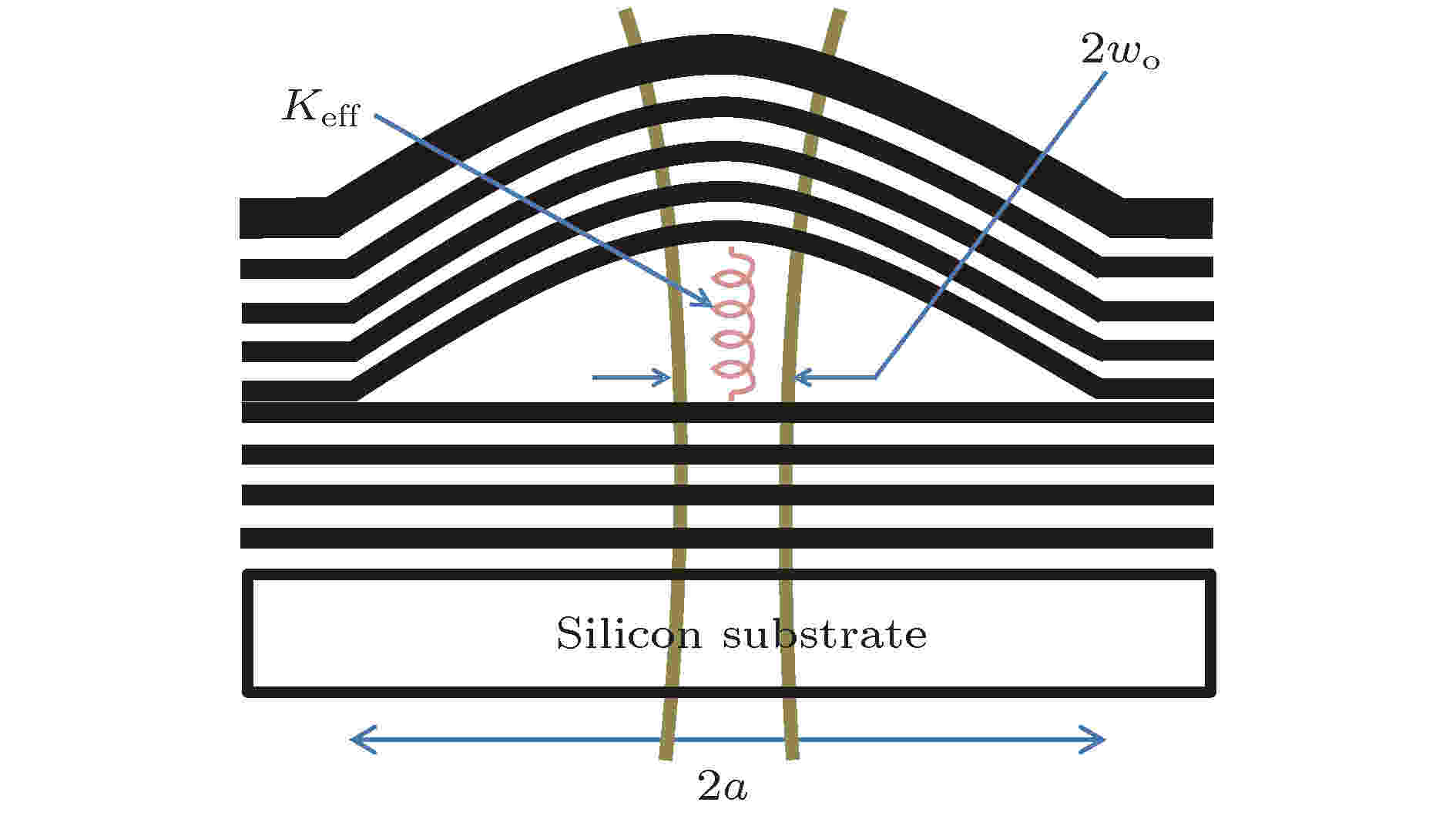图 5 Bitarafan[45]所提方案原理图Figure5. Schematic of proposal from Bitarafan[45].
2018年, Pontin等[46]提出一种长距离(100 m)、低精细度(仅为10)的光纤法布里-珀罗腔结构, 该结构采用悬浮式微盘腔作为机械振子, 达到与高精细度结构相同的基态冷却效果. 2019年, Deli?等[47]提出一种悬浮式粒子型的法布里-珀罗腔, 利用该结构可对悬浮粒子进行纳米水平的调控, 从而实现线性、二次、三次等多种光力相互作用, 且该结构可以获得强协同水平的性能表现, 其结构如图6所示.
图 6 悬浮式粒子型的法布里-珀罗腔实验结构图[47]Figure6. Experimental setup of F-P cavity with levitated particle[47].
2)回音壁腔(whisperinggallery mode cavity). 回音壁腔类型的腔光力系统也被称为环形微腔类型光力系统, 其中的模式也被称为呼吸模式, 腔的尺寸多为微米甚至纳米级, 属于近年来兴起且发展迅速的一种腔光力系统. 回音壁模式最初是声学研究中的概念, 指在类似于北京天坛、伦敦圣保罗大教堂等环形结构中, 声音可以在其中循环传播, 如图7所示. 后来, 光波也被证明具有类似的传播行为, 当光的入射角、介质折射率、相位等满足条件时, 光可在环内循环振荡, 该模式被称为回音壁模式. 回音壁腔的原理即在该种模式的光子作用下, 产生径向呼吸模式, 微环壁结构改变并同时影响该模式, 谐振后两者达到平衡.
图 7 回音壁模式示意图Figure7. Illustration of whispering gallery mode.
2003年, Vahala等[48]首次实验实现了芯片级的超高品质因数值(
图 8 (a)首个回音壁腔光力系统构造[48]; (b)其改进型构造[49]Figure8. (a) Structures of the first whispering gallery mode cavity[48]; (b) its enhanced version[49].
2013年, Henze等[50]提出一种在硅基上实现对系统自由频谱内任意频率进行回音壁模式的高Q值调谐的有效方法, 通过这个方法可以实现窄线宽激光或光谱线与硅基芯片级回音壁腔的高Q谐振模式间的简单有效的匹配. 2017年, Kavungal等[51]提出了一种基于聚合物线形回音壁腔的应力探测器, 回音壁模式的制备是通过光纤锥结构将光短暂地耦合到聚合物线中实现的, 该结构采用封装工艺, 简便易携, 其结构如图9所示.
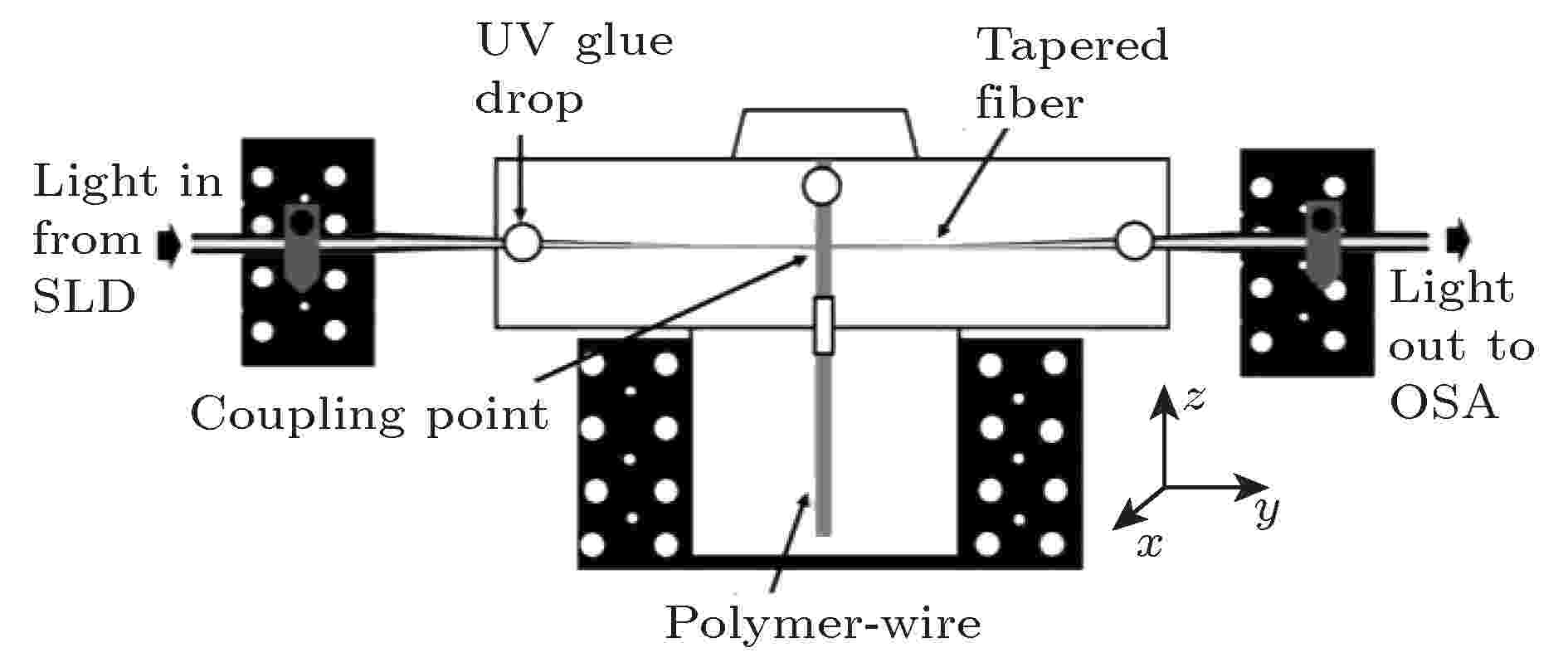图 9 光纤锥-聚合物线回音壁腔结构图[51]Figure9. Schematic of whispering gallery mode cavity formed by fiber taper and polymer wire[51].
2019年, Choi等[52]提出一种采用金属掺杂材料的高Q值硅基回音壁腔, 在增大腔材料拉曼增益的同时降低了光模式面积, 从而在保留低激光门限的同时极大地改善了反斯托克斯激光的生成效率, 其结构如图10所示.
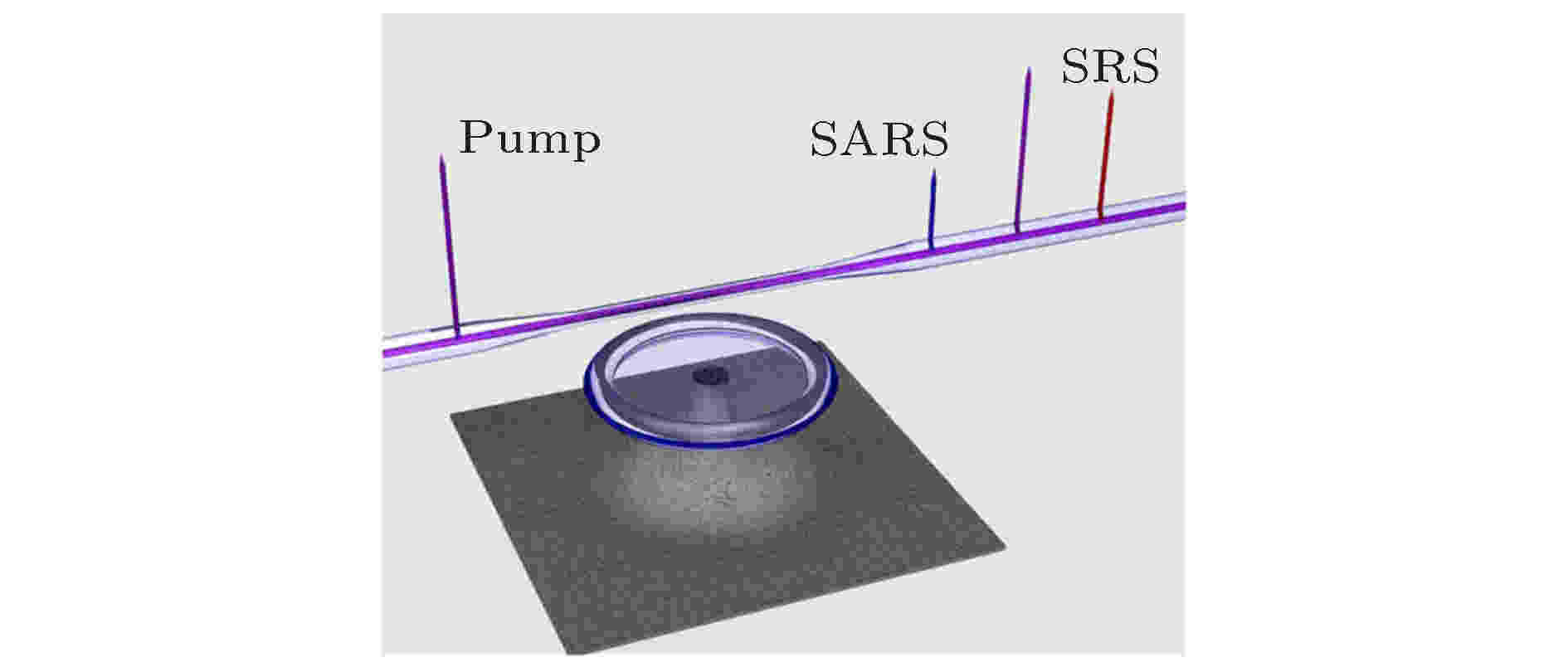图 10 金属掺杂材料回音壁腔[52]Figure10. Schematic of whispering gallery mode cavity formed by metal-doped material[52].
3)振动薄膜腔(vibrating membrane cavity). 事实上, 振动薄膜腔可认为是法布里-珀罗腔的一种变形结构, 即将F-P腔两端镜均固定, 而在腔中放置一个薄膜, 光压使得薄膜振动, 当振动平衡时, 形成稳定的机械振动模式和腔内光谐振模式. 2008年, Thompson等[53]提出一种结构, 其在两个介观尺度、固定、高精细度的刚性镜组成的腔中置入50 nm厚度的电介质薄膜构成腔光力系统, 该腔的频率失谐由薄膜控制, 有效地避免了光场和机械振动各自的性质的改变, 在观测量子跃迁等方面有很强的实用价值, 其原理及实验结构如图11所示.
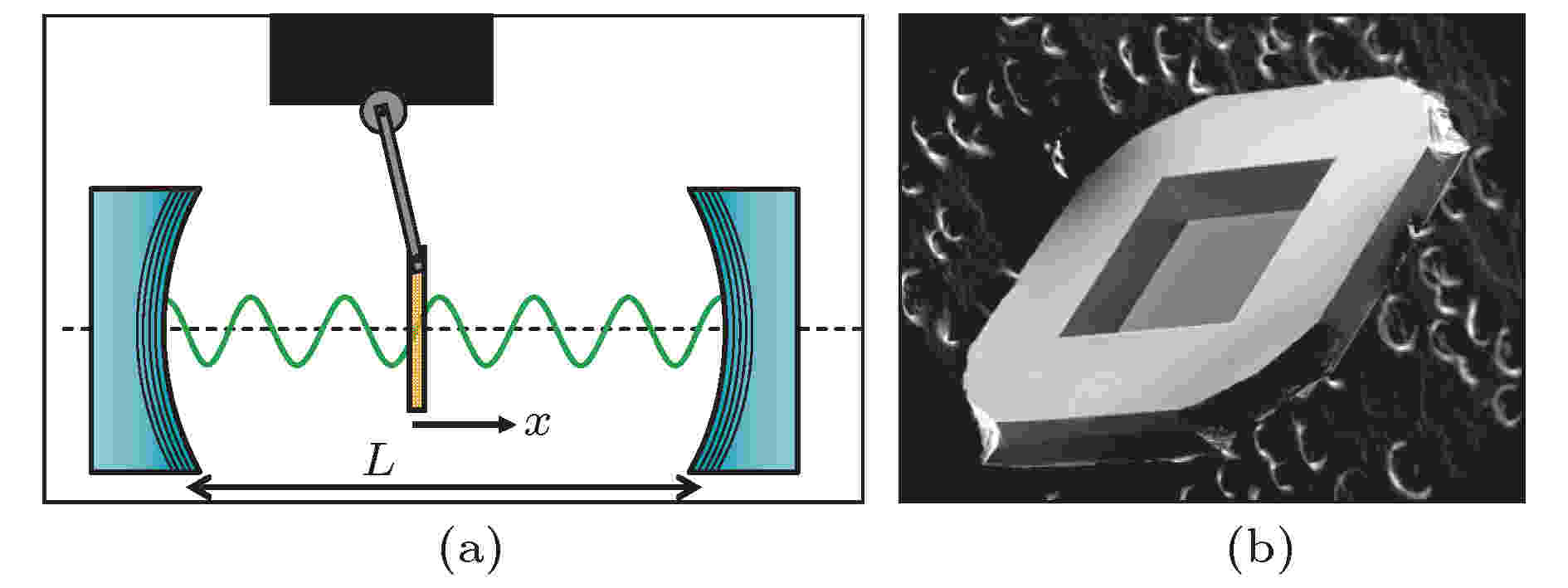图 11 (a) Thompson团队[53]所提振动薄膜原理图; (b)实验结构图[53]Figure11. Schematic[53](a) and experimental setup[53](b) of proposal from Thompson’s group.
2010年, Sankey等[54]仅使用一个含有灵活电介质薄膜的低损耗光力腔就实现了数种不同形式的光力耦合作用, 且所产生的二次方耦合作用强度比其他方案增强了3个数量级, 故可用于验证薄膜机械模式能量的量子化过程, 该方案如图12所示.
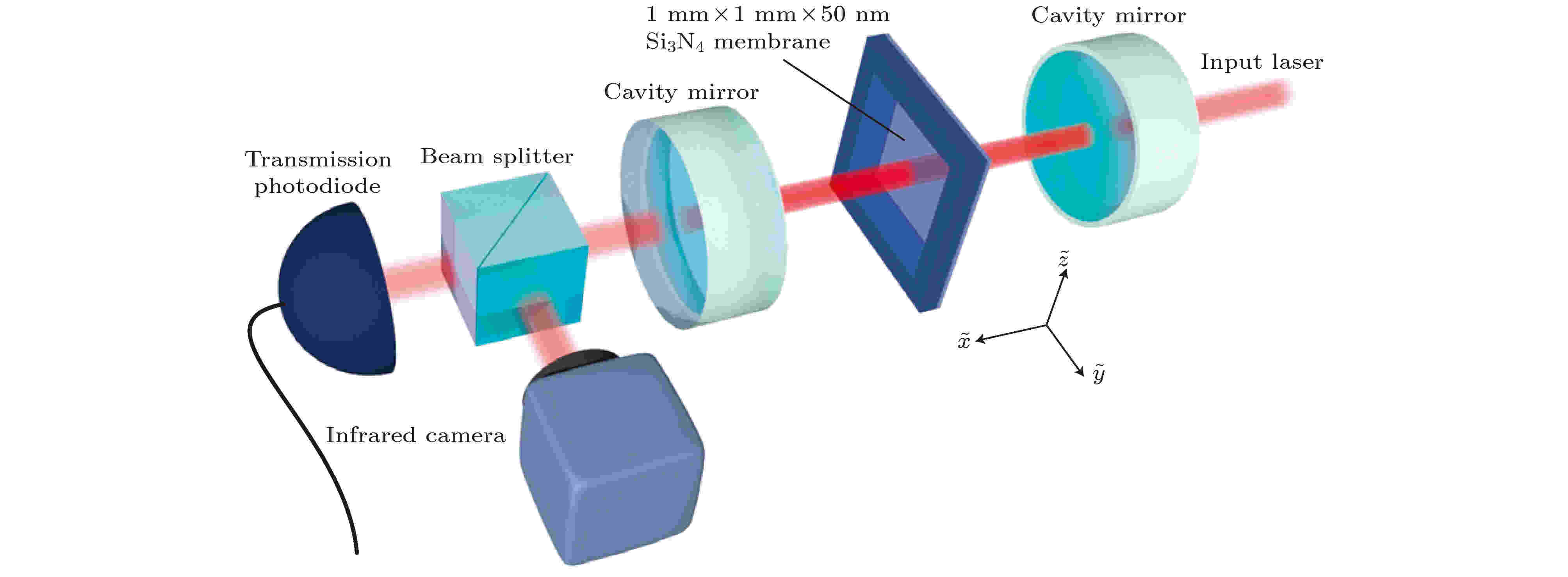图 12 Sankey团队[54]的方案示意图Figure12. Schematic of proposal from Sankey’s group[54].
2019年, Wang等[55]提出使用两束红失谐抽运同时驱动一个内含薄膜的腔光力系统以实现机械振子基态冷却的方案, 发现该方案在理论上可以取得超过单腔冷却极限的结果, 在合理选择腔耗散速率和抽运强度的情况下, 甚至可以将热噪声再降低一个数量级, 其原理如图13所示.
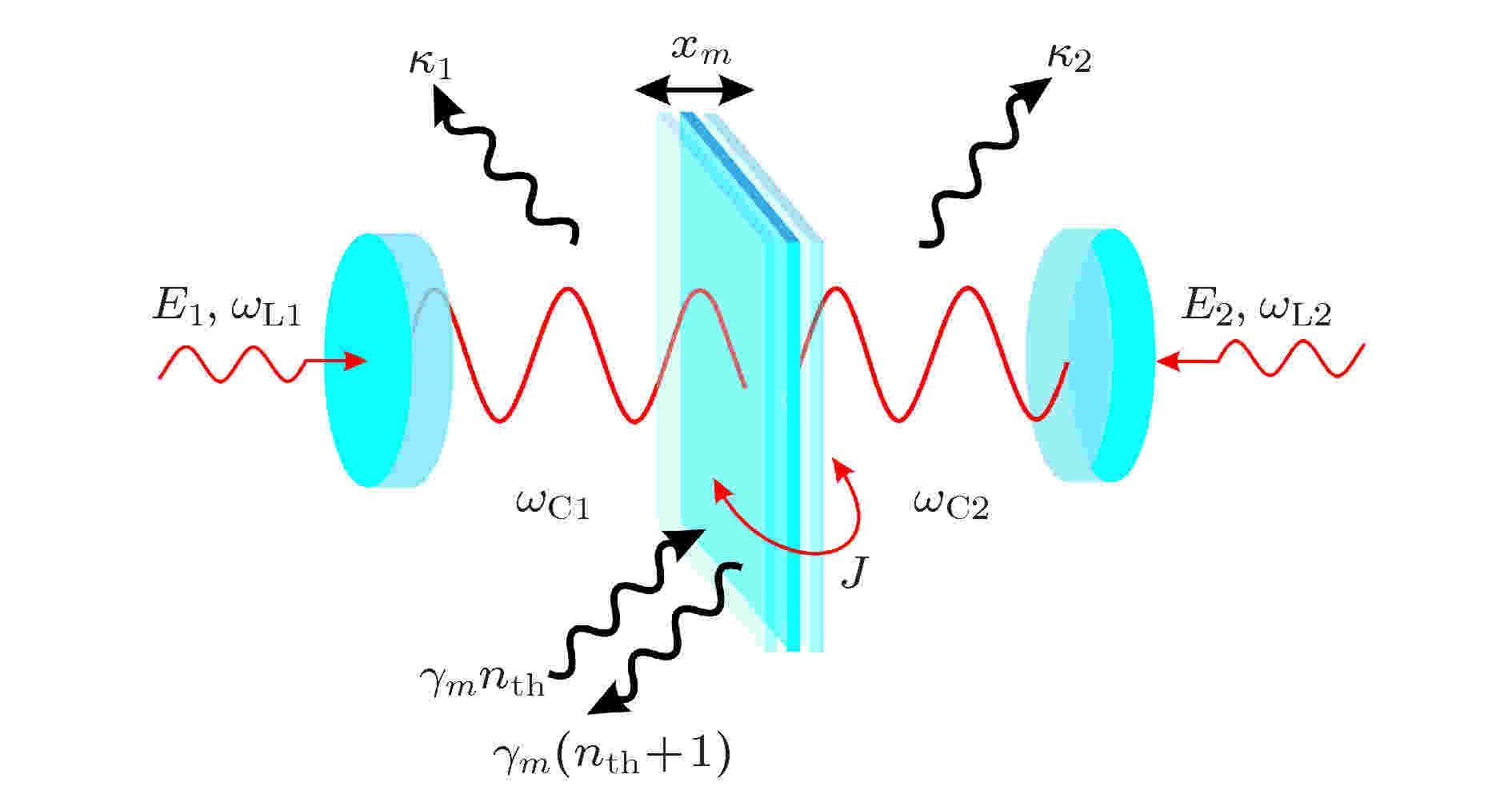图 13 双抽运驱动的振动薄膜腔原理图[55]Figure13. Schematic of vibrating membrane cavity with two pumps[55].
4)光子晶体腔(photonic crystal cavity). 光子晶体是指介电常数在空间分布上具有周期性的人工微纳材料, 不同的介电常数将对光子的传播具有不同的影响. 在光子晶体中通过打孔等方式有意引入一定缺陷后, 发现这样的光子晶体对光子的传播形成了能带与禁带, 从而形成光子带隙使之无法从中穿过, 即相当于光被局限, 从而形成了光子晶体微腔. 1999年, Painter[56]通过打孔的方式, 第一次实验实现了光子晶体微腔. 2009年, Eichenfield等[57]使用两个互相靠近的氮化硅纳米条构造了拉链式的光子晶体微腔, 重量和尺寸在皮克和纳米量级, 这样的结构产生了较大的光学弹簧效应, 其结构如图14所示.
图 14 拉链式光子晶体微腔结构图[57]Figure14. Structure of zipper-like photonic crystal cavity[57]
2014年, Safavi-Naeini等[58]在硅基片上实现了一种雪花形的平面光子晶体微腔, 腔内光模谐振频率可达195 THz, 有效的单光子-声子耦合速率为220 kHz, 机械振子的谐振频率达到了9.3 GHz的水平, 该微腔为微波X波段提供了全光子能带, 为近红外光提供了二维伪能带, 其结构如图15(a)所示. 2016年, Burek等[59]使用金刚石晶体NV色心结构, 加工出了一种稳定的光子晶体微腔, 与其他材料的光子晶体微腔相比, 其具有光子容量大(> 105)、光力耦合率高(协同参数室温下可达20)的优势, 该结构如图15(b)所示. 2018年, Riedinger等[60]使用两个相隔20 cm的芯片级纳米硅晶体腔光力结构, 成功将1550 nm光束产生的纠缠特性转移到这两个腔光力系统振动模式上, 且该纠缠态的相干时间达到毫秒级别, 该结构可以直接并入光学量子通信网络中, 应用于大规模量子组网. 2019年, Rajasekar等[61]利用一种六边形结构的光子晶体环状谐振腔进行压力和温度感知, 该结构具有高灵敏度、高传输效率和高品质因数的优势, 压力感知范围为0.04—6.00 GPa, 温度感知范围为5—540 °C, 极为适合在纳米技术中应用, 其结构如图15(c)所示.
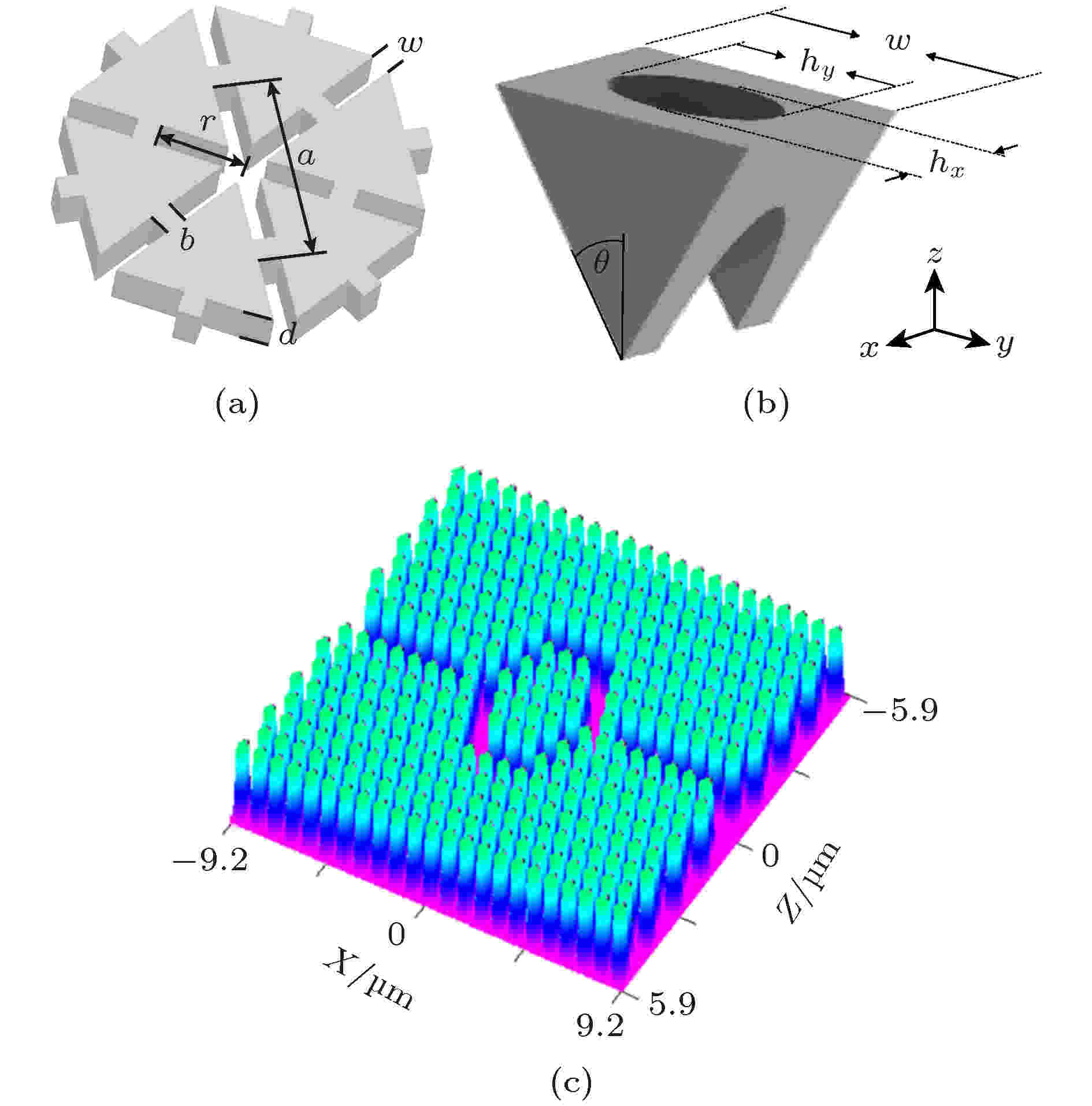图 15 (a)雪花形光子晶体微腔结构图[58]; (b)金刚石NV色心光子晶体微腔结构图[59]; (c)六边形结构的光子晶体环状谐振腔结构图[61]Figure15. Structures of (a) snowflake photonic crystal cavity[58], (b) diamond NV center photonic crystal cavity[59], and (c) hexagonal photonic crystal cavity[61].
5)超导微波腔(superconducting microwave cavity). 超导微波腔类型的腔光力系统由超导微波电路与纳米机械振子耦合构成, 故也被称为腔电力系统(cavity electromechanical system), 仍属于广义的腔光力系统, 其中超导微波电路多由超导传输线振子构成, 可等效为超导LC电路, 且腔谐振频率为
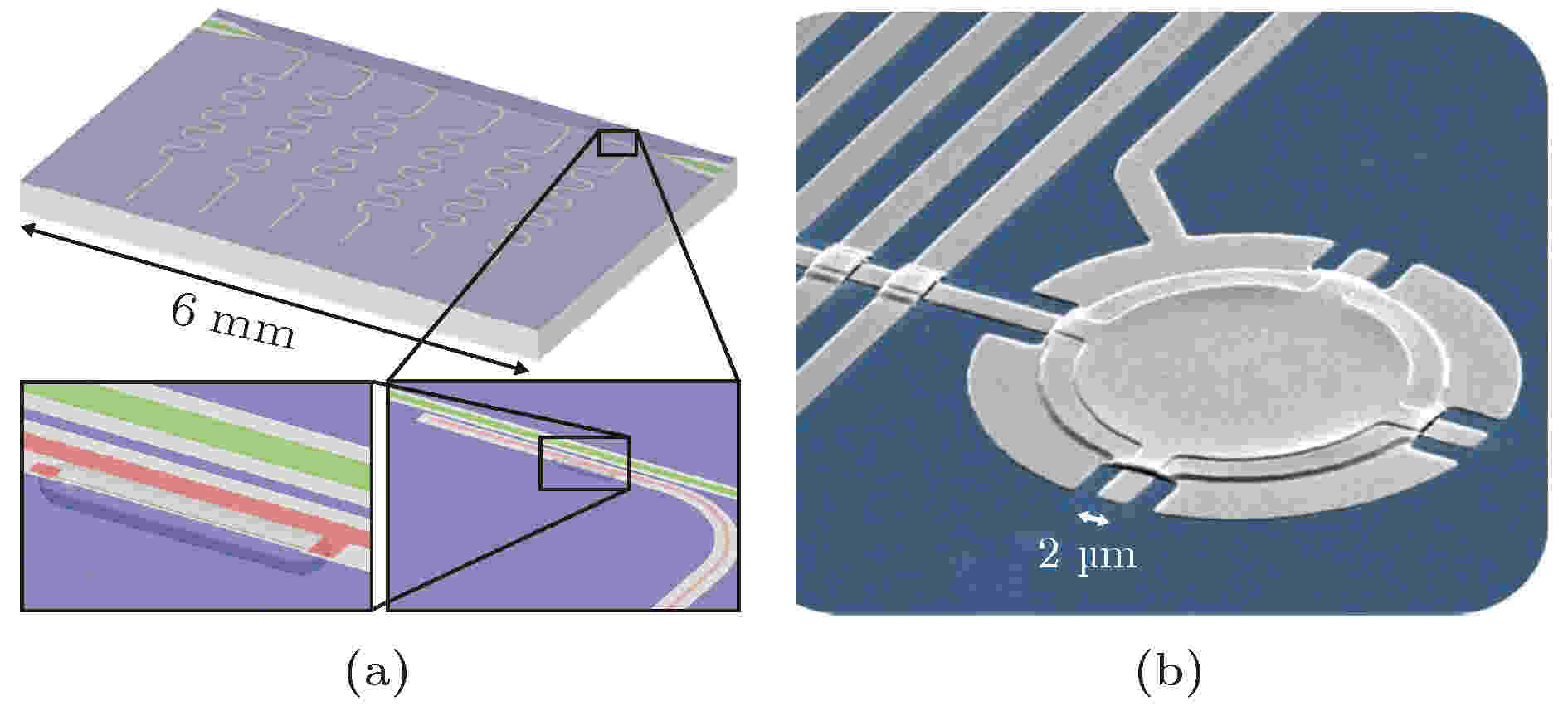图 16 (a)分布式超导微波腔结构图[62]; (b)鼓膜状超导微波腔结构图[63]Figure16. Structures of (a) distributed superconducting microwave cavity[62] and (b) drum-like superconducting microwave cavity[63].
2011年, Teufel等[63]通过将一个鼓膜状的超导微波腔同一个自由置入、灵活可变的铝薄膜耦合, 取得了比同类方案高出两个数量级的单光子-声子耦合强度, 这种结构为机械振子基态冷却、长时间量子态控制及量子态观测提供了一种有效途径, 其结构如图16(b)所示.
2016年, Fink等[64]设计了一种耦合了氮化硅纳米薄膜和平面声光材料超导微波电路的系统, 超导电路谐振频率为8 GHz, 在双抽运情况下可将机械振子冷却到0.32个声子的水平, 可用作芯片级的量子接口, 其原理及结构如图17(a)和图17(b)所示.
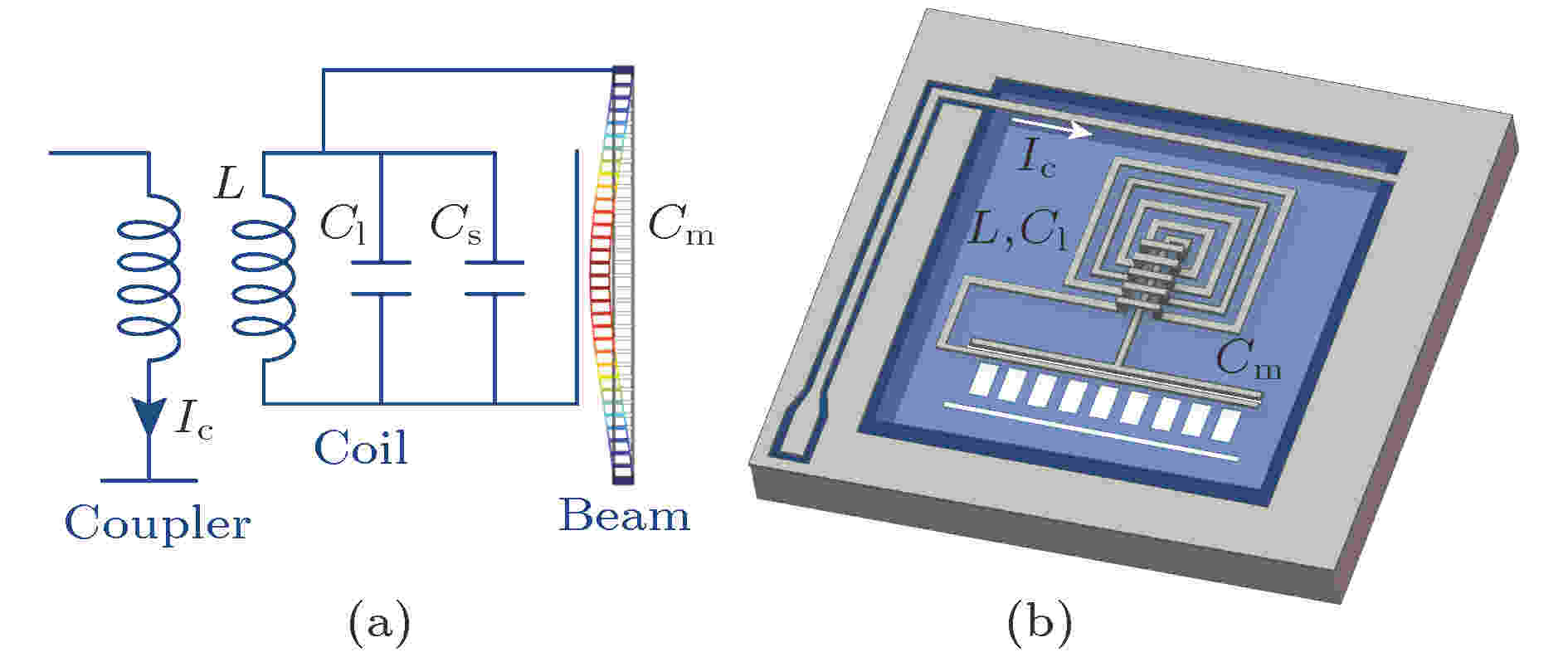图 17 氮化硅纳米薄膜超导微波腔(a)原理图和(b)结构图[64]Figure17. Schematic (a) and structure (b) of Si3N4 membrane superconducting microwave cavity[64].
2019年, Li等[65]构造了一种由悬浮超导薄膜与超导微波谐振腔电容性耦合而成的微尺度光力系统, 当增加抽运功率时, 机械振子频率与抽运功率之间的多样性依存关系都可被观察, 这种超导微波腔光力系统可以用在可控的微波-光接口等方面, 其结构如图18(a)所示. 同年, Bienfait等[66]设计了如图18(b)所示的双模超导微波腔光力系统. 两个超导微波腔中超导微波量子比特, 经由表面声波(surface-acoustic wave, SAW)声子构成的通道, 在声子的收发过程中实现了效率高达67%、保真度为84%的二比特超导微波量子态转移. 5种常见腔光力系统部分参数及研究进展的进一步总结说明如表1所示.
| 类别 | 品质因数水平 | 振子质量水平 | 振子频率水平 | 优势 | 不足 |
| 法布里-珀罗腔 | 104 | kg—pg | kHz—MHz | 技术成熟, 应用广泛 | 品质因数水平较低, 耗散较大、不易集成 |
| 回音壁腔 | 109 (微球腔) 108 (微环腔) | ng—fg | MHz—GHz | 光力耦合度高, 构造灵活, 腔内光子寿命长 | 工艺要求高、成本高 |
| 振动薄膜腔 | 105 | pg | MHz | 结构简单、灵活 | 耗散较大、不易集成 |
| 光子晶体腔 | 106 | fg | GHz | 可利用自由度多, 片上可扩展 性好, 精确的模式控制 | 工艺复杂 |
| 超导微波腔 | 107 | pg | MHz | 可高度集成, 与超导器件兼容, 腔的稳定性好, 热噪声水平低 | 超低温, 电磁噪声谱较宽 |
表15种主要腔光力系统的研究现状总结
Table1.Summary for current research states of 5 main cavity optomechanical systems.
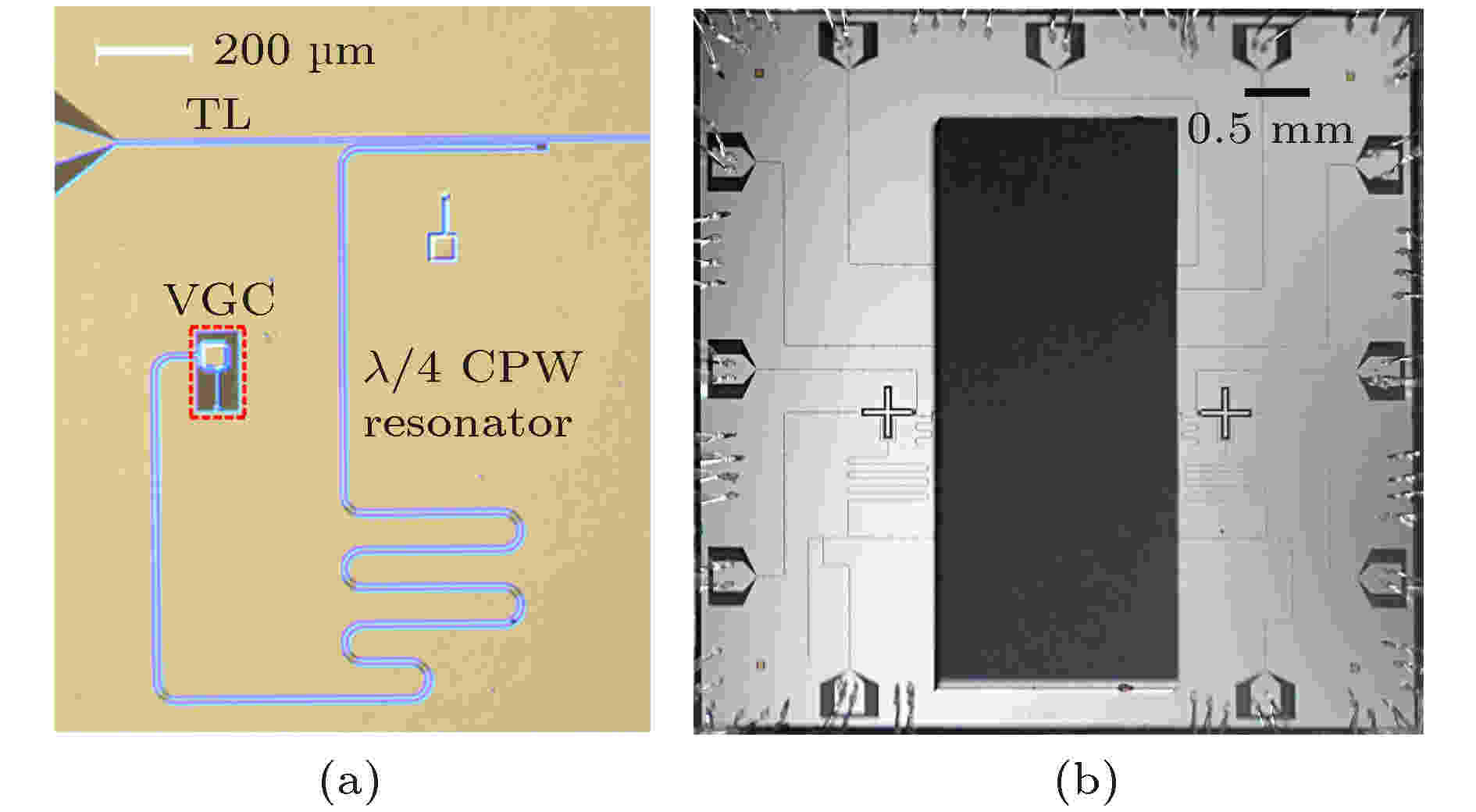图 18 (a) Li等[65]设计的超导微波腔结构图; (b) Bienfait等设计的实验结构图图[66]Figure18. (a) Structure of membrane superconducting microwave cavity designed by Li et al.[65]; (b) experimental setup designed by Bienfait et al.[66].
除上述分类外, 若以腔内的模式种类及数目为标准, 腔光力系统可划分为单模和多模两类, 单模类型中又可根据腔内模式频率分为光腔和微波腔两类; 多模类型中则可以分为光多模、微波多模和光-微波杂化多模3类, 而这些多模类型是通过腔光力系统制备微波非经典态的重要方法.
2
3.1.基于腔光力系统的微波非经典量子态制备
近年来, 微纳腔光力系统在制备微波非经典量子态上取得了较大进展, 显示出了巨大的应用潜力, 受到了广泛的关注, 由于其结构的灵活性, 各种方案层出不穷, 相关的实验也正在稳步推进, 主要可分为两类: 单纯腔电力系统制备方法和腔电光力系统(cavity electro-opto-mechanical system, cavity EOM system)制备方法.腔电力系统属于广义腔光力系统, 其纳米机械振子连接的是微波腔. 单纯腔电力系统制备法是指利用单个或两个超导微波电路腔与机械振子耦合, 通过腔内微波模式与机械谐振模式的相互作用实现对于微波非经典量子态的制备.
2011年, Ku等[73]设计并制出了两种微波无源器件, 分别由平面波导腔(coplanar waveguide cavity, CPWC)和支线所构成, 这两种无源器件的工作频率被分别设定在8 GHz和7 GHz, 其结构如图19(a)和图19(b)所示, 测试结果符合其设计预期, 可用在制备连续变量的双模压缩微波纠缠态等量子信息处理过程中. 在优化相应结构后, Ku等[74]在2015年利用改进结构成功制备了连续变量的双模压缩态纠缠微波. 如图19(c)所示, 其原理与光学中的制备方法类似, 即先通过约瑟夫森参量放大器(Josephson parametric amplifier, JPA)将两个传输微波场制成压缩态微波场, 再通过所设计的无源器件进行耦合, 生成双模压缩态.
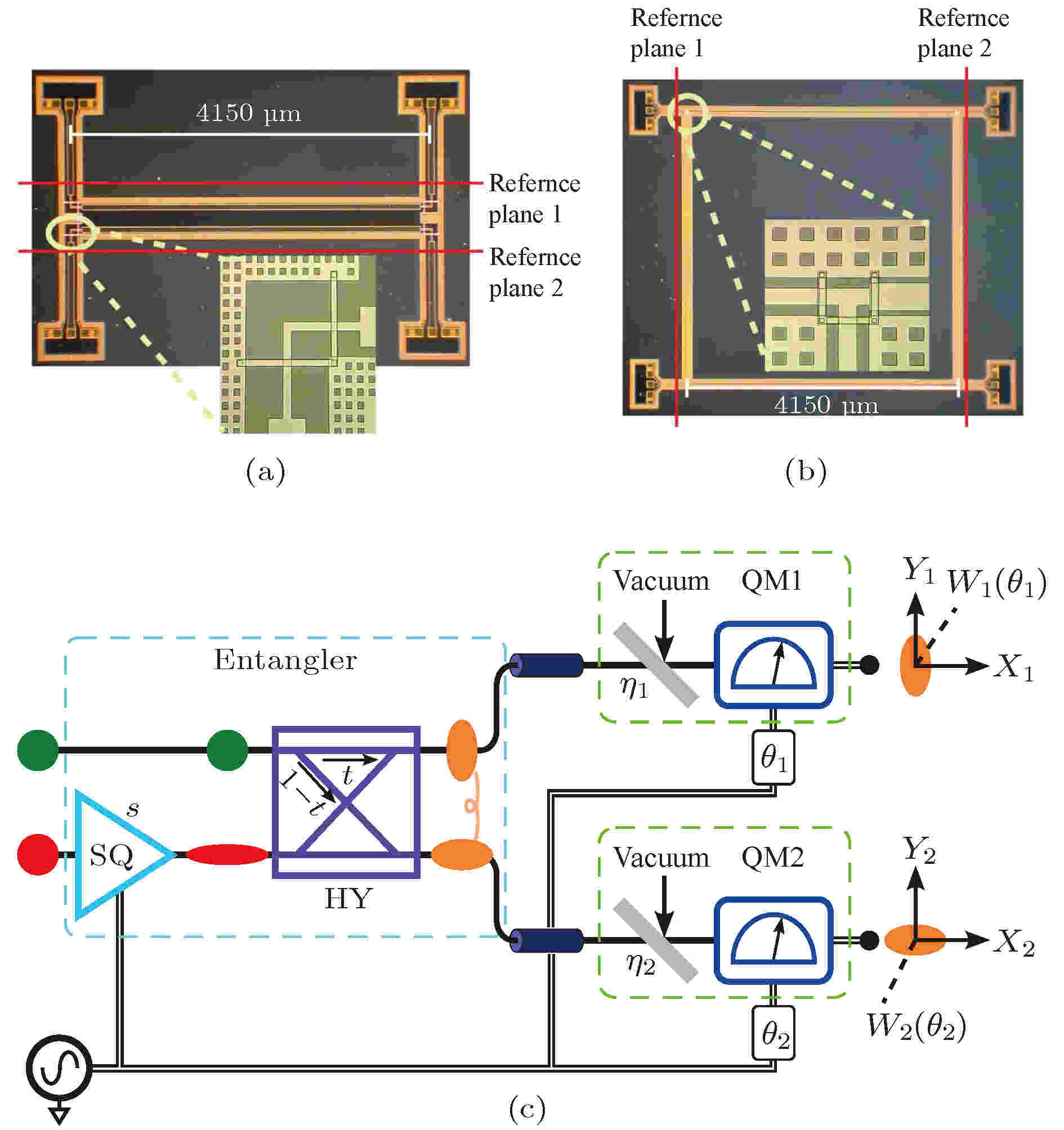图 19 (a)正交功分器结构图[73]; (b) 20 dB功分器结构图[73]; (c)微波EPR态制备方案示意图[74]Figure19. (a) Structure of quadrature hybrid coupler[73]; (b) structure of 20 dB directional coupler[73]; (c) schematic of microwave EPR state preparation[74].
2013年, Li等[75]利用两个超导平面波导腔与一个纳米机械振子电容性耦合的腔电力结构, 制备了稳定可控的微波连续变量纠缠态, 其结构如图20所示. 在强耦合条件下, 这种结构所制备的微波连续变量纠缠态, 可以通过系统动力学方法或者耗散型量子动力学过程得到确定性的控制, 且可由有效电力耦合强度控制所获得的纠缠程度.
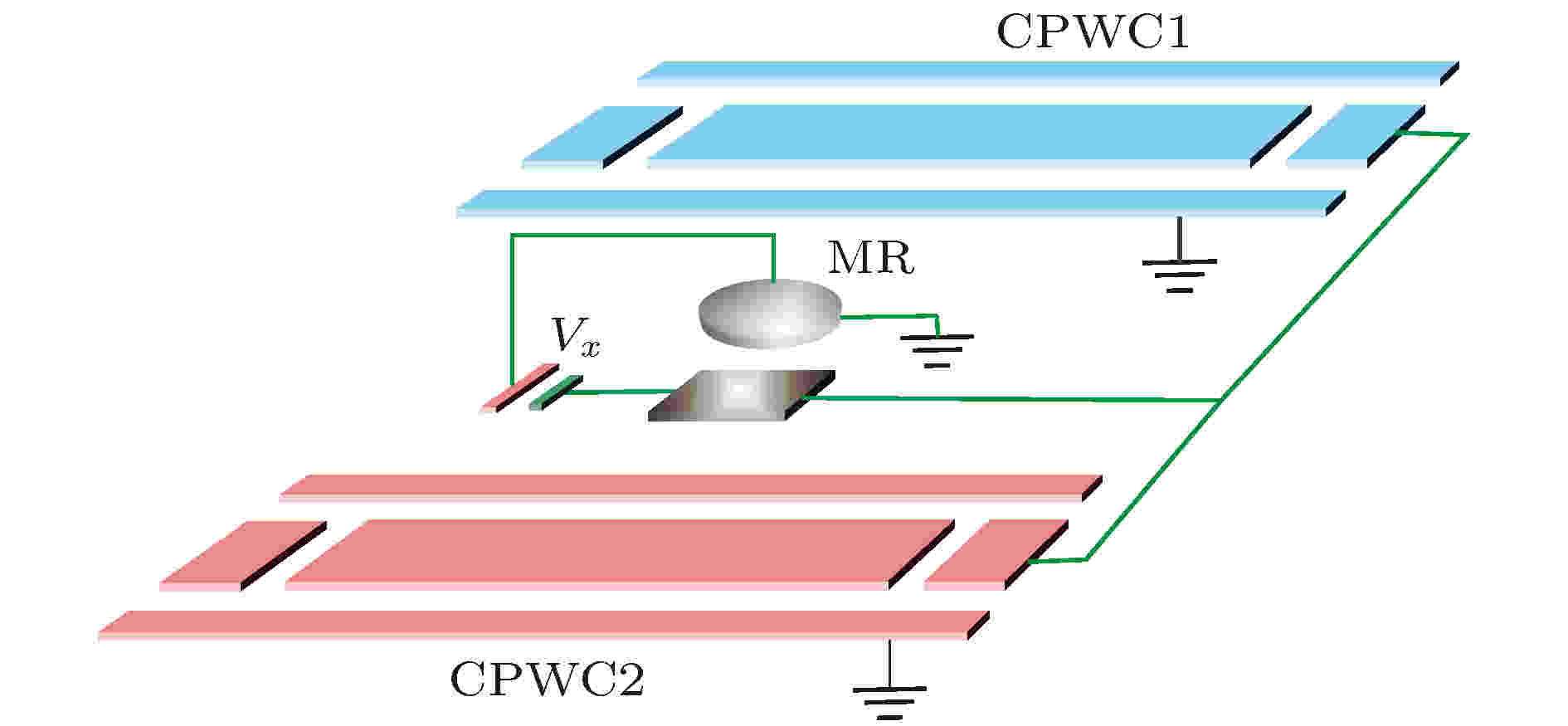图 20 Li等[75]提出的微波连续变量纠缠态制备方案原理图Figure20. Schematic of microwave continuous-variable entanglement state preparation proposed by Li et al.[75].
2013年, Palomaki等[76]通过如图21所示的腔电力结构, 制备了两个微波脉冲间的双模压缩纠缠态. 图21的腔电力系统可等效看作由左侧鼓膜状电容和螺旋状电感构成的超导LC电路腔同右侧绿色标注的微波传输线耦合而成, 该结构首先实现了一个微波脉冲与机械振子的动量间的纠缠, 然后机械振子将自己所存储的纠缠转移到另一个微波脉冲上, 通过测量发现这样的两个微波脉冲间符合双模压缩态的纠缠关系.
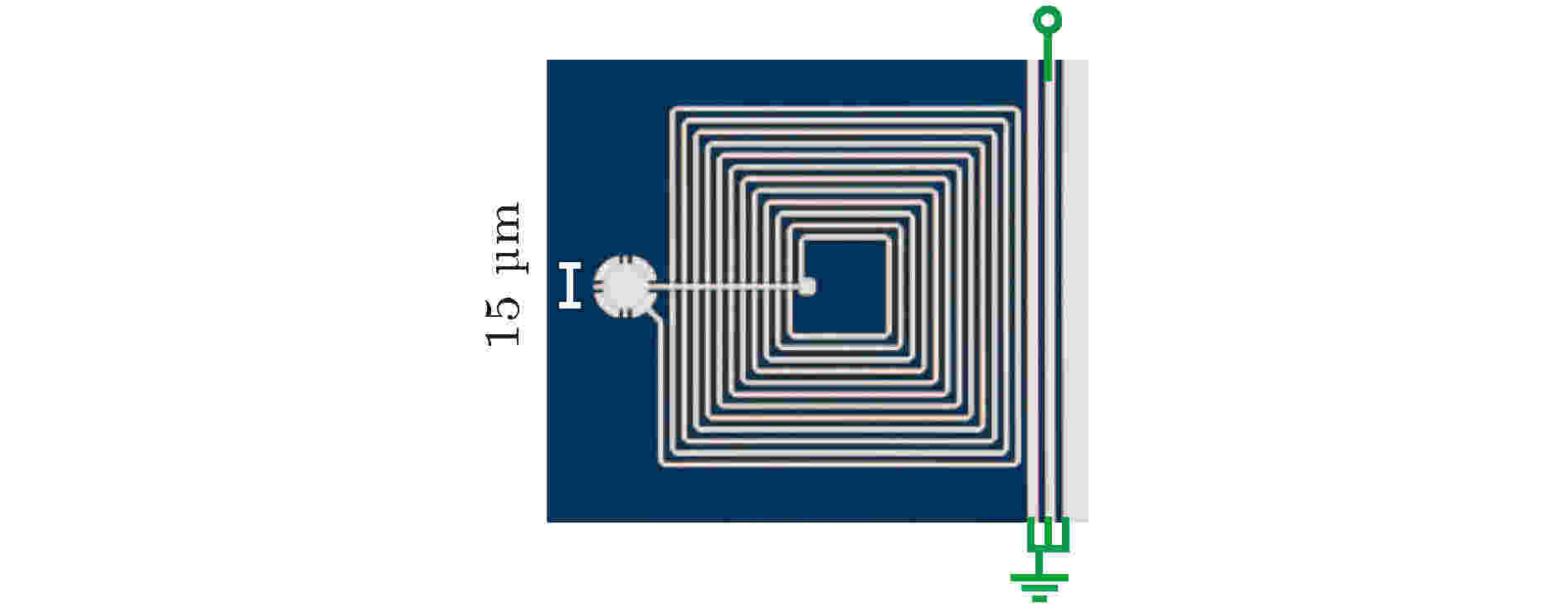图 21 Palomaki等[76]设计的超导微波腔结构图Figure21. Structure of superconducting microwave cavity designed by Palomaki et al.[76].
2014年, Sete等[77]利用如图22所示方案制备了微波压缩态以及微波-机械振子纠缠态. 方案通过将一个超导电荷比特与微波传输线腔及可移动纳米薄膜谐振腔耦合产生一个非线性相互作用, 同时可移动纳米薄膜谐振腔又与第二个微波谐振腔耦合产生电力非线性相互作用, 在这两种非线性效应的共同作用下, 一方面实现了对传输微波场的强压缩, 且压缩度可通过调整抽运微波场的功率来控制; 另一方面实现了鲁棒的微波-机械振子谐振模式纠缠.
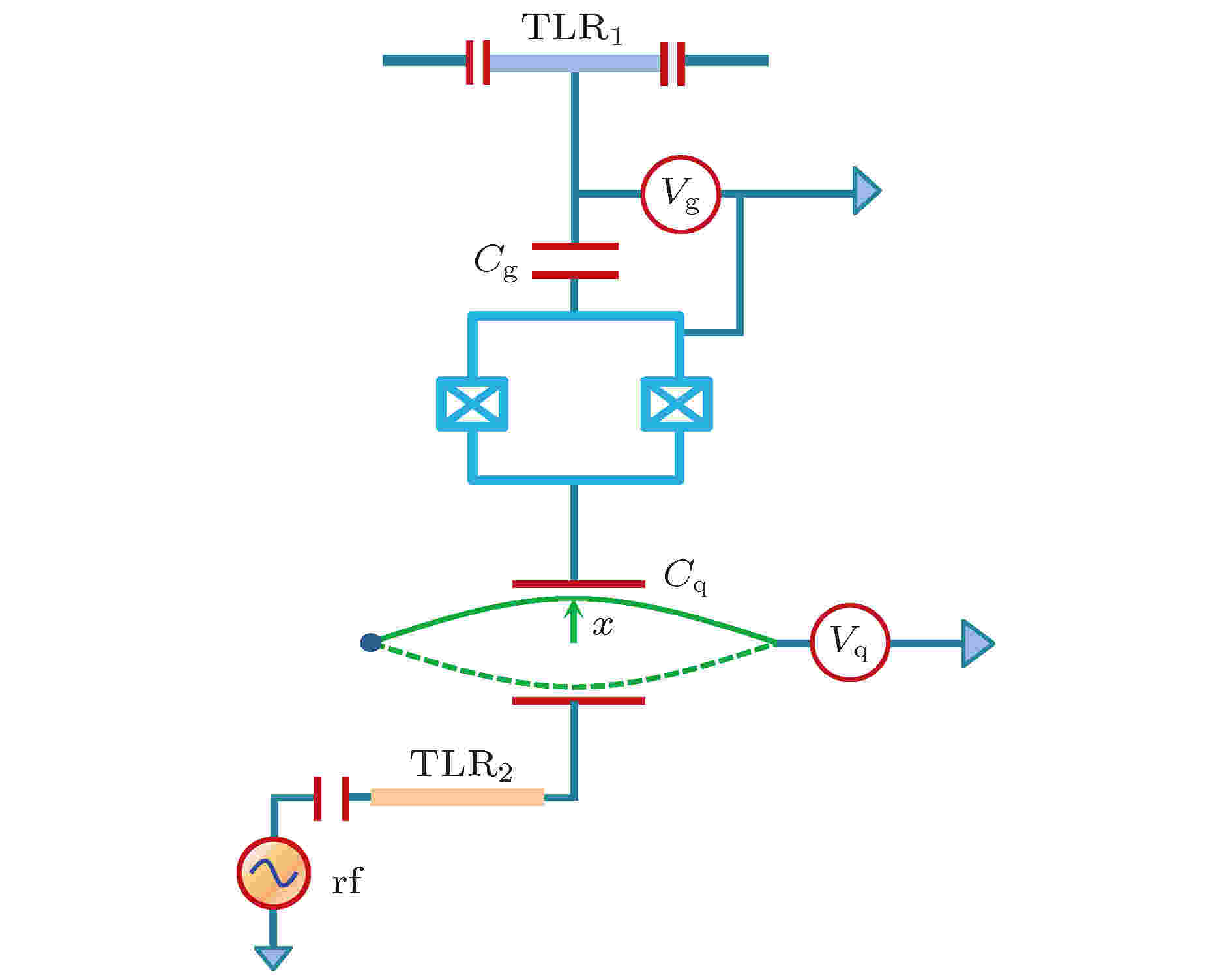图 22 Sete等[77]提出的微波压缩态及微波-机械振子谐振模式纠缠态制备方案示意图Figure22. Schematic of microwave squeezed state preparation and microwave-mechanical vibration mode entanglement preparation proposed by Sete et al.[77].
2017年, Ockeloen-Korppi等[78]通过腔电力结构, 制备了低于真空态8 dB的微波强压缩态, 其结构如图23所示. 该结构是由超导微波腔同薄膜振子耦合而成, 其中微波腔由双抽运驱动, 输入的抽运场与信号场在腔电力学系统的作用下, 将真空噪声进行压缩, 经低温条件进行相敏放大后, 在室温环境中利用矢量网络分析仪及频谱分析仪测量了噪声起伏, 验证了微波压缩态的产生.
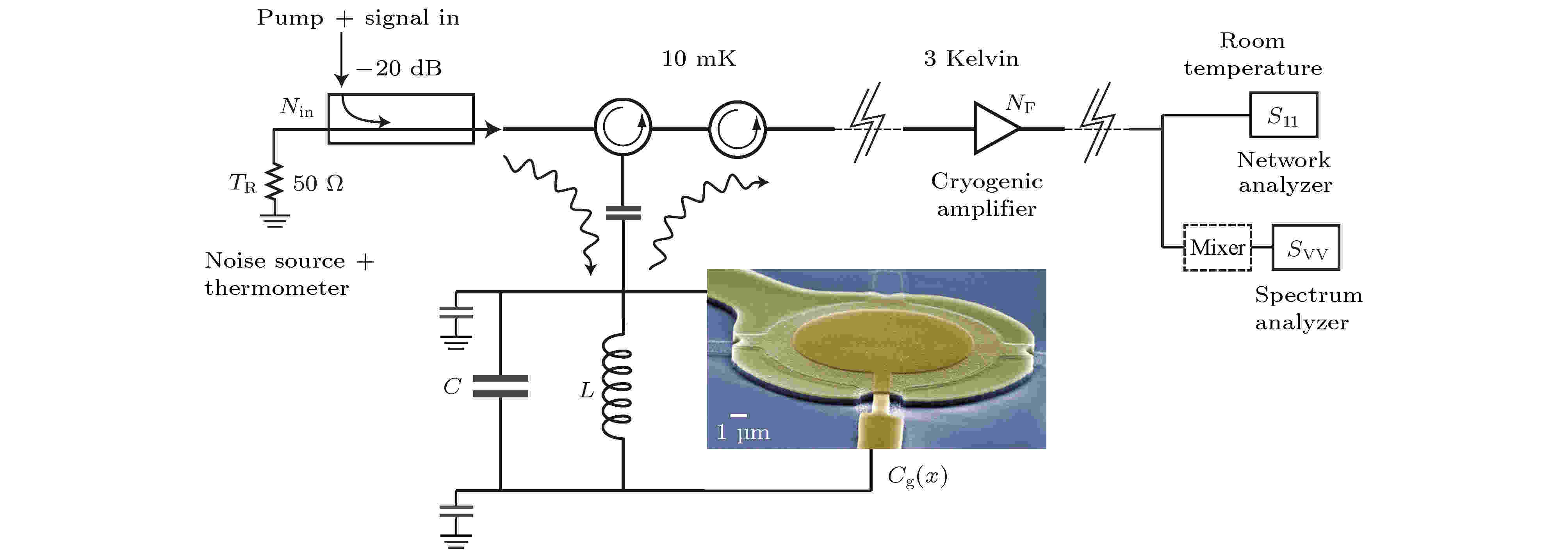图 23 微波强压缩态制备方案示意图[78]Figure23. Schematic of preparing highly squeezed state in microwave domain[78].
此外, 通过纳米机械振子同时与光腔和微波腔耦合, 构建腔电光力混合系统(也称为EOM转换器), 其基本结构如图24所示[79], 在红蓝失谐分别抽运两腔的情况下, 微波模式、光模式同时与机械振子谐振模式耦合, 可以实现跨频段的微波-光纠缠, 也可以利用EOM转换器的态转移和频段转移特性, 将光频段的非经典量子态转移到微波频段输出, 从而制备微波非经典量子态[80-82].
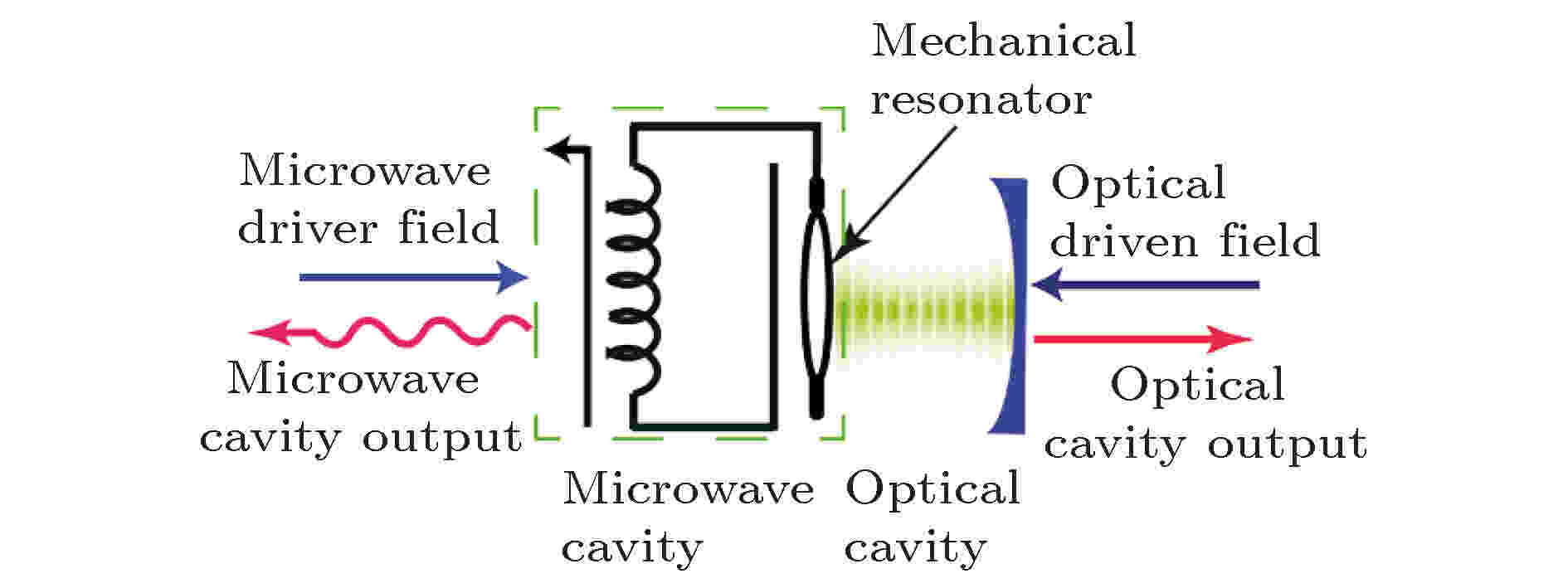图 24 腔电光力系统原理示意图[79]Figure24. Schematic of cavity electro-opto-mechanical system[79].
2013年, Tian[83]通过图25所示腔电光力混合量子接口, 探索了接口两端模式间的博戈留波夫暗模(Bogoliubov dark mode)激发及量子干涉相消问题, 并在强耦合条件下, 利用实验可达到的参数设置, 制备了抗机械声子激发的连续、离散类型微波-光纠缠态, 该研究在混合量子网络及量子态操控领域将具有极大应用潜力.
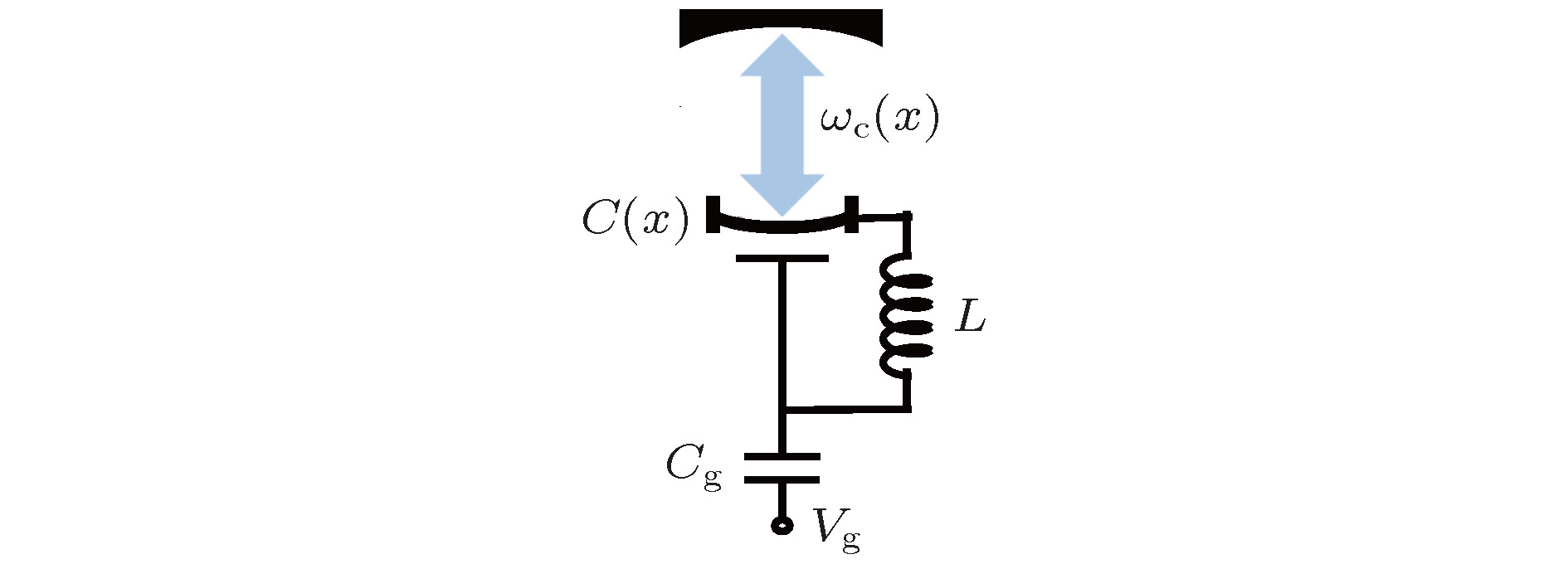图 25 Tian[83]提出的腔电光力混合量子接口示意图Figure25. Schematic of cavity electro-opto-mechanical hybrid quantum interface proposed by Tian[83].
2014年, Andrews等[84]利用图26所示腔电光力转换器在4 K的温度下第一次实验实现了微波-光双向可逆、相干、高效的频率转换能力, 并基于实验中的观测结果进一步分析指出, 当实验温度从当前的4 K降到40 mK时, 将同时实现微波-光信号间的量子态转移, 即在实现频段转移的同时转移脆弱的量子态, 这无疑提供了一种制备微波非经典量子态的新方法: 在足够高的态转移效率和保真度下, 通过将光量子态转移到微波信号上, 实现对应微波非经典量子态的制备.
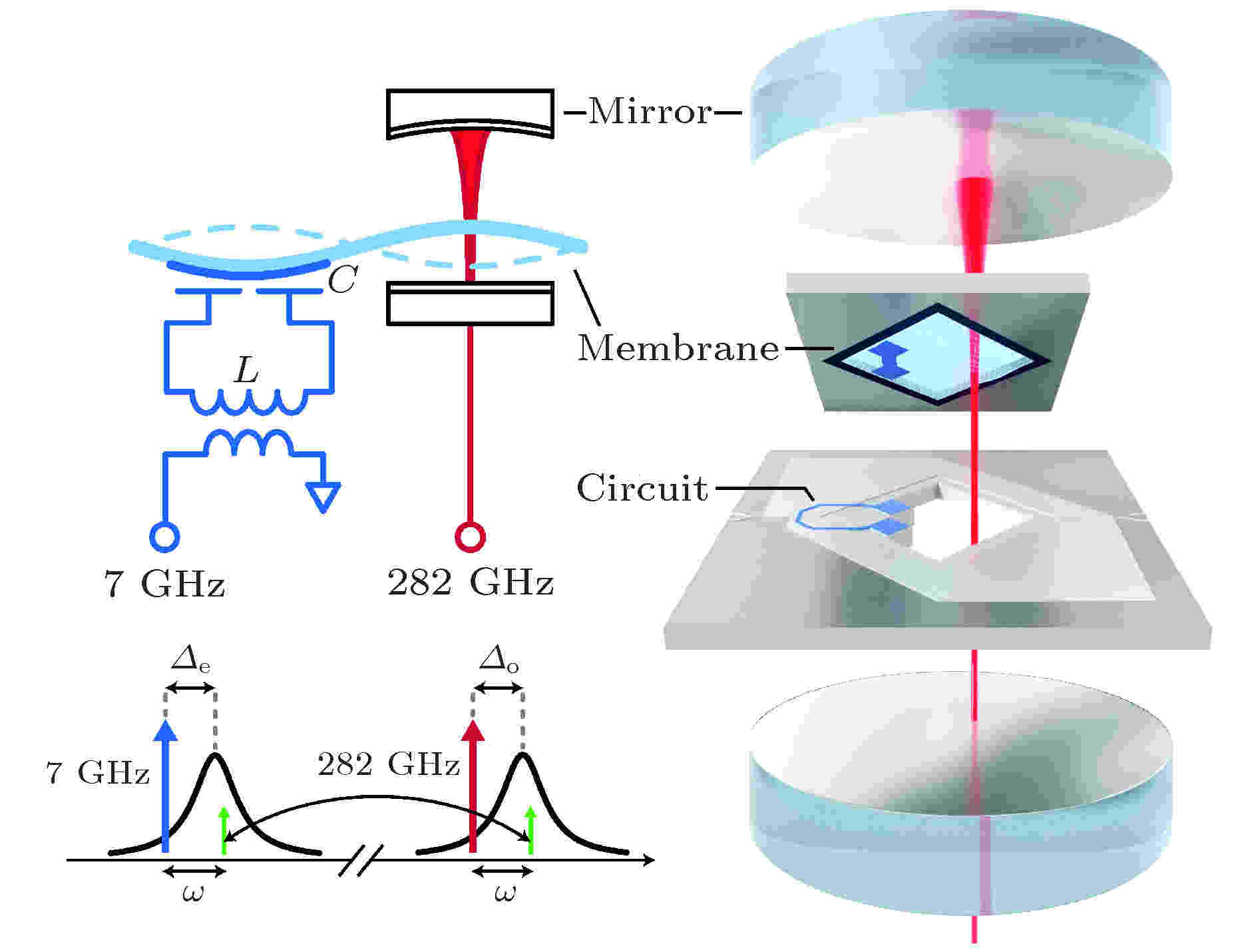图 26 Andrews等[84]设计的腔电光力转换器原理图及器件结构示意图Figure26. Schematic and structure of cavity electro-opto-mechanical converter designed by Andrews et al.[84].
2015年, Abdi等[85]采用两个四端口的腔电光力系统, 在纠缠交换协议下, 先制备出了稳定的微波-光纠缠态, 再通过纠缠交换实现了对两个远距离、无关联的微波场的纠缠, 成功制备了抗热光子的微波纠缠态, 其结构如图27所示. 这项研究可能为连接远程固态、超导量子比特提供有效方法.
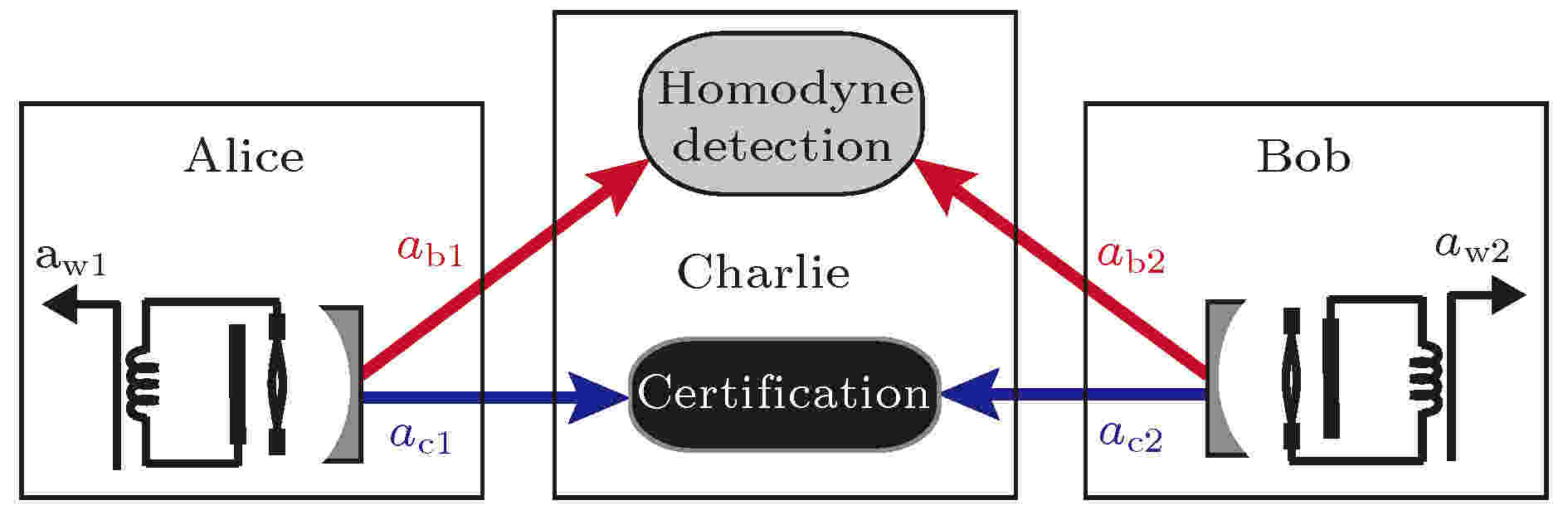图 27 Abdi等[85]提出的远距离微波场纠缠态制备方案示意图Figure27. Schematic of distant microwave fields entanglement preparation proposed by Abdi et al.[85].
2015年, Barzanjeh等[79]提出了基于双电光力转换器的量子微波照明方案, 该方案采用两个相同的电光力转换器, 一个作为发射端, 另一个作为接收端, 发射端在红蓝失谐边带抽运的驱动下, 制备了微波-光纠缠态, 而后将微波信号发射到自由空间传输, 将光信号保存在本地, 待微波信号遇到目标返回后由另一个电光力转换器接收, 并相共轭上转换为与反射微波纠缠的光输出, 与留在本地的光进行符合测量, 根据结果探知目标有无, 其原理如图28所示.
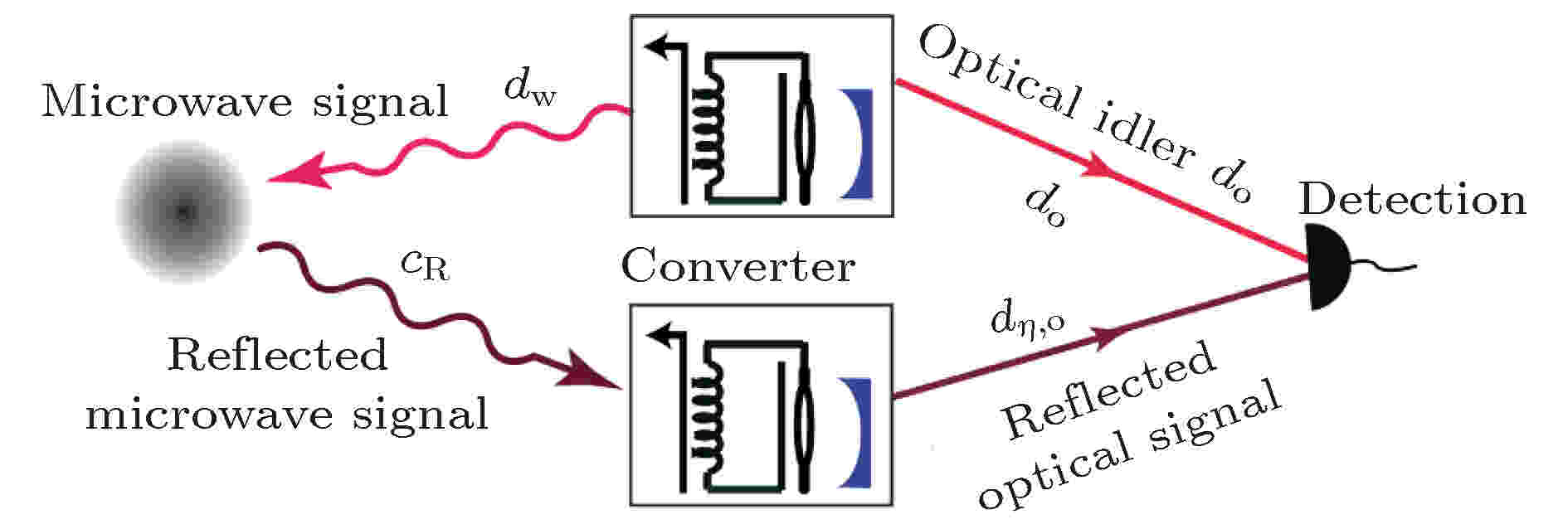图 28 基于双电光力转换器的量子微波照明方案示意图[79]Figure28. Schematic of microwave quantum illumination based on double cavity electro-opto-mechanical converters[79]
2015年, Huang[86]使用电光力转换器将高斯、非高斯量子态从光频段信号转移到微波频段信号, 实现了对高斯、非高斯微波量子态的制备, Sumei认为即使在量子噪声存在的情况下, 只要合理设计光腔、微波腔, 使其损耗速率小于其耦合速率、具有足够的耦合强度, 就可实现对量子态的高效转移, 其原理如图29所示.
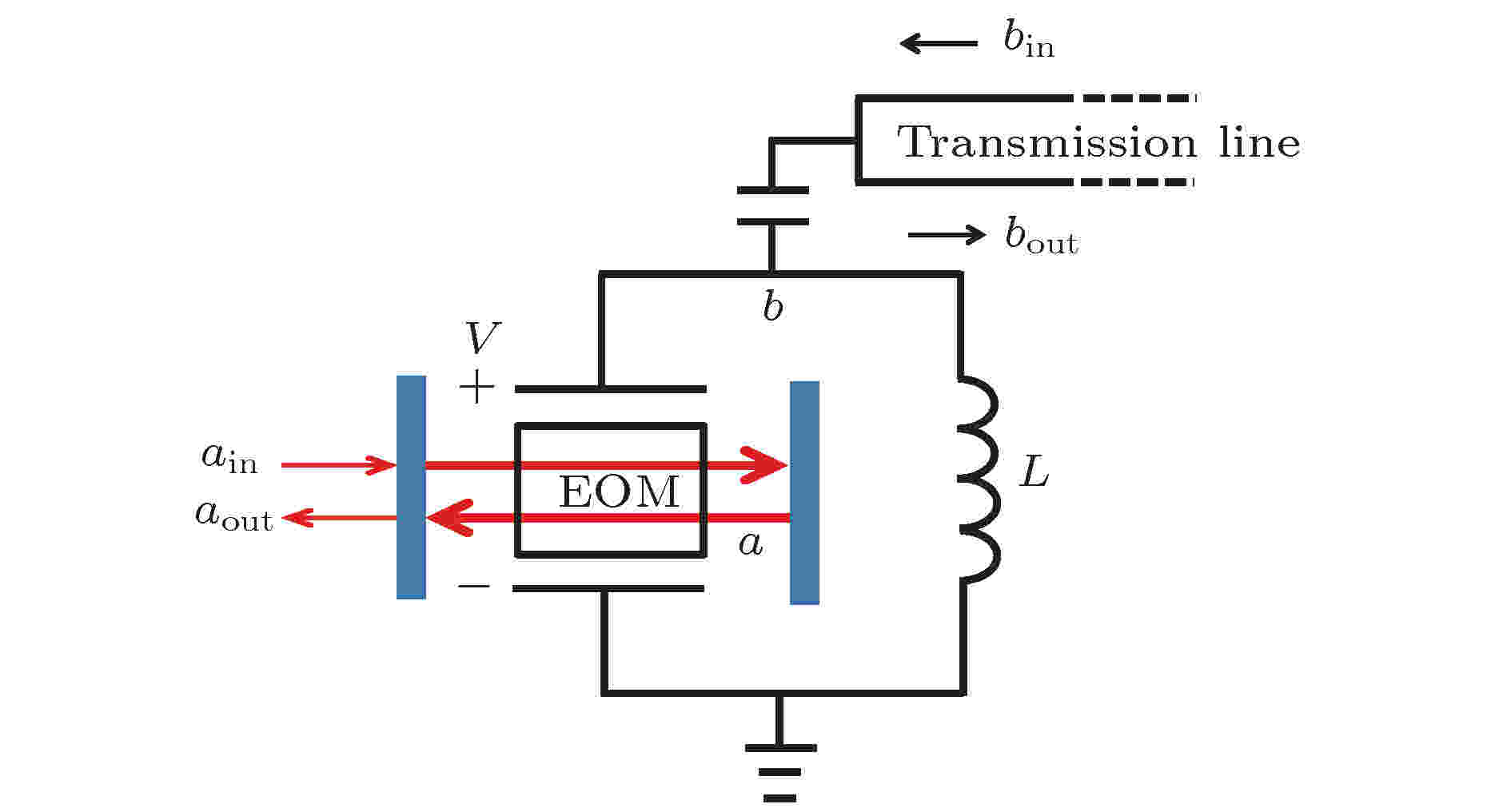图 29 基于电光力转换器的微波高斯、非高斯微波量子态制备方案示意图[86]Figure29. Schematic of Gaussian and non-Gaussian microwave quantum states preparation based on cavity electro-opto-mechanical converter[86].
2017年, Xiong等[87]提出在电光力转换器的F-P光腔中加入光学参量放大器制备了加强的微波-光纠缠态, 这是通过加入光学参量放大器之后, 微波光子-机械声子-光波光子间的耦合强度增大、转换效率上升实现的, 他们还分析了加强后的量子微波照明的性能, 理论上证明了这种方法增强电光力转换器制备的微波-光纠缠态有效性, 其原理图如图30所示.
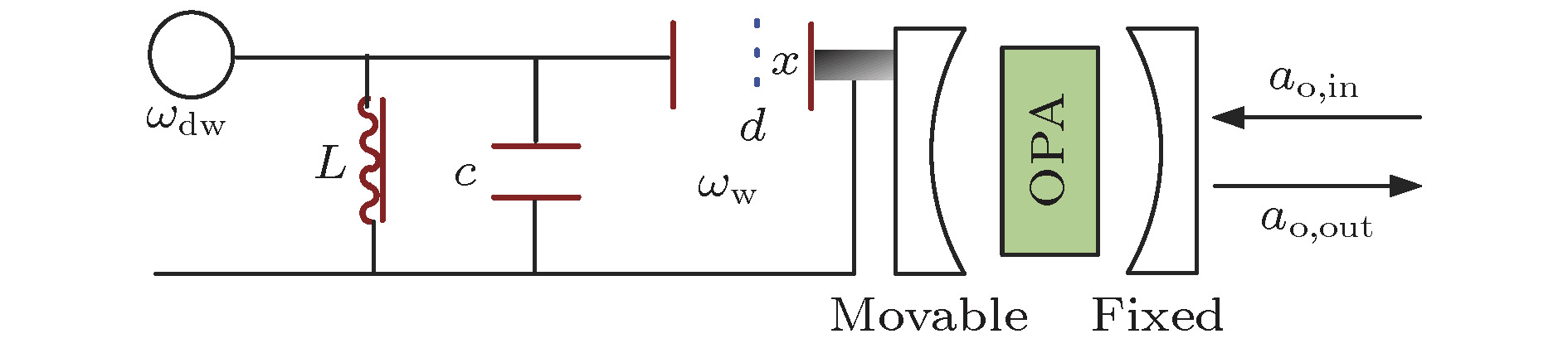图 30 引入光学参量放大器的电光力转换器示意图[87]Figure30. Schematic of cavity electro-opto-mechanical converter introducing optical parametric amplifier[87].
2018年, Regal团队[88]利用电光力转换器在100 mK温度下, 实现了可由纳米机械振子调节的微波-光态转移, 效率达到47%, 由于使用了前馈协议使得进入振子的热噪声光子减至38个, 且即使热噪声光子进入机械振子的速率大于微波-光态转移效率, 也能使量子态信息成功转移, 从而可以更好地制备微波非经典量子态, 其原理如图31所示.
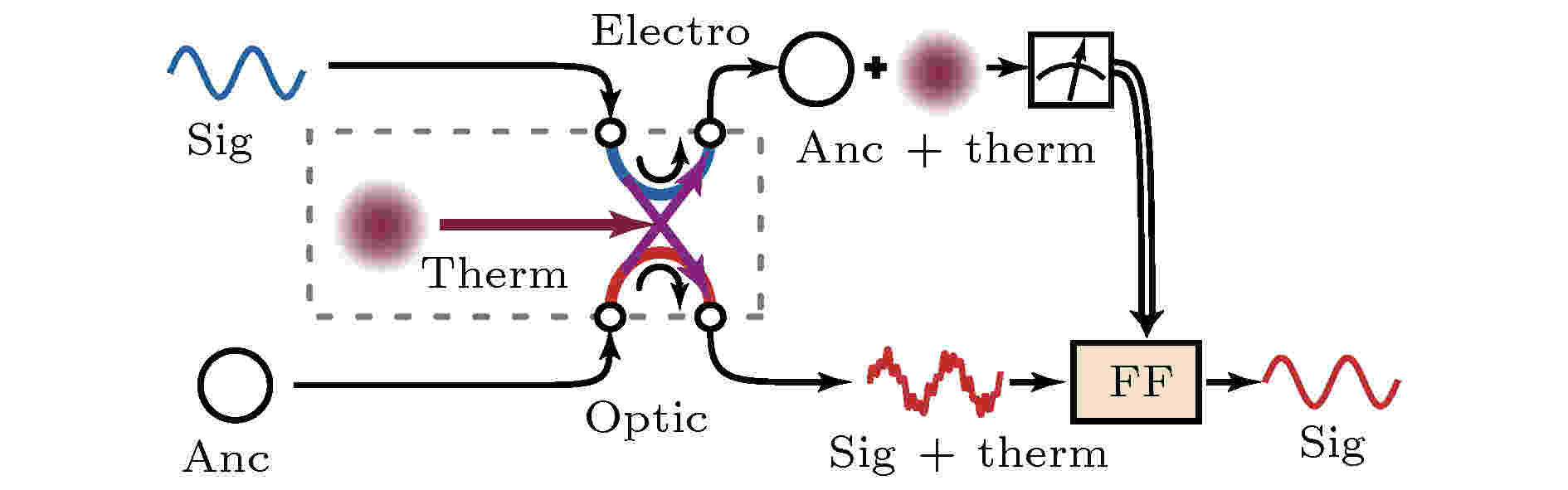图 31 Regal团队[88]提出的量子态转移方案示意图Figure31. Schematic of quantum state transferring proposed by Regal’sgroup[88].
2018年, Ma等[89]提出了一种基于腔电光力系统的多通道量子路由器, 该路由器由一个环形光腔和一个超导LC微波电路腔以电容耦合方式构成, 实现了微波单光子Fock态的制备, 并可实现微波-光的量子态的双向有效转换, 其结构如图32所示.
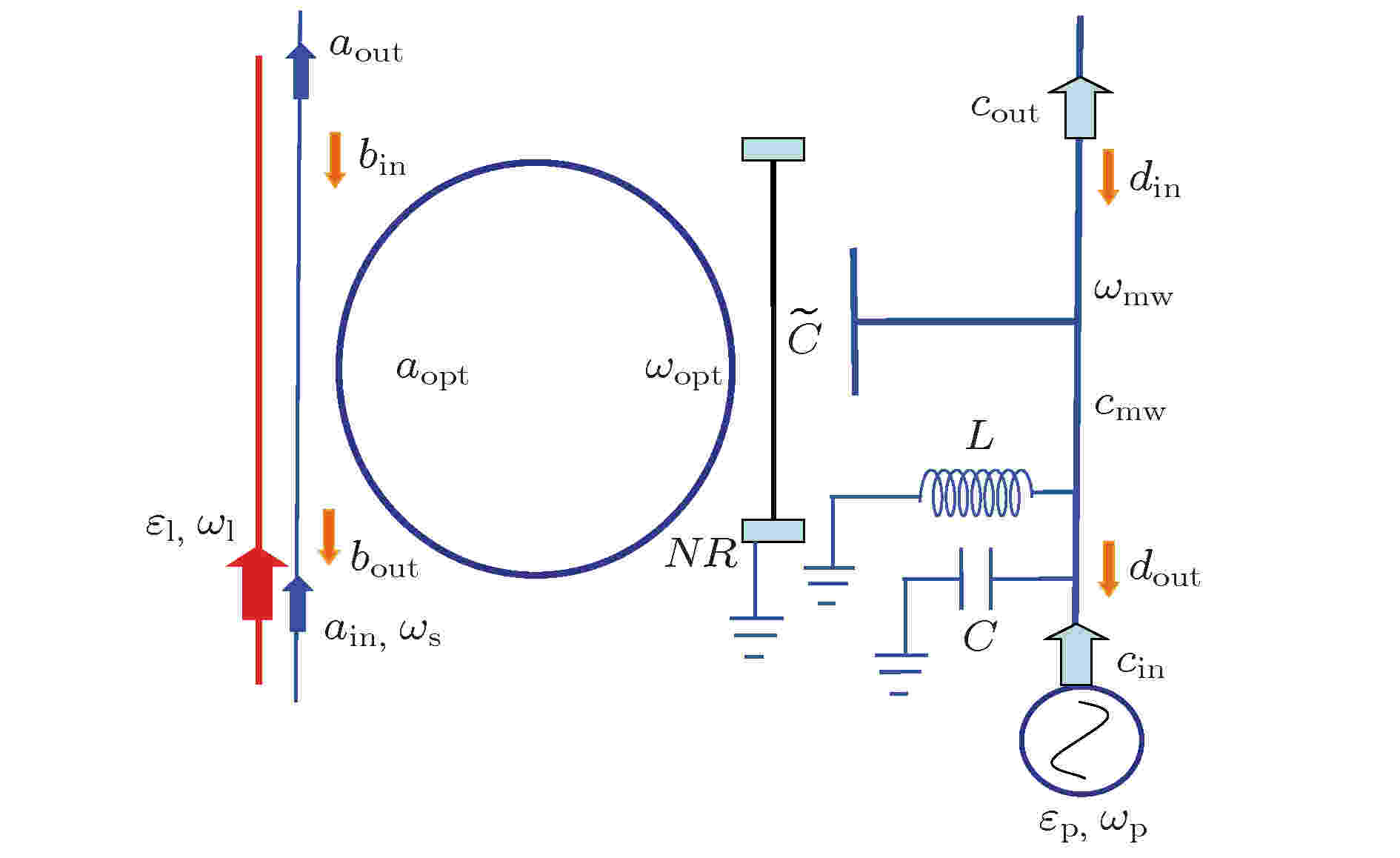图 32 基于腔电光力系统的多通道量子路由器示意图[89]Figure32. Schematic of multichannel quantum router based on cavity electro-opto-mechanical[89].
2019年, Zhong等[90]提出了一种基于电光力转换器的预报式微波-光纠缠态的制备方案, 该方案可以绕过直接态转移协议中的效率门限, 同时也对纠缠见证中的合适参数范围进行了验证, 有效制备了微波-光纠缠态, 这种方案也可以应用于许多其他系统, 是一个极好的量子特性研究平台, 其原理如图33所示. 为方便说明和比较, 现将上述方案进行分类总结, 并以表2列出.
| 腔光力系统类型 | 作用类型 | 模式数 | 腔类型 | 制备的微波非经典量子态 |
| 腔电力系统 | 光子-声子 | 2 | 微波腔 | 连续变量微波纠缠态, 微波压缩态, 微波-机械 振子谐振模纠缠态 |
| 腔电光力系统 | 光子-声子-光子 | 3 | 微波腔, 光腔 | 连续、离散变量微波纠缠态, 微波单光子Fock态, 微波-机械振子谐振模纠缠态, 微波-光纠缠态 |
表2基于腔光力系统的微波非经典量子态制备
Table2.Preparations of non-classical quantum statesof microwave based on cavity opto-mechanical system
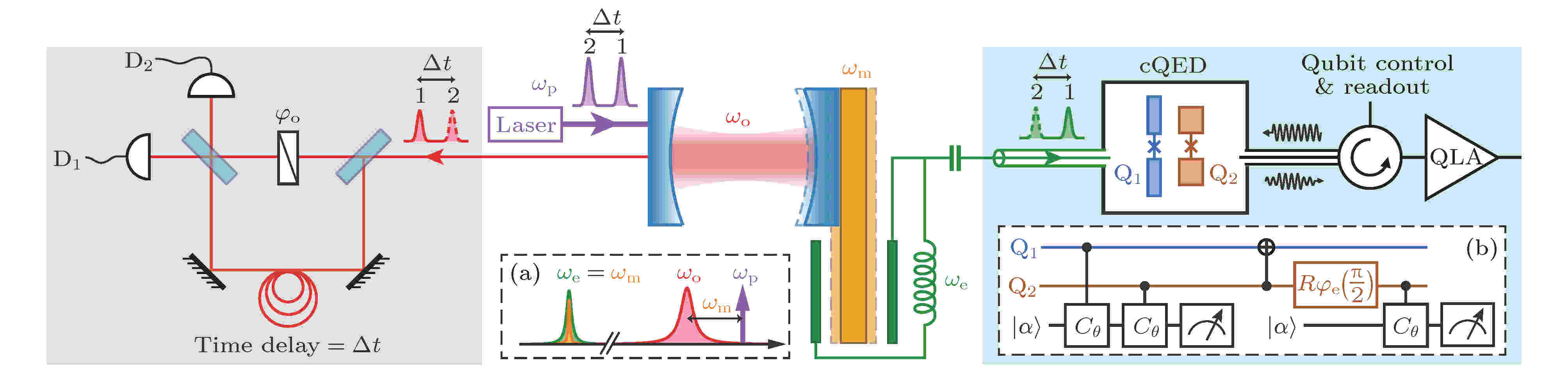图 33 基于电光力转换器的预报式微波-光纠缠态制备方案示意图[90]Figure33. Schematic of heraldedmicrowave-optical entanglement preparation based on cavity electro-opto-mechanical system[90].
2
3.2.性能优势与待解决问题
基于单纯腔电力系统和腔电光力系统的微波非经典量子态制备方法较之传统方法, 具有显而易见的性能优势, 同时也存在一定的待解决问题.基于单纯腔电力系统和腔电光力系统的微波非经典量子态制备方法, 其依靠超导技术、纳米技术、腔光力效应等最新技术, 所构建的系统具有超高的品质因数、超高的振动频率、超轻的质量以及超高的灵敏度, 使得其制备量子态环境具有噪声影响小、相干时间长、稳定优势, 同时超导微波腔还使得系统的设计灵活、适应性强. 同时, 基于腔电光力系统的微波非经典量子态制备方法具有许多独特的优势: 能够实现微波光子-机械声子-光波光子的强耦合, 从而实现有效的跨频段量子态转移, 有效降低微波量子态信号的制备的成本和技术难度; 能够有效地融合超导微波量子比特易操控和光子比特在光纤中可长距离传输的优势, 使得腔电光力系统可应用于量子计算以及量子通信组网中的跨频段信息交互, 如传输节点、中继、跨频段单光子路由等; 能够有效利用光学器件在制备与观测非经典量子态上成熟高效的优势, 同时也能很好地保留微波信号与超导器件兼容性及微波信号在自由空间中的传输性能, 使得基于量子微波信号的导航、雷达等应用成为可能, 从而提高甚至突破相关传统应用的性能.
基于单纯腔电力系统和腔电光力系统的微波非经典量子态制备方法也存在一些待解决的问题, 主要包括工作温度、机械振子激发声子、耦合强度、机械振子的品质因数等方面. 由于系统为了降低噪声光子对微波非经典量子态制备的影响而必须处于超低温环境下, 因此其工作条件比较苛刻, 尤其是在一些腔电光力系统中, 工作温度甚至在mK级别, 这对制冷设备要求比较高, 也将增加所需成本, 因此需要解决工作温度条件苛刻的问题. 同时, 在腔电光力系统中, 机械振子在与微波光子和光波光子相互作用过程中, 极易激发无关声子, 这将影响量子态转移效率, 从而影响微波量子态制备的效率, 目前在使用机械暗模规避声子激发上已经有相关的研究[91]. 另外, 一个强的耦合强度是保证量子态长时间相干、微波非经典量子态成功制备的前提, 目前已经有相关的努力, 即通过加入参量放大器达到增强耦合强度的目的[87]. 至于提高机械振子的品质因数, 则一直都是腔光力系统所追求的目标. 目前各种腔光力系统的品质因数发展水平, 已在表1中详细列出. 若以
2
3.3.相关应用
广义腔光力系统及其制备的微波非经典量子态在许多领域已经得到了应用, 并取得了令人振奋的成果, 尤其是腔电光力系统, 已经成为了各种量子实验的优良测试平台. 目前, 相关的应用场景包括量子微波照明[79,87]、微波-光量子接口[65,83,92]、量子精密测量[93,94]、引力波探测[34]、量子网络节点[85]、电磁诱导透明[95-97]、基态冷却[98,99]、跨频段单光子路由[89,100]、量子态存储[76]等. 其中, 量子微波照明、量子网络节点应用的是传播微波场, 其余应用中涉及的多为腔内微波场. 微波-光量子接口、量子态存储将助力于量子计算机的发展. 量子精密测量、引力波探测、电磁诱导透明、基态冷却、跨频段单光子路由、量子态存储等应用研究并非新近萌芽, 但广义腔光力系统(腔电力系统、混合腔电光力系统)为这些领域提供了新的方法、改善了相关性能, 其中跨频段单光子路由、量子态存储都创新性地将纳米机械振子作为了量子态的暂时存储器, 并利用光子-声子耦合进行信息的传递. 总体来看, 广义腔光力系统及其制备的微波非经典量子态的应用方兴未艾, 正处于大发展时期, 有望为经典领域甚至量子领域许多极具挑战性的课题提供新的可能.本文对腔光力学以及常见的腔光力系统进行了分类介绍, 主要综述了基于单纯腔电力系统以及混合腔电光力系统的微波非经典量子态制备方法及其研究进展, 详细分析了相关制备方法的性能优势和待解决问题, 总结了当前的应用场景和实际效果, 并进一步对未来可能的应用场景、研究方向进行了展望, 可为从事腔光力学、微波非经典量子态应用的研究人员提供参考.
