摘要:酸性环境引发的岩石孔隙表面溶解增加了孔隙内水溶液的盐离子浓度, 破坏了孔隙的表面结构. 本文采用分子动力学模拟的方法研究了纳米级岩石孔隙内水溶液的流动特性, 分析了盐离子浓度和孔隙表面结构对水流速度分布的影响及原因. 研究结果表明: 纳米级岩石孔隙内的水溶液流动符合泊肃叶流动特性, 流速呈“抛物线”分布; 随盐离子浓度增加, 水溶液内部氢键网络变得更为致密, 水黏度随其呈线性增长; 水溶液中离子浓度越大, 孔隙表面对水流动的阻力越大, 最大流速越小, 速度分布的“抛物线”曲率半径越大; 岩石孔隙表面结构的破坏改变了流动表面的粗糙程度, 增加了孔隙表面对H₂O分子的吸引力. 随表面结构破坏程度的增大, 水溶液在近壁区域的密度增大, 流速降低; 当表面破坏程度达到50%时, 水溶液在近壁区域出现了明显的负边界滑移现象.
关键词: 纳米级岩石孔隙/
表面溶解/
分子动力学/
流动

English Abstract

全文HTML

--> --> -->

压力驱动下的源生水和注入水可以在纳米级岩石孔隙内流动, 此现象在CO₂地质封存及石油和页岩气的水力开采等领域普遍存在^[1,2]. CO₂溶解于水^[3]及油层酸化解堵技术^[4]均会使岩石孔隙内水溶液呈酸性. 岩石孔隙壁面在酸性环境下易遭到腐蚀, 导致组成岩石表面的离子脱离孔隙壁面, 溶解于孔隙内的水溶液中, 增加了水溶液的离子浓度, 致使水溶液的微观溶剂化结构发生变化, 改变了水溶液的物化性质, 从而影响水溶液在岩石孔隙内的流动特性^[5,6]. 此外, 岩石孔隙壁面离子的脱落破坏了孔隙表面结构, 改变了壁面粗糙度和壁面与水分子间的相互作用势能强度, 进而导致孔隙内水溶液的流动特性产生变化^[7,8]. 因此, 研究岩石孔隙表面溶解对水溶液流动特性的影响, 可为CO₂地质封存选址及油气开采等领域提供一定的借鉴.
盖层岩石孔径小于50 nm的孔隙约占92.13%^[9], 属于纳米级孔隙^[10]. 纳米级孔隙具有极大的比表面积, 区别于宏观流动, 流体在纳米级孔隙内的流动受其自身物化性质和孔隙壁面性质的双重影响^[11]. 然而, 用实验方法观测纳米级孔隙中流动状态的难度较大, 分子动力学模拟则被认为是研究该尺度下流体流动的较好手段^[12,13]. 盐离子溶解于溶液所形成的溶剂化结构^[14]及纳米级孔隙壁面与离子之间的相互作用影响了孔隙内溶液的黏度和密度分布, 进而影响了溶液在纳米级孔隙内的流动特性. Ma等^[15]研究了NaCl水溶液在纳米孔隙内的离子输运能力, 发现随着NaCl浓度增加, 孔隙壁面对离子的移动阻力增大, 离子的去水合化效果增强. Vegt等^[16]通过实验研究了硫氰酸盐(SCN^–)水溶液的黏度随盐离子浓度的变化, 发现随盐离子浓度的增加, LiSCN和NaSCN水溶液的黏度增大, 而KSCN和CsSCN水溶液的黏度先减小后增大. 此外, Aryal等^[17]采用分子模拟方法研究了NaCl浓度对聚合物电解质膜内H₂O分子的扩散能力的影响, 结果表明随NaCl浓度增加, NaCl水溶液中的H₂O分子的扩散系数不断降低, 聚合物电解质膜内H₂O分子的扩散系数逐渐增加而后趋于平稳. 杨倩^[18]采用实验方法研究了石墨烯基二维纳米通道中的水合离子的输运性质, 结果显示不同离子在水溶液中的水合离子半径不同, 厚度为8 nm的氧化石墨烯膜能截留溶液中水合离子半径超过0.45 nm的离子. 综上所述, 研究者们已对纳米通道的离子输运性质进行了细致地讨论分析, 但盐离子对纳米级岩石孔隙内水溶液流动特性的影响机制尚未明晰.
纳米级孔隙表面粗糙度及孔隙表面与流体间的相互作用势均会影响流体在近壁区域的流动特性, 区别于流体在宏观尺度下的流动, 流体在纳米级孔隙中近壁区域的流动对其整体流动特性的影响不可忽略. 张烨等^[19]采用分子动力学方法研究了壁面刚度和金字塔型粗糙元对纳米通道内气体流动的影响, 发现壁面刚度的增加会减小气体在近壁区域速度峰值, 粗糙元高度的增加使得气体分子在近壁区域的聚集更加明显. Rahmatipour等^[20]采用分子动力学方法研究了纳米通道内壁面的肋高对流体密度分布的影响, 结果表明, 随肋高的增大, 粗糙壁面的近壁区域流体的密度波动范围逐渐增大, 但流体密度波动的峰值低于光滑壁面. 梅涛等^[21]采用分子动力学方法分析了纳米通道壁面粗糙度对流体流动的影响, 结果显示, 壁面粗糙度变化会改变固液界面位置, 肋高变化对通道中速度分布影响较大, 肋间距变化对通道内流体流动影响较小. 南怡伶等^[22]采用分子动力学方法研究了纳米狭缝内水溶液的流动特性, 结果表明, 随着壁面亲水性的增强, 壁面对水溶液的流动阻力增大, 水溶液的流速降低, 但速度在纳米孔隙高度方向仍然呈“抛物线”状分布. 王胜等^[23]采用分子动力学方法研究了流体在非对称浸润性粗糙纳米通道内的流动过程, 发现纳米通道上下壁面浸润性不对称导致了流体速度分布不呈中心对称, 通道壁面的纳米结构限制了流体的流动. 张冉等^[24]采用分子动力学方法研究了表面力场对纳米通道内气体流动的影响, 随着壁面对气体分子势能作用的增强, 气体分子在近壁区域形成吸附层, 速度滑移逐渐消失. Markesteijn等^[25]采用非平衡动力学模拟的方法研究了水在直径为4.3 nm的碳纳米管内的流动过程, 发现压力梯度驱动下水在碳纳米管道的流动符合泊肃叶方程, 并得到与实验数据吻合较好的水的黏度. 目前, 纳米孔隙内流体的流动特性在模拟^[26,27]和实验^[28,29]方面均已取得较多研究成果, 然而, 纳米级岩石表面结构破坏对孔隙内水溶液流动特性的影响机理鲜有研究.
考虑到CO₂地质封存及油气储层环境均具有较高温度和压力^[12,30], 本文采用分子动力学模拟的方法研究了温度为350 K、压强为20 MPa时, 水溶液在宽度为15 nm的岩石孔隙内的泊肃叶流动. 通过计算水溶液内部的氢键密度、原子对径向分布函数及其在孔隙内的密度分布, 本文从微观尺度分析了水溶液自身黏度和孔隙表面对其作用力的变化, 分别探讨了盐离子浓度增加和岩石孔隙表面结构破坏对水溶液流动特性的影响, 为调控岩石孔隙内水溶液的输运性质提供借鉴.

2

-->

2.1.模拟细节

镁橄榄石(Mg₂SiO₄)是CO₂地质封存盖层岩石的主要成分之一, 本文将镁橄榄石作为岩石固体相成分, 选取Mg₂SiO₄晶体最常见表面之一的(010)表面^[31]作为纳米级孔隙表面. 镁橄榄石纳米级孔隙宽度选为d = 15 nm, 孔隙两侧设置厚度为7 nm镁橄榄石层. 所构建的物理模型示于图1, 将模型中Y轴的坐标原点设置在孔隙宽度方向的中间平面上, 模型在X轴和Z轴方向的尺寸分别为3.8152 nm和3.6018 nm, 计算域孔隙内包含6772个H₂O分子. Mg₂SiO₄晶体(010)表面溶解会使其表面的Mg²⁺脱落, Mg²⁺进入纳米级孔隙增加了孔隙内水溶液的盐离子浓度. 因此, 本文在分析盐离子对孔隙内水溶液流动特性的影响时, 在水溶液中加入了不同浓度的Mg²⁺离子. 此外, 考虑到深部盐水层内阴离子中Cl^–的摩尔比高达90%—99%^[32], 故本文模型中的阴离子为Cl^–. 模型在X和Z方向均采用了周期性边界条件, 以在XZ平面形成无限大的镁橄榄石层, 而在Y方向形成宽度为d的岩石缝隙.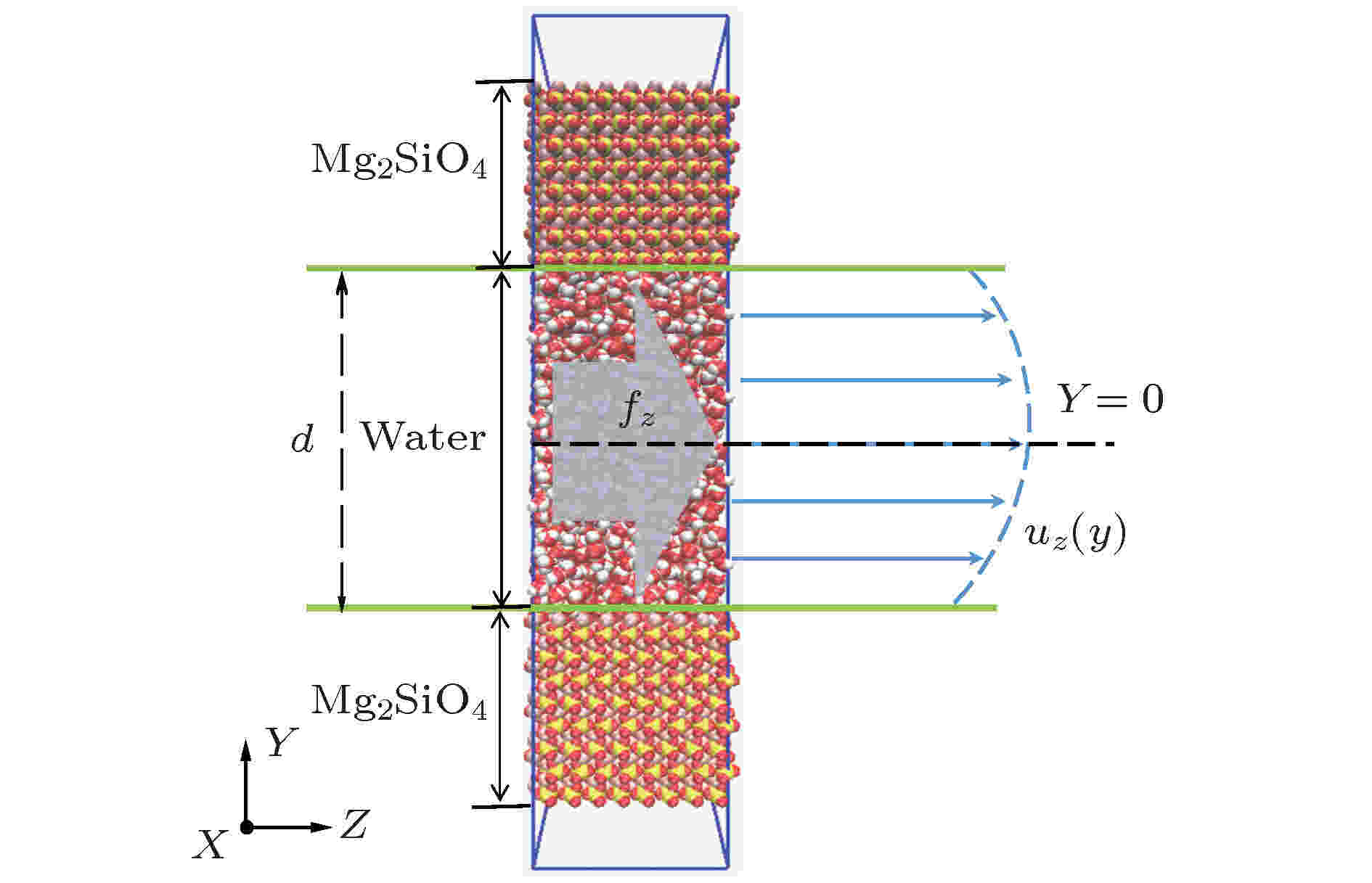
图 1 纳米级镁橄榄石孔隙内水溶液流动的模拟系统图
Figure1. The simulation system of water solution flow in the forsterite nanopore.

H₂O分子采用F3 C柔性模型^[33], 该模型有助于准确预测液固界面性质^[34,35]. Mg₂SiO₄及水溶液中的盐离子(Mg²⁺, Cl^–)采用CLAYFF力场^[36]. 模拟中考虑了分子内作用势和分子间作用势. 分子内作用势包括键拉伸和键角弯曲, 本文采用简谐势对其进行描述; 分子间作用势包括范德瓦耳斯相互作用势和静电相互作用势, 其中, 范德瓦耳斯相互作用采用兰纳-琼斯(Lennard-Jones potential, L-J)势^[37], 静电作用采用库仑作用势来进行描述, 分子间势能函数表达式为

$E = 4{\varepsilon _{ij}}\left[ {{{\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)}^{12}} - {{\left( {\frac{{{\sigma _{ij}}}}{{{r_{ij}}}}} \right)}^6}} \right] + \frac{{{q_i}{q_j}}}{{4{\text{π}}{\varepsilon _0}{r_{ij}}}}, $

其中ε_ij和σ_ij为原子间混合势参数, 采用Lorentz-berthelot混合法则^[38]计算, 即${\varepsilon _{ij}}={\left( {{\varepsilon _{ii}}{\varepsilon _{jj}}} \right)^{1/2}}$, ${\sigma _{ij}} = 0.5\left( {{\sigma _{ii}} + {\sigma _{jj}}} \right)$; ${r_{ij}}$为原子间的距离; q_i, q_j分别为原子i和j所带电荷; ε₀为真空介电常数. 模拟采用Particle Mesh Eward(PME)方法^[39]计算电荷相互作用. 范德瓦耳斯相互作用势和静电相互作用势的位能截断半径均为1.2 nm, 速度积分采用Velocity-Verlet算法, 时间步长为1 fs.
本文首先在温度为350 K、压强为20 MPa条件下, 应用定温定压系综(NPT)对初始模型进行了10 ns的平衡模拟, 使其达到稳定状态. 然后在正则系综(NVT)下进行非平衡分子动力学模拟, 使用Nose-Hoover热浴方法控制模拟温度(温度为350 K), 为防止Mg₂SiO₄晶体层在水溶液流动方向滑动, 非平衡模拟中固定了Mg₂SiO₄晶体的位置, 并对岩石孔隙内的盐离子和H₂O分子中的原子施加+Z方向大小为3.35 J/(mol·?)的作用力, 以模拟压力差驱动下孔隙内水溶液的流动. 系统运行30 ns后, 模型宏观物理量达到热力学稳定状态; 系统继续运行5 ns, 运行中每隔50 ps保存1次模型原子坐标, 用于对水溶液流动特性的分析. 模拟采用LAMMPS程序编写^[40].
2 -->

2.2.数据处理方法

为了获取纳米级镁橄榄石孔隙内水溶液的物理量参数, 本文将孔隙沿Y轴方向分为间距为0.2 nm的75个统计层, 某一统计层流体的Z向速度${u_z}\left( y \right)$以区间$y = [y, y + \Delta y)$内原子的平均速度来表征, 即

${u_z}\left( y \right) = \left\langle {\frac{{\sum\limits_{{y_i} \in [y,y + \Delta y)} {{u_{z,i}}} }}{{\sum\limits_{{y_i} \in [y,y + \Delta y)} {\varTheta ({y_i} - y)\varTheta (y + \Delta y - {y_i})} }}} \right\rangle, $

其中, ${u_{z, i}}$为i原子在Z方向的速度, $\varTheta ({y_i} - y)$和$\varTheta (y + \Delta y - {y_i})$为Heaviside阶跃分布函数.
本文非平衡模拟的结果表明镁橄榄石孔隙内水溶液的流速分布符合泊肃叶流动规律(见3.1节), 故关于水溶液黏度的计算采用Alvarez等^[41]的流体泊肃叶流动黏度求解方法. 当纳米级孔隙内每个原子受到沿+Z方向的作用力f_z后, 流体仅在Z方向存在稳态流动, 泊肃叶流动运动方程为

$\frac{{\rm{d}}}{{{\rm{d}}y}}\left( {\mu \frac{{{\rm{d}}{u_z}}}{{{\rm{d}}y}}} \right) = - N{f_z}, $

其中, ${u_z}$为流体沿+Z方向的流动速度, $\mu $为流体的黏度, N为受力的原子和离子总数目, ${f_z}$为每个原子所受的体积力. 根据(3)式可知, 镁橄榄石纳米级孔隙内流体的黏度为

$\mu = - \frac{{N{f_z}}}{{{{{{\rm{d}}^2}{u_z}} / {{\rm{d}}{y^2}}}}}. $

根据文献[21], 纳米级镁橄榄石孔隙内水溶液泊肃叶流动的u_z可表示为

${u_z} = \frac{{N{f_z}}}{{2\mu }}\left| y \right|\left( {\frac{d}{2} - \left| y \right|} \right) + {u_{\rm{s}}}, $

其中u_s为边界滑移速度.
为分析纳米级镁橄榄石孔隙内水溶液黏度变化的机理, 本文根据几何准则定义H₂O分子间的氢键. 其中, 当供体H₂O分子的氧原子O_w距离受体H₂O分子的氧原子O_w不大于0.35 nm, 且供体H₂O分子氢原子H_w、氧原子O_w与受体H₂O分子的氧原子O_w构成的夹角不大于30°时, 认为H₂O分子间形成氢键O_w—H_w···O_w.
2 -->

2.3.模型验证

为验证模型和计算方法的可靠性, 本文采用所建模型和方法计算了水溶液的密度和Mg₂SiO₄晶体的弹性模量. 模拟结果表明, NPT系综(温度为350 K, 压力为20 MPa)下水溶液的密度为982.3 kg/m³, 与美国标准与技术研究所(NIST)提供的水溶液在此温压下的实验密度(982.5 kg/m³)^[42]相符; 另外, NPT系综(温度为350 K, 压力为20 MPa)下Mg₂SiO₄晶体计算所得的应力-应变(σ-ε)曲线示于图2. 该图中Mg₂SiO₄晶体在拉伸过程中经历了弹性形变(ε ≤ 0.07)、塑性形变(0.07 < ε ≤ 0.125)和断裂(ε > 0.125) 3个阶段, 通过对图2弹性形变阶段曲线拟合计算, 得出Mg₂SiO₄晶体弹性模量E约为293 GPa, 与Liu等^[43]实验测得的Mg₂SiO₄晶体的弹性模量(约为287 GPa)吻合. 因此, 本文模拟所建模型和计算方法具有一定的准确性和可靠性.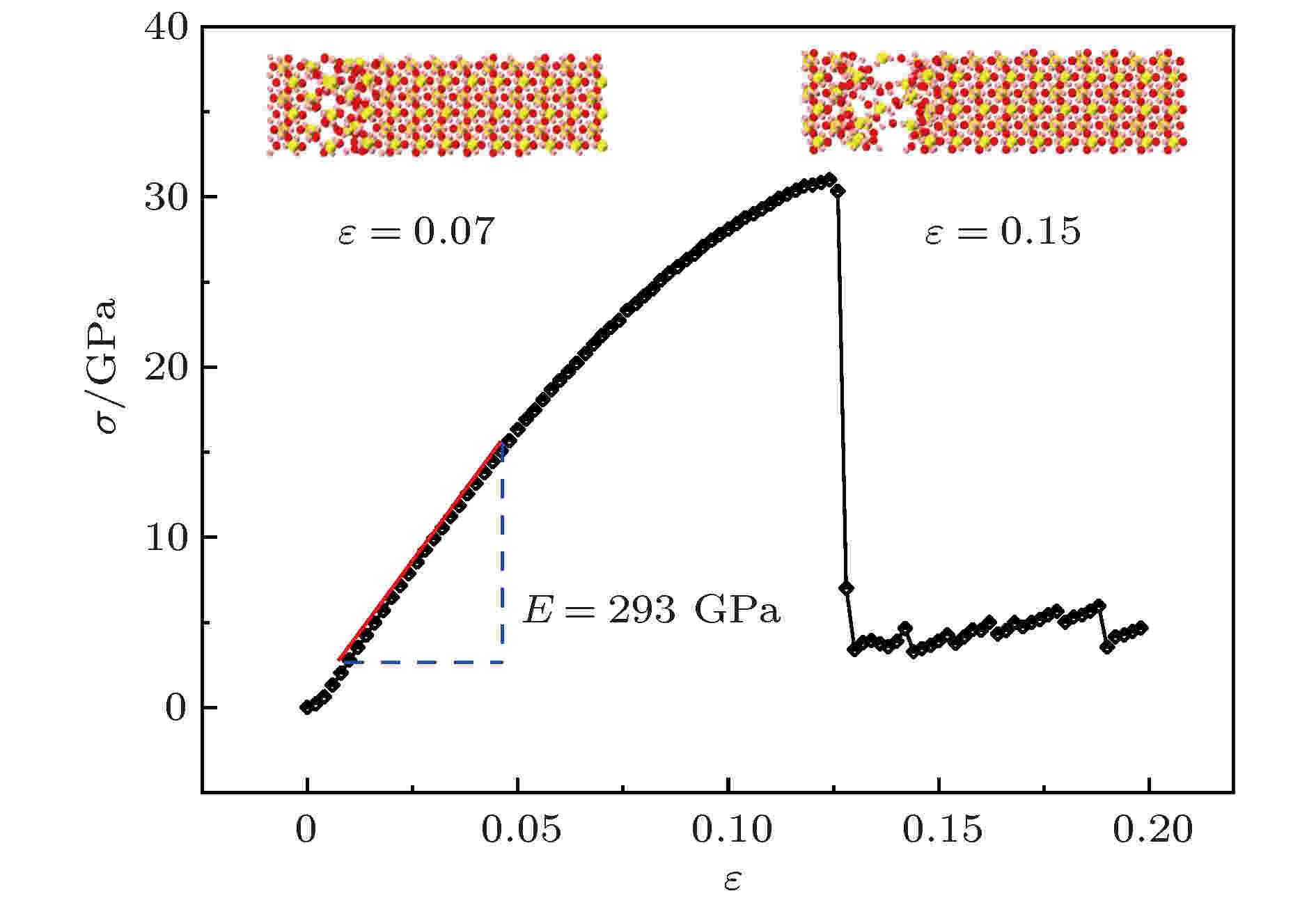
图 2 Mg₂SiO₄晶体拉伸的分子模拟应力-应变曲线
Figure2. The stress-strain curves of the Mg₂SiO₄ crystal stretching obtained using molecular dynamics simulation.

本文研究的岩石纳米级孔隙具有极大的比表面积, 孔隙内流体的流动特性与流体的自身物性(黏度)和孔隙表面对流体的作用力密切相关. 通过分析镁橄榄石孔隙内水溶液内的氢键密度、径向分布函数及密度分布, 本文从微观尺度探讨了盐离子浓度和孔隙表面结构对水溶液流动特性的影响机制.
2

-->

3.1.盐离子浓度对流动特性影响

为研究盐离子浓度对镁橄榄石孔隙内水溶液流动特性的影响, 本文分别模拟了盐离子(MgCl₂)浓度为0, 0.25, 0.50, 0.75, 1.00 mol/L的含盐水溶液的流动过程. 经数据处理, 模拟所得的纯水(盐离子浓度为0)和含盐水的微观结构示于图3(a). 由图3(a)可知, 在远离孔隙表面的主流区域纯水中的单一H₂O分子被约4.00个H₂O分子组成的水合壳包围; 在含盐水溶液中, 盐离子与极性H₂O间存在较强的静电力, 盐离子被具有特定分子取向的H₂O分子水合, 形成水合自由离子或水合离子对, 从而改变了水溶液的微观溶剂结构. 对模拟轨迹文件分析结果表明, 当含盐水溶液的盐离子(MgCl₂)浓度为1 mol/L时, 主流区域的单一H₂O分子水合壳内的H₂O分子数目增加至4.32个. 由此可知盐离子的存在改变了水溶液的微观结构, 进而导致了水溶液的宏观物化性质发生相应变化.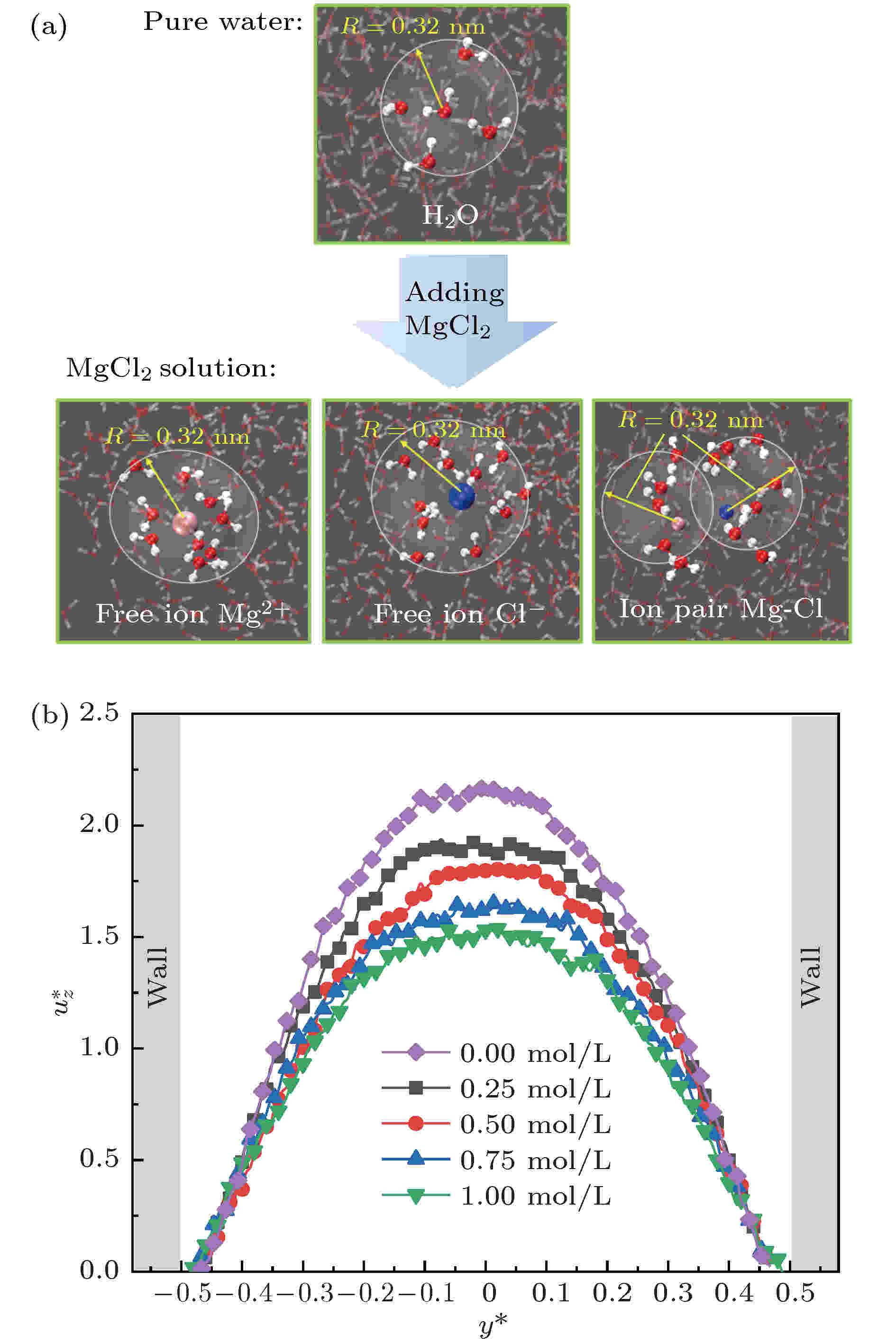
图 3 (a)纯水和MgCl₂含盐水中以0.32 nm半径的水合壳结构示意图; (b)不同MgCl₂浓度下纳米级镁橄榄石孔隙内纯水和含盐水的+Z向速度分布
Figure3. (a) Snapshots for the solvation shell with a radius of 0.4 nm in pure water and MgCl₂ solution, (b) the velocity profiles in the +Z direction of water solution in the forsterite nanopore with different MgCl₂ concentrations.

本文基于纯水在镁橄榄石纳米级孔隙内沿+Z向的流量Q, 求取纯水沿+Z向流动的平均速度u₀, 即u₀ = Q/A, A为孔隙XY截面面积, 计算可得u₀ = 163.14 m/s. 本文规定水溶液沿+Z向的约化速度$u_z^* = {{{u_z}}}/{{{u_0}}}$, 坐标y的约化坐标${y^*} = {y}/{{15}}$. 纯水和含盐水的$u_z^*$计算结果示于图3(b). 由图3(b)可知, 在相同的压力差驱动下, 流体的速度曲线均呈“抛物线”状, 表明不同离子浓度下含盐水的流速分布均符合泊肃叶方程; 随着MgCl₂盐离子浓度的增加, 近壁区域的速度差异较小, 但主流区的速度不断降低, 同时“抛物线”顶点处的曲率半径不断增大. 该变化较为明显, 与纯水溶液相比, 1 mol/L的含盐水流动时的最大约化速度$u_z^*$降低了29.72%; 抛物线顶点处曲率半径增加了43.99%, 由泊肃叶流动黏度求解方法可知, 孔隙内水溶液的黏度增大.
流体的流动特性与其自身黏度密切相关, 为分析盐离子对镁橄榄石纳米级孔隙内水溶液黏度的影响规律, 本文根据(4)式计算了图3(b)中不同盐离子浓度纯水和含盐水的黏度, 计算结果示于图4(a). 由图4(a)可知, 在0—1 mol/L的离子浓度区间内, 含盐水的MgCl₂浓度每增加0.25 mol/L, 含盐水的黏度约增长41.17 μPa·s, 故在该离子浓度区间内含盐水的黏度随MgCl₂盐离子浓度增加呈线性增长, 该线性规律可用公式y = 164.69x + 383.00 (y为含盐水黏度, x为MgCl₂浓度)描述.
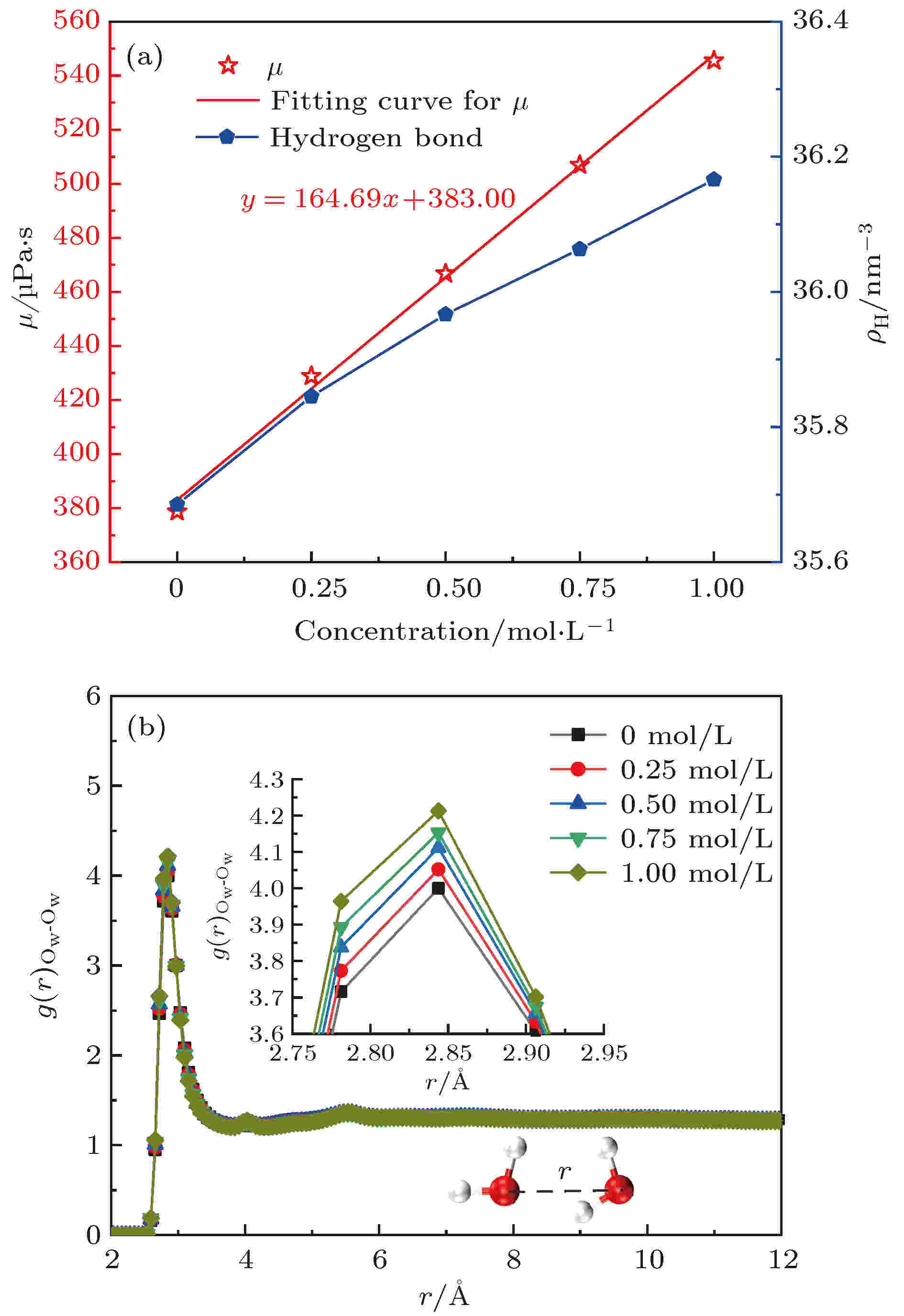图 4 (a)不同MgCl₂浓度含盐水的黏度及其内部氢键密度; (b)不同MgCl₂浓度含盐水O_w-O_w原子对的径向分布函数
Figure4. (a) The viscosity and hydrogen bond density of water solution with different MgCl₂ concentrations; (b) the radial distribution function of O_w-O_w near the wall of nanopores.

为深入分析MgCl₂浓度影响含盐水黏度的微观机制, 本文统计了不同MgCl₂浓度含盐水的氢键密度ρ_H, 统计结果示于图4(a), 并通过计算H₂O分子间O_w-O_w原子对的径向分布函数g(r)_Ow-Ow, 探讨了含盐水的氢键密度变化的微观机理, 计算结果示于图4(b). 图4(a)表明含盐水的氢键密度随盐离子浓度增加而不断增加, 但增加速率逐渐下降. 含盐水氢键密度的增加使其内部氢键网络变得更加致密, 进而导致了含盐水的黏度不断增加. 由图4(b)可知, g(r)_Ow-Ow第一峰值随离子浓度增加而逐渐增大, 但第一峰值的位置均在2.85 ? (1 ? = 0.1 nm)左右. 由此推断随MgCl₂盐离子浓度的增加, MgCl₂盐离子与H₂O分子间的静电作用使得更多的H₂O分子紧密地聚集在盐离子周围, 同时H₂O分子间的平均距离逐渐减小, 进而导致单一H₂O分子的第一层溶剂壳内的水分子数目增多, 但第一层溶剂壳的尺寸未发生改变, 故H₂O分子间的相互作用更加强烈, 单一H₂O分子与第一层溶剂壳内的其他H₂O更易形成氢键, 进而含盐水的氢键密度逐渐增大. 因此, 增加MgCl₂盐离子浓度可以改变含盐水溶液的微观结构, 使得H₂O分子间更易形成氢键, 进而增加了含盐水的黏度, 黏度的增加阻碍了含盐水在纳米级镁橄榄石孔隙内的流动, 导致含盐水的流动速度不断减小.
此外, 流动通道的流体流动阻力对流体的流动特性有重要影响. 为研究含盐水的盐离子浓度对H₂O分子与孔隙表面间相互作用强度的影响, 本文计算了以纳米级镁橄榄石孔隙表面的镁原子Mg为中心原子, H₂O分子中的氧原子O_w作为配位原子的Mg-O_W径向分布函数g(r)_Mg-Ow, 计算结果示于图5. g(r)_Mg-Ow第一峰值的位置代表镁橄榄石孔隙表面与近壁区域第一层H₂O分子间的距离, 峰值大小代表第一层H₂O分子排布的紧密程度. g(r)_Mg-Ow第一峰值的位置越小, 值越大表示镁橄榄石表面与H₂O分子间的相互作用越强. 由图5可以看出, 不同MgCl₂浓度的含盐水的g(r)_Mg-Ow均存在第一峰值(约在2.24 ?)和第二峰值(约在3.8 ?), 峰值位置无明显差异, 由此可以推断H₂O分子在镁橄榄石壁面附近存在明显的两个H₂O分子层, H₂O分子层不随离子浓度的变化而发生改变. 另外, g(r)_Mg-Ow第一峰值的大小随MgCl₂浓度的增加而增大, 这表明随着MgCl₂浓度增加, 孔隙表面附近H₂O分子排布更加紧密, 孔隙表面与H₂O分子间的相互作用不断增强, 即镁橄榄石表面对H₂O分子的吸引力更强, 增大了H₂O分子的流动阻力, 降低了纳米级镁橄榄石孔隙内含盐水的流动速度.
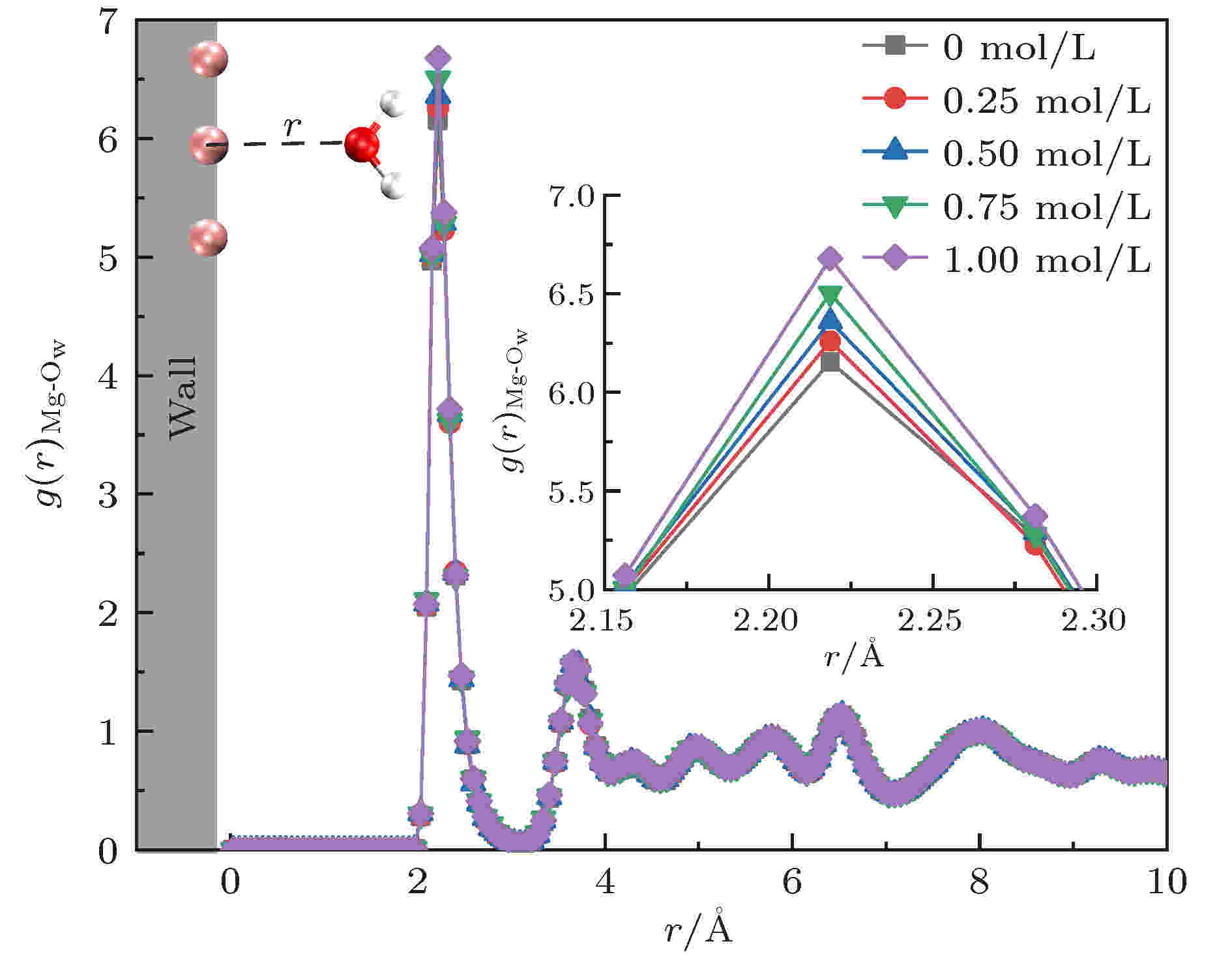图 5 Mg-O_w原子对的径向分布函数
Figure5. The radial distribution function of Mg-O_w near the wall of nanopores.

综上可知, 随着MgCl₂离子浓度增加, 含盐水的黏度呈线性增长, 且纳米级镁橄榄石孔隙表面对含盐水的流动阻力增强, 故含盐水在镁橄榄石纳米级孔隙内的流动速度逐渐降低.
2 -->

3.2.表面结构破坏对流动特性影响

纳米级岩石孔隙壁面溶解会导致孔隙表面结构的破坏, 为研究镁橄榄石纳米级孔隙表面结构破坏对纯水流动特性的影响, 本文构造孔隙不同破坏程度的粗糙表面, 以表示孔隙表面发生了不同程度的溶解和离子脱落, 所构建的5种镁橄榄石纳米级孔隙模型示于图6. 为便于比较, 本文构建了一侧为光滑表面, 一侧为粗糙表面的计算模型. 粗糙表面为发生不同程度溶解破坏的表面, 即发生不同程度结构破坏的粗糙表面, 粗糙表面结构破坏程度为0, 17%, 33%, 50%和67%, 分别用模型M1—M5表示.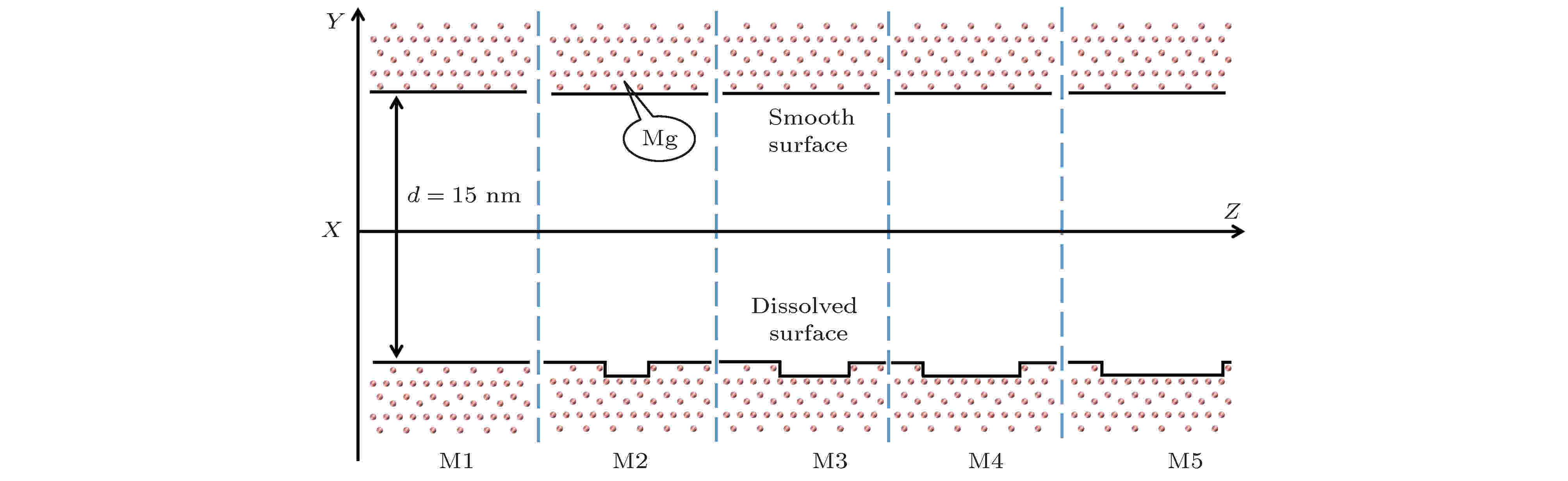
图 6 不同表面结构破坏程度的纳米级镁橄榄石孔隙示意图
Figure6. The schematic of forsterite nanopores with various degrees of surface structure destruction.

计算所得不同表面结构破坏程度下水溶液的+Z向速度分布示于图7. 从图7可以看出, 在距孔隙表面的距离相同时, 粗糙表面近壁区域水溶液的流速明显低于其在光滑表面近壁区域的流速. 随着镁橄榄石孔隙粗糙表面破坏程度的提高, 水溶液在粗糙表面近壁区域及主流区域的速度曲线逐渐偏离“抛物线”状, 流速不断降低, 并且当表面破坏程度达到50%以上时, 水溶液在粗糙表面附近存在负边界滑移, 模型M4和M5中水溶液在粗糙表面的边界负滑移约化速度u_s分别为0.29和0.34. 另外, 随着粗糙表面破坏程度增加, 水溶液流速降低的区域逐渐向光滑表面蔓延, 但在光滑表面近壁区域水溶液的流型和流速均未发生明显的变化, 表明光滑表面结构性质对其附近水的流速和流型有重要影响.
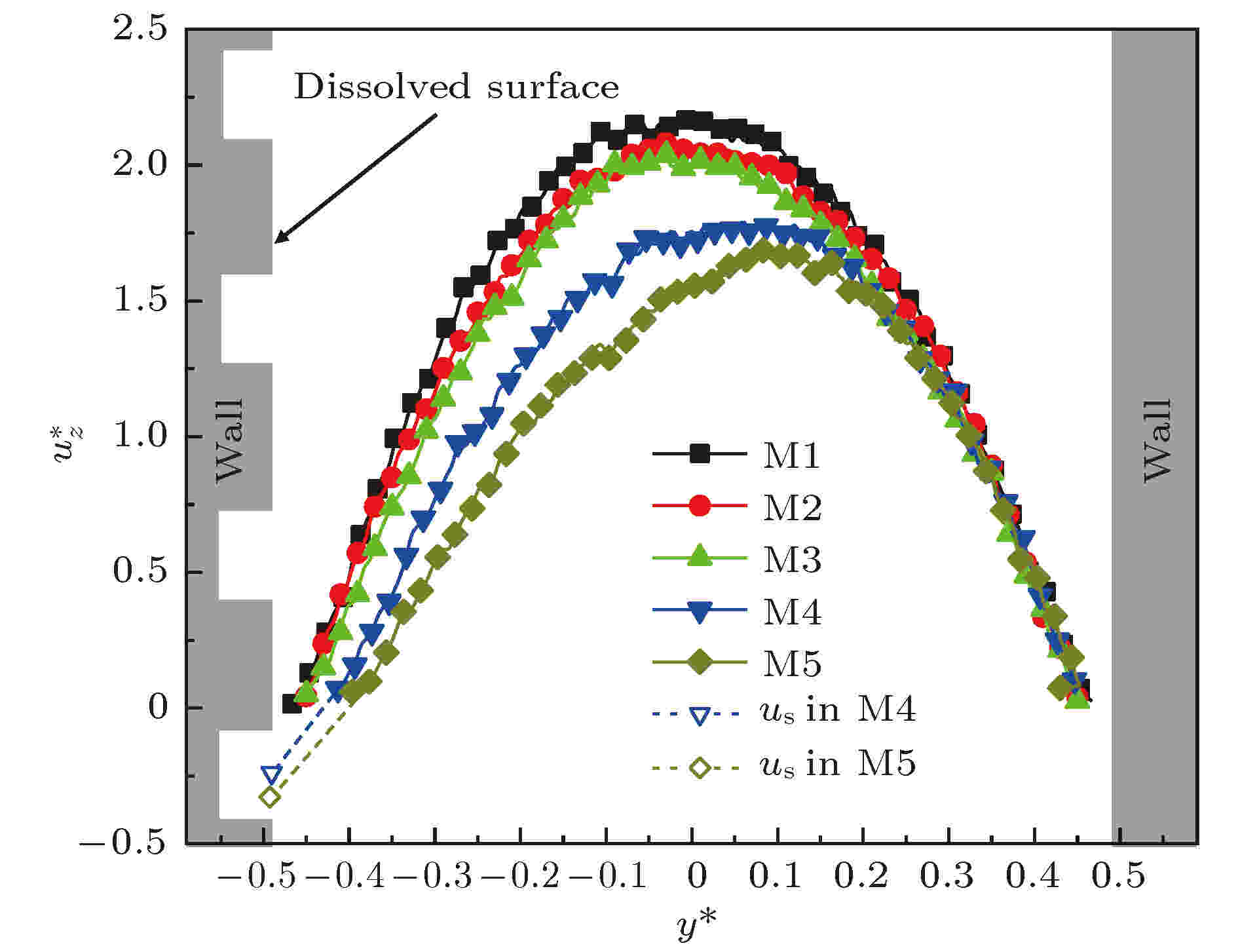图 7 不同表面结构破坏程度下纳米级镁橄榄石孔隙内水的+Z向速度分布
Figure7. The velocity profiles in the +Z direction of water solution in forsterite nanopores with various degrees of surface structure destruction.

为研究镁橄榄石纳米级孔隙表面结构破坏对水溶液流动阻力的影响机制, 本文以模型M2(表面破坏程度17%)和模型M3(表面破坏程度33%)为代表, 计算了水溶液在纳米级镁橄榄石孔隙内密度ρ的分布, 结果示于图8. 由图8可知, 随镁橄榄石孔隙表面破坏程度的提高, 粗糙表面附近水溶液密度振荡的第一峰值增大, 且粗糙表面附近的水溶液密度振荡不断向主流区域扩散, 振荡距离L不断增加, 而光滑表面附近水溶液的密度分布及密度振荡未收到明显影响, 水溶液在粗糙表面附近的密度比在光滑表面附近更大, H₂O分子在粗糙表面附近有聚集现象, 且聚集程度随孔隙表面结构破坏程度提高而不断增大. 由此可知, 随着纳米级镁橄榄石孔隙表面结构破坏程度的提高, 粗糙表面对H₂O分子的吸引力不断增强, H₂O分子在粗糙表面附近更加密集, H₂O分子倾向于“滞留”在粗糙表面附近, 此现象解释了图7中粗糙表面破坏程度为50%和67%的速度曲线存在负滑移的原因. 此外, 粗糙表面近壁区域水溶液密度的增加, 增大了粗糙表面附近H₂O分子间的相互碰撞频率, 导致水溶液在粗糙壁面附近的流动阻力不断增加, 降低了水溶液的流动速度.
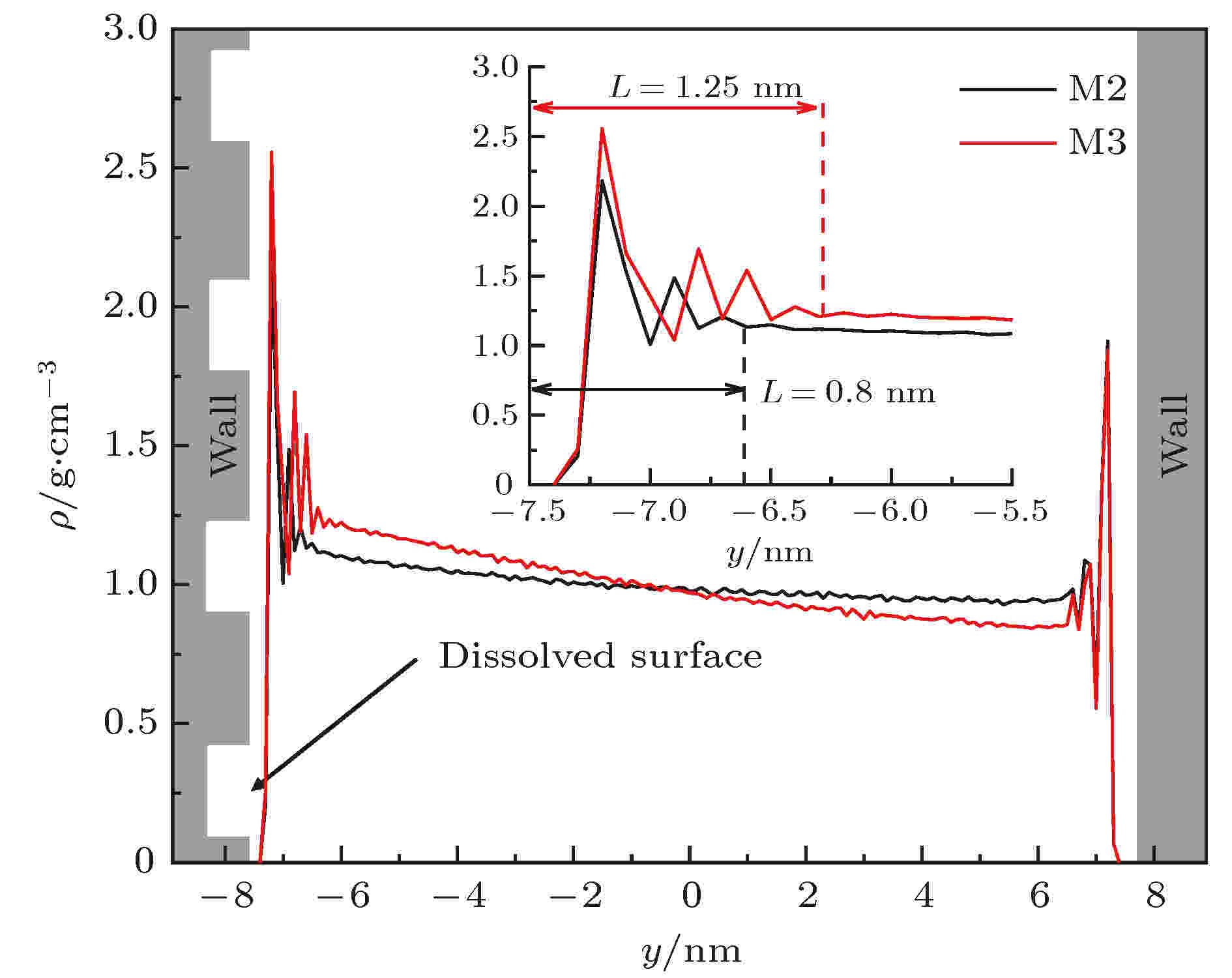图 8 不同表面结构破坏程度下纳米级镁橄榄石孔隙内水溶液的密度分布
Figure8. The density profiles of water solution in forsterite nanopores with various degrees of surface structure destruction.

采用分子动力学模拟的方法研究了纳米级镁橄榄石孔隙内水溶液的泊肃叶流动特性, 分析了水溶液的氢键密度、径向分布函数以及密度分布, 从黏度和孔隙表面流动阻力的角度探讨了MgCl₂盐离子浓度和孔隙表面结构破坏对水溶液流速分布的影响机制, 主要得到以下结论.
1) 含盐水在纳米级镁橄榄石孔隙内沿Y向的速度分布均为“抛物线”状; 随MgCl₂盐离子浓度的增加, 含盐水内氢键网络的致密性不断提高, 使得含盐水的黏度随盐离子浓度的增加呈线性增长; 同时孔隙表面对含盐水的流动阻力逐渐增大, 含盐水在主流区域的最大流速不断降低.
2) 随着纳米级镁橄榄石孔隙表面结构破坏程度提高, 粗糙表面对H₂O分子吸引力增强; 近壁区域水的密度不断增加, 粗糙表面对水的流动阻力不断增大, 水在近壁区域的流速不断降低; 当表面结构破坏程度达到50%时, 水在粗糙表面出现负边界滑移. 另外, 光滑表面近壁区域水的流速分布未发生明显变化, 表明光滑表面结构性质对其附近水的流速和流型有重要影响.