全文HTML
--> --> -->但我们对a-Si:H的认识仍不够深入, 其为非晶结构, 其结构和性能受制备过程中的工艺参数, 如衬底温度[6-8]、入射动能[9]、入射频率[10,11]等影响显著, 且其结构在后继使用和热处理过程中会发生变化, 典型的如光致衰减效应(Steabler-Wronski效应, S-W效应)[12]、热处理提高本征非晶硅层的钝化效果等[13,14]. 普遍认为薄膜中特殊的Si—H键中弱键断裂、迁移等机制是上述现象的可能原因[15]. 但在实验研究方面受限于制样和观测手段, 只能对薄膜的整体结构进行宏观统计上的分析, 难以得到进一步的微观结构信息, 更无法对不同工艺条件下制备的薄膜结构进行详细分类, 深入理解其性能随工艺演变的本质. 分子动力学模拟基于经典力学, 可追踪薄膜每个原子在相空间的运动规律和轨迹, 以及便于统计分析原子结构包括成键信息等优点, 是研究薄膜沉积生长和结构分析的有力工具. 本课题组前期利用分子动力学模拟研究了沉积参数对a-Si:H薄膜中悬挂键含量、H含量、晶化率和SiHx键合等微观结构的影响, 给出了本征非晶硅钝化晶体硅的钝化效果在适度的温度下热处理可获得改善的合理解释[6,9]. 本文在该研究基础上进一步模拟分析了a-Si:H/c-Si薄膜中SiyHx组态的种类、结构、稳定性, 及衬底温度对其含量的影响, 以期对非晶硅薄膜的结构和性能随工艺的演变规律有更进一步的认识.
2.1.薄膜沉积生长模型与方法
图1为a-Si:H/c-Si (001)薄膜生长的分子动力学模型示意图. 衬底尺寸为15a × 15a × 5.3a(a为硅的晶格常数), 共约9900个原子. 在Z方向, 衬底自下而上被分为三层: 1)底部为固定原子层, 以防止沉积过程中衬底模型受入射原子的冲击而飘移; 2)中间部分为恒温层, 在该层中采用Langevin方法控制其温度, 即为衬底温度, 防止由于沉积过程中入射原子的动能导致衬底温度的升高; 3)顶部为自由层, 在该部分的原子处于自由运动状态, 不对其施加其他约束条件以避免恒温算法可能引入的影响. 在X和Y方向上运用周期性边界条件, 用以模拟薄膜在无限大的表面上生长. 原子间相互作用采用由Murty和Atwater[16]在Tersoff势[17]的基础上修改得到的Murty-Tersoff势函数来描述, 时间步长设为0.001 ps. 现有研究表明, SiH3基团是获得高质量薄膜的主要自由基团, 因此仅采用SiH3基团进行沉积. 沉积时SiH3基团在衬底上方一定高度的空间区域内随机产生, 再垂直入射到衬底表面. 结构分析时, 体系将快冷至约0.01 K, 以消除热振动的影响.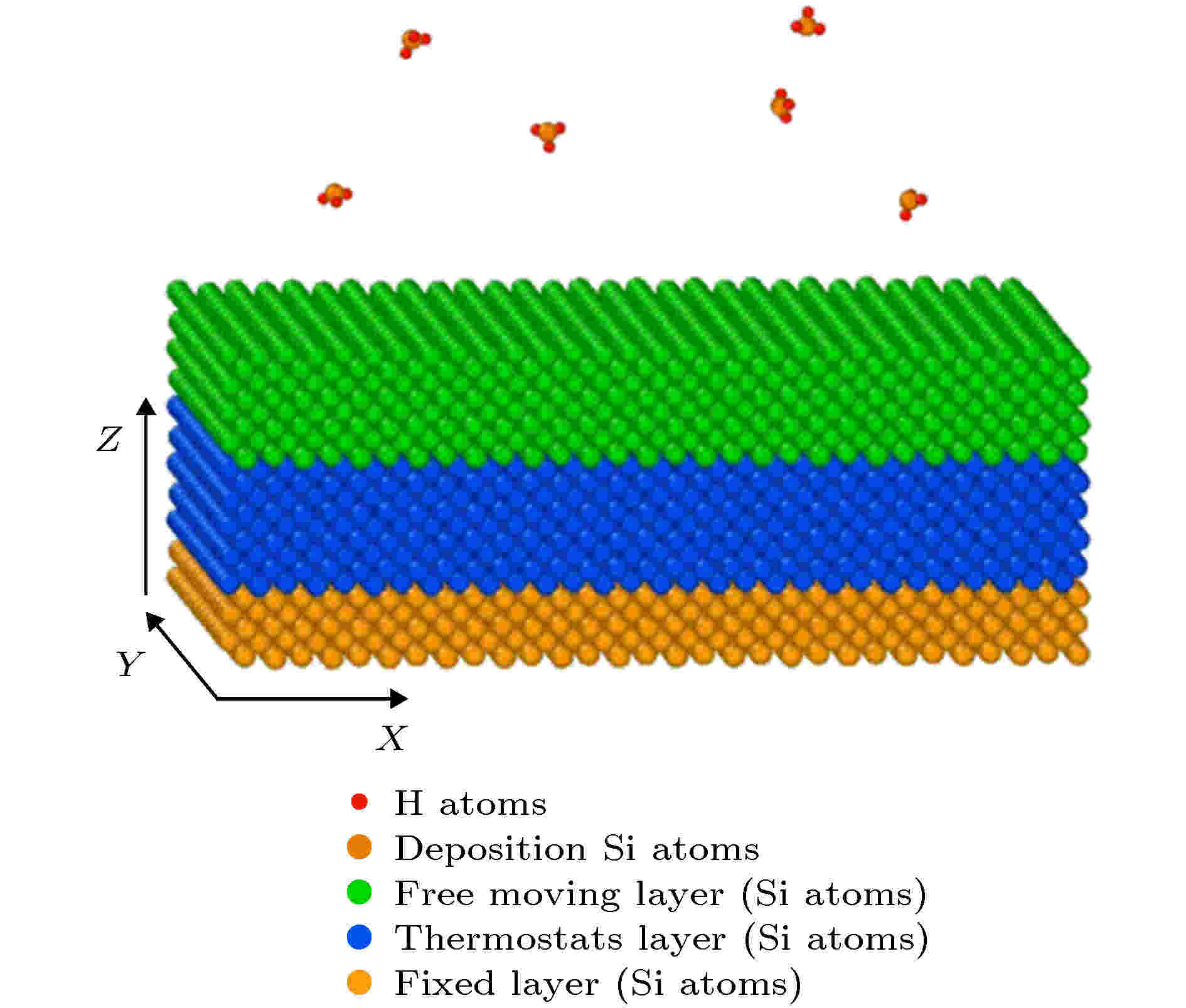
图 1 晶体硅衬底表面沉积生长a-Si:H/c-Si薄膜的模型结构示意图Figure1. Schematic diagram of the model structure about a-Si:H thin film deposited on the surface of crystalline silicon substrate.
2
2.2.结构分析及键能计算方法
SiyHx组态结构的键合状态、键长、键角均采用Mercury软件[18]进行分析. Mercury作为一款可视化软件, 可以提供体系所有原子成键的键长、键角信息. SiyHx组态中Si—H键的键能采用VASP软件[19]进行计算, 计算模型中Si—H键的键长键角均采用各SiyHx组态统计得到的平均值.3.1.a-Si:H/c-Si薄膜结构
在不同沉积参数下模拟沉积a-Si:H, 得到的a-Si:H/c-Si薄膜原子结构基本类似. 图2示出了模拟衬底温度为500 K时沉积得到a-Si:H/c-Si薄膜原子结构. 图中原子分为两部分, 底部为衬底层, 原子排列规则; 顶部为沉积生长的a-Si:H薄膜层, 原子排列混乱无序, 二者界面处在一定范围内Si原子从规则排列渐变为无序排列. 说明在模拟考察的沉积生长参数下, 均能形成非晶结构的薄膜, 没有出现结晶现象. 其中棕色原子和较小的红色原子分别为沉积的硅原子和氢原子, 可以发现氢原子主要分布在薄膜层的内部, 但因其半径小, 少部分可扩散进入衬底层. 图2(b)为薄膜层的径向分布函数. 图中径向分布函数曲线的第一峰为尖锐的高峰, 后续第二峰、第三峰非常弱, 说明该结构短程有序长程无序, 为典型的非晶结构的径向分布函数曲线, 进一步说明了薄膜为非晶结构.
图 2 衬底温度为500 K时, 入射约8000个基团得到的a-Si:H/c-Si薄膜的原子结构示意图(a) 和薄膜层的RDF图(b)Figure2. Atomic structure of a-Si:H/c-Si film after depositing about 8000 groups with the substrate temperature of 500 K (a) and RDF curve of the film layer (b).
2
3.2.SiyHx组态的结构分析
为研究H原子在a-Si:H/c-Si薄膜中的存在状态, 我们统计了Si-H键的键长分布, 如图3所示. 在图中Si-H键分布有两个明显的主峰, 以及之后两部分较矮的峰群, 分别处于1.42—1.49 ?, 1.49—1.57 ?, 1.57—1.69 ?和1.69—1.74 ?. 这可能对应于不同的SiyHx组态.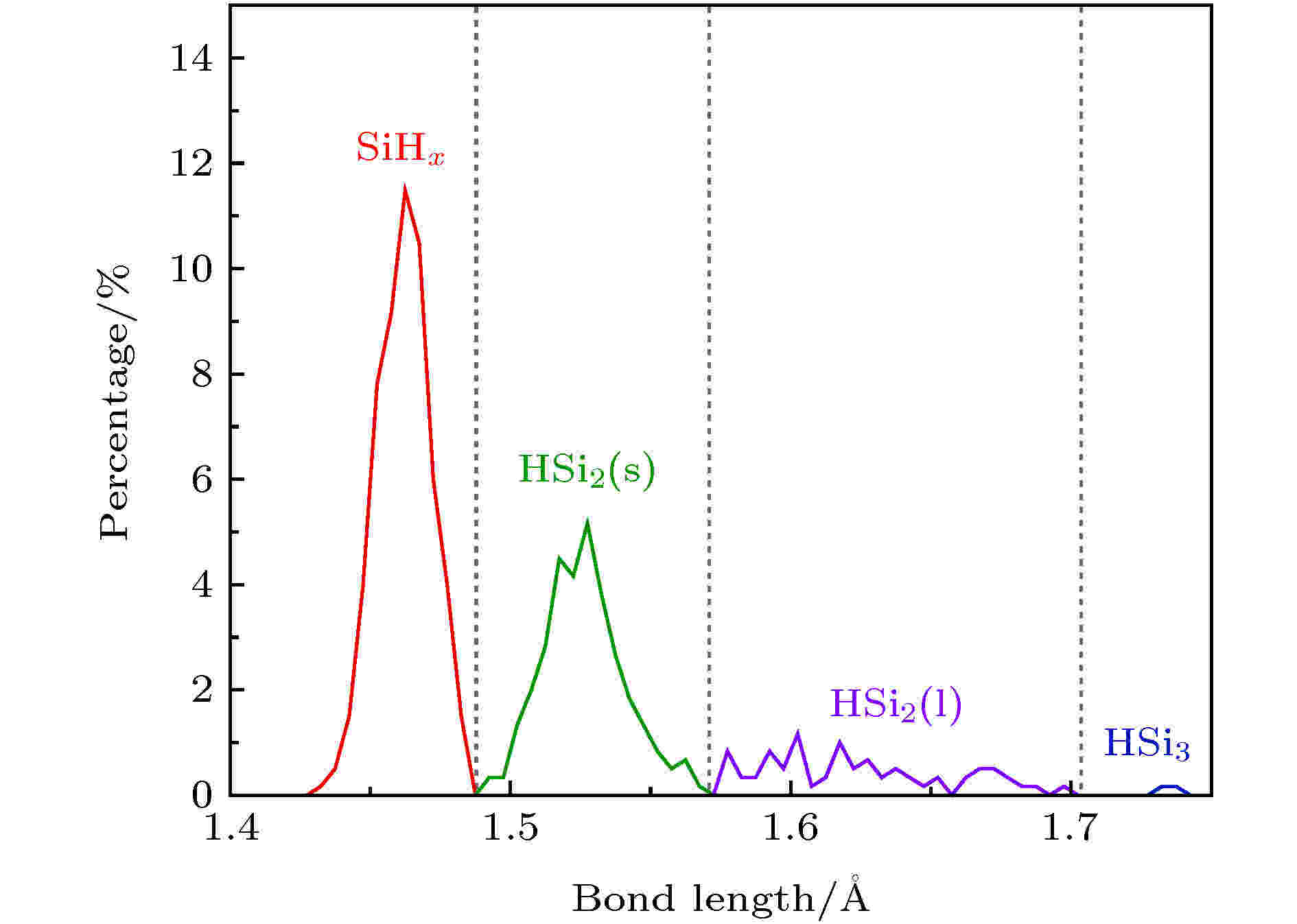
图 3 a-Si:H薄膜中Si-H键的键长分布 (沉积条件: 衬底温度为500 K, 入射动能为1.45 eV, 入射频率为1 ps/个基团)Figure3. The bond length distribution of the Si-H bond in the a-Si:H film (Deposition conditions: substrate temperature is 500 K, the incident kinetic energy is 1.45 eV, and the incident frequency is 1 ps/group).
为进一步分析a-Si:H/c-Si薄膜中的SiyHx组态, 利用Mercury软件对模拟沉积生长得到的a-Si:H薄膜中的Si—H的键合状态、键长、键角进行了统计分析, 发现H原子在连接不同数量的Si原子时, 其Si—H键的键长、键角呈现出不同的特征. 根据传统价键理论, 在Si—H结构中, 单个H原子通常只与一个Si原子形成化学键, 结合成三种组态: 分别为SiH, SiH2和SiH3, 记为SiHx组态. 这三类结构很容易鉴别出来, 其结构示于图4(a)—图4(c)中. 这三种组态中Si-H键的键长相近, 集中分布在1.46 ?附近, 对应于键长分布图(图3)中的第一峰, 在a-Si:H/c-Si薄膜中各SiyHx组态中长键角所占的比率最大. 除了上述三种化学键结合的SiHx组态外, 我们还发现了H与周围的Si原子形成物理键, 以氢桥Si-H-Si(HSi2)或HSi3的形式出现, 记为HSiy. a-Si:H薄膜中氢桥的存在曾被报道过[20,21], 但对于氢桥的结构特征分析不够明晰. 我们进一步分析还发现HSi2结构中存在两种具有不同键长键角特征的组态, 一种组态的Si—H键长处在1.49—1.57 ?范围, 键角集中分布在123°—137°之间, 因Si—H键长较短, 记为HSi2(s), 如图4(d)所示. 另一种组态Si—H键分布在1.5 —1.68 ?范围, Si—H—Si键角大于140°, 记为HSi2(l), 如图4(e)所示. 不难发现HSi2(s)和HSi2(l)两种组态对应于键长分布图(图3)中的第二峰和第三峰群, 其中HSi2(s)的含量明显高于HSi2(l). 图4(f)示出的是HSi3结构组态. 它的Si-H键在所有组态中最长, 大于1.7 ?. 同时它的Si-H-Si键角最小, 小于118°. HSi3组态对应于键长分布图(图3)中的最后一个小峰, 在所有组态中占比最少.
图 4 a-Si:H薄膜中SiyHx组态的结构示意图 (a) SiH; (b) SiH2; (c) SiH3; (d) HSi2(s); (e) HSi2(l); (f) HSi3Figure4. The structure Schematic diagram of SiyHx in the a-Si:H film: (a) SiH; (b) SiH2; (c) SiH3; (d) HSi2(s); (e) HSi2(l); (f) HSi3.
2
3.3.各SiyHx组态的稳定性
为分析以上六种SiyHx组态的稳定性, 我们采用第一性原理方法计算了它们的Si-H键能, 计算时各组态模型中的键长键角均采用统计得到的平均值. 同时将这些键能与太阳光的光子能量进行对比, 结果示于图5中. 通过键能的高低可以发现它们的稳定性由高到低的顺序为: SiH > SiH2 > SiH3 > HSi2(s) > HSi2(l) > HSi3. 只有SiH键的键能超出太阳光能量区间, 而SiH2, SiH3, HSi2(s), HSi2(l), HSi3组态的键能都处于该能量区间内. 但在实际非晶硅薄膜电池结构中, 非晶硅表面还有一层铟锡氧化物半导体透明导电膜(ITO)或加上一层玻璃层. 实验研究表明, ITO层或玻璃层几乎可以吸收掉太阳光中的全部紫外线[22]. 也就是说, 只有可见光和红外线可以真正照射到a-Si:H薄膜上. 从能量上正好对应于Si-H物理键的三种组态结构HSiy.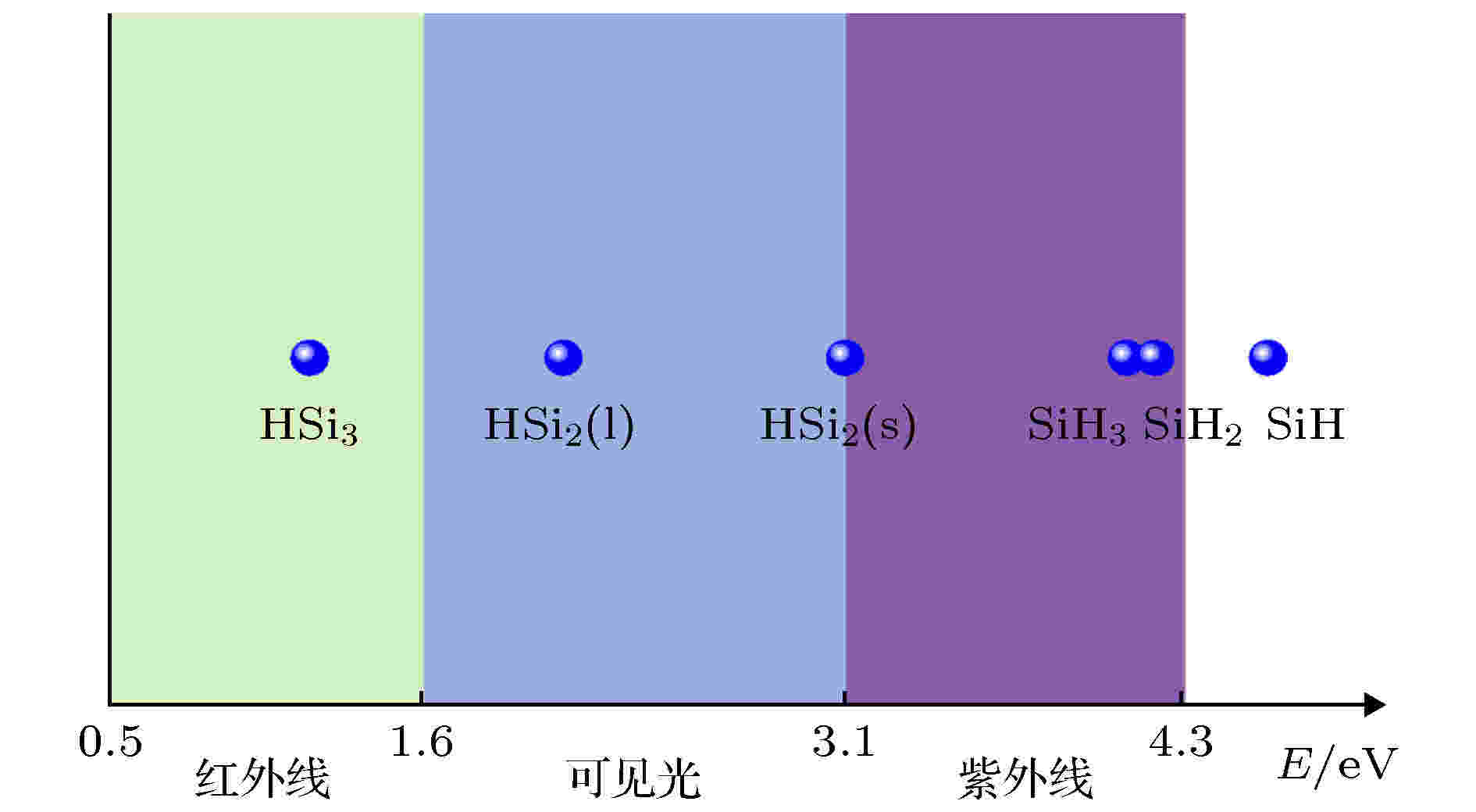
图 5 各SiyHx组态中Si-H键能与太阳光能量对比图Figure5. Comparisons of Si-H bond energy in each SiyHx configuration with solar energy
可以想象一下太阳光照射到电池上的场景: 首先紫外线被ITO或玻璃层全部吸收, 只有可见光和红外线透过ITO层到达a-Si:H薄膜表面. 它们因能量太低, 不会引起SiHx组态中Si—H键断键, 也就不会产生自由H原子; 但它们可与三种HSiy组态中Si—H物理键产生交互作用, 引起某个Si-H物理键断裂. 这种物理键的断裂, 只会让H原子位置产生偏移, 远离原成键Si原子, 偏向其余的Si原子, 同时引起Si原子电荷中心的变化. 对于断键的Si原子来说, 断键将增强其价电子的不饱和度, 类似于产生了一个强度较弱的Si悬挂键, 这将导致电池性能的下降. 因为光照断键的H原子仍被原HSiy组态中的其他Si原子约束, 不易发生长距离的扩散, 所以在没有光照的条件下, 经过结构弛豫, 原来的断裂的Si—H键又可能重新成键, 恢复电池的使用性能. 这个现象与非晶硅薄膜电池应用过程中的S-W效应的演化规律非常符合. 对于S-W效应起因, 人们已经做了大量的工作, 并提出了多种微观模型试图解释它, 但至今仍没有形成统一的观点. 而根据前面的分析结果, 我们认为光照引起HSiy组态中的Si—H物理键断裂, 才是S-W效应的主要机理.
2
3.4.衬底温度对SiyHx组态的影响
为了探讨沉积生长条件对SiyHx组态的影响规律, 我们选择衬底温度这一对薄膜结构影响较大的条件进行考察. 控制模拟参数: 衬底温度分别为300, 400, 500, 600和700 K, 基团入射频率为1个/ps, 入射动能为1.45 eV, 在Si(100)面上沉积约8000个基团. 然后统计了薄膜中悬挂键、SiHx和HSiy含量随衬底温度的变化, 如图6(a)所示. 该图以及后续图中各组态的含量都以其中的最大值为参考进行了归一化处理. 在不同衬底温度下, SiHx含量始终远大于HSiy的含量. 随温度升高, 薄膜中的SiHx和HSiy含量呈下降趋势, 这是因为衬底温度越高, 原子热振动加剧, Si—H弱键断裂形成氢气离开薄膜概率增加, 导致H原子含量降低的结果. 在500 K温度以下, 随温度升高, 悬挂键含量迅速降低; 500 K后, 下降趋势变得平缓. 这是因为虽然温度升高导致Si—H弱键断裂, H原子溢出, 会形成更多的Si悬挂键; 但高温有利于Si悬挂键之间也发生重组, 形成Si—Si强键, 使得Si悬挂键含量降低, 后者的作用大于前者, 总体上使得薄膜中Si悬挂键含量的降低.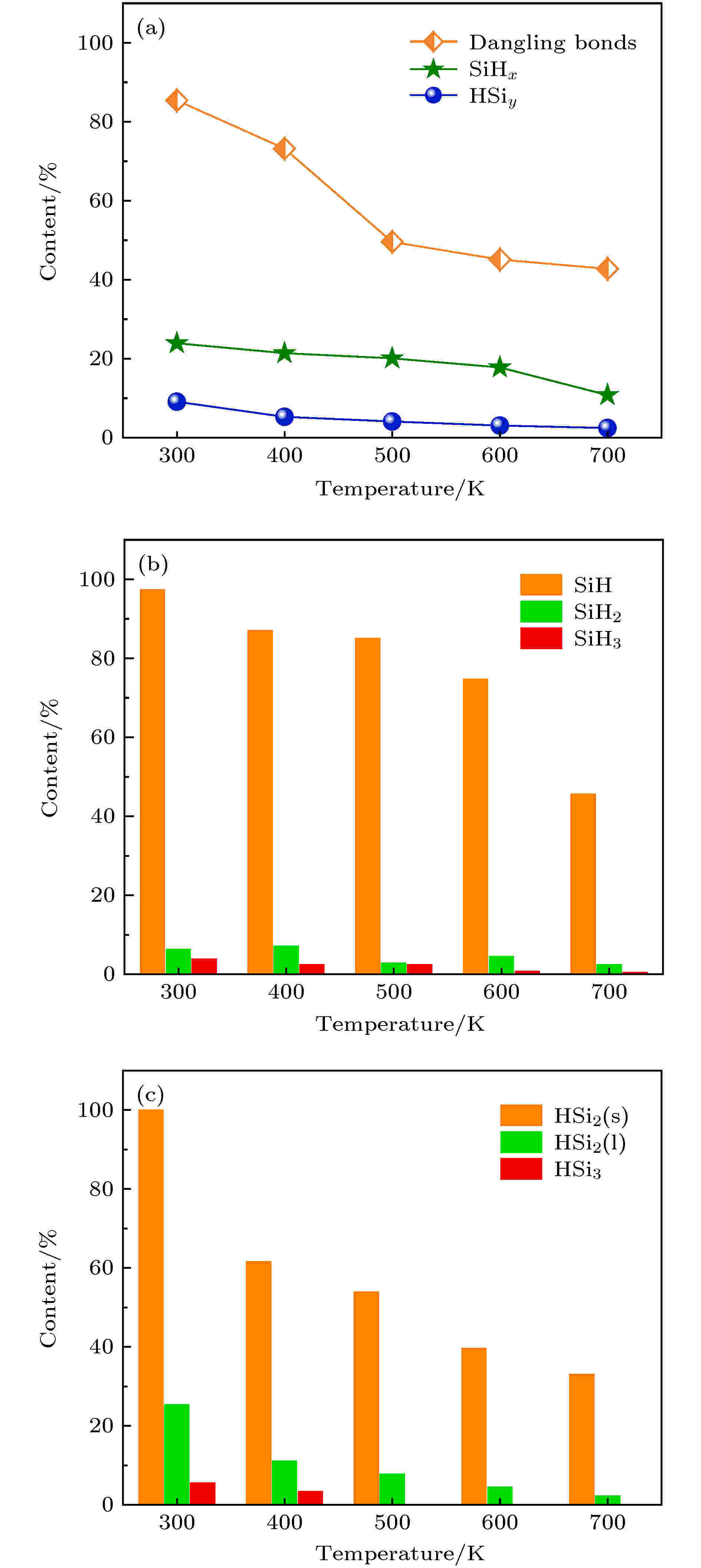
图 6 不同衬底温度下沉积生长的a-Si:H/c-Si薄膜中的悬挂键、SiHx和HSiy相对含量(a), SiH, SiH2和SiH3的相对含量(b)和HSi2(s), HSi2(l)和HSi3相对含量(c)Figure6. Relative contents of dangling bonds, SiHx and HSiy(a), relative contents of SiH, SiH2 and SiH3 (b), and relative content of HSi2(s), HSi2 (l) and HSi3 (c) in a-Si:H/c-Si films deposited with different substrate temperatures.
进一步分析了SiHx的三种组态和HSiy三种组态含量随衬底温度的变化, 分别示于图6(b)和图6(c)中. 从图6(b)中可发现, SiHx键合方式始终以SiH键为主, SiH2含量次之, SiH3含量最少. SiHx键含量随衬底温度的升高而降低. 同时SiH3含量随衬底温度的升高也有大幅的减少. 而HSiy中主要为HSi2(s)组态, HSi2(l)和HSi3含量很少. 随衬底温度的升高, 三种组态含量呈现明显的下降趋势. HSi2(l)在400 K之前含量迅速降低, 之后下降趋势变缓. HSi3在500 K后含量降为0, 这可能因为HSi3键能最低, 在高温下最不稳定.
