摘要:电子束照射下电介质/半导体样品的电子束感生电流(electron beam induced current, EBIC)是其电子显微检测的重要手段. 结合数值模拟和实验测量, 研究了高能电子束辐照下SiO₂/Si薄膜的瞬态EBIC特性. 基于Rutherford模型和快二次电子模型研究电子的散射过程, 基于电流连续性方程计算电荷的输运、俘获和复合过程, 获得了电荷分布、EBIC和透射电流瞬态特性以及束能和束流对它们的影响. 结果表明, 由于电子散射效应, 自由电子密度沿入射方向逐渐减小. 由于二次电子出射, 净电荷密度呈现近表面为正、内部为负的特性, 空间电场在表面附近为正而在样品内部为负, 导致一些电子输运到基底以及一些出射二次电子返回表面. SiO₂与Si界面处俘获电子导致界面附近负电荷密度高于周围区域. 随电子束照射样品内部净电荷密度逐渐降低, 带电强度减弱. 同时, 负电荷逐渐向基底输运, EBIC和样品电流逐渐增大, 电场强度逐渐减小. 由于样品带电强度较弱, 表面出射电流和透射电流随照射基本保持恒定. EBIC、透射电流及表面出射电流均随束流呈现近似正比例关系. 对于本文SiO₂/Si薄膜, 透射电流随束能的升高逐渐增大并接近于束流值, EBIC在束能约15 keV时呈现极大值.
关键词: 数值模拟/
电子束感生电流/
俘获/
输运

English Abstract

全文HTML

--> --> -->

现代微纳电子技术的发展对其制造工艺中的测试方法提出了较高要求^[1,2]. 基于电子束技术的扫描电子显微镜、透射电子显微镜可观测样品表面及内部结构. 在电子束辐照下, 通过激发产生电子-空穴对, 形成局部导电特性^[3-6]. 特别是对于透射电子束, 样品表面至导电衬底间将形成导电通道, 这种导电通道将导致入射电子、激发的次级电子在样品内部输运, 形成电子束感生电流(electron beam induced current, EBIC). 基于EBIC效应, 可实现半导体样品表面及内部结构的观测和检测^[7-11]. 更重要的是, EBIC是电子束照射下样品内部电荷积累及带电强度的重要指标和手段^[12].
对于微电子器件特有的具有多层结构电介质/半导体样品, 透射电子束照射下的EBIC受电子束条件、样品参数和结构的影响, 其瞬态值呈现复杂的变化特性. 这里, 电子束照射电介质/半导体结构样品时, 经非弹性散射激发的部分次级电子沉积在样品内部形成负空间电荷分布^[12-15], 其产生的静电场影响从表面出射的二次电子轨迹及透射电流的大小. 此外, 电介质样品的体缺陷会俘获电荷, 改变内部电场分布及EBIC的形成、瞬态特性及稳定值^[16-18]. 更重要的是, 电介质/半导体的分界面会俘获电荷, 产生的电场不仅影响电荷在电介质内部的累积和输运, 还决定最终通过半导体流向衬底的EBIC瞬态和稳态特性^[8]. 而且, EBIC瞬态特性和相关带电特性受电子束条件、样品参数和结构特性等多方面因素的影响, 呈现复杂的变化规律, 对其瞬态发展机理缺乏足够了解, 相关研究尚比较缺乏.
当前已有的电介质/半导体结构样品的EBIC特性研究主要是基于实验测量的稳态特性研究, 因此难以准确建立EBIC与电子束条件、样品参数和结构之间的定量关系, 限制了EBIC在微电子器件检测中的应用. 本文旨在揭示可穿透电子束照射下电介质/半导体结构样品的EBIC及相关带电瞬态特性, 阐明电子束条件对EBIC的影响规律. 研究结果对提高微电子器件检测准确性, 降低其带电效应具有理论和实用价值.
本文以SiO₂/Si结构样品为对象, 建立考虑电子散射、俘获和输运的数值计算模型, 结合实验测量, 研究可穿透电子束照射下电介质/半导体薄膜的EBIC及相关带电瞬态特性. 首先介绍数值模型和实验平台; 然后给出空间电场、表面出射电流、透射电流及EBIC的瞬态特性; 最后分析和讨论电子束条件和样品参数对EBIC特性的影响.

电子束入射样品后与样品材料发生一系列复杂的过程. Monte Carlo (MC)模拟是研究电子束与固体相互作用的常用方法. 本文结合MC模拟、有限差分法以及Runge-Kutta法计算电荷的散射、输运、俘获及二次电子的出射及返回过程^[19,20]. 电子束照射样品时, 表层、浅表层次级电子出射形成二次电子; 部分能量较高的入射电子穿透样品形成透射电流; 其余电子在样品内部经历复杂的输运和俘获过程. 采用Rutherford弹性散射模型描述电子的散射过程, 并建立电荷输运、俘获过程的有限差分法数值计算模型.
研究对象为微纳电子器件常见的SiO₂/Si结构, 样品结构及起因于电子束照射产生的各类电流如图1所示, 其中SiO₂和Si层的厚度分别取为400 nm和100 nm. 首先, 束流为I_B的电子束照射样品, 少量入射电子直接反射形成背散射电子电流I_BE; 部分激发产生的次级电子经表面出射形成二次电子电流I_SE, 但在表面电场的作用下, 部分出射电子可能返回表面形成I_RE, 因此有效出射电流I_I为

${I_{\rm{I}}} = {I_{{\rm{BE}}}} + {I_{{\rm{SE}}}} - {I_{{\rm{RE}}}}.$

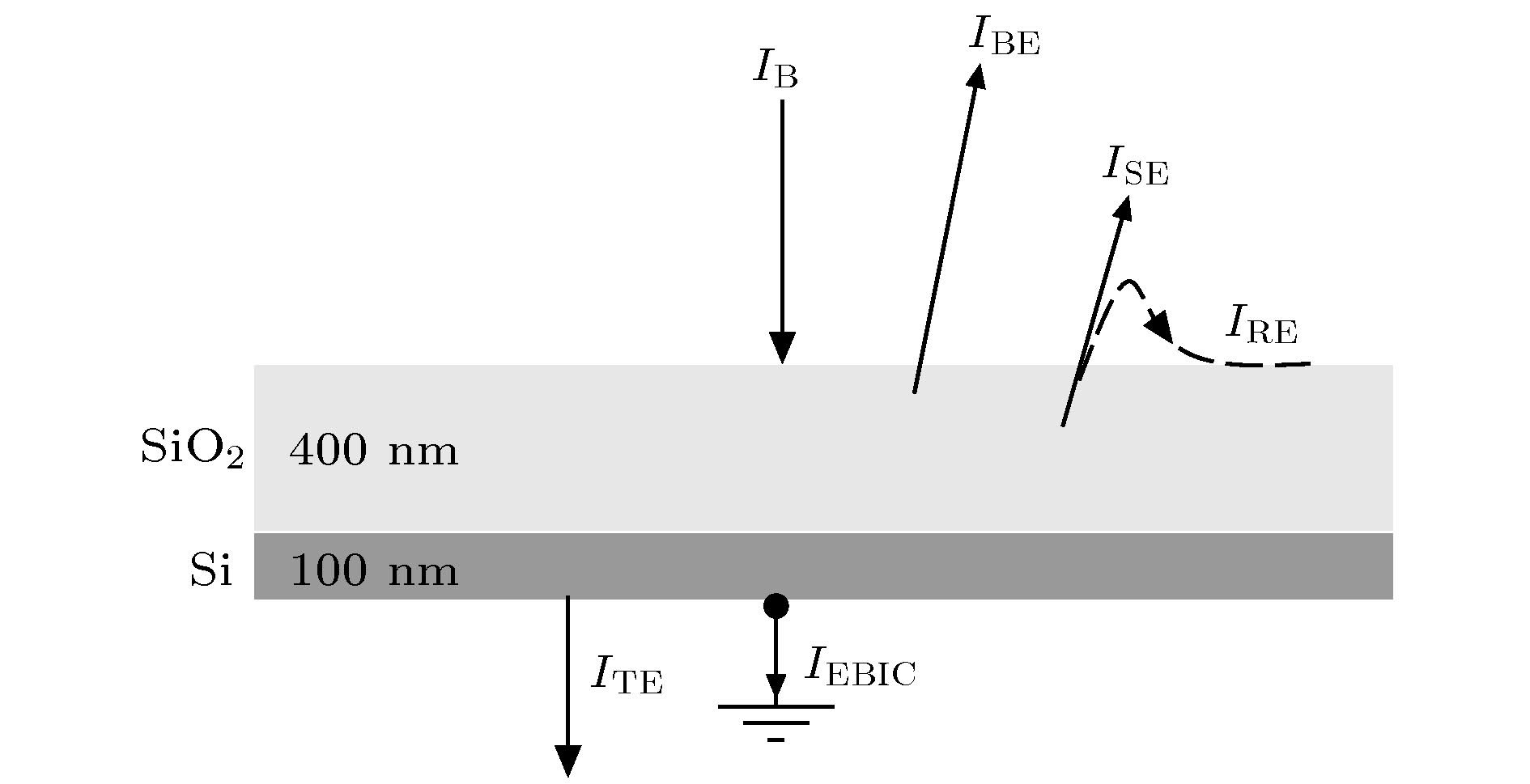图 1 电子束与样品相互作用产生的各类电流示意图
Figure1. Schematic of currents generated by the interaction of e-beams with samples.

部分能量较高的入射电子穿透样品形成透射电子电流I_TE. 部分自由电子经输运过程到达基板形成电子束感生电流I_EBIC. 因此本文中样品电流I_S可写为

${I_{\rm{S}}} = {I_{{\rm{TE}}}} + {I_{{\rm{EBIC}}}} + {I_{{\rm{RE}}}}.$

需要指出的是, 电子束辐照非导体样品时, 由于电荷累积在样品下表面的电场连续增大形成自由电子移动, 如果下表面接地会形成位移电流^[13]. 由于本文研究对象为电子迁移率较高的SiO₂和Si薄膜, 其内部沉积的负电荷量较小, 因而其内部电场强度较小, 故位移电流值较小, 对EBIC和样品电流的影响可忽略不计.
2

-->

2.1.电子散射及Monte Carlo模拟

电子束照射样品后, 与样品原子或分子发生复杂的散射过程. 入射电子与样品碰撞时, 受原子核库仑场的作用发生大角度弹性散射, 或者与原子的核外电子发生碰撞使原子受到激发发生非弹性散射. 这里, 非弹性散射主要与价电子激发相关.
弹性散射过程中, 入射电子在原子核的库仑势下折射, 不损失能量. 对于入射能量大于10 keV的高能电子弹性散射过程, Rutherford弹性散射截面为^[21]

${\sigma _{\rm{e}}} = 5.21 \times {10^{ - 21}}\frac{{{Z^2}}}{{{E^2}}}\frac{{4{\text{π}}}}{{\alpha (1 + \alpha )}}{\left( {\frac{{E + 511}}{{E + 1024}}} \right)^2}, $

其中$\alpha= 3.4 \times {10^{ - 3}}{Z^{0.67}}/E$, E为电子携带能量, Z是样品原子序数. 由(3)式可得到弹性散射平均自由程为

${\lambda _{\rm{e}}} = \frac{A}{{{N_a}\rho {\sigma _{\rm{e}}}}},$

这里N_a为Avogadro常数, ρ为材料质量密度, A为原子质量.
采用单电子散射模型来模拟非弹性散射过程, 其微分散射截面为

$\frac{{{\rm{d}}{\sigma _{{\rm{in}}}}}}{{{\rm{d}}\varOmega }} = \;\frac{{{\text{π}}{e^{\rm{4}}}}}{{{E^2}}}\left[ {\frac{1}{{{\varOmega ^2}}}{\rm{ + }}\frac{1}{{{{(1 - \varOmega )}^2}}}} \right],$

这里e为单电子电量, Ω为归一化能量损失系数, 由散射截面可得到非弹性散射平均自由程为

${\lambda _{{\rm{in}}}} = \frac{A}{{{N_{\rm{a}}}\rho Z{\sigma _{{\rm{in}}}}}}.$

非弹性散射过程的能量损失采用修正Bethe连续能量损失经验公式来描述, 能量为E的电子相对于散射步长S的平均能量损失率为^[21]

$\frac{{{\rm{d}}E}}{{{\rm{d}}S}} = - \;\frac{{7.85 \times {{10}^4}\rho \bar Z }}{{E \bar A}}\ln [1.166(E + 0.85 \bar J )/\bar J ],$

其中$\bar A $, $\bar J $和$\bar Z $分别为样品的平均原子量、平均电离能和平均原子序数, 平均电离能的计算式为

$\bar J = \left[ {9.76\bar Z + \frac{{58.5}}{{{{\bar Z}^{0.19}}}}} \right] \cdot {10^{ - 3}}\;({\rm{keV}}).$

对于本文研究的样品, 相关参数取值如表1所列.

参数	SiO2	Si
ρ/g·cm–3	2.26	2.32
$\bar A $/g·mole–1	20	28.1
$\bar J $/keV	0.139	0.173
$\bar Z $	10	14

表1电子散射过程参数默认设置
Table1.Default values of parameters in the scattering process.

采用MC模拟电子的散射过程. 电子散射中的运动轨迹由步长、散射角及方位角来确定, 一个电子在两次散射之间的步长S用下式来表示:

$S = - \;{\lambda _{\rm{T}}}\ln {R_1},$

其中R₁为随机数, ${\lambda _{\rm{T}}}$为总的平均自由程, 满足$\lambda _{\rm{T}}^{{\rm{ - 1}}} = \lambda _{\rm{e}}^{{\rm{ - 1}}} + \lambda _{{\rm{in}}}^{ - 1}$.
电子散射类型利用随机数R₂来决定. 假如${R_2} < \lambda _{\rm{e}}^{{\rm{ - 1}}}/\lambda _{\rm{T}}^{{\rm{ - 1}}}$, 则为弹性散射; 否则为非弹性散射. 弹性散射的散射角θ由随机数R₃来确定:

$\cos \theta = 1 - \frac{{2\alpha {R_3}}}{{(1 + \alpha - {R_3})}}\;.$

方位角满足:

$\psi = 2{\text{π}}{R_4},$

其中R₄为随机数.
对于由两种元素组成的SiO₂样品, 电子与其中第i种元素的原子的碰撞概率为

${p_i} = {{{C_i}{\sigma _i}}\bigg/{\sum\limits_{i = 1}^2 {{C_i}{\sigma _i}} }},$

其中${C_i}$和${\sigma _i}$分别表示第i种元素的原子百分比和弹性散射截面. 如果随机数R₅满足:

$\sum\limits_{j = 1}^{i - 1} {{p_j}} < {R_5} < \sum\limits_{j = 1}^i {{p_j}},$

则电子与样品中第i种元素的原子碰撞, $j = 0$时${p_0} = 0$. 上述随机数均为区间[0, 1]上的均匀分布.
2 -->

2.2.俘获与漂移

样品的体缺陷或者不同介质分界面的表面俘获能量耗尽的电子. 对于体缺陷的俘获, 采用基于Poole-Frenkel效应的俘获截面模型^[22], 俘获电子密度T(t)随时间变化表示为

${{{\rm{d}}T(t)}}/{{{\rm{d}}t}} = C \cdot N(t)\left( {{N_{{\rm{trap}}}} - T(t)} \right),$

其中N_trap为陷阱中心密度, C为俘获系数.
不同介质分界面的表面会俘获电荷. 当自由电子运动到该区域时, 只要该俘获点为空, 则该自由电子会被表面俘获.
输运特性是影响样品EBIC的关键^[23]. 未被俘获的自由电子及空穴在内部电场下迁移和密度梯度作用下扩散, 影响样品内部电荷分布以及表面出射电子、透射电子运动及EBIC特性. 电荷的迁移和扩散满足电流连续性方程^[8]:

$\frac{{{\rm{d}}N(t)}}{{{\rm{d}}t}} = \nabla {{{J}}_{\rm{e}}}(t)/e,$

$\frac{{{\rm{d}}P(t)}}{{{\rm{d}}t}} = \nabla {{{J}}_{\rm{p}}}(t)/e,$

${{{J}}_{\rm{e}}}(t) = - e{\mu _{\rm{e}}}N(t)\nabla V(t) + e{D_{\rm{e}}}\nabla N(t),$

${{{J}}_{\rm{p}}}(t) = - e{\mu _{\rm{p}}}P(t)\nabla V(t) + e{D_{\rm{p}}}\nabla P(t),$

其中${{{J}}_{\rm{e}}}(t)$和${{{J}}_{\rm{p}}}(t)$分别代表电子电流密度和空穴电流密度; μ_e和D_e分别是电子迁移率和扩散系数; μ_p和D_p分别是空穴迁移率和扩散系数, 二者之间满足爱因斯坦关系式.
空间电位满足泊松方程:

${\nabla ^2}V(t) = - [P(t) - N(t) - T(t)] e/\varepsilon,$

其中ε表示介电常数. 此外, 自由电子还可能与空穴发生复合. 为简化计算, 本文采用直接复合模型, 计算式为

$\frac{{\partial P(t)}}{{\partial t}} = - RP(t)N(t),$

$\frac{{\partial N(t)}}{{\partial t}} = - RP(t)N(t),$

式中R代表电子空穴复合率. 对微分方程组(14)—(21)采用有限差分法求解. 有限差分法的网格大小会影响最终结果及计算速度. 为了兼顾计算速度和准确性, 网格取5 nm.
对于三维坐标系统(x, y, z), z方向为入射方向, EBIC电流的计算式如下:

${I_{{\rm{EBIC}}}}(t) = - \int\!\!\! {\int {{{{J}}_{\rm{e}}}(t) \cdot z{\rm{d}}x{\rm{d}}y} } .$

2 -->

2.3.出射电子轨迹计算

对于电介质及半导体样品, 电子束照射下产生的空间电场有可能吸引部分能量较低的出射电子返回样品表面. 同时, 收集器电压也会影响出射电子的轨迹. 根据样品上方的空间电场F_x, F_y和F_z, 出射电子的运动方程为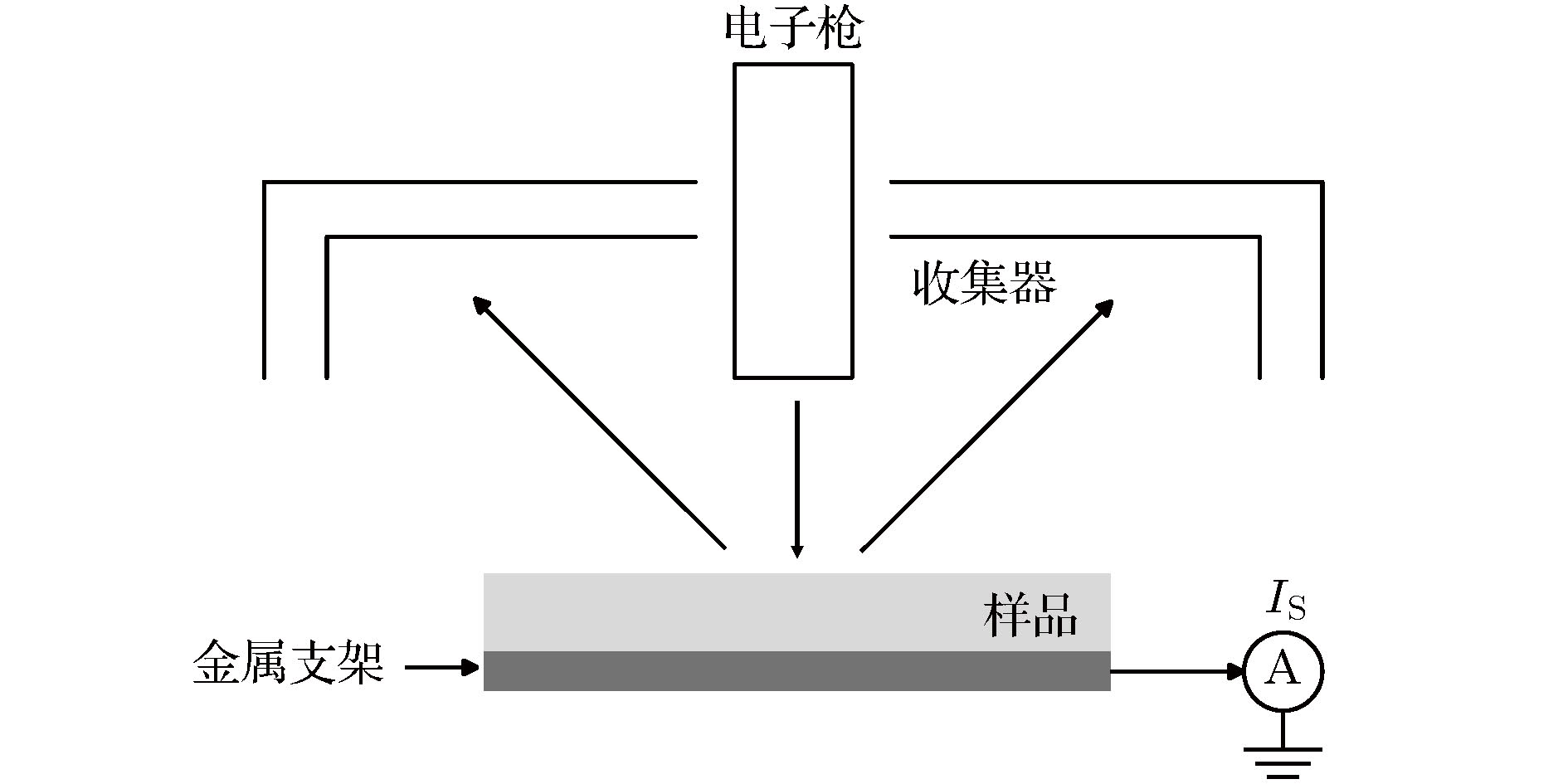

$m\ddot x = - e{F_x},\;m\ddot y = - e{F_y},m\ddot z = - e{F_z}.$

(23)式采用四阶龙格库塔法求解, 最终可得到返回表面电子电流I_RE以及有效出射电流I_I.

采用湿氧化法在硅基片上热生长二氧化硅薄膜, 样品结构和参数见图1. 图2是简化实验装置示意图, 用于测量表面出射电流以及样品电流. 整个装置放置于高真空实验舱内. 电子枪为热场发射电子枪, 束斑直径为100 nm. 样品放置于具有良好导电性能的金属平台, 下方连接安捷伦B2981A皮安计用于收集和测量样品电流. 样品上方为法拉第杯, 用于收集表面出射电子. 实验参数如表2所列.
图 2 实验装置示意图
Figure2. Schematic diagram of the experimental device.

束能EB/keV	束流IB/nA	扫描区域/mm2	扫描周期/s
10, 15, 20, 30	1.6	1 × 1	1.2

表2实验参数默认设置
Table2.Default values of parameters.

数值计算中的电子束照射方向为z方向. SiO₂的电子迁移率取10^–1 cm² · V^–1 · s^–1, Si的电子迁移率取10² cm² · V^–1 · s^–1, 未作说明的模拟参数默认值见表3. 需要说明的是, SiO₂与Si的界面陷阱密度受生长条件影响有所不同, 且远大于体缺陷俘获中心密度^[24,25].

参数	取值
束能EB/keV	10
束流IB/nA	1.6
体缺陷密度/cm–3	1017
界面俘获密度/cm–2	1014

表3数值计算参数默认设置
Table3.Default values of parameters.

2

-->

4.1.电子产额

影响EBIC大小的关键是入射电子束辐照产生的内部电荷和电场分布. 在高能电子束照射下, EBIC特性取决于流出样品电子电流大小. 对于电介质/半导体样品, 流出样品电流包括表面出射电子电流以及从样品衬底流出的电子电流.
从样品表面出射电子包括背散射电子和二次电子. 对于电介质或半导体样品, 长时间照射引起电荷的积累产生样品表面和内部带电, 因而出射电子电流和产额会动态变化. 图3是初始时刻电子总产额σ的模拟和实验结果, 实线是模拟结果, 方块符号是测量结果. 这种情况下, 可近似认为样品不带电, 理论上出射电子全部被收集器收集. 从图3可发现, σ 随束能E_B的增大而减小. 这是因为, 随着E_B的增大, 通过非弹性散射激发的次级电子分布在样品内更深区域, 因而更难从样品表面出射形成二次电子, 导致σ减小. 这一变化规律基本适用于所有金属、电介质样品. 需要指出的是, σ的计算结果略大于实际测量结果. 这主要是由于实际的电子收集器并不能收集所有的出射电子, 特别是出射角度(与入射方向夹角)较大的二次电子更可能离开收集器的有效视场, 无法被收集器收集.
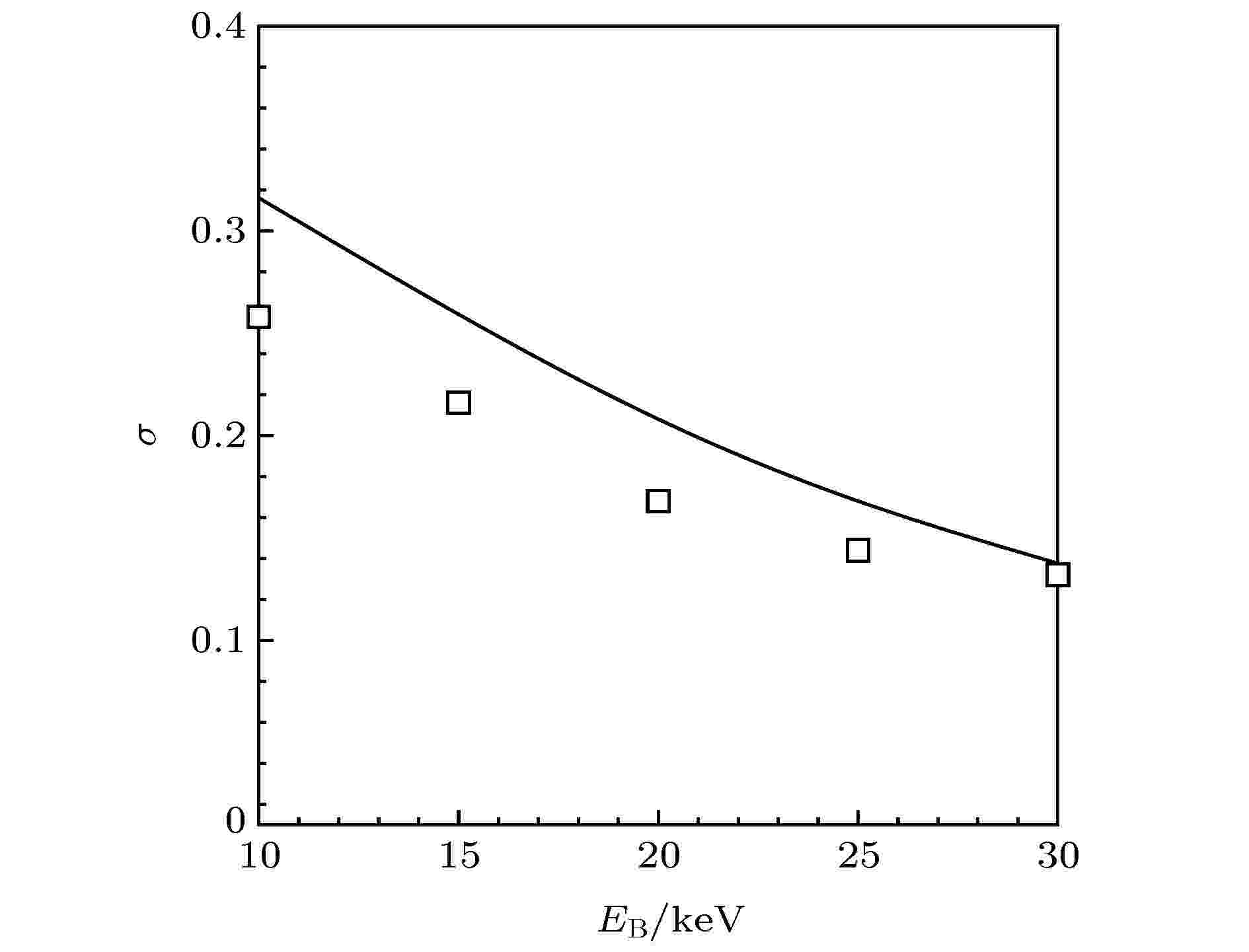图 3 电子总产额的模拟(直线)和实验(方块)结果
Figure3. Simulated (lines) and experimental (squares) results of total electron yield.

从样品衬底流出的电子电流首先是透射电子电流. 这里, 电子束的入射深度决定透射电流的大小, 最大入射深度λ可近似用下式计算^[21]:

$\lambda = \frac{{700E_{\rm{B}}^{{{1}}{{.66}}}}}{\rho }.$

基于样品参数, 束能大于10 keV时, 由(24)式计算得到的最大入射深度大于样品厚度, 因此电子束照射产生的透射电流不可忽略.
2 -->

4.2.空间电荷分布

经散射后自由电子在样品内部经历输运和俘获. 样品内部不同时刻自由电子密度N(t)的分布见图4. 从图4可知, 沿着入射z方向, 自由电子密度(不含俘获电子密度)总体上逐渐降低. 这是因为, 通过非弹性散射产生的次级电子一般主要发生在表面、近表面; 随着入射深度的增加, 入射电子能量逐渐衰减, 因而产生的次级电子数量逐渐减小. 此外, 随着电子束持续照射, 自由电子密度逐渐增大. 同时样品内部将沉积更多的电子, 负电荷量逐渐增大; 虽通过复合、迁移和扩散等作用自由电子密度会降低, 但总体上并不会改变随电子束持续照射自由电子密度增大的趋势.
图 4 自由电子密度N(t)沿入射方向分布
Figure4. Simulated free charge densities N(t) along the incident direction.

图5是模拟得到的不同时刻样品内部净电荷密度分布. 这里, 净电荷密度是空穴密度P(t)与电子密度N(t)之差. 由于空穴迁移率远小于电子迁移率, 因而相对于电子, 空穴可认为基本静止. 首先, 由于近表面二次电子的出射, 净电荷密度在近表面为正; 而在样品内部, 由于电子产额小于1, 净电荷密度总体为负. 此外, 在400 nm处, 即SiO₂与Si介质分界面, 由于界面处俘获电子, 因而界面处的净电荷密度(负)较高. 最后, 样品表面及近表面(约$z < 30$ nm), 由于电子的输运效应电子向表面迁移, 表面及近表面正电荷密度逐渐减小; 同理, 由于电子迁移率相对较高, 通过输运、复合作用, 样品内自由电子逐渐向下方输运, 因而电荷分布在更深的区域, 且净电荷密度逐渐减小.
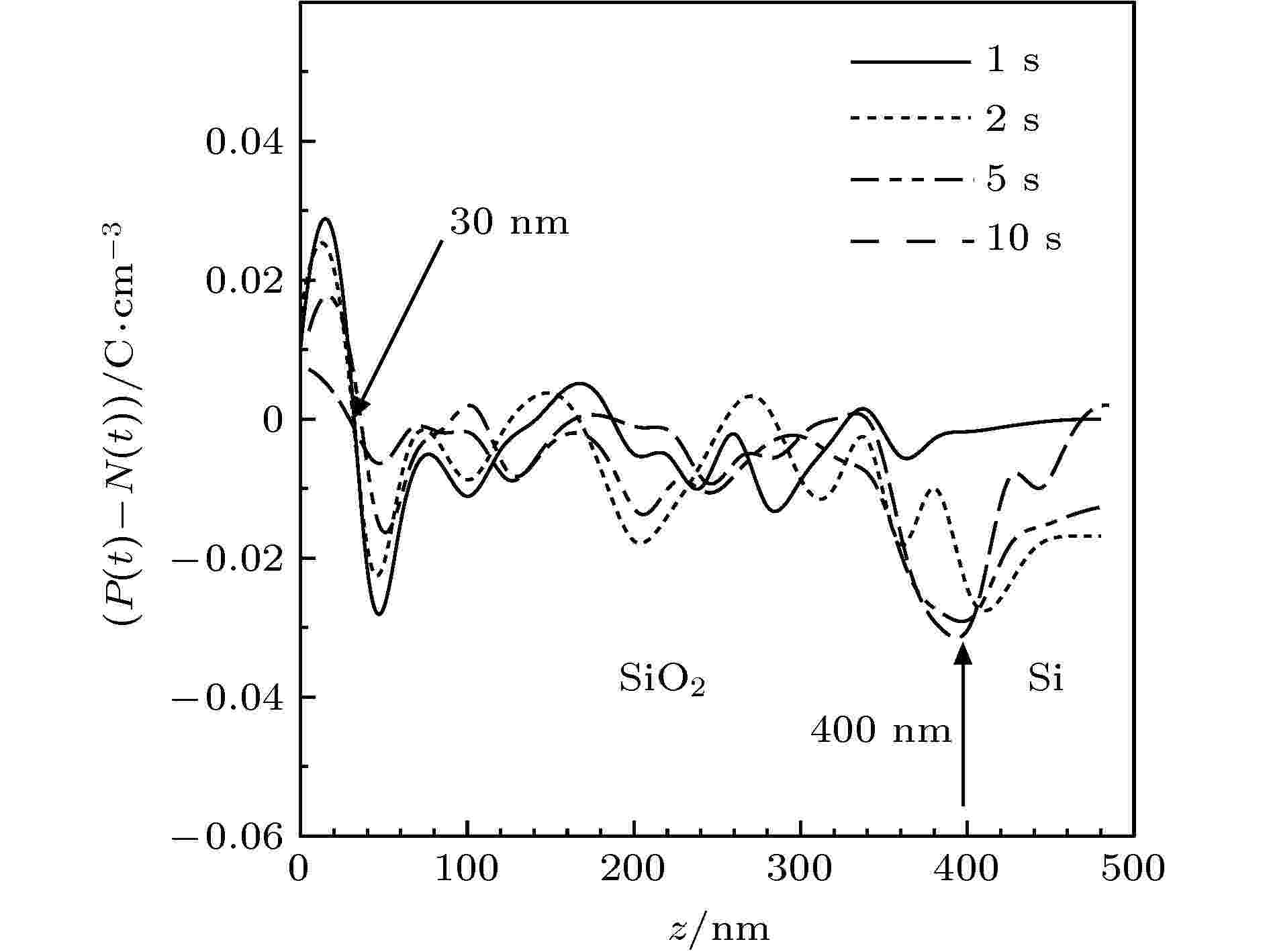图 5 净电荷密度(P(t) – N(t))沿入射方向分布
Figure5. Simulated net space densities (P(t) – N(t)) along the incident direction.

2 -->

4.3.空间电场分布

基于样品内部的净电荷分布, 可计算得到样品内部的电位和电场分布, 结果如图6所示. 从图6(a)可知, 空间电位沿入射方向先下降为极小值, 然后逐渐增大并趋于零, 这种分布形态由图5所示的净电荷分布形态所决定. 此外, 随着电子束持续照射, 样品内输运、复合作用的效应逐渐增强, 样品内的带电强度逐渐减弱, 空间电位逐渐升高并接近于零电位.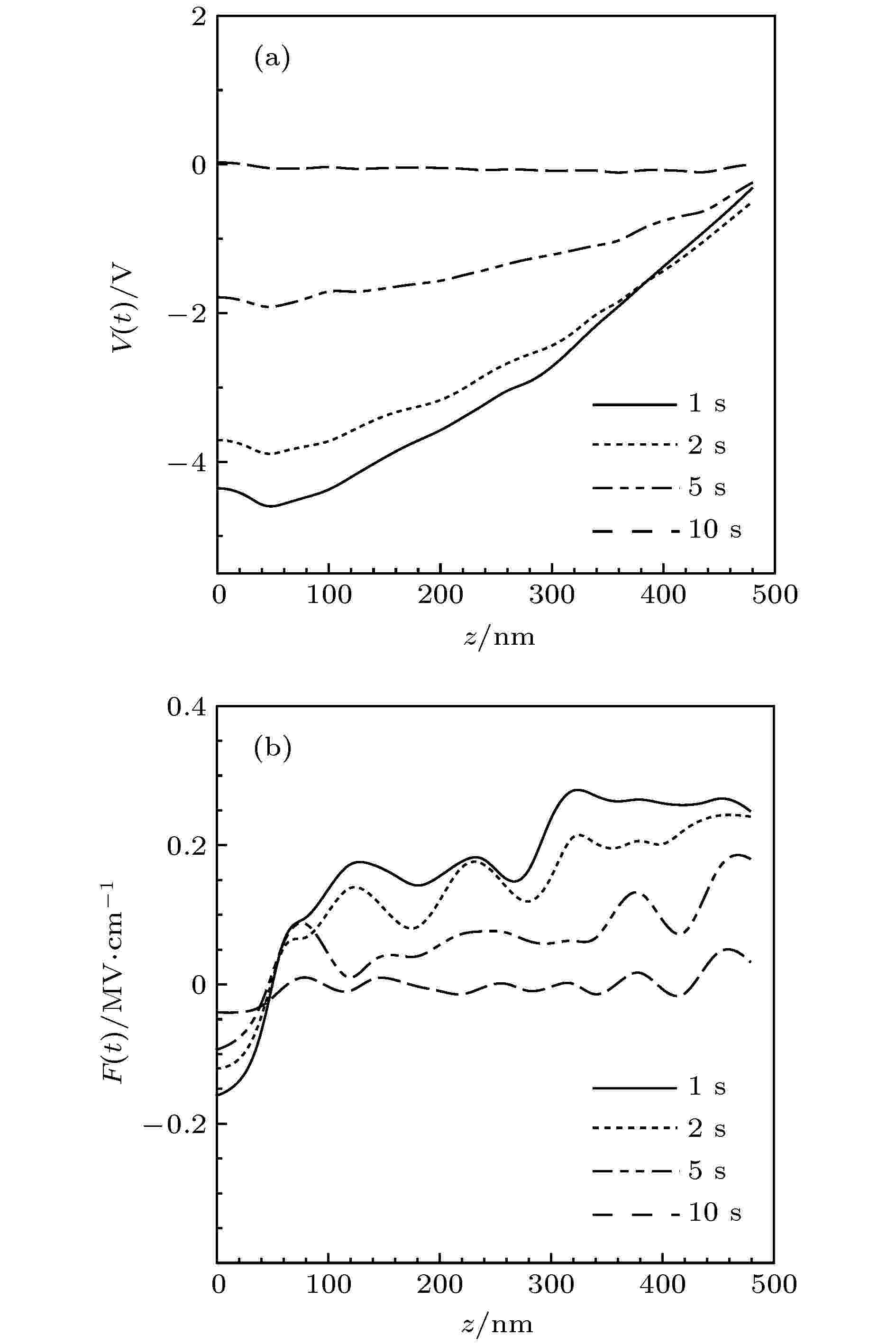
图 6 (a)空间电位V(t)和(b)空间电场F(t)沿入射方向分布模拟结果
Figure6. Simulated (a) space potentials V(t) and (b) space fields F(t) along the incident direction.

如图6(b)所示, 在样品内部约40 nm的浅表面, 电场强度为负值, 而在下方电场强度为正值. 这种电场形态一方面推动表面及近表面的电子向表面输运, 同时推动样品内部的自由电子向下输运并形成EBIC. 随着电子束持续照射, 尽管样品内部沉积的负电荷量逐渐增大, 但电场强度逐渐减小, 样品的带电强度将减弱. 而对于绝缘材料, 由于电子的输运能力较弱, 其样品内部电场强度随照射将逐渐增大, 其值远大于本文电介质样品, 因而有可能导致样品被击穿^[26]. 需要指出的是, 由于表面电场较小, 其对入射电子束的实际着陆能量及入射轨迹影响较小.
2 -->

4.4.表面出射电流

图7是不同时刻有效出射电流I_I的模拟和测量结果. 这里, 根据(1)式, I_I等于背散射电子电流和二次电子电流之和, 但需要减去返回表面的二次电子电流I_RE. 事实上, 尽管表面电场强度较弱(见图6(b)), 但依然会吸引部分二次电子返回表面. 但由于表面电场随照射逐渐减弱, 因而I_RE随着照射逐渐减小. 由于其值较小, 对有效出射电流I_I的影响较小, 因而I_I随照射基本保持在约0.35 nA.
图 7 有效出射电流I_I的模拟(直线)和测量(方块)结果
Figure7. Simulated (line) and experimental (squares) effective emission currents I_I.

2 -->

4.5.电子束感生电流

图8是不同时刻透射电流、EBIC及样品电流结果. 首先, 从图8(a)可看出, 透射电子电流I_TE随照射基本保持不变, 约为1.15 nA. 这是因为, 样品内的带电强度较弱, 对透射电子的轨迹影响较小. 此外, 电子束感生电流I_EBIC从零逐渐增大至一个稳定值. 这里, 在照射初期, 自由电子密度较小, 产生的EBIC也较小; 而随着电子束照射, 其值随自由电子密度的增大而增大; 在电子束照射后期, 由于自由电子分布在更广泛区域, 推动电子向下输运的空间电场强度较小, 因此I_EBIC将趋于稳定值.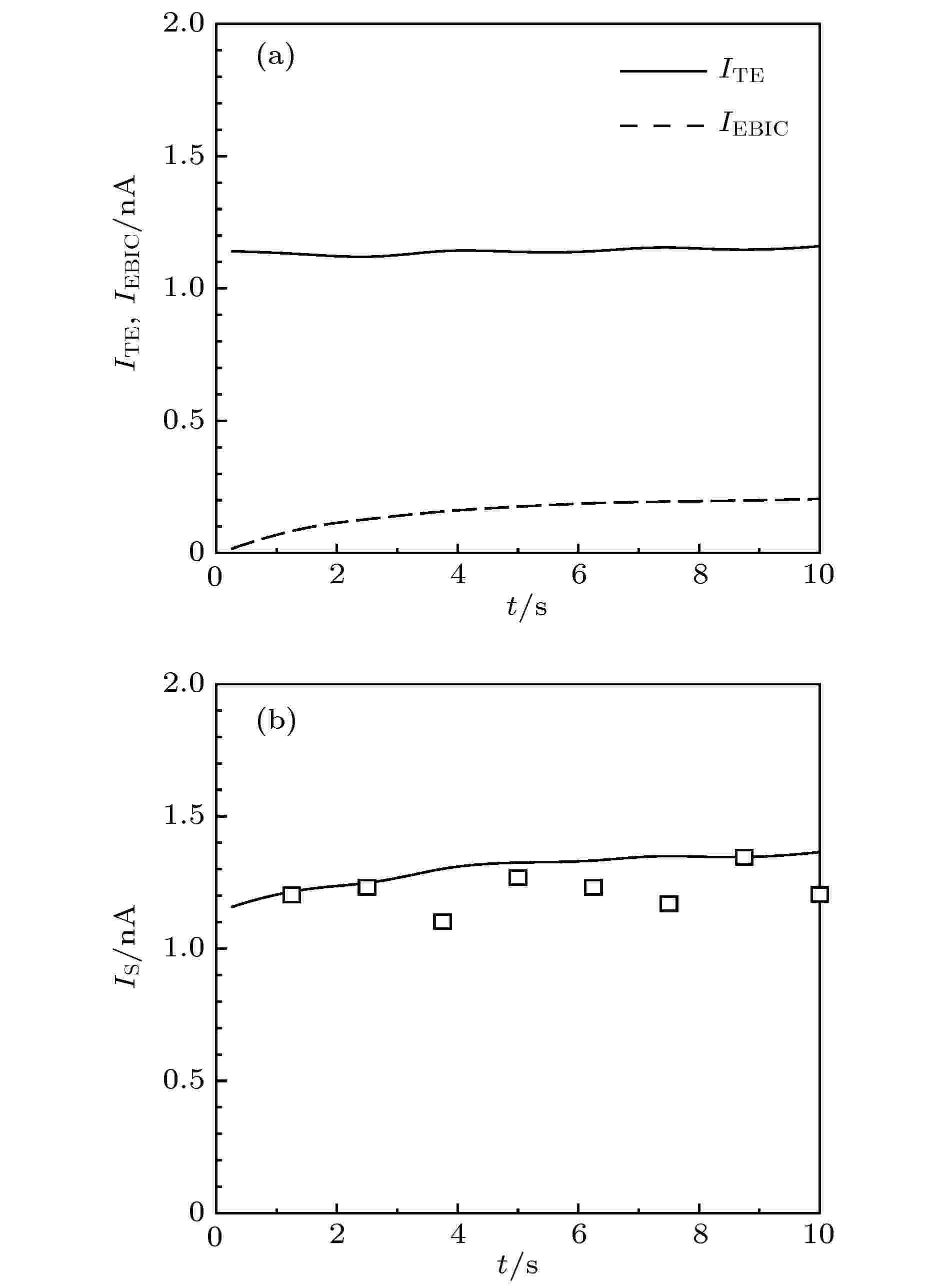
图 8 (a) I_EBIC及I_TE的模拟结果; (b) I_S的模拟(直线)和测量(方块)结果
Figure8. (a) Simulated I_EBIC and I_TE; (b) simulated (line) and experimental (squares) I_S.

此外, 如图8(b)所示, 样品电流从零逐渐增大至一个稳定值. 这里, 样品电流的模拟结果包含透射电流I_TE、电子束感生电流I_EBIC及返回表面的二次电子电流I_RE. 尽管由于表面正电场的减小I_RE随电子束照射逐渐减小, 但由于I_EBIC随照射逐渐增大, 因而总体上样品电流从零逐渐增大至一个稳定值.
需要指出的是, 对于具有较低迁移率的绝缘薄膜, 其内部积累的电荷浓度往往非常高, 表面电位较低, 因而其出射电流、透射电流的变化规律应该与本文高迁移率电介质薄膜的结论有较大差异^[19].
2 -->

4.6.电子束参数的影响

由于束流对电子散射、输运特性的影响较小, 因而平衡态时电子束感生电流I_EBIC与束流呈现近似正比例关系, 如图9所示. 类似地, 表面出射电子电流、样品电流随束流变化也呈现相同的正比例关系.
图 9 模拟得到的不同束流时电子束感生电流I_EBIC的稳态结果
Figure9. Simulated I_EBIC in the steady state under the different values of beam current I_B.

束能不仅决定电子产额也决定电子入射深度, 对带电特性的影响较为复杂. 图10是模拟得到的不同束能下透射电流I_TE时变特性, 当束能从10 keV增大到20 keV时, 由于电子入射深度的增大, 透射电子电流逐渐增大; 但从20 keV增加到30 keV时, 透射电子电流略小于入射电子电流I_B的稳定值. 这是因为, 在较高入射能量段, 背散射电子产额较低, 绝大多数入射电子将直接穿透样品, 因而透射电流接近于束流(1.6 nA).
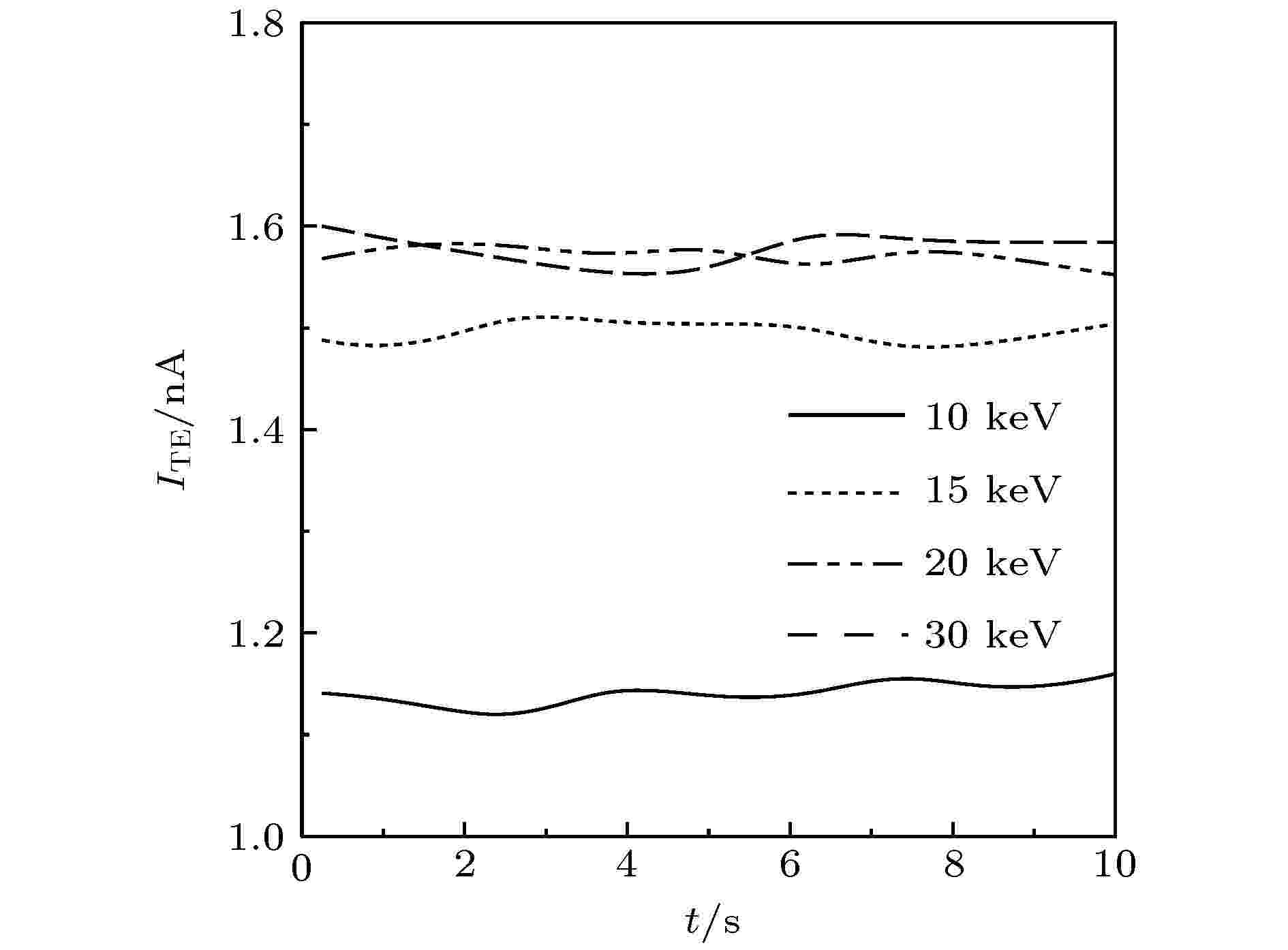图 10 模拟得到的不同束能时透射电流I_TE的时变特性
Figure10. Simulated I_TE as a function of the irradiation time in the different beam energies E_B.

图11是模拟得到的不同束能时电子束感生电流I_EBIC的时变特性, 在约15 keV处呈现极大值. 这里, 当束能从10 keV升至15 keV, 经非弹性散射激发的次级电子数量较大, 导致EBIC增大. 而随着束能的继续升高, 尽管次级电子数量较大但样品内激发的次级电子分布更为分散, 内部电场逐渐减小, 导致电子向下输运能力减弱, 因而EBIC反而减小, 故而在束能约为15 keV时EBIC呈现极大值.
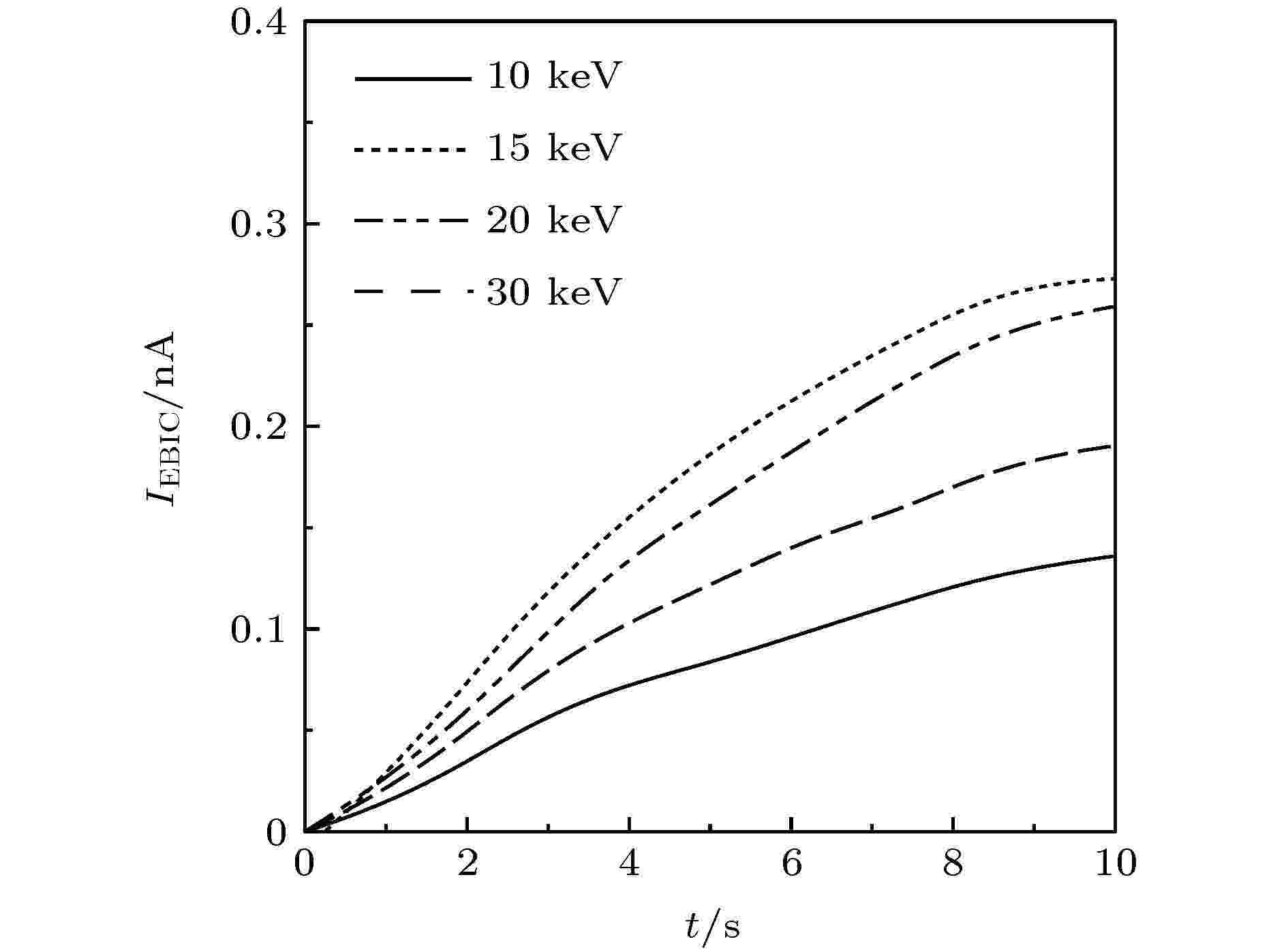图 11 模拟得到的不同束能时I_EBIC的时变特性
Figure11. Simulated I_EBIC as a function of the irradiation time in the different beam energies E_B.

本文研究对象为微电子器件常见的SiO₂/Si结构样品, 其电子迁移率一般远高于绝缘、聚合物样品. 由于绝缘样品的电子迁移率较低, 其内部自由电子的输运过程较为缓慢, 因而样品内的负带电强度较大, 样品内部、表面将强负带电. 这种强带电将严重影响入射电子轨迹及表面出射电子电流和透射电子电流, 其带电机理与电子迁移率较高的半导体样品有明显区别^[19,26].
文中的样品厚度为数百纳米级. 事实上, 介质样品厚度越大, 入射电子束的穿透能力越弱, 透射电流越小; 相反, 样品内部沉积的负电荷量会增大, 表面电位将明显下降.
由于生长条件不同, 实际中的样品参数可能与经验值有一定差别, 特别是陷阱密度等会影响样品内的散射、漂移和俘获过程. 样品陷阱密度及界面态俘获密度越大, 样品俘获的电子越多, 空间电位越低. 尽管由于参数不同导致得到的结果与实际有一定差异, 但本文研究结果并不影响所揭示的电介质/半导体样品EBIC特性的物理本质与规律.

研究了透射电子束照射下SiO₂/Si薄膜的EBIC及相关带电特性, 得到以下主要结论.
1) 在电子束照射下, 由于电子的散射效应, 自由电子密度沿入射方向逐渐减小. 由于表面、近表面二次电子的出射, 净电荷密度呈现近表面为正、随后为负的分布形态; 由于SiO₂与Si界面处俘获电子, 分界面附近的净电荷密度(负)低于周围区域; 样品内空间电场呈现在近表面为正, 内部为负的特性. 由于较高的电子迁移率, 随着电子束照射, 样品内部净电荷密度逐渐降低, 样品带电强度减弱.
2) 随电子束照射, 自由电子逐渐向基底输运, EBIC和样品电流逐渐增大. 由于样品带电强度较弱, 有效表面出射电流和透射电流随电子束照射基本保持恒定.
3) 随着束能增大, 入射电子具有更大的入射深度, 透射电子电流逐渐增大至接近于束流值; EBIC随束能的升高而增大, 但束能较高时, 电子向下输运的电场强度逐渐减小, EBIC反而减小, 对于本文样品在约15 keV处呈现极大值. EBIC等均随束流呈现近似正比例关系.
论文研究结果对于提高基于EBIC效应的样品检测可靠性以及降低扫描电镜、透射电镜观测中的带电效应具有指导意义和实用价值.