摘要:由于空间电荷效应的限制, 产生百飞秒的极短电子脉冲是超快电子衍射技术的一大难点. 同时, 电子的穿透深度随着电子能量的增加而增加, 而电子的散射几率却具有相反的规律. 因而, 除了时间分辨的提升, 还需要可宽范围调节的电子能量以优化不同厚度样品对其的需求. 基于此, 提出并设计了一种新型超紧凑电子枪, 结合均匀场阴极和可移动阳极的配置, 可在10—125 kV加速电压范围内实现100 fs量级时间分辨率. 通过优化设计高压电极轮廓, 使得其轴上和整个阴极面的场增强因子在不同阴阳极间距下均小于约4%, 从而保证了不同加速电压下最大轴上场强均可达10 MV/m量级, 有效地抑制了电子脉冲的展宽效应; 进一步将阳极小孔设计成可放置致密电镜载网的阶梯孔, 一方面可将载网支撑的样品紧贴小孔后方放置, 最大程度上缩短了电子从阴极到样品的时间弥散, 同时也可以有效地减弱阳极孔对电子束的散焦效应, 提升电子束的横向聚焦性能.
关键词: 超快过程/
分子电影/
均匀场电极/
超短电子源

English Abstract

全文HTML

--> --> -->

原子级空间和时间尺度微观结构演变的实时观测一直是超快科学的巨大挑战之一. 结合了泵浦-探测技术和电子衍射技术的超快电子衍射(ultrafast electron diffraction, UED)是实现该目标的最有力的工具之一, 自20世纪90年代以来, 已被广泛应用于有机化学、光诱导相变、电荷密度波以及温稠密物质等的超快动力学研究^[1-11]. UED技术的核心是产生超短电子脉冲的电子枪. 目前, 利用最小化电子传播距离提升时间分辨的紧凑型直流电子枪因结构简单、无需压缩且运行稳定等优势, 是使用最广泛的电子枪^[3,12-15]. 然而, 它的性能却受到电子传播过程中的空间电荷效应和真空色散的限制, 并且在很大程度上取决于阴阳极之间的最高的均匀电场强度^[16,17]. 由于局部场增强导致高压打火现象, 直流型UED的最高加速场强被限制在约10 MV/m量级^[16]. 为了减小场增强效应, Rogowski^[18,19]电极是直流UED系统使用最多的均匀场电极之一, 其轮廓与沿着表面的等势面一致, 最高的电场强度位于电极中心, 特别适用于固定电极间隙的情形. 最近, Gerbig等^[14]精心抛光不锈钢电极, 在加速电压为40 kV和阴阳极间距为(3.5 ± 0.2) mm下实现了(11.4 ± 0.7) MV/m的高电场强度, 最终在接近单电子领域可获得半峰全宽为130 fs (full width at half maxima, FWHM)的超高时间分辨率. Waldecker等^[15]设计了一个新的椭球状电极, 并抛光了电子枪的所有表面, 最终获得了100 keV的最大电子能量, 在阴阳极距离为8 mm时场强可达12.5 MV/m.
除了时间分辨的不断提升外, 不同类型的样品及超快过程对电子能量也提出了不同的要求. 可调的电子束能量可以针对不同样品优化电子的穿透深度、散射几率以及由非弹性散射事件引起的损伤等性能^[19]. 探测电子的能量越高, 可研究的样品厚度也越厚, 如复杂的生物分子. 而低能电子具有更大的散射截面, 可在超薄样品中更有效地散射, 如石墨烯等二维材料^[20]. 因此, 针对二维材料到复杂的生物分子等不同类型的样品, 还需要UED在保持高时间分辨率的同时实现可调谐的电子能量来满足各种实验的要求. 为此, 则需要在改变加速电压的同时实现阴阳极间距可调. 然而, 随着阴阳极间距的变化, 由于电极几何形状的曲率引起的局部场增强往往导致高压打火, 尤其是在能量高于50 keV的情况. 这也就导致了目前UED几乎都工作在某个特定电压而不可以在保持最佳电子脉冲特性的前提下调节加速电压. 因此, 如何设计出一款场增强效应小的电压可调型均匀场电极具有重要意义.
本文设计了一款兼具100 fs级时间分辨和10—125 kV量级可调节加速电压的紧凑型台式超快电子衍射仪. 通过分析目前UED所涉及的三类均匀场电极, 即Rogowski, Bruce和椭球形电极的轴上和阴极面的场分布与场增强效应, 设计并优化了一种新型的均匀场电极, 该阴极是Rogowski和Bruce电极的折衷, 可在中心轴附近以及整个阴极面产生恒定的均匀场区域. 结合可移动阳极, 可在10 和125 kV之间调节适用的加速电压, 满足不同样品的需要; 且不同加速电压下场强均可达10—12.5 MV/m量级, 抑制了时间展宽, 可产生100 fs量级的电子脉冲; 此外, 阳极孔的正后方设计了5个样品孔以尽量减小阴极与样品之间的距离, 同时, 在样品孔中使用致密的透射电子显微镜(transmission electron microscope, TEM)载网也有利于减轻阳极孔的散焦效应.

2

-->

2.1.设计理论

在设计直流型超快电子枪的过程中, 阴阳极间的均匀电场至关重要. 对电子脉冲起主要作用的是阴阳极中心轴上的电场, 因此电极设计的总体目标就是在阴极中心区域以最小的阴阳极间距产生尽可能高的均匀电场强度并最大限度减小高压电极组件任何其他部分相对于中心理想电场的局部场增强效应. 理想均匀电场指的是无限大的两平行平板之间的电场, 可用电位差U除以平板间的间距d来表示$\left( {E = {U}/{d}} \right)$, 这也是目前直流型UED系统估计加速场强的方法. 而实际中, 任何相对于中心电场的局部场增强将会导致电极中心处最大场强的降低.
图1(a)所示为一种平面型电极轮廓截面, 其由一段长为R₀的平行线与一个半径为R_e的半圆组成. 其总半径R和厚度T可表示为
图 1 常见UED用电极截面　(a) 平面型; (b) Rogowski型; (c) Bruce型; (d) 椭球型
Figure1. Definition of the (a) Plane; (b) Rogowski; (c) Bruce; (d) elliptical electrode profiles for UED.

$\left\{ {\begin{aligned}& {R = {R_0} + {R_{\rm{e}}},}\\& {T = 2{R_{\rm{e}}}.}\end{aligned}} \right.$

然而, 由于简单的平面型电极的尺寸有限, 边缘的场增强效应很严重, 因此需要设计更好的电极轮廓以在中心区域与中心附近产生均匀场分布, 并抑制光电阴极和阳极之间所有点处的局部场增强效应. 均匀场电极设计的关键是适当弯曲光电阴极, 以尽量减少局部场增强的影响. 为此, 研究人员已经开发了Rogowski, Bruce和椭球型等不同的电极轮廓.
早在1923年, Rogowski^[19]就提出了一种解析电极几何形状, 由Rogowski轮廓部分和一个圆形部分组成, 其轮廓基本上沿着由有限板和无限平面组成的平板电极产生等位面, 如图1(b)所示. 典型的90° Rogowski剖面轮廓即与$\psi = {\text{π}}/2$等位面相对应, 可表示为

$ \left\{ {\begin{aligned} & {x = \frac{A}{{\text{π}}}\phi ,}\\ & {y = \frac{A}{{\text{π}}}\left( {\frac{{\text{π}}}{2} + {{\rm{e}}^\phi }} \right),} \end{aligned}} \right. $

其中?代表电力线, A为有限平面和无限地平面之间的间距.
Rogowski电极的总半径R和电极厚度T可表示为

$\left\{ {\begin{aligned}& {R = {R_0} + {R_{\rm{e}}} = {R_0} + \frac{{\sqrt 2 }}{{\text{π}}}A,}\\& {T = \frac{{2 + \sqrt 2 }}{{\text{π}}}A.}\end{aligned}} \right.$

随后, Bruce^[21]提出了一种经验性的电极方案. 如图1(c)所示, 整个Bruce电极截面轮廓可分为三个部分, 每个部分切向并入下一个部分, 从半径为R₀的线性部分开始, 随后是一段径向延伸距离为A的正弦部分, 并以圆形部分终止. 参照图1(c)的坐标系, 正弦截面轮廓可表示为

$y = - {R_{\rm{e}}}\sin \left( {\frac{x}{{{x_0}}}\frac{{\text{π}}}{2}} \right),$

其中x₀为横坐标中心, R_e为圆形半径.
Bruce^[21]电极的总半径R和电极厚度T可表示为

$ \left\{ {\begin{aligned} & {R = {R_0} + A + {R_{\rm{e}}} = {R_0} + A + \frac{2}{{\text{π}}}\frac{A}{{{\rm{cos}}{\alpha _o}}}{\rm{tan}}{\alpha _o},}\\ & {T = A \cdot {\rm{tan}}{\alpha _o} + {R_{\rm{e}}} = A \cdot {\rm{tan}}{\alpha _o}\left( {1 + \frac{2}{{\text{π}}}\frac{1}{{{\rm{cos}}{\alpha _o}}}} \right),} \end{aligned}} \right. $

其中R_e与x₀分别定义为${R_{\rm{e}}} = \dfrac{2}{{\text{π}}}{x_0}{\rm{tan}}{\alpha _o}$, $ {x_0} = $ $\dfrac{A}{{{\rm{cos}}{\alpha _o}}}$, α_o是过渡段的特征角.
椭球形电极^[15]的截面轮廓近似于Bruce电极. 不同之处在于第二段为椭圆形, 而非正弦截面, 如图1(d)所示. 这段不同的椭圆形部分可以表示为

$\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1.$

椭球电极的总半径R和电极厚度T可表示为

$\left\{ {\begin{aligned}& {R = {R_0} + b,}\\& {T = a + {R_{\rm{e}}}.}\end{aligned}} \right.$

借助于三维电磁场仿真软件 (computer simulation technology, CST), 首先准确建立了上述电极的物理模型, 其次模拟了各电极在不同尺寸下的场分布. 为了更好地比较, 假定所有电极具有相同的总半径, 对于Bruce和椭球状电极, 具有相同的平面区域. 此外, 从常用于UED的非对称型阴、阳极配置开始研究, 即具有弯曲截面的阴极与平面阳极的配置. 设计中, 在不同阴极电压(10— 125 kV)下, 阴阳极的距离均调节到最小可承受间距以最大化加速场, 从而保持最高时间分辨率. 在可实现的场强10—12.5 MV/m的条件下, 阴阳极间距最大值约为12.5—10 mm, 为了减少阳极和真空室尺寸引起的场畸变, 首先将阳极设置成直径为150 mm的平板进行高压电极设计, 同时尽可能保持光电阴极的紧凑性. 根据Rogowski, Bruce和椭球状三种电极的比较, 提出了一种新的电极, 该电极的几何轮廓是Bruce和Rogowski形式之间的折衷, 在中心区域具有接近均匀的轴向场分布, 并且在UED阴极截面的曲线部分没有明显的场增强效应. 在保证加速电场可实现最大化的同时, 可以通过调节阴阳极电位差, 并使用可移动阳极来精确调整间隙间距以获得不同的电子能量. 具体的研究结果如下.
2 -->

2.2.电极总半径对场增强的影响

一般来说, 高压电极尺寸越大, 场分布也均匀, 场增强越小. 但是, 高压电极的太大会严重影响整个电子枪的紧凑型, 一般需要在高压电极与腔室内壁之间预留2个电极尺寸以上以避免高压打火现象的出现. 因此, 设计时将电极的总半径限制在50 mm以下. 本文采用场增强因子(E–E_T)/E_T%来表征电极的场增强效应, 其中E为轴上或沿着阴极表面上的由于场增强效应产生的实际最大电场强度, E_T为理论设计的轴上电场强度. 在加速电压125 kV, 阴阳极间距12.5 mm的条件下模拟并比较了Bruce, Rogowski, 椭球形以及新电极的场分布. 图2(a)和图2(b)所示为三类常见电极结构(即90° Rogowski, Bruce和椭球型)和新电极的中心轴和沿阴极表面的场增强因子. 由图2(a)可知四种电极的轴上场增强效应均相对较小, 小于10%, 最大场增强效应均发生在阴极的曲面部分. 在总电极半径为30—50 mm的范围内, Bruce电极具有最优的轴上场增强性能, 均在2%以下. 对于沿整个阴极面上的最大场增强效应, 如图2(b)所示, 非均匀性Rogowski电极则相对较小, 在电极半径尺寸大于40 mm时场增强因子小于7%, 而Bruce电极和Elliptical电极均大于7%. 也就是说Bruce由于中心平面区域的存在而具有较好的轴上场分布, 而Rogowski电极曲线部分更优, 具有较小的场增强效应. 对于椭球状电极, 轴上和轴外场增强都相对比较高, 故不再考虑.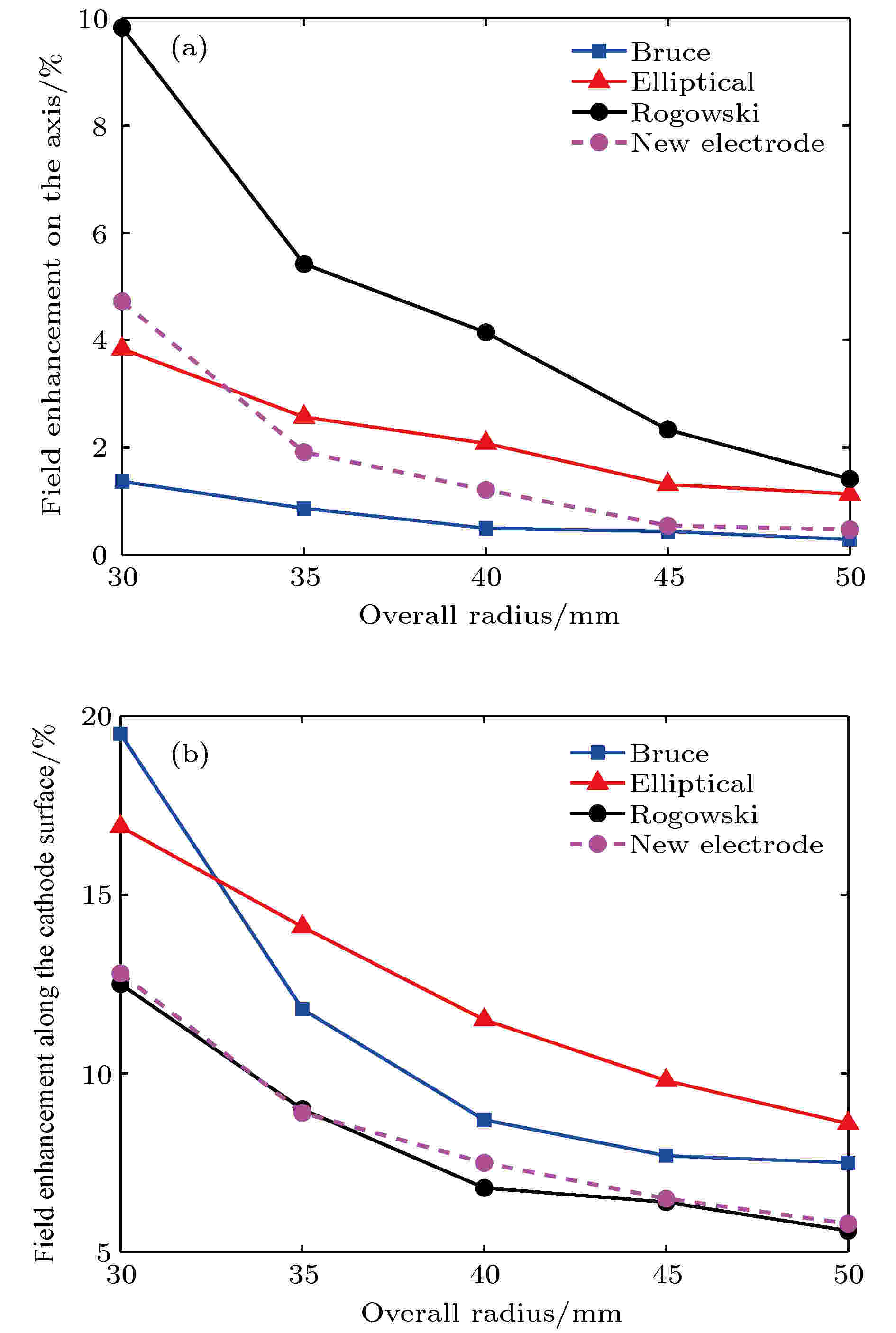
图 2 90° Rogowski, Bruce, 椭球型和新电极四类电极的场增强效应　(a)中心轴区域场增强因子; (b)沿阴极表面场增强因子
Figure2. Field enhancements of 90° Rogowski, Bruce, and elliptical electrode: (a) The central axis; (b) along the curved edge of cathode.

根据上述计算, 结合Bruce电极和Rogowski电极在各个区域的优势, 设计了一种新型均匀场电极, 将Bruce电极的中心部分与Rogowski电极的曲线部分相结合, 电极轮廓如图3所示. 新型电极的轴上与沿阴极表面的场增强因子如图2所示(紫色-方形线), 新电极的整个阴极面的场增强与Rogowski电极接近且远小于Bruce电极, 而沿着轴上的非均匀性比Rogowski电极的小很多. 此外, 新电极中心采用平面型更便于精确加工制作电极, 同时有利于安装背照式光电阴极.
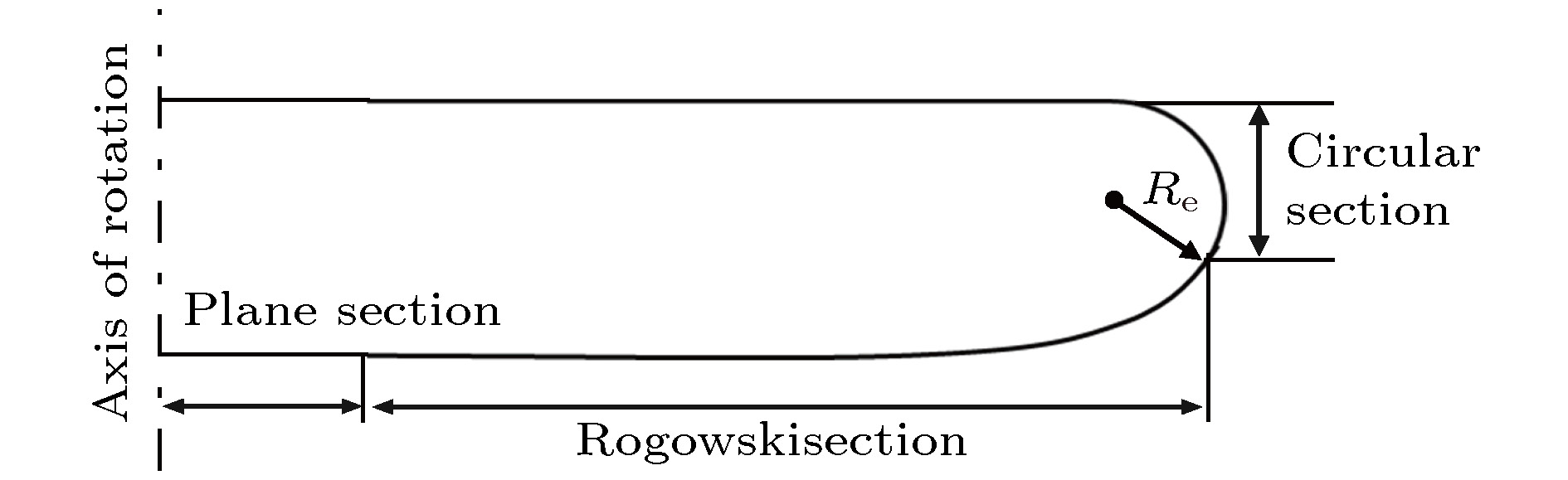图 3 新电极截面轮廓
Figure3. Geometry of the new high voltage electrode.

另外, 从图2可以看出电极尺寸越大场增强效应越小, 但在总半径大于45 mm时, 场增强效应的变化相对较小. 鉴于系统结构紧凑性与场增强效应的折衷, 电极总半径选择45 mm最为合适. 此时, 新电极具有最优的轴上和轴外场分布性能. 为了研究中心平面区域尺寸对场增强的影响, 固定新电极总半径而扫描平面区域的半径, 如图4所示, 可以看到轴上场增强因子随着平面区域的增加而减小, 而对于轴外沿阴极曲面的场增强效应, 在平面区域的半径超过7 mm后迅速上升. 考虑到光电阴极基底为光学镜片, 故选择平面区域尺寸半径6.35 mm.
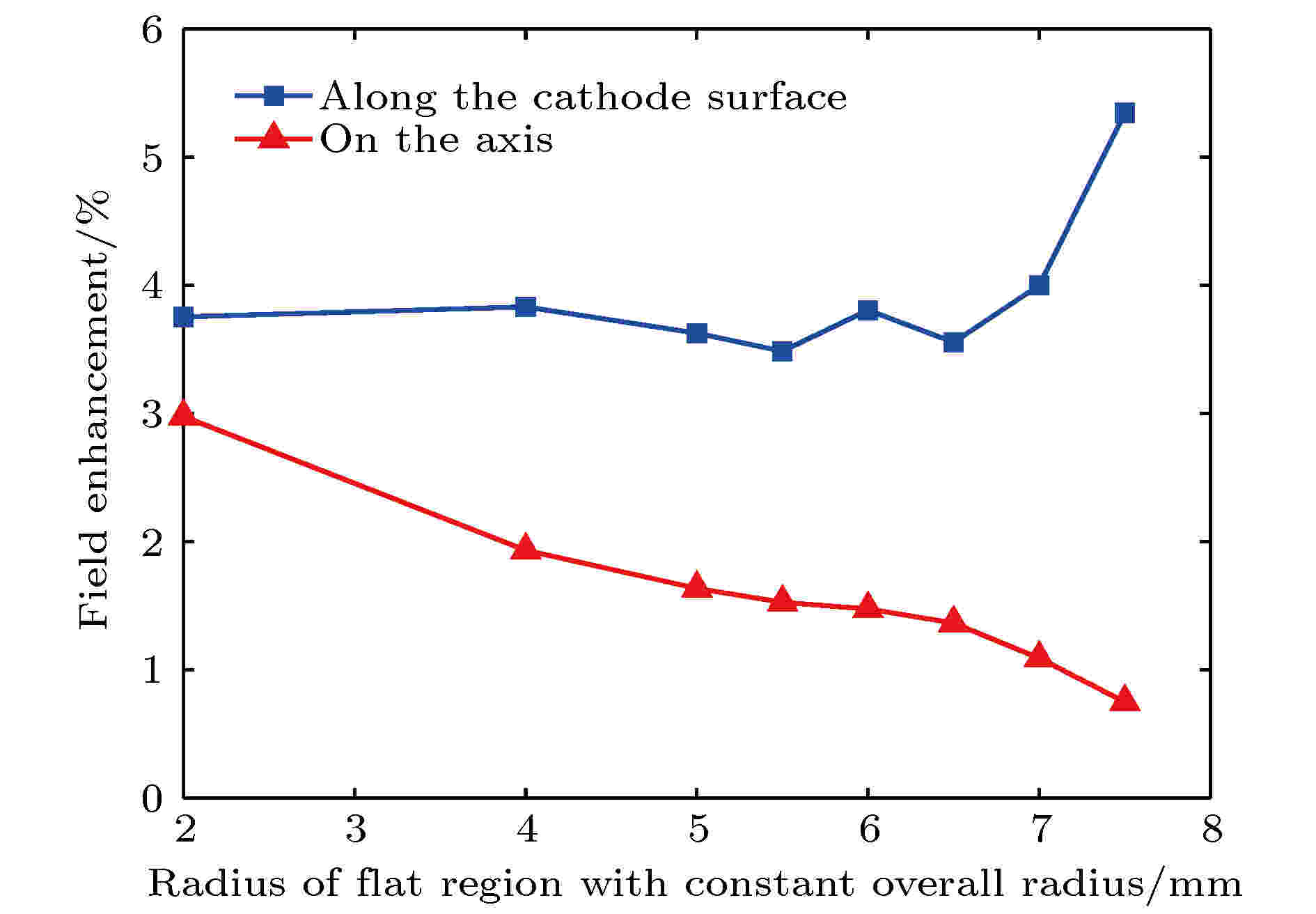图 4 总半径固定时中心平面区域尺寸变化对场增强的影响
Figure4. Effect of dimensional change of center plane area on field enhancement when the overall radius is constant.

2 -->

2.3.阴阳极间距(加速电压)对场增强效应的影响

根据上述讨论设置阴极平面区域半径值R₀ = 6.35 mm, 总半径R = 45 mm, 在不同的阴阳极间距下扫描计算中心轴与阴极表面上的场增强特性. 在调节阴阳极间距的同时, 其电位差也随之改变, 以保证电场强度恒定为约10 MV/mm. 图5所示为各个电极在不同阴阳极间距下轴上与沿着电极表面和轴上的场强因子. 由图5可知, 三种电极的轴上场增强相对较小, 而曲面部分场增强相对较大, 尤其是在间距大于约5 mm之后, 且随着阴阳极间距的增加而增大. Rogowski轴上场增强最大, 而Bruce电极和新电极的轴上场增强很小(1%内). 可以看到在间距小于15 mm时(即加速电压小于150 kV), Bruce电极和新电极几乎没有轴上场增强效应, 而沿着阴极表面, Bruce电极的最大场强比较大且增长较快. Rogowski电极虽然具有最小的轴外场增强因子, 但它的轴上场分布均匀性最差, 更重要的是它有一个不可避免的缺点, 即它的分段实际上是非光滑连接, 没有中心平面区域, 而对于背照式平面阴极, 往往需要在电极中心开一圆孔来安装阴极, 这将导致交接点处场增强明显增大, 特别是在100 kV以上的高压. 具有中心平面区域的新电极的综合性能较好, 在低电压区和高压区场增强效应均相对平缓, 在150 kV以下轴上的最大场增强小于 0.1%, 整个阴极面的场增强效应小于4.5%. 如前所述, 新电极在轴上和阴极面的场增强分别接近Bruce电极和Rogowski电极, 总体上具有最佳的性能.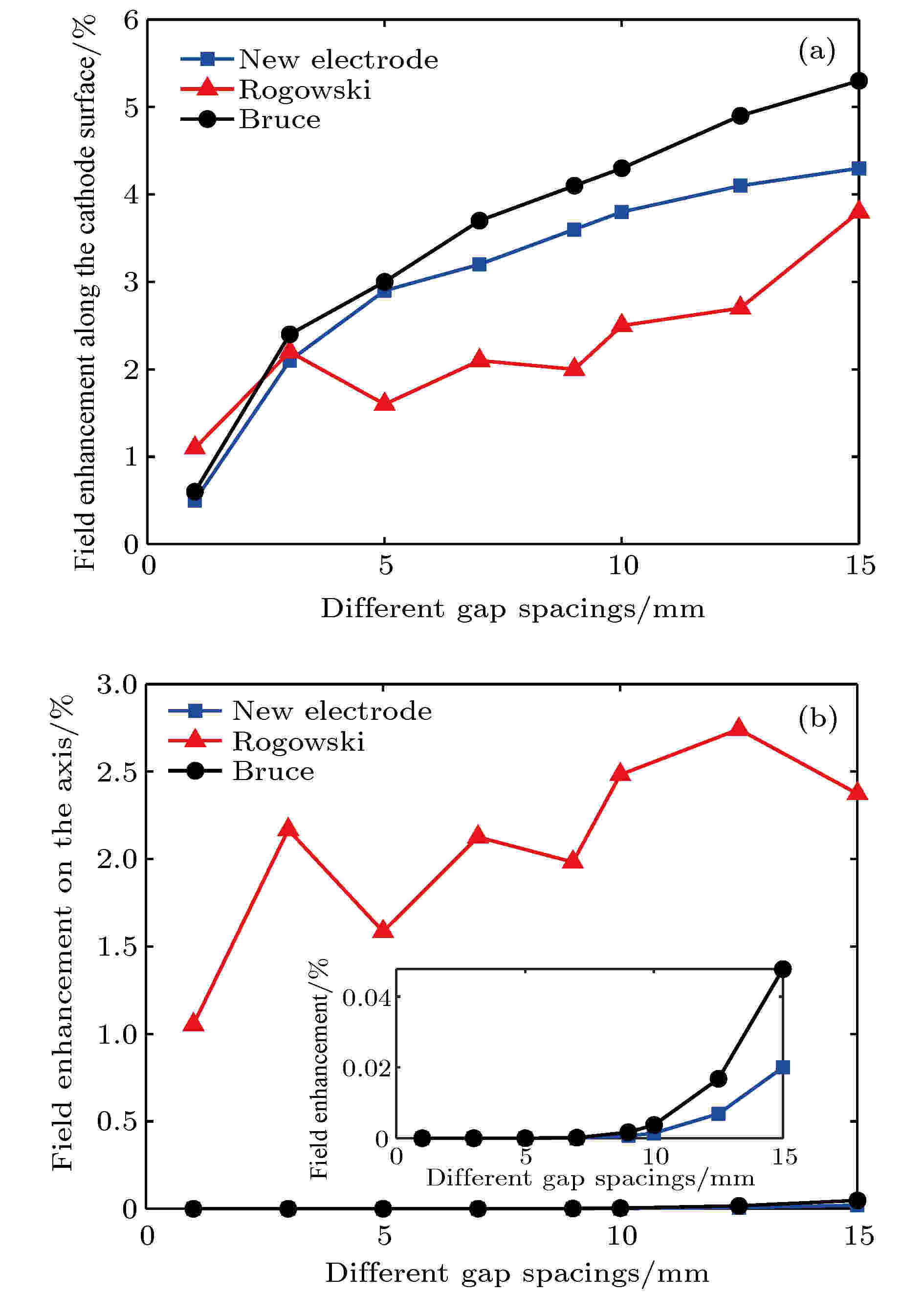
图 5 不同阴阳极间距下的场增强效应　(a) 沿阴极面的场增强; (b)轴上场增强
Figure5. Field enhancement effect at different cathode-anode spacings: (a) Field enhancement on the axis; (b) field enhancement along the cathode surface.

2 -->

2.4.阴阳极配置对场分布的影响

一般情况下, UED电极采用曲面阴极电极与平面阳极电极的非对称型配置, 然而, 根据场增强理论, 采用曲面电极对称配置时场分布会更均匀, 所谓对称配置, 即阳极采用与阴极完全相同的结构. 图6比较了相同电极参数下最高加速电压下(125 kV)非对称配置和对称配置对场增强效应的影响. 非对称配置时将阳极设置成前文所述的直径150 mm的平板. 显然, 非对称配置的场增强效应比对称配置时大, 但在125 kV电压以下时, 二者相差很小. 考虑到加工和装配简单, 一般选择平面阳极结构.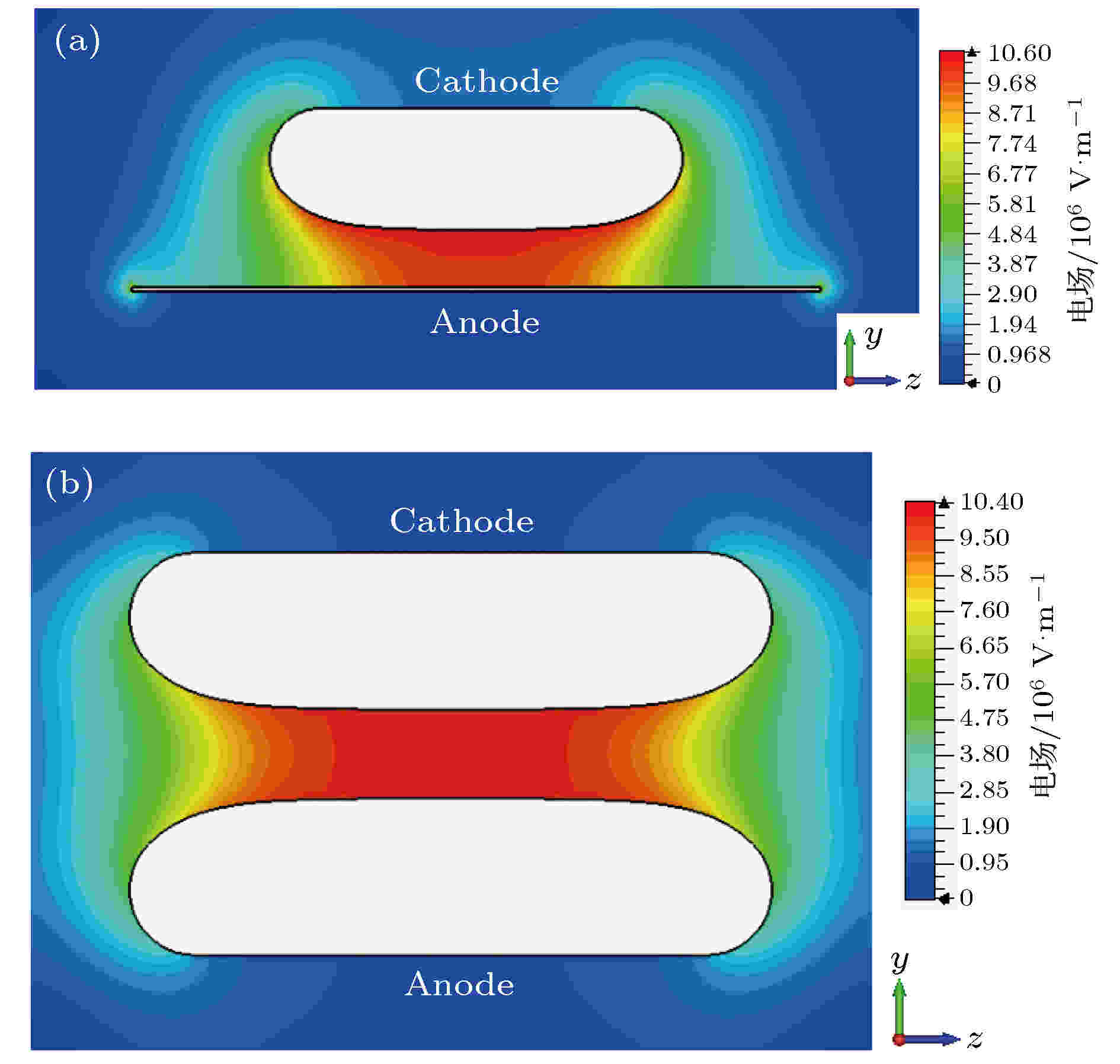
图 6 电极配置对场增强的影响　(a) 非对称配置; (b) 对称配置
Figure6. Influence of the electrode configuration on field enhancement: (a) Asymmetric electrode configuration; (b) symmetric electrode configuration.

2 -->

2.5.阳极小孔设计

超快电子源的特性与其受到的电磁场作用密切相关. 对于超紧凑型UED, 由于结构简单, 因此, 最为关键的便是阴阳极之间的电场分布. 在详细研究了阴阳极间场增强效应之后, 阳极小孔处的场分布成为另一关注点. 因实验透过电子需要, 阳极部分不可避免地需引入了一个小孔, 该小孔不仅会减弱中心轴上的电场强度, 还会造成电子束斑的横向发散. 如图7(a)所示, 可以清晰地看到小孔处的电场分布有类似于凹透镜的使电子束散焦的作用. 为了减小阳极小孔处的电场畸变, 将阳极小孔后端设计成标准TEM载网(直径3 mm)大小的阶梯孔, 引入不同目数的载网进行研究. 此处目数指的是在每2.54 mm范围内网格孔的数量, 目数越大网格孔越多且越小. 图7(b)为50目载网装载于阳极小孔后方的电场分布, 对比图7(a), 导电载网的引入大幅减小了小孔处的场畸变. 图7(c)所示为小孔处沿x轴的x方向的电场分布, 随着载网目数的增加, 场分布越来越均匀, 当载网目数大于150时, 电场分布基本不再改变, 因此实验中只要载网目数大于150目, 便可以很好的消除阳极小孔处的散焦效应.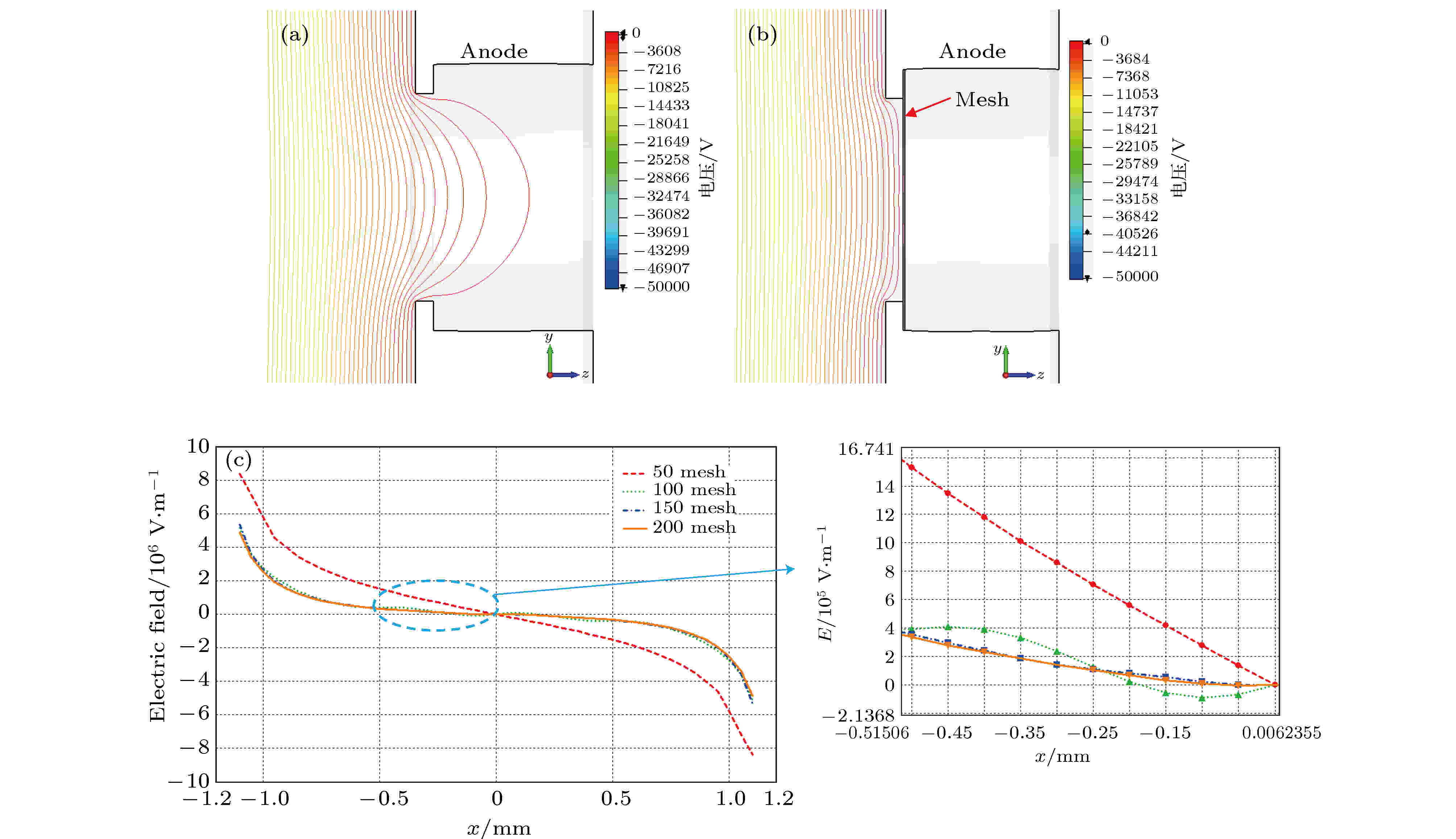
图 7 小孔处的电场分布　(a) 无载网; (b) 50目载网; (c) 不同目数载网的对比
Figure7. Electric field distribution at the anode pinholes: (a) Without TEM grid; (b) 50 mesh TEM grid; (c) comparison of different meshes of TEM grid.

该载网除了可以减小电子束发散特性, 还可以在其背面放置另一带有样品的载网进行UED实验. 如此一来, 阴极至该样品的距离几乎等同于阴阳极间距, 有效抑制了电子脉冲的展宽, 尤其是对于低能电子十分有利. 为了减少换样、打开真空系统等操作, 提高实验效率, 在阳极小孔正后方设置了5个对称分布的载网孔, 用于放置纯载网或载网支撑的超薄样品, 如图8所示. 计算发现在所设计的5个小孔范围内横向移动阳极对样品孔场分布的影响可以忽略不计, 而实际系统中阳极整体可放置于一个可高精度控制的三维移动平台上.
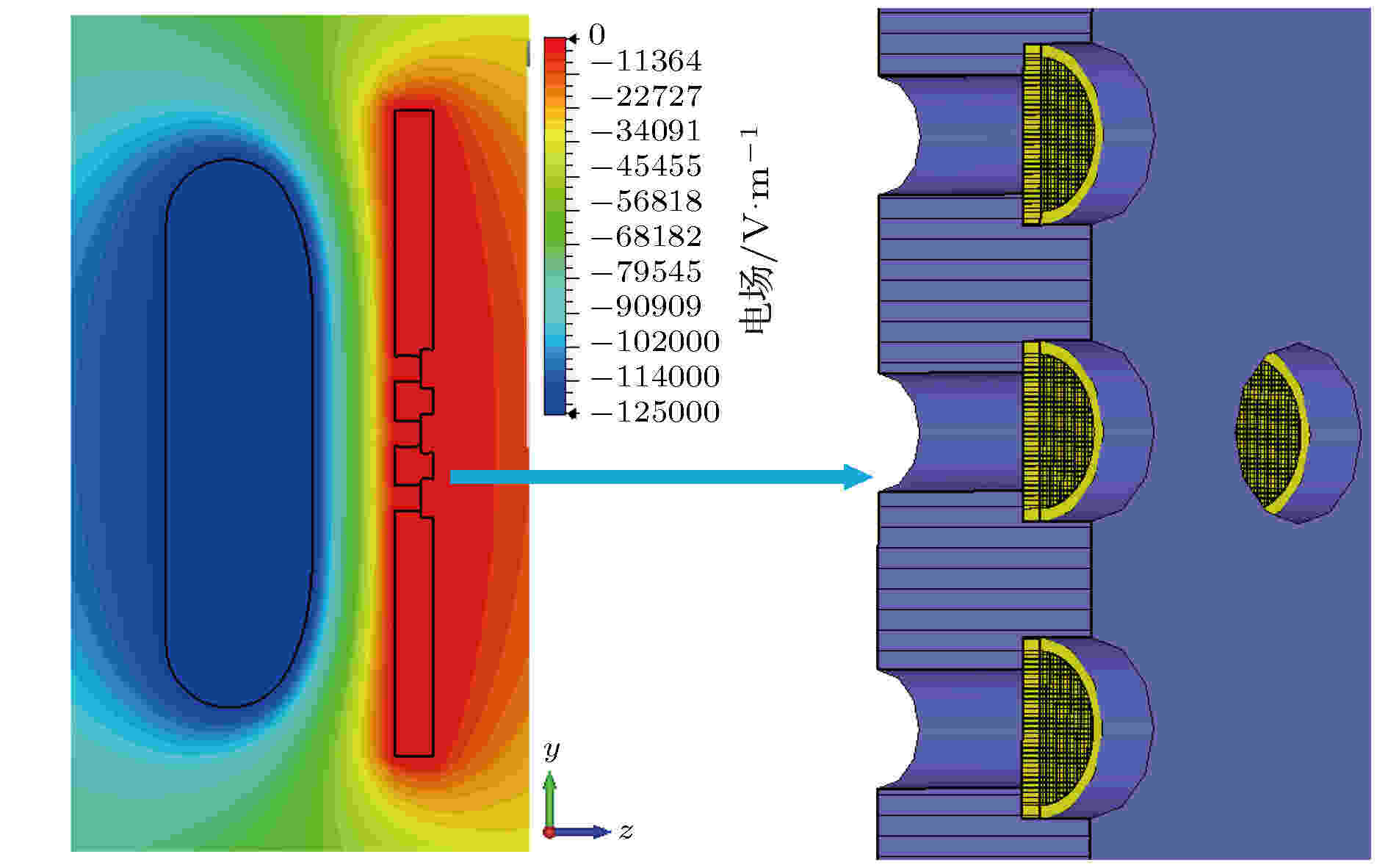图 8 阳极小孔设计
Figure8. Design of anode pinholes.

2

-->

3.1.系统结构

基于以上均匀场电极和可移动阳极的研究, 进一步模拟了超紧凑型UED系统在最低10 kV和最高125 kV加速电压时的电子束特性. 该紧凑型UED系统原理如图9所示, 主要由飞秒激光器、抽运-探测光路、阴阳极、样品托、三维位移台、磁透镜、探测系统等组成. 在新设计中, 样品可以放置于两个位置, 其一是紧贴着阳极设置, 且将磁透镜置于样品之后, 从而最大限度地缩短了电子从阴极出射到样品处的行程, 使得真空色散和库仑排斥造成的时空展宽最小化, 有效提高了时间分辨率, 此位置主要是针对低电压情形设计. 由于样品与阴极距离极短, 因此在二者中间不需要磁透镜, 简化了系统的调节过程, 而且将磁透镜置于样品之后荧光屏之前可用来提高衍射图分辨率. 其二是紧贴磁透镜之后放置, 这种设置虽然稍微增加了阴极-样品距离, 但是对样品的可操作性更好, 而且在较高加速电压下, 样品的微小后移对时间分辨率影响不大.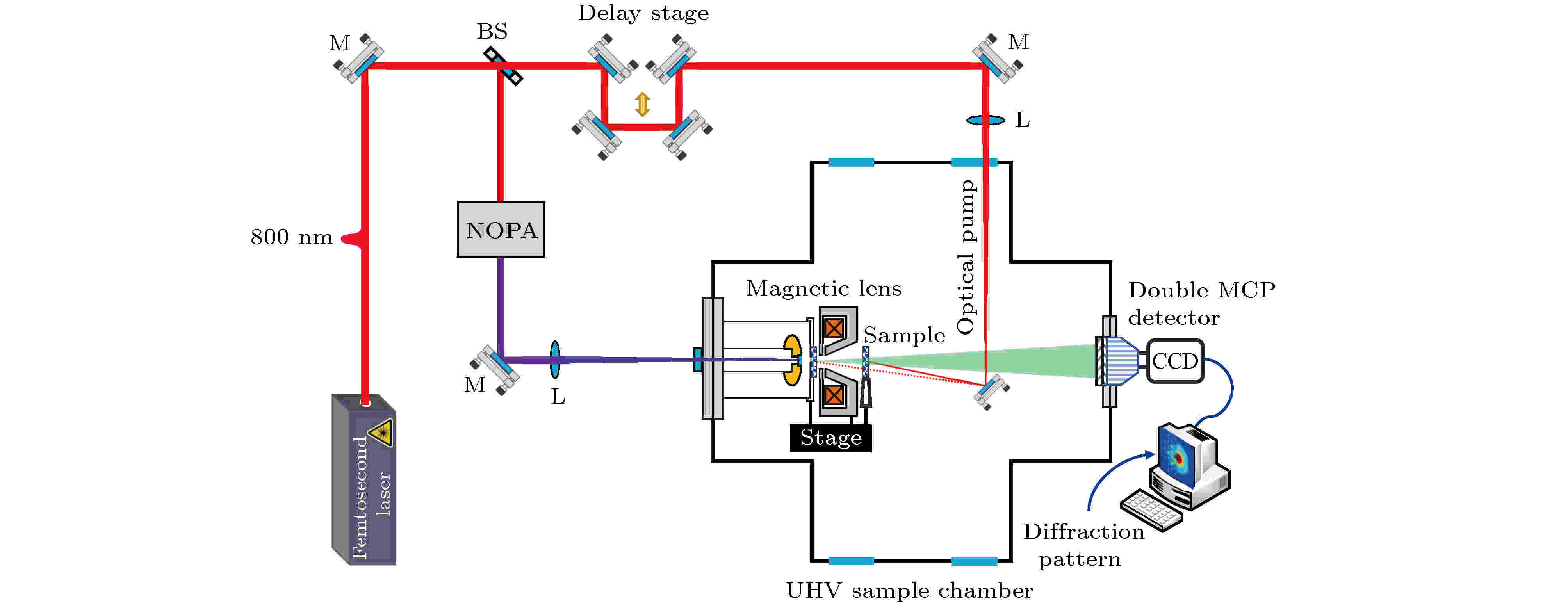
图 9 间距可调型超快电子衍射仪示意图
Figure9. Schematic diagram of anode movable ultrafast electron diffractometer.

2 -->

3.2.时空分辨特性

借助粒子轨迹追踪软件(general particle tracer, GPT)^[22]对系统性能进行了表征, 利用五阶龙格-库塔法模拟追踪了电子运行轨迹, 计算了电子束的时空特性, 并且研究了这些性质随主要参数变化的规律. 为了精确模拟空间电荷效应的影响, 采用粒子相互作用的N体模型模拟了空间电荷效应, 该模型下计算时间与粒子数量呈线性关系, 计算较快, 并且对于小能量弥散的情形十分可靠. 其次, 基于输入激光束斑与阴极的光电发射模型, 定义了电子源. 实验中采用波长约266 nm的紫外激光脉冲, 根据阴极的功函数, 便可估算初始电子能量弥散. 计算中将会研究不同电子数目下的性能, 当电子数目较大时, 引入宏粒子以提高计算效率. 因激光脉冲在时间上具有高斯形状, 所以电子的初始时间分布也采用高斯分布. 初始发射速度通过相对论参数定义, 它们都具有相同的速度, 各速度分量均匀地分布在半球上. 电子在空间方向的分布采用与激光束斑分布相同的高斯分布, 如图10所示为电子源的空间分布, 其中包含的电子总数目为10000, 半径为47 μm (FWHM).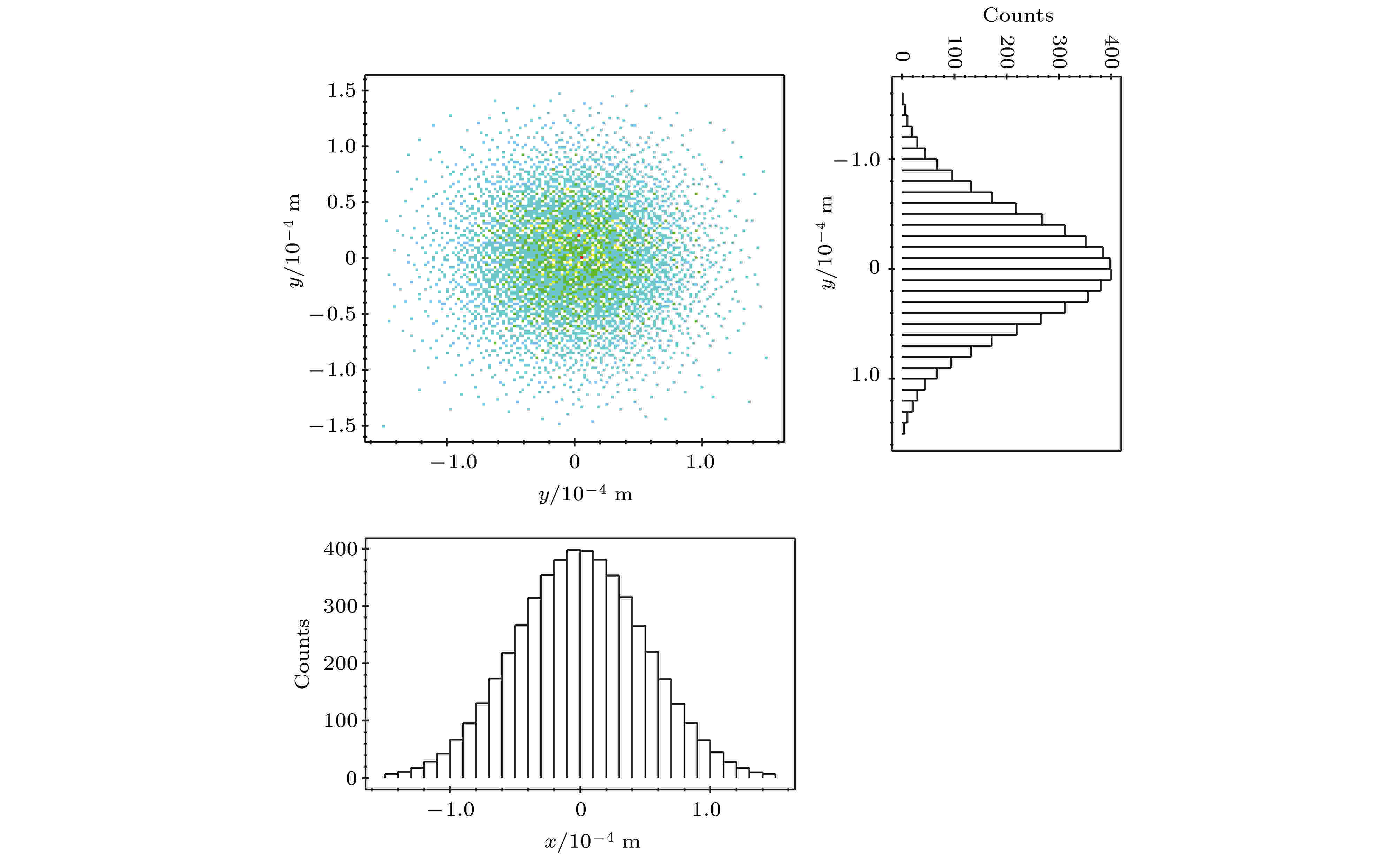
图 10 时间为0时电子源的空间分布
Figure10. Spatial distribution of electron source at time = 0.

设定了电子源的时间、速度和空间分布之后, 便可以模拟电子的运行轨迹, 计算系统主要性能参数. 为了分析该紧凑型UED在不同加速电压、电子初始能量和电子数目下的性能参数, 研究了不同参数下的电子脉冲脉宽和束斑尺寸的变化. 图11所示为不同加速电压V、初始能量弥散?E以及电子数目n对电子脉宽的影响. 其中, 图11(a)为加速电压为10 kV时, 初始能量弥散分别为0.1 和0.6 eV以及电子数目为1000和10000时, 电子束长在运行过程中的变化规律. 由于在电压为10 kV的情况下, 阴阳极间距约为1 mm, 因此图11中所选范围为z = 0—5 mm, 可以看出在相同初始能量弥散下, 电子数目越多, 电子脉冲展宽越快, 这是受到空间电荷效应的影响, 与预期一致. 对于相同电子数目, 不同初始能量弥散, 如n = 1000时对应的蓝色实线与紫色虚线所示, 可以看出小的初始能量弥散在最初有助于电子脉长的减小, 但当运行距离逐渐增加时, 较大的初始能量弥散更有利于抑制电子脉冲在纵向的快速展宽, 同样可以在n = 10000时得到相同的结论. 可见对于较长系统, 一味减小初始能量弥散并没有优势. 图11(b)所示为加速电压为125 kV时电子初始能量弥散与电子数目对电子脉冲长度的影响, 类似地, 受到空间电荷效应的影响, 电子数目越多, 电子束纵向展宽越严重. 图11(c)与图11(d)分别对应图11(a)和图11(b), 但具有更大的范围以观察电子运行更远距离后的效果. 从图11(d)中可明显观察到在电子运行距离较远时, 或阴极-样品间距较大时, 初始电子能量弥散适当增大反而有利于电子脉冲长度的减小.
图 11 加速电压、初始能量弥散以及电子数目对电子脉宽的影响　(a) V = 10 kV, z = 0?5 mm; (b) V = 125 kV, z = 0?20 mm; (c) V = 10 kV, z = 0?20 mm; (d) V = 125 kV, z = 0?100 mm
Figure11. Effect of accelerating voltage, initial electron dispersion and number of electrons on the length of the electron pulse: (a) V = 10 kV, z = 0?5 mm; (b) V = 125 kV, z = 0?20 mm; (c) V = 10 kV, z = 0?20 mm; (d) V = 125 kV, z = 0?100 mm.

图12为不同加速电压、初始能量弥散以及电子数目对电子束斑尺寸的影响. 分别统计了加速电压为10, 125 kV, 初始能量弥散为0.1, 0.6 eV, 电子数目为1000, 10000时的电子束斑尺寸. 显然, 电子数目越多, 束斑尺寸展宽越快, 电子初始能量弥散越大, 束斑尺寸展宽越快, 电子加速电压越小, 束斑尺寸展宽越快.
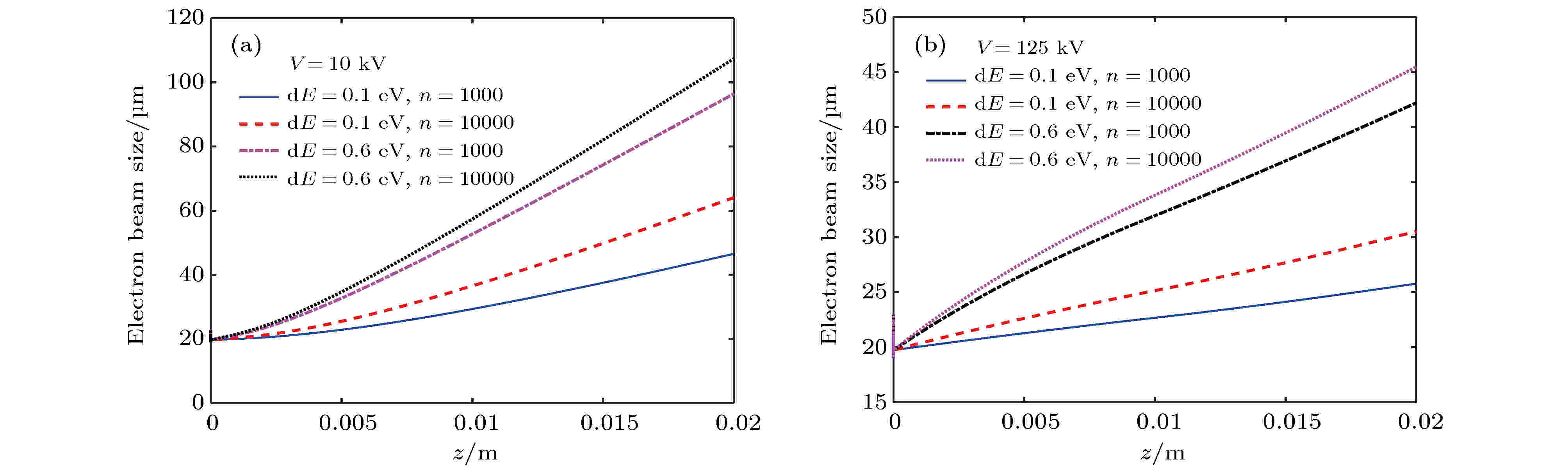图 12 加速电压、初始能量弥散以及电子数目对电子束斑尺寸的影响　(a) V = 10 kV, z = 0?0.02 m; (b) V = 125 kV, z = 0?0.02 m
Figure12. Effect of accelerating voltage, initial electron dispersion, and number of electrons on beam spot size: (a) V = 10 kV, z = 0?0.02 m; (b) V = 125 kV, z = 0?0.02 m.

2 -->

3.3.磁聚焦透镜的影响

上面分析了样品紧贴阳极时的情况, 但该系统的另一种工作模式便是类似于普通紧凑型UED, 即样品置于磁透镜后的情况. 此时, 系统一般工作在高电压模式(125 kV), 在阳极之后、样品之前设置磁透镜以约束电子束的横向发散. 图13为不同聚焦磁场下对应的电子脉冲长度的变化, 图13(a)和图13(b)分别对应电子数n = 1000与n = 10000的情况(初始能量弥散0.6 eV). 由图13可见, 不同聚焦透镜磁场强度对电子脉冲的纵向展宽的影响较小, 只有当系统较长时才有一定的影响, 且对电子数目较多的情况影响更大. 此时样品大致位于0.03 m处, 即使电子束达到10000个, 系统仍具有百飞秒量级的时间分辨能力.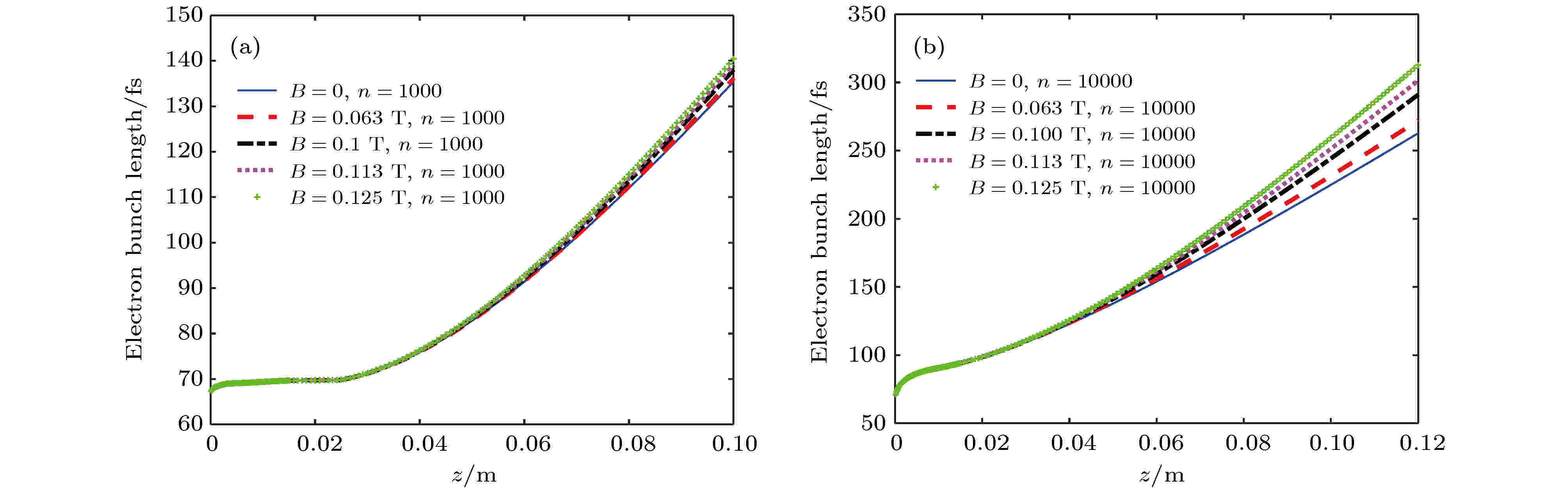
图 13 磁透镜对电子脉冲长度的影响　(a) n = 1000; (b) n = 10000
Figure13. Effect of magnetic lens on electronic pulse length: (a) n = 1000; (b) n = 10000.

图14所示为不同聚焦磁场下对应的电子束斑尺寸的变化, 图14(a)和图14(b)分别对应于电子数n = 1000与n = 10000的情形. 在B = 0.125 T时, 图14(a)和图14(b)两种情况下都实现了电子束在z = 0.01—0.06 m的范围内平行聚焦的现象, 在z > 0.07 m后, 由于空间电荷效应的影响继续展宽. 而对比图14(a)和图14(b)不难发现在磁透镜的聚焦作用下, 电子数目的增加对电子束横向尺寸的影响大大减小, n = 1000与n = 10000时, 电子束横向聚焦效果基本相同, 有效抑制了空间电荷效应对电子束横向展宽的影响.
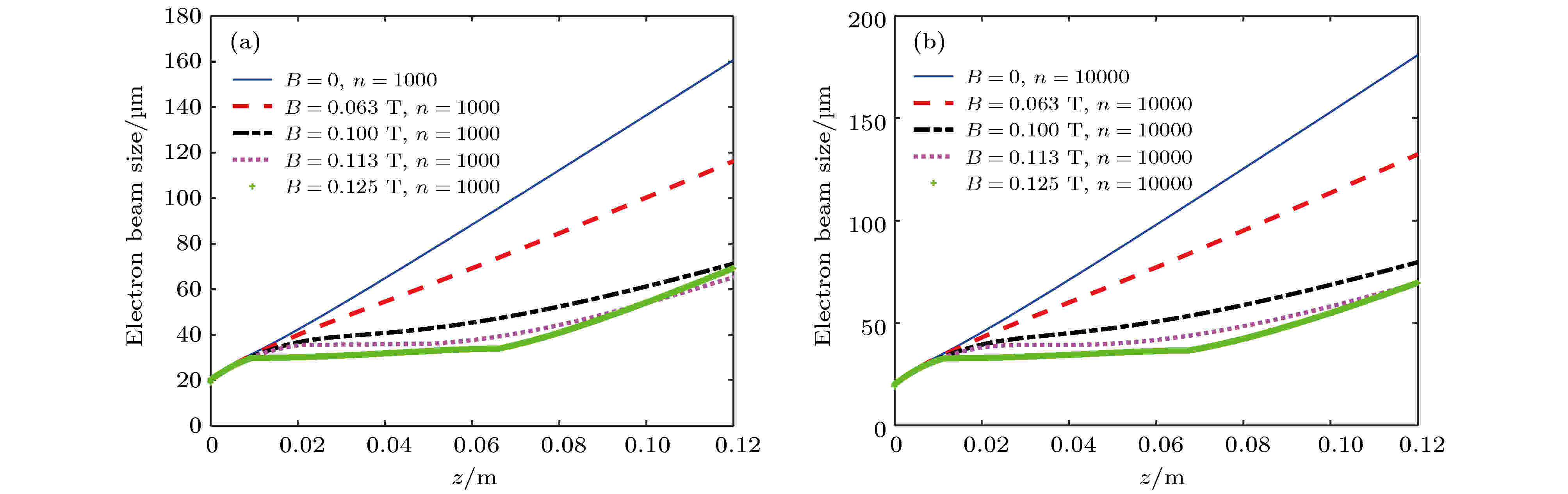图 14 磁透镜对电子束斑尺寸的影响　(a) n = 1000; (b) n = 10000
Figure14. Effect of magnetic lens on beam spot size: (a) n = 1000; (b) n = 10000.

为了设计出适合在宽电压范围、可调阴阳极间距、小型真空室等条件下使用的紧凑型电极形状, 研究了目前UED所涉及的三类均匀场电极: Rogowski, Bruce和椭球形电极的轴上和阴极面的场分布与场增强效应, 通过分析比较优化了一种新型的均匀场电极. 该电极的优化设计使得场增强因子在轴上和轴附近低于0.1%, 在整个阴极面上小于约4%, 可有效避免高压打火问题, 在10和125 kV之间均可实现约10 MV/m的最大直流加速场强. 此外, 在可移动阳极的正后方设计了5个样品孔, 以尽量减小阴极与样品之间的距离, 抑制时间展宽; 同时, 在样品孔中使用致密的TEM载网有效减弱了阳极孔的散焦效应. 本文采用超紧凑型设计缩短电子传播距离, 优化高压电极形状, 提高加速电压等途径, 可产生100 fs量级的10—125 keV电子脉冲, 适用于从超薄单层材料至生物样品的超快动力学研究, 为推动国内外, 尤其是国内的材料科学、凝聚态物理和生物医学等相关领域的发展提供有力工具.