全文HTML
--> --> -->
除了通过新的制备技术来提高材料的热电性能外, 掺杂也是提高材料热电性能的有效途径. 稀土元素被认为是提高Bi2Te3基合金热电性能的重要的掺杂元素[14,15], 因此, 深入研究稀土元素掺杂对n型Bi2Te3基合金的晶体结构和热电性能的作用机制就显得非常重要. 但是, 目前关于采用高压烧结技术制备稀土元素掺杂的n型Bi2Te3基合金的研究还鲜见报道. 本研究采用高压烧结技术制备了稀土元素Tb掺杂的Bi2Te2.7Se0.3块体材料, 系统研究了Tb不同的掺杂量对Bi2Te2.7Se0.3材料的晶体结构及热电性能的影响, 以期通过Tb掺杂提高Bi2Te2.7Se0.3材料的ZT值及ZTmax的发生温度, 从而制备出可用于发电领域的高性能的n型Bi2Te3基材料.
采用X射线衍射分析仪(XRD, D/max 2500)表征高压烧结样品的物相. 采用场发射扫描电子显微镜(FE-SEM, JSM-7001F)对样品的显微组织形貌进行观察. 在氩气气氛保护下于热电性能测试仪上测量样品的Seebeck系数和电导率. 热导率κ根据实测的热扩散系数λ, 定压比热容cp及密度d, 根据公式
3.1.样品的物相及显微形貌分析
图1是采用高压烧结技术制备的Tb不同掺杂量的XRD图谱. 通过与标准PDF卡片(PDF#50-0954)比对可知, 样品的衍射峰与Bi2Te2.7Se0.3的标准衍射峰峰位吻合, 这表明高压烧结制备的样品其主晶相为Bi2Te2.7Se0.3, 且未发现Tb单质的衍射峰, 说明Tb已进入Bi2Te2.7Se0.3的晶格, 实现了掺杂的目的. 此外, 从图1还可看到通过高压烧结制备的样品的衍射峰峰形明显宽化, 说明样品由很多细小的晶粒组成, 根据衍射峰的数据, 计算得到高压烧结样品的晶粒尺寸为29.77 nm.
图 1 高压烧结样品(Bi1–xTbx)2(Te0.9Se0.1)3 (x = 0, 0.002, 0.004, 0.008)的XRD图谱Figure1. XRD patterns of the (Bi1–xTbx)2(Te0.9Se0.1)3 (x = 0, 0.002, 0.004, 0.008) HPS samples.
根据衍射峰的数据, 计算了Tb不同掺杂量的高压烧结样品的晶格常数, 结果列于表1. 从表1可以看出样品的晶格常数a和c随着Tb掺杂量的增加而增大, 从而导致样品的晶胞体积随着Tb掺杂量的增加而变大. 原因在于Tb原子半径为1.78 ?, 较Bi (1.70 ?)大, 另外由于超高压力的作用, 使样品晶格发生了畸变, 这说明了稀土元素Tb微量的掺杂和高压对Bi2Te2.7Se0.3晶体结构的作用.
| Sample | x = 0 | x = 0.002 | x = 0.004 | x = 0.008 |
| a/? | 4.3748 | 4.38086 | 4.38205 | 4.38468 |
| c/? | 30.3456 | 30.34931 | 30.35013 | 30.35389 |
| V/?3 | 502.96 | 504.41 | 504.70 | 505.37 |
表1(Bi1–xTbx)2(Te0.9Se0.1)3 (x = 0, 0.002, 0.004, 0.008)样品的晶格常数
Table1.Lattice constants of (Bi1–xTbx)2(Te0.9Se0.1)3 (x = 0, 0.002, 0.004, 0.008).
图2给出了当Tb掺杂量为x = 0.004时高压烧结样品的高分辨微观形貌(FE-SEM)照片. 由图2可见, Tb掺杂的高压烧结样品由众多细小晶粒团聚而成, 这与XRD衍射峰宽化的结果一致, 即采用高压烧结技术能制备出纳米晶块体材料. 高压烧结形成纳米晶的机理在我们以前的工作中已经进行了阐述[16]. 高压烧结技术在实现样品良好烧结并获得高致密度的同时, 可以有效地抑制晶粒长大. 致密的微结构有利于获得良好的电学性能, 而细小的晶粒可以使声子散射增强, 降低材料的晶格热导率, 从而提高材料的ZT值.
图 2 Tb掺杂量为x = 0.004的高压烧结样品(Bi1–xTbx)2(Te0.9Se0.1)3的FE-SEM照片Figure2. FE-SEM of the (Bi1–xTbx)2(Te0.9Se0.1)3 HPS sample (x = 0.004).
2
3.2.Tb成分调控对热电性能的影响
图3给出了Tb不同掺杂量的高压烧结(HPS)样品的电导率随温度变化的关系. 从图3可见所有的HPS样品的电导率均随温度的升高而减小, 表现出简并半导体的导电行为. 未掺杂样品的电导率在室温下是60.82 × 103 S/m, 随着Tb掺杂量的增加, 样品的电导率呈现出增大的趋势. 当Tb掺杂量为x = 0.008时, 样品的电导率于298 K时取得最大值为105.99 × 103 S/m. 相较于未掺杂的Bi2Te2.7Se0.3样品, 增幅达到约74%.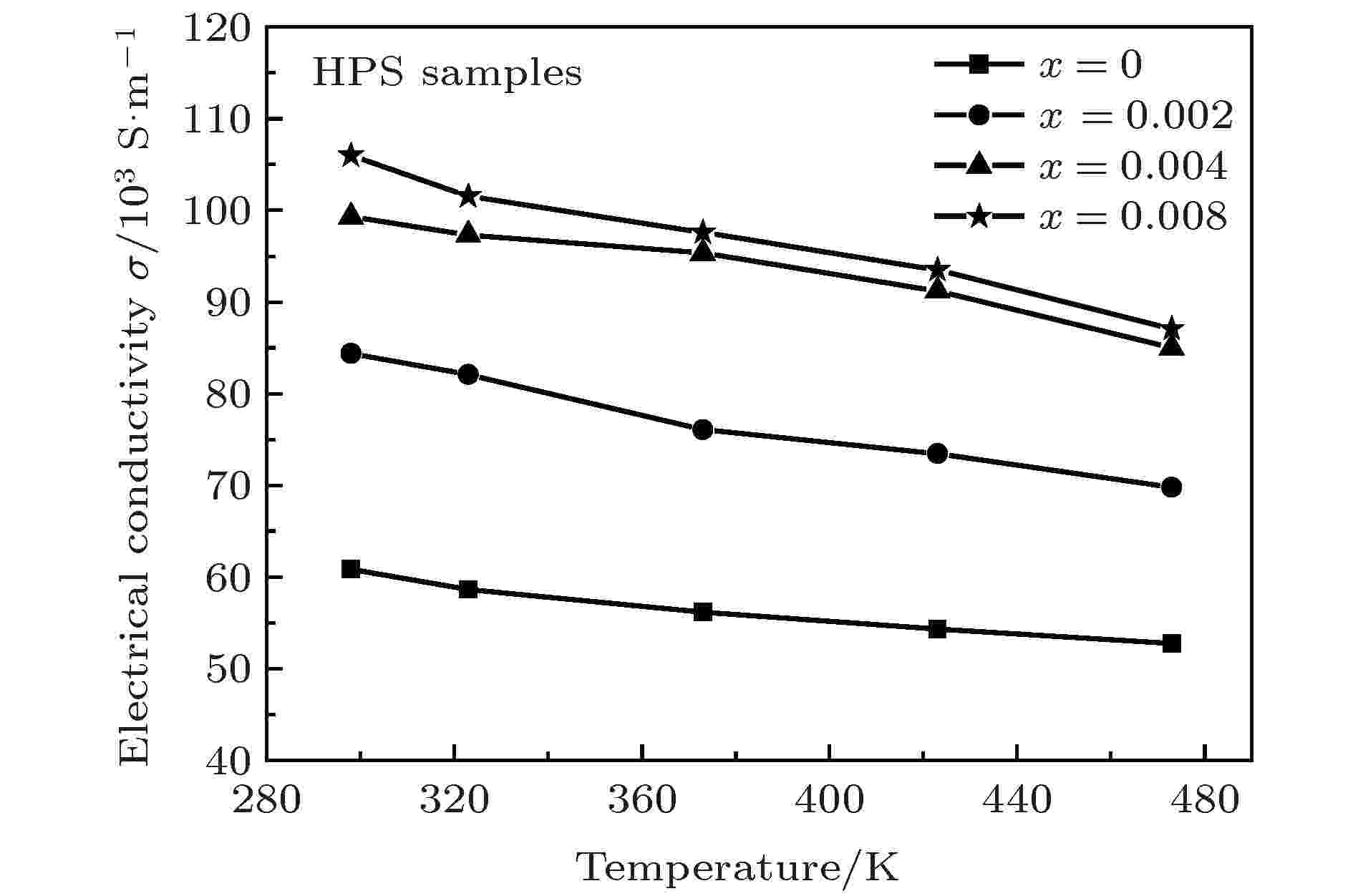
图 3 Tb不同掺杂量的高压烧结样品的电导率随温度的变化Figure3. The temperature dependences of electrical conducti-vities for the HPS samples doped with different Tb contents.
为了进一步研究Tb掺杂量对样品电输运性能的影响, 测试并计算了(Bi1－xTbx)2(Te0.9Se0.1)3系列样品的载流子浓度和载流子迁移率, 列于表2. 其中n为样品的载流子浓度, μ为载流子迁移率.
| Samples | Carrier concentrationn/1019 cm–3 | Carrier mobility μ/cm2·V–1·s–1 |
| x = 0 (HPS) | 1.92 | 197.98 |
| x = 0.002 (HPS) | 3.95 | 133.53 |
| x = 0.004 (HPS) | 6.51 | 95.31 |
| x = 0.008 (HPS) | 7.17 | 92.39 |
| x = 0.004 (Annealed) | 1.36 | 599.34 |
| x = 0.008 (Annealed) | 1.77 | 491.17 |
表2(Bi1–xTbx)2(Te0.9Se0.1)3样品的载流子浓度和迁移率
Table2.Carrier concentrations and mobility of (Bi1–xTbx)2(Te0.9Se0.1)3 samples.
由表2可见, 未掺杂Tb的HPS样品的载流子浓度为1.92 × 1019 cm–3, 随着掺杂量的增加, 样品的载流子浓度也随之增大, 当掺杂量为x = 0.008时, 样品的载流子浓度达到最大为7.17 × 1019 cm–3. 载流子浓度的升高, 是因为呈+3价的Tb掺杂Bi位后, 由于Tb占据了范德瓦耳斯层的间隙位置, 使Tb成为施主, 从而显著提高了样品的载流子浓度. 材料的电导率与载流子浓度和载流子迁移率成正比. 载流子浓度及载流子迁移率的变化共同决定了材料电导率的大小. 稀土元素掺杂会使合金散射增强, 从而使载流子的迁移率降低[17]. 因此, HPS样品的电导率随着Tb掺杂量的增加而增大可归因于呈+3价的Tb掺杂Bi位后, 大幅提高了体系中载流子浓度, 如表2所列, 从而使电导率随着Tb掺杂量的增加而增大. 即在决定HPS样品电导率大小的因素中载流子浓度起决定作用. 因此, Bi2Te2.7Se0.3材料通过Tb掺杂可使样品的电导率大幅提高.
图4显示了Tb不同掺杂量的HPS样品的Seebeck系数随温度变化的关系. 可见, 所有HPS样品的Seebeck系数均为负值, 说明HPS样品是通过n型载流子传导来实现电输运的. 所有HPS样品的Seebeck系数的绝对值均随温度升高而增大. 值得注意的是, 掺杂样品的Seebeck系数的绝对值均小于未掺杂样品的Seebeck系数, 且随着Tb掺杂量的增加, HPS样品的Seebeck系数的绝对值减小. 这与载流子浓度和电导率的变化趋势是一致的. 在所有HPS样品中, 未掺杂的Bi2Te2.7Se0.3的Seebeck系数的绝对值于473 K时达到最大值, 为125.15 μV/K. Seebeck系数可以表示为[18]
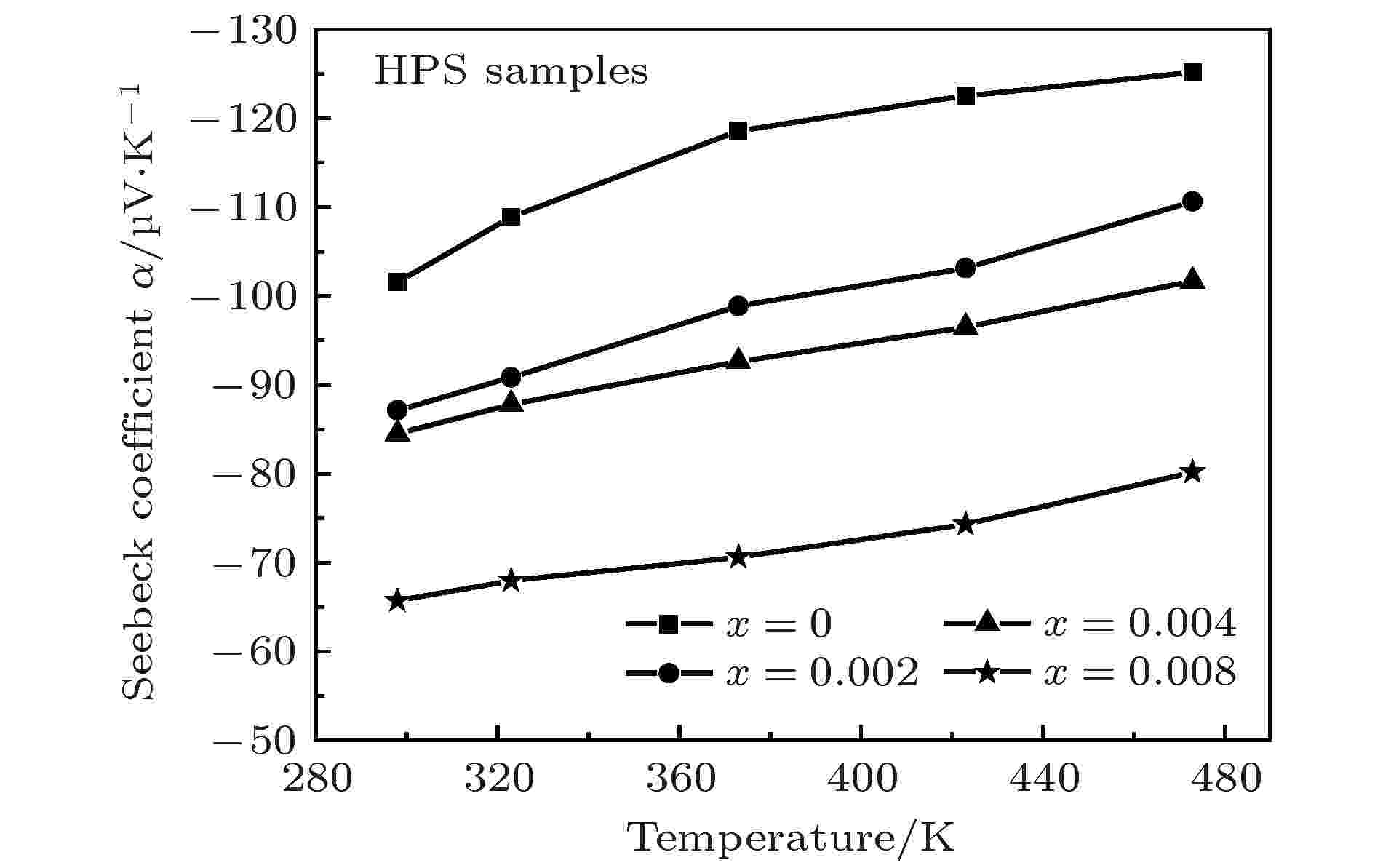图 4 Tb不同掺杂量的高压烧结样品的Seebeck系数随温度的变化Figure4. The temperature dependence of Seebeck coefficient for the HPS samples doped with different Tb contents.
图5显示了Tb不同掺杂量的HPS样品的功率因子随温度变化的关系. 从图5可见, HPS样品的功率因子随Tb掺杂量的增加而增大, 当Tb的掺杂量为x = 0.004时, 样品的功率因子在473 K时达到最大值为0.88 mW·K–2·m–1. 当Tb的掺杂量增大到x = 0.008时样品的功率因子大幅降低, 在473 K时仅为0.56 mW·K–2·m–1. 由此可知Tb掺杂量为x = 0.004是最优的掺杂量, 在该掺杂量时样品可获得较好的电学性能.
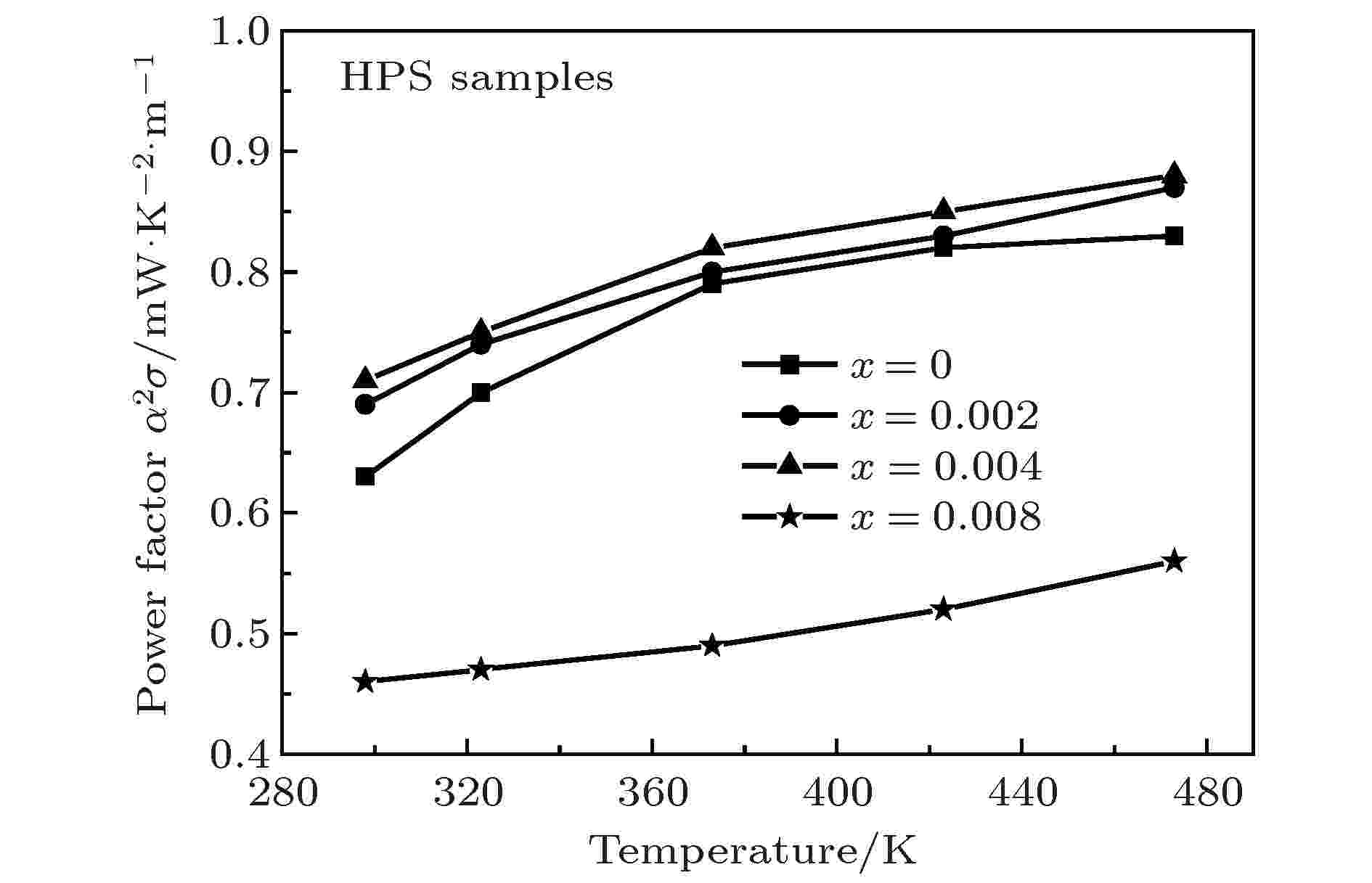图 5 Tb不同掺杂量的高压烧结样品的功率因子随温度的变化Figure5. Temperature dependence of power factor for the HPS samples doped with different Tb contents.
热电材料的热导率可表示为
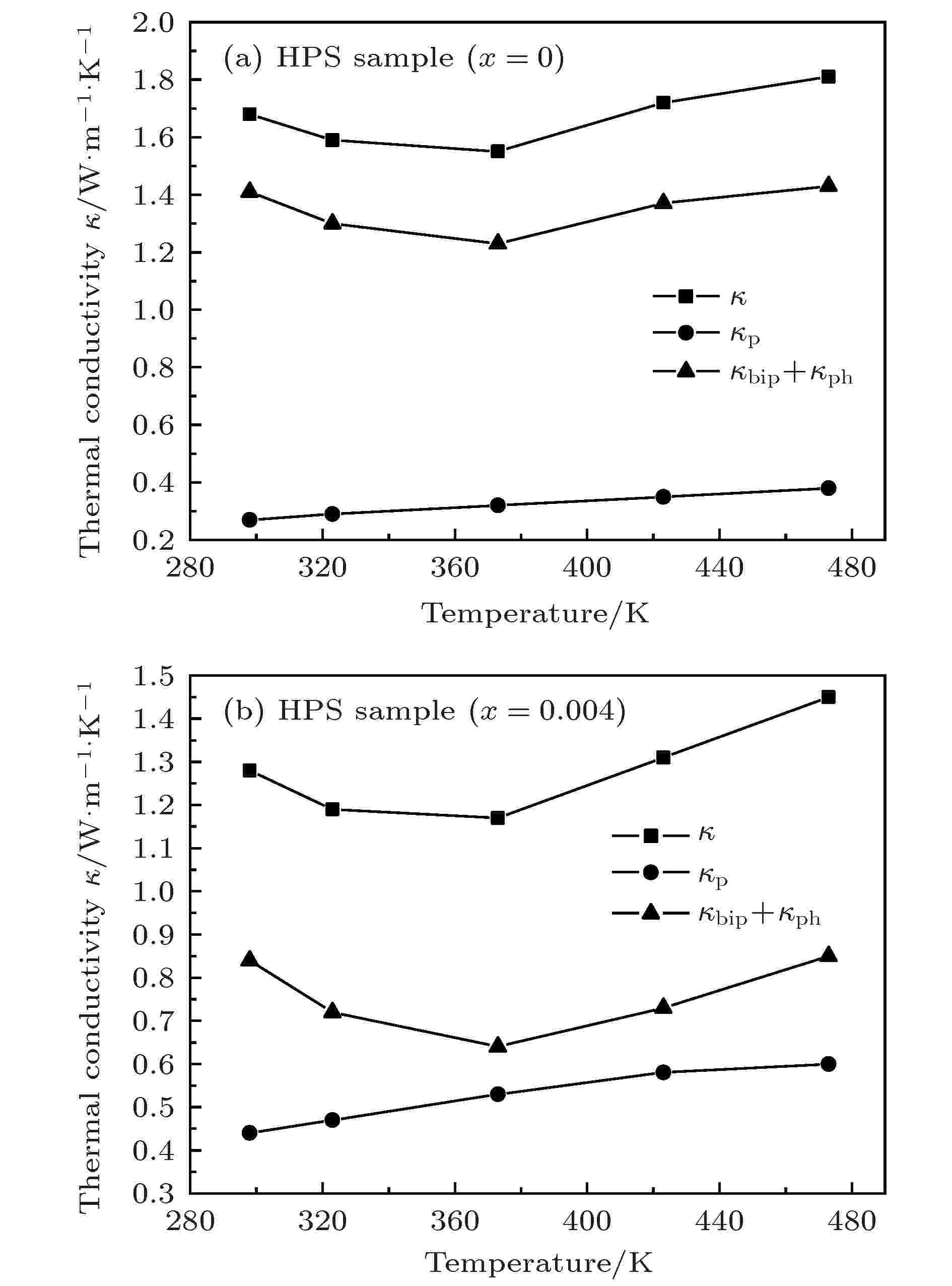图 6 高压烧结样品的热导率随温度变化 (a) 未掺杂样品; (b) 掺杂量为x = 0.004的样品Figure6. Temperature dependence of thermal conductivities for the HPS samples: (a) Tb-free sample (x = 0); (b)Tb-doped sample (x = 0.004).
从图6可见当测试温度从室温升高到373 K时, 未掺杂Tb及Tb掺杂量为x = 0.004的HPS样品的总热导率κ均随温度的升高而降低, 但是当温度高于373 K时, 上述样品的总热导率κ均随温度的升高而增大. 这是因为当温度较低时, 随着温度升高, 晶格振动增强, 声子的传输受到晶格的散射加剧, 从而使热导率κ逐渐降低; 当温度高于373 K时, 由于本征激发的作用使载流子浓度增加, 双极扩散的影响加剧, 从而使热导率κ急剧升高. 从图6(a)还可见, 当温度为373 K时, 未掺杂样品的总热导率为1.55 W·m–1·K–1, 而Tb掺杂量为x = 0.004的样品的总热导率为1.17 W·m–1·K–1, 如图6(b)所示, 相比于未掺杂样品, 降低了约25%. 这是因为在Bi2Te2.7Se0.3样品中通过在Bi的位置掺杂稀土元素Tb, 引入了点缺陷, 会对短波声子产生强烈的散射作用. 另外, 样品中大量的纳米晶(如图2所示)也会对短波声子产生强烈的散射作用, 从而使晶格热导率大幅降低, 最终导致总的热导率大幅降低. 这一结果说明通过Tb掺杂可以有效地降低样品的热导率.
未掺杂样品及Tb掺杂量为x = 0.004的样品的ZT值随温度变化的关系由图7给出. 由图7可见, HPS样品的ZT值随温度升高而增大, 并且掺杂样品的ZT值比未掺杂样品的ZT值有所提高. Tb掺杂量为x = 0.004的HPS样品的ZT值在473 K时达到最大为0.29, 相较于未掺杂样品, 增幅达到约32%. 即通过稀土元素Tb掺杂, 可以有效地提高样品的热电性能. 这是因为通过稀土元素Tb掺杂后, 材料的载流子浓度得到优化, 使得电学性能有所提高, 同时由于重原子散射使热导率大幅降低, 因此ZT值有所增大.
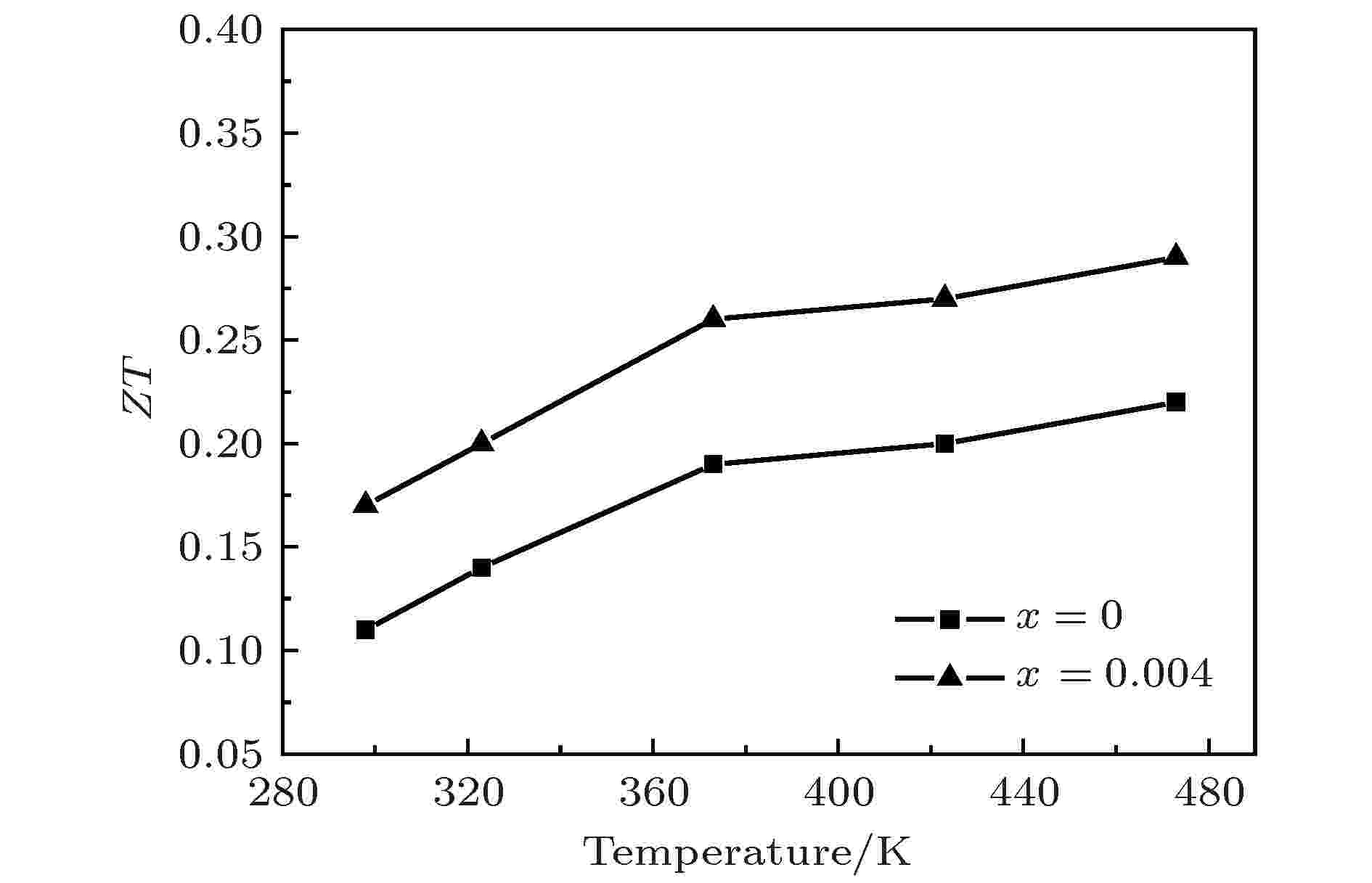图 7 未掺杂及掺杂量为x = 0.004的样品的ZT值随温度变化的关系Figure7. Temperature dependence of the figure of merit ZT for the Tb-free HPS sample and Tb-doped HPS sample with x = 0.004.
2
3.3.退火对样品热电性能的影响
图8给出了Tb不同掺杂量的HPS样品经退火处理后的电导率随温度变化的关系. 从图可见, 所有退火样品的电导率均远高于HPS样品的电导率. Tb掺杂量为x = 0.008的HPS样品经退火处理后, 电导率于298 K时取得最大值为139.1 × 103 S/m. 如表2所示, 掺杂量x = 0.004和x = 0.008的HPS样品经过退火处理后, 其载流子的迁移率分别从退火前的95.31 cm2/V·s和92.39 cm2/V·s提高到599.34 cm2/V·s和491.17 cm2/V·s. 载流子迁移率的大幅提升是因为样品经退火处理后, 缺陷减少, 晶格完美度提高, 缺陷对载流子的散射减少. 因此, 载流子迁移率较退火前有所提高成为必然. 对退火样品来说, 载流子浓度较退火前大幅降低, 而迁移率却大幅提高, 如表2所列. 因此退火样品电导率的大幅提高是由于载流子的迁移率较退火前有明显地提高所导致的, 从而可知载流子的迁移率在决定退火样品电导率大小的因素中起主要作用.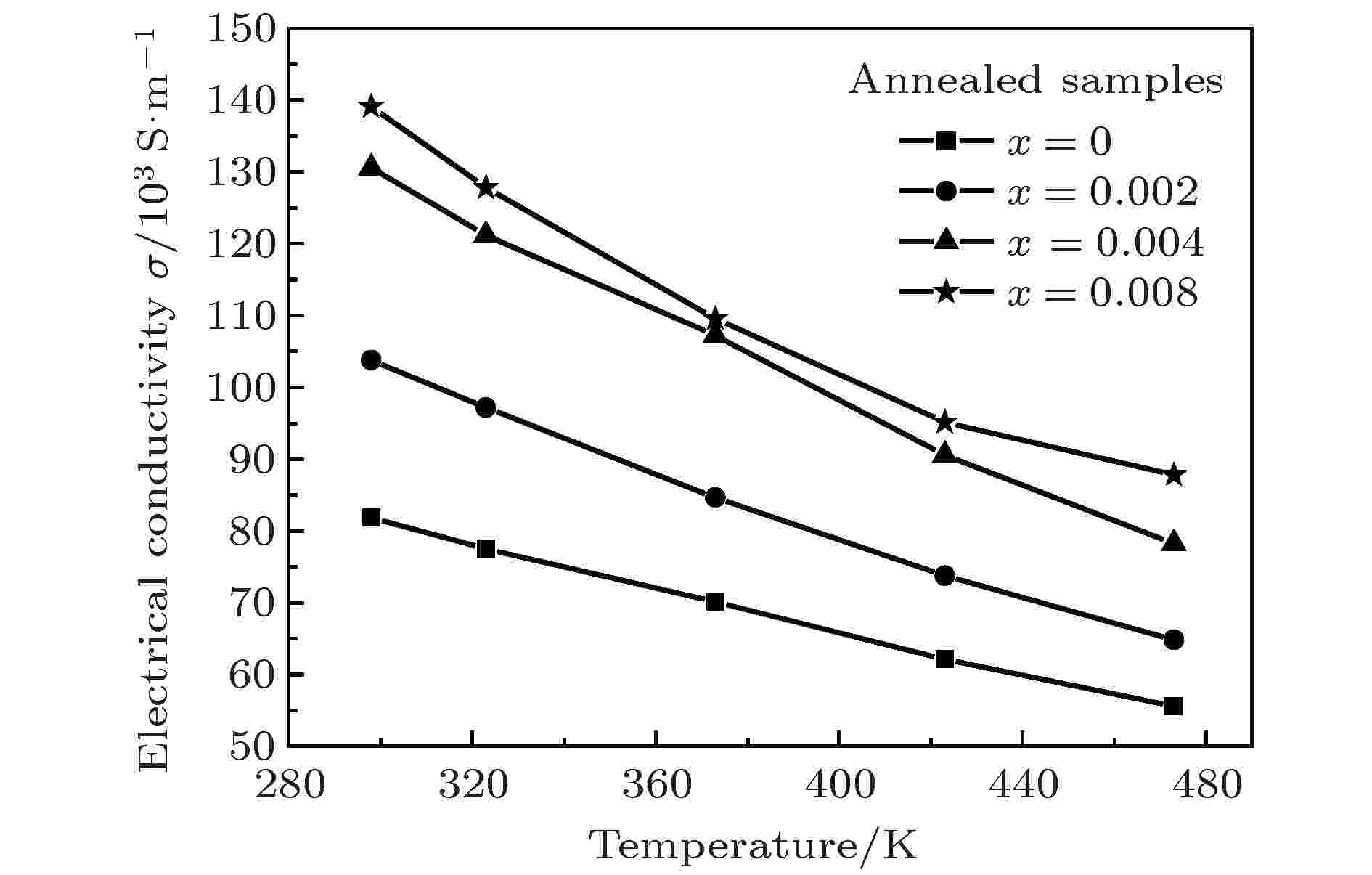
图 8 Tb不同掺杂量的退火样品的电导率随温度的变化Figure8. Temperature dependence of electrical conductivity for the annealed samples doped with different Tb contents.
Tb不同掺杂量的HPS样品经退火处理后的Seebeck系数随温度变化的关系如图9所示. 从图9可见, 所有退火样品的Seebeck系数的绝对值均明显大于HPS样品的Seebeck系数的绝对值. 如表2所列, 退火样品的载流子浓度相比于HPS样品的载流子浓度大幅降低, 根据(1)式可知, Seebeck系数与载流子浓度成反比例关系, 因此退火样品的Seebeck系数相较于HPS样品的Seebeck系数有了大幅提高. 此外, 退火样品的Seebeck系数的绝对值仍然是随Tb掺杂量的增加而减小, 未掺杂样品的Seebeck系数的绝对值在所有样品中最大. 退火样品Bi2Te2.7Se0.3的Seebeck系数的绝对值于473 K时达到最大值, 为181.15 μV·K–1.
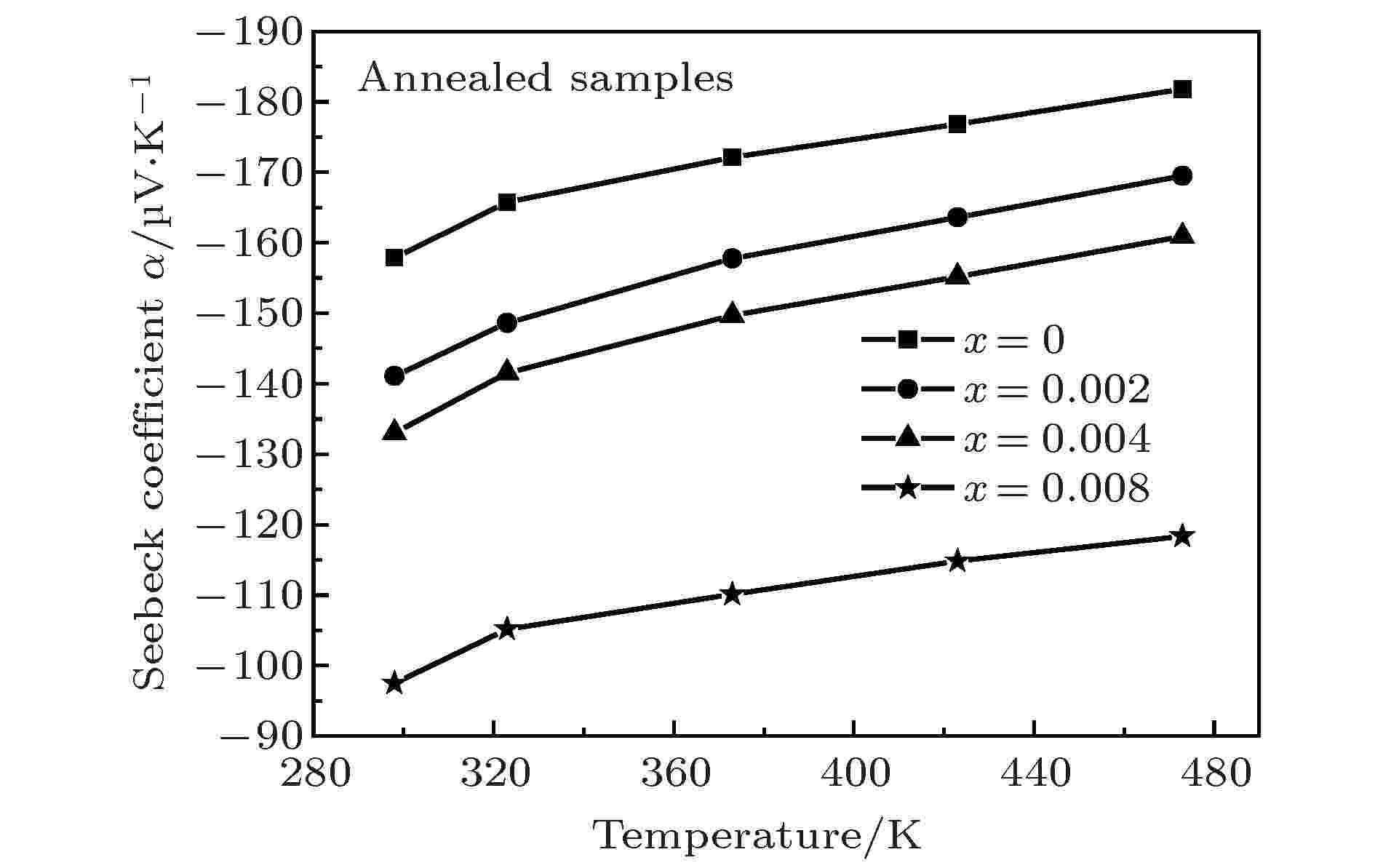图 9 Tb不同掺杂量的退火样品的Seebeck系数随温度的变化Figure9. Temperature dependence of Seebeck coefficient for the annealed samples doped with different Tb contents.
图10给出了Tb不同掺杂量的HPS样品经退火处理后的功率因子随温度变化的关系. 如图10所示, 退火样品的功率因子远高于HPS样品的功率因子. HPS样品经过退火处理后, 电导率和Seebeck系数较退火前均明显增大, 因此其功率因子也大幅提高. 掺杂量为x = 0.004的退火样品的功率因子在323 K时取得最大值为2.43 mW·K–2·m–1.
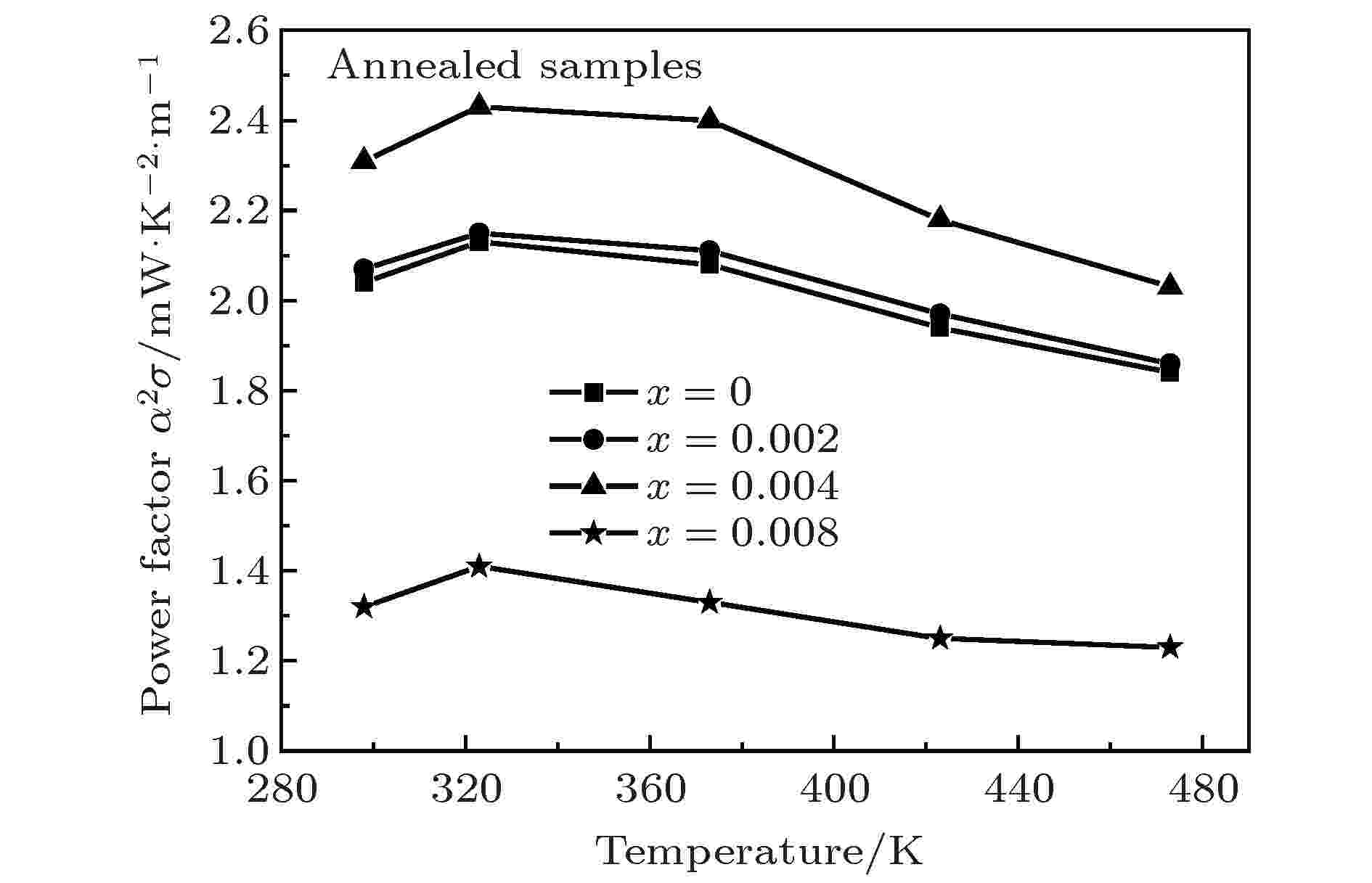图 10 Tb不同掺杂量的退火样品的功率因子随温度的变化Figure10. Temperature dependence of power factor for the annealed samples doped with different Tb contents.
图11给出了Tb掺杂量为x = 0.004的HPS样品经退火处理后的热导率随温度变化的关系. 从图11可见, 退火样品的总热导率的变化趋势与HPS样品的总热导率的变化趋势一致, 均是随温度升高, 样品的热导率κ先降低, 在373 K时热导率最低, 为0.9 W·m–1·K–1; 当温度高于373 K时, 热导率κ又开始增大. 从图11还可见, 对于退火样品来说, 从室温至473 K范围内电子热导的贡献大于双极扩散热导和晶格热导之和. 这是因为HPS样品经退火处理后, 样品的电导率有大幅提高. 值得注意的是退火样品的总热导率κ相较于HPS样品的总热导率明显降低. 例如, HPS样品的热导率κ在373 K时为1.17 W·m–1·K–1, 而退火样品的热导率κ在373 K时为0.9 W·m–1·K–1, 与HPS样品相比降低了约23%. 样品经真空长时间退火处理后, 反位缺陷等缺陷数目减少, 即带隙中杂质能级减少, 从而导致退火样品载流子浓度降低, 双极扩散受到抑制, 因此κbip降低. 另一方面, 在退火过程中由于应力释放及有微量的元素挥发产生了少量的气孔(高压烧结样品的相对密度为99.16%, 而样品经退火处理后相对密度减小为97.68%), 这些气孔能有效地散射声子, 从而使晶格热导率κph降低. 以上两个因素最终使退火样品的κbip+κph大幅降低, 从而使退火样品的总热导率κ大幅降低.
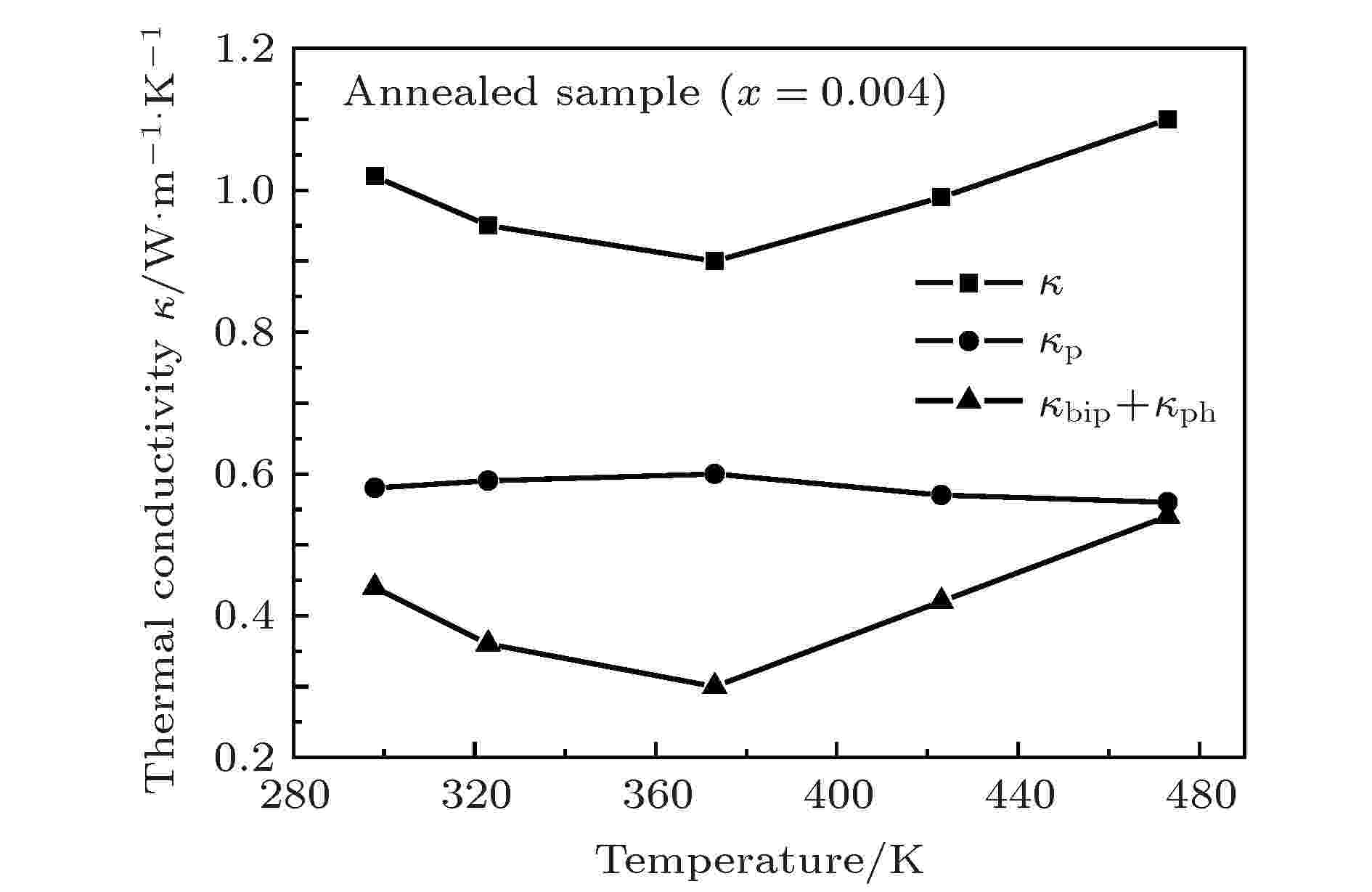图 11 Tb掺杂量为x = 0.004的退火样品的热导率随温度变化的关系Figure11. Temperature dependence of thermal conductivity for the annealed sample with x = 0.004.
图12给出了未掺杂及Tb掺杂量为x = 0.004的HPS样品经退火处理后的ZT值随温度变化的关系. 从图12可见, 退火样品的ZT值随温度升高先增大后减小. 此外, 退火样品的ZT值远大于HPS样品的ZT值. 这是因为HPS样品经退火处理后, 功率因子提高, 而热导率降低, 因此其ZT值大于HPS样品的ZT值. 掺杂量为x = 0.004的退火样品的ZT值在373 K时达到最大为0.99, 相比于Ce掺杂的n型Bi2Te2.7Se0.3的最大ZT值0.85[21], 提高了16%. 更为重要的是, 当温度高于323 K时, 退火样品的ZT值均大于0.8, 为应用于发电领域创造了条件.
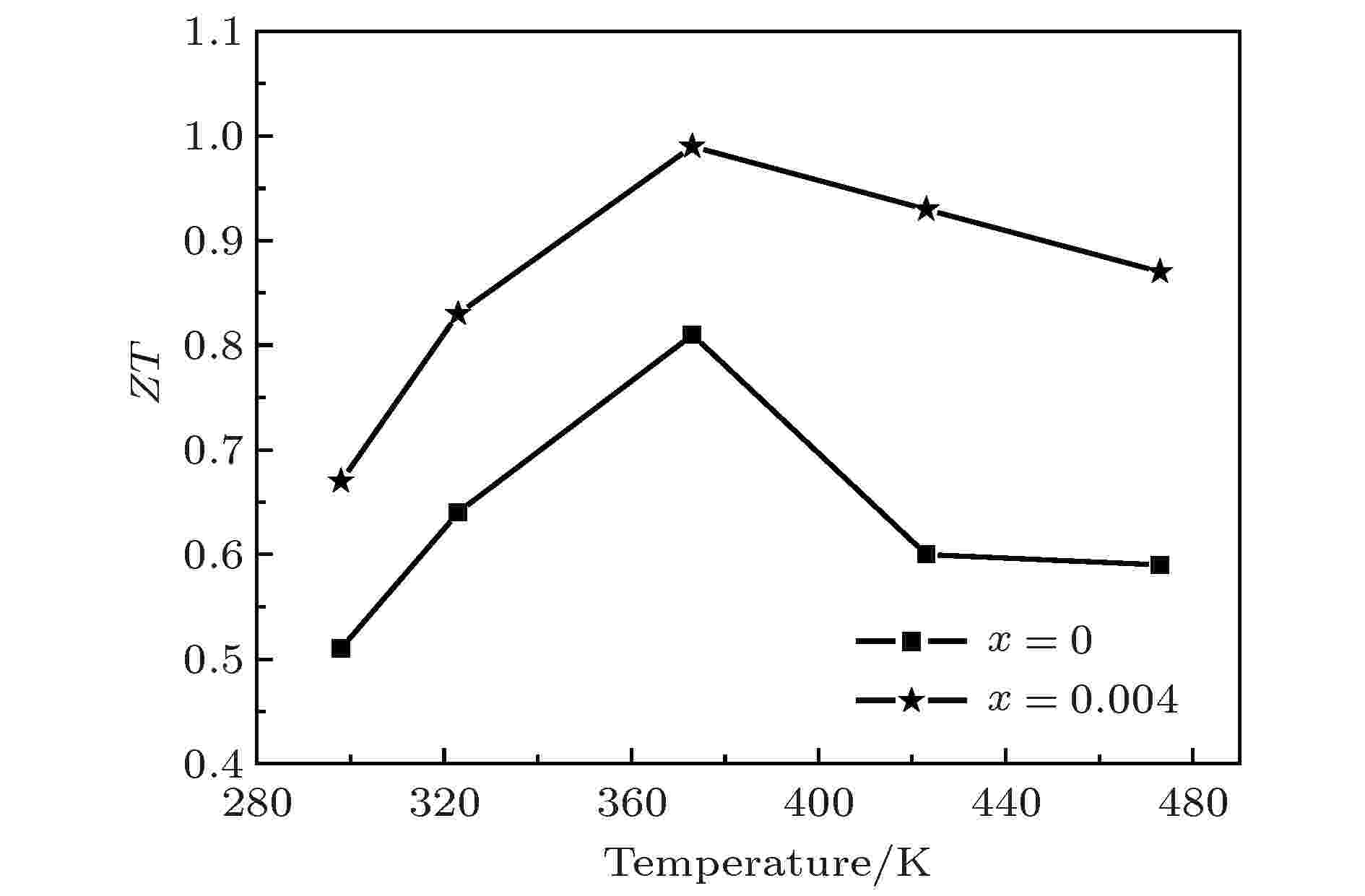图 12 未掺杂及掺杂量为x = 0.004的退火样品的ZT值随温度变化的关系Figure12. Temperature dependence of the figure of merit ZT for the Tb-free annealed sample and Tb-doped annealed sample with x = 0.004.
