删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

第一性原理软件北京原子技术模拟工具包的重构进展

本站小编 Free考研考试/2021-12-29
摘要:基于第一性原理的理论方法的研究, 代表了材料计算、分子模拟等领域的科学高地, 相应的第一性原理计算软件直接关系到该领域相关理论、算法的积累. 本文汇报了我们在重构第一性原理计算模拟软件—北京原子技术模拟工具包(BSTATE)的一些最新进展. 重构的核心思想是降低用户使用门槛、扩展软件适用范围、增加软件对于流行计算框架的支持. 基于此思路, 在BSTATE原有Makefile编译系统的基础上添加了CMake编译环境, 并支持各种数学函数库的自动和交互式配置; 通过在原有内置泛函基础上增添Libxc泛函库的支持, 使BSTATE支持的泛函数量有了数量级上的增长; 分析测试BSTATE在集群的并行特点, 并以更新数学库接口(FFTW3、Cufftw)的形式提供对于流行异构框架的初步支持.
关键词: 第一性原理软件/
密度泛函理论/
北京原子技术模拟工具包/
软件重构

English Abstract


全文HTML

--> --> -->
1.引　言
电子结构计算的理论依据是量子力学理论. 量子力学建立了微观粒子运动变化的基本规律, 将人类对自然的认识扩展到原子尺度的微观世界. 非相对论量子力学最流行的表述形式是Schr?dinger 的波动力学形式, 它的核心是波函数的概念及其运动方程Schr?dinger方程. 但电子体系的Schr?dinger方程是高维奇异问题, 很难直接求解. 于是人们又通过各种手段对Schr?dinger方程进行等价转换或近似, 其中最基本的近似是绝热近似或称Born-Oppenheimer近似. 它的基本思想是将整个问题分成两部分来考虑, 考虑电子运动时原子核是处在它们的瞬时位置上, 而考虑核的运动时则不考虑电子在空间的具体分布. 目前实际计算中用于求解Schr?dinger方程的各种方法大都是在这个近似基础上进行的. 根据是否使用经验参数和实验数据, 求解Schr?dinger方程的近似方法主要分为3类: 第一性原理方法、半经验方法和经验方法. 第一性原理方法是指不使用任何经验参数和实验数据, 只利用基本物理常数和原子量计算Schr?dinger方程的方法, 求解后得到体系的一系列性质, 如晶体结构、结合能和电子结构等.
众所周知, 化学和材料科学是现代科学技术和国民经济发展的重要基石, 基于第一性原理的分子、材料模拟是研究化学反应和材料物性最重要的方法之一, 为目标功能导向的材料设计提供了可能. 第一性原理计算方法在材料的性质研究和预测方面发挥着越来越大的作用, 已经成为继实验和理论分析之外的最为重要的研究方法和手段之一. 尤其是对于新型的拓扑材料的预测和研究, 第一性原理方法发挥了无可替代的作用.
当前我国在材料计算、反应模拟领域仍然缺乏核心的竞争力和影响力, 一个重要的原因就是成熟的第一性原理系列计算软件的缺失, 仍处于利用国外成熟商业软件, 如: GAUSSIAN[1], VASP[2] (Vienna Ab-initio Simulation Package, 维也纳从头算模拟程序包), 进行研究工作的下游. 这也导致相关基础人才储备不足、后劲缺乏, 影响到计算研究进一步的发展. 虽然目前国内的许多研究小组已经在该领域做出了出色的工作, 也有越来越多的相关程序包发布(如BDF[3], ABACUS[4], BSTATE[5]等), 但是目前有关这方面的研究积累仍然不足, 尤其是国产的适用于大型计算集群、支持异构框架的大规模并行软件仍然缺失. 这极大限制了可计算模拟的材料尺度或者分子大小, 进而制约了相关材料和化学科学的发展.
BSTATE (Beijing Simulation Tool for Atom Technology), 中文名为北京原子技术模拟工具包, 是基于密度泛函理论和平面波赝势(包括模守恒赝势[6]和超软赝势[7,8])方法的第一性原理计算程序包, 主体程序在20世纪90年代由中国科学院物理所方忠研究员及其合作者共同开发. BSTATE主要用于周期性晶体结构下能量、电子密度、能带结构等的计算模拟, 进而得到物质的电、磁、光等其他特性. 除了可以很好地处理一般的基态电子结构计算, 该程序包的长处在于能比较好的处理各种磁有序、轨道序、强自旋轨道耦合体系, 包含了独创的处理强关联体系的LDA+Gutzwiller[9-11]方法, 大幅提高了计算效率[5]. 基于BSTATE程序包, 以物理所凝聚态研究组为主体的研究人员针对Bi2Te3, Bi2Se3和Sb2Te3等拓扑材料进行了第一性原理的计算, 其研究结果表明这些体系是首次发现的三维拓扑绝缘体, 并且在其二维磁性掺杂薄膜中能实现量子化的反常霍尔效应. 这也为极低能量耗散的自旋电子器件设计指出了一个新的发展方向[12-15].
虽然BSTATE程序包已经在拓扑绝缘体的计算中取得了很好的成绩, 但是BSTATE的使用主要局限在少数课题组内, 有必要进行进一步的推广. 当前BSTATE局限性的主要在于用户门槛较高; 泛函数量较为单一, 不好满足特定材料的计算要求; 以及暂时没有考虑流行的硬件框架. 针对上述问题, 我们拟对中科院物理所的第一性原理材料计算软件包BSTATE进行重构. 以期提高软件的易用性和适用范围、降低用户门槛、优化其对流行计算框架的支持.
2.BSTATE程序的基本原理
BSTATE程序为大型的第一性原理程序包, 有近30万行的Fortran代码. 程序使用了FFTW (the Faster Fourier Transform in the West)函数库、Intel MKL (Math Kernel Library)等多种数学函数和MPI (Message Passing Interface)来提高计算效率. 程序的核心部分是对交换关联势做了LDA[16] (Local Density Approximation)或者GGA[17,18](Generalized Gradient Approximations)近似的KS (Kohn-Sham)方程的自洽求解[19].
2
2.1.Schr?dinger方程与DFT理论
-->

2.1.Schr?dinger方程与DFT理论

波恩-奥本海默近似下, 体系中电子的定态可以由满足非含时Schr?dinger方程的N电子波函数$\varPsi ({ r_1}, \cdots , { r_N})$来描述, 即
$\begin{split}{\rm H}\varPsi \;& = [T + V + U]\varPsi \\&= \left[ {\sum\limits_i^N { - \frac{{{\hbar ^2}}}{{2m}}\nabla _i^2 + \sum\limits_i^N {V\left( {{{ r}_i}} \right) + \sum\limits_{i < j} {U\left( {{{ r}_i},{{ r}_j}} \right)} } } } \right]\varPsi \\& = E\varPsi .\\[-10pt]\end{split}$
其中, H为体系哈密顿算符, 包含动能T(拉普拉斯算符$\nabla $)、势能V、电子相互作用U 三部分. 由于电子之间的相互作用会让体系成为很难处理的多体问题, 无法精确求解. DFT可以将含U的多体问题转化为不含U的单体问题, 从而成为解决此类问题的一个有效方法. 密度泛函理论中, 关键的变量为粒子的密度, 即
$\begin{split}\rho ( r) =\, & N\int {{\rm d^3}{r_2}} \int {{\rm d^3}r} \cdots\int {{\rm d^3}{r_N}} \\& \cdot {\varPsi ^*}\left( {{{ r}_{}},{{ r}_2}, \cdots ,{{ r}_N}} \right)\varPsi \left( {{{ r}_{}},{{ r}_2}, \cdots,{{ r}_N}} \right),\end{split}$
(2)式的关系也可以反过来, 即给出电子的密度$\rho ( r)$, 原则上也可以计算出对应的波函数$\varPsi $. 基于此, Hohenberg与Kohn(HK定理[20])指出存在电子密度$\rho ( r)$的总能量泛函$E(\rho )$ , 其中$E(\rho )$可以写成外势${V_{{\rm{ext}}}}$的形式, 即
$E[\rho ] = \int {\rho ( r)} {V_{{\rm{ext}}}}{\rm{d}}r + J[\rho ] + G[\rho ], $
其中, ${V_{{\rm{ext}}}}$由$\rho ( r)$唯一确定, $J[\rho ]$为经典的库伦排斥能. 此时可以通过最小化$E(\rho )$, 来获得体系的能量、电子密度以及其他所有性质. 相比于计算量随粒子数指数次增长的波函数方法, 电子密度方法的计算量与电子数目无关, 仅与在三维空间(x, y, z)内找到电子的概率有关. 由于泛函$G(\rho )$是未知的, HK定理并没有给出计算$E(\rho )$的实际方法.
2
2.2.KS-DFT与泛函近似
-->

2.2.KS-DFT与泛函近似

KS理论下$G[\rho ]$可以表示为${T_{\rm{s}}}[\rho ] + {E_{{\rm{xc}}}}[\rho ]$的形式[21,22], 其中${T_{\rm{s}}}[\rho ]$是假想无相互作用体系的动能泛函, ${E_{{\rm{xc}}}}[\rho ]$是交换关联能量. ${E_{{\rm{xc}}}}[\rho ]$的求解需要交换关联势(${\nu _{{\rm{xc}}}}(r) = {\rm{\delta }}{E_{{\rm{xc}}}}[\rho ]/\text{δ}\rho (r)$)的近似形式, 其最简单的近似就是局域密度近似, 即LDA. LDA近似下$\rho $用均匀电子气模型来处理. LDA交换关联能$E_{{\rm{xc}}}^{{\rm{LDA}}}$只与$\rho $有关, 表示为
$E_{{\rm{xc}}}^{{\rm{LDA}}}[\rho ] = \int {{\varepsilon _{{\rm{xc}}}}(\rho ( r))} \rho ( r){\rm{d}}r, $
其中, ${\varepsilon _{{\rm{xc}}}}(\rho ( r))$是均匀原子气单粒子的交换关联能. 在LDA中, 具有相反自旋的电子占据相同的KS空间轨道.
为了校正电子密度分布不均匀带来的误差, 将表示电子密度不均匀性的密度梯度($\nabla \rho $)作为半局域变量, 引入到${E_{{\rm{xc}}}}$, 此为含广义密度梯度校正的近似即GGA, 得到的泛函即为GGA泛函. GGA交换关联能$E_{{\rm{xc}}}^{{\rm{GGA}}}$是${\rho _{}}$和$\nabla {\rho _{}}$的泛函, 即$E_{{\rm{xc}}}^{{\rm{GGA}}}[{\rho _{}}, \nabla {\rho _{}}]$; 考虑到电子自旋后GGA泛函需要由四个参数确定, 即$E_{{\rm{xc}}}^{{\rm{GGA}}}[{\rho _ \uparrow }, {\rho _ \downarrow }, \nabla {\rho _ \uparrow }, \nabla {\rho _ \downarrow }]$; 也因此相比于LDA泛函, GGA泛函在计算结合能方面明显提高了计算精度.
除了LDA和GGA泛函, meta-GGA和hybrid-GGA[23,24]以及双杂化泛函都是重要的泛函形式. 当前BSTATE暂时没有用到后三种形式的泛函. 泛函确定后, 体系的波函数需要通过求解${\rm H}\varphi = E\varphi $形式的KS方程来得到, 具体形式为
$\left( { - \frac{{{\hbar ^2}}}{{2m}}\nabla _{}^2 + {\nu _{{\rm{eff}}}}(r)} \right){\varphi _i}({r_i}) = {\varepsilon _i}{\varphi _i}({r_i}), $
其中${\nu _{{\rm{eff}}}}$为泛函确定后的有效势.
2
2.3.BSTATE程序框架
-->

2.3.BSTATE程序框架

作为第一性原理计算程序包, BSTATE程序包的核心部分是对交换关联势做了LDA或者GGA近似的KS方程的自洽求解. 其基本流程示意图如图1所示.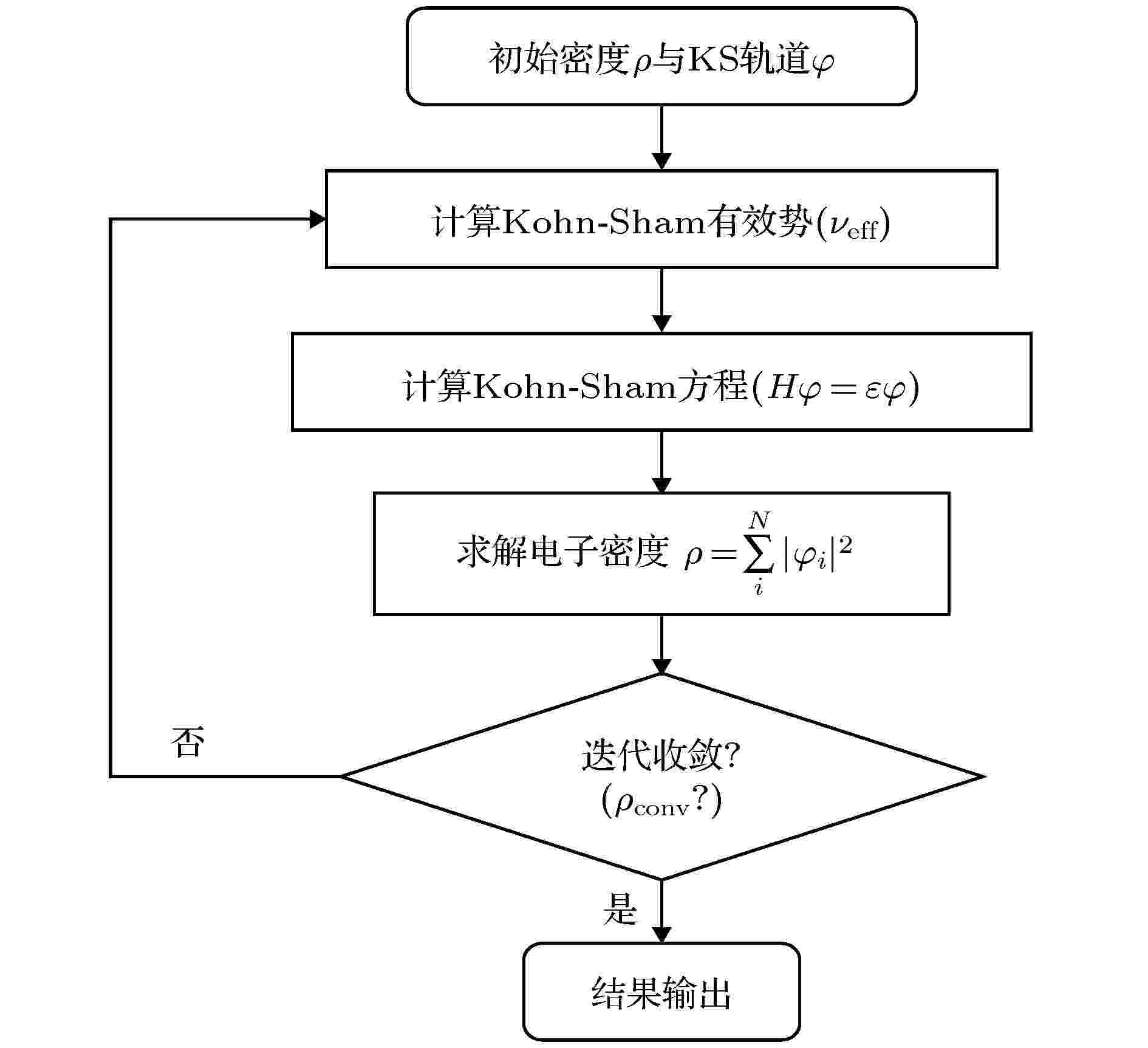
图 1 BSTATE计算流程示意图
Figure1. Flowchart of BSTATE package.

以上数值求解的过程中必须把连续量离散化, 如系统实空间原胞划分成足够细的网格, k空间的布里渊区的k点离散化. 在迭代求解KS方程的过程中需要初始化电荷密度$\rho $与KS轨道, 可以利用单原子的电子密度分布作为初始值. 有HK定理保证, KS势可以表示成电荷密度的泛函; 所以很容易得到离散网格上的KS势, 进而可以求解固定KS势场的单电子本征方程获得KS轨道信息. 一般情况, 求解出来的KS轨道与初始KS轨道是不相同的. 轨道求解出来以后可以根据DFT波函数为单行列式的性质求得电子密度信息$\rho $. 获得新的电子密度后, 使用HK定理重新计算KS势, 重新求解KS方程获得KS轨道信息, 最后重新利用KS轨道和电子排布获得电子密度信息. 更新重复上面的过程, 直到所求出的新的电荷密度与输入的电荷密度在判据范围内一致, 即可认为收敛. 这时候体系的波函数信息包括KS轨道和电子占据, 在此基础上可以得到系统的总能、电子态密度、能带图、布洛赫波、费米面、光电导等一系列结果.
3.BSTATE程序分析与重构进展报告
2
3.1.编译系统
-->

3.1.编译系统

重构前的BSTATE仅能采用GNU make进行程序构建和管理. Makefile文件描述了整个工程的编译、连接等规则. 使用Makefile时, BSTATE的编译步骤是:
1)通过预编译指令(GNU的cpp或者intel的fpp), 生成编译时使用的Fortran代码. 值得注意的是, BSTATE的mlwf(Maximally Localised Wannier Functions)部分需要使用自由格式的预编译; 其余需要使用固定格式的预编译. 此外, 预编译后实际生成的代码会受条件编译的控制.
2)预编译后的源代码(.f90, .for)被统一为.f后缀的Fortran代码. BSTATE编译的过程中首先会编译整个程序所需要的模块函数(module), 之后继续编译和连接所有的程序文件.
针对不同的计算机构架和编译环境, BSTATE有着不同的Makefile模板. 并支持Intel MKL和FFTW2等一系列的函数库. 针对不同的编译环境, 用户需要重新修改所有的编译选项. 这对于非计算机专业的用户存在不低的使用门槛, 同时使得跨平台和交叉编译复杂化.
重构后的BSTATE在保留旧版Makefile编译流程的基础上, 提供全新的CMake编译系统支持[25]. CMake全称是“cross platform make”, 是一个开源的跨平台自动化构建系统. 新版的BSTATE使用指定名为CMakeLists.txt的配置文件来控制软件的预编译、编译、连接等流程. 与此同时, CMake天生跨平台的特征, 使得仅需要对于CMakeList.txt进行简单配置, 原则上即可以生成不同目标平台(如Linux, Windows, Mac)的程序文件. 这可以大大简化跨平台和交叉编译方面的工作. 重构后的BSTATE编译系统的特点主要有:
1)保留原版Makefile的编译流程. 使用cmake或者ccmake时可以指定预编译环境(cpp、fpp). 预编译时可以指定条件编译的选项, 生成编译BSTATE时使用的有效代码.
2)内置了不同优化等级的预编译和编译方案(如debug, release等); 支持多线程编译.
3)提供Libxc、FFTW2/3、CUFFT/CUFFTW等外接函数库开关选项; 支持不同语言的混合编译.
4)通过cmake-curses-gui提供图形交互式(GUI)的预编译和编译支持.
5)通过对“MATH_ROOT”或类似关键环境变量的查找, 提供对于常见数学函数库的自动搜索和支持功能. 该功能默认开启, 并按照“MKL, ESSL, OPENBLAS, ATLAS, ACML, SYSTEM_NATIVE”的默认顺序进行数学函数库的自动配置.
通过以上的调整, 重构后的BSTATE可以通过CMake实现自动和快速编译. 比如终端中键入FC = mpif90 ccmake [BSTATE_CMakeList.txt], 即可开启预编译和编译的GUI, 进行自动配置或按提示修改编译选项.
在表1中我们也总结了BSTATE新老编译系统的对比. 可以看出重构后的编译系统相对于旧版, 无论是在代码维护、扩展性、用户使用等等方面均有长足的进步.
项目重构前重构后
编译系统GNUMakeCMake
图形GUI不支持支持
跨平台手工修改Makefile文件提供支持原生支持
数学库手工配置自动配置
外置函数库手工配置支持自动配置
异构支持否是
高级编译选项手工配置支持GUI配置
多线程编译不支持支持
用户门槛高低


表1重构前后BSTATE编译系统的对比
Table1.Comparison of BSTATE compilation system.

2
3.2.接口升级、函数库整合
-->

3.2.接口升级、函数库整合

重构前的BSTATE程序已经可以调用多种函数库来实现额外的功能或加速计算过程, 例如傅里叶变换FFTW函数库, 但其仅支持老旧的FFTW2接口. 因此, 首先在BSTATE里面增加FFTW3[26]的调用接口, 以便使用常用的SSE2和AVX指令集, 加速运算. 同时, 也初步接入了基于CUDA的傅里叶变换函数库(CUFFTW和CUFFT), 已可取得同CPU版本一致的计算结果, 但是效率仍有很大的提升空间.
重构前的BSTATE已经支持LDA, GGA, LDA+U, GGA+U等计算. 但其仅通过固定的代码支持ldapw91和ggapbe两个泛函. 因此将Libxc库[27]接入BSTATE, 使其可以支持流行的各种泛函. Libxc是当前最为全面的交换关联泛函库. 该泛函库由ETSF(European Theoretical Spectroscopy Facility)维护, 并几乎收录了主流期刊公开报道的所有交换关联泛函.
Libxc内部函数相互依赖, 调用需要编译为库文件后才能在子程序中调用. 因此重构时主要通过预编译的方式在多个子程序中配置, 然后再进行调用. 在重构的BSTATE程序中, LDA和GGA泛函通过新添加的extern_functionals.f90接口程序接入. 对于LDA泛函, 势能仅仅依赖于电子的密度(即$E_{{\rm{xc}}}^{{\rm{LDA}}} = E_{{\rm{xc}}}^{{\rm{LDA}}}[\rho ({r})]$ ); 对于GGA泛函, 势能会依赖于电子的密度和电子密度的梯度(即$E_{{\rm{xc}}}^{{\rm{GGA}}} = $$ E_{{\rm{xc}}}^{{\rm{GGA}}}[\rho ( r), \nabla \rho ( r)]$ ). 接口程序定位在BSTATE中的xc_gga.f90源程序中. 除了电子密度、梯度等信息, k点信息、自旋等也要在接口中传递.
作为测试, 使用砷化镓体系(GaAs, 见图2)和石墨烯片段作为测试的算例. 测试的结果表明重构后的BSTATE在DFT计算中性能可以与之前持平(表2和表3), 无论是单核、多核还是MPI并行计算, 性能均没有明显差距. 此外, 受益于FFTW3对于SSE2和AVX系列指令集的支持, 在Intel异构众核平台(MIC)的计算结果会有一定的提升.
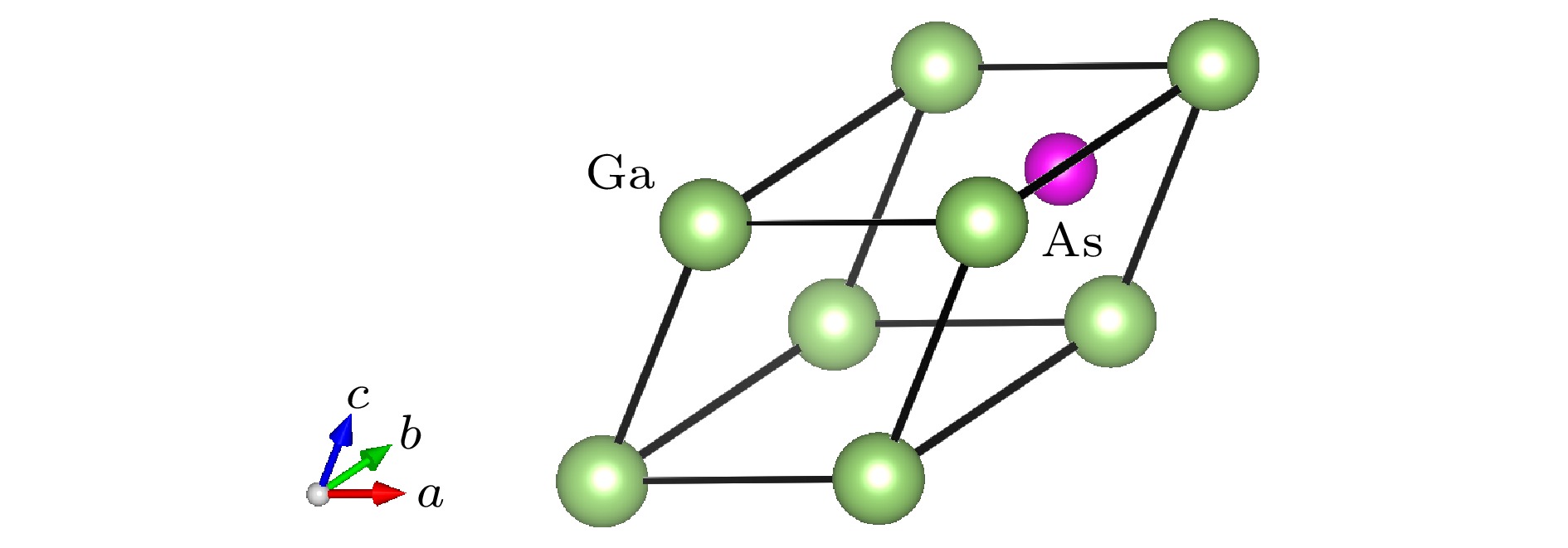图 2 闪锌矿结构的GaAs双原子化合物
Figure2. GaAs compound with zinc blende structure.

项目单核/s多核/s
BSTATE42.422.6
BSTATE+Libxc43.623.4
性能比0.970.97
* 测试机器为AMD A10 PRO-7800 B R7 (4核); GaAs体系


表2Libxc版本与原始版本性能比较
Table2.Benchmarks between BSTATEs with/without Libxc.

项目CPU平台/sMIC平台/s
FFTW211811717
FFTW3+Libxc11791593
性能比1.001.08
* CPU平台为Intel至强E7-4830v3 (56核); 石墨烯体系
* MIC平台为Intel Phi-7210 (64核); 石墨烯体系


表3FFTW3+Libxc版本与原始FFTW2版本性能比较
Table3.Benchmarks between V.FFTW2 and V.FFTW3+ Libxc.

使用整合Libxc和FFTW3的BSTATE版本, 我们在原有的lpw91(LDA)和ggapbe(GGA)泛函的基础上使用相对论(lda_x_rel[28])和自适应(lda_x_rae[29])的LDA泛函计算了GaAs的态密度. 其计算结果列于图3, 可以看出对于该体系不同的泛函会得到整体相似的态密度结果, 主要区别在–6 eV、0—4 eV能量区间.
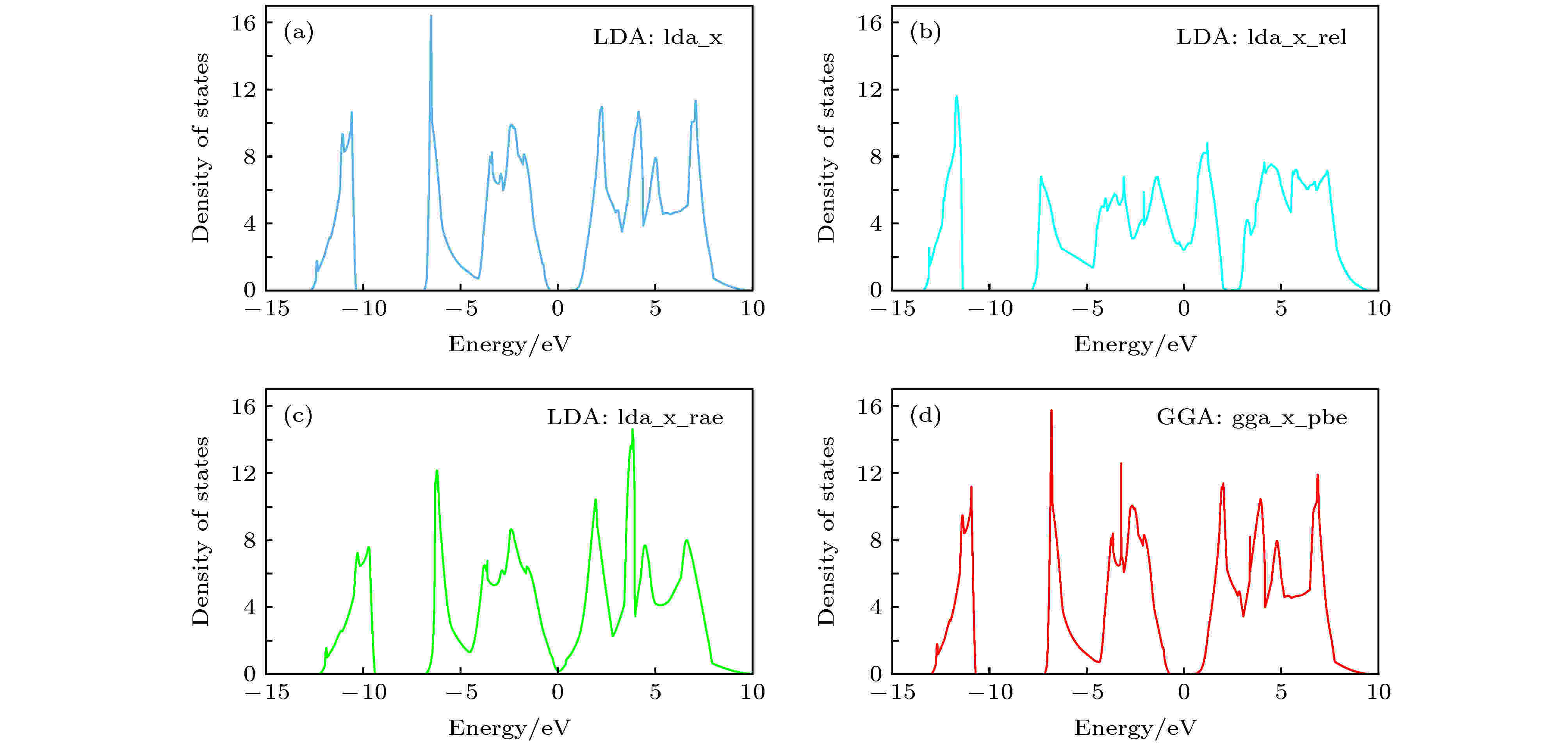图 3 多种泛函计算的GaAs的态密度 (a) (b) (c) (d)
Figure3. Calculated density of states (DOS): (a); (b); (c); (d)

2
3.3.并行分析和测试
-->

3.3.并行分析和测试

提高第一性原理计算模拟软件的计算效率一直是计算科学领域的一大挑战. 其主要原因是电子的强相互作用导致能量和波函数只能在哈密顿构造完之后才可以求解; 而且构造和求解的过程中也涉及各种数据结构或者数值代数方面的问题. BSTATE软件在设计之初就已经很好地考虑这些方面的问题, 并已经可以通过MPI模块按照k点进行分布式求解. 所谓 k点并行化, 即将k点均匀分配给(并行环境中的)多个 CPU, CPU 之间的数据交换较少, 计算效率高.
为了详细分析BSTATE的并行性能, 我们选用GaAs晶体和石墨烯片段分别进行小规模和大规模的测试计算. 对于较小体系如GaAs晶体, 使用个人PC在多核(4线程)计算, 分析过程中的各个大类模块所占时间比例统计于图4中(编译采用-O2优化). 可以看出, 傅里叶变换时间占比接近58%, 紧随其后为特征值求解, 时间占比约为12%左右, 态密度、球贝塞尔函数计算部分合计占比均为15%左右. 对于较大体系如石墨烯片段的计算(图4), 我们使用56核MPI并行的集群进行了测试, 测试结果表明特征值求解部分占用最多的时间比例, 约为65%, 同时傅里叶变换时间占比下降到18%左右.
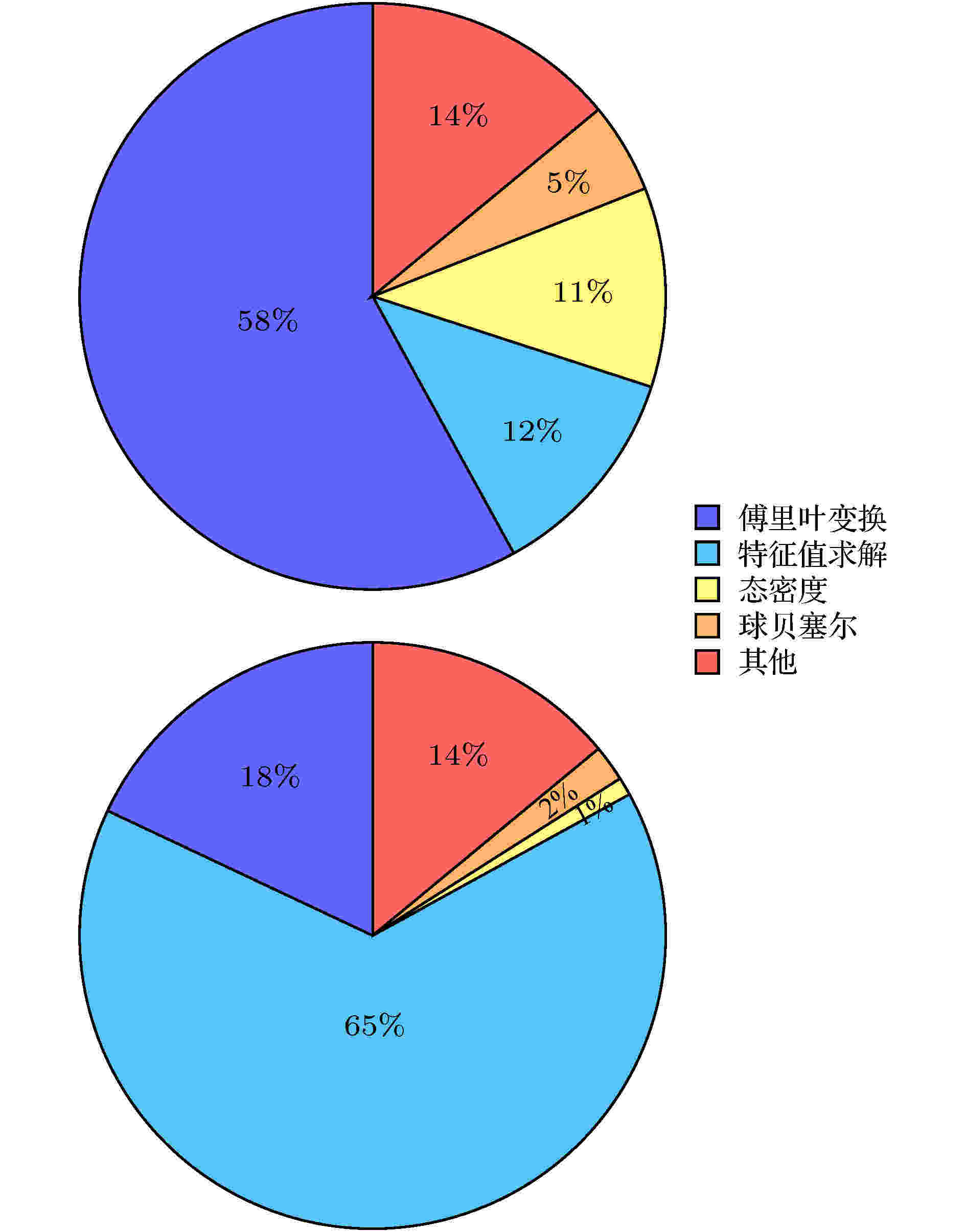图 4 个人PC (左图)及集群MPI (右图)测试中BSTATE各模块的时间占比统计
Figure4. Time percentages of subroutines in BSTATE using PC (left) and Cluster (right).

在图4中集群MPI的并行模式下面, 我们也通过使用TAU ( Tuning and Analysis Utilities; 重构的BSTATE通过CMake可以整合TAU模块) 分析了BSTATE并行时各个线程的执行情况, 并示于图5中. 可以看出在按照现有的基于k点的并行策略, BSTATE各个线程有着较好的负载均衡, 各个计算核心的计算能力都得到很好的发挥.
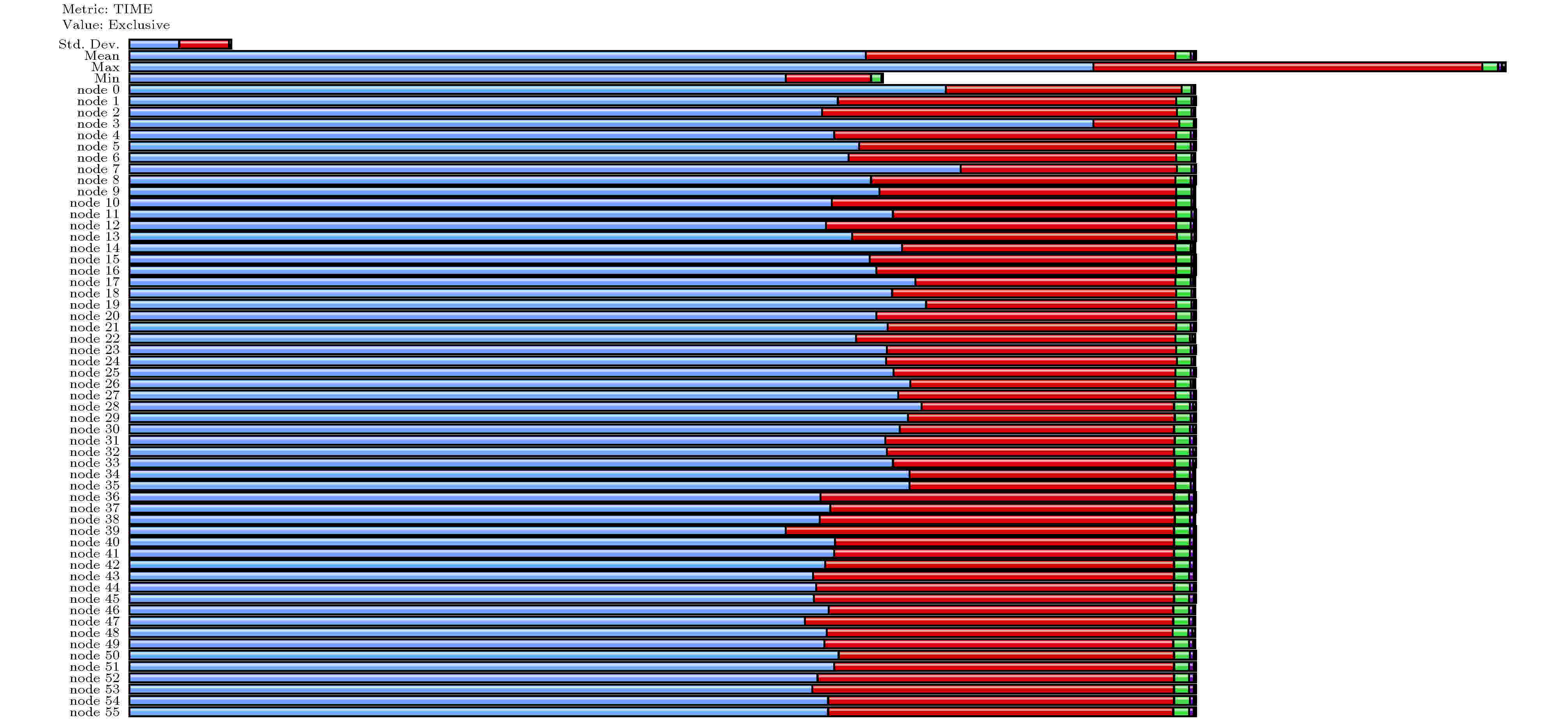图 5 BSTATE的MPI多线程并行分析; 其中蓝色、红色、黄色、黑色分别代表application(BSTATE), MPI_barrier, MPI_reduce以及MPI_allreduce.
Figure5. Analysis via TAU performance system framework for BSTATE

最后, 我们使用重构的BSTATE版本(即包含CMake+TAU+FFTW3+Libxc的版本), 在中国科学院的“元”集群上对石墨烯片段体系进行了更大规模的测试, 以验证新的版本可以稳定的执行计算任务. 该测试平台基于曙光TC4600 E刀片平台, 采用Intel Xeon E5 2680 V3处理器(2.5 GHz、12核). 测试的结果示于图6中. 可以看出, 重构的BSTATE相对于重构前基于FFTW2的版本在跨节点并行方面有着一定的性能提升(0—17%左右的加速). 这应该得益于新的FFTW3调用接口以及基于Libxc的泛函求解方案. 同时我们也注意到当前基于k点的并行求解方案在核心过多的情况下效率下降很快, 这也是实际计算中特别要注意的方面.
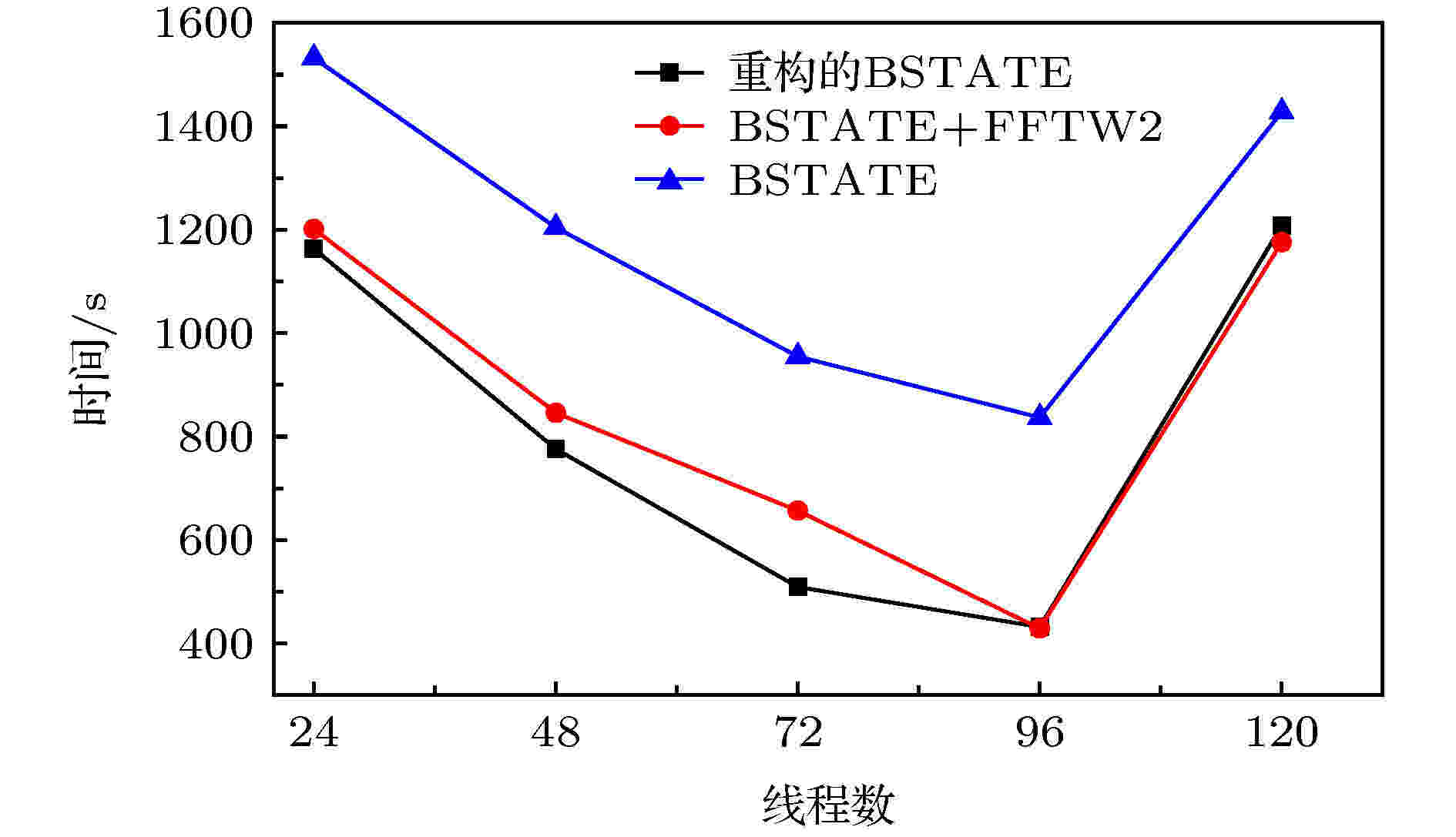图 6 重构前后的BSTATE跨节点并行测试
Figure6. Benchmark of MPI parallel for BSTATE with and without refactoring.

4.结　论
本文汇报了我们在重构第一性计算模拟软件BSTATE的一些最新进展. 根据重构的核心思想(降低用户使用门槛、扩展软件适用范围、提高软件计算效率), 我们的工作主要集中在编译、配置部分的自动化, 增加泛函类别, 以及优化程序接口3个方面. 重构后的BSTATE通过CMake的引入可以实现跨平台、简单图形化的编译; 通过Libxc和FFTW3的引入和更新实现了程序功能的扩展和对更多计算平台的支持; 最后的并行分析和稳定性测试, 验证了重构后的BSTATE可以更好地胜任第一性原理方面的计算任务, 并在跨节点并行方面有着一定的性能提升.
在重构的进程中, 也注意到BSTATE仍有较大的改进空间. 比如在原理层面上的哈密顿的构造、子空间迭代等自洽迭代改进方案, 以及技术层面上的CPU-GPU协同计算方面. 这些需要更多的第一性原理算法上的积累和深入, 也是我们后面需要进一步考虑的方面.
感谢徐顺博士关于程序优化方面的指导和讨论.
相关话题/计算 电子 程序 软件 测试
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 高熵合金短程有序现象的预测及其对结构的电子、磁性、力学性质的影响
    摘要:如何有效预测高熵合金的稳态结构,是开展研究其物理及化学等性能的基础.以FeCuCrMnMo合金为例,在有限晶胞尺寸内,采用蒙特卡洛结合密度泛函理论杂化计算方法(MonteCarlo/densityfunctionaltheory,MC/DFT)预测高熵合金的平衡态结构.与准随机近似方法(spe ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 石墨烯纳米网电导特性的能带机理：第一原理计算
    摘要:通过第一原理电子结构计算来研究有序多孔纳米网的电导特性变化的能带机理.能带结构分析结果表明:石墨烯纳米网超晶格(3m,3n)(m和n为整数)的电子本征态在布里渊区中心点发生四重简并;碳空位孔洞规则排列形成的石墨烯纳米网具有由简并态分裂形成的宽度可调带隙,无论石墨烯的两个子晶格是否对等.在具有磁 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Tl<sub>0.33</sub>WO<sub>3</sub>电子结构和太阳辐射屏蔽性能第一性原理研究
    摘要:节能减排已成为当今社会发展的主题,对节约能源、提高太阳能的高效综合利用的新型窗用透明隔热材料的理论设计和研究尤其重要.本文采用基于密度泛函理论的计算方法,研究了六方相三氧化钨Tl掺杂前、后的晶格参数、电子能带结构、形成能和光学性质.研究结果表明,Tl掺杂后晶格体积增大,系统能量降为负值,体系具 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • AlGaN/GaN高电子迁移率晶体管温度传感器特性
    摘要:本文制作了基于无栅AlGaN/GaN高电子迁移率晶体管结构的温度传感器,并对其温度相关的电学特性进行了表征.实验测试了器件从50℃到400℃的变温电流-电压特性,研究了器件灵敏度随着器件沟道长宽比的变化,并研究了在300—500℃高温的空气和氮气中经过1h恒温加热后器件的电学特性变化.理论与实 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 锐真空-等离子体边界倾角对激光尾波场加速中电子注入的影响
    摘要:超短超强激光脉冲在气体等离子体中激发的尾波场加速在过去40年里有了长足的发展,人们已经在厘米加速距离内获得了数GeV的准单能电子加速,激光尾波加速的最高电子能量已经达到8GeV.为了进一步提升加速电子束的稳定性和品质,多种电子注入方式先后被提出.本文研究了基于锐真空-等离子体边界面的密度跃变注 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 典型磁性材料价电子结构研究面临的机遇与挑战
    摘要:目前在磁性材料磁有序现象研究中广泛使用的交换作用、超交换作用和双交换作用模型形成于1950年代及其以前,这些模型都涉及材料中的价电子状态,但那时还没有充分的价电子状态实验依据.1970年代以来,有关价电子结构实验结果的报道越来越多,这些实验结果表明传统的磁有序模型需要改进.首先,大量电子谱实验 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 天线方向系数的一类计算逼近方法
    摘要:天线的方向系数是天线的核心性能指标之一,准确计算方向系数是高性能天线应用的核心要求.本文基于平面近场测试理论、实测数据和快速傅里叶变换算法,系统阐述基于近场测试来数值计算天线方向系数的原理,并进行深入的误差分析.本文选择一种方向图函数和方向系数已知的被测天线,来检验所讨论的误差评估方案.评估分 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光子对撞机产生正负电子对的数值方法
    摘要:光子对撞产生正负电子对的Breit-Wheeler过程,是由能量直接产生物质的过程,在物质的起源与光子物理理论的研究中有着极为重要的作用.随着激光与物质作用产生γ光源品质的提升,使得在实验室首次观测双光子对撞的Breit-Wheeler过程成为可能.针对光子对撞机的数值模拟方法,本文提出了一种 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • TiAl电子态结构的<i>ab initio</i>计算
    摘要:应用完全活动基自洽场方法,结合N电子价态微扰近似(NEVPT2),对TiAl金属二聚体的基态和若干最低电子激发态的势能曲线进行了计算.完全活动空间由Al的3个价电子(3s23p1)轨道和Ti的4个价电子(3d24s2)轨道构成,计算基组选用Karlsruhegroup的价分裂全电子基组def2 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 空位及氮掺杂二维ZnO单层材料性质:第一性原理计算与分子轨道分析
    摘要:采用基于密度泛函理论的第一性原理计算方法,系统地研究了带缺陷的二维类石墨烯结构的ZnO(graphenelike-ZnO,g-ZnO)的几何结构、电子结构、磁性性质和吸收光谱性质.研究的缺陷类型包括锌原子空位(VZn_g-ZnO)、氧原子空位(VO_g-ZnO)、氮原子取代氧原子(NO_g-Z ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.