摘要: 本文较为详细地介绍了作者之一及其合作者近期在Type II弦理论中有关D膜间相互作用, 开弦对产生以及这种对产生在一定情况下的增强效应的系列研究工作. 具体包括计算了带有一般世界体常数电磁场情况下平行放置且有一定间距的两张D膜间的相互作用, 讨论了相关特性, 比如相互作用的吸引或排斥情况. 当其中至少一张膜带电场时, 这种相互作用振幅通常有一个虚部, 反映了该系统的一种不稳定性即开弦对的产生, 并给出相应的衰变率和开弦对产生率. 另外, 探讨了这种开弦对产生率的增强效应, 发现其与所加的电场和磁场的方向和大小相关联. 当其中一个膜的空间维度为3, 另一个膜的空间维度为1时, 这种开弦对产生率可以大到人类实验室条件下得以检验. 开弦对的产生率与两膜沿额外维方向的间距密切关联, 如果假定弦理论的正确性及人类的4维时空可以看成一张D3膜的话, 测量开弦对产生所给出的(比如)电流并验证其与所加电磁场的关系符合预言, 由此可以检验额外维的存在性. 同时, 这也为弦理论提供了一种实验检验, 并且这是一种无须将该理论紧化到四维时空的全新方式.
关键词: D膜 /
弦与膜 English Abstract D-brane interaction, the open string pair production and its enhancement plus its possible detection Lu Jian-Xin Zhang Nan Peng Huanwu Center for Fundamental Theory, The Interdisciplinary Center for Theoretical Study, University of Science and Technology of China, Hefei 230026, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11775212, 11947301)Received Date: 06 January 2020Accepted Date: 01 March 2020Published Online: 20 May 2020Abstract: This review article reports the recent studies, based on a series of publications by one of the present authors along with his collaborators, regarding the interaction between two D-branes, the open string pair production and its possible enhancement in Type II superstring theories. Specifically, computed is the interaction amplitude between two D-branes, placed parallel at a separation, with each carrying a general worldvolume constant flux, and discussed are the amplitude properties, say, the repulsive or attractive nature of the interaction. When at least one of the D-branes carries an electric flux, the interaction amplitude can have an imaginary part, reflecting the instability of the underlying system via the open string pair production. The decay rate and the pair production rate are both computed. In addition, the enhancement of the latter is found when the added electric and magnetic fluxes are correlated in both magnitude and direction in a certain manner. In particular, when one of the branes is D3 and the other is D1, the corresponding pair production rate becomes large enough to be tested in an earthbound laboratory. Note that the pair production rate is related to the brane separation along the direction transverse to both branes, therefore, to the extra-dimensions with respect to the brane observer. So if the underlying string theory is relevant and the D3 can be taken as our own 4-dimensional world, measuring, say, the electric current due to the pair production and comparing it against the added electric and magnetic fields to see if the measurements agree with the prediction of the computations. This can be used to verify the existence of extra-dimensions. Further, this provides also a potential new means to test the underlying string theory without the need of compactifying it to four dimensions.Keywords: D-branes /strings and branes 全文HTML --> --> --> 1.引 言 引力的量子化是一个迄今没有解决的物理学基本问题. 引力的量子行为涉及相互作用的本质及其统一, 是理解比如黑洞奇点和宇宙学奇点以及暗能量本质的出发点. 目前存在两种比较认可的量子化引力尝试. 一种是圈量子引力, 另一种是弦/M-理论. 如果从物质和相互作用的统一的角度, 弦/M-理论是目前惟一的量子引力候选理论.$ (2, 0) $ 共形场论. 另外, 最近基于弦理论的研究告诉我们, 当考虑引力相互作用时, 并不是任何一个有效理论都具备紫外完备推广, 即使其在没有考虑引力时具有紫外完备.[1 -5 ] 的相关动力学. 这是基于作者之一和其合作者近期的一系列工作[6 -15 ] . 讨论将局限于第二类(Type II)超弦理论中的非微扰Dp 膜, 这里p 代表该D膜的空间维度. 在我们的讨论中, Dp 膜是沿p 维空间方向无穷延展的. 比如, 从膜图景来看, D3膜可以是我们生活的4维时空, 因此可能与我们的现实世界有关. 我们有两种第二类超弦理论, 通常称为IIA和IIB超弦理论. 除相应的非微扰Dp 膜和NS5膜外, 每一个仅包括闭弦, 都要求时空维度为10, 具有两个时空超对称. 它们的区别是前者不是一个手征理论(即两个超对称具有相反的手征性)而后者是(两个超对称具有同样的手征性). 对于IIA理论, p 可分别取$ 0, 2, 4, 6, 8 $ , 而对于IIB, $ p = -1, 1, 3, 5, 7, 9 $ . 这里$ p = -1 $ 代表D瞬子, $ p = 9 $ 通常又称为时空填充(spacetime-filling)膜. 除$ p = 9 $ 外, 一般总有$ p - p' = 2\, k $ (假定$ p \geqslant p' $ ), 这里$ k = 0, 1, 2, 3, 4 $ .p 膜, 其具有如下张力[5 ] :$ g_{\rm{s}} $ 是闭弦的耦合常数, 与后面提到的D膜的开弦描述的开弦耦合常数的关系为$ g_{\rm{o}} = g^{1/2}_{\rm{s}} $ . 具有长度平方量纲的常数$ \alpha' $ 与基本弦的张力关系为$ T_{\rm{F}} = 1/(2{\text{π}} \alpha') $ . 弦基本长度$ l_{\rm{s}} = \sqrt{\alpha'} $ 也是弦理论的一个基本常数.p 膜放入10维平坦时空时, 它也会引起周围的时空弯曲. 如果坚持沿垂直于膜的方向上有渐近平坦的行为, 要求$ p \leqslant 6 $ [3 ,4 ] . 对于$ p > 6 $ , 时空都会有不好的奇异行为, 比如圆锥奇点. 基于这一点以及后面要考虑的内容, 从现在开始限制$ 0 \leqslant p \leqslant 6 $ . $ p = - 1 $ , 即D瞬子, 与要考虑的内容没有特别关系, 将不考虑它.N 张重叠的Dp 膜放入10维平坦时空, 得到的时空度规为[3 ,4 ] r 是垂直于膜方向的径向距离, $ x_\| $ 是Dp 膜时空延展的方向, 而$ x_\bot $ 是垂直膜的方向. 这里参数$ k_{p} \approx N g_{\rm{s}} \alpha'^{(7-p)/2} $ (见文献[6 ]中的讨论). 如果弦耦合常数$ g_{\rm{s}} \ll 1 $ 使得$ g_{\rm{s}} N \ll 1 $ , 即使探测的距离$ r \approx l_{\rm{s}} = \alpha'^{1/2}\gg (N g_{\rm{s}})^{1/(7 - p)}\alpha'^{1/2} $ , 上述度规基本是平坦的. 换句话说, 在弱耦合情况下把N 张重叠的D膜放入平坦时空, 该时空即使在弦尺度下仍然保持平坦. 也就是说在弱耦合下可以把D膜看成是刚性的. 这也是后面讨论的出发点.1 )式表示的张力与开弦的耦合常数平方成反比, 但仅仅与闭弦的耦合常数本身成反比. 因此严格来说, D膜不完全是闭弦的孤子而应看成开弦的孤子. 当弦的耦合常数很小时, 如上文所述D膜本身可看成是刚性的, 其动力学可以用闭弦或开弦的微扰理论来研究. 从闭弦角度, D膜可以用所谓的边界态来描述(一种弦理论的相干态, 见文献[16 ,17 ]). 除最低阶的一些研究, 通常用这种描述还是很困难的. 从开弦角度, D膜的动力学可以用一个满足一定边界条件的微扰开弦来刻画[5 ] . 这是D膜作为一个非微扰客体最重要的特性, 即一个非微扰的动力学客体存在一个微扰理论的描述. 这也是弦理论中特有的现象.p 延展的方向满足所谓的纽曼(Neumann)边界条件而在垂直膜方向上满足所谓的狄里克莱(Dirichlet)边界条件, 如图1 所示. 当考虑一张Dp 膜时, 这种开弦的无质量态给出的就是$ (1 + p) $ 维下的$ U(1) $ 超对称规范理论① $ (p - 1) $ 矢量自由度, $ (9 - p) $ 标量自由度, 总共给出8个玻色自由度, 另外还有8个无质量费米自由度. 如图1 所示, 开弦的两个端点分别带大小相等、方向相反的U (1)电荷, 因此开弦整体来说没有净余的电荷. 通常又称这样的开弦为电中性开弦. 第二类超弦理论中描述D膜的开弦都是这种电中性开弦.图 1 D膜Figure1. D-braneN 张重叠的)这种Dp 膜保持1/2时空超对称, 称为1/2 BPS态, 因此本身是稳定的, 类似稳定真空态. 如同量子电动力学(QED)真空中虚的正反电子对涨落, 该Dp 膜本身也有量子涨落, 表现为所谓的虚的正反开弦对, 如图2 所示(暂时忽略图中膜上加的电场).图 2 虚开弦对Figure2. Virtual open string pair[18 ] . 这里自然会问, 如果在该Dp 膜上加一个电场(该电场会作用在虚的正反开弦对的带电的端点), 是否也有一定的几率把虚的正反开弦对拉开成为实的正反开弦对?对单张Dp 膜, 答案一般是否定的. 这是因为每一个开弦两端带的电荷大小相等但符号相反, 所加的电场至多只能把每一个开弦拉直, 但无法把该虚的正反开弦对分离. 有一种例外就是如果所加的电场达到所谓的临界值, 即由弦张力决定的电场, 这时该临界电场可以把开弦拉断, 由此可以产生正反开弦对.$ 10^{10} \;{\rm{V}}/{\rm{m}}$ ), 这也是至今未能在实验上观察到施温格对产生的主要原因(需要的电场 约$ 10^{18} \;{\rm{V}}/{\rm{m}}$ ). 在可以预见的将来不可能在实验室条件下实现弦理论临界电场, 它的值比现有的实验室可以实现的最大电场至少大20个数量级.[19 ,20 ] 作出了回答, 答案是肯定的. 由于所涉及的开弦没有取向, 开弦的两个端点所带的电荷不必大小相等、方向相反, 因此没有这里出现的问题. 但要把这种开弦对的产生与四维时空的观察联系起来, 必须要把26维的玻色弦或10维的第一类超弦紧致到四维时空. 这与我们的出发点不一样. 我们希望提供一种不需要紧致化时空来检验弦理论的手段. 这也是我们考虑具有取向的第二类超弦理论中D膜的原因.p 膜. 这时的开弦涨落有三种可能. 其中的两种是涨落的虚的正反开弦对的四个带电端点分别落在第一张Dp 膜或第二张Dp 膜上. 但这两种中的任一种与单张Dp 膜一样不可能给出开弦对的产生. 还有一种情况就是虚的开弦对其中的两个端点落在一张Dp 膜上, 另外两个端点落在另一张Dp 膜上. 在没有加任何膜上电场的情况下, 这种开弦涨落描述的是两膜间的开弦单圈环带相互作用(annulus amplitude). 它可以看成一根虚的开弦, 一个端点落在第一张Dp 膜上而第二个端点落在第二张Dp 膜上, 绕时间方向转了一个闭合时间圈. 由于弦理论具有共形对称性, 这种开弦的真空单圈效应等价于第一张Dp 膜在某时刻发出一根虚的闭弦, 传播一段时间, 然后被第二张Dp 膜吸收(类似于用量子场论计算两个电荷间的库仑相互作用或两个静止质量间的牛顿相互作用). 这种相互作用通常被称为闭弦的树图柱面相互作用(cylinder amplitude), 可以由图3 表示. 这种开弦单圈相互作用(因此是量子的)与闭弦的树图相互作用(因此是经典的)的等价性是所谓开弦/闭弦对偶的基础. 把这种对偶性应用到$ p = 3 $ 情形并考虑所谓的退耦极限就给出著名的AdS/CFT对应.图 3 闭弦树图相互作用与开弦单圈相互作用的等价性Figure3. The equivalence of a closed string tree-level cylinder amplitude and an open string one-loop annulus amplitudep 膜系统, 无论用开弦描述还是用闭弦描述, 两者间的相互作用有两部分贡献. 一部分来自所谓R-R分部(sector), 给出的是两张Dp 膜带同样所谓R-R电荷引起的排斥相互作用. 另一部分来自所谓的NS-NS分部(sector), 给出的是两张Dp 膜具有张力(因此有质量)引起的相互吸引作用. 由于每一张膜都是1/2 BPS, 其质量和RR电荷在一定单位制下相同, 由此给出这两张Dp 膜间的两部分相互作用大小相等但符号相反, 因此总的相互作用为零. 换句话说, 平行放置有一定间距的两张Dp 膜间没有相互作用, 因此与单张Dp 膜一样仍然是1/2 BPS.图4 . 如果在第一张Dp 膜上加的电场不同于第二张Dp 膜上加的电场, 不难看出这两根虚的开弦端点所受的力会使它们分离, 因此存在一定的几率产生正反开弦对. 换句话说, 即使不做任何计算(后面会用计算证实这一点), 这种简单的物理分析会告诉我们这样的简单系统一定会产生正反开弦对.图 4 一根虚开弦转一个闭合时间圈等价于虚正反开弦对的产生和湮灭Figure4. A virtual open string circulating a closed time loop can be viewed as a pair of virtual open stringand virtual anti open string creating and annihilating.p 膜和另一张${\rm{D}}p'$ 膜(不失一般性假设$ p \geqslant p' $ )间的相互作用. 这里“横向”的意思是指垂直于Dp 膜的方向或对Dp 膜上的观察者来说是额外维空间的方向.2.D膜边界态及一般闭弦树图柱面振幅的计算 利用D膜的边界态表示来讨论计算前述两张D膜间的相互作用. 本节将参照文献[14 ]对D膜边界态给一个简单介绍. 有关D膜边界态较全面的介绍, 请参看文献[16 ,17 ]. 如前所述, 描述一个D膜有两部分, 称为NS-NS分部(sector)和R-R分部(sector). 对于每一分部, 对D膜的边界条件还有两种选取的方式, 给出两个边界态$ |B, \eta\rangle $ , 这里$ \eta = \pm $ . 然而, 只有下面的组合:p 膜, 上述边界态$ |B, \eta\rangle $ 可以表述为物质部分和鬼部分贡献的乘积, 具体为[16 ,17 ,21 ] ,$ c_p = \sqrt{{\text{π}}}\left(2{\text{π}} \sqrt{\alpha'}\right)^{3 - p} $ .17 ,22 ]所指出, 上述Dp 膜边界态的算子结构即使在带有一般世界体常电磁通量情况下也是成立的, 对玻色物质场$ X^{\mu} $ , 有如下一般的形式:$ \psi^{\mu} $ , 对NS-NS分部, 有21 ]. 膜上电磁通量的信息分别由上述M $ |B_X\rangle_0 $ 和R-R分部的费米零膜$ |B_{\psi}, \eta\rangle_{0{\rm{R}}} $ 所刻画[17 ,22 -25 ] . 具体为$ \alpha, \beta, \cdots $ 标记的是膜延展的时空方向$ 0, 1, \cdots, p $ 而拉丁指标$ i, j, \cdots $ 代表的是垂直于膜的空间方向, 即$ p + 1, \cdots, 9 $ . $ |A \rangle |\tilde B\rangle $ 代表R-R分部的真空态. 还定义了无量纲的电磁通量$ \hat F = 2{\text{π}} \alpha' F $ , 其中F 是膜世界体上的通常常数电磁场. $ y^i $ 标记Dp 膜沿其横向方向的位置, C U $ ;\, \, ; $ 标记上面指数展开的每一项中的10维$ { {\varGamma}} $ 矩阵指标为反对称化. 另外, 注意上面的$ \eta $ 标记正反号$ \pm $ 或膜世界体闵氏平坦度规, 这很容易从相关表达式的具体形式看出.p 膜和一张${\rm{D}}p'$ 膜间的闭弦树图柱面相互作用振幅, 具体为D 是闭弦传播子$ L_0 $ 和$ {\tilde L}_0 $ 分别是考虑超鬼、鬼和物质场贡献的左行和右行总的零模Virasoro生存元. 比如$ L_0 = L^X_0 + L_0^\psi + L_0^{\rm{gh}} + L_0^{\rm{sgh}} $ , 这里$ L_0^X, \; L_0^\psi, \; L_0^{\rm{gh}} $ 和$ L_0^{\rm{sgh}} $ 分别为物质场$ X^\mu $ , 物质场$ \psi^\mu $ , 鬼b 和c , 以及超鬼$ \beta $ 和$ \gamma $ 对应的贡献, 它们的具体表达式可以在任何标准超弦理论的讨论中找到, 比如参考文献[16 ], 因此这里不再列出.$ { {\varGamma}}_{p, p'} ={ {\varGamma}}_{\rm{NSNS}} + { {\varGamma}}_{{\rm{RR}}} $ . 在计算$ { {\varGamma}}_{\rm{NSNS}} $ 或$ { {\varGamma}}_{{\rm{RR}}} $ , 要记住应该用(3 )式给的GSO投影边界态.$ { {\varGamma}} (\eta', \eta) = \langle B', \eta'| D |B, \eta\rangle $ , 其中$ \eta' \eta = + \; {\text{或}}\; - $ , $ B' = B_{p'} (\hat F') $ 和$ B = B_{p}(\hat F) $ . 将看到$ { {\varGamma}}(\eta', \eta) $ 其实仅仅依赖$ \eta' $ 和$ \eta $ 的乘积, 即$ { {\varGamma}}(\eta', \eta) = { {\varGamma}} (\eta' \eta) $ . 在NS-NS分部, 当$ \eta' \eta = \pm $ , 分别定义$ { {\varGamma}}_{\rm{NSNS}} (\pm) \equiv { {\varGamma}} (\pm) $ . 在R-R分部, 当$ \eta'\eta = \pm $ , 类似地有$ { {\varGamma}}_{{\rm{RR}}} (\pm) \equiv { {\varGamma}} (\pm) $ . 由此, 从(3 )式和(13 )式不难有$ { {\varGamma}} (\eta'\eta) $ 可有如下的因子化$ A^{\rm{bc}} $ 和超鬼矩阵元$ A^{\beta\varGamma} (\eta' \eta) $ 与所涉及的D膜维度以及所带电磁通量无关, 可以分别直接计算得到$ {}_{{\rm{R}}0}\langle B_{\rm{sgh}}, \eta'|B_{\rm{sgh}}, \eta\rangle_{\rm{0 R}} $ 标记超鬼的零模贡献, 通常其要求与本分部的物质场$ \psi^{\mu} $ 零模的贡献一道正规化. 将在后面讨论这种正规化.$ p = p' $ 情形下的闭弦树图柱面振幅. 我们将看到, 这一计算也为计算$ p \neq p' $ 情形下的相应振幅奠定了基础. 这里的讨论主要基于文献[11 ,14 ]给出的一般步骤. 一旦获得闭弦树图柱面振幅, 相应的开弦单圈环带(annulus)振幅可由该闭弦振幅通过一个雅可比变换得到. 将在接下来的两节讨论这些.3.相互作用振幅及其特性: $ p = p' $ 情形 由前节讨论不难知道闭弦树图柱面振幅的计算主要是计算(17 )式中物质场矩阵元$ A^{X} $ 和$ A^{\psi} $ . 为此, 我们希望指出(9 )式矩阵M y 的两个Dp 膜, 其中一个膜带一般电磁通量$ \hat F' $ 而另一个带$ \hat F $ , 在文献[11 ]中已经计算了$ {}_{R0}\langle B'_\psi, \eta' |B_\psi, \eta\rangle_{\rm{0 R}} $ 标记该分部的零模贡献. 前面提及该零模与超鬼零模贡献结合在一起需要进行正规化才能得到有意义的结果. 后面将简单讨论这一结果. 另外, 上面$ |z| = {\rm{e}}^{- {\text{π}} t} $ , $ V_{p + 1} $ 标记Dp 膜的世界体积和$ \lambda_\alpha $ 为矩阵$ { w}_{(1 + p) \times (1 + p)} $ 的本征值. 该矩阵的定义如下:M $ { {M}}' $ 由(9 )式给出, 对应的电磁通量分别为$ \hat F $ 或$ \hat F' $ , $ { {\mathbb{I}}} $ 代表单位矩阵. 矩阵$ { {w}}_{(1 + p) \times (1 + p)} $ 可用矩阵s $ s' $ 表述为$ { {s}}' $ 与s $ \hat F $ 换为$ \hat F' $ . 注意s $ ({ {\mathbb{I}}} - \hat F) $ 和$ ({ {\mathbb{I}}} + \hat F)^{-1} $ 是可以交换的, $ { {s}}' $ 也类似. 这里“$ { {\mathbb{I}}} $ ”代表$ (1 + p) \times (1 + p) $ 单位矩阵. 矩阵s $ { {s}}_{\alpha}\, ^{\gamma} ({ {s}}^{\rm T})_{{ {\gamma}}}\, ^{\beta} = \delta_{\alpha}\, ^{\beta} $ . 矩阵$ { {s}}' $ 和矩阵w W 22 )式或(23 )式或(24 )式的计算中通过对相关振动模式, 比如$ \tilde a_{n \nu} $ 的重新定义获得. 这种重新定义振动模式以及W 28 )式可以用来极大地简化相应矩阵元的计算. 下面将用一个具体例子来演示如何得到矩阵W 22 )式的$ A^X $ , 需要计算下列$ n > 0 $ 的矩阵元,$ |0\rangle $ 标记相应的真空态. 仅仅从简化上述等式右边矩阵元计算的角度, 基于$ { {M}}' $ 是一实矩阵, 可以定义$ \tilde{\alpha}'_{\pm n \mu} = ({ {M}}' )_{\mu}\, ^{\rho}\tilde{\alpha}_{\pm n \rho} $ . 因${ { M}}' $ 同样满足 (21 )式, 因此仍然有对易关系$ [\tilde{\alpha}'_{n\, \mu}, \tilde{\alpha}'_{m\, \nu}] = $ $ \eta_{\mu\nu} \delta_{n + m, 0} $ (这里$ n, \; m $ 可正、可负). 真空态$ |0\rangle $ 仍然为真空. 由上述的定义并利用矩阵$ { {M}}' $ 的性质(21 )式, 也有$ \tilde \alpha_{-n \mu} = ({ {M}}'^{\rm{T}})_{\mu}\, ^{\nu} \tilde\alpha'_{-n \nu} $ . 对$ n > 0 $ , 把$ \tilde\alpha_{n \mu} $ 和$ \tilde\alpha_{-n \mu} $ 分别用上面定义对应的$ \tilde\alpha'_{n\mu} $ 和$ \tilde \alpha'_{-n \mu} $ 取代并代入(29 )式的右边, 有W 25 )式给出的矩阵. 在(30 )式中已拿掉$ \tilde\alpha $ 上一撇的记号“′ ”. 文献[14 ]的第3 节及附录A中仔细地讨论了矩阵W 30 )式成为$ \lambda_{\rho} $ 中有$ (9 - p) $ 个为1, 另外$ (1 + p) $ 个对应(26 )式中定义的$ { {w}}_{(1 + p) \times (1 + p)} $ 矩阵的本征值, 且具有如下特性: 对每一个本征值$ \lambda $ , 它的倒数$ \lambda^{-1} $ 也是本征值. 换句话说, 该$ (1 + p) $ 个本征值是成对出现的. 当$ p $ 为偶数时, 其中必有一个本征值为1. 为讨论方便, 下面将按下列方式标记成对出现的本征值, 即记为$ \lambda_{\alpha} $ 和$ \lambda^{-1}_{\alpha} $ , 其中$ \alpha = 0, 1\cdots [(p - 1)/2] $ 且当$ p $ 为偶数时, 取最后一个本征值$ \lambda = 1 $ . 这里$ [(p - 1)/2] $ 标记$ (p - 1)/2 $ 的整数部分. 比如$ p = 6 $ 时, 它给出整数2.$ p \leqslant 6 $ 时, 至多需要三个方程来确定相应的本征值$ \lambda_{\alpha}, \; \lambda^{-1}_{\alpha} $ , 这里$ \alpha = 0, 1, \cdots, [(p - 1)/2] $ , 且当$ p $ 为偶数时还要加上一个本征值$ \lambda = 1 $ . 具体的情况列在表1 中.p 本征值满足的关系 0 $\lambda = 1$ 1 $\lambda_{0} + \lambda^{-1}_{0} = {\rm{tr} } { {w}}$ 2 $\lambda_{0} + \lambda^{-1}_{0} = {\rm{tr} } { {w}} - 1$, $\lambda = 1$ 3 $\displaystyle\sum_{\alpha =0}^{1} (\lambda_{\alpha} + \lambda^{-1}_{\alpha}) = {\rm{tr} } { {w}}, \;\;\displaystyle\sum_{\alpha =0}^{1} (\lambda^{2}_{\alpha} + \lambda^{-2}_{\alpha}) = {\rm{tr} } { {w}}^{2}$ 4 $\displaystyle\sum_{\alpha =0}^{1} (\lambda_{\alpha} + \lambda^{-1}_{\alpha}) = {\rm{tr} } { {w}} - 1, \;\;\displaystyle\sum_{\alpha =0}^{1} (\lambda^{2}_{\alpha} + \lambda^{-2}_{\alpha}) = {\rm{tr} } { {w}}^{2} - 1, \, \lambda = 1$ 5 $\displaystyle\sum_{\alpha =0}^{2} (\lambda_{\alpha} + \lambda^{-1}_{\alpha}) = {\rm{tr} } { {w}}, \;\;\displaystyle\sum_{\alpha =0}^{2} (\lambda^{2}_{\alpha} + \lambda^{-2}_{\alpha}) = {\rm{tr} } { {w}}^{2}, \;\;\displaystyle\sum_{\alpha =0}^{2} (\lambda^{3}_{\alpha} + \lambda^{-3}_{\alpha}) = {\rm{tr} } { {w}}^{3}$ 6 $\displaystyle\sum_{\alpha =0}^{2} (\lambda_{\alpha} + \lambda^{-1}_{\alpha}) = {\rm{tr} } { {w}} - 1, \;\;\displaystyle\sum_{\alpha =0}^{2} (\lambda^{2}_{\alpha} + \lambda^{-2}_{\alpha}) = {\rm{tr} } { {w}}^{2} - 1, $ $\displaystyle\sum_{\alpha =0}^{2} (\lambda^{3}_{\alpha} + \lambda^{-3}_{\alpha}) = {\rm{tr} } { {w}}^{3} - 1,$ $ \lambda = 1$
表1 对于$p \leqslant 6$ , 决定相应本征值所需要的方程Table1. The equations needed to determine the corresponding eigenvalues for $ p \leqslant 6$ .表1 中本征值所满足的方程就足够了, 并不需要具体求解相应的本征值. 下面举一个具体例子来给予说明. 为此, 考虑$ p = 3 $ 情形. 比如, (22 )式中的如下乘积可用$ {\rm{tr}} { {w}}, \; ({\rm{tr}} { {w}})^{2} $ 和$ {\rm{tr}} { {w}}^{2} $ 来表示w 16 )式的具体紧凑表达式. 对NS-NS分部, 利用$ bc $ 鬼矩阵元(18 )式, $ \beta\gamma $ 鬼矩阵元(19 )式, 物质场$ X^{\mu} $ 矩阵元(22 )式以及物质场$ \psi^{\mu} $ 矩阵元(23 )式, 对应的NSNS振幅为18 )式, (20 )式, (22 )式和(24 )式, 有5 )式后面给出的$ c_{p} $ 的显式以及前面给的$ |z| = {\rm{e}}^{- {\text{π}} t} $ . 上面R-R振幅中的零模贡献$ \hat F $ 和$ \hat F' $ , 利用 R-R 分部零模表达式(11 )式以及(12 )式并采纳文献[21 ,26 ]中给出的正规化手段, 有33 )式和(34 )式, 并利用(15 )式, 得到如下GSO投影的NSNS振幅:39 )式时, 利用了零模(37 )式只有当$ \eta\eta' = + $ 时才不为0的特性.$ \lambda_{\alpha} = {\rm{e}}^{2{\text{π}} {\rm{i}} \, \nu_{\alpha}} $ , 其中$ \alpha = 0, \cdots [(p - 1)/2] $ . 对每一个$ \nu_{\alpha} $ , 它的取值要么是实的, 要么是纯虚的. 对于前者, 考虑到RR振幅中零模的贡献(具体见文献[14 ]中附录B的讨论), 有$ \nu_{\alpha} \in [0, 1) $ . 对于后面这种情形, 可以证明(见文献[14 ]附录A)在所有的$ \nu_{\alpha} $ 中, 最多只有一个可以取虚值. 通常取$ \nu = \nu_{0} = {\rm{i}}\bar\nu_{0} $ . 因$ \lambda + \lambda^{-1} = 2 \cosh 2{\text{π}} \bar\nu_{0} $ , 只需取$ \bar\nu_{0} \in (0, \infty) $ . $ \nu_{\alpha} $ 中最多只有一个可以取虚值主要源于矩阵w 26 )式)是一个一般洛伦兹变换, 而计算的相互作用振幅是一个洛伦兹不变量. 当所加的电场一般不能通过一个洛伦兹变换消除时, 就有这样一个虚的$ \nu $ 出现.$ \theta $ 函数和Dedekind $ \eta $ 函数(这些函数的定义请参考文献, 比如文献[27 ])来简洁地表达NSNS振幅:39 )式), 也有14 ]附录B得$ 0 \leqslant p = p' \leqslant 6 $ , 有总相互作用振幅为$ \theta $ 函数的乘积. 为方便和明确起见, 在表2 中列出了每一种情况.p 振幅表达式((44 )式)方括号中$\theta$项及其简化 0 $\theta^{4}_{3} (0 |it) - \theta^{4}_{4} (0 |it) - \theta^{4}_{2} (0 | it) = 2\, \theta^{4}_{1} (0 | it) = 0$ 1 或 2 $\theta^{3}_{3} (0 |it) \theta_{3} (\nu_{0} |it) - \theta^{3}_{4} (0 |it) \theta_{4} (\nu_{0} |it) - \theta^{3}_{2} (0 |it) \theta_{2} (\nu_{0} | it) = 2\, \theta^{4}_{1} \left(\left.\dfrac{\nu_{0}}{2}\right| it \right)$ 3 或 4 $\theta^{2}_{3} (0 |it) \theta_{3} (\nu_{0} |it) \theta_{3} (\nu_{1} |it)- \theta^{2}_{4} (0 |it) \theta_{4} (\nu_{0} |it) \theta_{4} (\nu_{1} |it)- \theta^{2}_{2} (0 |it) \theta_{2} (\nu_{0} | it)\theta_{2} (\nu_{1} | it)$$= 2\, \theta^{2}_{1} \left(\left.\dfrac{\nu_{0} + \nu_{1} }{2}\right|it \right) \theta^{2}_{1} \left(\left.\dfrac{\nu_{0} - \nu_{1} }{2}\right|it \right)$ 5 或 6 $\theta_{3} (0 |it) \theta_{3} (\nu_{0} |it) \theta_{3} (\nu_{1} |it) \theta_{3} (\nu_{2} |it) - \theta_{4} (0 |it) \theta_{4} (\nu_{0} |it) \theta_{4} (\nu_{1} |it) \theta_{4} (\nu_{2} |it)$$ - \theta_{2} (0 |it) \theta_{2} (\nu_{0} | it)\theta_{2} (\nu_{1} | it) \theta_{2} (\nu_{2} | it) $ $= 2\, \theta_{1} \left(\left.\dfrac{\nu_{0} + \nu_{1} + \nu_{2} }{2}\right| it \right) \theta_{1} \left(\left.\dfrac{\nu_{0} - \nu_{1} + \nu_{2} }{2}\right| it \right) \theta_{1} \left(\left.\dfrac{\nu_{0} + \nu_{1} - \nu_{2} }{2}\right| it \right)\theta_{1} \left(\left.\dfrac{\nu_{0} - \nu_{1} - \nu_{2} }{2}\right| it \right) $
表2 振幅表达式((44 )式)方括号中$\theta$ 项及其简化Table2. The $\theta$ -terms in the square bracket in Eq. (44 ) and their simplification.表2 中, 还利用了文献[28 ]中有关$ \theta $ 函数的如下恒等式$ w', x', y' $ 和$ z' $ 与$ w, x, y, z $ 有如下的关系:$ \theta_{1} (0 |\tau) = 0 $ . 由表2 , 可以观测到$ p = 4 $ 或$ 3 $ , $ p = 2 $ 或$ 1 $ 及$ p = 0 $ 情形可以通过$ p = 6 $ 或$ 5 $ 情形分别取$ \nu_{2} = 0 $ , $ \nu_{2} = \nu_{1} = 0 $ 以及$ \nu_{2} = \nu_{1} = \nu_{0} = 0 $ 或它们相应的极限获得. 只要取相应的极限, 这一特性使得对应的$ p = p' < 5 $ 的振幅((44 )式)可以看成$ p = p' = 6 $ 或$ 5 $ 时的振幅在如下表达式意义下的一种特例:47 )式中的第一个等式, 通过积分变量t 的雅可比变换$ t \to t' = 1/t $ , 可以获得相应的开弦单圈环带(annulus)振幅为51 )式第一个等式时, 利用了$ \theta_{1} $ 函数和Dedekind $ \eta $ 函数的如下特性:51 )式第二个等式中, 已经去掉t 上的一撇. 在有电场出现时, 考虑其中一个$ \nu_{\alpha} $ , 比如$ \nu_{0} $ 是虚的情况. 为此, 取$ \nu_{0} = {\rm{i}} \bar\nu_{0} $ , 其中$ \bar\nu_{0} \in (0, \infty) $ . 对这种情况, 开弦单圈环带(annulus)振幅(51 )式的第二式可写为$ Z_{n} $ 仍由(52 )式给出, 只是现在$ \nu_{0} = {\rm{i}} \bar\nu_{0} $ . 考察振幅(56 )式中的被积函数, 注意到其分母中有一个因子$ \sin({\text{π}}\bar\nu_{0}t) $ , 它在正t 轴上(注意积分变量$ t > 0 $ )有无穷多零点, 发生在$ t_{k} = k/\bar\nu_{0} $ , 这里$ k = 1, 2, \cdots $ . 这些零点是该被积函数的单极点, 恰好反映前面讨论的在加电场时系统的不稳定性, 即系统在这些极点处产生正反开弦对, 释放由所加电场造成的多余能量使其衰变成能量更低的稳定状态. 由文献[19 ], 该系统单位体积非微扰衰变率是该被积函数在这些极点处留数的和并乘以$ {\text{π}} $ , 结果为$ |z_{k}| = {\rm{e}}^{-k{\text{π}}/\bar\nu_{0}} $ . 根据文献[27 ], 正反开弦对产生率由(57 )中第二等式首项($ k = 1 $ )给出为47 )式或(51 )式及正反开弦对产生率(59 )式的一般特性. 对每一具体p 的相互作用一般特性(排斥还是吸引)的讨论, 可参考文献[14 ]. 这里将主要相关结论总结一下. 采用的约定为: 振幅大于零对应吸引相互作用, 而振幅为负对应排斥相互作用. 研究[14 ] 发现: 1)当三个参数$ \nu_{0}, \nu_{1}, \nu_{2} $ 至少有一个为零或其中有一个为虚数时, 对应的相互作用为吸引; 2)仅当这三参数都为实且都不为零时, 排斥相互作用才有可能, 即仅当$ p = 6 $ 时才有可能. 具体分两种子情形来讨论: a) $ \nu_{0} + \nu_{1} + \nu_{2} < 2 $ , 这里$ \nu_{\alpha} \in [0, 1) $ , $ \alpha = 0, 1, 2 $ . 当这三个参数中最大的一个小于另外两个之和时, 对应的相互作用为排斥; 反之, 相互作用则为吸引. b) $ \nu_{0} + \nu_{1} + \nu_{2} > 2 $ . 不难验证, 给定$ \nu_{\alpha} \in [0, 1) $ , 三个参数中最大的只能小于另外两个之和, 这时对应的相互作用为吸引. 换句话说, 这种情况下相互作用只能是吸引的. 另外一种特殊情况是$ \nu_0 + \nu_1 + \nu_2 = 2 $ , 对应的相互作用为零.47 )式, 只要取前面提到的$ \nu_{2} = 0 $ 或$ \nu_{2} = \nu_{1} = 0 $ 或$ \nu_{2} = \nu_{1} = \nu_{0}$ $ = 0 $ 就可以得到$ p = p' < 5 $ 各种情形下对应的振幅. 在利用D膜边界态计算平行放置且有一定间距的两张同维度或不同维度的D膜间柱面振幅时, 对应每一个D膜世界体的维度信息仅体现在它的M 9 )式, 玻色零模(10 )式以及物质场RR分部费米零模(11 )式中. 其他的都与这一维度无关. 首先来仔细考察该M $ \alpha, \beta $ 标记沿膜的方向而$ i, j $ 标记垂直该膜的方向. 比如, 作为一个例子, 先考虑D6膜. 这里有$ \alpha, \beta = 0, 1, \cdots 6 $ 及$ i, j = 7, 8, 9 $ . 对其他的偶数$ p < 6 $ 的Dp 膜, 有沿膜方向$ \alpha', \beta' = 0, 1, \cdots p $ , 垂直膜方向$ i', j' = p + 1, \cdots 9 - p $ . 对应一般世界体电磁通量$ (\hat F_{p})_{\alpha'\beta'} $ 的$ { M}_{p} $ 矩阵可以看成为D6膜$ { M}_{6} $ 矩阵的一种特殊情形. 对偶数$ p < 6 $ 的Dp 膜, 有$ \alpha', \beta' = 0, 1, \cdots, p $ 扩展到$ \alpha, \beta = 0, 1, \cdots 6 $ 以及$ F_{p} $ 到$ F_{6} $ 并将之取如下特别的形式,$ k = 1, \cdots, (6 -p )/2 $ 对应磁通量取极限$ \hat g_{k} \to \infty $ , 该$ { M}_{6} $ 矩阵正好给出$ { M}_{p} $ 矩阵. 下面来具体看看细节. 对于所取特殊通量(62 )式, 有$ k = 1, \cdots, (6 - p)/2 $ 取极限$ g_{k} \to \infty $ , 上面的$ ({ M}_{6})_{\alpha\beta} = (({ M}_{p})_{\alpha'\beta'}, - \delta_{k'l'}) $ , 其中$k', l' \!=\! p \!+\! 1, \cdots 6$ . 这样就有$ { M}_{6} = (({ M}_{p})_{\alpha'\beta'}, - \delta_{i'j'}) ={ M}_{p} $ . 换句话说, $ { M}_{p} $ 实际上可看成为D6世界体通量取上述特殊情况下$ { M}_{6} $ 的一种特殊形式而已. 同样的讨论也适合从$ p = 5 $ 得到奇$ p < 5 $ 的情形.43 )式. 相关的具体讨论及细节请参考文献[14 ]中的附录B. 这两方面的考虑解释了振幅(47 )式中被积函数中的如下部分:64 )式对$ p = p' = 5 $ 或$ 6 $ 适用. 但只要对应的通量取如(62 )式的特殊形式并取相应的极限, (64 )式就会约化为$ p = p' < 5 $ 情形下期待的表达式. 然而, 玻色零模(10 )式的情况却不一样. 除整体因子$ [\det (\eta_{p} + \hat F_{p})]^{1/2} $ 外, 该零模的其他部分与所加通量无关, 因此上述对M $ V_{\rm{NN}} = V_{p + 1} $ 标记Dp 膜的世界体的体积(NN代表开弦的两个端点同时满足所谓纽曼边界条件涉及世界体时空方向的个数), DD代表开弦的两个端点同时满足狄里克莱边界条件空间方向的个数. 这里有DD$ = 9 - p $ . 很显然, $ p = p' < 5 $ 时振幅(47 )式中的被积函数因子$ t^{- (9 -p)/2} $ 是不可能通过取特殊通量及取相关极限从$ p = p' = 5 $ 或$ 6 $ 获得的. 由此解释了柱面振幅(47 )式为何对$ p = p' < 5 $ 情形也适用.[8 ,10 ,11 ,13 ,14 ] (后面将以$ p = 3 $ 情况为例从物理角度给予解释), 给出最大增强效应的电磁场具有如下形式:$ (1 + p) \times (1 + p) $ 的方阵. 不难看出, 这一形式的电磁场要求$ p \geqslant 3 $ . 对这种形式的电磁场, 开弦对产生率(59 )式的具体表达式为$ Z (\bar\nu_{0}, \nu_{1}) = Z_{1} (\bar \nu_{0}, \nu_{1}, \nu_{2} = 0) $ (后者的定义见(58 )式和(59 )式), 其显式为$ \hat f' = 0, \; \hat g' = 0 $ . 另外, 目前实验室能实现的直流电场和磁场相对弦尺度来说都非常小$ e E \approx $ $e B \approx 10^{-8 }\; m^{2}_{\rm e} $ , 这里$ m_{\rm e} $ 为电子的质量(比如② 29 ]). 通常在QED中, 探测施温格对需要的电场为$ e E \approx m^{2}_{\rm e} $ , 对应前面给出的$ E \approx 10^{18}\; {\rm {V/m}} $ . 如果取实验允许的最低弦标度$ M_{\rm{s}} = 1/\sqrt{\alpha'} $ 约几个TeV[30 ] , 有$ \hat f = 2{\text{π}} \alpha' e E \approx \hat g $ $ = 2{\text{π}} \alpha' e B \approx 6 \times 10^{- 8}\; m^{2}_{\rm e} /M^{2}_{\rm{s}} \approx 10^{- 20} \ll 1 $ . 由(69 ) 式, 有$ {\text{π}} \bar \nu_{0} \approx 2 {\text{π}} \alpha' e E \ll 1, \; {\text{π}} \nu_{1} \approx 2{\text{π}} \alpha' e B\ll 1 $ , 因此$ \bar \nu_{0} \ll 1, \nu_{1} \ll 1 $ . 基于此, $ Z (\bar\nu_{0}, \nu_{1}) \approx 1 $ , 反映在这种情况下只有开弦最低模式对产生率有贡献. 对此, 无量纲的开弦对产生率为$ p \geqslant 3 $ 和$ \bar\nu_{0} \ll 1 $ , 由(70 ) 式不难看出, 如果对所有$ p \geqslant 3 $ 的膜所加的电场和磁场都一样, $ p = 3 $ 给出的无量纲产生率$ (2{\text{π}}\alpha')^{(1 + p)/2} {\cal{W}}^{(1)} $ 将最大, 比如$ p = 4 $ 与$ p = 3 $ 产生率之比为$ (\bar\nu_{0}/4{\text{π}})^{1/2} \approx 10^{- 11} $ . 因此, 如果这种对产生可以探测的话, $ p = 3 $ 将最有可能. 另外, 文献[12 ]也证明了, 对于$ p \geqslant 5 $ , 如果在4和5方向再加一个磁张量(选择(66 ) 式中的磁场为最大), 这种新加的磁场对产生率起到减弱而不是增强作用. 为此, 下面将局限$ p = 3 $ 来讨论. $ p = 3 $ 对应的是D3膜, 其时空维度与我们生活的(1 + 3)维世界一致, 因此探讨这种情形也有一定的现实意义.$ p = 3 $ , 开弦对产生率(70 ) 式可以用实验室下的电场E 和磁场B 重新写为69 ) 式在弱场下给出$ {\text{π}}\bar\nu_{0} = 2{\text{π}} \alpha' e E$ $ \ll 1, \; {\text{π}} \nu_{1} = 2{\text{π}} \alpha' e B \ll 1 $ , 并定义了开弦最低质量模式的质量为m 就是该粒子的质量. 下面从弦理论角度来理解上述产生率. 在没有电磁场时, 连接两张D3膜开弦的质量谱为$ p = (k, 0) $ , k 为沿世界体方向的时空动量, $ N_{\rm{R}} $ 和$ N_{\rm{NS}} $ 分别为R分部和NS分部的粒子数算子, 它们的标准表达式为:$ N_{\rm{R}} \geqslant 0 $ )给出的是费米自由度而NS分部($ N_{\rm{NS}} \geqslant 1/2 $ )给出的是玻色自由度. 当$ y = 0 $ 时, $ N_{\rm{R}} = 0, \; N_{\rm{NS}} = 1/2 $ 给出的就是4维N = 4 U (2)规范理论. 这里有$ 4 (8_{\rm{F}} + 8_{\rm{B}}) $ 无质量自由度, 其中下标F代表费米自由度而B代表玻色自由度. 因此有$ 32_{\rm{F}} + 32_{\rm{B}} $ . 当$ y \neq 0 $ , $ U(2) $ 自发破缺为$ U(2) \to U(1) \times U(1) $ , 两个破缺的生存元给出$ 2 (8_{\rm{F}} + 8_{\rm{B}}) $ 有质量自由度, 它们的质量都为$ m = T_{f} y = y/(2{\text{π}}\alpha') $ , 分别对应的是一根开弦和一根反开弦的最低质量自由度. 开弦的端点都带相应没有破缺的$ U(1) $ 电荷. 从一张D3膜上来看, 开弦和反开弦的端点分别对应4维$ N = 4 $ 具有同样质量超对称规范带正电和带负电的自由度(其中每一个包括5个有质量带电标量, 4个有质量带电旋量, 1个有质量带电矢量). 它们形成了8个正反费米子自由度对和8个正反玻色子自由度对, 共给出16个正反自由度对. 所有这些自由度具有同样质量, 源于规范破缺前后$ N = 4 $ 超对称没有破缺. 因此在弱场情况下, 对产生率是这16个自由度对的产生率, 其中包括5个有质量带正反电荷的标量对, 4个有质量带正反电荷的旋量对, 还有1个有质量带正反电荷的矢量对. 下面来验证这一点.71 ) 式与QED相关的对产生率分别做一比较. 在电场和磁场同时出现时, 带电QED标量对和QED旋量对产生率分别为[31 ,32 ] :[33 ] $ m_{\rm{s}} $ . 在没有磁场时($ B = 0 $ ), 如果取所有的质量相等为m , 不难检验有e ), 在没有磁场时每一个自由度正反荷对的产生率是一样的. 这一结论可以从$ {\cal{W}}_{\rm{scalar}} = {\cal{W}}_{\rm{spinor}}/2 = {\cal{W}}_{\rm{vector}}/3 $ 关系得出, 因一个标量具有一个物理自由度, 一个旋量有两个物理自由度, 而一个有质量的矢量有三个物理自由度. 同时这也解释了上面得到的$ {\cal{W}}^{(1)} $ 与其他产生率的关系(78 ) 式. 再考虑另外一种情况, 即当$ B/E $ 很大时(对给定的E , 这意味着大磁场或有限的B 但$ E \approx 0 $ ). 这时有:$ {\cal{W}}^{(1)} $ 与矢量情况完全一致. 下面将对这些差别和相同之处给出解释. 为此, 考虑一个质量为$ m_{\rm{s}} $ , 自旋为S 带正电e 的粒子放入弱磁场B 背景中的运动, 其能谱为(见参考文献[34 ])$ g_{\rm{S}} $ (gyromagnetic ratio)为回旋磁比(这里$ g_{\rm{S}} = 2 $ ), N 为朗道能级. 对最低朗道能级($ N = 0 $ ), 由(80 ) 式有最低的能量为$ B \cdot S = 0, \; B/2, \; B $ . 换句话说, 当$ S \neq 0 $ 时, 自旋沿着磁场方向的极化分量或自由度给出的是最低能量(对带负电荷的粒子对应自旋极化正好相反). 对自旋$ S = 0 $ 的标量, 加上磁场后, 其原有的能级提升, 源于该粒子在加磁场后零点运动的贡献; 对自旋$ S = 1/2 $ 的费米子, 自旋与磁场同方向极化的能级与磁场无关, 仍由其静止质量决定, 但其与磁场相反方向的极化对应的能量为$ E_{1/2} = 2 e B + m^{2}_{1/2} $ ; 对自旋$ S = 1 $ , 自旋与磁场同方向的极化降低其原有能级, 而对于另外两个极化$ B \cdot S = 0, - B $ , 对应的能级都比原有的提高. 由于这里没有考虑加电场, 因此可视为$ B/E \to \infty $ . 在这种情况下, 自旋$ S = 1/2 $ 的两个极化对相应的正反自由度对的产生来说, 它们的对产生率之比为$ {\rm{e}}^{- 2 e B/E} \to 0 $ . 换句话来说, 任何相对最低能量态高的能量态对产生率都可以视为零. 也就是说, 最多只需要考虑最低能量极化的对产生率. 这一结论同样适用自旋$ S = 1 $ 情况. 总结一下, 当$ B/E $ 很大时, 对每一给定自旋, 只有自旋沿磁场方向这一极化对对产生率有贡献, 对应的能量由(81 ) 式决定. 也就是说, 贡献给对产生的只有一个自由度. 这解释了为何(79 ) 式中各种自旋对产生率非指数因子完全一样, 这同时也解释了(79 ) 式中各种自旋对产生率中指数因子对磁场的关系. 当$ B/E $ 很大时, 不同自旋的对产生率可以统一表述为$ E_{\rm{S}} $ 对不同自旋对应(81 ) 式中相关量. 上面的讨论同时说明, 如果不同自旋的带电粒子具有同样的质量, 当$ B/E $ 很大时, 最低能量的矢量极化对产生率将远大于标量和旋量对产生率. 产生矢量粒子对将是最可能的. 这也解释了为何在$ B/E $ 大时, $ {\cal{W}}^{(1)} $ 与矢量对产生率一致.71 ) 式实际上是5个带电标量对, 4个带电旋量对以及1个带电矢量对的贡献, 这些自由度都具有同样的质量. 由此, 当取所有自由度具有同样质量m 时, 我们期待有下列关系71 ) 式和场论计算结果(75 ) 式—(77 ) 式对(83 ) 式给予直接检验, 发现的确正确. 注意(83 ) 式左边是弦理论计算结果而右边是场论计算结果, 计算方式完全不同, 但物理上的考虑它们应该一致. 这里验证了的确如此, 这也从另一个角度说明了计算的正确性, 理论上验证了弦理论的自洽性.71 ) 式是否有观测效应. 由于该系统在加电场和磁场前是超对称的, 欧洲核子中心大型强子对撞机目前没有发现超对称, 因此该公式中的质量参数m 应该不小于TeV. 而实验室的电场和磁场$ e E \approx e B \approx 10^{- 8}\; m^{2}_{\rm e} $ 远小于TeV, 因此在这种实验室条件下不可能探测到开弦端点给出的正反电荷对.4.相互作用振幅及其特性: $ p \neq p' $ 情形 本节将首先计算两个平行放置、有一定间距y 、空间维度不一样的Dp 膜和${\rm{D}}p'$ 膜间的相互作用, 其中每一个都带其膜上的一般常电磁通量. 不失一般性, 可以假设$ p > p' $ . 有$ p - p' = \kappa = 2, 4, 6 $ 且$ p \leqslant 6 $ . 本节将推广上节使用的计算技巧从而可以利用前节$ p = p' $ 计算的柱面(cylinder)振幅获得本节$ p \neq p' $ 对应的振幅. 一旦获得了该柱面振幅, 同样可以用一个雅可比变换得到相应的开弦单圈环带(annulus)振幅, 讨论相关振幅的特性并在有电场出现的情况下讨论对应的开弦对产生及探测的可能性.${\rm{D}}p'$ 膜上的一般通量$ \hat F'_{p'} $ , 按上节中把一个Dp 膜($ p < 5 $ )上的通量扩展到D5或D6膜上通量的类似方式, 扩展到Dp 膜上的通量$ F'_{p} $ . 换句话说, 首先把${\rm{D}}p'$ 膜上的通量$ F'_{p'} $ 做如下扩展:$ \alpha, \beta = 0, 1, \cdots, p $ ; $ \alpha', \beta' = 0, 1, \cdots p' $ 及$ \kappa = 2, 4, 6 $ . 与上节($ p = p' $ )的情况一样, 在计算的最后只要对每一个$ k = 1, \cdots, \kappa/2 $ 对应的磁通取极限$ \hat g'_{k} \to \infty $ , 这样的扩展就不会改变由(9 )式给出当前情况下对应的矩阵$ { M}'_{p'} $ 以及物质场RR分部零模对振幅的贡献. 进一步, 对物质玻色场零模做同样的考虑时, 与前一节不一样, 这里得到了意外的结果. 下面来对此给予具体的解释. 按常规, 如同(65 )式一样, 这里物质玻色场零模对振幅的贡献为$ V_{\rm{NN}} = V_{p' + 1} $ 和$ {{\rm{DD}}} = 9 - p $ . 如果采用前面提到的技巧, 则有t 的依赖关系完全一样. 它们的差别发生在对t 无关的部分. 由(84 )式 , 当对每一个$ k = 1, \cdots, \kappa/2 $ 对应的磁通量取极限$ \hat g'_{k} \to \infty $ , 有$ \det (\eta_{p} + \hat F'_{p}) = $ $ (1 + \hat g'^{2}_{1})\;\cdots\; (1 + \hat g'^{2}_{\kappa/2}) \;\det\;(\eta_{p'} + \hat F'_{p'}) \;=\; \hat g'^{2}_{1} \cdots \hat g'^{2}_{\kappa/2} $ $ \det(\eta_{p'} + \hat F'_{p'}) $ . 由此有$ V_{p + 1} = V_{p' + 1} V_{\kappa} $ . 对一个带通量(84 )式 的Dp 膜, 可以有各种耦合, 其中一个与${\rm{D}}p'$ 膜相关的耦合如下:$ \hat F' $ 的个数是$ (p -p')/2 $ 且$ C_{p ' +1} $ 是可与${\rm{D}}p'$ 膜耦合的$ (p' + 1) $ 形式的RR势. 很清楚, 如果对$ k = 1, \cdots, \kappa/2 $ 对应的所有磁通取极限$ \hat g'_{k} \to \infty $ , 在所有可能的耦合中, 起主导作用的耦合如下:$ p - p' = \kappa $ 且耦合前面的系数标记着${\rm{D}}p'$ 膜以其张力为单位的量子化荷N . 换句话说, 有86 ) 式可表述为$ T_{p'}/T_{p} = c_{p'}/c_{p} $ , 其中边界态归一化常数$ c_{p} = \sqrt{{\text{π}}} (2{\text{π}} \sqrt{\alpha'})^{3 - p} $ (见(5 )式后面). 因子$ c_{p'}/c_{p} $ 恰好把因子$ c^{2}_{p} $ (计算$ p = p' $ 时柱面振幅出现的因子(见(16 ) 式))转化为$ c^{2}_{p} \times c_{p'}/c_{p} $ $ = c_{p} c_{p'} $ , 后者是目前振幅的正确因子. 这里的量子化荷N 是一无穷大正整数, 采用的技巧实际计算了一张Dp 膜和N 张${\rm{D}}p'$ 膜之间的相互作用振幅③ p 和一张${\rm{D}}p'$ 膜之间的相互作用振幅, 需要对所计算的振幅除以整数N . 基于这些, 对$ p - p' = \kappa > 0 $ 的闭弦树图柱面振幅可由振幅(47 ) 式得到为[14 ] 93 )式的第一个等式中$ \varGamma_{p, p} $ 是用扩展的通量$ \hat F'_{p} $ ((84 ) 式)得到的柱面振幅(47 )式 , 在第二个等式中用了$ V_{p + 1} = V_{p' + 1} V_{\kappa} $ 以及(92 )式, 在第三个等式中用了表达式$ c_{p} = \sqrt{{\text{π}}} (2{\text{π}}\sqrt{\alpha'})^{3 - p} $ , 以及$ C_{n} $ 继续由(48 )式给出. 另外, 在上面取了必要的极限$ \hat g'_{k} \to \infty $ ($ k = 1, \cdots \kappa/2 $ ), 前节中有关$ \nu_{\alpha} $ 的讨论同样适用这里. 显然上面的柱面振幅的基本结构与前节讨论的$ p = p' $ 情形一致. 由此我们期待同样的振幅特性, 比如相互作用的本质(吸引还是排斥)以及可能的不稳定性. 相关的讨论见文献[14 ]且结论与前节$ p = p' $ 时一致, 这里不再重复. 对这里考虑的系统, 我们也期待一些新的特点出现, 将在本节的后面给予讨论.94 ) 式, 对应的开弦单圈环带振幅可从该式第一个等式通过一个标准的雅可比变换得到(具体见前节). 该开弦单圈环带振幅为$ Z_{n} $ 继续由(52 ) 式给出. 该开弦单圈环带振幅可以用来分析小y 时的行为, 比如快子不稳定性以及当$ \nu_{0} $ 为虚数的时候该系统通过产生开弦对衰变的情况. 下面就这两方面进行讨论.$ \nu_{0}, \nu_{1} $ 和$ \nu_{2} $ 都为实且$\nu_{0} + \nu_{1}$ $ + \nu_{2} < 2 $ 时, 如果这三个磁参数最大的大于另外两个之和, 对应的相互作用为吸引. 这时当膜间间距小于一定值时就会出现快子不稳定性. 当$ \nu_{0} + \nu_{1} + \nu_{2} > 2 $ 时, 尽管这时最大的参数只能小于两个之和且相互作用只能是吸引, 同样也有快子不稳定性出现. 由于振幅(95 ) 式对$ \nu_{0}, \nu_{1}, \nu_{2} $ 是对称的, 不失一般性, 可以假定$ \nu_{2} \geqslant \nu_{1} \geqslant \nu_{0} $ . 我们知道$ \nu_{\alpha} \in [0, 1) $ ($ \alpha = 0, 1, 2 $ ). 首先考虑$ \nu_{0} + \nu_{1} + \nu_{2} < 2 $ 和$ \nu_{2} > \nu_{0} + \nu_{1} $ . 这时振幅的被积函数对$ t \to \infty $ 表现为$ y < {\text{π}} \sqrt{2 (\nu_{2} - \nu_{1} - \nu_{0})\alpha'} $ 时为无穷大, 表明出现快子不稳定性. $ \nu_{0} + \nu_{1} + \nu_{2} > 2 $ 时, 一定有$ \nu_{2} < \nu_{0} + \nu_{1} $ . 简单地看, 似乎没有这种发散出现. 但实际上这时$ Z_1 $ 与其他$ Z_n $ ($ n \geqslant 2 $ )不一样会给出一个负的指数发散项, 从而也有快子不稳定性出现, 具体见文献[14 ]中的讨论. 这里的情况与前节$ p = p' $ 时情形一样[14 ] .$ \nu_{0} = i \bar\nu_{0} $ 为虚的(这里$ \bar\nu_{0} \in (0, \infty) $ ), 振幅(95 ) 式中的被积函数因子$ \sin{\text{π}}\nu_{0} /\sinh{\text{π}}\nu_{0} t $ 成为$ \sinh{\text{π}}\bar\nu_{0}/\sin{\text{π}}\bar\nu_{0} t $ , 表明出现了无穷多被积函数的单极点, 发生在$ t_{k} = k/\bar\nu_{0} $ ($ k = 1, 2, \cdots $ ). 这说明振幅有一虚部, 反映所考虑的系统通过所谓的开弦对产生进行衰变. 单位体积的衰变率可按前面的方式计算为$ |z_{k}| = {\rm{e}}^{- k {\text{π}}/\bar\nu_{0}} $ . 与前面一样, 开弦对产生率由上面$ k = 1 $ 项给出, 为$ p \geqslant 5 $ . 与上节类似, $ p = 3, 4 $ 时的振幅或开弦对产生率可以通过取$ \nu_{2} \to 0 $ 极限得到, 而$ p = 2 $ 时相应的量可以通过$ \nu_{1}, \nu_{2} \to 0 $ 极限得到. 对每一个具体情况的讨论参考文献[14 ]. 下面将集中讨论一种与生活的(1 + 3)维世界关联的情形$ p = 3, \; p' = 1 $ . 我们将看到这种系统产生的开弦对是有可能被生活在D3膜上的观察者所探测的, 因此可为上节末提出的问题提供一个可能的答案.94 )式第二等式得到($ \nu_{2} = 0 $ )闭弦柱面振幅为$ |z| = {\rm{e}}^{- {\text{π}} t} $ , 参数$ \bar\nu_{0} $ 和$ \nu_{1} $ 由下面相应的公式确定$ \bar\nu_{0} \in [0, \infty), \nu_{1} \in (0, 1) $ . 只要y 不是特别小, 指数因子$ {{\rm{Exp}}[- y^{2}/(2{\text{π}}\alpha' t)]} $ 告知上面振幅积分表示的积分贡献主要来自比较大t 的积分. 不难看出这时该振幅所有因子都是正的, 因此该振幅也是正的, 反映D3和D1间相互作用为吸引. 这也是期待的, 因D3和D1间只有NSNS (引力)相互作用引力, 没有RR-荷间的相互作用. 同时这也意味着该系统不保持任何超对称. 但当y 很小时, 情况有所不同. 这时小t 对该振幅可以有重要贡献. 在振幅(101)的被积函数中, 无穷乘积因子的分母有一个因子在小t 时可以小于零, 即$[1 - 2 |z|^{2 n} \cosh(2{\text{π}}\bar\nu_{0})$ $+ |z|^{4 n}] \approx 2 (1 - \cosh (2{\text{π}} \bar\nu_{0})) < 0$ . 这样该振幅就有无穷多个小于零的因子乘积, 其正负号难以确定. 这种不确定性通常暗示着新物理的出现, 但在闭弦柱面振幅下难以看出. 为此, 要将其转换为开弦单圈环带振幅. 由(95 )式, 有该开弦单圈环带振幅为$ \sin({\text{π}}\bar\nu_{0} t) $ 外, 其他因子都是正定的. 因子$ \sin({\text{π}}\bar\nu_{0} t) $ 沿着正t 轴具有无穷多个零点, 发生在$ t_{k} = k/\bar\nu_{0} $ , 其中$ k = 1, 2, \cdots $ . 这些零点是该被积函数的单极点, 表明该D3/D1系统相互作用振幅具有一个虚部, 反映该系统的不稳定性. 由前面的讨论不难知道, 这种系统的衰变正是由于所加电场导致的开弦对产生所引起. 与前面一样, 根据文献[19 ], 可计算对应的衰变率. 具体为振幅((103 ) 式)的被积函数在这些单极点的留数之和乘以$ {\text{π}} $ 并除以D1的体积$ V_{2} $ , 结果为$ |z_{k}| = {\rm{e}}^{- {\text{π}} k/\bar\nu_{0}} $ . 相应开弦对的产生率, 对应上面衰变率$ k = 1 $ 项[27 ] , 为97 )式和(99 )式取$ p = 3, p' = 1, \nu_{2} = 0 $ 以及通量为(97 )式的特殊情形.$ \hat f' = 0 $ . 相对弦尺度, D3膜上实验室电场和磁场都很小, 即$ |\hat f| \ll 1 $ 和$ |\hat g| \ll 1 $ . 由此, 从(102 ) 式有$ \bar\nu_{0} \!\approx\! |\hat f /{\text{π}}| \!\ll\! 1 $ 和$ \nu_{1} \!\lesssim\! 1/2 $ . 注意到$ |z_{1}| \!=\! {\rm{e}}^{- {\text{π}}/\bar\nu_{0}}\!\to\! 0 $ 以及$ \nu_{1}/\bar\nu_{0} \gg 1 $ , 开弦对产生率(106 ) 式成为$ |\hat f| = 2{\text{π}} \alpha' e E $ , 其中e 为通常正电子带的电荷, E 为实验室电场, $ m = T_{f} y = y/(2{\text{π}}\alpha') $ . 定义一个有效质量$ m^{2}_{\rm{eff}} = m^{2} - \nu_{1}/(2\alpha') $ . 磁通$ \hat g = 2{\text{π}} \alpha' e B \ll 1 $ , 其中B 是通常实验室中的磁场. 与质量为m 对应的产生率相比, 产生率(107 ) 式有一个指数增强因子$ {{\rm{Exp}}}[{\text{π}} \nu_{1}/(2\alpha' e E)] $ . 该因子对目前考虑的系统可以很大, 因此对产生率起了巨大的增强效应.107 ) 式的用处之前, 先来确定该产生率起源于哪些开弦模式. 为方便这里的讨论, 采用本节开始用的技巧, 即把这里的D1有效地看成带一个沿2和3方向无穷大的磁通的D3膜. 该磁通的具体形式如下:$ \hat g' \to \infty $ . 这里先取$ \hat g' $ 有限但很大(最后取$ \hat g' \to \infty $ 极限), 由(69 ) 式有$ \hat g' \to \infty $ , 就得到(102 ) 中的第二式. 对于一般大的$ \hat g' $ , 这里考虑的等效系统为D3/D3, 其中人们生活的D3带(100 )式中的第一个通量, 而等效的D3带上面(108 ) 式的通量. 类似前节对那里的D3/D3系统的讨论, 当D3膜上没有通量出现时, 连接两张D3膜的开弦质量谱为$ p = (k, 0) $ , 其中k 是沿膜方向上的动量, $ N_{\rm{R}} $ 和$ N_{\rm{NS}} $ 分别是标准的R分部和NS分部的粒子数算子, 它们的具体形式分别为:$ y = 0 $ , 每一个这种连接两张D3膜的超对称开弦, 除有无穷多的质量不为零的模式外, 还拥有16个无质量模式, 其中8个为玻色自由度($ 8_{\rm{B}} $ ), 8个为费米自由度($ 8_{\rm{F}} $ ). 如果用D3膜来描述这16个无质量自由度, 它们对应D = 4, N = 4超对称U (2)规范理论中一个U (2)生存元. 当$ y \neq 0 $ , 该生存元将破缺, 对应的无质量$ 8_{\rm{B}} $ (1个无质量的矢量, 6个标量)将获得质量, 成为1个有质量的矢量, 5个有质量的标量(其中的一个无质量标量获得真空期望值, 给出$ y \neq 0 $ ). 8个无质量$ 8_{\rm{F}} $ 将成为4个4维有质量Majorana费米子. 当$ y = 0 \to $ $ y \neq 0 $ , $ U(2) \to U(1) \times U(1) $ , 其中有两个生存元破缺, 对应的是两根开弦(正反开弦对)的无质量模式获得质量, 没有破缺的两个U (1), 一个对应的是人们生活的D3, 另一个对应的是等效的D3. 从D3膜上看, 一根开弦的16个($ 8_{\rm{B}} + 8_{\rm{F}} $ )有质量自由度每一个带有对应的没有破缺的U (1)正电荷, 另一根的16个($ 8_{\rm{B}} + 8_{\rm{F}} $ )自由度的每一个带负电荷, 构成了16对正反粒子对, 其中1个矢量正反粒子对, 5个标量正反粒子对, 4个Majorana正反旋量粒子对. 所有的这32个自由度都具有同样的质量$ m = T_{f} y = y/(2{\text{π}} \alpha') $ , 对应(110 )式中$ N_{\rm{R}} = 0, \; N_{\rm{NS}} = 1/2 $ . 所有这些自由度具有同样的质量源于规范对称破缺前后超对称没有变化.$ \hat g \ll 1 $ , 而在有效D3上加一个大的磁场$ \hat g' $ . 当$ y \neq 0 $ , R分部的能量是正定的, 其真空态由8个有质量的费米自由度$ 8_{\rm{F}} $ 或4个有质量的4维Majorana旋量构成. 如同QED情形一样[34 ,35 ] , 加磁场后所有费米自由度的质量都不会降低. 对NS分部, 情况将不一样. 相应的能级[34 ,35 ] 成为$ \nu_{1} $ 由(109 )式给定, 朗道能级$ N = b^{+}_{0} b_{0} $ , 沿23-向的自旋算子为$ N^{\perp}_{\rm{NS}} $ 标记除2和3方向以外其他方向对粒子数算子的贡献. 在加磁场情况下, 特别当$ y = 0 $ , GSO投影的超弦态可能成为快子的第一Regge轨迹[34 ] , 具体由下式给定:$ |0 \rangle_{\rm{NS}} $ 为NS分部的真空. 对这些态有$ S = \tilde n + 1 \geqslant 1 $ . 在没有磁通出现时, 上面给出的就是NS分部的质量谱$ S = 1 $ 的态$ d^{+}_{1/2} |0\rangle_{\rm{NS}} $ , $ y = 0 $ 给出的质量为零, 而$ y \neq 0 $ 给出的质量为非零. 后者也对应上面提到的规范对称性破缺$ U(2) \to U(1) \times U(1) $ , 其中矢量玻色子的质量$ m = y/(2{\text{π}} \alpha') $ .117 )式和(118 )式不难看出, 自旋$ S = 1 $ 的态$ d^{+}_{1/2} |0\rangle_{\rm{NS}} $ 具有最低能量, 为$ \nu_{1}/2 $ 通常称为快子移动(tachyonic shift). 不难考察, 该最低能量就是接着开弦产生率(107 )式后定义的有效质量$ m_{\rm{eff}} $ . 这也暗示开弦对产生率(107 )式来源于一对具有上述能量的正反矢量极化模式. 其他模式以及其他自旋的各种极化模式对的贡献在$ \bar\nu_{0} \ll 1 $ 和$ \nu_{1}/\bar\nu_{0} \gg 1 $ 的情况下都趋于零. 下面来解释为何$ \nu_{1}/\bar\nu_{0} \gg 1 $ .[13 ] , 即使对系统D3/D1中的D3膜上不加任何磁场, 也有一个固有的$ \nu_{1} = 1/2 $ . 这里的D1, 如上面的讨论, 等效地可看成一个带无穷大磁通的D3. 正是如此, 有$ \nu_{1}/\bar\nu_{0} \gg 1 $ . 因此在$ 2(8_{\rm{F}} + 8_{\rm{B}}) $ 中, 仅有一对具有相同最低能量或有效质量的正反矢量极化对产生率有贡献, 给出产生率(107 )式.32 ]以及文献[13 ]中的讨论)都很小, 因此一般有$ \bar \nu_{0} \ll 1 $ 以及从(102 )式有$ \nu_{1} \lesssim 1/2 $ (因$ \hat g = 2 {\text{π}} \alpha' e B \ll 1 $ ). 对于这种实验室所加的电场和磁场, 这里把前节中D3/D3系统的开弦对产生率(71 )式, QED有质量带电矢量场对产生率(77 )式[33 ] 和这里计算的D3/D1系统的产生率(107 )式列在下面来做一个对比,m . 由前节的讨论知, $ {\cal{W}}^{(1)} $ 是$ D = 4 $ , $ N = 4 $ 有质量超对称规范理论的对产生率, 包括5个带电标量对, 4个带电旋量对和1个带电矢量对的贡献, 而QED计算的$ {\cal{W}}_{\rm{vector}} $ 仅包括1个矢量对的贡献. 所以这两者的差异可以理解, 由(83 )得以反映. 尽管$ {\cal{W}}^{(1)} $ 是从弦理论计算得到的, 但在$ \bar\nu_{0} \ll 1 $ 极限下, 它与$ D = 4 $ , $ N = 4 $ 有质量带电规范理论的计算结果应该一样. 但$ {\cal{W}}^{(1)}_{{\rm{D3}}/{\rm{D1}}} $ 有所不同. 从本节上面的讨论知, 对其贡献的只有一对具有最低能量的正反矢量模式, 而不是矢量场的三对模式. 由前节的讨论知道, 如果$ B/E \gg 1 $ , 也只有一对最低能量的矢量模式对$ {\cal{W}}^{(1)} $ 和$ {\cal{W}}_{\rm{vector}} $ 有贡献, 且120 )式中的$ {\cal{W}}^{(1)}_{{\rm{D3}}/{\rm{D1}}} $ 完全不同. 由前节的讨论知, 对实验室的E 和B , 因m 是弦质量标度, 其平方远大于$ e E $ 或$ e B $ , 因此$ {\cal{W}}^{(1)} $ 和$ {\cal{W}}_{\rm{vector}} $ 都极小, 但这里的$ {\cal{W}}^{(1)}_{{\rm{D3}}/{\rm{D1}}} $ 可以较大, 只要$ e E \approx m^{2}_{\rm{eff}} =$ $ m^{2} - \nu_{1}/(2\alpha') $ (注意$ \nu_{1} \sim 1/2 $ ). 后者其实不难满足, 只要D1与D3间的间距满足$ y \gtrsim y_{0} \equiv $ $ {\text{π}} \sqrt{2 \nu_{1} \alpha'} \approx {\text{π}} \sqrt{\alpha'} $ . 由此可见, 尽管都是矢量模式的贡献, $ {\cal{W}}^{(1)}_{{\rm{D3}}/{\rm{D1}}} $ 与通常场论计算结果很不一样, 起因是D3附近出现了D1, 反映了非微扰弦理论的信息. 因此, 可以把这种起源于弦理论的开弦对产生率$ {\cal{W}}^{(1)}_{{\rm{D3}}/{\rm{D1}}} $ 以及其与所加电场和磁场的关系看成为一种弦理论的标志. 也就是说, 如果可以探测这种对产生以及验证其与所加电场和磁场的关系(107 )式及(107 )式中$ \nu_{1} $ 与所加磁场的关系, 就发现了一种不需要紧化时空而提供检验弦理论的特征方式. 另外, 因这里的开弦对是沿额外维方向, 因此这也是一种发现额外维的手段.$ y \gtrsim y_{0} \equiv {\text{π}} \sqrt{2 \nu_{1} \alpha'} \approx {\text{π}} \sqrt{\alpha'} $ . 一方面这种要求使得D3膜上任何实验室宏观区域上的均匀电场和磁场都可以看成计算中使用的均匀电场和磁场(因这样的宏观尺度远远大于膜间距y ), 但另一方面这一要求对实现这样要求的D3/D1系统提出了挑战. 在快子凝聚发生前$ y > y_{0} $ , D3和D1间的相互作用一般是吸引的, 这从(101 )式或(103 )式不难看出. 这一吸引力总可以使比较大的y 能够达到$ y\gtrsim y_{0} $ . 我们期待在量子引力起主导作用期间, 比如宇宙极早期, D3和D1都会充满10维时空. 在宇宙演化到今天(物质为主以后), D3和D1间的吸引可能早已让y 达到$ y_{0} $ , 并经历了快子凝聚, 形成了所谓1/2 BPS (D1, D3)束缚态. 换句话说, D3膜附近目前还存在这种D1的几率应该不大, 这也使得探测这种正反开弦对不可能那么容易, 更细节的讨论见文献[15 ].5.讨论与总结 本文系统地讨论了作者之一及其合作者近10年来关于平行放置、有一定间距且带一般世界体常电磁通量的两个D膜间的相互作用及其特性的研究工作. 这两个D膜的空间维度可以一样, 也可以不一样, 比如一个为Dp 膜, 另一个为 ${\rm{D}}p'$ 膜, 且$ p - p' = \kappa = 0, 2, 4, 6 $ . 不失一般性, 假设$ p \geqslant p' $ . 为保证在弱弦耦合情况下, 相关的D膜在不远小于弦尺度下可以看成是刚性的, 则要求$ p \leqslant 6 $ .$ C_{n} $ 继续由(48 )式给定. 对每一对p 和$ p' $ ($ p - p' = 0, 2, 4, 6 $ 及$ p \leqslant 6 $ ), 对应的振幅, 如前两节描述的, 可以看成上面一般公式(122 )式的特殊情形. 对应的开弦单圈环带振幅可以由(122 )式通过所谓雅可比变换$ t \to t' = 1/t $ 以及对应的$ \theta_{1} $ 函数和Dedekind $ \eta $ 函数关系(55 )式给出为t 上的一撇, 且$ Z_{n} $ 也继续由(52 )式给定. 如果三参数$ \nu_{0}, \nu_{1}, \nu_{2} $ 其中之一, 比如$ \nu_{0} $ , 是虚的, 对应的系统要经历所谓的开弦对产生过程. 对应系统的衰变率为$ Z_{k}(\bar\nu_0, \nu_1, \nu_2) $ 由(98 )式给定. 对应的开弦对产生率由(124 )式的领头项($ k = 1 $ )给定为$ p' \leqslant p = 6 $ 且$ \nu_{0}, \nu_{1}, \nu_{2} $ 三参数都为非零实数以及$ \nu_{0} + \nu_{1} + \nu_{2} < 2 $ 时, 如果其中最大的参数大于另外两个参数之和, 对应的相互作用为吸引, 反之则为排斥. 当相互作用为吸引且两膜间的间距小于一定距离时, 开弦快子不稳定性就会出现. 如果相互作用为排斥, 则没有快子不稳定性. 然而, 当$ \nu_{0} + \nu_{1} + $ $\nu_{2} > 2 $ 时, 这时最大的参数只能小于其余两个之和且相互作用是吸引的, 同样也有快子不稳定出现. 当$ p'\leqslant p < 6 $ 时, 膜间相互作用只能是吸引. 相关的物理原因已在正文中讨论, 这里不再重复.$ \nu_{0}, \nu_{1}, \nu_{2} $ 其中之一为虚数时, 对应的系统将通过产生开弦对衰变. 这体现在开弦单圈振幅有一个虚部. 不失一般性, 取$ \nu_{0} = {\rm i} \bar \nu_{0} $ , 其中$ \bar\nu_{0} \in (0, \infty) $ . 振幅虚部的出现源于所加的电场. 当所加的电场达到其临界值时, 有$ \bar\nu_{0} \to \infty $ , 这时不难从(125 )式看出开弦对产生率变为无穷大, 开弦对这时将雪崩式地产生, 给出系统的另一种不稳定性. 对于一般的非临界电场, 开弦对产生率在加一定的磁场时会有增强效应. 这种增强效应从弦理论角度来看, 与加磁场时出现的快子移动有关, 在一般情况下为$ |\nu_{2} - \nu_{1}|/2 $ , 其中$ \nu_{1}, \nu_{2} \in [0, 1) $ . 这一移动的出现, 可以把有些开弦态的质量平方减小$ |\nu_{2} - \nu_{1}|/(2\alpha') $ . 正是由于这些虚开弦模式对的质量减少, 使得它们在加同样电场的情况下更容易从虚对被拉成实的正反开弦对.$ \nu_{1} $ 和$ \nu_{2} $ 中最大的一个, 而取相应的磁场使得其中小的一个为零, 这样给出的快子移动$ |\nu_{1} - \nu_{2}|/2 $ 为最大. 不失一般性, 通常取$ \nu_{2} = 0 $ . 现在的问题是加什么样的电场和磁场可以给出最大的增强效应.$ \bar\nu_{0} \ll 1 $ 很小. 从(98 )式不难看出, $ Z_{1} (\bar\nu_{0}, \nu_{1}, \nu_{2} = 0) \approx 1 $ . 根据第三 节讨论的情形, 这时也有$ \nu_{1} \ll 1 $ , 且D3/D3系统会给出最大开弦对产生率. 但由于该系统在加实验室电场和磁场前保持一般时空超对称, 因此连接这两个D3的最低开弦质量应不小于几个TeV[32 ] , 远大于实验室电场或磁场对应的标度. 换句话说, 实验室所加的电场和磁场不可能使虚的开弦对成为实的, 从而不能被探测到. 第3 节仔细讨论了这种情况. 在第4 节中, 讨论了$ p - p' = 2 $ 系统. 我们发现对D3/D1系统, 即使在D3上不加任何电磁场, D1对连接D3和D1间开弦所起的作用相当于加了一个弦尺度的磁场使得$ \nu_{1}/2 = 1/4 $ , 因此可以给出一个大的增强效应. 也正是由于这样一个大的等效磁场的出现, 使得开弦最低质量谱中的有质量带电矢量模的其中一个极化的质量被压低(对反开弦对应的是反极化模式), 给出一个可以比较小的等效质量, 从而使得所加实验室电场给出的$ e E $ 可以与该等效质量的平方相比拟, 因此有可能产生对应矢量模式的正反极化对. 第4 节给出了详细的讨论. 我们希望强调对应的产生率与所加电场和磁场的关系完全不同于通常QED的计算结果, 因此可以看成为一种弦理论的特征行为. 如果我们的确验证了这种行为, 比如验证由正反极化模式给出的电流与实验室所加电场和磁场的关系符合计算, 这对弦理论是一种检验, 同时也预言了额外维的存在. 另外, 我们要强调的是每一个矢量极化模式的实际质量至少为TeV, 其能被探测的原因是由于D1给出一个大的等效磁场从而把该质量压低到一个比较小的等效质量. 然而, 如文献[15 ]中讨论的, 要实现这种探测还是有一定难度的, 主要是实现所期待的D3/D1系统并不容易. 





























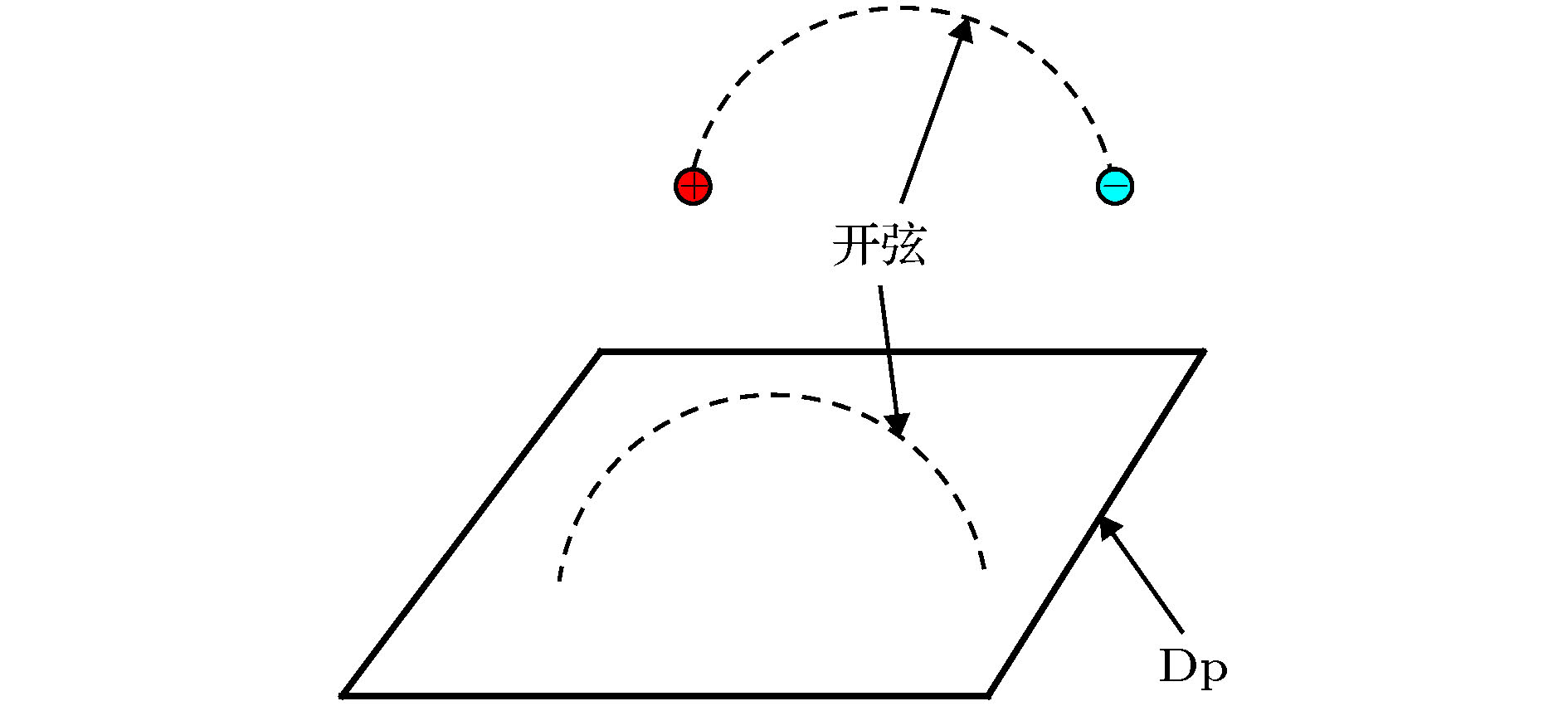 图 1 D膜
图 1 D膜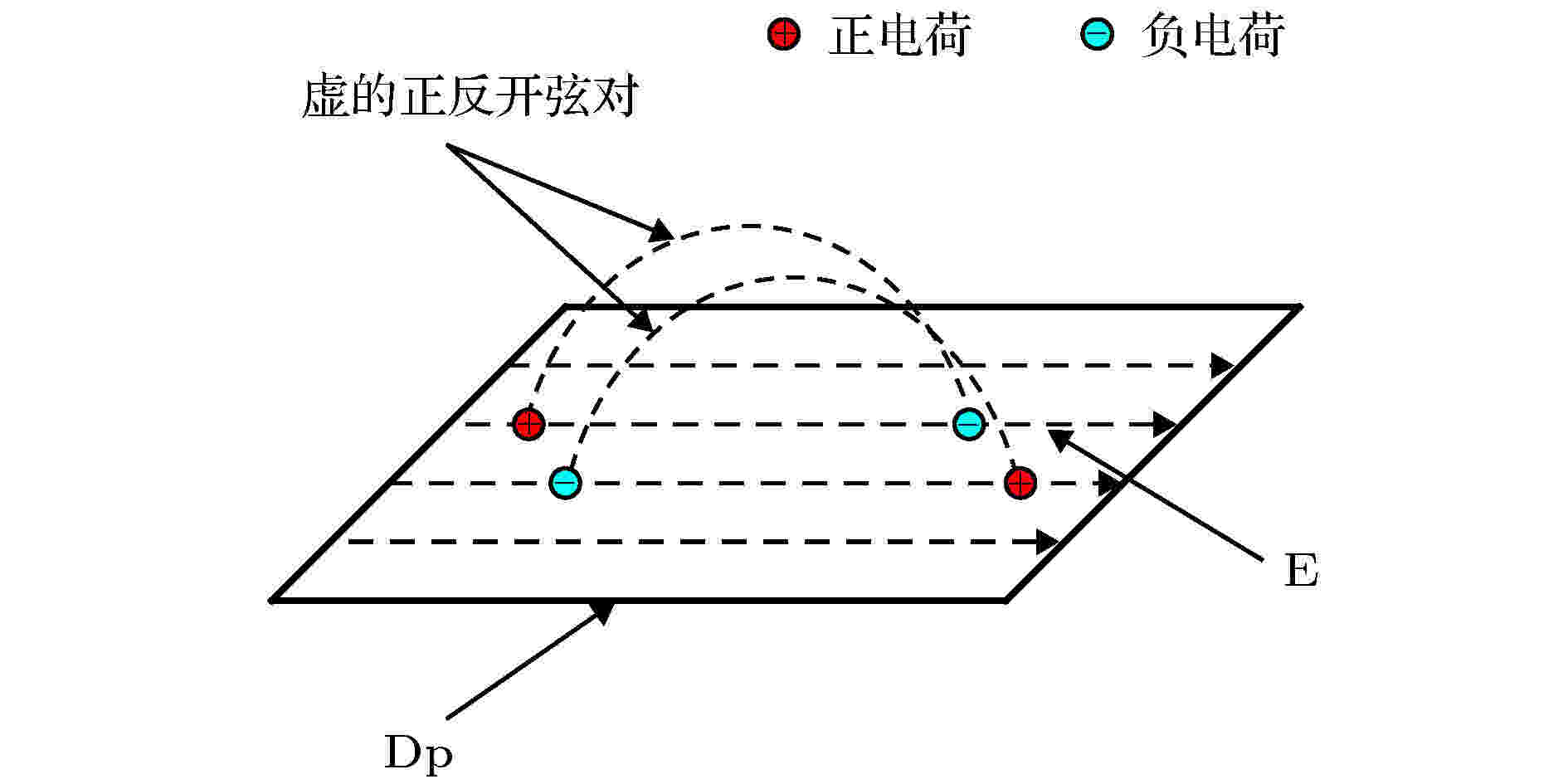 图 2 虚开弦对
图 2 虚开弦对


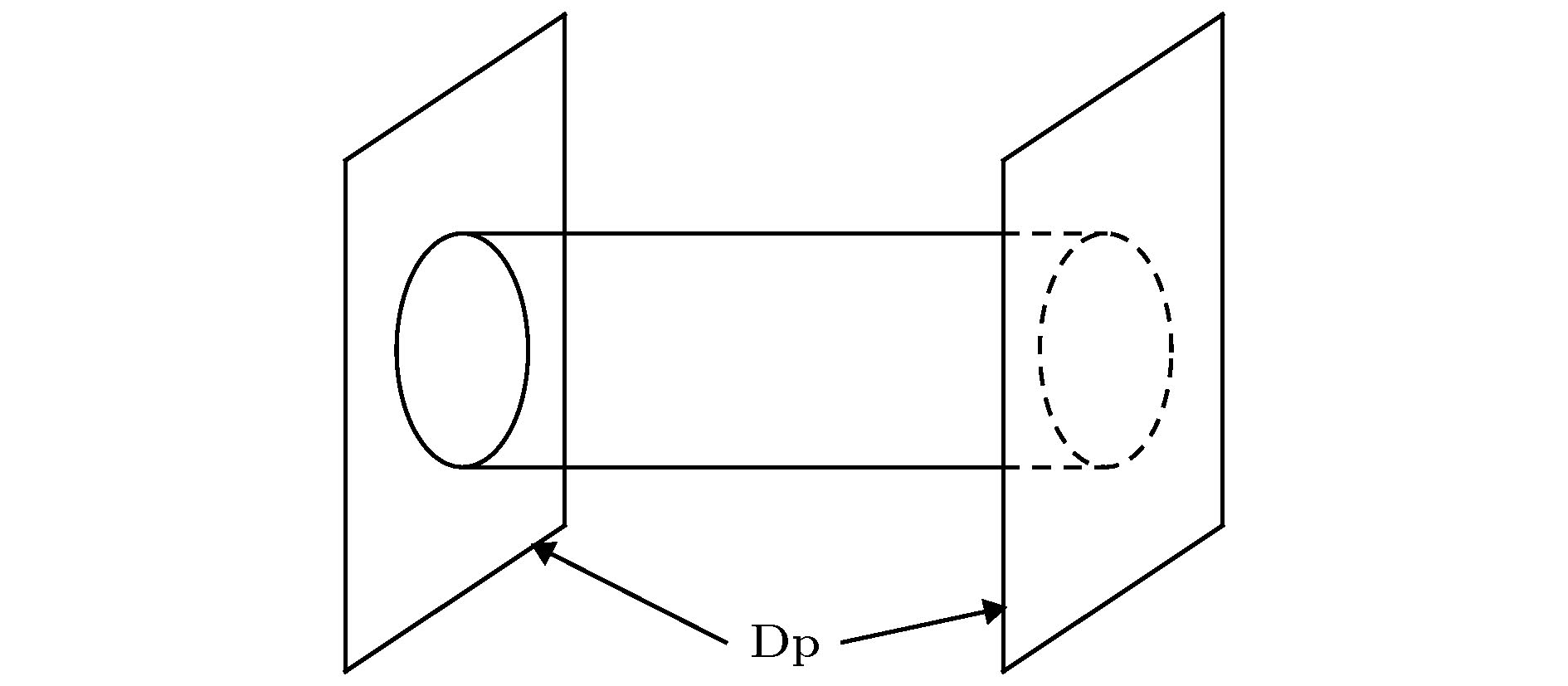 图 3 闭弦树图相互作用与开弦单圈相互作用的等价性
图 3 闭弦树图相互作用与开弦单圈相互作用的等价性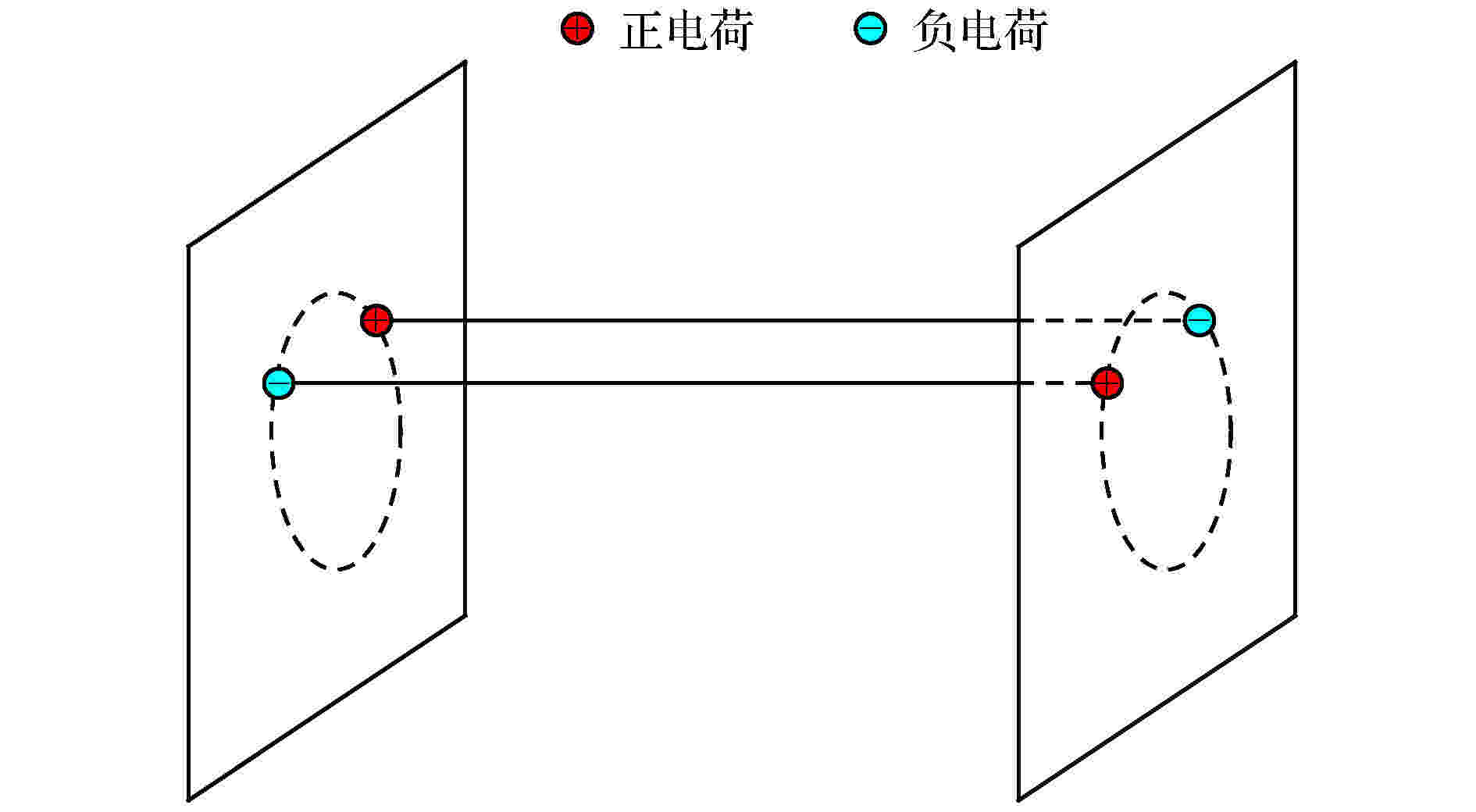 图 4 一根虚开弦转一个闭合时间圈等价于虚正反开弦对的产生和湮灭
图 4 一根虚开弦转一个闭合时间圈等价于虚正反开弦对的产生和湮灭



















































































































































































































































































































































































































































































































































































































































































