摘要: 节律行为, 即系统行为呈现随时间的周期变化, 在我们的周围随处可见. 不同节律之间可以通过相互影响、相互作用产生自组织, 其中同步是最典型、最直接的有序行为, 它也是非线性波、斑图、集群行为等的物理内在机制. 不同的节律可以用具有不同频率的振子(极限环)来刻画, 它们之间的同步可以用耦合极限环系统的动力学来加以研究. 微观动力学表明, 随着耦合强度增强, 振子同步伴随着动力学状态空间降维到一个低维子空间, 该空间由序参量来描述. 序参量的涌现及其所描述的宏观动力学行为可借助于协同学与流形理论等降维思想来进行. 本文从统计物理学的角度讨论了耦合振子系统序参量涌现的几种降维方案, 并对它们进行了对比分析. 序参量理论可有效应用于耦合振子系统的同步自组织与相变现象的分析, 通过进一步研究序参量的动力学及其分岔行为, 可以对复杂系统的涌现动力学有更为深刻的理解.
关键词: 同步 /
序参量 /
涌现 /
分岔 English Abstract Synchronization of coupled phase oscillators: Order parameter theory Zheng Zhi-Gang 1,2 ,Zhai Yun 3,1,2 ,Wang Xue-Bin 1,2 ,Chen Hong-Bin 1,2 ,Xu Can 1,2 1.Institute of Systems Science, Huaqiao University, Xiamen 361021, China Received Date: 26 December 2019Accepted Date: 31 January 2020Published Online: 20 April 2020Abstract: Rhythmic behaviors, i.e. temporally periodic oscillations in a system, can be ubiquitously found in nature. Interactions among various rhythms can lead to self-organized behaviors and synchronizations. This mechanism is also responsible for many phenomena such as nonlinear waves, spatiotemporal patterns, and collective behaviors in populations emerging in complex systems. Mathematically different oscillations are described by limit-cycle oscillators (pacemakers) with different intrinsic frequencies, and the synchrony of these units can be described by the dynamics of coupled oscillators. Studies of microscopic dynamics reveal that the emergence of synchronization manifests itself as the dimension reduction of phase space, indicating that synchrony can be considered as no-equilibrium phase transition and can be described in terms of order parameters. The emergence of order parameters can be theoretically explored based on the synergetic theory, central manifold theorem and statistical physics. In this paper, we discuss the order-parameter theory of synchronization in terms of statistical physics and set up the dynamical equations of order parameters. We also apply this theory to studying the nonlinear dynamics and bifurcation of order parameters in several typical coupled oscillator systems.Keywords: synchronization /order parameter /emergence /bifurcation 全文HTML --> --> --> 1.引 言 节律, 即系统呈现的随时间周期变化, 广泛存在于我们生活的世界, 从钟摆、星体运动到生物钟, 都是不同系统典型的动力学行为. 复杂与非线性系统会表现出多种多样的自组织与群体性行为[1 -3 ] , 而不同的节律之间也可以通过相互作用涌现出各种集体的自组织现象, 其中同步是最典型、最直接的有序行为, 它也是诸如非线性波、时空斑图乃至各种生物集群行为(例如鸟群、鱼群、蜂群、蚁群、人类社会等)的内在物理机制[4 ,5 ] .[5 ] . Wiener[6 ] 在其专著中关于“脑电波与自组织系统”一章指出, 脑电波的出现是来自于不同频率的锁定(pulling together of frequencies), 而且这种行为与其他诸如萤火虫同步闪光、蟋蟀同声鸣唱等现象有着共同的机制. 而如何在极限环基础上来研究驱动或相互作用的振子间的同步在理论上就成为重要课题.[7 ] 于1967年提出了全局耦合振子模型. 他认识到, 在同步问题上, 极限环之间相互作用起作用的关键自由度是其相位, 因此只需要考虑耦合的相位振子模型即可揭示同步的动力学实质. Winfree模型的动力学方程可写为i = 1, 2, ···, N 来标记不同振子, {θi }代表振子的相位, {ωi }为振子的自然频率, 它们各不相同, 设符合某个统计分布函数g(ω ). Winfree发现, 自然频率分布较窄时振子之间会相互同步[7 ] . 这样, 在众多不同物理背景下出现于不同体系中的很多现象就都可以利用耦合相振子系统的同步动力学来得到非常好的解释. 大量相互作用振子出现的整体同步行为是一种典型的集体涌现, 如何解析刻画同步涌现是一个挑战性课题.[8 -10 ] 考虑振子数目N → ∞ (热力学极限), 自然频率$\{ {\omega _i}\} $ 为单峰分布g (ω ), 振子间相互作用是耦合强度为K 的全局性平均场形式, 并取最简单的相位差的正弦函数sin?(?θ )来描述相互作用. 平均场耦合相振子模型可写为[11 ] . 我们还引入振子的集体自然频率$\bar \omega = \displaystyle\frac{1}{N}\mathop \sum \nolimits_{i = 1}^N {\omega _i}$ . 一般情况下自然频率分布函数设为关于$\bar \omega$ 的对称分布. 为讨论方便, 通常设$\bar \omega=0$ , 分布对称性满足$g\left( \omega \right) = g\left( { - \omega } \right)$ .K ≠ 0)各振子的实际振动频率都会相应地从K = 0时的自然频率{ωi }处发生偏离, 并随耦合强度变化而变化. 可定义振子的平均频率Ωi 为R = |z |描述振子的相干性强弱, $\varTheta $ 为一任意相位.Ωi 都不等, 它们在任一时刻的相位都均匀分布于0— 2π之间, 如图1(a) 所示, 此时R = 0. 随着耦合强度的增加, 越来越多的振子会同步, 平均频率Ωi 相等, 这些同步的振子相位之间会靠近并保持固定相位关系, 振子不再均匀分布, 如图1(b) 所示. 当所有Ωi 都相等时, R 就不为零, 表明此时振子之间可保持固定的相位关系. 存在一个临界的耦合强度K c , 当K ≤ K c 时R = 0; 当K ≥ K c 时, R ≠ 0. 在很强的耦合下, 振子相位会靠得很近, 形成整体的同步大集团, 如图1(c) 所示. 大量耦合振子可以通过相互作用克服自然频率不同带来的无序而涌现出同步态实质上就是一种典型的非平衡相变. 在临界K c 处发生的相变在理论上可以处理. Kuramoto利用统计物理学方法和自洽方程成功求解[9 ,10 ] , 理论上得到了临界耦合强度Kc , 并得到在K c 附近序参量R 的临界行为.图 1 耦合振子同步示意图 (a) 在耦合强度很弱时, 大量振子不同步, 任一时刻相位均匀分布于0?2π之间; (b)随着耦合强度的增加, 越来越多的振子会同步, 振子不再均匀分布; (c) 在很强的耦合下, 振子相位会靠得很近, 形成整体的同步大集团; (d) 序参量随耦合强度的变化Figure1. A schematic diagram of synchronization of coupled oscillators: (a) Most of the oscillators are asynchronous and evenly distributed along the circle; (b) with increasing the coupling, more and more oscillators are synchronized and are no longer evenly distributed; (c) under a strong coupling, oscillators form a single synchronous cluster, and the phases of oscillators are close to each other; (d) dependence of the order parameter on the coupling strength[11 -17 ] . 人们研究了不同耦合函数[18 ,19 ] 、不同耦合网络拓扑结构[14 ,15 ,20 -25 ] 、脉冲耦合[26 ] 等情况下的同步, 探讨了同步涌现的玻璃态[27 ] 、非对称耦合及其行波和驻波波态[28 ,29 ] 、惯性效应[30 ,31 ] 、阻挫效应[32 -35 ] 、时间延迟效应[36 ] 、外场驱动效应[37 ] 、时变耦合[38 ] 等与实际物理背景密切相关的问题. 以Kuramoto模型为代表的耦合振子系统集体动力学问题时至今日一直是重要的研究热点.[39 -41 ] 和同步分岔树方法[42 -44 ] 可以对耦合振子的微观动力学进行研究. 当振子数目$N \gg 1 $ 时, 微观动力学分析会变得很繁杂, 可以利用统计物理和宏观方法开展研究. 早期Kuramoto基于统计物理学方法和自洽方程理论成功地对同步相变进行了解析研究[9 ] . 但自洽方程方法建立在同步态为定态的前提下, 近年来人们发现了大量非定态集体动力学行为, 因此有必要建立一套反映集体动态行为的统计与宏观理论[45 ] . 20世纪90年代初, Watanabe与Strogatz发现[46 ] , 一类具有对称性的耦合振子系统的高维动力学可以通过引入M?bius变换(后称为Watanabe-Strogatz变换, 简称WS变换)精确降维到三维空间, 这意味着系统的部分可积性. Ott与Antonsen[47 ,48 ] 提出了序参量拟设理论, 将高维微观动力学研究降维到二维序参量空间加以研究. 人们随后意识到, OA拟设下的二维动力学实际上是WS变换下的三维动力学的进一步降维[49 ,50 ] .[51 ] .2.Kuramoto自洽方程理论 首先来看Kuramoto如何通过引入序参量并利用求解自洽方程来解析处理同步问题. 自洽方法的基础是通过假设系统存在一个不随时间改变的定态, 在此状态下序参量为一个待定的定值, 通过序参量的定义和系统定态的运动方程, 得到待定的序参量的值, 并在分析的过程中得到此序参量与相应定态的存在条件. 自洽方法从其方法本身便限定了其适用范围, 虽然只能用于对定态的分析, 却可以不受具体动力学的限制, 是振子系统分析中广泛使用的方法之一.N 足够多情况下, 序参量(4 )式与N 无关且不随时间变化. 考虑到Kuramoto模型(2 )式相互作用的平均场形式, 很容易可以将方程(2 )重新写为R , 则方程(5 )完全可以求解, 但这不是一件简单的事. 一个可行的办法是带着未知R 继续讨论, 建立一个关于R 的方程来将其求解. 该方程即为自洽方程(self-consistent equation)[8 ,51 ] . 下面的讨论即是围绕这一主题展开.R = 0对应于无相互作用的情形(均匀分布解), 这个非相干态总是系统的一个解, 但不总是稳定. 当$K > {K_{\rm{c}}}$ 时均匀分布解失稳. 另外一个解是Ωi 都相等时的解, 此时振子之间可以保持固定的相位, R ≠ 0, 所有振子都以集体频率$\bar \omega $ 转动, $\varTheta = \bar \omega t$ . 此解在$K \leqslant {K_{\rm{c}}}$ 时不稳定. 只要有Ωi 不相等, ${\theta _i}$ 就总是均匀分布于0—2π之间.${\phi _i} = {\theta _i} - \bar \omega t$ , (5 )式可写为6 )描述的第i 个振子满足$\left| {{\omega _i} - \bar \omega } \right| \leqslant KR$ 时, 该振子的相位? 就会保持定值${\phi _i} = {\sin ^{ - 1}}[({\omega _i} - \bar \omega )/(KR)]$ , 这意味着所有满足该条件的振子都会以$\bar \omega$ 频率运动, 它们处于同步状态. 2) 非同步解. 当方程(6 )描述的振子i 满足$\left| {{\omega _i} - \bar \omega } \right| > KR$ 时, 则该振子的相位? 就会随时间变化, 且凡是自然频率满足该条件的振子都处于非同步状态.N →∞时, ${\phi _i}$ 在0—2π之间会形成分布. 设分布函数为P (? , ω , t ), 它不仅依赖于? , 还依赖于振子自然频率ω . 平均场由分布函数可表为? 的统计分布, 则需要进一步对频率做积分$P(\phi, t) = $ $ \displaystyle\int {P(\omega, \phi, t)g(\omega ){\rm{d}}\omega } $ . 这些振子相位的分布直接决定了相关的平均量, 例如序参量, 因而很重要的一点就是如何确定分布函数. 根据上面讨论的两类定态解, 可把分布P (? )分解为同步与非同步两部分:? 趋于不动点, 与时间无关, 因此${P_{\rm{s}}}(\phi )$ 可由自然频率分布得到:?i 则随时间变化, 因为?i 随时间变化是非均匀的, 单位时间内探测到? 在$\phi \to $ ? + d? 之间的概率反比于相速度$|\dot \phi |:\; p(\phi, \omega ) \propto |{\dot \phi } |^{-1}$ . 把运动方程(6 )式代入并归一化可得到$x = \omega - \bar \omega $ , 并考虑到$g(\bar \omega + x) = g(\bar \omega - x)$ , 将(11 )式代入(12 )式积分可写为9 )式可得14 )式中${P_{{\rm{as}}}}(\phi )$ 部分积分为零, 只有${P_{\rm{s}}}(\phi )$ 对积分有贡献. 进一步将积分实部和虚部分离, 可得到(注意R 为实):16 )式可以确定$\bar \omega $ (实际上在原方程中可通过对称性确定). (15 )式是一个自洽方程, 由此可以确定R 和同步临界耦合强度${K_{\rm{c}}}$ . 当$K \geqslant {K_{\rm{c}}}$ 时, R 由零连续变为一个小量, 因此可把$g(\omega )$ 在$\bar \omega $ 附近展开:$g''(\bar \omega ) = {\left. {{{\rm{d}}^2}g(\omega )/{\rm{d}}{\omega ^2}} \right|_{\omega = \bar \omega }}$ . 代入(17 )式可以得到$K \to {K_{\rm{c}}}$ 时, 由于R 2 项为高阶小量, R →0, 由此得到同步临界耦合强度为19 )式代回(18 )式可以确定在临界点K c 附近R 的行为:$g(\omega ) = {\{ {\text{π}}[{(\omega - \bar \omega )^2} + {\gamma ^2}]\} ^{ - 1}}\gamma $ 的情况, 临界耦合为K c = 2γ , 序参量$R = \sqrt {(1 - 2\gamma /K} )$ . 可以看出R 在K c 附近为典型的连续相变$R \propto {(K - {K_{\rm{c}}})^{1/2}}$ , 如图1(d) 所示. 需要指出的是, 这是一种非平衡相变, 是系统有序(耦合)压倒无序(自然频率随机分布)的结果.3.序参量及其涌现的自组织原理 耦合振子同步微观动力学的研究表明, 大量耦合振子随着耦合强度的增加会经历由部分同步到整体同步的过渡, 相空间维数随同步进程而逐渐降低, 整体同步时, 系统在相空间的复杂运动会落到一个极低维的空间[42 -44 ] . 降维意味着系统发生同步的时候, 只需要少数变量即可刻画耦合振子系统的同步. 该结果为多振子体系同步的宏观及序参量描述提供了事实基础.[27 ] . 热力学和统计物理学的思想和方法为处理耦合振子同步转变问题提供了思路. 由大量相互作用振子组成的系统通常是非平衡系统, 同步是大量振子整体动力学从无序向有序的非平衡相变. 非平衡行为研究自20世纪中期发展起来的以耗散结构理论[52 ,53 ] 、协同学[54 ,55 ] 以及多学科分支形成的自组织理论等为描述众多的非平衡相变现象的共同本质提供了重要依据.[53 ] .[54 ] . 协同学的基本原理是支配原理(slaving principle), 它认为, 协同系统的状态由一组状态参量来描述, 这些状态参量弛豫时间尺度是不相同的, 慢变的线性不稳定模称为慢变量(slow variable), 而快变的线性稳定模称为快变量(fast variable). 当系统接近于发生显著质变的临界点时, 慢模数目会减少为只有一个或少数几个, 这些慢变量可以完全确定系统的宏观行为并表征系统的有序化程度, 故而称为序参量. 而为数众多的快模则由慢模/序参量所支配, 并可将其绝热消去, 由此可以建立少自由度的协同学基本方程. 在序参量方程基础上, 我们就可来研究协同系统的各种非平衡定态/非定态、稳定性及其非平衡相变[55 ] .n 维动力学系统为例来简单介绍一下支配原理:${{x}}\left( t \right) = {({x_1}\left( t \right), {x_2}\left( t \right), \cdots, {x_n}\left( t \right))^{\rm{T}}}$ 为n 维状态矢量, A $n \times n$ 常数矩阵, B x x x A $\left\{ {{\lambda _i}, i = 1, 2, \cdots, n} \right\}$ , 其中本征值按照其实部由大到小排列. 如果所有本征值实部均为负, 即$\left\{ {{\rm{Re}}{\lambda _i} < 0, i = 1, 2, \cdots, n} \right\}$ , 那么x A m 个模失稳, 而其他模仍然保持稳定, 即假设该模对应的本征值$\{0 < {\rm{Re}}\lambda _k^u \ll 1$ ,$ {\rm{Re}}\lambda _i^s < 0, k = 1, 2, \cdots, m, i = 1, 2, \cdots, n - m\}$ , 且${\rm{Re}}\lambda _k^u \ll \left| {{\rm{Re}}\lambda _i^s} \right|$ . 通过引入一个T A λ u , s m × m 与(n – m ) × (n – m )对角子矩阵. 则(21 )式可改写为x t ) = (u t ), s t ))T , 其中u t ) = (u 1 (t ), u 2 (t ), ···, um (t ))T , s t ) = (s 1 (t ), s 2 (t ),··· , sn–m (t ))T , ${{{B}}_u} \!= \!{(B_1^u, B_2^u, \cdots, B_m^u)^{\rm{T}}}, \;{{{B}}_s}\! = \!{(B_1^s, B_2^s, \cdots, B_{n - m}^s)^{\rm{T}}}.$ s t )为满足(24b )式的快变量, 而u t )为满足(24a )式的慢变量. 按照支配原理绝热消去, 令(24b )式左边$\dot {{s}} = 0$ , 由此n – 1个方程可将n – m 维矢量s u 24a )式可得到m 维的非线性方程24 )式到(25 )式, 在理论上可以看作是从多变量方程到少数序参量方程的约化, 在动力学上也产生了极大简化, 这是支配原则在讨论相变点附近行为时给出的有益结果.4.序参量动力学理论 下面将从耦合振子微观动力学方程出发, 利用统计力学方法建立分布函数方程, 并通过统计平均引入各阶序参量, 建立相应的序参量方程, 并进一步讨论对方程的降维.4.1.广义序参量 4.1.广义序参量 从一般形式的全局耦合振子系统运动方程出发:j = 1, 2, ···, N , ${\xi _j}(t)$ 为作用于第j 个振子上的随机噪声, 设为振子间无关联的高斯白噪声, 满足$\left\langle {{\xi _i}(t)} \right\rangle = 0$ , $\left\langle {{\xi _i}(t){\xi _j}(t')} \right\rangle = 2 D{\delta _{ij}}\delta (t - t')$ . ${{\beta}} = \{{\beta _1}, $ ${\beta _2}, \cdots, {\beta _m}\} $ 为一组均匀控制参量, 这些参量对所有振子均相同, 如通常考虑振子间相互作用强度相同. ${{\gamma}} = \left\{ {{\gamma _1}, {\gamma _2}, \cdots, {\gamma _N}} \right\}$ 为一组非均匀控制参量, 它们对不同振子不一样. 例如振子的自然频率通常各不相同, 此时{γi = ωi }.α αn }, 其分量为如下的n 阶序参量:n = 1时, α 1 即是Kuramoto引入的相干因子. n > 1时αn 为高阶序参量[56 ] . 在热力学极限N →∞下, 可以引入振子相位的密度分布函数ρ (γ θ , t ), ρ (γ θ , t )dθ 为一个振子在时刻t 相位处于θ →θ + dθ 的概率或时刻t 相位处于θ →θ + dθ 内的振子数密度. 它满足(12 )式对应的Fokker-Planck方程:v = F (α θ , β γ D = 0)时, 分布函数方程退化为如下的连续性方程ρ (γ θ , t )与γ $\rho \left( {\theta, t} \right) = {\displaystyle\sum \nolimits _i}\rho \left( {{\gamma _i}, \theta, t} \right)$ . 例如, 如果$\left\{ {{\gamma _i} = {\omega _i}} \right\}$ , 则分布函数为g (ω)为自然频率分布. ρ (θ , t )包含了振子系统集体行为的所有信息. 在同步问题宏观层面, 我们最为关注序参量α αn }. 对于均匀系统即没有非均匀参量γ γ n 阶序参量αn 实际上就是exp(inθ )的统计平均, 或称为exp(iθ )的n 阶矩. 由于宏观量的各阶矩描述与分布函数描述等价, 可由一方信息推知另外一方的信息. 还可以看到, 广义序参量实际上就是分布函数ρ (θ , t )的傅里叶变换系数.4.2.Ott-Antonsen拟设 -->4.2.Ott-Antonsen拟设 下面先考虑全同振子系统的序参量运动方程. 利用序参量的定义(27 )式, 对其进行时间求导, 并利用振子运动方程(26 )式可以得到F (α θ , β θ 的2π周期函数, 因此可做傅里叶展开:33 )中可得序参量运动方程为34 )式的傅里叶分解中只需包含最低阶项:35 )简化为n ≥ 0, ${\alpha _{ - n}} = {\bar \alpha _n}$ .26 )通过上述变换可以化为运动方程(35 )和(37 ), 它们都是一组耦合的序参量方程, 处理该序参量方程组的难度等价于相位运动方程(26 ), 对其的简化需要新的条件.37 )显然存在一个平庸的非相干解αn ≡ 0, 对应于耦合振子的非同步态. 随着耦合强度的增加, 耦合振子会产生同步, 整体运动在相空间也会塌缩到一个低维空间中. 在广义序参量空间来看, 系统也必然会在低维空间运动. 根据协同学原理, 这些广义序参量中可能只有少数为慢变量, 其余为快变量, 其中慢变的广义序参量会成为系统状态的真正序参量. 由于快变量的变化都依赖于慢变量, 因此在发生同步转变的区域附近, 各阶序参量之间应存在一定的关系, 它们均依赖于慢变的序参量. 一种最简单的可能情形是所有的各阶序参量αn 都依赖于α 1 , 不妨设为αn = G (α 1 , n ). 将其代入运动方程(37 )中并比较每一阶函数的傅里叶展开系数可以得到[56 ] 37 )式的多个运动方程可简并为单一方程,38 )式正是Ott-Antonsen (OA)拟设(ansatz)[47 ,48 ] .4.3.Poisson和不变子流形 -->4.3.Poisson和不变子流形 OA拟设有什么物理意义呢?下面通过讨论分布函数来进行分析.αn :αn , 就可以利用上述求和来得到分布函数, 通常这需要无穷阶的傅里叶系数.ρ 的傅里叶展开系数即广义序参量αn 40 )式可以得到42 )式右边的求和为幂级数, 可以得到振子分布为泊松和形式r 为序参量α 1 (t )的幅度, Θ 为集体相位. 因而分布ρ (θ , t )完全由α 1 (t )决定.38 )式的解满足简并的运动方程(39 ), 则在动力学演化过程中形式(38 )一直得到满足. 振子的分布虽然随着系统的演化而改变, 但将始终具有泊松和分布的形式. 如果系统的初始相密度分布满足泊松分布, 那么不管在任何时刻系统的相密度分布将始终保持着这一性质. 序参量关系式(38 )式及简并运动方程(39 )被称为动力系统的Poisson和不变子流形. 这个不变子流形一个很重要的特点是虽然α 1 (t )可以不含时, 也可以含时, 但分布形式随时间演化保持不变. 这一结果将Kuramoto自洽理论仅仅讨论定态的结果拓展至一般情形.4.4.非全同振子系统的OA拟设 -->4.4.非全同振子系统的OA拟设 对于振子非全同的情形, 若振子自然频率各不相同, 即{γi = ωi }, 设它们满足分布g (ω ). 那么当N → ∞时, 引入密度分布函数ρ (ω , θ , t ), 广义序参量相应写为(32 )式, 其中αn (ω , t )为ρ (ω , θ , t )的n 阶傅里叶展开式, 也可以理解为自然频率在ω → ω + dω 之间的局域序参量. 利用连续性方程可以得到如下递归方程:44 )的一组特解. 一阶序参量为g (ω )的形式为ω 的有理分式时, 可将ω 从实轴延拓到复ω 平面中去, 在不引起发散的情形下(|α 1(t )| ≤ 1)直接得到α 1 (t )的演化方程.5.微观动力学对称性与Watanabe-Strogatz变换 耦合相振子系统在振子数$N \gg 1 $ 时的微观动力学研究会变得很困难. OA方法给出了一种有效的将高维耦合振子动力学降维的方案, 但高维系统降维到二维的序参量空间来研究是有前提和成立条件的.N 维方程中的每一条轨迹只能局限在一个三维子空间中, 这意味着原始的高维微观态可以通过一定方法降维至低维的宏观态[46 ] , 这就需要他们提出的后来被称为Watanabe-Strogatz(WS)变换的方法来实现. WS变换的提出在一定程度上为人们寻求高维动力系统的低维解提供了方向, 但早期没有引起人们足够重视, 且数学与物理意义均不明确. 2009年, 受Ott与Antonsen工作的启发, Marvel等[49 ,50 ] 成功将这类问题的解推广到一般形式, 给出了WS变换的数学意义, 并清晰地给出OA拟设的数学依据.5.1.WS变换 5.1.WS变换 WS变换实际上来自于复数M?bius变换[57 ] . 定义复分数的M?bius变换$F:{\mathbb{C}} \to {\mathbb{C}} $ 为36 )式对应的动力学方程重新写为如下形式:j = 1, 2, ···, N , f = f 1 (α )为光滑复函数, $\bar f$ 是其复共轭, g = f 0 (α )为实函数, 它们均不依赖于指标j . 方程(49 )定义了一个 N 维动力系统. Marvel和Strogatz[49 ] 指出, 方程(49 )的解满足如下M?bius群在复空间内单位圆上的含时M?bius变换Mt :φj , j = 1, 2, ···, N }是系统的一组运动常数, ψ (t )是实参量函数, α (t )是复函数, $\left| {\alpha \left( t \right)} \right| \leqslant 1$ , $\bar \alpha \left( t \right)$ 是α (t )的复共轭. (50 )式和(51 )式的变换就被称为WS变换. 对任意时刻t 都对应一个变换Mt , 这些变换构成的集合满足群的性质, 全体变换的集合{Mt }构成一个代数系统即M?bius变换群. 系统(49 )式的演化完全被变换(50 )式和(51 )式所支配.5.2.三维动力学 -->5.2.三维动力学 方程(49 )满足变换(50 )式和(51 )式, 说明了系统任一时刻的状态{θj (t )}可由一组运动不变量{φj }在WS变换{α (t ), ψ (t )}的作用下完全确定. 而运动常数或不变积分{φj }的存在则反映了WS变换下系统的可积性. M?bius群本质上是一个三参量(ψ (t ), Reα (t ), Imα (t ))的李群, 相轨迹{θj (t )}被{ψ (t ), α (t )}以及{φj }唯一地确定.ψ (t ), α (t )的运动方程. 根据方程(50 )有49 )式对比可得$\dot \alpha $ 和$\dot \psi $ , 则有N 维相振子方程约化为三维的闭合方程, 而振子数目N 可以是有限的, 也可以是无限大.5.3.从WS变换到OA拟设 -->5.3.从WS变换到OA拟设 WS变换是一个从N 维相空间向三维相空间的严格动力学变换. 不同于统计方法例如基于序参量的OA拟设, WS方法并不依赖于任何近似条件或者特定状态, 而是将整个系统的动力学完整而严格地投影到低维系统中[56 ] . 当振子数N → ∞时, OA拟设下单一复序参量α 1 满足的方程为(39 )式, 这是一个二维的闭合实方程. 可以看到, WS变换下的三维方程(56 )式中第一式即复序参量方程(39 ), 因此一个自然的问题是, 这两者之间是否存在某种联系?在什么情况下WS变换可以退化到OA拟设?下面来分析一下WS变换和OA拟设这两种降维方案之间的区别和联系.N 振子系统(49 )式, 通过WS变换可以将序参量α 1 (t )重新表示为φj }出发, 若初始状态已知, 则系统的动力学情况可以由三维方程(56 )描述. 取特定均匀分布{φj = 2π(j – 1)/N }, 则序参量(57 )式可简化为N 为偶数的情况, “+”对应于N 为奇数的情况. 当$N \gg 1 $ , $I \ll 1 $ , 序参量就可以取近似${\alpha _1}(t) \approx \alpha (t)$ . 因而, 当运动常数{φj }取均匀测度时, α 1 (t )与α (t )的方程完全一致, 方程(56 )中α (t )和ψ (t )的演化解耦, WS变换的三维方程流形退化到二维OA流形(39 )式.φj }不取均匀测度时, α (t )和ψ (t )的时间演化就会相互耦合而无法简单解耦, α (t )的动力学行为将会受到ψ (t )的影响, 此时系统的动力学在三维空间中进行, α (t )和ψ (t )的运动会变得非常复杂[50 ,58 ] . 采用直角坐标, 设α = x +iy , f = Ref +iImf , 则三维方程(40 )化为$u = 2 x\operatorname{Re} f + g - 2 y\operatorname{Im} f$ .图2 给出了方程(60 )的运动轨道在α 平面的Poincare截面落点分布. 可以很清楚看到在|α |比较小的区域均为环面, α 的演化为定态或周期振荡. 但在|α |较大的范围, 运动轨道是不规则、混沌的[58 ] . 在环面区域, 类似于哈密顿系统, 环面对应于低维的运动, OA拟设可以成立. 在混沌区域, α (t )和ψ (t )的演化相互耦合, OA拟设不适用.图 2 序参量α 相空间的Poincare截面落点分布, 可以看到闭合环面和混沌散点Figure2. The Poincare section of the order parameter α in phase space, where one can find the closed tori and chaotic scattered points.6.序参量理论在几个同步问题研究中的应用 26.1.经典Kuramoto模型的同步相变 6.1.经典Kuramoto模型的同步相变 对于经典Kuramoto模型, 即平均场耦合振子系统, Kuramoto已成功地通过自洽方程理论得到了临界点及其临界行为. 下面利用OA拟设来研究该同步转变问题. 由于自然频率非均匀, 因此需用非均匀参数情况下的拟设. 利用序参量39 )式可以得到g (ω )为 Lorentz 分布63 )式有64 )式的积分可以将ω 延拓到复平面的上半平面进行, 利用留数定理可以得到$z(t) = {\alpha _1}(\omega = i, t)$ , 将其代入到(63 )式和 (64 )式中有K c = 2, 当K ≤ K c 时, 系统有唯一不动点z ≡ 0, 此即非相干态; 当K ≥ K c 时, z ≡ 0解失稳, 系统分岔到新解6.2.奇异态研究 -->6.2.奇异态研究 奇异态(chimera state)是近年来发现的一类对称性破缺导致的时空斑图涌现行为, 它描述了结构全同的单元(如相振子, 其振子的自然频率以及耦合方式都相同)在非局域耦合下会产生相干(coherence)和非相干(incoherence)共存的态[59 ,60 ] . 这种对称性自发破缺的现象在很多生物系统中可以看到, 例如海豚与其他海洋哺乳动物、迁徙的候鸟等都具有一类有趣的半脑睡眠现象[61 ] , 即它们可以在左(右)脑休息的时候让右(左)脑保持清醒的状态. 人们在Kuramoto模型以及其他很多振子系统特别是神经系统中均发现了奇异态[62 -67 ] , 并在光学混沌实验 [68 ] 和化学Belousov-Zhabotinsky (BZ)反应实验[69 ] 实现.? (x , t )为t 时刻位于空间x 处振子的相位, ω 为振子自然频率, 设为空间均匀且ω = 0. 积分代表空间不同位置振子间的耦合, $\Delta x = x - x'$ , $\Delta \phi = \phi \left( {x, t} \right) - \phi \left( {x', t} \right)$ . α 为振子间的相移(阻挫), 设0 < α < π/2. 非负耦合核函数G (x ) ≥ 0反映空间不同位置振子之间的非局域相互作用, 通常设为归一化且随|x |增加而衰减的偶函数:67 )式的奇异态动力学[62 ,70 ,71 ] . 设振子分布函数为f (x , ?, t ), 它满足连续性方程$Z(x, t)$ 可表示为70 )式, (69 )式的相速度$v(x, t)$ 可表示为? 的2π周期性, 可将分布函数表为相位? 的傅里叶级数形式:[47 ] , 系数hn 相互之间不独立, 它们满足幂律关系:$h(x, t) = {h_1}(x, t)$ . 将(73 )式代入(72 )式可得74 )式代入连续性方程(68 )式, 并比较两边exp?(i? )的不同阶系数可得74 )式也可将序参量重新表达为75 )式和(76 )式可得到序参量的演化动力学行为. 位于x 处振子的相位长时分布函数为$|h(x, t)| < 1$ 时, 对(77 )式求和并做归一化可得h 的幅角. 上述分布函数为与(43 )式形式相同的Poisson核函数, 其中心位于argh 处, |h |刻画分布的非均匀性. 当|h |=0时, f (? )为均匀分布; 当0 < |h | < 1时, f (? )为单峰分布; 当|h |=1时, 由于分布(78 )式分子分母均趋于零, 可求极限得f (? )简并为δ函数 f (? )=δ (? – argh ), 它代表所有振子的锁相.h (x , t )也可以看作是在空间x 处exp(i? )的统计平均, 即70 )式定义的序参量Z (x , t )相比较, h (x , t )没有对空间的积分, 即没有考虑非局域效应. 因此h (x , t )量度的是空间x 处附近的同步相干性, 是一种局域序参量. 若对某一x 处有|h (x , t )|=1, 则在$\left( {x - \varepsilon, x + \varepsilon } \right)\left( {\varepsilon \ll 1} \right)$ 范围内的振子会处于锁相(相干态), 而当|h (x , t )| < 1时, 则在$ \left( {x - \varepsilon, x + \varepsilon } \right) $ 范围内的振子处于非相干态, 以此可以给出两种态共存的奇异态.76 )式可以得到序参量R (x )的自洽方程, 进一步可以确定其空间分布. 当然, 也可用Kuramoto自洽方程理论来进行讨论, 可以得到与上述OA方法在定态时一致的结果. 进一步的计算需要借助于数值方法, 详细讨论可见我们的专著[51 ] 与综述文章[59 ,60 ] .6.3.高阶序参量及其动力学 -->6.3.高阶序参量及其动力学 很长时间以来, 人们聚焦于Kuramoto模型中的简单耦合函数情形开展研究. 在多数情况下, 振子间相互作用并不是简单的一阶正弦耦合函数. 对于一般的耦合函数, 在第4 节中已经看到, 不同阶序参量之间是复杂的相互依赖关系. Daido[72 ] 早在20世纪90年代初就通过对一般耦合函数的Fourier展开提出了广义序参量, 但没有进一步讨论不同序参量之间的关系, 而是使用传统的Kuramoto自洽方程方法进一步讨论. Pikovsky和Rosenblum[73 ] 讨论了如下具有相同自然频率耦合振子的Kuramoto-Daido模型:αn }. Pikovsky在该工作中早于Ott等[47 ] 提出了序参量之间的依赖关系(拟设条件), 即高阶序参量{αn , |n | ≥ 2}均依赖于α ±1 . 把(79 )式中的耦合函数写为Fourier级数形式, 则动力学方程可写为αn }为(27 )式定义的广义序参量. 考虑只有其中第l 阶Fourier分量耦合的情形, 则动力学方程可写为H (t )依赖于序参量αl .[74 ] . 动力学方程(81 )可以重新写为83 )式可变换为{φk }, α 及其时间导数$\left\{ {{{\dot \varphi }_k}} \right\}$ , $\dot \alpha $ :φk }的方程右边不依赖于k , 说明变换后的相角{φk }均以相同角速度运动, 因此可引入新变量$\psi \left( t \right) = {\varphi _k}\left( t \right) - \varphi _k^0$ , 其中{φk 0 }为一组运动常数. 显然$\dot \psi = {\dot \varphi _k}$ , 说明M?bius变换映射可写为l 因子.[75 ,76 ] 81 )中l = 2, H (t )=α 1 2 的情形, 因而可利用序参量方程(84 )进行讨论.[58 ] γ 为相移因子, 代表阻挫效应. 对于这种情况, $l = 2, \;H\left( t \right) = {\rm{exp}}\left( {2{\rm{i}}\gamma } \right){\alpha _2}$ . 二阶或高阶简谐耦合函数在很多系统中都存在, 因此近年来的研究很多[58 ,77 -79 ] , 也有相应的一些实验研究[80 -83 ] , 这里不再展开.7.结 论 综上所述, 大自由度复杂系统的同步是一类典型、基本的涌现行为. 这种涌现行为的出现是大量个体或自由度共同参与、通过相互作用自组织形成的整体有序. 有序意味着复杂系统低维宏观行为的出现, 它往往是以序参量的出现作为标志的, 可借助于统计物理学思想和方法来加以研究. 就序参量的涌现机制来看, 协同学的理论与方法揭示了大量自由度的复杂系统如何通过内部自组织与竞争产生出有序, 其中非常重要的理论任务就是对复杂系统通过集体变量的分析来甄别快慢变量, 并利用支配原理来进行降维, 得到序参量的动力学. 降维方法的精髓在于尺度的可分离性, 特别是时间尺度的快慢可区分性, 这种特性可以其他形式体现出来, 如拓扑流形中中心流形的出现、变量中守恒律的存在等等.[84 ] . 我们不妨以此为例进行说明. 神经元的主体微观动力学是电信号的积累发放, 目前实验方面已经可以采集大量实时数据并进行分析整合. 对于脑电波及其各种动力学协同行为的研究, 可以先抽取不同部位采样的脉冲时间序列, 再定义对应的相位, 就可以建立相位的时间序列信息, 据此计算不同序参量, 通过分析序参量的低维行为进行讨论. 就目前的研究来看, 很重要的一个课题是序参量动力学模型的重构, 这一问题至今无论在神经科学还是其他领域都还没有很大的突破, 但已有一些具有启发性的研究思路. 例如, Zhang等[85 ] 和Chen等[86 ] 近几年提出了主超前相位方法、动力学权重因子方法以及网络动力学重构方法, 以此可以分析复杂系统的动力学并结合序参量层次的动力学描述, 完全有可能提供一个可行的图景. 这些工作还需要大力推进. 





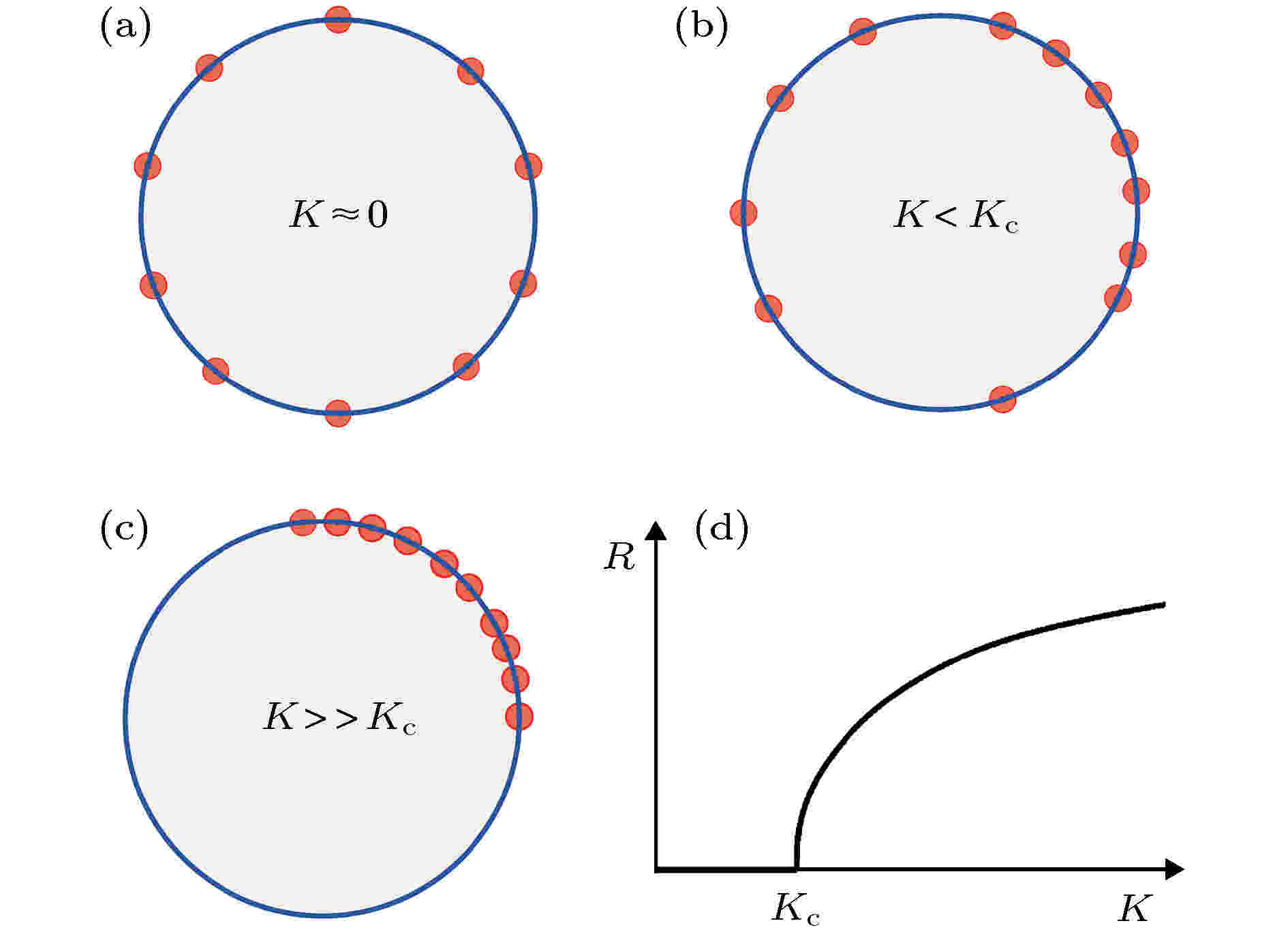 图 1 耦合振子同步示意图 (a) 在耦合强度很弱时, 大量振子不同步, 任一时刻相位均匀分布于0?2π之间; (b)随着耦合强度的增加, 越来越多的振子会同步, 振子不再均匀分布; (c) 在很强的耦合下, 振子相位会靠得很近, 形成整体的同步大集团; (d) 序参量随耦合强度的变化
图 1 耦合振子同步示意图 (a) 在耦合强度很弱时, 大量振子不同步, 任一时刻相位均匀分布于0?2π之间; (b)随着耦合强度的增加, 越来越多的振子会同步, 振子不再均匀分布; (c) 在很强的耦合下, 振子相位会靠得很近, 形成整体的同步大集团; (d) 序参量随耦合强度的变化





























































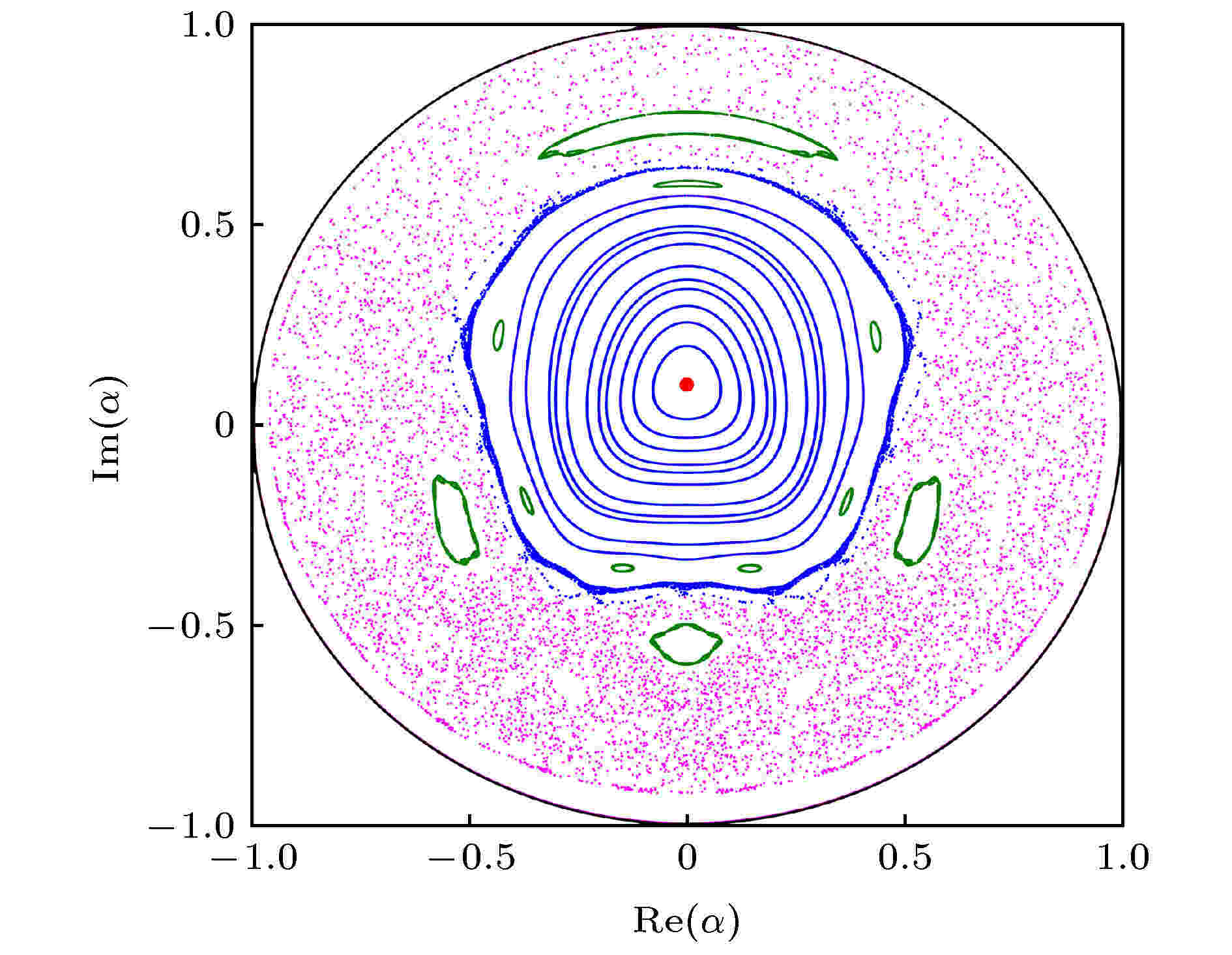 图 2 序参量α相空间的Poincare截面落点分布, 可以看到闭合环面和混沌散点
图 2 序参量α相空间的Poincare截面落点分布, 可以看到闭合环面和混沌散点













