全文HTML
--> --> --> 图 1 电力电子化电力系统示意图
图 1 电力电子化电力系统示意图Figure1. Schematic diagram of power electronic dominated power systems
电力电子设备为电力系统带来高效的同时, 也因其复杂性给电力系统的安全稳定运行带来了巨大的挑战. 作为国际上最近报道的一次大电网事故, 2019年8月9日英国Little Wymondley一条线路发生单相短路故障引发了伦敦在内的英格兰和威尔士大部分地区停电, 约110万人受到停电影响. 英国国家电网(NationalgridESO)的报告指出, 风电、直流输电等无惯性的电力电子并网电源高占比是本次事故的深层次原因[6]. 当前电力电子化电力系统受到短路故障等各种大扰动后暂态行为机理尚未明确, 传统继电保护装置无法快速抑制事故影响的扩散, 电网时刻面临失稳风险. 基于传统电力系统的基本认识和基础理论将无法适应全新的装备, 寻找电力电子化电力系统较直观的物理图像和机理分析亟需解决.
电力系统受到各种扰动后保持安全稳定运行是电网面临的最核心的问题之一[7,8]. 工程中一般根据电力系统的特点对电力系统稳定性分析进行分类和简化. 对于某一特定的运行状态, 将遭受一个微小扰动后系统能否恢复扰动前状态称为小干扰稳定性分析. 其本质为研究系统运行点(不动点)附近的局部稳定性, 一般将系统的非线性方程组在工作点处进行线性化, 然后用线性系统理论方法, 如特征值, 加以分析. 与之相对应, 对某一稳定运行状态施加特定的大的扰动, 研究扰动后系统是否可以达到一个可以接受的(新的或旧的)运行状态称为暂态稳定分析, 或者称为大扰动稳定分析. 其本质为系统全局稳定性, 需要确定故障后运行点吸引子稳定边界与故障恢复时刻的状态之间的关系, 在分析的过程中需保留原始的非线性关系.
在传统电力系统动态研究中, 不同元件及控制器耦合相互作用引发振荡问题的研究通常属于小干扰稳定分析范畴, 用线性系统理论加以研究. 人们根据不同的振荡机理和数学模型, 总结出低频振荡和次同步振荡等不同问题, 并形成相应的分析方法和控制策略. 对于暂态稳定性分析, 同步发电机等电磁变换装备在一次调频时间尺度内的暂态特性主要由转子机电动态所决定. 由此同步发电机转子在不平衡功率(即: 原动机的输入机械功率与同步机的电磁输出功率)下的转子运动被认为是暂态稳定分析的核心内容. 针对单同步机连接到无穷大母线系统, 可以用等面积定则来分析[7,8], 并通过加速和减速面积来提供基本物理图像. 进一步对于多同步机耦合系统, 学术界曾发展出多种分析方法, 主要有基于李雅普诺夫能量函数的直接法和基于多机空间映射的扩展等面积法[9-14]. 传统电力系统稳定分析经过五、六十年的发展, 已经形成了较为严格的数学理论, 并为电网部门在线运行和事故预判方面提供帮助.
与传统电力系统小干扰稳定性分析相对应, 电力电子化电力系统同样对非线性系统动力方程组在工作点处线性化, 通过研究线性系统的稳定性来判断系统稳定性. 其中包括状态空间法、阻抗法、幅相运动方程法等. 其中, 状态空间分析法(又称模态分析)是线性控制系统中常用的分析方法[15]. 这种方法能精确分析振荡现象, 并适用于复杂多机系统, 但较缺乏对振荡机理的解释, 而且当系统结构发生改变(如投入或切除一条线路)时, 都需重新列写状态方程. 尤其重要的, 实际电力电子装备通常由不同的厂商生产, 内部控制方式和控制参数都不可能精确得到, 利用状态空间分析法来分析不太现实. 为克服这些不足, 工程上大量有实际应用的是基于复频率域分析的阻抗法[16-18]. 其将电力电子设备黑箱化, 以电压和电流作为设备输入和输出变量, 以阻抗传递函数矩阵的形式来看待设备, 然后根据广义奈奎斯特判据或简单的波特图来判断整个系统的稳定性. 然而当前研究人员对于不同坐标系下的多种阻抗分析方法、交流运行点的处理、设备非线性系统线性化、如何推广用于多个电力电子设备系统、分析结果的准确性等也仍有诸多激烈的争论. 此外, 幅相运动方程法[19,20]则推广传统的转子运动方程形式, 认为多样化电力电子设备也可统一表现为不平衡瞬时功率驱动下的内电势运动, 采用输入有功和无功功率与输出内电动势幅值和相位的形式. 由于在电气领域, 基于非正弦时变电压和电流信号的功率理论还远未完备, 从功率的转换、储存、耗散等角度来分析大系统也仍然面临巨大的挑战. 后两种频域分析方法都是对不同设备和传输线网络分开来建模, 方便网络结构发生改变情况下的分析, 但是应用到多机系统仍可能面临传递函数阶数过高和广义奈奎斯特判据判断不方便等问题. 近期我们的文章具体比较了状态空间分析、阻抗法和幅相运动方程法三种方法对系统小扰动稳定的分析结果, 用数学的相似矩阵变换、数值符号运算和实际算例证明了其结果的一致性[21].
对于更加复杂的电力电子化电力系统暂态稳定问题, 由于控制器的切换与限幅、坐标变换等非线性环节、多时间尺度序贯控制方式间的复杂相互作用、机电与电磁暂态相互作用、复杂保护与控制主导的暂态控制方式等, 这些都使得传统暂态稳定分析理论难以适应当前电力电子化电力系统动态分析. 据作者们所知, 现阶段学术界对暂态稳定的研究主要针对特定简单场景下的零散研究, 仍然缺乏直观实用的方法来解释系统受扰后的物理过程[22-32]. 如文献[23,24]参照等面积定则, 从低维动力系统的角度分别分析了装备在功率同步控制和下垂控制的VSC系统的暂态稳定性. 文献[26]发现了电压源型变换器(VSC)在遭受电压突然跌落故障后存在一种突变分岔现象. 文献[29—31]总结了电力电子设备接入电网对同步机稳定的影响规律和对振荡的影响. 文献[32]仍然借鉴传统的转子运动方程和等面积定则, 具体针对VSC内部的锁相环(PLL)动态, 得到了暂态稳定分析的一些简单结果.
2017年国家电力调度控制中心主任李明节等[33]总结了新能源并网系统引发的复杂振荡问题及其对策, 并归纳了振荡的一些新特点. 如可出现不同的振荡频率, 甚至是超同步振荡(超出工频的振荡); 振荡频率可漂移; 振荡可发生在电网不同位置; 振荡特性(频率、阻尼及稳定性)受多变流器(群)聚合效应以及电网诸多参数、乃至风光等外部条件的影响, 具有影响因素复杂、大范围时变等特征; 振荡极易进入控制限幅, 导致振荡往往始于小信号负阻尼失稳, 而终于非线性自持续振荡; 振荡在机理上可能涉及到多变流器间及其与大电网之间的动态相互作用等. 由此可见, 为解决电力电子化电力系统复杂振荡问题, 我们可能必须对付和处理系统的固有非线性问题. 另外, 2015年9月第8届FEPPCON VIII国际会议(The Future of Electronic Power Processing and Conversion)也明确指出: 由于电力系统中的变流器越来越多, 二者之间的交互作用越来越复杂, 对传统电网运行特性的改造也越来越明显. 如何分析、设计、控制、集成, 才能确保电力电子化的供电系统仍然能够维持安全、稳定、高效地长期运行? 这是摆在电力电子、电力系统等学科研究人员面前的世纪难题.
在另一方面, 物理、数学和自动控制背景的研究人员近些年也积极进入到复杂电力网络领域之中, 在电力系统与复杂系统交叉方面开展了一系列卓有成效的研究, 如德国Menck等[34]和 Schultz等 [35]、德国Rohden等[36]和Schafer等 [37]、美国Motter等[38]和Yang等[39]、瑞士Dorfler等[40]和Grob等[41]、英国Carareto等[42]. 但是他们多以智能电网同步稳定问题为背景, 研究复杂网络上相互耦合的二阶Kuramoto相振子的同步化过程, 较多地从网络动力学的角度研究智能电网的网络拓扑结构如何影响整个系统的同步能力等问题. 国际上著名的复杂系统圣地圣塔菲研究所也于2012年召开学术沙龙: Power Grids as Complex Networks, 召集了智能电网和复杂系统两方面的专家, 探讨这两个领域共同关心的核心问题, 以促进复杂系统和电力系统的相互融合和进步.
针对上述研究背景及现状, 我们研究小组近些年已经开展了一些工作[21,43-50]. 本文将首先介绍以同步发电机为主导的传统电力系统单机及多机系统暂态分析的基本理论, 然后通过电力电子化电力系统单机无穷大母线系统电压突然跌落和再恢复的具体场景, 结合我们近期完成的一些研究结果, 对其暂态行为进行对比研究, 由此揭示出电力电子化电力系统受扰后的典型特征. 进一步将建立同时包含电力电子设备与同步机的多机系统模型, 突出和比较这两种设备在暂态分析中的异同. 最后, 将归纳和总结电力电子化电力系统暂态分析面临的基本问题与挑战, 以期引起复杂系统和统计物理背景的研究人员对这一重要前沿问题的兴趣.
2.1.单机系统暂态分析模型
同步发电机是电力系统中最核心的元件[7,8], 其转子磁链与定子磁链的交链实现了机械能与电能之间的相互变换. 设转子励磁绕组中心轴为d轴, 沿转子旋转方向领先d轴90电角度的坐标轴为q轴. 转子在d轴上有励磁绕组f及等值阻尼绕组D, 在q轴上有等值阻尼绕组Q. 不考虑零序分量, 定子





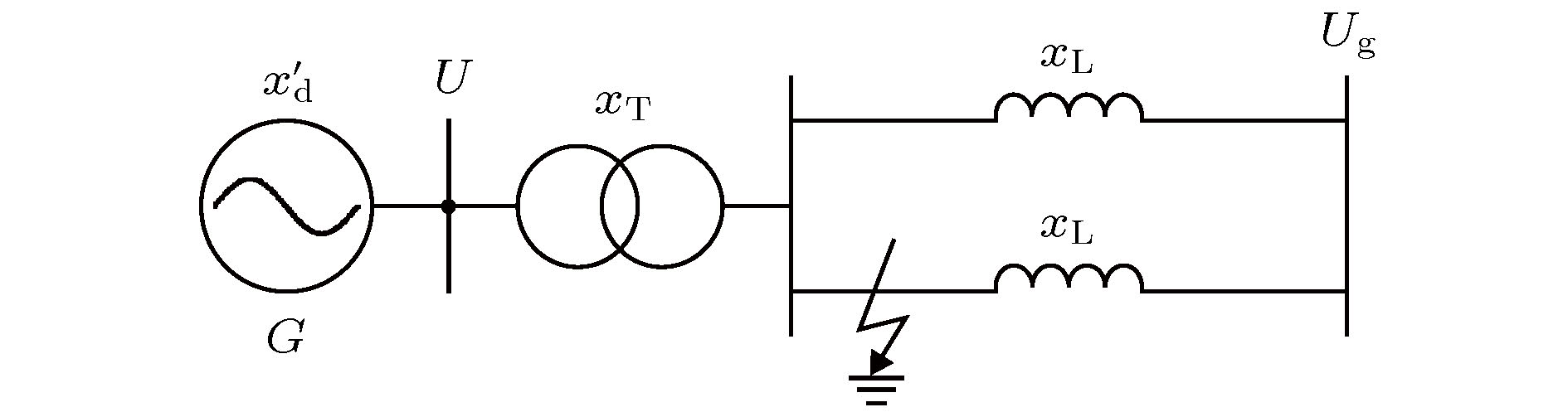 图 2 一台同步发电机经变压器升压后串联双回线路接入无穷大电网的示意图
图 2 一台同步发电机经变压器升压后串联双回线路接入无穷大电网的示意图Figure2. Schematic show for a single-machine-infinite-bus (SMIB) system
1) 近似认为发电机暂态电抗


2) 发电机的机械输入功率

3) 网络采用准稳态模型, 在这种模型下电感上的电压电流关系为代数关系;
4) 忽略变压器电阻及线路电阻, 忽略发电机的机械阻尼.
发电机转子的运动方程, 又称摇摆方程, 表示为[7]





图3绘制了电磁功率














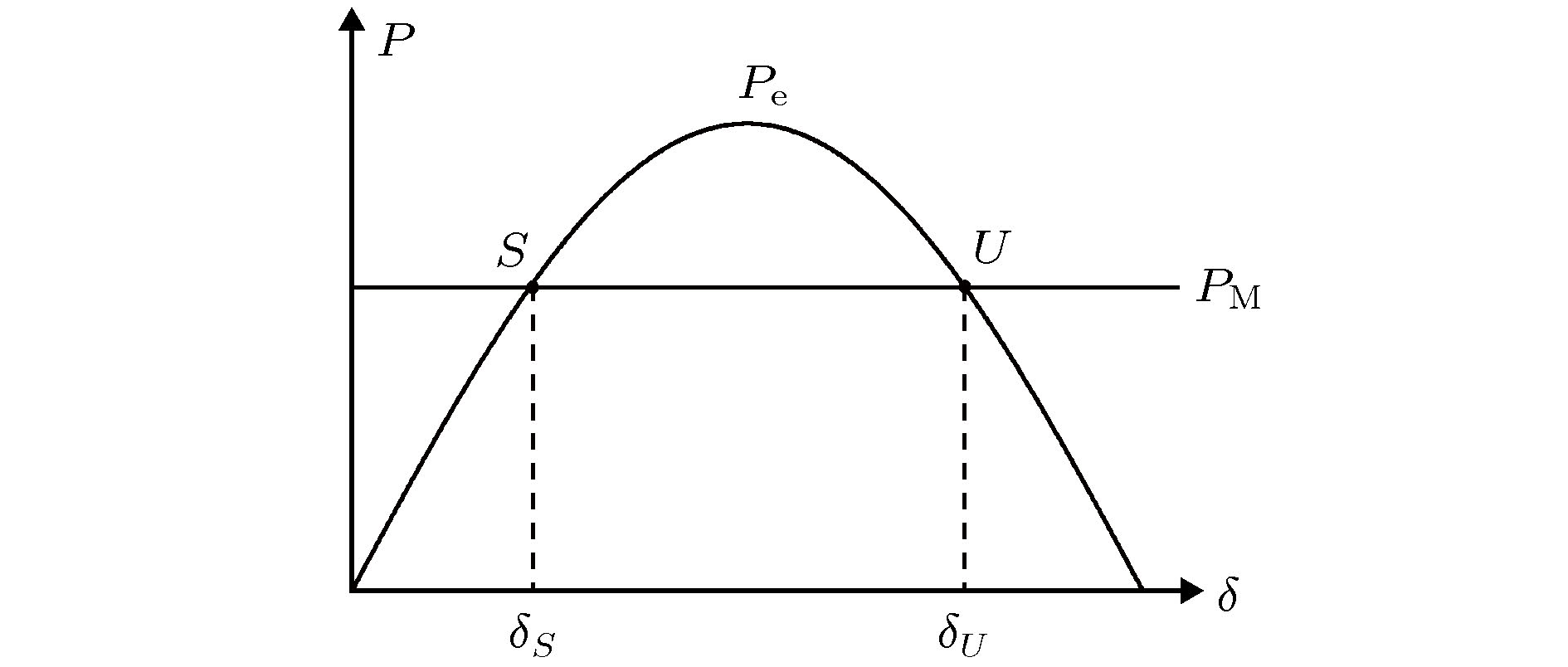 图 3 系统的功率特性曲线[7]
图 3 系统的功率特性曲线[7]Figure3. Power-angle relationship[7].
2
2.2.单机系统等面积定则
小干扰稳定保证电力系统在工作点处线性化区域内的稳定运行, 暂态稳定分析则研究电力系统在遭受大扰动下, 能否恢复至新的运行状态. 传统电力系统暂态稳定分析主要有两种方法, 即时域仿真和直接法. 时域仿真法将电力系统各原件的数学模型联立得到一组微分代数方程组, 通过逐步积分求得各状态量随时间变化的轨迹, 根据状态量最终是否回到稳定工作点上来判断其稳定性. 时域仿真法适用于各种不同复杂的设备, 但是较难进行机理分析. 直接法不必计算系统整个运行轨迹(但通常仍然需对从故障发生到故障恢复过程作数值积分), 而通过计算故障恢复时刻的状态满足的条件来直接判断稳定性. 其简化了故障恢复后的轨迹数值积分, 可对稳定性作快速判断, 并能提供稳定裕度和安全运行警告. 直接法从设备运动的规律出发, 更能说明暂态稳定的机理. 本文将重点介绍单机系统和多机系统暂态稳定的几种直接法.对于暂态稳定分析, 一般认为故障前系统工作于稳定状态, 稳定功角设为








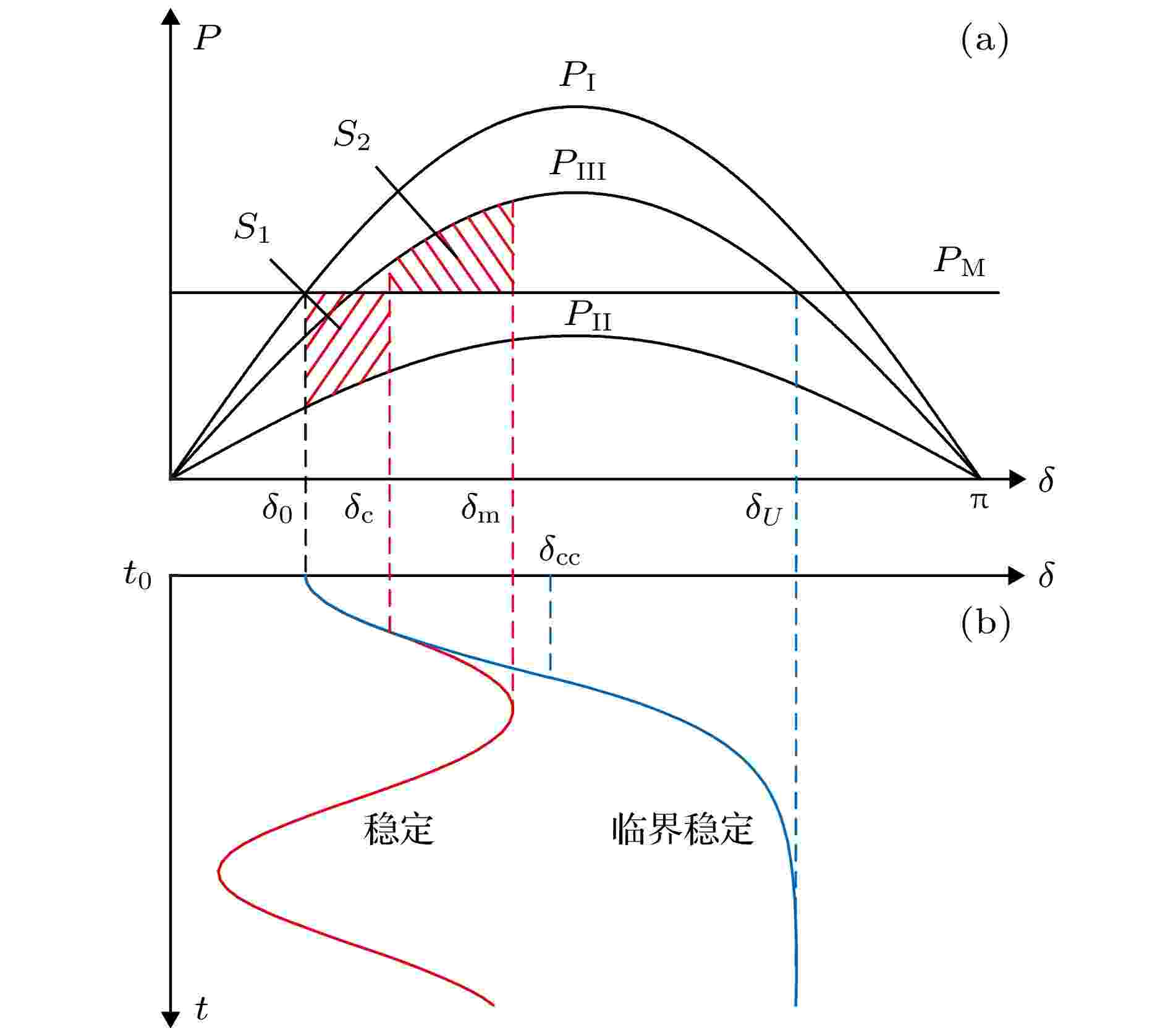 图 4 (a) 简单系统在故障前、故障中、故障后的三条不同功率特性曲线; (b) 暂态稳定(红色曲线)和临界稳定(蓝色曲线)情况下的功角的时域波形[9]
图 4 (a) 简单系统在故障前、故障中、故障后的三条不同功率特性曲线; (b) 暂态稳定(红色曲线)和临界稳定(蓝色曲线)情况下的功角的时域波形[9]Figure4. (a) Power-angle relationships for three different states of before-fault (




故障中由于







等面积定则本质上是不考虑阻尼条件下的能量守恒. 我们也可直接从势能函数的角度来解释. 故障恢复阶段系统的势能函数为

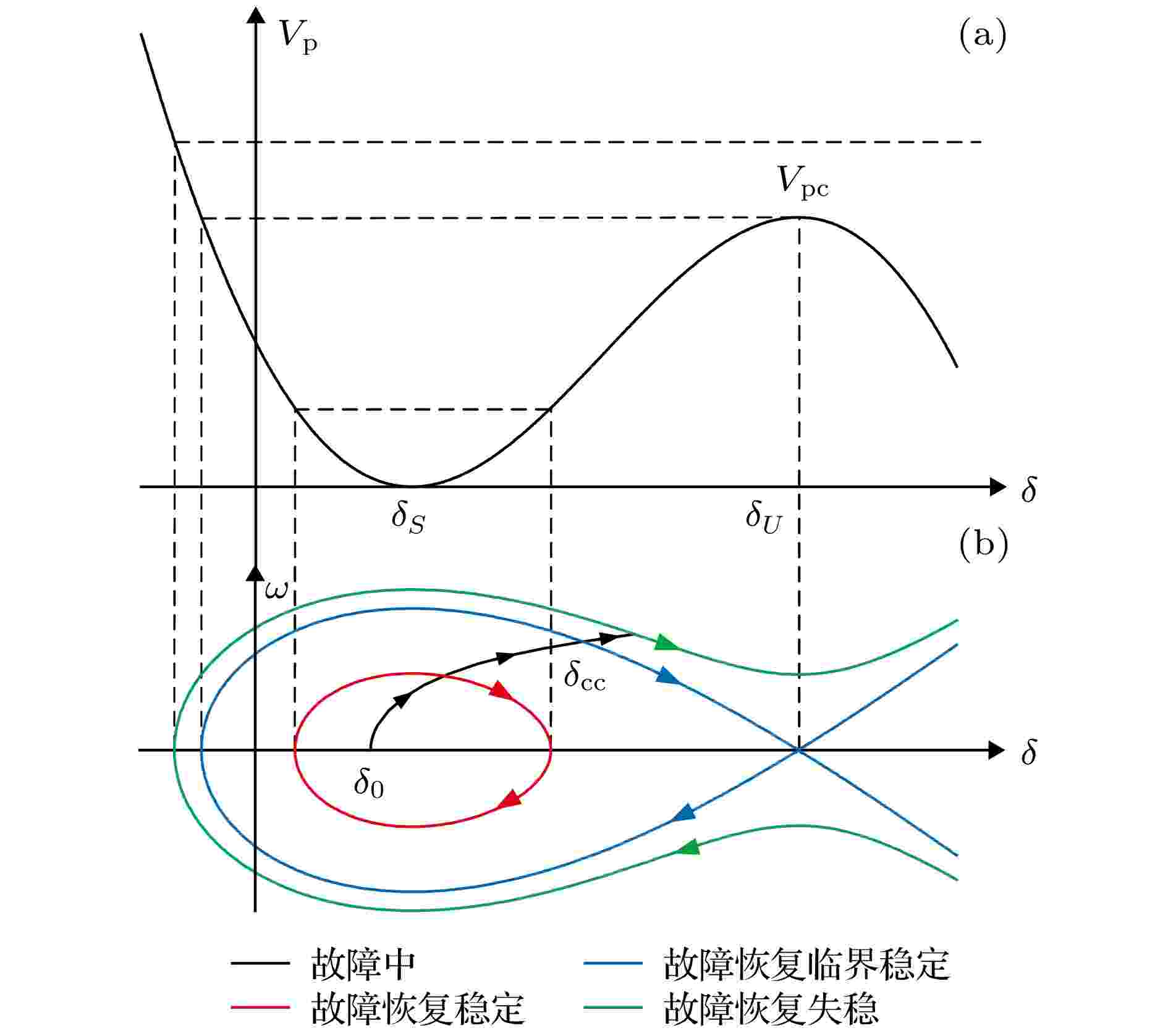 图 5 (a)势能函数曲线;(b)不同状态下的轨迹[10]
图 5 (a)势能函数曲线;(b)不同状态下的轨迹[10]Figure5. (a) Potential energy function curve; (b) trajectories in state space corresponding different states: stable, critically stable, and unstable[10].
2
2.3.多机系统暂态稳定分析
多同步机电力系统被描述为一组非线性微分代数方程, 其中微分方程由每台同步机的摇摆方程构成:



多台同步机通过网络实现功率交换, 由潮流方程所决定:

直接法仍需对故障中过程运行轨迹进行数值积分, 相比完全数值仿真方法的优点在于, 根据故障切除时刻的状态对稳定性直接判断. 由此其核心为对故障后稳定运行状态的吸引域的估计. 多年来, 电力系统研究人员提出了多种暂态稳定分析直接法, 具有代表性的方法有: 最近不稳定平衡点法(closest UEP)、 主导不稳定平衡点法(controlling UEP)[10]、位能界面曲线方法(potential energy boundary surface, PEBS)[12]、基于稳定边界的主导不稳定平衡点法(boundary of stability region based controlling UEP, BCU)[13]、扩展等面积定则(extended equal area criterion, EEAC)[14]等.
通常直接法判断暂态稳定的步骤为: 首先认为系统故障前工作于稳定状态, 通过逐步积分法计算故障中的故障轨迹, 然后根据不同直接法的计算步骤计算相应的临界能量值, 进一步将故障切除时刻的能量函数值与临界能量值相比较, 若小于临界能量值则暂态稳定, 反之则暂态失稳. 其中关键问题在于如何计算相应故障下的临界能量值. 早期方法有最近不稳定平衡点法和主导不稳定平衡点法, 这两种方法基于这样的事实: 稳定平衡点的稳定边界是由系统不稳定平衡点的稳定流形并集所构成. 最近不稳定平衡点法采用计算所有不稳定平衡点中最小的能量函数值为临界能量值. 这种估计方法独立于故障时的轨迹, 结果过于保守而无法广泛应用. 主导不稳定平衡点定义为稳定流形包含故障时轨线在稳定边界上的出口点的平衡点. 主导不稳定平衡点法采用主导不稳定平衡点的能量函数值为临界能量值. 这种方法针对故障特性类型来估计稳定域, 因而有更高的精度. 在后续发展的位能界面曲线方法中, 位能界面曲线为从稳定平衡点出发沿任意方向联结位能最大值点形成的曲面, 将故障中轨迹与位能界面曲线的交点的能量函数值为临界能量. 但有时可能给出错误的估计, 为克服这一困难, 人们将基于稳定边界的主导不稳定平衡点法结合主导不平衡点法和位能界面曲线法, 利用故障中轨线与位能界面曲线的交点找到原系统的主导不稳定平衡点. 这种方法保证稳定域的精确估计, 并提高了计算速度.
在另一方面, 20世纪80年代中期, 我国薛禹胜院士和比利时Pavella教授提出了扩展等面积定则方法, 将系统中的多台机划分为两互补群, 并用每个群所属机相角的加权平均值作为该群等值机的相角, 原多机空间被映射至等值两机空间, 这种概念被称为部分惯量中心(PCOI)映射. 不同的划分机群的方法会有不同的两机映像子系统, 其中最严重的映像子系统的临界条件就是原多机系统的稳定极限条件, 所以PCOI映射保留了稳定特性和临界条件. 每个映像子系统稳定的充要条件为当次摆动不经过映像加速功率为零值的动态鞍点, 这与传统等面积定则方法类似, 通常被称为扩展等面积定则.
3.1.VSC的系统模型
三相电压源型功率变化器(VSC)具有控制交流与直流系统之间功率交换的能力, 是电力电子化系统中最常见的设备, 广泛应用于光伏发电、风力发电、柔性输电、无功补偿中[4,5]. 本文将以VSC为例介绍电力电子设备暂态行为的基本特点. 图6为一个典型的单机VSC并网系统的电路图和控制框图. VSC的控制器工作在







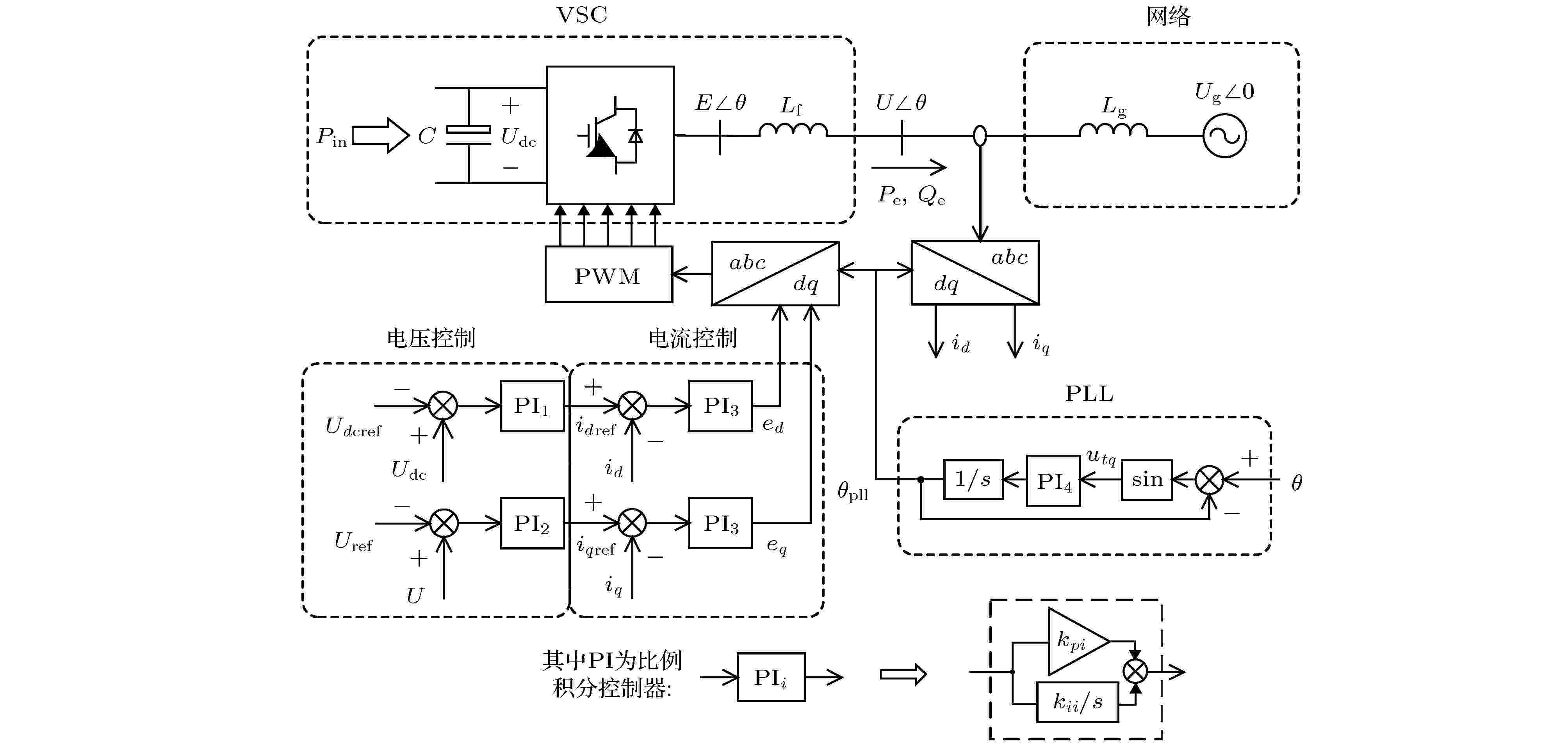 图 6 VSC单机并网系统控制框图
图 6 VSC单机并网系统控制框图Figure6. Schematic show of a grid-connected VSC system and its controllers
VSC的控制环路和所控制的电气量展现出多时间尺度的特性. 这里我们强调, 多时间尺度是一般非线性系统的普遍特征[51,52]. 一般而言, 内环电流控制器的响应速度最快, 为10 ms左右; 外环直流电压控制器、端电压控制器和锁相环的速度稍慢, 为100 ms左右. 根据不同控制器的响应速度, 可将VSC设备划分为电压控制时间尺度和电流控制时间尺度. 对于电力系统的短路故障, 相应的保护动作时间为几百毫秒到几秒, 在这一时间尺度下电压控制环将主导系统动态. 本文将重点考虑电压时间尺度的动态, 并与全时间尺度模型仿真相比较. 模型假设如下:
1) 直流侧的输入功率

2) 忽略电流环动态, 有功和无功电流值将始终等于其参考值(

3) 电感用相量描述; 在这一条件下电感的电压电流关系为代数关系, (

4) 变流器采用平均模型, 忽略变流器损耗和线路电阻损耗.
由此, 在电压时间尺度下, 模型得到简化. 其控制框图如图7所示, 符号的意义已在图6中标注. 根据该控制框图, 以下将推导系统的状态方程. 选取状态变量为


 图 7 VSC电压时间尺度模型系统控制框图
图 7 VSC电压时间尺度模型系统控制框图Figure7. Schematic show of the control diagram of the VSC system within the voltage timescale

直流电容通过吸收不平衡的功率来维持直流侧电压在正常范围:









2
3.2.分岔分析
首先令状态方程右侧等于零来得到平衡点. 观察到方程组(23)右侧多项式中的每一项都含有以下因式中的一项:












































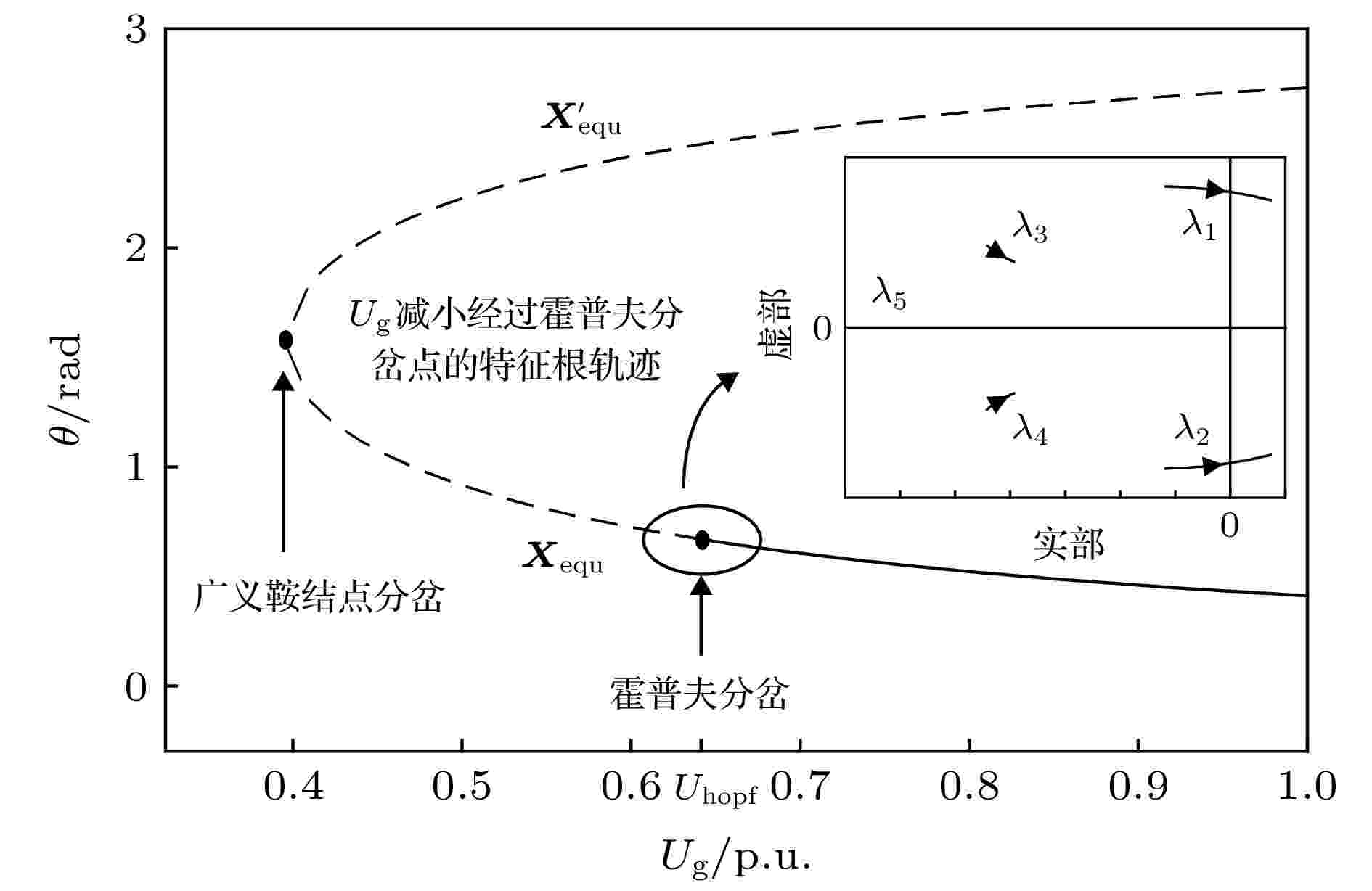 图 8 参数
图 8 参数



Figure8. Bifurcation diagram with the variation of




2
3.3.暂态稳定分析
33.3.1.暂态现象特征
我们在Matlab/SIMULINK中分别按照图6和图7搭建了VSC单机并网系统的详细模型和只考虑电压控制时间尺度的简化模型. 设置典型故障为:





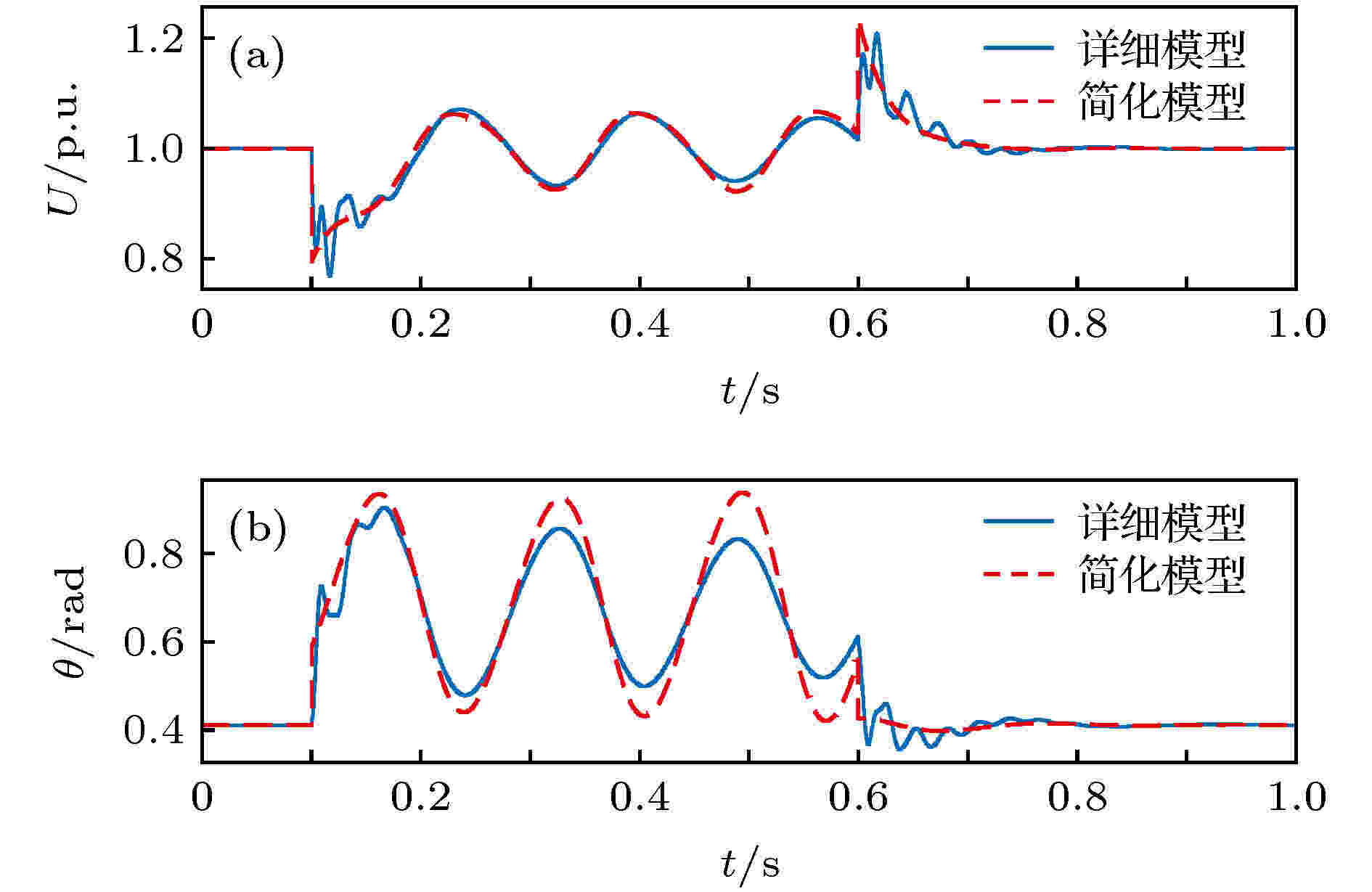 图 9 VSC电压时间尺度模型与详细模型在暂态故障后的响应对比
图 9 VSC电压时间尺度模型与详细模型在暂态故障后的响应对比Figure9. Response comparison between the voltage timescale VSC system and the detailed VSC system after transient fault
如图9所示, 电力电子设备在暂态扰动的过程中表现出明显的多时间尺度特征. 显然详细模型的时域波形含有两种不同频率的振荡成分: 即由电压控制环主导的10 Hz左右的低频振荡和由电流环主导的50 Hz左右的高频振荡, 尤其高频振荡在故障发生(


观察图9中故障发生时和故障切除时的波形, 可发现其端电压幅值和相角展现出不连续跳跃的特征. 进一步从控制框图(图7)可看出, 系统中的积分环节输出是连续的, 而代数环节的输出则完全由当前时刻的输入决定. 在本例中VSC端电压中PI环节的比例支路与网络代数方程形成了反馈控制环路, 构成了完整的代数环. 当该代数环中一个量发生突变(如文中考虑的电压跌落), 其他变量将立即随之发生改变. 故在故障发生和故障切除的两个时刻, 代数环中的状态变量出现突变, 并将为之前的耦合微分方程组(22)提供新的初始值. 由此可见, 微分-代数关系将决定整个系统的暂态行为, 而代数环的存在将使电力电子设备的暂态分析变得更加复杂.
3
3.3.2.临界故障切除时间
进一步地, 可通过分析不同故障深度和故障持续时间下的系统稳定性, 来获得工程上感兴趣的临界故障切除时间. 显然故障深度越深和故障持续时间越长, 系统越不稳定. 对于跌落较深的故障, 只有及时切除才能保证系统的稳定性. 随着故障深度变浅, 临界故障切除时间将趋向于无穷, 我们通过数值计算发现临界参数


我们还发现VSC在失稳的过程中表现出与同步机暂态稳定相类似的多摆现象. 由于故障深度越深,

2
3.4.VSC与同步机多机系统模型
同2.3节中传统的多机系统一样, 含有VSC的电力系统依然可描述为一组非线性微分代数方程组. 图10(a)所示为一个同时含有VSC和同步机的多机耦合系统. 同步机节点相关方程已在之前讲述, 如(11)式—(13)式. 假设第j节点为VSC节点, 由单机模型中(14)式, (15)式和 (17)式可进一步整理得微分方程组: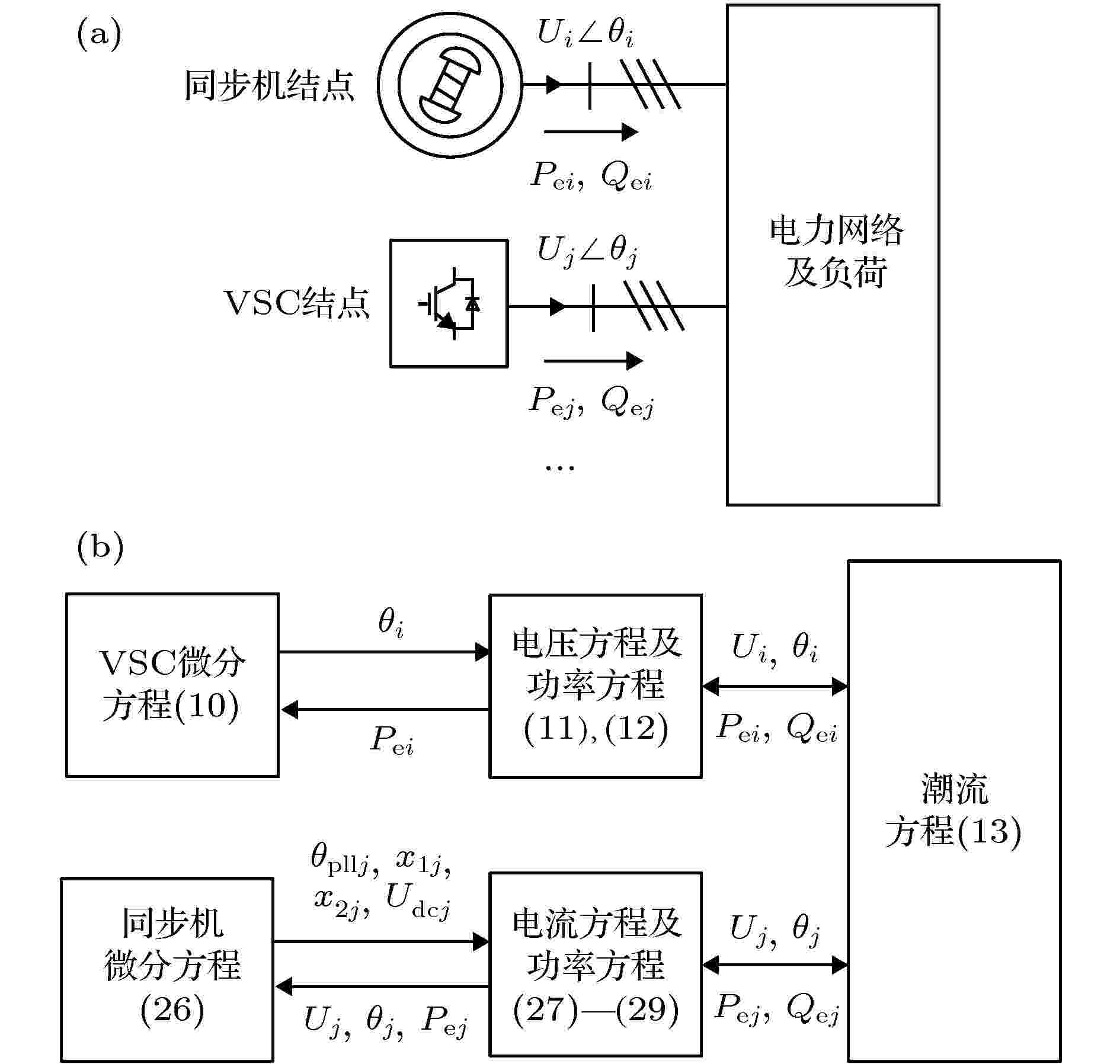 图 10 (a)VSC与同步机多机耦合系统和(b)其微分代数方程组中变量传递关系
图 10 (a)VSC与同步机多机耦合系统和(b)其微分代数方程组中变量传递关系Figure10. (a) A multi-machine power system with VSC devices and synchronous generators and (b) its variable relations in differential algebraic equations


因此VSC向网络中注入的有功功率和无功功率为:
| 复杂性 | 时间尺度 | 系统阶数 | |
| 传统电力系统 | 非线性项较少且单一 | 机电与电磁时间尺度较好分离 | 同步机二阶模型 |
| 电力电子化电力系统 | 非线性项分布广泛且复杂 | 多时间尺度间强耦合 | 装备多样化且高阶 |
表1电力电子化系统与传统电力系统暂态问题初步比较
Table1.Comparison of transient problems between Power-electronic-based power systems and traditional power systems
传统电力系统中节点电压与注入电磁功率之间关系(潮流方程)是最主要的非线性环节. 而在电力电子化电力系统中, PLL同步方式、保护控制的切换和限幅与坐标变换等非线性环节经过反馈控制环路相互交织在一起, 使得非线性作用关系变得极为复杂. 本文中得到了只考虑电压时间尺度下的五阶微分方程, 从非线性动力学的角度来看已经非常复杂, 其中包括了十余个非线性函数. 其显然不同于非线性物理界熟知的低阶非线性系统, 如洛伦兹振子、卢瑟振子、达芬振子等. 电力电子化电力系统的非线性环节的处理将非常棘手, 为进一步理论分析带来了巨大困难. 另外, 需强调的, 本文只是针对并网变换器这一小模块在通常矢量控制方式下开展了建模分析, 并未考虑更为复杂的限幅环节、附加暂态辅助控制、风机的机侧变换器、风机的机械转子动态等.
传统电力系统中同步机转子的惯性时间常数远大于电磁元件, 如电感的时间常数, 由此可划分出独立的机电时间尺度与电磁时间尺度. 在通常电力系统动态分析中, 研究人员可以集中针对机电时间尺度下的动力学行为来研究. 由此, 摇摆方程才在传统电力系统动态分析中处于中心地位. 而与之相对应, 电力电子化电力系统级联矢量控制的多样化控制器参数和其控制的物理量共同决定了时间尺度的划分, 如电流控制环与交流电感共同决定了电流时间尺度动态, 电压控制环与直流电容共同决定了电压时间尺度动态, 对于双馈风机还有转速控制器与机械转子共同决定的机电时间尺度等. 这些不同时间尺度受控制参数与系统参数的影响, 相互作用明显. 如何做多时间尺度分离, 或者在什么条件下可以这样做都是值得研究的课题. 当前我们还未有普遍接受的类似于同步发电机的不同阶数的实用动力学模型. 另外值得指出的, 图10中的多VSC与同步机模型可以看成是传统电力系统暂态模型在电力电子化电力系统中的推广, 具有普遍适用性, 但其还只是适用于电压控制时间尺度下的动态分析, 如果要包含考虑更快的电流时间尺度动态, 不光VSC模型部分将变得更为复杂, 原有网络部分准稳态代数模型也将用详细的电磁暂态微分模型来替代, 由此将造成理论分析上的更大的困难. 如何克服电力电子化电力系统动态网络部分的分析问题无疑是一大核心挑战.
同步发电机在受扰后, 表现出由转子运动方程决定的二阶特性, 考虑多机系统, 虽然系统阶数也随着同步机数量的增多而增多, 但是各同步机的特性相似, 相互耦合作用也较为清晰. 而在电力电子化系统中, 装备受到故障扰动后多时标控制器状态量间关系紧密, 系统响应特性将明显区别于二阶系统. 虽然当前有不少研究工作将电力电子装备动态特性类比于人们所熟悉的二阶线性动态系统, 如只针对其中的锁相环动态, 或直流电容上的电压动态等, 从而得到简化模型. 但是, 电力电子装备本质上都是由控制器所决定的高维动力系统, 这样简化是值得怀疑的. 而另一方面, 考虑到多机系统时的高维系统特性将更加明显, 若不经任何简化, 又往往会面临维数灾困难. 举一个典型的例子, 一个风电场通常由上百台双馈风机或直驱风机所构成, 如何分析其动态相互作用以及可能的振荡无疑是非常有挑战的问题.
综上, 电力电子化电力系统是一个非线性、多时标、复杂性特征明显的高维动力系统, 具有多样化设备跨尺度相互作用的特点. 类似的复杂系统问题也普遍存在于如机械振动分析、气象预报、地震监测、生物神经网络、人类经济行为等众多复杂性学科之中, 不同时间和空间尺度上节点的多样性和其复杂耦合相互作用关系是二十一世纪复杂系统学科的共同挑战. 由此急需尝试借鉴复杂系统等学科的研究成果, 从物理机理出发, 探索电力电子化电力系统稳定性分析和控制方法, 建立起新的动态研究的框架和体系. 本文抛砖引玉, 希望能够得到复杂系统和统计物理研究同行的关注, 共同开展电力网络与复杂系统的交叉研究, 为国家的能源转型贡献一份力量.





VSC系统参数:












控制参数: 1) 直流电压控制








工作点:




同步机参数:
















